1 Introduction

Many technological applications operating/generating high energy require removal of some amount of heat from the medium through conventional equipment of fins/extended surfaces by increasing the area of surface to be cooled. Some of these include computer engineering [1], industrial engineering [2, 3], micro-macro mechanical engineering [4], mechanical engineering [5, 6], solar energy engineering [7], automotive engineering [8] and nuclear engineering [9]. Numerically simulating the highly nonlinear convective-radiative temperature equation demands too much time of an engineer while designing fins. To ease the designers task, prescribing the temperature in terms of basic polynomials and determining the spatially distributed (temperature dependent) heat transfer coefficient/thermal conductivity along the inhomogeneous fin may be an alternative tool, as proposed in this research paper.

Constructing governing heat transfer equation for a fin of given cross section can be found in the open access books [10] and [11]. Abundant research papers are available now in the literature on the classical fin problem by means of numerical/semi-analytical solution of the governing equation. Some of these, such as [12,13,14,15] employ the simplifying assumption that material properties are uniformly set. Since addition of radiation term makes the problem quartic and more nonlinear, the radiation effects are generally ignored in the fin analysis, refer to the publications [16,17,18,19]. Taking into these two omitted effects into account, on the other hand, is important to get more realistic temperature solutions, as implied from the publications [20,21,22,23,24,25,26]. It was reported in [27] that the physical quantities of base heat transfer rate and fin efficiency can be directly accessible without fully simulating the heat equation for some special circumstances. Other interesting treatments and physical applications of various kinds of fins in different geometries can be seen in the recent articles [28,29,30,31,32,33,34,35].

The literature survey indicates obviously that the capability of heat dissipation of fins attached to the bodies of heat removal inherently depends on their geometry and functionally graded material properties. Imposing these beforehand and looking for the temperature response of a fin may not be a friendly approach from a designer point of view, since governing highly nonlinear heat transfer equation necessitates numerical simulation of full energy equation in that case, as has been fulfilled by the above researchers, or for instance, [36] for the pin fin arrangement simulations concerning a heat sink of flat plate kind. On the other hand, from an inverse problem thinking, prescribing a desired temperature distribution defined by simple polynomial functions and seeking for the corresponding axially changing (or temperature dependent) thermal conductivity/heat transfer coefficient across the fin under consideration may facilitate the engineer’s job while designing the fin shape influenced by the certain physical parameters, like the Biot number and radiation parameter. The variation in thermal conductivity/heat transfer coefficient along the fin surface becomes vital especially when the temperature gradient is large enough. In this way, the efficiency of heat transfer will be under control by resultant material properties. The prime objective here thus is to work out the responsive thermal conductivities for an imposed temperature solution associated with the non-homogeneous longitudinal cooling rectangular and triangular fin shapes, as well as a more general tapered fin family from a highly nonlinear conductive-radiative heat equation. It is exhibited that once the other parameters/quantities are fixed, the ideal variable thermal conductivity along the longitudinal fins can be determined by a direct integration. The validity region of solutions can later be sorted out by loading physical constraints on the temperature and variable properties. It is particularly deduced that adjusting the tip fin temperature acquires a control on the rest of the fin properties.

2 Governing Equations

Fig. 1
figure 1

Geometries of longitudinal fins of rectangular cross section (a) and triangular cross section (b)

Full size image

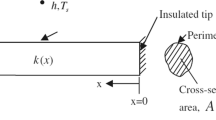
The heat loss problem by the thermal enhancement instrument of longitudinal rectangular or triangular fin as shown in Fig. 1(a,b) is considered. The heat conduction takes place in the direction of decreasing X along the fin of length L and width W. As in the usual practical applications, fin is maintained with a hot base temperature \(T_b\) at \(X=L\) and insulated at the fin tip \(X=0\) with no heat flux. Temperature of the fluid in the neighborhood of the fin is \(T_a\) (the ambient temperature) and radiation temperature to the environment occurs with \(T_r\). A variable thermal conductivity K(X) and a variable heat transfer coefficient H(X) influence the temperature distribution T(X) along the axial locations. Moreover, the Stefan–Boltzmann law constant is \(\sigma \) and the emissivity of the fin is \(\varepsilon \). In addition to these, the fin shape and thickness are governed by the function F(X).

In place of optimizing the fin geometry with uniform K and H, changing the material properties like the thermal conductivity or heat transfer coefficient along the fin could be another approach to enhance the heat transfer and fin efficiency. In the present work, we prefer allocating the temperature distribution under a constant heat transfer coefficient, and determining the axially variable thermal conductivity, although dependence of both physical properties on the spatial variable could be searched. Eventually, assuming that the fin thickness is much smaller as compared the fin length so that the one-dimensional heat transfer model can be adopted, and also taking into account the dimensionless quantities

$$\begin{aligned} \theta= & {} {T\over T_b},\quad x={X\over L},\quad F=\delta f,\nonumber \\ K= & {} k_0 k(x),\quad H = h_0 h(x), \end{aligned}$$
(1)

the temperature equation of an inhomogeneous fin whose thermal performance is affected by the heat losses due to conductive, convective and radiative heat transfer can be expressed in the following form (see; [20, 22, 23, 25, 26])

$$\begin{aligned}{}[f(x)k(x)\theta '(x)]'&{=}&Nc h(x)(\theta (x){-}\theta _a){+}Nr(\theta ^4(x)-\theta _r^4),\nonumber \\ \theta (1)&{=}&1,\quad \theta '(0) {=} 0. \end{aligned}$$
(2)

Keeping in mind that \(\delta \) is the half-fin thickness at the location that the fin is attached to the hot surface (refer to the configurations in Fig. 1(a,b)), \(k_0\) and \(h_0\) are the reference values of thermal conductivity and convective heat transfer coefficient, the followings hold true

$$\begin{aligned} f(1)= & {} k(1)\;=\;h(1)\;=\;1. \end{aligned}$$
(3)

Additionally, as a consequence non-dimensionalization via the transformations in (1), the following thermo geometric parameters arise

$$\begin{aligned} Nc= & {} {h_0L^2\over \delta k_0},\quad Nr = {\sigma \varepsilon L^2T_b^3\over \delta k_0},\nonumber \\ \theta _a= & {} {T_a\over T_b},\quad \theta _r = {T_r\over T_b}, \end{aligned}$$
(4)

where they are called, respectively, Nc the Biot number, Nr the conductive-radiative parameter, \(\theta _a\) the sink temperature parameter and \(\theta _r\) the radiation parameter.

The heat loss at the fin surface (that fin base minus fin tip) due to Fourier’s heat law is

$$\begin{aligned} q= & {} K(L)W F(L)T'(X=L), \end{aligned}$$
(5)

whereas the ideal case of the whole temperature at the base temperature (with an infinite thermal conductivity) yields the heat flux

$$\begin{aligned} q= & {} 2H(L)LW(T_b-T_a)+2\sigma \varepsilon LW(T_b^4-T_a^4). \end{aligned}$$
(6)

Taking into consideration the scalings in (1), the ratio of (5) to (6) gives rise to the definition of fin efficiency \(\eta \)

$$\begin{aligned} \eta= & {} {\int _0^1(Nch(x)(\theta (x)-\theta _a)+Nr(\theta (x)^4-\theta _r^4))dx \over Nc(1-\theta _a)+Nr(1-\theta _r^4)}\nonumber \\= & {} {\theta '(1)\over Nc(1-\theta _a)+Nr(1-\theta _r^4)}. \end{aligned}$$
(7)

3 Exact Solutions

We should remark that imposition of temperature function in terms of elementary polynomials will lead to more convenient formulae at the disposal of engineers; otherwise, results would appear in implicit forms in terms of advanced mathematical functions represented by infinite series, as can be referred to the literature. For instance, Taylor polynomial approximation was reported in [14], which had to be simultaneously justified from the numerical simulations. In the case of simultaneous convecting-radiating scenario, no exact solution so far in any scientific form is known owing to the quartic nonlinearity. On the other hand, simply accessible solutions are desirable as the present work adheres. Therefore, the temperature distribution \(\theta (x)\) satisfying the boundary conditions in (2) is assumed in the form

$$\begin{aligned} \theta (x)= & {} 1+a(1-x^2)+b(1-x^3), \end{aligned}$$
(8)

where a and b are the shape parameters whose validity range to be identified later. With the prescribed temperature solution (8), the corresponding dimensionless thermal conductivity spatially distributed over the entire fin of arbitrary shape can be obtained by integrating once Eq. (2)

$$\begin{aligned}&k(x)\nonumber \\&\quad = {\int _1^x(Nc(\theta (x)-\theta _a)+Nr(\theta (x)^4-\theta _r^4)dx+ \theta '(1)\over f(x)\theta '(x)}.\nonumber \\ \end{aligned}$$
(9)

Without losing the generality, we assume \(\theta _a=\theta _r=0\) to ease the analysis in what follows.

3.1 Longitudinal Rectangular Fin Profile

For this specific fin geometry, we have a constant cross section at all spatial locations as inferred from Fig. 1(a), so

$$\begin{aligned} f(x)= & {} 1. \end{aligned}$$
(10)

On substitution of (8) and (10) into (9), the material conductivity across the longitudinal rectangular fin is given by the formula

$$\begin{aligned} k(x)= & {} -\Big (-3 b-\text {Nc}-\frac{3 b \text {Nc}}{4}-\frac{2}{3} a (3+\text {Nc})-\text {Nr}\nonumber \\&-\Big (2288 a (105+2 a (63+4 a (9+2 a)))\nonumber \\&+1287 (210+a (490+a (413+121 a))) b\nonumber \\&+39 (8910+a (14740+6397 a)) b^2\nonumber \\&+858 (243+208 a) b^3+48114 b^4\Big ) \text {Nr}\big / 90090\nonumber \\&+(1+a+b)\left( \text {Nc}+(1+a+b)^3 \text {Nr}\right) x\nonumber \\&-\frac{1}{3} a \left( \text {Nc}+4 (1+a+b)^3 \text {Nr}\right) x^3\nonumber \\&-\frac{1}{4} b \left( \text {Nc}+4 (1+a+b)^3 \text {Nr}\right) x^4\nonumber \\&+\frac{6}{5} a^2 (1+a+b)^2 \text {Nr} x^5+2 a b (1+a+b)^2 \text {Nr} x^6\nonumber \\&-\frac{2}{7} (1+a+b) \left( 2 a^3-3 (1+a) b^2-3 b^3\right) \text {Nr} x^7\nonumber \\&-\frac{3}{2} a^2 b (1+a+b) \text {Nr} x^8 \nonumber \\&+\frac{1}{9} a \left( a^3-12 (1+a) b^2-12 b^3\right) \text {Nr}x^9\nonumber \\&-\frac{2}{5} b \left( -a^3+(1+a) b^2+b^3\right) \text {Nr} x^{10}+\frac{6}{11} a^2 b^2 \text {Nr} x^{11}\nonumber \\&+\frac{1}{3} a b^3 \text {Nr} x^{12}+ \frac{1}{13} b^4 \text {Nr} x^{13}\Big )\Big /(x (2 a+3 b x)). \end{aligned}$$
(11)

Because denominator of k(x) in (11) is zero, numerator should also vanish to get realistic solutions, leading to the restriction on the conductive-radiative parameter Nr

$$\begin{aligned} \text {Nr}= & {} -\Big ((15015 (12 \text {Nc}+8 a (3+\text {Nc})+9 b (4+\text {Nc}))) \nonumber \\&\Big /\Big (\Big (572 (315+8 a (105+2 a (63+4 a (9+2 a))))\nonumber \\&+2574 (210+a (490+a (413+121 a))) b\nonumber \\&+78 (8910+a (14740+6397 a)) b^2\nonumber \\&+1716(243+208 a) b^3+96228 b^4\Big )\Big )\Big ). \end{aligned}$$
(12)

Moreover, the physical parameter Nr in (12) should be positive, permitted to be zero only when

$$\begin{aligned} \text {Nct}= & {} -\frac{12 (2 a+3 b)}{12+8 a+9 b}, \end{aligned}$$
(13)

which gives the threshold for the Biot number Nc. In addition to this, the requirements on the temperature \(\theta (x)\), thermal conductivity k(x), Nr and Nc, keeping in mind (8), (11) and (12)

$$\begin{aligned} 0\le \theta (x),k(x)\le 1,\qquad 0\le x\le 1,\nonumber \\ \text {Nc}\ge 0,\quad \text {Nr}\ge 0 \end{aligned}$$
(14)

result in the domain of validity of parameters in the intervals

$$\begin{aligned} -1< b\le 0,\quad -1-b\le a< 0,\quad 0\le \text {Nc} \le \text {Nct},\nonumber \\ 0< b\le 2,\quad -1-b\le a< -{3b\over 2},\quad 0\le \text {Nc} \le \text {Nct}, \end{aligned}$$
(15)

which imply that the allowable range of \(a\times b=(-1,2]\times (-3,0]\).

3.2 Longitudinal Triangular Fin Profile

The only difference between the rectangular and triangular fin shapes is that there appears \(x^2\) term for the thermal conductivity in the denominator of Eq. (11) in the latter, since the fin thickness is given by \(f(x)=x\). Therefore, not only the numerator of k(x) but also its derivative should disappear, forcing the Biot number to completely vanish. Therefore, the heat transfer occurs through only radiation mechanism with the supplemented formulas

$$\begin{aligned} b= & {} -(1+a),\nonumber \\ \text {Nr}= & {} \frac{6435 (3+a)}{495+a (-165+a (45+(-9+a) a))},\nonumber \\ \theta (x)= & {} x^2 (a (-1+x)+x),\nonumber \\ k(x)= & {} \frac{(3+a) x^7 \left( 715 a^4-2574 a^3 (1+a) x+3510 a^2 (1+a)^2 x^2-2145 a (1+a)^3 x^3+495 (1+a)^4 x^4\right) }{(495+a (-165+a (45+(-9+a) a))) (-2 a+3 (1+a) x)}. \end{aligned}$$
(16)

It should be alerted that to maintain the convective heat transfer route over longitudinal fin of triangular cross section one should consider higher order terms in the prescribed temperature function (8), which can be implemented with an extra effort.

Fig. 2
figure 2

Thresholds for the physical solutions for fixed parameter b

Full size image

4 Results and Discussion

Results of the previous analysis will be presented separately in regard to the longitudinal rectangular fin and the longitudinal triangular fin. It is noted that the cited literature on the 0studied fin problem numerically solves it always by fixing the fin parameters under restricted thermal conductivities like linearly varying with temperature. However, the present approach does not pose any such confinement to neither the fin parameters nor the material properties, but only preassigns a suitable temperature profile. From this respect, the present approach is not directly comparable with the available results, otherwise a more general space/temperature-dependent thermal conductivity result would be needed for a potential comparison.

4.1 Longitudinal Rectangular Fin

Critical boundaries for Nc in (13) in the domain of definition given by (15) are shown in Fig. 2. Solution domains lie underneath piece of the curve shown for a particular value of parameter b. For instance, when \(b=-0.5\) to be presented solutions are valid in the domain \(a\in [-0.5,0)\), when \(b=0\) in \(a\in [-1,0)\) and when \(b=0.5\) in \(a\in [-1.5,-0.75)\). Obviously, as b increases within the interval (-1,2] the effective range of Nc decreases. Indeed, when \(b=2\), \(a=-3\) and \(Nc=0\). On the other hand, when \(b=0\), \(Nc\in [0,6]\).

Knowing the existence of physical solutions from the range of parameters via the relation in (15) and from Fig. 2, it is easy to control the variation of temperature and thermal conductivity within the functionally graded longitudinal rectangular fin profile from the exact expressions in (8) and (11). To serve the fin designer, the fin tip values can be assigned from the formulas

$$\begin{aligned} \theta (0)= & {} 1+a+b,\nonumber \\ k(0)= & {} \Big (180180 (1+a+b)^4 (2 a+3 b)\nonumber \\&+(1+a+b) \Big (572 a (315+a (567+41a (9+2 a)))\nonumber \\&+1287 (105+a (455+a (469+143 a))) b\nonumber \\&+39 (6435+a(14410+6841 a)) b^2\nonumber \\&+168597 (1+a) b^3+38907 b^4\Big ) \text {Nc}\Big )\nonumber \\&\Big /\Big (4 a \Big (286 (315+8 a (105+2 a (63+4 a (9+2 a))))\nonumber \\&+1287(210+a (490+a (413+121 a))) b\nonumber \\&+39 (8910+a (14740+6397 a)) b^2\nonumber \\&+858(243+208 a) b^3+48114 b^4\Big )\Big ). \end{aligned}$$
(17)
Fig. 3
figure 3

Radiation parameter Nr against Nc and a are shown for \(b=-0.5\) in (a). Part b Depicts the entire temperature distribution for the parameters in (a)

Full size image

To illustrate the practical use of the formulae obtained in this section, valid region of physical parameters Nc, Nr, a and the corresponding complete temperature field are revealed at \(b=-0.5\) in Fig. 3(a,b). In compliance with Fig. 2, Fig.  3(a) clearly indicates that higher values of conductive-radiative parameter Nr can be picked by fixing the Biot number small and parameter a in the vicinity of \(a=-0.5\), which signify radiation-dominated heat transfer. Otherwise, convective-dominated heat transfer takes place at higher values of Biot numbers Nc at comparatively smaller values of Nr. Proper choices of fin temperature distribution can be taken from the assigned value of a in Fig. 3(b). It is anticipated that the fin tip temperature can be reduced to the lowest value of zero provided that a is set -0.5, otherwise, increase in a will lead to increase in tip temperature, and hence the increase in the whole temperature. Figure 3(a,b) shows also evidence that most of the heat transfer will happen by pure convective mechanism, rather than radiation mechanism as also concluded in [20].

Fig. 4
figure 4

Prescribed temperature profiles and loaded thermal conductivities for some selected parameters a at \(b=-0.5\). a, b \(a=-0.5\), c, d \(a=-0.25\) and e, f \(a=-0.1\)

Full size image

Having fixed the physical parameters from Fig. 3(a) and imposing a temperature distribution from Fig. 3(b), the corresponding spatial loading of thermal conductivity can be fulfilled from Eq. (11). Some selected cross-sectional temperature profiles and corresponding thermal conductivity variation are demonstrated in Fig. 4(a–f). It is interesting to observe that for tip temperatures close to zero, the tip thermal conductivity should also be reduced to zero at all stations Nc and Nr, enforcing a monotonically increasing non-uniform thermal conductivity distribution from tip to the base of the rectangular fin. On the other hand, increase in the fin tip temperature makes it possible to load axially varying thermal conductivity whose tip value may exceed the base value, particularly for increasing Biot numbers.

Fig. 5
figure 5

Radiation parameter Nr against Nc and a are shown for \(b=0\) in (a). Part b depicts the entire temperature distribution for the parameters in (a)

Full size image

The valid region of physical parameters Nc, Nr, a and the corresponding temperature field are next exhibited at \(b=0\) in Fig. 5(a,b). Figure 5a is consistent with Fig. 2 and makes it clear that smaller radiation effects are achieved as compared to \(b=-0.5\) in Fig. 3(a). This is possible by enhancing the temperature profiles as witnessed from Fig. 5(b) (see the one for \(b=-0.5\) in Fig. 3(b)).

Some selected cross-sectional temperature profiles and corresponding thermal conductivity variation are demonstrated in Fig. 6(a–f) for \(b=0\). Similar scenario as above holds for smaller values of a, but no matter the prescribed temperature distribution, the tip thermal conductivity is always less than the fin base one. It is worthy of noting the phenomenon that one is able to increase the fin tip temperature and hence enhance the temperature distribution over the rectangular fin as high as possible by imposing the parameter a close to zero.

Fig. 6
figure 6

Prescribed temperature profiles and loaded thermal conductivities for some selected parameters a at \(b=0\). a, b \(a=-1\), c, d \(a=-0.5\) and e, f \(a=-0.1\)

Full size image

Finally, the valid region of physical parameters Nc, Nr, a and the corresponding temperature field are revealed at \(b=0.5\) in Fig. 7(a,b). The unique feature here distinct from the above cases of b is that it enables prescription of temperature profiles having inflectional character. This is achieved by sharply varying thermal conductivity distribution close to the hot body and relaxing it to zero in most of the rest of the fin up to the tip, refer to Fig. 8(a–f).

Fig. 7
figure 7

Radiation parameter Nr against Nc and a is shown for \(b=0.5\) in (a). Part b depicts the entire temperature distribution for the parameters in (a)

Full size image
Fig. 8
figure 8

Prescribed temperature profiles and loaded thermal conductivities for some selected parameters a for \(b=0.5\). a, b \(a=-1.5\), c, d \(a=-1\) and e, f \(a=-0.76\)

Full size image

For the purpose of qualitative referencing, some explicit elegant formulae from the selection of unity Biot number and special parameters are outlined below; \((a,b)=(-0.5,-0.5)\)

$$\begin{aligned} \text {Nr}= & {} 227370/9439=24.0884,\nonumber \\ \theta (x)= & {} {1\over 2} x^2 (1 + x),\nonumber \\ k(x)= & {} \frac{x^2 \left( 37756+28317 x+53 x^6 (715+3 x (858+5 x (234+11 x (13+3 x))))\right) }{113268 (2+3 x)}. \end{aligned}$$
(18)

\((a,b)=(-1,0)\)

$$\begin{aligned} \text {Nr}= & {} 15 ,\nonumber \\ \theta (x)= & {} x^2,\nonumber \\ k(x)= & {} {1\over 6} (x^2 + 5 x^8). \end{aligned}$$
(19)

\((a,b)=(-3/2,1/2)\)

$$\begin{aligned} \text {Nr}= & {} 4290/521=8.23417,\nonumber \\ \theta (x)= & {} -{1\over 2} (-3 + x) x^2,\nonumber \\ k(x)= & {} \frac{x^2 \left( -2084{+}521 x{-}3 x^6 (6435{+}x (-7722{+}5 x (702{+}11 (-13{+}x) x)))\right) }{6252 (-2{+}x)}. \end{aligned}$$
(20)

Figure 9 demonstrates mutual temperature profiles and thermal conductivity variations for \(Nc=1\) from (18-20).

Further Fig.  10(a,b) illustrates mutual temperature profiles and thermal conductivity variations for \(Nc=1\), corresponding to the formulae \((a,b)=(-0.25,-0.5)\)

$$\begin{aligned} \text {Nr}= & {} 2539680/206287=12.3114,\nonumber \\ \theta (x)= & {} \frac{1}{4} \left( 1+x^2+2 x^3\right) ,\nonumber \\ k(x)= & {} \Big (1475817 + 730034 x^2 \nonumber \\&+ 1095051 x^3 + 285714 x^4\nonumber \\&+ 952380 x^5 +952380 x^6 + 714285 x^7 \nonumber \\&+ 1296295 x^8 + 952380 x^9 \nonumber \\&+ 519480 x^10 +634920 x^11\nonumber \\&+ 293040 x^12\Big )\Big /2475444 (1 + 3 x). \end{aligned}$$
(21)

\((a,b)=(-0.5,0)\)

$$\begin{aligned} \text {Nr}= & {} 105/83=1.26506 ,\nonumber \\ \theta (x)= & {} \frac{1}{2} \left( 1+x^2\right) ,\nonumber \\ k(x)= & {} \frac{2307+1084 x^2+378 x^4+180 x^6+35 x^8}{3984}. \end{aligned}$$
(22)

\((a,b)=(-9/8,1/2)\)

$$\begin{aligned} \text {Nr}= & {} 1281280/2590949=0.494522,\nonumber \\ \theta (x)= & {} \frac{1}{8} \left( 3+9 x^2-4 x^3\right) ,\nonumber \\ k(x)= & {} -\Big (15951099+17167314 x^2-5722438 x^3\nonumber \\&+4378374 x^4-3243240 x^5+6872580 x^6\nonumber \\&-7297290 x^7+6531525 x^8-6222216 x^9\nonumber \\&+3538080 x^{10}-960960 x^{11}+98560 x^{12}\Big )\nonumber \\&\Big /31091388 (-3 + 2 x). \end{aligned}$$
(23)

Interestingly, a more cooled fin possessing less temperature is supported via a non-monotonic thermal conductivity distribution, dissimilar to the other cases shown. This indicates that a better fin may demand more care during manufacturing.

The fin efficiency regarding the inhomogeneous longitudinal rectangular fin from (7) turns out to be

$$\begin{aligned} \eta= & {} -\Big (\Big (2 (2 a+3 b) \Big (286 (315+8 a (105+2 a (63+4 a \nonumber \\&(9+2 a))))+1287 (210+a (490+a (413+121 a))) b\nonumber \\&+39 (8910+a (14740+6397 a))b^2\nonumber \\&+858 (243+208 a) b^3+48114 b^4\Big )\Big )\nonumber \\&\Big /\Big (-180180 (2 a+3b)\nonumber \\&+\Big (1144 a (315+8 a (63+4 a (9+2 a)))\nonumber \\&+1287 (315+2 a (490+a(413+121 a))) b\nonumber \\&+78 (8910+a (14740+6397 a)) b^2\nonumber \\&+1716 (243+208 a) b^3+96228 b^4\Big ) \text {Nc}\Big )\Big ). \end{aligned}$$
(24)

The resulting fin efficiencies from (24) are exhibited in Fig. 11(a–c). Expectedly, smaller Biot numbers lead to highest fin efficiencies owing to the shortest fin heights. Higher fin efficiencies are also as a result of higher surface radiation, whose thermal conductivity variations are shown in Figs. 4, 6 and 8. From the fin designing point of view, Fig. 11(a–c) has the utmost significance, since the fin designers can easily decide what parameters should be selected for the prescribed fin temperature from (8) giving rise to the optimal non homogenous thermal conductivity distributions from (11).

4.2 Longitudinal Triangular Fin

It should be recalled from (16) that solutions are valid in the absence of convective heat transfer with \(Nc=0\), so pure radiative heat loss is present. The domain of existence of solutions relies upon the illustrated graph in Fig. 12. It is easy to deduce that radiative heat transfer happens over the longitudinal triangular fin cross sections with the solutions (16) when \(a\in [-3,0]\) and \(Nr\in [0,39]\).

From the determined validity region in Fig. 12, temperature distribution and thermal conductivity variation over a triangular fin shape are shown in Fig. 13(a,b). Inflectional prescribed temperature distributions close to \(a=-3\) in Fig. 13(a) are available supported by largely varying thermal conductivities adjacent the attached surface in Fig. 13(b). Otherwise, for values of a near 0, monotonically increasing temperature and thermal conductivity profiles can be made use to construct non-homogeneous longitudinal triangular fin sections.

Fig. 9
figure 9

Mutual temperature profiles and thermal conductivity variations at chosen parameters for \(Nc=1\)

Full size image
Fig. 10
figure 10

At chosen parameters for \(Nc=1\). a Temperature and b thermal conductivity

Full size image

Some explicit cute solutions are given, for instance at \(a=-2\)

$$\begin{aligned} \text {Nr}= & {} 6435/1093,\nonumber \\ \theta (x)= & {} -(-2 + x) x^2,\nonumber \\ k(x)= & {} -\frac{x^7 \left( 11440-20592 x+14040 x^2-4290 x^3+495 x^4\right) }{1093 (-4+3 x)},\nonumber \\ \end{aligned}$$
(25)

at \(a=-1\)

$$\begin{aligned} \text {Nr}= & {} 18,\nonumber \\ \theta (x)= & {} x^2,\nonumber \\ k(x)= & {} x^7, \end{aligned}$$
(26)

and at \(a=0\)

$$\begin{aligned} \text {Nr}= & {} 39,\nonumber \\ \theta (x)= & {} x^3,\nonumber \\ k(x)= & {} x^{10}. \end{aligned}$$
(27)

Fin efficiency from (7) computed for triangular fins is given by the formula

$$\begin{aligned} \eta= & {} \frac{495-165 a+45 a^2-9 a^3+a^4}{6435}. \end{aligned}$$
(28)

Figure 14 eventually reveals the corresponding fin efficiency from (28). Interesting, the smaller the value of a, the fin efficiency becomes higher with an inflectional temperature distribution along the triangular fin shape.

Finally, we should state that the present analysis is not confined to the longitudinal rectangular or triangular fin profiles, but a general tapered longitudinal fin family could be considered with the thickness function

$$\begin{aligned} f(x)= & {} 1-\alpha (1-x), \quad 0\le \alpha \le 1, \end{aligned}$$
(29)

The controlling fin shape parameter \(\alpha =0\) and \(\alpha =1\) are special cases just studied here. Hence, the thermal response of such inhomogeneous tapered fin coolants can be guessed from these limiting fin surface results. It is also noteworthy to mention that a linear function of heat transfer coefficient \(h(x)=1+\beta x\) could be taken to investigate the effects of variable function of convective heat transfer.

Fig. 11
figure 11

Fin efficiencies for the longitudinal rectangular fin profiles. a \(b=-0.5\), b \(b=0\) and c \(b=0.5\)

Full size image

5 Conclusions

The present research considers the classical fin problem concerning longitudinal rectangular and triangular profiles taking into account the conductive, convective and radiative effects. Instead of uniform and homogenous fin material, inhomogeneous and spatially variable thermal properties such as the heat transfer coefficient and the thermal conductivity of the fin. With the above effects in the functionally graded fin surface, the governing equation of the heat conduction through the fin is highly nonlinear and no explicit or implicit form of the solution can be rewritten except in some special cases, or numerical methods were consulted by the researchers.

Fig. 12
figure 12

Threshold for the physical solutions

Full size image
Fig. 13
figure 13

Longitudinal triangular fins. a Temperature distribution and b Thermal conductivity variation

Full size image

On the other hand, a fin designer always hopes to have explicit formulae to understand the impacts of physical parameters on the fin shape under consideration. Not only the thermal solutions satisfied by the highly nonlinear differential equation are desired, but also an adjustable route of purely convective or radiative-dominated heat transfer mechanisms is required, accounting for mutual heat losses. To avoid the heavily involved numerical computations, a prescribed temperature distribution is therefore assumed within the present approach in terms of elementary polynomials. Then, the corresponding axially varying thermal conductivity is elaborated from the fin equation. The mathematical task of such an analysis only necessitates the determination of the thresholds of the thermo-geometric parameters inherent in the equation. As a result, unique features of temperature and thermal conductivity along the longitudinal convecting-radiating fins can be viewed by the fin analyst. Besides, having fixed the Biot number and conductive-radiative parameter, the corresponding fin efficiency can be realized from the explicit elegant formulas. To conclude, the great advantage of elementary solutions of highly nonlinear fin provided here can be taken granted by the scientific community actively working on the fin problem.

Fig. 14
figure 14

Fin efficiency

Full size image

We should finally emphasize that the present approach can be extended to other fin profiles, such as the pin fins, and to other physical mechanisms, such as the moving fins. Moreover, the present work can further be utilized interchangeably for determining the conventional/optimal shape of a desired fin, when all other physical quantities and parameters are given.