Design of an optimized fractional high-order differential feedback controller for an AVR system

Abstract

This paper proposes a high-order differential feedback controller (HODFC) and a fractional high-order differential feedback controller (FHODFC) to improve regulating ability of a commonly used automatic voltage regulator (AVR) system. In controller design process, particle swarm optimization (PSO) algorithm is utilized together with analytic approach. A constrained optimization problem is solved by PSO algorithm considering a specified objective function to obtain a less setting time, percentage overshoot, and regulation error. In order to test the performance of the proposed controllers, optimally tuned (proportional–integral–derivative) PID controllers available in the literature are implemented. The results demonstrate that the proposed FHODFC provides less percentage overshoot, settling time, rise time, and peak time than other proposed controllers, i.e., HODFC. Furthermore, the performance of the several available PID controllers is significantly worse than both of the proposed controllers in terms of transient response characteristics.

1 Introduction

An automatic voltage regulator (AVR) system may solve the problem of minimizing real power losses in power generating units by controlling generator voltage level with great accuracy. Providing this accuracy leads to improve durability of equipments designed considering rated voltage in a power system network [21]. It is, therefore, important to keep the output voltage of a synchronous generator at a desired level, and in addition to the robustness of the AVR system, the stability of the AVR system significantly affects the safety of the power system [25].

Several control schemes such as (proportional–integral–derivative) PID controller [5, 16, 20, 33, 36], fuzzy logic controller [18], fuzzy-PID controller [3], sliding mode controller [30], fractional-order PID controller [36, 43], and iterative learning controller [14] have been presented to control generator voltage level of an AVR system. Although there is such a variety of control methods for the AVR system, researchers have paid more attention to PID controller. Because either PID controller or its combinations have been commonly preferred in industrial control applications [6], thanks to its functionality, simplicity, applicability, and easy of use [4]. In light of this motivation, researchers have attempted to tune gain parameters of the PID controller to obtain desired transient and steady-state response of the AVR system. Genetic algorithm (GA) [16], particle swarm optimization (PSO) [16, 32, 43], chaotic ant swarm algorithm (CAS) [36, 44], chaotic optimization approach (COA) [33], artificial bee colony (ABC) [17], (cuckoo search algorithm (CSA) [7], teaching learning-based optimization (TLBO) [10], kidney-inspired algorithm (IKA) [13], and reinforcement learning automata (RLA) [19] are some of the intelligent approaches utilized to tune the parameters of PID controller used in an AVR system.

In addition to aforementioned control approaches, a model-free control scheme called as high-order differential feedback controller (HODFC) [28] has been proved to be an attractive solution in many control, synchronization, and estimation studies. Some of these studies can be briefly stated as follows: A HODFC was designed in simulation environment to control DC-bus voltage in active power filter and they obtained strong adaptability and robustness in results with the proposed controller type [41]. Synchronization of chaotic systems using hybrid HOD active control method was made in [11]. HODFC was used to control velocity and position of a DC motor by comparing the results with PID and fuzzy logic controller [24]. A cascaded model of HODFC for the main steam temperature control was proposed in [40]. The effectiveness of HODFC in terms of robustness, disturbance rejection, and system response were validated in simulation compared to PID-P cascade control structure. Shi et al. implemented and simulated HODFC and PID controller application in servo control system of NC machine tools and they showed better dynamic response of HODFC [34]. Faradja et al. tested the robustness of sliding mode controller (SMC) and HODFC in synchronization of nonlinear systems [15]. In the study, SMC had a poor performance in terms of convergence and robustness compared to HODFC. A HODFC was designed and implemented to control a flexible-joint manipulator in real time [1]. The results showed increased trajectory tracking performance of HODFC over traditional PID controller. Agee et al. [2] improved the performance of HODFC by using its distributed model on the same system given in [1].

Considering the above-mentioned HODFC studies, it is possible by HODFC to achieve a substantially robust and better system response than PID and fuzzy logic controller in both transient and steady-state regions. Although these studies had successful results, their results may be improved by using optimization techniques. Because none used any optimization approach while determining some required gain values of HODFC. Rather, these gain values were decided by trial and error method.

Therefore, this study mainly aims to further improve the regulating ability of a commonly used AVR system. To achieve this main purpose successfully, the following is carried out in this study:

• 1. An optimized HODFC for the AVR system is designed by utilizing PSO algorithm with a specified objective function to obtain a less setting time, percentage overshoot, and regulation error.

• 2. A fractional HODFC (FHODFC) is proposed for the same system, and it is optimally designed by using PSO algorithm as in the HODFC design.

• 3. Reference tracking and robustness performance of the proposed controllers in the AVR system are compared to each other and the optimally tuned PID controllers [5, 16, 20, 33, 36] available in the literature.

The main contributions of the study are fivefold.

• 1. The first HODFC design for the AVR system is proposed and the effectiveness of HODFC is shown.

• 2. In HODFC design process, an optimization algorithm is utilized for the first time.

• 3. FHODFC, which is a fractional approach of the HODFC, is proposed for the first time in the literature. Furthermore, implementation of FHODFC to the AVR system is performed.

• 4. Using an optimization algorithm in FHODFC design process is presented for the first time.

• 5. Comparison of the results obtained by the proposed controllers and the optimally tuned PID controllers [5, 16, 20, 33, 36] available in the literature is made and effectiveness of the proposed controllers over traditional approach is shown.

The rest of the paper is organized as follows. Section 2 overviews the concepts of AVR system, fractional-order operator, and PSO algorithm and presents new proposed FHODFC. Optimal design of the proposed HODFC and FHODFC controller for the AVR system using PSO algorithm is presented in Sect. 3. Section 4 is devoted to simulation results and discussion. Finally, conclusion remarks are given in Sect. 5.

2 Basic concepts, materials, and methods

2.1 AVR system model

An AVR system, which is an essential part of an excitation system, keeps output voltage of a synchronous generator at a desired level. A simple AVR system is composed of four different subsystems: amplifier, exciter, generator, and sensor [16, 25, 31]. Each subsystem can be modeled by a first-order transfer function T(s) in the form of $T(s)=K/(1+\tau s)$, where K and $\tau$ represent gain and time constant of the transfer function, respectively. Ranges of the gain and time constant values of the subsystems are provided in the literature [5, 9, 25, 31, 36]. The transfer function of each subsystem and typical gain and time constant value ranges are given in Table 1. Closed-loop structure of an AVR system without controller is shown in Fig. 1, where $V_\mathrm{ref}(s), V_\mathrm{g}(s)$, and $V_\mathrm{s}(s)$ are desired reference voltage, output voltage of the generator, and measured output voltage of the generator in Laplace domain, respectively. $V_\mathrm{e}(s)$ corresponding error voltage, i.e., the difference between the reference and the measured voltages, is required to be zero in both transient and steady-state regions.

Table 1 Transfer functions of the AVR subsystems [5, 9, 25, 31, 36]

By considering the studies [5, 9, 16, 25, 31, 36], the parameters of the AVR subsystems used in this study are set to $K_\mathrm{a}=10$, $\tau _\mathrm{a}=0.1$, $K_\mathrm{e}=1$, $\tau _\mathrm{e}=0.4$, $K_\mathrm{g}=1$, $\tau _\mathrm{g}=1.0$, $K_\mathrm{s}=1$, and $\tau _\mathrm{s}=0.01$. Using these values, step response of the AVR system without any controller is demonstrated in Fig. 2, where one can observe that the output voltage of the generator has a high overshoot, approximately $50\%$, long settling time, and steady-state error. Therefore, these transient response characteristics and steady-state error required to be improved.

Fig. 1

Block diagram of an AVR system

Fig. 2

Step response of the AVR system without controller

2.2 Fractional-order operator

Fractional-order operators are the basic components of fractional calculus getting more importance in engineering area [35], because these operators provide a more flexible design opportunity while modeling or controlling physical systems [38]. In addition, fractional-order methodologies may show better robustness and applicability when compared to their integer counterparts [8, 23].

A fractional-order operator is represented by $_{t_0}\text {D}_{t_\mathrm{f}}^\alpha$, where $t_0$ and $t_\mathrm{f}$ denote lower and upper time bounds of the calculus and $\alpha$ represents order of the fractional calculus. A continuous-time fractional-order operator $_{t_0}\text {D}_{t_\mathrm{f}}^\alpha$ can be written as in (1),where $\mathrm{Re}(\alpha )$ denotes the real part of the order $\alpha$. Riemann–Liouville, Grunwald–Letnikov, and Caputo definitions are commonly used definitions of the fractional-order operator $_{t_0}\text {D}_{t_\mathrm{f}}^\alpha$ [22].

(1)

Although both fractional-order integrator and differentiator are the essential elements of the fractional-order operators, in the following subsection, only fractional-order integrator is briefly introduced since the proposed control scheme, i.e., FHODFC, only contains integrator blocks.

2.2.1 Fractional-order integrator

A fractional-order integrator (FOI) is represented by the following transfer function:

$$\begin{aligned} {{G}_\mathrm{FOI}}(s)=\frac{1}{{{s}^{\lambda }}}, \end{aligned}$$

(2)

where $\mathrm{Re}(\lambda )>0$ [39]. Time response computation of a system containing fractional variable $s^\lambda$, $\lambda \in \mathfrak {R}$, is a challenging problem since an analytic solution is not available. Therefore, approximation methods such as Oustaloup’s method, Matsuda’s method, continued fractional expansion method, Carlson’s method, and Chareff’s method are proposed to obtain a solution of such fractional systems [42].

As the approximation method, Oustaloup’s approximation based on recursive distribution of poles and zeros [26, 27] is utilized in this study. Essential point of this method is to design a band-pass filter considering a specified frequency range $[\omega _\mathrm{b}, \omega _\mathrm{h}]$, where $\omega _\mathrm{b}$ and $\omega _\mathrm{h}$ are lower and upper frequency bounds, respectively, to approximate fractional-order operator $s^\lambda$, $\lambda \in \mathfrak {R}$, by following integer-order transfer function having poles, zeros, and gain:

$$\begin{aligned} {{s}^{\lambda }}= & {} K\prod \limits _{k=-N}^{N}{\frac{s+\omega _{k}^\mathrm{z}}{s+\omega _{k}^\mathrm{p}}},\nonumber \\ \omega _{k}^\mathrm{z}= & {} {{\omega }_\mathrm{b}}{{\left( \frac{{{\omega }_{h}}}{{{\omega }_\mathrm{b}}} \right) }^{\frac{k+N+0.5(1-\lambda )}{2N+1}}}, \nonumber \\ \omega _{k}^\mathrm{p}= & {} {{\omega }_\mathrm{b}}{{\left( \frac{{{\omega }_\mathrm{h}}}{{{\omega }_\mathrm{b}}} \right) }^{\frac{k+N+0.5(1+\lambda )}{2N+1}}},\nonumber \\ K= & {} {{\left( \frac{{{\omega }_\mathrm{h}}}{{{\omega }_\mathrm{b}}} \right) }^{-0.5\lambda }}\prod \limits _{k=-N}^{N}{\frac{\omega _{k}^\mathrm{p}}{\omega _{k}^\mathrm{z}}}, \end{aligned}$$

(3)

where $\omega _{k}^\mathrm{p}$ and $\omega _{k}^\mathrm{z}$ are the pole and zero of the sequence k. This integer-order transfer function has $(2N+1)$ zeros and $(2N+1)$ poles.

In this study, a tenth order, i.e., $N=10$,-approximated transfer function is designed in the frequency range of $\omega \in \left[ 10^{-6},10^{6} \right]$ rad/s by using Oustaloup’s method.

2.3 Fractional high-order differential feedback controller

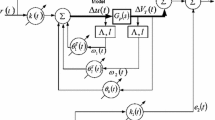
FHODFC is a fractional design of a HODFC based on high-order differentiator (HOD) proposed by Qi et al. [28]. A closed-loop control system containing FHODFC is given in Fig. 3 where $y_\mathrm{r}, y, e, \hat{\mathbf{e }}, \mathbf{K }, u$, and d denote reference input signal, measured output signal, error signal obtained as a difference of the reference input and the measured output signals, fractionally calculated error differential vector, gain vector, produced control signal, and bounded disturbance, respectively. In order to present an FHODFC scheme, it is required to explain fractional HOD (FHOD) depending on the design of HOD. Therefore, in the following subsections, the first design of the HOD is provided. After then, design of the fractional HOD (FHOD) is introduced, and finally, an FHODFC scheme containing the FHOD is proposed.

Fig. 3

The block diagram representation of a closed-loop control system containing FHODFC scheme

2.3.1 High-order differentiator design

A HOD extracts differentials up to system order, i.e., $n\hbox {th}$ order, by using $m\hbox {th}$-order dynamic system given in (4), where $m\ge n+1$, and (5) [28, 29].

$$\begin{aligned} \sum \left\{ \begin{array}{l} \dot{z_i}=z_{i+1}+a_i(y-z_1), 1\le i\le m-1\\ \dot{z_m}=a_m(y-z_1)) \end{array}\right. \end{aligned}$$

(4)

$$\begin{aligned} \left\{ \begin{array}{l} {\hat{y}}=z_1\\ {\hat{y}}^{(i)}=z_{i+1}+a_i(y-z_1), i=1,2,...,n \end{array}\right. \end{aligned}$$

(5)

where $z_i$ and $a_i$, $(1\le i\le m)$, represent the states and parameters of $\sum$, respectively, and y, ${\hat{y}}$, and ${\hat{y}}^{(i)}$ are measured output signal of the system, estimated output signal of the system, and estimated high-order differentials of the output signal y, respectively. The parameters $a_i$, $(1\le i\le m)$, are estimated by

$$\begin{aligned} \begin{aligned} a_i&=KC_{i-1}^{m-1}a_0^{i-1}, i=1,2,...,m\\ K&=\frac{m^ma_0}{(m-1)^{m-1}}, \end{aligned} \end{aligned}$$

(6)

where $C_{i-1}^{m-1}$ represents combination expression $\left( {\begin{array}{c}m-1\\ i-1\end{array}}\right) , i=1,2,...,m$ and $a_0 \in [5, 30]$ suggested in [28] via experience.

It should be noted that the HOD does not rely on the system since to implement a HOD, only m and $a_0$ parameters which are independent of the system are required. In addition, the HOD is an asymptotically stable system and satisfies the convergence $\lim _{t \rightarrow \infty }{\hat{y}}^{(i)}=y^{(i)},i=1,2,...,m$ [28, 29, 34].

2.3.2 Fractional high-order differentiator design

An FHOD extracts fractional differentials up to system order n by using mth-order dynamic system given in (7), where $m\ge n+1$, and (8).

In this manner, fractional state equations of an FHOD is reconstructed by

$$\begin{aligned}&\sum \left\{ \begin{matrix} z_i^{{(\lambda _i)}}=z_{i+1}+a_i(y-z_1), 1\le i\le m-1\\ z_m^{{(\lambda _i)}}=a_m(y-z_1)) \end{matrix},\right. \end{aligned}$$

(7)

$$\begin{aligned}&\left\{ \begin{matrix} {\hat{y}}=z_1\\ {\hat{y}}^{(\lambda _k)}=z_{k+1}+a_k(y-z_1), k=1,2,...,n \end{matrix},\right. \end{aligned}$$

(8)

where $z_i$, $z_i^{(\lambda _i)}$, and $a_i$, $(1\le i\le m)$, represent the ith state, fractional-order differential of the ith state where ${\lambda _i} \in \left[ {0,1} \right]$, and parameters of $\sum$, respectively, and y, ${\hat{y}}$, and ${\hat{y}}^{(\lambda _k)}$ are measured output signal of the system, estimated output signal of the system, and estimated fractional high-order differentials of the output signal y where ${\lambda _k} \in \left[ {0,n} \right]$, respectively. Both $a_i$ and $a_k$ are calculated using (6).

Block diagram representation of the FHOD is demonstrated in Fig. 4, where y is the input of the FHOD, and ${\hat{y}}$ and ${\hat{y}}^{(\lambda _k)}, k=1,2,...,n$ are the outputs of the FHOD.

Fig. 4

The block diagram of an FHOD. y is the input and ${\hat{y}}$ and ${\hat{y}}^{(\lambda _k)}, k=1,2,...,n$ are the outputs of the FHOD

2.3.3 FHODFC scheme design

As demonstrated in Fig. 3, an FHODFC scheme contains three main components, i.e., the FHOD, the gain vector $\mathbf{K }$, and the filter, to track reference input, $y_\mathrm{r}$, for a plant. Note that the plant is required to be modeled in control-affine form and high-order differentials of the input reference signal $y_\mathrm{r}$ up to system order n can be calculated directly or softening the signal.

By considering the definition of HODFC given in [28] (Theorem 1), control signal u for time-varying nonlinear control-affine system is

$$\begin{aligned} u={\mathbf {K}}\hat{{\mathbf {e}}}+{\tilde{u}}, \end{aligned}$$

(9)

where ${\mathbf {K}}=[k_n, k_{n-1},...,k_1,1] \in \mathfrak {R}^{1xn}$ is required to satisfy stability condition and ${\tilde{u}}$ represents filtered control signal satisfying

$$\begin{aligned} \dot{{\tilde{u}}}=-\lambda {\tilde{u}}+\lambda u, \end{aligned}$$

(10)

with a large positive constant $\lambda$ [28, 29].

When considered the given FHODFC scheme, estimated error differential vector $\hat{\mathbf{e }}$ is calculated; thanks to FHOD of which the input is error signal e, i.e., the difference of input reference signal $y_\mathrm{r}$ and actual output signal y, $e=y_\mathrm{r}-y$. The error differential vector is written as $\hat{\mathbf{e }}=[{\hat{e}}^{(\lambda _n)}, {\hat{e}}^{(\lambda _{n-1})}, ..., {\hat{e}}^{(\lambda _2)}, {\hat{e}}^{(\lambda _1)}, {\hat{e}}]^T \in \mathfrak {R}^n$ where ${\hat{e}}^{(\lambda _k)}, k=1,2,...,n$ is the estimated high-order differentials of the error signal e.

2.4 Particle swarm optimization algorithm

Particle swarm optimization algorithm developed by Kennedy and Eberhart [12] is a stochastic evolutionary optimization algorithm based on simulating the movements of a swarm like fish schooling and bird flocking. In order to model the movements of the swarm, position and velocity update equations of the particles are used. The equations of the velocity and position are given below, respectively.

$$\begin{aligned} V_{i}^{k+1}= & {} w^{k}V_{i}^{k}+c_{1}r_{1}(P_\mathrm{best}^{k}-X_{i}^{k})+c_{2}{r}_{2}(G_\mathrm{best}^{k}-X_{i}^{k}),\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned} X_{i}^{k+1}= & {} X_{i}^{k}+V_{i}^{k+1}, \end{aligned}$$

(12)

where k is the iteration number, i is the index of the particle, w is the inertia weight that directly affect the velocity, $c_1$ and $c_2$ are the acceleration factors called cognition and social constants, respectively, $r_1$ and $r_2$ are the random numbers between 0 and 1, $P_\mathrm{best}$ is the best local solution, $G_\mathrm{best}$ is the best global solution, and $V_{i}$ and $X_{i}$ are the velocity and position of the particle i, respectively.

Considering the velocity and position equations, it can be inferred that population size, inertia weight w, and acceleration factors $c_1$ and $c_2$ affect the result of the algorithm. In general, $c_1$ and $c_2$ are set to 2 and the inertia weight w which balances the global and local search is linearly decreased from about 0.9 to 0.4 [16].

The implementation of the PSO algorithm is described as follows:

• Step 1. Initialize the particles with random velocities and positions.

• Step 2. Evaluate and compare objective values of the particles in the population and obtain the local best value ($P_\mathrm{best}$) of the population for current iteration and keep the $P_\mathrm{best}$ value in memory.

• Step 3. Compare the $P_\mathrm{best}$ value to global best ($G_\mathrm{best}$) value, which is initially assigned to $P_{best}$ value, and assign global best ($G_\mathrm{best}$) value to the position of the particle with the best objective function value.

• Step 4. Update the velocities of the particles by using (11).

• Step 5. Move each particle to their new position by using (12).

• Step 6. Increase iteration number, go to step 2 and repeat the steps until stopping criterion is met.

3 Design of proposed controllers for AVR system

In this section, in order to improve the performance characteristics of the AVR system in addition to its robustness against model uncertainties, both HODFC and FHODFC are optimally designed using PSO algorithm. First, design of the FHODFC is presented, then details of HODFC design process is provided in the following subsections, respectively.

As mentioned in the introduction part of the Sect. 2.3, the difference of a HODFC and FHODCD originates from the type of the HOD. Considering that HOD is classical or fractional, the gain vector $\mathbf{K }$ is set. However, the low-pass filter seen in Fig. 3 can be used as same in both of the controllers. Hence, the transfer function of the low-pass filter is set to $\frac{20}{s+20}$ in both.

3.1 Optimized FHODFC design for AVR system

As indicated in Sect. 2.3.3, to design an FHODFC, it is required to consider each component of the FHODFC, i.e., the fractional differentiator FHOD, the gain vector $\mathbf{K }$, and the low-pass filter which is set to $\frac{20}{s+20}$, separately.

3.1.1 FHOD design

The design process of an FHODFC starts with the implementation of an FHOD in Matlab/Simulink platform. Note that the verification of the FHOD performance is required to ensure estimation results of error differential vector $\hat{\mathbf{e }}$ shown in Fig. 3.

The parameters $a_0$ and m are selected as 8 and 5 in (6), respectively. The FHOD extracts differentials up to system order, which is set to 4 by considering AVR system given in Fig. 1. To verify FHOD with these parameters, $y(t)=sin(t)$ is differentiated by using the designed FHOD with $\lambda _1=1, \lambda _2=1, \lambda _3=1$, and $\lambda _4=1$ in Matlab/Simulink. The $\lambda _i, i=1,2,3,4$ values are selected as integer instead of fractional to observe and compare the obtained differentiated signal better. Therefore, the output of the FHOD consists of ${\hat{y}}$, ${\hat{y}}^{(1)}$, ${\hat{y}}^{(2)}$, ${\hat{y}}^{(3)}$, and ${\hat{y}}^{(4)}$ corresponding to estimated output signal (${\hat{y}}(t)=sin(t))$, estimated first-order derivative of the output signal (${\hat{y}}^{(1)}=cos(t)$), estimated second-order derivative of the output signal (${\hat{y}}^{(2)}=-sin(t)$), estimated third-order derivative of the output signal (${\hat{y}}^{(3)}=-cos(t)$), and estimated fourth-order derivative of the output signal (${\hat{y}}^{(4)}=sin(t)$), respectively. Figure 5 shows the obtained signals which have unwanted rapid transients at the initial behavior. To overcome these produced peaking impulses, adding restraint to (5) is suggested by [28]. Therefore, restraint is added to (8) and amended FHOD is obtained by using (13), where $\sigma _i(t)$ is called as restraint and $\rho$ is a large positive constant [28]. Using the modified FHOD in which $\rho$ was set to 100, $y(t)=sin(t)$ is again differentiated to see the effect of the restraint. Figure 6 demonstrates the obtained ${\hat{y}}$, ${\hat{y}}^{(1)}$, ${\hat{y}}^{(2)}$, ${\hat{y}}^{(3)}$, and ${\hat{y}}^{(4)}$ all of which have restrained peaking impulses at the initial behavior. Figures 5 and 6 verify the performance of the designed FHOD.

$$\begin{aligned} \left\{ \begin{matrix} {\hat{y}}=z_1\\ {\hat{y}}^{(\lambda _k)}=z_{k+1}+a_k(y-z_1)\sigma _k(t), k=1,2,...,n \\ \sigma _k(t)=(1-exp(-\rho t^{2i}))/(1+exp(-\rho t^{2i})) \end{matrix}.\right. \end{aligned}$$

(13)

Fig. 5

Verification of the FHOD implemented for $y(t)=sin(t)$

Fig. 6

Verification of the amended FHOD implemented for $y(t)=sin(t)$

3.1.2 Optimally tuning of FHOD and gain vector $\mathbf{K }$

Having verified the FHOD with integer-order integrators, the orders of the integrators in the FHOD are required to be optimally tuned to obtain a more robust and effective controller. While tuning these five different orders, gain vector $\mathbf{K }$ which also contains five different gain variable, should be considered. Therefore, the optimization process involves tuning of ten different variables of $\varvec{\theta }=[\lambda _1,\lambda _2,\lambda _3\lambda _4\lambda _5,K_1,K_2,K_3,K_4,K_5]$, five for the FHOD, and five for the gain vector $\mathbf{K }$.

In the literature, there are several objective functions used in controller design process. Integral of absolute error (IAE), integral of squared error (ISE), integral of time-weighted absolute error (ITAE), and integral of time-weighted squared error (ITSE) are the basic and commonly used objective functions [37]. In addition, other objective functions including time domain and frequency domain characteristics such as overshoot, rise time, settling time, phase margin, and gain margin are also available [16, 25, 43].

Fig. 7

Block diagram representation of the FHODFC optimization process

In this study, PSO algorithm is employed to solve the following constrained optimization problem:

$$\begin{aligned}&\underset{\varvec{\theta } \in \mathfrak {R}}{min} f(\varvec{\theta }), \, \varvec{\theta }= [\theta _1, \theta _2, ..., \theta _{10}] \nonumber \\&\quad \text {subject to:} \, \left| u \right| \le 1 \, \text {and} \, \theta _i \in [{\theta _{iL}},{\theta _{iU}}] ,\ i=1, 2, ...,10 , \nonumber \\ \end{aligned}$$

(14)

where f() and u represent objective function and produced control signal, respectively, and $\theta _{iL}$ and $\theta _{iU}$ are lower and upper boundaries of each variable $\theta _i$, respectively. The specified objective function for the AVR system is

$$\begin{aligned} f(\theta )=\omega _1M_\mathrm{p}+\omega _2t_\mathrm{s}+\omega _3\mathrm{ITAE}, \end{aligned}$$

(15)

where $\omega _1, \omega _2$, and $\omega _3$ are the weights of percentage overshoot ($M_\mathrm{p}$), settling time ($t_\mathrm{s}$), and ITAE calculated as

$$\begin{aligned} \mathrm{ITAE}=\int _{0}^{t}t\left| e(t) \right| \mathrm{d}t, \end{aligned}$$

(16)

for error signal e(t). Note that the selection of the weights changes the characteristics of AVR system response. An increment in a weight factor results in the improvements in the corresponding characteristic [43]. Therefore, the weights $\omega _1, \omega _2$, and $\omega _3$ are selected as 5, 50, and 50, respectively, by considering the AVR system requirements and general magnitude scale of each characteristic. The lower and upper boundaries of $\varvec{\theta }$ are set to [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] and [1, 1, 1, 1, 1, 1000, 600, 300, 10, 10], respectively.

The PSO algorithm parameters $c_1$ and $c_2$ are set to 2 and the inertia weight w is linearly decreased from about 0.9 to 0.4 as recommended in [16]. In the optimization process, population size and maximum number of iterations are set to 50.

Figure 7 shows the block diagram representation of the FHODFC optimization process carried out in Matlab/Simulink platform. A unit step input $y_\mathrm{r}$ is applied during 4 s as the reference signal to be tracked. Since the PSO algorithm starts with randomly assigned particle positions, the obtained minimum objective function value may be a local minimum rather than global minimum. Therefore, repeating the algorithm more than once would be meaningful, and thus optimization algorithm ran 20 times. The change in the objective function for the best trial of 20 attempts is demonstrated in Fig. 8. The minimum objective function was attained as $f(\theta )=39.8272$ at the 45th iteration of the best trial. The optimized parameters for the FHOD, i.e., the order of the integrators, are $\lambda _1=0.8651$, $\lambda _2=0.8693$, $\lambda _3=0.6495$, $\lambda _4=0.9875$, and $\lambda _5=0.3010$. The optimized parameters for the gain vector $\mathbf{K }$ are $K_1=134.6488$, $K_2=509.1594$, $K_3=193.8084$, $K_4=9.7874$, and $K_5=0.1431$.

Fig. 8

The change in the objective function for the best trial of 20 attempts. OF objective function value

3.2 Optimized HODFC design for AVR system

The optimized HODFC design process is very similar to that of FHODFC design process. In this control scheme, a HOD is required rather than an FHOD shown in Fig. 7. Since the FHOD has already been designed in the previous section, i.e., Sect. 3.1.1, setting the orders of the integrators inside the FHOD to the integer value of 1 is sufficient to obtain a HOD. Therefore, the general parameters such as $a_0$, m, and $\rho$ are kept stationary in their previous values, and the orders of the integrators are set to 1. Albeit the fact that Fig. 6 is provided to show the verification of the designed amended FHOD, it actually demonstrates the verification of the designed amended HOD for the AVR system since the orders of the integrators, i.e., $\lambda _i, i=1,2,3,4$, are set to 1.

The HODFC optimization process can be represented by Fig. 7 with some modifications such as removing $\lambda _i, i=1,2,3,4$ parameters given in red rectangle since their values are set to 1 and replacing the FHOD block with the HOD block. Beside the low-pass filter which is set to $\frac{20}{s+20}$, the cost function and parameters of the PSO algorithm are same as the FHODFC optimization process. In this case, the optimization process involves tuning of five different variables of $\varvec{\theta }=[K_1,K_2,K_3,K_4,K_5]$ belonging to the gain vector $\mathbf{K }$. The lower and upper boundaries of $\varvec{\theta }$ are set to [0, 0, 0, 0, 0] and [1000, 600, 300, 10, 10], respectively.

The optimization process of the HODFC is performed in Matlab/Simulink platform. A unit step input $y_r$ is applied during 4 s as the reference signal to be tracked. The optimization algorithm ran 20 times since the PSO algorithm starts with randomly assigned particle positions. The minimum objective function was obtained as $f(\theta )=66.6481$ in the best trial. As a result of the optimization, the optimized parameters for the gain vector $\mathbf{K }$ are $K_1=134.2902$, $K_2=310.0338$, $K_3=81.3272$, $K_4=0.1254$, and $K_5=0.1142$.

4 Simulation results and discussion

In this section, to verify the effectiveness of the proposed HODFC and FHODFC in the AVR system, experiments are carried out in simulation platform. In the experiments, time domain analysis, consisting of both transient and steady-state response characteristics, and robustness analyses are performed. In addition, the performance of the both controllers are compared to optimally tuned different PID controllers [5, 16, 20, 33, 36] whose parameters were tuned using meta-heuristic optimization algorithms.

The parameters of the AVR subsystems used in this study are set to $K_\mathrm{a}=10$, $\tau _\mathrm{a}=0.1$, $K_\mathrm{e}=1$, $\tau _\mathrm{e}=0.4$, $K_\mathrm{g}=1$, $\tau _\mathrm{g}=1.0$, $K_\mathrm{s}=1$, and $\tau _\mathrm{s}=0.01$ as in the available studies [5, 16, 20, 33, 36] to which comparisons are made.

4.1 Digital implementation

The realization of the proposed controllers and their implementations are performed in Matlab/Simulink platform with sampling period $T_\mathrm{s}=1$ ms. The proposed controllers are compared to each other in addition to the available base controller in the literature. As in the published studies [5, 16, 20, 33, 36], PID controller is utilized as the base controller. The parameters of the different PID controllers were optimally tuned by the researchers using PSO [16], CAS [36], frequency domain approach (FDA) [5], COA [33], and hybrid genetic algorithm and bacterial foraging (GA–BF) [20] for AVR system. Since the base controller is a controller containing a differentiator component, the produced control signal must be considered carefully.

To briefly explain this crucial produced control signal fact in a separate paragraph, consider the differentiator component in PID controller which calculates

$$\begin{aligned} \frac{\varDelta e}{\varDelta t}=\frac{e(t)-e(t_\mathrm{prev})}{t-t_\mathrm{prev}}, \end{aligned}$$

(17)

where e(t) and $e(t_\mathrm{prev})$ represent error signal value at the current time t and previous time $t_\mathrm{prev}$ and $t-t_\mathrm{prev}$ corresponds to sampling time. Therefore, as the sampling time decreased, higher value of $\frac{\varDelta e}{\varDelta t}$ is obtained for the same error signal e. Furthermore, when the transient region of a response resulting because of instantaneously changed reference signals such as step signal considered, peak values with high magnitude occur as a result of $\frac{\Delta e}{\Delta t}$. Because of the fact that the control signal is a bounded signal, these peak values saturate the control signal in the real-time applications, whereas these peak values should provide a better response in simulation environment. Therefore, in order to make a feasible controller design in simulation platform, boundaries of the control signal should be considered either by adding control signal constraints in optimization process or saturation block after the designed controller. In this study, control signal constraint is added in the optimization process (Sects. 3.1.2 and 3.1.2) as $\left| u \right| \le 1$ where u is the produced control signal.

Fig. 9

Step response of the AVR system controlled by the proposed controllers (FHODFC and HODFC) and different PID controllers: PID–PSO [16], PID–CAS [36], PID–FDA [5], PID–COA [33], and PID–GA–BF [20]

Table 2 Controller parameters and obtained transient response characteristics, steady-state error, and performance metrics

4.2 Time domain analysis

Unit step responses of the same AVR system controlled by both proposed controllers, i.e., FHODFC and HODFC, and different PID controllers optimally tuned by using PSO [16], CAS [36], FDA [5], COA [33], and hybrid GA–BF [20] are analyzed in both transient and steady-state regions. The obtained responses and corresponding transient characteristics such as percentage overshoot ($M_\mathrm{p}$), settling time ($t_\mathrm{s}$), rise time ($t_\mathrm{r}$), and peak time ($t_\mathrm{p}$)) are represented in Fig. 9 and Table 2, respectively. Table 2 also contains the values of the controller parameters, steady-state errors ($E_\mathrm{ss}$), error-based performance metrics (IAE, ISE, and ITAE), and defined objective function ($f(\theta )$). The performance metrics IAE and ISE are calculated as

$$\begin{aligned} IAE= & {} \int _{0}^{t}\left| e(t) \right| \mathrm{d}t, \end{aligned}$$

(18)

$$\begin{aligned} ISE= & {} \int _{0}^{t} e(t)^2 \mathrm{d}t, \end{aligned}$$

(19)

for error signal e(t).

That the proposed FHODFC has the best step response can be observed from Fig. 9 in which a zoomed region is available to make the analysis more clear. In addition, the proposed HODFC follows the FHODFC and shows an outstanding step response compared to other optimally tuned PID controllers. When the numerical results given in Table 2 considered, it is clear that the best step response performance in terms of $M_\mathrm{p}$, $t_\mathrm{s}$, $t_\mathrm{r}$, and $t_\mathrm{p}$ is obtained by the proposed FHODFC which is followed by another proposed controller, i.e., HODFC. Moreover, performance metrics verify the superiorities of the proposed controllers over optimally tuned PID controllers [5, 16, 20, 33, 36]. Bold and italic in the table show the best and second-best results.

Figure 10 demonstrates the error signals obtained from the step response of the AVR system. The produced control signals by the whole controllers are presented in Fig. 11. From the figure, it can be observed that the control signals produced by the proposed FHODFC and HODFC satisfy the control signal constraint $\left| u \right| \le 1$.

Fig. 10

Error signal obtained from step response of the AVR system controlled by the proposed controllers (FHODFC and HODFC) and different PID controllers: PID–PSO [16], PID–CAS [36], PID–FDA [5], PID–COA [33], and PID–GA–BF [20]

Fig. 11

Control signals produced by the proposed controllers (FHODFC and HODFC) and different PID controllers: PID–PSO [16], PID–CAS [36], PID–FDA [5], PID–COA [33], and PID–GA–BF [20]

Fig. 12

Step response of the AVR system having uncertainty in the amplifier time constant $\tau _\mathrm{a}$ ranging from $-\,50\%$ to $+\,50\%$ and controlled by a FHODFC; b HODFC

Fig. 13

Step response of the AVR system having uncertainty in the exciter time constant $\tau _\mathrm{e}$ ranging from $-\,50\%$ to $+\,50\%$ and controlled by a FHODFC; b HODFC

Fig. 14

Step response of the AVR system having uncertainty in the generator time constant $\tau _\mathrm{g}$ ranging from $-\,50\%$ to $+\,50\%$ and controlled by a FHODFC; b HODFC

Fig. 15

Step response of the AVR system having uncertainty in the sensor time constant $\tau _\mathrm{g}$ ranging from $-\,50$ to $+\,50\%$ and controlled by a FHODFC; b HODFC

4.3 Robustness analysis

Robustness of the proposed controllers against uncertainties in some AVR system parameters is analyzed in this section. It is expected that the controllers can handle the available uncertainties and provide a reasonable stable response. Time constants of the AVR system, i.e., $\tau _\mathrm{a}, \tau _\mathrm{e}, \tau _\mathrm{g}$, and $\tau _\mathrm{s}$, are changed separately in the range of $\mp 50 \%$ of their nominal values with a $25\%$ step size as if there exist uncertainties. Figures 12, 13, 14 and 15 represent step responses of the AVR system with uncertainties in time constants of amplifier, exciter, generator, and sensor, respectively. Transient response characteristics of the AVR system having different uncertainties are also given in Table 3.

Table 3 Results of robustness analysis of the AVR system controlled by FHODFC/HODFC

Considering obtained step responses given in Figs. 12, 13, 14 and 15, that the uncertainties in the time constant values of the AVR system resulting in small deviations in generator voltage compared to nominal case are concluded. In particular, there are almost no deviations for the sensor time constant. Although some reasonable deviations from nominal case occur in the responses, the AVR system still works in stable region even having large uncertainties. Therefore, both FHODFC and HODFC can ensure the stability of the AVR system and tracking the specified reference signal.

Table 3 showing transient response characteristics of the AVR system supports the aforementioned results. In addition, Table 3 shows that both FHODFC and HODFC having superiority over optimally tuned PID controllers [5, 16, 20, 33, 36] is concluded. Because both of the proposed controllers perform a better transient response than these PID controllers (Table 2) even having large uncertainties.

5 Conclusion

In this paper, generator voltage control of a commonly used AVR system has been presented. A high-order differential feedback control scheme and its fractional version are proposed in order to improve the regulating performance of the AVR system rather than using optimally tuned conventional PID controller [5, 16, 20, 33, 36].

It is shown that the proposed controllers, i.e., FHODFC and HODFC, could provide high accuracy in controlling the generator voltage of the AVR system. In the controller design process, PSO algorithm is utilized to find the minimum value of the specified cost function defined by considering important parameters in AVR system such as percentage overshoot, settling time, and regulating error. Moreover, a constraint is imposed on the control signal in the optimization process in order to obtain more realistic simulation results (see Sect. 4.1). This constraint has not been discussed for an AVR system in the literature yet.

The performance of the proposed FHODFC and HODFC is compared to each other in addition to the available optimally tuned PID controllers [5, 16, 20, 33, 36]. Simulation results show that the FHODFC has a better performance in generator voltage control of the AVR system than both the proposed HODFC and several optimized PID controllers [5, 16, 20, 33, 36]. Moreover, the robustness of the proposed controllers are analyzed and it is concluded that both the FHODFC and HODFC can ensure from the stability of the AVR system and track the specified reference signal even having large uncertainties.