1 Introduction

Model-based fault diagnosis has become an important and critical topic in industrial applications. Fault diagnosis procedure consists of three stages including detection, isolation and identification [1, 2]. The fault detection stage is the first step, and the two other stages are dependent on this step and will initiate after fault occurrence declaration in the first step.

On the other hand, fault detection for nonlinear systems has drawn much attention in recent years due to this fact that industrial applications are nonlinear systems. Different methods for fault detection of nonlinear systems are given in the literature such as nonlinear observer method, neural networks, fuzzy systems, bond graph method, etc.

Observer method may be considered as the main class of the model-based fault detection methods. Different classes for nonlinear systems are investigated in the literature and different observer methods are proposed for state and output estimation of the nonlinear systems. The Luenberger observer for the Lipschitz nonlinear systems are proposed in [3,4,5]. In [6], sensor fault estimation observer design for the Lipschitz nonlinear system with finite-frequency specifications is considered in which the disturbances are attenuated in the finite-frequency domain. The fault detection problem for discrete-time Lipschitz nonlinear systems with additive white Gaussian noise channels subject to signal-to-noise ratio constraints is addressed based on the mixed \(H_-/H_\infty \) performance index in [7]. In [8], a new observer design approach for the Lipschitz nonlinear systems is proposed in the form of LMI optimization problem, which is robust against some nonlinear uncertainty. Application of robust fault detection for heat recovery steam generator as a Lipschitz nonlinear system is studied in [9].

A robust nonlinear observer for systems with Lipschitz nonlinearity is addressed in [10], which is robust in the sense that its state estimation error decays to almost zero even in the face of large external disturbances. An alternative to solve the speed sensorless control of a surface-mounted synchronous motor based on localization of compact invariant sets and the Thau observer is presented in [11]. The state estimation problem for a class of globally Lipschitz nonlinear systems with time-varying delayed output based on sliding mode observer is considered in [12]. The unscented Kalman filter (UKF) for state estimation of nonlinear system is addressed in [13].

Unknown input observers (UIO) are used for disturbance decoupling in nonlinear systems. Two approaches including a novel UIO and an \(H_\infty \) observer for robust state estimation of a class of Lipschitz nonlinear systems are presented in [14] wherein the minimum value of the disturbance attenuation levels is obtained through solving optimization problem. Simultaneous state and fault estimation and disturbances influences minimization are considered in the UIO-based robust fault estimation approach for the Lipschitz nonlinear systems which are subjected to both process and sensor disturbances in [15]. The problem of UIO design for the Lipschitz nonlinear systems is considered in [16], in which additional degrees of freedom offered that used to deal with the Lipschitz nonlinearity. A new nonlinear approach for robust sensor fault detection is proposed in [17] in which a nonlinear UIO method is used.

Adaptive observers for nonlinear systems are also considered in several studies. In [18], an adaptive \(H_\infty \) observer is developed for estimating the states, unknown input and measurement noise simultaneously in a class of the Lipschitz nonlinear systems. An adaptive \(H_\infty \)-based observer for Lipschitz and dissipative nonlinear systems in the presence of disturbances and sensor noise is proposed in [19]. An adaptive observer synthesis for the Lipschitz nonlinear systems is noticed in [20].

In another approach, the reduced-order observers for the Lipschitz nonlinear systems are studied. The design of reduced-order observers for the Lipschitz nonlinear systems, which is dependent on the solution of the Riccati equation, is considered in [21].

In this study, the robust observer-based FD for the Lipschitz nonlinear systems is studied. The main reasons for this study may be given as twofold.

  • Nonlinear systems are studied in different classes with different approaches. The Lipschitz nonlinear systems may be considered as the most common form of these classes wherein a combination of the linear and nonlinear terms determines the governing equations of the system. Exact determination of the values of these nonlinear models (linear and nonlinear parts) is a difficult task, which leads to robust study of these systems. This issue may highlight the importance of the robustness in model-based FD system design as well. In the previous studies on the FD system design for the Lipschitz nonlinear systems, the Lipschitz constant is assumed as a known fixed value, which may lead to the sensitivity of the FD system against the variation of the Lipschitz constant. Hence, any uncertainties in this parameter may deteriorate the performance of the FD system and will result in false or missed alarms due to the problem of exact value determination of the Lipschitz constant.

  • The second issue that must be pointed out in the FD scheme for the Lipschitz nonlinear systems is considering the parametric uncertainties in the linear parts of the governing equations, which may lead to more conservatism about minimum achievable disturbance attenuation and maximum achievable fault sensitivity of the FD system. This aspect is noticed in two manners in this study. Firstly, the parametric uncertainties in linear parts of the state equation, i.e., the uncertainties in A and B matrices, are included in the nonlinear term of the system, which further reduce the conservatism of the observer design. Secondly, using the projection lemma may also lead to less conservatism in the observer design, which is noticed in some of the previous studies for linear systems. The projection lemma can reduce the conservatism in the observer design by introducing new variables by which some freedom degrees are gained.

Finally, to the best of our knowledge, the problem of robust fault detection for nonlinear systems with optimal selection of the disturbance attenuation level and the Lipschitz constant using the projection lemma is not studied in the literature.

In this paper, new robust fault detection for the Lipschitz nonlinear systems using projection lemma is proposed wherein the disturbance attenuation level and the new defined Lipschitz constant are obtained in an optimal manner by definition of the observer design as a weighted LMI optimization problem. Projection lemma will lead to less conservatism in the observer design as mentioned in [22,23,24]. The disturbance attenuation level is also achieved in trade-off with the Lipschitz constant which leads to maintaining the fault sensitivity and robustness of the FD system against the parametric uncertainties and nonlinear uncertainty as well. In general, maximization of the Lipschitz constant will lead to the following benefits in the FD system.

  • By considering the parametric uncertainties in A and B as a part of nonlinear term, the robustness against parametric uncertainties are also achieved.

  • Due to the fact that the obtaining the exact value of the Lipschitz constant is hard to be find in practical nonlinear systems, the FD system is robust against this value which further reduce the sensitivity of the FD system against the Lipschitz constant.

  • The observer design by considering the disturbance attenuation level will not lead to an optimal FD system, since the disturbance attenuation-level minimization will lead to reduce the fault sensitivity in the system as well. In this paper, the optimal value of the disturbance attenuation level is determined in trade-off with the Lipschitz constant, which maintains the fault sensitivity in addition to the robustness of the FD system against parametric and nonlinear uncertainties.

The remainder of current paper is as follows. In Sect. 2, problem formulation and some preliminaries and lemmas are given. The proposed robust fault detection is presented in Sect. 3. The simulation results of the proposed method for a single-link manipulator with revolute joints actuated by a DC motor as a Lipschitz nonlinear system is given in Sect. 4, followed by conclusion in Sect. 5.

2 Problem formulation and preliminaries

Consider the following Lipschitz nonlinear system:

$$\begin{aligned} \dot{x}(t)= & {} (A+\Delta A)x(t)+(B+\Delta B)u(t)\nonumber \\&+\,\psi (x,u) + D_1 d(t)+Q_1 f(t) \end{aligned}$$
(1)
$$\begin{aligned} y(t)= & {} Cx(t)+D_2 d(t)+Q_2 f(t). \end{aligned}$$
(2)

where \(x\in R^n\), \(u\in R^m\), \(y \in R^l\), \(d\in R^{k1}\) and \(f \in R^{k2}\), which are considered for states, inputs, outputs, unknown exogenous disturbances and different actuator and sensor faults in the system, respectively. A, B, C, \(D_1\), \(Q_1\), \(D_2\) and \(Q_2\) are matrices of appropriate dimensions. \(D_1\), \(Q_1\), \(D_2\) and \(Q_2\) are disturbance and fault distribution matrices on the states and on the outputs of the system. The nonlinear term of the state space model is assumed as \(\psi (x,u)\), which is locally Lipschitz with respect to x in a region D containing the origin, uniformly in u, i.e.,

$$\begin{aligned} \left\| \psi \left( x,u^*\right) -\psi \left( \hat{x},u^*\right) \right\| \le \gamma _1 \left\| x-\hat{x}\right\| \end{aligned}$$
(3)

where \(\gamma _1\) is the Lipschitz constant and \(u^*\) is any admissible control signal [25]. The region D may be the operational region of the system or the interest region. The parametric uncertainties in A and B are defined in the following form.

$$\begin{aligned} \Delta A= & {} M_1FN_1 \end{aligned}$$
(4)
$$\begin{aligned} \Delta B= & {} M_2FN_2 \end{aligned}$$
(5)

where \(M_1\), \(M_2\), \(N_1\) and \(N_2\) are constant matrices and F is a time-varying matrix that has 2-bounded norm as \(\Vert F^{\mathrm{T}}F\Vert \le I\). It is also assumed that the considered uncertainties cannot lead to instability in the system.

The considered term \(\psi (x,u)\) is the nonlinear term which is assumed to satisfy the Lipschitz equation as (3). In (3), the Lipschitz constant \(\gamma _1\) is given as a fixed value, which is hard to be finding in industrial applications [26]. If we integrate the uncertainties parts into the nonlinear term of (1), we may obtain:

$$\begin{aligned} \dot{x}(t)= & {} Ax(t)+Bu(t)+\varPsi (x,u) + D_1 d(t)+Q_1 f(t) \end{aligned}$$
(6)
$$\begin{aligned} y(t)= & {} Cx(t)+D_2 d(t)+Q_2 f(t). \end{aligned}$$
(7)

in which

$$\begin{aligned} \varPsi (x,u)=\psi (x,u)+\Delta Ax(t)+\Delta B u(t) \end{aligned}$$
(8)

The new nonlinear term also satisfies the Lipschitz condition but with a new Lipschitz constant, which is called \(\gamma \). The proof is given in “Appendix” section of the paper. The greater values of the new Lipschitz constant indicate the more robustness of the proposed observer and therefore the FD system. If we can maximize the new Lipschitz constant in the observer design approach, the abovementioned desired specifications are achieved in the FD system. The simulation results also justify the abovementioned specifications of the proposed method. Thus, we have:

$$\begin{aligned} \Vert \varPsi (x,u)-\varPsi \left( \hat{x},u\right) \Vert \le \gamma \Vert x-\hat{x}\Vert \end{aligned}$$
(9)

The nonlinear Luenberger observer according to [3,4,5] may be given as (10):

$$\begin{aligned} \dot{\hat{x}}(t)=A \hat{x}(t)+B u(t)+\varPsi \left( \hat{x}(t),u(t)\right) +L(y(t)-\hat{y}(t)).\nonumber \\ \end{aligned}$$
(10)

in which

$$\begin{aligned} \hat{y}(t)=C\hat{x}(t) \end{aligned}$$
(11)

The state and output estimation errors are defined as (12) and (13), respectively.

$$\begin{aligned}&e(t)=x(t)-\hat{x}(t) \end{aligned}$$
(12)
$$\begin{aligned}&e_y(t)=y(t)-\hat{y}(t)=Ce(t)+D_2d(t)+Q_2f(t) \end{aligned}$$
(13)

Therefore, the state estimation error dynamic in the presence of disturbances and faults may be achieved as (14).

$$\begin{aligned} \dot{e}(t)= & {} (A-LC)e(t)+\varPsi (x,u)-\varPsi \left( \hat{x},u\right) \nonumber \\&+\,\,(D_1-LD_2)d(t)+(Q_1-LQ_2)f(t). \end{aligned}$$
(14)

The residual is defined as the output estimation error of the observer in (15).

$$\begin{aligned} r(t)=e_y(t) \end{aligned}$$
(15)

The effect of disturbances in the state estimation error dynamic of the observer must be attenuated while the sensitivity of the concerned faults is maintained. The disturbance attenuation level criterion is defined as an \(H_\infty \) problem as follows:

$$\begin{aligned} \Vert r(t)\Vert _2 \le \mu \Vert d(t)\Vert _2 \end{aligned}$$
(16)

which can be written as (17).

$$\begin{aligned} r(t)^{\mathrm{T}}r(t)-\mu ^2 d(t)^{\mathrm{T}}d(t) \le 0 \end{aligned}$$
(17)

The new Lipschitz constant is considered as unknown variable which must be maximized in the observer design.

The following lemmas are used in this paper.

Lemma 1

[27] Let D, S and F as real matrices with appropriate dimensions, which F satisfies \(F^{\mathrm{T}}F \le I\). Then, for any scalar \(\epsilon >0\) and vectors \(x,y\in R^n\), the following inequality can be deduced:

$$\begin{aligned} 2x^{\mathrm{T}}DFSy \le \frac{1}{\epsilon } x^{\mathrm{T}}DD^{\mathrm{T}}x+\epsilon y^{\mathrm{T}}S^{\mathrm{T}}Sy \end{aligned}$$
(18)

Lemma 2

[28] Given a symmetric matrix \(Z \in S_m\) (\(m \times m\)) and two matrices U and V of column dimension m. There exists matrix X that is unstructured and satisfies (19)

$$\begin{aligned} U^{\mathrm{T}}XV+V^{\mathrm{T}}X^{\mathrm{T}}U+Z < 0 \end{aligned}$$
(19)

if and only if the inequalities (20) and (21) with respect to X are satisfied.

$$\begin{aligned}&N_U^{\mathrm{T}}ZN_U < 0 \end{aligned}$$
(20)
$$\begin{aligned}&N_V^{\mathrm{T}}ZN_V < 0 \end{aligned}$$
(21)

in which \(N_U\) and \(N_V\) are arbitrary matrices and their columns are a basis for null spaces of U and V, respectively.

This lemma is called the projection lemma, which leads to less conservatism in the observer design.

3 Main results

In this section, the proposed FD system is presented which will attenuate the disturbances level while maintaining the fault sensitivity and is robust against parametric and nonlinear uncertainties as well. The proposed approach is given as an LMI optimization problem in the following theorem.

Theorem

Given the Lipschitz nonlinear system (6)–(7) with the unknown but lower limit-bounded Lipschitz constant and Luenberger observer as (10), the state estimation error dynamic is asymptotically stable with the \(H_\infty \) performance criterion as (16) for any disturbance signal \(\Vert d(t)\Vert _2 <\infty \) and with a maximized Lipschitz constant, if for given \(\lambda >0\), there exists the scalars values \(\epsilon >0\), \(\gamma >0\) and the matrices \(P>0\), X and N such that the following weighted LMI optimization problem has solution

$$\begin{aligned}&{\mathop {\min }\nolimits _{{P,X,N,\mu ,\gamma }}} w\epsilon -(1-w)\gamma \nonumber \\&\mathrm{s.t.} \quad \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varPi _{11} &{} \gamma I &{} P &{} \varPi _{14} &{} \varPi _{15} \\ *&{} -I &{} 0 &{} 0 &{} 0\\ *&{} *&{} -I &{} 0 &{} 0 \\ *&{} *&{} *&{} \varPi _{44} &{} \varPi _{45}\\ *&{} *&{} *&{} *&{} \varPi _{55} \\ \end{array} \right] <0 \end{aligned}$$
(22)
$$\begin{aligned}&\gamma _1 - \gamma <0 \end{aligned}$$
(23)

where

$$\begin{aligned} \varPi _{11}= & {} C^{\mathrm{T}} C+A^{\mathrm{T}}X+X^{\mathrm{T}}A-NC-C^{\mathrm{T}}N^{\mathrm{T}} \end{aligned}$$
(24)
$$\begin{aligned} \varPi _{14}= & {} \lambda A^{\mathrm{T}}X-\lambda C^{\mathrm{T}}N^{\mathrm{T}}+P-X^{\mathrm{T}} \end{aligned}$$
(25)
$$\begin{aligned} \varPi _{15}= & {} C^{\mathrm{T}}D_2+X^{\mathrm{T}}D_1-ND_2 \end{aligned}$$
(26)
$$\begin{aligned} \varPi _{44}= & {} -\lambda X- \lambda X^{\mathrm{T}} \end{aligned}$$
(27)
$$\begin{aligned} \varPi _{45}= & {} \lambda X^{\mathrm{T}}D_1- \lambda N D_2 \end{aligned}$$
(28)
$$\begin{aligned} \varPi _{55}= & {} -\epsilon I+D_2^{\mathrm{T}}D_2 \end{aligned}$$
(29)

The weighting factor \(0 \le w \le 1\) is chosen according to following cost function, which considers the ratio and difference between the criteria

$$\begin{aligned} {\mathop {\min }\nolimits _{w}}\left( \frac{\epsilon }{\gamma }+\frac{1}{|\epsilon -\gamma |}\right) . \end{aligned}$$
(30)

The maximized Lipschitz constant lower bound is also defined as \(\gamma _1\), which is the obtained Lipschitz constant of the Lipschitz nonlinear system.

The observer gain and disturbance attenuation level of the observer are also obtained as:

$$\begin{aligned} L=X^{-T}N, \quad \mu =\sqrt{\epsilon } \end{aligned}$$
(31)

Proof

The Lyapunov function is assumed as (32), and its derivative may be obtained as (33) given as follows.

$$\begin{aligned} V(t)= & {} e(t)^{\mathrm{T}}Pe(t) \end{aligned}$$
(32)
$$\begin{aligned} \dot{V}(t)= & {} \dot{e}(t)^{\mathrm{T}}Pe(t)+e(t)^{\mathrm{T}}P\dot{e}(t) \end{aligned}$$
(33)

Using the state estimation error dynamic in (14), we have:

$$\begin{aligned} \dot{V}(t)= & {} e(t)^{\mathrm{T}}(A-LC)^{\mathrm{T}}Pe(t)+e(t)^{\mathrm{T}}P(A-LC)e(t)\nonumber \\&+\,\,2e(t)^{\mathrm{T}}P\left( \varPsi -\hat{\varPsi }\right) +2e(t)^{\mathrm{T}}P(D_1-LD_2)d(t)\nonumber \\&+\,\,2e(t)^{\mathrm{T}}P(Q_1-LQ_2)f(t) \end{aligned}$$
(34)

For convenience, it is assumed that \(\hat{\varPsi }=\varPsi \left( \hat{x},u\right) \).

In fault-free case, the disturbance attenuation-level criterion must be satisfied by assumption that the Lipschitz constant is an unknown variable, which must be maximized.

Therefore, the Lyapunov derivative function may be obtained as:

$$\begin{aligned} \dot{V}(t)= & {} e(t)^{\mathrm{T}}\left( A_{cl}^{\mathrm{T}}P+PA_{cl}\right) e(t)\nonumber \\&+\,\,2e(t)^{\mathrm{T}}P_1\left( \varPsi -\hat{\varPsi }\right) +2e(t)^{\mathrm{T}}PD_{cl}d(t) \end{aligned}$$
(35)

in which

$$\begin{aligned} A_{cl}= & {} A-LC \end{aligned}$$
(36)
$$\begin{aligned} D_{cl}= & {} D_1-LD_2 \end{aligned}$$
(37)

By using Lemma 1 and the given results in [29], it can be concluded that:

$$\begin{aligned} 2e^{\mathrm{T}}P\left( \varPsi -\hat{\varPsi }\right) \le e(t)^{\mathrm{T}}PPe(t)+\gamma ^2 e(t)^{\mathrm{T}}e(t) \end{aligned}$$
(38)

By substituting (38) in (35), one may obtain that:

$$\begin{aligned} \dot{V}(t)\le & {} e(t)^{\mathrm{T}}(A_{cl}^{\mathrm{T}}P+PA_{cl}\nonumber \\&+\,\,\gamma ^2 I+PP)e(t) +2e(t)^{\mathrm{T}}PD_{cl}d(t) \end{aligned}$$
(39)

According to [30], it can be concluded that:

$$\begin{aligned} r(t)^{\mathrm{T}}r(t)-\mu ^2 d(t)^{\mathrm{T}}d(t)+\dot{V} \le 0 \end{aligned}$$
(40)

By calculating \(r(t)^{\mathrm{T}} r(t)\) as (41), (40) can be written as (42).

$$\begin{aligned}&r(t)^{\mathrm{T}}r(t) = e(t)^{\mathrm{T}}C^{\mathrm{T}}Ce(t)+2e(t)^{\mathrm{T}}C^{\mathrm{T}}D_2d(t)\nonumber \\&\quad +\,d(t)^{\mathrm{T}}D_2^{\mathrm{T}}D_2d(t) \end{aligned}$$
(41)
$$\begin{aligned}&e(t)^{\mathrm{T}}\left( A_{cl}^{\mathrm{T}}P+PA_{cl}+\gamma ^2 I+PP+C^{\mathrm{T}}C\right) e(t)\nonumber \\&\quad +\,\,2e(t)^{\mathrm{T}}(PD_{cl}+C^{\mathrm{T}}D_2)d(t)\nonumber \\&\quad +\,\,d(t)^{\mathrm{T}} \left( D_2^{\mathrm{T}}D_2-\mu ^2 I\right) d(t) \le 0 \end{aligned}$$
(42)

By writing (42) in matrix inequality form, one can obtain (43).

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c} A_{cl}^{\mathrm{T}}P+PA_{cl}+PP +\gamma ^2 I &{} PD_{cl}\\ *&{} 0\\ \end{array} \right] \nonumber \\&\quad + \left[ \begin{array}{c@{\quad }c} C^{\mathrm{T}}C &{} C^{\mathrm{T}}D_2\\ *&{} D_2^{\mathrm{T}}D_2-\mu ^2I\\ \end{array} \right] <0 \end{aligned}$$
(43)

Equation (44) may be achieved by some simplifications in (43).

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c} I &{} A_{cl}^{\mathrm{T}}\\ 0 &{} D_{cl}^{\mathrm{T}}\\ \end{array} \right] \left[ \begin{array}{c@{\quad }c} \gamma ^2 I+PP &{} P\\ P&{} 0\\ \end{array} \right] \left[ \begin{array}{c@{\quad }c} I &{} 0\\ A_{cl} &{} D_{cl}\\ \end{array} \right] \nonumber \\&\quad + \left[ \begin{array}{c@{\quad }c} 0 &{} C^{\mathrm{T}}\\ I &{} D_2^{\mathrm{T}}\\ \end{array} \right] \left[ \begin{array}{c@{\quad }c} -\mu ^2 I &{} 0\\ 0 &{} I\\ \end{array} \right] \left[ \begin{array}{c@{\quad }c} 0 &{} I\\ C &{} D_2\\ \end{array} \right] <0 \end{aligned}$$
(44)

By assuming (44) as \(N_U^{\mathrm{T}} ZN_U\), it can be written as:

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c} I &{} A_{cl}^{\mathrm{T}} &{} 0\\ 0 &{} D_{cl}^{\mathrm{T}} &{} I\\ \end{array} \right] \left[ \begin{array}{c@{\quad }c@{\quad }c} \gamma ^2 I+ PP + C^{\mathrm{T}} C &{} P &{} C^{\mathrm{T}}D_2\\ *&{} 0 &{} 0\\ *&{} *&{} -\mu ^2 I+D_2^{\mathrm{T}}D_2\\ \end{array} \right] \nonumber \\&\quad \cdot \left[ \begin{array}{c@{\quad }c} I &{} 0\\ A_{cl} &{} D_{cl}\\ 0 &{} I\\ \end{array} \right] <0 \end{aligned}$$
(45)

Thus, Z is obtained as (46).

$$\begin{aligned} Z=\left[ \begin{array}{c@{\quad }c@{\quad }c} \gamma ^2 I+ PP + C^{\mathrm{T}} C &{} P &{} C^{\mathrm{T}}D_2\\ *&{} 0 &{} 0\\ *&{} *&{} -\mu ^2 I+D_2^{\mathrm{T}}D_2\\ \end{array} \right] \end{aligned}$$
(46)

U is obtained as follows given that \(N_U\) columns are basis for its null space.

$$\begin{aligned} U=\left[ A_{cl} \quad -I \quad D_{cl}\right] \end{aligned}$$

The other variables \(N_V\) and V are assumed as follows according to [30]:

$$\begin{aligned} N_V= \left[ \begin{array}{c@{\quad }c} \lambda I &{} 0 \\ 0 &{} 0 \\ 0 &{} I \\ \end{array} \right] V=\left[ 0 \quad \lambda I \quad 0\right] \end{aligned}$$

According to the projection lemma, (19) may be given as (47) considering the abovementioned obtained variables.

$$\begin{aligned}&\left[ \begin{array}{c} A_{cl}^{\mathrm{T}}\\ -I\\ D_{cl}^{\mathrm{T}}\\ \end{array} \right] X \left[ 0 ~ \lambda I ~ 0\right] +\left[ \begin{array}{c} 0\\ \lambda I\\ 0\\ \end{array} \right] X^{\mathrm{T}} [A_{cl} ~ -I ~ D_{cl}]\nonumber \\&\quad + \left[ \begin{array}{c@{\quad }c@{\quad }c} \gamma ^2 I+ PP + C^{\mathrm{T}} C &{} P &{} C^{\mathrm{T}}D_2\\ *&{} 0 &{} 0\\ *&{} *&{} -\mu ^2 I+D_2^{\mathrm{T}}D_2\\ \end{array} \right] <0\nonumber \\ \end{aligned}$$
(47)

By simplifying (47) and substituting (36) and (37), a nonlinear matrix inequality is obtained as (48).

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c} \Lambda &{} P-X^{\mathrm{T}}+\lambda A^{\mathrm{T}}X-\lambda C^{\mathrm{T}}N^{\mathrm{T}} &{} C^{\mathrm{T}}D_2+X^{\mathrm{T}}D_1-ND_2\\ *&{} -\lambda X- \lambda X^{\mathrm{T}} &{} \lambda X^{\mathrm{T}}D_1- \lambda N D_2\\ *&{} *&{} -\epsilon I+D_2^{\mathrm{T}}D_2\\ \end{array} \right] <0\nonumber \\ \end{aligned}$$
(48)

where

$$\begin{aligned} N= & {} X^{\mathrm{T}}L \end{aligned}$$
(49)
$$\begin{aligned} \epsilon= & {} \gamma ^2 \end{aligned}$$
(50)
$$\begin{aligned} \Lambda= & {} \gamma ^2 I+ PP + C^{\mathrm{T}} C+A^{\mathrm{T}}X+X^{\mathrm{T}}A\nonumber \\&-\,NC-C^{\mathrm{T}}N^{\mathrm{T}} \end{aligned}$$
(51)

Finally, by applying the Schur complement, (22) may be achieved, and the proof is completed. \(\square \)

Fig. 1
figure 1

Lipschitz constant and disturbance attenuation level of the optimization problem versus weighting factor

Full size image

The residual evaluation function is assumed in the form of (52).

$$\begin{aligned} J_L(t)=\sqrt{\int _{t_0}^{t_0+L_W}{r(t)^{\mathrm{T}}r(t)\hbox {d}t}} \end{aligned}$$
(52)

in which \(t_0\) is the initial sample and \(L_W\) is the window length of the residual. The threshold for fault declaration on the residual evaluation function is given as (53).

$$\begin{aligned} J_{th}=\sup _{d(t),u(t) \in l_2,f(t)=0}{J_L(t)} \end{aligned}$$
(53)

4 Simulation results

In this section, a single-link manipulator with revolute joints actuated by a DC motor is considered to show the effectiveness of the proposed method. The considered case study is a common example in the Lipschitz nonlinear systems study, which is noticed in several papers such as [15, 31,32,33,34].

The state space representation of the system is given by [15]:

$$\begin{aligned} \dot{q}_m= & {} \omega _m \end{aligned}$$
(54)
$$\begin{aligned} \dot{\omega }_m= & {} \frac{k}{J_m}\left( q_l-q_m\right) -\frac{B}{J_m}\omega _m+\frac{k_\tau }{J_m}u \end{aligned}$$
(55)
$$\begin{aligned} \dot{q}_l= & {} \omega _l \end{aligned}$$
(56)
$$\begin{aligned} \dot{\omega }_l= & {} -\frac{k}{J_l}\left( q_l-q_m\right) -\frac{mgh}{J_l}\sin {q_l} \end{aligned}$$
(57)

where \(\omega _l\) is the angular velocity of the link, \(\omega _m\) is the angular velocity of the motor, \(q_l\) is the angular position of the link, \(q_m\) is the angular position of the motor, k is torsional spring constant, B is the viscous friction, \(k_\tau \) is the amplifier gain, g is the gravity constant and h is the distance from rotor to the center of the gravity to the link. The inertia of the motor and link are given as \(J_m\) and \(J_l\), respectively. u is the input of the system, which is the torque of the motor.

The matrices of the Lipschitz nonlinear system are considered as follows [34]:

$$\begin{aligned}A= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 1 &{} 0 &{} 0\\ -\,48.6 &{} -\,1.25 &{} 48.6 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ 19.5 &{} 0 &{} -\,19.5 &{} 0\\ \end{array} \right] ,\quad B= \left[ \begin{array}{c} 0\\ 21.6\\ 0 \\ 0\\ \end{array} \right] \\ C= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ \end{array} \right] ,\quad \psi = \left[ \begin{array}{c} 0\\ 0\\ 0 \\ -\,3.33 \sin {x_3} \\ \end{array} \right] \end{aligned}$$

in which \(x=[q_m \quad \omega _m \quad q_l \quad \omega _l ]\).

Different sensor and actuator faults can be detected by the proposed method. In this paper, an actuator fault is considered to show the efficiency of the proposed method. The vector f and distribution matrices may be modified to consider sensor faults as well. The fault and disturbance matrices are assumed as follows as in [15].

$$\begin{aligned}D_1= \left[ \begin{array}{c@{\quad }c@{\quad }c} -\,0.2 &{} 0.01 &{} -\,0.02\\ -\,0.1 &{} 0.02 &{} -\,0.04\\ 0.1 &{} -\,0.02 &{} 0.04\\ 0.2 &{} 0.02 &{} -\,0.04\\ \end{array} \right] ,\quad Q_1= \left[ \begin{array}{c} 0\\ 21.6\\ 0 \\ 0\\ \end{array} \right] \end{aligned}$$

The distribution matrices of fault and disturbance on the output are assumed as zero.

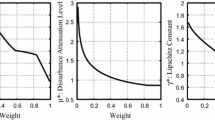
The obtained results by the given theorem for the Lipschitz constant and the disturbance attenuation level of the observer against weighting factor for \(\lambda =0.2\) are given as Fig. 1.

The optimal trade-off curve between the Lipschitz constant and disturbance attenuation level is depicted as Fig. 2.

Fig. 2
figure 2

Optimal trade-off curve

Full size image
Fig. 3
figure 3

Output estimation error of the observer in normal case and in the presence of disturbances

Full size image

Regarding the defined cost function of the theorem, the optimal value of the weighting factor is obtained as \(w=0.89\), which leads to the following results:

$$\begin{aligned} \mu =0.2324,\quad \gamma =3.9471 \end{aligned}$$

The gain of the observer is also achieved as:

$$\begin{aligned}L=\left[ \begin{array}{c@{\quad }c} 13.2085 &{} -\,6.0834 \\ -\,61.7967 &{} 43.9014 \\ -\,5.9194 &{} 38.1352 \\ 18.9590 &{} 6.1787 \\ \end{array} \right] \end{aligned}$$

The obtained Lipschitz constant is 3.9471 by the proposed method, which is improved by a factor of 1.18. In other words, the proposed FD system is robust against any parametric uncertainties and nonlinearity that satisfies the obtained maximized Lipschitz constant.

The single-link manipulator system is simulated in Matlab/Simulink platform in normal and faulty situations taking into account the abovementioned results. According to [15], the disturbances on the system are assumed as follows, which have large values.

$$\begin{aligned} d(t)= & {} \left[ d_1(t) \quad d_2(t) \quad d_3(t)\right] ^{\mathrm{T}}\nonumber \\= & {} \left[ 5 \sin {10t} \quad 2 \sin {10t} \quad \sin {20t}\right] \end{aligned}$$
(58)

Simulation results are given for \(u=2\sin {\pi t}\) with the initial state as \(x(0)=[0.01 \quad -5 \quad 0.01 \quad 5]^{\mathrm{T}}\) [15].

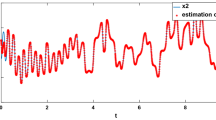
The residuals (output estimation errors) of the observer in normal case and in the presence of disturbances are given in Fig. 3.

As can be seen from the figures, the residuals have small values regarding the large values of the disturbances in the system.

The residual evaluation function in (52) is calculated by trapezoidal rule for a moving fixed length window of the residuals as \(L_W=10\) and the initial sample as \(t_0=50\), which leads to the following threshold as Table 1 using (53).

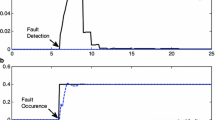
Table 1 Threshold on the residual evaluation function
Full size table

In faulty case simulation, an actuator fault is injected in the system as a step signal with unit amplitude at \(t=4\) s. In other words, an abrupt actuator fault is considered in the system. The residuals are depicted in Fig. 4.

Fig. 4
figure 4

Residuals of the FD system in abrupt actuator fault

Full size image
Fig. 5
figure 5

Residual evaluation function of the FD system in abrupt actuator fault

Full size image

It is obvious from the figure that the fault can be discriminated efficiently from the disturbances in the considered residuals of the FD system. In model-based fault detection methods, the decision of whether a fault is occurred is made based upon the residual evaluation function, which is compared with a fixed or adaptive threshold. The obtained residual evaluation functions in comparison to the defined fixed thresholds are given as Fig. 5.

Table 2 Threshold on the residual evaluation function in the case without Lipschitz maximization
Full size table

As can be seen from the figure, the residuals are exceeded from their thresholds and the fault occurrence is declared.

Fig. 6
figure 6

Residual evaluation function of the proposed method in normal case

Full size image
Fig. 7
figure 7

Residual evaluation function of the method without Lipschitz maximization in normal case

Full size image

In order to compare the results between the proposed method and the method without the Lipschitz constant maximization, an observer is designed based on disturbance attenuation level minimization. The gain of the observer, which is called \(L_{\mathrm{c}}\) is achieved as:

$$\begin{aligned} L_{\mathrm{c}}=1e3 \left[ \begin{array}{c@{\quad }c} 2.4361 &{} 1.1047 \\ 1.1804 &{} 0.8242 \\ -\,1.2739 &{} -\,0.3585 \\ -\,2.3115 &{} -\,0.7341 \\ \end{array} \right] \end{aligned}$$

The disturbance attenuation level is also obtained as \(2.83\hbox {e}{-}5\).

Fig. 8
figure 8

Residual evaluation function of the proposed method in normal case

Full size image
Fig. 9
figure 9

Residual evaluation function of the method without Lipschitz maximization in normal case

Full size image

It should be noted that the observer is defined with no constraint on the observer gain, which leads to large values for the gains of the observer. The larger values of the observer may lead to better performance of the observer, although its implementation may have some limitations. In fact, to show the great performance of the proposed method, an ideal situation is considered to compare the results.

Same as the proposed method, the thresholds on the residual evaluation function for the method without the Lipschitz constant maximization may be obtained as Table 2.

Fig. 10
figure 10

Residual evaluation function of the proposed method in normal case

Full size image
Fig. 11
figure 11

Residual evaluation function of the method without Lipschitz maximization in normal case

Full size image

As it is clear from Table 2, the thresholds have smaller values in comparison with the proposed method (Table 1), since the effects of disturbances are attenuated more efficiently in this method.

Robustness analysis of the proposed method in comparison with the method without Lipschitz constant maximization is studied with considering uncertainties in the parameters of the system and the Lipschitz constant as well. Three scenarios including parametric uncertainties in A and B and uncertainty in the Lipschitz constant are considered for robustness analysis of the proposed method.

In the first scenario, the parametric uncertainties are assumed as 5% increase in A as \(\Delta A\) in the normal case, which leads to the following residual evaluation functions for the proposed method and the method without Lipschitz maximization as Figs. 6 and 7, respectively.

It can be concluded from the figures that the proposed method maintains its performance in the presence of parametric uncertainty, while in the method without Lipschitz maximization, the uncertainty is declared as a fault occurrence. In other words, the parametric uncertainties may lead to false alarm in the method without Lipschitz maximization.

In the second scenario, the parametric uncertainty is considered as 5% increase in B as \(\Delta B\). The residuals evaluation functions are given in Figs. 8 and 9.

As can be observed from the figures, the second residual of the proposed method is exceeded in a limit time from the threshold, while there are several false alarms for the method without Lipschitz constant maximization.

In the third scenario, a nonlinear uncertainty as 5% increase in nominal value of the Lipschitz constant is considered in the system, which leads to a new value of the Lipschitz constant as 3.4965. The simulation results are shown in Figs. 10 and 11.

As can be observed from the figures, the proposed method has great performance in this case as well. The performance of the method without Lipschitz constant maximization has great sensitivity against nonlinear uncertainty, which is presented as the uncertainty in the Lipschitz constant.

In overall, a fault detection method is proposed in which the disturbance attenuation level is minimized in trade-off with the Lipschitz constant maximization. The conservatism of the observer is reduced using the new defined nonlinear Lipschitz term and using the projection lemma by introducing some new variables in the observer design, which is defined as an LMI optimization problem. This optimal disturbance attenuation level leads to greater thresholds on the residuals as Table 1, while maintaining the fault sensitivity of the FD system, which is shown in Figs. 4 and 5. On the other hand, the proposed method by the Lipschitz constant maximization is made robust against parametric uncertainties in A and B matrices and against nonlinear uncertainties as well, which are shown in Figs. 6, 8 and 10, respectively. The fault sensitivity of the proposed method maintain at a noticeable value in comparison with the method without Lipchitz constant maximization.

5 Conclusion

A new robust fault detection approach based on the observer method has been proposed in this study. The proposed method has shown great performance in disturbance attenuation level, fault sensitivity and robustness against parametric and nonlinear uncertainties. The observer has been designed by considering the optimal values of the Lipschitz constant and disturbance attenuation level, which has been defined as a weighted LMI optimization problem. The conservatism of the proposed FD system has been reduced by using the projection lemma. The parametric and nonlinear uncertainties have been included in the nonlinear Lipschitz term of the system with unknown but fixed lower bounded value of the Lipschitz constant. This approach has resolved the problem of finding the exact value of the Lipschitz constant in industrial applications, which leads to robustness of the FD system as well. The simulation results for a single-link manipulator with revolute joints actuated by a DC motor have shown the effectiveness of the proposed method in fault detection of the Lipschitz nonlinear system.

In order to develop the proposed method, the problem of robust fault detection for Lipschitz nonlinear systems by optimal maximized Lipschitz constant, disturbance attenuation level and other FD criteria such as fault sensitivity using \(H_-\) index and false alarm rate (FAR) may be considered in the future works.