Robust Fault Detection of Uncertain Lipschitz Nonlinear Systems with Simultaneous Disturbance Attenuation Level and Enhanced Fault Sensitivity and Lipschitz Constant

Abstract

In this paper, the problem of optimal robust fault detection (FD) for uncertain Lipschitz nonlinear systems is considered. A robust active fault detection approach for a class of the Lipschitz nonlinear systems in the presence of disturbances and parametric uncertainties is proposed, wherein the Lipschitz constant is assumed as one of the optimization parameters in the observer design. In addition to disturbance attenuation level, the fault sensitivity criterion based on $H_-$ index is also defined in the FD system design. Different criteria are defined as a weighted multi-objective linear matrix inequality optimization problem, and the optimal variables of the FD system are derived based on a newly defined cost function. A numerical example is provided to demonstrate the effectiveness of the proposed FD system. The results show the robustness of the proposed method against parametric uncertainty and nonlinear uncertainty as well.

1 Introduction

Over the past three decades, fault detection and isolation (FDI) has been the subject of numerous studies for different classes of dynamic systems and industrial applications as well [4, 16, 21, 38]. FDI methods can be categorized as model-based and data-driven methods [38]. Model-based FDI is further divided into qualitative and quantitative approaches [31]. In this paper, the model-based quantitative FDI approach is investigated, which has the advantages of representing a complete view of the system and efficiently showing different anomalies in the system.

FDI design for linear systems has been comprehensively investigated [12]. Industrial processes have nonlinear behavior, which makes it difficult to monitor and control the system. This challenge may be highlighted in the presence of disturbances in the system and uncertainties of the model. Recently, much attention has been given to study of nonlinear systems [11]. FDI system design for nonlinear systems may be categorized as three approaches: 1) linearization of the nonlinear system and using developed theories for the linear systems [3, 22]; 2) specialized approaches for nonlinear systems such as nonlinear observers and analytical redundancy relations (ARRs) [9, 13, 23, 35]; and 3) intelligent methods such as neural networks and fuzzy logics [19, 20, 28].

In this paper, the problem of fault detection (FD) system design for a class of Lipschitz nonlinear systems is tackled via robust observer approach. Due to the presence of uncertainties (parametric or nonparametric), disturbances and noises in the system, robustness may be considered as a critical feature of an FD system, which may be highlighted for nonlinear systems. Therefore, the robust FD system design for nonlinear systems has received much attention in the recent decades, resulting in an active area of research.

A complete survey on robust fault diagnosis with emphasis on linear systems is presented in [17], wherein different methods for robust residual generation and decision making are summarized. In [14], an effective fault estimation technique is developed to simultaneously estimate the system states and the concerned faults, while minimizing the influences from process/sensor disturbances. The proposed robust fault estimation techniques are addressed for the Lipschitz nonlinear systems subjected to both process and sensor disturbances. A robust fault diagnosis scheme for nonlinear systems is designed, and a new algorithm for a robust fault diagnosis observer is proposed in [24].

Robust fault detection is classified as active and passive approaches [5]. In the active approach, the robustness of an FD system is considered in the residual generation stage, while the robustness of the FD system is applied in the decision-making stage in the passive approach. According to [5], some conservatism is considered for achieving the robustness of the FD system in the passive methods and thus it cannot be regarded as a realistic robust method.

In the active robust approach, two different methods may be introduced. In the first method, different criteria for the robustness and other purposes of the FD system are defined based on a Lyapunov function [6, 7, 35, 37]. In the second approach, the effects of unwanted terms are considered as unknown terms and are removed in the error dynamics in the design procedure [29, 33, 36].

It is worth noting that dealing with the disturbance attenuation level without consideration of the fault sensitivity may lead to reduction in the fault sensitivity of the FDI system, which further causes several missed alarms. Therefore, several researches concentrated on the simultaneous disturbance attenuation level and fault sensitivity maximization in the FD system design. For example, simultaneous enhanced fault sensitivity and disturbance attenuation level are noticed in the FD system design for linear switching systems in [8], and mixed $H-/H_{\infty }$ fault detection observer design for the Lipschitz nonlinear systems is given in [39].

One issue that must be highlighted in the previous studies on the FD schemes of the Lipschitz nonlinear systems is that the considered criteria such as fault sensitivity and disturbance attenuation level are not obtained in an optimal manner. In fact, one of the values is calculated based on the known value of another one. Another issue in the FD design of the Lipschitz nonlinear systems is the Lipschitz constant, which is considered as a fixed value in the FD system design, while this constant is dependent on the parameters of the system and obtaining its exact value is difficult in practical applications [27]. As mentioned, the Lipschitz constant is dependent on the parameters of the system. Hence, considering the parametric uncertainties in the mathematical model of the system leads to uncertain Lipschitz constant as well, which may highlight the robustness issue in this regard.

In this paper, a robust active FD approach for the Lipschitz nonlinear systems in the presence of disturbances and parametric uncertainties is proposed. The Lipschitz constant, disturbance attenuation level and the fault sensitivity are assumed as the optimization parameters in the observer design. The proposed FD system is robust against both parametric and nonlinear uncertainties. The FD system is considered as a weighted multi-objective optimization problem based on the aforementioned criteria in linear matrix inequalities (LMIs) form.

In brief, the main contributions of the paper may be stated as follows:

• Optimal robust fault detection for a class of the Lipschitz nonlinear systems in the presence of disturbance, faults, parametric uncertainties and uncertainty in the Lipschitz constant.

• Maximization of the Lipschitz constant in the FDI system design.

• Defining the FD system as a weighted multi-objective optimization LMI problem, in which a new sufficient condition is derived.

The maximization of the Lipschitz constant leads to robustness of the observer and subsequently results in the robustness of the FD system. In other words, the proposed FD system is relying on a robust observer in which the robustness against nonlinear uncertainties is also considered in the design process. To solve the robust observer design problem considering disturbances, uncertainties in the parameter, uncertainties in the Lipschitz constant and faults for the Lipschitz nonlinear system, LMI technique is used in this paper. The fault sensitivity and disturbance attenuation are defined in LMI form as an $H_-/H_\infty$ index by considering the Lipschitz constant as one of the unknown variables of the problem. The effect of parametric uncertainties is considered in LMI derivation based on the lemma that is given in the next section. To use this lemma, a new constraint is imposed on the problem, which may be satisfied by defining and selecting proper value for a weighting matrix on the residuals. Finally, the obtained results are defined as a multi-objective weighted LMI optimization problem. The optimization LMI problem may be solved using available software packages. Several solutions may be obtained based on the weighting factor, and the optimal one is selected considering a new defined cost function.

The organization of the paper is as follows: In Sect. 2, problem definition and some preliminaries are given. Robust active FD system design based on the observer approach and the defined optimization problem in the LMI form as a new theorem, as well as a new condition that must be satisfied are presented in Sect. 3. Simulation results for a numerical example are given in Sect. 4, followed by conclusion and some remarks.

2 Problem Definition and Some Preliminaries

Consider the following Lipschitz nonlinear system.

$$\begin{aligned} \dot{x}(t)= & {} (A+\Delta A)x(t)+\psi (x,u) + D_1 d(t)+Q_1 f(t), \end{aligned}$$

(1)

$$\begin{aligned} y(t)= & {} (C+\Delta C)x(t)+D_2 d(t)+Q_2 f(t), \end{aligned}$$

(2)

where $x\in R^n$ is state, $u\in R^m$ is input, $y \in R^l$ is output, and $d\in R^{k1}$ and $f \in R^{k2}$ are unknown exogenous disturbances and different faults in the system, respectively. A, $C,D_1,Q_1,D_2$ and $Q_2$ are matrices of appropriate dimensions. The nonlinear term in (1) is locally Lipschitz, i.e.,

$$\begin{aligned} ||\psi (x,u)-\psi (\hat{x},u)|| \le \gamma ||x-\hat{x}||, \end{aligned}$$

where $\gamma$ is the Lipschitz constant.

$\Delta A$ and $\Delta C$ are unknown matrices representing the parametric uncertainties of the system, which have the following forms [1].

$$\begin{aligned} \Delta A= & {} M_1 F N_1, \end{aligned}$$

(3)

$$\begin{aligned} \Delta C= & {} M_2 F N_2, \end{aligned}$$

(4)

in which $M_1$, $N_1$, $M_2$ , $N_2$ and F are matrices with appropriate dimensions. $M_1$, $N_1$, $M_2$ and $N_2$ are known matrices. F is an unknown time-varying matrix satisfying $||F(t)||_2 \le I~ \forall t \in [0,\infty )$.

Any nonlinear system of the form $\dot{x}(t)=f(x,u)$ may be expressed as (1)–(2), as long as f(x, u) is differentiable with respect to x [26]. In other words, the nonlinear system as in (1) can be regarded as a general class of nonlinear systems, at least locally [26], and thus noticed here.

The Luenberger observer for the nonlinear Lipschitz systems is studied in some papers such as [25, 26, 30]. The Luenberger observer for the considered class of the Lipschitz nonlinear systems is expressed as (5):

$$\begin{aligned} \dot{\hat{x}}(t)=A \hat{x}(t)+\psi (\hat{x}(t),u(t))+L(y(t)-\hat{y}(t)), \end{aligned}$$

(5)

where $\hat{x}(t)$ is the state estimation and $\hat{y}(t)$ is the output estimation error of the observer that is defined as (6).

$$\begin{aligned} \hat{y}(t)=C \hat{x}(t), \end{aligned}$$

(6)

where L is the gain of the observer and will be designed regarding the desired criteria. The error dynamic of the observer can be easily obtained as (8) with the error definition in (7).

$$\begin{aligned} e(t)= & {} x(t)-\hat{x}(t), \end{aligned}$$

(7)

$$\begin{aligned} \dot{e}(t)= & {} (A-LC)e(t)+\psi (x,u)-\psi (\hat{x},u)+ (D_1-LD_2)d(t)\nonumber \\&+(Q_1-LQ_2)f(t)+(\Delta A - L\Delta C)x(t). \end{aligned}$$

(8)

The residuals of the FD system are assumed as (9).

$$\begin{aligned} r(t)=He_y(t)=HCe(t)+HM_2FN_2x(t)+HD_2d(t)+HQ_2f(t), \end{aligned}$$

(9)

in which H is the weighting matrix on the output estimation error for the residual generation. H is chosen as an arbitrary matrix to satisfy a constraint, which will be mentioned in the final theorem of the paper. It is also worth noting that the number of rows of H determines the number of the residuals for the FD system.

In the next section, the robust FD system is presented.

3 Robust Fault Detection Based on Nonlinear Observer

In this paper, the robustness issue in the FD system design is concerned with the disturbance attenuation level and maximization of the Lipschitz constant in the presence of parametric uncertainties. The observer gain is obtained via optimal selection of the different criteria.

In fault-free case, the disturbance attenuation level, which is represented as $\mu$, is expressed as:

$$\begin{aligned} ||r(t)||_2 \le \mu ||d(t)||_2. \end{aligned}$$

(10)

The fault sensitivity criteria using $H_-$ index are defined in (11).

$$\begin{aligned} ||r(t)||_2 \ge \beta ||f(t)||_2, \end{aligned}$$

(11)

where $\beta$ is defined as the minimum effect of faults on the residual.

To summarize, the following criteria are noticed in the FD system design.

• Asymptotic stability of the observer with a fixed decay rate.

• Disturbance attenuation level as given in (10).

• Satisfying $H_-$ index for fault sensitivity as (11).

• Maximization of the Lipschitz constant in order to enhance the robustness of the FD system against nonlinear uncertainty.

Regarding the parametric uncertainties in the state space representation of the system, the following Lyapunov function is considered.

$$\begin{aligned} V(t)=V_1(t)+V_2(t), \end{aligned}$$

(12)

where

$$\begin{aligned} V_1(t)=e(t)^TP_1e(t) \quad V_2(t)=x(t)^TP_2x(t). \end{aligned}$$

(13)

Therefore, the derivative of the Lyapunov function will be:

$$\begin{aligned} \dot{V}_1(t)= & {} \dot{e}(t)^TP_1e(t)+e(t)^TP_1\dot{e}(t), \end{aligned}$$

(14)

$$\begin{aligned} \dot{V}_2(t)= & {} \dot{x}(t)^TP_2x(t)+x(t)^TP_2\dot{x}(t). \end{aligned}$$

(15)

By substituting (8) into (14), we obtain the following equation:

$$\begin{aligned} \dot{V}_1(t)= & {} e(t)^T(A-LC)^TP_1e(t)+e(t)^TP_1(A-LC)e(t) +2e(t)^TP_1(\psi -\hat{\psi })\nonumber \\&+2e(t)^TP_1(D_1-LD_2)d(t)+2e(t)^TP_1(Q_1-LQ_2)f(t)\nonumber \\&+2e(t)^TP_1M_1FN_1x(t)-2e(t)^TP_1LM_2FN_2x(t). \end{aligned}$$

(16)

For the simplicity, it is assumed that $\hat{\psi }=\psi (\hat{x},u)$.

For the asymptotic stability of the observer, the following equation is considered.

$$\begin{aligned} (A-LC)^TP_1+P_1(A-LC)=-Q. \end{aligned}$$

(17)

Equation (17) is modified as (18) in order to consider the decay rate of the observer, which is defined as $\upsilon$.

$$\begin{aligned} A^TP_1+P_1A-P_1LC-C^TL^TP_1+2\upsilon P_1 =-Q. \end{aligned}$$

(18)

It is noted that both L and $P_1$ are unknown matrix variables that are multiplied by each other in the above equation, which leads to nonlinear matrix inequality. For solving this problem, a new matrix variable is defined as $G=P_1L$, leading to the following equation.

$$\begin{aligned} A^TP_1+P_1A-GC-C^TG+2\upsilon P_1 =-Q. \end{aligned}$$

(19)

In order to continue we use the following result:

Lemma

[32] Consider D, S and F as real matrices with proper dimensions. Matrix F satisfies the following condition.

$$\begin{aligned} F^TF \le I. \end{aligned}$$

Then, for any scalar $\epsilon >0$ and vectors $x,y\in R^n$, the following inequality can be concluded:

$$\begin{aligned} 2x^TDFSy \le \frac{1}{\epsilon } x^TDD^Tx+\epsilon y^TS^TSy. \end{aligned}$$

(20)

According to the lemma and the results of [2], we have:

$$\begin{aligned}&2e^TP_1(\psi -\hat{\psi }) \le e(t)^TP_1P_1e(t)+\gamma ^2 e(t)^Te(t), \end{aligned}$$

(21)

$$\begin{aligned}&2e(t)^TP_1M_1FN_1x(t) \le e(t)^TP_1M_1M^T_1P_1e(t)+x(t)^TN^T_1N_1x(t), \end{aligned}$$

(22)

$$\begin{aligned}&2e(t)^TP_1LM_2FN_2x(t) \le e(t)^TGM_2M^T_2G^Te(t)+x(t)^TN^T_2N_2x(t). \end{aligned}$$

(23)

Thus, the upper bound of $\dot{V}_1$ can be obtained as (24).

$$\begin{aligned} \dot{V}_1\le & {} -e(t)^TQe(t)+e(t)^TP_1P_1e(t)+x(t)^TN_2N^T_2x(t)+e(t)^TP_1M_1M^T_1P_1e(t)\nonumber \\&+e(t)^TGM_2M^T_2G^Te(t) +x(t)^TN^T_1N_1x(t) +2e(t)^TP_1(D_1-LD_2)d(t)\nonumber \\&+\gamma ^2 e(t)^Te(t)+2e(t)^TP_1(Q_1-LQ_2)f(t). \end{aligned}$$

(24)

By substituting the required terms in $\dot{V}_2$, it can be achieved in the form of (25).

$$\begin{aligned} \dot{V}_2= & {} x(t)^TA^TP_2x(t)+x(t)^TP_2Ax(t)+2x(t)^TP_2\psi + 2 x(t)^TP_2D_1d(t)\nonumber \\&+2x(t)^TP_2Q_1f(t)+2x(t)^TP_2M_1FN_1x(t). \end{aligned}$$

(25)

Similar to $\dot{V}_1$ and using the aforementioned lemma, the following equations can be concluded.

$$\begin{aligned}&2x(t)^TP_2M_1FN_1x(t) \le x(t)^TP_2M_1M^T_1P_2x(t)+x(t)^TN_1N^T_1x(t), \end{aligned}$$

(26)

$$\begin{aligned}&2x(t)^TP_2\psi \le x(t)^TP_2P_2x(t)+\gamma ^2 x(t)^T x(t). \end{aligned}$$

(27)

Therefore, the upper bound of $\dot{V}_2$ is given as (28).

$$\begin{aligned} \dot{V}_2\le & {} x(t)^T(A^TP_2+P_2A+P_2M_1M^T_1P_2+N_1N^T_1+P_2P_2+\gamma ^2 I)x(t)\nonumber \\&+2x(t)^TP_2D_1d(t)+2x(t)^TP_2Q_1f(t). \end{aligned}$$

(28)

By adding (24) and (28), the upper bound of the Lyapunov function derivative can be obtained as:

$$\begin{aligned} \dot{V}\le & {} e(t)^T(-Q+P_1P_1+\gamma ^2 I+P_1M_1M^T_1P_1+GM_2M^T_2G^T)e(t)+x(t)^T(A^TP_2\nonumber \\&+P_2A+P_2M_1M^T_1P_2+2N_1N^T_1+P_2P_2+\gamma ^2 I+N_2N^T_2)x(t)\nonumber \\&+2e(t)^TP_1(D_1-LD_2)d(t) +2e(t)^TP_1(Q_1-LQ_2)f(t)+2x(t)^TP_2D_1d(t)\nonumber \\&+2x(t)^TP_2Q_1f(t). \end{aligned}$$

(29)

Considering (30) as stated in [1], (29) can be written as (31).

$$\begin{aligned}&I+M_1M^T_1=J_1J^T_1,M_2M^T_2=J_2J^T_2. \end{aligned}$$

(30)

$$\begin{aligned}&\dot{V} \le e(t)^T(-Q+\gamma ^2 I+P_1J_1J^T_1P_1+GJ_2J^T_2G^T)e(t) +2e(t)^TP_1(D_1\nonumber \\&\quad -LD_2)d(t)+x(t)^T(A^TP_2+P_2A+P_2J_1J^T_1P_2+2N_1N^T_1+\gamma ^2I\nonumber \\&\quad +N_2N^T_2)x(t)+ 2e(t)^TP_1(Q_1-LQ_2)f(t)+2x(t)^TP_2D_1d(t)\nonumber \\&\quad +2x(t)^TP_2Q_1f(t). \end{aligned}$$

(31)

In the coming subsections, three concerned criteria are considered for the FD system design and the final theorem is presented based on the obtained results.

3.1 Disturbance Attenuation Level in Fault-Free Case

In fault-free case, i.e., $f=0$, the disturbance attenuation level in (10) must be satisfied. Thus, it can be written as:

$$\begin{aligned} r(t)^Tr(t)-\mu ^2 d(t)^Td(t) \le 0. \end{aligned}$$

(32)

Based on [2], we have:

$$\begin{aligned}&(HCe(t)+HM_2FN_2x(t)+HD_2d(t))^T(HCe(t)+HM_2FN_2x(t)\nonumber \\&\quad +HD_2d(t)) -\mu ^2 d(t)^Td(t) + \dot{V} \le 0. \end{aligned}$$

(33)

By simplifying the first term of (32), i.e., $r(t)^Tr(t)$, we have:

$$\begin{aligned} r(t)^Tr(t)= & {} e(t)^TC^TH^THCe(t)+e(t)^TC^TH^THM_2FN_2x(t)\nonumber \\&+e(t)^TC^TH^THD_2d(t)+x(t)^TN^T_2F^TM^T_2H^THCe(t)\nonumber \\&+x(t)^TN^T_2F^TM^T_2H^THM_2FN_2x(t)+x(t)^TN^T_2F^TM^T_2H^THD_2d(t)\nonumber \\&+d(t)^TD^T_2H^THCe(t)+d(t)^TD^T_2H^THM_2FN_2x(t)\nonumber \\&+d(t)^TD^T_2H^THD_2d(t). \end{aligned}$$

(34)

By applying the previous lemma, the upper bound of (34) is given as:

$$\begin{aligned} r(t)^Tr(t)\le & {} e(t)^TC^TH^THCe(t)+ e(t)^TC^TH^THM_2FN_2x(t)\nonumber \\&+e(t)^TC^TH^THD_2d(t)+x(t)^TN^T_2F^TM^T_2H^THCe(t)\nonumber \\&+d(t)^TD^T_2H^THD_2d(t)+x(t)^TN^T_2F^TM^T_2H^THM_2FN_2x(t)\nonumber \\&+x(t)^TN^T_2F^TM^T_2H^THD_2d(t)+d(t)^TD^T_2H^THCe(t)\nonumber \\&+d(t)^TD^T_2H^THM_2FN_2x(t). \end{aligned}$$

(35)

It should be stated that for using the aforementioned lemma, the following condition must be satisfied, which is a reachable condition and can be achieved by proper selection of the weighting matrix H.

$$\begin{aligned} ||F^TM^T_2H^THM_2F|| \le I. \end{aligned}$$

This condition is imposed by the following equation.

$$\begin{aligned}&x(t)^TN^T_2F^TM^T_2H^THM_2FN_2x(t)=x(t)^TN^T_2\acute{F}N_2x(t)\nonumber \\&\quad \le x(t)^TN^T_2N_2x(t)+x(t)^TN^T_2N_2x(t)=2x(t)^TN^T_2N_2x(t), \end{aligned}$$

(36)

where $\acute{F}$ is also an unknown time-varying matrix satisfying $||\acute{F}(t)||_2 \le I~ \forall t \in [0,\infty )$.

Therefore, we have:

$$\begin{aligned} r(t)^Tr(t)-\mu ^2 d(t)^Td(t)+\dot{V} \le 0. \end{aligned}$$

(37)

By substituting the upper bound of $r(t)^Tr(t)$ as (35) and $\dot{V}$ as (31) in (32), we have:

$$\begin{aligned}&e(t)^T(-Q+\gamma ^2I+P_1J_1J_1^TP_1+GJ_2J_2^TG^T+C^TH^THC\nonumber \\&\quad +2C^TH^THM_2M_2^TH^THC)e(t)+x(t)^T(A^TP_2+P_2A+P_2J_1J_1^TP_2\nonumber \\&\quad +2N_1N_1^T+\gamma ^2I+7N_2^TN_2)x(t)+2e(t)^T(P_1D_1-P_1LD_2+C^TH^THD_2)d(t)\nonumber \\&\quad +2x(t)^TP_2D_1d(t)+ d(t)^T(2D_2^TH^THM_2M_2^TH^THD_2\nonumber \\&\quad +D_2^TH^THD_2-\mu ^2I)d(t) \le 0. \end{aligned}$$

(38)

By writing (38) in matrix inequality form, a nonlinear matrix inequality is achieved. Finally, by using (38) and Schur complement, the linear form of matrix inequality may be obtained as follows.

$$\begin{aligned} LMI(1): \left[ \begin{array}{ccc} \Omega _{11} &{}\quad 0 &{} \quad \Omega _{13}\\ * &{} \quad \Omega _{22} &{} \quad \Omega _{23}\\ * &{}\quad * &{} \quad \Omega _{33}\\ \end{array} \right] \le 0, \end{aligned}$$

(39)

where

$$\begin{aligned}&\Omega _{11}= \left[ \begin{array}{cccc} \Pi &{} \quad \gamma I &{} \quad P_1J_1 &{} \quad GM_2\\ * &{} \quad -I &{} \quad 0 &{}\quad 0\\ * &{} \quad * &{}\quad -I &{}\quad 0\\ * &{}\quad * &{}\quad * &{}\quad -I\\ \end{array} \right] , \end{aligned}$$

(40)

$$\begin{aligned}&\Omega _{22}= \left[ \begin{array}{ccc} A^TP_2+P_2A+2N_1N^T_1+7N_2N^T_2 &{} \quad \gamma I &{} \quad P_2J_1\\ * &{}\quad -I &{}\quad 0\\ * &{}\quad * &{}\quad -I\\ \end{array} \right] , \end{aligned}$$

(41)

$$\begin{aligned}&\Omega _{13}=\left[ \begin{array}{c} P_1D_1-GD_2+C^TH^THD_2\\ 0\\ 0\\ 0\\ \end{array} \right] , \end{aligned}$$

(42)

$$\begin{aligned}&\Omega _{23}=\left[ \begin{array}{c} P_2D_1 \\ 0\\ 0\\ \end{array} \right] , \end{aligned}$$

(43)

$$\begin{aligned}&\Omega _{33}=D^TH^THD_2 + 2 D^T_2H^THM_2M^T_2H^THD_2-\alpha I, \end{aligned}$$

(44)

$$\begin{aligned}&\Pi = -Q+C^TH^THC+2C^TH^THM_2M^T_2H^THC. \end{aligned}$$

(45)

The linear matrix inequality is achieved by assuming a new parameter $\alpha$ as the squared value of $\mu$.

3.2 Fault Sensitivity Criterion Based on $H_-$ Index

In order to satisfy the fault sensitivity criterion in the FD system, $H_-$ index is used in this paper. As in [7], enhanced fault sensitivity based on $H_-$ index leads to an increase in fault detection rate (FDR), which is defined as (46).

$$\begin{aligned} FDR=\frac{\beta \delta _{fmin}}{J_{th}}, \end{aligned}$$

(46)

where $J_{th}$ is a predefined threshold, $\delta _{fmin}$ is the minimum size of f which is defined as the fault to be detected, and $\beta$ is called the $H_-$ index with assumption that there is no disturbance and uncertainties in the system [10].

$H_-$ index is defined in the form of (47) as mentioned in [18].

$$\begin{aligned} \beta =\mathop {inf}_{f \ne 0}~ \frac{||r||_2}{||f||_2}. \end{aligned}$$

(47)

In other words, the following equation must be satisfied with the assumption that there is no disturbance and uncertainties in the system [10].

$$\begin{aligned} r(t)r(t)^T-\beta ^2 f(t) f(t)^T \ge 0. \end{aligned}$$

(48)

The Lyapunov function in this case is contemplated as (49), which is negative semi-definite.

$$\begin{aligned} V=-e(t)^TP_1e(t) \le 0. \end{aligned}$$

(49)

It can be achieved that:

$$\begin{aligned} r(t)r(t)^T-\beta ^2 f(t) f(t)^T+\dot{V} \ge 0. \end{aligned}$$

(50)

By substituting $\dot{V}$ and (35) in the absence of uncertainty and disturbance and the presence of fault in (50), the subsequent matrix inequality may be obtained.

$$\begin{aligned} \left[ \begin{array}{cc} \Lambda &{}\quad C^TH^THQ_2-P_1Q_1+GQ_2 \\ * &{}\quad Q^T_2H^THQ_2-\beta ^2 I \\ \end{array} \right] \ge 0, \end{aligned}$$

(51)

where

$$\begin{aligned} \Lambda =C^TH^THC-P_1A-A^TP_1+GC+C^TG^T -\gamma ^2 I-P_1P_1. \end{aligned}$$

(52)

The following LMI is achieved by using Schur complement and some simplifications in (51), which defines the fault sensitivity criterion.

$$\begin{aligned} LMI(2): \left[ \begin{array}{cccc} \Xi _{11} &{}\quad \gamma I &{} \quad P_1 &{} \quad \Xi _{14}\\ * &{} \quad -I &{}\quad 0 &{}\quad 0 \\ * &{}\quad * &{}\quad -I &{}\quad 0\\ * &{} \quad * &{}\quad * &{}\quad \Xi _{44} \\ \end{array} \right] \le 0, \end{aligned}$$

(53)

in which

$$\begin{aligned} \Xi _{11}= & {} P_1A+A^TP_1-GC-C^TG^T-C^TH^THC. \end{aligned}$$

(54)

$$\begin{aligned} \Xi _{14}= & {} -C^TH^THQ_2+P_1Q_1-GQ_2. \end{aligned}$$

(55)

$$\begin{aligned} \Xi _{44}= & {} -Q^T_2H^THQ_2+\tau I. \end{aligned}$$

(56)

$$\begin{aligned} \tau= & {} \beta ^2. \end{aligned}$$

(57)

3.3 Lipschitz Constant Maximization

The previous methods on the fault detection for the Lipschitz nonlinear systems rely on a fixed Lipschitz constant, which may be obtained from the nonlinear term of the state space representation of the system. This nonlinear term, and subsequently the considered Lipschitz constant, may also contain some uncertainties due to the fact that this value is dependent on the parameters of the system, which may lead to false and missed alarms in the FD system. In this paper, the FD system is obtained by maximization of the Lipschitz constant which indicates the more robustness of the proposed method. In other words, the fixed obtained value for the Lipschitz constant is considered as the minimum value of the unknown Lipschitz constant. The maximized Lipschitz constant, in which the larger values mean the more robustness against nonlinear uncertainties, is obtained by solving the multi-objective optimization problem.

3.4 Final Theorem

Finally, by considering the results of three previous subsections, the following theorem can be achieved.

Theorem

Consider the uncertain Lipschitz nonlinear system (1)–(2) along with the observer as (5). The state estimation error dynamics (8) are asymptotically stable with a predefined decay rate, and the output estimation error satisfies $||r(t)||_2 \le \mu ||d(t)||_2$ and $||r(t)||_2 \ge \beta ||f(t)||_2$ for any nonzero $d \in l _2[0,\infty )$ if there exist scalars $\alpha >0$ , $\tau > 0$, $\gamma > 0$ and matrices $P_1>0$, $P_2>0$ and G such that the following LMI optimization problem has solution.

$$\begin{aligned}&\mathbf{min } ((1-W)\alpha -W(\tau +\gamma ))\\&\quad \quad \hbox {subject to:}\\&LMI(1) \le 0 , LMI(2) \le 0\\&||F^TM^T_2H^THM_2F|| \le I, \end{aligned}$$

where $0 \le W \le 1$ is defined as the weighting factor of the optimization problem, whose value is obtained by minimization of the following cost function.

$$\begin{aligned} J=\min _W \frac{k_1 \mu }{k_2 \beta +k_3 \gamma }, \end{aligned}$$

where $k_1$, $k_2$ and $k_3$ are used to place more or less emphasis on the considered criteria and may be selected based on the studied system.

Finally, the desired values of the unknown parameters are obtained as follows.

$$\begin{aligned} \mu =\sqrt{\alpha } , L=P^{-1}_1 G , \beta = \sqrt{\tau }. \end{aligned}$$

The maximized Lipschitz constant ($\gamma$ ) is also achieved from the optimization problem, which means that the FD system is robust against all Lipschitz nonlinear terms in (1) that have the Lipschitz constant equal to or less than obtained $\gamma$ . Note that the obtained constraint in the theorem will be satisfied by proper selection of matrix H. Then, the other parameters can be calculated by solving the LMI optimization problem.

4 Simulation Results

A numerical example as in [7] is given in this section to illustrate the performance of the proposed method. The simulation results of the proposed method for an active suspension system are given in Appendix of the paper as well. The development of a method to derive the optimal values of $k_1$ to $k_3$ for an experimental setup of the active suspension system is considered as the future work of the proposed method.

4.1 System Description and Obtained Results

The state space representation of the system is given by:

$$\begin{aligned}&A=\left( \begin{array}{ccc} -\,6.5 &{}\quad 3.9 &{} \quad 5.2 \\ 0 &{}\quad -\,9.1 &{}\quad 3.9 \\ 1.3 &{}\quad 3.9 &{}\quad -\,7.8 \\ \end{array} \right) , C=\left( \begin{array}{ccc} 1 &{}\quad 2 &{}\quad -\,1 \\ 2 &{}\quad -\,1 &{}\quad 3 \\ \end{array} \right) , \psi (x,u)=\left( \begin{array}{c} 0.5 \sin x \\ 0.5 \cos x \\ 0 \\ \end{array} \right) \\&M_1=\left( \begin{array}{c} 0.2 \\ 0.3 \\ 0.15 \\ \end{array} \right) , N_1=\left( \begin{array}{ccc} 0.25 &{}\quad 0.1 &{}\quad 0.33 \\ \end{array} \right) , M_2=\left( \begin{array}{c} 0.38 \\ 1 \\ \end{array} \right) ,\nonumber \\&N_2=\left( \begin{array}{ccc} 0.25 &{}\quad 0.1 &{}\quad 0.33 \\ \end{array} \right) \\&D_1=\left( \begin{array}{ccc} -\,0.3 &{} \quad 1 &{}\quad 0.6 \\ 0 &{}\quad 0.3 &{}\quad 0.5 \\ 0.4 &{}\quad 0 &{}\quad -\,0.2 \\ \end{array} \right) , D_2=\left( \begin{array}{ccc} 0.7 &{}\quad 1 &{}\quad -\,0.3 \\ 0 &{}\quad 0.6 &{}\quad 0.2 \\ \end{array} \right) \\&Q_1=\left( \begin{array}{cc} 1.3 &{}\quad 0.65 \\ -\,0.390 &{}\quad 1.04 \\ 0.78 &{}\quad -\,1.17 \\ \end{array}\right) , Q_2=\left( \begin{array}{cc} 1.6 &{}\quad 0 \\ 0 &{} \quad -\,1.6 \\ \end{array}\right) . \end{aligned}$$

Other parameters of the FD system design including the decay rate of the observer and weighting matrix on the residuals are considered as:

$$\begin{aligned} \upsilon = 0.55 , H=\left( \begin{array}{cc} 0.18 &{}\quad 0.18\\ 0.36 &{}\quad 0.18\\ -\,0.18 &{}\quad 0.36\\ \end{array} \right) . \end{aligned}$$

The fixed Lipschitz constant of the system is given as 0.5. The obtained results for the FD system without considering the maximization of the Lipschitz constant are valid for any nonlinearity which satisfies this value for $\psi (x,u)$.

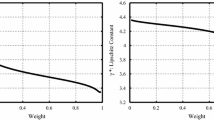
The obtained results of the theorem for different weighting factors of the optimization problem are given in Figs.1 and 2.

Fig. 1

Different criteria of the optimization problem versus weighting factor

Fig. 2

Optimal trade-off curves

The optimal value of the weighting factor is obtained as $W=0.4$ by assuming $k_1=2, k_2=0.5$ and $k_3=1$, which means the more emphasis on the fault sensitivity and disturbance attenuation in comparison with the Lipschitz constant. The following results are obtained by assuming the above-mentioned parameters.

$$\begin{aligned} P_1= & {} \left( \begin{array}{ccc} 2.8643 &{}\quad -\,1.7311 &{}\quad -\,1.2421 \\ -\,1.7311 &{} \quad 2.9924 &{} \quad 2.5429 \\ -\,1.2421 &{}\quad 2.5429 &{} \quad 4.7105 \\ \end{array} \right) ,\\ P_2= & {} \left( \begin{array}{ccc} 2.3973 &{} \quad -\,2.7380 &{}\quad -\,1.4343 \\ -\,2.7380 &{} \quad 9.6380 &{} \quad -\,0.6920 \\ -\,1.4343 &{}\quad -\,0.6920 &{} \quad 5.3254 \\ \end{array} \right) \\ G= & {} \left( \begin{array}{cc} 2.3767 &{}\quad -\,0.7859 \\ -\,0.8727 &{} \quad 0.8834 \\ 0.5243 &{} \quad 1.8861 \\ \end{array} \right) , L= \left( \begin{array}{cc} 0.9544 &{} \quad -\,0.2045 \\ -\,0.0886 &{} \quad -\,0.2171 \\ 0.4108 &{} \quad 0.4637 \\ \end{array} \right) \\ \gamma ^*= & {} 1.1302 , \mu =1.0770 , \beta = 0.6249. \end{aligned}$$

The admissible Lipschitz constant is obtained as 1.1302 by the proposed method, which means that it is improved by a factor of 2.26. In other words, the proposed FD system is robust against any nonlinearity that satisfies the maximized Lipschitz constant, which means the better performance and more robustness of the proposed method.

The given system is simulated in MATLAB/Simulink platform in normal and faulty situations taking into account the results of the theorem. The disturbance is simulated as a sine wave as (58) for $d_1$.

$$\begin{aligned} d_1(t)=0.25\sin {(10t)}u(t). \end{aligned}$$

(58)

$d_2$ and $d_3$ are also simulated as a step signal of amplitude 0.5 at $t=0$ and a signal which takes value randomly from a uniform distribution between $[-\,0.1,0.1]$, respectively.

The initial states of the system and the observer are assumed as:

$$\begin{aligned} x_{Obs}^T(0)=\left( \begin{array}{ccc} 0 &{}\quad -\,3 &{}\quad 2\\ \end{array} \right) , x_{Plant}^T(0)=\left( \begin{array}{ccc} 5 &{}\quad 1 &{}\quad -\,2\\ \end{array} \right) . \end{aligned}$$

The residuals are evaluated using (59).

$$\begin{aligned} J_L(t)=\sqrt{\int ^{t_0+L_W}_{t_0}r(t)^Tr(t)dt}, \end{aligned}$$

(59)

where $t_0$ is the initial sample and $L_W$ is the window length of the residuals. The above integral is calculated by trapezoidal rule for a moving fixed length window of the residuals. The simulation results are given for $t_0=0$ and $L_W=20$ samples.

The threshold on the residual evaluation function is assumed as fixed values as follows [34]:

$$\begin{aligned} J_{th}=\sup _{d(t),u(t) \in l_2,f(t)=0} J_L(t). \end{aligned}$$

(60)

4.2 Normal Situation

In fault-free case, the obtained results for the residuals and their evaluation functions in the presence of disturbances and parametric uncertainties are shown in Figs. 3 and 4, respectively.

Fig. 3

Residuals in fault-free case

Fig. 4

Residuals evaluation in fault-free case

The obtained thresholds are tabulated in Table 1.

4.3 Faulty Situation

Different fault scenarios can be simulated to demonstrate the effectiveness of the proposed FD system. In this paper, two scenarios are investigated.

In the first scenario, an abrupt fault is injected in the system at $t=6s$, which is simulated as a step signal of amplitude 0.5 in $f_2$. The simulated results of the residual evaluation functions are plotted in Fig. 5.

Table 1 Thresholds of the FD system

Fig. 5

Residuals evaluation in the first scenario (abrupt fault in $f_2$)

As can be observed from the figure, the injected fault can be detected in an efficient manner by using constant thresholds on the evaluation functions of the residuals. The FD system satisfies different criteria associated with robustness of the FD system against disturbance, parametric uncertainties and uncertainty in the Lipschitz constant as well. The considered fault can be detected using the third residual ($r_3$), which can be used for fault isolation purposes.

In the second scenario, an incipient fault is injected in the system, which is simulated as a ramp signal of $f_1$ as shown in Fig. 6.

Fig. 6

Injected incipient fault of $f_1$ in the second scenario

The evaluation function of the residuals is depicted in Fig. 7.

Fig. 7

Residual evaluation in the second scenario (incipient fault in $f_1$)

As shown in Fig. 7, the fault occurrence is declared due to exceeded residuals from the predefined thresholds in both $r_1$ and $r_2$. The residual $r_3$ is not sensitive to $f_1$ fault, which can be used for fault isolation purpose.

4.4 Robustness Against Nonlinear Uncertainties

In order to show the effectiveness of the proposed method, a comparison between the proposed method and the previous studies is made.

In the previous studies on the fault detection of the Lipschitz nonlinear systems based on the observer method, the fault sensitivity of the FD system is obtained for a given fixed disturbance attenuation level and fixed Lipschitz constant as well. Considering these assumptions, the observer gain for this example is obtained as follows:

$$\begin{aligned} L= \left( \begin{array}{cc} 0.5712 &{} 0.4187 \\ -\,0.4138 &{} 0.5462 \\ 0.6158 &{} -\,0.2219 \\ \end{array} \right) . \end{aligned}$$

The fixed thresholds on the residual evaluation function as (59) are given in Table 2.

Table 2 Thresholds on the residual evaluation without Lipschitz constant maximization

As can be seen from the table, the obtained thresholds are generally smaller than the corresponding values in Table 1, which indicates the less conservatism in the FD system design. The more conservatism of the proposed method is due to considering the nonlinear uncertainties, i.e., the uncertainty in the Lipschitz constant.

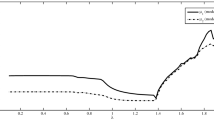
The simulation results show the effectiveness of the proposed method against nonlinear uncertainties. For a better comparison between the proposed method and the FD system without Lipschitz constant maximization, the obtained residuals and thresholds in the case that some nonlinear uncertainties are considered in the non-faulty system are depicted in Fig. 8.

Fig. 8

Comparison between residual evaluation in the proposed method and FD system without Lipschitz constant maximization in fault-free case in the presence of nonlinear term uncertainties

As shown in the figure, the FD system without Lipschitz constant maximization declared a fault occurrence in the system, while there is no fault in the system. In other words, the presence of nonlinear uncertainty leads to false alarm in the FD system.

Some remarks may be given from the simulation results as follows:

• There is a great sensitivity against the Lipschitz constant in the FD system design without Lipschitz constant maximization. In other words, any nonlinear uncertainty may lead to false alarm. This sensitivity is reduced in the proposed method by maximization of the Lipschitz constant in the observer design.

• The cost of this improvement by the proposed method may be stated as the greater thresholds on the residuals, which is compensated by enhanced fault sensitivity in the FD system design.

• The proposed method can also show great performance for linearized model of a system in the cases that the operating point of the system is changed.

• The proposed method satisfies simultaneous enhanced fault sensitivity and disturbance attenuation level.

• Some trade-off may be considered between desired criteria according to the studied system, which may be defined by setting appropriate values for $k_1$, $k_2$ and $k_3$ in the defined cost function J.

• The fault sensitivity criterion is a limit that can be clearly discriminated from disturbances or uncertainties in the system. The residuals are generated in a robust manner; therefore, setting fixed thresholds on the residual evaluation function is justifiable.

In this paper, the robust FD of the Lipschitz nonlinear systems is studied considering the different issues including disturbances, parametric uncertainties and faults. Although the robustness of the FD system against parametric uncertainties has been noticed in several studies for the Lipschitz nonlinear systems, the impact of these parametric uncertainties on the Lipschitz constant is not considered in the literature. As it is shown in the simulation results, the uncertainty in the Lipschitz constant, which may be due to the parametric uncertainties, will lead to false alarm in the FD system. This point may be stated as the main result of this study. The proposed method may be used for real-world examples in the Lipschitz nonlinear form such as active suspension system and single-link manipulator. The effect of parametric uncertainties on the performance of the FD system may be evaluated for such real systems.

It is also worth noting that the fault isolation can also be achieved by creating isolation logic table for different fault injection scenarios, which is not considered in this current paper. As an example, $r_1$ and $r_2$ exceeded their threshold in $f_1$ fault injection, while $r_3$ exceeded its threshold in $f_2$ fault injection, which can be used to isolate $f_1$ from $f_2$.

5 Conclusions

The optimal robust active fault detection for a class of uncertain Lipschitz nonlinear systems has been studied via observer-based approach. The FD system has been designed by considering different criteria such as disturbance attenuation level, enhanced fault sensitivity and FDR using $H_-$ index and also maximization of the Lipschitz constant.

The robustness of the FD system against nonlinear uncertainties has been obtained by maximization of the Lipschitz constant. The overall results have been presented as a weighted multi-objective LMI problem, wherein the observer has been designed by solving the obtained LMI using optimal selection of the parameters. The simulation results have shown that the effect of nonlinear uncertainties may lead to false alarm in the FD system. Although the proposed method has imposed some conservatism on the thresholds, the enhanced fault sensitivity may reduce this conservatism. The considered criteria including the presence of parametric and nonlinear uncertainties and disturbances are in accordance with practical cases. Different faults in abrupt or incipient natures can be detected in an efficient manner by using the predefined thresholds on the residual evaluation signal. The proposed FD system can be utilized for industrial applications that can be represented as uncertain Lipschitz nonlinear systems.

Appendix

In this section, the proposed method is applied to an active suspension system as a real-world system. The configuration of the system is depicted in Fig. 9.

Fig. 9

A quarter car model [15]

State space representation of the system is given by

$$\begin{aligned} \dot{x}(t)=\left( \begin{array}{cccc} 0 &{}\quad 0 &{}\quad 1 &{}\quad -\,1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ -\frac{k_s}{m_s} &{}\quad 0 &{}\quad -\frac{C_s}{m_s} &{}\quad \frac{C_s}{m_s} \\ \frac{k_s}{m_u} &{}\quad -\frac{k_t}{m_u} &{}\quad \frac{C_s}{m_u} &{}\quad -\frac{C_s+C_t}{m_u} \\ \end{array} \right) x(t)+ \left( \begin{array}{c} 0\\ -\,1\\ 0\\ \frac{C_t}{m_u}\\ \end{array} \right) w(t)+\left( \begin{array}{c} \psi _1 \\ \psi _2 \\ \frac{1}{m_s}u+\psi _3 \\ -\frac{1}{m_u}+\psi _4\\ \end{array} \right) \end{aligned}$$

(61)

$$\begin{aligned} y(t)=\left( \begin{array}{cccc} 1 &{}\quad 0 &{}\quad 0 &{} \quad 0 \\ 0 &{}\quad \frac{k_t}{(m_s+m_u)g} &{}\quad 0 &{}\quad 0\\ \end{array} \right) x(t). \end{aligned}$$

The states of the system are defined as suspension deflection, tire deflection, sprung mass speed and unsprung mass speed, respectively, which are represented as the following equations.

$$\begin{aligned} x_1(t)= & {} z_x(t)-z_u(t), \end{aligned}$$

(62)

$$\begin{aligned} x_2(t)= & {} z_u(t)-z_r(t), \end{aligned}$$

(63)

$$\begin{aligned} x_3(t)= & {} \dot{z}_s(t), \end{aligned}$$

(64)

$$\begin{aligned} x_4(t)= & {} \dot{z}_u(t). \end{aligned}$$

(65)

Disturbance is considered as

$$\begin{aligned} w(t)=\dot{z}_r(t), \end{aligned}$$

(66)

which is simulated as follows.

$$\begin{aligned} w(t)=0.05 \sin t. \end{aligned}$$

(67)

The nonlinear term of the state space equation is defined as the subsequent equation.

$$\begin{aligned} \psi (t)=\left( \begin{array}{c} 0.09 \sin t \\ 0.04 \cos t \\ 0.07 \sin t \\ 0.01 \sin t \\ \end{array} \right) . \end{aligned}$$

(68)

According to [15], the parameters of the system, their definition and considered values of the active suspension system are tabulated in Table 3.

Table 3 Parameters of active suspension system

By using the values in the table, the matrices of the system can be obtained as:

$$\begin{aligned} A=\left( \begin{array}{cccc} 0 &{}\quad 0 &{}\quad 1&{}\quad -\,1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ -\,43.905 &{}\quad 0 &{} \quad -\,1.125 &{} \quad 1.125 \\ 374.736 &{} \quad -\,886.973 &{} \quad 9.605 &{} \quad -\,9.733 \\ \end{array} \right) . \end{aligned}$$

The disturbance and fault distribution matrices are defined as:

$$\begin{aligned} D_1= & {} \left( \begin{array}{c} 0.3 \\ 0.6 \\ 0.1 \\ 0.4 \\ \end{array} \right) , Q_1=\left( \begin{array}{cc} 0 &{} \quad 0.4 \\ 0.8 &{} \quad 0.8 \\ 0.7 &{} \quad 0 \\ 0.3 &{} \quad 0.6 \\ \end{array} \right) \\ D_2= & {} \left( \begin{array}{c} 0.4 \\ 0.5 \\ \end{array} \right) , Q_2=\left( \begin{array}{cc} 0.7 &{} 0.5 \\ -\,0.6 &{} 0.5 \\ \end{array} \right) . \end{aligned}$$

Two actuator and sensor faults are considered for the system. The disturbance distribution matrices are assumed as $D_1$ and $D_2$ that is different from (61), which is considered for more strict conditions wherein disturbance can influence all states of the system instead of $x_2$ and $x_4$. It is also worth noting that the selection of disturbance and fault distribution matrices has a direct effect on the disturbance attenuation level, fault sensitivity and achievable Lipschitz constant as well.

The parametric uncertainties in the matrices of the system in (61) are assumed as follows.

$$\begin{aligned} M_1= & {} \left( \begin{array}{cccc} 0.11 &{}\quad -\,0.04 &{} \quad 0.02 &{} \quad 0.11 \\ 0.15 &{} \quad 0.13 &{} \quad 0.12 &{} \quad 0.02\\ 0.0.1 &{} \quad -\,0.11 &{} 0.03 &{} \quad 0.04 \\ 0.03 &{} \quad -\,0.08 &{} \quad 0.11 &{} \quad -\,0.06 \\ \end{array} \right) \\ N_1= & {} \left( \begin{array}{cccc} 0.063 &{} \quad -\,0.055 &{} \quad 0.074 &{} \quad 0.094 \\ 0.015 &{} \quad 0.012 &{} \quad 0.011 &{} \quad 0.064\\ 0.073 &{} \quad -\,0.101 &{} \quad 0.043 &{} \quad 0.045 \\ 0.034 &{} \quad -\,0.028 &{} \quad 0.083 &{} \quad -\,0.061 \\ \end{array} \right) \\ M_2= & {} \left( \begin{array}{c} 0.38 \\ 0.1\\ \end{array} \right) , N_2=\left( \begin{array}{cccc} 0.15 &{} \quad 0.1 &{} \quad 0.13 &{} \quad 0.1 \\ \end{array} \right) . \end{aligned}$$

The parameters for the observer design are considered as:

$$\begin{aligned} \beta = 0.29, H=\left( \begin{array}{cc} -\,0.18 &{}\quad 0.35 \\ -\,0.35 &{} \quad 0.28 \\ -\,0.35 &{} \quad 0.70 \\ 0.35 &{} \quad 0.11 \\ \end{array} \right) . \end{aligned}$$

The obtained results of the theorem for different weighting factors of the optimization problem are given in Figs. 10 and 11.

Fig. 10

Different criteria of the optimization problem versus weighting factor

Fig. 11

Optimal trade-off curves

The optimal value for the weighing factor is obtained as $W=0.9$. One can obtain the following optimal values by solving the LMI problem.

$$\begin{aligned} \mu =0.926 , \gamma =0.091 , \beta =0.237. \end{aligned}$$

The observer gain is achieved as:

$$\begin{aligned} L=\left( \begin{array}{cc} -\,0.193 &{} \quad 0.750 \\ 0.243 &{} \quad 1.411 \\ 1.669 &{} \quad 0.119 \\ 2.365 &{} \quad -\,0.582 \\ \end{array} \right) . \end{aligned}$$

The given values are obtained for $k_1=k_2=k_3=1$. The optimal values of these coefficients and validation of the proposed method for an experimental setup are considered as future works of this study.