Re-examining the effects of switching costs

Abstract

Consumers often incur costs when switching from one product to another. Recently, there has been renewed debate within the literature about whether these switching costs lead to higher prices. We build a theoretical model of dynamic competition and solve it analytically for a wide range of switching costs. We provide a simple condition which determines whether switching costs raise or lower long-run prices. We also show that even if switching costs reduce prices in the long run, they may still increase prices in the short run. Finally, switching costs redistribute surplus across time, and as such are shown to sometimes increase consumer welfare.

1 Introduction

In many markets, consumers incur costs if they switch from the product they currently purchase to another product sold by a different company. For example, in the US auto insurance industry, Honka (2013) estimates an average switching cost of $116, whilst in the US pay-TV market Shcherbakov (2009) estimates switching costs of $109 for cable and $186 for satellite. These amount to, respectively, 20, 32 and 52 % of what a typical consumer would spend annually on these products. Evidence of significant switching costs has also been found in several other industries, including cell phones and bank deposits (Shy 2002) and also domestic gas (Giulietti et al. 2005).

Switching costs partially lock consumers to their initial supplier, creating the well-known trade-off between ‘harvesting’ and ‘investing’. On the one hand, a firm might charge a high price and harvest its existing customers, exploiting their reluctance to switch. On the other hand, since consumers tend not to switch, there is a strong relationship between current market share and future profitability. A firm might therefore prefer to invest in market share by charging a low price. The conventional wisdom has been that the harvesting effect dominates, such that switching costs increase prices (Farrell and Klemperer 2007). Such wisdom typically draws on two-period models, in which firms offer ‘bargains’ to consumers when they are young, and ‘rip-offs’ when they become old. However, one drawback of these models is that they artificially separate out the investment and harvesting motives into the first and second periods, respectively. In reality, firms often compete over a long time horizon and at any moment are trying to both attract new consumers and sell to old ones. Therefore, the subsequent literature has emphasized models with infinite horizons and has offered some findings where small switching costs can reduce prices.

In this paper, we re-examine the effect of switching costs on prices, profits and consumer surplus within a more general model of dynamic competition. This approach has several distinctive features. Firstly, in contrast to other papers which typically focus only on very small or very large switching costs, or which use numerical simulations, it permits analytical results for a very wide range of switching costs. Secondly, it also allows both firms and consumers to be forward-looking, whereas many other papers make the restrictive assumption that consumers are myopic. Thirdly, it allows us to study the impact of switching costs in both the short run and long run, whereas the existing literature has tended to focus only on the latter. Distinguishing between the two is important—we show that switching costs can affect prices differently, depending upon the time horizon considered. Finally, it enables us to consider how switching costs affect not only prices but also welfare. To this end, we provide a novel explanation for why switching costs can be beneficial to consumers.

In more detail, the model considers two infinitely lived firms who sell to overlapping generations of consumers. In each period, the market is covered and product differentiation is modelled using a linear Hotelling line. Linearity is important because it enables us to find a closed form solution for equilibrium prices. It also allows us to be very general in other dimensions. In particular, all agents in the model—including consumers—are forward-looking, and we are able to state our results for very general levels of the switching cost. We first show that the impact of switching costs on steady state prices is almost always ambiguous and depends upon how patient consumers are relative to firms. We then derive a necessary and sufficient condition for when switching costs are pro-competitive, and show that it is satisfied unless consumers are significantly more patient than firms. The intuition, which we expand upon below, is that a firm’s incentive to ‘lock-in’ consumers far outweighs a consumer’s incentive to avoid being locked in. We therefore find a general presumption that in the long run, switching costs make markets more competitive.

In the short run, the relationship between switching costs and prices is generally more complicated and has rarely been studied within the previous literature. Additional complexities arise because firms may start with unequal market shares, and therefore have different pricing incentives. Compared with what happens in the long run, the firm with larger market share charges a higher price, whilst the firm with the smaller market share charges a lower price. This implies that the average (i.e. consumption weighted) price can initially be quite high. However, over time firms’ market shares become more symmetric, and the average price decreases monotonically. We provide a condition which determines whether average price is higher with switching costs than without. We also demonstrate that switching costs can be anti-competitive in the short run and yet pro-competitive in the long run.

It is natural to ask whether switching costs can reduce prices by so much that they actually benefit consumers. Young consumers gain if switching costs reduce prices. However, old consumers always lose out—they bear the brunt of switching costs and are never fully compensated for this by any price reductions. Therefore, switching costs have a tendency to transfer surplus from the old to the young. When consumers have a preference for current over future consumption, this transfer is beneficial. Consequently for a wide range of parameters, a consumer’s lifetime expected surplus is larger with switching costs than without.

Our modelling approach is most closely related to papers by Beggs and Klemperer (1992), To (1996), Doganoglu (2010), Somaini and Einav (2013) and Fabra and García (2014). They also use Hotelling-style models and, with the exception of the first and last papers, have overlapping generations of consumers. Beggs and Klemperer (1992) and To (1996) restrict attention to a special case where switching costs are so high that no consumer ever actually switches. They both find that steady state prices are higher compared to a market that has no switching cost.¹ Doganoglu (2010) restricts attention to another special case where switching costs are very low. Using a model of experience goods, he shows that starting from zero, a small increase in the switching cost leads to a decrease in the steady state price. Our approach in this paper is very different, because we solve our model for a considerably wider range of switching costs. We show that away from the two extremes which these other papers focus on, the impact of switching costs on prices is ambiguous. We then derive and interpret a condition on parameters which determines whether that impact is positive or negative. Somaini and Einav (2013) solve a model which is even more general than ours, and which allows for cost asymmetries and many (potentially multiproduct) firms. However, they are interested in antitrust policy in dynamic markets, rather than in determining analytically how switching costs affect prices and welfare. We also note that by working with a simplified version of their model, we are able to derive all our main results analytically and are able to go beyond looking at just steady state outcomes. Finally, Fabra and García (2014) develop a continuous-time model, in which consumers randomly have the opportunity to switch firms. Like us the authors also distinguish between the short run and the long run. They find that switching costs can lead to higher prices in the short run, if firms’ market shares are sufficiently asymmetric.

Several other recent papers are also related. Cabral (2014) proves that switching costs can lead to lower prices, and like us he shows this for a wide range of switching costs. However, in his model firms can price discriminate. This means that, for the most part, consumers behave myopically when deciding which product to buy. As a result, an important effect in our model—namely consumers’ fear of becoming locked in to a high-price firm—is absent from his model. Arie and Grieco (2014) show that firms with low market shares are more likely to be harmed by small switching costs, and to respond by reducing their price. Using a logit model, Pearcy (2014) derives a closed form solution for steady state prices and shows that switching costs are more likely to be pro-competitive in markets that have many firms. Finally, Bouckaert et al. (2012) and Biglaiser et al. (2013) explore the consequences of heterogeneity in switching costs. They show that an increase in the distribution of switching costs can lead to lower industry profits.

The paper proceeds as follows. Section 2 outlines the model, whilst Sect. 3 proves existence and uniqueness of an equilibrium in affine strategies. We then examine how switching costs affects prices and profits (in Sect. 4) and consumer surplus (in Sect. 5). Section 6 then checks the robustness of our results, whilst Sect. 7 concludes with some directions for future research. All omitted proofs are provided either in the Appendix, or in the working paper version (Rhodes 2014).

2 Model

Time is discrete and there are infinitely many periods, denoted by $t=1,2,\ldots$. There are two firms $A$ and $B$ that are located on a Hotelling line at positions $x=0$ and $x=1$, respectively. The marginal cost of production is normalized to zero for both firms. Each period a unit mass of new consumers is born, who then live for two periods before exiting the market. Consequently at any moment, there are (equal-sized) overlapping generations of ‘young’ and ‘old’ consumers in the economy. At the start of period $t$, each consumer is randomly assigned a location $x^{t}$ on the Hotelling line, which (for old consumers) is independent of their location in the previous period. A consumer with location $x^{t}$ values product $A$ at $V-x^{t}$ and product $B$ at $V-\left( 1-x^{t}\right)$. $V$ is sufficiently large that the market is always covered. If an ‘old’ consumer bought from firm $i$ when young but now wants to buy from firm $j\ne i$, she must incur a switching cost $s\in \left( 0,7/10\right]$.² As explained more fully below, we assume $s\le 7/10$ in order to ensure that in the equilibrium which we solve for, each firm always loses some of its past customers due to switching. Finally, consumers and firms are both risk-neutral and have discount factors $\delta _{c}$ and $\delta _{f}$, respectively, which lie in $\left( 0,1\right)$.

The share of young consumers who buy product $A$ in period $t$ is denoted by $\tilde{x}^{t}$ (Hence, $\tilde{x}^{t}$ also denotes the mass of old consumers who are ‘locked’ into firm $A$ at the start of period $t+1$, and who must pay a switching cost in order to buy the other product.). We assume that in the first period $\tilde{x}^{0}\in \left[ 0,1\right]$ old consumers are locked to firm $A$, whilst the remaining $1-\tilde{x}^{0}$ are locked to firm $B$. The timing of the model is as follows. In each period $t=1,2,\ldots$, the two firms simultaneously and non-cooperatively choose prices $p_{A}^{t}$ and $p_{B}^{t}$, in order to maximize their respective discounted sum of current and future profits. Firms cannot commit to any future prices. Consumers then observe $p_{A}^{t}$ and $p_{B}^{t}$ as well as their own personal location $x^{t}$. Young consumers buy whichever product maximizes their expected lifetime utility. Old consumers either stay with their initial supplier or pay the switching cost and buy from the competitor.

We focus on equilibria in Markov strategies, in which the past influences current prices only via its effect on a pay-off-relevant state variable. In our problem, the natural state variable for period $t$ is $\tilde{x}^{t-1}$. The solution concept used will be Markov perfect equilibrium (MPE). In more detail, we will conjecture (and then verify) existence of a MPE in which firms’ equilibrium prices are stationary, symmetric and linear functions of the state variable. Note that this is a restriction on equilibrium and not on strategy spaces. In particular when we verify subgame perfection of the proposed equilibrium strategies, we allow a firm to make an arbitrary (one-shot) deviation in its price. A couple of remarks are in order. Firstly, the Markovian restriction means that we rule out more collusive equilibria, in which firms may earn higher profits by conditioning their prices on the entire history of the game. Secondly, as is standard, our analysis does not rule out the possibility that there could exist other, nonlinear MPE as well.³

This is a simplified version of the set-up in Somaini and Einav (2013), which also allows for arbitrarily many firms whose marginal costs may differ. Their paper is primarily concerned with antitrust policy in markets with switching costs and does not analytically determine how these switching costs affect equilibrium prices and welfare. One advantage of our simpler set-up is that we are able to derive all our main results analytically. Our set-up is also isomorphic to Doganoglu (2010) when in our model $\delta _{c}=\delta _{f}$, and when in his model $\varDelta =2$ ($\varDelta$ is a parameter in his model which captures heterogeneity in consumers’ product valuations.). However, in his model firms sell experience goods, and therefore, consumers only learn their match with a product after consuming it. As such, the foundations of our two models are very different. In addition, Doganoglu focuses on comparative statics of the steady state price around the point $s=0$. Since our model does not have experience goods, we have one less parameter (namely $\varDelta$); this allows us to study prices both in and out of steady state, as well as consumer surplus, and we do this for all $s\in \left( 0,7/10\right]$.

3 Solving the model

As explained above, we look for MPE in which firms’ equilibrium prices are stationary, symmetric and linear functions of the state variable. In particular, we hypothesize that firms’ equilibrium prices are, respectively,

$$\begin{aligned} p_{A}^{t}\left( \tilde{x}^{t-1}\right)&= J+K\left( \tilde{x} ^{t-1}-1/2\right) \end{aligned}$$

(1)

$$\begin{aligned} p_{B}^{t}\left( \tilde{x}^{t-1}\right)&= J-K\left( \tilde{x} ^{t-1}-1/2\right) \end{aligned}$$

(2)

and that their equilibrium value functions can be expressed as

$$\begin{aligned} V_{A}^{t}\left( \tilde{x}^{t-1}\right)&= M+N\left( \tilde{x} ^{t-1}-1/2\right) +R\left( \tilde{x}^{t-1}-1/2\right) ^{2} \end{aligned}$$

(3)

$$\begin{aligned} V_{B}^{t}\left( \tilde{x}^{t-1}\right)&= M-N\left( \tilde{x} ^{t-1}-1/2\right) +R\left( \tilde{x}^{t-1}-1/2\right) ^{2} \end{aligned}$$

(4)

These equations can be interpreted as follows. When $\tilde{x}^{t-1}=1/2$, each firm sold to half of the young consumers born in period $t-1$. From period $t$ onwards, the two firms are symmetric, each charging the same price $J$ and earning the same discounted profits $M$. When instead $\tilde{x}^{t-1}>1/2$, firm $A$ sold to more than half of young consumers in period $t-1$. We prove later on that $K$ and $N$ are both positive. Therefore, whenever $\tilde{x} ^{t-1}>1/2$, firm $A$ charges a higher price in period $t$ than firm $B$ and also enjoys higher discounted profits.

Consider an arbitrary period $t$, and fix the state variable $\tilde{x} ^{t-1}$. To begin with, let us suppose that in period $t$, the two firms charge (potentially off-path prices) $p_{A}$ and $p_{B}$, respectively. Let us also suppose that both firms are expected to play the equilibrium pricing strategies (1) and (2) from period $t+1$ onwards. Given these assumptions, we now solve for each firm’s demand in period $t$.

Behaviour of old consumers Suppose an old consumer bought product $A$ when she was young. When old, she can again buy $A$ and enjoy a surplus $V-x^{t}-p_{A}$, or she can switch to product $B$ and get $V-\left( 1-x^{t}\right) -p_{B}-s$. Therefore, buying $A$ again is optimal if and only if $x^{t}\le \dot{x}^{t}=\left( 1+p_{B}-p_{A}+s\right) /2$. Similarly, an old consumer who bought $B$ when she was young optimally switches to $A$ if and only if $x^{t}\le \ddot{x}^{t}=\left( 1+p_{B}-p_{A}-s\right) /2$. We will show that since the switching cost is not too large, in equilibrium $\dot{x}^{t},\ddot{x}^{t}\in \left( 0,1\right)$, i.e. generically each firm has some consumers switching away from it and others switching towards it.

Behaviour of young consumers Consumers born in period $t$ form expectations about the prices they will face in the following period. For now, let us simply denote these price expectations by $Ep_{A}^{t+1}$ and $Ep_{B}^{t+1}$. If a young consumer buys $A$, she gets an immediate pay-off $V-x^{t}-p_{A}$; when old, she will stay with $A$ and get $V-x^{t+1}-Ep_{A}^{t+1}$ if $x^{t+1}$ is sufficiently low, otherwise she will switch to $B$ and get $V-\left( 1-x^{t+1}\right) -Ep_{B}^{t+1}-s$. Taking an expectation over all possible values of $x^{t+1}$, the young consumer can calculate her expected lifetime pay-off from buying product $A$. She can similarly calculate the expected utility from product $B$ and buys whichever product is best.

Lemma 1

In any period $t$, there exists a threshold $\tilde{x}^{t}$ such that young consumers with location $x^{t}\le \tilde{x} ^{t}$ buy product $A$, and young consumers with location $x^{t}>\tilde{x} ^{t}$ buy product $B$. The threshold is

$$\begin{aligned} \tilde{x}^{t}=\frac{1}{2}+\frac{p_{B}-p_{A}+\delta _{c}s\left( Ep_{B}^{t+1}-Ep_{A}^{t+1}\right) }{2} \end{aligned}$$

(5)

Young consumers located at $\tilde{x}^{t}$ expect to get the same lifetime utility from both products and are therefore indifferent between them. People located to the left (respectively, the right) of $\tilde{x}^{t}$ have a stronger initial preference for product $A$ (respectively, product $B$ ) and therefore buy it.

It only remains to specify how consumers form price expectations. Recall from above that by assumption, even if consumers observe prices in period $t$ which are off the equilibrium path, these consumers still believe that firms will use the equilibrium pricing strategies (1) and (2) from period $t+1$ onwards. In other words, we assume that regardless of $p_{A}$ and $p_{B}$, consumers expect to pay $Ep_{A}^{t+1}=J+K\left( \tilde{x }^{t}-1/2\right)$ and $Ep_{B}^{t+1}=J-K\left( \tilde{x}^{t}-1/2\right)$ in the following period. Substituting this into Eq. (5) and rearranging, we find that firm $A$’s market share amongst young consumers in period $t$ is equal to

$$\begin{aligned} \tilde{x}^{t}\left( p_{A},p_{B}\right) =\frac{1}{2}+\frac{p_{B}-p_{A}}{ 2\left( 1+K\delta _{c}s\right) } \end{aligned}$$

(6)

Behaviour of firms We know from above that in period $t$, product $A$ is bought by $\tilde{x}^{t}$ young consumers and by $\tilde{x} ^{t-1}\dot{x}^{t}+\left( 1-\tilde{x}^{t-1}\right) \ddot{x}^{t}$ old consumers. We can therefore write the demand for product $A$ in period $t$ as

$$\begin{aligned} D_{A}^{t}\left( p_{A},p_{B},\tilde{x}^{t-1}\right) =1+\left( p_{B}-p_{A}\right) \frac{2+K\delta _{c}s}{2\left( 1+K\delta _{c}s\right) } +s\left( \tilde{x}^{t-1}-1/2\right) \end{aligned}$$

(7)

In order for the strategies in (1) and (2) to constitute a MPE, they must be subgame perfect (see Fudenberg and Tirole 1991). In particular suppose that in period $t$, firm $B$ plays the equilibrium strategy given by Eq. (2), i.e. $p_{B}=p_{B}^{t}\left( \tilde{x}^{t-1}\right)$. Subgame perfection requires that for any history, and hence for any state variable $z$,

$$\begin{aligned} p_{A}^{t}\left( z\right) =\arg \max _{p_{A}}~p_{A}D_{A}^{t}\left( p_{A},p_{B}^{t}\left( z\right) ,z\right) +\delta _{f}V_{A}^{t+1}\left( \tilde{x }^{t}\left( p_{A},p_{B}^{t}\left( z\right) \right) \right) \end{aligned}$$

(8)

Differentiating the right-hand side with respect to $p_{A}$ and imposing $p_{A}=p_{A}^{t}\left( z \right)$ gives a first order condition. Equations (1), (2), (3) and (6) can then be used to substitute out for $p_{A}^{t}\left( z \right)$, $p_{B}^{t}\left( z \right)$ and $V_{A}^{t+1}\left( \tilde{x}^{t}\right)$. This leaves a single equation which is a function only of $z$ and underlying parameters. Since this one equation must hold for all values of $z$, we can use the method of undetermined coefficients to get two conditions on underlying parameters. In addition it should be the case that

$$\begin{aligned} V_{A}^{t}\left( z\right) =p_{A}^{t}\left( z\right) \times D_{A}^{t}\left( p_{A}^{t}\left( z\right) ,p_{B}^{t}\left( z\right) ,z\right) +\delta _{f}V_{A}^{t+1}\left( \tilde{x}^{t}\left( p_{A}^{t}\left( z\right) ,p_{B}^{t}\left( z\right) \right) \right) \end{aligned}$$

(9)

Again after making appropriate substitutions, Eq. (9) can be expressed only in terms of $z$ and underlying parameters. Since this one equation must hold for all values of $z$, we can use the method of undetermined coefficients to get three more conditions on underlying parameters. Full details of these manipulations are available in the Appendix.

A symmetric linear Markovian strategy is characterized by the parameters $J,K,M,N$ and $R$. We can obtain (implicit) expressions for these parameters by solving the five conditions mentioned above. This then allows us to state the following result.⁴

Proposition 1

For any $s\in \left( 0,7/10\right]$, there is a unique MPE in linear strategies as given by Eqs. (1) and (2). The behavioural parameter $J$ satisfies

$$\begin{aligned} J=\frac{2+2K\delta _{c}s+\delta _{f}K}{2+K\delta _{c}s+\delta _{f}s} \end{aligned}$$

(10)

whilst $K$ lies in $\left[ s/3,3s/8\right)$ and satisfies the following equation

$$\begin{aligned} \delta _{f}K^{3}\left( 2+K\delta _{c}s\right) -3K\left( 2+K\delta _{c}s\right) \left( 1+K\delta _{c}s\right) ^{2}+2s\left( 1+K\delta _{c}s\right) ^{3}=0 \end{aligned}$$

(11)

Proposition 1 imposes the restriction $s\le 7/10$. This is because when setting up demand in Eq. (7), we assumed that generically each firm has both some consumers switching to it and others switching from it. However, switching in both directions can only happen in equilibrium if the difference in prices $\left| p_{B}^{t}\left( \tilde{x}^{t-1}\right) -p_{A}^{t}\left( \tilde{x} ^{t-1}\right) \right| =K\left| 2\tilde{x}^{t-1}-1\right|$ is not too large. Since $K$ is related to $s$, this means that $s$ cannot be too large either. We show in the Appendix that it is sufficient to restrict attention to switching costs that are less than $7/10$.⁵ To put this into perspective, we show in the next section that although a wide range of prices may be charged by the two firms, in equilibrium no firm will ever charge more than about $1.2$. Consequently, the equilibrium in Proposition 1 is (at a bare minimum) valid for any switching cost between about 0 and $60\,\%$ of market prices. Most real-world estimates of switching costs, some of which were summarized in the introduction, comfortably lie in this interval.

Proposition 2

For any initial $\tilde{x}^{0}$, the market converges to a steady state in which firms split demand equally and charge a price $J$. In period $t$, the location of the marginal young consumer satisfies

$$\begin{aligned} \tilde{x}^{t}-1/2=-\frac{K}{1+K\delta _{c}s}\left( \tilde{x}^{t-1}-1/2\right) \end{aligned}$$

(12)

Proof

To derive Eq. (12), simply substitute (1) and (2) into (6). Proposition 1 says that $K\in \left[ s/3,3s/8\right)$ and therefore $K<1+K\delta _{c}s$. This implies that ${\lim }_{t\rightarrow \infty }\tilde{x}^{t}=1/2$ and, using Eqs. 1 and 2, also implies that ${\lim }_{t\rightarrow \infty } p_{A}^{t}={\lim }_{t\rightarrow \infty }p_{B}^{t}=J$. $\square$

If at the beginning of the game $\tilde{x}^{0}=1/2$, the market is always in steady state, with firms charging $J$ in every period and splitting the market equally. If instead at the beginning $\tilde{x}^{0}\ne 1/2$, over time the market converges to the aforementioned steady state. During this convergence process, the position of the marginal young consumer $\tilde{x} ^{t}$ oscillates around $1/2$. Consequently, the prices set by the two firms also oscillate around $J$. This oscillatory behaviour arises because in each period, the firm which previously sold to more than half of young consumers exploits this fact by charging a higher price than its rival. As a result, it then sells to fewer than half of the current young consumers.

4 The effect of switching costs on prices

4.1 Steady state

Remark 1

When $s=0$, the steady state price is equal to 1. The steady state price is also decreasing in $s$ at $s=0$.

Proof

Using Eqs. (10) to (11), it is straightforward to show that $J=1$ and $K=0$ when $s=0$. Totally differentiate Eq. (11) with respect to $s$; after substituting in $s=K=0$, this simplifies to $\left. \partial K/\partial s\right| _{s=0}=1/3$. Totally differentiate Eq. (10) with respect to $s$; after again substituting in $s=K=0$, this simplifies to $\left. \partial J/\partial s\right| _{s=0}=\left( \delta _{f}/2\right) \left( -1+\left. \partial K/\partial s\right| _{s=0}\right) =-\delta _{f}/3<0$. $\square$

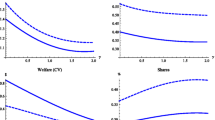
Several recent papers have shown that starting from $s=0$, steady state price is decreasing in the switching cost. The same is also true in our model. Other papers then use numerical simulations to show that the steady state price is lower for somewhat larger switching costs as well. However, as Fig. 1 makes clear, away from $s=0$ the effect of switching costs on steady state price is ambiguous and depends upon the specific parameter values that we choose. To interpret Fig. 1, note that the discount factors $\delta _{c}$ and $\delta _{f}$ both affect the (unique) steady state price and can both take values anywhere on $\left( 0,1\right)$. Therefore, for any given value of the switching cost, we can compute the infimum and supremum over $\left( \delta _{c},\delta _{f}\right) \in \left( 0,1\right) ^{2}$ of the steady state price. Figure 1 then plots the infimum and supremum for each switching cost in $\left[ 0,7/10\right]$. Notice that even when the switching cost is close to zero, steady state price can be either above or below 1, depending upon the values assigned to $\delta _{c}$ and $\delta _{f}$. Moreover as the switching cost grows, so does the gap between the highest and lowest steady state prices that we could observe. For example depending upon the specific values attached to $\delta _{c}$ and $\delta _{f}$, when $s=7/10$ steady state price can be as much as 8 % higher or 17 % lower than it is when $s=0$. Therefore, comparative statics around $s=0$ are rather special.

Fig. 1

A plot showing the infimum and supremum over $\left( \delta _{c},\delta _{f}\right) \in \left( 0,1\right) ^{2}$ of the steady state price, for each value of the switching cost

It is convenient to split up the impact of switching costs on price, into the following four effects, all of which are mentioned in various parts of the literature. These are the harvesting, poaching, investment and consumer price effects.⁶ The first two reflect pricing incentives on old customers. According to the harvesting effect, firms should charge a high price and exploit their old customers’ reluctance to switch away. However, according to the poaching effect, firms should charge a low price and poach some of their rival’s customers (using the low price to overcome their reluctance to switch). It turns out that since each firm has exactly half of the old customers, in steady state the harvesting and poaching effects cancel out.⁷ Two assumptions are crucial in this respect. First, we assumed that $s$ is small enough to guarantee that switching actually occurs. By contrast in Beggs and Klemperer (1992) and To (1996), the switching cost is so large that nobody ever switches. Poaching is therefore impossible, and both firms just harvest. Second, we assumed that preferences change independently over time. In Sect. 6, we show that if preferences are positively correlated, harvesting can dominate poaching.

Since the harvesting and poaching effects cancel, the steady state price is driven only by pricing incentives on young consumers. It is simple to show that $V_{A}^{t+1}\left( \tilde{x}^{t}\right)$ and $V_{B}^{t+1}\left( \tilde{ x}^{t}\right)$ are, respectively, increasing and decreasing in $\tilde{x}^{t}$, i.e. market share in one period is valuable in the next. Therefore, according to the investment effect, firms should charge lower prices, as they try to win market share and thereby improve their future profitability. On the other hand, if a firm cuts its price, consumers understand that it is only temporary and will be followed by a price increase in the next period (c.f. Eqs. 1 and 2). Young consumers therefore have relatively inelastic demands, and according to the consumer effect, firms should respond by charging higher prices.

Lemma 2

The steady state price strictly decreases in $\delta _{f}$ and strictly increases in $\delta _{c}$.

Discount factors affect the steady state price as one would expect.⁸ A higher $\delta _{f}$ means that firms care more about future profits, and therefore, both cut their prices in an attempt to increase their market shares. A higher $\delta _{c}$ means that consumers put less weight on temporary price cuts, such that firms face less elastic demand curves and therefore charge a higher price. The real question—which the next proposition addresses—is which of the investment and consumer effects dominates.

Proposition 3

For any $\delta _{c}$ and $s\in \left( 0,7/10 \right]$, there exists a $\widetilde{\delta _{f}}\in (\delta _{c}s / 2, 3\delta _{c}s / 5)$ such that the steady state price is less than 1 if and only if $\delta _{f}>\widetilde{\delta _{f}}$.

Proposition 3 confirms analytically that price can be either higher or lower depending upon parameters. However, we expect that in practice, firms are more patient than consumers, and therefore that $\delta _{f}\ge \delta _{c}>\widetilde{\delta _{f}}$. The model would then predict that steady state price is lower with switching costs than without. Equivalently, the investment effect outweighs the consumer effect. The interpretation is that firms cut their price as a defensive measure, to prevent their rival from stealing valuable market share.

To understand why the investment effect dominates, recall from Sect. 3 that old consumers definitely buy product $A$ if $x^{t+1}\le \left( 1-s\right) /2$ and definitely buy product $B$ if $x^{t+1}\ge \left( 1+s\right) /2$. We also know that if old consumers are in the ‘lock-in region’ $x^{t+1}\in \left[ \left( 1-s\right) /2,\left( 1+s\right) /2\right]$, they stay with their initial supplier. Consider the investment effect. If firm $i$ captures a few extra young consumers, they are valuable in the next period (i) if they buy product $i$ when old and (ii) if, but for buying $i$ when young, they would buy $j\ne i$ when old. Equivalently, these extra young consumers are valuable if and only if they lie in the lock-in region in the next period. The probability of actually being in the lock-in region is $s$. Moreover, the value created for the firm by these additional young consumers is $J$ since this is what they will contribute to future revenue. Therefore, if a firm acquires a few extra young consumers, the direct effect on future profits is $J\delta _{f}s$.⁹

Now consider the consumer effect. According to Eq. (6), the marginal young consumer has location

$$\begin{aligned} \tilde{x}^{t}\left( p_{A},p_{B}\right) =\frac{1}{2}+\frac{p_{B}-p_{A}}{2+2K\delta _{c}s} \end{aligned}$$

(13)

where the term $2K\delta _{c}s$ in the denominator measures the consumer effect. Intuitively, if firm $i$ slightly reduces its price, it will increase its market share. Using Eqs. (1) and (2), young consumers can infer that in the following period, $i$’s price will be higher and $j\left( \ne i\right)$’s price will be lower. In particular, $p_{i}^{t+1}-p_{j}^{t+1}$ increases in proportion to $2K$. However, a young consumer who buys product $i$ only incurs an expected future loss of $2K\delta _{c}s$. Intuitively only when a consumer finds herself in the lock-in region, does her initial decision to choose $i$ over $j$ actually cause her to pay the extra $2K$.¹⁰ Since the probability of ending up in the lock-in region is only $s$, the consumer effect is only on the order of $2K\delta _{c}s$.

Comparing the investment and consumer effects is just like comparing a level with a difference. Notice that everybody cares about what happens when a consumer becomes ‘locked in’. However, whilst the benefit of lock-in to a firm is a level (namely the price paid to it by the consumer), the cost to the consumer is only a difference (namely the extra amount she must pay). Intuitively if the switching cost is not too large, the level effect must swamp the difference effect. This is because for small $s$, the link between current market share and future prices is small, i.e. the additional amount that a locked-in consumer pays is also small. Put slightly differently, since we expect firms to be more patient than consumers, a firm’s incentive to lock people in will outweigh a consumer’s incentive to avoid being locked in. Consequently, switching costs are pro-competitive in steady state.

Two other points are worth briefly making. First, recall that around $s=0$ switching costs are pro-competitive irrespective of how large $\delta _{f}$ is relative to $\delta _{c}$. The reason is that whilst the investment effect $J\delta _{f}s$ is first order in $s$, the consumer effect $2K\delta _{c}s$ is only second order because $K$ is of the same order as $s$. Hence around $s=0$, the investment effect must dominate. Secondly, note that whilst the investment effect is roughly linear in $s$, the consumer effect is more-than-linear in $s$. This suggests that the investment effect will dominate initially, but then later the consumer effect will become more powerful. Therefore, by solving the model analytically, we are able to shed some light on why Doganoglu (2010) and Somaini and Einav (2013) both find (numerically) that steady state price is U shaped in the switching cost.

Finally, our intuition can also shed light on the broader question of why switching costs can be pro-competitive when they are relatively small, but (as shown by Beggs and Klemperer 1992 and To 1996) not when they are very large.¹¹ As discussed earlier, one reason is that when switching costs are very large, firms are unable to poach from their rival. Consequently, they focus more on harvesting, which is a force for higher prices. A second related reason is that when switching costs are very large, the link between a firm’s market share and its price will become stronger. Equivalently, the consumer effect will be stronger than in our model, and eventually probably dominates the investment effect. This again explains why very large switching costs lead to a higher steady state price. It is worth noting again, however, that all our results are valid (at a minimum) for any switching cost between about 0 and $60\,\%$ of the steady state price. Therefore, a very large switching cost is required to overturn our results.

4.2 Outside of steady state

Suppose that at the beginning of the game, the state variable is $\tilde{x} ^{0}\ne 1/2$. Proposition 2 guarantees that the market will converge to a steady state where firms split the market equally. Nevertheless, it is important to understand how switching costs affect competition during this convergence process. Since in each period firms will generally face different demand schedules, they will not charge the same price. At any point in time, the firm with the larger market share focuses more on harvesting and less on poaching, and consequently charges more than its smaller rival. In fact, a simple calculation reveals that depending upon parameters, one firm might charge as much as 33 % more than its rival.

One natural measure of market competition is the average (transaction) price. In period $t$, the average price paid by consumers is

$$\begin{aligned} J+\left( \tilde{x}^{t-1}-1/2\right) ^{2}K{ \left( s-K\frac{2+K\delta _{c}s}{1+K\delta _{c}s}\right) } \end{aligned}$$

(14)

which (weakly) exceeds the average price $J$ which consumers pay in the long-run steady state outcome. This is because even though $p_{A}^{t}\left( \tilde{x}^{t-1}\right) +p_{B}^{t}\left( \tilde{x}^{t-1}\right) =2J$ in every time period, in the short run one firm is able to both charge a higher price and sell to more than half of the market. However, $\left( \tilde{x}^{t-1}-1/2\right) ^{2}$ decreases monotonically over time (recall Proposition 2), so it is clear from Eq. (14) that the average price decreases over time.

We showed earlier in Proposition 3 that the long-run price is below 1 if and only if $\delta _{f}$ exceeds a threshold $\tilde{\delta }_{f}$. The corresponding result for the short run is as follows:

Proposition 4

For any $\delta _{c}$, any $\tilde{x}^{t-1}\ne 1/2$, and any $s\in \left( 0,7/10\right]$, there exists a threshold $\hat{\delta } _{f}\left( \left| \tilde{x}^{t-1}-1/2\right| \right) \in \left( \tilde{\delta }_{f},1\right)$ such that the average price in period $t$ is below 1 if and only if $\delta _{f}>\hat{\delta }_{f}\left( \left| \tilde{x}^{t-1}-1/2\right| \right)$. The threshold strictly increases in $\left| \tilde{x}^{t-1}-1/2\right|$ and tends to $\tilde{ \delta }_{f}$ as $\tilde{x}^{t-1}\rightarrow 1/2$.

Thus, the short-run impact of switching costs is also ambiguous, and again depends upon a comparison of firm and consumer discount factors. Compared to the case of no switching cost, average price is higher in all periods if $\delta _{f}<\tilde{\delta }_{f}$ but lower in all periods if $\delta _{f}>\hat{\delta }_{f}\left( \left| \tilde{x}^{0}-1/2\right| \right)$. More interestingly when $\delta _{f}\in \left( ~\tilde{\delta } _{f},\hat{\delta }_{f}\left( \left| \tilde{x}^{0}-1/2\right| \right) ~\right)$, the average price starts out above 1, but then falls as the market matures and at some point drops below 1. Consequently under these circumstances, switching costs are anti-competitive in the short run and yet pro-competitive in the long run.

The intuition for why switching costs can have different short- and long-run effects is as follows. In the long run, all that matters is the relative strengths of the investment and consumer effects. Therefore, switching costs are pro-competitive whenever $\delta _{f}/\delta _{c}$ is sufficiently large, even if in absolute terms $\delta _{c}$ and $\delta _{f}$ are both small. However, in the short run, the larger firm’s emphasis on harvesting provides an additional upward boost to prices. In order to counteract this, the investment effect has to be big in absolute terms as well. Therefore, a large $\delta _{f}/\delta _{c}$ is no longer sufficient to guarantee that switching costs are pro-competitive—$\delta _{f}$ has to be sufficiently large in absolute terms as well. To illustrate this point, suppose $\tilde{x} ^{0}=1$, $s=7/10$ and $\delta _{c}=0$, i.e. consumers are myopic. Consider two cases, one where $\delta _{f}=1/20$ and another where $\delta _{f}=1/10$. In the long run, switching costs are pro-competitive (prices are, respectively, $0.989$ and $0.977$) because $\delta _{f}$ is larger than $\delta _{c}$. However, in the short run, switching costs are anti-competitive in the first case (average price initially exceeds $1.002$) yet pro-competitive in the second case (average price does not exceed $0.992$).

In light of Proposition 4, it is natural to ask whether a switching cost could cause both firms to charge a lower price.

Remark 2

Start with $s=0$ and introduce a small switching cost. Provided $\delta _{f}>1/2$ both firms charge a strictly lower price in every period. This is true for any $\delta _{c}$ and any initial condition $\tilde{x}^{0}$.

Proof

Recalling the proof of Remark 1, $\left. \partial K/\partial s\right| _{s=0}=1/3$ and $\left. \partial J/\partial s\right| _{s=0}=-\delta _{f}/3$. Note that $\left. \partial p_{i}^{t}\left( \tilde{x}^{t-1}\right) /\partial s\right| _{s=0}\le \left. \partial J/\partial s\right| _{s=0}+\left. \partial K/\partial s\right| _{s=0}/2$ which is strictly negative whenever $\delta _{f}>1/2$. $\square$

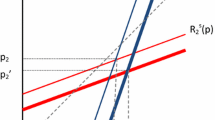
One interesting benchmark is when $\tilde{x}^{0}=1$, i.e. at the start of the game, all old consumers are locked to firm $A$. This could happen if firm $A$ were previously a monopolist, and $V$ was sufficiently high to induce it to sell to all young consumers.¹² Using Eq. (1) firm $A$ would charge $J+K/2$ in the first period. It is also clear from Eqs. (1) and (2) that in all other time periods and for all other initial conditions $\tilde{x}^{0}$, both firms would charge strictly less than $J+K/2$. This is intuitive because out of everybody, a (recent) monopolist has the strongest incentive to harvest its customer base via a high price. Surprisingly however, Remark 2 shows that even an incumbent monopolist (which faces a brand new entrant) may respond to a small switching cost by reducing its price. This is because if the incumbent cares enough about the future, it will follow the entrant and cut its price as a defensive measure to avoid losing too much market share. Of course one would expect that as the switching cost grows, the incumbent’s power over its old customers grows and therefore the harvesting effect should strengthen. This is shown graphically in Fig. 2. In particular for a given value of the switching cost, we can compute the infimum and supremum over $\left( \delta _{c},\delta _{f}\right) \in \left( 0,1\right) ^{2}$ of the price charged by an incumbent monopolist. Figure 2 plots the infimum and supremum, for each switching cost in $\left[ 0,7/10\right]$. As $s$ increases, there is a trend towards higher prices. However, even for very high switching costs, there are combinations of $\delta _{c}$ and $\delta _{f}$ such that the incumbent’s price is below the frictionless benchmark 1. Therefore, even very large switching costs may cause both firms in the market to charge a lower price in every period.

Fig. 2

A plot showing the infimum and supremum over $\left( \delta _{c},\delta _{f}\right) \in \left( 0,1\right) ^{2}$ of an incumbent monopolist’s price, for each value of the switching cost

To summarize, we have shown that the average price paid by consumers is higher in the short run when the market is outside steady state. We then derived a condition which determines whether this average price is higher or lower compared to a market where consumers do not incur switching costs. Finally, we demonstrated that under certain conditions, even a firm with a very large customer base may respond to switching costs by lowering its price.

4.3 Profits

Since there is a close connection between prices and profits, the previous two subsections suggest that firms are probably made worse off by switching costs. Firstly in steady state, each firm charges a price $J$ and sells to one unit of consumers in every period. Therefore, switching costs reduce long-run profits if and only if they reduce long-run price. Proposition 3 then implies that switching costs are bad for firms except when consumers are especially patient. Secondly outside of steady state, total industry profit in any individual period $t$ is equal to $p_{A}^{t}\left( \tilde{x}^{t-1}\right) \times D_{A}^{t}\left( .\right) +p_{B}^{t}\left( \tilde{x}^{t-1}\right) \times D_{B}^{t}\left( .\right)$. The latter is proportional to the average price charged in period $t$, which we defined earlier in Eq. (14). Therefore, Proposition 4 says that unless firms are sufficiently impatient, industry profit will be lower in every period. Of course if firms start off with unequal market shares, the larger firm may still benefit from switching costs. However, analogous to Remark 2, we can show that provided $\delta _{f}>1/2$, a small switching cost reduces every firm’s (discounted sum of) profits. In particular, even a recent monopolist can be harmed by the introduction of a small switching cost.

5 The effect of switching costs on consumer welfare

It is natural to ask whether switching costs could reduce prices so much, that they actually benefit consumers. To answer this question, we will focus on steady state consumer welfare.

In steady state, both firms charge the same price, so Eq. (6) shows that young consumers buy from $A$ if $x^{t}\le 1/2$ and buy from $B$ if $x^{t}>1/2$. However, these are exactly the same choices that they would make in a market without switching costs. Therefore, when consumers are young, they benefit from switching costs if and only if the equilibrium price is lower. This is obviously not true for old consumers, because some of them incur the switching cost (a direct loss), whilst others of them keep buying an inferior product to avoid paying the switching cost (an indirect loss). In principle, old consumers could still benefit from switching costs, if the steady state price falls enough to compensate them for these other losses. However, the following lemma shows that this never happens:

Lemma 3

In steady state, switching costs make old consumers worse off.

Therefore, in most relevant cases, switching costs have three effects. (1) They benefit all consumers through a lower market price, (2) they harm old consumers who either have to incur these costs or avoid them by sticking with an inferior product, and (3) they transfer utility from the old to the young. The net effect will depend largely on how we weight the pay-offs of young and old consumers. We now discuss two natural alternatives.

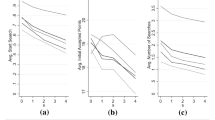
One natural way to measure consumer surplus is to simply add the pay-offs of young and old consumers, i.e. look at consumer welfare at a specific point in time. In this case, only the first two effects identified above are relevant. For example starting from $s=0$, a small switching cost reduces the market price by $\delta _{f}/3$ but forces half of old consumers to incur the cost when switching suppliers. Consequently, consumer surplus changes by $2\left( \delta _{f}/3\right) -1/2$, which is positive provided $\delta _{f}>3/4$. As another example when moving from $s=0$ to $s=1/4$, consumers are better off in aggregate provided that $\left( \delta _{f}, \delta _{c} \right)$ lie in the shaded area in Fig. 3. Figure 4 performs the same exercise when moving from $s=0$ to $s=1/2$.¹³ We note in passing that Somaini and Einav (2013) solve their related model numerically for $\delta _{f}=1/2$ and $\delta _{c}=7/10$, and find that switching costs reduce consumer surplus. Our analysis shows that this result can be overturned if firms are more patient than consumers.

Fig. 3

Increasing the switching cost from 0 to $1/4$ raises (unweighted) consumer surplus if and only if $\left( \delta _{f}, \delta _{c}\right)$ lie in the shaded region

Fig. 4

Increasing the switching cost from 0 to $1/2$ raises (unweighted) consumer surplus if and only if $\left( \delta _{f}, \delta _{c}\right)$ lie in the shaded region

Another natural measure of consumer surplus is the ex ante lifetime expected utility of a young consumer who is about to enter the market (i.e. weights of 1 and $\delta _{c}$ on young and old consumption, respectively). With this alternative measure, all three effects identified above are relevant.

Proposition 5

For any $\delta _{f}$ and $s$, there exists a threshold $\widetilde{\delta _{c}}>0$ such that in steady state, switching costs raise discounted lifetime consumer surplus if and only if $\delta _{c}<\widetilde{ \delta _{c}}$.

Proposition 5 is intuitive. When $\delta _{c}$ is very low, a consumer’s lifetime utility is mainly affected by how well off she is when young. Moreover, Proposition 3 says that for sufficiently small $\delta _{c}$, the steady state price must be lower with switching costs, and therefore that consumers are better off when young. Two things change as $\delta _{c}$ increases. Firstly, the steady state price increases and so consumers become worse off in both periods of their life. Secondly, consumers care more about utility in their second period. This implies that the intertemporal benefit of switching costs (namely transferring utility from the future to the present, when consumers value it most) becomes less important.

Example 1

Starting from $s=0$, a small switching cost increases discounted lifetime consumer surplus if and only if $\delta _{c}<\widetilde{ \delta _{c}}=2\delta _{f}/\left[ 3-2\delta _{f}\right] .$

Note that the condition $\delta _{c}<2\delta _{f}/\left[ 3-2\delta _{f} \right]$ is definitely satisfied if either $\delta _{f}>3/4$, or if $\delta _{f}\in \left[ 1/2,3/4\right]$ and firms are more patient than consumers. Therefore, as expected, a small switching cost increases consumer surplus for a wider range of parameters under this alternative measure. To further illustrate this point, Figs. 5 and 6 plot the critical threshold $\tilde{\delta }_{c}$ for the cases where $s=1/4$ and $s=1/2$. In both diagrams, the respective switching cost benefits consumers whenever $\left( \delta _{f}, \delta _{c} \right)$ lies in the shaded area. It turns out (although this is a little difficult to see from the diagrams) that when $\delta _{f}$ is low the critical discount factors satisfy $\left. \widetilde{ \delta _{c}}\right| _{s=1/2}>\left. \widetilde{\delta _{c}}\right| _{s=1/4}$, whereas when $\delta _{f}$ is higher they satisfy $\left. \widetilde{\delta _{c}}\right| _{s=1/2}<\left. \widetilde{\delta _{c}} \right| _{s=1/4}$. In either case provided consumers discount the future a little more than firms, they are definitely better off.

Fig. 5

Increasing the switching cost from 0 to $1/4$ raises lifetime discounted consumer surplus if and only if $\left( \delta _{f}, \delta _{c}\right)$ lie in the shaded region

Fig. 6

Increasing the switching cost from 0 to $1/2$ raises lifetime discounted consumer surplus if and only if $\left( \delta _{f}, \delta _{c}\right)$ lie in the shaded region

In summary, switching costs benefit the young but harm the old. For a fairly wide range of parameters, the net effect on consumers is positive. Cabral (2014) also shows that a small switching cost can benefit consumers, if firms are sufficiently patient. However, in his model, consumers are infinitely lived, so he considers only per-period welfare. We have overlapping generations of consumers, and we consider two different ways to measure their surplus. This allows us to identify an additional channel through which switching costs can benefit consumers (namely the intertemporal transfer of surplus), which is not present in Cabral’s analysis.

6 Discussion

6.1 Relaxing independence

We now relax the assumption that consumer preferences evolve independently over time. There is lot of evidence that a consumer’s valuation for any given product is often serially correlated across time. Moreover, Dubé et al. (2010) have shown that after controlling for switching costs, this persistence in preferences offers an additional explanation for why consumers exhibit inertia in their brand choices.

In order to be as general as possible, we model correlation in the following way. We continue to assume that when young consumers are born, their position on the Hotelling line is drawn randomly. However, when a young consumer with location $x^{t}$ becomes old, she is assigned a new location $x^{t+1}$ which is now drawn using a conditional density $f\left( \left. x^{t+1}\right| x^{t}\right)$. The joint density $f\left( x^{t},x^{t+1}\right)$ is continuous, atomless, strictly positive and satisfies the following two restrictions. Firstly, we assume that $f\left( y,z\right) =f\left( z,y\right)$. This ensures that in each period, the population of old consumers is unconditionally uniformly distributed along the Hotelling line.¹⁴ This facilitates comparison with the base model, in which old consumers were also assumed to be uniformly distributed along the line. Secondly, we assume that $f\left( y,z\right) =f\left( 1-y,1-z\right)$ for all $y,z\in \left[ 0,1\right]$, which is sometimes called radial symmetry. To motivate this assumption, consider two symmetrically located young consumers, one a distance $d$ from firm $A$ and the other the same distance $d$ away from firm $B$. It seems natural that when these consumers become old, their preferences will also be symmetric. When the first consumer becomes old, her distance from $A$ is $d_{A}^{t+1}$ which has conditional density $f\left( \left. d_{A}^{t+1}\right| d\right)$. Similarly when the second consumer becomes old, her distance from $B$ is $d_{B}^{t+1}$ which has conditional density $f\left( \left. 1-d_{B}^{t+1}\right| 1-d\right)$. Radial symmetry ensures that these conditional densities are equal, and therefore that ‘future’ preferences are symmetric. To gain some insights into how these two restrictions interact, consider a plot of the joint density function. Take any two points in $\left[ 0,1\right] ^{2}$ which lie on a ray through $\left( 1/2,1/2\right)$, and which are also located equidistantly from $\left( 1/2,1/2\right)$. Then, reflect both these points in the line $x^{t}=x^{t+1}$. This leaves us with four points, each of which represents the vertex of a rectangle. The above restrictions imply that $f\left( x^{t},x^{t+1}\right)$ is the same when evaluated at each of these four points.¹⁵ Note that although this places a certain amount of structure on the joint density, it allows for $x^{t}$ and $x^{t+1}$ to be positively correlated.

A firm’s demand is no longer a linear function of its past market share, and consequently, there does not exist an equilibrium in linear strategies. The difficulty of formally proving existence of a Markovian equilibrium in this more general setting is well known (see Dutta and Sundaram 1998 for a comprehensive discussion). For this reason, we take the following approach. When $s=0$, there are no pay-off-relevant state variables, so a MPE does trivially exist, and it involves the two firms playing the (static) Hotelling equilibrium in each period. Assuming that a (continuous) MPE also exists in the neighbourhood of $s=0$, we can derive first order conditions and use them to study comparative statics in this neighbourhood.

Proposition 6

Starting from $s=0$, a small switching cost reduces steady state price if and only if

$$\begin{aligned} \frac{1}{2}\frac{\partial \Pr \left( X\ge 1/2|Y=1/2\right) }{\partial Y}+ \frac{\delta _{c}}{2}\frac{\partial \Pr \left( X\ge 1/2|Y=1/2\right) }{\partial Y}-\delta _{f}\frac{f\left( 1/2|1/2\right) }{3}<0 \end{aligned}$$

(15)

To interpret Proposition 6, $\Pr \left( X\ge 1/2|Y\right) =1/2$ when preferences are independent, and so the inequality (15) definitely holds. When instead preferences are positively correlated, we expect that a consumer who is more attached to product $B$ in one period is also more likely to prefer $B$ over $A$ in another period. Equivalently, we expect that $\partial \Pr \left( X\ge 1/2|Y\right) /\partial Y\ge 0$, in which case (15) might not be satisfied. Before commenting further on this, we provide some brief intuition behind expression (15).

The first term in (15) is a combination of the harvesting and poaching effects, whilst the second term is the consumer effect, and the third term is the investment effect. The harvesting and poaching effects are therefore now (weakly) positive, and the intuition is as follows. As explained earlier, firms can exploit their own old consumers with a high price, or poach some of their rival’s customers with a low price. With independent preferences, half of old consumers are locked in to the ‘wrong’ firm, and the incentives to exploit and poach cancel. When instead preferences are positively correlated, fewer marginal consumers are locked in to the ‘wrong’ firm. This makes it more profitable to harvest and less profitable to poach, so the former effect now dominates.

The second term of (15) is the consumer effect and it too is now positive. As reported earlier, the standard explanation is that young consumers are less responsive to price cuts, because they expect a price rise to follow in the next period. Starting from $s=0$, we showed that this effect is only second order when consumer tastes evolve independently over time; for similar reasons, it is also second order even when tastes are correlated across time. Instead, the positive consumer effect in (15) is caused by a quite different mechanism which, to our knowledge, has not previously been mentioned in the literature. It arises due to expected changes in future preferences. For example, suppose that firm $A$ reduces $p_{A}^{t}$ and tries to attract some young consumers located slightly to the right of $x^{t}=1/2$. Since preferences are positively correlated, these young consumers expect to prefer product $B$ in the next period. This makes them more reluctant to buy $A$ now, which causes demand to become less elastic.

The final term of (15) is the investment effect. As in the base model, firms compete for the marginal young consumer who is located at $x^{t}=1/2$. As argued previously, this marginal consumer is valuable in future if she turns out to be located in the lock-in region. Starting from $s=0$, a small increase in the switching cost changes her probability of being in the lock-in region by $f\left( 1/2|1/2\right)$. Since preferences are correlated, we expect that $f\left( 1/2|1/2\right) >1$, i.e. the investment effect is stronger than in our earlier model.

To summarize when consumer preferences are correlated over time, the first two terms of inequality (15) are positive, and therefore even very small switching costs are not necessarily pro-competitive. Note, however, that only the behaviour of $f\left( \left. x^{t+1}\right| x^{t}\right)$ around the point $x^{t}=1/2$ is relevant for whether (15) holds. Correlation on the other hand is a global concept, which summarizes the behaviour of $f\left( \left. x^{t+1}\right| x^{t}\right)$ for all $x^{t}$. This immediately implies that the amount of correlation has no direct bearing on whether switching costs are pro- or anti-competitive.¹⁶ What matters instead is whether $\partial \Pr \left( X\ge 1/2|Y=1/2\right) /\partial Y$ is large or small. As an example, suppose that if a young consumer is almost indifferent about which product to buy, she is also equally likely to prefer $A$ or $B$ when she becomes old. Then, $\partial \Pr \left( X\ge 1/2|Y=1/2\right) /\partial Y$ is zero and switching costs are definitely pro-competitive, even if in the wider population there is a strong positive correlation between $x^{t}$ and $x^{t+1}$. Therefore, although our earlier assumption of independence is not innocuous, it can be substantially relaxed without changing the conclusion that small switching costs are pro-competitive. Furthermore, whenever consumer tastes are correlated, fewer old consumers need to actually incur the switching cost because they are already locked into the ‘correct’ firm. This means that conditional on switching costs being pro-competitive, there is again a good chance that they improve consumer welfare.

6.2 Relaxing the overlapping generations set-up

We have assumed throughout the paper that consumers live for just two periods. We now briefly consider what happens when a single generation of infinitely lived consumers enters the market in the first period. As in the main model, we assume that their preferences evolve independently over time. Generally there no longer exists an equilibrium in linear strategies, so we follow the same approach that we did with correlation.

In the working paper version (Rhodes 2014), we prove that starting from $s=0$, a small switching cost reduces steady state price by $2\delta _{f}/3$. Small switching costs are therefore more pro-competitive than in the overlapping generations model, where price fell by only $\delta _{f}/3$. The intuition for this stronger price response is as follows. As before, in each period there is a ‘lock-in region’, such that a consumer who finds herself located within it, stays with her previous supplier. The difference is that now a consumer could become locked in for any number $T=1,2,\ldots$ consecutive periods. Nevertheless, the probability of actually being locked in for any $T\ge 2$ consecutive periods is very small when $s$ is close to zero. Therefore, firms and consumers still only care about lock-in during the following period. Using similar arguments as in the base model, the consumer effect is second order whilst the investment effect is first order. Now consider the investment effect in more detail. Suppose firm $i$ reduces $p_{i}^{t}$ slightly and acquires some extra consumers. When these consumers are infinitely lived, all of them survive to the next period and have a chance of becoming locked in; when these consumers live for two periods, only half survive to the next period and have a chance of becoming locked in. Therefore, the investment motive is twice as strong as in the base model, and small switching costs are doubly pro-competitive. Although the model cannot be solved for larger switching costs, our intuition is that the investment effect will dominate the consumer elasticity effect even more than in the base model.¹⁷

We also find that starting from $s=0$, a small switching cost increases per-period consumer surplus whenever $\delta _{f}>3/4$. This is exactly the same condition that we found in the overlapping generations framework. However, when consumers are infinitely lived, switching costs no longer induce an intertemporal transfer of surplus. This is because once a market already exists, consumers are ‘old’ in every period, and therefore always face the threat of having to incur switching costs.

In some sense, the base model represents a market in which the population of consumers changes frequently or a market in which technology changes a lot (such that products quickly become obsolete, so consumers often need to start afresh with new products); the extension with infinitely lived consumers represents a market with the opposite characteristics. We therefore cautiously suggest that switching costs are more likely to be pro-competitive in markets which are ‘stable’ in terms of technology or the identities of buyers.

7 Conclusion

We have presented a tractable model of dynamic competition and solved it for a very wide and empirically relevant set of switching costs. In general, the long-run impact of switching costs is ambiguous and depends upon how patient are firms and their consumers. We provided a condition which determines whether in the long run switching costs are pro- or anti-competitive. Given that we would expect firms to be more patient than consumers, we found a presumption that in steady state switching costs lead to lower prices. This is because a firm’s incentive to lock-in consumers strongly outweighs any single consumer’s incentive to avoid being locked in. We then used the model to address some other issues which have been largely neglected by the previous literature. We showed that short-run prices can be extremely heterogeneous, and that focusing on steady state may lead to biased conclusions about the pro-competitiveness of switching costs. We also examined the wider effects of switching costs, on for example consumer welfare. Switching costs often act as a way of transferring surplus from old to young consumers. When consumers are relatively impatient, this trade-off is favourable and consumer welfare is increased. Finally, we investigated how our conclusions might change when consumer tastes are correlated over time and when consumers are long-lived.

Throughout the paper, we have assumed that the switching cost is exogenously given. However, in practice, retailers can make it more or less easy for their customers to cancel subscriptions or move to another provider. Therefore, an interesting way to extend the current model would be to allow each firm to influence how easily its customers can switch to its rival. Our existing results show that for a wide range of parameters, profits are maximized when consumers are able to switch costlessly. However, we conjecture that firms may end up playing a Prisoner’s dilemma. In particular, each firm might benefit from making it slightly more difficult for its existing customers to switch. However, once both firms do this, price competition is intensified and they both earn less profit. We hope to think more about this in future work.

Appendix

1.1 Main Proofs

Proof of Lemma 1

Suppose that firms charge prices $p_{A}$ and $p_{B}$, respectively, in period $t$. Then, a young consumer’s expected lifetime pay-off from buying product $A$ in period $t$ is:

$$\begin{aligned} V-x^{t}-p_{A}+\delta _{c}\left[ V- \int _{0}^{\dot{x}^{t+1}}\left( y+Ep_{A}^{t+1}\right) \mathrm{d}y-\int _{\dot{x}^{t+1}}^{1}\left( \left( 1-y\right) +Ep_{B}^{t+1}+s\right) \mathrm{d}y\right] \end{aligned}$$

(16)

where $\dot{x}^{t+1}=\left( 1+Ep_{B}^{t+1}-Ep_{A}^{t+1}+s\right) /2$. (16) can be rewritten as

$$\begin{aligned} V-x^{t}-p_{A}+\delta _{c}\left[ V-\frac{1}{2}-Ep_{A}^{t+1}+\int _{\dot{x} ^{t+1}}^{1}\left[ -\left( 1-2y\right) +Ep_{A}^{t+1}-Ep_{B}^{t+1}-s\right] \mathrm{d}y \right] \end{aligned}$$

(17)

Similarly, the expected lifetime pay-off from buying product $B$ in period $t$ is

$$\begin{aligned} V-\left( 1-x^{t}\right) -p_{B}+\delta _{c}\left[ V-\frac{1}{2} -Ep_{B}^{t+1}+\int _{0}^{\ddot{x}^{t+1}}\left[ \left( 1-2y\right) +\varDelta _{e}^{t+1}-s\right] \mathrm{d}y\right] \end{aligned}$$

(18)

where $\varDelta _{e}^{t+1}=Ep_{B}^{t+1}-Ep_{A}^{t+1}$ and $\ddot{x}^{t+1}=\left( 1+\varDelta _{e}^{t+1}-s\right) /2$. The difference between (17) and (18) is clearly decreasing in $x^{t}$. Therefore, provided $\left| p_{B}-p_{A}\right|$ is not too large, there exists an $\tilde{x}^{t}\in \left( 0,1\right)$ such that (17) and (18) are equal when evaluated at $x^{t}=\tilde{x}^{t}$ (This also means that (17) exceeds (18) when $x^{t}<\tilde{x}^{t}$, whilst the opposite is true when $x^{t}>\tilde{x}^{t}$.). To get Eq. (5), equate (17) and (18), then substitute in $x^{t}=\tilde{x}^{t}$ and simplify. $\square$

Proof of Proposition 1

Lemma 4 below derives expressions for $J,M,N,R$ as a function of $K$, which must hold in any equilibrium. Lemma 5 then shows there is a unique $K$ consistent with our problem, and shows that it lies on $\left[ s/3,3s/8\right)$. $\square$

Lemma 4

Equations (8) and (9) jointly imply that in any linear symmetric MPE, $J$ satisfies Eq. (10), $K$ satisfies Eq. (11), and

$$\begin{aligned} M&= \frac{J}{1-\delta _{f}} \end{aligned}$$

(19)

$$\begin{aligned} N&= \frac{2s\left( 1+K\delta _{c}s\right) -K\left( 2+K\delta _{c}s\right) }{ 2+K\delta _{c}s+\delta _{f}s} \end{aligned}$$

(20)

$$\begin{aligned} R&= \frac{K^{2}}{2}\left( \frac{2+K\delta _{c}s}{1+K\delta _{c}s}\right) \end{aligned}$$

(21)

Proof

First consider Eq. (8), and set $z=\tilde{x}^{t-1}$. Use Eqs. (3) and (6) to substitute out for $V_{A}^{t+1}\left( \tilde{x}^{t}\right)$, and then differentiate the right-hand side with respect to $p_{A}$. This gives the following first order condition¹⁸

$$\begin{aligned} D_{A}^{t}\left( .\right) -\frac{p_{A}}{2}\frac{2+K\delta _{c}s}{1+K\delta _{c}s}-\frac{ \delta _{f}N}{2\left( 1+K\delta _{c}s\right) }-\frac{\delta _{f}R\left( p_{B}^{t}\left( \tilde{x}^{t-1}\right) -p_{A}\right) }{2\left( 1+K\delta _{c}s\right) ^{2}}=0 \end{aligned}$$

(22)

Impose $p_{A}=p_{A}^{t}\left( \tilde{x}^{t-1}\right)$, then use Eqs. (1) and (2) to substitute out for $p_{A}^{t}\left( \tilde{x}^{t-1}\right)$ and $p_{B}^{t}\left( \tilde{x}^{t-1}\right)$. After collecting terms, this yields one equation of the form $\alpha _{1}+\alpha _{2}\left( \tilde{x}^{t-1}-\frac{1}{2}\right) =0$. Setting $\alpha _{1}=\alpha _{2}=0$ gives the following conditions

$$\begin{aligned} 1-\frac{J}{2}\frac{2+K\delta _{c}s}{1+K\delta _{c}s}-\frac{\delta _{f}N}{ 2\left( 1+K\delta _{c}s\right) }&= 0 \end{aligned}$$

(23)

$$\begin{aligned} s-\frac{3K}{2}\frac{2+K\delta _{c}s}{1+K\delta _{c}s}+\frac{\delta _{f}RK}{ \left( 1+K\delta _{c}s\right) ^{2}}&= 0 \end{aligned}$$

(24)

Secondly consider Eq. (9), and set $z=\tilde{x}^{t-1}$. Again use Eqs. (3) and (6) to substitute out for $V_{A}^{t+1}\left( \tilde{x}^{t}\right)$. Then, use Eqs. (1) and (2) to eliminate $p_{A}^{t}\left( \tilde{x} ^{t-1}\right)$ and $p_{B}^{t}\left( \tilde{x}^{t-1}\right)$. After collecting terms, $A$’s period-$t$ valuation can be expressed in the form $\alpha _{3}+\alpha _{4}\left( \tilde{x}^{t-1}-\frac{1}{2}\right) +\alpha _{5}\left( \tilde{x}^{t-1}-\frac{1}{2}\right) ^{2}$. Since we assumed in Eq. (3) that this value equals $M+N\left( \tilde{x}^{t-1}- \frac{1}{2}\right) +R\left( \tilde{x}^{t-1}-\frac{1}{2}\right) ^{2}$, we can equate coefficients and get three equations

$$\begin{aligned} \alpha _{3}&= J+\delta _{f}M=M \end{aligned}$$

(25)

$$\begin{aligned} \alpha _{4}&= Js-JK\frac{2+K\delta _{c}s}{1+K\delta _{c}s}+K-\frac{\delta _{f}KN}{1+K\delta _{c}s}=N \end{aligned}$$

(26)

$$\begin{aligned} \alpha _{5}&= Ks-K^{2}\frac{2+K\delta _{c}s}{1+K\delta _{c}s}+\frac{\delta _{f}RK^{2}}{\left( 1+K\delta _{c}s\right) ^{2}}=R \end{aligned}$$

(27)

Since $s>0$ Eq. (24) implies that $K\ne 0$. Therefore, rewrite Eq. (24) as

$$\begin{aligned} R=\frac{3\left( 2+K\delta _{c}s\right) \left( 1+K\delta _{c}s\right) }{ 2\delta _{f}}-\frac{s\left( 1+K\delta _{c}s\right) ^{2}}{\delta _{f}K} \end{aligned}$$

(28)

and then substitute this into Eq. (27) and rearrange to find $\phi \left( K\right) =0$ where

$$\begin{aligned} \phi \left( K\right) =\delta _{f}K^{3}\left( 2+K\delta _{c}s\right) -3K\left( 2+K\delta _{c}s\right) \left( 1+K\delta _{c}s\right) ^{2}+2s\left( 1+K\delta _{c}s\right) ^{3} \end{aligned}$$

(29)

Setting $\phi \left( K\right) =0$ gives Eq. (11) in the text. Substituting Eq. (28) into the left-hand side of (27) gives the expression for $R$ in Eq. (21). To get the expressions for $J$ and $N$ in (10) and (20), jointly solve Eqs. (23) and (26). $\square$

Lemma 5

The maximization problem in Eq. (8) assumes that in every period and for every possible history, each firm sells to some young consumers, and each firm loses some but not all of its old customers due to switching. Equation (11) has a unique solution consistent with this, and it lies in $\left[ s/3,3s/8\right)$.

Proof

The maximization problem (8) uses the demand expression (7). This demand expression (7) is valid if and only if $\left| K\right| \le 1-s$. To see this, note firstly that (7) is only well defined if $1+K\delta _{c}s\ne 0$, which is satisfied provided $\left| K\right| \le 1-s$. Secondly, (7) assumes that each firm sells to a positive mass of young consumers. This requires that $\tilde{x}^{t}\in \left( 0,1\right)$ which, using Eq. (6), is equivalent to $\left| K\right| <1+K\delta _{c}s$. This is again satisfied provided $\left| K\right| \le 1-s$. Thirdly, (7) assumes that generically (i.e. whenever $\tilde{x}^{t-1}\not \in \left\{ 0,1\right\}$) each firm has old consumers both switching to and away from it. Using Sect. 3, this requires $\ddot{x}>0$ and $\dot{ x}<1$. $\ddot{x}>0$ is equivalent to $1-s>2K\left( \tilde{x} ^{t-1}-1/2\right)$: A necessary and sufficient condition for this to hold for any $\tilde{x}^{t-1}\in \left( 0,1\right)$ is that $\left| K\right| \le 1-s$. $\dot{x}<1$ is also shown to hold under the same condition.

Aim show that Eq. (11) has a unique solution on $\left[ -\left( 1-s\right) ,1-s\right]$, and that it lies in $\left[ s/3,3s/8\right)$. Note then that $K\le 1-s$ holds, because by assumption $s\le 7/10$.

Step 1 Show that Eq. (11) has exactly one solution on the interval $\left[ 0,1-s\right]$.

Step 1a Using Eq. (29), we find that $\frac{1}{2}\frac{\partial \phi \left( K\right) }{ \partial K}$ equals:

$$\begin{aligned} K^{2}\delta _{f}\left( 3+2K\delta _{c}s\right) +3\left( 1+K\delta _{c}s\right) \left[ -1-4K\delta _{c}s-2\left( K\delta _{c}s\right) ^{2}+\delta _{c}s^{2}+K\delta _{c}^{2}s^{3}\right] \nonumber \\ \end{aligned}$$

(30)

Since we are considering $K\ge 0$, $3+2K\delta _{c}s\le 3\left( 1+K\delta _{c}s\right)$ and therefore

$$\begin{aligned} \frac{1}{2}\frac{\partial \phi \left( K\right) }{\partial K}\le 3\left( 1+K\delta _{c}s\right) \left[ K^{2}\delta _{f}-1-4K\delta _{c}s-2\left( K\delta _{c}s\right) ^{2}+\delta _{c}s^{2}+K\delta _{c}^{2}s^{3}\right] \qquad \end{aligned}$$

(31)

Notice that $-4K\delta _{c}s+K\delta _{c}^{2}s^{3}<0$ since $\delta _{c}s^{2}<4$, and that $K^{2}\delta _{f}-1+\delta _{c}s^{2}\le \left( 1-s\right) ^{2}-1+s^{2}=2s\left( s-1\right) <1$. Therefore, $\frac{\partial \phi \left( K\right) }{\partial K}<0$ for all $K\in \left[ 0,1-s\right]$.

Step 1b Note that $\phi \left( 0\right) =2s>0$. Now prove that $\phi \left( 1-s\right) <0$. Substituting $K=1-s$ into $\phi \left( K\right)$ and then simplifying, we find that $\phi \left( 1-s\right)$ equals

$$\begin{aligned} \delta _{f}\left( 1\!-\!s\right) ^{3}\left[ 2\!+\!\delta _{c}s\left( 1\!-\!s\right) \right] \!-\!\left[ 1\!+\!\delta _{c}s\left( 1\!-\!s\right) \right] ^{2}\left( 6-8s\!+\!3\delta _{c}s\!-\!8\delta _{c}s^{2}\!+\!5\delta _{c}s^{3}\right) \nonumber \\ \end{aligned}$$

(32)

Clearly $\left[ 2+\delta _{c}s\left( 1-s\right) \right] /\left[ 1+\delta _{c}s\left( 1-s\right) \right] ^{2}\le 2$ because $\left[ 2+X\right] /\left[ 1+X\right] ^{2}$ decreases in $X$ for any $X\ge 0$. Therefore, to show that $\phi \left( 1-s\right) <0$, it is sufficient to prove that

$$\begin{aligned} 2\left( 1-s\right) ^{3}<6-8s+3\delta _{c}s-8\delta _{c}s^{2}+5\delta _{c}s^{3} \end{aligned}$$

(33)

First, if $s\in \left[ 0,3/5\right]$ then the right-hand side of (33) increases in $\delta _{c}$. Therefore, if (33) holds for $\delta _{c}=0$ it will also hold for any $\delta _{c}\in \left[ 0,1\right]$. When $\delta _{c}=0$ (33) becomes $2\left( 1-s\right) ^{3}<6-8s$, which is easily shown to hold for any $s\in \left[ 0,3/5\right]$. Second, if instead $s\in \left[ 3/5,7/10\right]$ then the right-hand side of (33) decreases in $\delta _{c}$. Therefore, if (33) holds for $\delta _{c}=1$, it will also hold for any $\delta _{c}\in \left[ 0,1\right]$. When $\delta _{c}=1$ (33) becomes $0<4+s-14s^{2}+7s^{3}$ which is easily seen to hold for any $s\in \left[ 3/5,7/10\right]$. Therefore, $\phi \left( 1-s\right) <0$ for any $s\in \left[ 0,7/10\right]$.

Step 1c Combining steps 1a and 1b, there is a unique $K\in \left[ 0,1-s\right]$ that solves $\phi \left( K\right) =0$.

Step 2 Show that the solution on $\left[ 0,1-s\right]$ to $\phi \left( K\right) =0$, actually lies on $\left[ s/3,3s/8\right)$.

Step 2a Show that $\phi \left( s/3\right) >0$. The terms $-3K\left( 2+K\delta _{c}s\right) \left( 1+K\delta _{c}s\right) ^{2}+2s\left( 1+K\delta _{c}s\right) ^{3}$ become $\left. \left( 1+K\delta _{c}s\right) ^{2}K\delta _{c}s^{2}\right| _{K=s/3}>0$. Also $\delta _{f}K^{3}\left( 2+K\delta _{c}s\right) >0$ since $K>0$.

Step 2b Show that $\phi \left( 3s/8\right) <0$. Letting $Y=3\delta _{c}s^{2}/8$, $\phi \left( \frac{3s}{8}\right)$ equals

$$\begin{aligned}&\left( \frac{27}{512}\right) \delta _{f}s^{3}\left( 2+Y\right) -\frac{13s }{500}\left( 2+Y\right) \left( 1+Y\right) ^{2}-\frac{1099s}{1000}\left( 2+Y\right) \\&\quad \left( 1+Y\right) ^{2}+2s\left( 1+Y\right) ^{3} \end{aligned}$$

The first two terms are negative provided that $27s^{2}/512<13/500$, and this holds because $s<7/10$. The final two terms are negative if and only if $Y<198/901\approx 0.21$, and this holds because $Y\le \left( 3/8\right) \left( 7/10\right) ^{2}=0.18375$. Therefore, $\phi \left( 3s/8\right) <0$.

Step 2c Since $\phi \left( K\right)$ strictly decreases on $\left[ 0,1-s\right]$, and $\phi \left( s/3\right) >0$ but $\phi \left( 3s/8\right) <0$, the solution to $\phi \left( K\right) =0$ must lie on $\left[ s/3,3s/8\right)$.

Step 3 Now show there is no solution to $\phi \left( K\right) =0$ for $K\in \left[ -\left( 1-s\right) ,0\right]$.

Step 3a Using Step 1a, we can write that $\frac{1}{6}\frac{\partial ^{2}\phi \left( K\right) }{\partial K^{2}}$ equals:

$$\begin{aligned} 2K\delta _{f}\left( 1+K\delta _{c}s\right) +\delta _{c}s\left( -5-12K\delta _{c}s-6\left( K\delta _{c}s\right) ^{2}+2\delta _{c}s^{2}+2K\delta _{c}^{2}s^{3}\right) \end{aligned}$$

(34)

Since $K\in \left[ -\left( 1-s\right) ,0\right]$, the first term $2K\delta _{f}\left( 1+K\delta _{c}s\right)$ is negative. To show the remainder is also negative, it is sufficient to show that $-5-12K\delta _{c}s+2\delta _{c}s^{2}<0$. The latter is toughest to satisfy when $K$ is very negative and $\delta _{c}$ is large, so substitute in $K=-\left( 1-s\right)$ and $\delta _{c}=1$. It is then sufficient to prove that $-5+12s\left( 1-s\right) +2s^{2}<0$: This is easily shown to hold for any $s\in \left[ 0,7/10\right]$. Therefore, $\partial ^{2}\phi \left( K\right) /\partial K^{2}<0$ ($\phi \left( K\right)$ is concave) for all $K\in \left[ -\left( 1-s\right) ,0\right]$.

Step 3b Using substitution, we find that $\phi \left( -\left( 1-s\right) \right) >0$ equals:

$$\begin{aligned} \left( 1-s\right) \left( 2-\delta _{c}s\left( 1-s\right) \right) \left[ 3\left( 1-\delta _{c}s\left( 1-s\right) \right) ^{2}-\delta _{f}^{2}\left( 1-s\right) ^{2}\right] +2s\left( 1-\delta _{c}s\left( 1-s\right) \right) \end{aligned}$$

which by inspection in positive. We also showed in Step 1b that $\phi \left( 0\right) >0$. Therefore, since $\phi \left( K\right)$ is concave on $\left[ -\left( 1-s\right) ,0\right]$ and positive at the boundaries of that set, it must be true that $\phi \left( K\right) >0\forall K\in \left[ -\left( 1-s\right) ,0\right]$; hence there is no root to $\phi \left( K\right)$ on that interval. $\square$

The Proof of Lemma 2

is available in the working paper (Rhodes 2014). $\square$

Proof of Proposition 3

From Eq. (10), steady state price is 1 when $s=0$. First, using Eq. (10) $J<1$ if and only if

$$\begin{aligned} K\delta _{c}s-\delta _{f}\left( s-K\right) <0 \end{aligned}$$

(35)

which is harder to satisfy as $K$ increases. We also know from Proposition 1 that $K<3s/8$. Therefore, if inequality (35) holds when evaluated at $K=3s/8$, it always holds. Substituting $K=3s/8$ into (35), we get a condition $\delta _{f}> (3\delta _{c}s) / 5$. Second, $J>1$ if and only if

$$\begin{aligned} K\delta _{c}s-\delta _{f}\left( s-K\right) >0 \end{aligned}$$

(36)

which is easier to satisfy as $K$ increases. We again know from Proposition 1 that $K\ge s/3$. Therefore, if inequality (36) holds when evaluated at $K=s/3$, it always holds. Substituting $K=s/3$ into (36), we get a condition $\delta _{f}< (\delta _{c}s) / 2$. Therefore, steady state price is definitely lower if $\delta _{f}> ( 3\delta _{c}s) / 5$ and definitely higher if $\delta _{f}< (\delta _{c}s) / 2$. Lemma 2 says that the steady state price strictly decreases in $\delta _{f}$. Therefore, there exists a unique threshold between $(\delta _{c}s) / 2$ and $(3\delta _{c}s) / 5$ such that $J=1$ when $\delta _{f}=\widetilde{\delta _{f}}$. $\square$

Proof of Proposition 4

Step 1 Show that the average price strictly decreases in $\delta _{f}$. Totally differentiate (14) with respect to $\delta _{f}$:

$$\begin{aligned} \frac{\mathrm{d}J}{\mathrm{d}\delta _{f}}+\left( \tilde{x}^{t-1}-1/2\right) ^{2}\left[ s-2K-K \frac{2+K\delta _{c}s}{\left( 1+K\delta _{c}s\right) ^{2}}\right] \frac{ \partial K}{\partial \delta _{f}} \end{aligned}$$

(37)

We know that $\mathrm{d}J/\mathrm{d}\delta _{f}<0$ from Lemma 2, and we can also prove that $\partial K/\partial \delta _{f}>0$. Therefore, it is sufficient to show that the square-bracketed term is negative, which is easily done.

Step 2 It is simple (though tedious) to show that for any $\delta _{c}$, and $\tilde{x}^{t-1}\ne 1/2$ and any $s\in \left( 0,7/10\right]$: (a) average price exceeds 1 as $\delta _{f}\rightarrow \tilde{\delta }_{f}$ and (b) average price is below 1 as $\delta _{f}\rightarrow 1$. Since average price strictly decreases in $\delta _{f}$, the threshold $\hat{\delta }_{f}\left( \left| \tilde{x}^{t-1}-1/2\right| \right)$ exists and is unique.

Step 3 Since the average price strictly increases in $\left| \tilde{x}^{t-1}-1/2\right|$ and strictly decreases in $\delta _{f}$, the threshold $\hat{\delta }_{f}\left( \left| \tilde{x}^{t-1}-1/2\right| \right)$ strictly increases in $\left| \tilde{x}^{t-1}-1/2\right|$. $\square$

The Proof of Lemma 3

is available in the working paper (Rhodes 2014). $\square$

Proof of Proposition 5

The proof follows from arguments in the text, and Lemma 2 which says that $J$ increases in $\delta _{c}$. $\square$

1.2 Proof of Proposition 6

The solution concept will again be Markov perfect equilibrium. We conjecture that firms’ equilibrium prices $p_{A}^{t}\left( \tilde{x}^{t-1}\right)$ and $p_{B}^{t}\left( \tilde{x}^{t-1}\right)$ are symmetric, i.e. $p_{A}^{t}\left( y\right) =p_{B}^{t}\left( 1-y\right)$. We also conjecture that their value functions $V_{A}^{t}\left( \tilde{x}^{t-1}\right)$ and $V_{B}^{t}\left( \tilde{x}^{t-1}\right)$ are symmetric, i.e. $V_{A}^{t}\left( y\right) =V_{B}^{t}\left( 1-y\right)$. As before, we consider pricing in some arbitrary period $t$, where firms use (potentially off-path) prices $p_{A}$ and $p_{B}$, respectively, but are expected to use equilibrium pricing strategies from period $t+1$ onwards. To simplify notation, we use the shorthand $\varDelta =p_{B}-p_{A}$ and $\varDelta _{e}^{t+1}=Ep_{B}^{t+1}-Ep_{A}^{t+1}$. We start with some preliminary lemmas.

Lemma 6

suppose that in period $t-1$ all young consumers with $x^{t-1}\le \tilde{x}^{t-1}$ bought from $A$ and all others bought from $B$. Then, demand for the product $A$ in period $t$, denoted by $D_{A}^{t}\left( p_{A},p_{B},\tilde{x}^{t-1}\right)$, is:

$$\begin{aligned} \int _{0}^{\tilde{x} ^{t-1}}F\left( \left. \frac{1+\varDelta +s}{2}\right| z\right) \mathrm{d}z+\int _{ \tilde{x}^{t-1}}^{1}F\left( \left. \frac{1+\varDelta -s}{2}\right| z\right) \mathrm{d}z+\tilde{x}^{t} \end{aligned}$$

(38)

where $\tilde{x}^{t}$ is implicitly defined by the equation

$$\begin{aligned} 1-2\tilde{x}^{t}+\varDelta +\delta _{c}\psi _{1} -\delta _{c}\psi _{2} =0 \end{aligned}$$

(39)

with $\psi _{1}$ and $\psi _{2}$ defined as follows

$$\begin{aligned} \psi _{1} = s+\int _{\dot{x}^{t+1}}^{1}f\left( z|\tilde{x}^{t}\right) \left( 2z-1-\varDelta _{e}^{t+1}-s\right) \mathrm{d}z \\ \psi _{2} = \int _{\ddot{x}^{t+1}}^{1}f\left( z|\tilde{x}^{t}\right) \left( 2z-1-\varDelta _{e}^{t+1}+s\right) \mathrm{d}z \end{aligned}$$

and where $\dot{x}^{t+1}$ and $\ddot{x}^{t+1}$ are as defined earlier, namely $\dot{x}^{t+1}=\left( 1+\varDelta _{e}^{t+1}+s\right) /2$ and $\ddot{x} ^{t+1}=\left( 1+\varDelta _{e}^{t+1}-s\right) /2$.

Proof

The first two terms of (38) are demand from old consumers. In the previous period, $A$ sold to all young consumers with $x^{t-1}\le \tilde{x}^{t-1}$; as shown earlier, they will buy $A$ in period $t$ if and only if $x^{t}\le \left( 1+p_{B}-p_{A}+s\right) /2$. In the previous period, $B$ sold to all young consumers with $x^{t-1}\ge \tilde{x}^{t-1}$; as shown earlier, they will switch to $A$ in period $t$ if and only if $x^{t}\le \left( 1+p_{B}-p_{A}-s\right) /2$. The last term of (38) is demand from young consumers. Let us define $W_{A}^{t+1}=V-E\left( \left. x^{t+1}\right| x^{t}\right) -Ep_{A}^{t+1}$. Using the same arguments as when proving Lemma 1, a young consumer in period $t$ with location $x^{t}$ has expected pay-offs from buying $A$ and $B$ given by:

$$\begin{aligned}&V-x^{t}-p_{A}+\delta _{c}\left[ W_{A}^{t+1}+\int _{\dot{x} ^{t+1}}^{1}f\left( z|x^{t}\right) \left( 2z-1-\varDelta _{e}^{t+1}-s\right) \mathrm{d}z \right] \end{aligned}$$

(40)

$$\begin{aligned}&V-\left( 1-x^{t}\right) -p_{B}+\delta _{c}\left[ W_{A}^{t+1}-s+\int _{\ddot{ x}^{t+1}}^{1}f\left( z|x^{t}\right) \left( 2z-1-\varDelta _{e}^{t+1}+s\right) \mathrm{d}z \right] \nonumber \\ \end{aligned}$$

(41)

Now (40) minus (41) is strictly decreasing in $x^{t}$ when $s=0$ (and therefore by continuity, when $s$ is sufficiently close to zero). Hence, there exists an $\tilde{x}^{t}$ such that all consumers in period $t$ with location $x^{t}\le \tilde{x}^{t}$ buy $A$, and all others buy $B$. Substituting $x^{t}=\tilde{x}^{t}$ into (40) and (41) and then equating them gives Eq. (39) in the lemma. $\square$

Lemma 7

Recall the definition of the marginal young consumer $\tilde{x}^{t}$ in Lemma 6. In steady state (i) when $s=0$, $\mathrm{d}\tilde{x}^{t}/\mathrm{d}p_{A}=-1/2$, and (ii) the following holds:

$$\begin{aligned} \left. \frac{\partial \left( \mathrm{d}\tilde{x}^{t}/\mathrm{d}p_{A}\right) }{\partial s} \right| _{s=0}=\frac{\delta _{c}}{2}\frac{\partial \Pr \left( z\ge 1/2|x^{t}=1/2\right) }{\partial x^{t}} \end{aligned}$$

(42)

Proof

Totally differentiate (39) with respect to $p_{A}$. Then, impose $p_{A}=p_{A}^{t}\left( 1/2\right)$, $p_{B}=p_{B}^{t}\left( 1/2\right)$ and $\tilde{x}^{t}=1/2$. This gives:

$$\begin{aligned} \frac{\mathrm{d}\tilde{x}^{t}}{\mathrm{d}p_{A}}=-\frac{1}{\bar{\gamma }} \end{aligned}$$

(43)

where

$$\begin{aligned} \bar{\gamma }&= 2+\delta _{c}\psi _{3}+\delta _{c}\psi _{4} \nonumber \\&-\delta _{c}\frac{\mathrm{d}\varDelta _{e}^{t+1}\left( x^{t}=1/2\right) }{\mathrm{d}x^{t}}\int _{ \frac{1-s}{2}}^{\frac{1+s}{2}}f\left( z|x^{t}=1/2\right) \mathrm{d}z \end{aligned}$$

(44)

and where

$$\begin{aligned} \psi _{3}&= - \int _{\frac{1+s}{2}}^{1}\frac{\partial f\left( z|x^{t}=1/2\right) }{\partial x^{t}}\left( 2z-1-s\right) \mathrm{d}z \\ \psi _{4}&= \int _{\frac{1-s}{2}}^{1}\frac{\partial f\left( z|x^{t}=1/2\right) }{\partial x^{t}} \left( 2z-1+s\right) \mathrm{d}z \end{aligned}$$

For part (i) note that $\bar{\gamma }=2$ when $s=0$. For part (ii) note that when $s=0$ there is a MPE in which $\varDelta _{e}^{t+1}=0$ for all $x^{t}$. Therefore, $\mathrm{d}\varDelta _{e}^{t+1}\left( x^{t}=1/2\right) /\mathrm{d}x^{t}$ is zero when $s=0$. Also note that the integral in the final term of (44) is zero when $s=0$. Therefore, the derivative of the final term in (44) with respect to $s$ around $s=0$, is zero. Consequently:

$$\begin{aligned} \frac{1}{\delta _{c}}\left. \frac{\partial \bar{\gamma }}{\partial s} \right| _{s=0}&= 2\int _{1/2}^{1}\frac{\partial f\left( z|x^{t}=1/2\right) }{\partial x^{t}}\mathrm{d}z=2\frac{\partial \Pr \left( z\ge 1/2|x^{t}=1/2\right) }{\partial x^{t}}\\ \left. \frac{\partial \left( \mathrm{d}\tilde{x}^{t}/\mathrm{d}p_{A}\right) }{ \partial s}\right| _{s=0}&= \frac{1}{\left( \left. \bar{\gamma }\right| _{s=0}\right) ^{2}}\left. \frac{\partial \bar{\gamma }}{\partial s} \right| _{s=0}=\frac{\delta _{c}}{2}\frac{\partial \Pr \left( z\ge 1/2|x^{t}=1/2\right) }{\partial x^{t}} \end{aligned}$$

$\square$

Lemma 8

In steady state (i) when $s=0$, $\mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}=-1$ and (ii) the following holds

$$\begin{aligned} \left. \frac{\partial \left( \mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}\right) }{\partial s}\right| _{s=0}=\frac{1+\delta _{c}}{2}\frac{\partial \Pr \left( z\ge 1/2|x^{t}=1/2\right) }{\partial x^{t}} \end{aligned}$$

(45)

Proof

Differentiate the demand expression in Eq. (38) with respect to $p_{A}$. Then, impose $p_{A}=p_{A}^{t}\left( 1/2\right)$, $p_{B}=p_{B}^{t}\left( 1/2\right)$, $\tilde{x}^{t-1}=\tilde{x}^{t}=1/2$. Using $\bar{\gamma }$ defined in Lemma 7 this gives:

$$\begin{aligned} \frac{\mathrm{d}D_{A}^{t}}{\mathrm{d}p_{A}}=-\frac{1}{\bar{\gamma }}-\frac{1}{2} \int _{0}^{1/2}f\left( \left. \frac{1+s}{2}\right| z\right) \mathrm{d}z-\frac{1}{2 }\int _{1/2}^{1}f\left( \left. \frac{1-s}{2}\right| z\right) \mathrm{d}z \end{aligned}$$

(46)

To prove part (i) note that given our assumptions on $f\left( x^{t},x^{t+1}\right)$, we have that $\int _{0}^{1}f\left( x^{t+1}=1/2|x^{t}=z\right) \mathrm{d}z=1$. To prove part (ii) note that again given our assumptions on $f\left( x^{t},x^{t+1}\right)$, we can write

$$\begin{aligned} \int _{0}^{1/2}f\left( \left. \frac{1+s}{2}\right| z\right) \mathrm{d}z+\int _{1/2}^{1}f\left( \left. \frac{1-s}{2}\right| z\right) \mathrm{d}z =2\Pr \left( z\ge 1/2\left| x^{t}=\frac{1-s}{2}\right. \right) \end{aligned}$$

Therefore, differentiating Eq. (46) with respect to $s$ around $s=0$, gives

$$\begin{aligned} \left. \frac{\partial \left( \mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}\right) }{\partial s}\right| _{s=0}=\frac{\delta _{c}}{2}\frac{\partial \Pr \left( x^{t+1}\ge 1/2|x^{t}=1/2\right) }{\partial x^{t}}+\frac{\partial \Pr \left( x^{t+1}\ge 1/2|x^{t}=1/2\right) }{\partial x^{t}} \end{aligned}$$

(47)

$\square$

Lemma 9

In steady state:

$$\begin{aligned} \left. \frac{\partial D_{A}^{t}/\partial \tilde{x}^{t-1}}{\partial s}\right| _{s=0}=f\left( \left. \frac{1}{2}\right| \frac{1}{2}\right) \end{aligned}$$

(48)

Proof

Differentiate the demand expression (38) with respect to $\tilde{x}^{t-1}$:

$$\begin{aligned} \frac{\partial D_{A}^{t}}{\partial \tilde{x}^{t-1}}=F\left( \left. \frac{ 1+\varDelta +s}{2}\right| \tilde{x}^{t-1}\right) -F\left( \left. \frac{ 1+\varDelta -s}{2}\right| \tilde{x}^{t-1}\right) \end{aligned}$$

(49)

Substitute in $\tilde{x}^{t-1}=1/2$ and $\varDelta =p_{B}^{t}\left( 1/2\right) -p_{A}^{t}\left( 1/2\right) =0$, then differentiate the resulting expression with respect to $s$. $\square$

Lemma 10

In steady state, the derivative of $\frac{ \partial \left( \mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}\right) }{\partial \tilde{x}^{t-1}}$ with respect to $s$ is zero at $s=0$.

Proof

Differentiate Eq. (49) with respect to $p_{A}$ to get

$$\begin{aligned} \frac{\partial \left( \mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}\right) }{\partial \tilde{x}^{t-1}}= \frac{1}{2}\left[ -f\left( \left. \frac{1+\varDelta +s}{2}\right| \tilde{x} ^{t-1}\right) +f\left( \left. \frac{1+\varDelta -s}{2}\right| \tilde{x} ^{t-1}\right) \right] \end{aligned}$$

(50)

Then, substitute in $\tilde{x}^{t-1}=1/2$ and $\varDelta =p_{B}^{t}\left( 1/2\right) -p_{A}^{t}\left( 1/2\right) =0$. Now differentiate with respect to $s$, and note that radial symmetry implies $f^{\prime }\left( 1/2|1/2\right) =0$. $\square$

Now for the main proof.

Proof of Proposition 6

In this problem, the pay-off-relevant state variable in period $t$ is $\tilde{x }^{t-1}$. As stated earlier, we hypothesize a symmetric MPE which is continuous around $s=0$, and where the steady state has $\tilde{x}^{t}=1/2$ and both firms charging the same price in every period $t$.

In period $t$, firm $A$ chooses $p_{A}$ to maximize $p_{A}D_{A}^{t}\left( p_{A},p_{B},\tilde{x}^{t-1}\right) +\delta _{f}V_{A}^{t+1}\left( \tilde{x} ^{t}\right)$, which gives a first order condition

$$\begin{aligned} D_{A}^{t}\left( p_{A},p_{B},\tilde{x}^{t-1}\right) +p_{A}\frac{\mathrm{d}D_{A}^{t}}{ \mathrm{d}p_{A}}+\delta _{f}\frac{\mathrm{d}V_{A}^{t+1}\left( \tilde{x}^{t}\right) }{\mathrm{d}\tilde{x} ^{t}}\frac{\mathrm{d}\tilde{x}^{t}}{\mathrm{d}p_{A}}=0 \end{aligned}$$

(51)

Firstly, impose $p_{A}=p_{A}^{t}\left( 1/2\right)$, $p_{B}=p_{B}^{t}\left( 1/2\right)$ and $\tilde{x}^{t-1}=\tilde{x}^{t}=1/2$. Then, differentiate the resulting expression with respect to $s$ around $s=0$. In doing this, note (i) that in steady state $D_{A}^{t}\left( .\right) =1$, (ii) the properties of $\mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}$ given in Lemma 8, (iii) that when $s=0$ firm $A$ charges a price of 1 and has value $V_{A}^{t+1}=1/\left( 1-\delta _{f}\right)$ which is not a function of $\tilde{x}^{t}$, and (iv) that $\mathrm{d}\tilde{x}^{t}/\mathrm{d}p_{A}=-1/2$ when $s=0$ (Lemma 7). Letting $\bar{p}$ be the steady state price, we find that:

$$\begin{aligned} \left. \frac{\partial \bar{p}}{\partial s}\right| _{s=0}=\frac{1+\delta _{c}}{2}\frac{\partial \Pr \left( x^{t+1}\ge 1/2|x^{t}=1/2\right) }{ \partial x^{t}}-\frac{\delta _{f}}{2}\left[ \left. \frac{\partial \left( \mathrm{d}V_{A}^{t+1}\left( 1/2\right) /\mathrm{d}\tilde{x}^{t}\right) }{\partial s} \right| _{s=0}\right] \nonumber \\ \end{aligned}$$

(52)

Secondly, substitute $p_{A}=p_{A}^{t}\left( \tilde{x} ^{t-1}\right)$ and $p_{B}=p_{B}^{t}\left( \tilde{x}^{t-1}\right)$ into Eq. (51) and call the left-hand side $F.O.C.$ Then, differentiate the expression with respect to $\tilde{x}^{t-1}$ to get:

$$\begin{aligned} \frac{d\left( F.O.C.\right) }{\mathrm{d}p_{A}^{t}}\frac{\mathrm{d}p_{A}^{t}}{\mathrm{d}\tilde{x}^{t-1}}+ \frac{\mathrm{d}\left( F.O.C.\right) }{\mathrm{d}p_{B}^{t}}\frac{\mathrm{d}p_{B}^{t}}{\mathrm{d}\tilde{x}^{t-1}}+ \left[ \frac{\partial D_{A}^{t}}{\partial \tilde{x}^{t-1}}+p_{A}^{t}\frac{ \partial \left( \mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}^{t}\right) }{\partial \tilde{x}^{t-1}} \right] =0\quad \end{aligned}$$

(53)

The aim now is to differentiate this equation with respect to $s$ around $s=0$. To do this note that when $s=0$, (i) $F.O.C.=1+p_{B}^{t}-2p_{A}^{t}$, (ii) $p_{A}^{t}$ and $p_{B}^{t}$ both equal 1 and so are not a function of $\tilde{x}^{t-1}$, and (iii) that according to Lemma 10, both $\partial \left( \mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}\right) /\partial \tilde{x} ^{t-1}$and its derivative with respect to $s$, are zero. Also use Lemma 9 which gives an expression for the derivative of $\partial D_{A}^{t}/\partial \tilde{x}^{t-1}$ with respect to $s$. Then,

$$\begin{aligned} -2\left. \frac{\partial \left( \mathrm{d}p_{A}^{t}/\mathrm{d}\tilde{x}^{t-1}\right) }{\partial s}\right| _{s=0}+\left. \frac{\partial \left( \mathrm{d}p_{B}^{t}/\mathrm{d}\tilde{x} ^{t-1}\right) }{\partial s}\right| _{s=0}+f\left( \left. \frac{1}{2} \right| \frac{1}{2}\right) =0 \end{aligned}$$

(54)

We look for a symmetric equilibrium in which $p_{A}^{t}\left( y\right) =p_{B}^{t}\left( 1-y\right)$ therefore $\mathrm{d}p_{A}^{t}/\mathrm{d}\tilde{x}^{t-1}\left( \frac{1}{2}\right) =-\mathrm{d}p_{B}^{t}/\mathrm{d}\tilde{x}^{t-1}\left( \frac{1}{2}\right)$. So differentiating the above equation with respect to $s$ at $s=0$, gives:

$$\begin{aligned} \left. \frac{\partial \left( \mathrm{d}p_{A}^{t}\left( \frac{1}{2}\right) /\mathrm{d}\tilde{x} ^{t-1}\right) }{\partial s}\right| _{s=0}=\frac{f\left( \left. \frac{1}{ 2}\right| \frac{1}{2}\right) }{3} \end{aligned}$$

(55)

Thirdly, consistency of the value functions requires that

$$\begin{aligned} V_{A}^{t}\left( z\right) =p_{A}^{t}\left( z\right) \times D_{A}^{t}\left( p_{A}^{t}\left( z\right) ,p_{B}^{t}\left( z\right) ,z\right) +\delta _{f}V_{A}^{t+1}\left( \tilde{x}^{t}\left( p_{A}^{t}\left( z\right) ,p_{B}^{t}\left( z\right) \right) \right) \end{aligned}$$

(56)

Totally differentiating with respect to $z$, using the envelope theorem and then substituting $z=\tilde{x}^{t-1}$, gives:

$$\begin{aligned} \frac{\mathrm{d}V_{A}^{t}}{\mathrm{d}\tilde{x}^{t-1}}=\left[ p_{A}^{t}\frac{\mathrm{d}D_{A}^{t}}{ \mathrm{d}p_{B}^{t}}+\delta _{f}\frac{\mathrm{d}V_{A}^{t+1}}{\mathrm{d}\tilde{x}^{t}}\frac{\mathrm{d}\tilde{x} ^{t}}{\mathrm{d}p_{B}^{t}}\right] \frac{\mathrm{d}p_{B}^{t}}{\mathrm{d}\tilde{x}^{t-1}}+p_{A}^{t}\frac{ \partial D_{A}^{t}}{\partial \tilde{x}^{t-1}} \end{aligned}$$

(57)

Since $D_{A}^{t}\left( \cdot \right)$ and $\tilde{x}^{t}$ only depend upon current prices through $\varDelta$, $\mathrm{d}D_{A}^{t}/\mathrm{d}p_{B}^{t}=-\mathrm{d}D_{A}^{t}/\mathrm{d}p_{A}^{t}$ and $\mathrm{d}\tilde{x} ^{t}/\mathrm{d}p_{B}^{t}=-\mathrm{d}\tilde{x}^{t}/\mathrm{d}p_{A}^{t}$. Therefore, we can make use of Eq. (51) (evaluated at $p_{A}=p_{A}^{t}\left( \tilde{x }^{t-1}\right)$ and $p_{B}=p_{B}^{t}\left( \tilde{x}^{t-1}\right)$) to rewrite the above as:

$$\begin{aligned} \frac{\mathrm{d}V_{A}^{t}}{\mathrm{d}\tilde{x}^{t-1}}=D_{A}^{t}\frac{\mathrm{d}p_{B}^{t}}{\mathrm{d}\tilde{x} ^{t-1}}+p_{A}^{t}\frac{\partial D_{A}^{t}}{\partial \tilde{x}^{t-1}} \end{aligned}$$

(58)

Next consider steady state and substitute $\mathrm{d}p_{B}^{t}/\mathrm{d}\tilde{x} ^{t-1}\left( \frac{1}{2}\right) =-\mathrm{d}p_{A}^{t}/\mathrm{d}\tilde{x}^{t-1}\left( \frac{1}{ 2}\right)$ into Eq. (58). Then, differentiate the resulting expression with respect to $s$ at $s=0$. Finally, combine this last equation with Eqs. (55) and (52), to get the required expression for $\left. \partial \bar{p} /\partial s\right| _{s=0}$. $\square$