1 Introduction

Real-time kinematic (RTK) or postprocessing kinematic (PPK) solutions could achieve centimeter-level accuracy once integer carrier-phase ambiguity resolved, which is one of the best choices for mobile surveying and mapping (Puente et al. 2013). However, the integer property of the ambiguity in precise point positioning (PPP) is destroyed by the satellite- and receiver-dependent fractional cycle bias (FCB); thus, only float ambiguity PPP technology was widely used. Fortunately, several methods for integer ambiguity resolution (IAR)-enabled PPP have been developed during the last decade. According to the description of principles relevant to PPP-RTK methods from Teunissen and Khodabandeh (2015), there are two types of IAR-PPP models, i.e., the integer recovery clock/decoupled satellite clock (IRC/DSC) model and the uncalibrated phase delay/fractional cycle bias (UPD/FCB) model. The basic idea of these models is to separate fractional parts from float ambiguities to recover the integer nature. In accordance with the benefit of the very precise carrier phase, PPP also has the potential of providing a reliable centimeter-level positioning accuracy, whose performance is close to RTK or PPK precision (Geng et al. 2011). However, there are enormous challenges through mobile mapping by the kinematic PPP in the case of dealing with restrictive physical environment. The obstructive conditions encompassing urban canyon, tunnels or high receiver dynamics will trigger loss of tracking locks for satellites. As a result, frequent interruptions and cycle slips lead to re-initialization of the corresponding ambiguities; therefore, a long re-convergence period to a satisfactory precision of float solution is required for IAR (Geng et al. 2010). Moreover, the partial ambiguity-fixed subset with insufficient satellite visibility and limited spatial geometry may bring risks to positioning accuracy and reliability.

In order to enhance ambiguity resolution for kinematic PPP, various efficient methods and schemes are proposed. First of all, if atmospheric delay augmentation information derived from dense regional reference network is provided, instantaneous ambiguity resolution could be realized and kinematic PPP does not undergo signal-degrading circumstances readily (Li et al. 2011). Secondly, multi-GNSS and triple-frequency observations are straightforward to improve PPP results and furthermore its ambiguity resolution. Integrating multi-GNSS provides more satellites to strengthen spatial geometry when single constellation lacks in enough satellites, thereby making float ambiguities estimated precisely (Li et al. 2014a). Compared with GPS-only PPP, the positioning availability with quad-constellations is increased from 40% to more than 99.5% when elevation cutoff is set to 40° to simulate corresponding constrained conditions (Li et al. 2015). On this basis, Li et al. (2017c) accomplished multi-GNSS phase delay estimation including BDS GEO and Galileo satellites and concluded that 13.4 min for fixing is achievable for GCRE four-system solutions in the case of 30° cutoff elevation, while the GPS-only results are unreliable. Liu et al. (2017) investigated some combined IAR-PPP strategies using GPS, GLONASS and BDS (IGSO, MEO) hybrid constellations. For kinematic PPP with a 10-min observation time, only 16.2% fixed epochs could be obtained with GPS alone, while it reaches up to 75.9% with adding GLONASS and 90% with BDS collaboration. Meanwhile, the correct fixing rate is also improved from 51.7% for GPS alone, to 98.3% for three systems. Similar results on multi-GNSS IAR-PPP can be found in Geng and Shi (2017), Li et al. (2017a) and Yi et al. (2017). Unlike multi-GNSS, the main purpose of changing from a dual- to a triple-frequency model is to reduce the ambiguity dilution of precision (ADOP) and improve model strength for successful ambiguity resolution (Teunissen et al. 2014). By using simulated data, Geng and Bock (2013) constructed an ambiguity-fixed ionosphere-free observable, which was treated as precise pseudo-range to assist in speeding up narrow-lane ambiguity resolution. Ambiguity-fixed solutions at a success rate of 78% were achieved within 2 min in triple-frequency PPP, whereas the success rate was almost zero in dual-frequency PPP. Li et al. (2014b) adopted the similar cascading IAR strategy in Geng and Bock (2013) to implement triple-frequency IAR-PPP. The difference is that a longer wavelength wide-lane model is constructed by the optimal triple-frequency pseudo-range linear combination, which shows that 99.15% of 2592 stations could surpass the success rate critical value in 10 s. Gu et al. (2015) and Laurichesse and Blot (2016) also presented that real triple-frequency GNSS data were conducive to fast ambiguity resolution and convergence in PPP. Finally, cycle slips always have impact on positioning accuracy, where continuously and precisely estimated ambiguities are broken. Geng et al. (2010) developed a cycle slip correction (CSC) method based on precisely predicted ionospheric delays for rapidly integer resolution. In addition, Zhang and Li (2012) proposed the WL-L3-LX cascade cycle slip resolution strategy to connect phase segments. Ye et al. (2016) as well as Zhang and Li (2016) analyzed the improvement in GPS + GLONASS observations for cycle slip fixing and the benefits of triple-frequency observations on cycle ship correction, respectively. These CSC methods could achieve high-accuracy kinematic PPP continuously without re-initialization.

Obviously, none of the above solutions are beyond the perspective of GNSS itself. In fact, GNSS integrated with strapdown inertial navigation system (INS) has become a standard mode in modern navigation systems. The self-contained manner makes INS free from the external abrupt changes, the impact of signal deteriorating and blocking environment. Therefore, its superior and stable positioning accuracy in a short timescale improves position and float ambiguity estimation when tightly coupled integration is applied. For instance, in RTK positioning, the INS-aided IAR and its performance have been extensively investigated. Grejner-Brzezinska et al. (1998) utilized separation between INS-predicted and candidate position to exclude some suspicious candidates and shorten on-the-fly ambiguity search time. Scherzinger (2000) presented that integer ambiguity recovery time was 1–4 s in INS-aided RTK, which was compared to 10–15 s in standard RTK after full outages lasting up to 60 s. Han et al. (2017) proposed INS-aided partial ambiguity resolution with GPS and BDS data. Consequently, a success rate greater than 90% and fast ambiguity recovery within 5 s for a 19-s outage could be obtained with inertial aiding. However, as far as we know, few researches focus on the technique and performance evaluation of IAR-PPP with INS aiding. Liu et al. (2016) introduced INS to ambiguity-fixed PPP for the first time, but only provided model description and initial results. Therefore, a comprehensive analysis and assessment of IAR with INS aiding for kinematic PPP are still required.

2 PPP/INS tightly coupled model and integer ambiguity resolution

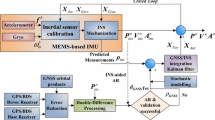
Tightly coupled (TC) integration is characterized by a single Kalman filter, which fuses both measurement information from GNSS and inertial sensor directly. When inertial sensor inherent biases and systematic errors are well calibrated along with the convergent filtering, INS is capable of predicting high-accuracy position using mechanization. With the precisely predicted position information, kinematic PPP is augmented in terms of positioning continuity, availability and reliability. System and measurement model construction are essential prerequisites for implementing integrated filtering. So the PPP/INS TC model is described in this section, followed by IAR strategy and procedures.

2.1 System model

The system model is established in the WGS-84 ECEF reference frame, where GNSS usually operates position calculation. System states of TC model can be classified into three categories: navigation parameters, INS-dependent parameters and GNSS-dependent parameters. The components of GNSS-dependent parameters rely on which positioning mode is adopted, such as short- or long-baseline double-differenced positioning, ionosphere-free or uncombined PPP. In our method, ionosphere-free PPP model with single differenced (SD) between simultaneously observed satellites is embedded into TC architecture. Therefore, receiver clock bias is eliminated, while single-differenced float ambiguities become estimated states.

The phi angle error equations describing a dynamics process of navigation parameters are expressed as follows:

$$ \left\{ \begin{aligned} & \delta \dot{\varvec{r}}^{e} = \delta \varvec{v}^{e} +\varvec{\xi}_{\varvec{r}} \hfill \\ & \delta \dot{\varvec{v}}^{e} = \varvec{N}\delta \varvec{r}^{e} - \text{2}\varvec{\omega}_{ie}^{e} \times \delta \varvec{v}^{e} + \varvec{f}^{e} \times\varvec{\phi}+ \varvec{R}_{b}^{e} \varvec{a}^{b} +\varvec{\xi}_{\varvec{v}} \hfill \\ & \dot{\varvec{\phi }} = -\varvec{\omega}_{ie}^{e} \times\varvec{\phi}- \varvec{R}_{b}^{e}\varvec{\varepsilon}^{b} +\varvec{\xi}_{\varvec{\phi}} \hfill \\ \end{aligned} \right. $$
(1)

where dots denote the time derivations, the cross product operator makes a vector to a skew-symmetric matrix, superscript and subscript e, i, b stand for ECEF, earth-centered inertial (ECI) and inertial sensor body frames, respectively, the b-frame is defined as right–front–up axis set which is aligned with the pitch, roll and yaw. \( \delta \varvec{r}^{e} \), \( \delta \varvec{v}^{e} \) and \( \varvec{\phi} \) are the position, velocity and misalignment error vectors in the e-frame, the misalignment \( \varvec{\phi} \) is the attitude error of b-frame with respect to e-frame, \( \varvec{R}_{b}^{e} \) is the rotation matrix from b-frame to e-frame, using the rotation matrix \( \varvec{R}_{b}^{e} \), the specific force in b-frame is transformed to \( \varvec{f}^{e} \), rotation rate of earth \( \varvec{\omega}_{ie}^{e} \) relative to i-frame is expressed in e-frame, \( \varvec{N} \) is the tensor of the gravitational gradients, \( \varvec{a}^{b} \) and \( \varvec{\varepsilon}^{b} \) are synthetic systematic errors of accelerometer and gyroscope; here, only biases are considered and other inertial sensor errors like scale factor and non-orthogonality are neglected, \( \varvec{\xi}_{\varvec{r}} \), \( \varvec{\xi}_{\varvec{v}} \) and \( \varvec{\xi}_{\varvec{\phi}} \) indicate random walk process driving noise vectors for the position, velocity and attitude, respectively.

The INS-dependent parameter, only including accelerometer and gyroscope biases, is described as random walk process:

$$ \left\{ \begin{aligned} \dot{\varvec{a}}^{b} =\varvec{\xi}_{\varvec{a}} \hfill \\ \dot{\varvec{\varepsilon }}^{b} =\varvec{\xi}_{\varvec{\varepsilon}} \hfill \\ \end{aligned} \right. $$
(2)

where \( \varvec{\xi}_{\varvec{a}} \) and \( \varvec{\xi}_{\varvec{\varepsilon}} \) denote noise vectors of random walk process. Those spectral densities of process noise vary with different grade inertial sensors, dynamic conditions and physical environments. The technical specification of inertial sensors and Allan variance analysis technique provide a coarse approximate value, and in the case of known reference trajectory, fine-tuning is followed by analyzing quality indicators of TC filtering results.

The SD float ambiguity errors \( \delta \varvec{N}_{n \times 1} \) and tropospheric zenith wet delay error (ZWD) δTw both belong to the GNSS-dependent parameters and are modeled as random walk process:

$$ \left\{ \begin{aligned} & \delta \dot{\varvec{N}}_{n \times 1} =\varvec{\xi}_{\varvec{N}} \hfill \\ & \delta \dot{T}_{w} = \xi_{{T_{w} }} \hfill \\ \end{aligned} \right. $$
(3)

where \( \varvec{\xi}_{\varvec{N}} \) and \( \xi_{{T_{w} }} \) show the process noise of SD float ambiguities and ZWD.

2.2 Measurement model

Single-differenced ionosphere-free measurement model is built, where the healthy satellite with the highest elevation and without cycle slip is selected as reference satellite. For the pseudo-range and carrier-phase measurements, the linearized equations for one satellite–receiver pair can be written as follows:

$$ \left\{ \begin{aligned} & v_{P}^{i,r} = \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }^{i,r} \cdot \delta \varvec{r}^{e} + \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }^{i,r} \left( {\varvec{l}^{e} \times } \right) \cdot\varvec{\phi}+ MF^{i,r} \cdot \delta T_{w} + \eta_{P}^{i,r} \hfill \\ & v_{L}^{i,r} = \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }^{i,r} \cdot \delta \varvec{r}^{e} + \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }^{i,r} \left( {\varvec{l}^{e} \times } \right) \cdot\varvec{\phi}+ MF^{i,r} \cdot \delta T_{w} + \delta N^{i,r} + \eta_{L}^{i,r} \hfill \\ \end{aligned} \right. $$
(4)

where (·)i,r = (·)i − (·)r refers to a variable between satellites i and r, the superscript r denotes reference satellite, vP (m) and vL (m) are the observed-minus-computed pseudo-range and carrier-phase measurements, which contain errors correction such as relativistic effect, phase windup, tide loading, phase center offsets and variations of satellite and receiver (Kouba and Heroux 2001), \( \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} } \) represents the direction cosines of the unit vector from receiver to satellite, \( \varvec{l}^{e} \) symbolizes the lever arm vector expressed in e-frame and \( \left( {\varvec{l}^{e} \times } \right) \) is the skew-symmetric matrix with respect to \( \varvec{l}^{e} \), MF indicates the tropospheric mapping function and global mapping function (GMF) is applied, ηP and ηL are measurement errors of un-differenced pseudo-range and carrier phase, they are regarded as white Gaussian noise and the elevation-dependent weighting scheme is used (Li et al. 2017a), a priori precision of 3 mm and 0.9 m is set for pseudo-range and carrier phase in kinematic PPP; then, the single-differenced covariance matrix is obtained by means of the covariance propagation law.

One can form the final mathematical equations of measurement model for all satellite–receiver pairs at present epoch according to Eq. (4). Meanwhile, continues-time system Eqs. (1)–(3) are transformed into discrete-time formulations. With the system propagation and measurement update, the closed-loop extent Kalman filter is employed to maintain optimal estimate of the state vector and covariance matrix in PPP/INS TC integration. Despite the fact that only position and misalignment error states exist in measurement Eq. (4), the remaining error states can be still estimated precisely because of the error covariance matrix. The covariance matrix represents the degree of correlation between error states themselves. This kind of highly coupled information may be used to infer one error state from others.

2.3 Integer ambiguity resolution

Compared to PPP-alone IAR, the natural attribute of SD float wide-lane (SDWL) and ionosphere-free (SDIF) ambiguities in the PPP/INS TC integration is unchanged so that they could share the same procedure and strategy for IAR. Here, the similar IAR algorithm and strategy in PPP described by Li et al. (2014a, 2016, 2017a) are adopted. The flowchart of IAR-PPP/INS TC integration illustrated in Fig. 1 shows methodology procedures.

Fig. 1
figure 1

Flowchart of IAR-PPP/INS TC integration. The block with dotted line and color denotes IAR module. The red line is to eliminate the confusion of process sequence related to PPP/INS TC filtering module. All ambiguities are SD form, and “SD” is omitted

Full size image

In the partial IAR strategy based on LAMBDA method (Teunissen 1995), some adjustments are made for IAR-PPP/INS TC integration. Firstly, a narrow-lane (NL) ambiguity is discarded, if filtering epochs of the corresponding IF ambiguity are less than five and the success rate of integer rounding is less than 0.99. These two criterions are used mainly to exclude emerging NL ambiguities of lower precisions. Therefore, the ambiguity involved in IAR for the first time will be also suspected, if attempt of full ambiguity resolution fails at this time. Secondly, it is more possible that satellites of low elevation suffer from contaminated measurements because of low signal-to-noise ratio and multi-path effect. So satellites below an elevation angle of 15° are rejected one by one from low to high angle, until partial IAR satisfies predefined condition of successfully fixed or there are no relevant satellites. If the two previous steps fail to fix ambiguities, the remaining SDNL ambiguities will be decorrelated by Z-transformation in LAMBDA and their decorrelated variances are obtained simultaneously. According to the value of decorrelated variances from large to small, decorrelated ambiguities are excluded one by one to form a subset for integer candidates searching. The successful ambiguity resolution is defined that both bootstrapping success rate and ratio test could pass the threshold of 0.99 and 2.0, respectively. For fear of poor spatial geometry, only if at least five fixed ambiguities are validated successfully, can IAR at this epoch be attained finally. Otherwise, none of the ambiguities is fixed, and float state is kept.

Other non-ambiguity states in PPP/INS TC filter are correlated with SDIF ambiguities, while SDIF ambiguities are correlated with fixed SDNL ambiguities. The chained correlation information could make other non-ambiguity states and SDIF ambiguities refined by fixed SDNL ambiguities, which are treated as virtual measurements. Indeed, this state updating strategy is widely used for ambiguity resolution in PPP as well as double-differenced positioning (Takasu and Yasuda 2010; Geng et al. 2011; Li et al. 2017a). The refined SDIF ambiguities could bring a tight constraint in the float ambiguity estimation of subsequent epochs and thus improve the fixing ratio especially in kinematic positioning. Such approach is called “hold ambiguity” mode. However, a successful but not correct fixed ambiguity will lead to negative impact on subsequent states estimation when the “hold ambiguity” mode is used. Therefore, dual parallel processing lines are designed, including an “updating” processing line and a “hold ambiguity” processing line. The “updating” processing line is in charge of updating a copy of filtering states using all of the successfully fixed ambiguities. Its primary purpose is to output navigation and positioning parameters at each epoch, while “hold ambiguity” processing line is designed to update filtering states directly with “correct” fixed ambiguities for transmitting this tight constraint to next epoch. In our algorithm, one is regarded as the “correct” fixed ambiguity at a high confidence level when the ambiguity is fixed successfully to an identical integer over three successive epochs. Similarly, at least five “correct” fixed ambiguities are required to activate the “hold ambiguity” processing line.

It is worth indicating that the adopted strategies and parameter setting above are based on empirical consideration in practice. They are relatively effective for reliable IAR in PPP or PPP/INS TC integration, but may not be suitable for other applications, such as double-differenced RTK.

3 Theoretical analysis of INS-aided IAR

In this section, theoretical analysis is presented for the improvement in IAR with INS aiding. As we know, IAR performance relies on reliable and precise float ambiguity information. In our PPP/INS TC integration, float ambiguity updating is based on different priori information in three situations. Firstly, the float ambiguities are estimated continuously and constrained by previous accurate float ambiguities. Secondly, the “hold ambiguity” mode is activated and current float ambiguities are constrained tightly by previous “correct” fixed ambiguities. Finally, the signal tracking interruption occurs and all ambiguities are re-initialized with pseudo-range observations. Obviously, float ambiguities in the first two situations have been estimated precisely by PPP itself, and adding INS information is barely of extra use. However, in the third situation, float ambiguities are in the absence of constrain; thus, INS which retained the high-accuracy position information from previous results could assist in retrieving initial float ambiguities with acceptable precision. With the more reliable and precise float ambiguities, IAR performance is improved automatically. Consequently, the next part was concentrated on the third condition, where all float ambiguities are re-initialized during GNSS outages.

To be more explicit, the system and measurement model of PPP/INS TC integration are rewritten. The filtering states are partitioned as:

$$ \varvec{x} = \left( {\delta \tilde{\varvec{r}},\delta \varvec{N},\varvec{x}_{\text{oth}} } \right)^{\text{T}} $$
(5)

where \( \delta \tilde{\varvec{r}} \) is the position error with respect to GNSS antenna, the position of GNSS antenna can be inferred from the inertial sensor center and the lever arm, and \( \delta \tilde{\varvec{r}} \) can be expressed as \( \delta \varvec{\tilde{r} = }\delta \varvec{r}^{e} + \left( {\varvec{l}^{e} \times } \right) \cdot\varvec{\phi} \), \( \delta \varvec{N} \) is SDIF ambiguity errors, \( \varvec{x}_{\text{oth}} \) represents all of the remaining errors.

Because the float ambiguities are all re-initialized, there is no correlation between float ambiguities and other states, and the priori state covariance \( \varvec{P}_{x}^{ - } \) with respect to \( \varvec{x} \) can be partitioned as:

$$ \varvec{P}_{\varvec{x}}^{ - } = \left( {\begin{array}{lll} {\varvec{P}_{{\delta \tilde{\varvec{r}}}}^{ - } } & \quad {\mathbf{0}} &\quad {\varvec{P}_{{\delta \tilde{\varvec{r}},{\text{oth}}}}^{ - } } \\ {\mathbf{0}} &\quad {\varvec{P}_{{\delta \varvec{N}}}^{ - } } &\quad {\mathbf{0}} \\ {\varvec{P}_{{{{\rm oth}},\delta \tilde{\varvec{r}}}}^{ - } } &\quad {\mathbf{0}} & \quad {\varvec{P}_{{\rm oth}}^{ - } } \\ \end{array} } \right) $$
(6)

Considering that tropospheric zenith wet delay varies slowly and could be predicted for subsequent epochs during GNSS outages, the corresponding state error is removed from Eq. (4), which is simplified as:

$$ \left\{ \begin{aligned} & v_{P}^{i,r} = \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }^{i,r} \cdot \delta \tilde{\varvec{r}} + \eta_{P}^{i,r} \hfill \\ & v_{L}^{i,r} = \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }^{i,r} \cdot \delta \tilde{\varvec{r}} + \delta N^{i,r} + \eta_{L}^{i,r} \hfill \\ \end{aligned} \right. $$
(7)

In fact, the pseudo-range equation is merely used to calculate \( \delta \tilde{\varvec{r}} \), such measurement information has been expressed with a priori information \( \varvec{P}_{{\delta \tilde{\varvec{r}}}}^{ - } \) in Eq. (6). Besides, INS could predict precise position and code solution is not required. Therefore, the decision is to remove the pseudo-range equation from Eq. (7). Note that these simplified operations are only for facilitating analysis.

Assuming there are n satellites (excluding the reference satellite), the final measurement equation is:

$$ \varvec{v}_{L} = \left( {\begin{array}{lll} {\varvec{H}_{{\delta \tilde{\varvec{r}}}} } & \varvec{I} & {\mathbf{0}} \\ \end{array} } \right)\left( {\begin{array}{l} {\delta \tilde{\varvec{r}}} \\ {\delta \varvec{N}} \\ {\varvec{x}_{\text{oth}} } \\ \end{array} } \right){ + }\varvec{\eta}_{L} $$
(8)

where \( \varvec{v}_{L} \) is the measurement error vector, \( \varvec{\eta}_{L} \) refers to the measurement noise vector, whose covariance matrix is expressed as \( \varvec{R}_{L} \), \( \varvec{I} \) is (n × n) identity matrix.

An alternative form for the posteriori state covariance \( \varvec{P}_{{}}^{ + } \) in Kalman filter was applied (Crassidis and Junkins 2011):

$$ \varvec{P}^{ + } = \varvec{P}^{ - } - \varvec{P}^{ - } \varvec{H}^{\text{T}} \left( {\varvec{HP}^{ - } \varvec{H}^{\text{T}} + \varvec{R}} \right)^{ - 1} \varvec{HP}^{ - } $$
(9)

Substituting Eqs. (6) and (8) into Eq. (9) obtains the updated float ambiguity covariance \( \varvec{P}_{{\delta \varvec{N}}}^{ + } \):

$$ \varvec{P}_{{\delta \varvec{N}}}^{ + } = \varvec{P}_{{\delta \varvec{N}}}^{ - } - \varvec{P}_{{\delta \varvec{N}}}^{ - } \varvec{R}_{{\delta \varvec{N}}}^{ - 1} \varvec{P}_{{\delta \varvec{N}}}^{ - } $$
(10)

with

$$ \varvec{R}_{{\delta \varvec{N}}}^{{}} = \varvec{H}_{{\delta \tilde{\varvec{r}}}} \varvec{P}_{{\delta \tilde{\varvec{r}}}}^{ - } \varvec{H}_{{\delta \tilde{\varvec{r}}}}^{T} + \varvec{P}_{{\delta \varvec{N}}}^{ - } + \varvec{R}_{L} $$
(11)

An examination of Eq. (10) reveals that \( \varvec{P}_{{\delta \varvec{N}}}^{ + } \) is only influenced by the satellite geometry \( \varvec{H}_{{\delta \tilde{\varvec{r}}}} \) and the priori positioning information \( \varvec{P}_{{\delta \tilde{\varvec{r}}}}^{ - } \) due to the fact that items \( \varvec{P}_{{\delta \varvec{N}}}^{ - } \) and \( \varvec{R}_{L} \) are deterministic. It implies that better satellite geometry and high-accuracy positioning information could improve float ambiguity estimation. For the INS-aided IAR, improving the priori positioning information is dominant.

Presuming that \( \varvec{P}_{{\delta \varvec{\tilde{r},s}}}^{ - } \) denotes the priori positioning information from INS mechanization, \( \varvec{P}_{{\delta \varvec{\tilde{r},c}}}^{ - } \) from a code solution, two float ambiguity covariance associated with two priori positioning information are obtained and the difference is expressed as follows:

$$ \begin{aligned} \varvec{P}_{{\delta \varvec{N,s}}}^{ + } - \varvec{P}_{{\delta \varvec{N,c}}}^{ + } &= \varvec{P}_{{\delta \varvec{N}}}^{ - } \left( {\varvec{R}_{{\delta \varvec{N,c}}}^{ - 1} - \varvec{R}_{{\delta \varvec{N,s}}}^{ - 1} } \right)\varvec{P}_{{\delta \varvec{N}}}^{ - }\\ &= \varvec{P}_{{\delta \varvec{N}}}^{ - } \varvec{R}_{{\delta \varvec{N,c}}}^{ - 1} \left( {\varvec{R}_{{\delta \varvec{N,s}}}^{{}} - \varvec{R}_{{\delta \varvec{N,c}}}^{{}} } \right)\varvec{R}_{{\delta \varvec{N,s}}}^{ - 1} \varvec{P}_{{\delta \varvec{N}}}^{ - } \\ &= \varvec{P}_{{\delta \varvec{N}}}^{ - } \varvec{R}_{{\delta \varvec{N,c}}}^{ - 1} \varvec{H}_{{\delta \tilde{\varvec{r}}}} \left( {\varvec{P}_{{\delta \varvec{\tilde{r},s}}}^{ - } - \varvec{P}_{{\delta \varvec{\tilde{r},c}}}^{ - } } \right)\varvec{H}_{{\delta \tilde{\varvec{r}}}}^{T} \varvec{R}_{{\delta \varvec{N,s}}}^{ - 1} \varvec{P}_{{\delta \varvec{N}}}^{ - } \\ \end{aligned} $$
(12)

In Eq. (12), \( \varvec{P}_{{\delta \varvec{N}}}^{ - } \), \( \varvec{R}_{{\delta \varvec{N,c}}}^{ - 1} \) and \( \varvec{R}_{{\delta \varvec{N,s}}}^{ - 1} \) are positive definite matrices, so that the sign of the left side is determined by the quadratic form \( \varvec{H}_{{\delta \tilde{\varvec{r}}}} \left( {\varvec{P}_{{\delta \varvec{\tilde{r},s}}}^{ - } - \varvec{P}_{{\delta \varvec{\tilde{r},c}}}^{ - } } \right)\varvec{H}_{{\delta \tilde{\varvec{r}}}}^{\text{T}} \) in the right formulation. Then it is easy to derive a matrix inequality:

$$ \varvec{P}_{{\delta \varvec{N,s}}}^{ + } \text{ < }\varvec{P}_{{\delta \varvec{N,c}}}^{ + } \;{\text{iff:}}\;\varvec{P}_{{\delta \varvec{\tilde{r},s}}}^{ - } \text{ < }\varvec{P}_{{\delta \varvec{\tilde{r},c}}}^{ - } $$
(13)

It is concluded that the more precise the priori positioning information is, the better the float ambiguity estimation will be.

The ADOP and the volume of the ambiguity search space are defined as follows, respectively (Teunissen et al. 1996, 2014):

$$ \text{ADOP = }\left( {\sqrt {\left| {\varvec{P}_{\text{NL}} } \right|} } \right)^{{\frac{1}{n}}} \quad \left( {\text{cycle}} \right) $$
(14)
$$ V = \chi^{n} U_{n} \sqrt {\left| {\varvec{P}_{\text{NL}} } \right|} $$
(15)

where \( \varvec{P}_{\text{NL}} \) is the SDNL ambiguity covariance with the unit in cycle, which is converted from the SDIF ambiguity covariance \( \varvec{P}_{{\delta \varvec{N}}}^{ + } \) using the covariance propagation law in Eq. (6), |·| denotes the determinant, n indicates the dimension of the ambiguity vector, χ is a parameter, which controls the search space size to contain the solution, Un symbolizes the volume of the unit sphere in the n-dimensional real space.

It can be found obviously that ADOP and V have a positive correlation with \( \varvec{P}_{{\delta \tilde{\varvec{r}}}}^{ - } \). That means the ADOP and the size of integer ambiguity search space would be reduced in the case of \( \varvec{P}_{{\delta \varvec{\tilde{r},s}}}^{ - } \text{ < }\varvec{P}_{{\delta \varvec{\tilde{r},c}}}^{ - } \).

Theoretical analysis above shows that INS-aided IAR outperforms unaided IAR when positioning accuracy of INS solutions is superior to code solutions for float ambiguity estimation during GNSS outages. However, INS suffers from accumulative position errors with increasing GNSS outage periods. Consequently, the position error drift exceeds SPP accuracy level, which leads to an adverse impact on IAR performance. Similar issues have been discussed in the inertially aided RTK and reached the same conclusion about the improvement in INS-aided IAR in many studies (Scherzinger 2002; Lee et al. 2005; Li et al. 2017b).

4 Data processing and discussion

4.1 Experiment description

In order to adequately assess such assisted IAR performance, we utilized two sets of integrated navigation equipment to conduct three different experiments. A ring laser gyroscope (RLG)-based navigation-grade IMU and a fiber optic gyroscope (FOG)-based tactical-grade IMU were tested to analyze the impact of IMU grades on INS-aided IAR. The land vehicle and airborne data sets were collected to validate the performance of INS-aided IAR in different dynamic environments. Three experiments were labeled as A, B and C, which refer to vehicular test with RLG-IMU, vehicular test with FOG-IMU and airborne test with FOG-IMU, respectively.

The well-known commercial product SPNA-FSAS from NovAtel Company was adopted in the FOG-IMU-based experiments. The SPNA-FSAS system tightly couples dual-frequency GPS + GLONASS receiver and a tactical-grade IMU from iMAR GmbH Company, which consists of three closed-loop fiber optic gyroscopes and three servo accelerometers. The RLG-based equipment is a prototype system, which integrates NovAtel OEM4 receiver, three ring laser gyroscopes and three servo accelerometers. The main technical parameters about two IMUs are listed in Table 1.

Table 1 Technical parameters of RLG and FOG IMUs
Full size table

In order to avoid other adverse effects on INS-aided IAR, three experiments were conducted in open-sky environments. The collected data, including IMU measurements at 200 Hz and GPS measurements at 1 Hz, were free from interrupts and exceptions. Since many researches have demonstrated that multi-GNSS is beneficial for PPP ambiguity resolution, in this work, only measurements from GPS system were processed. In this way, the role of INS aiding for PPP ambiguity resolution is possible to be truly revealed. PPK solutions are provided as a reference trajectory using NovAtel GrafNav software. It is reported by NovAtel technical documents that GrafNav could achieve 2–6 cm positioning accuracy when baseline length is shorter than 130 km and DD ambiguities can be fixed correctly (Gao et al. 2015). In fact, points on this reference trajectory refer to GNSS antenna phase center, while a navigation solution in PPP/INS TC integration points toward inertial sensor center. There is a requirement to convert the navigation solution from INS to GNSS antenna using lever arm and attitudes.

Figure 2 shows the basic positioning information about three experiments, including the number of available GPS satellites, position dilution of precision (PDOP) and DD ambiguity fixed status. Despite an open-sky environment on the ground, experiment B was influenced by some trees along the road, which resulted in a degraded signal acquisition, or signal blockage for some satellites. Therefore, the number of available GPS satellites is not stable compared with the other two experiments. Overall, the spatial geometry configuration in the three experiments was appropriate for positioning. Thus, applying the GrafNav software makes all DD ambiguities fixed, whose status is shown in Fig. 2.

Fig. 2
figure 2

Number of available satellites, PDOP and DD ambiguity-fixed status in vehicular experiment A with RLG-IMU (top), vehicular experiment B with FOG-IMU (middle) and airborne experiment C with FOG-IMU (bottom), respectively. Here, available satellites refer to ones involved in position calculation, excluding those satellites of low quality, such as low elevation angles and large priori residuals

Full size image

It is widely known that GNSS/INS integrated system can provide position, velocity and attitude information. However, the estimation of velocity and attitude is mainly based on the dynamic information from INS, while the positioning absolute accuracy depends on the precisely estimated ambiguities in GNSS carrier-phase observables (Zhang et al. 2017; Liu et al. 2016). Liu et al. (2016) have concluded that ambiguity fixing for the PPP/INS integration could only improve positioning accuracy rather than velocity and attitude. Therefore, this research only focuses on the analysis of positioning result.

4.2 INS aiding effect on IAR for clean observation data

The clean observation data of three experiments were processed in PPP and PPP/INS TC mode. Regardless of PPP or PPP/INS TC, float ambiguity estimation is critical for high-accuracy positioning and IAR performance. Note that the standard deviations (STDs) output by Kalman filter reflects the accuracy of estimated float ambiguities. Hereinafter, the results of experiment B were presented as a representative example. Figure 3 shows the STD time series of ionosphere-free ambiguity for each satellite using PPP-only and PPP/INS TC mode. Taken as a whole, the STD variation in the plots is similar to each other, especially at the beginning stage. Furthermore, all STD values converge to 0.1 m in 15 min, and a sudden drop occurs at about 40 min. This is because ambiguities are fixed correctly at this epoch and “hold ambiguity” mode is activated for the first time. The jumps are more obvious for those ambiguities with slow convergence. Due to newly observed satellites or cycle slips, ambiguities which are initialized or re-initialized arise large STDs in the following stage. However, adding INS information can accelerate STD convergence and decrease their values to below 0.1 m during those periods.

Fig. 3
figure 3

Standard deviation of ionosphere-free ambiguity for each satellite, the left panel refers to PPP, the right panel refers to PPP/INS TC; different colors correspond to different satellites; these results are acquired from experiment B: vehicular test with FOG-IMU

Full size image

Figure 4 depicts the ADOP changes of SDNL ambiguities and the number of ambiguity-fixed satellites with and without INS aiding. The ADOP is to measure the intrinsic precision of float ambiguities and the intrinsic model strength for successful IAR (Teunissen et al. 2014). Since PPP/INS TC behaves merely a little better than PPP-only mode in terms of estimated ambiguities, there is only 5% average ADOP enhancement. However, a more obvious enhancement up to 14% is obtained during the middle periods, where ambiguity initialization or re-initialization is present. Similarly, a sudden drop at about 40 min can be found in the ADOP time series. The number of ambiguity-fixed satellites keeps zero during the initial convergence and appears intermittently from 15 to 40 min, and then remains a constant value of 9 for a while. Beginning from these epochs, stable ambiguity fixing is achieved and the average number of ambiguity-fixed satellites is around 6.6 for both PPP-only and PPP/INS TC modes.

Fig. 4
figure 4

ADOP time series of SDNL ambiguities and the number of ambiguity-fixed satellite for PPP and PPP/INS TC, respectively; these results were obtained from experiment B: vehicular test with FOG-IMU

Full size image

The position accuracy improvement is a crucial indicator to evaluate INS aiding effect on IAR. Figure 5 shows the ambiguity-fixed solutions for PPP and PPP/INS TC. The position errors in three components are calculated with respect to the reference trajectory. Both PPP and PPP/INS TC take about 15 min to get the first ambiguity-fixed solutions. But the ambiguity fixing is not continuously available until the solutions arrive at 40 min. After achieving the stable fixing, the position errors keep around zero all the time. Our designed dual parallel processing method for PAR is responsible for the emergence of first and stable fixing. At the place of first fixing, the fixed ambiguities are merely used to update the float PPP-derived position. This “updating” processing line is independent of delivering ambiguity-fixed information to subsequent filtering. When “correct” ambiguities are recorded to satisfy the condition in aforementioned section, the “hold ambiguity” processing line is activated and regards the fixed integer as a tight constraint in Kalman filtering. In this paper, the time of stable fixing is defined as the time to first fix (TTFF), which is also the first time of activated “hold ambiguity” mode in our program. From the view of position accuracy improvement and TTFF, the performance of PPP and PPP/INS TC is roughly the same. As shown in Fig. 4, the number of fixed ambiguities is reduced to zero at about 1.3 h, where the fixed failure is marked in Fig. 5 accordingly. Figure 2 shows that only six satellites are available during these periods of time. Therefore, the main reason is that available observations in float PPP decrease suddenly due to the environmental obstructions and the satisfied ambiguities may be insufficient for successful PAR. Compared with IAR-PPP solutions, the influence of fixed failure on large position errors is weakened for PPP/INS TC.

Fig. 5
figure 5

Comparison of ambiguity-fixed solutions for PPP and PPP/INS TC in terms of position bias in east, north and up components; these results were acquired from experiment B: vehicular test with FOG-IMU

Full size image

The statistical results of three experiments are given in Table 2 in aspects of the position RMS (root-mean-square), TTFF and correct fixing rate (CFR). The TTFF in this analysis has been defined above as the first time to achieve stable fixing. Likewise, the RMS of epoch-wise position errors and CFR are both computed with removal of those results before stable fixing. The CFR is expressed as the ratio of the number of correctly fixed epochs to the number of total epochs. A correctly fixed solution is identified when the ambiguity-fixed position agrees well with the reference coordinate, and its accuracy is better than that of ambiguity-float PPP.

Table 2 RMS of epoch-wise position errors with ambiguity-fixed solutions, TTFF and CFR values for PPP and PPP/INS TC; the reference trajectory is obtained from PPK solutions
Full size table

According to the statistical values in Table 2, the average RMS for the east, north and up components with INS aiding are reduced by 5.0%, 5.0% and 19.2% from (2.0, 2.0, 7.3) to (1.9, 1.9, 5.9) cm, respectively. Likewise, the difference of the TTFF and CFR between PPP-only and PPP/INS TC mode is also slight. The TTFF is more than 27 min up to 40 min with a mean value of 33 min. The CFR for three experiments ranges from 91.36 to 99.98%. Regardless of the accuracy improvement in the vertical direction, taking the horizontal accuracy, TTFF and CFR values to evaluate IAR performance, three experiments indicate that adding INS only achieves very little improvement when the GPS data are clean.

4.3 INS-aided ambiguity re-fixing performance

The GPS outages in urban areas maybe lead to all ambiguities re-initialized simultaneously. As a result, a long convergence time of 30 min or more is required again to achieve ambiguity fixing. In contrast, the INS solutions will not suffer from such re-initialization and could retain the continuous and high accuracy during a short time. To some extent, the precision of INS solution at this epoch is approximately equivalent to ambiguities before re-initialization. It means that the prediction information from the INS solution is superior to re-initialized ambiguities whose precisions are determined by pseudo-range observations. Hence, not only ambiguity estimation but also ambiguity re-fixing performance is enhanced with the support of INS aiding.

In order to evaluate INS-aided ambiguity re-fixing performance, three indicators including ADOP, bootstrapping success rate (BSSR) and time to fix are analyzed in detail. The BSSR has been proved as a lower bound for the integer least squares (ILS) success rate. The data discontinuity is simulated by means of manually raising the elevation mask to 90° as well as compulsively interrupting all ambiguities during GPS outages. Consequently, five complete outage durations including 1, 5, 10, 30 and 60 s were considered, respectively.

Firstly, float ambiguity estimation is compared between PPP and PPP/INS TC solutions for experiment B, as an example. The re-convergence of their ambiguity STDs during five GPS outages is shown in Fig. 6. Beginning from 40 min, five GPS outages are inserted orderly into the observation data every 20 min. For PPP float ambiguities, a process similar to the initialization with long convergence time is yielded no matter how short GPS outage durations are. Even when using 20-min observation data, the STDs of some ambiguities are still larger than 1 cm. By contrast, in the case of 1-s and 5-s outages, although the STDs of PPP and PPP/INS TC solutions are close initially, a faster re-convergence is obtained for all ambiguities, and all STDs values reach below 0.1 cm in 20 min. Nevertheless, along with the outage duration increasing from 1 to 60 s, ambiguity STDs of two solutions tends to be the same.

Fig. 6
figure 6

Comparison of ionosphere-free ambiguity STDs for PPP (top) and PPP/INS TC (bottom) solutions during five GPS outages; different colors correspond to different satellites; this result is from experiment B: vehicular test with FOG-IMU; here, the outage is also referred to as gap

Full size image

Secondly, we analyzed ADOP and BSSR indicators, which represent ambiguity fixing performance indirectly and are shown in Figs. 7 and 8. Five GPS outages are simulated individually at a same time point for three experiments. As expected, the ADOP and BSSR of PPP-only solutions are interrupted at the place of GPS outages. It takes about 313 s, 322 s and 100 s for the BSSR values to recover to 99.0%, while the mean time of the ADOP values decreasing to 0.12 cycles are 446 s, 426 s and 143 s for experiments A, B and C, respectively. Here, the BSSR value of 99.0% is used because it is one of the thresholds for successful IAR in our integer ambiguity validation, and the ADOP value below 0.12 cycle level is another theoretical indication of successful IAR (Teunissen et al. 2014). For PPP/INS TC solutions, the rapid recovery of ADOP and BSSR can be achieved with the outage duration less than 10 s. At the first epoch after interruption, the average values are (0.21, 0.20, 0.20) cycles for ADOP and (84.36, 78.82, 87.71) % for BSSR, in the case of 1-s, 5-s and 10-s outages, respectively. Moreover, with the better initial values, the mean time spent on convergence to a desired level is only (16, 23, 12) s for the ADOP and (7, 28, 6) s for the BSSR. When the outage duration prolongs to 30 s and 60 s, there is a little improvement on the ADOP and BSSR with the INS aiding.

Fig. 7
figure 7

PPP-only mode-derived ADOP and bootstrapping success rate (BSSR) time series for three experiments during five GPS outages; subplots from left to right denote the results of experiments A, B and C, respectively. The ADOP and BSSR are computed for SDNL ambiguities

Full size image
Fig. 8
figure 8

PPP/INS TC mode-derived ADOP and bootstrapping success rate (BSSR) time series for three experiments during five GPS outages; subplots from left to right denote the results of experiments A, B and C, respectively. The ADOP and BSSR are computed for SDNL ambiguities

Full size image

The ADOP and BSSR analyzed above are merely two kinds of measurements of successful IAR in theory. Nevertheless, smaller ADOP and higher BSSR values do not guarantee that ambiguity can be fixed correctly. The position errors and time to re-fix (shown in Figs. 9, 10) are eventually utilized as the most reasonable indicators to conduct the assessment of INS-aided ambiguity re-fixing performance. It is interesting to note that experiment C outperforms the other two in terms of the ADOP and BSSR, but has a poor performance in ambiguity re-fixing as shown in Fig. 9. This suggests the fact again that there is no absolute correlation between a successful IAR and the ADOP as well as the BSSR. For the same experiment data processed in PPP mode, ambiguity re-fixed time exhibits good repeatability and stability across different outages. The time to re-fix recorded in each case are shown in Figs. 9 and 10. The mean time to re-fix is about 29 min, 33 min and 32 min for the PPP solutions of three experiments.

Fig. 9
figure 9

PPP-only mode-derived position errors time series and ambiguity re-fixed time for three experiments during five GPS outages; subplots from left to right denote the results of experiments A, B and C, respectively. The arrows point to the place of ambiguity re-fixing

Full size image
Fig. 10
figure 10

PPP/INS TC mode-derived position errors time series and ambiguity re-fixed time for three experiments during five GPS outages; subplots from left to right denote the results of experiments A, B and C, respectively. The arrows point to the place of ambiguity re-fixing

Full size image

When using PPP/INS TC mode, the mean time to re-fix is significantly reduced; especially in the case of outage durations shorter than 10 s, nearly instantaneous ambiguity re-fixing is realized only using five epochs, except for experiments B and C with 10-s outage. These two cases spend 26 s and 28 s to achieve ambiguity re-fixed solutions, which are still much better than PPP-only performance. Moreover, because of high accuracy in a short time, the continuous navigation information provided by the INS makes experiment C solutions more stable and precise. If the outage durations increased to 30 s and 60 s, ambiguity re-fixing improvement is clearly related to IMU grade and dynamic movement. For the vehicular test, ambiguity re-fixing can be obtained in 6.2 min and 10.7 min using the navigation-grade IMU, but it requires 11.2 min and 17.6 min to attain the same goal using the tactical-grade IMU, while for the same grade IMU, the time to re-fix of the airborne test is longer than that of the vehicular test by 1.7 min and 15.3 min. It is noted that the INS aiding in the case of 60-s outage fails to improve ambiguity re-fixing performance for experiment C, but brings an adverse effect instead. The time to re-fix is extended by 72 s compared with that of PPP solutions.

4.4 Discussion on ambiguity re-fixing

From the preceding analysis, it is confirmed that the shorter the outages, the greater the ambiguity re-fixing improvement with the introduction of the INS dead reckoning information. The position error accumulates dramatically along with time for dead reckoning techniques when operated in a stand-alone mode. In essence, the ambiguity re-fixing improvement relies on the position accuracy predicted by the INS. The high-accuracy information could contribute to decorrelation between the position and float ambiguity parameters; such float ambiguities with enhanced observability facilitate the rapid identification of correct integer candidates (Geng and Shi 2017). Intuitively, the position solution is simply updated by quadratic time integration of IMU raw data. However, there are many factors to influence position accuracy. All errors in navigation parameters and INS-dependent parameters would degrade position accuracy ultimately by means of error propagation functions. Table 3 lists the simplified relationship between position drifts in north direction and each error component; furthermore, similar expressions can also be derived for the east channel. For the INS-derived position, it is acknowledged that vertical accuracy can be maintained much better than the horizontal accuracy during outages. Hence, the horizontal errors in the INS-derived position are the greatest impediment to INS-aided ambiguity re-fixing performance.

Table 3 Position error drifts in north direction with respect of each error component.
Full size table

Table 3 illustrates that position errors are made up of a constant term and other six drift terms, among which the drift terms are described as a power function of integration time with different orders. The IMU grade is classified by the bias and bias instability of accelerometers and gyroscopes. The higher the IMU grades are, the smaller the bias and bias instability are. For the low-grade IMU, the remaining uncalibrated biases will enlarge drift of position errors in both accelerometers and gyroscopes, as Table 3 displays in last three equations. In addition, according to the expression of Λ, position error components in north direction with respect of the initial yaw error and the vertical gyroscope bias are related to east velocity yet. In the aerial investigation, the average velocity of aircraft was 80 m/s, which was faster than ground vehicles; as a result, it led to larger position errors. The previous discussion is merely based on theoretical analysis; however, in practice, position error drifts will become more complicated due to many unexpected factors. Figure 11 displays the actual position error drifts in horizontal and vertical components during 60-s outage compared with the SPP position errors. This simulated outage is the same as that in Figs. 9 and 10.

Fig. 11
figure 11

Position error drifts during 60-s outage for horizontal and vertical components, dL and dH denote the horizontal and vertical components; subplots from left to right indicate the results of experiments A, B and C, respectively

Full size image

Obviously, the position error drifts depend on IMU grades, integration time as well as dynamic motion. Furthermore, the ambiguity re-fixing enhancement is consistent with position accuracy changes. Figure 11 demonstrates the position errors of INS prediction are less than that of SPP throughout the 60-s outage period for experiments A and B. For experiment C, the horizontal errors accumulate too rapidly to exceed the accuracy level of SPP when the integration time reaches to 60 s. Consequently, float ambiguity estimation is worse rather than better under the influence of the contaminated position information from INS prediction. It explains why the ambiguity re-fixing performance of 60-s outage is impaired by INS aiding for experiment C. The outage duration of 10 s is another interesting cutoff point, where the accumulated errors are within 3.0 cm, 6.7 cm and 13.6 cm for three experiments, respectively. These position errors are better than or approximately equal to half wavelength of L1 GPS carrier phase, which is also the one half of the NL cycle. In this situation, float ambiguities deduced from observed-minus-computed (OMC) carrier-phase observations will become quite close to correct integer candidates. The caused constant bias in NL ambiguity determination could be limited within a half cycle. Meanwhile, with the reduced volume of the ambiguity search space, rapid ambiguity re-fixing will be achieved eventually.

In order to demonstrate the repeatability of INS-aided ambiguity re-fixing performance, we selected five different time points to conduct GPS outages simulated experiments. Figure 12 shows the time to re-fix statistics of PPP/INS TC solutions and the corresponding average values are calculated and given in Table 4. When the outage durations are 1 s and 5 s, the ambiguity re-fixing with INS aiding has a stable performance for three experiments. Nearly instantaneous ambiguity re-fixing can be always achieved with a re-convergence time of about 5 s. In fact, our IAR strategy will reject fixing a NL ambiguity if the corresponding IF ambiguity is estimated less than five epochs. Without this restriction, it is potential to shorten the ambiguity re-fixed time further. Nevertheless, the risk of false ambiguity fixing also follows. Therefore, improving ambiguity validation is a crucial task to ensure rapid and correct fixing. With the outage duration increasing from 10 to 30 s, there is a quite significant degradation of the ambiguity re-fixing performance, which is presented clearly in Fig. 12. The 10-s outage can be regarded as a turning point in terms of the ambiguity re-fixing with INS aiding. The re-fixed time deteriorates from tens of seconds level to tens of minutes level if outage duration exceeds 10 s. Looking into the statistical values in Table 4, because of inertial position error growth, ambiguity re-fixing performance degrades gradually to that of PPP-only solutions along with increasing GPS outage duration. In spite of performance degradation, adding INS information is still helpful for PPP-only solutions in the case of 60-s outage, where the ambiguity re-fixed time is decreased by 16.4, 13.8 and 8.3 min for three experiments. Especially for the navigation-grade IMU, its average time to re-fix is kept around 10 min, which is close to the PPP-only result of 9.21 min by employing GCRE four-system data (Li et al. 2017c). It implies that a joint processing of multi-GNSS and high-grade IMU will promise faster ambiguity re-fixing, without the support of other sophisticated approaches, such as cycle slip correction.

Fig. 12
figure 12

Time to re-fix statistics for five GPS outages, subplots from left to right denote the PPP/INS TC results of experiments A, B and C, respectively

Full size image
Table 4 Comparison of average time to re-fix
Full size table

In conclusion, for the navigation- and tactical-grade IMU, the INS-aided ambiguity re-fixing performance can be classified as three levels: significant improvement for the outage duration less than 10 s, moderate improvement for the outage duration from 10 to 60 s, a little or zero improvement for the outage duration longer than 60 s. Strictly speaking, the performance improvement in ambiguity re-fixing is determined by the position accuracy maintained by the INS solution during the GPS outage.

4.5 INS-aided IAR-PPP in real urban environment

We also performed the INS-aided IAR-PPP in real urban environment. From the preceding analysis in Sect. 4.2, there is only a little improvement for the TTFF with INS aiding information. It still takes about 30 min to achieve first stable fixing. Therefore, the experimental vehicle was driven in open-sky environment at the beginning 45 min and then entered into urban area. The equipment is still the commercial product SPNA-FSAS.

Figures 13 and 14 show the trajectory in urban environment and the number of available satellites. Four GPS outages in the enlarged panels are presented as representative examples. Place A is a long tunnel in the mountains and place D is a short tunnel, the overpasses and high buildings in the places B and C make the satellite signals blocked. There are totally nine places with data interruptions in the trajectory, whose gaps are listed in Table 5. Figure 14 displays that the number of available GPS satellites is not stable compared with the previous clean data. During some periods with complex environment, available GPS satellites are less than six and the PDOP values are large. Besides, more cycle slips and outliers in observations are detected.

Fig. 13
figure 13

Field test in urban environment. The trajectory is from GPS-alone PPP solutions. Different colors on the trajectory correspond to different number of satellites. Red represents n ≤ 5, yellow represents n ≤ 7, purple represents n ≤ 9, and green represents n > 9, where n is the number of satellites. Four data outages are regarded as representative examples, which are labeled as A, B, C and D

Full size image
Fig. 14
figure 14

PDOP and number of available satellites

Full size image
Table 5 Statistics of time to re-fix for each outage
Full size table

We performed the IAR-PPP with and without INS aiding. The four solutions are compared in Fig. 15, including ambiguity-float and ambiguity-fixed results for PPP and PPP/INS TC. And Fig. 16 shows the ambiguity-fixed status. The RTS smoothed coordinates of DGPS/INS TC are regarded as reference trajectory. Obviously, the ambiguity-float position time series suffers from large errors and intermittent re-convergences. In contrast, the high short-term accuracy provided by INS is capable of bridging the gaps caused by re-initialization. At about 1.5 h, the experimental vehicle passed though the long tunnel with an outage duration of 68 s, which is place D in Fig. 13. The horizontal position error accumulates to about 3 m. Taken as a whole, the PPP/INS TC solutions are with the better continuity. Due to the good quality data at the beginning stage, both PPP-only and PPP/INS TC mode can achieve first ambiguity fixing successfully. The TTFF is 28.7 min for PPP and 27.0 min for PPP/INS TC integration. When the experimental vehicle was driven in urban area, environmental obstructions appears intermittently to make satellite signal blocked. As we know, the integer ambiguity recovery for PPP usually requires 30 min. However, the span of each clean data is shorter than 30 min due to intermittent interruptions. Therefore, ambiguity re-fixing for PPP always fails and the ambiguity-float solutions are kept from the first interruption, which is shown in Fig. 16. For the INS-aided IAR-PPP, a significant improvement on position accuracy is shown in Fig. 15. The position RMS of ambiguity-fixed solutions is 2.7 cm, 5.8 cm and 3.6 cm for the east, north and up components. Although the ambiguity is not resolved continuously, the CFR with a value of 68.87% is still obtained. If we remove these epochs during the re-convergence stage, the statistical value of CFR increases to 80.30%.

Fig. 15
figure 15

Comparison of ambiguity-float and ambiguity-fixed solutions for PPP and PPP/INS TC. The left plots are PPP results, while the right plots are PPP/INS TC results. The top and bottom are ambiguity-float and ambiguity-fixed results, respectively. The yellow vertical line represents the time to first fix

Full size image
Fig. 16
figure 16

Number of ambiguity-fixed satellite and ambiguity-fixed status for PPP and PPP/INS TC, respectively

Full size image

The time to re-fix with INS aiding for each outage is listed in Table 5. There are four outages associated with the four scenarios selected in Fig. 13. Since PPP is unable to recover integer ambiguity after the first interruption in our urban test, there is no value for time to re-fix in Table 5. However, nearly instantaneous ambiguity re-fixing can be achieved with INS aiding in the case of the first five outages. For the outage duration of 11 s and 5 s, the time to re-fix is relatively longer with a value of 18 s and 50 s. The longest outage duration of 68 s occurred when the experimental vehicle passed through the tunnel in the mountains. It takes 835 s to achieve ambiguity re-fixing with INS aiding. This time to re-fix is close to the result in the case of 60 s simulated outage in Table 4, whose average ambiguity re-fixed time is 896.4 s for the tactical-grade IMU in the vehicular test. It indicates that the analysis on simulated outages is beneficial to some degree. For the last outage duration of 10 s, the time to re-fix is abnormal with a value as large as 322 s, which happens at about 1.93 h. The main reason is that some satellites are interrupted frequently by the environmental obstructions and the satisfied ambiguities are insufficient for successful PAR. Nevertheless, Fig. 15 shows that the position accuracy for INS-aided IAR-PPP does not degrade.

In summary, INS-aided IAR-PPP could achieve an excellent performance in urban environment. For more complex urban areas, however, only integrating INS for PPP may be insufficient. Adding other navigation sensors such as distance measurement indicator (DMI) or stereo camera is expected to enhance ambiguity re-fixing and positioning performance further for kinematic PPP.

5 Conclusions

In this study, the PPP/INS TC model with integer ambiguity resolution is described in detail. In order to use the ambiguity-fixed information reasonably, we designed dual parallel processing lines: one line to update non-ambiguity states using all of the successfully fixed ambiguities and another one to hold ambiguities using “correct” fixed ambiguities. Besides, the partial IAR strategy and some identification criterions of correct integer candidates are introduced to make the ambiguities as fixed correctly as possible.

On the other hand, the theoretical analysis states that the IAR-PPP performance with INS aiding can be improved in the case of GNSS outages, when the position accuracy maintained by the INS solution is superior to SPP solutions. Real data experiments equipped with navigation-grade and tactical-grade IMUs were conducted in an open-sky environments and urban area. For the clean GPS data, since the float ambiguities of PPP-only solutions have been estimated precisely, adding INS information is unable to improve ambiguity fixing. However, owing to the ability of dead reckoning in a stand-alone mode, the INS could deliver position with high accuracy over a short period. As a result, during the GPS outage, this high-accuracy information is used to assist in accelerating re-convergence for re-initialized float ambiguities. According to the INS prediction accuracy, the INS aiding effect on ambiguity re-fixing can be classified into three levels roughly. Firstly, when the position accuracy is better than one half cycle, nearly instantaneous or rapid ambiguity re-fixing is achieved. In practice, the outage duration is required less than 10 s. Secondly, for the outage duration from 10 to 60 s, the average time to re-fix for INS aiding is shorter than that of PPP-only solutions. It is regarded as a moderate improvement. Finally, if the outage duration continues to increase, the INS drift error is close to that of SPP solutions. As a result, the contribution of INS aiding will become less and less. Moreover, there is an adverse impact on ambiguity re-fixing performance for the large INS prediction error. In essence, the INS-predicted position accuracy is the critical factor for ambiguity recovery performance, where an accuracy better than 0.1 m and 1.0 m is required for the significant and moderate improvement. For the urban environments, the span of clean data is often shorter than 30 min due to intermittent signal interruptions; thus, ambiguity re-fixing for PPP always fails, while INS-aided information could bridge the data gaps and achieve fast ambiguity re-fixing.

In practice, especially for the real kinematic scenario, the observation environment is more complex due to a variety of unexpected problems. In order to enhance kinematic PPP, future studies are focused on the combination of multi-GNSS, multi-frequency and multi-sensor and its effects on PPP model strengthening. Besides, the quality control for reliable integer ambiguity resolution is also crucial.