Introduction

The DGNSS/INS system which provides precise position and attitude solutions has been widely investigated (Petovello et al. 2004; Scherzinger 2006; Skaloud 1999). The core of the DGNSS/INS system is fusion of double-difference (DD) code, carrier and Doppler observations from reference and rover receivers with INS data. Once the DD ambiguities are correctly fixed to integers, the system can obtain centimeter-level positioning accuracy.

However, there are two restrictions weakening the application of the DGNSS/INS system: First, one or more local reference stations are needed to offer raw observations, which increases the system cost; second, the distance between the rover receiver and the reference stations should be within tens of kilometers to ensure successful and reliable integer ambiguity resolution. For airborne surveying over large area, several reference stations have to be deployed at control points, which is quite a complex work. For shipboard surveying, deploying reference stations at control points may not be feasible if the work is far offshore.

Over the past decades, precise point positioning (PPP) has been presented to be an efficient tool to deliver high-accuracy positioning globally with ionospheric-free code and phase observations from a single GNSS receiver (Kouba and Héroux 2001; Zumberge et al. 1997). Since local reference stations are no longer necessary, PPP is suitable for surveying applications over large area and even globally. In studies by Du and Gao (2010), Kjørsvik et al. (2010), Abd Rabbou and El-Rabbany (2014), Roesler and Martell (2009), Shin and Scherzinger (2009), and Zhang and Gao (2008), the focus was on ambiguity-float PPP and its integration with INS. This approach has two drawbacks: One is that the significant convergence time is required to achieve high-precise positioning solutions, and the other one is that the positioning accuracy is unstable which varies between decimeter and centimeter level even after a lengthy convergence period. The two drawbacks mentioned above severely prevent the popularity of the PPP/INS system.

Recently, PPP ambiguity fixing techniques (Collins et al. 2010; Ge et al. 2008; Geng et al. 2010a; Laurichesse et al. 2009) have been developed and illustrated that ambiguity fixing for PPP can dramatically shorten the convergence time and improve the positioning accuracy. Therefore, if we integrate the ambiguity-fixed PPP with INS, the new system will overcome the restrictions of the DGNSS/INS system and the drawbacks of the ambiguity-float PPP/INS system. In other words, the ambiguity-fixed PPP/INS system is capable of implementing high-accuracy positioning and attitude determination with no local reference stations and without distance limitation, and its performance will be comparable to that of the DGNSS/INS system.

Unfortunately, little attention has been given to studying the model of ambiguity-fixed PPP/INS integration and to assessing its performance. We, therefore, establish the model of tightly coupled ambiguity-fixed PPP/INS integration. The observation model of ambiguity-fixed PPP is derived first, and the ambiguity fixing strategy is outlined. The equations of motion and the INS error equations are presented in a separate section. We then present the details of the model of tightly coupled PPP/INS integration. Two carborne tests are used to evaluate the performance of the ambiguity-fixed PPP/INS integration.

Ambiguity-fixed PPP observation model

Several PPP ambiguity fixing methods have been developed in recent years. The uncalibrated phase delay method (Ge et al. 2008), the decoupled clock model (Collins et al. 2010), and the integer phase clock method (Laurichesse et al. 2009) are three representative techniques. Geng et al. (2010b) proved the theoretical equivalence between the uncalibrated phase delay method and the integer phase clock method. Shi and Gao (2014) gave a comprehensive comparison of these three PPP ambiguity fixing methods, and the equivalence of them in the user solution was concluded.

Currently only Center National d’Etudes Spatiales (CNES), as one of International GNSS Service (IGS) Analysis Centers (AC), regularly provides users with products to perform PPP ambiguity fixing using the integer phase clock method at the undifferenced level (Loyer et al. 2012). Therefore, the products provided by CNES are adopted for PPP ambiguity fixing herein. In order to establish the integration model, the observation model of ambiguity-fixed PPP is derived first.

The standard GPS dual-frequency code and phase observation equations can be written as:

$$P_{\text{j}} = \rho + cdt_{\text{r}} - cdt^{\text{s}} + T + \gamma_{\text{j}} I + B_{{{\text{r}},P_{\text{j}} }} - B_{{P_{\text{j}} }}^{\text{s}} + \varepsilon_{{P_{\text{j}} }}$$
(1)
$$L_{\text{j}} = \rho + cdt_{\text{r}} - cdt^{\text{s}} + T - \gamma_{\text{j}} I - \lambda_{\text{j}} N_{\text{j}} + B_{{{\text{r}},L_{\text{j}} }} - B_{{L_{\text{j}} }}^{\text{s}} + \varepsilon_{{L_{\text{j}} }}$$
(2)

where the subscript r indicates the receiver and the superscript s indicates the satellite, the subscript j indicates frequency index and equals 1 or 2 for GPS, P is the raw code observation (m), L is the raw phase observation scaled to distance, ρ is the geometric distance from receiver to satellite, c is the speed of light in vacuum, dt r is the receiver clock error, dt s is the satellite clock error, T is the tropospheric delay, γ j = f 21 /f 2j and f j is the frequency, I is the first-order ionospheric delay on frequency f 1, λ j is the wavelength of frequency f j, N j is the integer ambiguity in cycles, \(B_{{{\text{r}},P_{\text{j}} }}\) is the receiver code bias, \(B_{{P_{\text{j}} }}^{\text{s}}\) is the satellite code bias, \(B_{{{\text{r}},L_{\text{j}} }}\) is the receiver phase bias, \(B_{{L_{\text{j}} }}^{\text{s}}\) is the satellite phase bias, and the ɛ-terms denote unmodeled errors including multipath effect and observation noise. The code bias is caused by the code hardware delay. The phase bias is caused by the phase hardware delay and the initial phase offset. The effects of earth tide, phase windup, relativity, sagnac and antenna phase center offsets and variations are not listed in (1) and (2), as they can sufficiently be modeled or calibrated (Kouba 2009).

By (1) and (2), the ionospheric-free linear combinations can be formed to remove the first-order ionospheric delay as:

$$P_{\text{IF}} = \alpha P_{1} + \beta P_{2} = \rho + cdt_{\text{r}} - cdt^{\text{s}} + T + B_{{{\text{r}},P_{\text{IF}} }} - B_{{P_{\text{IF}} }}^{\text{s}} + \varepsilon_{{P_{\text{IF}} }}$$
(3)
$$L_{\text{IF}} = \alpha L_{1} + \beta L_{2} = \rho + cdt_{\text{r}} - cdt^{\text{s}} + T - N_{\text{IF}} + B_{{{\text{r}},L_{\text{IF}} }} - B_{{L_{\text{IF}} }}^{\text{s}} + \varepsilon_{{L_{\text{IF}} }}$$
(4)

where the subscript IF denotes the ionospheric-free combination, P IF is the ionospheric-free code observation, L IF is the ionospheric-free phase observation, α = f 21 /(f 21  − f 22 ) and β = −f 22 /(f 21  − f 22 ) are the combination coefficients, \(B_{{{\text{r}},P_{\text{IF}} }}\), \(B_{{P_{\text{IF}} }}^{\text{s}}\), \(B_{{{\text{r}},L_{\text{IF}} }}\) and \(B_{{L_{\text{IF}} }}^{\text{s}}\) are the corresponding ionospheric-free combinations of the biases, and N IF is the ionospheric-free ambiguity, which has been scaled to distance in meters, and can be resolved as:

$$N_{\text{IF}} = \alpha \cdot \lambda_{1} N_{1} + \beta \cdot \lambda_{2} N_{2} = \lambda_{\text{NL}} N_{1} - \frac{{\lambda_{2} }}{{\gamma_{2} - 1}}\left( {N_{2} - N_{1} } \right) = \lambda_{\text{NL}} N_{1} - \frac{{\lambda_{2} }}{{\gamma_{2} - 1}}N_{\text{WL}}$$
(5)

where N WL is the wide-lane ambiguity (cycle), and λ NL is the wavelength of the narrow-lane ambiguity so that N 1 herein is called the narrow-lane ambiguity (cycle). Note that the unit of N IF is in meters which is different from the units of N 1 and N WL in cycles. For the simplicity of the following derivation and description, four kinds of clock error are predefined as:

$$dt_{{{\text{r}},P_{\text{IF}} }} = dt_{\text{r}} + b_{{{\text{r}},P_{\text{IF}} }}$$
(6)
$$dt_{{P_{\text{IF}} }}^{\text{s}} = dt^{\text{s}} + b_{{P_{\text{IF}} }}^{\text{s}}$$
(7)
$$dt_{{{\text{r}},L_{\text{IF}} }} = dt_{\text{r}} + b_{{{\text{r}},L_{\text{IF}} }}$$
(8)
$$dt_{{L_{\text{IF}} }}^{\text{s}} = dt^{\text{s}} + b_{{L_{\text{IF}} }}^{\text{s}}$$
(9)

where \(dt_{{{\text{r}},P_{\text{IF}} }}\) denotes the receiver code clock error, \(dt_{{P_{\text{IF}} }}^{\text{s}}\) denotes the satellite code clock error, \(dt_{{{\text{r}},L_{\text{IF}} }}\) denotes the receiver phase clock error, \(dt_{{L_{\text{IF}} }}^{\text{s}}\) denotes the satellite phase clock error, and b-terms denote the time delay biases derived from b = B/c.

We can obtain the traditional ambiguity-float PPP model by substituting (6) and (7) into (3) and (4):

$$P_{\text{IF}} = \rho + cdt_{{{\text{r}},P_{\text{IF}} }} - cdt_{{P_{\text{IF}} }}^{\text{s}} + T + \varepsilon_{{P_{\text{IF}} }}$$
(10)
$$L_{\text{IF}} = \rho + cdt_{{{\text{r}},P_{\text{IF}} }} - cdt_{{P_{\text{IF}} }}^{\text{s}} + T - N_{\text{IF}} + \left( {B_{{{\text{r}},L_{\text{IF}} }} - B_{{{\text{r}},P_{\text{IF}} }} } \right) - \left( {B_{{L_{\text{IF}} }}^{\text{s}} - B_{{P_{\text{IF}} }}^{\text{s}} } \right) + \varepsilon_{{L_{\text{IF}} }}$$
(11)

With the traditional PPP model, the satellite code clock \(dt_{{P_{\text{IF}} }}^{\text{s}}\) by means of the precise satellite clock provided by IGS (Collins et al. 2010) is applied to the ionospheric-free code and phase observations, and the receiver code clock \(dt_{{{\text{r}},P_{\text{IF}} }}\) is estimated together with the ionospheric-free ambiguities, which leads to the case that the estimated ambiguity is the combination of N IF and \(\left( {B_{{{\text{r}},L_{\text{IF}} }} - B_{{{\text{r}},P_{\text{IF}} }} } \right) - \left( {B_{{L_{\text{IF}} }}^{\text{s}} - B_{{P_{\text{IF}} }}^{\text{s}} } \right)\). In other words, the ionospheric-free ambiguity that we actually estimated is not unbiased, but contaminated by \(\left( {B_{{{\text{r}},L_{\text{IF}} }} - B_{{{\text{r}},P_{\text{IF}} }} } \right) - \left( {B_{{L_{\text{IF}} }}^{\text{s}} - B_{{P_{\text{IF}} }}^{\text{s}} } \right)\), which means the estimated ionospheric-free ambiguity cannot precisely be resolved into the combination of two integer ambiguities as shown in (5). As a result, ambiguity fixing in the traditional PPP model is not possible.

However, if we follow the approach of the decoupled clock model and the integer phase clock method, which feature different clock terms for code and phase observations (Shi and Gao 2014), then the estimated ionospheric-free ambiguities will no longer be contaminated and could be fixed. By substituting (6) and (7) into (3), and (8) and (9) into (4), the ambiguity-fixed PPP model is given by:

$$P_{\text{IF}} = \rho + cdt_{{{\text{r}},P_{\text{IF}} }} - cdt_{{P_{\text{IF}} }}^{\text{s}} + T + \varepsilon_{{P_{\text{IF}} }}$$
(12)
$$L_{\text{IF}} = \rho + cdt_{{{\text{r}},L_{\text{IF}} }} - cdt_{{L_{\text{IF}} }}^{\text{s}} + T - N_{\text{IF}} + \varepsilon_{{L_{\text{IF}} }}$$
(13)

If we estimate these four kinds of clocks in (12) and (13) together, then we can fix ionospheric-free ambiguities. If we use the precise phase clock from CNES to correct the ionospheric-free phase observations and use the precise code clock from IGS to correct the ionospheric-free code observations and estimate two kinds of receiver clocks, the estimated ionospheric-free ambiguity recovers the fixable property of the combination of two integers. As a consequence, PPP ambiguity fixing becomes feasible.

In order to avoid estimating two kinds of receiver clocks at one epoch, single-difference (SD) between-satellites operator can be used for eliminating receiver-dependent errors including receiver clocks. If the satellite clock error has been corrected by using precise clock products, then we can rewrite (12) and (13) to get the SD ionospheric-free observations:

$$P_{\text{IF}}^{pi} = \rho^{pi} + T^{pi} + \varepsilon_{{P_{\text{IF}} }}^{pi}$$
(14)
$$L_{\text{IF}}^{pi} = \rho^{pi} + T^{pi} - N_{\text{IF}}^{pi} + \varepsilon_{{L_{\text{IF}} }}^{pi}$$
(15)

where the superscript p represents the reference satellite index, the superscript i represents the index of non-reference satellite, and the superscript pi denotes the SD term calculated by i-term minus p-term.

Additionally, the SD ionospheric-free Doppler observation should also be used in the tight integration of PPP and INS to update the INS-mechanized velocity; its observation equation is directly given by:

$$D_{\text{IF}}^{pi} = \dot{\rho }^{pi} + \varepsilon_{{D_{\text{IF}} }}^{pi}$$
(16)

where \(D_{\text{IF}}^{pi}\) is the SD ionospheric-free Doppler observation (m/s) and \(\dot{\rho }\) is the range rate between the receiver and the satellite. Nevertheless, Eqs. (14) to (16) cannot be directly used in the conventional extended Kalman filter (EKF) and should be expanded by using Taylor series around initial parameters as:

$$P_{\text{IF}}^{pi} - P_{{{\text{IF}}0}}^{pi} = - \varvec{e}^{pi} \delta \varvec{r} + m_{\text{w}}^{pi} \delta T_{\text{w}} + \varepsilon_{{P_{\text{IF}} }}^{pi}$$
(17)
$$L_{\text{IF}}^{pi} - L_{{{\text{IF}}0}}^{pi} = - \varvec{e}^{pi} \delta \varvec{r} + m_{\text{w}}^{pi} \delta T_{\text{w}} - \delta N_{\text{IF}}^{pi} + \varepsilon_{{L_{\text{IF}} }}^{pi}$$
(18)
$$D_{\text{IF}}^{pi} - D_{{{\text{IF}}0}}^{pi} = - \varvec{e}^{pi} \delta \varvec{v} + \varepsilon_{{D_{\text{IF}} }}^{pi}$$
(19)

where \(P_{\text{IF0}}^{pi},\,L_{\text{IF0}}^{pi},\,and\, D_{\text{IF0}}^{pi}\) are the approximations, and in integrating of PPP and INS, these approximations are calculated from the INS-mechanized position and velocity; \(\varvec{e}^{pi}\) is the SD direction cosine vector (DCV) from the receiver to the satellite; \(\delta \varvec{r}\) is the position error vector; \(\delta \varvec{v}\) is the velocity error vector; T w is the zenith wet delay (ZWD) supposing that the dry zenith delay has been corrected; and \(m_{\text{W}}^{pi}\)is the SD value of the wet delay mapping function. Equations (17), (18), and (19) will be used for establishing the observation model of tightly coupled PPP/INS integration.

Recent investigations showed that the combined GPS/GLONASS PPP can significantly reduce the convergence time compared with the GPS-only PPP (Cai and Gao 2013; Li and Zhang 2014; Jokinen et al. 2013). Therefore, in our investigation, the GLONASS satellites will also be included to aid ambiguity fixing of GPS PPP. Nevertheless, the ionospheric-free ambiguity of GLONASS will not be fixed since it is difficult to be fixed at present (Li and Zhang 2014). The observation model of GLONASS PPP also takes the form of GPS PPP, but only uses conventional precise clock products from IGS.

PPP ambiguity fixing strategy

From the derivation above, the ionospheric-free ambiguity can recover its fixable property by separating the satellite code clock and satellite phase clock. However, its recovery of fixable property does not mean the ionospheric-free ambiguity is already fixed. The fixing of the ionospheric-free ambiguity is based on the primary fixing of the wide- and narrow-lane ambiguities. The strategy is at the SD level and is summarized as follows:

  1. 1.

    SD float ionospheric-free ambiguity calculating. The SD float ionospheric-free ambiguities with their variance–covariance (VC) matrix are calculated from the standard EKF. If we do not need the fixed solutions, then the following three steps will no longer be carried out and the solutions from EKF is directly used as the final results.

  2. 2.

    SD wide-lane ambiguity fixing. The SD float wide-lane ambiguities are computed from the Hatch–Melbourne–Wübbena (HMW) combinations (Hatch 1982; Melbourne 1985; Wübbena 1985) and then are corrected by the wide-lane biases provided by CNES to recover their integer property (Loyer et al. 2012). The fixing decision is made according to Dong and Bock (1989). Typically, a simple rounding method is used for fixing the SD wide-lane ambiguity because of its relatively long wavelength.

  3. 3.

    SD narrow-lane ambiguity fixing. The SD float narrow-lane ambiguities are derived from their relationship with the SD float ionospheric-free ambiguities and the SD-fixed wide-lane ambiguities. In detail, the SD float narrow-lane ambiguities can be calculated from (5):

    $$\hat{\varvec{N}}_{1}^{pi} = {{\left( {\hat{\varvec{N}}_{\text{IF}}^{pi} + \frac{{\lambda_{2} }}{{\gamma_{2} - 1}}\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} }_{\text{WL}}^{pi} } \right)} \mathord{\left/ {\vphantom {{\left( {\hat{\varvec{N}}_{\text{IF}}^{pi} + \frac{{\lambda_{2} }}{{\gamma_{2} - 1}}\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} }_{\text{WL}}^{pi} } \right)} {\lambda_{\text{NL}} }}} \right. \kern-0pt} {\lambda_{\text{NL}} }}$$
    (20)

    where \(\hat{\varvec{N}}_{\text{IF}}^{pi}\) is the SD float ionospheric-free ambiguities with their VC matrix denoted by \(\varvec{Q}_{{\hat{\varvec{N}}_{\text{IF}}^{pi} }}\), and \(\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} }_{\text{WL}}^{pi}\) is the SD-fixed wide-lane ambiguities. The VC matrix of the SD float narrow-lane ambiguities is obtained by applying the covariance propagation law:

    $$\varvec{Q}_{{\hat{\varvec{N}}_{1}^{pi} }} = \frac{1}{{\lambda_{\text{NL}}^{2} }}\varvec{Q}_{{\hat{\varvec{N}}_{\text{IF}}^{pi} }}$$
    (21)

    Unlike the PPP ambiguity fixing method developed by Ge et al. (2008), there is no need to correct the narrow-lane ambiguities with the satellite narrow-lane biases since they have been absorbed in the satellite phase clocks. The SD float narrow-lane ambiguities and their VC matrix are then used as the input to the well-known Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) method (Teunissen 1995) to perform integer ambiguity resolution. Fixing decisions are made by the popular ratio test and the success rate (Teunissen 1998). Because of the relatively short wavelength of narrow-lane ambiguities, some biases will prevent the successful resolution of the whole set of the ambiguities. Instead of fixing all the SD narrow-lane ambiguities, a subset of the ambiguities is fixed to integers. A partial ambiguity resolution (PAR) algorithm proposed by Parkins (2011) is used in our fixing strategy. In order to increase the reliability of correct fixing of the SD narrow-lane ambiguities, this step will not be carried out until the position variance from EKF is below a threshold.

  4. 4.

    SD ionospheric-free ambiguity fixing. After successful fixing of the SD wide- and narrow-lane ambiguities, the SD ionospheric-free ambiguities can be fixed by using (5), and then the other parameters including positions, ZWD, and remnant unfixed ambiguities can be updated by their correlation with the fixed ambiguities.

Inertial navigation system model

Unlike GNSS, INS is a completely autonomous system and is immune to the outside interference. However, the navigation performance of INS degrades with time rapidly. In order to restrict the INS error growth, external observations from GNSS receiver are required. For the integration of PPP and INS, the equations of motion and the INS error equations will be studied first. The equations of motion expressed in the earth-centered earth-fixed (ECEF) frame are given by:

$$\left[ {\begin{array}{*{20}l} {\dot{\varvec{r}}^{e} } \\ {\dot{\varvec{v}}^{e} } \\ {\dot{\varvec{C}}_{b}^{e} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varvec{v}^{e} } \\ {\varvec{C}_{b}^{e} \varvec{f}_{ib}^{b} - 2\varvec{\varOmega}_{ie}^{e} \varvec{v}^{e} + \varvec{g}^{e} } \\ {\varvec{C}_{b}^{e}\varvec{\varOmega}_{eb}^{b} } \\ \end{array} } \right]$$
(22)

where the rotation rate of frame a relative to frame b expressed in frame c is denoted as \(\varvec{\omega}_{ba}^{c}\), \(\varvec{\varOmega}_{ba}^{c}\) is the skew-symmetric form of \(\varvec{\omega}_{ba}^{c}\), the three symbols i, b, and e in the subscript or superscript indicate the inertial frame, the body frame, and the ECEF frame, respectively, a dot represents a time derivative, \(\varvec{r}^{e}\) is the position vector expressed in the e frame, \(\varvec{v}^{e}\) is the velocity vector expressed in the e frame, \(\varvec{C}_{b}^{e}\) represents the rotation matrix to rotate a vector from the b frame to the e frame, \(\varvec{f}_{ib}^{b}\) is the specific force vector obtained from the accelerometers expressed in the b frame, \(\varvec{\varOmega}_{ie}^{e}\) is the skew-symmetric form of the earth rotation rates \(\varvec{\omega}_{ie}^{e}\), \(\varvec{g}^{e}\) is the gravity vector expressed in the e frame, and \(\varvec{\varOmega}_{eb}^{b}\) is the skew-symmetric form of the rotation rate vector \(\varvec{\omega}_{eb}^{b}\) which can be calculated by:

$$\varvec{\omega}_{eb}^{b} =\varvec{\omega}_{ib}^{b} - \varvec{C}_{e}^{b}\varvec{\omega}_{ie}^{e}$$
(23)

where \(\varvec{\omega}_{ib}^{b}\) is the angular rate vector obtained from the gyros.

The mechanization equations are used to solve the equations of motion to obtain the position, velocity, and attitude when the initial conditions of the system are known. The details of the mechanization equations are available in Groves (2008). The equations of motion are then linearized to obtain the INS error equations:

$$\left[ {\begin{array}{*{20}c} {\delta \dot{\varvec{r}}^{e} } \\ {\delta \dot{\varvec{v}}^{e} } \\ {\dot{\varvec{\varphi }}^{e} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\delta \varvec{v}^{e} } \\ { - 2\varvec{\varOmega}_{ie}^{e} \delta \varvec{v}^{e} + S(\varvec{C}_{b}^{e} \varvec{f}_{ib}^{b} )\varvec{\varphi }^{e} - \varvec{C}_{b}^{e} \delta \varvec{f}_{ib}^{b} } \\ { -\varvec{\varOmega}_{ie}^{e} \varvec{\varphi }^{e} + \varvec{C}_{b}^{e} \delta\varvec{\omega}_{ib}^{b} } \\ \end{array} } \right]$$
(24)

where δ in front of a parameter indicates an error quantity, \(\varvec{\varphi }^{e}\) is the vector of misalignment angles, S is the function of calculating the skew-symmetric matrix of a vector, \(\delta \varvec{f}_{ib}^{b}\) is the accelerometer sensor error vector, and \(\delta\varvec{\omega}_{ib}^{b}\) is the gyro sensor error vector. In the following section, it will be found that (24) is the basis of establishing the system model for the tight integration of PPP and INS.

Tight integration of PPP and INS

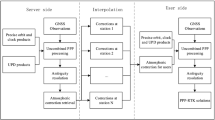
The loose and tight integration architectures are most commonly used in integrating PPP with INS (Du and Gao 2010). They differ in the type of information shared between GNSS and INS (Petovello et al. 2004). In the loose integration architecture, the PPP-derived navigation information and INS-mechanized navigation information are inputted into the fusing filter to generate the error state vector. In contrast to the loose integration architecture, the tight architecture uses the ionospheric-free observations from GNSS and the INS-predicted observations as inputs of the fusing filter to yield the error state vector.

Although the tight integration architecture is complex and increases the computational burden due to the increased size of the state vector, it has three major advantages in comparison with the loose one: First, it directly uses the observations (code, phase, and Doppler) that exhibit less temporal correlation than the navigation solutions (position and velocity); second, its fusing filter can still be updated in situations when less than four satellites are visible; and third, it enhances the ability of INS-aided fault detection, cycle slip correction, and re-fixing. As a consequence, we aim to model and implement the tight architecture for the PPP/INS integration.

An estimator is needed to fuse the GNSS and INS data together. EKF is the most widely used estimator for the GNSS/INS integration. EKF consists of two parts: a system model and an observation model. The system model is obtained from the INS error Eqs. (24) by augmenting with new error states:

$$\left[ {\begin{array}{*{20}c} {\delta \dot{\varvec{r}}^{e} } \\ {\delta \dot{\varvec{v}}^{e} } \\ {\dot{\varvec{\varphi }}^{e} } \\ {\delta \dot{\varvec{b}}_{\text{a}} } \\ {\delta \dot{\varvec{b}}_{\text{g}} } \\ {\delta \dot{T}_{\text{w}} } \\ {\delta \dot{\varvec{N}}_{\text{IF}}^{G,pi} } \\ {\delta \dot{\varvec{N}}_{\text{IF}}^{R,qj} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} \varvec{0} & \varvec{I} & \varvec{0} & \varvec{0} & \varvec{0} & 0 & \varvec{0} & \varvec{0} \\ \varvec{0} & { - 2\varvec{\varOmega}_{ie}^{e} } & {S(\varvec{C}_{b}^{e} \varvec{f}_{ib}^{b} )} & { - \varvec{C}_{b}^{e} } & \varvec{0} & 0 & \varvec{0} & \varvec{0} \\ \varvec{0} & \varvec{0} & { -\varvec{\varOmega}_{ie}^{e} } & \varvec{0} & {\varvec{C}_{b}^{e} } & 0 & \varvec{0} & \varvec{0} \\ \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & 0 & \varvec{0} & \varvec{0} \\ \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & 0 & \varvec{0} & \varvec{0} \\ \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & 0 & \varvec{0} & \varvec{0} \\ \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & 0 & \varvec{0} & \varvec{0} \\ \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & 0 & \varvec{0} & \varvec{0} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\delta \varvec{r}^{e} } \\ {\delta \varvec{v}^{e} } \\ {\varvec{\varphi }^{e} } \\ {\delta \varvec{b}_{\text{a}} } \\ {\delta \varvec{b}_{\text{g}} } \\ {\delta T_{\text{w}} } \\ {\delta \varvec{N}_{\text{IF}}^{G,pi} } \\ {\delta \varvec{N}_{\text{IF}}^{R,qj} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} \varvec{0} & \varvec{0} & 0 \\ { - \varvec{C}_{b}^{e} } & \varvec{0} & 0 \\ \varvec{0} & {\varvec{C}_{b}^{e} } & 0 \\ \varvec{0} & \varvec{0} & 0 \\ \varvec{0} & \varvec{0} & 0 \\ \varvec{0} & \varvec{0} & 1 \\ \varvec{0} & \varvec{0} & 0 \\ \varvec{0} & \varvec{0} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{\varepsilon}_{\text{a}} } \\ {\varvec{\varepsilon}_{\text{g}} } \\ {\varvec{\varepsilon}_{{T_{\text{w}} }} } \\ \end{array} } \right]$$
(25)

where I is the identity matrix, b a is the accelerometer biases expressed in the b frame, b g is the gyro biases expressed in the b frame, b a and b g are modeled as random constants for the tactical grade inertial measurement unit (IMU) used in the following tests, ε a is accelerometer noise vector, ε g is the gyro noise vector, T w is modeled as random walk process and its driving noise is denoted by \(\varepsilon_{{T_{\text{w}} }}\), the superscripts G and R denote GPS and GLONASS, respectively, the superscript q denotes the reference satellite of GLONASS, the superscript j denotes the non-reference satellites of GLONASS, \(\varvec{N}_{\text{IF}}^{G,pi}\) is the vector formed by the SD ionospheric-free ambiguities of GPS, \(\varvec{N}_{\text{IF}}^{R,qj}\) is the vector formed by the SD ionospheric-free ambiguities of GLONASS, and all the ionospheric-free ambiguities are modeled as constant.

The observation model is obtained from the PPP error Eqs. (17), (18) and (19) by augmenting with new error states:

$$\left[ {\begin{array}{*{20}c} {\varvec{P}_\text{IF}^{G,pi} - \varvec{P}_\text{INS}^{G,pi} } \\ {\varvec{L}_\text{IF}^{G,pi} - \varvec{L}_\text{INS}^{G,pi} } \\ {\varvec{D}_\text{IF}^{G,pi} - \varvec{D}_\text{INS}^{G,pi} } \\ {\varvec{P}_\text{IF}^{R,qj} - \varvec{P}_\text{INS}^{R,qj} } \\ {\varvec{L}_\text{IF}^{R,qj} - \varvec{L}_\text{INS}^{R,qj} } \\ {\varvec{D}_\text{IF}^{R,qj} - \varvec{D}_\text{INS}^{R,qj} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \varvec{E}^{G,pi} } & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & {\varvec{m}_{w}^{G,pi} } & \varvec{0} & \varvec{0} \\ { - \varvec{E}^{G,pi} } & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & {\varvec{m}_{w}^{G,pi} } & { - \varvec{I}^{G} } & \varvec{0} \\ \varvec{0} & { - \varvec{E}^{G,pi} } & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} \\ { - \varvec{E}^{R,qj} } & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & {\varvec{m}_{w}^{R,qj} } & \varvec{0} & \varvec{0} \\ { - \varvec{E}^{R,qj} } & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & {\varvec{m}_{w}^{R,qj} } & \varvec{0} & { - \varvec{I}^{R} } \\ \varvec{0} & { - \varvec{E}^{R,qj} } & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} & \varvec{0} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\delta \varvec{r}^{e} } \\ {\delta \varvec{v}^{e} } \\ {\varvec{\varphi }^{e} } \\ {\delta \varvec{b}_{\text{a}} } \\ {\delta \varvec{b}_{\text{g}} } \\ {\delta T_{\text{w}} } \\ {\delta \varvec{N}_{\text{IF}}^{G,pi} } \\ {\delta \varvec{N}_{\text{IF}}^{R,qj} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\varvec{\varepsilon}_{{P_{\text{IF}} }}^{G,pi} } \\ {\varvec{\varepsilon}_{{L_{\text{IF}} }}^{G,pi} } \\ {\varvec{\varepsilon}_{{D_{\text{IF}} }}^{G,pi} } \\ {\varvec{\varepsilon}_{{P_{\text{IF}} }}^{R,qj} } \\ {\varvec{\varepsilon}_{{L_{\text{IF}} }}^{R,qj} } \\ {\varvec{\varepsilon}_{{D_{\text{IF}} }}^{R,qj} } \\ \end{array} } \right]$$
(26)

where \(\varvec{P}_{\text{IF}}^{G,pi}\) is the vector formed by the SD ionospheric-free code observations of GPS, \(\varvec{L}_{\text{IF}}^{G,pi}\) is the vector formed by the SD ionospheric-free phase observations of GPS, \(\varvec{D}_{\text{IF}}^{G,pi}\) is the vector formed by the SD ionospheric-free Doppler observations of GPS, the subscript INS on the equation left indicates the INS-predicted observations derived from the INS-mechanized position and velocity, \(\varvec{E}^{G,pi}\) is the matrix formed by the SD DCV, \(\varvec{e}^{pi}\), of the GPS satellites, \(\varvec{m}_{\text{w}}^{G,pi}\) is the vector formed by the SD wet mapping function value of GPS, and \(\varvec{P}_{\text{IF}}^{R,qj}\), \(\varvec{L}_{\text{IF}}^{R,qj}\), \(\varvec{D}_{\text{IF}}^{R,qj}\), \(\varvec{E}^{R,qj}\) and \(\varvec{m}_{\text{w}}^{R,qj}\), are the corresponding denotations of GLONASS.

Therefore, the PPP/INS integration model is established by (25) and (26). Note that the model presented above is used for not only the ambiguity-float PPP/INS integration but also the ambiguity-fixed PPP/INS integration. The difference is that the ambiguity-float PPP/INS integration only uses the precise clock products from the IGS and its SD ionospheric-free ambiguities are unfixed, while the ambiguity-fixed PPP/INS integration additionally needs the precise clock products from CNES to recover the fixable property of the ionospheric-free ambiguities as described above. Note that the ambiguities of GLONASS satellites will not be fixed.

Results and analysis

To validate the tight integration model of the ambiguity-fixed PPP and INS, two carborne tests were carried out in different environments. With each test, a NovAtel OEM4 GNSS dual-frequency receiver and a tactical grade LCI-IMU were installed in the vehicle. The raw dual-frequency code, phase, and Doppler observations were logged from the GNSS receiver at 1 Hz. The raw specific increments and angle increments were logged from the IMU at 200 Hz. The specifications for the IMU are listed as follows: The gyro bias of the IMU is 1°/h, the angular random walk is 0.05°/\(\sqrt {\text{h}}\), the accelerometer bias is 1 mg, and the velocity random walk is 50 μg/\(\sqrt {\text{Hz}}\).

In order to properly evaluate the performance of the PPP/INS integration, both of the two tests deployed reference stations so that the reference solution including position, velocity, and attitude can be calculated with the commercial software package, Inertial Explorer (IE), in the tightly coupled DGNSS/INS mode. The nominal accuracy of the reference solution provided by IE is at the level of 1 cm for horizontal position and 1.5 cm for vertical position, 1 cm/s for velocity, and <0.01° for attitude. Another reference solution, which is used to evaluate the performance of PPP-only solution, was calculated from IE in the DGNSS mode.

Carborne test I

The first test was conducted on November 14, 2013, on a small square in Wuhan, China, lasting about 4000 s. The horizontal routing is shown in Fig. 1. The lever arm from the navigation center of the IMU to the phase center of the receiver antenna was measured by using a total station and was corrected in the filtering. During the test, a reference station was deployed at a site with precisely known position. The maximum baseline during the test was about 10 km which ensures an accurate and reliable reference trajectory that can be generated by the commercial software.

Fig. 1
figure 1

Horizontal routing of the first test

Full size image

The static period of about 9 min of the collected IMU data was used for the initial alignment. The successive IMU data were used to fuse with the GNSS raw observations in two integration modes, namely the ambiguity-float PPP/INS integration and the ambiguity-fixed PPP/INS integration. The total number of satellites and the numbers of fixed SD wide- and narrow-lane ambiguities are given in Fig. 2. The figure shows that the number of the fixed SD narrow-lane satellites is sometimes less than the number of the fixed SD wide-lane satellites, which means PAR was carried out in the filtering.

Fig. 2
figure 2

Total satellite number and fixed SD wide- and narrow-lane satellite numbers

Full size image

The position, velocity, and attitude differences between the two modes and the reference solution were calculated. The position differences of the two modes are shown in Figs. 3 and 4, respectively. Figure 4 shows that it takes about 10 min for the ambiguity-fixed PPP/INS integration to obtain its first-fixed solution. Once the ambiguities are correctly fixed, the position difference observably falls from decimeter to centimeter level compared with the ambiguity-float PPP/INS integration. Furthermore, the ambiguity-fixed PPP/INS integration presents a more accurate and stable solution after the first-fixed solution as is illustrated in Fig. 4.

Fig. 3
figure 3

Position difference of the ambiguity-float PPP/INS integration

Full size image
Fig. 4
figure 4

Position difference of the ambiguity-fixed PPP/INS integration

Full size image

Table 1 shows the statistics of the position difference from the time of the first-fixed solution to the end of the data. The tabular result indicates that the positioning difference of ambiguity-fixed PPP/INS integration is at centimeter level which is comparable to that of DGNSS/INS integration, while the position difference of the ambiguity-float PPP/INS integration is not stable.

Table 1 Statistics of position difference
Full size table

Figure 5 shows the velocity difference between the ambiguity-fixed PPP/INS integration and the reference solution, and Fig. 6 shows the corresponding attitude difference. The advantage of ambiguity fixing for the PPP/INS integration mainly results in an improvement of the positioning accuracy. Therefore, the velocity difference and the attitude difference of the ambiguity-float PPP/INS integration are not illustrated. The RMS for the north, east, and up components are 3.52, 4.13, and 4.85 mm/s, respectively, and the RMS for pitch, roll, and yaw are 0.0030°, 0.0029°, and 0.0265°, respectively. Both statistics used the data segment covering from the first-fixed solution to the end of the data. Although the differences are not the true errors, they still imply that the velocity and attitude accuracy is consistent with that of the reference solution. However, the yaw difference is slightly larger than the pitch and roll differences because of the poor observability degree of the yaw angle.

Fig. 5
figure 5

Velocity difference of the ambiguity-fixed PPP/INS integration

Full size image
Fig. 6
figure 6

Attitude difference of the ambiguity-fixed PPP/INS integration

Full size image

Carborne test II

The second test was carried out on December 14, 2013, in the suburban environment of Zunyi, China, lasting about 4000 s. Figure 7 shows the plan view of the trajectory. The maximum baseline length for this run was within 5 km. The GNSS receivers and the IMU used in the second test were the same type as those used in the first test. The other settings of the second test were the same as those of the first test. Figure 8 shows the total satellite number and the fixed SD wide-lane and narrow-lane satellite numbers.

Fig. 7
figure 7

Horizontal routing of the second test

Full size image
Fig. 8
figure 8

Total satellite number and fixed SD wide- and narrow-lane satellite numbers

Full size image

The first 7 min of the IMU data was in static and was used for the initial alignment. Then, the IMU data were fused with the raw observations from the rover GNSS receiver in two modes as described in the first test. The position differences between the two modes and the reference solution are shown in Figs. 9 and 10, respectively. Figure 10 shows that it takes about 14 min for the ambiguity-fixed PPP/INS integration to achieve its first-fixed solution. Table 2 shows the statistics of the position difference from the first-fixed solution to the end of the data. It is shown that after the first-fixed solution, the position difference of the ambiguity-fixed PPP/INS integration is stable and around centimeter level.

Fig. 9
figure 9

Position difference of the ambiguity-float PPP/INS integration

Full size image
Fig. 10
figure 10

Position difference of the ambiguity-fixed PPP/INS integration

Full size image
Table 2 Statistics of position difference
Full size table

Figure 11 shows the velocity difference and Fig. 12 the attitude difference. The RMS of the velocity differences in east, north, and up are 2.10, 2.07, and 2.01 mm/s, respectively, and the RMS attitude differences in pitch, roll, and yaw are 0.0070°, 0.0026°, and 0.0098°, respectively. Also, both statistics used the data segment covering from the first-fixed solution to the end of the data. It is also found that the velocity and attitude accuracy is comparable to that of the reference solution.

Fig. 11
figure 11

Velocity difference of the ambiguity-fixed PPP/INS integration

Full size image
Fig. 12
figure 12

Attitude difference of the ambiguity-fixed PPP/INS integration

Full size image

Rapid re-fixing aided by INS

Both PPP and the PPP/INS integration will face GNSS outages in carborne applications, because the GNSS signals are vulnerable to be obstructed by bridges and high buildings. The phase observations will have cycle slips after the GNSS signals are re-acquired. Typically, the ambiguity parameters will be reset in the PPP filter. However, it will cost several or even tens of minutes to achieve re-convergence and re-fixing, which prevents the popularity of PPP. For the PPP/INS integration, the accuracy of the INS-mechanized position can maintain centimeter to decimeter level over a short period of GNSS outage. Although the ambiguity parameters are also reset in the PPP/INS filter, rapid re-convergence and re-fixing are aided by INS.

The carborne test I was used to evaluate the performance of INS-aided re-convergence and re-fixing. Two GNSS outages were simulated in the raw GNSS data. The first GNSS outage was from 09:49:50 to 09:50:00 and the second from 09:59:50 to 10:00:00. Every GNSS outage is 10 s long. The GNSS data with GNSS outages and the INS data were calculated in the four modes, namely the ambiguity-float PPP, the ambiguity-fixed PPP, the ambiguity-float PPP/INS integration, and the ambiguity-fixed PPP/INS integration. The position differences between the four modes and the reference solutions are shown in Figs. 13, 14, 15, and 16.

Fig. 13
figure 13

Position difference of the ambiguity-float PPP with two GNSS outages

Full size image
Fig. 14
figure 14

Position difference of the ambiguity-fixed PPP with two GNSS outages

Full size image
Fig. 15
figure 15

Position difference of the ambiguity-float PPP/INS integration with two GNSS outages

Full size image
Fig. 16
figure 16

Position difference of the ambiguity-fixed PPP/INS integration with two GNSS outages

Full size image

As can be seen in Fig. 13, PPP requires re-convergence to get better position results after the two GNSS outages. The two re-convergence periods are obvious, and the maximum position difference is over 1 meter. In contrast, Fig. 15 shows that rapid re-convergence is achievable due to INS aiding. The two re-convergence periods are not obvious. Figure 14 shows that it takes several minutes to get the re-fixed solutions, while Fig. 16 shows that it only costs about 1 min to get the re-fixed solutions. The above comparison shows that the INS contributes to the re-fixing of ambiguities.

However, the four figures indicate that the initial convergence period is not accelerated by using the tactical grade INS, because the INS provides the position increment but not the absolute position, and that the initial position of INS is imprecise and has large uncertainty. By contrast, at the beginning of the GNSS outage, the position of INS already has a certain precision and can contribute to the re-convergence and re-fixing. It should be noted that the INS-mechanized position error increases rapidly with longer GNSS outage period, which also degrades the performance of INS-aided re-convergence and re-fixing.

Conclusions and prospects

In this study, we give a detailed description of establishing the model of the tight integration of the ambiguity-fixed PPP and INS. Two tests were carried out to evaluate the performance of the proposed ambiguity-fixed PPP/INS integration by comparing its navigation solution with that of the DGNSS/INS integration from the commercial software. The results indicate that the efficiency of positioning and attitude determination of the ambiguity-fixed PPP/INS integration is comparable to that of the DGNSS/INS integration, the ambiguity-fixed PPP/INS integration has much shorter convergence time than the ambiguity-float PPP/INS integration, and rapid re-convergence and re-fixing are achievable due to INS aiding after a short period of GNSS outage.

For applications over large area, the proposed ambiguity-fixed PPP/INS integration will be an ideal alternative to the DGNSS/INS integration. Because local reference stations are no longer required, it will significantly decrease the system complexity and cost.

Compared with the well-developed and widely used DGNSS/INS system, the ambiguity-fixed PPP/INS system will face several problems to be solved. One of the problems is the reliability and quality control of the ambiguity fixing, which is crucial for high-accuracy applications and will be further investigated in future work.