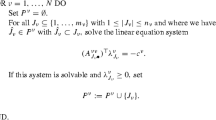Computing equilibria of Cournot oligopoly models with mixed-integer quantities

Abstract

We consider Cournot oligopoly models in which some variables represent indivisible quantities. These models can be addressed by computing equilibria of Nash equilibrium problems in which the players solve mixed-integer nonlinear problems. In the literature there are no methods to compute equilibria of this type of Nash games. We propose a Jacobi-type method for computing solutions of Nash equilibrium problems with mixed-integer variables. This algorithm is a generalization of a recently proposed method for the solution of discrete so-called “2-groups partitionable” Nash equilibrium problems. We prove that our algorithm converges in a finite number of iterations to approximate equilibria under reasonable conditions. Moreover, we give conditions for the existence of approximate equilibria. Finally, we give numerical results to show the effectiveness of the proposed method.

1 Introduction

Cournot oligopolies can be modeled as Nash equilibrium problems, see e.g. Başar and Olsder (1989), Tirole (1988). The Nash equilibrium problem is a key model in game theory and several algorithms have been proposed for its solution, see e.g. the monograph (Facchinei and Pang 2003) and the references therein. Also for its generalized version (the generalized Nash equilibrium problem) can be found in the literature many solution methods, see e.g. Aussel and Sagratella (2017), Dreves et al. (2011, 2012), Dreves and Kanzow (2011), Facchinei and Kanzow (2010), Facchinei et al. (2012, 2014), Facchinei and Lampariello (2011), Facchinei and Sagratella (2011), Nabetani et al. (2011), Pang and Fukushima (2009). But all these methods assume that the feasible region of all the players is continuous. Besides some specific procedures for some particular applications (see e.g. Fabrikant et al. 2004; Stengel 2002), recently some numerical methods for the solution of Nash equilibrium problems with discrete strategy spaces have been proposed (Sagratella 2016).

We consider the most challenging case of Nash equilibrium problems in which each player solves a mixed-integer nonlinear problem (see e.g. Belotti et al. 2013, 2009; Bienstock 1996; Lazimy 1982; Nowak 2006; Tawarmalani and Sahinidis 2002 as excellent references on this type of optimization problems) since some of its variables represent indivisible quantities. In particular, we generalize the Jacobi-type algorithm proposed in Sagratella (2016) for discrete so-called “2-groups partitionable” Nash equilibrium problems.

In Sect. 2 we describe the Cournot oligopoly model with mixed-integer quantities. In Sect. 3 we define the Jacobi-type method for computing solutions of the Nash model with mixed-integer variables and we prove that it converges in a finite number of iterations to an approximate equilibrium under reasonable conditions. In Sect. 4 we give numerical results to show the effectiveness of the proposed method.

Notation: $M \in \mathbb {R}_{m \times n}$ is a matrix with m rows and n columns; $M_{j*}$ denotes the jth row of M and $M_{*i}$ denotes the ith column of M; given a set of row indices $J_r$ and a set of column indices $J_c, M_{J_r J_c}$ is the submatrix with rows in $J_r$ and columns in $J_c$; given $v \in {{\mathbb {R}}}^n, D_v$ denotes the square matrix whose diagonal entries are those of v.

2 A Cournot oligopoly model

Consider a market in which N firms produce multiple goods in order to increase their profits as much as possible. Assuming that the firms act rationally, there is no explicit collusion among them, and all of them have complete information, then the Nash equilibrium paradigm fits well within this framework, see e.g. Tirole (1988).

Each firm $\nu \in \{1, \ldots , N\}$ produces $n_\nu$ goods and must decide the amount of all its goods it will produce. Namely, by considering the realistic case of an initial stage (which is not an equilibrium) in which each firm $\nu$ produces quantities ${\widehat{q}}^\nu \in {{\mathbb {R}}}^{n_\nu }_+$ of its goods, the decision variables of each firm $\nu$ are $x^\nu \in {{\mathbb {R}}}^{n_\nu }$ which represent deviations from ${\widehat{q}}^\nu$, so that the amounts of produced goods are actually $q^\nu \triangleq x^\nu + {\widehat{q}}^\nu$. We further define the vector $\mathbf{x}^{-\nu } \triangleq (x^{\mu })_{\nu \ne \mu =1}^N$ and write ${\mathbb {R}}^{n}\ni \mathbf{x}\triangleq (x^\nu ,\mathbf{x}^{-\nu })$, where $n \triangleq n_1 + \cdots + n_N$.

The consumers’ inverse demand function for each firm $\nu \in \{1, \ldots , N\}$ is linear:

$$\begin{aligned} p^\nu (x^\nu ,\mathbf{x}^{-\nu }) \triangleq a^\nu - \sum _{\mu = 1}^N C^{\nu \mu } (x^\mu + {\widehat{q}}^\mu ), \end{aligned}$$

where $a^\nu \in {{\mathbb {R}}}^{n_\nu }, C^{\nu \mu } \in \mathbb {R}_{n_\nu \times n_\mu }$ for all $\mu$, and $p^\nu (x^\nu ,\mathbf{x}^{-\nu })$ indicates the market prices corresponding to deviations $\mathbf{x}$. Notice that, if $C^{\nu \mu }_{ij} \ge 0$ then the jth product of firm $\mu$ is a substitute for the ith product of firm $\nu$ since the price of the second product decreases as the quantity of the first product increases. On the other hand, if $C^{\nu \mu }_{ij} \le 0$ then the jth product of firm $\mu$ is a complement for the ith product of firm $\nu$.

Each firm $\nu \in \{1, \ldots , N\}$ has quadratic production costs:

$$\begin{aligned} \text {Cost}_\nu (x^\nu ) \triangleq (x^\nu + {\widehat{q}}^\nu )^{\scriptscriptstyle T}c^\nu - (x^\nu + {\widehat{q}}^\nu )^{\scriptscriptstyle T}D_{k^\nu } (x^\nu + {\widehat{q}}^\nu ), \end{aligned}$$

where $c^\nu , k^\nu \in {{\mathbb {R}}}^{n_\nu }_+$. This structure for the production costs allows to model, for example, the presence of economies of scale.

The overall profit of each firm $\nu \in \{1, \ldots , N\}$ is the following:

$$\begin{aligned} \text {Profit}_\nu (x^\nu ,\mathbf{x}^{-\nu }) \triangleq p^\nu (x^\nu ,\mathbf{x}^{-\nu })^{\scriptscriptstyle T}(x^\nu + {\widehat{q}}^\nu ) - \text {Cost}_\nu (x^\nu ). \end{aligned}$$

Observe that $\text {Profit}_\nu (x^\nu ,\mathbf{x}^{-\nu })$ is a quadratic function.

Assume, without loss of generality, that the first $i_\nu$ goods of each firm $\nu$ are indivisible (like houses, cars and machines) or must be produced in lots, while the remaining $n_\nu - i_\nu$ goods are perfectly divisible. Namely, we assume that $x^\nu _j, {\widehat{q}}^\nu _j \in {{\mathbb {Z}}}$ for all $j \le i_\nu$.

The optimization problem faced by each firm $\nu \in \{1, \ldots , N\}$ is the following:

$$\begin{aligned} \displaystyle \text {minimize}_{x^\nu }&\; \theta _\nu (x^\nu ,\mathbf{x}^{-\nu }) \triangleq - \text {Profit}_\nu (x^\nu ,\mathbf{x}^{-\nu }) \nonumber \\&l^\nu \le x^\nu \le u^\nu \nonumber \\&x^\nu _j \in {{\mathbb {Z}}}, \quad j = 1, \ldots , i_\nu , \end{aligned}$$

(1)

where $l^\nu , u^\nu \in {{\mathbb {R}}}^{n_\nu }$ are suitable bounds, namely, $-{\widehat{q}}^\nu \le l^\nu \le u^\nu$ and $l^\nu _j, u^\nu _j \in {{\mathbb {Z}}}$ for all $j \le i_\nu$. Each (1) is a mixed-integer nonlinear problem, specifically, it is a mixed-integer quadratic problem (MIQP), see e.g. Bienstock (1996), Lazimy (1982). The whole game is a standard Nash equilibrium problem (NEP) since the objective function of each player $\nu$ depends on the rivals’ variables $\mathbf{x}^{-\nu }$.

Let us introduce the best response set at ${\overline{\mathbf{x}}} \in X$ for each firm $\nu$:

$$\begin{aligned} {\widehat{x}}^\nu ({\overline{\mathbf{x}}}^{-\nu }) \triangleq \arg \min _{x^\nu \in X^\nu } \theta _\nu (x^\nu , {\overline{\mathbf{x}}}^{-\nu }), \end{aligned}$$

where

$$\begin{aligned} X^\nu \triangleq \left\{ x^\nu \in {{\mathbb {R}}}^{n_\nu }: \, l^\nu \le x^\nu \le u^\nu , \, x^\nu _j \in {{\mathbb {Z}}}, \, j = 1, \ldots , i_\nu \right\} \; \text { and } \; X \triangleq \prod _{\nu =1}^N X^\nu . \end{aligned}$$

Given $\varepsilon > 0$, we say that ${\overline{\mathbf{x}}} \in X$ is an $\varepsilon$-approximate equilibrium if, for all $\nu \in \{1, \ldots , N\}$, it holds that

$$\begin{aligned} \theta _\nu ({\overline{x}}^\nu , {\overline{\mathbf{x}}}^{-\nu }) - \theta _\nu ({\widehat{x}}^\nu , {\overline{\mathbf{x}}}^{-\nu }) \le \varepsilon , \end{aligned}$$

where ${\widehat{x}}^\nu \in {\widehat{x}}^\nu ({\overline{\mathbf{x}}}^{-\nu })$.

3 A Jacobi-type algorithm

To compute approximate equilibria of NEP (1), we propose the Jacobi-type method defined in Algorithm 1. This algorithm is an extension of Algorithm 7 in Sagratella (2016) for the mixed-integer case. The non-standard choice of the subset ${{\mathcal {J}}}^k$ of the firms that “play” at each iteration makes Algorithm 1 really flexible. Namely, as special cases, by selecting only one firm at each iteration we get a Gauss–Southwell scheme, while if the firms take turns to move their variables we get a Gauss–Seidel scheme, and, finally, if at each iteration all the firms solve their optimization problems simultaneously we get a Jacobi scheme.

It is well known that best response methods, like Algorithm 1, do not lead to solutions of NEPs in general, even in a totally continuous setting. However, as witnessed by Theorem 1 below, and similarly to what done in Sagratella (2016), we can define an interesting class of Cournot models with mixed-integer variables for which Algorithm 1 effectively works.

Definition 1

We say that the NEP defined by (1) is 2-groups partitionable if X is non-empty and compact, $Q^\nu \triangleq C^{\nu \nu } - D_{k^\nu } \succeq 0$ for all $\nu$, and a partition of the variables indices into two groups, $G_1$ and $G_2$, exists such that, for all $(\nu ,i) \ne (\mu ,j)$:

$$\begin{aligned}&C^{\nu \mu }_{ij} \le 0 \; \text { if } \, (\nu ,i) \in G_1 \ni (\mu ,j) \, \text { or } \, (\nu ,i) \in G_2 \ni (\mu ,j), \end{aligned}$$

(2)

$$\begin{aligned}&C^{\nu \mu }_{ij} \ge 0 \; \text { if } \, (\nu ,i) \in G_1 \not \ni (\mu ,j) \, \text { or } \, (\nu ,i) \in G_2 \not \ni (\mu ,j). \end{aligned}$$

(3)

The assumption $Q^\nu \succeq 0$ in Definition 1 is strong but quite standard in a Nash game setting, since it entails the convexity of the objective function of any player’s problem (1). Anyhow, it can be noted that the objective function of any player $\nu$ can always be reformulated as a convex function, regarding the discrete variables, by adding a term $\alpha (l^\nu - x^\nu )^{\scriptscriptstyle T}(u^\nu - x^\nu )$, with $\alpha$ sufficiently large, that vanishes in case of binary constraints $x^\nu \in \{l^\nu , u^\nu \}$.

Conditions (2) and (3) in Definition 1 simply require that all the goods must be divided into two groups such that: two goods of the same group are complements, while two goods of different groups are substitutes. See Sect. 2 for a definition of complements and substitutes.

We give a small example of a 2-groups partitionable Cournot model.

Example 1

There are three firms with the following data: $n_\nu = 1, {\widehat{q}}^\nu = 0, a^\nu = 2, c^\nu = 1, k^\nu = \frac{1}{2}, i_\nu = 1, l^\nu = 0$, and $u^\nu = 1$, for all $\nu \in \{1, 2, 3\}; C^{11} = 1, C^{12} = 0, C^{13} = -1, C^{21} = 1, C^{22} = 1, C^{23} = 0, C^{31} = 0, C^{32} = 1$, and $C^{33} = 1$. This Cournot model is 2-groups partitionable since: X is non-empty and compact, $Q^\nu = C^{\nu \nu }-k^\nu = \frac{1}{2}$ for all $\nu$, and, by partitioning the variables indices into $G_1 = \{(1,1), (3,1)\}$ and $G_2 = \{(2,1)\}$, conditions (2) and (3) are satisfied. Notice that the good produced by firm 1 is a complement for that of firm 3 and vice versa (they are both in $G_1$). On the other hand, the good of firm 2 is a substitute for that produced by firm 1 and for that produced by firm 3 and vice versa (the good of firm 2 is not in $G_1$).

The following theorem gives sufficient conditions for the convergence of Algorithm 1.

Theorem 1

Assume that the NEP defined by (1) is 2-groups partitionable with groups $G_1$ and $G_2$.

For all $\nu \in \{1,\ldots ,N\}$ and all $i \in \{1,\ldots ,n_\nu \}$, let $x^{0,\nu }_i = l^\nu _i$ if $(\nu ,i) \in G_1$, and let $x^{0,\nu }_i = u^\nu _i$ if $(\nu ,i) \in G_2$. Let a finite positive integer h exist such that $\nu \in \cup _{t = k}^{k + h} {{\mathcal {J}}}^t$ for each player $\nu$ and each iterate k.

Then, for each iterate k and each player $\nu \in {{\mathcal {J}}}^k$, a best response ${\widehat{x}}^{k,\nu } \in {\widehat{x}}^\nu (\mathbf{x}^{k,-\nu })$ can be computed such that

$$\begin{aligned} {\widehat{x}}^{k,\nu }_i \ge x^{k,\nu }_i, \quad \forall \, (\nu ,i) \in G_1, \qquad {\widehat{x}}^{k,\nu }_i \le x^{k,\nu }_i, \quad \forall \, (\nu ,i) \in G_2. \end{aligned}$$

(4)

By computing ${\widehat{x}}^{k,\nu }$ for all k and all $\nu \in {{\mathcal {J}}}^k$ such that (4) holds, Algorithm 1 converges, in a finite number of iterations, to an $\varepsilon$-approximate equilibrium of the NEP, given any $\varepsilon > 0$.

Proof

First of all note that the set ${\widehat{x}}^\nu ({\overline{\mathbf{x}}}^{-\nu })$ is non-empty for any $\nu$ and any ${\overline{\mathbf{x}}} \in X$ since X is non-empty and compact.

Let us consider the first iteration. Since $\mathbf{x}^1 \in X$ then it holds that $x^{1,\nu }_i \ge x^{0,\nu }_i$ if $(\nu ,i) \in G_1$, and $x^{1,\nu }_i \le x^{0,\nu }_i$ if, otherwise, $(\nu ,i) \in G_2$.

Now let us consider the second iteration. In order to prove that, for all $\nu$, a best response ${\widehat{x}}^{1,\nu } \in {\widehat{x}}^\nu (\mathbf{x}^{1,-\nu })$ exists such that for all $i \in \{1,\ldots ,n_\nu \}$:

$$\begin{aligned} {\widehat{x}}^{1,\nu }_i \ge x^{1,\nu }_i, \quad \text { if } \, (\nu ,i) \in G_1, \qquad \text { and, } \qquad {\widehat{x}}^{1,\nu }_i \le x^{1,\nu }_i, \quad \text { if } \, (\nu ,i) \in G_2, \end{aligned}$$

(5)

we have to consider two possibilities. If $\nu \notin {{\mathcal {J}}}^0$, or, in general, $x^{1,\nu }$ is not updated as in line 7 of the algorithm, then $x^{1,\nu } = x^{0,\nu }$ and then (5) is trivially satisfied. Otherwise $\nu \in {{\mathcal {J}}}^0$ and $x^{1,\nu }$ is updated as in line 7 of the algorithm, then we suppose by contradiction that for all $y^\nu \in {\widehat{x}}^\nu (\mathbf{x}^{1,-\nu })$ a non-empty set of indices $J \subseteq \{1, \ldots , n_\nu \}$ exists such that for all $i \in J$ it holds that $y^\nu _i < x^{1,\nu }_i$ if $(\nu ,i) \in G_1$ and $y^\nu _i > x^{1,\nu }_i$ if $(\nu ,i) \in G_2$. Now we show that this is impossible. Let ${\bar{J}} \triangleq \{1, \ldots , n_\nu \} \setminus J$, for all $j \in {\bar{J}}$ we have $y^\nu _j \ge x^{1,\nu }_j$ if $(\nu ,j) \in G_1$ and $y^\nu _j \le x^{1,\nu }_j$ if $(\nu ,j) \in G_2$. We define ${\bar{y}}^\nu , {\widetilde{y}}^\nu \in X^{\nu }$ such that ${\bar{y}}^\nu _J = y^\nu _J, {\bar{y}}^\nu _{{\bar{J}}} = x^{1,\nu }_{{\bar{J}}}, {\widetilde{y}}^\nu _J = x^{1,\nu }_J$ and ${\widetilde{y}}^\nu _{{\bar{J}}} = y^\nu _{{\bar{J}}}$. Recalling $Q^\nu \triangleq C^{\nu \nu } - D_{k^\nu }$, the following chain of inequalities holds:

$$\begin{aligned}&\left[ ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu \right] - \left[ (x^{1,\nu })^{\scriptscriptstyle T}Q^\nu (x^{1,\nu }) - ({{\bar{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\bar{y}}^\nu \right] \nonumber \\&\quad =\left[ 2 \left( (y^\nu _J)^{\scriptscriptstyle T}\; (y^\nu _{{\bar{J}}})^{\scriptscriptstyle T}\right) \, \left( \begin{array}{c} Q^\nu _{JJ} \\ Q^\nu _{{\bar{JJ}}} \end{array} \right) \, \left( x^{1,\nu }_J - y^\nu _J \right) + \left( x^{1,\nu }_J - y^\nu _J \right) ^{\scriptscriptstyle T}Q^\nu _{JJ} \left( x^{1,\nu }_J - y^\nu _J \right) \right] \nonumber \\&\qquad -\left[ 2 \left( (y^\nu _J)^{\scriptscriptstyle T}\; (x^{1,\nu }_{{\bar{J}}})^{\scriptscriptstyle T}\right) \, \left( \begin{array}{c} Q^\nu _{JJ} \\ Q^\nu _{{\bar{JJ}}} \end{array} \right) \, \left( x^{1,\nu }_J - y^\nu _J \right) {+} \left( x^{1,\nu }_J - y^\nu _J \right) ^{\scriptscriptstyle T}Q^\nu _{JJ} \left( x^{1,\nu }_J - y^\nu _J \right) \right] \nonumber \\&\quad =2 \left( y^\nu _{{\bar{J}}} - x^{1,\nu }_{{\bar{J}}} \right) ^{\scriptscriptstyle T}Q^\nu _{{\bar{JJ}}} \left( x^{1,\nu }_J - y^\nu _J \right) \le 0, \end{aligned}$$

(6)

where the last inequality holds because:

• for all $j \in {\bar{J}}$: $\left( y^\nu _j - x^{1,\nu }_j \right) \ge 0$ if $(\nu ,j) \in G_1$ and $\left( y^\nu _j - x^{1,\nu }_j \right) \le 0$ if $(\nu ,j) \in G_2$,

• for all $j \in {\bar{J}}$ and all $i \in J$: $Q^\nu _{ji} \le 0$ if $(\nu ,j) \in G_1 \ni (\nu ,i)$ or $(\nu ,j) \in G_2 \ni (\nu ,i)$, by (2), and $Q^\nu _{ji} \ge 0$ if $(\nu ,j) \in G_1 \not \ni (\nu ,i)$ or $(\nu ,j) \in G_2 \not \ni (\nu ,i)$, by (3),

• for all $i \in J$: $\left( x^{1,\nu }_i - y^\nu _i \right) > 0$ if $(\nu ,i) \in G_1$ and $\left( x^{1,\nu }_i - y^\nu _i \right) < 0$ if $(\nu ,i) \in G_2$.

Let $b^\nu \triangleq 2 Q^\nu {\widehat{q}}^\nu - a^\nu + c^\nu + \sum _{\nu \ne \mu = 1}^N C^{\nu \mu } {\widehat{q}}^\mu$. By using (6), we can write the following chain of inequalities

$$\begin{aligned} 0&\ge ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu - (x^{1,\nu })^{\scriptscriptstyle T}Q^\nu (x^{1,\nu }) + ({{\bar{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\bar{y}}^\nu \\&\overset{(A)}{\ge } ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu + \left[ b^\nu + \sum _{\nu \ne \mu =1}^N C^{\nu \mu } x^{0,\mu }\right] _J^{\scriptscriptstyle T}(x^{1,\nu }_J - y^\nu _J) \\&\overset{(B)}{\ge } ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu + \left[ b^\nu + \sum _{\nu \ne \mu =1}^N C^{\nu \mu } x^{1,\mu }\right] _J^{\scriptscriptstyle T}(x^{1,\nu }_J - y^\nu _J) \\&= ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu + \left[ b^\nu + \sum _{\nu \ne \mu =1}^N C^{\nu \mu } x^{1,\mu }\right] ^{\scriptscriptstyle T}({\widetilde{y}}^\nu - y^\nu ), \end{aligned}$$

where (A) holds since $x^{1,\nu } \in {\widehat{x}}^\nu (\mathbf{x}^{0,-\nu })$ (remember that we are considering the case in which $\nu \in {{\mathcal {J}}}^0$ and $x^{1,\nu }$ is updated as in line 7 of the algorithm), and ${\bar{y}}^\nu$ is feasible for player $\nu$; while (B) is true since for all $i \in J$: if $(\nu ,i) \in G_1$ we have $\left[ \sum _{\nu \ne \mu =1}^N C^{\nu \mu } (x^{0,\mu }-x^{1,\mu })\right] _i \ge 0$ and $(x^{1,\nu }_i - y^\nu _i) > 0$, and if $(\nu ,i) \in G_2$ we have $\left[ \sum _{\nu \ne \mu =1}^N C^{\nu \mu } (x^{0,\mu }-x^{1,\mu })\right] _i \le 0$ and $(x^{1,\nu }_i - y^\nu _i) < 0$. Then we can conclude that $\theta _\nu ({\widetilde{y}}^\nu , \mathbf{x}^{1,-\nu }) \le \theta _\nu (y^\nu , \mathbf{x}^{1,-\nu })$ and, since ${\widetilde{y}}^\nu _i \ge x^{1,\nu }_i$ for all $(\nu ,i) \in G_1$ and ${\widetilde{y}}^\nu _i \le x^{1,\nu }_i$ for all $(\nu ,i) \in G_2$, this is a contradiction. Therefore, for all $\nu \in {{\mathcal {J}}}^1$, we can set ${\widehat{x}}^{1,\nu } \in {\widehat{x}}^\nu (\mathbf{x}^{1,-\nu })$ satisfying (5) for all $i \in \{1,\ldots ,n_\nu \}$, and then we obtain

$$\begin{aligned} x^{2,\nu }_i \ge x^{1,\nu }_i, \quad \forall \, (\nu ,i) \in G_1, \qquad x^{2,\nu }_i \le x^{1,\nu }_i, \quad \forall \, (\nu ,i) \in G_2. \end{aligned}$$

At a generic iterate $k \ge 2$, assuming that for all $t<k$

$$\begin{aligned} x^{k,\nu }_i \ge x^{t,\nu }_i, \quad \forall \, (\nu ,i) \in G_1, \qquad x^{k,\nu }_i \le x^{t,\nu }_i, \quad \forall \, (\nu ,i) \in G_2, \end{aligned}$$

we can do similar considerations in order to prove that we can get for all $(\nu ,i)$:

$$\begin{aligned} x^{k+1,\nu }_i \ge x^{k,\nu }_i, \quad \text { if } \, (\nu ,i) \in G_1, \qquad \text { and, } \qquad x^{k+1,\nu }_i \le x^{k,\nu }_i, \quad \text { if } \, (\nu ,i) \in G_2. \end{aligned}$$

(7)

Namely, we have the following two possibilities for any $\nu \in {{\mathcal {J}}}^k$: if $\nu \notin \cup _{t=0}^{k-1} {{\mathcal {J}}}^t$, or, in general, $x^{k,\nu } = x^{0,\nu }$, then (7) is trivially satisfied, otherwise, as above we can contradict the fact that any point $y^\nu$ in ${\widehat{x}}^\nu (\mathbf{x}^{k,-\nu })$ has a non-empty set of indices J such that for all $i \in J$ it holds that $y^\nu _i < x^{k,\nu }_i$ if $(\nu ,i) \in G_1$ and $y^\nu _i > x^{k,\nu }_i$ if $(\nu ,i) \in G_2$. We define ${\bar{y}}^\nu$ and ${\widetilde{y}}^\nu$ as above. Let $p<k$ be the last iterate at which $x^{\nu }$ is updated as in line 7 of the algorithm. By the same considerations made above, we can write the chain of inequalities

$$\begin{aligned} 0&\ge ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu - (x^{k,\nu })^{\scriptscriptstyle T}Q^\nu (x^{k,\nu }) + ({{\bar{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\bar{y}}^\nu \\&\ge ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu + \left[ b^\nu + \sum _{\nu \ne \mu =1}^N C^{\nu \mu } x^{p,\mu }\right] _J^{\scriptscriptstyle T}\left( x^{k,\nu }_J - y^\nu _J\right) \\&\ge ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu + \left[ b^\nu + \sum _{\nu \ne \mu =1}^N C^{\nu \mu } x^{k,\mu }\right] _J^{\scriptscriptstyle T}\left( x^{k,\nu }_J - y^\nu _J\right) \\&= ({{\widetilde{y}}^\nu })^{\scriptscriptstyle T}Q^\nu {\widetilde{y}}^\nu - ({y^\nu })^{\scriptscriptstyle T}Q^\nu y^\nu + \left[ b^\nu + \sum _{\nu \ne \mu =1}^N C^{\nu \mu } x^{k,\mu }\right] ^{\scriptscriptstyle T}\left( {\widetilde{y}}^\nu - y^\nu \right) , \end{aligned}$$

which proves the contradiction in the same way as above.

Therefore, we can say that the entire sequence $\{\mathbf{x}^k\}$ is such that $\mathbf{x}^k \in X$ and (7) is true for all $(\nu ,i)$. Now, let us suppose, by contradiction, that sequence $\{\mathbf{x}^k\}$ is infinite. In this case, by recalling that $\nu \in \cup _{t = k}^{k + h} {{\mathcal {J}}}^t$ for each player $\nu$ and each iterate k, for any k we obtain that an iteration t, with $k \le t \le k+h$, and a firm $\mu$ exist such that

$$\begin{aligned} \theta _\mu (x^{t,\mu }, \mathbf{x}^{t,-\mu }) - \theta _\mu (x^{t+1,\mu }, \mathbf{x}^{t,-\mu }) > \varepsilon . \end{aligned}$$

(8)

Let us denote

$$\begin{aligned} \displaystyle \tau \triangleq \max _{\nu \in \{1, \ldots , N\}} \max _{\mathbf{x}\in X} \left\| \nabla _{x^\nu } \theta _\nu (\mathbf{x}^t) \right\| _2. \end{aligned}$$

By the assumptions, $\tau$ is finite. Then (8) implies that

$$\begin{aligned} \varepsilon&< \theta _\mu (x^{t,\mu }, \mathbf{x}^{t,-\mu }) - \theta _\mu (x^{t+1,\mu }, \mathbf{x}^{t,-\mu }) \\&\overset{(A)}{\le } \nabla _{x^\mu } \theta _\mu (x^{t,\mu }, \mathbf{x}^{t,-\mu })^{\scriptscriptstyle T}(x^{t,\mu } - x^{t+1,\mu }) \\&\le \left\| \nabla _{x^\mu } \theta _\mu (x^{t,\mu }, \mathbf{x}^{t,-\mu }) \right\| _2 \left\| x^{t,\mu } - x^{t+1,\mu }\right\| _2 \\&\le \tau \left\| x^{t,\mu } - x^{t+1,\mu }\right\| _2, \end{aligned}$$

where (A) holds by the convexity of $\theta _\mu$. Then we obtain

$$\begin{aligned} \frac{\varepsilon ^2}{\tau ^2} < \left\| x^{t,\mu } - x^{t+1,\mu }\right\| _2^2 \le n \left\| x^{t,\mu } - x^{t+1,\mu }\right\| _\infty ^2. \end{aligned}$$

Therefore an index $i \in \{1, \ldots , n_\mu \}$ exists such that

$$\begin{aligned} x^{t+1,\mu }_i > x^{t,\mu }_i + \frac{\varepsilon }{\tau \sqrt{n}}, \; \text { if } \, (\mu ,i) \in G_1, \; \text { and, } \; x^{t+1,\mu }_i < x^{t,\mu }_i - \frac{\varepsilon }{\tau \sqrt{n}}, \; \text { if } \, (\mu ,i) \in G_2, \end{aligned}$$

but this contradicts the boundedness of X, and, therefore, $\{\mathbf{x}^k\}$ is finite. Thus, the point returned by Algorithm 1 is an $\varepsilon$-approximate equilibrium of the NEP. $\square$

It is worth to spend some words about the proof of Theorem 1. First of all, we note that the proof of Theorem 1 is very similar to that of Theorem 4.2 in Sagratella (2016). The main difference is that here we consider the mixed-integer setting and then, to prove that the sequence produced by the algorithm is finite, we focus on $\varepsilon$-approximate equilibria with $\varepsilon > 0$.

The first part of the proof is quite identical to that in Sagratella (2016), and it is devoted to proving that, starting from the point $\mathbf{x}^0$ (such that $x^{0,\nu }_i = l^\nu _i$ if $(\nu ,i) \in G_1$, and $x^{0,\nu }_i = u^\nu _i$ if $(\nu ,i) \in G_2$), then the algorithm can always produce a sequence $\{\mathbf{x}^k\}$ such that (7) is true for all $(\nu ,i)$. Therefore, once any variable $x^\nu _i$ leaves its starting bound during the iterations, it goes towards the other bound never coming back. It is important to notice that this behaviour is independent from the fact that $x^\nu _i$ is a continuous or a discrete variable.

The last part of the proof differs from that in Sagratella (2016) due to the presence of continuous variables. Here we show that, by exploiting the convexity and the smoothness of any $\theta _\nu$, and by recalling (7) and the compactness of X, the sequence produced by the algorithm must be finite. Finally, any point returned by the algorithm is, by definition, an $\varepsilon$-approximate equilibrium of the game.

Moreover, we observe that the starting points for which the convergence of the algorithm is proved in Theorem 1 are two: the one defined in the theorem and the other one that can be obtained by switching the two groups of indices.

Example 2

Consider again the model of example 1. The problems solved by the firms are the following

$$\begin{aligned}&\displaystyle \text {minimize}_{x^1} \; \theta _1(x^1, x^2, x^3) = \frac{1}{2} (x^1)^2 - x^1 x^3 - x^1, \quad \text { s.t. } x^1 \in \{0, 1\}, \\&\displaystyle \text {minimize}_{x^2} \; \theta _2(x^1, x^2, x^3) = \frac{1}{2} (x^2)^2 + x^1 x^2 - x^2, \quad \text { s.t. } x^2 \in \{0, 1\}, \\&\displaystyle \text {minimize}_{x^3} \; \theta _3(x^1, x^2, x^3) = \frac{1}{2} (x^3)^2 + x^2 x^3 - x^3, \quad \text { s.t. } x^3 \in \{0, 1\}. \end{aligned}$$

Starting from the point indicated in Theorem 1, that is (0, 1, 0), Algorithm 1, with any $\varepsilon < \frac{1}{2}$ and any order of play, produces the following sequence

$$\begin{aligned} \begin{array}{rccccccc} &{} \left( 0,1,0\right) &{} \rightarrow &{} \left( 1,1,0\right) &{} \rightarrow &{} \left( 1,0,0\right) &{} \rightarrow &{} \left( 1,0,1\right) \\ \theta _1: \quad &{} 0 &{} &{} -\frac{1}{2} \;\; &{} &{} -\frac{1}{2} \;\; &{} &{} -\frac{3}{2} \;\; \\ \theta _2: \quad &{} -\frac{1}{2} \;\; &{} &{} \frac{1}{2} &{} &{} 0 &{} &{} 0 \\ \theta _3: \quad &{} 0 &{} &{} 0 &{} &{} 0 &{} &{} -\frac{1}{2} \;\; \end{array} \end{aligned}$$

that terminates in (1, 0, 1) which is an $\varepsilon$-approximate equilibrium of the game. Notice that (1, 0, 1) is the other possible starting point for which the convergence is proved in Theorem 1. It is directly an equilibrium of the game.

Moreover, if we consider any possible other mixed-integer setting, e.g. $i_1 = 0, i_2 = 1$, and $i_3 = 1$, then the sequence produced by the algorithm is the same, and (1, 0, 1) is an equilibrium of the game.

The following result is about the complexity of Algorithm 1.

Proposition 1

Let us suppose that all the assumptions in Theorem 1 are fulfilled. Then Algorithm 1 converges to an $\varepsilon$-approximate equilibrium of the NEP defined by (1), with $\varepsilon > 0$, in at most

$$\begin{aligned} h \left[ \sum _{\nu =1}^N \sum _{i=1}^{n_\nu } (u^\nu _i-l^\nu _i) \frac{\tau \sqrt{n}}{\varepsilon } \right] \end{aligned}$$

iterations.

Proof

As stated in the proof of Theorem 1, sequence $\{\mathbf{x}^k\}$, generated by Algorithm 1, is such that $\mathbf{x}^k \in X$ and (7) is true for all $(\nu ,i)$. By recalling that $\nu \in \cup _{t = k}^{k + h} {{\mathcal {J}}}^t$ for each player $\nu$ and each iterate k, then, if for an iteration ${\bar{k}}$ it holds that $\mathbf{x}^{{\bar{k}}} = \mathbf{x}^{{\bar{k}}+h+1}$, then $\mathbf{x}^{{\bar{k}}+h+1}$ is a solution of the discrete NEP. Otherwise at least one $(\nu ,i)$ exists such that

$$\begin{aligned} x^{{\widetilde{k}}+1,\nu }_i > x^{{\widetilde{k}},\nu }_i + \frac{\varepsilon }{\tau \sqrt{n}}, \; \text { if } \, (\mu ,i) \in G_1, \; \text { and, } \; x^{{\widetilde{k}}+1,\nu }_i < x^{{\widetilde{k}},\nu }_i - \frac{\varepsilon }{\tau \sqrt{n}}, \; \text { if } \, (\mu ,i) \in G_2, \end{aligned}$$

where ${\bar{k}} \le {\widetilde{k}} \le {\bar{k}} + h$. Therefore Algorithm 1 can do no more than

$$\begin{aligned} h \left[ \sum _{\nu =1}^N \sum _{i=1}^{n_\nu } (u^\nu _i-l^\nu _i) \frac{\tau \sqrt{n}}{\varepsilon } \right] \end{aligned}$$

iterations before $x^{k,\nu }_i = u^\nu _i$ if $(\nu ,i) \in G_1$ and $x^{k,\nu }_i = l^\nu _i$ if $(\nu ,i) \in G_2$, for all $\nu \in \{1,\ldots ,N\}$ and all $i \in \{1,\ldots ,n_\nu \}$. $\square$

The following corollary gives conditions for the existence of $\varepsilon$-approximate equilibria. It is a direct consequence of Theorem 1.

Corollary 1

A 2-groups partitionable NEP has at least one $\varepsilon$-approximate equilibrium for any given $\varepsilon > 0$.

The following example shows that if the Cournot model is not partitionable into two groups then there is no hope to obtain the good results of Theorem 1, Proposition 1, and Corollary 1. In particular, the game in the example is partitionable into three, but not into two, groups and it does not have any equilibrium.

Example 3

Let us consider again the model of example 1, but with $C^{13} = 1$. In this case the good produced by firm 3 is no longer a complement for that of firm 1, but it is a substitute. Therefore the variables are partitionable into three groups, but not into two groups. In particular, we can partition the variables indices in this way: $G_1 = \{(1,1)\}, G_2 = \{(2,1)\}$, and $G_3 = \{(3,1)\}$. The problem solved by firm 1 is the following

$$\begin{aligned}&\displaystyle \text {minimize}_{x^1} \; \theta _1(x^1, x^2, x^3) = \frac{1}{2} (x^1)^2 + x^1 x^3 - x^1, \quad \text { s.t. } x^1 \in \{0, 1\}, \end{aligned}$$

while the other firms solve the same problems as before (see example 2). Starting from (0, 1, 0), Algorithm 1, with any $\varepsilon < \frac{1}{2}$ and any order of play, produces the following infinite sequence

$$\begin{aligned} \begin{array}{rccccccccccccccc} &{} \left( 0,1,0\right) &{} \rightarrow &{} \left( 1,1,0\right) &{} \rightarrow &{} \left( 1,0,0\right) &{} \rightarrow &{} \left( 1,0,1\right) &{} \rightarrow &{} \left( 0,0,1\right) &{} \rightarrow &{} \left( 0,1,1\right) &{} \rightarrow &{} \left( 0,1,0\right) &{} \rightarrow &{} \cdots \\ \theta _1: \quad &{} 0 &{} &{} -\frac{1}{2} \;\; &{} &{} -\frac{1}{2} \;\; &{} &{} \frac{1}{2} &{} &{} 0 &{} &{} 0 &{} &{} 0 \\ \theta _2: \quad &{} -\frac{1}{2} \;\; &{} &{} \frac{1}{2} &{} &{} 0 &{} &{} 0 &{} &{} 0 &{} &{} -\frac{1}{2} \;\; &{} &{} -\frac{1}{2} \;\; \\ \theta _3: \quad &{} 0 &{} &{} 0 &{} &{} 0 &{} &{} -\frac{1}{2} \;\; &{} &{} -\frac{1}{2} \;\; &{} &{} \frac{1}{2} &{} &{} 0 \end{array} \end{aligned}$$

While starting from (0, 0, 0) or (1, 1, 1), which are the only other points that are not in the sequence above, the algorithm never stops since they are not $\varepsilon$-approximate equilibria for any $\varepsilon < \frac{1}{2}$. Therefore, starting from any feasible point, the algorithm does not converge. However, the game does not have any $\varepsilon$-approximate equilibrium with $\varepsilon < \frac{1}{2}$, and this indicates that no method can be more effective than Algorithm 1 on this game.

4 Numerical experiments

Models described in this paper are particularly relevant if the number of players is small, and challenging if the number of decision variables of each of these few players is large. Thus, in our experiments we assume that there are $N=3$ firms each producing $n_\nu =100$ products. For any player $\nu$, the first $i_\nu =50$ products are indivisible, while the other 50 are modeled with continuous variables. We assume that any product, of any firm, belongs to one of two groups following assumptions (2) and (3). We recall that two products of the same group are complements, while two products of different groups are substitutes. The first group of products is made up of the first 50 products of firm 1, the first 25 products of firm 2 and the first 75 products of firm 3. The second group is made up of the other products. Let $h^\nu \in \{-1,1\}^{100}$ be a vector, for any firm $\nu$, whose entries are equal to 1 if the corresponding product belongs to the first group, or are equal to -1 otherwise. For any couple of firms $\nu$ and $\mu$, we computed matrix $C^{\nu \mu }$ in the following way: $C^{\nu \mu } = - \left[ \left( w^\nu \circ h^\nu \right) \, \left( v^{\nu \mu } \circ h^\mu \right) ^{\scriptscriptstyle T}\right] \circ M^{\nu \mu }$, where $w^\nu , v^{\nu \mu } \in {{\mathbb {R}}}^{100}_+, \circ$ denotes the element-wise product, and $M^{\nu \mu } \in \mathbb {R}_{n_\nu \times n_\mu }$ has the following entries:

$$\begin{aligned} M^{\nu \mu }_{ij} = \left\{ \begin{array}{ll} 5 &{}\quad \text { if } \nu \ne \mu \quad \text { and } \quad h^\nu _i h^\mu _j < 0 \\ 0.05 &{}\quad \text { if } \nu \ne \mu \quad \text { and }\quad h^\nu _i h^\mu _j > 0 \\ 0.5 &{}\quad \text { if } \nu = \mu . \end{array}\right. \end{aligned}$$

Matrix $M^{\nu \mu }$ is intended to emphasize the effect of substitute goods of different firms and to decrease the effect of complement ones. Moreover, in order to get any $Q^{\nu } \succ 0$, we set the diagonal elements of $Q^{\nu }$ equal to 10 times the sum of the absolute values of the corresponding (off-diagonal) row elements of the symmetric part of $Q^{\nu }$.

For any firm $\nu$, the parameters were generated in the following way: $a^\nu$ were randomly generated in $[10\,000,20\,000]^{100}$ by using the uniform distribution, and then rounded off to the nearest integer values; $c^\nu = 0.5 \, a^\nu$; $w^\nu$ and $v^{\nu \mu }$, for all $\mu$, were randomly generated in $[0.9,1.1]^{100}$ and $[0,1]^{100}$ respectively by using the uniform distribution; ${\widehat{q}}^\nu = {\widehat{x}}^\nu (0)$ in the case of null initial quantities and lower bounds, and large upper bounds ($=100$); $l^\nu = \max \{- {\widehat{q}}^\nu , -10\}$ and $u^\nu = 10$.

We generated 3 different instances of the game (denoted by A, B, and C), and solved them by using Algorithm 1 in 4 different variants: pure Jacobi (Ja), Gauss–Seidel in which the order of play is: firm 1 for first, firm 2 for second and firm 3 for third (GS123), Gauss–Seidel in which the order of play is: firm 2 for first, firm 3 for second and firm 1 for third (GS231), and Gauss–Seidel in which the order of play is: firm 3 for first, firm 1 for second and firm 2 for third (GS312). We considered 3 different starting points: quantity deviations of the first group goods start from their lower bounds and the others from their upper bounds (sp1); quantity deviations of the first group goods start from their upper bounds and the others from their lower bounds (sp2); all the quantity deviations start from zero (sp3). Notice that (sp1) and (sp2) are the two starting points for which the convergence is proved in Theorem 1, while starting from (sp3) Algorithm 1 could not converge.

All the experiments were carried out on an Intel Core i7-4702MQ CPU @2.20 GHz $\times$ 8 with Ubuntu 14.04 LTS 64-bit and by using Matlab 7.14.0.739 (R2012a). We implemented Algorithm 1 by using AMPL and we computed all the best responses by using the convex mixed-integer quadratic programming solver of CPLEX 12.6.0.1 with default options. We set $\varepsilon = 1e-4$.

Table 1 Amount of best responses computed (CPU time in seconds consumed) by Algorithm 1 to return an $\varepsilon$-approximate equilibrium

Fig. 1

A-Ja-sp3

Fig. 2

A-GS123-sp3

Fig. 3

A-GS231-sp3

Fig. 4

A-GS312-sp3

Fig. 5

B-Ja-sp3

Fig. 6

B-GS123-sp3

Fig. 7

B-GS231-sp3

Fig. 8

B-GS312-sp3

Fig. 9

C-Ja-sp3

Fig. 10

C-GS123-sp3

Fig. 11

C-GS231-sp3

Fig. 12

C-GS312-sp3

In Table 1 we report the amount of best responses computed (i.e. the amount of optimization problems solved with CPLEX), and the total CPU time consumed, by Algorithm 1 to return an $\varepsilon$-approximate equilibrium of the game. We considered all the pairs “(algorithm variant)-(starting point)” and all the instances. An $\varepsilon$-approximate equilibrium is computed for any run of the algorithm except for B-Ja-sp3, which is a case not covered by Theorem 1. In Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 we plot the profits of all the firms for any iteration. Note that, although for B-Ja-sp3 there is no convergence, it computes points that are close to the equilibrium computed in the other cases, see the figures. All in all, the different versions of Algorithm 1 computed $\varepsilon$-approximate equilibria of the game in few iterations and few seconds. The different Gauss–Seidel versions perform similarly and they are faster than the Jacobi one.