Computing all solutions of linear generalized Nash equilibrium problems

Abstract

In this paper we consider linear generalized Nash equilibrium problems, i.e., the cost and the constraint functions of all players in a game are assumed to be linear. Exploiting duality theory, we design an algorithm that is able to compute the entire solution set of these problems and that terminates after finite time. We present numerical results on some academic examples as well as some economic market models to show effectiveness of our algorithm in small dimensions.

1 Introduction

Generalized Nash equilibrium problems (GNEPs) have been considered recently in many papers, and we refer to Facchinei and Kanzow (2010), Facchinei and Pang (2009) and Fischer et al. (2014) for survey articles. Quite often GNEPs where all players have the same constraints, which are then called shared constraints, are considered in literature, since this problem class seems to have a larger number of applications. GNEPs with shared constraints that have a common convex feasible set are also called jointly convex GNEPs. For those one can define normalized solutions in the sense of Rosen (1965), which are particular solutions. Meanwhile, there is a number of algorithms available to compute solutions of GNEPs, see for example Dreves et al. (2011, 2012), Facchinei and Kanzow (2010), Facchinei et al. (2009), Han et al. (2012), Izmailov and Solodov (2014), Krawczyk and Uryasev (2000) and Schiro et al. (2013) to mention just a few. In particular there are methods available which are globally and local quadratic convergent, namely the Newton method from Dreves et al. (2013) to compute normalized solutions of jointly convex GNEPs, or the hybrid method from Dreves et al. (2014) for the general case.

Nearly all existing algorithms are able to compute one solution of a GNEP, or if they are started with different parameters a number of different solutions, as for example Facchinei and Sagratella (2011), Nabetani et al. (2011). But since the total number of solutions is typically infinite, see Dorsch et al. (2013) for a discussion on this topic, they are not able to compute the entire solution set of the problem in finite time. An exception are affine generalized Nash equilibrium problems (AGNEPs), where the cost functions of all players are quadratic functions and the common constraints are affine linear. Here, following Nabetani et al. (2011), the entire solution set can be represented as the finite union of polyhedral sets via KKT conditions. Then, in principal a vertex enumeration algorithm could be used to obtain the entire solution set, by deciding which of the polyhedral sets are empty. A second method for so called AGNEP1s was presented in Dreves (2014). This algorithm is able to compute all solutions of AGNEPs with shared constraints, where each player has exactly one variable, with the help of sign conditions for the derivatives of the cost and constraint functions.

In this paper we consider linear generalized Nash equilibrium problems (LGNEPs) with not necessarily shared constraints, i.e., problems of the form:

$$\begin{aligned} \min _{x^\nu } \, \langle c^\nu , x^\nu \rangle \quad \text {s.t.} \quad A^{\nu \nu } x^\nu + \sum _{\mu \ne \nu } A^{\nu \mu } x^\mu \le b^{\nu } \end{aligned}$$

for all players $\nu =1,\ldots ,N.$ We have the problem dimensions $A^{\nu \mu } \in \mathbb {R}^{m_\nu \times n_\mu },$ $c^\nu \in \mathbb {R}^{n_\nu }, b^{\nu } \in \mathbb {R}^{m_\nu }.$ Further the dimension of the considered LGNEPs is described by $n := n_1 + \cdots +n_N$ and $m:= m_1 + \cdots +m_N$. LGNEPs were very recently considered in Stein and Sudermann-Merx (2015) and a nonsmooth optimization reformulation was given there. Further in Dreves and Sudermann-Merx (2016) different numerical approaches to solve LGNEPs were introduced and in particular a potential reduction algorithm and some subgradient method were recommended to find one generalized Nash equilibrium. Let us concatenate the matrices and vectors to define

$$\begin{aligned} A:=\begin{pmatrix} A^{11} &{} \ldots &{} A^{1N} \\ \vdots &{} &{}\vdots \\ A^{N1} &{} \ldots &{} A^{NN} \end{pmatrix} \in \mathbb {R}^{m \times n}, \quad b:=\begin{pmatrix} b^1 \\ \vdots \\ b^N \end{pmatrix} \in \mathbb {R}^m \end{aligned}$$

and the feasible set

$$\begin{aligned} X:= \left\{ x \in \mathbb {R}^n \mid A x \le b \right\} . \end{aligned}$$

If one has the special case, where the constraints are shared by all players, one has $m_1=\cdots =m_N, A^{1 \mu }=\cdots =A^{N \mu }$ for all $\mu =1,\ldots ,N$ and $b^1=\cdots =b^N.$ Then each linear constraint in X is repeated N times, and one can remove all the redundant rows except one in the description of the common closed and convex feasible set X. Hence the LGNEP with shared constraints has the equivalent form

$$\begin{aligned} \min _{x^\nu } \, \langle c^\nu , x^\nu \rangle \quad \text {s.t.} \quad (x^\nu ,x^{-\nu }) \in X \qquad \forall \nu =1,\ldots ,N. \end{aligned}$$

In the following we will design an algorithm that is able to compute all solutions of LGNEPs, allowing more than one variable for each player, in contrast to the AGNEP1 approach in Dreves (2014). To know the entire solution set is important if one tries to select one specific equilibrium out of the typically infinite number of solutions of the LGNEP that maximizes some selection criteria, like the total social benefit. For further selection criteria in the context of LGNEPs and transportation problems we refer to Sudermann-Merx (2016).

Let us introduce some of our notations: With $\mathbb {R}^k_+$ we denote the orthant of nonnegative vectors in $\mathbb {R}^k.$ For an index set $J \subseteq \{1,\ldots ,m\}$ we will denote by |J| the number of elements of J and by $A_{J \bullet }$ the matrix, where all rows with indices that are not in J are dropped. Further $\mathop {\mathrm {vert}}(X)$ is the set of all vertices of the polyhedral set X and $\mathop {\mathrm {conv}}(M)$ is the convex hull of a set M.

In the next section we will present our algorithm and show that it terminates in finite time with the entire solution set of an LGNEP. In Sect. 3 we present several examples of academic problems and economy market models that can be solved. Finally we conclude in Sect. 4.

2 The algorithm and its convergence

Inspecting the setting in Dreves (2014), where the Sign Bingo algorithm was designed for AGNEP1, we see that the cost functions are assumed to be quadratic and can not be linear. However, it is possible to show that a slight modification of the algorithm also works for LGNEPs with one-dimensional strategy spaces and shared constraints. But since we can exploit more structure in the linear setting, we will design here a new algorithm that can also handle more than one-dimensional strategy spaces and also non-shared constraints. An LGNEP is defined via the vectors $b^1,\ldots ,b^N,c^1,\ldots ,c^N$ and the matrices $A^{\nu \mu },\nu ,\mu \in \{1,\ldots ,N\}$ which are the input data for our algorithm. Let us define the vectors

$$\begin{aligned} \lambda := \begin{pmatrix} \lambda ^1 \\ \vdots \\ \lambda ^N \end{pmatrix} \in \mathbb {R}^{m_1+\ldots +m_N} \qquad \text {and} \qquad w:= \begin{pmatrix} w^1 \\ \vdots \\ w^N \end{pmatrix} \in \mathbb {R}^{m_1+\ldots +m_N} . \end{aligned}$$

From duality theory for linear programs we directly obtain necessary and sufficient optimality conditions for the coupled linear programs in an LGNEP:

Lemma 1

$\bar{x} \in \mathbb {R}^{n}$ is a solution of the LGNEP if and only if there exist $(\lambda , w) \in \mathbb {R}^{m_1+\cdots +m_N} \times \mathbb {R}^{m_1+\cdots +m_N}$ such that

$$\begin{aligned} (A^{\nu \nu })^\top \lambda ^\nu= & {} - c^\nu \qquad \forall \nu =1,\ldots ,N,\\ A \, \bar{x} + w= & {} b, \\ \lambda \ge 0, \quad w \ge 0, \quad \lambda ^\top w= & {} 0. \end{aligned}$$

Remark 1

A simple approach to solve these conditions is to compute for all indexsets $J \subseteq \{1,\ldots ,m\}$, with the complement $\bar{J}:=\{1,\ldots ,m\} {\setminus } J$, the vertices of the polyhedral sets defined by

$$\begin{aligned} (A^{\nu \nu })^\top \lambda ^\nu= & {} - c^\nu \qquad \forall \nu =1,\ldots ,N,\\ A \, \bar{x} + w= & {} b, \\ \lambda \ge 0, \quad w \ge 0, \quad \lambda _{\bar{J}}=0, \quad w_{J}= & {} 0, \end{aligned}$$

and obtain the primal solutions as projections on the x-space. This simple procedure requires $2^{m}$ times the computation of all vertices of a polyhedron, which can be done by a vertex enumeration algorithm. However, it is possible to exploit more structure in order to split the full problem in smaller subproblems and to avoid the full computation for all index sets. This is done in our new algorithm that we state next.

Algorithm 1

Computing all solutions of LGNEPs

• (S.1)

  

• (S.2) For all $J=(J_1,\ldots ,J_N) \in P^1 \times \ldots \times P^N$ compute the sets

  $$\begin{aligned} V(J) := \left\{ v \in \mathop {\mathrm {vert}}(X) \Bigg | \bigcup \limits _{\nu =1,\ldots ,N} J_\nu \subseteq I(v) \right\} , \end{aligned}$$

  with

  $$\begin{aligned} I(v):=\left\{ i \in \{1,\ldots ,m\} \mid A_{i \bullet } \, v =b_i \right\} , \end{aligned}$$

  and define the set

  $$\begin{aligned} M:= \bigcup _{J \in P^1 \times \ldots \times P^N} \{V(J)\}. \end{aligned}$$

• (S.3) The set $\tilde{M}$ is obtained by deleting duplicates and all sets $\{V(J)\} \in M$ that are contained in a larger set $\{V(\tilde{J})\} \in M,$ i.e., that satisfy $V(J) \subset V(\tilde{J}).$ The output set is

  $$\begin{aligned} S:= \bigcup _{q \in \tilde{M}} \mathop {\mathrm {conv}}(q). \end{aligned}$$

Before stating theoretical results for Algorithm 1 we first discuss a simple example in detail to better understand and illustrate the behavior of the algorithm.

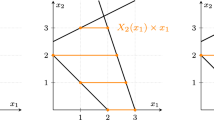
Example 1

We consider a 2-player game with shared constraints that is defined by the data

$$\begin{aligned} c^1=\begin{pmatrix} -1 \\ -2 \end{pmatrix}, \quad c^2=-1, \quad A=\begin{pmatrix} 1 &{}\quad 2 &{}\quad -1\\ 3 &{}\quad 2 &{}\quad 1\\ -1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad -1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -1\end{pmatrix}, \quad b=\begin{pmatrix} 14 \\ 30 \\ 0 \\ 0 \\ 0 \end{pmatrix}. \end{aligned}$$

Hence the LGNEP has the form

$$\begin{aligned} \min _{x_1^1,x_2^1}&-x_1^1 -2 x_2^1&\quad \text { s.t. }A \, x \le b, \\ \min _{x^2}&-x^2&\text { s.t. } A \, x \le b. \end{aligned}$$

The common feasible set is $X=\left\{ x \in \mathbb {R}^3 \big | A x \le b \right\} .$

In (S.1) we start with $\nu =1$ and we have to solve for

$$\begin{aligned} J_1 \in \{\{1\},\{2\},\{3\},\{4\},\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{2,4\},\{3,4\} \} \end{aligned}$$

the equation system

$$\begin{aligned} (A_{J_1, \{1,2\}})^\top \lambda ^1_{J_1} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}. \end{aligned}$$

Now we see that for $J_1=\{1\}$ we find $\lambda ^1_{J_1}=1 \ge 0,$ and hence we have $\{1\} \in P^1.$ Now it is obvious that we do not have to compute solutions of equation systems with sets $J_\nu$ containing 1 and therefore we do not have to compute the solutions for $J_1 \in \{ \{1,2\},\{1,3\},\{1,4\} \}.$ For $J_1 \in \{ \{2\},\{3\},\{4\},\{2,4\},\{3,4\} \}$ we do not find nonnegative solutions, but for $J_1= \{2,3\}$ we have

$$\begin{aligned} \begin{pmatrix} 3 &{}\quad -1 \\ 2 &{}\quad 0 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}. \end{aligned}$$

Thus we obtain

$$\begin{aligned} P^1= \{ \{1\}, \{2,3\} \}. \end{aligned}$$

For $\nu =2$ we have to consider

$$\begin{aligned} J_2 \in \{ \{1\}, \{2\}, \{5\} \}, \end{aligned}$$

and it is easy to see that we obtain

$$\begin{aligned} P^2 = \{ \{2\} \}. \end{aligned}$$

In (S.2) we now have to find all vertices whose active constraints include one of the sets $\{1,2\}, \{2,3\}.$ Therefore we search for feasible vertices with the active constraints in

$$\begin{aligned} \{\{1,2,3\},\{1,2,4\},\{1,2,5\} \} \quad \text {or} \quad \{\{1,2,3\},\{2,3,4\},\{2,3,5\}\}. \end{aligned}$$

Note that we get the index set $\{1,2,3\}$ twice, but in our implementation we solve the corresponding linear system of course only once. We find the vertices given in Table 1.

Table 1 vertices computed in (S.2)

Therefore we get in (S.2)

$$\begin{aligned} V(\{1,2\}, \{2\})= & {} \{ (0,11,8), (8,3,0)\}, \\ V(\{2,3\}, \{2\})= & {} \{ (0,11,8), (0,0,30)\}, \end{aligned}$$

and hence

$$\begin{aligned} M = \{ \{ (0,11,8), (8,3,0)\} , \{ (0,11,8), (0,0,30)\} \}. \end{aligned}$$

Finally, since we do not have to remove duplicates here, the solution set from (S.3) is given by

$$\begin{aligned} S = \mathop {\mathrm {conv}}\{ (0,11,8), (8,3,0) \} \cup \mathop {\mathrm {conv}}\{ (0,11,8), (0,0,30)\} . \end{aligned}$$

We have seen in this example that the algorithm terminates after finite time. This holds in general as we will show now. Since we describe the solution set as convex hull of vertices, we will need boundedness of the feasible set X. For GNEPs with shared constraints this implies that $n_\nu \le m_\nu$ for all $\nu =1,\ldots ,N.$ In the case of nonshared constraints this is not necessarily true. Since we will state the next result in general form we need the binomial coefficients $\left( {\begin{array}{c}m_\nu \\ n_\nu \end{array}}\right) .$ To get them well-defined, we can, by the boundedness of X, formally introduce additional box constraints that are always satisfied to obtain $n_\nu \le m_\nu .$

Proposition 1

Algorithm 1 is well-defined and terminates after finite time, if X is bounded.

Proof

(S.1) is the solution of a finite number of at most $\sum _{\nu =1}^N \sum _{i=1}^{n_\nu } \left( {\begin{array}{c}m_\nu \\ i\end{array}}\right)$ linear equation systems. Since X is a bounded and polyhedral set, the computation of all vertices corresponding to active constraints in $P^1 \times \ldots \times P^N$ is possible in finite time by solving at most $\left( {\begin{array}{c}m\\ n\end{array}}\right)$ linear equation systems and checking feasibility of the solutions. Hence (S.2) terminates after finite time. (S.3) is finitely often checking a set inclusion. Hence we see that Algorithm 1 is well-defined and terminates after finite time. $\square$

For our main result we need the following lemma.

Lemma 2

Let $A \in \mathbb {R}^{n \times k}, b \in \mathbb {R}^n$ with $k > n.$ Further let $\tilde{\lambda } \in \mathbb {R}^k_{+}$ be a solution of $A \tilde{\lambda } = b$ with $\tilde{\lambda }_i>0$ for $i=1,\ldots ,\tilde{k}$ and $\tilde{\lambda }_i=0$ for $i=\tilde{k} + 1,\ldots , k.$ Then there exists a $\lambda \in \mathbb {R}^k_{+}$ which has at most n nonzero elements and satisfies $A \lambda = b.$

Proof

If $\tilde{k} \le n$ there is nothing to show. Therefore assume $\tilde{k} > n.$ We have by assumption

$$\begin{aligned} b= \sum _{i=1}^{k} \tilde{\lambda }_i A_{\bullet i} = \sum _{i=1}^{\tilde{k}} \tilde{\lambda }_i A_{\bullet i} \qquad \text {and} \qquad \tilde{\lambda }_i >0 \quad \forall i=1,\ldots ,\tilde{k}. \end{aligned}$$

Since $\tilde{k} >n$ the columns of A must be linearly dependent and hence we can find $\alpha _i \in \mathbb {R}$ such that

$$\begin{aligned} 0 = \sum _{i=1}^{\tilde{k}} \alpha _i A_{\bullet i}. \end{aligned}$$

Without loss of generality we can assume that at least for one $i \in \{1,\ldots ,\tilde{k}\}$ we have $\alpha _{i} > 0,$ since otherwise we can multiply the equation by $-1,$ or we have $A=0,$ where the assertion of this lemma is trivially satisfied. Then we define

$$\begin{aligned} \beta :=\min _{1 \le i \le \tilde{k}} \left\{ \frac{\tilde{\lambda }_i}{\alpha _i} \Bigg | \alpha _i>0 \right\} =: \frac{\tilde{\lambda }_{i_0}}{\alpha _{i_0}}>0, \end{aligned}$$

and we obtain

$$\begin{aligned} b = \sum _{i=1}^{\tilde{k}} (\tilde{\lambda }_i A_{\bullet i} - \beta \alpha _i A_{\bullet i}) =\sum _{i=1}^{\tilde{k}} (\tilde{\lambda }_i - \beta \alpha _i) A_{\bullet i} =\sum _{i=1, i \ne i_0}^{\tilde{k}} (\tilde{\lambda }_i - \beta \alpha _i) A_{\bullet i}. \end{aligned}$$

Now we have $\lambda _{i_0}=0$ and $\lambda _i:=\tilde{\lambda }_i - \beta \alpha _i \ge 0$ for all $i \in \{1,\ldots ,\tilde{k} \} \setminus \{i_0\},$ and with $\lambda _i=0$ for $i=\tilde{k}+1,\ldots ,n$ we have reduced the number of nonzero elements from $\tilde{\lambda }$ to $\lambda$ by at least one. Repeating this argument as long as the remaining columns of A are linearly dependent, we can reduce the number of nonzero elements to at most n,  which completes the proof. $\square$

Now let us show that the set S computed by Algorithm 1 is the entire solution set of the LGNEP.

Theorem 1

Let X be bounded. Then the set S computed by Algorithm 1 coincides with the solution set of the LGNEP.

Proof

First, let $\bar{x}$ be an element of S. Then we have $\bar{x} \in \mathop {\mathrm {conv}}(q)$ for some $q \in \tilde{M} \subseteq M.$ This, in turn, means that we have some tuple of index sets $J=(J_1,\ldots ,J_N) \in P^1 \times \ldots \times P^N$ such that

$$\begin{aligned} q = V(J)= \left\{ v \in \mathop {\mathrm {vert}}(X) \Bigg | \bigcup \limits _{\nu =1,\ldots ,N} J_\nu \subset I(v) \right\} . \end{aligned}$$

Now we get for every $\nu =1,\ldots ,N$ by $J_\nu \in P^\nu$ a $\lambda _{J_\nu }^\nu \ge 0$ such that

$$\begin{aligned} (A^{\nu \nu }_{J_\nu \bullet })^\top \lambda ^\nu _{J_\nu } = - c^\nu . \end{aligned}$$

Defining $\lambda _i^\nu = 0$ for all $i \not \in J_\nu$ we therefore have $\lambda ^\nu \ge 0$ and

$$\begin{aligned} (A^{\nu \nu })^\top \lambda ^\nu = - c^\nu \end{aligned}$$

(1)

for all $\nu =1,\ldots ,N.$

Since $q=V(J)$ and the number of vertices of X is finite, we can find K vertices $v_1,\ldots ,v_K$ of X with $q=\{v_1,\ldots ,v_K\}.$ Thus we have $\bigcup \limits _{\nu =1,\ldots ,N} J_\nu \subset I(v_k)$ for all $k=1,\ldots ,K$ and the definition of $I(v_k)$ yields

$$\begin{aligned} A_{i \bullet } v_k = b_i \qquad \forall i \in \bigcup _{\nu =1,\ldots ,N} J_\nu , \quad \forall k=1,\ldots ,K. \end{aligned}$$

Now exploiting that $\bar{x} \in \mathop {\mathrm {conv}}(q)=\mathop {\mathrm {conv}}(v_1,\ldots ,v_K)$ and setting $w_i=0$ for all $i \in \bigcup \limits _{\nu =1,\ldots ,N} J_\nu$ we get

$$\begin{aligned} A_{i \bullet } \bar{x} + w_i= b_i \qquad \forall i \in \bigcup _{\nu =1,\ldots ,N} J_\nu . \end{aligned}$$

Further, the feasibility $v_k \in X,$ implies

$$\begin{aligned} b_i - A_{i \bullet } v_k \ge 0 \qquad \forall i \not \in \bigcup _{\nu =1,\ldots ,N} J_\nu , \quad \forall k=1,\ldots ,K. \end{aligned}$$

Again using $\bar{x} \in \mathop {\mathrm {conv}}(q)=\mathop {\mathrm {conv}}(v_1,\ldots ,v_K)$ we get

$$\begin{aligned} w_i:=b_i-A_{i \bullet } \bar{x} \ge 0 \qquad \forall i \not \in \bigcup _{\nu =1,\ldots ,N} J_\nu . \end{aligned}$$

Therefore we defined a $w \ge 0$ such that

$$\begin{aligned} A \bar{x} + w= b. \end{aligned}$$

(2)

Further we have by construction

$$\begin{aligned} \lambda \ge 0, \quad w \ge 0, \quad \lambda ^\top w = 0. \end{aligned}$$

(3)

Altogether, we have shown that $\bar{x}$ together with $(\lambda , w)$ satisfies the conditions (2), (1), and (3), which are the necessary and sufficient optimality conditions of the LGNEP. Hence $\bar{x}$ is a solution of the LGNEP.

Now let $\bar{x}$ be a solution of the LGNEP. Then there exists some $(\tilde{\lambda },w)$ such that the optimality conditions (2), (1), and (3) are satisfied. Hence we can define for every $\nu =1,\ldots ,N$ the index set $\tilde{J}_\nu \subset \{1,\ldots ,m_\nu \}$ with $\tilde{\lambda }^\nu _{\tilde{J}_\nu } > 0$ and $w^\nu _{\tilde{J}_\nu }=0.$ If $|\tilde{J}_\nu | > n_\nu$ we can use Lemma 2 to construct a $J_\nu \subset \tilde{J}_\nu$ with $|J_\nu | \le n_\nu$ and $\lambda ^\nu _{J_\nu } \ge 0, \lambda ^\nu _i = 0$ for all $i \not \in J_\nu$ and $(A^{\nu \nu })^\top \lambda ^\nu = - c^\nu .$ If we take the smallest possible subset $J_\nu$ we have $J_\nu \in P^\nu$ in (S.1), and this can be done for all $\nu =1,\ldots ,N.$ Further $(\bar{x}, \lambda ,w)$ still satisfies the optimality conditions.

Since $\bar{x} \in X,$ we can find vertices $\{v_1,\ldots ,v_K\}$ of the polyhedral set X such that

$$\begin{aligned} \bar{x} =\sum _{k=1}^K \alpha _k v_k, \qquad \alpha _k >0, \qquad \sum _{k=1}^K \alpha _k=1. \end{aligned}$$

Since all these vertices are feasible and $\alpha _k >0$ we obtain from (2)

$$\begin{aligned} A_i v_k = b_i \qquad \forall i \in \bigcup _{\nu =1,\ldots ,N} J_\nu , \quad \forall k=1,\ldots ,K. \end{aligned}$$

This shows that $\bigcup \limits _{\nu =1,\ldots ,N}J_\nu \subset I(v_k)$ for all $k=1,\ldots ,K,$ implying that $v_1,\ldots ,v_K \in V(J),$ with $J:=(J_1,\ldots ,J_N).$ Thus (S.2) and (S.3) yield that $\mathop {\mathrm {conv}}(v_1,\ldots ,v_K)$ is in the set S,  and thus also $\bar{x}$ is contained in S. $\square$

Let us comment on the algorithm:

• In (S.1) in the worst case if none of the equation systems with $|J_\nu | < n_\nu$ was solvable, one has to solve $\sum _{i=1}^{n_\nu } \left( {\begin{array}{c}m_\nu \\ i\end{array}}\right)$ linear equation systems with dimensions from $n_\nu \times 1$ to $n_\nu \times n_\nu$. This will become difficult in larger dimensions. However, note that we have to solve linear equation systems in the smaller dimension $n_\nu$ and not in the full dimension n here. Furthermore, one has to solve these equation systems for all players $\nu =1,\ldots ,N.$ Therefore the computational effort of (S.1) is, in the worst case, the solution of $\sum _{\nu =1}^N \sum _{i=1}^{n_\nu } \left( {\begin{array}{c}m_\nu \\ i\end{array}}\right)$ linear equation systems, which however do not all have full dimension. If we use a standard linear equation solver for a system of dimension $n_\nu \times i$ the main computational effort is approximately $i^2 \left( n_\nu - \frac{1}{3} i \right)$ and therefore the computational effort of a worst case in (S.1) is approximately

  $$\begin{aligned} \sum _{\nu =1}^N \sum _{i=1}^{n_\nu } i^2 \left( n_\nu - \frac{1}{3} i \right) \left( {\begin{array}{c}m_\nu \\ i\end{array}}\right) . \end{aligned}$$

  Note that, since the calculations of different players are independent, (S.1) can be easily parallelized. For some problems, as the economy market models introduced in Dreves and Sudermann-Merx (2016), it is possible to compute the sets $P^\nu$ analytically, and then (S.1) is also possible for larger dimensional problems.

• In (S.2) one has to compute all tuples $J=(J_1,\ldots ,J_N) \in P^1 \times \ldots \times P^N$ and each of them contains the indices of constraints that have to be active at a component of the solution set. If |J| is the number of active indices and |J| is smaller than n one can choose $n-|J|$ out of the $m-|J|$ remaining indices to get n active ones and in each case by solving a linear equation system and checking if the solution is feasible, one can decide weather one has the index set of a vertex of X. To avoid the solution of the same linear system several times we store all computed vertices together with the active constraints in a list. Then we check if the current set of active constraints is already in the list before solving the equation system. Depending on the number of tuples and the size of |J| we have to solve a large number of linear equation systems of dimension $n \times n.$ If we have all possible tuples this results in the computation of all vertices of the set X. Hence, using a linear equation solver with main effort $\frac{2}{3} n^3$ the main computational effort of (S.2) is in the worst case approximately

  $$\begin{aligned} \frac{2}{3} n^3 \left( {\begin{array}{c}m\\ n\end{array}}\right) . \end{aligned}$$

  In Example 2 we present such a worst case example, where all vertices are contained in the solution set and therefore have to be computed in (S.2). However, typically we observe much less than all possible tuples in $P^1 \times \ldots \times P^N$and (S.2) is faster than computing all vertices of X.

• Note that at the end of (S.2) we already have a representation of the solution set, which however can be simplified. This is done in (S.3), where we delete duplicates and those sets that are included in larger sets. This results in the comparison of list elements, which is much faster than the computations in (S.2).

• Let us compare Algorithm 1 to the simple procedure suggested in Remark 1. Any subset $J =(J_1,\ldots ,J_N) \in P^1 \times \ldots \times P^N$ that we have at (S.2) corresponds to one of the subsets $J \subset \{1,\ldots ,m\}$ in the procedure of Remark 1. For J we have computed in (S.1) the solution of the problems

  $$\begin{aligned} (A^{\nu \nu }_{J_\nu \bullet })^\top \lambda ^\nu _{J_\nu } =-c^\nu , \quad \lambda ^\nu _{J_\nu } \ge 0 \qquad \forall \nu =1,\ldots ,N \end{aligned}$$

  and in (S.2) we compute the vertices of

  $$\begin{aligned} \{x \in \mathbb {R}^n \mid Ax \le b, A_J x = b_J\}. \end{aligned}$$

  This is also computed in the vertex enumeration for the index set J in the procedure of Remark 1, where it is done all at once and with the additional variables w in larger dimensions. Therefore the computational effort of (S.1) and (S.2) is for the index set J at least not larger than that of the simple procedure.

  Note that, at least for GNEPs with nonshared constraints, where each player has at least two constraints, we will not get all possible subsets of $\{1,\ldots ,m\}$ in $P^1 \times \ldots \times P^N$, since by (S.1) if one set $J_\nu$ is in $P^\nu$ we do not have any of its subsets in $P^\nu$.

  Moreover for all index sets $J \subseteq \{1,\ldots ,m\}$ that are not in $P^1 \times \ldots \times P^N$, we have at most solved the small linear equation systems in (S.1), which is much cheaper than vertex enumeration of the full dimensional problem of the simple procedure from Remark 1 for the index set J. Therefore the overall computational effort of the simple procedure is higher than that of Algorithm 1.

3 Examples

We implemented Algorithm 1 in Wolfram Mathematica ^® 9, which can handle large lists of points well. We then computed the entire solution sets of a few academic problems, that we present now.

Example 2

For the 2-player game

$$\begin{aligned} \max x^1 \quad \text {s.t.} \quad \begin{pmatrix} 1 &{}\quad -3 \\ -3 &{}\quad 1 \\ 1 &{}\quad 1 \end{pmatrix} x\le & {} \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} \\ \max x^2 \quad \text {s.t.} \quad \begin{pmatrix} 1 &{}\quad -3 \\ -3 &{}\quad 1 \\ 1 &{}\quad 1 \end{pmatrix} x\le & {} \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} \end{aligned}$$

we obtain the solution set

$$\begin{aligned} \{(-1,-1)\} \cup \mathop {\mathrm {conv}}\left\{ \left( \frac{5}{4},-\frac{1}{4} \right) ,\left( -\frac{1}{4},\frac{5}{4} \right) \right\} . \end{aligned}$$

Since the feasible set X is a triangle and all vertices are contained in the solution set, we compute all vertices of X in (S.2). Further in this example we have to check all possible 1-dimensional subsets $J_\nu$ of $\{1,2,3\}$ for both players in (S.1). Hence this is as a worst case example for the computational effort of Algorithm 1. In our implementation we have to solve 9 linear equation systems, 6 with dimension $1 \times 1$ (and check that the solution is non-negative) and 3 of dimension $2 \times 2$ (and check that the solution is feasible). Note that a naive implementation of the simple approach of Remark 1 requires $2^6$ times a vertex enumeration algorithm.

Example 3

Let us define

$$\begin{aligned} \hat{A}:=\begin{pmatrix} 4 &{}\quad -1 &{}\quad 0 &{}\quad 2 &{}\quad 1 &{}\quad -3 \\ 1 &{}\quad 2 &{}\quad 3 &{}\quad 1 &{}\quad -1 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad -2 &{}\quad 0 &{}\quad 1 &{}\quad -2 \end{pmatrix} \quad \text {and} \quad \hat{b}:=\begin{pmatrix} 10 \\ 10 \\ 10 \end{pmatrix}. \end{aligned}$$

Then we obtain for the 2-player game

$$\begin{aligned} \min&-x_1^1+3x_2^1+x_3^1&\text {s.t. } 0 \le x^1 \le 10, \, \hat{A} x \le \hat{b}, \\ \min&-2x_1^2+x_2^2+2x_3^2&\text {s.t. } 0 \le x^2 \le 10, \, \hat{A} x \le \hat{b}, \end{aligned}$$

the solution set

$$\begin{aligned}&\mathop {\mathrm {conv}}\left\{ (0,0,0,8,0,2),(0,2,0,6,0,0) \right\} \\&\cup \mathop {\mathrm {conv}}\left\{ (0,0,0,8,0,2), \left( \frac{40}{7},0,0,0,0,\frac{30}{7} \right) \right\} \\&\cup \mathop {\mathrm {conv}}\left\{ (0,2,0,6,0,0),(0,8,0,4,10,0) \right\} \\&\cup \mathop {\mathrm {conv}}\left\{ \left( \frac{40}{7},0,0,0,0,\frac{30}{7} \right) ,(8,0,0,0,8,10) \right\} . \end{aligned}$$

Our implementation of Algorithm 1 requires the solution of 1302 linear equation systems with a maximal dimension of $6 \times 6$ for this problem.

Example 4

With $\hat{A}$ and $\hat{b}$ from Example 3 we get for the 3-player game

$$\begin{aligned} \min&-x^1&\text {s.t. } 0 \le x^1 \le 10, \, \hat{A}x \le \hat{b}, \\ \min&3x_1^2+x_2^2&\text {s.t. } 0 \le x^2 \le 10, \, \hat{A}x \le \hat{b}, \\ \min&-2x_1^3+x_2^3+2x_3^3&\text {s.t. } 0 \le x^3 \le 10, \, \hat{A}x \le \hat{b}, \end{aligned}$$

the solution set

$$\begin{aligned}&\mathop {\mathrm {conv}}\left\{ (0,0,0,8,0,2),(0,2,0,6,0,0),\left( \frac{40}{7},0,0,0,0,\frac{30}{7} \right) ,\left( \frac{10}{3},\frac{10}{3},0,0,0,0 \right) \right\} \\&\cup \mathop {\mathrm {conv}}\left\{ (0,2,0,6,0,0),(0,8,0,4,10,0),\left( \frac{10}{3},\frac{10}{3},0,0,0,0 \right) , \left( \frac{20}{9},\frac{80}{9},0,0,10,0 \right) \right\} \\&\cup \mathop {\mathrm {conv}}\left\{ \left( \frac{40}{7},0,0,0,0,\frac{30}{7} \right) ,(8,0,0,0,8,10) , \left( \frac{10}{3},\frac{10}{3},0,0,0,0 \right) , \right. \\&\qquad \quad \left. \left( \frac{20}{9},\frac{80}{9},0,0,10,0 \right) , \left( \frac{70}{9},\frac{10}{9},0,0,10,10 \right) \right\} . \end{aligned}$$

Here we need to solve 961 linear equation systems with a maximal dimension of $6 \times 6$.

Example 5

With the matrix A and the vector b from Example 1, we consider a 2-player game with shared constraints which is by definition not an LGNEP:

Introducing two additional variables this can be equivalently reformulated as an LGNEP with non-shared constraints:

$$\begin{aligned} \min _{y^1}&y^1_3&\text {s.t. } \begin{pmatrix} 1&{}\quad 2&{}\quad 0&{}\quad -1&{}\quad 0\\ 3&{}\quad 2&{}\quad 0&{}\quad 1&{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 2 &{}\quad 1 &{}\quad -1 &{}\quad 1 &{}\quad 0 \\ -2 &{}\quad -1 &{}\quad -1 &{}\quad -1 &{}\quad 0 \\ 1 &{}\quad 2 &{}\quad -1 &{}\quad 1 &{}\quad 0 \\ -1 &{}\quad -2 &{}\quad -1 &{}\quad -1 &{}\quad 0 \end{pmatrix} \begin{pmatrix} y_1^1\\ y_2^1\\ y_3^1 \\ y_1^2 \\ y_2^2 \end{pmatrix} \le \begin{pmatrix} 14\\ 30 \\ 0 \\ 0 \\ 25 \\ -25 \\ 38 \\ -38 \end{pmatrix}, \\ \min _{y^2}&y^2_2&\text {s.t. } \begin{pmatrix} 1&{}\quad 2&{}\quad 0&{}\quad -1&{}\quad 0\\ 3&{}\quad 2&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -1 &{}\quad 0 \\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 2 &{}\quad -1 \\ -1 &{}\quad -1 &{}\quad 0 &{}\quad -2 &{}\quad -1 \end{pmatrix} \begin{pmatrix} y_1^1\\ y_2^1\\ y_3^1 \\ y_1^2 \\ y_2^2 \end{pmatrix} \le \begin{pmatrix} 14\\ 30 \\ 0 \\ 25 \\ -25 \end{pmatrix}. \end{aligned}$$

The computed solution set for this LGNEP is

$$\begin{aligned}&\mathop {\mathrm {conv}}\{ (8,3,24,0,14),(1,10,10,7,0) \} \\&\cup \mathop {\mathrm {conv}}\left\{ (0,11,8,8,2),(1,10,10,7,0), \left( 0,\frac{53}{5},\frac{48}{5},\frac{36}{5},0 \right) \right\} , \end{aligned}$$

from which we obtain the solution set of the original problem by dropping the additionally introduced variables:

$$\begin{aligned} \mathop {\mathrm {conv}}\{ (8,3,0),(1,10,7) \} \cup \mathop {\mathrm {conv}}\left\{ (0,11,8),(1,10,7),\left( 0,\frac{53}{5},\frac{36}{5} \right) \right\} . \end{aligned}$$

For the computation of this set we solved 192 linear equation systems with maximal dimension $5 \times 5$.

Further we want to solve some instances of economy markets that can be modeled as LGNEPs with shared constraints and were introduced in Dreves and Sudermann-Merx (2016). In these LGNEPs we have N players and player $\nu$ has the optimization problem

$$\begin{aligned} \max _{x^\nu \in \mathbb {R}^K} \langle p^\nu ,x^\nu \rangle \quad \text {s.t.}\quad x^\nu \ge 0, \quad \sum _{k=1}^K x_k^\nu \le C^\nu , \quad \sum _{\nu =1}^N x_k^\nu \le D_k \quad \forall k=1,\ldots ,K. \end{aligned}$$

As mentioned in Dreves and Sudermann-Merx (2016) the model can be used for example if several travel agencies offer flight seats for the same flight, in different price categories depending on the remaining time until departure. For these problems it is possible to exploit the structure in order to compute (S.1) very efficiently. In detail: by Dreves and Sudermann-Merx (2016, Lemma 5.3) one can explicitly get all vertices (at most $K+1$) of the sets

$$\begin{aligned} \left\{ \lambda ^\nu \in \mathbb {R}^{m_\nu } \mid (A^{\nu \nu })^\top \lambda ^\nu = -c^\nu , \lambda ^\nu \ge 0\right\} \end{aligned}$$

and by taking the corresponding indices of positive components, one can directly get the index sets $P^\nu$ in (S.1) without solving linear equation systems. We solve some instances of these problems, that were randomly generated by a procedure described in Dreves and Sudermann-Merx (2016, Section 6.1), and we report details for some small problems in Table 2. Each column contains one example with the dimensions given in the first row, and the specifications of the constants $p^\nu , C^\nu$ and D below. The solution set always consists of a convex combination of “Sol” elements and our algorithm has to solve “LES” linear equation systems of a maximal dimension $N \cdot K$, and these numbers are reported in the last two rows of Table 2.

Table 2 Problem data and results for economy market LGNEPs

4 Conclusions

We presented an algorithm that is able to compute the entire solution set of an LGNEP in finite time. This algorithm exploits the linear structure via duality theory and requires the solution of typically a large number of linear equation systems. Therefore its application is limited to smaller dimensional problems. However, to the best of our knowledge there is currently no other algorithmic realization available, that is able to compute the entire solution set of an LGNEP.