Goodness-of-fit testing of a count time series’ marginal distribution

Abstract

Popular goodness-of-fit tests like the famous Pearson test compare the estimated probability mass function with the corresponding hypothetical one. If the resulting divergence value is too large, then the null hypothesis is rejected. If applied to i. i. d. data, the required critical values can be computed according to well-known asymptotic approximations, e. g., according to an appropriate $\chi ^2$-distribution in case of the Pearson statistic. In this article, an approach is presented of how to derive an asymptotic approximation if being concerned with time series of autocorrelated counts. Solutions are presented for the case of a fully specified null model as well as for the case where parameters have to be estimated. The proposed approaches are exemplified for (among others) different types of CLAR(1) models, INAR(p) models, discrete ARMA models and Hidden-Markov models.

1 Introduction

In many applications, one is interested in testing a hypothesis with respect to the marginal distribution of a given count time series $X_1,\ldots ,X_T$. This might be done by looking at a specific feature of the hypothetical count distribution, e. g., at the Poisson index of dispersion as in Schweer and Weiß (2014), or by deriving a test statistic which considers any kind of deviation from the null model. In Meintanis and Karlis (2014), such tests are developed based on probability generating functions (pgf), while here, we follow the textbook approach and consider goodness-of-fit statistics based on the hypothetical and estimated probability mass function (pmf). As an important example within the power-divergence family (Cressie and Read 1984; Read and Cressie 1988), we shall concentrate on Pearson’s goodness-of-fit statistic, but the presented approach could be adapted to other pmf-based statistics as well.

In Sect. 2, an approach is presented of how to explicitly compute the asymptotic distribution of Pearson’s goodness-of-fit statistic (so no bootstrap implementation is required). This approach covers both scenarios, where the model parameters are either specified, or where they have to be estimated from the available data. The approach can be applied if the process satisfies certain mixing and moment conditions, and if the h-step-ahead conditional distributions (and corresponding moments) can be computed. A number of examples are presented, including types of CLAR(1) models, INAR(p) models, discrete ARMA models and Hidden-Markov models, also see the summaries in Appendix A. The goodness of the resulting asymptotic approximations to the actual Pearson statistic’s distribution is investigated in Sect. 3, where results from a simulation study are presented. There, we also analyze the size and power of the test if applied in practice, and we briefly discuss two real-data examples. Finally, we conclude in Sect. 4.

2 Goodness-of-fit testing

Many common goodness-of-fit test statistics fall within the power-divergence family as discussed by Cressie and Read (1984) and Read and Cressie (1988). Since the asymptotic behavior of these statistics is the same as that of the famous Pearson’s goodness-of-fit statistic $G^2$ to be defined below (Cressie and Read 1984; Read and Cressie 1988), we shall focus on the latter in the sequel.

If the given data $X_1,\ldots ,X_T$ are independent and identically distributed (i. i. d.), and if the Pearson statistic $G^2$ is constructed by using k categories, it is known that its asymptotic distribution is a $\chi ^2$-distribution (Cressie and Read 1984; Read and Cressie 1988) [also note the results by Kißlinger and Stummer (2016) about statistics within the family of scaled Bregman divergences having such a limiting $\chi ^2$-distribution]. More precisely, if the hypothetical distribution is fully specified, then $G^2$ converges to the $\chi ^2_{k-1}$-distribution with $k-1$ degrees of freedom. If, in contrast, the hypothetical distribution has $r\ge 1$ unspecified parameters, which have to be estimated from the same data, the degrees of freedom have to be further reduced by r, i. e., the distribution of $G^2$ is approximated by the $\chi ^2_{k-1-r}$-distribution.

In the sequel, we shall consider both scenarios, i. e., a fully specified hypothetical distribution, or a distribution with estimated parameters, but in the case of serially dependent time series data $X_1,\ldots ,X_T$. Such a scenario (although referring to continuous-valued data) was also considered by Moore (1982), where it was shown that the asymptotic distribution of the Pearson statistic (under rather general conditions) can be formally derived; however, the involved matrices appeared “intractible” such that explicit computations were presented only for a Gaussian AR(1) process (first-order autoregressive) with fully specified null distribution. In this work, an approach is presented for explicitly computing the limit distribution for a variety of count time series models and under parameter estimation, such that the Pearson test can be applied in all these cases without the need for a bootstrap implementation.

2.1 Pearson’s goodness-of-fit test

Let $(X_t)_{\mathbb {Z}}$ be a stationary count process. With a goodness-of-fit test based on $X_1,\ldots ,X_T$, we want to test the hypothesis that the marginal distribution satisfies $P(X_t=i)=p_i$ for some pmf $(p_i)_{i}$. First, we define an appropriate set of categories, e. g., following one of the rules of thumb surveyed in Horn (1977). Like in Kim and Weiß (2015), we shall assume $b-a+2$ categories of the form

$$\begin{aligned} \{0,\ldots ,a\},\ \{a+1\}, \ldots ,\ \{b\},\ \{b+1,\ldots \} \quad \text {with some } 0\le a<b. \end{aligned}$$

(1)

Then the hypothetical probabilities for $X_t$ falling into one of these categories are computed from ${\varvec{p}}=(p_0,\ldots ,p_b)^{\top }$ as

$$\begin{aligned}&{\varvec{\pi }}:= \left( \begin{array}{c} \pi _a\\ \pi _{a+1}\\ \vdots \\ \pi _b\\ \pi _{b+1}\\ \end{array}\right) \,:=\, \left( \begin{array}{c} p_0+\cdots +p_a\\ p_{a+1}\\ \vdots \\ p_b\\ 1-p_0-\ldots -p_b \end{array}\right) =\ {\mathbf{A }}\,{\varvec{p}}+ {\varvec{e}}_{b-a+2} \nonumber \\&\text {with } {\varvec{e}}_{b-a+2}:=(0,\ldots ,0,1)^{\top },\quad \text {and} \\ \nonumber&{\mathbf{A }}:={\mathbf{A }}(a,b) :=\ \underbrace{\left( \begin{array}{ccc} 1 &{} \cdots &{} 1 \\ 0 &{} \cdots &{} 0 \\ \vdots &{} &{} \vdots \\ 0 &{} \cdots &{} 0 \\ -1 &{} \cdots &{} -1\\ \end{array}\right. }_{a+1} \underbrace{\left. \begin{array}{ccc} 0 &{} \cdots &{} 0\\ 1 &{} &{} \vdots \\ &{} \ddots &{} 0 \\ 0 &{} &{} 1 \\ -1 &{} \cdots &{} -1\\ \end{array}\right) }_{b-a} \left. \begin{array}{c} \\ \\ \\ \\ \\ \end{array}\right\} b-a+2. \end{aligned}$$

(2)

Defining $\hat{p}_i$ as the relative frequency of i within $X_1,\ldots ,X_T$, i. e., $\hat{p}_i$$= \frac{1}{T}\,\sum _{t=1}^{T} \mathbb {1}_{\{X_t=i\}}$ with $\mathbb {1}$ denoting the indicator function, and setting $\hat{{\varvec{\pi }}}\,:=\,{\mathbf{A }}\,\hat{{\varvec{p}}} + {\varvec{e}}_{b-a+2}$ with $\hat{{\varvec{p}}}=(\hat{p}_0,\ldots ,\hat{p}_b)^{\top }$, Pearson’s goodness-of-fit statistic is computed as

$$\begin{aligned} G^2 =\ T\,(\hat{{\varvec{\pi }}}-{\varvec{\pi }})^{\top }\,\text{ diag }({\varvec{\pi }})^{-1}\,(\hat{{\varvec{\pi }}}-{\varvec{\pi }}). \end{aligned}$$

(3)

This can be rewritten

$$\begin{aligned} G^2 =\ T\,{\varvec{G}}^{\top }\,{\varvec{G}}\qquad \text {with } {\varvec{G}}\,:=\,\text{ diag }\big (\pi _a^{-1/2},\ldots , \pi _{b+1}^{-1/2}\big )\,{\mathbf{A }}(\hat{{\varvec{p}}}-{\varvec{p}}). \end{aligned}$$

(4)

From now on, let us assume that the marginal pmf is determined by some parameter ${\varvec{\theta }}\in \mathbb {R}^r$, i. e., ${\varvec{p}}={\varvec{p}}({\varvec{\theta }})$ and ${\varvec{\pi }}={\varvec{\pi }}({\varvec{\theta }})={\mathbf{A }}\,{\varvec{p}}({\varvec{\theta }}) + {\varvec{e}}_{b-a+2}$. We shall distinguish the two scenarios, where either ${\varvec{\theta }}$ is specified (so fully specified pmf), or ${\varvec{\theta }}$ has to be estimated from $X_1,\ldots ,X_T$ (goodness-of-fit with estimated parameters). In the latter case, we shall use simple moment estimators, i. e., we assume that $\hat{{\varvec{\theta }}}$ is expressed as a differentiable function ${\varvec{h}}: \mathbb {R}^r\rightarrow \mathbb {R}^r$ applied to the empirical marginal raw moments $\hat{\mu }_1=\bar{X}=\frac{1}{T}\,\sum _{t=1}^{T} X_t$, ..., $\hat{\mu }_r=\frac{1}{T}\,\sum _{t=1}^{T} X_t^r$. The ultimate aim is to derive the asymptotic distributions of $\sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},{\varvec{\theta }})$ and $\sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})$, respectively, as well as of $G^2(\hat{{\varvec{p}}},{\varvec{\theta }})$ and $G^2(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})$, respectively.

2.2 A central limit theorem

To derive the asymptotic distributions of $\sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},{\varvec{\theta }})$ and $\sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})$, respectively, we start with a central limit theorem. For this purpose, we assume that $(X_t)_{\mathbb {Z}}$ satisfies appropriate mixing and moment conditions: in the examples considered below, it is sufficient to assume, e. g., that $(X_t)_{\mathbb {Z}}$ is $\alpha$-mixing with geometrically decreasing weights, and that the $(2r+\delta )$-moments with some $\delta >0$ exist. Then we can apply Theorem 1.7 in Ibragimov (1962) to obtain the required limit distribution.

Special attention is given to the case, where the lagged bivariate probabilities $P(X_t=i, X_{t-h}=j)$ are symmetric in i, j (property “SYM”), since then more simple closed-form expressions can be obtained. Note that SYM is implied by time reversibility. But our approach also works if the optional property SYM is violated, computations are just more complex in that case.

In view of (4), we define the $(b+1+r)$-dimensional process

$$\begin{aligned} {\varvec{Z}}_t =\ \left( \begin{array}{c} \mathbb {1}_{\{X_t=0\}} \\ \vdots \\ \mathbb {1}_{\{X_t=b\}} \\ X_t \\ \vdots \\ X_t^r \end{array}\right) \qquad \text {with}\quad {\varvec{\mu }}_{{\varvec{Z}}} := E[{\varvec{Z}}_t] =\ \left( \begin{array}{c} p_0 \\ \vdots \\ p_b \\ \mu _1 \\ \vdots \\ \mu _r \end{array}\right) , \end{aligned}$$

(5)

where $\mu _k:=E[X_t^k]$ with $\mu :=\mu _1$ (marginal raw moments). The idea is to choose r sufficiently large such that all parameters in ${\varvec{\theta }}$ can be estimated by the method-of-moments. Note that the mixing properties of $(X_t)_{\mathbb {Z}}$ carry over to $({\varvec{Z}}_t)_{\mathbb {Z}}$ such that Theorem 1.7 in Ibragimov (1962) is applicable.

Theorem 2.2.1

Let $(X_t)_{t\in \mathbb {Z}}$ be a stationary count process, which is $\alpha$-mixing with geometrically decreasing weights and has existing $(2r+\delta )$-moments with some $\delta >0$, and let ${\varvec{Z}}_t$ be given by (5). Then

$$\begin{aligned} \frac{1}{\sqrt{T}}\,\sum \limits _{t=1}^{T}({\varvec{Z}}_t-{\varvec{\mu }}_{{\varvec{Z}}})\ \xrightarrow {D}\ {\text{ N }}({\varvec{0}}, {\varvec{\varSigma }}), \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rl} \sigma _{ij} =&{} E[Z_{0,i} \cdot Z_{0,j}]-\mu _{{\varvec{Z}},i}\,\mu _{{\varvec{Z}},j}\\ &{}\displaystyle \quad + \mathop {\sum }\limits _{h=1}^\infty \big (E[Z_{0,i} \cdot Z_{h,j}]\ +\ E[Z_{h,i} \cdot Z_{0,j}]-2\,\mu _{{\varvec{Z}},i}\,\mu _{{\varvec{Z}},j}\big ) \\ {\mathop {=}\limits ^{\text {SYM}}}&{} E[Z_{0,i} \cdot Z_{0,j}]-\mu _{{\varvec{Z}},i}\,\mu _{{\varvec{Z}},j}\ +\ 2 \, \displaystyle \mathop {\sum }\limits _{h=1}^\infty \big (E[Z_{h,i} \cdot Z_{0,j}]-\mu _{{\varvec{Z}},i}\,\mu _{{\varvec{Z}},j}\big ). \end{array} \end{aligned}$$

Note that $\frac{1}{\sqrt{T}}\,\sum _{t=1}^{T} {\varvec{Z}}_t \,=\, \sqrt{T}\,(\hat{p}_0,\ldots ,\hat{p}_b,\ \hat{\mu }_1,\ldots ,\hat{\mu }_r)^{\top }$. Assuming some differentiable function ${\varvec{h}}: \mathbb {R}^r\rightarrow \mathbb {R}^r$ such that ${\varvec{\theta }}={\varvec{h}}(\mu _1, \ldots , \mu _r)$, the moment estimator of ${\varvec{\theta }}$ follows as $\hat{{\varvec{\theta }}}={\varvec{h}}(\hat{\mu }_1,\ldots ,\hat{\mu }_r)$. Applying the Delta method, Theorem 2.2.1 leads to the asymptotic result

$$\begin{aligned} \sqrt{T}\,\big ((\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})-({\varvec{p}},{\varvec{\theta }})\big )\ \xrightarrow {D}\ {\text{ N }}\big ({\varvec{0}}, {\varvec{\varSigma }}^*\big ) \qquad \text {with } {\varvec{\varSigma }}^*:={\mathbf{D }}{\varvec{\varSigma }}{\mathbf{D }}^{\top }, \end{aligned}$$

(6)

with ${\mathbf{D }}$ denoting the Jacobian of $\big (z_0,\ldots ,z_b,{\varvec{h}}(z_{b+1},\ldots ,z_{b+r})\big ){}^{\top }$ evaluated at $(p_0, \ldots , \mu _r)^{\top }$. If, in contrast, ${\varvec{\theta }}$ is specified, then it suffices to consider the asymptotic result

$$\begin{aligned} \sqrt{T}\,(\hat{{\varvec{p}}}-{\varvec{p}})\ \xrightarrow {D}\ {\text{ N }}\big ({\varvec{0}}, {\varvec{\varSigma }}^{({\varvec{p}})}\big ) \qquad \text {with } {\varvec{\varSigma }}^{({\varvec{p}})}:=(\sigma _{ij})_{i,j=0,\ldots ,b}. \end{aligned}$$

(7)

So formally, the asymptotic distributions (6) and (7) are easily derived, also see the analogous results by Moore (1982); in Sect. 2.4, we shall pick up again these asymptotic distributions for $\sqrt{T}\,(\hat{{\varvec{p}}}-{\varvec{p}})$ and $\sqrt{T}\,\big ((\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})-({\varvec{p}},{\varvec{\theta }})\big )$, respectively, and derive the resulting asymptotic distribution of the Pearson statistic with specified or estimated parameters. But before continuing in this direction, it is crucial to ask if the covariances occurring in Theorem 2.2.1 can be computed at all in practice, since otherwise we could not benefit from this result in applications. Therefore, in Sect. 2.3, it is shown that for many different types of count processes, explicit results are easily obtained.

2.3 Intermezzo: application and implementation of Theorem 2.2.1

The required moments $E[Z_{h,i} \cdot Z_{0,j}]$ with $h\ge 0$ in Theorem 2.2.1 are easy to compute in many practically relevant cases. As outlined in the sequel, the minimal requirement for computability is that the h-step-ahead conditional probabilities $p_{i|j}{}^{(h)}:=P(X_t=i\ |\ X_{t-h}=j)$ are available.

For $i,j\in \{0,\ldots ,b\}$, we have

$$\begin{aligned} \begin{array}{rl} E[Z_{h,i} \cdot Z_{0,j}]-\mu _{{\varvec{Z}},i}\mu _{{\varvec{Z}},j}\ =&{} P(X_t=i, X_{t-h}=j) - p_i\,p_j\\ =&{} \left\{ \begin{array}{ll} (\delta _{i,j}-p_i)\,p_j &{}\quad \text {if } h=0,\\ (p_{i|j}^{(h)}-p_i)\,p_j &{}\quad \text {if } h>0,\\ \end{array}\right. \end{array} \end{aligned}$$

(8)

where $\delta _{i,j}$ denotes the Kronecker delta. So if being able to compute the $p_{i|j}{}^{(h)}$, then all $\sigma _{ij}$ with $i,j=0,\ldots ,b$ [and hence ${\varvec{\varSigma }}{}^{({\varvec{p}})}$ from (7)] are available.

Next, for $i,j\in \{1,\ldots ,r\}$, we have $\mu _{{\varvec{Z}},b+i}=\mu _i$ as well $\mu _{{\varvec{Z}},b+j}=\mu _j$, and we obtain

$$\begin{aligned} E[Z_{h,b+i} \cdot Z_{0,b+j}] =\ E[X_t^i\cdot X_{t-h}^j] =\ \left\{ \begin{array}{ll} \mu _{i+j} &{}\quad \text {if } h=0,\\ E[X_t^i\cdot X_{t-h}^j] &{}\quad \text {if } h>0.\\ \end{array}\right. \end{aligned}$$

(9)

So joint moments of sufficiently high order need to be computed. For $r=1$, it is indeed sufficient to compute the autocovariance function. If closed-form moment expressions are not available, a numerical computation based on the h-step-ahead bivariate distributions is possible, e. g., by truncating the summation after $M+1$ summands with M sufficiently large.

Finally, for the remaining moments, the optional property SYM would be particularly useful, because then

$$\begin{aligned} E[Z_{h,i} \cdot Z_{0,b+j}]\, {\mathop {=}\limits ^{\text {SYM}}}\, E[Z_{h,b+j} \cdot Z_{0,i}] \end{aligned}$$

holds for $i=0,\ldots ,b$ and $j=1,\ldots ,r$. For the latter moments, we obtain

$$\begin{aligned} E[Z_{h,b+j} \cdot Z_{0,i}] =\ E[X_t^j\,\mathbb {1}_{\{X_{t-h}=i\}}]\ =\ \left\{ \begin{array}{ll} i^j\,p_i &{} \quad \text {if } h=0,\\ E[X_t^j\ |\ X_{t-h}=i]\,p_i &{}\quad \text {if } h>0.\\ \end{array}\right. \end{aligned}$$

(10)

Note that such conditional moments (10) are often easy to compute in practice, as illustrated by the subsequent examples. If the “nice-to-have” property SYM does not hold, then $E[Z_{h,i} \cdot Z_{0,b+j}] = \sum _{x=0}^{\infty } x^j\,p_{i|x}^{(h)}\,p_x$ has to be calculated (numerically) from the h-step-ahead bivariate distribution.

Example 2.3.1

(i. i. d. Counts) Let $(X_t)_{\mathbb {Z}}$ be i. i. d. Then $p_{i|j}{}^{(h)}-p_i=0$ for $h>0$, so (8) simplifies and we obtain the well-known result that $\sigma _{ij}=(\delta _{i,j}-p_i)\,p_j$ for $i,j=0,\ldots ,b$. Similarly, (9) simplifies because of $E[X_t^i\cdot X_{t-h}^j]=\mu _i\,\mu _j$ for $h>0$, so $\sigma _{b+i,b+j}=\mu _{i+j}-\mu _i\,\mu _j$ for $i,j=1,\ldots ,r$. Finally, the independence implies SYM, and $E[X_t^j\ |\ X_{t-h}=i]=\mu _j$ if $h>0$. So $\sigma _{i,b+j}=(i^j-\mu _j)\,p_i$ because of (10).

Example 2.3.2

(CLAR(1) Model) Let $(X_t)_{\mathbb {Z}}$ follow a CLAR(1) model (Grunwald et al. 2000) as described in Appendix A.1. Applying (A.2) to (10), we obtain for $j=1$ (referring to the estimation of the mean $\mu$) that

$$\begin{aligned} E[Z_{h,b+1} \cdot Z_{0,i}] =\ \big (\alpha ^h\cdot i + (1-\alpha ^h)\,\mu \big )\,p_i, \end{aligned}$$

which also holds for $h=0$. Hence, if SYM holds, $\sigma _{i,b+1}$ in Theorem 2.2.1 becomes

$$\begin{aligned} \begin{array}{rl} \sigma _{i,b+1} =&{} E[Z_{0,b+1} \cdot Z_{0,i}]-\mu \,p_i\ +\ 2 \, \displaystyle \mathop {\sum }\limits _{h=1}^\infty \big (E[Z_{h,b+1} \cdot Z_{0,i}]-\mu \,p_i\big )\\ =&{} (i-\mu )\,p_i\ +\ 2 \,\displaystyle \mathop {\sum }\limits _{h=1}^\infty \alpha ^h\, (i-\mu )\,p_i =\ (i-\mu )\,p_i\,\frac{1+\alpha }{1-\alpha }. \end{array} \end{aligned}$$

Furthermore, (9) leads to $E[Z_{h,b+1} \, Z_{0,b+1}]-\mu ^2=Cov[X_t, X_{t-h}]=\sigma ^2\,\rho (h)$, where $\rho (h)=\alpha ^h$ according to (A.2). So $\sigma _{b+1,b+1}$ in Theorem 2.2.1 becomes

$$\begin{aligned} \sigma _{b+1,b+1}=\ \sigma ^2\ +\ 2 \, \sum \limits _{h=1}^\infty \sigma ^2\,\alpha ^h =\ \sigma ^2\,\frac{1+\alpha }{1-\alpha }. \end{aligned}$$

As we have seen in Example 2.3.2, the covariances $\sigma _{i,b+1}$ and $\sigma _{b+1,b+1}$ directly follow from the CLAR(1) property, without further distributional assumptions. To evaluate the remaining expressions, let us consider two particular instances within the CLAR(1) family, which date back to McKenzie (1985) and are often used in applications.

Example 2.3.3

(Poisson INAR(1) Model) Let $(X_t)_{\mathbb {Z}}$ follow the Poisson INAR(1) model from Appendix A.2. Then the marginal distribution $p_i=e^{-\mu }\,\mu ^i/i!$ is determined by only one parameter, the mean parameter $\mu$. So it suffices to consider only one estimator (thus $r=1$), $\hat{\mu }=\bar{X}$. The results of Example 2.3.2 hold with an additional simplification: because of the Poisson’s equidispersion property, we have $\sigma ^2=\mu$.

The remaining entries $\sigma _{ij}$ in Theorem 2.2.1 for $i,j\in \{0,\ldots ,b\}$ simplify with (8) to

$$\begin{aligned} \sigma _{ij} =\ (\delta _{i,j}-p_i)\,p_j\ +\ 2\,p_j \, \sum \limits _{h=1}^\infty (p_{i|j}{}^{(h)}-p_i) \end{aligned}$$

which are computed by either using (A.3) for the Poisson INAR(1)’s h-step-ahead transition probabilities, or by utilizing that $(X_t,X_{t-h})$ are bivariately Poisson distributed according to ${\text{ BPoi }}\big (\alpha ^h\,\mu ;\ (1-\alpha ^h)\,\mu , (1-\alpha ^h)\,\mu \big )$. Since a closed-form expression for $\sigma _{ij}$ is rather complex, in practice, one approximates

$$\begin{aligned} \sigma _{ij} \ \approx \ (\delta _{i,j}-p_i)\,p_j\ +\ 2\,p_j \, \sum \limits _{h=1}^M (p_{i|j}{}^{(h)}-p_i)\qquad \text {with { M} sufficiently large}. \end{aligned}$$

Example 2.3.4

(Binomial AR(1) Model) Let $(X_t)_{\mathbb {Z}}$ follow the binomial AR(1) model from Appendix A.3, i. e., with binomial marginal distribution $p_i=\left( {\begin{array}{c}n\\ i\end{array}}\right) \,\pi ^i\,(1-\pi )^{n-i}$. The results of Example 2.3.2 hold with $\mu =n\pi$, $\sigma ^2=n\pi (1-\pi )$ as well as $\alpha$ replaced by $\rho$. The required moment estimator of $\pi$ is defined as $\hat{\pi }:= \bar{X}/n$. As a result, the Jacobian ${\mathbf{D }}$ used for (6) takes a very simple form, ${\mathbf{D }}=\text{ diag }(1,\ldots ,1,\ 1/n)$.

The entries $\sigma _{ij}$ in Theorem 2.2.1 for $i,j\in \{0,\ldots ,b\}$ are computed as in Example 2.3.3, but using formula (A.7) for the h-step-ahead transition probabilities. Note that in this particular example, the asymptotic covariance matrix ${\varvec{\varSigma }}{}^{({\varvec{p}})}$ from (7) can also be computed by using a result in Tavaré and Altham (1983) for finite Markov chains, see Kim and Weiß (2015) for details.

A CLAR(1) process not being time reversible is the geometric INAR(1) process.

Example 2.3.5

(Geometric INAR(1) Model) If $(X_t)_{\mathbb {Z}}$ follows the geometric INAR(1) model from Appendix A.2, then, in contrast to Example 2.3.3, the property SYM does not hold. So numerical approximations are required for Theorem 2.2.1. These include the computation of the $p_{i|j}{}^{(h)}$, since a simple closed-form formula is not available: for N sufficiently large, define $\tilde{{\mathbf{P }}}:=(p_{i|j})_{i,j=0,\ldots ,N}$ with the transition probabilities (A.5); then the h-step-ahead transition probabilities $(p_{i|j}{}^{(h)})_{i,j=0,\ldots ,N}$ are approximated by the matrix $\tilde{{\mathbf{P }}}{}^h$.

The geometric marginal distribution satisfies $\mu =(1-\pi )/\pi$ and $\sigma ^2=(1-\pi )/\pi ^2$, and it requires one estimator (thus $r=1$), $\hat{\pi }=1/(1+\bar{X})$. The Jacobian ${\mathbf{D }}$ used for (6) equals ${\mathbf{D }}=\text{ diag }\big (1,\ldots ,1,\ -\pi ^2\big )$.

In an analogous way as in Example 2.3.5, one can also handle INAR(1) processes with other types of non-Poisson marginal distribution, e. g., a negative binomial distribution (McKenzie 1986). In the latter case, the main difference to Example 2.3.5 is the fact that the negative binomial distribution has two parameters, i. e., now $r=2$ moments have to be considered for parameter estimation. The required formulae for higher-order joint moments can be found in Schweer and Weiß (2014).

The next examples demonstrate that the count processes to be considered are not limited to Markov chains. As an illustrative example for a higher-order AR-type model, the Poisson INAR(2) model by Alzaid and Al-Osh (1990) is presented.

Example 2.3.6

(Poisson INAR(2) Model) Let $(X_t)_{\mathbb {Z}}$ follow the Poisson INAR(2) model from Appendix A.2, especially Example A.2.2. Like any Poisson INAR(p) process in the sense of Alzaid and Al-Osh (1990), this process is time reversible such that the property SYM holds. All computations can be done in complete analogy to the INAR(1) case in Example 2.3.3, by using that $(X_t,X_{t-h})\, \sim \, {\text{ BPoi }}\Big (\rho (h)\,\mu ;\, \big (1-\rho (h)\big )\,\mu ,\, \big (1-\rho (h)\big )\,\mu \Big )$ and $E[X_t\ |\ X_{t-h}]\, =\, \rho (h)\,X_{t-h}+\big (1-\rho (h)\big )\,\mu$, where the ACF satisfies $\rho (1)=\alpha _1$ and $\rho (h)\, =\, \alpha _1\,\rho (h-1) + \alpha _2\,\rho (h-2)$ for $h\ge 2$.

It should be pointed out that the argumentation in Example 2.3.6 is easily adapted to the family of Poisson INMA(q) processes (moving-average-type models), which are non-Markovian but q-dependent. The latter property implies that the infinite sums in Theorem 2.2.1 reduce to finite ones, with non-zero summands for $h\le q$. For such Poisson INMA(q) processes, Weiß (2008) showed that again $(X_t,X_{t-h})\, \sim \, {\text{ BPoi }}\Big (\rho (h)\,\mu ;\, \big (1-\rho (h)\big )\,\mu ,\, \big (1-\rho (h)\big )\,\mu \Big )$ holds, where the ACF has to be determined from the specific INMA(q) model. Note that the bivariate distributions of $(X_t,X_{t-1}),\ldots ,(X_t,X_{t-q})$ require knowledge only about $\mu$ and $\rho (1),\ldots ,\rho (q)$, which are easily estimated from given time series data.

A completely different approach than INARMA for obtaining ARMA-like count processes is given by the NDARMA models by Jacobs and Lewis (1983).

Example 2.3.7

(NDARMA Model) Let $(X_t)_{\mathbb {Z}}$ be an NDARMA(p, q) process as described in Appendix A.4. According to (A.8), these models satisfy the property SYM with $p_{i|j}{}^{(h)}-p_i\, =\,(\delta _{i,j}-p_i)\,\rho (h)$. Defining $c:=1+2\,\sum _{h=1}^{\infty } \rho (h)$, the entries $\sigma _{ij}$ in Theorem 2.2.1 for $i,j\in \{0,\ldots ,b\}$ become $\sigma _{ij}=c\,(\delta _{i,j}-p_i)\,p_j$. Note that this result coincides with the i. i. d. case from Example 2.3.1 except the additional factor c, also see formula (14) in Weiß (2013).

The conditional moments in (10) follow as

$$\begin{aligned} E[X_t^j | X_{t-h}=i] = \sum \limits _{x=0}^{\infty }\, x^j\,\big (p_x + (\delta _{x,i}-p_x)\,\rho (h)\big ) = \mu _j + \rho (h)\,(i^j-\mu _j). \end{aligned}$$

So $\sigma _{i,b+j}$ in Theorem 2.2.1 becomes $\sigma _{i,b+j} = c\,(i^j-\mu _j)\,p_i$, compare again with the i. i. d. result from Example 2.3.1. Finally, the joint moments in (9) are computed as

$$\begin{aligned} E[X_t^i X_{t-h}^j]= & {} \sum \limits _{x,y=0}^{\infty } x^i y^j \big (p_x + (\delta _{x,y}-p_x) \rho (h)\big ) p_y = \mu _i \mu _j \\&+\, \rho (h) (\mu _{i+j}-\mu _i \mu _j), \end{aligned}$$

so $\sigma _{b+i,b+j}$ in Theorem 2.2.1 becomes $\sigma _{b+i,b+j} = c\,(\mu _{i+j}-\mu _i\,\mu _j)$. Hence, throughout, we obtain the i. i. d. results from Example 2.3.1 together with the additional factor c.

Another non-Markovian example, which could be relevant in practice, is a Hidden-Markov model for counts, see Zucchini and MacDonald (2009) for detailed information. If ${\mathbf{A }}$ denotes the transition matrix of the hidden Markov chain with ${\varvec{\pi }}$ being the corresponding stationary marginal distribution, and if ${\mathbf{P }}(i) := \text{ diag }\big (p(i|\cdot )\big )$ denotes the diagonal matrix of all state-dependent probabilities leading to the count $i\in \mathbb {N}_0$, then the marginal and lagged bivariate probabilities are computed as

$$\begin{aligned} \begin{array}{rl} P(X_t=i) =&{} {\varvec{1}}^{\top }\,{\mathbf{P }}(i)\,{\varvec{\pi }},\\ P(X_t=i, X_{t-h}=j) =&{} {\varvec{1}}^{\top }\,{\mathbf{P }}(i)\,{\mathbf{A }}^h\,{\mathbf{P }}(j)\,{\varvec{\pi }}, \end{array} \end{aligned}$$

(11)

where ${\varvec{1}}$ denotes the vector of ones. So formulae (8)–(10) are again easily computed in practice.

Remark 2.3.8

A further model family commonly used for ARMA-like count time series are INGARCH models (integer-valued generalized autoregressive conditional heteroscedasticity), see Ferland et al. (2006) and Weiß (2018) for background information. Although these models typically satisfy the moment and mixing conditions of Theorem 2.2.1, see Ferland et al. (2006) and Neumann (2011), goodness-of-fit tests w.r.t. to the counts’ marginal distribution are not applicable. INGARCH models are defined in terms of their conditional distribution (given the available past), e. g., by requiring a conditional Poisson distribution for Poisson INGARCH models. But analytic expressions concerning the resulting marginal distribution are not known, so marginal goodness-of-fit statistics cannot be computed for these models.

2.4 Asymptotic distribution of Pearson statistic

In Sect. 2.2, we ended up with the asymptotic normal distribution (6) for $\sqrt{T}\,\big ((\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})-({\varvec{p}},{\varvec{\theta }})\big )$. This is now used to derive the asymptotic distributions of $\sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},{\varvec{\theta }})$ and $\sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})$, respectively, remember (4). For this purpose, let ${\varvec{z}}=({\varvec{z}}_1,{\varvec{z}}_2)$ with ${\varvec{z}}_1\in \mathbb {R}^{b+1}$ and ${\varvec{z}}_2\in \mathbb {R}^{r}$, and define the function

$$\begin{aligned} {\varvec{g}}({\varvec{z}}) := {\varvec{g}}({\varvec{z}}_1,{\varvec{z}}_2) :=\ \text{ diag }\big (\pi _a({\varvec{z}}_2)^{-1/2},\ldots , \pi _{b+1}({\varvec{z}}_2)^{-1/2}\big )\,{\mathbf{A }}\big ({\varvec{z}}_1-{\varvec{p}}({\varvec{z}}_2)\big ) \end{aligned}$$

such that ${\varvec{G}}(\hat{{\varvec{p}}},{\varvec{\theta }})={\varvec{g}}(\hat{{\varvec{p}}},{\varvec{\theta }})$ and ${\varvec{G}}(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})={\varvec{g}}(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})$. To be able to apply the Delta method to (6), the Jacobian of ${\varvec{g}}$ is required. Note that the kth component of ${\varvec{g}}({\varvec{z}})$, $k=a,\ldots ,b+1$, equals

$$\begin{aligned} g_k({\varvec{z}}) =\ \sum \limits _{l=0}^b\, a_{kl}\, \pi _k({\varvec{z}}_2)^{-1/2}\, \big (z_{1,l}-p_l({\varvec{z}}_2)\big ). \end{aligned}$$

So we obtain the partial derivatives

$$\begin{aligned} {\begin{array}{rl} \tfrac{\partial }{\partial z_{1,i}}\,g_k({\varvec{z}}) =&{} a_{ki}\, \pi _k({\varvec{z}}_2)^{-1/2} \qquad \text {for } i=0,\ldots ,b,\\ \tfrac{\partial }{\partial z_{2,j}}\,g_k({\varvec{z}})=&{} \displaystyle \mathop {\sum }\limits _{l=0}^b\, a_{kl}\, \Big (\big (z_{1,l}-p_l({\varvec{z}}_2)\big )\, \tfrac{\partial }{\partial z_{2,j}}\,\pi _k({\varvec{z}}_2)^{-1/2}\ -\ \pi _k({\varvec{z}}_2)^{-1/2}\, \tfrac{\partial }{\partial z_{2,j}}\,p_l({\varvec{z}}_2)\Big )\\ =&{} -\displaystyle \mathop {\sum }\limits _{l=0}^b\, \tfrac{a_{kl}}{2}\,\big (z_{1,l}-p_l({\varvec{z}}_2)\big )\,\pi _k({\varvec{z}}_2)^{-3/2}\, \displaystyle \mathop {\sum }\limits _{m=0}^b a_{km}\,\tfrac{\partial }{\partial z_{2,j}}\,p_m({\varvec{z}}_2)\\ &{}-\displaystyle \mathop {\sum }\limits _{l=0}^b\, a_{kl}\,\pi _k({\varvec{z}}_2)^{-1/2}\, \tfrac{\partial }{\partial z_{2,j}}\,p_l({\varvec{z}}_2) \qquad \text {for } j=1,\ldots ,r. \end{array} } \end{aligned}$$

In the specified-parameter case, we evaluate the reduced Jacobian

$$\begin{aligned} {\mathbf{J }}_{{\varvec{g}}}({\varvec{z}}_1) =\ \big (\tfrac{\partial }{\partial z_{1,i}}\,g_k({\varvec{z}}_1,{\varvec{\theta }})\big ){}_{k=a,\ldots ,b+1,\ i=0,\ldots ,b} \end{aligned}$$

in ${\varvec{p}}$. Together with (7), this leads to

$$\begin{aligned} \sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},{\varvec{\theta }})\ \xrightarrow {D}\ {\text{ N }}\Big ({\varvec{0}}, {\mathbf{D }}_{\text{ kn }}{\varvec{\varSigma }}^{({\varvec{p}})}{\mathbf{D }}_{\text{ kn }}^{\top }\Big ) \quad \text {with } {\mathbf{D }}_{\text{ kn }} =\ \text{ diag }\Big ({\varvec{\pi }}({\varvec{\theta }})^{-1/2}\Big )\,{\mathbf{A }}. \end{aligned}$$

(12)

Here, ${\varvec{\pi }}({\varvec{\theta }})^{-1/2}$ is computed by applying “${}^{-1/2}$” (i. e., $1/\sqrt{\cdot }$) separately in each component of ${\varvec{\pi }}({\varvec{\theta }})$.

In the estimated-parameter case, we evaluate the full Jacobian

$$\begin{aligned} {\mathbf{J }}_{{\varvec{g}}}({\varvec{z}}) =\ \big (\tfrac{\partial }{\partial z_{l}}\,g_k({\varvec{z}})\big ){}_{k=a,\ldots ,b+1,\ l=0,\ldots ,b+r} \end{aligned}$$

in $({\varvec{p}},{\varvec{\theta }})$. Denoting the Jacobian of ${\varvec{p}}({\varvec{z}}_2)$ by ${\mathbf{J }}_{{\varvec{p}}}({\varvec{z}}_2)$, we obtain together with (6) that

$$\begin{aligned} \sqrt{T}\,{\varvec{G}}(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})\ \xrightarrow {D}\ {\text{ N }}\Big ({\varvec{0}}, {\mathbf{D }}_{\text{ est }}{\varvec{\varSigma }}^*{\mathbf{D }}_{\text{ est }}^{\top }\Big ) \quad \text {with } {\mathbf{D }}_{\text{ est }} =\ \Big ({\mathbf{D }}_{\text{ kn }},\ -{\mathbf{D }}_{\text{ kn }}\,{\mathbf{J }}_{{\varvec{p}}}({\varvec{\theta }})\Big ) \end{aligned}$$

(13)

being a block matrix. Let us illustrate the computation of ${\mathbf{J }}_{{\varvec{p}}}({\varvec{\theta }})$ and hence ${\mathbf{D }}_{\text{ est }}$ with some common types of hypothetical marginal distribution.

Example 2.4.1

(Poisson Marginal) If the hypothetical marginal distribution is a Poisson one, i. e., $X_t\sim {\text{ Poi }}(\mu )$ with $p_i(\mu )=e^{-\mu }\,\mu ^i/i!$, like for the Poisson INAR models in Examples 2.3.3, 2.3.6 and Appendix A.2, then the Jacobian ${\mathbf{J }}_{{\varvec{p}}}$ is easily computed:

$$\begin{aligned} \tfrac{\partial }{\partial \mu }\,p_i(\mu ) =\,\ e^{-\mu }\,\frac{\mu ^{i-1}}{(i-1)!}-e^{-\mu }\,\frac{\mu ^i}{i!} =\,\ p_{i-1}(\mu )-p_i(\mu ), \end{aligned}$$

which also holds for $i=0$ with the convention $p_{j}(\mu )=0$ for $j<0$.

Example 2.4.2

(Binomial Marginal) If the hypothetical marginal distribution is a binomial one, i. e., $X_t\sim {\text{ Bin }}(n,\pi )$, i. e., $p_{n,i}(\pi )=\left( {\begin{array}{c}n\\ i\end{array}}\right) \,\pi ^i\,(1-\pi )^{n-i}$, like for the binomial AR(1) model in Example 2.3.4 and Appendix A.3, then again the Jacobian ${\mathbf{J }}_{{\varvec{p}}}$ is easily computed:

$$\begin{aligned} \begin{array}{rl} \tfrac{\partial }{\partial \pi }\,p_{n,i}(\pi ) =&{} i\,\left( {\begin{array}{c}n\\ i\end{array}}\right) \,\pi ^{i-1}\,(1-\pi )^{n-i}-(n-i)\,\left( {\begin{array}{c}n\\ i\end{array}}\right) \, \pi ^i\,(1-\pi )^{n-i-1}\\ =&{} n\,\big (p_{n-1,i-1}(\pi )-p_{n-1,i} (\pi )\big ), \end{array} \end{aligned}$$

which also holds for $i=0,n$ as well as $n=1$ with the conventions $p_{0,0}(\pi )=1$ and $p_{m,j}(\pi )=0$ for $j<0$ or $j>m$.

Example 2.4.3

(Geometric Marginal) If the hypothetical marginal distribution is the geometric distribution ${\text{ Geom }}(\pi )$, i. e., $p_i(\pi )=\pi \,(1-\pi )^i$, like for the geometric INAR(1) model in Example 2.3.5 and Appendix A.2, then the Jacobian ${\mathbf{J }}_{{\varvec{p}}}$ is computed by using

$$\begin{aligned} \tfrac{\partial }{\partial \pi }\,p_i(\pi ) =\ (1-\pi )^i - i\,\pi \,(1-\pi )^{i-1} =\ \tfrac{1}{\pi }\,p_i(\pi )-i\,p_{i-1}(\pi ), \end{aligned}$$

which also holds for $i=0$ with the convention $p_{j}(\pi )=0$ for $j<0$.

As the final step, we apply Theorem 3.1 in Tan (1977) to (12) and (13) to obtain the asymptotic distribution of Pearson’s goodness-of-fit test statistic (4) in both scenarios. This is a quadratic-form distribution, i. e., the distribution of an expression of the form $\sum _{i=1}^u \lambda _i\,Z_i^2$ with $Z_1,\ldots ,Z_r$ being i. i. d. ${\text{ N }}(0,1)$-variates [also see Moore (1982)]. In the specified-parameter case, it holds that

$$\begin{aligned} G^2(\hat{{\varvec{p}}},{\varvec{\theta }})\ \xrightarrow {D}\ \sum \limits _{i=1}^u\,\lambda _i\,Z_i^2, \end{aligned}$$

(14)

where $\lambda _1,\ldots ,\lambda _u$ are the non-zero eigenvalues of ${\mathbf{D }}_{\text{ kn }}{\varvec{\varSigma }}^{({\varvec{p}})}{\mathbf{D }}_{\text{ kn }}^{\top }$ according to (12). Note that in the particular case of a binomial AR(1) process (Example 2.3.4 and Appendix A.3), the asymptotic distribution in (14) can also be computed according to the approach of Kim and Weiß (2015).

In the estimated-parameter case, it holds that

$$\begin{aligned} G^2(\hat{{\varvec{p}}},\hat{{\varvec{\theta }}})\ \xrightarrow {D}\ \sum \limits _{j=1}^v\,\lambda _j^*\,Z_j^2, \end{aligned}$$

(15)

where $\lambda _1^*,\ldots ,\lambda _v^*$ are the non-zero eigenvalues of ${\mathbf{D }}_{\text{ est }}{\varvec{\varSigma }}^*{\mathbf{D }}_{\text{ est }}^{\top }$ according to (13).

To evaluate such quadratic-form distributions, the R package CompQuadForm (Duchesne and Micheaux 2010) can be used, e. g., the functions davies or imhof. This is also done in the next Sect. 3, where we investigate the asymptotic distributions (14) and (15) from various viewpoints. Before doing this, we conclude with a brief remark concerning the NDARMA models from Example 2.3.7.

Example 2.4.4

(NDARMA Model) Since the involved covariance matrices of an NDARMA(p, q) process differ from those of the i. i. d. case only by the unique factor c as defined in Example 2.3.7, goodness-of-fit testing based on NDARMA processes, with or without estimated parameters, is done by computing the respective critical values for the i. i. d. case and by multiplying them by c, also see Weiß (2013).

3 Computations and simulations

In the sequel, some results from a simulation study are presented to demonstrate the goodness of the asymptotic approximations (14) and (15) to the Pearson statistic’s distribution, and to illustrate the application of the Pearson test in practice.

3.1 Finite-sample performance of asymptotic approximations

Since the above approach concerning the distribution of Pearson’s goodness-of-fit test statistic (4) relies on asymptotic results for sample size $T\rightarrow \infty$, the first question to be analyzed is the one about the performance of the resulting approximation for time series of finite length T. For this purpose, diverse types of count process were simulated (always with 10,000 replications), the Pearson statistics with specified or estimated parameters, respectively, were computed, and empirical properties of the resulting samples are now compared to the corresponding asymptotic properties according to (14) or (15), respectively.

Table 1 Quantiles of Pearson statistic (estimated parameters) for binomial AR(1) process: asymptotic versus simulated values, where the latter are taken from Table 1 in Kim and Weiß (2015)

Our first comparison refers to Kim and Weiß (2015), who derived the asymptotic distribution of the Pearson statistic for the special case of a binomial AR(1) process (Example 2.3.4 and Appendix A.3) with specified parameters. In the last four lines of their Table 1, however, Kim and Weiß (2015) gave simulated values of the quantiles $q_{0.25},q_{0.50},q_{0.75},q_{0.95},q_{0.99}$ also for the case of estimating the binomial parameter $\pi$ by $\hat{\pi }:= \bar{X}/n$. With the novel approach derived in this paper, see Example 2.3.4, we are able to also compute these quantiles asymptotically. This is shown in Table 1, where we see a rather good agreement between the asymptotic and the simulated quantiles, although the sample size $T=70$ is rather small in a time series context.

Table 2 Mean, standard deviation and quantiles of Pearson statistic for Poisson INAR(1) process with $\mu =3$: asymptotic versus simulated values

Table 3 Mean, standard deviation and quantiles of Pearson statistic for geometric INAR(1) process with $\mu =3$: asymptotic versus simulated values

Table 4 Mean, standard deviation and quantiles of Pearson statistic for Poisson INAR(2) process with $\mu =3$: asymptotic versus simulated values

Next, we check the finite-sample performance for a number of count models with an unbounded range: the Poisson INAR(1) model (Example 2.3.3 and Appendix A.2) as a first-order model satisfying the property “SYM”, the geometric INAR(1) model (Example 2.3.5 and Appendix A.2) as a first-order model violating the property “SYM”, and the Poisson INAR(2) model (Example A.2.2 and Appendix A.2) as a second-order model satisfying the property “SYM”. In each case, the design parameters were chosen such that Cochran’s rule is satisfied, i. e., the expected count per category is $\ge 5$. For each of these models, selected results are shown in Tables 2, 3 and 4 for illustration; further results can be obtained from the author upon request.

The results in Tables 2, 3 and 4 show a rather good agreement between the asymptotic approximation and the simulated values of mean, standard deviation as well as the quantiles $q_{0.25},\ldots ,q_{0.99}$ throughout, with slightly increasing discrepancy for increasing autocorrelation level. This agreement is better in the estimated-parameter case, which is more relevant for practice anyway.

Fig. 1

Critical values (asymptotic approximation) with respect to Poisson or geometric marginal distribution having mean $\mu =3$, sample size $T=200$, see Sect. 3.2

3.2 Approximate critical values

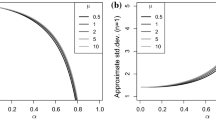
After having demonstrated the goodness of the asymptotic approximation, let us next investigate the resulting (asymptotic) critical values in more detail, as they are required for applying the Pearson test. The graphs in Fig. 1 show the critical values (level 5%) for the Pearson statistic based on a time series of length $T=200$, which stems from either a Poisson INAR(1), a geometric INAR(1), or a Poisson INAR(2) process. All processes have the marginal mean $\mu =3$, and the INAR(2) process satisfies $\alpha _1=\alpha , \alpha _2=0.2$. In view of Cochran’s rule, we have two further categories for the geometric marginal distribution.

The respective solid graphs in Fig. 1 show the critical values for the case of specified parameters, while the dashed graphs refer to the estimated-parameter case. Like in the i. i. d. case, we have smaller critical values if the parameters have to be estimated; so ignoring the fact of estimated parameters (just plugging-in estimates instead of true parameter values) would lead to a (very) conservative test procedure. Furthermore, the critical values increase (without bound) with increasing dependence parameter $\alpha$ (note the analogous result in Moore (1982) for a fully-specified Gaussian AR(1) process). So if one would apply the i. i. d.-asymptotics to serially dependent data, the test performance would be severely deteriorated. Finally, comparing the graphs for the Poisson INAR models, we see that the additional dependence caused by $\alpha _2=0.2$ leads to a further increase of the critical values.

3.3 Size and power in practice

Finally, we investigate the size and power of the Pearson test if applied in practice: since parameter values are usually not known, they have to be estimated from the available time series, and parameter estimates are also required for evaluating the asymptotic approximations (“plug-in approach”). The presented results rely on simulations (again with 10,000 replications), with $\mu$ being estimated by the arithmetic mean, and with $\alpha$ or $\alpha _1,\alpha _2$, respectively, being estimated from the sample autocorrelation function.

Table 5 Simulated size of Pearson test (level 5%) for Poisson INAR(1), Poisson INAR(2) (also if underfitted by Poisson INAR(1)), and geometric INAR(1) process; all having mean $\mu =3$

Table 5 shows the simulated sizes for diverse models if the Pearson tests are designed by assuming the level 5%. For the Poisson INAR(2) model as a data-generating process (DGP), also the robustness w.r.t. to a misspecification of the autoregressive order was investigated: the model order was chosen too small, i. e., the test design was done by falsely assuming a Poisson INAR(1) process. For the correctly specified model types and orders (but always with estimated parameters), the simulated sizes are very close to the nominal level of 5%. An exception is the scenario $\alpha =0.75$ and $T=200$ (strong autocorrelation), where somes sizes are slightly too large. More discrepancy is observed if the Poisson INAR(2) DGP is underfitted, so the model order should not be chosen too small in practice. Later in this section, we also analyze the effect of an overfitting as well as of misspecifying the model type.

Table 6 Simulated size of Pearson test (level 5%) for Poisson INAR(1) process ($I=1$), and simulated power for NB-INAR(1) process ($I>1$) or Poisson INARCH(1) process, respectively; all having mean $\mu =3$

Next, let us investigate the power of the Pearson test. If the test assumes Poisson INAR(1) but the data are generated by a geometric INAR(1) process (having the same mean and ACF), or vice versa, the power was equal to 1.000 in nearly any case (therefore, these values are not tabulated here). So such kind of alternative scenario is nearly always detected. More refined alternative scenarios are analyzed in Table 6. There, the Pearson test assumed a Poisson INAR(1) model, but if a value larger than 1 is given for the index of dispersion, $I=\sigma ^2/\mu$, then the true DGP was a negative binomial (NB) INAR(1) process. More precisely, the innovations $(\epsilon _t)$ are NB-distributed in such a way that the observations exhibit the given values of $\mu$, I and $\rho (1)$. It can be seen that the power increases with increasing I, and the increase is faster for larger sample sizes T, as expected. In applications, however, one has to be aware of the fact that the power of detection becomes worse with an increasing level of autocorrelation. Our conclusions slightly differ for the second power scenario considered in Table 6: there, the DGP was a Poisson INARCH(1) process (see Remark 2.3.8), which shows increasing overdispersion with increasing autocorrelation level (we have the relation $I=1/\big (1-\rho (1)^2\big )$). Thus, it is plausible that now the power improves with increasing autocorrelation.

Table 7 Simulated size and power of Pearson test (level 5%) for i. i. d. Poisson ($I=1$) and i. i. d. NB counts ($I>1$), respectively. Left part: correctly specified i. i. d. model; right part: overfitted INAR(1) model

Table 8 Simulated size and power of Pearson test (level 5%) for Poisson INAR(1) process ($I=1$) and NB-INAR(1) process ($I>1$), respectively; all having mean $\mu =3$. Left part: correctly specified INAR(1) model; right part: overfitted INAR(2) model

Let us now return to the discussion of Table 5. There, we observed that an underfitting of the actual DGP is problematic and may lead to considerably increased sizes. So it is natural to ask for the effect of overfitting the model order instead. Table 7 provides results if an i. i. d. DGP (“model order 0”) is overfitted by an INAR(1) model, and Table 8 if an INAR(1) DGP is overfitted by an INAR(2) model. It can be seen that the effect on size and power is very small, sometimes these values are slightly reduced if the model order is unnecessarily large. But the amount of reduction does not appear to be of practical relevance. So an overfitting of the DGP is substantially less problematic than an underfitting. Thus, we conclude that in practice, one should better choose a somewhat larger model order in case of doubt.

Table 9 Simulated size of Pearson test (level 5%) under model misspecification: true DGP Poisson INMA(1), but test assumes Poisson INAR(1) (left table); true DGP geometric AR(1) using either negative-binomial thinning (“NT-AR(1)”) or iterated thinning (“IT-AR(1)”), but test assumes geometric INAR(1) (right table); all having mean $\mu =3$

The previous robustness study allowed for a misspecification of the model order, but it assumed that the model family was chosen correctly. So finally, we also consider the case where the model type is misspecified, see Table 9. The considered types of misspecification are chosen such that in practice, there is a large risk of choosing the wrong model: the marginal distribution of the DGP is the same as that of the wrong model, and also the autocorrelation structure is very similar or even identical. In the left part of Table 9, the DGP is Poisson INMA(1), so it has a Poisson marginal distribution, and its autocorrelation structure might be confused with the one of a Poisson INAR(1) process. In the right part of Table 9, two types of DGP having a geometric marginal distribution and an AR(1)-like ACF are chosen (and confused with the geometric INAR(1) model): the geometric AR(1) process proposed by Ristić et al. (2009) is defined by an INAR(1)-like recursion but using negative-binomial thinning instead of binomial thinning (hence we abbreviate it as “NT-AR(1)” in Table 9), the one proposed by Al-Osh and Aly (1992) uses some kind of “iterated thinning” (“IT-AR(1)”), where first a binomial thinning and then a negative binomial thinning is applied at each time t. The sizes of the misspecified Poisson INAR(1) model in the left part of Table 9 are still very close to 5%, so erroneously treating the INMA(1) as INAR(1) data is not problematic. For the misspecified geometric INAR(1) models, the sizes become visibly smaller than 5% for large autocorrelation levels. So the Pearson test becomes conservative in these cases. On the other hand, for increasing autocorrelation, it is usually also more easy to distinguish between the different models, since then, e. g., sample paths or conditional variances are more pronounced.

Fig. 2

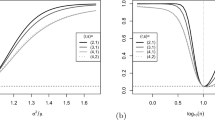
Time series plot and PACF plot (against lag k) of data examples from Sect. 3.4: a download counts, b counts of iceberg orders

3.4 Real-data examples

We conclude our investigations with two real-data examples. The count time series $x_1,\ldots ,x_T$ shown in Fig. 2a is taken from the book by Weiß (2018). It consists of the daily numbers of downloads of a tex editor for the period Jun. 2006 to Feb. 2007 (hence length $T=267$). As can be seen from the PACF plot, we are concerned with an AR(1)-like autocorrelation structure, with a rather low autocorrelation level: $\hat{\rho }(1)\approx 0.245$. The download counts have the mean $\approx 2.401$ and the large dispersion index $\approx 3.127$. In view of the autocorrelation structure, the INAR(1) family appears to be a plausible choice for the data, and in view of the strong degree of overdispersion, it appears plausible to test the null hypothesis of a geometric marginal distribution within this INAR(1) family (on level 5%).

The same null hypothesis is also to be tested for the second data example, plotted in Fig. 2b, which consists of $T=800$ counts of so-called iceberg orders concerning the Deutsche Telekom shares traded in the XETRA system of Deutsche Börse, measured every 20 minutes for 32 consecutive trading days in the first quarter of 2004 (Jung and Tremayne 2011). According to the plotted PACF, we again have an AR(1)-like autocorrelation structure, but now of larger extend ($\hat{\rho }(1)\approx 0.635$). Mean and dispersion index equal $\approx 1.406$ and $\approx 1.551$, respectively.

Fig. 3

Pmf plot (against count x) for data examples from Sect. 3.4: sample pmf (in black) and geometric pmf (in gray) for a download counts, b counts of iceberg orders

For the download counts, we estimate the parameter of the hypothetical geometric distribution as $\hat{\pi }\approx 0.294$. The Pearson statistic is computed for the nine categories defined by $a=0$ and $b=7$, and it takes the value $\approx 1.179$. The critical value obtained for the hypothetical geometric INAR(1) model equals $\approx 14.504$ such that we cannot reject the null hypothesis. In fact, looking at Fig. 3a, where the sample pmf (black) is compared to the pmf of ${\text{ Geom }}(\hat{\pi })$ (gray), we see a rather good agreement. It should also be noted that the critical value under an i. i. d.-assumption would only be slightly smaller than the above critical value: $\approx 14.067$ (95% quantile of $\chi _{9-1-1}^2$-distribution). This small discrepancy is plausible in view of Fig. 1, where the critical values show a small slope for low values of $\alpha$ (here, we have $\hat{\alpha }\approx 0.245$).

Things differ for the second data example. The estimated geometric parameter equals $\hat{\pi }\approx 0.416$, so we choose the same categorization as before ($a=0$, $b=7$) and, thus, obtain the same critical value under an i. i. d.-assumption: $\approx 14.067$. The critical value for the hypothetical geometric INAR(1) model is now much larger, $\approx 21.106$, which is confirmed by Fig. 1 and the rather large estimate $\hat{\alpha }\approx 0.635$. The Pearson statistic, however, becomes even larger, $\approx 67.286$, so this time, we have to reject the null of a geometric marginal distribution. Considering the pmf plots in Fig. 3b, this decision appears plausible as both pmfs deviate visibly from each other, especially for low counts $x\le 2$.

4 Discussion

If Pearson’s goodness-of-fit test statistic is applied to data stemming from a count process, its distribution can be asymptotically approximated with the help of a quadratic-form distribution. The specific distribution can be explicitly computed for a number of practically relevant count process models. The approach does not only cover the situation where the null model is fully specified, but also where parameters have to be estimated. The simulation study showed that the obtained asymptotic approximation works rather well for time series of finite length, and that the test can be successfully applied in practice to uncover model violations. Also the effect of different types of model misspecification was investigated. It turned out that an overfitting was clearly less problematic than an underfitting, so the model order should not be chosen too small. Also cases of misspecifying the model type have been analyzed, where the test’s performance is affected especially for large autocorrelation levels. So careful model selection is recommended before applying the test to the given count time series.

For future research, it would be interesting to analyze how to best choose the categories (1) for the Pearson statistic such that the asymptotic approximation works well and we obtain an optimal power; in this work, we used the popular Cochran’s rule for simplicity. Another research direction could be to investigate if and how the presented approach applies to the family of scaled Bregman divergences (Kißlinger and Stummer 2016). In view of Remark 2.3.8, an important question would be to analyze if a Pearson-like test could also be developed for the conditional distribution of a count process, since many important count time series models, like INGARCH and regression models, are defined by specifying the conditional distribution. Finally, returning to the possible problem of a model misspecification, it would be desirable for practice to have a nonparametric way of estimating the covariance matrices ${\varvec{\varSigma }}^{({\varvec{p}})},{\varvec{\varSigma }}^*$ involved in computing the Pearson statistic’s asymptotics. In this context, the Editor pointed out the work by Francq and Zakoïan (2013), where the estimation of the parameter vector (say, ${\varvec{\theta }}$) for a time series’ marginal distribution is considered. In addition, a nonparametric estimator for $\hat{\varvec{\theta }}$’s covariance matrix is developed. For future research, it should be tried to develop an analogous approach for nonparametrically estimating ${\varvec{\varSigma }}^{({\varvec{p}})},{\varvec{\varSigma }}^*$.

Appendices

Specific models for count processes

The subsequent models are used in the main part of this article to illustrate the derivation of the asymptotic distributions of the considered goodness-of-fit tests.

1.1 CLAR(1) model

Many important models for count Markov chains belong to the class of conditional linear autoregressive models of order one (CLAR(1) models) as discussed by Grunwald et al. (2000). The homogeneous count Markov chain $(X_t)_{\mathbb {Z}}$ is said to have CLAR(1) structure if the conditional mean of $X_t$ is linear in $X_{t-1}$, i. e., if

$$\begin{aligned} E[X_t\ |\ X_{t-1}] =\ \alpha \cdot X_{t-1} + \beta \qquad \text {for some } \alpha \in \mathbb {R}\text { and } \beta >0. \end{aligned}$$

(A.1)

The condition $|\alpha |<1$ guarantees a finite stationary mean given by $\mu :=E[X_t]=\beta /(1-\alpha )$. If also the stationary variance of $X_t$ is finite, i. e., $\sigma ^2:=V[X_t]<\infty$, then the autocorrelation function (ACF) is of AR(1)-type, i. e., it altogether holds that

$$\begin{aligned} \rho (h):=Corr[X_t,X_{t-h}] =\ \alpha ^h,\qquad E[X_t\ |\ X_{t-h}]\ =\ \alpha ^h\cdot X_{t-h} + (1-\alpha ^h)\,\mu . \end{aligned}$$

(A.2)

1.2 INAR models

If X is a discrete random variable with range $\mathbb {N}_0$ and if $\alpha \in (0;1)$, then the random variable $\alpha \circ X := \sum _{i=1}^{X} Z_i$ is said to arise from X by binomial thinning (Steutel and Harn 1979). Here, the $Z_i$ are i. i. d. binary random variables with $P(Z_i=1)=\alpha$, which are also independent of X. Hence, $\alpha \circ X$ has a conditional binomial distribution given the value of X, i. e., $\alpha \circ X|X\ \sim {\text{ Bin }}(X,\alpha )$. The boundary values $\alpha =0$ and $\alpha =1$ might be included into this definition by setting $0\circ X := 0$ and $1\circ X := X$.

Using the random operator “$\circ$”, McKenzie (1985) defined the INAR(1) model in the following way.

Definition A.2.1

(INAR(1) Model) Let the innovations$(\epsilon _t)_{\mathbb {Z}}$ be an i. i. d. process with range $\mathbb {N}_0$, denote $E[\epsilon _t]=\mu _{\epsilon }$, $V[\epsilon _t]=\sigma _{\epsilon }^2$. Let $\alpha \in (0;1)$. A process $(X_t)_{\mathbb {Z}}$ of observations, which follows the recursion

$$\begin{aligned} X_t =\ \alpha \circ X_{t-1}\ +\ \epsilon _t, \end{aligned}$$

is said to be an INAR(1) process if all thinning operations are performed independently of each other and of $(\epsilon _t)_{\mathbb {Z}}$, and if the thinning operations at each time t as well as $\epsilon _t$ are independent of $(X_s)_{s<t}$.

The most popular instance of the INAR(1) family is the Poisson INAR(1) model (McKenzie 1985), which assumes the innovations $(\epsilon _t)_{\mathbb {Z}}$ to be i. i. d. according to the Poisson distribution ${\text{ Poi }}(\lambda )$. A Poisson INAR(1) process is an irreducible and aperiodic Markov chain with a unique stationary marginal distribution for $(X_t)_{\mathbb {Z}}$, the Poisson distribution ${\text{ Poi }}(\mu )$ with $\mu =\frac{\lambda }{1-\alpha }$. It is also $\alpha$-mixing with geometrically decreasing weights (Schweer and Weiß 2014). Furthermore, the Poisson INAR(1) model constitutes the only instance within the INAR(1) family, which is time reversible (McKenzie 1985; Schweer 2015).

The (Poisson) INAR(1) model belongs to the class of CLAR(1) models, so it satisfies (A.2). The h-step-ahead transition probabilities are given by (Freeland and McCabe 2004)

$$\begin{aligned} p_{i|j}^{(h)} =\ \sum \limits _{m=0}^{\min {\{i,j\}}}\ \left( {\begin{array}{c}j\\ m\end{array}}\right) \alpha ^{h\,m}\,(1-\alpha ^h)^{j-m}\cdot e^{-\mu \,(1-\alpha ^h)}\,\frac{\big (\mu \,(1-\alpha ^h)\big )^{i-m}}{(i-m)!}, \end{aligned}$$

(A.3)

and $(X_t,X_{t-h})$ are bivariately Poisson distributed (Johnson et al. 1997) according to ${\text{ BPoi }}\big (\alpha ^h\,\mu ;\ (1-\alpha ^h)\,\mu , (1-\alpha ^h)\,\mu \big )$ (Alzaid and Al-Osh 1988). Here, ${\text{ BPoi }}(\lambda _0;\ \lambda _1, \lambda _2)$ refers to the joint distribution of $(Y_0+Y_1, Y_0+Y_2)^{\top }$ with independent Poisson variates $Y_i\sim {\text{ Poi }}(\lambda _i)$ for $i=0,1,2$.

A simple example of an INAR(1) process not being time reversible is the geometric INAR(1) process (McKenzie 1985, 1986), which has marginal distribution ${\text{ Geom }}(\pi )$, i. e., $P(X_t=x)=\pi \,(1-\pi )^x$. Here, the innovations stem from a zero-inflated geometric distribution,

$$\begin{aligned} \epsilon _t :=\ B_t\,G_t \qquad \text {with independent } B_t\sim {\text{ Bin }}(1,1-\alpha ),\ G_t\sim {\text{ Geom }}(\pi ), \end{aligned}$$

(A.4)

with pmf $P(\epsilon =x) = \delta _{x,0}\,\alpha + (1-\alpha )\,\pi \,(1-\pi )^x$. Hence, the 1-step-ahead transition probabilities are computed as

$$\begin{aligned} p_{i|j} =\ \sum \limits _{m=0}^{\min {\{i,j\}}}\ \left( {\begin{array}{c}j\\ m\end{array}}\right) \alpha ^{m}\,(1-\alpha )^{j-m}\cdot P(\epsilon =i-m). \end{aligned}$$

(A.5)

It is also possible to obtain any other member of the family of negative binomial distributions as a marginal distribution by choosing an appropritae innovations’ distribution, see McKenzie (1986) for details.

It is also possible to extend the INAR(1) recursion in Definition A.2.1 to a pth-order autoregression of the form

$$\begin{aligned} X_t =\ \alpha _1\circ X_{t-1}\ +\cdots +\ \alpha _p\circ X_{t-p}\ +\ \epsilon _t \qquad \text {with } \alpha _{\bullet }:=\sum \limits _{j=1}^p \alpha _j\ <1. \end{aligned}$$

(A.6)

Due to the stochastic nature of the thinnings involved in (A.6), however, additional assumptions concerning the thinnings $(\alpha _1\circ X_{t},\ldots , \alpha _p\circ X_{t})$ are required. While the INAR(p) model by Du and Li (1991) assumes the conditional independence of $(\alpha _1\circ X_{t},\ldots , \alpha _p\circ X_{t})$ given $X_t$, the one by Alzaid and Al-Osh (1990) supposes a conditional multinomial distribution. As shown by Schweer (2015), only the latter model continues the INAR(1)’s property that we have time reversibility exactly in the case of Poisson innovations (then also the observations are Poisson-distributed), while the INAR(p) model by Du and Li (1991) is neither time reversible nor does it have Poisson marginals. For this reason, we shall focus here on the time reversible Poisson INAR(p) model according to Alzaid and Al-Osh (1990), where the innovations are i. i. d. ${\text{ Poi }}(\lambda )$ and, hence, the observations have the stationary marginal distribution ${\text{ Poi }}(\mu )$ with $\mu =\lambda /(1-\alpha _{\bullet })$.

Example A.2.2

(Poisson INAR(2) Model) Solving the Yule–Walker-type equations (3.6) and (3.8) in Alzaid and Al-Osh (1990), the ACF of the Poisson INAR(2) model becomes

$$\begin{aligned} \rho (1)\,=\,\alpha _1,\qquad \rho (h) =\ \alpha _1\,\rho (h-1)\,+\,\alpha _2\,\rho (h-2)\quad \text {for } h\ge 2. \end{aligned}$$

As shown in Appendix B, the lagged observations $X_t$ and $X_{t-h}$ with $h\in \mathbb {N}$ are bivariately Poisson distributed,

$$\begin{aligned} (X_t,X_{t-h})\ \sim \ {\text{ BPoi }}\Big (\rho (h)\,\mu ;\ \big (1-\rho (h)\big )\,\mu ,\ \big (1-\rho (h)\big )\,\mu \Big ), \end{aligned}$$

with conditional mean $E[X_t\ |\ X_{t-h}]\, =\, \rho (h)\,X_{t-h}+\big (1-\rho (h)\big )\,\mu$.

1.3 Binomial AR(1) model

In many applications, it is known that the observed count data cannot become arbitrarily large, but their range has a natural upper bound $n\in \mathbb {N}$ that can never be exceeded. For the case of such time series of counts supported on $\{0,\ldots ,n\}$, McKenzie (1985) proposed the binomial AR(1) model.

Definition A.3.1

(Binomial AR(1) Model) Let $\rho \in \big (\max {\{-\frac{\pi }{1-\pi }, -\frac{1-\pi }{\pi }\}}\ ;\ 1\big )$ and $\pi \in (0;1)$. Define $\beta :=\pi \cdot (1-\rho )$ and $\alpha :=\beta +\rho$. Fix $n\in \mathbb {N}$. The process $(X_t)_{\mathbb {Z}}$, defined by the recursion

$$\begin{aligned} X_t =\ \alpha \circ X_{t-1}\ +\ \beta \circ (n-X_{t-1}), \end{aligned}$$

where all thinnings are performed independently of each other, and where the thinnings at time t are independent of $(X_s)_{s<t}$, is referred to as a binomial AR(1) process.

The condition on $\rho$ guarantees that the derived parameters $\alpha ,\beta$ satisfy $\alpha ,\beta \in (0;1)$, i. e., these parameters can indeed serve as thinning probabilities.

It is known that $(X_t)_{\mathbb {Z}}$ is a stationary, ergodic and $\phi$-mixing finite Markov chain (again with geometrically decreasing weights), the marginal distribution of which is ${\text{ Bin }}(n,\pi )$ (McKenzie 1985; Kim and Weiß 2015). The binomial AR(1) model belongs to the class of CLAR(1) models, so it satisfies (A.2), and it is time reversible (McKenzie 1985). The h-step-ahead transition probabilities are given by (Weiß and Pollett 2012)

$$\begin{aligned} p_{i|j}^{(h)} =\! \sum \limits _{m=\max {\{0,i+j-n\}}}^{\min {\{i,j\}}}\ \left( {\begin{array}{c}j\\ m\end{array}}\right) \ \left( {\begin{array}{c}n-j\\ i-m\end{array}}\right) \ \alpha _h^m (1-\alpha _h)^{j-m}\ \beta _h^{i-m} (1-\beta _h)^{n-j+m-i}, \end{aligned}$$

(A.7)

where $\beta _h:=\pi \cdot (1-\rho ^h)$ and $\alpha _h:=\beta _h +\rho ^h$.

1.4 NDARMA model for counts

The “new” discrete ARMA (NDARMA) models have been proposed by Jacobs and Lewis (1983). They generate an ARMA-like dependence structure through some kind of random mixture.

Definition A.4.1

(NDARMA Model for Counts) Let the observations $(X_t)_{\mathbb {Z}}$ and the innovations $(\epsilon _t)_{\mathbb {Z}}$ be count processes, where $(\epsilon _t)_{\mathbb {Z}}$ is i. i. d. with $P(\epsilon _t=i)=p_i$, and where $\epsilon _t$ is independent of $(X_s)_{s<t}$. The random mixture is obtained through the i. i. d. multinomial random vectors

$$\begin{aligned} (\alpha _{t,1},\ldots ,\alpha _{t,{\text{ p }}},\beta _{t,0},\ldots ,\beta _{t,{\text{ q }}}) \quad \sim \ {\text{ MULT }}(1;\ \phi _1, \ldots ,\phi _{{\text{ p }}},\varphi _0,\ldots ,\varphi _{{\text{ q }}}), \end{aligned}$$

which are independent of $(\epsilon _t)_{\mathbb {Z}}$ and of $(X_s)_{s<t}$. Then $(X_t)_{\mathbb {Z}}$ is said to be an NDARMA(p, q) process if it follows the recursion

$$\begin{aligned} X_t =\ \alpha _{t,1}\cdot X_{t-1}+\cdots +\alpha _{t,{\text{ p }}}\cdot X_{t-{\text{ p }}}\ +\ \beta _{t,0}\cdot \epsilon _{t}+\cdots +\beta _{t,{\text{ q }}}\cdot \epsilon _{t-{\text{ q }}}. \end{aligned}$$

The stationary marginal distribution of $X_t$ is identical to that of $\epsilon _{t}$, i. e., $P(X_t=i)=p_i=P(\epsilon _t=i)$, and we always have

$$\begin{aligned} p_{i|j}^{(h)} =\ p_i\cdot \big (1-\rho (h)\big )\ +\ \delta _{i,j}\cdot \rho (h). \end{aligned}$$

(A.8)

The autocorrelations are non-negative and can be determined from the Yule–Walker equations (Jacobs and Lewis 1983)

$$\begin{aligned} \rho (h) =\ \sum \limits _{j=1}^{{\text{ p }}}\ \phi _j\cdot \rho (|h-j|)\ +\ \sum \limits _{i=0}^{{\text{ q }}-h}\ \varphi _{i+h}\cdot r(i)\qquad \text {for } h\ge 1, \end{aligned}$$

where the r(i) satisfy

$$\begin{aligned} r(i) =\ \sum \limits _{j=\max {\{0,i-{\text{ p }}\}}}^{i-1}\ \phi _{i-j}\cdot r(j)\ +\ \varphi _i\,\mathbb {1}(0\le i\le {\text{ q }}), \end{aligned}$$

which implies $r(i)=0$ for $i<0$, and $r(0)=\varphi _0$. Mixing properties have been established by Weiß (2013).

Bivariate distributions of INAR(2) model

We pick up the derivations of Alzaid and Al-Osh (1990) and extend them to obtain the bivariate distribution of $X_t$ and $X_{t-h}$ for $h\in \mathbb {N}$. Let $(X_t)_{\mathbb {Z}}$ follow an INAR(2) model, where we first do not further specify the innovations’ distribution. Define the sequence of weights $(w_j)_{j\ge -1}$ by

$$\begin{aligned} w_{-1}=0,\quad w_0=1,\quad w_j =\ \alpha _1\,w_{j-1}+\alpha _2\,w_{j-2}\quad \text {for } j=1,2,\ldots , \end{aligned}$$

(B.1)

which satisfy $\sum _{j=0}^{\infty } w_j\,=\,1/(1-\alpha _{\bullet })$ (Alzaid and Al-Osh 1990 [p. 317]). Let us introduce a further sequence of coefficients $({\varvec{a}}_j)_{j\ge -1}$ with ${\varvec{a}}_j=(a_{j,1},a_{j,2})^{\top }$:

$$\begin{aligned} {\varvec{a}}_{-1}=(0,1)^{\top },\quad {\varvec{a}}_{0}=(1,0)^{\top },\quad {\varvec{a}}_j =\ \alpha _1\,{\varvec{a}}_{j-1}+\alpha _2\,{\varvec{a}}_{j-2}\quad \text {for } j=1,2,\ldots \end{aligned}$$

(B.2)

Obviously, the first components are identical to the weights (B.1), $a_{j,1}=w_j$ for all $j\ge -1$, while the second components satisfy $a_{j,2}=\alpha _2\,a_{j-1,1}=\alpha _2\,w_{j-1}$ for $j\ge 0$.

Following Alzaid and Al-Osh (1990), p. 320, we define the bivariate process $({\varvec{X}}_t)_{\mathbb {Z}}$ by ${\varvec{X}}_t=(X_t, \alpha _2\circ X_{t-1})^{\top }$, which is a Markov chain satisfying

$$\begin{aligned} { E\big [z_1^{X_{t,1}}\,z_2^{X_{t,2}}\ \big |\ {\varvec{X}}_{t-1},\ldots \big ] =\ {\text{ pgf }}_{\epsilon }(z_1)\,\big (1+\alpha _1\,(z_1-1)+\alpha _2\,(z_2-1)\big )^{X_ {t-1,1}}\,z_1^{X_{t-1,2}}. } \end{aligned}$$

(B.3)

In a first step, we extend this result to arbitrary time lags $h\in \mathbb {N}$. Using the coefficients (B.2), we rewrite (B.3) as

$$\begin{aligned}&E\Big [\big (1+a_{0,1}\,(z_1-1)+a_{0,2}\,(z_2-1)\big )^{X_{t,1}}\,\nonumber \\&\quad \big (1+a_{-1,1}\,(z_1-1)+a_{-1,2}\,(z_2-1)\big )^{X_{t,2}}\ \Big |\ {\varvec{X}}_{t-1},\ldots \Big ]\nonumber \\&\quad =\ {\text{ pgf }}_{\epsilon }\big (1+a_{0,1}\,(z_1-1)+a_{0,2}\,(z_2-1)\big )\nonumber \\&\qquad \cdot \big (1+a_{1,1}\,(z_1-1)+a_{1,2}\,(z_2-1)\big )^{X_{t-1,1}}\,\nonumber \\&\qquad \big (1+a_{0,1}\,(z_1-1)+a_{0,2}\,(z_2-1)\big )^{X_{t-1,2}}. \end{aligned}$$

(B.4)

Using the law of total expectation, we apply (B.4) and obtain

$$\begin{aligned}&E\big [z_1^{X_{t,1}}\,z_2^{X_{t,2}}\ \big |\ {\varvec{X}}_{t-h}\big ] =\ {\text{ pgf }}_{\epsilon } \quad \big (1+a_{0,1}\,(z_1-1)+a_{0,2}\,(z_2-1)\big )\nonumber \\&\quad \cdots E\Big [\big (1+a_{1,1}\,(z_1-1)+a_{1,2}\,(z_2-1)\big )^{X_{t-1,1}}\,\nonumber \\&\qquad \big (1+a_{0,1}\,(z_1-1)+a_{0,2}\,(z_2-1)\big )^{X_{t-1,2}}\ \Big |\ {\varvec{X}}_{t-h}\Big ]\nonumber \\&=\cdots =\ \prod _{j=0}^{h-1}\ {\text{ pgf }}_{\epsilon }\big (1+a_{j,1}\,(z_1-1)+a_{j,2}\,(z_2-1)\big )\nonumber \\&\qquad \cdot \big (1+a_{h,1}\,(z_1-1)+a_{h,2}\,(z_2-1)\big )^{X_{t-h,1}}\,\nonumber \\&\qquad \big (1+a_{h-1,1}\,(z_1-1)+a_{h-1,2}\,(z_2-1)\big )^{X_{t-h,2}}. \end{aligned}$$

(B.5)

On the one hand, this implies the marginal pgf as

$$\begin{aligned} \begin{array}{l} {\text{ pgf }}_{{\varvec{X}}}({\varvec{z}}) =\ \prod _{j=0}^{\infty }\ {\text{ pgf }}_{\epsilon }\big (1+w_j\,(z_1-1)+\alpha _2\,w_{j-1}\,(z_2-1)\big ),\\ {\text{ pgf }}_{X}(z) =\ {\text{ pgf }}_{{\varvec{X}}}(z,1) =\ \prod _{j=0}^{\infty }\ {\text{ pgf }}_{\epsilon }\big (1+w_j\,(z-1)\big ), \end{array} \end{aligned}$$

(B.6)

also see (4.4) and Theorem 2.1 in Alzaid and Al-Osh (1990). On the other hand, we compute from (B.5) the lagged bivariate pgf as

$$\begin{aligned}&{\text{ pgf }}_{{\varvec{X}}_t,{\varvec{X}}_{t-h}}({\varvec{z}},{\varvec{y}}) =\\&\prod _{j=0}^{h-1}\ {\text{ pgf }}_{\epsilon }\big (1+w_j\,(z_1-1)+\alpha _2\,w_{j-1}\,(z_2-1)\big )\cdot E\Big [y_1^{X_{t-h,1}}\,y_2^{X_{t-h,2}}\\&\qquad \cdot \big (1+w_{h}\,(z_1-1)+\alpha _2\,w_{h-1}\,(z_2-1)\big )^{X_{t-h,1}}\,\\&\qquad \big (1+w_{h-1}\,(z_1-1)+\alpha _2\,w_{h-2}\,(z_2-1)\big )^{X_{t-h,2}}\Big ]\\&=\ \prod _{j=0}^{h-1}\ {\text{ pgf }}_{\epsilon }\big (1+w_j\,(z_1-1)+\alpha _2\,w_{j-1}\,(z_2-1)\big )\\&\qquad \cdot {\text{ pgf }}_{{\varvec{X}}}\Big (y_1\,\big (1+w_{h}\,(z_1-1)+\alpha _2\,w_{h-1}\,(z_2-1)\big )\ ,\ \\&\qquad y_2\,\big (1+w_{h-1}\,(z_1-1)+\alpha _2\,w_{h-2}\,(z_2-1)\big )\Big ). \end{aligned}$$

This implies that

$$\begin{aligned} {\text{ pgf }}_{X_t,X_{t-h}}(z,y)= & {} {\text{ pgf }}_{{\varvec{X}}}\Big (y\,\big (1+w_{h}\,(z-1)\big )\ ,\ 1+w_{h-1}\,(z-1)\Big ) \, \nonumber \\&\quad \prod _{j=0}^{h-1} {\text{ pgf }}_{\epsilon }\big (1+w_j\,(z-1)\big ). \end{aligned}$$

(B.7)

Now, we turn to the special case of the Poisson INAR(2) model (Example A.2.2), i. e., where the innovations $(\epsilon _t)_{\mathbb {Z}}$ satisfy ${\text{ pgf }}_{\epsilon }(z)\,=\,\exp {\big (\lambda \,(z-1)\big )}$. Using that $\sum _{j=0}^{\infty } w_j\,=\,1/(1-\alpha _{\bullet })$ and that $\mu =\lambda /(1-\alpha _{\bullet })$, (B.6) simplifies to

$$\begin{aligned} {\text{ pgf }}_{{\varvec{X}}}({\varvec{z}}) =\ \exp {\Big (\mu \,\big ((z_1-1)+\alpha _2\,(z_2-1)\big )\Big )},\quad {\text{ pgf }}_{X}(z) =\ \exp {\big (\mu \,(z-1)\big )}, \end{aligned}$$

(B.8)

also see (5.1) in Alzaid and Al-Osh (1990). In particular, the stationary marginal distribution is ${\text{ Poi }}(\mu )$. The bivariate pgf (B.7) becomes

$$\begin{aligned}&{\text{ pgf }}_{X_t,X_{t-h}}(z,y) =\ \exp {\Big (\mu \,\big (y-1+w_{h}\,y\,(z-1)+\alpha _2\,w_{h-1}\,(z-1)\big )\Big )} \, \\&\quad \exp {\Big (\lambda \,(z-1)\,\mathop {\sum }\limits _{j=0}^{h-1} w_j\Big )}. \end{aligned}$$

This expression can be further simplified by considering (B.1). It follows that

$$\begin{aligned} (1-\alpha _{\bullet })\,\mathop {\sum }\limits _{j=0}^{h-1} w_j= & {} \mathop {\sum }\limits _{j=0}^{h-1} w_j\ -\ \alpha _2\,w_{h-1} - \alpha _1\,w_0 \\&- \mathop {\sum }\limits _{j=2}^h\, (\alpha _1\,w_{j-1}+\alpha _2\,w_{j-2})\\= & {} 1+\alpha _1+\mathop {\sum }\limits _{j=2}^{h-1} w_j\ -\ \alpha _2\,w_{h-1} - \alpha _1 - \mathop {\sum }\limits _{j=2}^h w_j\ \\= & {} 1 - \alpha _2\,w_{h-1} - w_h, \end{aligned}$$

so we continue

$$\begin{aligned} { \begin{array}{rl} {\text{ pgf }}_{X_t,X_{t-h}}(z,y) =&{} \exp {\Big (\mu \,\big (y-1\ +\ z-1\ +\ w_{h}\,(y-1)(z-1)\big )\Big )}\\ =&{} \exp {\Big (\mu \,\big ((1-w_h)\,(y-1)\ +\ (1-w_h)\,(z-1)\ +\ w_{h}\,(yz-1)\big )\Big )}. \end{array} } \end{aligned}$$

(B.9)

Obviously, this pgf is symmetric in z and y, confirming the time reversibility. For $h=1$, it simplifies to (5.3) in Alzaid and Al-Osh (1990). In particular, (B.9) shows that $(X_t,X_{t-h})$ are bivariately Poisson distributed according to ${\text{ BPoi }}\big (w_h\,\mu ;\ (1-w_h)\,\mu , (1-w_h)\,\mu \big )$, see Johnson et al. (1997). This implies the conditional mean

$$\begin{aligned} E[X_t\ |\ X_{t-h}]\ =\ w_h\,X_{t-h}+(1-w_h)\,\mu . \end{aligned}$$

The proof of Example A.2.2 is completed by noting that the weights in (B.1) follow the same recursion as the ACF of the Poisson INAR(2) model, so $w_h=\rho (h)$ for $h\ge 0$ in this special case.