Testing the dispersion structure of count time series using Pearson residuals

Abstract

Pearson residuals are a widely used tool for model diagnostics of count time series. Despite their popularity, little is known about their distribution such that statistical inference is problematic. Squared Pearson residuals are considered for testing the conditional dispersion structure of the given count time series. For two popular types of Markov count processes, an asymptotic approximation for the distribution of the test statistics is derived. The performance of the novel tests is analyzed and compared to relevant competitors. Illustrative data examples are presented, and possible extensions of our approach are discussed.

1 Introduction

The analysis and modeling of count time series, i.e., of quantitative time series having the range $\mathbb {N}_0=\{0,1,\ldots \}$, has become a popular area in research and applications; see the books by Davis et al. (2016) and Weiß (2018). An important step during model fitting is diagnostic checks with regard to the considered candidate model, to find out, e.g., a possible misspecification of the model order or the dispersion structure. In the present paper, we are concerned with the latter task, i.e., the aim is to detect a misfit of the (conditional) variance of the actual data-generating process (DGP) $(X_t)_{\mathbb {Z}}$. In this context, we speak about overdispersion (underdispersion) if the DGP has more (less) variance than captured by the fitted model. If concentrating on the marginal dispersion of a stationary DGP, the use of an appropriate type of dispersion index is quite common among practitioners. For example, to check for a marginal equidispersion, Fisher’s dispersion index might be used, which is defined as the quotient of the (sample) variance to the mean, i.e., as $I=\sigma ^2/\mu$ or $\hat{I}=S^2/\bar{X}$, respectively. The distribution of $\hat{I}$ for count time series data was analyzed by Schweer and Weiß (2014), among other works.

If also considering the conditional dispersion structure, statistics based on the (standardized) Pearson residuals appear as a reasonable choice (Harvey and Fernandes 1989; Czado et al. 2009; Jung and Tremayne 2011; Jung et al. 2016; Weiß 2018). Let the candidate model (depending on some parameter vector ${\varvec{\theta }}\in \mathbb {R}^m$) have the conditional mean $E[X_t\ |\ X_{t-1},\ldots ;\ {\varvec{\theta }}]$ and variance $V[X_t\ |\ X_{t-1},\ldots ;\ {\varvec{\theta }}]$. Inserting the estimated parameter $\hat{{\varvec{\theta }}}$ into these functions of ${\varvec{\theta }}$, the Pearson residuals are defined as

$$\begin{aligned} R_t:=R_t(\hat{{\varvec{\theta }}})\ =\ \frac{X_t-E\big [X_t\ |\ X_{t-1},\ldots ;\ \hat{{\varvec{\theta }}}\big ]}{\sqrt{V\big [X_t\ |\ X_{t-1},\ldots ;\ \hat{{\varvec{\theta }}}\big ]}}. \end{aligned}$$

(1)

Note that these residuals are computed from the same set of data that was used for parameter estimation.

Assuming that the type of candidate model was chosen adequately, the “true” Pearson residuals $R_t({\varvec{\theta }})$ have mean 0, variance 1, and they are serially uncorrelated. So it is natural to also analyze the estimated Pearson residuals $R_t(\hat{{\varvec{\theta }}})$ for these properties. For example, Harvey and Fernandes (1989) suggest to “check on whether the sample variance of the residuals is close to 1. A value greater than 1 indicates overdispersion relative to the model that is being fitted.” (p. 413). This conclusion, however, has to be done with some caution. In a recent work, Weiß et al. (2019) did a comprehensive simulation study and showed that statistics based on Pearson residuals offer a good potential for detecting certain misspecifications, but a decision for or against the actual candidate model is difficult because of considerable deviations from the above target values even under model adequacy. Comparing the distributions of statistics based on either $R_t({\varvec{\theta }})$ or $R_t(\hat{{\varvec{\theta }}})$, they also showed that main parts of these deviations are caused by estimation uncertainty. Therefore, in this work, we aim at capturing the effect of the estimated parameters on the residuals’ distribution for certain types of count process model. To the best of our knowledge, such derivations have only been done for classical regression models up to now, e.g., by Pierce and Schafer (1986) and Cordeiro and Simas (2009).

Remark 1

Pearson residuals are very popular in practice, also because they are universally applicable in some sense: As long as the conditional mean and variance required for (1) can be computed for the considered model, the Pearson residuals can be used for checking the model adequacy. On the other hand, because of their general definition, they do not use further model properties beyond conditional mean and variance. Therefore, it might be possible to define alternative (and perhaps refined) types of residuals for specific model classes. As an example, Jung et al. (2016) define “component residuals” for the so-called INAR model (to be defined in Sect. 2), which allow to infer on the parts of the INAR recursion separately. Similarly, Zhu and Wang (2010) define residuals being tailor-made for the so-called INARCH model (see Sect. 2). If being concerned with such types of DGP (under the null), it is certainly recommended to also apply these (and further) diagnostic tools in addition to the Pearson residuals.

Furthermore, if not only the null model is specified but also the class of alternative models, this information might be used for constructing a hypothesis test, e.g., in the spirit of Sun and McCabe (2013), who consider INAR models based on the Katz family of distributions. But as mentioned before, here, our focus is on the widely applicable Pearson residuals, which we investigate analytically for certain INAR and INARCH models, and where possible extensions (e.g., to different model classes) are also briefly discussed. Furthermore, our simulation study (Sect. 4) shows that the considered tests show a rather good performance despite the general nature of the Pearson residuals.

Let the computed residuals $R_t$ be indexed by $t=1,\ldots ,n$. Since our focus is on the conditional dispersion structure, we consider the statistics

$$\begin{aligned} \textstyle \mathrm{MS}_R\ =\ \frac{1}{n}\,\mathop {\sum }\limits _{t=1}^n R_t^2 \qquad \text {and}\qquad S_R^2\ =\ \mathrm{MS}_R\ -\ \bar{R}^2, \end{aligned}$$

(2)

where $\bar{R}\, =\, \frac{1}{n}\,\sum _{t=1}^n R_t$. For an adequately chosen model type, both statistics in (2) should take a value “close to 1.” For the two types of Markov count process described in Sect. 2, the aim is to derive closed-form formulae providing an asymptotic approximation to the distribution of (2). This is done in Sect. 3, where we also analyze these asymptotics and illustrate their application with some real-data examples. The finite-sample performance of the asymptotic approximations and the power of the dispersion tests implied by (2) are investigated in Sect. 4. Sect. 5 outlines possible extensions of our approach, and Sect. 6 provides concluding remarks on the residual-based dispersion tests.

2 Markov count processes

The computation of conditional mean and variance, as required for calculating the Pearson residuals (1), is particularly simple if being concerned with a pth-order Markov process. Certainly, the computation is also possible for many further processes, for example, Hidden-Markov processes, see p. 112 in Weiß (2018). But in the present work, we restrict on count-data Markov chains i.e., $p=1$), where the distribution of $X_t$ only depends on the previous observation $X_{t-1}$. Many models for count-data Markov chains have been proposed in the literature (Weiß 2018), where especially such having a conditional linear autoregressive (CLAR(1)) structure are widely used in practice, i.e., where the conditional mean is of the form $E[X_t\ |\ X_{t-1}] = \alpha \,X_{t-1}+\beta$ (see Grunwald et al. 2000). Two popular instances of CLAR(1) models are INAR(1) and INARCH(1) model (integer-valued autoregressive (conditional heteroscedasticity)); see McKenzie (1985), Ferland et al. (2006) and Weiß (2018).

The INAR(1) model is defined by the recursion $X_t\, =\, \alpha \circ X_{t-1} + \epsilon _t$ with $\alpha \in (0;1)$, where the innovations $\epsilon _t$ are i. i. d. count random variables satisfying $E[\epsilon _t]=\mu _{\epsilon }>0$ and $V[\epsilon _t]=\sigma _{\epsilon }^2>0$. The involved binomial thinning operation “$\circ$” (Steutel and van Harn 1979) is defined by requiring that $\alpha \circ X|X\, \sim Bin (X,\alpha )$, where X is a count random variable. Conditional mean and variance are given by

$$\begin{aligned} \begin{array}{rl} M_t\ =\ E[X_t\ |\ X_{t-1}]\ =&{} \alpha \cdot X_{t-1}\ +\ \mu _{\epsilon },\\ V_t\ =\ V[X_t\ |\ X_{t-1}]\ =&{} \alpha (1-\alpha )\cdot X_{t-1}\ +\ \sigma _{\epsilon }^2, \end{array} \end{aligned}$$

(3)

which are both linear functions of $X_{t-1}$. A Poi-INAR(1) model assumes Poisson-distributed innovations, say $\epsilon _t\sim Poi (\beta )$ with $\mu _{\epsilon }=\sigma _{\epsilon }^2=\beta$. Then also the observations $X_t$ are Poisson-distributed, now $X_t\sim Poi (\mu )$ with $\mu =\sigma ^2=\frac{\beta }{1-\alpha }$. In this case, the parameter vector ${\varvec{\theta }}$ is given by $(\beta ,\alpha )$.

The INARCH(1) model assumes that the conditional mean is linear in the previous observation, i.e.,

$$\begin{aligned} M_t\ =\ \alpha \cdot X_{t-1}\ +\ \beta \quad \text {with } \beta >0 \text { and } \alpha \in (0;1), \end{aligned}$$

(4)

whereas the conditional variance follows from the chosen conditional distribution of $X_t$ given $X_{t-1}$. If choosing a Poisson distribution, i.e., if $X_t\,\sim \,Poi (\alpha \cdot X_{t-1} + \beta )$, then we obtain the Poi-INARCH(1) model satisfying $V_t=M_t=\alpha \cdot X_{t-1} + \beta$. The two-dimensional parameter vector ${\varvec{\theta }}$ is again commonly chosen as $(\beta ,\alpha )$. Note that the unconditional distribution of $X_t$ is not Poisson, actually, we have $I=1/(1-\alpha ^2)>1$ (overdispersion) and $\mu =\frac{\beta }{1-\alpha }$.

Remark 2

There are many ways of estimating the model parameters of a Poi-INAR(1) or INARCH(1) model, respectively. In this work, the main aim is to obtain closed-form formulae for the asymptotic distribution of the residual-based dispersion tests (2), enabling a detailed analysis of these asymptotics (to be done in Sect. 3). For this reason, we decided to use moment estimators, which are easy to compute by simple formulae (in exactly the same way for both models!), and for which explicit expressions for the asymptotic distribution are readily available, see Weiß and Schweer (2016). These moment estimators use the empirical mean $\bar{X}$, variance $\hat{\gamma }(0)$, and first-order autocovariance $\hat{\gamma }(1)$, and they estimate $\alpha$ by $\hat{\rho }(1)=\hat{\gamma }(1)/\hat{\gamma }(0)$ as well as $\beta$ by $\bar{X}\big (1-\hat{\rho }(1)\big )$.

But other types of estimators might be used as well for computing the Pearson residuals, e.g., maximum likelihood (ML) estimators as this was done in the simulation study by Weiß et al. (2019). Then, however, it is not possible anymore to find closed-form formulae for the asymptotics of (2), because both the ML estimators themselves as well as their asymptotic distribution can only be computed numerically. In addition, one has to be aware that the Pearson residuals based on ML estimators will behave differently (not necessarily worse) than those based on moment estimators in some situations. This was observed by Weiß et al. (2019); see the last paragraph of their Sect. 3, where deviations in the dispersion structure also affected the mean and autocorrelation of the ML-based residuals. Since the asymptotics for an ML-based implementation of (2) are not explicitly available, hypothesis testing is only possible based on a bootstrap implementation. But this causes a considerable amount of additional computational efforts, whereas the moment-based implementation of (2) only requires to evaluate a few formulae. Nevertheless, we also did some simulation experiments regarding such bootstrap implementations, and these are presented in Sect. 5.

3 Approximating the squared Pearson residual’s distribution

Let $X_0,\ldots ,X_n$ be the available time series, which is assumed to originate from a Markov count DGP. These data are used to estimate the DGP’s model parameter vector ${\varvec{\theta }}$ on the one hand, and to compute the Pearson residuals $R_1,\ldots ,R_n$ according to (1) on the other hand. Then, we compute the statistics (2) to check the adequacy of the fitted model’s dispersion structure. For this purpose, we need to approximate the distribution of the statistics (2) under the null hypothesis of having fitted the correct type of model to the data. Our approach for doing this is as follows. Since $\bar{R}^2$ is expected to produce values being very close to zero, the values of $S_R^2$ and $\mathrm{MS}_R$ will usually nearly coincide; also see the examples and simulations as follows. Hence, we approximate the distribution of the empirical variance $S_R^2$ by the one of $\mathrm{MS}_R = \frac{1}{n}\,\sum _{t=1}^n R_t(\hat{{\varvec{\theta }}})^2$. The latter, in turn, is derived in two steps. First, we derive an asymptotic approximation for the joint distribution of $\frac{1}{n}\,\sum _{t=1}^n R_t({\varvec{\theta }})^2$ (mean of squared “true” residuals) and $\hat{{\varvec{\theta }}}$. Then, in analogy to Weiß et al. (2017), we approximate $\mathrm{MS}_R$ linearly in $\hat{{\varvec{\theta }}}-{\varvec{\theta }}$ by

$$\begin{aligned} \textstyle \mathrm{MS}_R(\hat{{\varvec{\theta }}}) \ \approx \ \mathrm{MS}_R({\varvec{\theta }})\ -\ \mathop {\sum }\limits _{i=1}^m\, E\big [\tfrac{\partial V_t}{\partial \theta _i}\,\tfrac{1}{V_t}\big ]\,(\hat{\theta }_i-\theta _i), \end{aligned}$$

(5)

see Appendix A.1. This general expression is finally adapted to the considered types of DGP and used to compute an asymptotic approximation for the distribution of $\mathrm{MS}_R$. The results obtained for a Poi-INAR(1) DGP are presented in Sect. 3.2, the ones for a Poi-INARCH(1) DGP in Sect. 3.2. The detailed derivations are provided by Appendices A and B, respectively. Since it is not clear in advance that our approximation approach works successfully in practice, its performance has to be checked with simulations, which is done later in Sect. 4.

3.1 Approximation for Poi-INAR(1) DGP

For the Poi-INAR(1) DGP with conditional mean $M_t=\alpha \, X_{t-1} + \beta$ and variance $V_t=\alpha (1-\alpha )\, X_{t-1} + \beta$, which was briefly surveyed in Sect. 2, the statistic $\mathrm{MS}_R$ from (2) is computed as

$$\begin{aligned} \mathrm{MS}_R=\mathrm{MS}_R(\hat{\beta },\hat{\alpha }) \ =\ \frac{1}{n}\,\sum _{t=1}^n \frac{(X_t-\hat{\alpha }\, X_{t-1} - \hat{\beta })^2}{\hat{\alpha } (1-\hat{\alpha })\, X_{t-1} + \hat{\beta }}, \end{aligned}$$

(6)

see (3). In Appendix A.1, we show that (5) implies the following linear approximation for $\mathrm{MS}_R(\hat{\beta },\hat{\alpha })$:

$$\begin{aligned} \begin{array}{rl} \mathrm{MS}_R(\hat{\beta },\hat{\alpha }) \ \approx &{} \mathrm{MS}_R(\beta ,\alpha ) \ -\ (1-2\alpha )\, E\big [\frac{X_{t-1}}{V_t}\big ]\,(\hat{\alpha }-\alpha ) \\ &{} -\ \frac{1}{\beta }\, \Big (1-\alpha (1-\alpha )\,E\big [\frac{X_{t-1}}{V_t}\big ]\Big )\,(\hat{\beta }-\beta ). \end{array} \end{aligned}$$

(7)

This approximation allows us to separate the randomness of the residuals from the one of the estimated parameters. The required moment

$$\begin{aligned} E\Big [\frac{X_{t-1}}{V_t}\Big ] \ \overset{(3)}{=}\ E\Big [\frac{X_{t-1}}{\alpha (1-\alpha )\, X_{t-1} + \beta }\Big ] \ =\ (1-\alpha )^{-1}\,E\Big [\frac{X_{t-1}}{\alpha \, X_{t-1} + \mu }\Big ] \end{aligned}$$

can be computed numerically as $(1-\alpha )^{-1}\,\sum _{x=0}^M \frac{x}{\alpha \, x + \mu }\, p_x$ with M sufficiently large, where the marginal probabilities $p_x = P(X_{t-1}=x)$ are from the $Poi (\mu )$-distribution. For $\alpha \rightarrow 0$, we have $E\big [\frac{X_{t-1}}{V_t}\big ]\rightarrow 1$.

(7) immediately implies the following approach for bias correction,

$$\begin{aligned} \begin{array}{rl} E\big [\mathrm{MS}_R(\hat{\beta },\hat{\alpha })\big ] \ \approx &{} 1\ -\ (1-2\alpha )\, E\big [\frac{X_{t-1}}{V_t}\big ]\,E\big [\hat{\alpha }-\alpha \big ] \\ &{} -\ \frac{1}{\beta }\, \Big (1-\alpha (1-\alpha )\,E\big [\frac{X_{t-1}}{V_t}\big ]\Big )\,E\big [\hat{\beta }-\beta \big ], \end{array} \end{aligned}$$

(8)

where bias approximations for $E\big [\hat{\alpha }-\alpha \big ], E\big [\hat{\beta }-\beta \big ]$ are to be inserted. For the case of the moment estimators used here (Sect. 2), such bias formulae are provided by Weiß and Schweer (2016).

To derive an approximate distribution for (7), we need the following result.

Theorem 1

Let $(X_t)_{\mathbb {Z}}$ be a Poi-INAR(1) process with $\mu =\frac{\beta }{1-\alpha }$, and let $\hat{\beta },\hat{\alpha }$ be moment estimators of $\beta ,\alpha$; see Sect. 2. Then,

$$\begin{aligned} \sqrt{n}\,\left( \frac{1}{n}\,\sum _{t=1}^n \frac{(X_t-M_t)^2}{V_t}\ -1,\ \hat{\beta }-\beta ,\ \hat{\alpha }-\alpha \right) \end{aligned}$$

is asymptotically normally distributed with mean ${\varvec{0}}$ and covariance matrix ${\varvec{\Sigma }}=(\sigma _{ij})_{i,j=1,2,3}$, where

$$\begin{aligned} \begin{array}{rl} \sigma _{11}\ =&{} 2+\frac{1}{\mu (1-\alpha )}-\frac{\alpha }{\mu }\, E\big [\frac{X_{t-1}}{V_t}\big ]-6\alpha ^2(1-\alpha )^2\, E\big [\frac{X_{t-1}}{V_t^2}\big ] ,\\ \sigma _{12}\ =&{} 1+2\alpha \mu -2\alpha (1-\alpha )\big (\alpha +(1+\alpha )\mu \big )\, E\big [\frac{X_{t-1}}{V_t}\big ],\\ \sigma _{13}\ =&{} -2\alpha +2\alpha (1-\alpha ^2)\, E\big [\frac{X_{t-1}}{V_t}\big ], \qquad \sigma _{22}\ =\ (1-\alpha )\mu + (1-\alpha ^2)\mu ^2, \\ \sigma _{23}\ =&{} -(1-\alpha ^2)\mu , \qquad \sigma _{33}\ =\ 1-\alpha ^2 + \frac{\alpha (1-\alpha )}{\mu }. \end{array} \end{aligned}$$

The proof of Theorem 1 is given in Appendix A.3. The covariances $\sigma _{22},\sigma _{23},\sigma _{33}$ have first been derived by Freeland and McCabe (2005).

Next, we combine the linear approximation (7) with Theorem 1 and derive the following normal approximation (see Appendix A.4).

Theorem 2

Let $(X_t)_{\mathbb {Z}}$ be a Poi-INAR(1) process with $\mu =\frac{\beta }{1-\alpha }$, and let $\hat{\mu },\hat{\alpha }$ be moment estimators of $\mu ,\alpha$; see Sect. 2. Then, the distribution of the linear approximation (7) for $\mathrm{MS}_R(\hat{\beta },\hat{\alpha })$ can be approximated by a normal distribution with mean 1 and variance $\sigma _{\mathrm{MS}_R}^2/n$, where

$$\begin{aligned} \begin{array}{@{}rl} \sigma _{\mathrm{MS}_R}^2\ =&{} \frac{3-5\alpha }{1-\alpha } \ +\ (1-\alpha ) \big ( (1-5\alpha )(1-\alpha ^2) + \frac{\alpha (1-3\alpha )}{\mu } \big )\, E\big [\frac{X_{t-1}}{V_t}\big ]^2 \\ &{}-\ 6 \alpha ^2 (1-\alpha )^2\, E\big [\frac{X_{t-1}}{V_t^2}\big ] \ -\ \big (\frac{\alpha (1-4 \alpha )}{\mu }+2(1-4\alpha -\alpha ^2)\big )\,E\big [\frac{X_{t-1}}{V_t}\big ] . \end{array} \end{aligned}$$

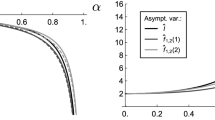
A plot of approximate bias and standard deviation (SD) of $\mathrm{MS}_R$, as implied by (8) and Theorem 2, is shown in Fig. 1 (where we set $n=1$). It becomes clear that the actual marginal mean $\mu$ has only little effect on these approximations, whereas the effect of the dependence parameter $\alpha$ is very strong. Note that for $\alpha \rightarrow 0$, we have $E\big [\frac{X_{t-1}}{V_t^2}\big ]\rightarrow 1/\mu$. So the limiting value of $\sigma _{\mathrm{MS}_R}$ for $\alpha \rightarrow 0$ is given by $\sqrt{2}$, which can also be recognized from Fig. 1b.

Fig. 1

Approximate bias in (a) and SD in (b) of $\mathrm{MS}_R$ for Poi-INAR(1) DGP (setting $n=1$), plotted against $\alpha$ for different mean levels $\mu$

In applications, the normal distribution implied by Theorem 2, together with the bias-corrected mean (8), can now be used to approximate the true distribution of both statistics $\mathrm{MS}_R$ and $S_R^2$ from (2) under the null hypothesis of a Poi-INAR(1) DGP. The performance of this approximation is investigated in Sect. 4, where results from a simulation study are presented.

Example 1

Let us consider a time series of monthly counts (Jan. 1987 to Dec. 1994, so 96 observations) of claims caused by burn-related injuries in the heavy manufacturing industry, which was presented in Example 2.5.1 by Freeland (1998) as an illustration for the Poi-INAR(1) model. Under this assumption, together with the moment estimates $\hat{\mu }\approx 8.604$ and $\hat{\alpha }\approx 0.452$, we compute 95 Pearson residuals, see (6), where both $\mathrm{MS}_R$ and $S_R^2$ take the value $\approx 1.310$. Following Harvey and Fernandes (1989), this indicates that the data exhibit more variation than captured by the Poi-INAR(1) model. But does 1.310 constitute a significant deviation from 1?

The same data were also analyzed in Schweer and Weiß (2014) by using Fisher’s dispersion index, and they ended up with a “quite narrow decision” against the Poi-INAR(1) model. Let us complement this result by a residual-based test concerning the alternative $\mathrm{MS}_R,S_R^2>1$. Using the asymptotics of (8) and Theorem 2 (and plugging-in the above moment estimates instead of the unknown model parameters), we approximate the mean and standard deviation of $\mathrm{MS}_R$ as 0.971 and 0.177, respectively. On a 5%-level, the critical value computes as 1.263, so we actually have a “less narrow” decision (P value 0.028) against the Poi-INAR(1) model than in Schweer and Weiß (2014).

3.2 Approximation for Poi-INARCH(1) DGP

For the Poi-INARCH(1) DGP, conditional mean and variance are equal to each other, both given by $M_t=\alpha \, X_{t-1} + \beta$, see Sect. 2. So this time, the statistic $\mathrm{MS}_R$ from (2) is computed as

$$\begin{aligned} \mathrm{MS}_R(\hat{\beta },\hat{\alpha }) \ =\ \frac{1}{n}\,\sum _{t=1}^n \frac{(X_t-\hat{\alpha }\, X_{t-1} - \hat{\beta })^2}{\hat{\alpha }\, X_{t-1} + \hat{\beta }}, \end{aligned}$$

(9)

see (4). In Appendix B.1, we again use (5) to derive the following linear approximation of $\mathrm{MS}_R(\hat{\beta },\hat{\alpha })$:

$$\begin{aligned} \begin{array}{rl} \mathrm{MS}_R(\hat{\beta },\hat{\alpha }) \ \approx &{} \mathrm{MS}_R(\beta ,\alpha ) \ -\ E\big [\frac{X_{t-1}}{M_t}\big ]\,(\hat{\alpha }-\alpha ) \\ &{} -\ \frac{1}{\beta }\, \Big (1-\alpha \,E\big [\frac{X_{t-1}}{M_t}\big ]\Big )\,(\hat{\beta }-\beta ). \end{array} \end{aligned}$$

(10)

Like before, this approximation allows us to separate the randomness of the residuals from the one of the estimated parameters. The required moment

$$\begin{aligned} E\Big [\frac{X_{t-1}}{M_t}\Big ] \ \overset{(4)}{=}\ E\Big [\frac{X_{t-1}}{\alpha \, X_{t-1} + \beta }\Big ] \end{aligned}$$

can be computed numerically as $\sum _{x=0}^M \frac{x}{\alpha \, x + \beta }\, p_x$ with M sufficiently large. The marginal probabilities $p_x=P(X_{t-1}=x)$ can be approximated based on the invariance equation of the INARCH(1) model; see Sect. 3.3 in Weiß et al. (2017) or Remark 2.1.3.4 in Weiß (2018). For $\alpha \rightarrow 0$, we have $E\big [\frac{X_{t-1}}{V_t}\big ]\rightarrow 1$.

Like in the INAR(1) case, (10) would also imply a bias correction, namely

$$\begin{aligned} \begin{array}{rl} E\big [\mathrm{MS}_R(\hat{\beta },\hat{\alpha })\big ] \ \approx &{} 1\ -\ E\big [\frac{X_{t-1}}{M_t}\big ]\,E\big [\hat{\alpha }-\alpha \big ] \\ &{} -\ \frac{1}{\beta }\, \Big (1-\alpha \,E\big [\frac{X_{t-1}}{M_t}\big ]\Big )\,E\big [\hat{\beta }-\beta \big ], \end{array} \end{aligned}$$

(11)

where bias approximations for $E\big [\hat{\alpha }-\alpha \big ], E\big [\hat{\beta }-\beta \big ]$ are to be inserted. For the case of the moment estimators used here (Sect. 2), such bias formulae are provided by Weiß and Schweer (2016). But our simulations to be presented in Sect. 4 show that this time, the bias correction does not work satisfactorily.

To derive an approximate distribution for (10), we again proceed in a stepwise manner and first derive the following result.

Theorem 3

Let $(X_t)_{\mathbb {Z}}$ be a Poi-INARCH(1) process with $\mu =\frac{\beta }{1-\alpha }$, and let $\hat{\beta },\hat{\alpha }$ be moment estimators of $\beta ,\alpha$; see Sect. 2. Then,

$$\begin{aligned} \sqrt{n}\,\left( \frac{1}{n}\,\sum _{t=1}^n \frac{(X_t-M_t)^2}{M_t}\ -1,\ \hat{\beta }-\beta ,\ \hat{\alpha }-\alpha \right) \end{aligned}$$

is asymptotically normally distributed with mean ${\varvec{0}}$ and covariance matrix ${\varvec{\Sigma }}=(\sigma _{ij})_{i,j=1,2,3}$, where

$$\begin{aligned} \begin{array}{rl} \sigma _{11}\ =&{} 2+ \frac{1}{\mu (1-\alpha )} \big (1-\alpha \, E\big [\frac{X_{t-1}}{M_t}\big ]\big ) , \qquad \sigma _{12}\ =\ 1,\qquad \sigma _{13}\ =\ 0, \\ \sigma _{22}\ =&{} \frac{1+2\alpha ^4}{1+\alpha +\alpha ^2}\,\mu + (1-\alpha ^2)\mu ^2, \qquad \sigma _{23}\ =\ -\frac{\alpha ^3(1+2\alpha )}{1+\alpha +\alpha ^2} - (1-\alpha ^2)\mu ,\\ \sigma _{33}\ =&{} 1-\alpha ^2+\frac{\alpha (1+\alpha )(1+2\alpha ^2)}{\mu (1+\alpha +\alpha ^2)} . \end{array} \end{aligned}$$

The proof of Theorem 3 is given in Appendix B.3. The covariances $\sigma _{22},\sigma _{23},\sigma _{33}$ have first been derived by Weiß (2010).

Next, we combine the linear approximation (10) with Theorem 3 and derive the following normal approximation (see Appendix B.4).

Theorem 4

Let $(X_t)_{\mathbb {Z}}$ be a Poi-INARCH(1) process with $\mu =\frac{\beta }{1-\alpha }$, and let $\hat{\mu },\hat{\alpha }$ be moment estimators of $\mu ,\alpha$; see Sect. 2. Then, the distribution of the linear approximation (10) for $\mathrm{MS}_R(\hat{\beta },\hat{\alpha })$ can be approximated by a normal distribution with mean 1 and variance $\sigma _{\mathrm{MS}_R}^2/n$, where

$$\begin{aligned} \begin{array}{rl} \sigma _{\mathrm{MS}_R}^2\ =&{} \frac{3-\alpha }{1-\alpha } + \frac{\alpha ^3(1+2\alpha )}{\mu (1-\alpha )(1-\alpha ^3)} \ -\ (1+\alpha ) \big ( \frac{2}{1-\alpha } + \frac{\alpha (1-\alpha +3\alpha ^2)}{\mu (1-\alpha )(1-\alpha ^3)} \big )\, E\big [\frac{X_{t-1}}{M_t}\big ]\\ &{}+\ \big (\frac{1+\alpha }{1-\alpha } + \frac{\alpha (1+\alpha ^2+\alpha ^3)}{\mu (1-\alpha )(1-\alpha ^3)}\big )\, E\big [\frac{X_{t-1}}{M_t}\big ]^2. \end{array} \end{aligned}$$

A plot of approximate bias and SD of $\mathrm{MS}_R$, as implied by (11) and Theorem 4, is shown in Fig. 2 (where we set $n=1$). The dependence parameter $\alpha$ has again a very strong effect on these quantities, but in contrast to Fig. 1 for a Poi-INAR(1) DGP, they are also notably influenced by the marginal mean $\mu$ this time. The limiting value of $\sigma _{\mathrm{MS}_R}$ for $\alpha \rightarrow 0$ again equals $\sqrt{2}$, which can also be recognized from Fig. 2b.

Fig. 2

Approximate bias in (a) and SD in (b) of $\mathrm{MS}_R$ for Poi-INARCH(1) DGP (setting $n=1$), plotted against $\alpha$ for different mean levels $\mu$

In applications, the normal distribution implied by Theorem 4 can now be used to approximate the true distribution of both statistics $\mathrm{MS}_R$ and $S_R^2$ from (2) under the null hypothesis of a Poi-INARCH(1) DGP. The performance of this approximation is investigated in Sect. 4, where results from a simulation study are presented. There, also the possible bias correction using (11) is investigated.

Example 2

Jung and Tremayne (2011) presented a time series of counts of iceberg orders (per 20 min for 32 consecutive trading days in 2004, so 800 observations) with respect to the Deutsche Telekom shares traded in the XETRA system of Deutsche Börse. These overdispersed data were also analyzed by Weiß (2015), where a Poi-INARCH(1) model turned out to be a reasonable candidate model¹. So we compute the 799 (squared) Pearson residuals under this model assumption, see (9), where we have the moment estimates $\hat{\mu }\approx 1.406$ and $\hat{\alpha }\approx 0.635$. Both $\mathrm{MS}_R$ and $S_R^2$ take the value $\approx 1.088$, which is rather close to 1. But because of the large sample size, we have a significant though narrow violation of the null hypothesis on a 5%-level, because the P value equals 0.049 (with bias correction: 0.043). This goes along with the results in Weiß (2015), who finally preferred another model for these data.

Example 3

Recalling Example 1, the claims counts time series requires a model with more variation than provided by a Poi-INAR(1) model, and such a model is given by the Poi-INARCH(1) model (also see the conclusions in Schweer and Weiß (2014)). Proceeding as in Example 2, we compute $\mathrm{MS}_R$ and $S_R^2$ as $\approx 1.050$, so again only a small exceedance of 1. But this time, the sample size is much smaller, and the critical value on a 5%-level becomes rather large, namely 1.239 (with bias correction: 1.238). Also the P value 0.365 (with bias correction: 0.363) shows that there is no contradiction against a Poi-INARCH(1) model for the claims counts data.

4 Results from a simulation study

We conducted a simulation study, the aim of which was twofold: to check the finite-sample performance of the approximations for mean and variance of $\mathrm{MS}_R$ and $S_R^2$ derived in Sect. 3, and to investigate size and power of the diagnostic tests based on $\mathrm{MS}_R$ and $S_R^2$. For each considered scenario, we simulated $10^5$ replications. As a general result, it turned out that the difference between $\mathrm{MS}_R$ and $S_R^2$ from (2) was virtually negligible. For example, if we observed a difference in power at all, this difference was very small and followed a regular pattern. Since $S_R^2 = \mathrm{MS}_R - \bar{R}^2\ < \mathrm{MS}_R$, $\mathrm{MS}_R$ lead to equal or slightly better power if an upper-sided test against overdispersion is done, and $S_R^2$ lead to equal or slightly better power if a lower-sided test against underdispersion is done. So to save some space, the summarizing tables collected in Appendix C are restricted to $\mathrm{MS}_R$ only.

The first part of our simulations refers to a hypothetical Poi-INAR(1) model, i.e., the Pearson residuals and the asymptotics for $\mathrm{MS}_R$ are computed as described in Sect. 3.1. The results in Table 1 for the marginal means $\mu \in \{2,5\}$ and the autocorrelation parameters $\alpha \in \{0.25,0.5,0.75\}$ show a negative bias for $\mathrm{MS}_R$, but this bias is captured quite well by the asymptotic approximation (8), at least for sample size $n\ge 250$. An analogous conclusion applies to the standard errors of $\mathrm{MS}_R$, where the approximation quality slightly deteriorates with increasing $\alpha$. In practice, these approximations are used for testing the hypothetical Poi-INAR(1) model, in analogy to Example 1. So the performance of such a test (size & power) is crucial for applications. This is investigated for diverse alternative scenarios: We use upper-sided tests to uncover overdispersion as generated by an NB-INAR(1) DGP in Table 2 or by a ZIP-INAR(1) DGP as in Table 3, and lower-sided tests to uncover underdispersion as generated by a Good-INAR(1) DGP in Table 4. Here, the INAR(1) innovations follow a negative binomial or zero-inflated Poi-or Good distribution, respectively; for background information on these distributions, see Weiß (2018). As a competitor, we use the $\hat{I}$-test relying on the sample dispersion index as derived by Schweer and Weiß (2014).

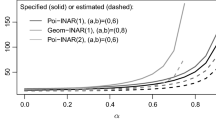
The size values in Table 2 (columns $I=1$; replicated in Table 3) for the $\mathrm{MS}_R$-test are always very close to the nominal 5%-level, whereas those of the $\hat{I}$-test are either somewhat larger than 5% for $\alpha =0.25$, or smaller than 5% for $\alpha =0.75$. Also concerning the lower-sided tests, see Table 4, the size values the $\mathrm{MS}_R$-test are usually more close to the 5%-level than those of the $\hat{I}$-test. In particular, with only few exceptions, the $\mathrm{MS}_R$-test has better power values than the $\hat{I}$-test, both for under- and overdispersion, and also for the case if overdispersion is actually caused by an excessive number of zeros. So we can give a clear recommendation for using the $\mathrm{MS}_R$-test instead of the $\hat{I}$-test in the INAR(1) case.

The second part of our simulation study refers to a hypothetical Poi-INARCH(1) DGP, see Sect. 3.1. Here, we do not consider the dispersion index as a competitor, because it is known to perform poorly for such INARCH processes. Instead, we consider the $\widehat{C}_{1;2}$-test proposed by Weiß et al. (2017), and we also use the parametrizations given there, i.e., $\mu \in \{2.5,5\}$ and $\alpha \in \{0.2,0.4,0.6,0.8\}$. Table 5 compares the simulated means and standard errors with the asymptotic approximations implied by (11) and Theorem 4. While the approximation of the standard errors works rather well, especially for $\mu =5$, the mean approximation is not satisfactory: In most cases, the simulated bias is clearly stronger, but for $\mu =2.5$ and $\alpha =0.8$, we also find the opposite deviation. For this reason, we did not further use the bias correction when executing the $\mathrm{MS}_R$-test in the INARCH(1) case. The size values of the $\mathrm{MS}_R$-test (without bias correction) are given in Table 6 (column “$\theta =1$”). Most often, they are reasonably close to the nominal 5%-level, and in case of a notable deviation (essentially for $T=100$ or $\mu =2.5$, $\alpha =0.8$), the $\mathrm{MS}_R$-test is conservative. This differs from the $\widehat{C}_{1;2}$-test, the size of which often exceeds the 5%-level, especially for large $\alpha$.

For power analysis, we use an alternative DGP with additional conditional variation, namely the same NB-INARCH(1) process as in Weiß et al. (2017):

$$\begin{aligned} X_t\ \big |\ X_{t-1}, X_{t-2},\ldots \quad \sim \ NB \left( \frac{\beta +\alpha \, X_{t-1}}{\theta -1},\ \frac{1}{\theta }\right) \quad \text {with }\theta >1. \end{aligned}$$

The corresponding power values in Table 6 show that the $\mathrm{MS}_R$-test has better power values in most cases despite its tendency to being conservative. The advantage to the $\widehat{C}_{1;2}$-test is particularly large for a highly correlated process ($\alpha =0.8$). So taking all results together, we clearly recommend the $\mathrm{MS}_R$-test for uncovering a misfit of the DGP’s dispersion structure.

5 Possible extensions

In view of their good performance, as demonstrated in Sect. 4, it appears to be a promising direction for future research to extend the residual-based dispersion tests also to other relevant types of count process. This could be done in two ways. On the one hand, analogous asymptotic approximations could be derived for different types of DGP. For example, if appropriately parametrized, the non-Markovian Poi-INMA(1) process (a moving-average-type process) has the same formulae for 1-step-ahead conditional mean and variance as the Poi-INAR(1) process, see (3). Hence, we also get the same formulae for the test statistic and its linear approximation, namely (6) and (7), respectively. So it remains to compute an asymptotic result analogous to Theorem 1, where the asymptotics derived by Aleksandrov and Weiß (2019) constitute a starting point. Another idea could be to consider models for bounded counts, i.e., having a finite range of the form $\{0,\ldots ,N\}$ with some $N\in \mathbb {N}$, like the finite Markov chains binomial AR(1) or INARCH(1); see Weiß (2018) for details and references. These processes, however, have slightly different expressions for the conditional variance (if choosing the model parameters to match the conditional mean), thus also the expressions for the residuals slightly differ from the ones discussed in this article. For $N\rightarrow \infty$, these formulae converge to those of the respective Poisson counterpart.

A second solution for doing residual-based tests for count DGPs could be based on a parametric bootstrap implementation (regarding the respective hypothetical model for the DGP). This would allow to consider further types of DGP, such as higher-order INAR and IN(G)ARCH models or Hidden-Markov models, or to use different estimation approaches for computing the residuals, e.g., ML instead of moment estimators. To get an idea about the performance of such a bootstrap implementation, we did a simulation experiment for the Poi-INAR(1) case, by comparing the above asymptotic approximation with the parametric bootstrap scheme described in Jentsch and Weiß (2018). Since the bootstrap implementation requires much more computing time, we did only 5 000 Monte Carlo replicates this time (and always 500 bootstrap replicates). The results are summarized in Table 7, where the columns “asym” refer to the asymptotic approximation and are taken from Table 2, and where the columns “boot” contain the new simulation results. Although showing more fluctuations, the sizes for this upper-sided bootstrap test are close to the 5%-level, and the power values regarding an NB-INAR(1) DGP agree quite well with those of the asymptotic approximation (with some deterioration for increasing $\alpha$). It should be noted, however, that the lower-sided bootstrap test suffers from oversizing, especially for $\alpha =0.75$ (see Table 8), so further refinements would be required here.

In addition, we also combined the above bootstrap implementation (Poi- against NB-INAR(1) DGP) with ML-based residuals; also recall the discussion in Remark 2. This, however, caused a further increase in computing time because of the numerical optimizations required for each simulation and each bootstrap run. The obtained simulation results are summarized in Table 9. Again, the sizes show a bit more fluctuations than in the case of the asymptotic implementation based on moment estimators (see Table 7), but are sufficiently close to 0.050. The ML-based power values are nearly the same as those obtained using moment estimators for the low autocorrelation level $\alpha =0.25$, but they become more and more superior with increasing $\alpha$. This result appears plausible in view of a better performance of the ML estimators than the moment estimators for highly correlated INAR(1) processes; see the discussion in Weiß and Schweer (2016). So if the computational burden caused by the ML-based bootstrap implementation can be managed, this type of residual-based dispersion test seems to be even more powerful in detecting neglected dispersion than the more simple moment-based implementation.

6 Conclusions

For doing model diagnostics with respect to the conditional dispersion structure of the given count time series, we used statistics based on the squared Pearson residuals. To allow for hypothesis testing, we derived asymptotic approximations for the distribution of the test statistics under the null of a Poi-INAR(1) or INARCH(1) DGP. The simulations demonstrated that the resulting tests show a very good performance for uncovering diverse over- and underdispersion scenarios. Although we concentrated on Poi-INAR(1) and INARCH(1) DGPs (and computed the residuals based on moment estimators), we also argued that extensions to other types of count processes (or to other types of estimators) are possible (e.g., based on an appropriate bootstrap implementation). A more detailed study of such extensions and their performance should be done in a future research.

Appendices

Proofs for Poi-INAR(1) DGP

1.1 Linear approximation for squared residuals

Before turning to the specific case of a Poi-INAR(1) DGP, let us first consider the general case described in the beginning of Sect. 3, i.e., Let $M_t=E[X_t\ |\ X_{t-1},X_{t-2},\ldots ]$ and $V_t=V[X_t\ |\ X_{t-1},\ldots ]$ depend on some parameter vector ${\varvec{\theta }}$, then

$$\begin{aligned} \mathrm{MS}_R({\varvec{\theta }})\ =\ \frac{1}{n}\sum \limits _{t=1}^n\frac{\big (X_t-M_t({\varvec{\theta }})\big )^2}{V_t({\varvec{\theta }})}, \end{aligned}$$

where $M_t({\varvec{\theta }})$ and $V_t({\varvec{\theta }})$ denote the conditional mean and variance, respectively, as functions of ${\varvec{\theta }}$. To derive a linear approximation for the statistic $\mathrm{MS}_R(\hat{{\varvec{\theta }}})$, we consider a first-order Taylor approximation of the function $\mathrm{MS}_R({\varvec{\theta }})$ in ${\varvec{\theta }}$. The first-order partial derivative in $\theta _i$ equals

$$\begin{aligned} \tfrac{\partial }{\partial \theta _i}\,\mathrm{MS}_R\ =\ -\frac{1}{n}\sum \limits _{t=1}^n\frac{(X_t-M_t)^2}{V_t^2}\, \frac{\partial V_t}{\partial \theta _i}-\ \frac{2}{n}\sum \limits _{t=1}^n \frac{(X_t-M_t)}{V_t}\,\frac{\partial M_t}{\partial \theta _i}. \end{aligned}$$

The means of the summands are

$$\begin{aligned} \begin{array}{@{}rl} E\Big [\frac{(X_t-M_t)^2}{V_t^2}\, \frac{\partial V_t}{\partial \theta _i}\Big ]\ =&{} E\Big [\frac{\partial V_t}{\partial \theta _i}\,\frac{1}{V_t^2}\,E\big [(X_t-M_t)^2\ |\ X_{t-1},\ldots \big ]\Big ] \ =\ E\big [\frac{\partial V_t}{\partial \theta _i}\,\frac{1}{V_t}\big ],\\ E\Big [\frac{(X_t-M_t)}{V_t}\,\frac{\partial M_t}{\partial \theta _i}\Big ] \ =&{} E\Big [\frac{\partial M_t}{\partial \theta _i}\,\frac{1}{V_t}\,E[X_t-M_t\ |\ X_{t-1},\ldots ]\Big ]\ =\ 0, \end{array} \end{aligned}$$

where the first equation used that $E\big [(X_t-M_t)^2\ |\ X_{t-1},\ldots \big ] = V_t$. This is used to conclude that

$$\begin{aligned} \frac{1}{n}\sum \limits _{t=1}^n\left( \frac{(X_t-M_t)^2}{V_t^2}\, \frac{\partial V_t}{\partial \theta _i}\ -\ E\left[ \frac{\partial V_t}{\partial \theta _i}\,\frac{1}{V_t}\right] \right)= & {} o_P(1),\\ \frac{2}{n}\sum \limits _{t=1}^n \frac{(X_t-M_t)}{V_t}\,\frac{\partial M_t}{\partial \theta _i}= & {} o_P(1). \end{aligned}$$

Thus, the linear Taylor approximation

$$\begin{aligned} \mathrm{MS}_R(\hat{{\varvec{\theta }}})= & {} \textstyle \mathrm{MS}_R({\varvec{\theta }})\ +\ \sum \limits _{i=1}^m\, \tfrac{\partial }{\partial \theta _i}\,\mathrm{MS}_R({\varvec{\theta }})\,(\hat{\theta }_i-\theta _i) \ +\ o\big (\Vert \hat{{\varvec{\theta }}}-{\varvec{\theta }}\Vert \big )\\= & {} \textstyle \mathrm{MS}_R({\varvec{\theta }})\ -\ \sum \limits _{i=1}^m\, E\big [\tfrac{\partial V_t}{\partial \theta _i}\,\tfrac{1}{V_t}\big ]\,(\hat{\theta }_i-\theta _i) \ +\ o\big (\Vert \hat{{\varvec{\theta }}}-{\varvec{\theta }}\Vert \big )\\&\textstyle -\ \sum \limits _{i=1}^m\, \biggl (\frac{1}{n}\sum \limits _{t=1}^n\Big (\frac{(X_t-M_t)^2}{V_t^2}\, \frac{\partial V_t}{\partial \theta _i}\ -\ E\big [\frac{\partial V_t}{\partial \theta _i}\,\frac{1}{V_t}\big ]\Big )\biggl )\,(\hat{\theta }_i-\theta _i) \\&\textstyle -\ \sum \limits _{i=1}^m\, \Big (\frac{2}{n}\sum \limits _{t=1}^n \frac{(X_t-M_t)}{V_t}\,\frac{\partial M_t}{\partial \theta _i}\Big )\,(\hat{\theta }_i-\theta _i), \end{aligned}$$

together with Slutsky’s lemma, implies the linear approximation (5).

Now, consider the special case of a Poi-INAR(1) DGP, i.e., ${\varvec{\theta }}=(\beta ,\alpha )$. According to (5), we require the partial derivatives of $V_t=\beta +\alpha (1-\alpha )\,X_{t-1}$, which equal $\frac{\partial }{\partial \alpha }\,V_t=(1-2\alpha )\,X_{t-1}$ and $\frac{\partial }{\partial \beta }\,V_t=1$. Thus, it follows that

$$\begin{aligned} \textstyle E\big [\frac{\partial V_t}{\partial \alpha }\,\frac{1}{V_t}\big ]\ =\ (1-2\alpha )\,E\big [\frac{X_{t-1}}{V_t}\big ],\qquad E\big [\frac{\partial V_t}{\partial \beta }\,\frac{1}{V_t}\big ]\ =\ E\big [\frac{1}{V_t}\big ]. \end{aligned}$$

This implies the linear approximation (7). Note that $E\big [\frac{1}{V_t}\big ]$ can be rewritten as $\frac{1}{\beta }\big (1-\alpha (1-\alpha )\,E\big [\frac{ X_{t-1}}{V_t}\big ]\big )$.

1.2 Joint distribution of residuals and moments

In order to prepare the asymptotic results to be derived for Sect. 3, we use a central limit theorem (CLT) for the four-dimensional vector-valued process $({\varvec{Y}}_t)_{\mathbb {Z}}$ given by

$$\begin{aligned} {\varvec{Y}}_t\ :=\ \left( \begin{array}{c} Y_{t,0}\\ Y_{t,1}\\ Y_{t,2}\\ Y_{t,3}\\ \end{array}\right) \ :=\ \left( \begin{array}{c} \frac{(X_t-M_t)^2}{V_t} - 1\\ X_t - \mu \\ X_t^2 - \mu (0)\\ X_t X_{t-1} - \mu (1) \end{array}\right) \end{aligned}$$

(A.1)

with $\mu (k) := E[X_t X_{t-k}]$. Note that the Poi-INAR(1) process is $\alpha$-mixing with exponentially decreasing weights, and it has existing moments of any order (Weiß and Schweer 2016). So the CLT by Ibragimov (1962) can be applied to $\frac{1}{\sqrt{T}} \sum _{t=1}^T {\varvec{Y}}_t$. The following lemma summarizes the resulting asymptotics.

Lemma 1

Let $(X_t)_{\mathbb {Z}}$ be a Poi-INAR(1) process with $\mu =\frac{\beta }{1-\alpha }$, $\mu (k)=\mu (\alpha ^k+\mu )$ and

$$\begin{aligned} Y_{t,0}\ =\ \frac{(X_t-M_t)^2}{V_t} - 1 \ =\ \frac{(X_t-\alpha \, X_{t-1} - \beta )^2}{\alpha (1-\alpha )\, X_{t-1} + \beta } - 1. \end{aligned}$$

Then, $\frac{1}{\sqrt{n}} \sum _{t=1}^n {\varvec{Y}}_t$ is asymptotically normally distributed with mean ${\varvec{0}}$ and covariance matrix $\tilde{{\varvec{\Sigma }}} = (\tilde{\sigma }_{ij})$, where

$$\begin{aligned} \begin{array}{@{}rl} \tilde{\sigma }_{00}\ =&{} 2+\frac{1}{\mu (1-\alpha )}-\frac{\alpha }{\mu }\, E\big [\frac{ X_{t-1}}{V_t}\big ]-6\alpha ^2(1-\alpha )^2\, E\big [\frac{ X_{t-1}}{V_t^2}\big ], \\ \tilde{\sigma }_{01}\ =&{} \frac{1}{1-\alpha }-2\alpha ^2\, E\big [\frac{ X_{t-1}}{V_t}\big ], \\ \tilde{\sigma }_{02}\ =&{} \frac{2(3\alpha +2)\mu }{1+\alpha } +\frac{1}{1-\alpha } +\frac{2\alpha ^2(-3+2\alpha )}{1+\alpha }\, E\big [\frac{ X_{t-1}}{V_t}\big ], \\ \tilde{\sigma }_{03}\ =&{} \frac{2\mu (1+2\alpha +2\alpha ^2)}{1+\alpha }+\frac{\alpha }{1-\alpha }+2\alpha \mu (1-\alpha )^2\, E\big [\frac{ X_{t-1}}{V_t}\big ]+\frac{2\alpha ^3(-3+2\alpha )}{1+\alpha }\, E\big [\frac{ X_{t-1}}{V_t}\big ]. \end{array} \end{aligned}$$

The expressions for $\tilde{\sigma }_{11},\ldots ,\tilde{\sigma }_{33}$ can be found in Theorem 2.1 of Weiß and Schweer (2016).

1.2.1 Proof of Lemma 1

Note that the conditional variance and the conditional mean are related to each other in several ways, namely:

$$\begin{aligned} (M_t-\beta )(1-\alpha )+\beta= & {} V_t,\end{aligned}$$

(A.2)

$$\begin{aligned} M_t(1-\alpha )+\alpha \beta= & {} V_t,\end{aligned}$$

(A.3)

$$\begin{aligned} M_t-V_t= & {} \alpha ^2 X_{t-1},\end{aligned}$$

(A.4)

$$\begin{aligned} 1-\alpha (1-\alpha )\, E\big [\tfrac{ X_{t-1}}{V_t}\big ]= & {} \beta \, E\big [\tfrac{1}{V_t}\big ]. \end{aligned}$$

(A.5)

We first need to calculate some conditional moments. Obviously, we have $E\left[ X_t^2\ |\ X_{t-1}\right] =V_t+M_t^2$. Since for Poisson and binomial variates, factorial moments take a particularly simple form, we shall use the falling factorials $(x)_{(k)}=x\cdots (x-k+1)$ in the sequel. We have

$$\begin{aligned} E\left[ X_t^3\ |\ X_{t-1}\right]= & {} E[(\alpha \circ X_{t-1}+\epsilon _t)^3\ | \ X_{t-1}]\nonumber \\= & {} E[(\alpha \circ X_{t-1})^3\ | \ X_{t-1}]+3E[(\alpha \circ X_{t-1})^2\ | \ X_{t-1}]E[\epsilon _t]\nonumber \\&+\,3E[(\alpha \circ X_{t-1})\ | \ X_{t-1}]E[\epsilon _t^2]+E[\epsilon _t^3],\nonumber \\= & {} \alpha X_{t-1}+3\alpha ^2(X_{t-1})_{(2)}+\alpha ^3(X_{t-1})_{(3)} +3\alpha X_{t-1}(\beta ^2+\beta )\qquad \qquad \nonumber \\&+\,3(\alpha X_{t-1}+\alpha ^2(X_{t-1})_{(2)})\beta +(\beta +3\beta ^2+\beta ^3)\nonumber \\= & {} M_t^3+\alpha X_{t-1}+3\alpha ^2( X_{t-1})_{(2)}+\alpha ^3(-3 X_{t-1}^2+2 X_{t-1})\nonumber \\&+\,3(\alpha X_{t-1}-\alpha ^2 X_{t-1})\beta +3\alpha X_{t-1}\beta +(\beta +3\beta ^2)\nonumber \\= & {} M_t^3+3M_t V_t+\alpha X_{t-1}-3\alpha ^2 X_{t-1}+2\alpha ^3 X_{t-1}+\beta \nonumber \\= & {} M_t^3+3M_t\cdot V_t+(1-2\alpha )V_t+2\beta \alpha , \end{aligned}$$

(A.6)

where we used the moment formulae from Johnson et al. (2005), page 110, and the following simplification

$$\begin{aligned} M_t^3= & {} \beta ^3+3\beta ^2\alpha X_{t-1}+3\beta \alpha ^2 X_{t-1}^2+\alpha ^3 X_{t-1}^3,\\ M_t\cdot V_t= & {} \beta ^2+\alpha \beta (2-\alpha ) X_{t-1}+\alpha ^2(1-\alpha ) X_{t-1}^2. \end{aligned}$$

Analogously, we get for the fourth conditional moment

$$\begin{aligned} E[X_t^4\ | \ X_{t-1}]= & {} E[(\alpha \circ X_{t-1}+\epsilon _t)^4\ | \ X_{t-1}] \nonumber \\= & {} E[(\alpha \circ X_{t-1})^4\ | \ X_{t-1}]+4E[(\alpha \circ X_{t-1})^3\ | \ X_{t-1}]E[\epsilon _t]+E[\epsilon _t^4]\nonumber \\&+\,6E[(\alpha \circ X_{t-1})^2\ | \ X_{t-1}]E[\epsilon _t^2]+4E[(\alpha \circ X_{t-1})\ | \ X_{t-1}]E[\epsilon _t^3]\nonumber \\= & {} \alpha ^4( X_{t-1})_{(4)}+6\alpha ^3( X_{t-1})_{(3)}+7\alpha ^2( X_{t-1})_{(2)}+\alpha X_{t-1}\nonumber \\&+\,4(\alpha ^3( X_{t-1})_{(3)}+3\alpha ^2( X_{t-1})_{(2)}+\alpha X_{t-1})\cdot \beta \nonumber \\&+\,6(\alpha ^2( X_{t-1})_{(2)}+\alpha X_{t-1})\cdot (\beta +\beta ^2)\nonumber \\&+\,4\alpha X_{t-1}\cdot (\beta +3\beta ^2+\beta ^3)+(\beta ^4+6\beta ^3+7\beta ^2+\beta )\nonumber \\= & {} M_t^4+6M_t^2 V_t+M_t V_t(7-11\alpha )+V_t(1+11\alpha \beta )\nonumber \\&+\,2\alpha ^2(-3-3\alpha ^2+6\alpha +4\alpha \beta ) X_{t-1}. \end{aligned}$$

(A.7)

We are now in a position to compute the asymptotic covariances required for Lemma 1. The CLT by Ibragimov (1962) implies that

$$\begin{aligned} \tilde{\sigma }_{00}= & {} E\big [(\tfrac{(X_{t}-M_{t})^2}{V_{t}}-1)^2\big ]\ +\ 2\sum \limits _{k=1}^\infty E\big [(\tfrac{(X_{t+k}-M_{t+k})^2}{V_{t+k}}-1) \cdot (\tfrac{(X_{t}-M_{t})^2}{V_{t}}-1)\big ]\\= & {} E\big [\tfrac{(X_t-M_t)^4}{V_t^2}\big ]-1\\&+\,2\sum \limits _{k=1}^\infty \left( E\Big [\tfrac{(X_{t}-M_{t})^2}{V_{t}}\cdot \tfrac{\overbrace{E[(X_{t+k}-M_{t+k})^2\ |\ X_{t+k-1}, \ldots ]}^{=V_{t+k}}}{V_{t+k}}\Big ]-1\right) \\= & {} \tfrac{1}{ V_t^2}\,E\big [E[(X_t-M_t)^4 \ | \ X_{t-1} ]\big ]-1\\= & {} 2+E\big [\tfrac{1}{V_t}\big ]-6\alpha ^2(1-\alpha )^2\,E\big [\tfrac{ X_{t-1}}{V_t^2}\big ]\\= & {} 2+\tfrac{1}{\beta }(1-\alpha (1-\alpha )E[\tfrac{ X_{t-1}}{V_t}])-6\alpha ^2(1-\alpha )^2\,E\big [\tfrac{ X_{t-1}}{V_t^2}\big ], \end{aligned}$$

where we used that $E\left[ \frac{(X_t-M_t)^2}{V_t}\right] =1$ and

$$\begin{aligned}&E\Big [(X_t-M_t)^4 \ | \ X_{t-1} \Big ]\\&\quad =E[X_t^4\ | \ X_{t-1} ]-4E[X_t^3\ | \ X_{t-1} ]M_t+6E[X_t^2\ | \ X_{t-1} ]M_t^2-3M_t^4\\&\quad =M_t^4+6M_t^2 V_t+M_t V_t(7-11\alpha )+V_t(1+11\alpha \beta )\\&\qquad +\,2\alpha ^2(-3-3\alpha ^2+6\alpha +4\alpha \beta ) X_{t-1}\\&\qquad -\,4M_t(M_t^3+3M_t\cdot V_t+(1-2\alpha )V_t+2\beta \alpha )+6M_t^2(M_t^2+V_t^2)-3M_t^4\\&\quad =3(1-\alpha )M_tV_t+V_t(1+11\alpha \beta )-8\beta \alpha M_t+2\alpha ^2(-3-3\alpha ^2+6\alpha +4\alpha \beta ) X_{t-1}\\&\quad \overset{(A.4)}{=}3(1-\alpha )(\tfrac{V_t-\beta }{1-\alpha }+\beta )V_t+V_t(1+11\alpha \beta )-8\beta \alpha (\tfrac{V_t-\beta }{1-\alpha }+\beta )\\&\qquad +\,2(-3-3\alpha ^2+6\alpha +4\alpha \beta )((\tfrac{V_t-\beta }{1-\alpha }+\beta )-V_t)\\\\&\quad =3V_t^2+V_t+6\alpha (1-\alpha )(\beta -V_t)\\&\quad =3V_t^2+V_t-6\alpha ^2(1-\alpha )^2 X_{t-1}. \end{aligned}$$

Here, we used formulas (A.7) and (A.6) for the conditional moments.

For the next covariance, we need

$$\begin{aligned} E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_t\right]= & {} E\left[ \tfrac{1}{V_{t}}\, E\left[ (X_t-M_t)^2\ X_t\ |\ X_{t-1}\right] \right] \nonumber \\= & {} E\left[ \tfrac{1}{V_{t}} \big (E\left[ X_t^3\ |\ X_{t-1}\right] -2M_tE\left[ X_t^2\ |\ X_{t-1}\right] \right. \nonumber \\&\left. +M_t^2E\left[ X_t\ |\ X_{t-1}\right] \big )\right] \nonumber \\&\overset{(A.6)}{=}&E\left[ \tfrac{1}{V_{t}}(M_t^3+3M_tV_t\right. \nonumber \nonumber \\&\left. +(1-2\alpha )V_t+2\beta \alpha -2M_t(V_t+M_t^2)+M_t^3)\right] \qquad \nonumber \\= & {} E\left[ \tfrac{1}{V_{t}}(M_tV_t+(1-2\alpha )V_t+2\beta \alpha \right] \nonumber \\= & {} E[M_t]+1-2\alpha +2\beta \alpha E[\tfrac{1}{V_t}]\nonumber \\&\overset{(A.5)}{=}&\mu +1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}]. \end{aligned}$$

(A.8)

So it follows that

$$\begin{aligned} \tilde{\sigma }_{01}= & {} E\left[ (\tfrac{(X_t-M_t)^2}{V_{t}}-1)\cdot (X_t-\mu )\right] +\sum \limits _{k=1}^\infty E\left[ (\tfrac{(X_t-M_t)^2}{V_{t}}-1)\cdot ( X_{t+k}-\mu )\right] \\&+\,\sum \limits _{k=1}^\infty E\left[ (\tfrac{(X_{t+k}-M_{t+k})^2}{V_{t+k}}-1) \cdot (X_{t}-\mu )\right] \\= & {} E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_t\right] -\mu +\sum \limits _{k=1}^\infty \left( E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}\right] -\mu \right) \\&+\,\sum \limits _{k=1}^\infty \left( E\left[ \tfrac{(X_{t+k}-M_{t+k})^2}{V_{t+k}} \cdot X_{t}\right] -\mu \right) . \end{aligned}$$

Now, let us take a look at

$$\begin{aligned} E\left[ \tfrac{(X_{t+k}-M_{t+k})^2}{V_{t+k}} \cdot X_{t}\right] -\mu =E\left[ \tfrac{X_{t}}{V_{t+k}}\,E\left[ (X_{t+k}-M_{t+k})^2|\ X_{t+k-1},\ldots \right] \right] -\mu = 0, \end{aligned}$$

thus the last infinite sum vanishes. And the terms inside the first infinite sum can be calculated in the following way:

$$\begin{aligned}&E\Big [\tfrac{(X_t-M_t)^2}{V_{t}}\cdot \underbrace{E\left[ X_{t+k}|\ X_{t+k-1},\ldots \right] }_{\beta +\alpha X_{t+k-1}}\Big ]\nonumber \\&\quad =\ldots \ =\ \beta +\alpha \beta +\alpha ^2\beta +\ldots +\alpha ^{k-1}\beta +\alpha ^k E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_t\right] \nonumber \\&\quad \overset{(A.8)}{=}\tfrac{\beta (1-\alpha ^k)}{1-\alpha }+\alpha ^k(\mu +1-2\alpha ^2(1-\alpha )\,E[\tfrac{ X_{t-1}}{V_t}])\nonumber \\&\quad =\mu +\alpha ^k(1-2\alpha ^2(1-\alpha )\,E[\tfrac{ X_{t-1}}{V_t}]). \end{aligned}$$

(A.9)

Note that (A.9) also holds for $k=0$, see (A.8). So we get

$$\begin{aligned} \tilde{\sigma }_{01}= & {} \sum \limits _{k=0}^\infty (E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}\right] -\mu ) \ =\ \sum \limits _{k=0}^\infty \alpha ^k(1-2\alpha ^2(1-\alpha )\,E[\tfrac{ X_{t-1}}{V_t}])\nonumber \\= & {} \frac{1}{1-\alpha }-2\alpha ^2\,E[\tfrac{ X_{t-1}}{V_t}]. \end{aligned}$$

(A.10)

Now, let us look at

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_t^2\right] =E\left[ \tfrac{1}{V_{t}} E\left[ (X_t-M_t)^2\ X_t^2\ |\ X_{t-1}\right] \right] \nonumber \\&\quad =E\left[ \tfrac{1}{V_{t}}\, \big (E\left[ X_t^4\ |\ X_{t-1}\right] -2M_tE\left[ X_t^3\ |\ X_{t-1}\right] +M_t^2E\left[ X_t^2\ |\ X_{t-1}\right] \big )\right] \nonumber \\&\quad =E\Big [\tfrac{1}{V_{t}}\,\big (M_t^4+6M_t^2 V_t+M_t V_t(7-11\alpha )+V_t(1+11\alpha \beta )+M_t^2(V_t+M_t^2)\nonumber \\&\qquad +\,2\alpha ^2(-3-3\alpha ^2+6\alpha +4\alpha \beta ) X_{t-1}-2M_t(M_t^3+3M_t\cdot V_t+(1-2\alpha )V_t+2\beta \alpha )\big )\Big ]\nonumber \\&\quad =E[M_t^2]+E[M_t](5-7\alpha )+1+11\alpha (1-\alpha )\mu +2\alpha ^2(-3(1-\alpha )^2\nonumber \\&\qquad +\,4\alpha \mu (1-\alpha ))E[\tfrac{ X_{t-1}}{V_t}]-4\alpha \beta E[\tfrac{M_t}{V_t}]\nonumber \\&\quad =\alpha ^2\mu +\mu ^2+\mu (5-7\alpha )+1+11\alpha (1-\alpha )\mu \nonumber \\&\qquad +\,2\alpha ^2(1-\alpha )(-3+3\alpha +4\alpha \mu )E[\tfrac{ X_{t-1}}{V_t}]-4\alpha \mu (1-\alpha )(1+\alpha ^2 E[\tfrac{ X_{t-1}}{V_t}])\nonumber \\&\quad =(-6\alpha ^2+5+\mu )\mu +1+2\alpha ^2(1-\alpha )(-3+3\alpha +2\alpha \mu )E[\tfrac{ X_{t-1}}{V_t}], \end{aligned}$$

(A.11)

where we used (A.6) and (A.7) for the conditional moments, and $M_t=V_t+\alpha ^2 X_{t-1}$. This will be used for

$$\begin{aligned} \tilde{\sigma }_{02}= & {} \sum \limits _{k=0}^\infty E\left[ \left( \tfrac{(X_t-M_t)^2}{V_{t}}-1\right) \cdot ( X_{t+k}^2-\mu -\mu ^2)\right] \nonumber \\= & {} \sum \limits _{k=0}^\infty \left( E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}^2\right] -\mu -\mu ^2\right) . \end{aligned}$$

(A.12)

Now, let us take a look at the terms inside the infinite sum.

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}^2 \right] =E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot E\left[ X_{t+k}^2|\ X_{t+k-1},\ldots \right] \right] \nonumber \\&\quad = E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot (V_{t+k}+M_{t+k}^2)\right] \nonumber \\&\quad = E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot \big [(\beta +\alpha (1-\alpha ) X_{t+k-1})+(\beta +\alpha X_{t+k-1})^2\big ]\right] \nonumber \\&\quad =\beta (1+\beta )+\alpha (1-\alpha +2\beta ) E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1}\right] +\alpha ^2E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1}^2 \right] \nonumber \\&\quad \overset{A.9}{=}\beta (1+\beta )+\alpha (1-\alpha +2\beta ) (\mu +\alpha ^{k-1}(1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}]))\nonumber \\&\qquad +\,\alpha ^2E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1}^2 \right] \nonumber \\&\quad =\mu (1-\alpha )(1+\mu (1-\alpha ))+\alpha (1-\alpha )(1+2\mu )\mu \nonumber \\&\qquad +\,\alpha ^k(1-\alpha )(1+2\mu )(1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}])+\alpha ^2E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1}^2 \right] \nonumber \\&\quad =\mu (\mu +1)(1-\alpha ^2)+\alpha ^k(1-\alpha )(1+2\mu )(1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}])\nonumber \\&\qquad +\,\alpha ^2E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1}^2 \right] . \end{aligned}$$

(A.13)

The above relationship can be viewed as a recurrence. Let us define $g_k:= E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}^2 \right]$ with

$$\begin{aligned} g_0:=(-6\alpha ^2+5+\mu )\mu +1+2\alpha ^2(1-\alpha )(-3+3\alpha +2\alpha \mu )E\left[ \frac{ X_{t-1}}{V_t}\right] \end{aligned}$$

according to (A.11). Then, the first-order linear difference equation

$$\begin{aligned} g_k=\mu (\mu +1)(1-\alpha ^2)+\alpha ^k(1-\alpha )(1+2\mu )(1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}])+\alpha ^2\,g_{k-1} \end{aligned}$$

has the unique solution given by

$$\begin{aligned} g_k= & {} \textstyle g_0\cdot \prod _{i=0}^{k-1}\alpha ^2+\sum \limits _{j=0}^{k-1}\Big (\mu (\mu +1)(1-\alpha ^2)\nonumber \\&\textstyle +\,\alpha ^{j+1}(1-\alpha )(1+2\mu )\big (1-2\alpha ^2(1-\alpha )\,E[\tfrac{ X_{t-1}}{V_t}]\big )\Big )\cdot \prod _{w =j+1}^{k-1}\alpha ^2\nonumber \\= & {} \textstyle g_0\cdot \alpha ^{2k}+\mu (\mu +1)(1-\alpha ^2)\sum \limits _{j=0}^{k-1}\alpha ^{2(k-1-j)}\nonumber \\&\textstyle +(1-\alpha )(1+2\mu )\big (1-2\alpha ^2(1-\alpha )\,E[\tfrac{ X_{t-1}}{V_t}]\big )\sum \limits _{l=0}^{k-1} \alpha ^{l+1}\cdot \alpha ^{2(k-1-l)}\nonumber \\= & {} g_0\cdot \alpha ^{2k}+\mu (\mu +1)(1-\alpha ^2)\cdot \tfrac{1-\alpha ^{2k}}{1-\alpha ^2}\nonumber \\&+\,(1-\alpha )(1+2\mu )\big (1-2\alpha ^2(1-\alpha )\,E[\tfrac{ X_{t-1}}{V_t}]\big )\cdot \alpha ^k\cdot \tfrac{1-\alpha ^k}{1-\alpha }\nonumber \\= & {} g_0\cdot \alpha ^{2k}+\mu (\mu +1)(1-\alpha ^{2k})\nonumber \\&+\,(1+2\mu )\big (1-2\alpha ^2(1-\alpha )\,E[\tfrac{ X_{t-1}}{V_t}]\big )(\alpha ^k-\alpha ^{2k}). \end{aligned}$$

(A.14)

If we insert (A.14) into Eq. (A.12), we get

$$\begin{aligned} \tilde{\sigma }_{02}= & {} \sum \limits _{k=0}^\infty (g_k-\mu -\mu ^2)\\= & {} \sum \limits _{k=0}^\infty \Big (g_0\cdot \alpha ^{2k}-\mu (\mu +1)\alpha ^{2k}\\&+\,(1+2\mu )\big (1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}]\big )(\alpha ^k-\alpha ^{2k})\Big )\\= & {} \frac{g_0}{1-\alpha ^2}-\frac{\mu (\mu +1)}{1-\alpha ^2}+\frac{(1+2\mu )\big (1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}]\big )\alpha }{1-\alpha ^2}. \end{aligned}$$

Together with $g_0$ according to (A.11), it follows that

$$\begin{aligned} \tilde{\sigma }_{02}= & {} \frac{(-6\alpha ^2+5+\mu )\mu +1+2\alpha ^2(1-\alpha )(-3+3\alpha +2\alpha \mu )E[\tfrac{ X_{t-1}}{V_t}]}{1-\alpha ^2}\\&-\,\frac{\mu (\mu +1)}{1-\alpha ^2}+\frac{(1+2\mu )(1-2\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}])\alpha }{1-\alpha ^2}\\= & {} \frac{(-6\alpha ^2+2\alpha +4)\mu +1+\alpha +2\alpha ^2(1-\alpha )(-3+2\alpha )E[\tfrac{ X_{t-1}}{V_t}]}{1-\alpha ^2}\\= & {} \frac{2(3\alpha +2)\mu }{1+\alpha } +\frac{1}{1-\alpha } +\frac{2\alpha ^2(-3+2\alpha )}{1+\alpha }E[\tfrac{ X_{t-1}}{V_t}]. \end{aligned}$$

Now, we have to calculate $\tilde{\sigma }_{03}$. For this purpose, we start with

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_t X_{t-1}\right] =E\left[ \tfrac{ X_{t-1}}{V_{t}}\, E\left[ (X_t-M_t)^2X_t \ | \ X_{t-1}\right] \right] \nonumber \\&\overset{(A.8)}{=}&E\left[ \tfrac{ X_{t-1}}{V_{t}}\cdot (M_t^3+3M_tV_t+(1-2\alpha )V_t+2\beta \alpha -2M_t(V_t+M_t^2)+M_t^3)\right] \nonumber \\&\quad =E[ X_{t-1} M_t]+2\beta \alpha \, E[\tfrac{ X_{t-1}}{V_t}]+(1-2\alpha )\mu \nonumber \\&\quad =(1-\alpha )\mu ^2+\alpha (\mu ^2+\mu )+2\beta \alpha \, E[\tfrac{ X_{t-1}}{V_t}]+(1-2\alpha )\mu \nonumber \\&\quad =\mu (\mu -\alpha +1)+2\mu (1-\alpha )\alpha \, E[\tfrac{ X_{t-1}}{V_t}]. \end{aligned}$$

(A.15)

Then,

$$\begin{aligned} \tilde{\sigma }_{03}= & {} \sum \limits _{k=0}^\infty E\left[ (\tfrac{(X_t-M_t)^2}{V_{t}}-1)\cdot ( X_{t+k}X_{t+k-1}-\alpha \mu -\mu ^2) \right] \\&+\,\sum \limits _{k=1}^\infty E\left[ (\tfrac{(X_{t+k}-M_{t+k})^2}{V_{t+k}}-1)\cdot ( X_{t}X_{t-1}-\alpha \mu -\mu ^2) \right] ,\\ \end{aligned}$$

where

$$\begin{aligned}&E\left[ (\tfrac{(X_{t+k}-M_{t+k})^2}{V_{t+k}}-1)\cdot ( X_{t}X_{t-1}-\alpha \mu -\mu ^2) \right] \\&\quad =E\left[ \tfrac{X_{t}X_{t-1}}{V_{t+k}}\cdot E\left[ (X_{t+k}-M_{t+k})^2\ | \ X_{t+k-1}, \ldots \right] \right] -\alpha \mu -\mu ^2\\&\quad =E\left[ X_{t}X_{t-1} \right] -\alpha \mu -\mu ^2\ =\ 0. \end{aligned}$$

Furthermore,

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}X_{t+k-1} \right] -\alpha \mu -\mu ^2\\&\quad = E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1}\cdot E\left[ X_{t+k}\ | \ X_{t+k-1},\ldots \right] \right] -\alpha \mu -\mu ^2\\&\quad = E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1} (\beta +\alpha X_{t+k-1})\right] -\alpha \mu -\mu ^2\\&\quad = \mu (1-\alpha )\, E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1} \right] +\alpha \, E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k-1}^2\right] -\alpha \mu -\mu ^2. \end{aligned}$$

Thus, using that $\alpha \mu +\mu ^2=\alpha (\mu +\mu ^2)+(1-\alpha )\mu ^2$, we obtain

$$\begin{aligned} \tilde{\sigma }_{03}= & {} E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t}X_{t-1}\right] -\alpha \mu -\mu ^2\\&+\,\sum \limits _{k=0}^\infty \left( \mu (1-\alpha )\, E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k} \right] +\alpha \, E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}^2\right] -\alpha \mu -\mu ^2\right) \\= & {} E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t}X_{t-1}\right] -\alpha \mu -\mu ^2+(1-\alpha )\mu \, \sum \limits _{k=0}^\infty \left( E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k} \right] -\mu \right) \\&+\,\alpha \, \sum \limits _{k=0}^\infty \left( E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t+k}^2\right] -\mu -\mu ^2\right) \\= & {} E\left[ \tfrac{(X_t-M_t)^2}{V_{t}}\cdot X_{t}X_{t-1}\right] -\alpha \mu -\mu ^2+(1-\alpha )\mu \, \tilde{\sigma }_{01}+\alpha \, \tilde{\sigma }_{02}, \end{aligned}$$

where we used (A.10) and (A.12) in the last step. Plugging-in $\tilde{\sigma }_{01}, \tilde{\sigma }_{02}$ from Lemma 1 as well as (A.15), it follows that

$$\begin{aligned} \tilde{\sigma }_{03}= & {} \mu (\mu -\alpha +1)+2\mu (1-\alpha )\alpha \, E[\tfrac{ X_{t-1}}{V_t}]-\alpha \mu -\mu ^2\\&+\,(1-\alpha )\mu \, \big (\frac{1}{1-\alpha }-2\alpha ^2\,E[\tfrac{ X_{t-1}}{V_t}]\big )\\&+\,\alpha \, \big (\tfrac{2(3\alpha +2)\mu }{1+\alpha } +\tfrac{1}{1-\alpha } +\tfrac{2\alpha ^2(-3+2\alpha )}{1+\alpha }E[\tfrac{ X_{t-1}}{V_t}]\big ) \\= & {} 2\mu (1-\alpha )+2\alpha (1-\alpha )^2\mu \, E[\tfrac{ X_{t-1}}{V_t}]+\tfrac{2\alpha (3\alpha +2)\mu }{1+\alpha } +\tfrac{\alpha }{1-\alpha } +\tfrac{2\alpha ^3(-3+2\alpha )}{1+\alpha }E[\tfrac{ X_{t-1}}{V_t}]\\= & {} \tfrac{2\mu }{1+\alpha }\,(1+2\alpha +2\alpha ^2)+\tfrac{\alpha }{1-\alpha }+2\alpha \mu (1-\alpha )^2\, E[\tfrac{ X_{t-1}}{V_t}]+\tfrac{2\alpha ^3(-3+2\alpha )}{1+\alpha }\,E[\tfrac{ X_{t-1}}{V_t}]. \end{aligned}$$

So the proof of Lemma 1 is complete.

1.3 Proof of Theorem 1

We use the Delta method the same way as described in the proof of Corollary 1 in Weiß et al. (2017), page 599. Let ${\varvec{g}}:\mathbb R^4\rightarrow \mathbb R^3$ be defined as

$$\begin{aligned} {\varvec{g}}(y_1,\ y_2,\ y_3,\ y_4)\ =\ (y_1,\ y_2\frac{y_3-y_4}{y_3-y_2^2},\ \frac{y_4-y_2^2}{y_3-y_2^2})^{\top }, \end{aligned}$$

where

$$\begin{aligned} {\varvec{g}}(1,\mu ,\mu +\mu ^2,\alpha \mu +\mu ^2)\ =\ (1,\ \beta ,\alpha ). \end{aligned}$$

Then, the Jacobian of ${\varvec{g}}$ is given by

$$\begin{aligned} \mathbf J _{{\varvec{g}}}(y_1,\ y_2,\ y_3,\ y_4)\ =\ \left( \begin{array}{cccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \frac{(y_3-y_4)(y_3+y_2^2)}{(y_3-y_2^2)^2} &{}\quad \frac{y_2(y_4-y_2^2)}{(y_3-y_2^2)^2} &{}\quad \frac{-y_2}{y_3-y_2^2} \\ 0 &{}\quad \frac{2y_2(y_4-y_3)}{(y_3-y_2^2)^2} &{}\quad \frac{y_2^2-y_4}{(y_3-y_2^2)^2} &{}\quad \frac{1}{y_3-y_2^2} \\ \end{array} \right) , \end{aligned}$$

such that

$$\begin{aligned} \mathbf D :=\mathbf J _{{\varvec{g}}}(1,\mu ,\mu +\mu ^2,\alpha \mu ^2+\mu ^2)=\left( \begin{array}{cccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad (1-\alpha )(1+2\mu ) &{} \quad \alpha &{} -1 \\ 0 &{}\quad -2(1-\alpha ) &{}\quad -\frac{\alpha }{\mu } &{}\quad \frac{1}{\mu } \\ \end{array} \right) . \end{aligned}$$

We need to calculate the covariance matrix ${\varvec{\Sigma }}=\mathbf D \tilde{\varvec{\Sigma }}\mathbf D ^{\top }$ with $\tilde{\varvec{\Sigma }}$ from the previous Lemma 1. The components $\sigma _{22},\sigma _{23},\sigma _{33}$ are provided by Weiß and Schweer (2016), page 127. Furthermore, it obviously holds that $\sigma _{11}=\tilde{\sigma }_{00}$. Then,

$$\begin{aligned} \sigma _{12}= & {} \left( 0,\ (1-\alpha )(1+2\mu ),\ \alpha ,\ -1\right) \cdot \left( \tilde{\sigma }_{00},\ \tilde{\sigma }_{01},\ \tilde{\sigma }_{02},\ \tilde{\sigma }_{03} \right) ^{\top }\\= & {} 1+2\mu -2\alpha ^2(1-\alpha )(1+2\mu )E[\tfrac{ X_{t-1}}{V_t}]+\tfrac{2\mu (3\alpha ^2+2\alpha )}{1+\alpha }\\&-\,\tfrac{2\mu (1+2\alpha +2\alpha ^2)}{1+\alpha }-2\alpha \mu (1-\alpha )^2 E[\tfrac{ X_{t-1}}{V_t}]\\= & {} 1+2\mu -\tfrac{2\mu (1-\alpha ^2)}{1+\alpha }-2(1-\alpha )\alpha (\alpha +\mu \alpha +\mu )E[\tfrac{ X_{t-1}}{V_t}]\\= & {} 1+2\alpha \mu -2\alpha (1-\alpha )(\alpha +\mu \alpha +\mu )E[\tfrac{ X_{t-1}}{V_t}]. \end{aligned}$$

Finally,

$$\begin{aligned} \sigma _{13}= & {} \left( 0,\ -2(1-\alpha ),\ -\tfrac{\alpha }{\mu },\ \tfrac{1}{\mu } \right) \cdot \left( \tilde{\sigma }_{00},\ \tilde{\sigma }_{01},\ \tilde{\sigma }_{02},\ \tilde{\sigma }_{03} \right) ^{\top }\\= & {} -2+4\alpha ^2(1-\alpha )E[\tfrac{ X_{t-1}}{V_t}]-\tfrac{2(3\alpha ^2+2\alpha )}{1+\alpha }+\tfrac{2(1+2\alpha +2\alpha ^2)}{1+\alpha }+2\alpha (1-\alpha )^2 E[\tfrac{ X_{t-1}}{V_t}]\\= & {} -2\alpha +2\alpha (1-\alpha ^2) E[\tfrac{ X_{t-1}}{V_t}]. \end{aligned}$$

1.4 Proof of Theorem 2

Using Theorem 1 and the Cramer–Wold device with

$$\begin{aligned} \textstyle {\varvec{l}}\ =\ \Big (1\ , -\frac{1}{\mu (1-\alpha )}(1-\alpha (1-\alpha )E[\frac{ X_{t-1}}{V_t}]),\ -(1-2\alpha )\,E[\frac{X_{t-1}}{V_{t}}]\Big )\in \mathbb R^3, \end{aligned}$$

it follows for the linear approximation (7) that

$$\begin{aligned} \textstyle \sqrt{n}\Big (\mathrm{MS}_R(\beta ,\alpha )-1-(\hat{\alpha }-\alpha )(1-2\alpha )E[\frac{X_{t-1}}{V_{t}}]-(\hat{\beta }-\beta )\frac{1}{\beta }(1-\alpha (1-\alpha )E[\frac{ X_{t-1}}{V_t}])\ \Big ) \end{aligned}$$

converges to the normal distribution with mean 0 and variance $\sigma _{\mathrm{MS}_R}^2={\varvec{l}}{\varvec{\Sigma }}{\varvec{l}}^{\top }$, where ${\varvec{\Sigma }}$ is the covariance matrix from Theorem 1. After tedious calculations, the variance simplifies to

$$\begin{aligned} \sigma _{\mathrm{MS}_R}^2= & {} \frac{3-5\alpha }{1-\alpha }-6 (1-\alpha )^2 \alpha ^2 E[\tfrac{X_{t-1}}{V_t^2}]+\big (\tfrac{\alpha (2 \alpha (\mu +2)+8 \mu -1)}{\mu }-2\big )E[\tfrac{X_{t-1}}{V_t}]\\&+\,\tfrac{(1-\alpha )}{\mu }\left( 5 \alpha ^3 \mu -\alpha ^2 (\mu +3)-5 \alpha \mu +\alpha +\mu \right) E[\tfrac{X_{t-1}}{V_t}]^2. \end{aligned}$$

The proof is complete.

Proofs for Poi-INARCH(1) DGP

1.1 Linear approximation for squared residuals

We proceed in the same way as in Appendix A.1. To apply the linear approximation (5) to the special case of a Poi-INARCH(1) DGP, we require the partial derivatives of $V_t=M_t=\beta +\alpha \,X_{t-1}$, which equal $\frac{\partial }{\partial \alpha }\,V_t=X_{t-1}$ and $\frac{\partial }{\partial \beta }\,V_t=1$. Thus, it follows that

$$\begin{aligned} \textstyle E\big [\frac{\partial V_t}{\partial \alpha }\,\frac{1}{V_t}\big ]\ =\ E\big [\frac{X_{t-1}}{M_t}\big ],\qquad E\big [\frac{\partial V_t}{\partial \beta }\,\frac{1}{V_t}\big ]\ =\ E\big [\frac{1}{M_t}\big ]. \end{aligned}$$

This implies the linear Taylor approximation (10). Note that $E\big [\frac{1}{M_t}\big ]$ can be rewritten as $\frac{1}{\beta }\big (1-\alpha \,E\big [\frac{ X_{t-1}}{M_t}\big ]\big )$.

1.2 Joint distribution of residuals and moments

The Poi-INARCH(1) process satisfies the same mixing and moment conditions as stated for the Poi-INAR(1) process in Appendix A.2. So again, we can use a CLT in the same way as described in Appendix A.2 for the vectors from Eq. (A.1). Note that in the INARCH(1) case, $V_t$ equals $M_t$.

Lemma 2

Let $(X_t)_{\mathbb {Z}}$ be a Poi-INARCH(1) process with $\mu =\frac{\beta }{1-\alpha }$, $\mu (k)=\frac{\mu \,\alpha ^k}{1-\alpha ^2}+\mu ^2$ and

$$\begin{aligned} Y_{t,0}\ =\ \frac{(X_t-M_t)^2}{M_t} - 1 \ =\ \frac{(X_t-\alpha \, X_{t-1} - \beta )^2}{\alpha \, X_{t-1} + \beta } - 1. \end{aligned}$$

Then, $\frac{1}{\sqrt{n}} \sum _{t=1}^n {\varvec{Y}}_t$ is asymptotically normally distributed with mean ${\varvec{0}}$ and covariance matrix $\tilde{{\varvec{\Sigma }}} = (\tilde{\sigma }_{ij})$, where

$$\begin{aligned} \begin{array}{@{}rl@{\qquad }rl} \tilde{\sigma }_{00}\ =&{} 2+E[\frac{1}{M_t}], &{} \tilde{\sigma }_{01}\ =&{} \frac{1}{1-\alpha }, \\ \tilde{\sigma }_{02}\ =&{} \frac{1+4\beta +2\alpha \beta }{(1-\alpha )^2(1+\alpha )}, &{} \tilde{\sigma }_{03}\ =&{} \frac{\alpha +2\beta +4\alpha \beta }{(1-\alpha )^2 (1+\alpha )}. \end{array} \end{aligned}$$

The expressions for $\tilde{\sigma }_{11},\ldots ,\tilde{\sigma }_{33}$ can be found in Theorem 2.2 of Weiß and Schweer (2016).

1.2.1 Proof of Lemma 2

The proof is done in complete analogy to the proof of Lemma 1 in Appendix A.2. For computing conditional moments, we use that the conditional distribution of $X_t$ given $X_{t-1}$ is $Poi (M_t)$, so we use the formulae for Poisson moments in Johnson et al. (2005). Like in Appendix A.2, using that $E\big [\tfrac{(X_t-M_t)^2}{M_t}\big ]=1$, we get

$$\begin{aligned} \tilde{\sigma }_{00}= & {} E\big [\tfrac{(X_t-M_t)^4}{M_t^2}\big ]-1 \ =\ E\big [\tfrac{1}{M_t^2}\,E[(X_t-M_t)^4 \ | \ X_{t-1} ]\big ]-1\\= & {} E\big [\tfrac{1}{M_t^2}\,E[X_t^4-4X_t^3M_t+6X_t^2M_t^2-4X_tM_t^3+M_t^4\ |\ X_{t-1}\ldots ]\big ]-1\\= & {} E\big [\tfrac{1}{M_t^2}\,\big (M_t+7M_t^2+6M_t^3+M_t^4-4(M_t+3M_t^2+M_t^3)M_t\\&+\,6(M_t+M_t^2)M_t^2-3M_t^4\big )\big ]-1\\= & {} E\big [\tfrac{1}{M_t^2}\,(M_t+3M_t^2)\big ]-1 \ =\ 2+E[\frac{1}{M_t}]. \end{aligned}$$

To compute $\tilde{\sigma }_{01}$, we first need

$$\begin{aligned} E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_t\right]= & {} E\left[ \tfrac{1}{M_t} E\left[ (X_t-M_t)^2\ X_t\ |\ X_{t-1}\right] \right] \nonumber \\= & {} E\left[ \tfrac{1}{M_t}(M_t+3M_t^2+M_t^3-2M_t^2-2M_t^3+M_t^3)\right] \nonumber \\= & {} 1+E[M_t]\ =\ 1+\mu . \end{aligned}$$

(B.1)

Then, like in Appendix A.2, it follows that

$$\begin{aligned} \tilde{\sigma }_{01} \ =\ \sum \limits _{k=0}^\infty \left( E\left[ \tfrac{(X_t-M_t)^2}{M_{t}}\cdot X_{t+k}\right] -\mu \right) . \end{aligned}$$

(B.2)

The terms inside the infinite sum can be calculated as

$$\begin{aligned}&E\Big [\tfrac{(X_t-M_t)^2}{M_t}\cdot \underbrace{E\left[ X_{t+k}|\ X_{t+k-1},\ldots \right] }_{\beta +\alpha X_{t+k-1}}\Big ]-\mu \nonumber \\&\quad = \cdots \ =\ \beta +\alpha \beta +\alpha ^2\beta +\cdots +\alpha ^{k-1}\beta +\alpha ^k\, E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_t\right] -\mu \nonumber \\&\overset{(B.1)}{=}&\tfrac{\beta (1-\alpha ^k)}{1-\alpha }+\alpha ^k(1+\mu )-\mu =\alpha ^k+\tfrac{\beta }{1-\alpha }-\mu \ =\ \alpha ^k. \end{aligned}$$

(B.3)

So we get

$$\begin{aligned} \tilde{\sigma }_{01} \ =\ \sum \limits _{k=0}^\infty \left( E\left[ \tfrac{(X_t-M_t)^2}{M_{t}}\cdot X_{t+k}\right] -\mu \right) \ \overset{(B.3)}{=}\ \sum \limits _{k=0}^\infty \alpha ^k \ =\ \frac{1}{1-\alpha }. \end{aligned}$$

(B.4)

Now, let us look at

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_t^2\right] \ =\ E\left[ \tfrac{1}{M_t}\, E\left[ (X_t-M_t)^2\, X_t^2\ |\ X_{t-1}\right] \right] \nonumber \\&\quad =E\left[ \tfrac{1}{M_t}\,\big (M_t+7M_t^2+6M_t^3+M_t^4-2M_t(M_t+3M_t^2+M_t^3)+M_t^2(M_t+M_t^2)\big )\right] \nonumber \\&\quad =1+5\,E[M_t]+E[M_t^2] = 1+5\mu +\alpha ^2\,V[X_{t-1}]+\mu ^2 \nonumber \\&\quad = 1+5\mu +\mu ^2+\alpha ^2\,\tfrac{\mu }{1-\alpha ^2}. \end{aligned}$$

(B.5)

This will be used for

$$\begin{aligned} \tilde{\sigma }_{02} \ =\ \sum \limits _{k=0}^\infty (E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k}^2\right] -\tfrac{\mu }{1-\alpha ^2}-\mu ^2). \end{aligned}$$

(B.6)

We can rewrite the terms inside the infinite sum as

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k}^2 \right] \ =\ E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot E\left[ X_{t+k}^2|\ X_{t+k-1},\ldots \right] \right] \nonumber \\&\quad = E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot (M_{t+k}+M_{t+k}^2)\right] \nonumber \\&\quad = E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot \big [(\beta +\alpha X_{t+k-1})+(\beta +\alpha X_{t+k-1})^2\big ]\right] \nonumber \\&\quad = \beta (1+\beta )+\alpha (1+2\beta )\, E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k-1}\right] +\alpha ^2\,E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k-1}^2 \right] \nonumber \\&\quad \overset{(B.3)}{=} \mu (1-\alpha )\,(1+\beta )+\alpha (1+2\beta )\, (\mu +\alpha ^{k-1})+\alpha ^2\,E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k-1}^2 \right] \nonumber \\&\quad = \mu \,(1+\beta +\alpha \beta )+(1+2\beta )\,\alpha ^k+\alpha ^2\,E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k-1}^2 \right] . \end{aligned}$$

(B.7)

This relationship can be viewed as a recurrence, where $1+\beta +\alpha \beta =1+\mu (1-\alpha ^2)$. Defining $g_k= E\left[ \frac{(X_t-M_t)^2}{M_t}\cdot X_{t+k}^2 \right]$ with

$$\begin{aligned} g_0\ =\ E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_t^2\right] \ =\ 1+5\mu +\mu ^2+\alpha ^2\,\tfrac{\mu }{1-\alpha ^2} \end{aligned}$$

according to (B.5), we have the first-order linear difference equation

$$\begin{aligned} g_k\ =\ \mu \,(1+\mu (1-\alpha ^2))+(1+2\beta )\,\alpha ^k\ +\ \alpha ^2\,g_{k-1}. \end{aligned}$$

It has the unique solution

$$\begin{aligned} g_k= & {} \textstyle g_0\cdot \prod \limits _{i=0}^{k-1}\alpha ^2+\sum \limits _{j=0}^{k-1}[\mu \,(1+\mu (1-\alpha ^2))+(1+2\beta )\,\alpha ^{j+1}]\cdot \prod \limits _{w =j+1}^{k-1}\alpha ^2\nonumber \\= & {} \textstyle g_0\cdot \alpha ^{2k}+\mu \,(1+\mu (1-\alpha ^2))\sum \limits _{j=0}^{k-1}\alpha ^{2(k-1-j)}+(1+2\beta )\,\sum \limits _{l=0}^{k-1} \alpha ^{l+1}\cdot \alpha ^{2(k-1-l)}\nonumber \\= & {} g_0\cdot \alpha ^{2k}+\mu \,(1+\mu (1-\alpha ^2))\cdot \tfrac{1-\alpha ^{2k}}{1-\alpha ^2}+(1+2\beta )\,\alpha ^k\cdot \tfrac{1-\alpha ^k}{1-\alpha }\nonumber \\= & {} g_0\cdot \alpha ^{2k}+\big (\tfrac{\mu }{1-\alpha ^2}+\mu ^2\big )\,(1-\alpha ^{2k})+\tfrac{1+2\beta }{1-\alpha }\cdot (\alpha ^k-\alpha ^{2k}), \end{aligned}$$

(B.8)

which also holds for $k=0$. Thus,

$$\begin{aligned} \tilde{\sigma }_{02}= & {} \sum \limits _{k=0}^\infty (g_k-\tfrac{\mu }{1-\alpha ^2}-\mu ^2)\nonumber \\= & {} \sum \limits _{k=0}^\infty \Big (g_0\cdot \alpha ^{2k} +\big (\tfrac{\mu }{1-\alpha ^2}+\mu ^2\big )\,(1-\alpha ^{2k}) +\tfrac{1+2\beta }{1-\alpha }\cdot (\alpha ^k-\alpha ^{2k})-\tfrac{\mu }{1-\alpha ^2}-\mu ^2\Big ). \end{aligned}$$

All the terms without the power k can be added together:

$$\begin{aligned} \big (\tfrac{\mu }{1-\alpha ^2}+\mu ^2\big )-\tfrac{\mu }{1-\alpha ^2}-\mu ^2\ =\ 0. \end{aligned}$$

So we can further calculate

$$\begin{aligned} \tilde{\sigma }_{02}= & {} \sum \limits _{k=0}^\infty \big (g_0\cdot \alpha ^{2k}-\big (\tfrac{\mu }{1-\alpha ^2}+\mu ^2\big )\,\alpha ^{2k}+\tfrac{1+2\beta }{1-\alpha }\,(\alpha ^k-\alpha ^{2k})\big )\\&\overset{(B.5)}{=}&\big (1+5\mu +\mu ^2+\alpha ^2\,\tfrac{\mu }{1-\alpha ^2}-\tfrac{\mu }{1-\alpha ^2}-\mu ^2-\tfrac{1+2\beta }{1-\alpha }\big )\,\sum \limits _{k=0}^\infty \alpha ^{2k} \ +\ \tfrac{1+2\beta }{1-\alpha }\,\sum \limits _{k=0}^\infty \alpha ^k\\= & {} \big (1+4\mu -\tfrac{1+2\beta }{1-\alpha }\big )\,\tfrac{1}{1-\alpha ^2} \ +\ \tfrac{1+2\beta }{1-\alpha }\,\tfrac{1}{1-\alpha } \ =\ \big (2\mu -\tfrac{\alpha }{1-\alpha }\big )\,\tfrac{1}{1-\alpha ^2} \ +\ \tfrac{1+2\beta }{(1-\alpha )^2}\\= & {} \tfrac{2\beta -\alpha }{(1-\alpha )^2(1+\alpha )} \ +\ \tfrac{(1+2\beta )(1+\alpha )}{(1-\alpha )^2(1+\alpha )} \ =\ \tfrac{1+4\beta +2\alpha \beta }{(1-\alpha )^2(1+\alpha )}. \end{aligned}$$

So it remains to calculate $\tilde{\sigma }_{03}$. First,

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_t X_{t-1}\right] =E\left[ \tfrac{ X_{t-1}}{M_t}\,E\left[ (X_t-M_t)^2X_t \ | \ X_{t-1}\right] \right] \nonumber \\&\quad = E\left[ \tfrac{ X_{t-1}}{M_t}\cdot (M_t+3M_t^2+M_t^3-2M_t(M_t+M_t^2)+M_t^3)\right] \nonumber \\&\quad = \mu +E\left[ X_{t-1} M_t\right] \ =\ \mu (1+\beta )+\alpha \,\mu (0) \nonumber \\&\quad = \mu (1+\beta )+\alpha \,\big (\tfrac{\mu }{1-\alpha ^2}+\mu ^2\big ) \ =\ \mu (1+\mu )+\tfrac{\alpha \,\mu }{1-\alpha ^2}. \end{aligned}$$

(B.9)

Then, like in Appendix A.2, we have

$$\begin{aligned} \tilde{\sigma }_{03} \ =\ \sum \limits _{k=0}^\infty (E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k}X_{t+k-1} \right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2). \end{aligned}$$

Here,

$$\begin{aligned}&E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k}X_{t+k-1} \right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2\\&\quad =E\left[ \tfrac{(X_t-M_t)^2}{M_t}\,X_{t+k-1} \cdot E\left[ X_{t+k}\ | \ X_{t+k-1}, \ldots \right] \right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2\\&\quad =E\left[ \tfrac{(X_t-M_t)^2}{M_t}\,X_{t+k-1} \cdot (\beta +\alpha X_{t+k-1})\right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2\\&\quad =\beta \, E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k-1} \right] +\alpha \, E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k-1}^2\right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2. \end{aligned}$$

Thus, it follows that

$$\begin{aligned} \tilde{\sigma }_{03}= & {} E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t}X_{t-1} \right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2\\&+\sum \limits _{k=0}^\infty \Big (\beta \, E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k} \right] +\alpha \, E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t+k}^2\right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2\Big ). \end{aligned}$$

Comparing with (B.2) and (B.6), and using that

$$\begin{aligned} \beta \,\mu \ +\ \alpha \,\big (\tfrac{\mu }{1-\alpha ^2}+\mu ^2\big ) \ =\ \tfrac{\alpha \,\mu }{1-\alpha ^2}+\mu ^2, \end{aligned}$$

it follows that

$$\begin{aligned} \tilde{\sigma }_{03} \ =\ E\left[ \tfrac{(X_t-M_t)^2}{M_t}\cdot X_{t}X_{t-1} \right] -\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2 \ +\ \beta \,\tilde{\sigma }_{01} \ +\ \alpha \,\tilde{\sigma }_{02}. \end{aligned}$$

Plugging-in $\tilde{\sigma }_{01},\tilde{\sigma }_{02}$ from Lemma 2 as well as (B.9), we obtain

$$\begin{aligned} \tilde{\sigma }_{03}= & {} \mu (1+\mu )+\tfrac{\alpha \,\mu }{1-\alpha ^2}-\tfrac{\alpha \,\mu }{1-\alpha ^2}-\mu ^2 \ +\ \beta \,\tfrac{1}{1-\alpha } \ +\ \alpha \,\tfrac{1+4\beta +2\alpha \beta }{(1-\alpha )^2(1+\alpha )}\\= & {} 2\mu \ +\ \alpha \,\tfrac{1+4\beta +2\alpha \beta }{(1-\alpha )^2(1+\alpha )} \ =\ \tfrac{2\beta (1-\alpha ^2)}{(1-\alpha )^2(1+\alpha )}\ +\ \tfrac{\alpha +4\alpha \beta +2\alpha ^2\beta }{(1-\alpha )^2(1+\alpha )} \ =\ \tfrac{\alpha +2\beta +4\alpha \beta }{(1-\alpha )^2 (1+\alpha )}. \end{aligned}$$

This completes the proof of Lemma 2.

1.3 Proof of Theorem 3

The proof follows the same steps as in Appendix A.3, and the required matrix $\mathbf D$ can be directly taken from page 599 in Weiß et al. (2017):

$$\begin{aligned} \mathbf D =\left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} (1-\alpha )\big (1+2\mu (1-\alpha ^2)\big )&{} \alpha (1-\alpha ^2) &{} -(1-\alpha ^2) \\ 0 &{} -2(1-\alpha )^2(1+\alpha ) &{} -(1-\alpha ^2)\,\frac{\alpha }{\mu } &{} (1-\alpha ^2)\,\frac{1}{\mu } \\ \end{array} \right) . \end{aligned}$$

Then, we calculate the covariance matrix ${\varvec{\Sigma }}=\mathbf D \tilde{\varvec{\Sigma }}\mathbf D ^{\top }$ with $\tilde{\varvec{\Sigma }}$ from the previous Lemma 2. The components $\sigma _{22},\sigma _{23},\sigma _{33}$ are provided by Weiß and Schweer (2016), page 129, or by Weiß et al. (2017), page 599. Furthermore, it obviously holds that $\sigma _{11}=\tilde{\sigma }_{00}$. Then,

$$\begin{aligned} \sigma _{12}= & {} \left( 0,\ (1-\alpha )\big (1+2\mu (1-\alpha ^2)\big ),\ \alpha (1-\alpha ^2),\ -(1-\alpha ^2) \right) \cdot \left( \tilde{\sigma }_{00},\ \tilde{\sigma }_{01},\ \tilde{\sigma }_{02},\ \tilde{\sigma }_{03} \right) ^{\top }\\= & {} 1+2\mu (1-\alpha ^2)+\frac{\alpha (1+4\beta +2\alpha \beta )}{1-\alpha }-\frac{\alpha +2\beta +4\alpha \beta }{1-\alpha }\\= & {} 1+2\mu (1-\alpha ^2)+\frac{-2\beta +2\alpha ^2\beta }{1-\alpha }\ =\ 1. \end{aligned}$$

Finally,

$$\begin{aligned} \sigma _{13}= & {} \left( 0,\ -2(1-\alpha )^2(1+\alpha ),\ -(1-\alpha ^2)\,\tfrac{\alpha }{\mu },\ (1-\alpha ^2)\,\tfrac{1}{\mu } \right) \cdot \left( \tilde{\sigma }_{00},\ \tilde{\sigma }_{01},\ \tilde{\sigma }_{02},\ \tilde{\sigma }_{03} \right) ^{\top }\\= & {} -2(1-\alpha ^2)-\frac{1+4\beta +2\alpha \beta }{1-\alpha }\,\frac{\alpha }{\mu }+\frac{\alpha +2\beta +4\alpha \beta }{1-\alpha }\,\frac{1}{\mu }\\= & {} -2(1-\alpha ^2)+2(-\alpha ^2+1)\ =\ 0. \end{aligned}$$

1.4 Proof of Theorem 4

Using Theorem 3 and the Cramer–Wold device with

$$\begin{aligned} \textstyle {\varvec{l}}\ =\ \Big (1,\ -\frac{1}{\mu (1-\alpha )}\, \big (1-\alpha \,E\big [\frac{X_{t-1}}{M_t}\big ]\big ),\ -E[\frac{X_{t-1}}{M_t}] \Big )\in \mathbb {R}^3, \end{aligned}$$

it follows for the linear approximation (10) that

$$\begin{aligned} \textstyle \sqrt{n} \Big (\mathrm{MS}_R(\beta ,\alpha ) - E\big [\frac{X_{t-1}}{M_t}\big ]\,(\hat{\alpha }-\alpha ) - \frac{1}{\beta }\, \Big (1-\alpha \,E\big [\frac{X_{t-1}}{M_t}\big ]\Big )\,(\hat{\beta }-\beta )\ -1\Big ) \end{aligned}$$

converges to the normal distribution with mean 0 and variance $\sigma _{\mathrm{MS}_R}^2={\varvec{l}}{\varvec{\Sigma }}{\varvec{l}}^{\top }$, where ${\varvec{\Sigma }}$ is the covariance matrix from Theorem 3. After tedious calculations, the variance simplifies to

$$\begin{aligned} \sigma _{\mathrm{MS}_R}^2= & {} \frac{\alpha ^4 (\mu +2)+\alpha ^3 (1-3 \mu )-\alpha \mu +3 \mu }{(1-\alpha )(1-\alpha ^3)\, \mu }\\&+\frac{(1+\alpha ) \left( \alpha ^3 (2 \mu -3)+\alpha ^2-\alpha -2 \mu \right) }{(1-\alpha )(1-\alpha ^3)\, \mu }\,E[\tfrac{X_{t-1}}{M_t}]\\&+\,\frac{\alpha ^4 (1-\mu ) +\alpha ^3(1-\mu )+\alpha \mu +\alpha +\mu }{(1-\alpha )(1-\alpha ^3)\, \mu }\,E[\tfrac{X_{t-1}}{M_t}]^2. \end{aligned}$$

Tables

See Tables 1, 2, 3, 4, 5, 6, 7, 8 and 9.

Table 1 Hypothetical model: Poi-INAR(1); DGP: Poi-INAR(1)

Table 2 Hypothetical model: Poi-INAR(1); DGP: Poi-INAR(1) (if $I=1$) or NB-INAR(1) (if $I>1$)

Table 3 Hypothetical model: Poi-INAR(1); DGP: Poi-INAR(1) (if $I=1$) or ZIP-INAR(1) (if $I>1$)

Table 4 Hypothetical model: Poi-INAR(1); DGP: Poi-INAR(1) (if $I=1$) or Good-INAR(1) (if $I<1$)

Table 5 Hypothetical model: Poi-INARCH(1); DGP: Poi-INARCH(1)

Table 6 Hypothetical model: Poi-INARCH(1); DGP: Poi-INARCH(1) (if $\theta =1$) or NB-INARCH(1) (if $\theta >1$)

Table 7 Hypothetical model: Poi-INAR(1); DGP: Poi-INAR(1) (if $I=1$) or NB-INAR(1) (if $I>1$)

Table 8 Hypothetical model: Poi-INAR(1); DGP: Poi-INAR(1)

Table 9 Hypothetical model: Poi-INAR(1); DGP: Poi-INAR(1) (if $I=1$) or NB-INAR(1) (if $I>1$)