Dynamic matching pennies on networks

Abstract

We consider a network game based on matching pennies with two types of agents, conformists and rebels. Conformists prefer to match the action taken by the majority of her neighbors while rebels like to match the minority. We investigate the simultaneous best response dynamic focusing on the lengths of limit cycles (LLC for short). We show that $\hbox {LLC}=1$ or 2 when all agents are of the same type, and $\hbox {LLC}=4$ when there is no conformist-rebel edge and no two even-degreed agents (if any) are neighboring each other. Moreover, $\hbox {LLC}=1$ for almost all type configurations when the network is a line or a ring, which implies that a pure strategy Nash equilibrium is reached from any initial action profile. However, $\hbox {LLC}=4$ for about one half of the type configurations with star networks.

1 Introduction

The theory of network games has become a booming field and attracted increasing attention from social and computer scientists.¹ One direction of research in this field is to model social interactions by letting two-player games be simultaneously played by players connected through network structures. In this paper, we study such a network extension of matching pennies.² There is generally no pure strategy Nash equilibrium (PNE for short) in this model, so we study its best-response dynamics, which are mimics of individuals’ adaptive behaviors and the limit cycles of which to be introduced soon could also be viewed as extensions of PNE.

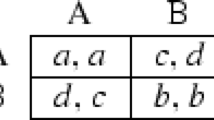
Matching pennies is an asymmetric game. It can be intuitively interpreted as that the row player (called a conformist) preferring to coordinate with her opponent’s action, while the column player (called a rebel) preferring to anti-coordinate. Therefore, in a network extension of matching pennies, it is natural to assume that a pair of conformists play a coordination game, a pair of rebels play an anti-coordination game, and a conformist-rebel pair plays matching pennies. With this in mind, the model, to be referred to as the network matching pennies game (NMP for short), can be decomposed into three elementary base games, namely, matching pennies, a coordination game, and an anti-coordination game, among which matching pennies is the most essential one, because it is the only one that has both types of players. The NMP model is originally proposed by Jackson (2008, P.271) for the analysis of the phenomenon of fashion and subsequently analyzed by Cao et al. (2013), Cao and Yang (2014), and Zhang et al. (2018). However, the potential applications of NMP are not restricted to fashion. For example, the dynamics of NMP, as studied in this paper, may be viewed as learning processes of heterogeneous agents with different learning rules. Conforming and rebelling behaviors are also closely related to herding and contrarian behaviors, which are well recognized as being critical to understanding financial markets (Park and Sabourian 2011). In fact, there are at least three types of conforming/rebelling behaviors, namely, pure conformity/rebellion, instrumental conformity/rebellion, and informational conformity/rebellion, as detailed in Young (2001) and Zhang et al. (2018).

1.1 Results

We mainly focus on the simultaneous best response dynamics (simultaneous BRD for short). Since the simultaneous BRD is deterministic, and there are a total of finitely many states, it will eventually enter a cycle, which is usually called a limit cycle in the literature on dynamic systems. We are mainly concerned with the lengths of limit cycles (LLC for short) under simultaneous BRD. It is clear that a PNE must exist for the corresponding NMP when $\hbox {LLC}=1$.

Dynamic analyses on general network structures are usually very complicated. For the particular model that we are interested in, even the static problem of deciding whether a PNE exists is computationally hard (Cao and Yang 2014). For this reason, we shall investigate two benchmark cases: the case with a single type of agents and the case without direct interaction among agents of the same type, and three special network structures: lines, rings or stars. Although these network structures seem simple, some of the analyses are nontrivial. In addition, they are frequently analyzed in the literature on social learning and cultural dynamics, a field that is closely related to this paper.³

Our main findings are summarized as follows. (i) We show that $\hbox {LLC}=1$ or 2 when all agents are of the same type (Theorem 1).⁴ (ii) We generalize the simple fact that matching pennies has $\hbox {LLC}=4$ to NMPs with all edges being conformist-rebel ones under certain additional conditions (Theorem 2). (iii) When the underlying network is a line or a star, all the possible LLCs for NMPs are 1, 2 and 4 (Theorems 3, 5). When the network is a ring, however, LLC can be as large as twice the size of the network (Remark 5), although in most cases the properties with rings are similar to those with lines (Theorem 4). (iv) If a network is sufficiently large, then regardless of the initial action profiles, NMP has $\hbox {LLC}=1$ for almost all type configurations when the network is a line or a ring (Theorem 6(a)), and $\hbox {LLC}=4$ for approximately one half of the type configurations when the network is a star (Theorem 6(b)).

In an appendix, we also investigate the sequential BRD. It turns out that when the underlying network is a line or a ring, NMP is an ordinal potential game, which implies that the sequential BRD converges to a PNE, if and only if the network is not completely heterophilic (i.e., not all edges are conformist-rebel ones) (Theorem 7). For star networks, we consider a particular sequential BRD, where at each time step unsatisfied agents are randomly selected to deviate with the probability that each unsatisfied agent is selected being positive. We show that when the underlying network is a star, the probability that the above sequential BRD converges is one if and only if at least one half of the peripheral agents are of the same type as the central agent, a condition that is equivalent to the existence of a PNE (Theorem 8).

1.2 Related work

The NMP model is originally proposed by Jackson (2008), who observed that when each agent has no fewer conformist neighbors than rebel neighbors, the existence of a PNE is guaranteed. Applying a partial potential analysis, Zhang et al. (2018) established an improvement of the above observation by showing that we only need to require each conformist have no fewer conformist neighbors than rebel neighbors to guarantee the existence of a PNE. The major difference between this paper and Zhang et al. (2018) is that the latter paper studies sequential BRD by transforming the discrete dynamic into a system of ordinary differential equations, whereas the present paper mainly focuses on simultaneous BRD, a dynamic that is much less understood in the literature than its sequential counterpart. In addition, the present paper also carries out a rigorous analysis, instead of an approximate analysis as in Zhang et al. (2018), of the sequential BRD. The major difference between this paper and Cao and Yang (2014) is that the latter focuses on computational issues. While we are concerned with LLC and convergence of BRDs, Cao et al. (2013) concentrated on the cooperation level problem in NMP through numerical simulations.

Since the coordination game and the anti-coordination game are both base games, NMP can also be viewed as a combination of the network coordination game and the network anti-coordination game. The literature on network coordination games is too vast for us to give a complete survey here. In particular, Apt et al. (2017) considered general coordination games on networks where agents typically have different action sets. Several other related useful results for this paper will be introduced when they are applied. The network anti-coordination game, in contrast, attracts considerably less attention. The most influential papers on this topic are Bramoullé et al. (2004) and Bramoullé (2007).⁵ In the field of social physics, a closely related and extensively studied model is the minority game (also known as the El Farol Bar problem), a model that was proposed by Arthur (1994) and developed by Challet and Zhang (1997) with numerous follow-ups. We refer the reader to Szabó et al. (2014) for a recent study of the evolutionary matching pennies game on bipartite regular networks.

Our research falls into the booming field of network games. The NMP model is a mixture of a network game with strategic complements and a network game with strategic substitutes, the two most extensively studied classes of network game models. Indeed, it exhibits a simple form of strategic complement for conformists and a simple form of strategic substitute for rebels. In a recent paper by Bramoullé et al. (2014), mixtures of strategic complements and strategic substitutes are allowed, but action sets in their paper are continuous. In Hernandez et al. (2013), both strategic complement and strategic substitute are considered. However, for any specific values of parameters in their model, strategic complement and strategic substitute do not coexist. Other recent related works include Southwell and Cannings (2013), Ramazi et al. (2016), Haslegrave and Cannings (2017), and Shirado and Christakis (2017).⁶

The rest of this paper is organized as follows. Section 2 formally introduces the NMP model. Section 3 deals with two benchmark cases for the simultaneous BRD. Section 4 considers three special network structures for the simultaneous BRD. Section 5 concludes the paper with several further discussions. Most of the proofs and the investigation of the sequential BRD are organized in an appendix.

2 The model

In the NMP model, there are two types of agents, conformists and rebels, located on a fixed network. Conformists like to match the majority action of her neighbors, while rebels prefer to match the minority. Each agent has two available actions, named 0 and 1, which can be interpreted as wearing white or black skirts, buying or not buying an iphone, etc.⁷ According to their types, each pair of neighboring agents play one of the three base games, the payoffs of which are described in Fig. 1. We assume that each agent takes the same action in all of the base games she plays. The overall payoff of each agent is simply the sum of the payoffs that she receives in all the games she plays.

Fig. 1

The three base games. (1) The coordination game (left): a conformist versus a conformist; (2) the anti-coordination game (middle): a rebel versus a rebel; (3) matching pennies (right): a conformist versus a rebel. Conformists are represented by circles, and rebels by triangles

Formally, we use $\{C,R\}$ to denote the type set, where C stands for conformists and R for rebels. For each agent i, $T_i\in \{C,R\}$ is her type. An NMP is represented by a triple $G=(N,\mathrm{g},{\mathbf {T}})$, where

• $N=\{1,2,\ldots ,n\}$ is the set of agents;

• $\mathrm{g}\subseteq N\times N$ is the set of links (edges);

• ${\mathbf {T}}=(T_1,T_2,\ldots ,T_n)\in \{C,R\}^n$ is the configuration of agents’ types.

The underlying network $(N,\mathrm{g})$ is undirected. That is, ij and ji represent the same link. Two agents $i,j\in N$ are neighboring each other if and only if $ij\in \mathrm{g}$. We also use $N_i$ to denote the set of neighbors of agent i, i.e., $N_i=\{j\in N: ij\in \mathrm{g}\}$. In simultaneous BRD, time elapses discretely. Agents’ types do not change over time, but their actions may change. We use

$$\begin{aligned} {\mathbf {x}}(0)=(x_1(0),x_2(0),\ldots ,x_n(0))\in \{0,1\}^n \end{aligned}$$

to denote the initial action profile, where $x_i(0)$ is the initial action of agent i. We define $x_i(t)\in \{0,1\}$ as the action of agent i at time t, and write ${\mathbf {x}}(t)=(x_1(t),x_2(t),\ldots ,x_n(t))$.

Define $L_i({\mathbf {x}}(t))\subseteq N_i$ as the subset of neighbors at time t that are liked by agent i. Since conformists like those taking the same action while rebels the opposite, we have

$$\begin{aligned} L_i({\mathbf {x}}(t))=\left\{ \begin{array}{ll}\{j\in N_i: x_j(t)=x_i(t)\} &{}\quad if\ T_i=C,\\ \{j\in N_i: x_j(t)\ne x_i(t)\}&{}\quad if\ T_i=R.\end{array}\right. \end{aligned}$$

Set $D_i({\mathbf {x}}(t))=N_i{\setminus } L_i({\mathbf {x}}(t))$ as the subset of neighbors that are disliked by agent i at time t. According to the payoff settings in Fig. 1, agent i gains 1 unit from interacting with each neighboring agent in $L_i({\mathbf {x}}(t))$ but loses 1 unit from interacting with each of those in $D_i({\mathbf {x}}(t))$. Thus, given an action profile ${\mathbf {x}}(t)$ at time t, the utility of agent i is given by

$$\begin{aligned} u_i({\mathbf {x}}(t))=|L_i({\mathbf {x}}(t))|-|D_i({\mathbf {x}}(t))|. \end{aligned}$$

When $u_i({\mathbf {x}}(t)\ge 0$, we may also say that agent i is satisfied (at time t). Otherwise, she is called unsatisfied. Under the simultaneous BRD, agent i switches her action at time t if and only if she is unsatisfied:

$$\begin{aligned} x_i(t+1)=\left\{ \begin{array}{ll}1-x_i(t)&{}\quad if\ u_i({\mathbf {x}}(t))<0,\\ x_i(t)&{}\quad otherwise.\end{array}\right. \end{aligned}$$

The focus of our analysis is on the limit cycle, a basic concept from dynamic systems. Intuitively, a limit cycle is an ordered set of action profiles such that starting from each of these profiles the system will evolve into its immediate successor (the successor of the last action profile is the first one). Since there are a total of finitely many action profiles in the NMP and simultaneous BRD is deterministic, some profile will reappear after a certain number of steps. From that time on, everything will be repeated just as that state is reached for the first time. Therefore, limit cycle always exists and it is unique for any NMP and an initial action profile.

In the rest of this paper, we also use ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ to denote an initialized NMP. Below is the formal definition of a limit cycle.

Definition 1

Let ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ be an initialized NMP, and $t({\mathcal {I}})\ge 1$ be the first time such that

$$\begin{aligned} {\mathbf {x}}(t({\mathcal {I}}))\in \{{\mathbf {x}}(0),{\mathbf {x}}(1),\ldots , {\mathbf {x}}(t({\mathcal {I}})-1)\}. \end{aligned}$$

Let $r({\mathcal {I}})<t({\mathcal {I}})$ be the time such that ${\mathbf {x}}(t({\mathcal {I}}))={\mathbf {x}}(r({\mathcal {I}}))$. We call the ordered set of states $({\mathbf {x}}(r({\mathcal {I}})),{\mathbf {x}}(r({\mathcal {I}})+1),\ldots , {\mathbf {x}}(t({\mathcal {I}})-1))$ the limit cycle of ${\mathcal {I}}$.

In the rest of this paper, we use $\ell ({\mathcal {I}})=t({\mathcal {I}})-r({\mathcal {I}})$ to denote the length of the limit cycle (LLC for short) of ${\mathcal {I}}$. When time goes beyond $r({\mathcal {I}})$, we say that simultaneous BRD enters the limit cycle. For an initialized NMP ${\mathcal {I}}$, it is clear that a PNE will be eventually reached via simultaneous BRD if and only if $\ell ({\mathcal {I}})=1$, in which case we also say that the simultaneous BRD converges.

Example 1

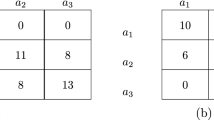
Matching pennies, when viewed as an NMP with exactly one conformist and one rebel who are connected, has $\hbox {LLC}=4$. See Fig. 2 for an illustration.

Fig. 2

$\text {LLC}=4$ in matching pennies. Conformists and rebels are represented by circles and triangles, respectively. Actions are indicated by colors: black for 1 and white for 0

Remark 1

A closely related model to NMP that has been extensively studied is the threshold model (Granovetter 1978). In the threshold model, there is a threshold for each agent and she prefers action 1 over action 0 if and only if the number of her neighbors choosing action 1 is greater than or equal to this threshold. When the threshold is one half of the degree for each agent, the corresponding simultaneous BRD is also known as the majority dynamic. It is worth noting that the preference of a conformist in NMP is not exactly the same as in the majority dynamic. The subtle difference lies in the tie-breaking rules: when the number of action 1 neighbors of an agent is exactly the threshold, action 1 is biased in the majority dynamic, but action 1 and action 0 are symmetric in NMP. It has been pointed out that the tie-breaking rule may be very critical in global behaviors of the dynamic and other tie-breaking rules have also been studied in the literature (Gärtner and Zehmakan 2017).

3 Simultaneous BRD: two benchmark cases

In this section, we consider two benchmark cases. (i) The case where either all agents are conformists (a network coordination game) or all agents are rebels (a network anti-coordination game). Note that in this case all interactions are inner-type ones, i.e., there is no conformist-rebel edge. (ii) The case where all interactions are cross-type ones, i.e., all edges are conformist-rebel ones. In terms of homophily, the first benchmark is the completely homophilic case and the second benchmark is the completely heterophilic case.⁸

3.1 The completely homophilic case

It is well-known that any threshold model has an LLC of either one or two via a Lyapunov function method (Poljak and Sura 1983; Goles 1987; Berninghaus and Schwalbe 1996). It was pointed out by Cannings (2009) that the same Lyapunov function works for anti-threshold models, deriving an LLC of either one or two. However, as we have pointed out in Remark 1, there is a subtle difference between the tie-breaking rules of a threshold model and the network coordination game. As a result, the Lyapunov functions constructed in Poljak and Sura (1983), Goles (1987) and Berninghaus and Schwalbe (1996) do not apply to the network coordination game or the network anti-coordination game. Yet, the $LLC\le 2$ property still holds.

Theorem 1

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP such that all agents are of the same type. Then LLC equals 1 or 2.

Our proof is based on the Lyapunov function applied in a recent paper by Haslegrave and Cannings (2017), who studied a mixture of a threshold model and an anti-threshold model, which has different tie-breaking rules with our model.

For each agent $i\in N$ and time $t\ge 1$, we use $n_i^1(t)$ to denote the number of i’s neighbors that use action 1 at time t. The following observations are critical.

Observation 1

Suppose i is a conformist. (i) If $x_i(t+1)=1,$ then $n_i^1(t) \ge n_i/2$. (ii) If $x_i(t+1)=0,$ then $n_i^1(t)\le n_i/2$.

Note that the other way around is incorrect in both cases of the observation, because $x_i(t+1)=x_i(t)$ when $n_i^1(t)=n_i/2$. In addition, if $n_i$ is odd, the two inequalities are both strict. We have an analogous observation for rebels.

Observation 2

Suppose i is a rebel. (i) If $x_i(t+1)=1,$ then $n_i^1(t) \le n_i/2$. (ii) If $x_i(t+1)=0,$ then $n_i^1(t)\ge n_i/2$.

Using the above two observations, it can be shown that the proof of Haslegrave and Cannings (2017) can be adapted for Theorem 1 (Appendix A).

Remark 2

Theorem 1 may not be valid in the general case, even if there is only one conformist-rebel edge. The example in Fig. 3 provides an illustration.

Fig. 3

$\text {LLC}=6$ in an NMP with one conformist-rebel edge. Conformists and rebels are represented by circles and triangles, respectively. Actions are indicated by colors: black for 1 and white for 0. Unhappy faces indicate that the corresponding agents are unsatisfied

3.2 The completely heterophilic case

As illustrated in Fig. 2, matching pennies always has $\hbox {LLC}=4$ under simultaneous BRD. Theorem 2 of this subsection is a generalization of this simple fact. Before presenting this result, we provide a formal definition of complete heterophily.

Definition 2

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP. If $T_i\ne T_j$ for all $ij\in \mathrm{g}$, i.e., the neighbors of any conformist are all rebels and the neighbors of any rebel are all conformists, we say that G is completely heterophilic.

If G is completely heterophilic, then the underlying network $(N,\mathrm{g})$ is a bipartite network with one side of all conformists and the other side of all rebels.⁹ This structure is a natural generalization of that in the matching pennies game, because only matching pennies will be played in this NMP but the other two base games do not occur.

Theorem 2

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be a completely heterophilic NMP. If no two even-degreed agents (if any) are neighboring each other,  then $\hbox {LLC}=4$.

Proof

We prove in two steps. In the first step we show via a new Lyapunov function that $x_i(t-1)\ne x_i(t+1)$ for any agent i with an odd degree and large enough t such that a limit cycle is reached at time $t-1$. This implies that the period of the action series of agent i in the limit cycle is 4. In the second step, we show that the action series of an even-degreed agent is of either period 1 or period 4, if her neighbours are all odd-degreed. The proof is completed by combining these two steps.

Step 1: Denote $\alpha _C(t)=\sum _{i\in C: x_i(t)=1}n_i^1(t-1)$ as the number of ij links such that $i\in C, x_i(t)=1$ and $j \in R, x_j(t-1)=1$, and $\beta _C(t)=\sum _{i\in C: x_i(t)=1 \text{ or } x_i(t-1)=0}n_i/2$. Analogously, denote $\alpha _R(t)=\sum _{i\in R: x_i(t)=1}n_i^1(t-1)$ as the number of ij links such that $i\in R, x_i(t)=1$ and $j \in C, x_j(t-1)=1$, and $\beta _R(t)=\sum _{i\in R: x_i(t)=1 \text{ or } x_i(t-1)=0}n_i/2$. Define a Lyapunov function

$$\begin{aligned} \gamma (t)=[\alpha _C(t)-\beta _C(t)]-[\alpha _R(t)-\beta _R(t)]. \end{aligned}$$

It can be checked that

where

$$\begin{aligned} C_{1\rightarrow 1}(t)=\{i\in C: x_i(t-1)=1, x_i(t+1)=1\} \end{aligned}$$

is the set of conformists who take action 1 at time $t-1$ and time $t+1$, and $C_{0\rightarrow 0}(t), R_{1\rightarrow 1}(t)$ and $R_{0\rightarrow 0}(t)$ are analogously defined.

By Observations 1 and 2, $\gamma (t+1)-\gamma (t)$ is always nonnegative. Consequently, $\gamma (t)$ must be a constant in a limit cycle. In particular, if $n_i$ is odd, then we must have $x_i(t-1)\ne x_i(t+1)$ in the limit cycle, i.e, $C_{1\rightarrow 1}(t), C_{0\rightarrow 0}(t), R_{1\rightarrow 1}(t)$ and $R_{0\rightarrow 0}(t)$ are all empty. This implies that the action series of agent i has the form of $00110011\cdots$ in the limit cycle, i.e., with a period of 4.

Step 2: We now consider the case that every neighbour of an even-degreed agent j has an odd degree. Suppose that agent j has k neighbours, among whom $k_{j0}(t)$ agents use action 0 and $k_{j1}(t)$ agents use action 1 at time t. Let $k_{j}(t)=k_{j0}(t)-k_{j1}(t)$ be the value of the number of j’s action 0 neighbors minus the number of j’s action 1 neighbors at time t. From Step 1, the period of the action series of any of agent j’s neighbor i is 4 in a limit cycle, leading to $x_i(t-1)\ne x_i(t+1)$. This implies that $k_{j0}(t-1)=k_{j1}(t+1)$ and $k_{j1}(t-1)=k_{j0}(t+1)$, and hence $k_{j}(t)=-k_{j}(t+2)=k_{j}(t+4)$. For simplicity, we denote the time series of $k_{j}(t)$ by $[k_{j}(t), k_{j}(t+1), -k_{j}(t), -k_{j}(t+1)]$.

The action of agent j at time $t+1$, $x_j(t+1)$, is determined by the type of j, $x_j(t)$ and the sign of $k_{j}(t)$. Since $k_{j}(t)$ and $k_{j}(t+1)$ can be either positive, negative or 0, there are 9 cases for the sign series of $[k_{j}(t), k_{j}(t+1), -k_{j}(t), -k_{j}(t+1)]$. For each case, it can be checked that the action series of agent j displays either period 1 or period 4, regardless of j’s type or $x_j(t)$ (we omit the easy but tedious details). This implies that $\hbox {LLC}=4$ if there is no link between even-degreed agents. $\square$

Remark 3

The condition that even-degreed agents are not neighboring each other is necessary to the correctness of Theorem 2. In fact, $\hbox {LLC}=12$ is possible even if there are exactly two such agents, as shown in Fig. 4.

Fig. 4

$\text {LLC}=12$ in a completely heterophilic NMP with two even-degreed agents that are neighboring each other. Conformists and rebels are represented by circles and triangles, respectively. Actions are indicated by colors: black for 1 and white for 0. The third conformist and the third rebel are the only even-degreed agents and they are neighboring each other. Unhappy faces indicate that the corresponding agents are unsatisfied

4 Simultaneous BRD: three special network structures

In this section, we consider three special network structures, lines, rings, and stars.¹⁰ The simultaneous BRD of NMP can be understood more clearly with these networks. Note first that if $(N,\mathrm{g})$ is a line or a ring, then complete heterophily means that conformists and rebels are alternate; and for star networks, complete heterophily means that all the peripheral agents are of the opposite type to the central one. The following basic results will be frequently used in later discussions.

Lemma 1

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP,  ${\mathbf {x}}(0)$ an initial action profile,  and ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ the corresponding initialized NMP. Suppose also $n\ge 2$.

• (a) G is an exact potential game if and only if there is no conformist-rebel link; 

• (b) If no agent is initially satisfied,  i.e.,  $u_i({\mathbf {x}}(0))<0$ for all $i\in N,$ then $\ell ({\mathcal {I}})=2;$

• (c) If $(N,\mathrm{g})$ is a line,  then G does not have a PNE if and only if it is completely heterophilic; 

• (d) If $(N,\mathrm{g})$ is a ring,  then G does not have a PNE if and only if it is completely heterophilic and n / 2 is odd; 

• (e) If $(N,\mathrm{g})$ is a star,  then G has a PNE if and only if at least one half of the peripheral agents are of the same type as the central agent.

Lemma 1(a) is provided in Zhang et al. (2018). In particular, Lemma 1(a) implies that a PNE exists in NMP when there is only one type of agents. Lemma 1(b) is trivial: because when no agent is initially satisfied, they switch to the other actions simultaneously, leading to a new state where no agent is satisfied either. In the next round, all agents switch back to the initial state. Therefore, the system keeps oscillating between the two states, all agents are in eternal flux and no agent is ever satisfied. Evidently, coordination failure is caused by simultaneous moves. Lemma 1(c) and Lemma 1(d) are proved in Cao and Yang (2014). Lemma 1(e) is simple: since each peripheral agent has the central agent as her unique neighbor, the utility of the central agent in any PNE must be the number of agents that are of the same type minus that of the opposite type; this happens if and only if at least one half of the peripheral agents are of the same type as the central agent.

Certain simple local structures turn out to play crucial roles in the convergence of BRDs. To ease later discussions, we introduce them formally in the definitions below.

Definition 3

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP, and the underlying network $(N,\mathrm{g})$ be a line or a ring. Any component of two adjacent agents that are of the same type is called a weak cluster, and G is called weakly clustered if it has at least one weak cluster. Obviously, G is weakly clustered if and only if it is not completely heterophilic.

Definition 4

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP, and the underlying network $(N,\mathrm{g})$ be a line. A strong cluster of G is defined as any of the following components: (i) the left-most two agents that are of the same type; (ii) the right-most two agents that are of the same type; and (iii) three adjacent agents that are of the same type. G is called strongly clustered if it has at least one strong cluster.

Definition 5

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP, and the underlying network $(N,\mathrm{g})$ be a ring. A strong cluster of G is defined as a component of three adjacent agents that are of the same type. G is called strongly clustered if it has at least one strong cluster.

Since NMP with any network structure has $\hbox {LLC}\le 2$ (Theorem 1) and is an exact potential game when there is only one type of agents (Lemma 1(a)), it is intuitive that the existence of clusters may be in favor of the convergence of BRDs. It is indeed the case.

4.1 Lines

Below are the main results of this subsection, which give a fairly complete characterization for the simultaneous BRD of NMP with line structures.

Theorem 3

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP with the underlying network $(N,\mathrm{g})$ being a line,  ${\mathbf {x}}(0)$ an initial action profile,  and ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ the corresponding initialized NMP. Suppose also $n\ge 2$.

• (a) If G is completely heterophilic,  then $\ell ({\mathcal {I}})=4$ for all ${\mathbf {x}}(0);$

• (b) If G is not completely heterophilic,  i.e.,  it is weakly clustered,  then $\ell ({\mathcal {I}})\in \{1,2,4\}$ for all ${\mathbf {x}}(0)$. In particular, 

  • (i) $\ell ({\mathcal {I}})=2$ if and only if all agents are of the same type and they are all initially unsatisfied,  i.e.,  $u_i({\mathbf {x}}(0))<0$ for all $i\in N;$

  • (ii) If there exists a weak cluster such that the corresponding two agents initially like each other,  then $\ell ({\mathcal {I}})=1;$

  • (iii) If G is strongly clustered and the condition in (i) is not true,  then $\ell ({\mathcal {I}})=1;$

  • (iv) In all the other cases that G is weakly clustered,  i.e.,  G is not strongly clustered and the condition in (ii) is not true,  $\ell ({\mathcal {I}})\in \{1,4\}$.

Proofs of the above results are relatively easy, except cases (a) and (b)(iv), whose basic ideas are sketched in the following. Detailed rigorous proofs of all results of Theorem 3 are presented in Appendices B.1 and B.2.

The proofs of cases (a) and (b)(iv) rely crucially on two technical lemmas, Lemma 6 and Lemma 7 (Appendix B.2). Suppose now the underlying network is a completely heterophilic line. In the two lemmas, we focus on utility sequences rather than on action profiles. Roughly speaking, Lemma 6 states that certain utility sequences will never occur. Lemma 7 shows further that no agent has utility zero in the limit cycle.

The basic idea to prove Theorem 3(a) goes as follows. Recall first that a PNE does not exist in this case (Lemma 1(d)). By Lemma 7, none of the agents has a utility of zero in the limit cycle. Due to Lemma 6, 2 will never be adjacent with 2 and neither will $-2$ be adjacent with $-2$ in any utility sequence. Thus, it can be concluded that, the whole sequence of utilities will consist of alternate 2 and $-2$ (except for the ending agents, whose utilities are 1 or $-1$) once a limit cycle is entered. And hence at any step of the limit cycle, either none conformist is satisfied but every rebel is, or none rebel is satisfied but every conformist is. Based on this argument, it can be checked easily that $\hbox {LLC}=4$.

To prove Theorem 3(b)(iv), a “cutting technique” is explored. Observe first that, due to (b)(i) and (b)(iii), NMPs discussed in this case cannot be strongly clustered. Since $\hbox {LLC}=2$ implies that all agents are of the same type and further that G is strongly clustered, we must have $\ell ({\mathcal {I}})\ne 2$. In addition, there are no three adjacent agents that are of the same type, and neither the left-most two agents nor the right-most two ones are of the same type. So, if we cut the line at all the conformist-conformist links and at all the rebel-rebel ones into sublines, then each subline is completely heterophilic, and no isolated agent will be produced. To prove Theorem 3(b)(iv), it suffices to show that “$\ell ({\mathcal {I}})\ge 3$ implies $\ell ({\mathcal {I}})=4$”. Suppose now $\ell ({\mathcal {I}})\ge 3$. Since each of the sublines has $\hbox {LLC}=4$ (Theorem 3(a)), and piecing them together does not affect the dynamic of each other, provided that $\ell ({\mathcal {I}})\ge 3$ (Lemma 5 in Appendix B.1), we complete the proof of Theorem 3(b)(iv).

Theorem 3(b)(i), though simple, possesses several features that are in general not owned by other network structures (e.g., the star, see Theorem 5(a)): to have $\hbox {LLC}=2$, it must be true that (i) the limit cycle is entered immediately at the very beginning of the dynamic. There is no possibility to evolve for certain periods of time and then enter a length two limit cycle; (ii) no agent is ever satisfied; and (iii) all agents are of the same type.

Remark 4

Let G be an NMP with the underlying network being a line. Combining Theorem 3 with Lemma 1(c) yields an interesting property: if G does not possess any PNE, then $\hbox {LLC}=4$ for all initial action profiles. Note that this property is not covered by Theorem 2.

4.2 Rings

The results in Theorem 3(b) for lines are still valid for rings. We summarize them in the following theorem.

Theorem 4

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP with the underlying network $(N,\mathrm{g})$ being a ring,  ${\mathbf {x}}(0)$ an initial action profile,  and ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ the corresponding initialized NMP. Suppose also $n\ge 3$. If G is weakly clustered,  then $\ell ({\mathcal {I}})\in \{1,2,4\}$ for all ${\mathbf {x}}(0)$. In particular, 

• (i) $\ell ({\mathcal {I}})=2$ if and only if all agents are of the same type and they are all initially unsatisfied,  i.e.,  $u_i({\mathbf {x}}(0))<0$ for all $i\in N;$

• (ii) If G is weakly clustered and the two agents in some cluster initially like each other,  then $\ell ({\mathcal {I}})=1;$

• (iii) If G is strongly clustered and the condition in (i) is not true,  then $\ell ({\mathcal {I}})=1;$

• (iv) In the other cases that G is weakly clustered,  i.e.,  G is not strongly clustered and the condition in (ii) is not true,  we have $\ell ({\mathcal {I}})\in \{1,4\}$.

Note that when the number of agents n is odd, G with a ring structure cannot be completely heterophilic. Therefore, Theorem 4 provides a fairly complete characterization for the simultaneous BRD of NMP on ring structures when n is odd. The characterization is not as complete when n is even.

Proofs of Theorem 4(i), (ii) and (iii) are the same as of their counterparts in Theorem 3. However, the result that is parallel to Theorem 3(a) does not hold for rings: if the ring is completely heterophilic, we do not have in general that $\hbox {LLC}=4$ (see Fig. 5 for a counter example). The key reason is that rings do not have ending nodes, and thus we are unable to get a result that is parallel to Lemma 7 (Appendix B.1), which plays a crucial role in the proof of Theorem 3(a).

Fortunately, a similar cutting technique can still be applied. This technique helps us to cut a ring into completely heterophilic lines without affecting its LLC, when $\ell ({\mathcal {I}})\ge 3$ (note that while cutting a line for k times leads to $k+1$ smaller separate lines, cutting a ring for k times leads to k separate lines). Using a similar argument as in the proof of Theorem 3(b)(iv), we can show that Theorem 4(iv) is valid. The detailed proof is presented in Appendix B.1.

Remark 5

When n is even, numerical simulations suggest that simultaneous BRD on completely heterophilic rings behaves very differently from that on completely heterophilic lines. To be specific, (i) if n / 2 is also even, then LLC could be 1, 4 and n, (ii) if n / 2 is odd, then LLC could be 4 and 2n. Figure 5 illustrates two limit cycles with lengths n and 2n, respectively.

Fig. 5

Limit cycles for completely heterophilic rings. Conformists and rebels are represented by circles and triangles, respectively. Actions are indicated by colors: black for 1 and white for 0. In the left example, $n=8$ and $\hbox {LLC}=n$. In the right example, $n=6$ and $\hbox {LLC}=2n$. Unhappy faces indicate that the corresponding agents are unsatisfied

4.3 Stars

When the underlying network is a star, simultaneous BRD can be understood even more clearly than with lines and rings.

Theorem 5

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP with the underlying network $(N,\mathrm{g})$ being a star,  ${\mathbf {x}}(0)$ an initial action profile,  and ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ the corresponding initialized NMP. Suppose also $n\ge 4$.

• (a) If more than one half of the peripheral agents are of the opposite type to the central agent,  then $\ell ({\mathcal {I}})=4$ for all ${\mathbf {x}}(0);$

• (b) If more than one half of the peripheral agents are of the same type as the central agent,  and initially the central agent is unsatisfied,  then $\ell ({\mathcal {I}})=2;$

• (c) In all the other cases,  $\ell ({\mathcal {I}})=1$.

The proof of Theorem 5(a) has some similarity to Theorem3(a). It can be shown that either only the central agent is satisfied or only the central agent is unsatisfied in the limit cycle. Using this fact, it can be checked easily that $\hbox {LLC}=4$. Limit cycles in this case are illustrated in Fig. 6.

Theorem 5(b) is parallel to Theorem 3(b)(i) and Theorem 4(i), all characterizing the $\hbox {LLC}=2$ case. The condition used in Theorem 5(b) is weaker than the one used for lines and rings, which requires all agents be initially unsatisfied (and hence be of the same type), as for the general case in Lemma 1(c). The reason that this weaker condition is still sufficient for deriving $\hbox {LLC}=2$ is that, for star networks, after one round of deviations of the initially unsatisfied agents, the peripheral ones, no matter whether initially satisfied or not, are all unsatisfied. Since the peripheral agents that are of the same type as the central agent outnumber those of the opposite type, it follows that the central agent is still unsatisfied at the second step, leading to the general condition in Lemma 1(c) that no agent is satisfied. This shows that Theorem 5(b) is correct.

Fig. 6

Illustrations of the $\text {LLC}=4$ cases for star networks. Conformists and rebels are represented by circles and triangles, respectively. Actions are indicated by colors: black for 1 and white for 0

To prove Theorem 5(c), suppose now the central agent is a conformist. Due to Theorem 5(a)(b), there are two cases to discuss, (i) more than one half of the peripheral agents are conformists, and initially the central conformist is satisfied, and (ii) precisely one half of the peripheral agents are conformists and one half of them are rebels. Case (i) is easy: at the first step only possibly some of the peripheral agents deviate, but not the central conformist. Thus, at the second step, all of the peripheral agents are satisfied, and consequently so is the central conformist, leading to the convergence of the simultaneous BRD. To show case (ii), suppose on the contrary that $\ell ({\mathcal {I}})\ge 2$. Then, there exists some time t in the limit cycle such that the central conformist is unsatisfied; suppose w.l.o.g. that she takes action 1. It can be observed that, peripheral agents that are of the same type must take the same action in the limit cycle (Lemma 8(a) in Appendix B.3). It follows that all of the peripheral agents take action 0 at time t. At time $t+1$, all of the peripheral conformists switch to action 1 and the central conformist switches to action 0, making the central conformist satisfied but all the peripheral ones unsatisfied. Thus, at time $t+2$, all the peripheral agents switch, making all agents happy and $\ell ({\mathcal {I}})=1$, contradicting the hypothesis that $\ell ({\mathcal {I}})\ge 2$. The other scenario that the central agent is a rebel can be similarly proved.

The detailed proof of Theorem 5 is presented in Appendix B.3. Due to Theorem 5, we can see that the central agent plays a much more important role than the peripheral ones. This is very reasonable.

Remark 6

Let G be an NMP with the underlying network being a star. Combining Theorem 5 with Lemma 1(e) yields a property similar to the one in Remark 4 for lines: if G does not possess a PNE, then $\hbox {LLC}=4$ for all initial action profiles.

4.4 A summary

We have seen the crucial roles of weak and strong clusters. Other factors that might affect LLC include network size, population composition, network structure, and initial action profile.

As discussed in Remark 5, network size may sometimes play a very critical role. LLC could be arbitrarily long as the network size n goes to infinity. However, this happens only to ring networks in our study, not to the line or star networks, where LLC is always bounded above by 4. Even for the ring networks, an LLC that is larger than 4 may only possibly occur when the ring is completely heterophilic. Nevertheless, being completely heterophilic with ring structures is very rare if the configuration of agents’ types is randomly determined. To be more specific, let each agent be a conformist with probability $c\in [0,1]$ and be a rebel with probability $1-c$. We use $\mathbb {T}$ to denote this random type configuration. Note that there are $2^n$ configurations in total. Thus, a random type configuration is a distribution of these $2^n$ configurations, where the probability of a configuration with $n_C$ conformists and $n-n_C$ rebels is $c^{n_C}(1-c)^{n-n_C}$. Then, the probability that a ring is completely heterophilic (i.e., $T_i \ne T_{i+1}$ for $i=1,\ldots ,n-1$ in the type configuration $\mathbb {T}$) is $2c^{n/2}(1-c)^{n/2}$, which tends to 0 as n goes to infinity (assume for simplicity that n is even). Thus, if the network has a line, ring, or star structure, then in almost all cases its size does not affect LLC.

To discuss the effects of other factors, we use a similar probability approach. Note that when $c=1/2$, the random type configuration $\mathbb {T}$ obeys the uniform distribution. A general c makes us able to investigate the factor of population composition. For any real number $x\in [0,1]$, denote

$$\begin{aligned} \overline{x}=\max \{x,1-x\} \quad \text {and}\quad \underline{x}=\min \{x,1-x\}. \end{aligned}$$

Observe that $\underline{x}\le 0.5 \le \overline{x}$ and $\overline{x}+\underline{x}=1$ for all $x\in [0,1]$.

We also use $\mathbb {X}$ as a random initial action profile such that each agent is independently assigned an initial action 0 with probability $b\in [0,1]$ and action 1 with probability $1-b$. There are $2^n$ initial action profiles in total. Thus, similarly to $\mathbb {T}$, $\mathbb {X}$ is a distribution of these $2^n$ action profiles, where the probability of an action profile with $n_0$ agents using action 0 and $n-n_0$ agents using action 1 is $b^{n_0}(1-b)^{n-n_0}$. In the following, we also use subscripts c and b for the probability function Prob[$\cdot$] to indicate the distribution parameters in $\mathbb {T}$ and $\mathbb {X}$.

Theorem 6

The following results on the probabilities of LLC hold for all $c,b\in [0,1]$.

• (a) If the underlying network $(N,\mathrm{g})$ is a line or a ring,  then

  $$\begin{aligned} \lim _{n\rightarrow \infty } \text {Prob}_{c} \left[ \ell (N,g,\mathbb {T},{\mathbf {x}}(0))=1, \forall {\mathbf {x}}(0)\in \{0,1\}^n\right] =1. \end{aligned}$$

• (b) If the underlying network $(N,\mathrm{g})$ is a star,  then

  $$\begin{aligned}&\text{ Prob }_{c} \left[ \ell (N,g,\mathbb {T},{\mathbf {x}}(0))=m, \forall {\mathbf {x}}(0)\in \{0,1\}^n\right] =0,\quad \forall m\ne 4,\\&\lim _{n\rightarrow \infty } \text{ Prob }_{c} \left[ \ell (N,g,\mathbb {T},{\mathbf {x}}(0))=4, \forall {\mathbf {x}}(0)\in \{0,1\}^n\right] =\underline{c},\\&\lim _{n\rightarrow \infty } \text{ Prob }_{c,b} \left[ \ell (N,g,\mathbb {T},\mathbb {X})=2\right] =\overline{c}(c\underline{b}+(1-c)\overline{b}),\\&\lim _{n\rightarrow \infty } \text{ Prob }_{c,b} \left[ \ell (N,g,\mathbb {T},\mathbb {X})=1\right] =\overline{c}(c\overline{b}+(1-c)\underline{b}). \end{aligned}$$

Using Theorems 3 and 4, Theorem 6(a) can be easily shown, because the probability that there is at least one strong cluster tends to 1, as n goes to infinity. Using Theorem 5, the correctness of Theorem 6(b) is also easy. The detailed proof is provided in Appendix B.4.

Observe that when type configuration and initial action profile are uniformly selected, i.e., $c=b=0.5$, the probabilities in the latter three formulas of Theorem 6(b) are respectively 0.5, 0.25 and 0.25. According to Theorem 6, we know that network structure alone can play a very important role. If we are told that the underlying network is a line or a ring, then almost always $\hbox {LLC}=1$, namely, the simultaneous BRD converges. If it is known that the network is a star and type configuration and initial action profile are uniformly selected, then $\hbox {LLC}=4$ with probability 0.5.

When the network is a star, population composition plays some role in determining LLC: All the latter three probabilities are significantly affected by it. A not so intuitive fact is that the roles of conformists and rebels are sometimes symmetric, which is not the case in Zhang et al. (2018), where, under the dynamic of sequential BRD, they found that conformists tend to widen the gap between the number of agents choosing action 0 and the number of agents choosing action 1, while rebels tend to narrow this gap. For example, the second formula in Theorem 6(b) indicates that the roles of the proportion of conformists and the proportion of rebels are symmetric in deciding the probability of $\hbox {LLC}=4$: this probability reaches its highest value when the two proportions are the most balanced ($c=0.5$) and reaches its lowest value when the two proportions are the most unbalanced ($c\in \{0, 1\}$).

For star networks, the population composition parameter c has to work together with the initial action parameter b in order to decide the probabilities of $\hbox {LLC}=2$ and $\hbox {LLC}=1$. For example, when $c=1$, i.e., all of the agents are conformists, the probability for $\hbox {LLC}=1$ is approximately $\overline{b}$, which achieves its highest value when all agents initially take the same action ($b\in \{0,1\}$), and it achieves its lowest value when each agent uniformly chooses between action 0 and action 1 ($b=0.5)$.

5 Conclusion

In this paper, we have studied the matching pennies game on networks. Two benchmark cases and three simple network structures have been investigated. Our results demonstrate that network structures play a very critical role for both the simultaneous and sequential BRD. Indeed, even some very simple local structures, i.e., weak and strong clusters, may play crucial roles. These results may help us understand various phenomena in the real world including fashion.

The NMP is a relatively new model that is concise, interesting and useful. Much work is needed for more completely understanding the model and for exploring applications. First, how often is it to have $\hbox {LLC}=1$ in NMPs with a single type of agents? Second, it is meaningful to understand completely heterophilic NMPs with at least two linked even-degreed agents. Finally, it is interesting to investigate properties of other familiar dynamics, such as fictitious play and logit response, for NMP.

Appendices

Appendix A: Proof of Theorem 1

Proof

Suppose now all agents are conformists. Denote $\alpha (t)=\sum _{i\in N: x_i(t)=1}n_i^1(t-1)$ as the number of edges ij such that $x_i(t)=1$ and $x_j(t-1)=1$, and $\beta (t)=\sum _{i\in N: x_i(t)=1}n_i/2$. Define a Lyapunov function

$$\begin{aligned} \gamma (t)=\alpha (t)-\beta (t)-\beta (t-1). \end{aligned}$$

It is elementary to check that

where

$$\begin{aligned} N_{0\rightarrow 1}(t)= & {} \{i\in N: x_i(t-1)=0, x_i(t+1)=1\}, \\ N_{1\rightarrow 0}(t)= & {} \{i\in N: x_i(t-1)=1, x_i(t+1)=0\}. \end{aligned}$$

By Observation 1, $\gamma (t+1)-\gamma (t)$ is always nonnegative. Consequently, $\gamma (t)$ is a constant in the limit cycle and the following observation holds.

Observation 3

Suppose that a limit cycle is reached at time $t-1$. If $i\in N_{0\rightarrow 1}(t)\cup N_{1\rightarrow 0}(t),$ i.e.,  i takes different actions at time $t-1$ and $t+1,$ then $n_i^1(t)=n_i/2$.

We show in the rest of the proof that $N_{0\rightarrow 1}(t)\cup N_{1\rightarrow 0}(t)=\emptyset$ in the limit cycle, i.e., the action of each agent will be back within two steps, implying that LLC equals 1 or 2.

Suppose on the contrary that $N_{0\rightarrow 1}(t)\cup N_{1\rightarrow 0}(t)\ne \emptyset$ for large enough t such that a limit cycle is reached. If there exists $i\in N_{0\rightarrow 1}(t)$, we must have $x_i(t+1)=1$ due to $x_i^1(t)=n_i/2$. Let $t+k$ be the first time after t such that $x_i(t+k)=0$ with $k\ge 2$. Then $x_i(t+k)=0$ and $x_i(t+k-2)=1$, implying that $i\in N_{1\rightarrow 0}(t+k-1)$ and hence $n_i^1(t+k-1)=n_i/2$ due to Observation 3. Therefore, $x_i(t+k-1)=0$. This contradicts the hypothesis that $t+k$ is the first time after t such that $x_i(t+k)=0$. Using the same logic, the case that $i\in N_{1\rightarrow 0}(t)$ is impossible as well.

When all agents are rebels, the same Lyapunov function $\gamma (t)$, which is nonincreasing due to Observation 2, still applies. We can show that $N_{0\rightarrow 1}(t)\cup N_{1\rightarrow 0}(t)=\emptyset$ holds in the limit cycle in a way similar to the all-conformist case. This finishes the proof. $\square$

Appendix B: Proofs in Sect. 4

We assume throughout this appendix that (i) $n\ge 2$ whenever the underlying network is a line, (ii) $n\ge 3$ whenever it is a ring, and (iii) $n\ge 4$ whenever it is a star.

1.1 Proofs of Theorems 3 and 4

We prove Theorems 3 and 4 simultaneously.

Definition 6

Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$, if $x_i(t)$ keeps unchanged when simultaneous BRD enters the limit cycle, we say agent i is immune w.r.t. ${\mathcal {I}}$.

The lemma below characterizes the convergence case.

Lemma 2

Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},T, {\mathbf {x}}(0)),$ and suppose the underlying network $(N,\mathrm{g})$ is either a line or a ring. The following statements are equivalent.

• (a) $\ell ({\mathcal {I}})=1;$

• (b) All agents are immune w.r.t. ${\mathcal {I}};$

• (c) At least one agent is immune w.r.t. ${\mathcal {I}}$.

Proof

The equivalence between (a) and (b) is obvious. It is trivial that (b) implies (c), so we are left to show that (c) implies (b). Suppose that i is immune. We claim that $j\in N_i$, an arbitrary neighbor of i, is also immune.

Suppose not, then there would exist some time $t_0\ge r({\mathcal {I}})$ such that $u_j({\mathbf {x}}(t_0))<0$. So i is not liked by agent j at time $t_0$, and j will switch, i.e., $x_j(t_0+1)=1-x_j(t_0)$. Since i is immune, we know that she never switches, i.e., $x_i(t_0+1)=x_i(t_0)$. Therefore, i is liked by agent j at time $t_0+1$, and $u_j({\mathbf {x}}(t_0+1))\ge 0$. Furthermore, the utility of j keeps being nonnegative after time $t_0+1$, because i never switches in the limit cycle and hence she is always liked by j after $t_0$. It follows that agent j will never switch any more, and the action $x_j(t_0)$ will never be taken again by j after $t_0$, contradicting the fact that a limit cycle is entered at time $t_0$. $\square$

Notice that the above lemma relies crucially on the fact that each agent has at most two neighbors in lines and rings. As long as one of her two neighbors is liked by her, she will be satisfied and will not deviate. This is generally not true for other structures. The following lemma characterizes length-two limit cycles.

Lemma 3

Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0)),$ and suppose the underlying network $(N,\mathrm{g})$ is either a line or a ring. The following statements are equivalent.

• (a) $\ell ({\mathcal {I}})=2;$

• (b) $\exists i\in N$ such that $u_i({\mathbf {x}}(t))<0$ holds for all $t\ge r({\mathcal {I}});$

• (c) $\exists t\ge 0$ such that $u_i({\mathbf {x}}(t))<0$ holds for all $i\in N;$

• (d) $u_i({\mathbf {x}}(0))<0$ holds for all $i\in N$.

Proof

(a) implies (b) trivially. Suppose (b) is true, then agent i keeps switching her action in the limit cycle. This can only happen when her neighbors keep switching actions too. Using this argument repeatedly, we know that no agent is satisfied at any step of the limit cycle, thus (c) is valid. Suppose now (c) is true, i.e., at some time t no agent is satisfied. This can only happen when all agents are of the same type, because for any two adjacent agents of different types, it is impossible for both of them to be unsatisfied. In addition, no agent should be initially satisfied, because otherwise the initially satisfied agent and one of her neighbors will both be immune. This indicates that (d) is valid. (d) implies (a) obviously. This finishes the proof. $\square$

Proofs of Theorem 3(b)(i) and Theorem 4(i)

The equivalence between (a) and (d) in Lemma 3 implies that Theorem 3(b)(i) and Theorem 4(i) are both valid. $\square$

Proof of Theorem 3(b)(ii)

Suppose two agents in some weak cluster initially like each other. Then it can be seen that the two agents are immune. It follows from Lemma 2 that $\ell ({\mathcal {I}})=1$. $\square$

Proof of Theorem 3(b)(iii)

Suppose G is strongly clustered and some agent (not necessarily in any strong cluster) is initially satisfied. Then at least one of the following must hold: (i) $T_1=T_2$; (ii) $T_{n-1}=T_n$; and (iii) there are three adjacent agents that are of the same type.

Suppose $T_1=T_2$ and they are both conformists. If at some step they take the same action, then they will both be immune. By Lemma 2, this means that $\ell ({\mathcal {I}})=1$ and we are done. So we suppose now they always take different actions. Since agent 1 has only one neighbor, this means that she will keep switching actions. By the equivalence between (a) and (b) in Lemma 3, we have $\ell ({\mathcal {I}})=2$ and hence no agent is initially satisfied (Lemma 3(d)), contradicting the hypothesis that some agent is initially satisfied. If agents 1 and 2 are both rebels, it can be shown by a similar argument. By symmetry, it is also valid for the case that $T_{n-1}=T_n$.

Suppose now there are three agents, $i,i+1$ and $i+2$, such that $T_i=T_{i+1}=T_{i+2}=C$. If there exists some time t such that either $x_i(t)=x_{i+1}(t)$ or $x_{i+1}(t)=x_{i+2}(t)$, then there will be immune agents and $\ell ({\mathcal {I}})=1$. So we assume that $x_i(t)=x_{i+2}(t)\ne x_{i+1}(t)$ holds for all time t. Therefore, the middle agent $i+1$ will switch her action at all steps. By Lemma 3, it follows that $\ell ({\mathcal {I}})=2$, contradicting the hypothesis that some agent is initially satisfied.

Suppose now there are three agents, $i,i+1$ and $i+2$, such that $T_i=T_{i+1}=T_{i+2}=R$. If there exists some time t such that either $x_i(t)\ne x_{i+1}(t)$ or $x_{i+1}(t)\ne x_{i+2}(t)$, then there will be immune agents and $\ell ({\mathcal {I}})=1$. So we assume that $x_i(t)=x_{i+2}(t)= x_{i+1}(t)$ holds for all time t. Therefore, the middle agent $i+1$ will switch her action at all steps. By Lemma 3, it follows that $\ell ({\mathcal {I}})=2$, contradicting the hypothesis that some agent is initially satisfied. $\square$

Proof of Theorem 4(iii)

The proof is exactly the same as that of Theorem 3(b)(iii), except that the first two cases do not occur. $\square$

To prove part (a) and (b)(iv) of Theorem 3, we need a property about LLC$\ge$3.

Lemma 4

Let ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ be an initialized NMP with the underlying network $(N,\mathrm{g})$ being either a line or a ring. If $\ell ({\mathcal {I}})\ge 3,$ then no agent switches in two consecutive steps,  i.e.,  there is no agent i and time t such that $u_i({\mathbf {x}}(t))=u_i({\mathbf {x}}(t+1)){<}0$.

Proof

We consider first the case that $(N,\mathrm{g})$ is a line. Suppose on the contrary that $u_i({\mathbf {x}}(t))=u_i({\mathbf {x}}(t+1))<0$. It can be shown easily that (i) if $i\in \{1,n\}$, then i is of the same type as her only neighbor, and (ii) if $i\notin \{1,n\}$, then i and her two neighbors must have the same type. Hence ${\mathcal {I}}$ is strongly clustered. Due to Theorem 3 (b)(i)(iii), we know that $\ell ({\mathcal {I}})\le 2$. A contradiction with the hypothesis that $\ell ({\mathcal {I}})\ge 3$. The case that $(N,\mathrm{g})$ is a ring can be proved in exactly the same approach. $\square$

The key method we use to deal with part (b)(iv) of Theorem 3 is the “cutting” technique. To ease the presentation, we need one more term. Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$, and suppose that $(N,\mathrm{g})$ is a line. For any agent i, $2\le i\le n-1$, let $\mathcal {I'}(i)=(N',\mathrm{g}',T',x'(0))$ be a new (smaller) initialized NMP constructed by the left i agents of ${\mathcal {I}}$ in the following natural way: $N'=\{1,2,\ldots ,i\}$; $\mathrm{g}'=\{ij: i,j\in N', ij\in \mathrm{g}\}$; $\forall 1\le j\le i$, $T'_j=T_j$; $\forall 1\le j\le i$, $x'_j(0)=x_j(0)$. Similarly, $\mathcal {I''}(i)$ is an initialized NMP constructed by the right $n-i$ agents of ${\mathcal {I}}$.

Definition 7

We say that $\mathcal {I'}(i)$ is a complete sub-instance of ${\mathcal {I}}$ if and only if $x'_j(t)=x_j(t)$ holds for all $t\ge 1$ and all $1\le j\le i$. $\mathcal {I''}(i)$ is called a complete sub-instance in an analogous way.

Lemma 5

Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0)),$ and suppose the underlying network is a line that is not completely heterophilic. Suppose also that $\ell ({\mathcal {I}})\ge 3$ and agents i and $i+1$ are of the same type ($2\le i\le n-2$). Then $\mathcal {I'}(i)$ and $\mathcal {I''}(i)$ are both complete sub-instances of ${\mathcal {I}}$.

Proof

By symmetry, we only consider $\mathcal {I'}(i)$. Suppose w.l.o.g. that i and $i+1$ are both conformists. In the simultaneous BRD of ${\mathcal {I}}$, i and $i+1$ will always take the opposite actions, because otherwise they will both be immune and the hypothesis that $\ell ({\mathcal {I}})\ge 3$ will be violated. Therefore, whether i will switch her action or not at step t is completely determined by the action of agent $i-1$. This is also true for the simultaneous BRD of $\mathcal {I'}(i)$, where $i-1$ is the only neighbor of i. Hence the lemma. $\square$

With the assistance of Lemma 6 and Lemma 7 that are to be presented in Appendix B.2, we are ready to prove the remaining parts of Theorem 3.

Proof of Theorem 3(a)

Suppose now ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ is an initialized NMP, and the underlying network is a completely heterophilic line. Recall first that a PNE does not exist in this case (Lemma 1(d)). Since none of the agents has a utility of zero in the limit cycle (Lemma 7), and 2 will never be adjacent with 2 and neither will -2 be adjacent with -2 in any utility sequence (Lemma 6(a)), the whole sequence of utilities will consist of alternate 2 and -2 (except for the ending agents, whose utilities are 1 or -1). At any step of the limit cycle, either none conformist is satisfied but every rebel is, or none rebel is satisfied but every conformist is. Based on the above discussion, it is easy to check that the length of any limit cycle is exactly 4, just as in the example of the matching pennies game that is illustrated in Fig. 2. $\square$

Proof of Theorem 3(b)(iv)

Suppose now ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ is an initialized NMP, and the underlying network is a line that is a neither strongly clustered nor completely heterophilic (note that this is exactly the case discussed in Theorem 3(b)(iv)). Since ${\mathcal {I}}$ is not strongly clustered, it follows from Theorem 3(b)(i) that $\ell ({\mathcal {I}})\ne 2$. To prove Theorem 3(b)(iv), it suffices to show that $\ell ({\mathcal {I}})\ge 3$ implies $\ell ({\mathcal {I}})=4$.

Suppose now $\ell ({\mathcal {I}})\ge 3$. We cut the line at an arbitrary conformist-conformist link or rebel-rebel link into two pieces. Notice that this cutting will not produce isolated agents because ${\mathcal {I}}$ is not strongly clustered. Due to Lemma 5, they are both complete sub-instances. If the two pieces are both completely heterophilic, then each of them has $\hbox {LLC}=4$, regardless of the initial action profiles (Theorem 3(a)). By the definition of a complete sub-instance, piecing them together gives Theorem 3(b)(iv) immediately. Otherwise, we cut them again into even smaller pieces, and use the same argument. Since the line is finite, this process will terminate and the proof is done. $\square$

Proof of Theorem 4(iv)

To prove Theorem 4(iv), we use a similar cutting technique. Observe that a ring discussed in this case will be cut into completely heterophilic lines instead of completely heterophilic rings. Therefore, although we do not have $\hbox {LLC}=4$ for completely heterophilic rings (see Remark 5), we can still use the same logic as in the proof of Theorem 3(b)(iv) to show that Theorem 4(iv) is correct. $\square$

1.2 Two technical lemmas

The two lemmas provided in this subsection are used in the proofs of Theorem 3(a) and (b)(iv). Since their proofs, mainly the latter one, are rather technical, we present them in this separate subsection.

In this subsection, we use $u_i(t)$ for short of $u_i({\mathbf {x}}(t))$. This is reasonable, because the utility of each agent is a function of the single variable of time t once the initial action profile is fixed.

Since the underlying network $(N,\mathrm{g})$ is a line, $u_i(t)$ takes five possible values, 2, 1, 0, $-1$, and $-2$. We call $[a_1,a_2,\ldots ,a_k]\in \{-2,2,0, -1,1\}^k$ a utility sequence, if there exists a time t and an agent i such that $[u_i(t),u_{i+1}(t),\ldots , u_{i+k-1}(t)]=[a_1,a_2,\ldots ,a_k]$. It is sometimes more convenient to deal with utility sequences than to deal with action sequences.

Lemma 6

Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0)),$ and suppose $(N,\mathrm{g})$ is a completely heterophilic line.

• (a) The following utility sequences never occur :  [2, 2],  $[-2,-2],$ [2, 0, 2],  $[2,0,\ldots ,0,2],$ [2, 0, 1],  $[2,0,\ldots ,0,1],$$[-2,0,-2],$$[-2,0,\ldots ,0,-2],$$[-2,0,-1],$$[-2,0,\ldots ,0,-1],$$[1,0,\ldots ,0,1],$ and $[-1,0,\ldots ,0,-1];$

• (b) If $u_i(t)=-2,$ then $u_i(t+1)=2;$

• (c) If $u_i(t)=0,$ then $u_i(t+1)\in \{-2,0\}$.

Proof

One nice property of the completely heterophilic line is that one agent likes her neighbor at some time if and only if her neighbor dislikes her. Using this property, it is easy to check that the sequences in (a) never occurs.

Since no pair of adjacent agents can be simultaneously unsatisfied, we know that if agent i switches her action at some step, then none of her neighbors switches at the same step. Using this fact, (b) is valid.

If $u_i(t)=0$, then i likes one of her neighbors and dislikes the other at time t. Suppose w.l.o.g. that $i-1\in L_i({\mathbf {x}}(t))$ and $i+1\in D_i({\mathbf {x}}(t))$. Accordingly, $i\in D_{i-1}({\mathbf {x}}(t))$ and $i\in L_{i+1}({\mathbf {x}}(t))$. Therefore, $u_{i-1}(t)\le 0$ and $u_{i+1}(t)\ge 0$. Since $i+1$ is satisfied at time t, she will not switch. In the case that $u_{i-1}(t)<0$, it is evident that $u_{i}(t+1)=-2$. And in the case that $u_{i-1}(t)=0$, we have $u_{i}(t+1)=0$. Hence (c) is correct. This finishes the proof. $\square$

Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$, let Z(t) be the set of agents whose utilities are zero at time t, i.e.,

$$\begin{aligned} Z(t)=\{i\in N: u_i(t)=0\}. \end{aligned}$$

Lemma 7

Given an initialized NMP ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0)),$ suppose the underlying network $(N,\mathrm{g})$ is a completely heterophilic line. Then $Z(t)=\emptyset$ for all $t\ge r({\mathcal {I}}),$ i.e.,  no agent has utility zero in the limit cycle.

Proof

First, it follows from Lemma 1(a) that PNE does not exist for ${\mathcal {I}}$ and hence $L({\mathcal {I}})\ne 1$. Due to Lemma 3, we obviously have $L({\mathcal {I}})\ne 2$. Hence

$$\begin{aligned} L({\mathcal {I}})\ge 3, \end{aligned}$$

(1)

and the results in Lemma 4, Lemma 5 and Lemma 6 are all valid. We prove in two steps.

(i) We prove first that the cardinality of Z(t) is non-increasing, i.e.,

$$\begin{aligned} |Z(t+1)|\le |Z(t)|. \end{aligned}$$

(2)

Let

$$\begin{aligned} Z^{+}(t)=Z(t+1){\setminus } Z(t), \end{aligned}$$

and

$$\begin{aligned} Z^{-}(t)=Z(t){\setminus } Z(t+1), \end{aligned}$$

we only need to show that

$$\begin{aligned} |Z^+(t)|\le |Z^{-}(t)|. \end{aligned}$$

If $Z^+(t)$ is empty, we are done. Suppose not. Take an arbitrary agent i from $Z^+(t)$, i.e., $u_i(t+1)=0$ and $u_i(t)\ne 0$. Then by Lemma 6(b), it can only be that $u_i(t)=2$. And it is obvious that $i\notin \{1,n\}$. So agent i does not switch her action at step t, and her utility changes from 2 at step t to 0 at step $t+1$. This can only happen when exactly one neighbor of i is unsatisfied at time t. Due to Lemma 6(a), utility sequence [2, 2] never occurs, so the neighbor of agent i who is satisfied at time t must have a utility of 0. Therefore, $\{u_{i-1}(t), u_{i+1}(t)\}=\{-2,0\}$ (we assume w.l.o.g. that $i-1\ne 1$ and $i+1\ne n$).

Claim 1 (i) If $[u_{i-1}(t),u_i(t), u_{i+1}(t)]=[-2,2,0],$ then $Z^-(t)\cap \{i+1,i+2,\ldots ,n\}\ne \emptyset$. (ii) If $[u_{i-1}(t),u_i(t), u_{i+1}(t)]=[0,2,-2],$ then $Z^-(t)\cap \{1,2,\ldots ,i-1\}\ne \emptyset$.

Suppose now $[u_{i-1}(t),u_i(t), u_{i+1}(t)]=[-2,2,0]$, and suppose on the contrary to Claim 1(i) that $Z^-(t)\cap \{i+1,i+2,\ldots ,n\}=\emptyset$. Then $i+1\notin Z^-(t)$. Since $i+1\in Z(t)$, this implies that $i+1\in Z(t+1)$, i.e., $u_{i+1}(t+1)=0$. As agent $i+1$ does not switch her action at step t, her left neighbor, agent i, does not switch either, and the utility of $i+1$ also keeps unchanged, we know that the right neighbor of agent $i+1$, namely, agent $i+2$, should not switch at step t either. Therefore, $u_{i+2}(t)\ge 0$. By Lemma 6(a), utility sequence [2, 0, 2] and [2, 0, 1] never occurs, implying it is impossible that $u_{i+2}(t)\in \{2,1\}$. It can only be that $u_{i+2}(t)=0$.

In addition, $Z^-(t)\cap \{i+1,i+2,\ldots ,n\}=\emptyset$ implies that $i+2\notin Z^-(t)$. It follows from $u_{i+2}(t)=0$ that $i+2\in Z(t)$. Using exactly the same argument as in the last paragraph, we know that $u_{i+3}(t)=0$. But this cannot continue for ever, because $u_n(t)\in \{1,-1\}$ for all time t. Hence a contradiction. Therefore, Claim 1(i) is valid. By symmetry, Claim 1(ii) is also valid.

Due to Claim 1, the following definition for each $i\in Z^+(t)$ is valid:

$$\begin{aligned} f(i)=\left\{ \begin{array}{llll}\min \big \{j: j\in Z^-(t)\cap \{i+1,i+2,\ldots ,n\}\big \}&{}if~[u_{i-1}(t),u_i(t), u_{i+1}(t)]=[-2,2,0]\\ \max \big \{j:j\in Z^-(t)\cap \{1,2,\ldots ,i-1\}\big \}&{}if~[u_{i-1}(t),u_i(t), u_{i+1}(t)]=[0,2,-2]\end{array}\right. . \end{aligned}$$

The facts below can also be observed from the above discussion. For all $i\in Z^-(t)$,

$$\begin{aligned} f(i)>i~\text { implies}~[u_{i-1}(t),\ldots ,u_{f(i)+1}(t)]=[-2,2,0,\ldots ,0,-2], \end{aligned}$$

(3)

$$\begin{aligned} f(i)<i~\text { implies}~[u_{f(i)-1}(t),\ldots ,u_{i+1}(t)]=[-2,0,\ldots ,0,2,-2], \end{aligned}$$

(4)

where the “$\ldots$”s on the right hand sides both denote a series of 0’s.

Since $f(\cdot )$ is a mapping from $Z^+(t)$ to $Z^-(t)$, if we could show that $i_1\ne i_2$ implies $f(i_1)\ne f(i_2)$, then $|Z^+(t)|\le |Z^-(t)|$ would be valid. Assume w.l.o.g. that $i_1<i_2$. We discuss in four cases.

• $f(i_1)<i_1$ and $f(i_2)>i_2$. Since $f(i_2)>i_2>i_1>f(i_1)$, it is true that $f(i_1)\ne f(i_2)$;

• $f(i_1)>i_1$ and $f(i_2)>i_2$. It can be seen from (3) that $u_j(t)=0$ for all $i_1<j\le f(i_1)$. It follows from $i_2>i_1$ and $u_{i_2}(t)\ne 0$ that $i_2>f(i_1)$. Hence $f(i_2)>i_2>f(i_1)$, and consequently $f(i_1)\ne f(i_2)$;

• $f(i_1)<i_1$ and $f(i_2)<i_2$. It can be seen from (4) that $u_j(t)=0$ for all $f(i_2)\le j<i_2$. It follows from $i_2>i_1$ and $u_{i_1}(t)\ne 0$ that $i_1<f(i_2)$. Hence $f(i_1)<i_1<f(i_2)$, and consequently $f(i_1)\ne f(i_2)$;

• $f(i_1)>i_1$ and $f(i_2)<i_2$. It can be seen from (3) that $u_{f(i_1)+1}(t)=-2$. But we know from (4) that $u_{f(i_2)+1}(t)\in \{0,2\}$, hence $f(i_1)\ne f(i_2)$.

This shows that (2) is indeed correct.

(ii) By the monotonicity property (2) we know immediately that the cardinality of Z(t) keeps unchanged in the limit cycle, i.e.,

$$\begin{aligned} |Z(t+1)|=|Z(t)|, \forall t\ge r({\mathcal {I}}). \end{aligned}$$

(5)

Consequently, we know that

$$\begin{aligned} \forall t\ge r({\mathcal {I}}),\forall j\in Z^-(t), \text{ there } \text{ exists } \text{ exactly } \text{ one } i\in Z^+(t)~ s.t.~ f(i)=j. \end{aligned}$$

(6)

Now, we are ready to prove the final result. We use the minimum counter-example argument. Suppose the lemma is not valid, and ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ is a counter-example with the smallest number of agents. Let $j^*$ be the agent with the largest index among all the agents having a utility of 0 for at least one time in the limit cycle.

First of all, it is verifiable that $j^*=n-1$, because otherwise we could construct a smaller counter-example. In fact, the choice of $j^*$ tells us that if $j^*\ne n-1$, then $x_{j^*+1}(t)\in \{2,-2\}$ holds for all $t\ge r({\mathcal {I}})$. In the limit cycle, if agent $j^*+1$ dislikes $j^*$, then her utility will be $-2$, because 0 is never attained, and she will switch her action. And when agent $j^*+1$ likes $j^*$, evidently she will not switch. Therefore, whether $j^*+1$ switches her action at time $t\ge r({\mathcal {I}})$ or not is completely determined by the action of $j^*$. Using the same argument as in the proof of Lemma 5, we know that $\mathcal {I'}(j^*+1)=(N',\mathrm{g}', T', x'(0))$ is also a qualified counter-example (a limit cycle is entered at the first step), where $N'=\{1,2,\ldots ,j^*+1\}$, $T'$ the corresponding sub-vector of T, $\mathrm{g}'$ the corresponding left part of $\mathrm{g}$, and $x'(0)=(x_1(r({\mathcal {I}})),x_2(r({\mathcal {I}}),\ldots ,x_{j^*+1}(r({\mathcal {I}}))))$. Since ${\mathcal {I}}$ is the smallest counter-example, this is impossible, and thus it can only be that $j^*=n-1$.

Suppose $u_{j^*}(t')=0$ for some $t'\ge r({\mathcal {I}})$, then there must exist $t^*\ge t'$ such that $u_{j^*}(t^*)=0$ and $u_{j^*}(t^*+1)\ne 0$. Because otherwise, the utility of $j^*$ would keep at 0 from time $t'$ on, and thus she would be immune. As a result, $\ell ({\mathcal {I}})=1$ and a PNE would be reached by the simultaneous BRD. This is a contradiction with (1).

Therefore, $j^*\in Z^-(t^*)$. Since $t^*\ge t'\ge r({\mathcal {I}})$, we know by (6) that there exists exactly one $i^*\in Z^+(t^*)$ such that $f(i^*)=j^*$. Since $j^*=n-1$, we know that $i^*<j^*$ (note that agent n never has utility 0, while $i^*\in Z^+(t^*)$ implies that agent $i^*$ has utility 0 at time $t^*+1$). Therefore, it follows from (4) that

$$\begin{aligned} {[}u_{i^*-1}(t^*),\ldots , u_{j^*}(t^*), u_n(t^*)]=[-2,2,0,\ldots ,0,-1]. \end{aligned}$$

By Lemma 6(c), it must hold that $u_{j^*}(t^*+1)=-2$. Therefore,

$$\begin{aligned} {[}u_{i^*-1}(t^*+1),\ldots , u_n(t^*+1)]=[2,0,0,\ldots ,-2,1]. \end{aligned}$$

(7)

It can be observed from (7) that $j^*-1\in Z^-(t^*+1)$. Again, using (6), we know that there is an agent $k^*\in Z^+(t^*+1)$ such that $f(k^*)=j^*-1$. It must hold that $k^*<j^*-1$, because (7) tells us that the sequence $[0,2,-2]$ never occurs on the right side of $j^*-1$ and (4) says that if $k^*>j^*-1$ we would have a sequence $[0,2,-2]$ on the right side of $j^*-1$ (note by definition that $f(i)\ne i$ for any $i\in Z^+(t)$). Furthermore, comparing (3) with (7), we know that $k^*=i^*-1$, which can only happen when $u_{i^*-2}(t^*+1)\in \{-2,-1\}$.

However, $u_{i^*-2}(t+1)=-1$, i.e., $i^*-2=1$, is not true. Because if otherwise, then we would have $[u_{i^*-2}(t^*+2),\ldots , u_n(t^*+2)]=[1,0,0,0,\ldots ,-2, 2,-1]$, which has $n-4$ 0s in total. However, it can be checked that we would further have $[u_{i^*-2}(t^*+3),\ldots , u_n(t^*+3)]=[1,0,0,0,\ldots ,-2,2,-2,1],$ which has $n-5$ 0s in total, a contradiction with (5).

Therefore, we have $u_{i^*-2}(t+1)=-2$ and

$$\begin{aligned} {[}u_{i^*-2}(t^*+2),\ldots , u_n(t^*+2)]=[2,0,0,0,\ldots ,-2, 2,-1]. \end{aligned}$$

(8)

It can be observed from (8) that $j^*-2\in Z^-(t^*+2)$. Again, there is no $[0,2,-2]$ on the right side of $j^*-2$, and so we can only have $f(j^*-2)=i^*-2$. This can only happen when $u_{i^*-3}(t^*+2)\in \{-2,-1\}$. Again, we can deduce that $u_{i^*-3}(t^*+2)=-2$ and

$$\begin{aligned} {[}u_{i^*-3}(t^*+3),\ldots , u_n(t^*+3)]=[2,0,0,0,\ldots ,-2, 2,-2,1]. \end{aligned}$$

(9)

This process will be repeated infinitely. But this is obviously impossible, because the line is finite. This establishes the lemma. $\square$

1.3 Proof of Theorem 5

Before presenting the main proof, we need a lemma that is similar to Lemma 2 and Lemma 3.

Lemma 8

Let ${\mathcal {I}}=(N,\mathrm{g},{\mathbf {T}},{\mathbf {x}}(0))$ be an initialized NMP and suppose the underlying network $(N,\mathrm{g})$ is a star. The following statements are true.

• (a) At every step of the limit cycle,  all the peripheral conformists choose the same action,  and so do all the peripheral rebels; 

• (b) $\ell ({\mathcal {I}})=1$ if and only if all agents are satisfied at some time,  if and only if some agent is always satisfied in the limit cycle.

• (c) $\ell ({\mathcal {I}})=2$ if and only if all agents are unsatisfied at some time,  if and only if some agent is always unsatisfied in the limit cycle.

Proof

• (a) We only prove for conformists, because the rebel half is analogous. Suppose on the contrary that at some step of the limit cycle, part of the peripheral conformists choose action 1 and the other peripheral conformists choose action 0. Since all the peripheral agents have the same single neighbor, namely, the central agent, it must be true that either all the action 1 peripheral conformists are satisfied but the action 0 ones are unsatisfied, or the opposite. Suppose w.l.o.g. the former case occurs. Then the action 1 peripheral conformists switch to action 0, while the action 0 ones keep their actions fixed at 0. Hence, all the peripheral conformists have an action of 0 at the next step. From that time on, at each step, either they simultaneously switch or simultaneously keep unchanged. So, in any of the following steps, they always share the same action, and hence the state we assume that part of the peripheral conformists choose action 1 and the others choose action 0 will never be reached again, contradicting our hypothesis that it is in the limit cycle.

• (b) The first part is straightforward, we only show the second part. The “only if” side is trivial. Suppose now some agent is always satisfied in the limit cycle, then the central agent is also always satisfied in the limit cycle, and consequently so are all the peripheral ones. This shows that the “if” side of the second part is also correct.

• (c) The “if” side of the first part is trivial. $\hbox {LLC}=2$ implies that if some agent is satisfied at some step of the limit cycle, then it is always satisfies in the limit cycle. Therefore, the “only if” side of the first part is true due to (a). The “only if” side of the second part is trivial due to the first part. The “if” side of the second part is also true, because some agent is always unsatisfied in the limit cycle implies that the central agent and furthermore all agents are unsatisfied in the limit cycle.$\square$

Proof of Theorem 5

• (a) Consider the case that the central agent is a rebel. Then peripheral conformists are more than peripheral rebels. Observe first that $\ell ({\mathcal {I}})\ge 2$, because a PNE exists for star networks if and only if at least one half of the peripheral agents are of the same type as the central one. Since all of the conformists choose the same action in the limit cycle (Lemma 8 (a)), it is impossible that $\ell ({\mathcal {I}})=2$, because at any step of the limit cycle, either all of the conformists are satisfied (when they take the same action as the central agent) or the central rebel is satisfied (when the peripheral conformists take a different action with the central rebel).

  Using Lemma 8(c), there must exist some time t in the limit cycle such that the central rebel is satisfied, say she chooses action 0. Since there are more peripheral conformists than peripheral rebels, we know that all peripheral conformists should choose action 1 at time t (hence they are also satisfied). We discuss in two cases about the peripheral rebels.

  • (i) All of the peripheral rebels are unsatisfied at time t. This implies that they all choose action 0 at time t. At time $t+1$, all the peripheral agents switch actions, making themselves happy but the central rebel unhappy. So at time $t+2$, the central rebel switches to action 1, making herself happy and all the peripheral agents unhappy. Similarly, at time $t+3$, all the peripheral agents, but not the central one, switch, and at time $t+4$, only the central rebel switches, leading back to the action profile at time t. Therefore, we have $\ell ({\mathcal {I}})=4$ in this case. This limit cycle is illustrated in the left part of Fig. 6.

  • (ii) All of the peripheral rebels are satisfied at time t. This implies that they all choose action 1 at time t. It can be checked that the state at time $t+1$ in this case is exactly that at time $t+1$ in case (i). However, the time t state in this case is none of the four states in the limit cycle of the previous case, so it will never be reached again, contradicting our hypothesis that a limit cycle has been entered at time t. Therefore, this case never occurs.

  The proof of the situation that the central agent is a conformist is quite similar and thus omitted. The limit cycle in this case is illustrated in the right part of Fig. 6.

• (b) Let’s consider the case that the central agent is a rebel.

  Suppose w.l.o.g. that the central rebel chooses action 1 initially. Since she is initially unsatisfied, at step 2 she will switch to action 0. So do the peripheral rebels who initially take action 1. For the peripheral rebels who initially take action 0, they are initially satisfied and do not switch at the first step. For the peripheral conformists who take action 1 initially, they are satisfied at the first step, and hence still have action 1 at the second step. For the peripheral conformists who take action 0 initially, they are unsatisfied at the first step, and hence switch to action 1 at the second step.

• (c) Naturally, we discuss in four cases.

  • (i) The central agent is a rebel, more than half of the peripheral agents are also rebels, and initially the central rebel is satisfied. Since the central rebel is initially satisfied, her action at the second step will be the same as in the first step. For the peripheral rebels, the ones initially taking the opposite action keep unchanged, and the other peripheral rebels switch to this action too at the second step. So, at the second step, each of the peripheral rebels takes an opposite action to the central rebel. Since more than one half of the central rebel’s neighbors are rebels, we know that all the rebels will be always satisfied from the second step on. Using Lemma 8(b), we have $\ell ({\mathcal {I}})=1$.

  • (ii) The central agent is a conformist, more than one half of the peripheral agents are also conformists, and initially the central conformist is satisfied. The proof is quite similar to that of case (i) and thus omitted.

  • (iii) The central agent is a rebel, and exactly one half of the peripheral agents are rebels and one half of them are conformists. Suppose on the contrary that $\ell ({\mathcal {I}})\ge 2$. It follows from Lemma 8(b) that there is some time t in the limit cycle such that the central rebel is unsatisfied. This must be the case that all the agents take the same action, say action 1, because when the peripheral conformists and the peripheral rebels take different actions, the central rebel is satisfied. So, at step $t+1$, all of the rebels switch to action 0, and the conformists still hold action 1. Therefore, the central rebel is the only satisfied agent at step $t+1$. At time $t+2$, the central rebel still has action 0, the peripheral rebels have action 1, and the conformists have action 0. It can be seen that all of the agents are satisfied at step $t+2$, contradicting the hypothesis that $\ell ({\mathcal {I}})\ge 2$.

  • (iv) The central agent is a conformist, and one half of the peripheral agents are rebels and one half of them are conformists. The proof is quite similar to that of case (iii) and thus omitted. $\square$

1.4 Proof of Theorem 6

Proof

• (a) Suppose now the underlying network is a line or a ring, then the probability that it is strongly clustered goes to 1, as n goes to infinity. This is true because the probability that there are three or more adjacent agents that are of the same type goes to 1, as n tends to infinity. Since $u_j({\mathbf {x}}(0))<0$ for all $j\in N$ can only happen when all agents are of the same type, an event that occurs with a probability $c^n+(1-c)^n\rightarrow 0$, it follows from Theorem 3(b)(iii) and Theorem 4(iii) that Theorem 6(a) is correct.

• (b) Suppose now the underlying network is a star. Since the probability that there are equal numbers of conformists and rebels in the peripheral agents goes to 0, as n goes to infinity, it follows from Theorem 5 that the first formula is valid.

Observe that $\underline{c}+\overline{c}(c\underline{b}+(1-c)\overline{b})+\overline{c}(c\overline{b}+(1-c)\underline{b})=1$ for all $b,c\in (0,1)$. Therefore, it suffices to show that the second and the third formulas are both correct.

Claim 2 The probability that more than one half of the peripheral agents are of the same type as the central agent tends to $\overline{c},$ as n goes to infinity.

Observe that the probability that there are equal numbers of conformists and rebels in the peripheral agents approaches 0, as n goes to infinity. To prove Claim 2, we discuss in three cases. (i) When $c=0.5$, it follows by symmetry that Claim 2 is correct. (ii) When $c>0.5$, using the Law of Large Numbers, the probability that there are more conformist peripheral agents than rebel ones approaches 1, as n goes to infinity. Thus, the probability that more than one half of the peripheral agents are of the same type as the central agent tends to the probability that the central agent is a conformist, which is $c=\overline{c}$. (iii) When $c<0.5$, using the Law of Large Numbers again, it can be seen that the probability that more than one half of the peripheral agents are of the same type as the central agent tends to the probability that the central agent is a rebel, which is $1-c=\overline{c}$. Due to the above discussions, we conclude that Claim 2 is valid.

Claim 3 When the central agent is a conformist,  the probability that she is initially unsatisfied tends to $\underline{b},$ as n goes to infinity.

Observe first that the probability that there are equal numbers of peripheral agents who choose 0 and those who choose 1 goes to 0, as n goes to infinity. We still discuss in three cases. (i) When $b=0.5$, Claim 3 is true by symmetry. (ii) When $b>0.5$, the probability that more than one half of the peripheral agents initially choose action 0 approaches 1. Therefore, the probability that the central agent is initially unsatisfied approaches the probability that she initially chooses action 1, which is $1-b=\underline{b}$, because the central agent is a conformist. (iii) When $b>0.5$, the probability that more than one half of the peripheral agents initially choose action 1 approaches 1. Therefore, the probability that the central agent is initially unsatisfied approaches the probability that she initially chooses action 0, which is $b=\underline{b}$. It follows from the previous discussions that Claim 3 is true.

Claim 4 When the central agent is a rebel,  the probability that she is initially unsatisfied tends to $\overline{b},$ as n goes to infinity.

The proof of Claim 4 is quite similar to that of Claim 3 and thus omitted.

Claim 2 implies that the probability that more than one half of the peripheral agents are of the opposite type to the central agent tends to $1-\overline{c}=\underline{c}$, as n goes to infinity. Combining with Theorem 5(a), it is clear that the second formula in Theorem 6(b) is valid. We are left to show the third formula in Theorem 6(a). By Claim 3 and Claim 4, the probability that the central agent is initially unsatisfied tends to $c\underline{b}+(1-c)\overline{b}$. Combining this with Theorem 5(b) and Claim 2, it can be seen that the third formula in Theorem 6(b) is valid. This finishes the proof. $\square$

Appendix C: Sequential BRD

In this appendix, we discuss properties of the sequential BRD with arbitrary deviation orders. Given an initialized NMP, at each time step, as long as PNE is not reached, we let an arbitrary unsatisfied agent switch her action. We say that the sequential BRD converges if and only if a PNE is reached for any deviation order. It is well known that the sequential BRD converges if and only if the corresponding game possesses an ordinal potential function (Monderer and Shapley 1996). While Zhang et al. (2018) discuss the two benchmark cases, where an NMP is either completely homophilic or completely heterophilic, we consider the line and the ring network structures in this section. We use a slightly weaker convergence concept, to be introduced later, for NMPs with a star network.

1.1 Lines and rings

Observe first that an NMP, in general, is not a potential game for the line or ring networks, because a PNE is not guaranteed in the two cases, while a potential game always possesses a PNE (Monderer and Shapley 1996). However, for a very wide class of situations, it is indeed the case. Lemma 1(a) states that an NMP is an exact potential game if and only if there is no conformist-rebel link, i.e., conformists only interact with conformists and rebels only interact with rebels. The following theorem concerns with ordinal potentials for NMPs with line or ring structures.

Theorem 7

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP. Suppose the underlying network $(N,\mathrm{g})$ is a line or a ring. The sequential BRD converges for G,  i.e.,  G is an ordinal potential game,  if and only if it is weakly clustered.

Proof

Suppose now the underlying network is a line. Due to Lemma 1(a), the “only if” part of Theorem 7 is straightforward. We show next the “if” part. That the line is not completely heterophilic implies that it is weakly clustered, i.e., there exist two agents, say i and $i+1$, who are adjacent and are of the same type. Suppose on the contrary that G is not an ordinal potential game. Then, there will be an infinite number of deviations from some initial action profile (for some particular deviating order). Since i and $i+1$ are of the same type, at most one of them ever deviates, and deviates for at most once. When neither of i and $i+1$ deviates, $i-1$ and $i+2$, the two neighbors of i and $i+1$, both deviate for at most once. When one of i and $i+1$ deviates, say at time $t_1$, then after $t_1$, $i-1$ and $i+2$ both deviate for at most once. Using the same logic, there exists some time $t_2$ such that after $t_2$ both $i-2$ and $i+3$, the two neighbors of $i-1$ and $i+2$, deviate for at most once. Using this logic repeatedly, we will get that there are a finite number of deviations in total, a contradiction. Thus the “if” part of Theorem 7 in this case is also true.

Suppose now the underlying network is a ring. The “if” part of Theorem 7 in this case can be shown to be correct in precisely the same way as for the line network. To verify the “only if” part, suppose now the underlying ring is completely heterophilic and all agents take the same initial action. Then the conformists are all satisfied and the rebels are all unsatisfied. We let the rebels deviate one by one, during which the payoffs of the conformists keep decreasing. After the last deviation of the rebels, all of them are satisfied, but all of the conformists are unsatisfied. Now it is the conformists’ turn to deviate one by one. When the conformists are satisfied, all of the rebels will be unsatisfied again. Hence under the above particular deviation orders, this process will be infinitely repeated. It follows that the sequential BRD does not converge and the game is not an ordinal potential game. This completes the whole proof.$\square$

When the underlying network $(N,\mathrm{g})$ is a line or a ring, it is very likely to have at least one weak cluster. Similar to Theorem 6(a), we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \text{ Prob }_{c} \left[ (N,\mathrm{g},\mathbb {T}) \text{ is } \text{ an } \text{ ordinal } \text{ potential } \text{ game }\right] =1. \end{aligned}$$

We also have the following nice characterization for the sequential BRD on lines. Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP with the underlying network $(N,\mathrm{g})$ being a line, then the following statements are equivalent: (i) a PNE exists for G; (ii) G is weakly clustered; (iii) the sequential BRD converges for all initial action profiles; and (iv) the sequential BRD converges for some initial action profile. We do not have such a nice characterization when the network is a ring.

1.2 Stars

Observe first that, when the underlying network is a star, an NMP may not be an ordinal potential game, even if a PNE exists. To see this, suppose that the central agent is a conformist, and there are two peripheral conformists and one peripheral rebel. This game has a PNE (e.g., all the conformists choose action 0 and the rebel chooses action 1). Suppose the central conformist initially takes action 1, the rebel takes action 0, one peripheral conformist takes action 0 and the other peripheral conformist takes action 1. We let the rebel have a priority in deviating over the peripheral conformists. Then, it can be seen that the sequential BRD will never converge. Indeed, the central conformist and the peripheral rebel will alternately deviate for ever, like in matching pennies.

Yet, if we slightly weaken the convergence concept, then a result that is similar to Theorem 7 still holds for star networks.

Definition 8

Suppose that we are given an initialized NMP. A (stochastic) sequential BRD is called regular, if in each round, as long as a PNE is not reached, exactly one unsatisfied agent is selected to switch, such that (i) the probability that each unsatisfied agent is selected is positive, and (ii) this stochastic process is Markovian, i.e., the probability that each unsatisfied agent is selected is independent of the history.

Theorem 8

Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP. If the underlying network $(N,\mathrm{g})$ is a star,  then each regular sequential BRD converges with probability one for all initial action profiles if and only if at least one half of the peripheral agents are of the same type as the central agent.

Proof

Since G has a PNE if and only if at least one half of the peripheral agents are of the same type as the central agent (Lemma 1(e)), the “only if” part of Theorem 8 is immediate. The “if” part is a direct application of absorbing Markov chains, as demonstrated below.

Suppose now at least one half of the peripheral agents are of the same type as the central agent. Then at least one PNE exists. In fact, it can be seen that there are exactly two PNEs. Taking the action profiles as states, and letting the transition probabilities be determined by the underlying dynamic, we have a well-defined (not necessarily time-homogeneous) Markov chain. The two PNEs correspond to the only absorbing states of the Markov chain. It remains to show that this Markov chain is absorbing, i.e., every state can reach one of the two absorbing states. This follows from the observation below: if we let the unsatisfied peripheral agents that are of the same type as the central agent deviate first (one by one in an arbitrary order), and the other unsatisfied peripheral agents deviate subsequently (one by one in an arbitrary order), then we will arrive at one of the two PNEs. Since the non-absorbing states are transient in absorbing Markov chains, we know immediately that a PNE will be reached with probability one. This completes the proof. $\square$

Given a star network $(N,\mathrm{g})$, let each agent uniformly choose a type, then the probability that at least one half of the peripheral agents are of the same type as the central agent tends to 0.5, as n goes to infinity. Combining this fact with Theorem 8, it can be seen that when the underlying network is a star and each agent is assigned as a conformist with probability 0.5, the probability that the sequential BRD converges almost surely for all initial action profiles approaches 0.5, as n goes to infinity.

We also have the following nice characterization for the sequential BRD on star networks. Let $G=(N,\mathrm{g},{\mathbf {T}})$ be an NMP with the underlying network $(N,\mathrm{g})$ being a star, then the following statements are equivalent: (i) a PNE exists for G; (ii) at least one half of the peripheral agents are of the same type as the central agent; (iii) the sequential BRD converges almost surely for all initial action profiles; and (iv) the sequential BRD converges almost surely for some initial action profile.

1.3 Simultaneous BRD V.S. sequential BRD

Let’s now make some comparisons between the simultaneous BRD and the sequential BRD. Generally speaking, the sequential BRD has been studied much more extensively than the simultaneous BRD, and it has been widely recognized that the simultaneous BRD is in general more complicated than the sequential BRD. This contrast is also reflected in this paper: while we have provided quite complete characterizations for the sequential BRD of NMP, it is not the case for the simultaneous BRD.

We can also argue that convergence of the simultaneous BRD is stronger than convergence of the sequential BRD in some sense, when the underlying network is a line or a star. (i) Given an NMP with the underlying network being a line, if the simultaneous BRD converges for some initial action profile, then the sequential BRD converges for all initial action profiles. This is true because the former condition implies that a PNE exists, which is equivalent to the latter condition. (ii) Suppose now the underlying network is a star. Similarly, if the simultaneous BRD converges for some initial action profile, then the sequential BRD converges almost surely for all initial action profiles.