On the relationship between p-dominance and stochastic stability in network games

Abstract

This paper examines the properties of networks that determine the uniqueness of long-run equilibria emerging from symmetric coordination games when players are myopic best responders. We identify the contagion threshold and the network diameter as two measures of finite networks that determine when strategies in the minimal p-best response set of a coordination game are uniquely stochastically stable. We show that when the contagion threshold is greater or equal to p, strategies in the minimal p-best response set are uniquely stochastically stable in strongly connected networks with diameter greater or equal to seven. The contagion threshold and the network diameter are easy to compute and their values are unique for every strongly connected network.

1 Introduction

The concept of Nash equilibrium plays a central role in the field of game theory and economics. However, many games, such as coordination games,¹ have multiple strict Nash equilibria. This raises the question of which outcomes should be regarded as more reasonable than others. To address this issue, Foster and Young (1990), Kandori et al. (1993) and Young (1993) proposed examining the process by which conventions (Nash equilibria of coordination games) become established using evolutionary models with persistent randomness. In this framework, persistent randomness ensures that all outcomes are likely, but as the amount of noise vanishes, some outcomes become more likely than others. Outcomes that retain a positive probability of being played in the long run as the amount of noise vanishes are said to be stochastically stable.

A notable observation in the aforementioned papers is that stochastic stability as a selection mechanism not only rules out unstable mixed equilibria, but also selects a unique outcome in coordination games with two strategies. This outcome being the risk-dominant equilibrium, which is a strategy that is a unique best response to any distribution that places on it a mass of at least one half. Recent studies show that the predictions of stochastic stability strictly depend on the interaction structure (Alós-Ferrer and Weidenholzer 2007; Peski 2010).² And for most coordination games, there can be multiple stochastically stable outcomes on a given interaction structure. Even for $2\times 2$ coordination games, it is easy to construct an interaction structure where uniform adoption of either strategy is stochastically stable.

This paper seeks to identify properties of the interaction structure that robustly determine the uniqueness of stochastically stable outcomes. We consider an evolutionary model of best response with mutations (BRM) in symmetric coordination games—a framework introduced by Young (1993) and Kandori et al. (1993)—where players interact locally through a social network. The social network is modeled as a graph consisting of the set of players as nodes and a set of edges/links connecting different pairs of players. For any pair of players i and j, a directed link from i to j implies that i observes strategies chosen by j. The central behavioural assumptions of the BRM model are: (i) players are myopic in that their strategy choices at any period depend on the profile of strategies chosen by their opponents (i.e., the set of players with whom a player directly interacts) in the previous period; (ii) players choose strategies that are best responses to opponents’ strategy profile with a high probability, and with a small probability, independent across players and time, they experiment (mutate) and choose any strategy at random. These behavioural assumptions capture some aspects of bounded rationality of decision makers (e.g., limited attention and the inability to make farsighted decisions) often observed in economics and psychology.³

We identify two network measures, the contagion threshold and network diameter, that determine when strategies in the minimal p-best response set are uniquely stochastically stable.⁴ The minimal p-best response set is a generalization of risk-dominance to games with more than two strategies. A set of strategies of a coordination game is a p-best response set if the best responses to distributions that place on them a mass of at least p are themselves within that set (Tercieux 2006). The minimal p-best response set is the p-best response set that does not contain another smaller subset that itself is a p-best response set. If the minimal p-best response set contains only one strategy, then that strategy is a p-dominant equilibrium (Morris et al. 1995). In a coordination game with only two strategies, a $\frac{1}{2}$-dominant equilibrium is also a risk-dominant equilibrium.

The contagion threshold of an unweighted and strongly connected network, G, is defined as follows (Opolot and Azomahou 2021).⁵ Denote the set of players by N and define the r-order neighbours of any player i as the set of players located at a distance of r steps from i (i.e. player j is an r-order neighbour of i if the shortest path from i to j consists of r consecutive links). Define also the rth-neighbourhood of i as the set of all players within r steps from i, with i included; and $d_i$ as the maximum shortest distance from i to any other player. The contagion threshold, ${\underline{\eta }}(G)$, of network G is the minimum over all $i\in N$, all $r=2,3,\ldots ,d_i$ and all r-order neighbours of i, of the proportion of the first-order neighbours of each r-order neighbour of i that are contained in the $(r-1)$th-neighbourhood of i.⁶ Every strongly connected network has a unique contagion threshold bounded from above by 1/2 and from below by $1/\Delta (G)$, where $\Delta (G)$ is the maximum number of first-order neighbours of any player in the network.

The diameter, d(G), of network G is the maximum shortest distance between any two players (i.e., the maximum over all $i\in N$ of $d_i$). The value of the network diameter is unique for every strongly connected network and it captures the density and centralization of the network. Centralized networks exhibit a core-periphery structure where a subset of densely interconnected players form the core, and the rest who are adjacent to the core but not to themselves form the periphery. Highly centralized networks have a short diameter (e.g. a star network with diameter of 2). The network density is the total number of connections relative to the number of players. For a fixed number of players, the lower the network density the larger the network diameter.

We show that an absorbing set of states containing only strategies in the minimal p-best response set is uniquely stochastically stable in undirected, unweighted and strongly connected networks with the contagion threshold greater or equal to p and diameter greater or equal to seven. We discuss in Sect. 5 how this result directly extends to directed and weighted networks.

The proof of this result relies on the properties of contagion dynamics in networks. We distinguish between three forms of contagion dynamics: full contagion, partial contagion, and step-by-step contagion. Full contagion is the spread of strategies to the whole network through best response starting from a group of players whose size is less than half the population size. Partial contagion is the spread of strategies through best response from a group of players, say $N^\prime$, whose size, $n^\prime$, is less than half the population size, to a group of players whose size is larger than $n^\prime$. Step-by-step contagion is the spread of strategies to the whole network through iterative application of partial contagion.⁷

The contagion threshold and the network diameter determine when strategies in the minimal p-best response set are uniquely stochastically stable because, firstly, when ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$, strategies in the minimal p-best response set spread through full and step-by-step contagion from the first-neighbourhood of any player. This implies that the minimum number of mutations that trigger the spread of strategies in the minimal p-best response set through full and step-by-step contagion is at most the size of the smallest first-neighbourhood of G. Secondly, when ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$, the cost of reaching the basin of attraction of an absorbing set of states containing only strategies in the minimal p-best response set from any other state is bounded from above by the minimum number of mutations that trigger full and step-by-step contagion.⁸ Thirdly, when ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$, the minimum number of mutations needed to leave the basin of attraction of an absorbing set of states containing only strategies in the minimal p-best response set is greater than the size of the smallest first-neighbourhood of G. Following Ellison (2000, Theorems 1 and 2), these three observations imply that an absorbing set of states containing only strategies in the minimal p-best response set is uniquely stochastically stable whenever ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$.⁹

The network measures that have previously been identified as determinants of the uniqueness of stochastically stable outcomes include the sizes of the smallest odd and the largest first-order neighbourhoods, and the maximum group cohesion of the network (Alós-Ferrer and Weidenholzer 2008; Peski 2010; Opolot 2020). Let $\delta _0(G)$ be the size of the smallest odd first-order neighbourhood of network G. Peski (2010, Theorem 2 and Corollary 1) shows that in a BRM model, a p-dominant strategy is uniquely stochastically stable in network G if p is less or equal to $\frac{1}{2}\left( 1-1/\delta _0(G)\right)$. In comparison, our results offer more accurate predictions of stochastically stable outcomes in sparsely connected networks (i.e. where $\Delta (G)$ is small so that the lower bound of the contagion threshold, $1/\Delta (G)$, is large), while Peski (2010, Theorem 2 and Corollary 1) offers more accurate predictions in densely connected networks (i.e., where $\delta _0(G)$ is large so that $\frac{1}{2}\left( 1-1/\delta _0(G)\right)$ is close to one half). For example, when $\delta _0(G)=1$, Peski (2010, Theorem 2 and Corollary 1) fails to predict the unique stochastically stable outcome.

Alós-Ferrer and Weidenholzer (2008) show that in a BRM model, a $1/\Delta (G)$-dominant strategy is uniquely stochastically stable.¹⁰ Our results generalize this special case from Alós-Ferrer and Weidenholzer (2008) since the lower bound of the contagion threshold of any network is $1/\Delta (G)$.¹¹ Opolot (2020) finds that for a BRM model on cyclic regular networks where the size of the first-order neighbourhoods is k, strategies in the smallest iterated p-best response set (i.e., a set of strategies that remain after iterative application of the notion of p-best response sets) are uniquely stochastically stable whenever p is less or equal to one minus the maximum group cohesion.¹² Opolot (2020) provides a counter example showing that the maximum group cohesion fails to predict the uniqueness of stochastically stable outcomes in some arbitrary networks. Since every strongly connected arbitrary network has a unique contagion threshold greater or equal to $1/\Delta$, our result provides a prediction of when the minimal p-best response set is uniquely stochastically stable in any strongly connected arbitrary network.

Besides the aforementioned papers, many other papers have examined long-run stability of the BRM model in networks.¹³ Ellison (1993, 2000) and Weidenholzer (2012) show that a $\frac{1}{2}$-dominant strategy is uniquely stochastically stable in cyclic regular networks where each player has an even number of neighbours; Blume (1995), Young (1998), Lee and Valentinyi (2000) and Lee et al. (2003) show that the risk-dominant strategy is uniquely stochastically stable in 2-dimensional grid lattices; and Alós-Ferrer and Weidenholzer (2007) show that a globally pairwise risk-dominant strategy of a $3\times 3$ coordination game is stochastically stable in a cyclic network where each player has two neighbours. In contrast to the present paper, these papers focus on specific (mostly regular) networks and do not identify the general network properties that determine the uniqueness of stochastically stable outcomes.

Finally, this paper is related to Morris (2000), Oyama and Takahashi (2015) and Opolot and Azomahou (2021) who study contagion in networks when players are myopic best responders. Morris (2000) finds that a p-dominant strategy of a $2\times 2$ coordination game is fully contagious on an unbounded network if p is less or equal to the contagion threshold. We discuss in Sect. 3.1 the difference between the contagion threshold for finite networks defined in this paper and the contagion threshold for unbounded networks as defined by Morris (2000). Oyama and Takahashi (2015) derive the conditions under which the risk-dominant and Pareto-dominant strategies of a $3\times 3$ coordination game containing a dominated strategy are fully contagious on unbounded networks; they also compare networks in terms of their power of inducing contagion in general supermodular games. Opolot and Azomahou (2021) show that a p-dominant strategy of an m-strategy coordination game is fully contagious on a finite network whenever p is less or equal to the contagion threshold. We build on the ideas of contagion dynamics developed in these papers and use them to derive the conditions under which the minimal p-best response set is uniquely stochastically stable.

The remainder of the paper is organized as follows. Section 2 outlines a model of evolutionary dynamics with best response and mutations. Section 3 defines the notion of contagion and contagion threshold, and discusses how contagion determines stochastically stable outcomes. Section 4 states the main results and discusses the intuition of the proof. Section 5 discusses the implications of our results and how they relate to the literature. Concluding remarks are offered in Sect. 6 and proofs are contained in the Appendix.

2 An evolutionary model of best response with mutations

We consider a finite set of players, $N = \{1, 2,\ldots , n\}$, connected through a social network. Each player plays a symmetric coordination game against her direct neighbours. Players revise their strategies simultaneously and independently at discrete times, $t=1, 2,\ldots$. We start with a description of an unperturbed evolutionary model where, at each t, each player chooses a pure strategy randomly from the set of pure strategies that are best responses to the profile of strategies played by the opponents at $t-1$. Players do not play mixed strategies. For the characterization of stochastically stable outcomes, we consider an evolutionary model of best response with mutations (BRM) where, with a fixed small probability $\varepsilon$, independent across players and across time, players choose any pure strategy at random, and with the complementary probability $1-\varepsilon$, they choose a strategy from the best response set. The following subsections formally outline these concepts.

2.1 The coordination game

We consider m-strategy 2-player symmetric strict coordination games with a set of pure strategies denoted by $A=\{a_1, \ldots , a_j, \ldots , a_m\}$, identical to all players. Let U be an $m\times m$ payoff matrix with the elements $u(a_j,a_l)$, for all $a_j, a_l \in A$, being the payoff to a player playing strategy $a_j$ against an opponent playing strategy $a_l$. The double (A, U) is a coordination game if $u(a_j , a_j) \ge u(a_l , a_j)$ for all $a_j, a_l \in A$ and $a_l \ne a_j$; it is a symmetric coordination game if, in addition, $u(a_j,a_l)$, for all $a_j, a_l \in A$, is identical for all players; and it is a strict symmetric coordination game if $u(a_j , a_j) > u(a_l , a_j)$, for all $a_j, a_l \in A$ and $a_l \ne a_j$, and $u(a_j,a_l)$ is identical for all players. This paper focuses on strict symmetric coordination games.

Let $\Sigma$ be the set of all distributions over A whereby, for any $a_j\in A$ and $\sigma \in \Sigma$, $\sigma (a_j)$ is the mass that $\sigma$ places on $a_j$, and $\sum _{a_k\in A}\sigma (a_k)=1$. We consider linear payoffs where the payoff to a player playing pure strategy $a_j$ against distribution $\sigma$ is given by $U(a_j\mid \sigma )=\sum _{a_k\in A}\sigma (a_k)u(a_j,a_k)$. The set of pure strategy best responses to $\sigma$ is defined as

$$\begin{aligned} BR(\sigma )=\{a_j\in A \mid U(a_j\mid \sigma )\ge U(a_l\mid \sigma ) \,\forall a_l\in A \}. \end{aligned}$$

2.2 The network game

The social network is represented by an exogenously given and fixed over time graph G(N, E), with N representing the set of players and E the set of edges linking different pairs of players.¹⁴ Let $N_i$ be the set of first-order neighbours of i—the set of players that i directly interacts with in G(N, E)—and let $n_i$ be the cardinality of $N_i$. A directed path from player i to j is a finite sequence of players $(i_1, i_2,\ldots ,i_r)$, with $i=i_1$ and $i_r=j$, that are connected through distinct directed links (i.e., no link appears more than once).

We focus on unweighted, undirected and strongly connected networks. A network is unweighted if a link between any pair of players $i,j\in N$ has a weight of one; it is undirected if the existence of a link from i to j implies existence of a reverse link from j to i; and it is strongly connected if there exists a directed path connecting any pair of players $i, j \in N$ and $i\ne j$.

Focusing on unweighted and undirected networks is for simplicity and we discuss in Sect. 5 how our results extend to weighted and directed networks. Requiring the network to be strongly connected is necessary for our results to hold. Networks that are not strongly connected may consist of disconnected subgroups, which affects convergence of an evolutionary process. By avoiding issues related to convergence, we can focus on examining structural properties of the network that determine the uniqueness of stochastically stable outcomes. One of the network measures that is relevant to our analysis is the diameter. Let $d_{ij}$ be the length of the shortest directed path from i to j (i.e. the distance from i to j), and $d_i=\max _{j\in N}d_{ij}$ be the maximum shortest distance from i to any other player. The diameter of G(N, E) is $d(G)=\max _{i\in N}d_i$, which is the maximum shortest distance between any two players.

In analogy to the linear payoffs defined above, let $\sigma _i=(\sigma _i(a_1),\ldots ,\sigma _i(a_m))$ be the distribution over A that represents the proportion of i’s direct neighbours playing each pure strategy. Then the total payoff that i receives from playing pure strategy $a_j$ against distribution $\sigma _i$ is (players do not play mixed strategies)¹⁵

$$\begin{aligned} U_i(a_j\mid \sigma _i)= \sum _{a_l\in A}\sigma _i(a_l)u(a_j, a_l). \end{aligned}$$

(1)

We refer to the quadruple (A, U, N, G), where each player’s payoff is given by (1), for all $\sigma _i\in \Sigma$, as a network game.

2.3 Unperturbed evolutionary process

The unperturbed evolutionary process is a myopic best response process where players revise their strategies simultaneously and independently over discrete times, $t = 1, 2, \ldots$. At each t, each player plays the symmetric strict coordination game against the same set of direct neighbours and selects a pure strategy randomly from a set of strategies that maximize (1). Players are myopic in that the strategies chosen at t are those that maximize the payoffs of the profiles of strategies chosen by their neighbours at $t-1$.

Formally, let ${\mathbf {x}}=(x^1,\ldots ,x^n)$ denote the profile/configuration of pure strategies, where $x^i$ is the pure strategy played by the ith player. Each strategy profile is a state of an evolutionary process, and we denote the set of all states by ${\mathbf {X}}$. For each ${\mathbf {x}}$, let $\sigma _i(a_l;{\mathbf {x}})$ be the proportion of i’s neighbours playing strategy $a_l$ in profile ${\mathbf {x}}$, and let $\sigma _i({\mathbf {x}})=(\sigma _i(a_1;{\mathbf {x}}),\ldots ,\sigma _i(a_m;{\mathbf {x}}))$ be the distribution over A representing the proportions of i’s neighbours playing different strategies in profile ${\mathbf {x}}$. Let also ${\mathbf {x}}(t)$ be the strategy profile at t, and $x^i(t)$ the respective strategy played by the ith player in profile ${\mathbf {x}}(t)$. In analogy to (1), $U_i\big (a_j\mid \sigma _i({\mathbf {x}}_t)\big )= \sum _{a_l\in A}\sigma _i(a_l;{\mathbf {x}}_t)u(a_j, a_l)$ is player i’s payoff from playing pure strategy $a_j$ against the profile of strategies chosen by the neighbours at t. Accordingly, $BR(\sigma _i({\mathbf {x}}(t)))$ is the best response set of $\sigma _i({\mathbf {x}}(t))$ (i.e. the set of all strategies, $a_j\in A$, that satisfy the inequality $U_i\big (a_j\mid \sigma _i({\mathbf {x}}_t)\big )\ge U_i\big (a_l\mid \sigma _i({\mathbf {x}}_t)\big )$, for all $a_l\in A$). Then, at period $t+1$, player i randomizes uniformly over the strategies in $BR(\sigma _i({\mathbf {x}}(t)))$.

The assumption of myopia is standard in the literature of evolutionary game theory and it is used to model agents with bounded rationality. That is, it assumes that agents are incapable of keeping track of the entire history of play and performing complex evaluations associated with forward-looking decision making.

The evolutionary framework described above is a finite time homogeneous Markov chain (i.e., the associated transition probability matrix is independent of time) on the state space ${\mathbf {X}}$. It is time homogeneous because the four components, A, U, N and G, that make up the network game are independent of time. Let P denote the transition probability matrix so that $P({\mathbf {x}},{\mathbf {y}})$ is the probability of transiting from state ${\mathbf {x}}$ to ${\mathbf {y}}$ in a single step. We refer to the tuple (A, U, N, G, P) as an unperturbed evolutionary process on network G. The equilibrium behaviour of (A, U, N, G, P) is fully described by its absorbing sets. A subset of states, $W\subseteq {\mathbf {X}}$, is an absorbing set of (A, U, N, G, P) if, once entered, is never exited. If an absorbing set is a singleton then it is called an absorbing state; that is, any state ${\mathbf {x}}\in {\mathbf {X}}$ for which $P({\mathbf {x}},{\mathbf {x}})=1$ is an absorbing state. Absorbing sets that are not absorbing states form an absorbing cycle. For example, a pair of states ${\mathbf {x}}$ and ${\mathbf {y}}$ form an absorbing cycle if $P({\mathbf {x}},{\mathbf {y}})=1$ and $P({\mathbf {y}},{\mathbf {x}})=1$. We denote by ${\mathbf {A}}$ a set of all absorbing sets.

2.4 Perturbed evolutionary process and stochastic stability

Following the literature, a perturbed evolutionary process is derived from the unperturbed evolutionary process by adding rare mutations. We follow the evolutionary framework of best response with mutations (BRM) by Young (1993) and Ellison (2000), whereby, with a fixed small probability $\varepsilon >0$, independent across players and time, a player chooses a strategy uniformly at random, and with a complementary probability $(1-\varepsilon )$, randomizes uniformly over the strategies in $BR(\sigma _i({\mathbf {x}}(t)))$.

Let $P_{\varepsilon }$ be the transition probability matrix of the associated Markov chain, so that $P_{\varepsilon }({\mathbf {x}},{\mathbf {y}})$ is the probability that profile ${\mathbf {x}}$ is followed by ${\mathbf {y}}$. Let $c({\mathbf {x}}, {\mathbf {y}})$ be the number of players for whom $y^i$, the ith strategy in ${\mathbf {y}}$, is not a best response to ${\mathbf {x}}$ (i.e. the number of mutations involved in a direct transition from ${\mathbf {x}}$ to ${\mathbf {y}}$). Then $P_{\varepsilon }({\mathbf {x}},{\mathbf {y}})$ can be expressed as follows, where we use the notation $b_i({\mathbf {x}})=|BR(\sigma _i({\mathbf {x}}))|$.¹⁶

$$\begin{aligned} P_{\varepsilon }({\mathbf {x}},{\mathbf {y}}) = \left( \frac{\varepsilon }{m}\right) ^{c({\mathbf {x}}, {\mathbf {y}})}\prod _{i=1}^{n-c({\mathbf {x}}, {\mathbf {y}})}\left( \frac{m+(b_i({\mathbf {x}})-m)\varepsilon }{mb_i({\mathbf {x}})}\right) \end{aligned}$$

(2)

The parameter $c({\mathbf {x}},{\mathbf {y}})$, for any pair ${\mathbf {x}},{\mathbf {y}}\in {\mathbf {X}}$, is also commonly referred to as the cost function of the stochastic evolutionary process. The cost, $c({\mathbf {x}},{\mathbf {y}})$, reflects how unlikely the direct transition from ${\mathbf {x}}$ to ${\mathbf {y}}$ is when $\varepsilon$ is small. For this reason, $c({\mathbf {x}},{\mathbf {y}})$ is formally defined as

$$\begin{aligned} c({\mathbf {x}},{\mathbf {y}}) = -\lim _{\varepsilon \rightarrow 0}\varepsilon \ln P_{\varepsilon }({\mathbf {x}},{\mathbf {y}}) \end{aligned}$$

(3)

Substituting for the expression of the transition probabilities from (2), we see that the limit on the right hand side of (3) exists. The definition of the cost function in (3) is not limited to the BRM model. Sandholm (2010) applies this definition to derive the cost functions of evolutionary models where the transition probabilities assume a logit and probit probability structures.

The tuple $(A,U,N,G,P_{\varepsilon })$ is here referred to as the perturbed evolutionary process on network G. The equilibrium behaviour of $(A,U,N,G,P_{\varepsilon })$ is fully described by its stationary distribution, $\pi _{\varepsilon }$, which is the probability distribution over the state space, ${\mathbf {X}}$, that describes the long-run average time spent in each state. For each ${\mathbf {x}}\in {\mathbf {X}}$, $\pi _{\varepsilon }({\mathbf {x}})$ is the proportion of time that $(A,U,N,G,P_{\varepsilon })$ spends in ${\mathbf {x}}$ in the long run. The stationary distribution of $(A,U,N,G,P_{\varepsilon })$ exists, and is unique, because $(A,U,N,G,P_{\varepsilon })$ is ergodic (i.e., it is possible to get from every state to every other state with positive probability). The ergodicity of $(A,U,N,G,P_{\varepsilon })$ follows because the incorporation of mutations that are independent across players and time ensures that $P_{\varepsilon }({\mathbf {x}},{\mathbf {y}})>0$, for all pairs ${\mathbf {x}},{\mathbf {y}}\in {\mathbf {X}}$.

We are interested in identifying the long-run or stochastically stable set of states of $(A,U,N,G,P_{\varepsilon })$, which is a set of states that maximize $\pi _{\varepsilon }$ when $\varepsilon$ is small. However, computing $\pi _{\varepsilon }$ is difficult, and the standard approach is to focus on the limit stationary distribution, $\pi ^*$, defined as $\pi ^*=\lim _{\varepsilon \rightarrow 0}\pi _{\varepsilon }$. The reason for this is that $\pi ^*$, which is easier to compute, provides an approximation to $\pi _{\varepsilon }$ when $\varepsilon$ is small. The limit stationary distribution exists and the set of states ${\mathbf {A}}^*\subset {\mathbf {X}}$, with $\pi ^*({\mathbf {A}}^*)>0$, is called a stochastically stable set (Young 1993; Ellison 2000). It is known that the stochastically stable set of $(A,U,N,G,P_{\varepsilon })$ is contained in ${\mathbf {A}}$ (Young 1993). If ${\mathbf {A}}^*=\{{\mathbf {x}}^*\}$, then ${\mathbf {x}}^*$ is a stochastically stable state. Accordingly, a set of strategies $A^*\subseteq A$ played in ${\mathbf {A}}^*$ are said to be stochastically stable strategies.

To compute the stochastically stable set of $(A,U,N,G,P_{\varepsilon })$, we employ the method developed by Ellison (2000), which involves computing the radius, coradius and modified coradius of the basins of attraction of absorbing sets. The basin of attraction, D(W), of $W\subseteq {\mathbf {A}}$, is the set of initial states from which the unperturbed evolutionary process, (A, U, N, G, P), converges to W with probability one.¹⁷

The radius, coradius and modified coradius are all cost functions that depend on the total costs of paths between states. Define a path from subset Z to W as a finite sequence of distinct states $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ with ${\mathbf {x}}_1\in Z$, ${\mathbf {x}}_T\in W$ and ${\mathbf {x}}_{\tau }\notin W$ for $2\le \tau \le T-1$. Let S(Z, W) be the set of all paths from Z to W. The cost $c({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ of path $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ is the sum of the costs of the transitions between pairs of states along $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$. That is, $c({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T) = \sum _{\tau =1}^{T-1}c({\mathbf {x}}_{\tau },{\mathbf {x}}_{\tau +1})$.

Recall that each $c({\mathbf {x}}_{\tau },{\mathbf {x}}_{\tau +1})$, defined in (3), reflects how unlikely the direct transition from ${\mathbf {x}}_{\tau }$ to ${\mathbf {x}}_{\tau +1}$ is when $\varepsilon$ is small. Accordingly, $c({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ reflects how unlikely it is for $(A,U,N,G,P_{\varepsilon })$ to reach ${\mathbf {x}}_{T}$ from ${\mathbf {x}}_{1}$ through the path $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ when $\varepsilon$ is small.

Let $C(Z,W) = \min _{({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)\in S(Z,W)}c({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ be the cost of the minimum cost path from Z to W. The radius, R(W), of W, is the minimum cost of any path from W out of the basin of attraction of W (i.e., the minimum number of mutations needed to exit D(W)):

$$\begin{aligned} R(W) =\min _{({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)\in S(W, {\mathbf {X}}-D(W))}c({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T) \end{aligned}$$

Intuitively, R(W) measures how likely it is for $(A,U,N,G,P_{\varepsilon })$ to leave the basin of attraction of W when $\varepsilon$ is small.

The coradius, CR(W), of W is the maximum over all other states of the minimum number of mutations required to reach W, and it measures how likely it is for $(A,U,N,G,P_{\varepsilon })$ to reach W from any other state when $\varepsilon$ is small:¹⁸

$$\begin{aligned} CR(W) = \max _{{\mathbf {x}}\notin W}\min _{({\mathbf {x}}_1,\ldots ,{\mathbf {x}}_T)\in S({\mathbf {x}},W)}c({\mathbf {x}}_1,\ldots ,{\mathbf {x}}_T)=\max _{{\mathbf {x}}\notin W}C({\mathbf {x}},W) \end{aligned}$$

Let $Z_1,Z_2,\ldots ,Z_q$, with ${\mathbf {x}}\in D(Z_1)$, $Z_q\subseteq W$ and $Z_l\not \subseteq W$ for $l<q$, be a sequence of absorbing sets through which some path, $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$, from ${\mathbf {x}}={\mathbf {x}}_1$ to ${\mathbf {x}}_{T}\in Z_q$ traverses consecutively. Define the modified cost, $c^*({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$, of the path $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ as the cost, $c({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$, minus the radius of the intermediate limit sets through which the path $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ passes. That is,

$$\begin{aligned} c^*({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T) = c({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)-\sum _{l=2}^{q-1}R(Z_l) \end{aligned}$$

(4)

The modified coradius, $CR^*(W)$, of W is the maximum over all ${\mathbf {x}}\notin W$ of the minimum modified cost of all paths from ${\mathbf {x}}$ to W. That is,

$$\begin{aligned} CR^*(W) = \max _{{\mathbf {x}}\notin W}\min _{({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)\in S({\mathbf {x}}, W)}c^*({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)=\max _{{\mathbf {x}}\notin W}C^*({\mathbf {x}},W) \end{aligned}$$

(5)

where $C^*({\mathbf {x}},W) = \min _{({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)\in S({\mathbf {x}}, W)}c^*({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ is the minimum modified cost of all paths from ${\mathbf {x}}$ to W. Like the coradius, the modified coradius measures how likely it is for $(A,U,N,G,P_{\varepsilon })$ to reach W from any other state when $\varepsilon$ is small. The following lemma summarize the results of Ellison (2000, Theorems 1 and 2).

Lemma 1

(Ellison 2000, Theorems 1 and 2) Let ${\mathbf {A}}^*\subseteq {\mathbf {A}}$ be a set of absorbing sets. If $R({\mathbf {A}}^*)>CR({\mathbf {A}}^*)$ and/or $R({\mathbf {A}}^*)>CR^*({\mathbf {A}}^*)$, then the unique stochastically states are contained in ${\mathbf {A}}^*$.

3 How contagion affects stochastically stable outcomes

3.1 p-best response sets, contagion and the contagion threshold

We aim to establish the relationship between p-best response/p-dominance and stochastic stability of the evolutionary process $(A,U,N,G,P_{\varepsilon })$. We derive the conditions under which the minimal p-best response set is uniquely stochastically stable on a given network. A p-best response set is a set of strategies that are best responses to distributions that place on them a mass of at least p. And for the network game (A, U, N, G), if at least proportion p of a player’s neighbours play strategies in the p-best response set, then all of a player’s best responses are themselves within that set. For any nonempty subset $A^\prime \subseteq A$ and any $\sigma \in \Sigma$, let $\sigma _{A^\prime }=\sum _{a_j\in A^\prime }\sigma (a_j)$ be the total mass that distribution $\sigma$ places on $A^\prime$.

Definition 1

A nonempty subset of strategies $A^\prime \subseteq A$ is a p-best response set of a symmetric strict coordination game (A, U) if for all $\sigma \in \Sigma$ with $\sigma _{A^\prime }\ge p$, $\text {BR}(\sigma )\subseteq A^\prime$. $A^\prime$ is a minimal p-best response set if $A^\prime$ does not contain any proper subset that is a p-best response set.

The definition of a p-best response set in Definition 1 implies that the strategy set, A, is, trivially, a p-best response set of (A, U) for all $p\in [0,1]$. A coordination game can have more than one p-best response set, and the minimal p-best response set is the one that does not contain another smaller subset that itself is a p-best response set.¹⁹ We denote by $A^p$ the minimal p-best response set of (A, U). Every coordination game has a unique minimal p-best response set when $p\le \frac{1}{2}$ (Tercieux 2006, Theorem 1). If, for some $p\le \frac{1}{2}$, $A^p=\{a\}$, then a is a p-dominant equilibrium.

Although the predictions of stochastic stability will be coarse when $A^p$ contains more than one strategy, it is useful to examine when strategies in $A^p$ are stochastically stable because, firstly, many coordination games do not have a p-dominant equilibrium but every coordination game has a unique minimal p-best response set for $p\le \frac{1}{2}$. Secondly, if only one strategy is indeed uniquely stochastically stable, then we would know that that strategy is in $A^p$. A more precise method can then be used to isolate the unique stochastically stable strategy from $A^p$. Thirdly, there are situations, such as technology adoption, where one may be interested in the diffusion of a combination of strategies. A firm that owns two technologies may be interested in the long-run market survival of both technologies if they are complementary or if producing both is cost-effective.

Consider the two examples of symmetric coordination games in Fig. 1. For the game in Fig. 1a, set $A^\prime =\{a_2,a_3\}$ is a p-best response set for $p>\frac{5}{18}$, and for $p>\frac{3}{8}$, both $A^\prime =\{a_2,a_3\}$ and $A^{\prime \prime }=\{a_3\}$ are p-best response sets. The minimal p-best response set is $A^p=A^{\prime \prime }$, which is also a p-dominant equilibrium since it is a singleton set. The game in Fig. 1b does not contain a p-dominant equilibrium for all $p\le \frac{1}{2}$, but it contains a minimal p-best response set $A^p=\{a_2,a_3\}$, for $p>\frac{1}{3}$. For this scenario, our analysis below establishes the conditions under which the unique stochastically stable strategy is contained in $A^p=\{a_2,a_3\}$.

Fig. 1

a A $3\times 3$ symmetric coordination game with strategy $a_3$ as the p-dominant equilibrium, for $p>\frac{3}{8}$; b A $3\times 3$ symmetric coordination game with $A^\prime =\{a_2,a_3\}$ as the minimal p-best response set, for $p>\frac{1}{3}$

Given $A^p\subseteq A$, let ${\mathbf {A}}^p\subseteq {\mathbf {A}}$ be the set of all absorbing sets of states containing only strategies in $A^p$. Strategies in $A^p$ are said to be uniquely stochastically stable if set ${\mathbf {A}}^p$ is uniquely stochastically stable. We derive conditions under which ${\mathbf {A}}^p$ is uniquely stochastically stable (i.e. under which $R({\mathbf {A}}^p)>CR({\mathbf {A}}^p),CR^*({\mathbf {A}}^p)$) by exploiting the properties of the process of contagion in networks. We distinguish between two forms of contagion that are both used in the derivation of the main results: full contagion and step-by-step contagion. Full contagion is the spread of strategies in $A^\prime \subset A$ to the whole network through best response starting from a group of players whose size is less than half the population size. Step-by-step contagion is derived by iteratively applying partial contagion, which is the spread of strategies in $A^\prime \subset A$ through best response from a group of players, say $N^\prime \subset N$, whose size, $n^\prime$, is less than half the population size, to a group of players whose size is larger than $n^\prime$. These three concepts are formally developed through the following series of definitions.

Definition 2

A sequence of strategy profiles $\left\{ {\mathbf {x}}_t \right\} _{t=0}^{{\bar{t}}}$ of (A, U, N, G, P), for some ${\bar{t}}\ge 2$, is a best response sequence if it satisfies the following properties: (i) for all $1\le t<{\bar{t}}$, there exists at least one $i\in N$ such that $x_t^i\ne x_{t-1}^i$; (ii) if $x_t^i\ne x_{t-1}^i$, then $x_t^i\in BR(\sigma _i({\mathbf {x}}_{t-1}))$.

According to Definition 2, a sequence of states is a best response sequence if, (i) for any pair of consecutive states ${\mathbf {x}}_{t}$ and ${\mathbf {x}}_{t+1}$ along the sequence, at least one player must play a strategy in state ${\mathbf {x}}_{t+1}$ that is different from a strategy played in state ${\mathbf {x}}_{t}$; (ii) players switch strategies through best response, that is, if i’s strategy in state ${\mathbf {x}}_{t+1}$ is different from the strategy played in state ${\mathbf {x}}_{t}$, then $x_{t+1}^i$ is a best response to $\sigma _i({\mathbf {x}}_{t})$.

Definition 3

Let (A, U, N, G, P) start from some ${\mathbf {x}}\in {\mathbf {X}}$. Strategies in $A^\prime \subset A$ spread through full contagion from a subgroup of players, ${\mathcal {M}}(A^\prime ;{\mathbf {x}})\subset N$, if there exists some ${\bar{t}}\ge 2$ such that every best response sequence $\left\{ {\mathbf {x}}_t \right\} _{t=0}^{{\bar{t}}}$ with ${\mathbf {x}}_0={\mathbf {x}}$ and $x_1^i\in A^\prime$ for all $i\in {\mathcal {M}}(A^\prime ;{\mathbf {x}})$ satisfies $x_{{\bar{t}}}^i\in A^\prime$ for all $i\in N$.

According to Definition 3, when (A, U, N, G, P) starts from ${\mathbf {x}}$, strategies in $A^\prime$ spread through full contagion from a subset ${\mathcal {M}}(A^\prime ;{\mathbf {x}})$ if they spread to the whole network through best response once all players in ${\mathcal {M}}(A^\prime ;{\mathbf {x}})$ play strategies in $A^\prime$. Let $\mu (A^\prime ;{\mathbf {x}})$ be the cardinality of ${\mathcal {M}}(A^\prime ;{\mathbf {x}})$ and let $\mu ^*(A^\prime ;{\mathbf {x}})$ be the size of the smallest group of players from which strategies in $A^\prime$ can spread through full contagion starting from ${\mathbf {x}}$. Equivalently, $\mu ^*(A^\prime ;{\mathbf {x}})$ is the minimum number of mutations needed to trigger evolution of (A, U, N, G, P) from ${\mathbf {x}}$ to some state in ${\mathbf {A}}^\prime$, a set of absorbing sets containing only strategies in $A^\prime$.

Definition 4

Strategies in $A^\prime \subset A$ are fully contagious on G if, starting from every ${\mathbf {x}}\notin {\mathbf {A}}^\prime$, they can spread through full contagion from a group of $\mu ^*(A^\prime ;{\mathbf {x}})<\frac{n}{2}$ players.

When $\max _{{\mathbf {x}}\notin {\mathbf {A}}^p}\mu ^*(A^p;{\mathbf {x}})\le \mu ^*$, we say that $\mu ^*$ mutations to strategies in $A^p$ trigger full contagion. From the definition of the coradius in Sect. 2.4, it follows from Definition 4 that when strategies in $A^p$ are fully contagious on a given network, the coradius of ${\mathbf {A}}^p$ is bounded from above by $\max _{{\mathbf {x}}\notin {\mathbf {A}}^p}\mu ^*(A^p;{\mathbf {x}})$. In the analysis that follows, we define a network measure, the contagion threshold, that determines when strategies in $A^p$ can spread through full contagion. Once such a measure is defined, it is then possible to establish an upper bound of $\max _{{\mathbf {x}}\notin {\mathbf {A}}^p}\mu ^*(A^p;{\mathbf {x}})$, and hence, the coradius of ${\mathbf {A}}^p$.

Although the notion of full contagion enables us to derive the upper bound of the coradius of ${\mathbf {A}}^p$, the coradius is a less accurate measure of the cost of reaching ${\mathbf {A}}^p$ from any other state compared to the modified coradius. In some networks, the value of $\max _{{\mathbf {x}}\notin {\mathbf {A}}^p}\mu ^*(A^p;{\mathbf {x}})$, and hence, the coradius of ${\mathbf {A}}^p$, can be large (i.e. close to $\frac{n}{2}$), which in turn requires imposing strict assumptions on the network structure to ensure that $R({\mathbf {A}}^p)>CR({\mathbf {A}}^p)$. Using the modified coradius can mitigate this problem because in most cases, the modified coradius is less than the coradius of an absorbing set.

Recall that the modified coradius of ${\mathbf {A}}^p$ is the cost of the minimum cost path that passes along absorbing sets that are different from ${\mathbf {A}}^p$. The notion of step-by-step contagion captures the costs of evolution along sequences of absorbing sets, and can thus be used to place an upper bound on the modified coradius of ${\mathbf {A}}^p$. Let $N(A^\prime ;{\mathbf {x}})$ be the set of players playing strategies in $A^\prime$ in configuration ${\mathbf {x}}$, and let $n(A^\prime ;{\mathbf {x}})$ be the cardinality of $N(A^\prime ;{\mathbf {x}})$. Then partial and step-by-step contagion are formally defined as follows.

Definition 5

Let (A, U, N, G, P) start from some ${\mathbf {x}}\in {\mathbf {X}}$ and let ${\mathbf {x}}\in D(W^\prime )$, where $W^\prime \in {\mathbf {A}}$ and $W^\prime \ne {\mathbf {A}}^\prime$. Strategies in $A^\prime \subset A$ spread through partial contagion from a subgroup of players, ${\mathcal {M}}(A^\prime ;{\mathbf {x}};W)\subset N$, to some absorbing set $W\ne W^\prime$, if there exists some ${\bar{t}}\ge 2$ such that every best response sequence $\left\{ {\mathbf {x}}_t \right\} _{t=0}^{{\bar{t}}}$ with ${\mathbf {x}}_0={\mathbf {x}}$ and $x_1^i\in A^\prime$ for all $i\in {\mathcal {M}}(A^\prime ;{\mathbf {x}};W)$ satisfies ${\mathbf {x}}_{{\bar{t}}}\in W$ and $n(A^\prime ;{\mathbf {x}}_{{\bar{t}}})>n(A^\prime ;{\mathbf {x}})$.

Let $\mu (A^\prime ;{\mathbf {x}};W)$ be the cardinality of ${\mathcal {M}}(A^\prime ;{\mathbf {x}};W)$. Definition 5 states that strategies in $A^p$ spread through partial contagion from a group ${\mathcal {M}}(A^p;{\mathbf {x}};W)$ of players, where ${\mathbf {x}}\in D(W^\prime )$, to an absorbing set $W\ne W^\prime$ if $\mu (A^p;{\mathbf {x}};W)$ mutations to strategies in $A^p$ trigger an iterative process of best response where (A, U, N, G, P) eventually converges to W. Let $\mu ^*(A^p;{\mathbf {x}};W)$ be the size of the smallest group of players from which strategies in $A^p$ can spread through partial contagion starting from ${\mathbf {x}}$ to W. Equivalently, $\mu ^*(A^p;{\mathbf {x}};W)$ is the minimum number of mutations to strategies in $A^p$ needed to trigger evolution of (A, U, N, G, P) from ${\mathbf {x}}$ to some state in W.

Definition 6

Strategies in $A^\prime \subset A$ are step-by-step contagious on G starting from ${\mathbf {x}}\notin {\mathbf {A}}^\prime$, if there exists a sequence of absorbing sets $W_1, W_2,\ldots ,W_J$, with ${\mathbf {x}}\in D(W_1)$ and $W_J={\mathbf {A}}^\prime$, and a corresponding sequence of strategy sets, $A_2, A_3,\ldots , A_J$, such that, for any ${\mathbf {y}}\in W_j$, strategies in $A_{j+1}$ spread through partial contagion from $\mu ^*(A_{j+1};{\mathbf {y}};W_{j+1})<\frac{n}{2}$ players.

Definition 6 states that strategies in $A^p$ are step-by-step contagious on a given network if they spread to the whole network through iterative application of partial contagion. That is, starting from ${\mathbf {x}}\in D(W)$, there exists a sequence of absorbing sets $W_1, \ldots , W_J$, with $W=W_1$ and $W_J={\mathbf {A}}^p$, and a corresponding sequence of strategy sets $A_2, A_3,\ldots ,A_J$, with $A_J=A^p$, such that along $W_1, \ldots , W_J$, (A, U, N, G, P) evolves from ${\mathbf {x}}$ to $W_2$ through best response once $\mu ^*(A_2;{\mathbf {x}};W_{2})<\frac{n}{2}$ players play (mutation to) strategies in $A_2$; and from any ${\mathbf {y}}\in W_2$ to $W_3$ through best response once $\mu ^*(A_3;{\mathbf {y}};W_{3})<\frac{n}{2}$ players play (mutation to) to strategies in $A_3$; and so on, until it eventually reaches ${\mathbf {A}}^p$. When $\mu ^*(A_{j+1};{\mathbf {y}};W_{j+1})\le \mu ^*$ for all $j=1,\ldots ,J-1$, we say that $\mu ^*$ mutations trigger step-by-step contagion of strategies in $A^p$ starting from ${\mathbf {x}}$.

We demonstrate that the contagion threshold not only determines when strategies in $A^p$ can spread through full contagion, but also when they can spread through partial, and hence, step-by-step contagion. The definition of the contagion threshold is based on the following reinterpretation of the definitions of full and partial contagion in Definitions 3 and 5. Given a network G and any subset of players $S\subset N$, let $N_i(S) = N_i\cap S$ be the set of i’s direct neighbours within G that belong to subgroup S. Let $n_i(S)$ be the corresponding cardinality of $N_i(S)$ and $\alpha _i(S) = \frac{n_i(S)}{n_i}$ be the proportion of i’s neighbours in S.

From Definition 3, strategies in $A^p$ spread through full contagion if, for every best response sequence $\{{\mathbf {x}} _{\tau }\}_{\tau =0}^{{\bar{t}}}$ satisfying the conditions in Definition 3, there exists a sequence of players $S_1, S_2,\ldots ,S_{{\bar{t}}}$, with $S_1={\mathcal {M}}(A^p;{\mathbf {x}})$ and $\cup _{\tau =1}^{{\bar{t}}}S_{\tau }=N$, such that for each $j\in S_{\tau }$, and all $\tau =2, 3,\ldots , {\bar{t}}$, $\alpha _j(\cup _{k=1}^{\tau -1}S_{k})\ge p$. That is, every player in $S_{\tau }$ has at least proportion p of their neighbours in $\cup _{k=1}^{\tau -1}S_{k}$. The inequality $\alpha _j(\cup _{k=1}^{\tau -1}S_{k})\ge p$, for all $j\in S_{\tau }$ and $\tau =2, 3,\ldots , {\bar{t}}$, ensures that once all players in $S_1={\mathcal {M}}(A^p;{\mathbf {x}})$ play strategies in $A^p$, all players in $S_1\cup S_2$ subsequently play strategies in $A^p$ since each $j\in S_2$ has at least proportion p of her neighbours in $S_1$; all players in $S_1\cup S_2\cup S_2$ subsequently play strategies in $A^p$ since each $j\in S_2\cup S_3$ has at least proportion p of her neighbours in $S_1\cup S_2$; this iterative process continues until the whole network eventually plays strategies in $A^p$.

Similarly, from Definition 5, strategies in $A^p$ spread through partial contagion from a group of players, ${\mathcal {M}}(A^p;{\mathbf {x}};W^\prime )$, where ${\mathbf {x}}\in D(W)$, to $W^\prime \ne W$ if, for every best response sequence $\{{\mathbf {x}} _{\tau }\}_{\tau =0}^{{\bar{t}}}$ satisfying the conditions in Definition 5, there exists a sequence of players $S_1, S_2,\ldots ,S_{{\bar{t}}}$, with $S_1={\mathcal {M}}(A^p;{\mathbf {x}};W^\prime )=N(A^p;{\mathbf {x}}_1), S_2=N(A^p;{\mathbf {x}}_2),\ldots ,S_{{\bar{t}}}=N(A^p;{\mathbf {x}}_{{\bar{t}}})$, such that for each $j\in S_{\tau }$, and all $\tau =2, 3,\ldots , {\bar{t}}$, $\alpha _j(S_{\tau -1})\ge p$. These sequences of players have two main properties: first, the sets $S_{\tau }$, for $\tau =1,\ldots , {\bar{t}}$, need not be disjoint sets, that is, for any pair $S_{\tau }$ and $S_{\tau +1}$ along the sequence, it is not necessary for $S_{\tau }\cap S_{\tau +1}=\emptyset$ to hold; second, $S_{{\bar{t}}}\subseteq N$, because for partial contagion, strategies in $A^p$ need not spread to the whole network.

Thus, the first step in defining the network measure that determines when strategies in $A^p$ can spread though full and step-by-step contagion involves choosing a set of players from which contagion can be triggered. We identify the first-neighbourhoods of players (i.e. the set of direct neighbours of each $i\in N$, with i included) as groups of players from which strategies in $A^p$ can spread through full and partial contagion.²⁰ For each $i\in N$, let $B_{i_r}$ be the rth-neighbourhood of i (i.e. the set of all players within r steps from i, with i included) and $N_{i_r}$ be the r-order neighbours of i (i.e. all players that are located at r steps from i). These definitions imply that $B_{i_r}=i\cup N_{i_1}\cup N_{i_2}\cup \ldots \cup N_{i_{r}}$. Let $b_{i_r}$ and $n_{i_r}$ be the respective cardinalities of $B_{i_r}$ and $N_{i_r}$.

Strategies in $A^p$ can spread from $B_{i_1}$ of any $i\in N$ through either full or partial contagion if the corresponding sequence, $B_{i_1}, N_{i_2},\ldots , N_{i_{d_i}}$, satisfies the conditions outlined in the above reinterpretations of Definitions 3 and 5. That is, starting from any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$, $b_{i_1}$ mutations to strategies in $A^p$ by all players in $B_{i_1}$ can trigger full contagion, if, along the sequence $B_{i_1}, N_{i_2},\ldots , N_{i_{d_i}}$, $\alpha _j(B_{i_{\tau -1}})\ge p$ for each $j\in N_{i_{\tau }}$ and all $\tau =2,\ldots ,d_i$ (i.e. $\min _{\tau \in [2,d_i]}\min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})\ge p$). Similarly, $b_{i_1}$ mutations to strategies in $A^p$ by all players in $B_{i_1}$ can trigger partial contagion, if, along the sequence, $S_1, S_2,\ldots ,S_{{\bar{t}}}$ with $S_1=B_{i_1}$, $S_2\subseteq B_{i_2},\ldots , S_{{\bar{t}}}\subseteq B_{i_{{\bar{t}}}}$, $\alpha _h(S_{\tau -1})\ge p$ for each $h\in S_{\tau }$ and all $\tau =2,\ldots ,{\bar{t}}$. The following lemma shows that such sequences are guaranteed to exist whenever $\min _{\tau \in [2,d_i]}\min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})\ge p$.

Lemma 2

Let G be unweighted and strongly connected. If $\min _{\tau \in [2,d_i]}\min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})\ge p$ for all $i\in N$, then there exist sequences of the form $S_1=B_{i_1}$, $S_2\subseteq B_{i_2}, S_3\subseteq B_{i_3},\ldots , S_{{\bar{t}}}\subseteq B_{i_{{\bar{t}}}}$, such that $\alpha _h(S_{\tau -1})\ge p$ for all $h\in S_{\tau }$ and all $\tau =2,\ldots ,{\bar{t}}$.

Proof

See Appendix 2$\square$

Fig. 2

An example of a network with the contagion threshold of ${\underline{\eta }}(G)=\frac{1}{3}$ and diameter of $d(G)=3$

The sufficient condition for strategies in $A^p$ to spread through either full or partial contagion from $B_{i_1}$ is then $\min _{\tau \in [2,d_i]}\min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})\ge p$. As in Opolot and Azomahou (2021), we define the contagion threshold, ${\underline{\eta }}(G)$, as the minimum $\min _{\tau \in [2,d_i]}\min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})$ over all $i\in N$ such that strategies in $A^p$ spread from $B_{i_1}$ of any $i\in N$ through either full or partial contagion whenever ${\underline{\eta }}(G)\ge p$.

Definition 7

The contagion threshold of a strongly connected network, G, is defined as ${\underline{\eta }}(G)=\min _{i\in N}\min _{r\in [2,d_i]}\min _{j\in N_{i_r}}\alpha _j(B_{i_{r-1}})$.

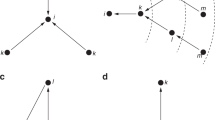
Example 1

Consider an example of the network in Fig. 2. Denote by $\eta _i(G)$, the contagion threshold of player i in network G. That is, $\eta _i(G)=\min _{r\in [2,d_i]}\min _{j\in N_{i_r}}\alpha _j(B_{i_{r-1}})$, so that the contagion threshold of network G is ${\underline{\eta }}(G)=\min _{i\in N}\eta _i(G)$. For player 1 in this network, the composition of the neighbourhoods is as follows: $B_{1_1}=\{1,2,3,8\}$, $N_{1_2}=\{4,6,7\}$, $N_{1_3}\,{=}\,\{5\}$. For each $j\,{\in }\,N_{1_2}$, we have $\alpha _j(B_{1_1})\ge \frac{1}{3}$; and for player 5 in $N_{1_3}$, we have $\alpha _5(B_{1_2})= 1$; and hence, $\eta _1(G)=\frac{1}{3}$. If (A, U, N, G, P) starts, at $t=1$, from any state where all players in $B_{1_1}$ play a $\frac{1}{3}$-dominant strategy, then these players will continue to play a $\frac{1}{3}$-dominant strategy for all $t\ge 2$. From $t=2$ onward, all players in $N_{1_2}$ switch to the $\frac{1}{3}$-dominant strategy because each has at least $\frac{1}{3}$ of their neighbours in $B_{1_1}$, all of whom play the $\frac{1}{3}$-dominant strategy at $t=1$; and from $t=3$ onwards, player 5 in $N_{1_3}$ also switches to the $\frac{1}{3}$-dominant strategy. Thus, a $\frac{1}{3}$-dominant strategy spreads through full contagion from a subset $B_{1_1}$ of players. Following the same steps, we find that, for this network, $\eta _i(G)=\frac{1}{3}$ for all $i\in N$, so that ${\underline{\eta }}(G)=\frac{1}{3}$. Consequently, a $\frac{1}{3}$-dominant strategy spreads through full contagion in this network.

The definition of the contagion threshold in Definition 7 is specific to finite networks but shares some similarities with the definition of the contagion threshold for unbounded networks according to Morris (2000). Morris (2000) defines the contagion threshold of an unbounded network as the maximum p such that a p-dominant strategy spreads to the whole network through best response starting from a finite group of players. The similarity between this definition and Definition 7 is that they both determine when a p-dominant strategy is fully contagious. The difference concerns the definition of the group of players from which a p-dominant strategy spreads contagiously. To be able to establish the bounds of the coradius, modified coradius and radius of ${\mathbf {A}}^p$ in finite networks, it is necessary to precisely define the set and the number of players from which contagion can be triggered. It is not sufficient, as in the case of unbounded networks, to require strategies in $A^p$ to spread contagiously from a finite group of players without defining the composition and the size of such a group.

3.2 Contagion, coradius, modified coradius and the radius of ${\mathbf {A}}^p$

This subsection discusses how full and step-by-step contagion determine the upper bounds of the coradius and modified coradius of ${\mathbf {A}}^p$, and the lower bound of the radius of ${\mathbf {A}}^p$. By definition of the contagion threshold, when ${\underline{\eta }}(G)\ge p$, strategies in $A^p$ spread from the first-neighbourhood of any player through either full or partial contagion. When full contagion is feasible on an undirected, unweighted and strongly network G, the coradius of ${\mathbf {A}}^p$ is bounded from above by $\max _{{\mathbf {x}}\notin {\mathbf {A}}^p}\mu ^*(A^p;{\mathbf {x}})$. And since full contagion can be triggered from $b_{i_1}$ of any $i\in N$, it follows that $CR({\mathbf {A}}^p)\le \max _{{\mathbf {x}}\notin {\mathbf {A}}^p}\mu ^*(A^p;{\mathbf {x}})\le \min _{i\in N}b_{i_1}={\underline{b}}_1$ for any G where full contagion of strategies in $A^p$ is feasible.

To see the connection between step-by-step contagion and the modified coradius of ${\mathbf {A}}^p$, consider any ${\mathbf {x}}\in D(W)$ and $W\ne {\mathbf {A}}^p$. If $W_1,\ldots ,W_J$, with $W_1=W$ and $W_J= {\mathbf {A}}^p$, is the sequence of absorbing sets along which some path, $({\mathbf {x}}_1,\ldots ,{\mathbf {x}}_T)$, from ${\mathbf {x}}={\mathbf {x}}_1$ to ${\mathbf {x}}_T\in {\mathbf {A}}^p$ passes, then $({\mathbf {x}}_1,\ldots ,{\mathbf {x}}_T)$ can be partitioned into sub-paths between absorbing sets. That is, $({\mathbf {x}}_1,\ldots ,{\mathbf {x}}_T)$ can be partitioned into $\bigcup _{j=1}^{J-1}({\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_{T^\prime }})$, where, for $j=1,\ldots ,J-1$, $({\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_{T^\prime }})$ is the sub-path of $({\mathbf {x}}_1,\ldots ,{\mathbf {x}}_T)$ that starts from ${\mathbf {x}}_{j_1}\in W_j$ and ends at ${\mathbf {x}}_{j_{T^\prime }}\in W_{j+1}$.²¹ From (4), the modified cost $c^*({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ of path $({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T)$ can then be rewritten as:

$$\begin{aligned} c^*({\mathbf {x}}_1,{\mathbf {x}}_2,\ldots ,{\mathbf {x}}_T) = c({\mathbf {x}}_{1_1},\ldots ,{\mathbf {x}}_{1_{T^\prime }}) +\sum _{j=2}^{J-1}c({\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_{T^\prime }}) - \sum _{j=2}^{J-1}R(W_j) \end{aligned}$$

Let $\Gamma ({\mathbf {x}},{\mathbf {A}}^p)$ be the set of all sequences of absorbing sets along which paths from ${\mathbf {x}}$ to ${\mathbf {A}}^p$ traverse. Then the minimum modified cost of all paths from ${\mathbf {x}}$ to ${\mathbf {A}}^p$ becomes

$$\begin{aligned} C^*({\mathbf {x}},{\mathbf {A}}^p)&= \min _{(W_1,\ldots ,W_J)\in \Gamma ({\mathbf {x}}, {\mathbf {A}}^p)}\Bigg [\min _{({\mathbf {x}}_{1_1},\ldots ,{\mathbf {x}}_{1_{T^\prime }})\in S({\mathbf {x}}, W_2)}c({\mathbf {x}}_{1_1},\ldots ,{\mathbf {x}}_{1_{T^\prime }}) \nonumber \\&+\sum _{j=2}^{J-1}\min _{({\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_{T^\prime }})\in S(W_j, W_{j+1})}c({\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_{T^\prime }}) - \sum _{j=2}^{J-1}R(W_j)\Bigg ] \end{aligned}$$

(6)

By definition of partial contagion above, we have

$$\begin{aligned} \min _{({\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_{T^\prime }})\in S(W_j, W_{j+1})}c({\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_{T^\prime }})=\min _{{\mathbf {y}}\in W_j}\mu ^*(A_{j+1};{\mathbf {y}};W_{j+1}) \end{aligned}$$

$$\begin{aligned} C^*({\mathbf {x}},{\mathbf {A}}^p)&=\min _{(W_1,\ldots ,W_J)\in \Gamma ({\mathbf {x}}, {\mathbf {A}}^p)}\nonumber \\&\qquad \Bigg [\mu ^*(A_{2};{\mathbf {x}};W_{2}) +\sum _{j=2}^{J-1}\left( \min _{{\mathbf {y}}\in W_j}\mu ^*(A_{j+1};{\mathbf {y}};W_{j+1})-R(W_j)\right) \Bigg ] \end{aligned}$$

(7)

We demonstrate in Sect. 4 below that when strategies in $A^p$ spread through step-by-step contagion, then, along the sequence of absorbing sets, $W_1, W_2,\ldots ,W_J$, that the minimum modified cost path from ${\mathbf {x}}\in D(W_1)$ to ${\mathbf {A}}^p$ traverses, $R(W_j)=\min _{{\mathbf {y}}\in W_j}\mu ^*(A_{j+1};{\mathbf {y}};W_{j+1})$. More specifically, we show that when strategies in $A^p$ are not fully contagious, there are two other possible categories of paths from any ${\mathbf {x}}\in D(W)$ to ${\mathbf {A}}^p$. The first category of paths traverse through a sequence of only three absorbing sets, $W, W^\prime , {\mathbf {A}}^p$, where $W^\prime$ is an absorbing cycle containing both strategies in $A^p$ and $A\backslash A^p$. Along this sequence, $R(W)=\min _{{\mathbf {y}}\in W}\mu ^*(A^p;{\mathbf {y}};W^\prime )$ and $R(W^\prime )=\min _{{\mathbf {y}}\in W^\prime }\mu ^*(A^p;{\mathbf {y}};{\mathbf {A}}^p)$. The second category of paths traverse through a sequence of four absorbing sets, $W, W^\prime , W^{\prime \prime }, {\mathbf {A}}^p$, where $W^\prime$ and $W^{\prime \prime }$ are absorbing cycles containing both strategies in $A^p$ and $A\backslash A^p$. Along this sequence, $R(W)=\min _{{\mathbf {y}}\in W}\mu ^*(A^p;{\mathbf {y}};W^\prime )$, $R(W^\prime )=\min _{{\mathbf {y}}\in W^\prime }\mu ^*(A\backslash A^p;{\mathbf {y}};W^{\prime \prime })$ and $R(W^{\prime \prime })=\min _{{\mathbf {y}}\in W^{\prime \prime }}\mu ^*(A^p;{\mathbf {y}};{\mathbf {A}}^p)$. For both categories of paths, it follows from (7) that $C^*({\mathbf {x}},{\mathbf {A}}^p)=\min _{W^\prime \ne W}\mu ^*(A^p;{\mathbf {x}};W^\prime )\le {\underline{b}}_1$, where the inequality follows because the partial contagion of strategies in $A^p$ can be triggered from the first-neighbourhood of any player. The modified coradius of ${\mathbf {A}}^p$ then becomes

$$\begin{aligned} CR^*({\mathbf {A}}^p)=\max _{{\mathbf {x}}\notin D({\mathbf {A}}^p)}C^*({\mathbf {x}},{\mathbf {A}}^p)=\max _{{\mathbf {x}}\notin D({\mathbf {A}}^p)}\min _{W^\prime \ne W}\mu ^*(A^p;{\mathbf {x}};W^\prime ) \le {\underline{b}}_1 \end{aligned}$$

(8)

Contagion not only determines the upper bounds of the coradius and modified coradius of ${\mathbf {A}}^p$ but also the lower bound of its radius. We demonstrate that when strategies in $A^p$ are fully or step-by-step contagious, the diameter of the network determines when the lower bound of the radius of ${\mathbf {A}}^p$ is greater than ${\underline{b}}_1$. Specifically, we show that when (A, U, N, G, P) starts from any ${\mathbf {x}}\in {\mathbf {A}}^p$, and $d(G)\ge 7$, $b_{i_1}$ mutations to strategies in $A\backslash A^p$ by all players in $B_{i_1}$ of any $i\in N$ are not sufficient to trigger an exit from the basin of attraction of ${\mathbf {A}}^p$.

The underlying intuition is that when $d(G)\ge 7$, each $i\in N$ has $d_i\ge 4$ (see Lemma 3 for the proof), which implies that for all $j\in N_{i_4}\cup N_{i_5}\cup \ldots \cup N_{i_{d_i}}$, $B_{j_2}\cap B_{i_1}=\emptyset$ (i.e. there is no overlap between the first-neighbourhood of i and the second-neighbourhood of j). This implies that, starting from any ${\mathbf {x}}\in {\mathbf {A}}^p$, if all players in $B_{i_1}$ mutate to strategies in $A\backslash A^p$, there exists at least one player $j\in N_{i_4}\cup N_{i_5}\cup \ldots \cup N_{i_{d_i}}$ for whom all players in $B_{j_2}$ play strategies in $A^p$. The definition of the contagion threshold implies that when ${\underline{\eta }}(G)\ge p$, (A, U, N, G, P) converges to ${\mathbf {A}}^p$ from any configuration where all players in $B_{j_2}$ of any $j\in N$ play strategies in $A^p$ (i.e., $b_{j_2}$ mutations to strategies in $A^p$ sufficiently trigger full contagion on any unweighted and strongly connected network).²² Thus, when ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$, more than $b_{i_1}$ mutations are required to trigger an exit from the basin of attraction of ${\mathbf {A}}^p$ so that $R({\mathbf {A}}^p)>{\underline{b}}_1\ge CR({\mathbf {A}}^p),CR^*({\mathbf {A}}^p)$.

4 Stochastic stability of the minimal p-best response set

This section presents the main results of this paper. The following Theorem provides the conditions under which strategies in $A^p$ are uniquely stochastically stable.

Theorem 1

Given an evolutionary process of best response with mutations, $(A,U,N,G,P_{\varepsilon })$, on an undirected, unweighted and strongly connected network G(N, E), the minimal p-best response set $A^p\subseteq A$ is uniquely stochastically stable whenever ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$.

The following steps provide the sketch and intuition of the proof of Theorem 1. A detailed exposition is provided in Appendix 3. The proof involves deriving the upper bounds of the coradius and modified coradius, and the lower bound of the radius of ${\mathbf {A}}^p$. It exploits the implications of the process of full and step-by-step contagion discussed in Sect. 3.

We show that the upper bound of both the coradius and modified coradius of ${\mathbf {A}}^p$ is ${\underline{b}}_1=\min _{i\in N}b_{i_1}$. To prove this result, we first show that when (A, U, N, G, P) starts from any ${\mathbf {x}}\notin {\mathbf {A}}^p$, $b_{i_1}$ mutations to strategies in $A^p$, for any $i\in N$, trigger either full contagion of strategies in $A^p$ or partial contagion where (A, U, N, G, P) converges to an absorbing cycle of states containing both strategies in $A^p$ and $A\backslash A^p$. For networks where $b_{i_1}$ mutations trigger full contagion, we have $C({\mathbf {x}},{\mathbf {A}}^p)= \mu ^*(A^p;{\mathbf {x}})\le \min _{i\in N}b_{i_1}={\underline{b}}_1$ and $CR({\mathbf {A}}^p)=\max _{{\mathbf {x}}\in {\mathbf {X}}\backslash {\mathbf {A}}^p}C({\mathbf {x}},{\mathbf {A}}^p)\le {\underline{b}}_1$.

Now, let ${\mathcal {C}}({\mathbf {A}})$ be the set of all absorbing cycles of states containing both strategies in $A^p$ and some strategies in $A\backslash A^p$. Let $N_{i_{\tau }}^r$, for $\tau < r$, $\tau =1,2,\ldots ,d_i-1$ and $r=2,\ldots ,d_i$, be the set of players in $N_{i_{\tau }}$ that lie along the paths of length greater or equal to r. Put differently, $N_{i_{\tau }}^r$ is the set of all $h\in N_{i_{\tau }}$ with $N_{h_{r-\tau }}\cap N_{i_r}\ne \emptyset$ (i.e. the set of players in $N_{i_{\tau }}$ with at least one $(r-\tau )$-order neighbour in $N_{i_{r}}$). For example, $N_{i_1}^3$ is the set of all $h\in N_{i_1}$ with at least one second-order neighbour in $N_{i_3}$ (i.e. $N_{h_{2}}\cap N_{i_3}\ne \emptyset$).²³ Let ${\bar{N}}_{i_{\tau }}^{r}=N_{i_{\tau }}\backslash N_{i_{\tau }}^{r}$ be the set of all players in $N_{i_{\tau }}$ that are not contained in $N_{i_{\tau }}^{r}$, and $n_{i_{\tau }}^{r}$ and ${\bar{n}}_{i_{\tau }}^{r}$ be the respective cardinalities of $N_{i_{\tau }}^{r}$ and ${\bar{N}}_{i_{\tau }}^{r}$.

We show that when $b_{i_1}$ mutations to strategies in $A^p$ fail to trigger full contagion, (A, U, N, G, P) converges to an absorbing cycle, $W\in {\mathcal {C}}({\mathbf {A}})$, where players in $N_{i_1}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ and $i\cup N_{i_2}^{3}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ alternate between strategies in $A^p$ and some strategies in A (i.e., including some strategies in $A\backslash A^p$), and the rest play some strategies in A. We then show that, firstly, $n_{i_1}^r$ mutations to strategies in $A^p$, for any $4\le r\le d_i$, sufficiently trigger an exit from the basin of attraction of W to some state in ${\mathbf {A}}^p$. Since this result holds for any $i\in N$, including player ${\underline{i}}=i\in \mathop {\mathrm {argmin}} b_{i_1}$ with the fewest number of direct neighbours, it follows that $C(W,{\mathbf {A}}^p)\le {\underline{n}}_{1}^{*}\le {\underline{n}}_{1}^r$, where ${\underline{n}}_1^r=\min _{i\in N}n_{i_1}^r$ and ${\underline{n}}_{1}^{*}=\min _{i\in N}\min _{r\in [4,d_i]}n_{i_1}^r$.

Secondly, if (A, U, N, G, P) exits the basin of attraction of W after less or equal to $\underline{n}_{1}^{*}$ mutations to strategies in $A\backslash A^p$, then it converges to an absorbing cycle where players in $N_{i_1}^{4}\cup N_{i_3}^4\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ and $i\cup N_{i_2}^{4}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ alternate between strategies in $A^p$ and some strategies in A, and the rest play some strategies in A. Denote this absorbing cycle by $W^\prime \in {\mathcal {C}}({\mathbf {A}})$. This implies that either $R(W) = C(W,{\mathbf {A}}^p),$ when $C(W,{\mathbf {A}}^p)\le C(W,W^\prime )$, or $R(W) = C(W,W^\prime )$ when $C(W,W^\prime )\le C(W,{\mathbf {A}}^p)$.

Thirdly, we show that $n_{i_1}^4$ mutations to strategies in $A^p$ sufficiently trigger an exit from the basin of attraction of $W^\prime$ to ${\mathbf {A}}^p$. However, $n_{i_1}^4$ mutations to strategies in $A\backslash A^p$ cannot trigger an exit from the basin of attraction of $W^\prime$. This implies that $R(W^\prime ) = C(W^\prime ,{\mathbf {A}}^p)\le {\underline{n}}_1^4$.

Thus, there are three possible minimum cost paths from any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$ to ${\mathbf {A}}^p$. First, ${\underline{b}}_1$ mutations to strategies in $A^p$ trigger full contagion from any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$ so that $CR({\mathbf {A}}^p)\le {\underline{b}}_1$. Second, (A, U, N, G, P) converges to some absorbing cycle $W\in {\mathcal {C}}({\mathbf {A}})$ after ${\underline{b}}_1$ mutations to strategies in $A^p$, and that the number of mutations to strategies in $A\backslash A^p$ needed to trigger an exit from D(W) is greater than ${\underline{n}}_1^*$. For this scenario, $R(W) = C(W,{\mathbf {A}}^p)$ so that

$$\begin{aligned} C^*({\mathbf {x}},{\mathbf {A}}^p)&= \min _{W\in {\mathcal {C}}({\mathbf {A}})}\Big [\min _{({\mathbf {x}}_{1},{\mathbf {x}}_{2},\ldots ,{\mathbf {x}}_{{T^\prime }})\in S({\mathbf {x}}, W)} c({\mathbf {x}}_{1},{\mathbf {x}}_{2},\ldots ,{\mathbf {x}}_{{T^\prime }}) \nonumber \\&\quad + \min _{({\mathbf {y}}_1, {\mathbf {y}}_2, \ldots , {\mathbf {y}}_T)\in S(W, {\mathbf {A}}^p)} c({\mathbf {y}}_1, {\mathbf {y}}_2, \ldots , {\mathbf {y}}_T)-R(W)\Big ]\nonumber \\&=\min _{W\in {\mathcal {C}}({\mathbf {A}})}\Big [C({\mathbf {x}},W)+C(W,{\mathbf {A}}^p)-R(W) \Big ] \nonumber \\&=\min _{W\in {\mathcal {C}}({\mathbf {A}})}C({\mathbf {x}},W)\le {\underline{b}}_1 \end{aligned}$$

(9)

Third, (A, U, N, G, P) converges to some absorbing cycle $W\in {\mathcal {C}}({\mathbf {A}})$ after ${\underline{b}}_1$ mutations to strategies in $A^p$, but the number of mutations to strategies in $A\backslash A^p$ needed to trigger an exit from D(W) is less or equal to ${\underline{n}}_1^*$. For this scenario, there exists another absorbing cycle, $W^\prime \in {\mathcal {C}}({\mathbf {A}})$ and $W^\prime \ne W$, where $C(W,W^\prime )\le C(W,{\mathbf {A}}^p)$ and $R(W) = C(W,W^\prime )$. And following the above discussion, $R(W^\prime ) = C(W^\prime ,{\mathbf {A}}^p)$ so that

$$\begin{aligned} C^*({\mathbf {x}},{\mathbf {A}}^p)=&\min _{W,W^\prime \in {\mathcal {C}}({\mathbf {A}})}\Big [\min _{({\mathbf {x}}_{1},{\mathbf {x}}_{2},\ldots ,{\mathbf {x}}_{{T^\prime }})\in S({\mathbf {x}}, W)} c({\mathbf {x}}_{1},{\mathbf {x}}_{2},\ldots ,{\mathbf {x}}_{{T^\prime }}) \nonumber \\&+ \min _{({\mathbf {y}}_1, {\mathbf {y}}_2, \ldots , {\mathbf {y}}_T)\in S(W, W^\prime )} c({\mathbf {y}}_1, {\mathbf {y}}_2, \ldots , {\mathbf {y}}_T)-R(W)\nonumber \\&+ \min _{({\mathbf {z}}_1, {\mathbf {z}}_2, \ldots , {\mathbf {z}}_T)\in S(W^\prime , {\mathbf {A}}^p)} c({\mathbf {z}}_1, {\mathbf {z}}_2, \ldots , {\mathbf {z}}_T)-R(W^\prime )\Big ]\nonumber \\ =&\min _{W,W^\prime \in {\mathcal {C}}({\mathbf {A}})}\Big [C({\mathbf {x}},W)+C(W,W^\prime )-R(W) +C(W^\prime ,{\mathbf {A}}^p)-R(W^\prime )\Big ]\nonumber \\ =&\min _{W\in {\mathcal {C}}({\mathbf {A}})}C({\mathbf {x}},W)\le {\underline{b}}_1 \end{aligned}$$

(10)

Since Eqs. (9) and (10) hold for any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$ from which ${\underline{b}}_1$ mutations cannot trigger full contagion, it follows that $CR^*({\mathbf {A}}^p)=\max _{{\mathbf {x}}\notin D({\mathbf {A}}^p)}\min _{W\in {\mathcal {C}}({\mathbf {A}})}C({\mathbf {x}},W)\le {\underline{b}}_1$. The following examples help to elaborate these steps.²⁴

Example 2

Consider the network depicted in Fig. 3, with the contagion threshold and diameter of ${\underline{\eta }}(G)=\frac{1}{3}$ and $d(G)=8$ respectively. The players with the smallest first-neighbourhood are 1 and 16, with $b_{1_1}=b_{16_1}={\underline{b}}_1=2$. Let $p\le \frac{1}{3}$, and let (A, U, N, G, P) start from some configuration ${\mathbf {x}}\notin D({\mathbf {A}}^p)$ (i.e. a configuration containing both strategies in $A^p$ and $A\backslash A^p$). If players in $B_{1_1}=\{1,2\}$ both mutate to strategies in $A^p$ at $t=1$, then (A, U, N, G, P) will evolve as follows:

$t=1$	All players in $B_{1_1}=\{1,2\}$ play strategies in $A^p$; all other players play strategies in A.
$t=2$	Player 1 plays a strategy in $A^p$ since $\alpha _1(B_{1_1})>p$; a player in $N_{1_1}=\{2\}$ plays a strategy in $A^p$ because $\alpha _2(B_{1_1})=\frac{1}{3}>p$. All $j\in N_{1_2}=\{3,4\}$ also play strategies in $A^{p}$ because each has $\alpha _j(B_{1_1})= \frac{1}{3}\ge p$. All other players play strategies in A.
$t=3$	All $j\in B_{1_3}=\{1,2,3,4,5,6,7\}$ play strategies in $A^p$ because each has $\alpha _j(B_{1_2})\ge \frac{1}{3}\ge p$ and that all players in $B_{1_2}$ play strategies in $A^p$ at $t=2$. All other players play strategies in A.
${-}-$
$t=8$	All players in $B_{1_8}=N=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16\}$ play strategies in $A^p$.

Thus, for this network, ${\underline{b}}_1$ mutations to strategies in $A^p$ sufficiently trigger full contagion, which implies that $C({\mathbf {x}},{\mathbf {A}}^p)\le {\underline{b}}_1$ for any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$, and that $CR({\mathbf {A}}^p)=\max _{{\mathbf {x}}\notin D({\mathbf {A}}^p)}C({\mathbf {x}},{\mathbf {A}}^p)\le {\underline{b}}_1$.

Example 3

Consider the network in Fig. 4, with the contagion threshold of ${\underline{\eta }}(G)=\frac{1}{2}$ and diameter of $d(G)=10$. Let (A, U, N, G, P) start from some configuration ${\mathbf {x}}$ where all players play strategies in $A\backslash A^p$, and let players in $B_{3_1}=\{1,3,5\}$ mutate to strategies in $A^p$ at $t=1$. For $p=\frac{1}{2}={\underline{\eta }}(G)$, (A, U, N, G, P) evolves from $t=2$ onward as follows:

Fig. 3

An example of a network with contagion threshold (computed using the matrix-based steps in Appendix 1) of ${\underline{\eta }}(G)=\frac{1}{3}$ and $d(G)=8$

Fig. 4

An example of a network with contagion threshold of ${\underline{\eta }}(G)=\frac{1}{2}$ and $d(G)=10$

$t=2$	Players in $3\cup N_{3_2}= \{2,3,4,6,7,8\}$ play strategies in $A^p$ since each has at least proportion $\frac{1}{2}= p$ of neighbours in $B_{3_1}$. All $j\in N_{3_1}=\{1,5\}$ switch back to strategies in $A\backslash A^p$ because each has $\alpha _j(B_{3_1})=\frac{1}{3}< p$. All other players play strategies in $A\backslash A^p$.
$t=3$	Players in $3\cup N_{3_2}$ play strategies in $A\backslash A^p$; players in $N_{3_1}$ play strategies in $A^p$; a player in $N_{3_3} =\{9\}$ plays a strategy in $A^p$; all other players play strategies in $A\backslash A^p$.
$t=4$	Players in $3\cup N_{3_2}\cup N_{3_4}$ play strategies in $A^p$; players in $N_{3_1}\cup N_{3_3}$ play strategies in $A\backslash A^p$; all other players play strategies in $A\backslash A^p$.
${-}-$
$t=9$	Players in $3\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A\backslash A^p$; and players in $N_{3_1}\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A^{p}$.

Thus, for this network, (A, U, N, G, P) converges to an absorbing cycle $W\in {\mathcal {C}}({\mathbf {A}})$ where players in $3\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ and $N_{3_1}\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ alternate between strategies in $A^p$ and $A\backslash A^p$.²⁵

We now show that ${\underline{n}}_1^*=1$ mutations²⁶ to strategies in $A^p$ sufficiently trigger an exit from D(W) to ${\mathbf {A}}^p$, but ${\underline{n}}_1^*$ mutations to strategies in $A\backslash A^p$ cannot trigger exit from D(W). Let (A, U, N, G, P) start (at $t=0$) from configuration ${\mathbf {y}}\in W$ where players in $3\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A\backslash A^p$ and players in $N_{3_1}\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A^{p}$. At $t=1$, let a player in $N_{3_1}^9=\{5\}$ mutate to a strategy in $A^p$. Then (A, U, N, G, P) evolves from $t=1$ onward as follows:

$t=1$	Players in $3\cup N_{3_1}^9\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A^p$; players in ${\bar{N}}_{3_1}^9\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A\backslash A^p$, where ${\bar{N}}_{3_1}^9=\{1\}$.
$t=2$	Players in $3\cup N_{3_1}\cup N_{3_2}\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A^p$, where players in $3\cup N_{3_1}\cup N_{3_2}\cup N_{3_3}$ all play strategies in $A^p$ because each has at least $\frac{1}{2}=p$ of their neighbours in $\{3,5\}\cup N_{3_2}$, all of whom play strategies in $A^p$ at $t=1$. Players in $N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A\backslash A^p$.
$t=3$	Players in $B_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A^p$; players in $N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A\backslash A^p$.
${-}-$
$t=7$	Players in $B_{3_8}$ play strategies in $A^p$; players in $N_{3_9}$ play strategies in $A\backslash A^p$.
$t=8$	All players in $B_{3_9}=N$ play strategies in $A^p$.

Thus, ${\underline{n}}_1^*$ mutations to strategies in $A^p$ sufficiently trigger an exit from D(W), which implies that $C(W,{\mathbf {A}}^p)\le {\underline{n}}_1^*$. Now, let (A, U, N, G, P) instead start (at $t=0$) from configuration ${\mathbf {z}}\in W$ where players in $3\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A^p$ and players in $N_{3_1}\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A\backslash A^{p}$.²⁷ At $t=1$, let a player in $N_{3_1}^9=\{5\}$ mutate to a strategy in $A\backslash A^p$. Then (A, U, N, G, P) evolves from $t=1$ onward as follows.

$t=1$	Players in ${\bar{N}}_{3_1}^9\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A^p$; players in $3\cup N_{3_1}^9\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A\backslash A^p$.
$t=2$	Players in $3\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A^p$. Player 3 and players in ${\bar{N}}_{3_2}^4=\{2,4\}$ all play strategies in $A^p$ because each has at least $\frac{1}{2}=p$ of their neighbours in ${\bar{N}}_{3_1}^9=\{1\}$ playing strategies in $A^p$ at $t=1$. Players in $N_{3_2}^4=\{6,7,8\}$ play strategies in $A^p$ because for each $k\in N_{3_2}^4$, there is a $j\in N_{3_4}=\{10,11,12\}$ where $N_{k_1}\cap N_{j_1}\subseteq N_{3_3}^4$. This implies that, for each $k\in N_{3_2}^4$, $\alpha _k(N_{3_3}^4)\ge \alpha _k(N_{j_1})=\alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)=p=\frac{1}{2}$. Since all players in $N_{3_3}^4\subseteq N_{3_3}$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{3_2}^4$. And since $N_{3_2}={\bar{N}}_{3_2}^4\cup N_{3_2}^4$, it follows that all players in $N_{3_2}$ play strategies in $A^p$ at $t=2$. Players in $N_{3_1}\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A\backslash A^p$.
$t=3$	Players in $N_{3_1}\cup N_{3_3}\cup N_{3_5}\cup N_{3_7}\cup N_{3_9}$ play strategies in $A^{p}$; and players in $3\cup N_{3_2}\cup N_{3_4}\cup N_{3_6}\cup N_{3_8}$ play strategies in $A\backslash A^p$.

Thus, (A, U, N, G, P) reverts to W after ${\underline{n}}_1^*$ mutations to strategies in $A\backslash A^p$. Exiting the basin of attraction of W through mutations to strategies in $A\backslash A^p$ requires more than ${\underline{n}}_1^*$ mutations, which implies that $R(W)=C(W,{\mathbf {A}}^p)\le {\underline{n}}_1^*$. Following the above discussion, and Eq. (9), it follows that $C^*({\mathbf {x}},{\mathbf {A}}^p)=\min _{W\in {\mathcal {C}}({\mathbf {A}})}C({\mathbf {x}},W)\le {\underline{b}}_1$.

The second part of the proof of Theorem 1 establishes a lower bound of the radius of ${\mathbf {A}}^p$. Following the implications of full and partial contagion discussed above, we show in Appendix 3 that when ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$, ${\underline{b}}_1$ mutations to strategies in $A\backslash A^p$ can not trigger an exit from the basin of attraction of ${\mathbf {A}}^p$, and hence, $R({\mathbf {A}}^p)\ge {\underline{b}}_1+\iota$, where $\iota$ is some integer greater or equal to one. The underlying intuition is that if $d(G)\ge 7$, which, according to Lemma 3, also implies that $d_i\ge 4$ for all $i\in N$, then there is no overlap between the first-neighbourhood of any $i\in N$ and the second-neighbourhood of any $j\in N_{i_4}\cup \ldots \cup N_{i_{d_i}}$ (i.e. $B_{i_1}\cap B_{j_2}=\emptyset$). As discussed in Sect. 3.1 (see also Footnote 22), when ${\underline{\eta }}(G)\ge p$, (A, U, N, G, P) converges to ${\mathbf {A}}^p$ from any configuration consisting of at least one $j\in N$ with all players in $B_{j_2}$ playing strategies in $A^p$. This implies that when (A, U, N, G, P) starts from any state in ${\mathbf {A}}^p$ and players in $B_{{\underline{i}}_1}$ mutate to strategies in $A\backslash A^p$, (A, U, N, G, P) will revert to ${\mathbf {A}}^p$ whenever ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$, so that $R({\mathbf {A}}^p)\ge {\underline{b}}_1+\iota$.

The above dynamics does not directly extend to networks with $d(G)\le 6$. Firstly, networks with $d(G)\le 4$ contain at least one $i\in N$ with $d_i=2$. For these networks, when all players in $B_{i_1}$ of any $i\in N$ with $d_i=2$ mutate to strategies in $A\backslash A^p$ starting from any ${\mathbf {x}}\in {\mathbf {A}}^p$, all players in $N_{i_2}$ can switch to strategies in $A\backslash A^p$ at $t=2$. This implies that $b_{i_1}$ mutations to strategies in $A\backslash A^p$ can trigger an exit from $D({\mathbf {A}}^p)$ to an absorbing state or cycle containing both strategies in $A^p$ and $A\backslash A^p$ or only strategies in $A\backslash A^p$. Secondly, networks with $5\le d(G)\le 6$ contain at least one $i\in N$ with $d_i=3$. For each $i\in N$ with $d_i=3$, $N_{j_2}\subseteq B_{i_1}$ for all $j\in N_{i_3}$. This implies that when all players in $B_{i_1}$ mutate to strategies in $A\backslash A^p$ starting from any ${\mathbf {x}}\in {\mathbf {A}}^p$, the resulting configuration consists of players in $B_{j_1}$, for all $j\in N_{i_3}$, playing strategies in $A^p$ and the rest play strategies in $A\backslash A^p$. From such a configuration, (A, U, N, G, P) can converge to an absorbing cycle containing both strategies in $A^p$ and $A\backslash A^p$ (see the proof of the upper bounds of $CR({\mathbf {A}}^p)$ and $CR^*({\mathbf {A}}^p)$ above). The following counter example helps to further illustrate this point.

Example 4

Consider an example of the network in Fig. 5 with ${\underline{\eta }}(G)=\frac{2}{5}$ and consisting of at least one player with $d_i=3$.²⁸ Let $p\le {\underline{\eta }}(G)$, and let (A, U, N, G, P) start from any ${\mathbf {x}}\in {\mathbf {A}}^p$. If all players in $B_{6_1}=\{4,5,6\}$, where player 6 has $d_6=3$, simultaneously mutate to strategies in $A\backslash A^p$ at $t=1$, then at $t=2$, all players in $\{2,3,6,7,8\}$ switch to strategies in $A\backslash A^p$ because each has at least proportion $\frac{2}{3}>\frac{3}{5}=(1-p)$ of their neighbours playing strategies in $A\backslash A^p$ at $t=1$. Still at $t=2$, all players in $\{1,4,5\}$ play strategies in $A^{p}$. From $t=3$ onward, these two sets of players (i.e. $\{2,3,6,7,8\}$ and $\{1,4,5\}$) alternate between strategies in $A^p$ and $A\backslash A^p$. A total of $b_{6_1}$ mutations to strategies in $A\backslash A^p$ are therefore sufficient to trigger an exit from $D({\mathbf {A}}^p)$ to an absorbing cycle containing both strategies in $A^p$ and $A\backslash A^p$.

Fig. 5

An example of a network with the contagion threshold of ${\underline{\eta }}(G)=\frac{2}{5}$ and diameter of $d(G)=3$

To conclude the proof of Theorem 1, we see from the above discussion that when $p\le {\underline{\eta }}(G)$ and $d(G)\ge 7$, $CR({\mathbf {A}}^p)\le {\underline{b}}_1$, $CR^*({\mathbf {A}}^p)\le {\underline{b}}_1$ and $R({\mathbf {A}}^p)\ge {\underline{b}}_1+\iota$. Thus, the inequalities $R({\mathbf {A}}^p)>CR({\mathbf {A}}^p)$ and $R({\mathbf {A}}^p)>CR^*({\mathbf {A}}^p)$ hold, which implies that the absorbing set ${\mathbf {A}}^p$, and hence, the subset $A^p\subseteq A$, is uniquely stochastically stable.

5 Discussion and relation to the literature

We now discuss the implications of each of the conditions in Theorem 1. The first condition requires the network to be undirected, unweighted and strongly connected. The results of Theorem 1 extend to directed networks that are unweighted and strongly connected. This is because the requirements we make in the proof of Theorem 1 regarding the diameter of an undirected network, also hold for directed networks. It follow from the proof of Lemma 3 that, for a directed, unweighted and strongly connected network G(N, E), if $d(G)\ge 7$, then $d_i\ge 4$ for all $i\in N$. Thus, the steps undertaken to derive the upper bounds of the coradius and modified coradius, and the lower bound of the radius of ${\mathbf {A}}^p$ hold for directed, unweighted and strongly connected networks as well.

Theorem 1 can also be extended to weighted and strongly connected networks but only after accounting for link weights in the definition of the contagion threshold. Specifically, for any $j\in N_{i_{r}}$, let $\phi _j(B_{i_{r-1}})$ be the proportion of j’s interactions with players in $B_{i_{r-1}}$. That is, if $w_{jk}$ is the weight of the directed link from j to k, then $\phi _j(B_{i_{r-1}})=\sum _{k\in B_{i_{r-1}}}w_{jk}/\sum _{l\in N_j}w_{jl}$. The contagion threshold of a weighted network G is then defined as ${\underline{\eta }}(G)=\min _{i\in N}\min _{r\in [2,d_i]}\min _{j\in N_{i_r}}\phi _j(B_{i_{r-1}})$. To account for the link weights in the total payoffs, the payoff to player i from playing strategy $a_j$ against configuration ${\mathbf {x}}$ can be expressed as $U_i\left( a_j\mid {\mathbf {x}}\right) =\sum _{k\in N_i}w_{ik}u(a_j,x^k)$, where $x^k$ is the strategy played by player k in configuration ${\mathbf {x}}$. These definitions of the contagion threshold and the total payoffs ensure that strategies in $A^p$ will be fully and step-by-step contagious on any weighted and strongly connected network G whenever ${\underline{\eta }}(G)\ge p$, and that Theorem 1 holds for weighted and strongly connected networks.²⁹

Unlike directedness and weightedness, requiring the network to be strongly connected is necessary for Theorem 1 to hold. When a network is not strongly connected, there is no guarantee that strategies in $A^p$ can spread contagiously from neighbourhood $B_{i_1}$ of every $i\in N$. Similarly, there is no guarantee that $d(G)\ge 7$ implies that $d_i\ge 4$ for all $i\in N$. The proof, and hence validity of Theorem 1, relies on these two conditions. Note, however, that if an undirected network is not strongly connected, then it consists of strongly connected components which can be analysed as separate networks. More specifically, if ${\mathcal {G}}$ is the set of all strongly connected components of G and $G_k$ is a typical element of ${\mathcal {G}}$, then, when $d(G_k)\ge 7$ and ${\underline{\eta }}(G_k)\ge p$ for all $G_k\in {\mathcal {G}}$, strategies in $A^p$ are uniquely stochastically stable in each component and in turn the whole network.

The second condition is a restriction on the diameter, $d(G)\ge 7$. This condition is sufficient but not necessary for Theorem 1 to hold. It is easy to construct examples of networks with $d(G)<7$ where strategies in $A^p$ are uniquely stochastically stable. The inequality, $d(G)\ge 7$, rules out highly centralized networks (e.g. a star network for which all strategies are stochastically stable) and densely connected networks (e.g. a complete network where each player interacts with every other player). Overall, this condition does not limit the applicability of the results of Theorem 1. This is because real-world networks (e.g. social media networks, collaboration networks in academia, etc.) are large and sufficiently localized that their diameters are greater than seven.

The last condition relates p to the contagion thresholds ${\underline{\eta }}(G)$. The inequality, $p\le {\underline{\eta }}(G)$, is sufficient but not necessary for strategies in $A^p$ to be uniquely stochastically stable. It is easy to construct an example where strategies in $A^p$ are uniquely stochastically stable in a network with $p>{\underline{\eta }}(G)$, but such examples cannot easily be generalized.

Our analysis and results are related to Opolot (2020) and Peski (2010) who also identify network measures that determine which and when strategies are uniquely stochastically stable. Opolot (2020) shows that for regular cyclic networks, if the maximum group cohesion is less or equal to $(1-p)$, then there exists a threshold network diameter above which strategies that form the smallest iterated p-best response set (i.e., a set of strategies that remain after iterative application of the notion of a p-best response set) are uniquely stochastically stable. And when the network diameter is greater or equal to two, strategies in the minimal p-best response set are uniquely stochastically stable whenever the maximum group cohesion is less or equal to $(1-p)$. Morris (2000) and Opolot (2020) define the maximum group cohesion as follows.

For some $Z\subset N$ and $i\in Z$ in network G, define $\eta _i(Z,G)$ as the proportion of i’s neighbours in Z. That is,

$$\begin{aligned} \eta _i(Z,G) = \frac{|N_i\cap Z|}{n_i} \end{aligned}$$

A group $Z\subset N$ of players is $\alpha$-cohesive if $\eta (Z,G)=\min _{i\in Z} \eta _i(Z,G)\ge \alpha$. The maximum group cohesion in G is then $\eta (G)=\max _{Z\subset N}\eta (Z,G)$.

Opolot (2020) also demonstrates with an example that although the maximum group cohesion predicts unique stochastically stable outcomes in regular cyclic networks, it fails to do so in some arbitrary networks. In contrast, since $1/\Delta (G)\le {\underline{\eta }}(G)\le \frac{1}{2}$ for all strongly connected networks with $d(G)\ge 7$, where $\Delta (G)=\max _{i\in N}n_i$, is the size of the largest first-order neighbourhood in G, Theorem 1 states that strategies in $A^p$, for $1/\Delta (G)\le p\le \frac{1}{2}$, are uniquely stochastically stable in any undirected, unweighted and strongly connected arbitrary network with ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$.³⁰

The contagion threshold can also be defined using alternative reference groups. For example, the cohesive subgroups, rather than the first-neighbourhoods of players, can be used as reference groups from which strategies in $A^p$ spread through contagion. That is, let ${\mathcal {Z}}(G)$ denote the set of all groups of players in G that are $\frac{1}{2}$-cohesive. For each $Z\in {\mathcal {Z}}(G)$, let $N_{Z_1}$ be the set of players in $N\backslash Z$ with at least one neighbour in Z; $N_{Z_2}$ is the set of players in $N\backslash \{Z\cup N_{Z_1}\}$ with at least one neighbour in $N_{Z_1}$; and more generally, $N_{Z_r}$ is the set of players in $N\backslash \{Z\cup N_{Z_1}\cup \ldots \cup N_{Z_{r-1}}\}$ with at least one neighbour in $N_{Z_{r-1}}$. Let $d_Z(G)$ be the diameter of Z in network G (i.e., the value of r at which $N_{Z_r}\ne \emptyset$ but $N_{Z_{r+1}}=\emptyset$). For any $j\in N_{Z_r}$, let $\eta _j^\prime (N_{Z_{r-1}})$ be the proportion of j’s neighbours in $N_{Z_{r-1}}$. Then the contagion threshold of G can also be defined as

$$\begin{aligned} \eta ^\prime (G)=\min _{Z\in {\mathcal {Z}}(G)}\min _{r\in [1,d_Z]}\min _{j\in N_{Z_r}}\eta _j^\prime (N_{Z_{r-1}}) \end{aligned}$$

(11)

This definition of the contagion threshold ensures that strategies in $A^p$ can spread on G through either full or partial contagion starting from any $Z\in {\mathcal {Z}}(G)$ whenever $\eta ^\prime (G)\ge p$. From the proof of Theorem 1 and the discussion in Opolot (2020, Sect. 5), we conjecture that when $\eta ^\prime (G)\ge p$, there exists a threshold value of the minimum group diameter (i.e., the minimum $d_Z(G)$ over all $Z\in {\mathcal {Z}}(G)$) above which $CR({\mathbf {A}}^p)\le \min _{Z\in {\mathcal {Z}}(G)}|Z|$, and $R({\mathbf {A}}^p)\ge \min _{Z\in {\mathcal {Z}}(G)}|Z|+\iota$, where $\iota \ge 1$ is some positive integer (i.e., the threshold diameter at which strategies in $A^p$ are uniquely stochastically stable). The exact proof of this conjecture is beyond the scope of this paper and is left as an avenue for future research.

Peski (2010, Theorem 2 & Corollary 1) shows that for the BRM model, a $\left( \frac{1}{2}-\delta ^*\right)$-dominant strategy is uniquely stochastically stable under local interactions, where $\delta ^*$ is defined below. That is, let strategy $a\in A$ be $\left( \frac{1}{2}-\delta ^*\right)$-dominant, and for any pair $i,j\in N$, let $g_{ij}=1$ if there is a link from i to j, and zero otherwise. Then configuration ${\mathbf {a}}$, where all players coordinate on strategy a, is uniquely stochastically stable on any network G with $\delta ^*=\max _{i\in N}\delta _i$ and

$$\begin{aligned} \delta _i = \inf \left\{ \delta : \forall _{S\subseteq N\backslash i}\forall _{j^*\in S} \,\text {if}\, \frac{\sum _{j\in S}g_{ij}}{\sum _{j\ne i}g_{ij}}> \frac{1}{2}+\delta , \, \text {then}\, \frac{\sum _{j\in S\backslash j^*}g_{ij}}{\sum _{j\ne i}g_{ij}}\ge \frac{1}{2}-\delta \right\} \nonumber \\ \end{aligned}$$

(12)

If we label $N_i$, the first-order neighbours of player $i\in N$, as $N_i=\{1,2,\ldots ,n_i\}$, then the set S satisfying (12) is such that when $n_i$ is even, $S=\{1,2,\ldots ,\frac{n_i}{2}\}$, and when $n_i$ is odd, $S=\{1,2,\ldots ,\lceil \frac{n_i}{2} \rceil \}$. This implies that:

$$\begin{aligned} \delta _i = {\left\{ \begin{array}{ll} 0 &{} \quad \text {if }n_i\text { is even} \\ \frac{1}{2n_i} &{} \quad \text {if }n_i\text { is odd} \end{array}\right. } \end{aligned}$$

(13)

where the equality for $n_i$ odd follows because when $S=\{1,2,\ldots ,\lceil \frac{n_i}{2} \rceil \}$, we have

$$\begin{aligned} \frac{\sum _{j\in S}g_{ij}}{\sum _{j\ne i}g_{ij}}=\frac{\lceil \frac{n_i}{2} \rceil }{n_i}=\frac{1}{2}+\frac{2\lceil \frac{n_i}{2} \rceil -n_i}{2n_i}=\frac{1}{2}+\frac{1}{2n_i} \end{aligned}$$

If we let $\delta _0(G)$ be the size of the smallest odd neighbourhood in G³¹ so that $\delta ^*=\frac{1}{2\delta _0(G)}$, then the results in Peski (2010, Theorem 2 & Corollary 1) essentially state that a p-dominant strategy is uniquely stochastically stable in network G if $p\le \frac{1}{2}\left( 1-\frac{1}{\delta _0(G)}\right)$.³² Thus, these results depend solely on the size of the smallest odd neighbourhood. Stated this way, the contrast with our results becomes apparent.

First, the results in Peski (2010) offer more accurate predictions for evolutionary dynamics in densely connected networks (i.e. where $\delta _0(G)$ is large)—by more accurate predictions we mean the upper bound of p at which a p-dominant strategy is uniquely stochastically stable is as close to $\frac{1}{2}$ as it can be for a given network. Our results instead offer more accurate predictions in sparsely connected networks. For example, when the smallest odd neighbourhood size is 3, Peski (2010, Theorem 2 and Corollary 1) predicts that a $\frac{1}{3}$-dominant strategy is uniquely stochastically stable. However, in the example of the network in Fig. 4 above with $\delta _0(G)=3$, Theorem 1 predicts that a $\frac{1}{2}$-dominant strategy is uniquely stochastically stable. Peski (2010, Theorem 2 and Corollary 1) fails to predict the unique stochastically stable outcome in any unweighted network containing at least one player with $n_i=1$. This is because for such networks, $\delta _0(G)=1$, and hence, $p=0$. An example of such a network is depicted in Fig. 3 above, where Theorem 1 instead predicts that a $\frac{1}{3}$-dominant strategy is uniquely stochastically stable.

Second, Theorem 1 establishes conditions under which the minumal p-best response set are stochastically stable and not just p-dominant strategies. This generalization is important because games with a p-dominant strategy are an exception rather than the rule. In the absence of a unique p-dominant strategy, the next best option may be to isolate strategies that form the minimal p-best response set.

6 Concluding remarks

Evolutionary models with persistent randomness provide a framework for equilibrium selection in games with multiple equilibria. These models employ stochastic stability as a solution concept. However, recent developments have highlighted the lack of robustness of stochastic stability to the interaction structure, to the extent that it fails to distinguish between equilibria in $2\times 2$ coordination games in some networks.

One approach that can lead to relatively robust predictions is to identify network parameters and aggregate measures that determine the conditions under which stochastically stable outcomes are unique. We adopt this approach and identify the contagion threshold as one of such aggregate network measures. Network structures can then be categorized based on their contagion thresholds and the predictions of stochastic stability will be identical for networks with the same contagion threshold. We show that, with mild restrictions on the network diameter and connectedness, strategies that form the minimal p-best response set are uniquely stochastically stable in networks with the contagion threshold of p.

The contagion threshold is just one among a potential list of network parameters and aggregate measures that can robustly predict unique stochastically stable outcomes. More research is thus needed to further explore the role of different network properties.

Appendices

A Matrix-based steps for computing the contagion threshold

The contagion threshold of a network can be computed through matrix-based representation of networks. The network G(N, E) can be represented by an adjacency matrix, which, with a slight abuse of notation, is here denoted by G. The adjacency matrix is a zero-one matrix with elements $g_{ij}=1$ if there is a link from i to j, and zero otherwise. Recall that the contagion thresholds is the minimum $\alpha _j(B_{i_{{\tau }-1}})$ over all $j\in N_{i_{\tau }}$, ${\tau }=2,\ldots ,d_i$, and $i\in N$, where $\alpha _j(B_{i_{{\tau }-1}})$ is the proportion of player j’s neighbours that are contained in $B_{i_{{\tau }-1}}$. For $\tau =2,3,\ldots ,d(G)$, the values of $\alpha _j(B_{i_{{\tau }-1}})$, for all $j\in N_{i_{\tau }}$ and $i\in N$, can be written in matrix form, here denoted by $W(\tau )$. That is, $W(\tau )$ is a matrix with each element $w_{ij}(\tau )=\alpha _j(B_{i_{\tau -1}})$ if $j\in N_{i_{\tau }}$ and zero otherwise. For this representation, the contagion threshold is given by ${\underline{\eta }}(G)=\min _{i\in N}\min _{\tau \in [2,d(G)]}\min _{j\ne i} w_{ij}(\tau )$. For any network with adjacency matrix G, the corresponding $W(\tau )$ matrices, for $\tau =2,\ldots ,d_i$, can be computed from G through the following matrix-based algorithmic step. These algorithmic steps involve matrix multiplication and addition, which makes them tractable – matrix multiplication can be executed in polynomial time of order three (Bini et al. 1979).

Let I denote the identity matrix, and D(G), or simply D where no confusion arises, be the diagonal matrix with the diagonal elements being the number of direct neighbours of each player. More precisely, if ${\mathbf {c}}$ is a column vector containing sums of rows of G (i.e. $c_i=\sum _{j\in N}g_{ij}$ for each $i\in N$), then D(G) is a square matrix whose diagonal is ${\mathbf {c}}$ and zero elsewhere. For any arbitrary matrix M, let $M^{[1]}$ be a matrix derived from M by replacing all elements of M that are greater than one with one, and let $M^{[0]}$ be a matrix derived from M by replacing all negative elements of M with zero. These two matrix operations can be extended to sums and products of matrices. For example, $[H\times M]^{[1]}$ is a matrix derived from the product $H\times M$ by replacing all elements of $H\times M$ that are greater than one with one, and $[H+ M]^{[1]}$ is a matrix derived from $H+ M$ by replacing all elements of $H+ M$ that are greater than one with one. The third operator that we use in the computation of $W(\tau )$ matrices is $\text {RepZero}[M; H]$, which takes two equal-sized square matrices M and H, and replaces the element $m_{ij}$ of M with zero if $h_{ij}=0$, otherwise $m_{ij}=m_{ij}$ if $h_{ij}\ne 0$. For $\tau =2, 3, \ldots d(G)$, each $W(\tau )$ is computed as follows.

To compute W(2), first notice that the entries of $G\times G$ are the number of two-step paths leading up to a given node (i.e. the ijth entry of $G\times G$ is the number of paths that start from i and end at j in two steps). Thus, if all elements of $G\times G$ that are greater than one are replaced by 1, then the ijth element of $[G\times G]^{[1]}$ is one if j is reachable in two steps from i, and zero otherwise. Note, however, that, for each $i\in N$, we aim to compute the values of $\alpha _j(B_{i_1})$ for all $j\in N_{i_2}$, where $N_{i_2}$ is the set of the second-order neighbours of i (i.e. players that are two steps away from i and are not contained in $B_{i_1}$). Note also that the ijth element of matrix $I+G$ is one if j is in $B_{i_1}$ and zero otherwise. Thus, if we subtract $I+G$ from $[G\times G]^{[1]}$, we end up with $[[G\times G]^{[1]}-(I+G)]^{[0]}$ whose ijth entry is equal to one if j is contained in $N_{i_2}$ and zero otherwise. The ijth entry of $G\times G$, which is the number of two-step paths from i to j, is equal to the number of direct neighbours of j that are contained in $B_{i_1}$. This implies that the ijth entry of $\text {RepZero}\big [G\times G; [[G\times G]^{[1]}-(I+G)]^{[0]} \big ]$ is the number of neighbours of $j\in N_{i_2}$ that are contained in $B_{i_1}$ and zero otherwise. The W(2) matrix is then equal to $\text {RepZero}\big [G\times G; [[G\times G]^{[1]}-(I+G)]^{[0]} \big ]$ with each ijth entry normalized by the number of neighbours of j. That is

$$\begin{aligned} W(2)=\text {RepZero}\big [G\times G; [[G\times G]^{[1]}-(I+G)]^{[0]} \big ]\times D(G)^{-1} \end{aligned}$$

The matrix W(3) is computed through the same steps above. To shorten notation, let $M(2)=[[G\times G]^{[1]}-(I+G)]^{[0]}$. The product $M(2)\times G$ is the number of three-step paths between pairs of players (i.e. the ijth entry is the number of paths that start from i and end at j in three steps); and the ijth element of $[M(2)\times G]^{[1]}$ is one if j is reachable in three steps from i, and zero otherwise. The ijth element of matrix $I+G+M(2)$ is one if j is in $B_{i_2}$, and zero otherwise. Thus, the ijth entry of $\left[ [M(2)\times G ]^{[1]}-\left( I+G+M(2)\right) \right] ^{[0]}$ is equal to one if $j\in N_{i_3}$. The matrix W(3) is then given by

$$\begin{aligned} W(3)=\text {RepZero}\big [M(2)\times G; \left[ [M(2)\times G ]^{[1]}-\left( I+G+M(2)\right) \right] ^{[0]} \big ]\times D(G)^{-1} \end{aligned}$$

Letting $M(3)=\left[ [M(2)\times G]^{[1]}-\left( I+G+M(2)\right) \right] ^{[0]}$, the product $M(3)\times G$ is the number of four-step paths between pairs of players, so that the ijth entry of $[M(3)\times G]^{[1]}$ is one if j is reachable in four steps from i, and zero otherwise. The ijth element of matrix $I+G+M(2)+M(3)$ is one if j is in $B_{i_3}$, and zero otherwise. Thus, the ijth entry of $\left[ [M(3)\times G ]^{[1]}-\left( I+G+M(2)+M(3)\right) \right] ^{[0]}$ is equal to one if $j\in N_{i_4}$. The matrix W(4) is then given by

$$\begin{aligned}&W(4)=\text {RepZero}\big [M(3)\\&\times G; \left[ [M(3)\times G ]^{[1]}-\left( I+G+M(2)+M(3)\right) \right] ^{[0]} \big ]\times D(G)^{-1} \end{aligned}$$

Let $M(\tau )=\left[ [M(\tau -1)\times G ]^{[1]}-\sum _{r=0}^{\tau -1}M(r)\right] ^{[0]}$, where $M(0)=I$ and $M(1)=G$. Then, following the same steps in the above iterative process, the $W(\tau )$ matrix, for $\tau =2,3,\ldots ,d(G)$ is given by

$$\begin{aligned} W(\tau )=\text {RepZero}\left[ M(\tau -1)\times G; \Big [[M(\tau -1)\times G ]^{[1]}-\sum _{r=0}^{\tau -1}M(r)\Big ]^{[0]} \right] \times D(G)^{-1} \end{aligned}$$

B Proof of Lemma 2

To prove Lemma 2, we first show that the following relation holds.

$$\begin{aligned}&\min _{r\in \{\tau ,\tau +1\}}\min _{j\in B_{i_{r}}} \alpha _j(B_{i_{r-1}}) \nonumber \\&\quad = \min \left\{ \min _{j\in N_{i_{\tau -1}}}\alpha _j(B_{i_{\tau -1}}), \min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}}), \min _{j\in N_{i_{\tau +1}}}\alpha _j(B_{i_{\tau }})\right\} \end{aligned}$$

(14)

To prove (14), first notice that

$$\begin{aligned} \min _{r\in \{\tau ,\tau +1\}}\min _{j\in B_{i_{r}}} \alpha _j(B_{i_{r-1}})=\min \left\{ \min _{j\in B_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}}), \min _{j\in B_{i_{\tau +1}}}\alpha _j(B_{i_{\tau }})\right\} . \end{aligned}$$

(15)

Second, since all direct neighbours of any $h\in B_{i_{\tau -2}}$ are contained within $B_{i_{\tau -1}}$, it follows that $\alpha _h(B_{i_{\tau -1}})=1$ for all $h\in B_{i_{\tau -2}}$. And if $\tau +1\le d_i$, so that $N_{i_{\tau +1}}\ne \emptyset$, then there exists at least one $k\in N_{i_{\tau -1}}\cup N_{i_{\tau }}$ with $\alpha _k(B_{i_{\tau -1}})<1$, so that

$$\begin{aligned} \min _{j\in B_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})= & {} \min _{j\in N_{i_{\tau -1}}\cup N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})\nonumber \\= & {} \min \left\{ \min _{j\in N_{i_{\tau -1}}}\alpha _j(B_{i_{\tau -1}}), \min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}})\right\} \end{aligned}$$

(16)

Similarly, $\min _{j\in B_{i_{\tau +1}}}\alpha _j(B_{i_{\tau }})=\min \left\{ \min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau }}), \min _{j\in N_{i_{\tau +1}}}\alpha _j(B_{i_{\tau }})\right\}$.

Third, note that $\alpha _k(B_{i_{\tau }})\ge \alpha _k(B_{i_{\tau -1}})$ for all $k\in N_{i_{\tau }}$. This is because some of the direct neighbours of $k\in N_{i_{\tau }}$ are contained within $N_{i_{\tau }}$, and that $N_{i_{\tau }}\subseteq B_{i_{\tau }}$ but $N_{i_{\tau }}\not \subseteq B_{i_{\tau -1}}$. This inequality implies that

$$\begin{aligned}&\min \left\{ \min _{j\in B_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}}), \min _{j\in B_{i_{\tau +1}}}\alpha _j(B_{i_{\tau }})\right\} \\&\quad =\min \left\{ \min _{j\in N_{i_{\tau -1}}}\alpha _j(B_{i_{\tau -1}}), \min _{j\in N_{i_{\tau }}}\alpha _j(B_{i_{\tau -1}}), \min _{j\in N_{i_{\tau +1}}}\alpha _j(B_{i_{\tau }})\right\} \end{aligned}$$

This proves Eq. (14).

Now, considering the minimum $\min _{j\in B_{i_{r}}} \alpha _j(B_{i_{r-1}})$ over all $r=3,\ldots ,d_i$, it follows from (14) that

$$\begin{aligned} \nonumber \min _{r\in [3,d_i]}\min _{j\in B_{i_{r}}} \alpha _j(B_{i_{r-1}})&= \min \left\{ \min _{j\in N_{i_{2}}}\alpha _j(B_{i_{2}}), \min _{r\in [3,d_i]}\min _{j\in N_{i_{r}}}\alpha _j(B_{i_{r-1}})\right\} \\&\ge \min _{r\in [2,d_i]}\min _{j\in N_{i_{r}}}\alpha _j(B_{i_{r-1}}) \end{aligned}$$

(17)

where the inequality on the right hand side of (17) follows because $\alpha _k(B_{i_{2}})\ge \alpha _k(B_{i_{1}})$ for all $k\in N_{i_{2}}$. Thus, when $\min _{r\in [2,d_i]}\min _{j\in N_{i_r}}\alpha _j(B_{i_{r-1}})\ge p$, $\min _{r\in [3,d_i]}\min _{j\in B_{i_{r}}} \alpha _j(B_{i_{r-1}})\ge p$, and since $S_{\tau }\subseteq B_{i_{\tau }}$ for all $\tau =2,\ldots ,d_i$, it follows that for any sequence $S_3\subseteq B_{i_3},\ldots , S_{d_i}\subseteq B_{i_{d_i}}$, $\alpha _h(S_{\tau -1})\ge p$ for each $h\in S_{\tau }$ and all $\tau =3,\ldots ,d_i$.

It then remains to show that when $\min _{r\in [2,d_i]}\min _{j\in N_{i_r}}\alpha _j(B_{i_{r-1}})\ge p$, there exists some $S_2\subseteq B_{i_2}$ with $\alpha _h(S_{1})=\alpha _h(B_{1})\ge p$ for each $h\in S_{2}$. Indeed, from (16), we have $\min _{j\in B_{i_{2}}}\alpha _j(B_{i_{1}})=\min \left\{ \min _{j\in N_{i_{1}}}\alpha _j(B_{i_{1}}), \min _{j\in N_{i_{2}}}\alpha _j(B_{i_{1}})\right\}$. Since $\min _{r\in [2,d_i]}\min _{j\in N_{i_r}}\alpha _j(B_{i_{r-1}})\ge p$ implies that $\min _{j\in N_{i_{2}}}\alpha _j(B_{i_{1}})\ge p$, it follows that there exists some subgroup of players $S_2$, where $N_2\subseteq S_2\subseteq B_{i_2}$, with $\alpha _h(B_{1})\ge p$ for each $h\in S_{2}$.

Thus, when $\min _{r\in [2,d_i]}\min _{j\in N_{i_r}}\alpha _j(B_{i_{r-1}})\ge p$, for any $i\in N$, there exist sequences of players, $S_1, S_2, S_3,\ldots , S_{{\bar{t}}}$, with $S_1=B_{i_1}$, $S_2\subseteq B_{i_2}, S_3\subseteq B_{i_3},\ldots , S_{{\bar{t}}}\subseteq B_{i_{{\bar{t}}}}$, such that $\alpha _h(S_{\tau -1})\ge p$ for all $h\in S_{\tau }$ and all $\tau =2,\ldots ,{\bar{t}}$, where ${\bar{t}}\le d_i$.

C Proof of Theorem 1

Before deriving the upper bounds of the cordadius and modified coradius and the lower bound of the radius of ${\mathbf {A}}^p$, we first show in the following lemma that, for an undirected, unweighted and strongly connected network G, $d(G)\ge 7$ implies that $d_i(G)\ge 4$ for all $i\in N$.

Recall that a directed path from i to j is a finite sequence $(i_1, i_2,\ldots ,i_r)$, with $i=i_1$ and $i_r=j$, that is connected through distinct directed links; $d_{ij}$ is the length of the maximum shortest path from i to j; $d_i=\max _{j\ne i}d_{ij}$ is the length of the shortest path from i to any other player; and $d(G)=\max _{i\in N}d_i$ is the diameter of G.

Lemma 3

For an undirected, unweighted and strongly connected network G, if $d(G)\ge 7$, then $d_i\ge 4$ for all $i\in N$.

Proof

We first show that, for an undirected, unweighted and strongly connected network G, if d(G) is even, then $d_i\ge \frac{d(G)}{2}$ for all $i\in N$, and if d(G) is odd, then $d_i\ge \frac{d(G)+1}{2}$ for all $i\in N$.

Consider any directed path that forms a diameter of G (there can be many such paths), and label the elements along this path as $i=i_1, i_2,\ldots ,i_{d(G)+1}=j$. Since $i,j\in N$ are the end points of this path, and that G is strongly connected and undirected, it follows that $j\in N_{i_{d_i}}$, $i\in N_{j_{d_j}}$ and $d_{ij}=d_i=d_j=d(G)$. If d(G) is even, then the distance (i.e. the number of steps) from $i_{\frac{d(G)}{2}+1}$ (the player at halfway point along $(i_1, i_2,\ldots ,i_{d(G)+1})$) to players i and j is exactly $\frac{d(G)}{2}$, That is, $d_{i_{\frac{d(G)}{2}+1}i}= d_{i_{\frac{d(G)}{2}+1}j}=\frac{d(G)}{2}$. If d(G) is odd, then $i_{\frac{d(G)+1}{2}}$ and $i_{\frac{d(G)+3}{2}}$ are the players at halfway point along $i_1, i_2,\ldots ,i_{d(G)+1}$. And the distances from $i_{\frac{d(G)+1}{2}}$ to j and $i_{\frac{d(G)+3}{2}}$ to i is exactly $\frac{d(G)+1}{2}$. That is, $d_{i_{\frac{d(G)+1}{2}}j}=d_{i_{\frac{d(G)+3}{2}}i}=\frac{d(G)+1}{2}$.

This implies that for every player, h, along $(i_1, i_2,\ldots ,i_{d(G)+1})$, $d_h\ge \frac{d(G)}{2}$ when d(G) is even, and $d_{h}\ge \frac{d(G)+1}{2}$ when d(G) is odd. And since the network is strongly connected, there exists a shortest path connecting every other player, $k\ne h$, that does not lie along $(i_1, i_2,\ldots ,i_{d(G)+1})$, to some h along $(i_1, i_2,\ldots ,i_{d(G)+1})$. For all such players, $d_k\ge d_{kh}+\frac{d(G)}{2}$ if d(G) is even, and $d_k\ge d_{kh}+\frac{d(G)+1}{2}$ if d(G) is odd. Thus, when d(G) is even, $d_i\ge \frac{d(G)}{2}$ for all $i\in N$, and when d(G) is odd, $d_i\ge \frac{d(G)+1}{2}$ for all $i\in N$, and hence, when $d(G)\ge 7$, $d_i\ge 4$ for all $i\in N$. $\square$

The upper bounds of the coradius and modified coradius of ${\mathbf {A}}^p$

We aim to show that, for the evolutionary processes (A, U, N, G, P) and $(A,U,N,G,P_{\varepsilon })$ on an undirected, unweighted and strongly connected G, if $p\le {\underline{\eta }}(G)$ and $d(G)\ge 7$, then $CR({\mathbf {A}}^p)\le {\underline{b}}_1$ and $CR^*({\mathbf {A}}^p)\le {\underline{b}}_1$, where ${\underline{b}}_1=\min _{i\in N}b_{i_1}$. The proof follows in four steps. First, we show that when (A, U, N, G, P) starts from any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$, ${\underline{b}}_1$ mutations to strategies in $A^p$ trigger either full contagion of these strategies or an iterative process of best response where (A, U, N, G, P) ultimately converges to an absorbing cycle of states containing both strategies in $A^p$ and $A\backslash A^p$.

Second, for a scenario where ${\underline{b}}_1$ mutations to strategies in $A^p$ fail to trigger full contagion, (A, U, N, G, P) converges to an absorbing cycle $W\in {\mathcal {C}}({\mathbf {A}})$ where players in $N_{i_1}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ and $i\cup N_{i_2}^{3}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ alternate between strategies in $A^p$ and some strategies in A, and the rest play some strategies in A. Third, at most ${\underline{n}}_1^*$ mutations to strategies in $A^p$ sufficiently trigger an exit from the basin of attraction of $W\in {\mathcal {C}}({\mathbf {A}})$, so that $C(W,{\mathbf {A}}^p)\le {\underline{n}}_1^*$. This implies that if the number of mutations to strategies in $A\backslash A^p$ that trigger an exit from D(W) is greater than ${\underline{n}}_1^*$, then $R(W)=C(W,{\mathbf {A}}^p)$.

Fourth, we show that in a scenario where the number of mutations to strategies in $A\backslash A^p$ that trigger an exit from the basin of attraction of W is less or equal to ${\underline{n}}_1^*$, there exists another absorbing cycle $W^\prime \in {\mathcal {C}}({\mathbf {A}})$ and $W^\prime \ne W$, where $R(W)=C(W,W^\prime )\le {\underline{n}}_1^*$. For any such $W^\prime \in {\mathcal {C}}({\mathbf {A}})$, ${\underline{n}}_1^4$ mutations to strategies in $A^p$ trigger an exit from $D(W^\prime )$ to ${\mathbf {A}}^p$, but ${\underline{n}}_1^4$ mutations to strategies in $A\backslash A^p$ cannot trigger exit from $D(W^\prime )$, which implies that $R(W^\prime )=C(W^\prime ,{\mathbf {A}}^p)\le {\underline{n}}_1^4$. Following the discussion in Sect. 4, together with Eqs. (9) and (10), we then demonstrate that these four results imply that $CR({\mathbf {A}}^p)\le {\underline{b}}_1$ and $CR^*({\mathbf {A}}^p)\le {\underline{b}}_1$.

Let (A, U, N, G, P) start from any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$, and at $t=1$, let all players in $B_{i_1}$ of any $i\in N$ mutate to strategies in $A^p$. Then from $t=2$ onward, (A, U, N, G, P) evolves as follows, where we write $i\rightarrow A^\prime$ and $N^\prime \rightarrow A^\prime$ to mean i and respectively each player in $N^\prime$ plays a strategy in $A^\prime$.

$t=1$	$B_{i_1}\rightarrow A^p$; $N_{i_2}\cup N_{i_3}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=2$	$i\cup N_{i_2}\rightarrow A^p$, where i plays a strategy in $A^p$ because all $j\in N_{i_1}$ play strategies in $A^p$ at $t=1$. Players in $N_{i_2}$ play strategies in $A^p$ because each $h\in N_{i_2}$ has $\alpha _h(B_{i_1})\ge {\underline{\eta }}(G)\ge p$, and that all $j\in N_{i_1}$ play strategies in $A^p$ at $t=1$. Note that no $h\in N_{i_2}^3$ will play a strategy in $A\backslash A^p$ even if all players in $N_{i_2}$ and $N_{i_3}$ play strategies in $A\backslash A^p$ at $t=1$. This is because for each $h\in N_{i_2}^3$, $\alpha _h(B_{i_1})\ge {\underline{\eta }}(G)\ge p$ implies that $(1-p)\ge (1-{\underline{\eta }}(G))\ge (1-\alpha _h(B_{i_1}))=\alpha _h(N_{i_2}\cup N_{i_3})$. Since $(1-p)\ge \alpha _h(N_{i_2}\cup N_{i_3})$, strategies in $A\backslash A^p$ are not best responses to any such h because they are best responses only when played by more than proportion $1-p$ of neighbours. $N_{i_1}\cup N_{i_3}\cup N_{i_4}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$. Note, however, that some players in $N_{i_1}$ will play strategies in $A^p$; for example, all $j\in {\bar{N}}_{i_1}^2$ (i.e. all $j\in N_{i_1}$ with $N_{j_1}\cap N_{i_2}=\emptyset$) play strategies in $A^p$ because each has all their direct neighbours within $B_{i_1}$, all of whom play strategies in $A^p$ at $t=1$. But since $A^p\subset A$, we simply write $N_{i_1}\rightarrow A$. Moreover, for the rest of the remaining analysis, it is sufficient to only keep track of the strategies played by the players in $i, N_{i_1}^3, N_{i_1}^4, N_{i_2}^3, N_{i_2}^4, N_{i_3}, N_{i_4},\ldots , N_{i_{d_i}}$.
$t=3$	$N_{i_1}^3\cup N_{i_3}\rightarrow A^p$. All $h\in N_{i_1}^3$ play strategies in $A^p$ because, firstly, each has at least one second-order neighbours in $N_{i_3}$ (i.e. $N_{h_2}\cap N_{i_3}\ne \emptyset$). This implies that, for each $h\in N_{i_1}^3$, there exists some $j\in N_{i_3}$ with $N_{h_1}\cap N_{j_1}=N_{h_1}\cap B_{j_1}\ne \emptyset$ and $N_{h_1}\cap N_{j_1}\subseteq N_{i_2}^3$ (i.e. all direct neighbours of $h\in N_{i_1}^3$ that are also direct neighbours of $j\in N_{i_3}$ are contained within $N_{i_2}^3$). It then follows that $\alpha _h(N_{i_2}^3)\ge \alpha _h(N_{j_1})= \alpha _h(B_{j_1})\ge \min _{k\in N_{j_2}}\alpha _k(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. The first inequality, $\alpha _h(N_{i_2}^3)\ge \alpha _h(N_{j_1})$, holds because, if there is more than one $j\in N_{i_3}$, then for each $h\in N_{i_1}^3$, it is not necessary for all $N_{h_1}\subset N_{i_2}^3$ (i.e. direct neighbours of h that are contained in $N_{i_2}$) to also be contained in $N_{j_1}$. Secondly, since all players in $N_{i_2}^3\subseteq N_{i_2}$ play strategies in $A^p$ at $t=2$, and by the above inequality, $\alpha _h(N_{i_2}^3)\ge {\underline{\eta }}(G)\ge p$ for each $h\in N_{i_1}^3$, strategies in $A^p$ are best responses to all $h\in N_{i_1}^3$. All players in $N_{i_3}$ play strategies in $A^p$ because each $l\in N_{i_3}$ has $\alpha _l(N_{i_2})=\alpha _l(B_{i_2})\ge {\underline{\eta }}(G)\ge p$ and all players in $N_{i_2}$ play strategies in $A^p$ at $t=2$. $i\cup {\bar{N}}_{i_1}^3\cup N_{i_2}\cup N_{i_4}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=4$	$i\cup N_{i_2}^3\cup N_{i_4}\rightarrow A^p$. Player i plays a strategy in $A^p$ because for each $j\in N_{i_2}^3$, $N_{i_1}\cap N_{j_1}\subseteq N_{i_1}^3$ (i.e. all direct neighbours of $j\in N_{i_2}^3$ that are also direct neighbours of i are contained within $N_{i_1}^3$). This implies that, for any $j\in N_{i_2}^3$, $\alpha _i(N_{i_1}^3)\ge \alpha _i(N_{j_1})= \alpha _i(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^3$ play strategies in $A^p$ at $t=3$, it follows that a strategy in $A^p$ is a best response to player i. Players in $N_{i_2}^3$ play strategies in $A^p$ for the similar reason. That is, for each $k\in N_{i_2}^3$, $N_{k_1}\cap N_{i_1}\subseteq N_{i_1}^3$, which implies that $\alpha _k(N_{i_1}^3)= \alpha _k(N_{i_1})= \alpha _k(B_{i_1})\ge {\underline{\eta }}(G)\ge p$, and hence, strategies in $A^p$ are best responses to all $k\in N_{i_2}^3$. Players in $N_{i_4}$ play strategies in $A^p$ because each $l\in N_{i_4}$ has $\alpha _l(N_{i_3})=\alpha _l(B_{i_3})\ge {\underline{\eta }}(G)\ge p$, and that all players in $N_{i_3}$ play strategies in $A^p$ at $t=3$. $N_{i_1}\cup {\bar{N}}_{i_2}^3\cup N_{i_3}\cup N_{i_5}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=5$	$N_{i_1}^3\cup N_{i_3}\cup N_{i_5} \rightarrow A^p$. Players in $N_{i_1}^3\cup N_{i_3}$ play strategies in $A^p$ for the same reasons outlined in $t=3$ above. Players in $N_{i_5}$ play strategies in $A^p$ because each $l\in N_{i_5}$ has $\alpha _l(N_{i_4})=\alpha _l(B_{i_4})\ge {\underline{\eta }}(G)\ge p$, and that all players in $N_{i_4}$ play strategies in $A^p$ at $t=4$. $i\cup {\bar{N}}_{i_1}^3\cup N_{i_2}\cup N_{i_4}\cup N_{i_6}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=6$	Following the same steps above, $i\cup N_{i_2}^3\cup N_{i_4}\cup N_{i_6}\rightarrow A^p$. $N_{i_1}\cup {\bar{N}}_{i_2}^3\cup N_{i_3}\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=7$	$N_{i_1}^3\cup N_{i_3}\cup N_{i_5}\cup N_{i_7} \rightarrow A^p$. $i\cup {\bar{N}}_{i_1}^3\cup N_{i_2}\cup N_{i_4}\cup N_{i_6}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$\text {{-}{-}}$
$t=d_{i}$	If $d_{i}$ is an odd number, then: $N_{i_1}^3\cup N_{i_3}\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}} \rightarrow A^p$ $i\cup {\bar{N}}_{i_1}^3\cup N_{i_2}\cup N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$. If $d_{i}$ is an even number, then: $i\cup N_{i_2}^3\cup N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_i}}\rightarrow A^p$. $N_{i_1}\cup {\bar{N}}_{i_2}^3\cup N_{i_3}\cup N_{i_5}\cup N_{i_7}\cup N_{i_9}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.

Thus, from $t=d_{i}$ iterations onward, if $d_{i}\ge 3$, then the iterative process will converge to either an absorbing state/cycle containing only strategies in $A^p$, or to an absorbing cycle containing both strategies in $A^p$ and some strategies in $A\backslash A^p$. Specifically, if players in $i\cup {\bar{N}}_{i_1}^3\cup N_{i_2}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$, for $d_i$ odd, and players in $N_{i_1}\cup {\bar{N}}_{i_2}^3\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}-1}}$, for $d_i$ even, all play strategies in $A^p\subset A$ after $t=d_i$ iterations, then (A, U, N, G, P) converges to an absorbing set containing only strategies in $A^p$. For this scenario, $b_{i_1}$ mutations, for any $i\in N$, to strategies in $A^p$ sufficiently trigger evolution from any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$ to ${\mathbf {A}}^p$ so that $CR({\mathbf {A}}^p)= \max _{{\mathbf {x}}\notin D({\mathbf {A}}^p)}C({\mathbf {x}},{\mathbf {A}}^p)\le {\underline{b}}_1$.

We use the following definitions and notation in the following steps where we examine the evolution of (A, U, N, GP) out of absorbing cycles containing both strategies in $A^p$ and some strategies in $A\backslash A^p$.

${\bar{N}}_{i_1}^r[N_{i_1}^r]$	For $r=3, 4,\ldots ,d_i$, ${\bar{N}}_{i_1}^r[N_{i_1}^r]$ is the set of players in ${\bar{N}}_{i_1}^r$ (i.e. the set of players in $N_{i_1}$ that are not contained in $N_{i_1}^r$) that are one step away from at least one player in $N_{i_1}^r$. That is, for each $j\in {\bar{N}}_{i_1}^r[N_{i_1}^r]$, there exists at least one $h\in N_{i_1}^r$ where $j\in N_{h_1}$. For example, in the network of Fig. 6, ${\bar{N}}_{1_1}^3[N_{1_1}^3]=\{7\}$
${\bar{N}}_{i_2}^r[N_{i_2}^r]$ ${\bar{N}}_{i_2}^r[N_{i_1}^r]$	For $r=3, 4,\ldots ,d_i$, ${\bar{N}}_{i_2}^r[N_{i_2}^r]$ is the set of players in ${\bar{N}}_{i_2}^r$ that are one step away from at least one player in $N_{i_2}^r$. That is, for each $j\in {\bar{N}}_{i_2}^r[N_{i_2}^r]$, there exists at least one $h\in N_{i_2}^r$ where $j\in N_{h_1}$. For example, in the network of Fig. 6, ${\bar{N}}_{1_2}^3[N_{1_2}^3]=\{3\}$. Similarly, ${\bar{N}}_{i_2}^r[N_{i_1}^r]$ is the set of players in ${\bar{N}}_{i_2}^r$ that are one step away from at least one player in $N_{i_1}^r$. That is, for each $j\in {\bar{N}}_{i_2}^r[N_{i_1}^r]$, there exists at least one $h\in N_{i_1}^r$ where $j\in N_{h_1}$. For example, in the network of Fig. 6, ${\bar{N}}_{1_2}^3[N_{1_1}^3]=\{3, 14\}$.
${\bar{N}}_{i_1}^r[{\bar{N}}_{i_1}^r[N_{i_1}^r]]$	For $r=3, 4,\ldots ,d_i$, ${\bar{N}}_{i_1}^r[{\bar{N}}_{i_1}^r[N_{i_1}^r]]$ is the set of players in ${\bar{N}}_{i_1}^r$ that are one step away from at least one player in $i\cup {\bar{N}}_{i_1}^r[N_{i_1}^r]$. That is, for each $j\in {\bar{N}}_{i_1}^r[{\bar{N}}_{i_1}^r[N_{i_1}^r]]$, where $j\in {\bar{N}}_{i_1}^r$ but $j\notin i\cup {\bar{N}}_{i_1}^r[N_{i_1}^r]$, there exists at least one $h\in i\cup {\bar{N}}_{i_1}^r[N_{i_1}^r]$ where $j\in N_{h_1}$. For example, in the network of Fig. 6, ${\bar{N}}_{1_1}^3[{\bar{N}}_{1_1}^3[N_{1_1}^3]]=\{8,10\}$.

Fig. 6

For player 1, the above defined subsets have the following composition: $N_{1_1}^3=\{2,13\}$; ${\bar{N}}_{1_1}^3[N_{1_1}^3]=\{7\}$; ${\bar{N}}_{1_2}^3[N_{1_1}^3]=\{3,14\}$; and ${\bar{N}}_{1_2}^4[N_{1_1}^4]=\{14\}$

Now, let $W\in {\mathcal {C}}({\mathbf {A}}^p)$ be an absorbing cycle where players in $N_{i_1}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ and $i\cup N_{i_2}^{3}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ alternate between strategies in $A^p$ and some strategies in A, and the rest play some strategies in A. More specifically, consider any two configurations ${\mathbf {y}},{\mathbf {z}}\in W\in {\mathcal {C}}({\mathbf {A}}^p)$ with $P({\mathbf {y}},{\mathbf {z}})=1$, where ${\mathbf {y}}$ consist of all players in $N_{i_1}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ playing strategies in $A^p$, and all players in $i\cup {\bar{N}}_{i_1}^{3}\cup N_{i_2}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ play strategies in A; and configuration ${\mathbf {z}}$ consists of all players in $i\cup N_{i_2}^{3}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ playing strategies in $A^p$, while all players in $N_{i_1}\cup {\bar{N}}_{i_2}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ play strategies in A. Let (A, U, N, G, P) start from ${\mathbf {y}}$, and let all players in $N_{i_1}^r$, for $4\le r\le d_i$, mutate to strategies in $A^p$ at $t=1$. Then for $d_{i_1}\ge 4$, (A, U, N, G, P) evolves from $t=1$ onward as follows:

$t=1$	$i\cup N_{i_1}^r\cup N_{i_2}^{3}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$; ${\bar{N}}_{i_1}^{r}\cup {\bar{N}}_{i_2}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=2$	$i\cup N_{i_1}^3\cup N_{i_2}^r\cup {\bar{N}}_{i_2}^3[N_{i_2}^{3}]\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. Player i plays a strategy in $A^p$ because for each $k\in N_{i_2}^r$, $N_{k_1}\cap N_{i_1}\subseteq N_{i_1}^r$, which implies that, for any $k\in N_{i_2}^r$, $\alpha _i(N_{i_1}^r)\ge \alpha _i(N_{k_1})= \alpha _i(B_{k_1})\ge \min _{l\in N_{k_2}}\alpha _l(B_{k_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^r$ play strategies in $A^p$ at $t=1$, a strategy in $A^p$ must be a best response to player i. Players in $N_{i_1}^3$ play strategies in $A^p$ because for each $k\in N_{i_1}^3$, there exists at least one $j\in N_{i_3}$ with $N_{k_1}\cap N_{j_1}\subseteq N_{i_2}^3$, which implies that $\alpha _k(N_{i_2}^3)\ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_2}^3$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_1}^3$. Players in $N_{i_2}^r$ play strategies in $A^p$ because for each $k\in N_{i_2}^r$, $N_{k_1}\cap N_{i_1}\subseteq N_{i_1}^r$, which implies that $\alpha _k(N_{i_1}^r)= \alpha _k(N_{i_1})= \alpha _k(B_{i_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^r$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_2}^r$. To see why players in ${\bar{N}}_{i_2}^3[N_{i_2}^{3}]$ play strategies in $A^p$, first observe that no $k\in {\bar{N}}_{i_2}^3[N_{i_2}^{3}]$ is a direct neighbour of any $j\in N_{i_3}$. That is, if $k\in {\bar{N}}_{i_2}^3[N_{i_2}^{3}]$, then $k\notin N_{j_1}$ for all $j\in N_{i_3}$. This observation implies that, for each $k\in {\bar{N}}_{i_2}^3[N_{i_2}^{3}]$, there exists at least one $j\in N_{i_3}$ where $N_{k_1}\cap N_{j_1}\subseteq N_{i_2}^{3}$, so that $\alpha _k(N_{i_2}^3)\ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$, and hence, strategies in $A^p$ are best responses. Players in $N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ play strategies in $A^p$ because each $h\in N_{i_3}$ and $l\in N_{i_r}$, for $r=5,7,\ldots ,d_i$, has $\alpha _h(N_{i_{2}}^3)=\alpha _h(N_{i_{2}})=\alpha _h(B_{i_{2}})\ge {\underline{\eta }}(G)\ge p$ and $\alpha _l(N_{i_{r-1}})=\alpha _l(B_{i_{r-1}})\ge {\underline{\eta }}(G)\ge p$ respectively. Since all players in $N_{i_{2}}^3$ and $N_{i_{r-1}}$, for all $r=5,7,\ldots ,d_i$, play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all players in $N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$. Finally ${\bar{N}}_{i_1}^3\cup {\bar{N}}_{i_2}^r\backslash {\bar{N}}_{i_2}^3[N_{i_2}^{3}]\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=3$	$i\cup N_{i_1}^r\cup {\bar{N}}_{i_1}^3[N_{i_1}^3]\cup N_{i_2}^3\cup {\bar{N}}_{i_2}^3[N_{i_1}^3]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^3]\right\} \cup {\bar{N}}_{i_2}^3[N_{i_2}^{r}]\cup N_{i_3}^r\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Players in $i\cup N_{i_1}^r\cup N_{i_2}^3\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ all play strategies in $A^p$ for the same reasons outlined in $t=2$ above. To see why players in ${\bar{N}}_{i_1}^3[N_{i_1}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^3]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^3]\right\}$ play strategies in $A^p$, first observe that for each $k\in {\bar{N}}_{i_1}^3[N_{i_1}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^3]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^3]\right\}$, where $k\notin {\bar{N}}_{i_2}^3[N_{i_2}^3]$, and any $j\in N_{i_2}^3$, we have $N_{k_1}\cap N_{j_1}\subseteq N_{i_1}^3\cup {\bar{N}}_{i_2}^3[N_{i_2}^{3}]$ (i.e., all direct neighbours of any $k\in {\bar{N}}_{i_1}^3[N_{i_1}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^3]$, that are also direct neighbours of some $j\in N_{i_2}^3$, are contained within $N_{i_1}^3\cup {\bar{N}}_{i_2}^3[N_{i_2}^{3}]$). This implies that for each $k\in {\bar{N}}_{i_1}^3[N_{i_1}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^3]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^3]\right\}$, there exists at least one $j\in N_{i_2}^3$ such that $\alpha _k\left( N_{i_1}^3\cup {\bar{N}}_{i_2}^3[N_{i_2}^{3}]\right) \ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^3\cup {\bar{N}}_{i_2}^3[N_{i_2}^{3}]$ play strategies in $A^p$ at $t=2$, strategies in $A^p$ are best responses to all $k\in {\bar{N}}_{i_1}^3[N_{i_1}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^3]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^3]\right\}$. Players in ${\bar{N}}_{i_2}^3[N_{i_2}^{r}]$ play strategies in $A^p$ because, firstly, no $k\in {\bar{N}}_{i_2}^3[N_{i_2}^{r}]$ is a direct neighbour of any $j\in N_{i_3}^r$. That is, if $k\in {\bar{N}}_{i_2}^3[N_{i_2}^{r}]$, then $k\notin N_{j_1}$ for all $j\in N_{i_3}^r$. This observation implies that, for each $k\in {\bar{N}}_{i_2}^3[N_{i_2}^{r}]$, there exists at least one $j\in N_{i_3}^r$ where $N_{k_1}\cap N_{j_1}\subseteq N_{i_2}^{r}$, so that $\alpha _k(N_{i_2}^r)\ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. Secondly, since all players in $N_{i_2}^r$ play strategies in $A^p$ at $t=2$, strategies in $A^p$ are best responses to all $k\in {\bar{N}}_{i_2}^3[N_{i_2}^{r}]$. Players in $N_{i_3}^r$ play strategies in $A^p$ because for each

	$h\in N_{i_3}^r$, $N_{h_1}\cap N_{i_2}\subseteq N_{i_2}^r$, which implies that $\alpha _h(N_{i_2}^r)= \alpha _h(N_{i_2})= \alpha _h(B_{i_2})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_2}^r$ play strategies in $A^p$ at $t=2$, strategies in $A^p$ are best responses to all $h\in N_{i_3}^r$. $\left\{ {\bar{N}}_{i_1}^r\backslash {\bar{N}}_{i_1}^3[N_{i_1}^3]\right\} \cup {\bar{N}}_{i_2}^3\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_2}^{r}]\cup {\bar{N}}_{i_2}^3[N_{i_1}^3]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^3]\right\} \right\} \cup {\bar{N}}_{i_3}^r\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=4$	$i\cup N_{i_1}\cup N_{i_2}^r\cup {\bar{N}}_{i_2}^3[N_{i_2}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^r]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^r]\right\} \cup N_{i_3}\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. Players in $i\cup N_{i_2}^r\cup {\bar{N}}_{i_2}^3[N_{i_2}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^r]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^r]\right\} \cup N_{i_3}\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}$ all play strategies in $A^p$ for the same reasons outlined in $t=2$ and $t=3$ above. To see why all players in $N_{i_1}$ play strategies in $A^p$, first notice that $N_{i_1}^3\cup {\bar{N}}_{i_1}^3[N_{i_1}^3]\cup {\bar{N}}_{i_1}^3[{\bar{N}}_{i_1}^3[N_{i_1}^3]] =N_{i_1}$; and similarly, $N_{i_1}^r\cup {\bar{N}}_{i_1}^r[N_{i_1}^r]\cup {\bar{N}}_{i_1}^r[{\bar{N}}_{i_1}^r[N_{i_1}^r]] =N_{i_1}$. Now, players in $N_{i_1}^3$ play strategies in $A^p$ for the same reasons outlined in $t=2$. Players in ${\bar{N}}_{i_1}^r[N_{i_1}^r]$ play strategies in $A^p$ because, firstly, for each $k\in {\bar{N}}_{i_1}^r[N_{i_1}^r]$, and any $j\in N_{i_2}^r$, we have $N_{k_1}\cap N_{j_1}\subseteq N_{i_1}^r\cup {\bar{N}}_{i_2}^r[N_{i_2}^{r}]$, where ${\bar{N}}_{i_2}^r[N_{i_2}^{r}]\subseteq {\bar{N}}_{i_2}^3[N_{i_2}^{r}]\cup N_{i_2}^{3}\backslash N_{i_2}^{r}$. This implies that for each $k\in {\bar{N}}_{i_1}^r[N_{i_1}^r]$, there exists at least one $j\in N_{i_2}^r$ such that $\alpha _k\left( N_{i_1}^r\cup {\bar{N}}_{i_2}^r[N_{i_2}^{r}]\right) \ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. Secondly, since all players in $N_{i_1}^r\cup {\bar{N}}_{i_2}^r[N_{i_2}^{r}]$ play strategies in $A^p$ at $t=3$, strategies in $A^p$ are best responses to all $k\in {\bar{N}}_{i_1}^r[N_{i_1}^r]$. Players in ${\bar{N}}_{i_1}^3[{\bar{N}}_{i_1}^3[N_{i_1}^{3}]]$ play strategies in $A^p$ because, firstly, each $k\in {\bar{N}}_{i_1}^3[{\bar{N}}_{i_1}^3[N_{i_1}^{3}]]$ is not directly connected to any player in $N_{i_1}^{3}$, but there exists at least one $j\in N_{i_1}^{3}$ where $N_{k_1}\cap N_{j_1}\subseteq {\bar{N}}_{i_1}^3[N_{i_1}^{3}]\cup {\bar{N}}_{i_2}^3[N_{i_1}^{3}]$. This implies that for each $k\in {\bar{N}}_{i_1}^3[{\bar{N}}_{i_1}^3[N_{i_1}^{3}]]$, there exists at least one $j\in N_{i_1}^{3}$ where $\alpha _k\left( {\bar{N}}_{i_1}^3[N_{i_1}^{3}]\cup {\bar{N}}_{i_2}^3[N_{i_1}^{3}]\right) \ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. Secondly, since all players in ${\bar{N}}_{i_1}^3[N_{i_1}^{3}]\cup {\bar{N}}_{i_2}^3[N_{i_1}^{3}]$ play strategies in $A^p$ at $t=3$, strategies in $A^p$ are best responses to all $k\in {\bar{N}}_{i_1}^3[{\bar{N}}_{i_1}^3[N_{i_1}^{3}]]$. Finally, since $N_{i_1}^r\subseteq N_{i_1}^3$ and ${\bar{N}}_{i_1}^r[{\bar{N}}_{i_1}^r[N_{i_1}^{r}]]\subseteq {\bar{N}}_{i_1}^3[{\bar{N}}_{i_1}^3[N_{i_1}^{3}]]\cup N_{i_1}^3\backslash N_{i_1}^r$, it follows that all players in $N_{i_1}^r\cup {\bar{N}}_{i_1}^r[N_{i_1}^r]\cup {\bar{N}}_{i_1}^r[{\bar{N}}_{i_1}^r[N_{i_1}^r]] =N_{i_1}$ play strategies in $A^p$ at $t=4$. ${\bar{N}}_{i_2}^r\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_2}^3]\cup {\bar{N}}_{i_2}^3[N_{i_1}^r]\backslash \left\{ {\bar{N}}_{i_2}^3[N_{i_1}^3]\cap {\bar{N}}_{i_2}^3[N_{i_2}^r]\right\} \right\} \cup N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=5$	$i\cup N_{i_1}\cup N_{i_2}\cup N_{i_3}^r\cup N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Players in $i\cup N_{i_1}\cup N_{i_3}^r\cup N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}$ all play strategies in $A^p$ for the same reasons outlined in $t=2$, $t=3$ and $t=4$ above. Players in $N_{i_2}$ play strategies in $A^p$ because each $k\in N_{i_2}$ has $\alpha _k(B_{i_1})\ge {\underline{\eta }}(G)\ge p$, and that all players in $B_{i_1}=i\cup N_{i_1}$ play strategies in $A^p$ at $t=4$. ${\bar{N}}_{i_3}^r\cup N_{i_5}\cup N_{i_7}\cup N_{i_9}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=6$	$B_{i_1}\cup N_{i_2}\cup N_{i_3}\cup N_{i_5}\cup N_{i_7}\cup N_{i_9}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. $N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup N_{i_{10}}\cup N_{i_{12}}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=7$	$B_{i_4}\cup N_{i_{6}}\cup N_{i_{8}}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. $N_{i_5}\cup N_{i_{7}}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
${-}-$
$t=d_{i}+2$	$B_{i_{d_{i}-1}}\rightarrow A^p$; and $N_{i_{d_{i}}}\rightarrow A$.
$t=d_{i}+3$	$B_{i_{d_{i}}}=N\rightarrow A^p$.

Thus, $n_{i_1}^r$ mutations to strategies in $A^p$ sufficiently trigger an exit from the basin of attraction of $W\in {\mathcal {C}}({\mathbf {A}})$ to ${\mathbf {A}}^p$. Since this holds for all $i\in N$, it follows that ${\underline{n}}_{1}^*\le {\underline{n}}_1^r$ mutations to strategies in $A^p$ also sufficiently trigger an exit from D(W) to ${\mathbf {A}}^p$, so that $C(W,{\mathbf {A}}^p)\le {\underline{n}}_1^*$.

Now, consider again the two configurations ${\mathbf {y}},{\mathbf {z}}\in W\in {\mathcal {C}}({\mathbf {A}})$ defined above, and let ${\mathbf {y}}$ be a subsequent configuration to ${\mathbf {z}}$ so that $P({\mathbf {z}},{\mathbf {y}})=1$. Let (A, U, N, G, P) start from ${\mathbf {z}}$ at $t=0$, and let a subset of players $S_{i_1}^r\subseteq N_{i_1}^r$, for $4\le r\le d_i$, mutate to strategies in $A\backslash A^p$ at $t=1$. Given that $d_i\ge 4$ for all $i\in N$, (A, U, N, G, P) evolves from $t=1$ onward as follows.

$t=1$	$N_{i_1}^3\backslash S_{i_1}^r\cup N_{i_3}\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. $S_{i_1}^r \rightarrow A\backslash A^p$. $i\cup {\bar{N}}_{i_1}^{3}\cup N_{i_2}\cup N_{i_4}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=2$	$N_{i_2}^4\cup N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Players in $N_{i_2}^4$ play strategies in $A^p$ because for each $k\in N_{i_2}^4$, there exists at least one $j\in N_{i_4}$ with $N_{k_1}\cap N_{j_1}\subseteq N_{i_3}^4$, which implies that$\alpha _k(N_{i_3}^4)\ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_3}^4\subseteq N_{i_3}$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_2}^4$. Players in $N_{i_4}$ play strategies in $A^p$ because for each $k\in N_{i_4}$, $\alpha _k(N_{i_3}^4)=\alpha _k(B_{i_3})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_3}^4\subseteq N_{i_3}$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_4}$. $i\cup N_{i_1}\cup {\bar{N}}_{i_2}^4\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$. Players in $N_{i_1}$, including players in $S_{i_1}^r$, play strategies in A because they are surrounded by direct neighbours in $i\cup S_{i_1}^r\cup {\bar{N}}_{i_1}^3\cup N_{i_2}$ that all play strategies in A at $t=1$. Similarly, there is no guarantee that players in ${\bar{N}}_{i_2}^4$, or even players in $N_{i_2}^3\backslash N_{i_2}^4$, will play strategies in $A^p$. For example, all players in ${\bar{N}}_{i_2}^4[N_{i_1}^4]$ play strategies in A because, although all their direct neighbours in $N_{i_3}\cup N_{i_1}^3\backslash N_{i_1}^4$ play strategies in $A^p$ at $t=1$, all their direct neighbours in $N_{i_1}^4$ play strategies in $A\backslash A^p$.
$t=3$	$N_{i_1}^4\cup N_{i_3}^4\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. Players in $N_{i_1}^4$ play strategies in $A^p$ because for each $k\in N_{i_1}^4$, there exists at least one $j\in N_{i_3}^4$ with $N_{k_1}\cap N_{j_1}\subseteq N_{i_2}^4$, which implies that $\alpha _k(N_{i_2}^4)\ge \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_2}^4$ play strategies in $A^p$ at $t=2$, strategies in $A^p$ are best responses to all $k\in N_{i_1}^4$. All $k\in N_{i_3}^4$ play strategies in $A^p$ because each has $\alpha _k(N_{i_2}^4)=\alpha _k(B_{i_2})\ge {\underline{\eta }}(G)\ge p$, and that all players in $N_{i_2}^4$ play strategies in $A^p$ at $t=2$. $i\cup {\bar{N}}_{i_1}^{4}\cup N_{i_2}\cup {\bar{N}}_{i_3}^4\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=4$	$i\cup N_{i_2}^4\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Player i plays a strategy in $A^p$ because for each $k\in N_{i_2}^4$, $N_{k_1}\cap N_{i_1}\subseteq N_{i_1}^4$, which implies that, for any $k\in N_{i_2}^4$, $\alpha _i(N_{i_1}^4)\ge \alpha _i(B_{k_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^4$ play strategies in $A^p$ at $t=1$, a strategy in $A^p$ must be a best response to player i. All $k\in N_{i_2}^4$ play strategies in $A^p$ because each has $\alpha _k(N_{i_1}^4)=\alpha _k(B_{i_1})\ge {\underline{\eta }}(G)\ge p$, and that all players in $N_{i_1}^4$ play strategies in $A^p$ at $t=3$. $N_{i_1}\cup {\bar{N}}_{i_2}^4\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=5$	$N_{i_1}^4\cup N_{i_3}^4\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. $i\cup {\bar{N}}_{i_1}^{4}\cup N_{i_2}\cup {\bar{N}}_{i_3}^4\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.

Thus, if (A, U, N, G, P) exits the basin of attraction of W after less or equal to ${\underline{n}}_{1}^{*}$ mutations (i.e., after a subset of players in $N_{i_1}^r$, for any $i\in N$, mutate) to strategies in $A\backslash A^p$, then it converges to an absorbing cycle, $W^\prime \in {\mathcal {C}}({\mathbf {A}}^p)$, where players in $N_{i_1}^{4}\cup N_{i_3}^4\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ and $i\cup N_{i_2}^{4}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ alternate between strategies in $A^p$ and some strategies in A, and the rest play some strategies in A. Depending on the network structure (e.g., when $N_{i_1}^{3}=N_{i_1}^{4}$, $N_{i_2}^{3}=N_{i_2}^{4}$ and $N_{i_3}=N_{i_3}^{4}$), it is also possible that (A, U, N, G, P) will revert to $W\in {\mathcal {C}}({\mathbf {A}}^p)$, an absorbing cycle where players in $N_{i_1}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ and $i\cup N_{i_2}^{3}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ alternate between strategies in $A^p$ and some strategies in A, in which case $R(W)=C(W,{\mathbf {A}}^p)$ (see the above discussion).

Now, let ${\mathbf {u}},{\mathbf {v}}\in W^\prime \in {\mathcal {C}}({\mathbf {A}}^p)$, with $P({\mathbf {u}},{\mathbf {v}})=1$, be two subsequent configurations where ${\mathbf {u}}$ consist of all players in $N_{i_1}^{4}\cup N_{i_3}^4\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ playing strategies in $A^p$, and all players in $i\cup {\bar{N}}_{i_1}^{4}\cup N_{i_2}\cup {\bar{N}}_{i_3}^{4}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ play strategies in A; and configuration ${\mathbf {v}}$ consists of all players in $i\cup N_{i_2}^{4}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ playing strategies in $A^p$, while all players in $N_{i_1}\cup {\bar{N}}_{i_2}^{4}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ play strategies in A. Let (A, U, N, G, P) start from ${\mathbf {u}}$, and let all players in $N_{i_1}^4$, mutate to strategies in $A^p$ at $t=1$. Then (A, U, N, G, P) evolves from $t=1$ onward as follows:

$t=1$

$i\cup N_{i_1}^4\cup N_{i_2}^{4}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$; ${\bar{N}}_{i_1}^{4}\cup {\bar{N}}_{i_2}^{4}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.

$t=2$

$i\cup N_{i_1}^4\cup N_{i_2}^4\cup N_{i_3}^4\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. Player i plays a strategy in $A^p$ because for each $k\in N_{i_2}^4$, $N_{k_1}\cap N_{i_1}\subseteq N_{i_1}^4$, which implies that, for any $k\in N_{i_2}^4$, $\alpha _i(N_{i_1}^4)\ge \alpha _i(N_{k_1})= \alpha _i(B_{k_1})\ge \min _{l\in N_{k_2}}\alpha _l(B_{k_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^4$ play strategies in $A^p$ at $t=1$, a strategy in $A^p$ must be a best response to player i. Players in $N_{i_1}^4$ play strategies in $A^p$ because for each $k\in N_{i_1}^4$, there exists at least one $j\in N_{i_3}^4$ with $N_{k_1}\cap N_{j_1}\subseteq N_{i_2}^4$, which implies that $\alpha _k(N_{i_2}^4)\ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_2}^4$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_1}^4$. Players in $N_{i_2}^4$ play strategies in $A^p$ because for each $k\in N_{i_2}^4$, $N_{k_1}\cap N_{i_1}\subseteq N_{i_1}^4$, which implies that $\alpha _k(N_{i_1}^4)= \alpha _k(N_{i_1})= \alpha _k(B_{i_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^4$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_2}^4$. Similarly, players in $N_{i_3}^4$ play strategies in $A^p$ because for each $k\in N_{i_3}^4$, $N_{k_1}\cap N_{i_2}\subseteq N_{i_2}^4$, which implies that $\alpha _k(N_{i_2}^4)= \alpha _k(B_{i_2})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_2}^4$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_3}^4$. Players in $N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}$ play strategies in $A^p$ because each $l\in N_{i_r}$, for $r=5,7,\ldots ,d_i$, has $\alpha _l(N_{i_{r-1}})=\alpha _l(B_{i_{r-1}})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_{r-1}}$, for all $r=5,7,\ldots ,d_i$, play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all players in $N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}$. ${\bar{N}}_{i_1}^4\cup {\bar{N}}_{i_2}^4\cup {\bar{N}}_{i_3}^4\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.

$t=3$	$i\cup N_{i_1}^4\cup N_{i_2}^4\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Players in $i\cup N_{i_1}^4\cup N_{i_2}^4\cup N_{i_3}^4\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ play strategies in $A^p$ for the same reasons outlined in $t=2$. To see why players in ${\bar{N}}_{i_3}^4[N_{i_3}^{4}]$ play strategies in $A^p$, first observe that no $k\in {\bar{N}}_{i_3}^4[N_{i_3}^{4}]$ is a direct neighbour of any $j\in N_{i_4}$. This observation implies that, for each $k\in {\bar{N}}_{i_3}^4[N_{i_3}^{4}]$, there exists at least one $j\in N_{i_4}$ where $N_{k_1}\cap N_{j_1}\subseteq N_{i_3}^{4}$, so that $\alpha _k(N_{i_3}^4)\ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. Secondly, since all players in $N_{i_3}^4$ play strategies in $A^p$ at $t=2$, strategies in $A^p$ are best responses to all $k\in {\bar{N}}_{i_3}^4[N_{i_3}^{4}]$. Similarly, players in $N_{i_4}$ all play strategies in $A^p$ because for each $k\in N_{i_4}$, $N_{k_1}\cap N_{i_3}\subseteq N_{i_3}^4$, which implies that $\alpha _h(N_{i_3}^4)= \alpha _h(B_{i_3})\ge {\underline{\eta }}(G)\ge p$. ${\bar{N}}_{i_1}^{4}\cup {\bar{N}}_{i_2}^{4}\cup \left\{ {\bar{N}}_{i_3}^{4}\backslash {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\right\} \cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=4$	$i\cup N_{i_1}^4\cup N_{i_2}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup N_{i_4}\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. Players in $i\cup N_{i_1}^4\cup N_{i_2}^4\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup N_{i_4}\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}$ play strategies in $A^p$ for the same reasons outlined in $t=2$ and $t=3$. Players in ${\bar{N}}_{i_2}^4[N_{i_2}^4]$ and ${\bar{N}}_{i_3}^4[N_{i_2}^4]\backslash \left\{ {\bar{N}}_{i_3}^4[N_{i_2}^4]\cap {\bar{N}}_{i_3}^4[N_{i_3}^4]\right\}$ play strategies in $A^p$ because for each $k\in {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup {\bar{N}}_{i_3}^4[N_{i_2}^4]\backslash \left\{ {\bar{N}}_{i_3}^4[N_{i_2}^4]\cap {\bar{N}}_{i_3}^4[N_{i_3}^4]\right\}$, there exists at least one $j\in N_{i_3}^4$ with $N_{k_1}\cap N_{j_1}\ne \emptyset$. For any $j\in N_{i_3}^4$ satisfying the preceding property, $N_{k_1}\cap N_{j_1}\subseteq N_{i_2}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^4]$, which implies that $\alpha _k\left( N_{i_2}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^4]\right) \ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_2}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^4]$ play strategies in $A^p$ at $t=3$, strategies in $A^p$ are best responses to all players in ${\bar{N}}_{i_2}^4[N_{i_2}^4]$ and ${\bar{N}}_{i_3}^4[N_{i_2}^4]\backslash \left\{ {\bar{N}}_{i_3}^4[N_{i_2}^4]\cap {\bar{N}}_{i_3}^4[N_{i_3}^4]\right\}$. ${\bar{N}}_{i_1}^4\cup \left\{ {\bar{N}}_{i_2}^4\backslash {\bar{N}}_{i_2}^4[N_{i_2}^4]\right\} \cup \left\{ {\bar{N}}_{i_3}^4\backslash \left\{ {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup {\bar{N}}_{i_3}^4[N_{i_3}^4]\right\} \right\} \cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=5$	$i\cup N_{i_1}^4\cup {\bar{N}}_{i_1}^4[N_{i_1}^4]\cup N_{i_2}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup {\bar{N}}_{i_2}^4[N_{i_1}^4]\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup N_{i_4}\cup N_{i_5}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Players in $i\cup N_{i_1}^4\cup N_{i_2}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup N_{i_4}\cup N_{i_5}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}$ play strategies in $A^p$ for the same reasons outlined in $t=2$, $t=3$ and $t=4$. Players in ${\bar{N}}_{i_1}^4[N_{i_1}^4]$ and ${\bar{N}}_{i_2}^4[N_{i_1}^4]\backslash \left\{ {\bar{N}}_{i_2}^4[N_{i_1}^4]\cap {\bar{N}}_{i_2}^4[N_{i_2}^4]\right\}$ play strategies in $A^p$ because for each $k\in {\bar{N}}_{i_1}^4[N_{i_1}^4]\cup {\bar{N}}_{i_2}^4[N_{i_1}^4]\backslash \left\{ {\bar{N}}_{i_2}^4[N_{i_1}^4]\cap {\bar{N}}_{i_2}^4[N_{i_2}^4]\right\}$, there exists at least one $j\in N_{i_2}^4$ with $N_{k_1}\cap N_{j_1}\ne \emptyset$. For any $j\in N_{i_2}^4$ satisfying the preceding property, $N_{k_1}\cap N_{j_1}\subseteq N_{i_1}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]$, which implies that $\alpha _k\left( N_{i_1}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]\right) \ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]$ play strategies in $A^p$ at $t=3$, strategies in $A^p$ are best responses to all players in ${\bar{N}}_{i_1}^4[N_{i_1}^4]$ and ${\bar{N}}_{i_2}^4[N_{i_1}^4]\backslash \left\{ {\bar{N}}_{i_2}^4[N_{i_1}^4]\cap {\bar{N}}_{i_2}^4[N_{i_2}^4]\right\}$. $\left\{ {\bar{N}}_{i_1}^4\backslash {\bar{N}}_{i_1}^4[N_{i_1}^4]\right\} \cup \left\{ {\bar{N}}_{i_2}^4 \backslash \left\{ {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup {\bar{N}}_{i_2}^4[N_{i_1}^4]\right\} \right\} \cup \left\{ {\bar{N}}_{i_3}^4\backslash \left\{ {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup {\bar{N}}_{i_3}^4[N_{i_3}^4]\right\} \right\} \cup N_{i_7}\cup N_{i_9}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=6$	$i\cup N_{i_1}\cup N_{i_2}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup {\bar{N}}_{i_2}^4[N_{i_1}^4]\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup N_{i_4}\cup N_{i_5}\cup N_{i_6}\cup N_{i_7}\cup N_{i_9}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. Players in $i\cup N_{i_2}^4\cup {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup {\bar{N}}_{i_2}^4[N_{i_1}^4]\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup N_{i_4}\cup N_{i_5}\cup N_{i_6}\cup N_{i_7}\cup N_{i_9}\cup \ldots \cup N_{i_{d_{i}}}$ play strategies in $A^p$ for the same reasons outlined in $t=2$, $t=3$, $t=4$ and $t=5$. To see why players in $N_{i_1}$

	all play strategies in $A^p$, first recall that $N_{i_1}=N_{i_1}^4\cup {\bar{N}}_{i_1}^4[N_{i_1}^4]\cup {\bar{N}}_{i_1}^4[{\bar{N}}_{i_1}^4[N_{i_1}^4]]$. Players in $N_{i_1}^4\cup {\bar{N}}_{i_1}^4[N_{i_1}^4]$ play strategies in $A^p$ for the same reasons outlined in $t=5$. Players in ${\bar{N}}_{i_1}^4[{\bar{N}}_{i_1}^4[N_{i_1}^4]]$ play strategies in $A^p$ because, firstly, each $k\in {\bar{N}}_{i_1}^4[{\bar{N}}_{i_1}^4[N_{i_1}^{4}]]$ is not directly connected to any player in $N_{i_1}^{4}$, but there exists at least one $j\in N_{i_1}^{4}$ where $N_{k_1}\cap N_{j_1}\subseteq {\bar{N}}_{i_1}^4[N_{i_1}^{4}]\cup {\bar{N}}_{i_2}^4[N_{i_1}^{4}]$. This implies that for each $k\in {\bar{N}}_{i_1}^4[{\bar{N}}_{i_1}^4[N_{i_1}^{4}]]$, there exists at least one $j\in N_{i_1}^{4}$ where $\alpha _k\left( {\bar{N}}_{i_1}^4[N_{i_1}^{4}]\cup {\bar{N}}_{i_2}^4[N_{i_1}^{4}]\right) \ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. Secondly, since all players in ${\bar{N}}_{i_1}^4[N_{i_1}^{4}]\cup {\bar{N}}_{i_2}^4[N_{i_1}^{4}]$ play strategies in $A^p$ at $t=5$, strategies in $A^p$ are best responses to all $k\in {\bar{N}}_{i_1}^4[{\bar{N}}_{i_1}^4[N_{i_1}^{4}]]$. $\left\{ {\bar{N}}_{i_2}^4\backslash \left\{ {\bar{N}}_{i_2}^4[N_{i_2}^4]\cup {\bar{N}}_{i_2}^4[N_{i_1}^4]\right\} \right\} \cup \left\{ {\bar{N}}_{i_3}^4\backslash \left\{ {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup {\bar{N}}_{i_3}^4[N_{i_3}^4]\right\} \right\} \cup N_{i_8}\cup N_{i_{10}}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=7$	$i\cup N_{i_1}\cup N_{i_2}\cup N_{i_3}^4\cup {\bar{N}}_{i_3}^4[N_{i_3}^{4}]\cup {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup N_{i_4}\cup N_{i_5}\cup N_{i_6}\cup N_{i_7}\cup N_{i_8}\cup N_{i_{10}}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$, where players in $N_{i_2}$ all play strategies in $A^p$ because for each $k\in N_{i_2}$, $\alpha _k(B_{i_1})\ge {\underline{\eta }}(G)\ge p$, and that all players in $B_{i_1}$ play strategies in $A^p$ at $t=6$. $\left\{ {\bar{N}}_{i_3}^4\backslash \left\{ {\bar{N}}_{i_3}^4[N_{i_2}^4]\cup {\bar{N}}_{i_3}^4[N_{i_3}^4]\right\} \right\} \cup N_{i_9}\cup N_{i_{11}}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=8$	$B_{i_2}\cup N_{i_3}\cup N_{i_4}\cup N_{i_5}\cup N_{i_6}\cup N_{i_7}\cup N_{i_8}\cup N_{i_9}\cup N_{i_{11}}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$, where players in $N_{i_3}$ all play strategies in $A^p$ because for each $k\in N_{i_3}$, $\alpha _k(B_{i_2})\ge {\underline{\eta }}(G)\ge p$, and that all players in $B_{i_2}$ play strategies in $A^p$ at $t=7$. $N_{i_{10}}\cup N_{i_{12}}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=9$	$B_{i_{10}}\cup N_{i_{12}}\cup N_{i_{14}}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. $N_{i_{11}}\cup N_{i_{13}}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
${-}-$
$t=d_{i}-2$	$B_{i_{d_{i}-1}}\rightarrow A^p$; and $N_{i_{d_{i}}}\rightarrow A$.
$t=d_{i}-1$	$B_{i_{d_{i}}}=N\rightarrow A^p$.

Thus, ${\underline{n}}_{1}^4$ mutations to strategies in $A^p$ sufficiently trigger an exit from the basin of attraction of $W^\prime$ to ${\mathbf {A}}^p$, so that $C(W^\prime ,{\mathbf {A}}^p)\le {\underline{n}}_{1}^4$. However, as we demonstrated in the dynamics of (A, U, N, G, P) from W to $W^\prime$ above, if, starting from $W^\prime$, ${\underline{n}}_{1}^4$ players mutate to strategies in $A\backslash A^p$, (A, U, N, G, P) will revert to $W^\prime$. Specifically, let (A, U, N, G, P) start from ${\mathbf {v}}$ at $t=0$, and let all players in $N_{i_1}^4$ mutate to strategies in $A\backslash A^p$ at $t=1$.³³ Given that $d_i\ge 4$ for all $i\in N$, (A, U, N, G, P) evolves from $t=1$ onward as follows.

$t=1$

$N_{i_3}^4\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. $i\cup N_{i_1}\cup N_{i_2}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.

$t=2$

$N_{i_2}^4\cup N_{i_4}\cup N_{i_6}\cup N_{i_8}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Players in $N_{i_2}^4$ play strategies in $A^p$ because for each $k\in N_{i_2}^4$, there exists at least one $j\in N_{i_4}$ with $N_{k_1}\cap N_{j_1}\subseteq N_{i_3}^4$, which implies that $\alpha _k(N_{i_3}^4)\ge \alpha _k(N_{j_1})= \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_3}^4\subseteq N_{i_3}$ play strategies in $A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_2}^4$. Players in $N_{i_4}$ play strategies in $A^p$ because for each $k\in N_{i_4}$, $\alpha _k(N_{i_3}^4)=\alpha _k(B_{i_3})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_3}^4\subseteq N_{i_3}$ play strategies in

	$A^p$ at $t=1$, strategies in $A^p$ are best responses to all $k\in N_{i_4}$. $i\cup N_{i_1}\cup {\bar{N}}_{i_2}^4\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=3$	$N_{i_1}^4\cup N_{i_3}^4\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. Players in $N_{i_1}^4$ play strategies in $A^p$ because for each $k\in N_{i_1}^4$, there exists at least one $j\in N_{i_3}^4$ with $N_{k_1}\cap N_{j_1}\subseteq N_{i_2}^4$, which implies that $\alpha _k(N_{i_2}^4)\ge \alpha _k(B_{j_1})\ge \min _{l\in N_{j_2}}\alpha _l(B_{j_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_2}^4$ play strategies in $A^p$ at $t=2$, strategies in $A^p$ are best responses to all $k\in N_{i_1}^4$. All $k\in N_{i_3}^4$ play strategies in $A^p$ because each has $\alpha _k(N_{i_2}^4)=\alpha _k(B_{i_2})\ge {\underline{\eta }}(G)\ge p$, and that all players in $N_{i_2}^4$ play strategies in $A^p$ at $t=2$. $i\cup {\bar{N}}_{i_1}^{4}\cup N_{i_2}\cup {\bar{N}}_{i_3}^4\cup N_{i_4} \cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.
$t=4$	$i\cup N_{i_2}^4\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A^p$. Player i plays a strategy in $A^p$ because for each $k\in N_{i_2}^4$, $N_{k_1}\cap N_{i_1}\subseteq N_{i_1}^4$, which implies that, for any $k\in N_{i_2}^4$, $\alpha _i(N_{i_1}^4)\ge \alpha _i(B_{k_1})\ge {\underline{\eta }}(G)\ge p$. And since all players in $N_{i_1}^4$ play strategies in $A^p$ at $t=1$, a strategy in $A^p$ must be a best response to player i. All $k\in N_{i_2}^4$ play strategies in $A^p$ because each has $\alpha _k(N_{i_1}^4)=\alpha _k(B_{i_1})\ge {\underline{\eta }}(G)\ge p$, and that all players in $N_{i_1}^4$ play strategies in $A^p$ at $t=3$. $N_{i_1}\cup {\bar{N}}_{i_2}^4\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A$.
$t=5$	$N_{i_1}^4\cup N_{i_3}^4\cup N_{i_5}\cup N_{i_7}\cup \ldots \cup N_{i_{d_{i}}}\rightarrow A^p$. $i\cup {\bar{N}}_{i_1}^{4}\cup N_{i_2}\cup {\bar{N}}_{i_3}^4\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}\rightarrow A$.

Thus, $n_{i_1}^4\ge {\underline{n}}_1^4$, for any $i\in N$, mutations to strategies in $A\backslash A^p$ are not sufficient to trigger an exit from the basin of attraction of $W^\prime$. This implies that $R(W^\prime )=C(W^\prime ,{\mathbf {A}}^p)\le {\underline{n}}_1^4$.

Putting the above three scenarios together, we see that, for any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$, ${\underline{b}}_1$ mutations can trigger evolution from ${\mathbf {x}}$ to ${\mathbf {A}}^p$ so that $C({\mathbf {x}},{\mathbf {A}}^p)\le {\underline{b}}_1$. Otherwise, there exists at least one absorbing cycle $W\in {\mathcal {C}}({\mathbf {A}})$, with $C({\mathbf {x}},W)\le {\underline{b}}_1$, where players in $N_{i_1}^{3}\cup N_{i_3}\cup N_{i_5}\cup \ldots \cup N_{i_{d_{i}}}$ and $i\cup N_{i_2}^{3}\cup N_{i_4}\cup N_{i_6}\cup \ldots \cup N_{i_{d_{i}-1}}$ alternate between strategies in $A^p$ and some strategies in A, and the rest play some strategies in A. For this scenario, the number of mutations to strategies in $A^p$ that trigger evolution from W to ${\mathbf {A}}^p$ is less or equal to ${\underline{n}}_1^*$, so that if the number of mutations to strategies in $A\backslash A^p$ needed to trigger an exit from D(W) is greater than ${\underline{n}}_1^*$, then $R(W)=C(W,{\mathbf {A}}^p)$. However, if the number of mutations to strategies in $A\backslash A^p$ needed to trigger an exit from the basin of attraction of W is less or equal to ${\underline{n}}_1^*$, then there exists another absorbing cycle $W^\prime \in {\mathcal {C}}({\mathbf {A}})$ and $W^\prime \ne W$, where $R(W)=C(W,W^\prime )\le {\underline{n}}_1^*$, and $R(W^\prime )=C(W^\prime ,{\mathbf {A}}^p)\le {\underline{n}}_1^4$. Since these three scenarios hold for any ${\mathbf {x}}\notin D({\mathbf {A}}^p)$, it follows from the discussion in Sect. 4, together with Eqs. (9) and (10), that $CR({\mathbf {A}}^p)\le {\underline{b}}_1$ and

$$\begin{aligned} CR^*({\mathbf {A}}^p)=\max _{{\mathbf {x}}\notin D({\mathbf {A}}^p)}C^*({\mathbf {x}},{\mathbf {A}}^p) = \max _{{\mathbf {x}}\notin D({\mathbf {A}}^p)}\min _{W\in {\mathcal {C}}({\mathbf {A}})}C({\mathbf {x}},W)\le {\underline{b}}_1. \end{aligned}$$

The lower bound of the radius of ${\mathbf {A}}^p$

We now show that when $p\le {\underline{\eta }}(G)$ and $d(G)\ge 7$, the radius of ${\mathbf {A}}^p$ is bounded from below by $R({\mathbf {A}}^p)\ge {\underline{b}}_1+\iota$, where $\iota \ge 1$ is some positive integer. Specifically, for an undirected, unweighted and strongly connected network G with $d(G)\ge 7$, which also means that $d_i\ge 4$ for all $i\in N$, if $p\le {\underline{\eta }}(G)$, then ${\underline{b}}_1$ mutations to strategies in $A\backslash A^p$ cannot trigger an exit from $D({\mathbf {A}}^p)$.

We first show that if (A, U, N, G, P) starts, at $t=0$, from any configuration, ${\mathbf {x}}\notin D({\mathbf {A}}^p)$, where all players in $B_{i_2}$ of any $i\in N$ play strategies in $A^p$, then it will converge to ${\mathbf {A}}^p$. Indeed, since, by definition of the contagion threshold, each $h\in B_{i_2}\cup N_{i_3}$ has $\alpha _h(B_{i_2})\ge {\underline{\eta }}(G)\ge p$ (i.e. each $h\in B_{i_2}\cup N_{i_3}$ has at least ${\underline{\eta }}(G)\ge p$ of her direct neighbours within $B_{i_2}$), and all players in $B_{i_1}$ have all their direct neighbours within $B_{i_2}$, it follows that all players in $B_{i_3}$ will play strategies in $A^p$ from $t=2$ onward. From $t=3$ onward, all players in $B_{i_4}$ play strategies in $A^p$ because each $h\in B_{i_3}\cup N_{i_4}$ has $\alpha _h(B_{i_3})\ge {\underline{\eta }}(G)\ge p$. This iterative process continues until $t=d_i-1$ when all players in $B_{i_{d_i}}=N$ play strategies in $A^p$ because each $h\in B_{i_{d_i-1}}\cup N_{i_{d_i}}$ has $\alpha _h(B_{i_{d_i-1}})\ge {\underline{\eta }}(G)\ge p$.

Now, for any $i\in N$, if $d_i\ge 4$, then for all $j\in N_{i_4}\cup N_{i_5}\cup \ldots \cup N_{i_{d_i}}$, we have $B_{j_2}\cap B_{i_1}=\emptyset$ (i.e. there is no overlap between the first-neighbourhood of i and the second-neighbourhood of j). This implies that, if (A, U, N, G, P) starts from any ${\mathbf {x}}\in {\mathbf {A}}^p$ at $t=0$, and all players in $B_{i_1}$ mutate to strategies in $A\backslash A^p$ at $t=1$, then (A, U, N, G, P) will revert to ${\mathbf {A}}^p$ (i.e. converge to some state within ${\mathbf {A}}^p$) because: firstly, there exists at least one player $j\in N_{i_4}\cup N_{i_5}\cup \ldots \cup N_{i_{d_i}}$ for whom all players in $B_{j_2}$ play strategies in $A^p$ at $t=1$; secondly, (A, U, N, G, P) converges to ${\mathbf {A}}^p$ from any configuration ${\mathbf {x}}\notin D({\mathbf {A}}^p)$ where all players in $B_{j_2}$ of any $j\in N$ play strategies in $A^p$.

Thus, when ${\underline{\eta }}(G)\ge p$ and $d(G)\ge 7$, more than $b_{i_1}$ mutations are required to trigger an exit from the basin of attraction of ${\mathbf {A}}^p$. Since this holds for all $i\in N$, it follows that $R({\mathbf {A}}^p)\ge {\underline{b}}_1+\iota$, for $\iota \ge 1$.

Stochastically stable set of states/strategies

Putting the above results together, we see that, for an undirected, unweighted and strongly connected network with $d(G)\ge 7$, if $p\le {\underline{\eta }}(G)$, then $CR^*({\mathbf {A}}^p)\le {\underline{b}}_ 1$ and $R({\mathbf {A}}^p)\ge b_{i_1}+\iota$, for $\iota \ge 1$, which implies that $R({\mathbf {A}}^p)>CR^*({\mathbf {A}}^p)$, and hence, ${\mathbf {A}}^p$, and strategies in $A^p$, are uniquely stochastically stable.