1 Introduction

Although hydrogen embrittlement is a well-known phenomenon, it still remains a significant problem in solid mechanics. Sometimes, even small concentrations of hydrogen in metal parts operating under extreme loads and in corrosive environments can lead to a decrease in strength followed by fracture and premature failure of structural elements [41, 45, 70]. In particular, this problem is very acute in oil and gas production, since hydrogen and its compounds are included in the oil products pumped through the pipelines [44]. Thus, the processes taking place inside metal parts during their use must be understood. In particular, the distribution of hydrogen must be known, since high local concentrations can lead to fracture [40].

As a rule, the effect of hydrogen on the properties of structural materials is examined by the use of the artificial saturation of these materials. In most cases, it is believed that several tens of hours is enough for uniform charging, but the uniformity of the concentration distribution at standardized charging with hydrogen is usually not checked [5]. However, according to direct measurements, there is a significant excess of hydrogen within a thin boundary layer of metal parts [5, 49, 54, 59, 68]. The experiments described in [4, 5, 59] showed that standard hydrogen saturation of cylindrical specimens in an electrolyte for 96 h results in an extremely nonuniform distribution of hydrogen across the specimen. In fact, what is saturated is only a thin surface layer with a thickness of the order of the characteristic grain size. Similar results were obtained on the basis of cathodic hydrogen charging [33, 49, 68], where a uniform distribution of hydrogen was obtained only after 500 h of saturation, that is, several times greater than the average duration of the cathodic hydrogen charging used in experiments. Highly nonuniform distribution of hydrogen within specimens was also observed in fatigue tests with non-hydrogen-charged specimens in air environment [11, 12]. The distribution of hydrogen was found to be nonuniform even in the absence of external loading, although the skin effect was not so obvious as in case of the artificial saturation.

The nonuniform distribution of hydrogen after charging the specimens can be explained by two types of hydrogen simultaneously present in the material, namely the diffusible hydrogen and the trapped hydrogen attached to microstructural inhomogeneities [33, 54, 69]. In contrast to the diffusible hydrogen, evenly distributed in the charged specimen, the trapped hydrogen is mainly located within a subsurface region of the specimen that contains vacancies [33]. Indeed, the lateral surfaces of specimens are known to be covered with crystal lattice defects leading to microcracks formation [13, 43, 63]. A detailed examination of the surface layer of a uniform monocrystal shows that its grains or particles rotate and create voids near the boundary [63]. According to [57], there is a wide range of atomic configurations and a large number of vacancies occurring in a surface layer of the material followed by weakening of interatomic interactions. From this point of view, the surface layer in a deformed solid can be considered as an independent subsystem [56, 57].

Numerous investigations indicate a strong coupling between diffusion and stress–strain state of the material [1, 15, 32, 47, 67]. According to [33], amount of the trapped hydrogen strongly increases with the applied strain. In [15, 32, 47], it was shown that mechanical stresses lead to the redistribution of the internal dissolved hydrogen. All these models assume the presence of mechanical stresses in the metal caused by the external tensile or cycling loading.

The stress field can be changed directly by hydrogen [14, 58]. A coupled problem involving a system of equations of the gradient-tensor type was solved in [62]. Here, correlations between the hydrogen concentration and the relative volume expansion (dilatation) of the metal and hydrostatic pressure were established, resulting in a nonuniform distribution of hydrogen. A bi-continual model considering the mutual influence of dissolved hydrogen and mechanical stresses was concerned in [59]. The first continuum represented the elastic medium, whereas the second continuum was the hydrogen of both types, namely the mobile hydrogen and the trapped hydrogen. The analytical solution describing the localization of hydrogen in the form of exponential decrease in hydrogen concentration from the border was obtained. Note that in both models only inner stresses due to hydrogen pressure were considered.

To take into account the inner stresses occurring due to the structural heterogeneity of the material, one can introduce an intrinsic length scale parameter characterizing the thickness of the boundary layer with a structure differing from the bulk material. This makes us go beyond classical elasticity, which does not deal with length scales. Various generalized continuum theories, such as the strain gradient theory [3, 7, 18,19,20], micropolar theory [6, 7, 23, 26], and surface theory [8, 24], have been successfully applied to a number of different problems with size effect. In particular, the general micropolar continuum theory takes into account couple stress, as well as internal rotational degrees of freedom. Rotation of individual regions caused by grain boundary migration is possible in materials with a large stress gradient and in the presence of substructures with a large number of defects [42].

This paper makes use of the micropolar continuum theory to explain a highly nonuniform stress–strain state of material. The lateral surface is supposed to be traction free and the distributed couple stress assumed to reflect the influence of the structural defects on the boundary. The problem statement makes it possible to explain the structural inhomogeneity by means of the continuum mechanics approach. The distribution of hydrogen is obtained by modeling a stress-induced diffusion following the Fick’s second law. As a result, a thin surface layer containing almost all the additional hydrogen from the environment appears. Thus, we consider internal stresses and strains as the reason of the nonuniform distribution of hydrogen.

In general, theoretical investigations of the stress-induced diffusion are based on the molecular dynamics methods [66] or on the continuum mechanics approach [16]. In the latter case, the mutual influence is due to the dependence of the diffusion coefficient on the local energy or due to the driving force in the diffusion equation [34, 52]. Within the frame of the present paper, the diffusion coefficient is dependent on the strain energy. Such a dependence for a classical theory of continuum mechanics was considered in [31, 51, 52, 64].

2 Basic equations of the linear micropolar continuum

Let us briefly recall the general relations for a micropolar continuum. A detailed description of the main ideas can be found in [2, 21, 24,25,26, 35, 50, 53, 65].

The micropolar theory employs the concept of local microrotation of a point particle, \(\mathbf {\theta }\), as well as classical translation of the particle, \(\mathbf {u}\). We deal with a geometrically linear micropolar continuum. In this case, the linear stretch tensor, \(\mathbf {\epsilon }\), and linear wryness tensor, \(\mathbf {\kappa }\), can be introduced as follows:

$$\begin{aligned} \mathbf {\epsilon }= & {} \nabla \otimes \mathbf {u}+\mathbf {I}\times \mathbf {\theta }, \end{aligned}$$
(1)
$$\begin{aligned} \mathbf {\kappa }= & {} \nabla \otimes \mathbf {\theta }, \end{aligned}$$
(2)

where \(\nabla \) is the gradient operator and \(\mathbf {I}\) is the unit tensor.

In the case of a physically linear micropolar elastic solid, the strain energy density, W, is a quadratic function of the strain measures:

$$\begin{aligned} W=\frac{1}{2}\mathbf {\epsilon }\cdot \cdot ^4{\mathbf {C}}\cdot \cdot \mathbf {\epsilon }+\mathbf {\epsilon }\cdot \cdot ^4{\mathbf {B}}\cdot \cdot \mathbf {\kappa }+\frac{1}{2}\mathbf {\kappa }\cdot \cdot ^4{\mathbf {D}}\cdot \cdot \mathbf {\kappa }, \end{aligned}$$
(3)

where \(^4{\mathbf {C}}\), \(^4{\mathbf {B}}\), and \(^4{\mathbf {D}}\) are the fourth-order tensors of elastic moduli of the micropolar continuum.

For an isotropic material, the tensors of elastic moduli are expressed as

$$\begin{aligned} ^4{\mathbf {C}}= & {} \lambda \mathbf {I}\otimes \mathbf {I}+{\widetilde{\mu }}\mathbf {e}_k\otimes \mathbf {I}\otimes \mathbf {e}_k+\left( {\widetilde{\mu }}+\kappa \right) \mathbf {e}_m\otimes \mathbf {e}_n\otimes \mathbf {e}_m\otimes \mathbf {e}_n, \nonumber \\ ^4{\mathbf {D}}= & {} \beta _1\mathbf {I}\otimes \mathbf {I}+\beta _2\mathbf {e}_k\otimes \mathbf {I}\otimes \mathbf {e}_k+\beta _3\mathbf {e}_m\otimes \mathbf {e}_n\otimes \mathbf {e}_m\otimes \mathbf {e}_n, \nonumber \\ ^4{\mathbf {B}}= & {} 0, \end{aligned}$$
(4)

where \(\lambda \), \({\widetilde{\mu }}\), \(\kappa \) and \(\beta _i\) (\(i=1, 2, 3\)) are independent elastic moduli. Here the Einstein rule of summation over repeated indices is used. Letting the four additional moduli \(\kappa \) and \(\beta _i\) go to zero will simplify the micropolar elasticity model to the classical elasticity model.

The extra moduli can be associated with engineering (technical) constants (Table 1). A comparison of notations used by various authors is given in [17]. The elastic modulus \(\kappa \) quantifies the degree of coupling between macro- and microrotation fields and allows to introduce the coupling number, N, which is a dimensionless measure of the degree of coupling between the translation and rotation fields. The limit value \(N=0\) (\(\kappa =0\)) corresponds to a decoupling of the rotational and translation degrees of freedom. In this case \({\widetilde{\mu }}\) is identical to the classical shear modulus, \(\mu \). The limit value \(N=1\) (\(\kappa \rightarrow \infty \)) corresponds to a micropolar media with constrained rotations, also known as “pseudo-Cosserat continuum” or “couple stress theory.” According to the couple stress theory, the microrotation vector coincides with the macrorotation vector, which is determined by the curl of the displacement field. The elastic moduli \(\beta _2\) and \(\beta _3\) allow to introduce characteristic lengths, \(l_t\) for torsion and \(l_b\) for bending, that reflect the effects of the couple stress. The polar ratio, \(\psi \), represents the ratio between elastic moduli \(\beta _1\), \(\beta _2\) and \(\beta _3\).

Table 1 Engineering constants in micropolar theory by [25, 37, 46]
Full size table

Substitution of Eqs. (4) into Eq. (3) yields

$$\begin{aligned} W= & {} \frac{\lambda }{2}\text {tr}^2(\mathbf {\epsilon })+\frac{{\widetilde{\mu }}}{2}\text {tr}(\mathbf {\epsilon }\cdot \mathbf {\epsilon })+\frac{{\widetilde{\mu }}+\kappa }{2}\text {tr}(\mathbf {\epsilon }\cdot \mathbf {\epsilon }^\top )+\nonumber \\&+\frac{\beta _1}{2}\text {tr}^2(\mathbf {\kappa })+\frac{\beta _2}{2}\text {tr}(\mathbf {\kappa }\cdot \mathbf {\kappa })+\frac{\beta _3}{2}\text {tr}(\mathbf {\kappa }\cdot \mathbf {\kappa }^\top ), \end{aligned}$$
(5)

where \(\text {tr}(\mathbf {A})\) stands for the trace of a second-order tensor \(\mathbf {A}\) and the superscript \(\top \) denotes the transpose.

The constitutive equations for the stress tensor, \(\mathbf {T}\), and couple stress tensor, \(\mathbf {M}\), can be found as the partial derivatives of the scalar-valued function W with respect to the second-order tensors \(\mathbf {\epsilon }\) and \(\mathbf {\kappa }\), respectively:

$$\begin{aligned} \mathbf {T}=\frac{\partial W}{\partial \mathbf {\epsilon }}, \quad \mathbf {M}=\frac{\partial W}{\partial \mathbf {\kappa }}. \end{aligned}$$
(6)

It follows that \(\mathbf {T}\) and \(\mathbf {M}\) can be expressed as

$$\begin{aligned} \mathbf {T}= & {} \lambda \text {tr}(\mathbf {\epsilon })\mathbf {I}+2 \mu \mathbf {\epsilon }^S + \kappa \mathbf {\epsilon }^A, \end{aligned}$$
(7)
$$\begin{aligned} \mathbf {M}= & {} \beta _1 \text {tr}(\mathbf {\kappa })\mathbf {I}+\beta _2 \mathbf {\kappa }^\top + \beta _3\mathbf {\kappa }, \end{aligned}$$
(8)

where \(\mu \) arises from \({\widetilde{\mu }}\) according to Table 1, the superscripts S and A indicate the symmetric and antisymmetric part of a second-order tensor, respectively.

In order to obtain the stress–strain state of the micropolar continuum, we use two equilibrium equations, balances of linear momentum and angular moment, which in the absence of body forces and body couples can be written as

$$\begin{aligned} \nabla \cdot \mathbf {T}= & {} 0, \end{aligned}$$
(9)
$$\begin{aligned} \nabla \cdot \mathbf {M}+\mathbf {T}_\times= & {} 0, \end{aligned}$$
(10)

where \(\left( \mathbf {a}\otimes \mathbf {b}\right) _\times =\mathbf {a}\times \mathbf {b}\).

Finally, the following system of equations for the displacement field and the independent microrotation vector can be obtained:

$$\begin{aligned}&(\lambda +\mu )\nabla \left( \nabla \cdot \mathbf {u}\right) +\mu \triangle \mathbf {u}+\kappa \left( \frac{1}{2}\left( \triangle \mathbf {u}-\left( \nabla \cdot \mathbf {u}\right) \nabla \right) +\mathbf {I}\times \cdot \left( \mathbf {\theta }\otimes \nabla \right) \right) =0, \end{aligned}$$
(11)
$$\begin{aligned}&\beta _1\nabla \left( \nabla \cdot \mathbf {\theta }\right) +\beta _2\nabla \cdot \left( \mathbf {\theta }\nabla \right) +\beta _3\triangle \mathbf {\theta }+\kappa \nabla \times \mathbf {u}-2\kappa \mathbf {\theta }=0, \end{aligned}$$
(12)

where \(\left( \mathbf {a}\otimes \mathbf {b}\right) \times \cdot \left( \mathbf {c}\otimes \mathbf {d}\right) =\left( \mathbf {a}\cdot \mathbf {d}\right) \mathbf {b}\times \mathbf {c}\) and \(\triangle =\nabla \cdot \nabla \) is the Laplacian.

3 Boundary value problem

Consider a circular cylinder of radius \(r_0\) and length L in the cylindrical coordinate system \(\left( r,\varphi ,z\right) \) (Fig. 1). Assuming that the lateral surface of the cylinder is traction free, so

$$\begin{aligned} \left. \mathbf {n}\cdot \mathbf {T}\right| _{r=r_0}=0, \end{aligned}$$
(13)

where \(\mathbf {n}\) is the outward normal to the lateral surface.

Fig. 1
figure 1

Boundary value problem in cylindrical coordinates

Full size image

The introduction of the additional rotational degree of freedom and accounting for the couple stress interaction lead to the necessity to formulate a suitable boundary condition at the surface, which can be static, kinematic or “mixed.” The static boundary condition suggests that the external couples \(\mathbf {M}_0\) are preset on the entire boundary S of the body or on its portion \(S_t\subset S\). The kinematic condition can also be imposed on the entire boundary or on some part of the boundary \(S_u\subset S\) and can be formulated as \(\mathbf {\theta }=\mathbf {\theta }_0\).

Setting the appropriate boundary condition that is consistent with experimental measurements causes technical problems. At the same time, it is known that the lateral surface of a metal detail is covered with a large amount of defects created during the preparation and leading to the surface microcracks appearance. The distributed couple stress may reflect the microcracks appearance and can be considered as the reason of the grains microrotations. To obtain experimental data it is necessary to relate the value of the distributed couple stress with the crack density and find an empirical dependence. The other way is to consider the grains microrotations on the border with respect to the position of the inner grains on the base of the microstructure data. Both of the boundary conditions, namely static and kinematic, are reasonable from mechanical point of view and should not affect the solution qualitatively. Within the frame of the present paper we do not provide any experimental data and use static boundary condition

$$\begin{aligned} \left. \mathbf {n}\cdot \mathbf {M}\right| _{r=r_0}=\mathbf {M}_0. \end{aligned}$$
(14)

In general, \(\mathbf {M}_0\) is a function of z and \(\varphi \). However, for simplicity, we assume that the surface microcracks are uniformly distributed across the surface of the cylinder. Hence, we treat the surface couple tension as constant.

We assume finite displacement and microrotation at the center of the cylinder,

$$\begin{aligned} \left. \mathbf {u}\right| _{r=0} \ll \infty , \qquad \left. \mathbf {\theta }\right| _{r=0}\ll \infty . \end{aligned}$$
(15)

According to the Saint–Venant’s principle, the stress state in a long cylinder loaded at its end faces is practically independent on the distribution of the surface forces acting on the end cross sections [48]. At a certain distance from the end faces the stress state is determined only by the principal force and the principal moment. Thus, the corresponding boundary conditions can be replaced by integral relationships. Since couple stress interactions occurring within the micropolar theory play a role only in the vicinity of the perturbation region [28, 29], let us consider the systems of forces and moments remaining statistically equivalent to zero, so

$$\begin{aligned}&\left. \int \int _S \mathbf {e}_z\cdot \mathbf {T} \mathrm{d}S\right| _{z=0, z=L}=0, \end{aligned}$$
(16)
$$\begin{aligned}&\left. \int \int _S \mathbf {e}_z\cdot \mathbf {M} \mathrm{d}S\right| _{z=0, z=L}=0. \end{aligned}$$
(17)

It is known [28, 29] that the difference between solutions with and without couple stresses depends on the characteristic lengths. The greater \(l_b\) and \(l_t\), the greater the difference. Generally, the characteristic lengths are small in comparison with the specimen dimensions, and the micropolar solution can be considered as a correction term to the classical solution to make sure it satisfies the additional boundary condition (14). Thus, the asymptotic behavior of the additional term can be assumed. The asymptotic expansion technique by introducing a boundary layer is commonly used in static and dynamic theories of micropolar bars, plates and shells [22, 60]. This technique considers asymptotic expansions in terms of the thickness of the solid and allows to suggest a rapid decay of function f, so the following conditions hold:

$$\begin{aligned} \frac{\partial ^2f}{\partial r^2}\gg \frac{\partial f}{\partial r}\gg f. \end{aligned}$$
(18)

On the basis of similarities between the micropolar theory and theories of plates and shells, we will use the assumptions (18) and take into account the smallness of the characteristic length to deal with the asymptotic solution for the boundary layer.

Since the zero displacement field satisfies the equilibrium conditions and guarantees a traction-free lateral surface, we only deal with the solution that describes the stress–strain state near the boundary. As long as solution for the boundary layer only changes along the radial direction due to additional external loading, we seek a solution to the equations of equilibrium (11) and (12) that has the form

$$\begin{aligned} \mathbf {u}= & {} \mathbf {u}\left( r\right) =u_r\left( r\right) \mathbf {e}_r+u_z\left( r\right) \mathbf {e}_z, \end{aligned}$$
(19)
$$\begin{aligned} \mathbf {\theta }= & {} \mathbf {\theta }\left( r\right) =\theta _r\left( r\right) \mathbf {e}_r+\theta _\varphi \left( r\right) \mathbf {e}_\varphi +\theta _z\left( r\right) \mathbf {e}_z, \end{aligned}$$
(20)

where \(\mathbf {e}_r\), \(\mathbf {e}_\varphi \) and \(\mathbf {e}_z\) are unit basis vectors.

According to the linear theory, an additional external loading can be added at the end faces of the cylinder. Then, the total solution is the sum of the two individual solutions. One of them corresponds to the load at the ends of the cylinder and describes the stress–strain state inside the body, while the other comes in action only within a thin surface layer and provides correction to ensure that the boundary condition, that is, distributed couple stress on the lateral surface is satisfied. The first term can be obtained by means of classical theory of elasticity, whereas the second one is determined by couple stress interactions and can be obtained only using a micropolar theory.

Thus, up to terms of the same order of smallness, Eqs. (11) and (12) become

$$\begin{aligned} \left( \lambda +2\mu \right) \frac{\partial ^2 u_r}{\partial r^2}= & {} 0, \nonumber \\ \left( \mu +\frac{\kappa }{2}\right) \frac{\partial ^2 u_z}{\partial r^2}+\kappa \frac{\partial \theta _\varphi }{\partial r}= & {} 0, \nonumber \\ \kappa \frac{\partial \theta _z}{\partial r}= & {} 0, \nonumber \\ (\beta _1+\beta _2+\beta _3)\frac{\partial ^2 \theta _r}{\partial r^2}-2\kappa \theta _r= & {} 0, \nonumber \\ \beta _3\frac{\partial ^2 \theta _z}{\partial r^2}-2\kappa \theta _z= & {} 0, \nonumber \\ \beta _3\frac{\partial ^2 \theta _\varphi }{\partial r^2}-2\kappa \theta _\varphi -\kappa \frac{\partial u_z}{\partial r}= & {} 0. \end{aligned}$$
(21)

Let us introduce non-dimensional parameters for the geometric characteristics and displacement field

$$\begin{aligned} x=1-\frac{r}{r_0}, \quad \xi =\frac{r_0}{L}, \quad u_x=\frac{u_r}{r_0}, \quad u_{\zeta }=\frac{u_z}{L}, \end{aligned}$$
(22)

as well as non-dimensional material parameters

$$\begin{aligned} {\widetilde{\lambda }}= & {} \frac{\lambda }{\mu },\qquad {\tilde{\kappa }}=\frac{\kappa }{2\mu }=\frac{N^2}{1-N^2}, \qquad \delta =\sqrt{\frac{\beta _3}{2\kappa r_0^2}}=\frac{\sqrt{1-N^2}}{N}\frac{l_b}{r_0}, \nonumber \\ \delta _{\Sigma }= & {} \sqrt{\frac{\beta _\Sigma }{2\kappa r_0^2}}=\frac{\sqrt{1-N^2}}{N}\frac{1}{\sqrt{2\psi }}\frac{l_t}{r_0}, \end{aligned}$$
(23)

where \(\beta _\Sigma =\beta _1+\beta _2+\beta _3\).

Since microrotation is a non-dimensional quantity, we have \(\theta _x=\theta _r\) and \(\theta _{\zeta }=\theta _z\).

Thus, we can rewrite Eqs. (21) as follows:

$$\begin{aligned} \frac{\partial ^2 u_x}{\partial x^2}= & {} 0,\nonumber \\ \frac{\left( 1+{\tilde{\kappa }}\right) }{\xi ^2}\frac{\partial ^2 u_{\zeta }}{\partial x^2}-\frac{2{\tilde{\kappa }}}{\xi }\frac{\partial \theta _\varphi }{\partial x}= & {} 0,\nonumber \\ \frac{\partial \theta _{\zeta }}{\partial x}= & {} 0,\nonumber \\ \delta _\Sigma ^2\frac{\partial ^2 \theta _x}{\partial x^2}-\theta _x= & {} 0,\nonumber \\ \delta ^2\frac{\partial ^2 \theta _{\zeta }}{\partial x^2}-\theta _{\zeta }= & {} 0,\nonumber \\ \delta ^2\frac{\partial ^2 \theta _\varphi }{\partial x^2}-\theta _\varphi +\frac{1}{2\xi }\frac{\partial u_{\zeta }}{\partial x}= & {} 0. \end{aligned}$$
(24)

The integration of Eq. (24)\(_1\) results in the linear function \(u_x=Ax+B\), which contradicts the assumptions (18). To overcome this contradiction, we set the constants of integration A and B equal to zero.

From Eqs. (24)\(_3\) and (24)\(_5\) it follows that

$$\begin{aligned} \theta _{\zeta }=0. \end{aligned}$$
(25)

Solution of Eq. (24)\(_4\) accounting for the boundary condition (15) is as follows:

$$\begin{aligned} \theta _x=C_{x}e^{-\frac{x}{\delta _\Sigma }}, \end{aligned}$$
(26)

where \(C_{x}\) is an integration constant.

Integrating Eq. (24)\(_2\) yields

$$\begin{aligned} \theta _\varphi =\frac{1+{\tilde{\kappa }}}{2\xi {\tilde{\kappa }}}\frac{\partial u_{\zeta }}{\partial x}+C_\varphi , \end{aligned}$$
(27)

where \(C_\varphi \) is the integration constant.

The last equation in (24) gives the following solution accounting for the boundary condition (15) and satisfying assumptions (18):

$$\begin{aligned} u_{\zeta }=Ce^{-\frac{x}{\delta \sqrt{{{{\tilde{\kappa }}}}+1}}}, \qquad C_\varphi =0, \end{aligned}$$
(28)

where C is the integration constant.

Finally, substituting Eq. (28) into Eq. (27) we obtain

$$\begin{aligned} \theta _\varphi =-C \frac{\sqrt{{{\tilde{\kappa }}}+1}}{2\xi \delta \tilde{\kappa }}e^{-\frac{x}{\delta \sqrt{{\tilde{\kappa }}+1}}}. \end{aligned}$$
(29)

As a result, the stress tensor becomes

$$\begin{aligned} \widetilde{{\mathbf{T}}}= & {} \frac{1}{\mu }\mathbf {T}=\frac{2 C}{\delta \xi \sqrt{{\tilde{\kappa }}+1}}e^{-\frac{x}{\delta \sqrt{{\tilde{\kappa }}+1}}} \mathbf {e}_z\otimes \mathbf {e}_r+\nonumber \\&+2 C_x {{\widetilde{\kappa }}} e^{-\frac{x}{\delta _\Sigma }}\left( \mathbf {e}_z\otimes \mathbf {e}_ \varphi -\mathbf {e}_\varphi \otimes \mathbf {e}_z\right) , \end{aligned}$$
(30)

and the boundary conditions (13) and (16) are satisfied automatically.

The couple stress tensor is

$$\begin{aligned} \widetilde{\mathbf {M}}= & {} \frac{1}{\mu L}\mathbf {M}=-2 C e^{-\frac{x}{\delta \sqrt{{\tilde{\kappa }}+1}}}\left[ \frac{\beta _2}{\beta _3}\mathbf {e}_\varphi \otimes \mathbf {e}_r+\mathbf {e}_r\otimes \mathbf {e}_\varphi \right] +\nonumber \\&+\frac{\sqrt{2\kappa }C_x}{\mu L}e^{-\frac{x}{\delta _\Sigma }}\left[ \sqrt{\beta _\Sigma }\mathbf {e}_r\otimes \mathbf {e}_r+\frac{\beta _1}{\sqrt{\beta _\Sigma }}\left( \mathbf {e}_\varphi \otimes \mathbf {e}_\varphi +\mathbf {e}_z\otimes \mathbf {e}_z\right) \right] . \end{aligned}$$
(31)

Satisfying the remaining boundary condition at the lateral surface (14) and solving for the integration constants, we get

$$\begin{aligned} \mathbf {e}_r\cdot \frac{1}{\mu L}\mathbf {M}\left| _{x = 0} \right.= & {} - \frac{ M_{0\varphi }}{\mu L}\mathbf {e}_\varphi , \qquad \rightarrow \nonumber \\ C= & {} \frac{M_{0\varphi }}{2\mu L}, \qquad C_x=0. \end{aligned}$$
(32)

Thus, boundary conditions at the cylinder end faces (17) are satisfied automatically.

Finally, we obtain

$$\begin{aligned} \mathbf {u}= & {} \frac{M_{0\varphi }}{2\mu }e^{-\frac{r_0-r}{l_b}N}\mathbf {e}_z, \end{aligned}$$
(33)
$$\begin{aligned} \mathbf {\theta }= & {} -\frac{M_{0\varphi }}{4\mu l_b N} e^{-\frac{r_0-r}{l_b}N}\mathbf {e}_\varphi , \end{aligned}$$
(34)
$$\begin{aligned} \mathbf {\epsilon }= & {} \frac{M_{0\varphi }}{4\mu l_b N}e^{-\frac{r_0-r}{l_b}N}\left[ \left( 2N^2-1\right) \mathbf {e}_r\otimes \mathbf {e}_z+\mathbf {e}_z\otimes \mathbf {e}_r\right] , \end{aligned}$$
(35)
$$\begin{aligned} \mathbf {\kappa }= & {} -\frac{M_{0\varphi }}{4\mu l_b}e^{-\frac{r_0-r}{l_b}N}\left[ \frac{1}{l_b}\mathbf {e}_r\otimes \mathbf {e}_\varphi -\frac{1}{rN}\mathbf {e}_\varphi \otimes \mathbf {e}_r\right] , \end{aligned}$$
(36)
$$\begin{aligned} \mathbf {T}= & {} \frac{M_{0\varphi }}{l_b}N e^{-\frac{r_0-r}{l_b}N}\mathbf {e}_z\otimes \mathbf {e}_r, \end{aligned}$$
(37)
$$\begin{aligned} \mathbf {M}= & {} -M_{0\varphi }e^{-\frac{r_0-r}{l_b}N}\left[ \frac{\beta _2}{\beta _3}\mathbf {e}_\varphi \otimes \mathbf {e}_r+\mathbf {e}_r\otimes \mathbf {e}_\varphi \right] . \end{aligned}$$
(38)

It is clear that the obtained solution changes the stress–strain state only in the vicinity of the lateral surface due to the exponential decay of the functions. Additional deformations, in turn, may change the inner structure of the material near the border and lead to void and defects appearance.

Note that in the limit case \(N=1\), Eqs. (33)–(38) reduce to

$$\begin{aligned} \mathbf {u}= & {} \frac{M_{0\varphi }}{2\mu }e^{-\frac{r_0-r}{l_b}}\mathbf {e}_z, \end{aligned}$$
(39)
$$\begin{aligned} \mathbf {\theta }= & {} -\frac{M_{0\varphi }}{4\mu l_b} e^{-\frac{r_0-r}{l_b}}\mathbf {e}_\varphi , \end{aligned}$$
(40)
$$\begin{aligned} \mathbf {\epsilon }= & {} \frac{M_{0\varphi }}{4\mu l_b}e^{-\frac{r_0-r}{l_b}}\left[ \mathbf {e}_r\otimes \mathbf {e}_z+\mathbf {e}_z\otimes \mathbf {e}_r\right] , \end{aligned}$$
(41)
$$\begin{aligned} \mathbf {\kappa }= & {} -\frac{M_{0\varphi }}{4\mu l_b}e^{-\frac{r_0-r}{l_b}}\left[ \frac{1}{l_b}\mathbf {e}_r\otimes \mathbf {e}_\varphi - \frac{1}{r}\mathbf {e}_\varphi \otimes \mathbf {e}_r\right] ,\nonumber \\ \mathbf {T}= & {} \frac{M_{0\varphi }}{l_b}e^{-\frac{r0-r}{l_b}}\mathbf {e}_z\otimes \mathbf {e}_r, \end{aligned}$$
(42)
$$\begin{aligned} \mathbf {M}= & {} -M_{0\varphi }e^{-\frac{r0-r}{l_b}}\left[ \frac{\beta _2}{\beta _3}\mathbf {e}_\varphi \otimes \mathbf {e}_r+\mathbf {e}_r\otimes \mathbf {e}_\varphi \right] . \end{aligned}$$
(43)

The same solution was obtained in [27] for a continuum with constrained rotations.

4 Diffusion problem

The pure diffusion of hydrogen follows the Fick’s second law

$$\begin{aligned} \frac{\partial c}{\partial t}=\nabla \cdot \left( D\nabla c\right) , \end{aligned}$$
(44)

where c is the hydrogen concentration, t is time, D is the diffusion coefficient.

According to the Arrhenius low, the diffusion coefficient depends on the activation energy for the reaction [30, 36, 39]. This energy, in turn, can be correlated with inelastic strain energy density [30] or with elastic potential energy [31, 51, 52, 64]. Within the frame of the present paper, the diffusion coefficient is supposed to depend on the strain energy in the following way [51, 52]:

$$\begin{aligned} D=D_0e^{\frac{\Delta V W}{RT}}, \end{aligned}$$
(45)

where \(D_0\) is the diffusion constant, \(\Delta V\)=m/\(\rho \) is the local volume change per 1 mole of substance (m is the molar mass of hydrogen and \(\rho \) is the metal density), \(R=8.31455\,\)J/(mol\(\cdot \)K) is the universal gas constant, T is the absolute temperature.

The boundary conditions are as follows:

$$\begin{aligned} \left. c \right| _{r=r_0}=c_0, \qquad \left. \frac{\partial c}{\partial r}\right| _{r=0}=0. \end{aligned}$$
(46)

Substituting Eqs. (35), (36) into Eq. (5), we get

$$\begin{aligned} W=\frac{M_{0\varphi }^2}{4\mu l_b^2}e^{-2\frac{r_0-r}{l_b}N} \end{aligned}$$
(47)

for a general micropolar theory, and

$$\begin{aligned} W=\frac{M_{0\varphi }^2}{4\mu l_b^2}e^{-2\frac{r_0-r}{l_b}} \end{aligned}$$
(48)

for the media with constrained rotations (\(N=1\)). Thus, the diffusion coefficient given by Eq. (45) depends on the radial coordinate r. It takes quit big values in the vicinity of the border within the area comparable to the characteristic length of the structural inhomogeneity and decreases away from the lateral surface to the constant value \(D_0\).

The solution of the diffusion problem is obtained numerically by an implicit finite difference method; the tridiagonal matrix algorithm was realized with MATLAB.

5 Experimental data and results

To verify the existence of a thin boundary layer, we carried out the following experiment, which was described in detail in [59]. A cylindrical specimen of radius 4 mm and length 40 mm made of the weather resistant steel 14HGNDC was charged with hydrogen according to NACE Standard TM0284-2106-SG in an accredited laboratory which is certified for industrial testing. Samples were incubated for 96 h in a deaerated solution based on distilled water with 5 wt% NaCl and 0.5 wt% CH3COOH. The gaseous hydrogen sulfide was purged through the solution by bubbling. A constant concentration of 2500 mg/l of hydrogen sulfide was maintained in the working chamber. After the saturation the specimen was taken out of the electrolyte solution and held in air for about 48 h. Then, it was cut manually with a hacksaw into four cylindrical parts of equal length. The cylindrical layers of thickness 0.06, 0.11 and 0.21 mm were removed from three out of the four parts, respectively. Each part was further cut into two cylindrical specimens for subsequent analysis.

Measurements of hydrogen concentration were carried out using the industrial mass spectrometric hydrogen analyzer AV-1, which utilizes the vacuum hot extraction method [38, 61]. The method of the analysis and the analyzer are detailed in [9, 10]. The specimens inside the extractor were heated gradually up to release temperatures of 400 \(^{\circ }\)C, 600 \(^{\circ }\)C and 800 \(^{\circ }\)C during 1 h per temperature. It can be stated that the temperature of 400 \(^{\circ }\)C is the upper bound for the first group of hydrogen maxima (diffusible or mobile hydrogen) and the temperature of 600 \(^{\circ }\)C is the upper bound for the second group of the hydrogen maxima, sometimes referred to as the trapped hydrogen, so that it is sufficient to completely extract the “overall” hydrogen from the reference samples [55, 59]. The temperature of 800 \(^{\circ }\)C was selected for the extraction of total hydrogen amount during the hot vacuum extraction. The amount of hydrogen released from all parts of the original specimen for each temperature was measured. The mean values for two specimens of the same diameter are shown in Table 2.

Table 2 The amount of extracted hydrogen, ppm w.r.t. mass
Full size table

It is apparent from the table that a nonuniform distribution of hydrogen concentrations over the sample volume takes place. It is known that a non-charged specimen always contains evenly distributed hydrogen. According to Table 2, the total amounts of hydrogen extracted from the cylindrical parts with the removed layers of thicknesses \(110\,\upmu \text {m}\) and \(210\,\upmu \text {m}\) are almost equal. So that, the initial concentration of hydrogen within the specimens may be posted as 0.47 ppm to focus only on the uneven distribution of the additional hydrogen. In this case, we can conclude that almost all hydrogen due to saturation is concentrated in a thin boundary layer with a thickness of about \(60{-}110\,\upmu \text {m}\). The removed layer of thickness \(110\,\upmu \text {m}\) contains overall additional hydrogen, whereas the layer of thickness \(60\,\upmu \text {m}\) contains about \(77.5\%\) (0.01\(\cdot \)(0.62–0.14 ppm)/0.62 ppm) of this amount.

To estimate the non-classical material parameters appearing in the present micropolar model and reflecting the skin effect, we can relate the experimental thickness of the boundary layer containing a large excess of hydrogen to the width of the layer with a changed stress–strain state. According to Eqs. (33)–(38), this layer is determined by the exponentiation function

$$\begin{aligned} e^{-\frac{r_0-r}{l_b}N}. \end{aligned}$$

Since components of \(\mathbf {u}\), \(\mathbf {\theta }\), \(\mathbf {\epsilon }\), \(\mathbf {\kappa }\), \(\mathbf {T}\) and \(\mathbf {M}\) decay exponentially to zero, but never be exactly equal to it, we suppose that they decrease by a factor of k times at the boundary of the experimentally obtained layer, \(r_*\), as compared to the corresponding components at the surface of the specimen, where they take their maximum values. It means that

$$\begin{aligned} \left. f\right| _{r=r_*}=\frac{1}{k}\left. f\right| _{r=r_0}, \end{aligned}$$

where f is corresponding to the rapidly decreasing components of vector and tensor fields. So that, k may correlate with a sufficiently small value of the considering component in comparison with its value at the border. It does not have any physical meaning and can be considered as a fading number of the solution. Then, we obtain

$$\begin{aligned} L_b=\frac{l_b}{N}=\frac{r_0-r_*}{\ln k}. \end{aligned}$$
(49)

Values of \(L_b\) corresponding to \(r_*=3.94\,\text {mm}\) and \(r_*=3.89\,\text {mm}\) for two values of the fading number, namely \(k=100\) and \(k=30\), are given in Table 3. The corresponding values of the dimensional thicknesses of the boundary layer, \(h_*=r_0-r_*\), and the dimensionless one, \(x_*=\left( r_0-r_*\right) /r_0\), are also indicated. The estimated values of the material parameters are much smaller than the radius of the cylinder and comparable to the grain size that can be considered as the characteristic size of the material.

Table 3 Material parameter \(L_b\) w.r.t. the geometrical parameters of the cylindrical specimen corresponding to the size of the hydrogenated area, namely inner border of the boundary layer, \(r_*\), dimensional thickness of the boundary layer, \(h_*\), dimensionless thickness of the boundary layer, \(x_*\), fading number of the solution, k
Full size table

For simplicity, we restrict ourselves to considering the displacement field to reflect the impact of the distributed couple stress on the border on the material behavior. Substituting relation (49) into Eq. (33) gives

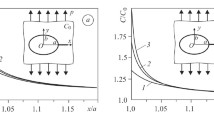
$$\begin{aligned} u_z=\frac{M_{0\varphi }}{2\mu }e^{-\frac{r_0-r}{r_0-r_*}\text {ln}(k)}. \end{aligned}$$
(50)

Figure 2 displays the longitudinal displacement against the dimensionless radius \(r/r_0\). The shear modulus \(\mu \) of the steel 14HGNDC was not measured, so we assume it equaling to \(80\,\text {GPa}\). We consider two thicknesses of the boundary layer, namely \(h_{*1}=60\,\upmu \text {m}\) and \(h_{*2}=110\,\upmu \text {m}\). The fading numbers \(k=100\) and \(k=30\) are taken. The curve is plotted for \(M_0=6.4\,\)MPa\(\cdot \)m. This boundary condition provides displacement on the border equal to 40 \(\upmu \text {m}\) that is of order of a few grains. Nevertheless, any other value of the distributed couple stress will also lead to the typical exponentiation decrease in the displacement field. The difference is quantitative rather than qualitative. The comparison of solutions provided by \(M_0=6.4\,\)MPa\(\cdot \)m, \(M_0=3.2\,\)MPa\(\cdot \)m, and \(M_0=1.6\,\)MPa\(\cdot \)m is presented in Fig. 3. The thickness of the boundary layer \(h_{*2}=110\,\upmu \text {m}\) and fading number \(k=100\) are considered. Note that according to Eq. (49), the distributed couple stress does not affect the material parameters used in the present model. Therefore, the difference is observed for the values of the displacements and does not affect the width of the area with a changed stress–strain state.

Fig. 2
figure 2

Dependence of the longitudinal displacement on the dimensionless radius for different values of the thickness of the boundary layer, \(h_*\), and fading numbers, k, namely \(h_*=h_{*1}=60\,\upmu \text {m}\), \(k=100\) (red curve) and \(k=30\) (black curve), \(h_*=h_{*2}=110\,\upmu \text {m}\), \(k=100\) (green curve) and \(k=30\) (blue curve) (colour figure online)

Full size image
Fig. 3
figure 3

Dependence of the longitudinal displacement on the dimensionless radius for different values of the distributed couple stress on the border, namely \(M_0=6.4\,\)MPa\(\cdot \)m (red curve), \(M_0=3.2\,\)MPa\(\cdot \)m (blue curve) and \(M_0=1.6\,\)MPa\(\cdot \)m (black curve) (colour figure online)

Full size image

In order to obtain the distribution of hydrogen within the thickness of the cylinder with respect to the diffusion problem explained in the previous section, let us consider the media with constrained rotations (\(N=1\)) to minimize the number of the unknown material parameters. Note that the difference between the solution of general Cosserat problem and Pseudo-Cosserat problem is quantitative but not qualitative. So, the elastic energy is determined by Eq. (48). We take the distributed couple stress on the border \(M_0=6.4\,\)MPa\(\cdot \)m and the material lengths for bending \(l_b=24\,\upmu \text {m}\) and \(l_b=13\,\upmu \text {m}\). The diffusion coefficient is given by Eq. (45). The saturation temperature, T, is set to be equal 300 K and the duration of the diffusion process is set to be equal 96 h according to the experimental data. The molar mass of hydrogen \(m=0.002\,\)kg/mol is a known value, \(\rho =7800\,\)kg/\(\hbox {m}^3\) is taken for the weather resistant steel 14HGNDC. There is a wide range of values of the constant diffusion coefficient \(D_0\). We use the value of \(D_0\) providing the lack of the inner concentration of hydrogen when considering the diffusion process with a constant diffusion coefficient to demonstrate the difference. The concentration profiles are shown in Fig. 4.

Fig. 4
figure 4

The concentration profiles of hydrogen w.r.t. the dimensionless radius after 96 h saturation, where the material length for bending \(l_b=13\,\upmu \text {m}\) (left-hand side, blue points) and \(l_b=24\,\upmu \text {m}\) (right-hand side, red points). The black points correspond to the constant diffusion coefficient (colour figure online)

Full size image

The results show a highly inhomogeneous distribution of hydrogen and an appearance of a thin saturated surface layer of a thickness about 20–\(30\,\upmu \text {m}\) (corresponding to \(r/r_0=0.9925\)–0.9950) that is a few times less than the one estimated on the base of the experimental data (60–\(110\,\upmu \text {m}\)). On the one hand, the value of the thickness layer predicted by the present model depends on the material parameters, in particular, the material length for bending. In case of a zero value of the parameter, the micropolar theory will provide a zero solution, so the surface layer will not appear. On the other hand, we can see that variation of the value of this parameter within the range of values comparable to the grain size does not affect the thickness.

To compare the obtained results with the experimental data quantitatively we estimate the mean inner concentration of hydrogen in ppm w.r.t. mass. Within the experiment a constant concentration of 50 ppm of hydrogen corresponding to 2500 mg/l of hydrogen sulfide was maintained on the border. The mean additional inner concentration of hydrogen predicted by the present model is as follows:

$$\begin{aligned} {\widetilde{c}}_\mathrm{ppm}=\frac{\int _0^L \int _0^{r_0} c_\mathrm{ppm}(r) 2\pi r \mathrm{d}z \mathrm{d}r}{\pi r_0^2 L}. \end{aligned}$$
(51)

where \(c_\mathrm{ppm}\) is the function of the inner concentration given in ppm.

Solving Eq. (51), we obtain the mean concentration of the additional hydrogen over the specimen to be equal to \(0.68\,\)ppm for \(l_b=24\,\upmu \text {m}\) and \(0.62\,\)ppm for \(l_b=13\,\upmu \text {m}\), while the amount estimated experimentally is about \(0.62\,\)ppm. Thus, we can see that the amount of the additional hydrogen due to saturation estimated theoretically and experimentally coincidence, while the theoretical thickness is smaller than the estimated experimentally.

6 Discussion and outlook

The proposed model explains the appearance of a thin boundary layer containing a significant excess of hydrogen based on of the micropolar continuum theory. Consideration of the distributed couple stress on the border and subsequent accounting for additional rotational degrees of freedom and inner couple stresses results in a highly inhomogeneous stress–strain state of the material. The distributed couple stress reflects the presence of a large number of defects leading to the grain rotations and microcracks appearance and can be posted as the boundary condition. The other way is to consider directly the grain microrotations on the border. According to Eq. (29), the corresponding solution will still decay exponentially from the lateral surface; only integration constants will differ. Further, additional deformations occurring in the vicinity of the border may change the bulk material microstructure. It can lead to voids and defects appearance that are known to be traps for hydrogen. Indeed, considering the dependence of the effective diffusion coefficient on the strain energy, we show that hydrogen accumulates within the area comparable to the size of the surface layer with additional stresses and strains. This area is determined by the additional material parameter appearing within the micropolar model. This material parameter is of order of the grain size that, in turn, can be considered as a characteristic size of the material inhomogeneity.

Thus, it follows that Cosserat-type continuum theories are capable of describing nonuniform distribution of hydrogen observed in experiments. Further investigation is necessary to study the mutual influence of stress–strain state and diffusion. So far, we have considered a stress-induced hydrogen diffusion, whereas the influence of hydrogen on the inner pressure was not taken into account. Thus, a coupled problem should be solved to explain the skin effect more accurately. In this case the initial nonuniform stress–strain state predicted by the micropolar theory due to the distributed couple stress or microrotations on the border may provide the fast diffusion within a thin surface layer with a high strain energy. The accumulated hydrogen, in turn, may cause additional self strains and change the stress–strain state within a wider area than observed initially, and so on. The steady state will prevent further fast hydrogen diffusion. In such a case, the thickness of the surface layer estimated theoretically may be wider than obtained within the frame of the present paper. Considering a coupled problem also makes it possible to take into account a strong dependence of elastic moduli on the hydrogen concentration.

Another issue is that so far we estimated the material parameters appearing in the micropolar model and reflecting the “size effect" related to the structural inhomogeneity by means of the measured hydrogenated surface layer. Indeed, comparison of the theoretical results with the experimental data on the hydrogenated surface layer makes it possible to estimate some ratios of the non-classical elastic modulus. Thus, according to Eq. (49) and data presented in Table 1, the ratio \(\beta _3/N^2\) can be expressed in terms of the relative boundary layer thickness as

$$\begin{aligned} \begin{aligned} \frac{\beta _3}{N^2}=4\mu \left( \frac{h_*}{\ln k}\right) . \end{aligned} \end{aligned}$$
(52)

In the case of material with constrained rotations \(N=1\), the elastic modulus \(\beta _3\) can be estimated. However, the material parameters appearing within the micropolar theory may depend only on the structural changes. Since the present paper focuses on nonuniform distribution of hydrogen caused only due to the structural inhomogeneity, one can assume that the thickness of the hydrogenated layer is comparable to the thickness of structural inhomogeneity. Then, it is necessary to estimate the values of the material parameters only within the model. To validate the estimated material parameters, additional experiments on specimens should be carried out. Thus, it is more correct to estimate its values on the base of the microstructure evolution than by means of the hydrogen concentration profile. In context of the model implemented in the present paper, the material constants shall be obtained on the base of the microstructure observed for the hydrogenated metal. Then, it will describe the field of the additional stresses and strains occurring due to the hydrogen accumulation. Size of this field may differ from the size of the hydrogenated layer that should be predicted by the diffusion problem. In case of the coupled problem mentioned earlier within the current section, the material parameters and, therefore, the initial thickness of the area with a changed stress–strain state may be estimated on the base of the microstructure data obtained for the non-hydrogen-charged metal. Then, it will explain only the “initial" skin effect due to the structural defects on the border. The thickness of the layer with the initial nonzero stress–strain state is supposed to be smaller than the final one. Additional self strains will appear away from the border due to the hydrogen diffusion resulting in a wider area with a changed microstructure and, finally, lead to a wider hydrogenated area.

7 Conclusions

The following tasks have been accomplished within the framework of the present paper:

  • The experimentally observed strong nonuniform distribution of hydrogen in metal specimens, that is, the appearance of a thin boundary layer containing a significant excess of hydrogen, has been explained by means of the micropolar continuum approach. The diffusion coefficient is to depend on the radially nonuniform strain energy.

  • While the classical elasticity does not explain the material behavior near the lateral surface, the micropolar theory describes it with the solution, which rapidly fades away from the boundary.