Mechanics of third-gradient continua reinforced with fibers resistant to flexure in finite plane elastostatics

Abstract

A third-gradient continuum model is developed for the deformation analysis of an elastic solid, reinforced with fibers resistant to flexure. This is framed in the second strain gradient elasticity theory within which the kinematics of fibers are formulated, and subsequently integrated into the models of deformations. By means of variational principles and iterated integrations by parts, the Euler equilibrium equation is obtained which, together with the constraints of bulk incompressibility, compose the system of the coupled nonlinear partial differential equations. In particular, a rigorous derivation of the admissible boundary conditions arising in the third gradient of virtual displacement is presented from which the expressions of the triple forces are derived. The resulting triple forces are, in turn, coupled with the Piola-type triple stress and are necessary to determine a unique deformation map. The proposed model predicts smooth and dilatational shear angle distributions, as opposed to those obtained from the first- and second-gradient theory where the resulting shear zones are either non-dilatational or non-smooth.

1 Introduction

Problems involving the mechanics of an elastic solid, reinforced with embedded fibers, have received a considerable amount of attention mainly because of their fundamental importance in materials science and engineering in general. Fiber-reinforced elastic solids, also known as fiber composites, are a special class of materials where the microstructure (fibers) dominates the general responses of the composites [1,2,3,4]. Traditional approaches to examining these microstructured materials include the direct estimations of an individual fiber–matrix system (see, for example, [5, 6]). Such local analyses are an effective means of characterizing the intrinsic properties of composite materials. However, they often rely heavily upon computationally expensive identification processes when predicting the mechanical responses of the materials subjected to certain types of boundary conditions (e.g., external loadings, edge conditions, etc.). Instead, a continuum description can be considered a promising alternative in a sense that, in most cases, fibers are densely distributed, so as to render the idealization of ‘continuous’ distribution. Within this prescription, the kinematics of fibers are mapped into the model of the continuum deformation. Since the continuum-based models offer the advantages of a compact mathematical frame work and the associated analyses, they have been adopted in a number of pertinent problems (see, for example, [7,8,9] and the references therein). However, as the energy function employed in the aforementioned studies is based on the classical deformation gradient accommodated by the first-gradient continua, when it is used in junction with the conditions of bulk incompressibility and fiber inextensibility, the corresponding deformation fields are often kinematically determinate without imposing boundary conditions [8, 9].

In recent years, anisotropic strain gradient elasticity theory [10,11,12] has received renewed attention for its application in the modeling and analysis of microstructured continua. Contemporary applications vis-a-vis the general theory and mathematical aspects of the subject matter can be found in [13,14,15,16,17,18,19]. The second-gradient continuum model, which describes the mechanics of an elastic solid reinforced with continuously distributed fibers, is explored by Spencer and Soldatos [20]. There the authors assign the bending resistance to the changes in curvature of fibers. The computation of the letter is facilitated by the second gradient of the continuum deformation through which the bending deformation of fibers is mapped in the form of a convected curve. The concept is further generalized to accommodate fibers resistant to flexure, stretch and twist within the confined scope of the Cosserat theory of nonlinear elasticity [21]. The second-gradient-based continuum models have been widely and successfully adopted for problems such as the mechanics of meshed structures [22,23,24], bending of bidirectional fiber composites [25] and composites reinforced with extensible fibers [26]. Further, the second-gradient continuum models predict smooth transitions in the shear angle distributions, whereas the classical (first-order) continuum theory results in discontinued distributions [23, 24, 27]. Although the second-gradient model produces reasonably accurate descriptions of microstructured continua, there exist physical phenomena for which the models are intrinsically limited in predictions, such as deformations induced by line forces, couples and, in particular, mechanical contact interactions on edges and points of Cauchy cuts [28,29,30]. In the case of fiber-reinforced composites, the latter would mean the mechanical interactions between the fiber and matrix through the interfacial region. Such contact interaction forces pose formidable challenges in the modeling and analysis of the composites, and therefore, to the best of the authors’ knowledge, little has been devoted in the literature.

In the present work, we develop a third-gradient continuum model for the deformation analysis of an elastic solid which is reinforced with fibers resistant to flexure and subjected to finite plane deformations. Hence, it is assumed that the fiber’s directors and the associated deformation map remain in a plane field, with no out-of-plane components and all material properties are independent of the out-of-plane coordinates. The kinematics of fibers are determined by their positions and director fields under the postulation of the continuously distributed spatial rods (fibers) of Kirchhoff type [31,32,33]. Within this prescription, we propose an energy density function that accommodates the third gradient of the continuum deformation in the sense of [20]. This is materialized by the third-gradient continua through which line forces, couples, double forces and triple forces are exerted in order to assimilate the mechanical interactions between the fibers and the matrix, in addition to the bending resistance of the fibers. The associated Euler equilibrium equation is then obtained by employing iterated integrations by parts and variational formulations of the second and third gradient of deformations [11, 29, 30, 34, 35]. In particular, the rate of change in curvature, defined at points on the convected curves of fibers, is computed in terms of the third gradient of deformation map explicitly, from which the contact interactions between the fibers and the surrounding matrix may be characterized. A rigorous derivation of the admissible and necessary boundary conditions arising in the third gradient of virtual displacement is also presented. There we show that the introduction of the third gradient of deformations gives rise to an additional set of mechanical interaction forces on the desired boundaries, unlike those obtained from the second-gradient model. In fact, these interaction forces are the energy couple to the Piola-type triple stresses that can be suitably sustained by the third-gradient continua (see, also, [28,29,30]).

Implementation of the proposed model is demonstrated by considering a fiber-reinforced solid of neo-Hookean type, subjected to finite plane deformations. A set of numerical solutions of the resulting system of coupled partial differential equations (PDEs) is obtained via finite element analysis (FEA), which demonstrate close agreement with the results in the literature [22, 36, 37]. In particular, the proposed model predicts smooth and dilatational shear angle distributions, in contrast to those obtained from the first- and second-gradient theory where the resulting shear zones are either non-dilatational or non-smooth. More precisely, the patterns of dilatational shear zones are configured by the applied triple forces, which are ultimately computed via the third gradient of the deformation map and its energy couple pertaining to the Piola-type triple stress. Case studies are also performed through the inhouse experimental settings of crystalline nanocellulose (CNC) fiber composites and Nylon-6 fiber Neoprene rubber composites, which illustrate that the obtained solutions successfully predict the deformation profiles of both composites. More importantly, we identify the unique characteristic constants for the composites that minimize the prediction errors. These coefficients are not responsive to either the applied loadings or the boundary conditions and may therefore be inferred as intrinsic properties of the examined composites pertaining to the Piola-type triple stress. Further investigations of the results extending to other materials may be of particular mechanical interest. Lastly, the proposed model bears close similarity to the theory of micropolar elasticity in the sense that the rotation of a local point (microstructure) is integrated into the model of deformations via the third gradient of the continuum deformation. Therefore, the proposed model can be regarded as an alternative 2D Cosserat theory of nonlinear elasticity [10, 38,39,40].

Throughout the manuscript, we use standard notation such as $\mathbf {A}^\mathrm{T},~ \mathbf {A}^{-1},\ \mathbf {A}^{*}$ and $tr(\mathbf {A}).$ These are the transpose, the inverse, the cofactor and the trace of a tensor $\mathbf {A}$, respectively. The tensor product of vectors is indicated by interposing the symbol $\otimes$, and the Euclidian inner product of tensors $\mathbf {A}$, $\mathbf {B}$ is defined by $\mathbf {A}\cdot \mathbf {B}=tr({\mathbf {AB}}^\mathrm{T})$; the associated norm is $\left| \mathbf {A}\right| =\sqrt{\mathbf {A}\cdot \mathbf {A}}$. The symbol$\ \left| *\right|$ is also used to denote the usual Euclidian norm of three-vectors. Latin and Greek indices take values in $\{1,2\}$ and, when repeated, are summed over their ranges. Lastly, the notation $F_{\mathbf {A}}$ stands for the tensor-valued derivatives of a scalar-valued function $F(\mathbf {A})$.

2 Kinematics

We introduce the vector field $\mathbf {D}$ representing the unit tangent to the fiber’s trajectory in the reference configuration. The orientation of particular fibers is then given by

$$\begin{aligned} \lambda =\left| \mathbf {d}\right| =\frac{\hbox {d}s}{\hbox {d}S} \quad {\text { and }}\quad {\varvec{\tau }}=\lambda ^{-1}\mathbf {d}, \end{aligned}$$

(1)

where

$$\begin{aligned} \mathbf {d}={\mathbf {FD}}. \end{aligned}$$

(2)

In the above, $\mathbf {d}$ is the unit tangent to the fiber trajectory in the current configuration and $\mathbf {F}$ is the first gradient of the deformation function $(\chi (\mathbf {X}))$, i.e.,

$$\begin{aligned} \mathbf {F}={\varvec{\nabla }}\chi (\mathbf {X}). \end{aligned}$$

(3)

Equation (2) can be derived by taking the derivative of $\mathbf {r}(S)= \varvec{\chi }(\mathbf {X}(S))$, upon making the identifications $\mathbf {D}=\mathbf {X} ^{\prime }(S)$ and $\mathbf {d}=\mathbf {r}^{\prime }(S)$. We denote that, unless otherwise specified, primes refer to derivatives with respect to arclength along a fiber (i.e., $(*)^{\prime }=\hbox {d}(*)/\hbox {d}S$). Accordingly, from Eq. (2), the geodesic curvature of an arc ($\mathbf {r}\left( S\right)$) is expressed in terms of $\mathbf {F}$ and $\mathbf {d}$ as

$$\begin{aligned} \mathbf {g}=\mathbf {r}^{\prime \prime }=\frac{\hbox {d}(\mathbf {r}^{\prime } \left( S\right) )}{\hbox {d}S}=\frac{\partial ({\mathbf {FD}})}{\partial \mathbf {X}}\frac{\hbox {d} \mathbf {X}}{\hbox {d}S} =\nabla [{\mathbf {FD}}]\mathbf {D}. \end{aligned}$$

(4)

In a typical environment, most of the fibers are straight prior to deformations. Even slightly curved fibers can be regarded as ‘fairly straight’ fibers considering their length scales against the matrix materials. This further leads to the assumption of vanishing gradient fields of the unit tangent in the reference configuration (i.e., $\nabla \mathbf {D}=\mathbf {0}$). Hence, Eq. (4) reduce to

$$\begin{aligned} \mathbf {g}={\varvec{\nabla }} \mathbf {F}(\mathbf {D}\otimes \mathbf {D}). \end{aligned}$$

(5)

We now introduce the commonly used conventions of the second gradient of deformations:

$$\begin{aligned} {\varvec{\nabla }}\mathbf {F}\equiv \mathbf {G}, \end{aligned}$$

(6)

where the compatibility condition of $\mathbf {G}$ can be seen as

$$\begin{aligned} G_{iAB}=F_{iA,B}=F_{iB,A}=G_{iBA}. \end{aligned}$$

(7)

Accordingly, Eq. (5) becomes

$$\begin{aligned} \mathbf {g}=\mathbf {G}(\mathbf {D}\otimes \mathbf {D})=\mathbf {g}(\mathbf {G},\mathbf {D}). \end{aligned}$$

(8)

Based on the above kinematical setting, authors in [20] propose the following energy density function in the continuum description of an elastic solid reinforced with fibers resistant to flexure:

$$\begin{aligned} W(\mathbf {F},\mathbf {G})=\widehat{W}(\mathbf {F})+W(\mathbf {G}),\ W(\mathbf {G}) \equiv \frac{1}{2}C\left( \mathbf {F}\right) \left| \mathbf {g}\right| ^{2}, \end{aligned}$$

(9)

where $C(\mathbf {F})$ refers to the material properties of the fibers and is, in general, independent of the deformation gradient, i.e.,

$$\begin{aligned} C(\mathbf {F})=C. \end{aligned}$$

(10)

In this model (Eq. (9)), the fibers’ bending energy is presumed to be dependent entirely on the second gradient of deformations, $\mathbf {G},$ which facilitates the development of the associated mathematical framework. The concept has been widely and successfully adopted in the relevant studies (see, for example, [19, 21, 26, 37, 41]).

In the present study, we propose a more comprehensive model by introducing the third gradient of deformations into the model of deformations. For this purpose, we compute the rate of changes in curvature (the third gradient of deformations) at points on the fibers as

$$\begin{aligned} \varvec{\alpha }=\mathbf {r}^{^{\prime \prime \prime }} =\frac{\hbox {d}(\nabla [{\mathbf {FD}}]\mathbf {D})}{\hbox {d}S} =\frac{\partial (\nabla [ {\mathbf {FD}}] \mathbf {D})}{\partial \mathbf {X}}\frac{\hbox {d}\mathbf {X}}{\hbox {d}S} =[\nabla \{\nabla [ {\mathbf {FD}}]\mathbf {D}\}]\mathbf {D} =[\nabla \{\nabla [ {\mathbf {FD}}]\}\mathbf {D} +\nabla [{\mathbf {FD}}](\nabla \mathbf {D})]\mathbf {D}, \end{aligned}$$

(11)

through which the interactions between the fibers and the surrounding matrix may be characterized. Further, we formulate the follow in the same sprit as Eqs. (5)–(8) that

$$\begin{aligned} \varvec{\alpha }= & {} \nabla (\nabla \mathbf {F})(\mathbf {D} \otimes \mathbf {D}\otimes \mathbf {D}), \nonumber \\ \nabla (\nabla \mathbf {F})= & {} \nabla (\mathbf {G})\equiv \mathbf {H},\text {and}\nonumber \\ \varvec{\alpha }= & {} \mathbf {H}(\mathbf {D}\otimes \mathbf {D}\otimes \mathbf {D}) =\alpha (\mathbf {H},\mathbf {D}). \end{aligned}$$

(12)

Thus, the energy potential associated with the third gradient of deformations is incorporated and yields

$$\begin{aligned} W(\mathbf {F},\mathbf {G},\ \mathbf {H})=\widehat{W}(\mathbf {F})+W(\mathbf {G}) +W(\mathbf {H}),\ \ W(\mathbf {G})\equiv \frac{1}{2}C\left( \mathbf {F}\right) \left| \mathbf {g}\right| ^{2},\ W(\mathbf {H})\equiv \frac{1}{2}A \left( \mathbf {F}\right) \left| \varvec{\alpha }\right| ^{2}. \end{aligned}$$

(13)

Here, the third gradient of deformations $\mathbf {H}$ is defined by

$$\begin{aligned} \nabla [\nabla \mathbf {G}]=\nabla \mathbf {G}\equiv \mathbf {H}, \end{aligned}$$

(14)

which accounts for the rate of change in the fibers’ curvature. The phenomenological implications vis-a-vis the third gradient of deformations (e.g., interactions between fibers and a matrix material) and the identification of the associated coefficient (here, denoted as A) are addressed in the literature [11, 29, 30, 34, 35, 42, 43]. Our emphasis here is on the development of a mathematical frame work, and the associated analyses, in order to provide the more general and comprehensive description of fiber composites with fibers resistant to flexure. It is also noted that, in the forgoing analysis, the parameter A is assumed to be independent of the deformation gradient, similar to Eq. (10). That is

$$\begin{aligned} A(\mathbf {F})=A. \end{aligned}$$

(15)

We adopt the variational principles in the derivations of the Euler equations and the associated boundary conditions. To obtain the desired expressions, we evaluated the induced energy variation of the response function with respect to $\mathbf {F}$, $\mathbf {G}$, and $\mathbf {H}$ as

$$\begin{aligned} \dot{W}(\mathbf {F}, \mathbf {G}, \mathbf {H})=W_{\mathbf {F}} \cdot \dot{\mathbf {F}}+W_{\mathbf {G}}\cdot \dot{\mathbf {G}} +W_{\mathbf {H}}\cdot \dot{\mathbf {H}}, \end{aligned}$$

(16)

where the superposed dot refers to the derivatives with respect to a parameter $\epsilon$ at a fixed value (e.g., $\epsilon =0$ at equilibrium) that labels a one-parameter family of deformations. Similarly, Eq. (13) $_{2,3}$ yields

$$\begin{aligned} \dot{W}(\mathbf {G})=C\mathbf {g}\cdot \dot{\mathbf {g}}\quad {\text { and }}\quad \dot{W}(\mathbf {H}) =A{\varvec{\alpha }} \cdot \dot{{\varvec{\alpha }}}. \end{aligned}$$

(17)

Now, taking derivatives of Eqs. (5) and (12)$_{3}$ with respect to $\epsilon$ (e.g., $\dot{\mathbf {g}}=\dot{\mathbf {G}} (\mathbf {D}\otimes \mathbf {D})$), and substituting them into Eq. (17), we obtain

$$\begin{aligned} \dot{W}(\mathbf {G})= & {} C\mathbf {g}\cdot \overset{\cdot }{\mathbf {g}}=Cg_{j} \mathbf {e}_{\mathbf {j}}\cdot \dot{G}_{iAB}D_{A}D_{B}\mathbf {e}_{i}=Cg_{i} \dot{G}_{iAB}D_{A}D_{B},\ \text {and} \nonumber \\ \dot{W}(\mathbf {H})= & {} A{\varvec{\alpha }} \cdot \overset{\cdot }{{\varvec{\alpha }}}=A\alpha _{j} \mathbf {e}_{\mathbf {j}}\cdot \dot{H}_{iABC}D_{A}D_{B}D_{C}\mathbf {e}_{i} =A\alpha _{i}\dot{H}_{iABC}D_{A}D_{B}D_{C}. \end{aligned}$$

(18)

But, the above are also equivalent to

$$\begin{aligned} \dot{W}(\mathbf {G})= & {} W_{\mathbf {G}}\cdot \overset{\cdot }{\mathbf {G}} =W_{G_{iAB}}(\mathbf {e}_{i}\otimes \mathbf {E}_{A}\otimes \mathbf {E}_{B} \otimes )\dot{G}_{jCD}(\mathbf {e}_{j}\otimes \mathbf {E}_{C}\otimes \mathbf {E}_{D}) =W_{G_{iAB}}\dot{G}_{iAB}\text { and} \nonumber \\ \dot{W}(\mathbf {H})= & {} W_{\mathbf {H}}\cdot \dot{\mathbf {H}}=W_{H_{iABC}} (\mathbf {e}_{i}\otimes \mathbf {E}_{A}\otimes \mathbf {E}_{B}\otimes \mathbf {E}_{C})\dot{H}_{jDEF}(\mathbf {e}_{j}\otimes \mathbf {E}_{D}\otimes \mathbf {E}_{E}\otimes \mathbf {E}_{F})=W_{H_{iABC}}\dot{H}_{iABC}.\nonumber \\ \end{aligned}$$

(19)

Hence, we compare Eqs. (18)–(19) and obtain

$$\begin{aligned} \frac{\partial W}{\partial G_{iAB}}=Cg_{i}D_{A}D_{B}\quad {\text { and }}\quad \frac{\partial W}{\partial H_{iABC}}=A\alpha _{i}D_{A}D_{B}D_{C}, \end{aligned}$$

(20)

or

$$\begin{aligned} W_{\mathbf {G}}=C\mathbf {g}\otimes \mathbf {D}\otimes \mathbf {D} \quad {\text { and }}\quad W_{\mathbf {G}}=A {\varvec{\alpha }} \otimes \mathbf {D} \otimes \mathbf {D}\otimes \mathbf {D}. \end{aligned}$$

(21)

In general, volumetric changes in the materials’ deformations are energetically expensive processes (see, for example, [44, 45]). Thus, for the desired application, the energy density function, Eq. (13), is augmented by the condition of bulk incompressibility such that

$$\begin{aligned} U(\mathbf {F}, \mathbf {G}, \mathbf {H},\ p)=W(\mathbf {F},\mathbf {G}, \ \mathbf {H})-p(J-1), \end{aligned}$$

(22)

where J is determinant of $\mathbf {F}$ and p is a Lagrange-multiplied filed. We continue by using the identity $\dot{J}=J_{\mathbf {F}}\ \cdot \dot{\mathbf {F}}=\mathbf {F}^{*} \cdot \dot{\mathbf {F}}$ and obtain the variational derivative of the above as

$$\begin{aligned} \dot{U}=(W_{\mathbf {F}}-p\mathbf {F}^{*})\cdot \dot{\mathbf {F}} +W_{\mathbf {G}}\cdot \dot{\mathbf {G}}+W_{\mathbf {H}}\cdot \dot{\mathbf {H}}, \end{aligned}$$

(23)

or, equivalently,

$$\begin{aligned} \dot{U}=(W_{F_{iA}}-pF_{iA}^{*})\dot{F}_{iA}+W_{G_{iAB}} \dot{G}_{iAB}+W_{H_{iABC}}\dot{H}_{iABC}. \end{aligned}$$

(24)

Clearly, the obtained variational form (23) is dependent on both the second and the third gradients of deformations as intended, i.e., the rate of change in curvature is now incorporated into the model of deformations via the third gradient of deformations.

3 Equilibrium

The derivation of the Euler equation and boundary conditions arising in second-gradient elasticity is well documented in [10,11,12, 34]. There authors formulate the weak form of the equilibrium equations by employing the principles of the virtual work statement:

$$\begin{aligned} \overset{\cdot }{E}=P, \end{aligned}$$

(25)

where P is the virtual work of the applied load and the superposed dot refers to the variational and/or Gateâux derivative. In this section, we present a variational formulation which accounts for the third gradient of the continuum deformation by means of iterated integrations by parts (see, for example, [11, 29, 30, 34, 35]). To proceed, we express the strain energy of the system as

$$\begin{aligned} E=\int _{\Omega }U(\mathbf {F}, \mathbf {G}, \mathbf {H},\ p)\hbox {d}A, \end{aligned}$$

(26)

where $\Omega$ is the domain occupied by a fiber–matrix material. Since the conservative loads are characterized by the existence of a potential L,  such that $P=\dot{L}$, the problem of determining equilibrium deformations is reduced to the problem of minimizing the potential energy $E-L.$ Hence, we find

$$\begin{aligned} \overset{\cdot }{E}=\int _{\Omega }\dot{U}(\mathbf {F}, \mathbf {G}, \mathbf {H},\ p)\hbox {d}A. \end{aligned}$$

(27)

Also, from Eq. (19), the energy variations with respect to the second and third gradients of deformations (i.e., $\mathbf {G}$ and $\mathbf {H}$) can be expressed as

$$\begin{aligned} \frac{\partial W}{\partial G_{iAB}}\overset{\cdot }{G}_{iAB}= & {} \frac{\partial W}{\partial G_{iAB}}u_{i,AB}\text { and} \nonumber \\ \frac{\partial W}{\partial H_{iABC}}\overset{\cdot }{H}_{iABC}= & {} \frac{\partial W}{\partial H_{iABC}}u_{i,ABC}, \end{aligned}$$

(28)

where

$$\begin{aligned} u_{i}=\dot{\chi }_{i} \end{aligned}$$

(29)

is the variation of the position field $\varvec{\chi }(\mathbf {X})$. Applying integration by parts, Eq. (28) yields

$$\begin{aligned} \frac{\partial W}{\partial G_{iAB}}u_{i,AB}= & {} \left( \frac{\partial W}{\partial G_{iAB}}u_{i,A}\right) _{,B}-\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}u_{i,A}\text { and} \nonumber \\ \frac{\partial W}{\partial H_{iABC}}u_{i,ABC}= & {} \left( \frac{\partial W}{\partial H_{iABC}}u_{i,AB}\right) _{,C}-\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,AB}. \end{aligned}$$

(30)

We now substitute Eqs. (24) and (30) into Eq. (27) and thereby obtain

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\Omega }\left[ \left( \frac{\partial W}{\partial F_{iA}} -pF_{iA}^{*}\right) \cdot \overset{\cdot }{F_{iA}} +\left( \frac{\partial W}{\partial G_{iAB}}u_{i,A}\right) _{,B} -\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}u_{i,A}\right. \nonumber \\&\left. +\left( \frac{\partial W}{\partial H_{iABC}}u_{i,AB}\right) _{,C} -\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,AB}\right] \hbox {d}A. \end{aligned}$$

(31)

Invoking Green–Stoke’s theorem, the above further reduces to

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\Omega }\left[ \frac{\partial W}{\partial F_{iA}} -pF_{iA}^{*}-\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}\right] u_{i,A}\hbox {d}A-\int _{\Omega }\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,AB}\hbox {d}A \nonumber \\&+\int _{\partial \Omega }\left[ \left( \frac{\partial W}{\partial G_{iAB}} u_{i,A}\right) N_{B}+\left( \frac{\partial W}{\partial H_{iABC}} u_{i,AB}\right) N_{C}\right] \hbox {d}S, \end{aligned}$$

(32)

where $\mathbf {N}$ is the rightward unit normal to the boundary $\partial \Omega$. To obtain the expression of the Piola stresses, we again apply the integration by parts on $\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,AB}$, i.e.,

$$\begin{aligned} \left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,AB} =\left( \left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,A}\right) _{,B} -\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,CB}u_{i,A}, \end{aligned}$$

(33)

and thus obtain from the second integral of Eq. (32) that

$$\begin{aligned} \int _{\Omega }\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C} u_{i,AB}\hbox {d}A=\int _{\Omega }\left( \left( \frac{\partial W}{\partial H_{iABC}} \right) _{,C}u_{i,A}\right) _{,B}-\left( \frac{\partial W}{\partial H_{iABC}} \right) _{,CB}u_{i,A}\hbox {d}A. \end{aligned}$$

(34)

But, Eq. (34) is equivalent to

$$\begin{aligned} \int _{\Omega }\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C} u_{i,AB}\hbox {d}A=\int _{\partial \Omega }\left( \left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,A}\right) N_{B}\hbox {d}S-\int _{\Omega }\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,CB}u_{i,A}\hbox {d}A, \end{aligned}$$

(35)

in which we again applied the Green–Stoke’s theorem. We then substitute Eq. (35) into Eq. (32) and subsequently obtain

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\Omega }\left[ \frac{\partial W}{\partial F_{iA}} -pF_{iA}^{*}-\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}\right] u_{i,A}\hbox {d}A\nonumber \\&-\left[ -\int _{\Omega }\left( \frac{\partial W}{\partial H_{iABC}} \right) _{,CB}u_{i,A}\hbox {d}A+\int _{\partial \Omega }\left( \left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}u_{i,A}\right) N_{B}\hbox {d}S\right] \nonumber \\&+\int _{\partial \Omega }\left[ \left( \frac{\partial W}{\partial G_{iAB}} u_{i,A}\right) N_{B}+\left( \frac{\partial W}{\partial H_{iABC}} u_{i,AB}\right) N_{C}\right] \hbox {d}S. \end{aligned}$$

(36)

Now, Eq. (36) may be recast as

$$\begin{aligned} \overset{\cdot }{E}=\int _{\Omega }P_{iA}\overset{\cdot }{F_{iA}} \hbox {d}A+\int _{\partial \Omega }\left[ \left\{ \frac{\partial W}{\partial G_{iAB}} -\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}\right\} u_{i,A}N_{B} +\frac{\partial W}{\partial H_{iABC}}u_{i,AB}N_{C}\right] \hbox {d}S, \end{aligned}$$

(37)

where

$$\begin{aligned} P_{iA}=\frac{\partial W}{\partial F_{iA}}-pF_{iA}^{*} -\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B} +\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,CB} \end{aligned}$$

(38)

is the expression of the Piola stress. It is evident from Eq. (38) that the resulting stress fields are dependent on both the second and third gradients of deformations. Also, it may be necessary to write the above equations in the tensorial form for the sake of clarity and completeness, especially for the terms which are obtained from the results of a multilinear transformations of higher-order tensors with mixed bases:

$$\begin{aligned} \overset{\cdot }{E}=\int _{\Omega }\mathbf {P}\cdot \overset{\cdot }{\mathbf {F}} \hbox {d}A+\int _{\partial \Omega }[W_{\mathbf {G}}^\mathrm{T}\mathbf {F}^\mathrm{T}\cdot \mathbf {N} +W_{\mathbf {H}}^\mathrm{T}(\nabla \mathbf {F})^\mathrm{T}\cdot \mathbf {N}-(\hbox {Div}(W_{\mathbf {H}}))^\mathrm{T} \mathbf {F}^\mathrm{T}\cdot \mathbf {N}]\hbox {d}S; \end{aligned}$$

(39)

and

$$\begin{aligned} \mathbf {P}=W_{\mathbf {F}}-p\mathbf {F}^{*}-\hbox {Div}(W_{\mathbf {G}}) +\hbox {Div}(\hbox {Div}(W_{\mathbf {H}})). \end{aligned}$$

(40)

In the case of initially straight fibers (i.e., $\nabla \mathbf {D}=\mathbf {0}$), we evaluate from Eq. (20) that

$$\begin{aligned} \left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}=Cg_{i,B}D_{A}D_{B} \quad {\text { and }}\quad \left( \frac{\partial W}{\partial H_{iABC}}\right) _{,CB} =A\alpha _{i,BC}D_{A}D_{B}D_{C}, \end{aligned}$$

(41)

and thus reduce Eq. (38) to

$$\begin{aligned} P_{iA}=\frac{\partial W}{\partial F_{iA}}-pF_{iA}^{*} -Cg_{i,B}D_{A}D_{B}+A\alpha _{i,BC}D_{A}D_{B}D_{C}. \end{aligned}$$

(42)

Finally, Eq. (42) satisfies

$$\begin{aligned} P_{iA,A}=0\quad {\text { or }}\quad \hbox {Div}(\mathbf {P})=0, \end{aligned}$$

(43)

which can be served as the Euler equilibrium equation for the reinforced solids occupying the domain of $\Omega$.

3.1 Example: neo-Hookean materials

In the case of neo-Hookean materials, the energy density function is given by

$$\begin{aligned} W(I_{1},I_{3})=\frac{\mu }{2}(I_{1}-3)-\mu \log I_{3}+\frac{\lambda }{2} (\log I_{3})^{2}, \end{aligned}$$

(44)

where $\mu$ and $\lambda$ are the material constants and $I_{1}$ and $I_{3}$ are, respectively, the first and third invariants of the deformation gradient tensor. By setting $I_{3}=1$, the incompressible model can be obtained as

$$\begin{aligned} W(I_{1})=\frac{\mu }{2}(I_{1}-3)=\frac{\mu }{2}(\mathbf {F}\cdot \mathbf {F}-3). \end{aligned}$$

(45)

Now taking the derivative of the above with respect to $\mathbf {F}$ and subsequently substituting it into Eq. (42), we find

$$\begin{aligned} P_{iA}=\mu F_{iA}-pF_{iA}^{*}-Cg_{i,B}D_{A}D_{B} +A\alpha _{i,BC}D_{A}D_{B}D_{C}, \end{aligned}$$

(46)

which is the expression of the Piola stress for the reinforced solid of neo-Hookean type. Hence, the corresponding Euler equilibrium equation satisfies

$$\begin{aligned} P_{iA,A}=\mu F_{iA,A}-p_{,A}F_{iA}^{*}-Cg_{i,AB}D_{A}D_{B} +A\alpha _{i,ABC}D_{A}D_{B}D_{C}=0, \end{aligned}$$

(47)

where we use the Piola’s identity (i.e., $F_{iA,A}^{*}=0$).

For example, we consider the reinforced solid which consists of initially straight fibers such that

$$\begin{aligned} \mathbf {D}=\mathbf {E}_{1}\ ({\text {i.e., }}D_{1}=1\quad {\text { and }}\quad D_{2}=0), \end{aligned}$$

(48)

and is subjected to finite plain deformations. Then, the equilibrium equation (47) reduces to

$$\begin{aligned} P_{iA,A}=\mu F_{iA,A}-p_{,A}F_{iA}^{*}-Cg_{i,11}+A\alpha _{i,111}=0. \end{aligned}$$

Further, we evaluate from Eqs. (5) and (12) that

$$\begin{aligned} g_{i}=F_{i1,1}, \alpha _{i}=F_{i1,11},\ F_{iA}=\chi _{i,A}, \ F_{iA}^{*}=\varepsilon _{ij}\varepsilon _{AB}F_{jB}, \end{aligned}$$

(49)

where $\varepsilon _{ij}$ is the 2-D permutation, $\varepsilon _{12}=-\varepsilon _{21}=1$, $\varepsilon _{11}=\varepsilon _{22}=0.$ Consequently, invoking Eqs. (48)–(49), together with the constraint of the bulk incompressibility (i.e., $\det \mathbf {F}=1$), we deliver the following system of PDEs,

$$\begin{aligned}&P_{iA,A}\mathbf {e}_{1}=(\mu \chi _{i,AA}-p_{,A}\varepsilon _{ij} \varepsilon _{AB}\chi _{j,B}-C\chi _{i,1111}+A\chi _{i,111111}) \mathbf {e}_{1}=0\; {\text { and }} \end{aligned}$$

(50)

$$\begin{aligned}&\chi _{1,1}\chi _{2,2}-\chi _{1,2}\chi _{2,1}=1, \end{aligned}$$

(51)

which solves for $\chi _{1}$, $\chi _{2}$ and p.

4 Boundary conditions

In this section, we present rigorous derivations vis-a-vis the admissible boundary conditions which arise in the third gradient of virtual displacement. Due to the presence of the high-order terms, the corresponding formulation turns out to be mathematically quite involved. However, the resulting expressions of boundary conditions are in relatively simple formats and thus mathematically tractable. To proceed, we apply the decomposition $P_{iA}u_{i,A}=(P_{iA} u_{i})_{,A}-P_{iA,A}u_{i}$ as in Eq. (30) and obtain from Eq. (37) that

$$\begin{aligned} \overset{\cdot }{E}{=}\int _{\partial \Omega }P_{iA}u_{i}N_{A}\hbox {d}S{-}\int _{\Omega } P_{iA,A}u_{i}\hbox {d}A{+}\int _{\partial \Omega }\left[ \left\{ \frac{\partial W}{\partial G_{iAB}} -\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}\right\} u_{i,A}N_{B} +\frac{\partial W}{\partial H_{iABC}}u_{i,AB}N_{C}\right] \hbox {d}S.\nonumber \\ \end{aligned}$$

(52)

Here, the Green–Stoke’s theorem is applied in the first term of Eq. (52). Since the Euler equation, $P_{iA,A}=0,$ holds in $\Omega$, the above reduces to

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial \Omega }P_{iA}u_{i}N_{A}\hbox {d}S+\int _{\partial \Omega }\left[ \left\{ \frac{\partial W}{\partial G_{iAB}}-\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}\right\} u_{i,A}N_{B}+\frac{\partial W}{\partial H_{iABC}}u_{i,AB}N_{C}\right] \hbox {d}S. \end{aligned}$$

(53)

Now, we project ${\varvec{\nabla }} \mathbf {u}$ onto the normal and tangential direction and thereby obtain

$$\begin{aligned} \nabla \mathbf {u}=\nabla \mathbf {u}(\mathbf {T}\otimes \mathbf {T}) +\nabla \mathbf {u}(\mathbf {N}\otimes \mathbf {N})=\mathbf {u}^{\prime } \otimes \mathbf {T}+\mathbf {u},_{\mathbf {N}}\otimes \mathbf {N}, \end{aligned}$$

(54)

such that $\mathbf {u}^{\prime }$and $\mathbf {u}_{,N}$ are, respectively, the tangential and normal derivatives of $\mathbf {u}$ on $\partial \Omega$, i.e.,

$$\begin{aligned} u_{i}^{\prime }=u_{i,A}T_{A},~u_{i,N}=u_{i,A}N_{A}, \end{aligned}$$

(55)

where $\mathbf {T}=\mathbf {X}^{\prime }(S)=\mathbf {k}\times \mathbf {N}$ defines the unit tangent to $\partial \Omega ,$ and $\mathbf {N}$ is the associated unit normal to the boundary. Thus, invoking Eqs. (54)–(55), $u_{i,A}$ can be decomposed into

$$\begin{aligned} u_{i,A}=\frac{\hbox {d}u_{i}}{\hbox {d}s}\frac{\hbox {d}s}{\hbox {d}X_{A}}+\frac{\hbox {d}u_{i}}{\hbox {d}N}\frac{\hbox {d}N}{\hbox {d}X_{A}} =u_{i}^{\prime }T_{A}+u_{i,N}N_{A}, \end{aligned}$$

(56)

and similarly for $u_{i,AB},$

$$\begin{aligned} u_{i,AB}=u_{i}^{\prime \prime }T_{A}T_{B}+u_{i}^{^{\prime }} (T_{A}^{\prime }T_{B}+T_{A,N}N_{B})+u_{i,N}(N_{A}^{^{\prime }} T_{B}+N_{A,N}N_{B})+u_{i,N}^{^{\prime }}(N_{A}T_{B}+T_{A}N_{B})+u_{i,NN}N_{A}N_{B}. \end{aligned}$$

(57)

Substituting the above results into Eq. (53) then yields

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\partial \Omega } P_{iA}u_{i}N_{A}\hbox {d}S+\int _{\partial w}\left\{ \left( \frac{\partial W}{\partial G_{iAB}}\right) -\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}\right\} \left( u_{i}^{\prime }T_{A}N_{B} +u_{i,N}N_{A}N_{B}\right) \hbox {d}S\nonumber \\&+\int _{\partial \Omega }\frac{\partial W}{\partial H_{iABC}} [u_{i}^{\prime \prime }T_{A}T_{B}+u_{i}^{\prime }(T_{A}^{^{\prime }} T_{B}+T_{A,N}N_{B})+u_{i,N}(N_{A}^{\prime }T_{B}+N_{A,N}N_{B}) \nonumber \\&+u_{i,N}^{\prime }(N_{A}T_{B}+T_{A}N_{B})+u_{i,NN}N_{A}N_{B}]N_{C}\hbox {d}S. \end{aligned}$$

(58)

In order to extract the admissible boundary conditions from Eq. (58), we make use of iterated integrations by parts. For example,

$$\begin{aligned}&\frac{\partial W}{\partial G_{iAB}}T_{A}N_{B}u_{i}^{\prime } =\left( \frac{\partial W}{\partial G_{iAB}}T_{A}N_{B}u_{i}\right) ^{\prime } -\left( \frac{\partial W}{\partial G_{iAB}}T_{A}N_{B}\right) ^{\prime }u_{i}, \end{aligned}$$

(59)

$$\begin{aligned}&\frac{\partial W}{\partial H_{iABC}} (N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})u_{i,N}^{\prime } \nonumber \\&\quad =\left[ \frac{\partial W}{\partial H_{iABC}} (N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})u_{i,N}\right] ^{\prime } -\left[ \frac{\partial W}{\partial H_{iABC}}(N_{A}T_{B}N_{C} +T_{A}N_{B}N_{C})\right] ^{\prime }u_{i,N}, \end{aligned}$$

(60)

$$\begin{aligned}&\frac{\partial W}{\partial H_{iABC}}T_{A}T_{B}N_{C}u_{i}^{\prime \prime } \nonumber \\&\quad =\left( \frac{\partial W}{\partial H_{iABC}}T_{A}T_{B} N_{C}u_{i}\right) ^{\prime \prime }+\left( \frac{\partial W}{\partial H_{iABC}} T_{A}T_{B}N_{C}\right) ^{\prime \prime }u_{i}-2\left[ \left( \frac{\partial W}{\partial H_{iABC}}T_{A}T_{B} N_{C}\right) ^{\prime }u_{i}\right] ^{\prime }, \end{aligned}$$

(61)

and similarly for other terms in Eq. (58). Consequently, Eq. (58) becomes

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\partial \Omega }\left[ P_{iA}N_{A}-\left\{ \frac{\partial W}{\partial G_{iAB}}T_{A}N_{B}-\left( \frac{\partial W}{\partial H_{iABC}} \right) _{,C}T_{A}N_{B}\right\} ^{\prime }\right] u_{i}\hbox {d}S \nonumber \\&-\int _{\partial \Omega }\left[ \left\{ \frac{\partial W}{\partial H_{iABC}} (T_{A}^{\prime }T_{B}N_{C}+T_{A,N}N_{B}N_{C})\right\} ^{\prime } +\left( \frac{\partial W}{\partial H_{iABC}}T_{A}T_{B} N_{C}\right) ^{\prime \prime }\right] u_{i}\hbox {d}S \nonumber \\&+\int _{\partial \Omega }\left[ \left\{ \frac{\partial W}{\partial G_{iAB}} T_{A}N_{B}-\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C} T_{A}N_{B}-2\left( \frac{\partial W}{\partial H_{iABC}} T_{A}T_{B}N_{C}\right) ^{\prime }\right\} u_{i}\right] ^{\prime }\hbox {d}S \nonumber \\&+\int _{\partial \Omega }\left[ \frac{\partial W}{\partial H_{iABC}} (T_{A}^{\prime }T_{B}N_{C}+T_{A,N}N_{B}N_{C})u_{i}\right] ^{\prime }\hbox {d}S \nonumber \\&+\int _{\partial \Omega }\left[ \frac{\partial W}{\partial H_{iABC}} (N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})u_{i,N}\right] ^{\prime }\hbox {d}S \nonumber \\&+\int _{\partial \Omega }\left[ \left\{ \left( \frac{\partial W}{\partial G_{iAB}} \right) -\left( \frac{\partial W}{\partial H_{iABC}}\right) _{,C}\right\} N_{A}N_{B}+\frac{\partial W}{\partial H_{iABC}}(N_{A}^{\prime } T_{B}+N_{A,N}N_{B})N_{C}\right] u_{i,N}\hbox {d}S \nonumber \\&-\int _{\partial \Omega }\left[ \left\{ \frac{\partial W}{\partial H_{iABC}} (N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})\right\} ^{\prime }\right] u_{i,N}\hbox {d}S \nonumber \\&+\int _{\partial \Omega }\left( \frac{\partial W}{\partial H_{iABC}} T_{A}T_{B}N_{C}u_{i}\right) ^{\prime \prime }\hbox {d}S+\int _{\partial \Omega } \frac{\partial W}{\partial H_{iABC}}u_{i,NN}N_{A}N_{B}N_{C}\hbox {d}S. \end{aligned}$$

(62)

But, in view of Eqs. (20) and (41) (e.g., $\frac{\partial W}{ \partial G_{iAB}}=Cg_{i}D_{A}D_{B}$, $\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B} =Cg_{i,B}D_{A}D_{B}$, etc.), the above may be recast as

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\partial \Omega }[P_{iA}N_{A}-\{(Cg_{i}-A \alpha _{i,C}D_{C})D_{A}T_{A}D_{B}N_{B}\}^{\prime }-\{A\alpha _{i}D_{C} N_{C}(D_{A}T_{A}^{\prime }D_{B}T_{B}+D_{A}T_{A,N}D_{B}N_{B})\}^{\prime }]u_{i}\hbox {d}S \nonumber \\&+\int _{\partial \Omega }[\left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}D_{C} N_{C}\right) ^{\prime \prime }]u_{i}\hbox {d}S+\sum \left\| A\alpha _{i} (D_{A}T_{A}^{\prime }D_{B}T_{B}D_{C}N_{C}+D_{A}T_{A,N}D_{B}N_{B}D_{C} N_{C})u_{i}\right\| \nonumber \\&+\sum \left\| [(Cg_{i}-A\alpha _{i,C}D_{C})D_{A}T_{A}D_{B}N_{B}-2 \left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}D_{C}N_{C}\right) ^{\prime }]u_{i}\right\| \nonumber \\&+\sum \left\| A\alpha _{i}(D_{A}N_{A}D_{B}T_{B}D_{C}N_{C}+D_{A}T_{A}D_{B} N_{B}D_{C}N_{C})u_{i,N}\right\| +\sum \left\| \frac{\hbox {d}}{\hbox {d}s} \left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}N_{C}D_{C}u_{i}\right) \right\| \nonumber \\&+\int _{\partial \Omega }\left[ (Cg_{i}-A\alpha _{i,C}D_{C})D_{A}N_{A}D_{B}N_{B}+A\alpha _{i}D_{C}N_{C} (D_{A}N_{A}^{\prime }D_{B}T_{B}+D_{A}N_{A,N}D_{B}N_{B})\right] u_{i,N}\hbox {d}S \nonumber \\&-\int _{\partial \Omega }[\left\{ A\alpha _{i}D_{A}D_{B}D_{C}(N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})\right\} ^{\prime } u_{i,N}]\hbox {d}S+\int _{\partial \Omega }(A\alpha _{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C}u_{i,NN})\hbox {d}S, \end{aligned}$$

(63)

where the double bar symbol refers to the jump across the discontinuities on the boundary $\partial \Omega$ (i.e., $\left\| *\right\| =\left( *\right) ^{+}-\left( *\right) ^{-}$) and the sum refers to the collection of all discontinuities. Since the virtual work statement ($\overset{\cdot }{E}=P$) implies that the admissible mechanical powers are of the form

$$\begin{aligned} P=\int _{\partial w_{t}}t_{i}u_{i}\hbox {d}S+\int _{\partial w} m_{i}u_{i,N}\hbox {d}S+\int _{\partial w}r_{i}u_{i,NN}\hbox {d}S+\sum f_{i}u_{i} +\sum h_{i}u_{i,N}, \end{aligned}$$

(64)

By comparing Eqs. (63) and (64), we find that

$$\begin{aligned} \mathbf {t}= & {} \mathbf {PN}+\frac{\hbox {d}^{2}}{\hbox {d}s^{2}}[A\varvec{\alpha } (\mathbf {D}\cdot \mathbf {T})^{2}(\mathbf {D}\cdot \mathbf {N})] \nonumber \\&-\frac{\hbox {d}}{\hbox {d}s}[(C\mathbf {g}-A(\nabla {\varvec{\alpha }} )\mathbf {D}) (\mathbf {D}\cdot \mathbf {T})(\mathbf {D}\cdot \mathbf {N})-A{\varvec{\alpha }} (\mathbf {D}\cdot \mathbf {N})(\mathbf {D}\cdot \mathbf {T})(\mathbf {D} \cdot \mathbf {T}^{\prime })+A{\varvec{\alpha }} (\mathbf {D} \cdot \mathbf {N})^{2}(\mathbf {D}\cdot \mathbf {T}_{,N})], \nonumber \\ \mathbf {m}= & {} (C\mathbf {g}-A(\nabla \alpha )\mathbf {D})(\mathbf {D}\cdot \mathbf {N}) ^{2}+A\varvec{\alpha }(\mathbf {D}\cdot \mathbf {N})[(\mathbf {D} \cdot \mathbf {N}^{\prime })(\mathbf {D}\cdot \mathbf {T})+(\mathbf {D} \cdot \mathbf {N}_{,N})(\mathbf {D}\cdot \mathbf {N})] \nonumber \\&-\frac{\hbox {d}}{\hbox {d}s}[2A\varvec{\alpha }(\mathbf {D}\cdot \mathbf {T}) (\mathbf {D}\cdot \mathbf {N})^{2}], \nonumber \\ \mathbf {r}= & {} A\varvec{\alpha }(\mathbf {D}\cdot \mathbf {N})^{3}, \nonumber \\ \mathbf {f}= & {} (C\mathbf {g}-A(\nabla {\varvec{\alpha }} )\mathbf {D}) (\mathbf {D}\cdot \mathbf {T})(\mathbf {D}\cdot \mathbf {N}) -\frac{\hbox {d}}{\hbox {d}s}[2A\varvec{\alpha }(\mathbf {D}\cdot \mathbf {T})^{2} (\mathbf {D}\cdot \mathbf {N})] \nonumber \\&+A{\varvec{\alpha }} [ (\mathbf {D}\cdot \mathbf {T}^{\prime }) (\mathbf {D}\cdot \mathbf {N})(\mathbf {D}\cdot \mathbf {N})+(\mathbf {D} \cdot \mathbf {T}_{,N})(\mathbf {D}\cdot \mathbf {N})^{2}],\nonumber \\ \frac{\hbox {d}}{\hbox {d}s}[\mathbf {f}]= & {} \frac{\hbox {d}}{\hbox {d}s}[A\varvec{\alpha }(\mathbf {D} \cdot \mathbf {N})(\mathbf {D}\cdot \mathbf {N})], \nonumber \\ \mathbf {h}= & {} 2A\varvec{\alpha }((\mathbf {D}\cdot \mathbf {T})(\mathbf {D} \cdot \mathbf {N})^{2}, \end{aligned}$$

(65)

where $\mathbf {t},\mathbf {m},$ and $\mathbf {f}$ are the expressions of edge tractions, edge moments and the corner forces, respectively. More importantly, unlike those from the second-gradient models, additional boundary conditions (i.e., $\mathbf {r}$, $\frac{\hbox {d}}{\hbox {d}s}[\mathbf {f}]$ and $\mathbf {h}$) appeared as a result of the introduction of the third gradient of deformations. These boundary conditions are the set of admissible contact interactions that can be sustained by third-gradient continua (see, also, [11, 30, 34] and references therein). In fact, such interaction forces are in conjugation with the Piola-type triple stress and are necessary to capture the internal energy contributions to the contact interactions on edges and points of Cauchy cuts [28,29,30]. In the present case, this would mean the effects of local interactions between the fiber and matrix on the adjoined deformation fields.

Remark

The proposed model has a close similarity to the theory of micropolar elasticity, which admits additional degrees of freedom associated with the rotation of a local point (microstructure) pertaining to couple stresses. Within the description of the proposed model, this is achieved via the computation of the third gradient of the continuum deformation, i.e., the rate of changes in curvature (local point rotations), which is determined by the imposition of the triple forces (e.g., $\mathbf {r},\mathbf {h}$) on the desired boundaries. Therefore, the proposed model can be used as an alternative 2D Cosserat theory of nonlinear elasticity.

In a typical environment where fibers are aligned along the directions of either normal and/or tangential to the boundary (e.g., rectangular boundaries), we compute

$$\begin{aligned} (\mathbf {D}\cdot \mathbf {T})(\mathbf {D}\cdot \mathbf {N})=0\quad {\text { and }}\quad \nabla \mathbf {T}={\varvec{\nabla }} \mathbf {N}=0, \end{aligned}$$

(66)

and thereby reduce Eq. (65) to

$$\begin{aligned} \mathbf {t}= & {} \mathbf {PN}, \nonumber \\ \mathbf {m}= & {} [C\mathbf {g}-A(\nabla {\varvec{\alpha }} )\mathbf {D}] (\mathbf {D}\cdot \mathbf {N})^{2}, \nonumber \\ \mathbf {r}= & {} A\varvec{\alpha }(\mathbf {D}\cdot \mathbf {N})^{3}, \nonumber \\ \mathbf {f}= & {} 0, \nonumber \\ \frac{\hbox {d}}{\hbox {d}s}[\mathbf {f}]= & {} 0, \nonumber \\ \mathbf {h}= & {} 0, \end{aligned}$$

(67)

where

$$\begin{aligned} P_{iA}= & {} \mu F_{iA}-pF_{iA}^{*}-Cg_{i,B}D_{A}D_{B} +A\alpha _{i,BC}D_{A}D_{B}D_{C}, \nonumber \\ g_{i}= & {} F_{iA,B}D_{A}D_{B}\quad {\text { and }}\quad \alpha _{i}=F_{iA,BC}D_{A}D_{B}D_{C}. \end{aligned}$$

(68)

Hence, in this case (Eq. (66)), $\mathbf {r}$ is the only meaningful boundary force associated with the third gradient of deformations (i.e., $\mathbf {f},~\mathbf {f}^{\prime }$ and $\mathbf {h}$ are identically vanishes), which is required to obtain the unique solution. We note here that the clarification of such triple forces and associated boundary conditions (Eq. (65)) may be of particular mechanical interest to practitioners and theoreticians alike. In this regard, a number of cases are examined throughout the following section. However, the attempts are intrinsically limited due to the paucity of experimental resources which certainly deserve further researches.

Lastly, by imposing the admissible set of boundary conditions (Eq. (67)), the solution of the PDE system (Eqs. (50)–(51)) can be obtained via commercial packages (e.g., Matlab, COMSOL, etc.). We reserve the details of numerical procedures in “Appendix” for the sake of coherence and consistency.

5 Results and discussion

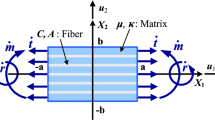
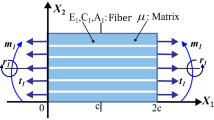
For the purpose of demonstration, we simulate a set of numerical solutions describing the deformations of a rectangular composite that is reinforced with fibers resistant to flexure and subjected to the double force $\mathbf {m}$ (bending moment) and triple force $\mathbf {r}$ (see Fig. 1). More precisely, a half problem is considered in which the corresponding boundary conditions are prescribed as

$$\begin{aligned} m_{1}= & {} C\chi _{1,11}-A\chi _{1,1111}=M/\mu , r_{1} =A\chi _{1,111}=r/\mu , \nonumber \\ m_{2}= & {} C\chi _{2,11}-A\chi _{2,1111}=0, r_{2}=A\chi _{2,111}=0,\nonumber \\ \chi _{1}= & {} 0, \chi _{2}=0,\text { at }x=c, \end{aligned}$$

(69)

and symmetric boundary conditions are imposed at $x=0$. It is noted that, unless otherwise specified, the corresponding data are obtained under the normalized setting (e.g., $\frac{C}{\mu }=150$, $\frac{A}{\mu }=50$, etc.). Also, here and henceforth, we conveniently refer to material constants associated with the Piola-type double stress and triple stress (i.e., C and A) as the ‘double stress parameter’ and ‘triple stress parameter,’ respectively.

Fig. 1

Schematic of problem

The obtained solutions in Fig. 2 illustrate gradual decreases in deformed configurations of the composite with increasing double stress parameter, C (bending stiffness of fibers), which also agrees with the results in [25, 37]. Further, the corresponding deformation fields in Figs. 3 and 4 demonstrate sensitivity to both the triple stress parameter, A,  and the triple force, $\mathbf {r}$, as intended, and accommodate the solutions from the second-gradient model [25, 37] when the third-gradient effects are removed (see Fig. 5).

Fig. 2

Deformed configurations with respect to $C/\mu$

Fig. 3

Deformed configurations with respect to $A/\mu$

Fig. 4

Deformed configurations with respect to $r/\mu$

Fig. 5

Comparison with the existing results [25, 37]

More importantly, we examine shear strain fields and the associated shear angle distributions over the domain of interest in order to have a more in-depth understanding of the influences of the third gradient of deformations. In the analysis, the shear strain gradients and shear angles are computed using the following relations [22]:

$$\begin{aligned} \phi ^{\prime }=\frac{u_{2}^{\prime \prime }(1+u_{1}^{\prime }) -u_{2}^{\prime }u_{1}^{\prime \prime }}{u_{2}^{\prime 2}+(1+u_{1}^{\prime })^{2}}, \end{aligned}$$

(70)

and

$$\begin{aligned} \phi =\tan ^{-1}\left( \frac{\chi _{2,1}-\chi _{1,1}}{2+\chi _{1,1}+\chi _{2,1}}\right) . \end{aligned}$$

(71)

It is shown in Fig. 6 that the magnitudes of shear strains either gradually increase or decrease with respect to the signs of applied triple force, i.e., the shear strain increases when $\mathbf {r}>0$ and decreases with $\mathbf {r}<0$. This further leads to the smooth and dilatational shear angle distributions throughout the entire domain of interest where the rate of dilatation is governed by the triple force $\mathbf {r}$ (Fig. 7). In other words, when the composite is subjected to the double force $\mathbf {m}$, the proposed model predicts multiple configurations of shear angle distributions, depending on the applied triple force $\mathbf {r}$, whereas only one configuration (smooth but non-dilatational distribution) is possible within the description of the strain gradient theory (see, for example, [23, 24, 27]). Indeed, the shear angle distribution from the result of the second-gradient continuum model is the special case of those predicted by the obtained solution in the limit of the vanishing triple force (i.e., $\mathbf {r}=0$, see Fig. 8). This also can be seen directly from Eqs. (47), (67) and (68). For example, by setting $\mathbf {r}=0$, we find from Eq. (67)$_{3}$ that,

Fig. 6

Shear strain gradients with respect to $\mathbf {r} : \mathbf {r}>0$ (left) and $\mathbf {r}<0$ (right)

Fig. 7

Shear angle contours with respect to $\mathbf {r} : \mathbf {r}>0$ (left) and $\mathbf {r}<0$ (right)

Fig. 8

Shear angle contours: first gradient (left), second gradient (middle), third gradient (right)

$$\begin{aligned} \mathbf {r}=A\varvec{\alpha }(\mathbf {D}\cdot \mathbf {N})^{3}=0. \end{aligned}$$

(72)

Accordingly, the boundary conditions in Eq. (67) and the expression of the Piola-type stress (Eq. (68)) reduce to

$$\begin{aligned} \mathbf {t}= & {} \mathbf {PN},\ \mathbf {m}=C\mathbf {g} (\mathbf {D}\cdot \mathbf {N})^{2},\text { and} \end{aligned}$$

(73)

$$\begin{aligned} P_{iA}= & {} \mu F_{iA}-pF_{iA}^{*}-Cg_{i,B}D_{A}D_{B}. \end{aligned}$$

(74)

Similarly, by invoking Eq. (72), the system of coupled PDEs (Eq. (47)) becomes

$$\begin{aligned} P_{iA,A}=\mu F_{iA,A}-p_{,A}F_{iA}^{*}-Cg_{i,AB}D_{A}D_{B}=0. \end{aligned}$$

(75)

Hence, the corresponding equations are now reduced to those obtained from the strain gradient theory (see Eqs. (24), (37), and (38) in [37]).

Remark

The triple force $\mathbf {r}$ is meaningful only if its conjugate pair exists: the Piola-type triple stress. In the present case, the stress expression in Eq. (46) is a combination of the Piola-type stress ($\mu F_{iA}$), double stress ($Cg_{i,B}D_{A}D_{B}$) and triple stress ($A\alpha _{i,BC}D_{A}D_{B}D_{C}$) such that the third gradient of the deformation term in Eq. (46) (i.e., $A\alpha _{i,BC}D_{A}D_{B}D_{C}$) can be interpreted as the energy pair of the applied triple force $\mathbf {r}$. The same statement holds in cases of the second-gradient continuum models. For example, the Piola-type double stress ($Cg_{i,B}D_{A}D_{B}$) is the energy conjugate to the double force $\mathbf {m}$ (see, also, [28, 29]).

Lastly, we summarize the associated field distributions predicted, respectively, by the first-, second- and third-gradient continuum models for the purpose of comparison. In the summary, the second strain gradient, strain gradient, shear angle, deformation gradient and boundary conditions are denoted as SSG, SG, SA, DG and BCs, respectively. It is evident from Table 1 that the Nth-order continuum model predicts continuous (but not necessarily smooth) shear strain gradient fields up to (${N-1}$)th order. For example, the second-order continuum model predicts the first gradient of the shear strain fields (SG), see case b) in Table 1. Further, in order to uniquely determine such fields, the corresponding Nth-order forces are required, which can be imposed on the desired boundaries only if there exists their energy couple, the Nth-order gradient of the deformation map (see DG and BCs in Table 1).

Table 1 Field distributions predicted by the Nth-order gradient continuum model

5.1 Characterization of the triple stress parameter

In the previous section, we observed that the responses of the composite and the associated shear strain and shear angle distributions are sensitive to boundary forces (i.e., double and triple forces) and, in particular, their energy couples via the Nth-order stress parameters (i.e., C and A ). The double stress parameter C represents the bending rigidity of a fiber such that each fiber family has their own unique C values, obtained from bending experiments. However, little has been devoted to the characterization of the parameter A mainly due to the complex nature of mechanical interactions on edges and points (see, also, [28,29,30]). Hence, in this section, we address this deficiency and investigate whether there exists a unique characteristic constant A associated with the Piola-type triple stress. The accuracy and utility of the proposed model are also examined via comparison with the experimental results.

Two sets of experiments were designed for this purpose (see Figs. 9, 10): a three-point bending test of a crystalline nanocellulose (CNC) fiber composite ($C=150\,\hbox {GPa}$, $\mu =1\,\hbox {GPa}$); and a bending test of a nylon-6 fiber neoprene rubber composite ($C=2000\,\hbox {MPa}$, $\mu =1\,\hbox {MPa}$), which is clamped on both ends. In both experiments, the out-of-plane direction ($x_{3}$) is aligned with either the loading cylinder or the guide clamps. This setting is a particular case of the proposed model when $c\gg d.$ The resulting displacements are simultaneously recorded via the MTS load cell and high-speed camera.

Fig. 9

CNC fiber composites bending test: experimental data and theoretical predictions

Fig. 10

Nylon-6 fiber neoprene rubber composite experimental setup

Figures 9 and 11 illustrate that the proposed model successfully predicts the deformation profiles of both the CNC fiber composite and nylon fiber composite with a maximum error of less then 2%. But more importantly, the results in Fig. 12 indicate that there exists a certain range of values for A which minimize the prediction errors. Further, we found that these characteristic numbers are unique for each composite and not affected by either the types of boundary conditions or the applied loadings (e.g., $\mathbf {r},\mathbf {m}$, see Fig. 12). Therefore, it is inferred that A is indeed an intrinsic property of the examined composites pertaining to the Piola-type triple stress, and can be uniquely determined for each case. For example, $A=127$ for CNC fiber composite and $A=0.825$ for nylon rubber composite. Here, we may refer to A as the triple modulus of composites for use in analogous studies.

Lastly, we note that the obtained results can be further extended to encompass more practically important problems: determining the triple modulus of the composites subjected to different loading conditions (e.g., bias extension); examining the existence of the triple modulus for an arbitrary composite; analyzing the effects of the residual Piola-type triple stresses on the mechanical responses of a composite. The researches on these subjects are currently underway, and our intention is to report elsewhere when we collect enough case studies.

Fig. 11

Nylon-6 fiber neoprene rubber composite: experimental data and theoretical predictions

Fig. 12

Maximum error with respect to A: CNC fiber composite (left), neoprene rubber composite (right)

Appendix: Finite element analysis of the fourth-order coupled PDE

The resulting systems of PDEs (Eqs. (50)–(51)) are sixth-order differential equations with coupled nonlinear terms. The case of such less regular PDEs deserves delicate mathematical treatment as done similarly in [25, 37] and is of particular practical interest. Therefore, it is not trivial to demonstrate numerical analysis procedures regarding FE analysis.

For preprocessing, Eqs. (50)–(51) may be recast as

$$\begin{aligned} \mu \left( Q+\chi _{1,22}\right) -A\chi _{2,2} +B\chi _{2,1}-CQ_{,11}+AS_{,11}= & {} 0, \nonumber \\ \mu \left( R+\chi _{2,22}\right) +A\chi _{1,2} -B\chi _{1,1}-CR_{,11}+AT_{,11}= & {} 0, \nonumber \\ Q-\chi _{1,11}= & {} 0, \nonumber \\ R-\chi _{2,11}= & {} 0, \nonumber \\ S-Q_{,11}= & {} 0, \nonumber \\ T-R_{,11}= & {} 0, \nonumber \\ A-\mu (Q+\chi _{1,22})-CS= & {} 0, \nonumber \\ B-\mu (R+\chi _{2,22})-CT= & {} 0, \end{aligned}$$

(76)

where $Q=\chi _{1,11}$, $R=\chi _{2,11}$, $S=Q_{,11}$ and $T=R_{,11}$. Thus, we reduced the order of deferential equations from three coupled equations of sixth order to eight coupled equations of second order. In particular, the nonlinear terms (e.g., $A\chi _{2,2}$, $B\chi _{2,1}$, etc.) in the above equations can be systematically treated via the Picard iterative procedure;

$$\begin{aligned} -A_{\mathrm{initial}}\chi _{2,2}^{\mathrm{initial}}+B_{\mathrm{initial}}\chi _{2,1}^{\mathrm{initial}}&\Longrightarrow&-A_{0}\chi _{2,2}^{0}+B_{0}\chi _{2,1}^{0}, \nonumber \\ A_{\mathrm{initial}}\chi _{1,2}^{\mathrm{initial}}-B_{\mathrm{initial}}\chi _{1,1}^{\mathrm{initial}}&\Longrightarrow&A_{0}\chi _{1,2}^{0}-B_{0}\chi _{1,1}^{0}, \end{aligned}$$

(77)

where the values of A and B continue to be updated based on their previous estimations (e.g., $A_{1}$ and $B_{1}$ are refreshed by their previous pair of $A_{0}$ and $B_{0})$ as iteration progresses. Hence, we generalize the above expression for N number of iterations as

$$\begin{aligned} -A_{N-1}\chi _{2,2}^{N-1}+B_{N-1}\chi _{2,1}^{N-1}&\Longrightarrow&-A_{N}\chi _{2,2}^{N}+B_{N}\chi _{2,1}^{N}, \nonumber \\ A_{N-1}\chi _{1,2}^{N-1}-B_{N-1}\chi _{1,1}^{N-1}&\Longrightarrow&A_{N}\chi _{1,2}^{N}-B_{N}\chi _{1,1}^{N}, \end{aligned}$$

(78)

in which the number of iteration can be determined by a convergence criteria.

In addition, the weighted forms of Eq. (76) are obtained by

$$\begin{aligned} 0= & {} \int \limits _{\Omega ^{e}}w_{1}(\mu \left( Q+\chi _{1,22}\right) -A\chi _{2,2}+B\chi _{2,1}-CQ_{,11}+AS_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{2}(\mu \left( R+\chi _{2,22}\right) +A\chi _{1,2}-B\chi _{1,1}-CR_{,11}+AT_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{3}(Q-\chi _{1,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{4}(R-\chi _{2,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{5}(S-Q_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{6}(T-R_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{7}(A-\mu (Q+\chi _{1,22})-CS)d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{8}(B-\mu (R+\chi _{2,22})-CT)d\Omega . \end{aligned}$$

(79)

Applying integration by parts and Green–Stoke’s theorem (e.g., $\mu \int _{\Omega ^{e}}w_{1}\chi _{1,22}d\Omega =-\mu \int _{\Omega ^{e}}w_{1,2}\chi _{1,2}d\Omega +\mu \int _{\Omega ^{e}}w_{1}\chi _{1,2}Nd\Gamma$), we obtain from the above that

$$\begin{aligned} 0= & {} \int \limits _{\Omega ^{e}}(\mu w_{1}Q-\mu w_{1,2}\chi _{1,2}-w_{1}A_{0} \chi _{2,2}+w_{1}B_{0}\chi _{2,1}+Cw_{1,1}Q_{,1}-Aw_{1,1}S_{,1})d\Omega \nonumber \\&+\int \limits _{\partial \Gamma ^{e}}\mu w_{1}\chi _{1,2}Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}Cw_{1}Q_{,1}Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}Aw_{1}S_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(\mu w_{2}R-\mu w_{2,2}\chi _{2,2}+w_{2}A_{0} \chi _{1,2}-w_{2}B_{0}\chi _{1,1}+Cw_{2,1}R_{,1}-Aw_{2,1}T_{,1})d\Omega \nonumber \\&+\int \limits _{\partial \Gamma ^{e}}\mu w_{2}\chi _{2,2}Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}Cw_{2}R_{,1}Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}Aw_{2}T_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{3}Q+w_{3,1}\chi _{1,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{3}\chi _{1,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{4}R+w_{4,1}\chi _{2,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{4}\chi _{2,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{5}S+w_{5,1}Q_{,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{5}Q_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{6}T+w_{6,1}R_{,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{6}R_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{7}(A_{0}-\mu Q-CS-\mu w_{7,2}\chi _{1,2})d\Omega -\int \limits _{\partial \Gamma ^{e}}\mu w_{7}\chi _{1,2}Nd\Gamma \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{8}(B_{0}-\mu R-CT-\mu w_{8,2}\chi _{1,2})d\Omega -\int \limits _{\partial \Gamma ^{e}}\mu w_{7}\chi _{2,2}Nd\Gamma , \end{aligned}$$

(80)

where $\Omega$, $\partial \Gamma$ and $\mathbf {N}$ are the domain of interest, the associated boundary, and the rightward unit normal to the boundary $\partial \Gamma$ in the sense of the Green–Stoke’s theorem, respectively. The unknowns, $\chi _{1}$, $\chi _{2}$, Q, R, S, T, A and B can be written in the form of Lagrangian polynomial as

$$\begin{aligned} (*)=\sum _{j=1}^{n=4}[(*)_{j}\Psi _{j}(x, y)]. \end{aligned}$$

(81)

Thus, the test function w is obtained by

$$\begin{aligned} w_{m}=\sum _{i=1}^{n=4}w_{m}^{i}\Psi _{i}(x, y)\quad {\text { and }}\quad m=1,2,3,\ldots ,8. \end{aligned}$$

(82)

Here, $w_{i}$ is weight of the test function and $\Psi _{i}(x,y)$ are the shape functions for the four-node rectangular elements such that

$$\begin{aligned} \Psi _{1}=\frac{(x-c)(y-d)}{cd},\Psi _{2}=\frac{x(y-d)}{-cd},~\Psi _{3} =\frac{xy}{cd}\quad {\text { and }}\quad \Psi _{4}=\frac{y(x-c)}{-cd}. \end{aligned}$$

(83)

By means of Eq. (81), Eq. (80) can be rewritten in terms of Lagrangian polynomial representation as

$$\begin{aligned} 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i}\Psi _{j} +C\Psi _{i,1}\Psi _{j,1})d\Omega \right\} Q_{j}\nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}} (\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{1j}-\sum _{i,j=1}^{n} \left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}A_{0}\Psi _{j,2}-\Psi _{i}B_{0}\Psi _{j,1})d\Omega \right\} \chi _{2j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(A\Psi _{i,1}\Psi _{j,1})d\Omega \right\} S_{j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{1,2})Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}(C\Psi _{i}Q_{,1})Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}A\Psi _{i}S_{,1}Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i}\Psi _{j} +C\Psi _{i,1}\Psi _{j,1})d\Omega \right\} R_{j}\nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{2j}+\sum _{i,j=1}^{n} \left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}A_{0}\Psi _{j,2}-\Psi _{i}B_{0}\Psi _{j,1})d\Omega \right\} \chi _{1j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(A\Psi _{i,1}\Psi _{j,1})d\Omega \right\} T_{j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{2,2})Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}(C\Psi _{i}R_{,1})Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}A\Psi _{i}T_{,1}Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} Q_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} \chi _{1j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}\chi _{1,1})Nd\Gamma ,\nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} R_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} \chi _{2j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}\chi _{2,1})Nd\Gamma ,\nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} S_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} Q_{j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}Q_{,1})Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} T_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} R_{j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}R_{,1})Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} A_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i} \Psi _{j})d\Omega \right\} Q_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(C\Psi _{i} \Psi _{j})d\Omega \right\} S_{j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{1j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{1,2})Nd\Gamma ,\nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} B_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i} \Psi _{j})d\Omega \right\} R_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(C\Psi _{i} \Psi _{j})d\Omega \right\} T_{j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{2j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{2,2})Nd\Gamma . \end{aligned}$$

(84)

Now, for the local stiffness matrices and forcing vectors for each elements, we find

$$\begin{aligned} \left[ \begin{array}{cccc} K_{11}^{11} &{}\quad K_{12}^{11} &{}\quad K_{13}^{11} &{}\quad K_{14}^{11} \\ K_{21}^{11} &{}\quad K_{22}^{11} &{}\quad K_{23}^{11} &{}\quad K_{24}^{11} \\ K_{31}^{11} &{}\quad K_{32}^{11} &{}\quad K_{33}^{11} &{}\quad K_{34}^{11} \\ K_{41}^{11} &{}\quad K_{42}^{11} &{}\quad K_{43}^{11} &{}\quad K_{44}^{11} \end{array}\right] _{\mathrm{Local}}\left[ \begin{array}{c} \chi _{1}^{1} \\ \chi _{1}^{2} \\ \chi _{1}^{3} \\ \chi _{1}^{4} \end{array}\right] _{\mathrm{Local}}=\left[ \begin{array}{c} F_{1}^{1} \\ F_{2}^{1} \\ F_{3}^{1} \\ F_{4}^{1} \end{array}\right] _{\mathrm{Local}}, \end{aligned}$$

(85)

or alternatively, in a compact form,

$$\begin{aligned} \left[ K_{ij}^{11}\right] [\chi _{1}^{i}]=[F_{i}^{1}]\text { for }i, j=1,2,3,4, \end{aligned}$$

(86)

where

$$\begin{aligned} \left[ K_{ij}^{11}\right] =\int \limits _{\Omega ^{e}}(\mu \Psi _{i,2} \Psi _{j,2})d\Omega , \end{aligned}$$

(87)

and

$$\begin{aligned} {[}F_{i}^{1}]=-\mu \int \limits _{\partial \Gamma ^{e}}\Psi _{i} \chi _{1,2}Nd\Gamma +C\int \limits _{\partial \Gamma ^{e}}\Psi _{i}Q_{,1}Nd \Gamma -\int \limits _{\partial \Gamma ^{e}}A\Psi _{i}S_{,1}Nd\Gamma . \end{aligned}$$

(88)

Accordingly, the unknowns (i.e., Q, R, S, T, A and B) can be expressed as

$$\begin{aligned} Q_{i}=\{\chi _{1}^{i}\}_{,11}, R_{i}=\{\chi _{2}^{i}\}_{,11}, S_{i}=\{Q^{i}\}_{,11}\text { etc.} \end{aligned}$$

(89)

Finally, we repeat the same procedures for the rest of components (e.g., $\left[ K_{ij}^{21}\right] [\chi _{2}^{i}]=[F_{i}^{2}]$, etc.) and thereby obtain the following systems of equations (in the Global form) for each individual elements.

$$\begin{aligned} \left[ \begin{array}{cccccccc} \left[ K^{11}\right] &{}\quad \left[ K^{12}\right] &{}\quad \left[ K^{13}\right] &{}\quad \left[ K^{14}\right] &{}\quad \left[ K^{15}\right] &{}\quad \left[ K^{16}\right] &{}\quad \left[ K^{17}\right] &{}\quad \left[ K^{18}\right] \\ \left[ K^{21}\right] &{}\quad \left[ K^{22}\right] &{}\quad \left[ K^{23}\right] &{}\quad \left[ K^{24}\right] &{}\quad \left[ K^{25}\right] &{}\quad \left[ K^{26}\right] &{}\quad \left[ K^{27}\right] &{}\quad \left[ K^{28}\right] \\ \left[ K^{31}\right] &{}\quad \left[ K^{32}\right] &{}\quad \left[ K^{33}\right] &{}\quad \left[ K^{34}\right] &{}\quad \left[ K^{35}\right] &{}\quad \left[ K^{36}\right] &{}\quad \left[ K^{37}\right] &{}\quad \left[ K^{38}\right] \\ \left[ K^{41}\right] &{}\quad \left[ K^{42}\right] &{}\quad \left[ K^{43}\right] &{}\quad \left[ K^{44}\right] &{}\quad \left[ K^{45}\right] &{}\quad \left[ K^{46}\right] &{}\quad \left[ K^{47}\right] &{}\quad \left[ K^{48}\right] \\ \left[ K^{51}\right] &{}\quad \left[ K^{52}\right] &{}\quad \left[ K^{53}\right] &{}\quad \left[ K^{54}\right] &{}\quad \left[ K^{55}\right] &{}\quad \left[ K^{56}\right] &{}\quad \left[ K^{57}\right] &{}\quad \left[ K^{58}\right] \\ \left[ K^{61}\right] &{}\quad \left[ K^{62}\right] &{}\quad \left[ K^{63}\right] &{}\quad \left[ K^{64}\right] &{}\quad \left[ K^{65}\right] &{}\quad \left[ K^{66}\right] &{}\quad \left[ K^{67}\right] &{}\quad \left[ K^{68}\right] \\ \left[ K^{71}\right] &{}\quad \left[ K^{72}\right] &{}\quad \left[ K^{73}\right] &{}\quad \left[ K^{74}\right] &{}\quad \left[ K^{75}\right] &{}\quad \left[ K^{76}\right] &{}\quad \left[ K^{77}\right] &{}\quad \left[ K^{78}\right] \\ \left[ K^{81}\right] &{}\quad \left[ K^{82}\right] &{}\quad \left[ K^{83}\right] &{}\quad \left[ K^{84}\right] &{}\quad \left[ K^{85}\right] &{}\quad \left[ K^{86}\right] &{}\quad \left[ K^{87}\right] &{}\quad \left[ K^{88}\right] \end{array}\right] _{\mathrm{Global}}\left[ \begin{array}{c} \{\chi _{1}^{i}\} \\ \{\chi _{2}^{i}\} \\ Q_{i} \\ R_{i} \\ A_{i} \\ B_{i} \\ S_{i} \\ T_{i} \end{array}\right] _{\mathrm{Global}}{=}\left[ \begin{array}{c} \{F_{i}^{1}\} \\ \{F^{2}\} \\ \{F^{3}\} \\ \{F^{4}\} \\ \{F^{5}\} \\ \{F^{6}\} \\ \{F^{7}\} \\ \{F^{8}\} \end{array}\right] _{\mathrm{Global}}\!. \end{aligned}$$

(90)

In the simulation, the following convergence criteria are used for both nonlinear terms;

$$\begin{aligned} \left| A_{n+1}-A_{n}\right| =e_{1}\le \varepsilon , \left| B_{n+1}-B_{n}\right| =e_{2}\le \varepsilon \quad {\text { and }}\quad \varepsilon =\text {maximum error}=10^{-4}, \end{aligned}$$

(91)

which demonstrate fast convergence within 20 iterations (see Table 2).

Table 2 Maximum numerical errors with respect to the number of iterations