Finite plane deformations of elastic solids reinforced with fibers resistant to flexure: complete solution

Abstract

A model for the deformation of an elastic solid reinforced by embedded fibers is presented in which elastic resistance of the fibers to bending is incorporated. Within the framework of strain-gradient elasticity, we formulated the equilibrium equations and necessary boundary conditions which describe the finite plane deformations of fiber-reinforced composite materials. The resulting nonlinear partial differential equations are numerically solved by employing the finite element method. A complete analytical solutions is also obtained within the limitation of superposed incremental deformations.

1 Introduction

Mechanics of elastic solids with distinct microstructures has consistently been the subject of intense research mainly because of their practical applications in materials science and engineering. It is widely believed that, in many cases, the microstructure of a material dominates the general mechanical responses of the material [1,2,3,4]. Examples of such materials include fiber-reinforced composites where fibers; microstructure of the composite; are embedded in a matrix material. These fibers are often so densely distributed so that they can be idealized as continuously distributed fibers. This allows for a continuum setting in the modeling of fiber-matrix composites, typically based on the concept of a simple anisotropic material. Within this prescription, the response functions depend on the conventional deformation gradient, possibly augmented by the constraints of bulk incompressibility or fiber inextensibility. In the latter case, the resulting prediction models are often so constrained that the final deformed configurations are determined essentially by their kinematic relations. As a result, the models were not able to capture the general behaviors of fiber composites, especially those arise in [5, 6].

In recent years, considerable advances in the continuum theory of fiber-reinforced solids were made by accounting bending resistance of the fibers explicitly [7]. This is based on the nonlinear strain-gradient theory [8,9,10] of anisotropic elasticity where elastic response is induced by the changes in curvature (flexure) of the fibers. The latter is computed from the second gradient of the continuum deformation in which the fibers are idealized as convected curves. Current applications of the general theory (Cosserat theory) are illustrated in [11,12,13,14], and mathematical aspects of the subject are presented in [15]. This framework may be used in conjunction with strain-gradient theory, which has also drawn increasing attention recently [16, 17]. To this end, the author in [18] developed a continuum-based model which integrates fibers resistant to twist in addition to flexure and stretch under the simplified setting of the Cosserat theory of nonlinear elasticity [8, 19]. However, the majority of the aforementioned studies have been conducted in a conceptual level that the actual implementation of the theory (including an analysis and solution) in relevant problems remains absent.

In the present work, we address the above-mentioned deficiency and present a continuum model that can accommodate fiber’s elastic resistance to flexure. The fibers are regarded as continuously distributed spatial rods of Kirchhoff type such that the kinematics are based on their position field and a director field. We seek a complete model describing the finite plane deformations of elastic solids reinforced with fibers resistant to flexure. Hence, we assume that the fiber’s directional field remains in a plane, with no components in the out of plane direction, and the corresponding deformations and all material properties are independent of the out of plane coordinate. Within this prescription, we consider a special case of a Neo-Hookian material reinforced with a single (unidirectional) family of fibers. This allows relatively simple formulations including linearization processes and offers reasonably accurate descriptions of the final deformed configurations. Via the method of virtual work and the computation of variational derivatives along the length of a fiber, the corresponding Euler equilibrium equation, in the form of coupled Partial Differential Equations (PDEs), is derived. The constraint of bulk incompressibility is also imposed by introducing Lagrange multiplier. With the Euler equation satisfied, we present a rigorous analysis for the derivation of the necessary boundary conditions. A set of numerical solutions is obtained via a finite element analysis which demonstrate reasonable predictions of the deformed configurations. In addition, a comparison of the proposed model with an experiment is presented in order to demonstrate the applicability of the model to related engineering problems. Lastly, the development of a linear theory of the present model is discussed. This includes the derivation of a linearized Euler equation, corresponding boundary conditions and material incompressibility. A complete analytical solution of the linearized system is obtained for the case when the fiber composite is subjected to bending loads on its edge. We note that the presented model can serve as an alternative 2D Cosserat theory of nonlinear elasticity [8, 19,20,21].

Throughout the manuscript, we use standard notation such as $\mathbf {A}^\mathrm{T},~ \mathbf {A}^{-1},\ \mathbf {A}^{*}$ and $tr(\mathbf {A}).$ These are the transpose, the inverse, the cofactor and the trace of a tensor $\mathbf {A}$, respectively. The tensor product of vectors is indicated by interposing the symbol $\otimes ,\$and the Euclidian inner product of tensors $\mathbf {A}$, $\mathbf {B}$ is defined by ${\mathbf {A\cdot B=}}\,tr({\mathbf {AB}}^\mathrm{T})$; the associated norm is$\ \left| \mathbf {A}\right| =\sqrt{\mathbf {A\cdot A }}$. The symbol$\ \left| \mathbf {\cdot }\right|$ is also used to denote the usual Euclidian norm of vectors. Latin and Greek indices take values in $\{1,2\}$ and, when repeated, are summed over their ranges. Lastly, the notation $F_{\mathbf {A}}$ stands for the tensor-valued derivatives of a scalar-valued function $F(\mathbf {A})$.

2 Kinematics and equilibrium equations

We consider from [7] that the energy density for a fiber-reinforced solid is of the form

$$\begin{aligned} W(\mathbf {F},\mathbf {G})=\widehat{W}(\mathbf {F})+W(\mathbf {G}),\ \ W(\mathbf {G})\equiv \frac{1}{2}C\left( \mathbf {F}\right) \left| \mathbf {g} \right| ^{2}, \end{aligned}$$

(1)

where $\mathbf {F}$ is the gradient of the deformation function ($\mathbf {\chi }(\mathbf {X})$) and $\mathbf {G}$ is the second gradient of the deformation (i.e. $\mathbf {G}=\nabla \mathbf {F}$). Further, C refers to the material property of fibers which, in general, independent of the deformation gradient (i.e. $C=C(\mathbf {F})$). The advantage of adopting above form of energy function is that the bending energy of the fibers is solely accounted by the strain gradient so that it allows one to compute energy variations induced by first gradient ($\mathbf {F}$) and second gradient ($\mathbf {G}$) in a separate manner. This approach has been widely and successfully used in the relevant studies [17, 18, 22].

The orientation of a particular fiber is given by

$$\begin{aligned} \lambda =\left| \mathbf {d}\right| \text { and }\mathbf {\tau }=\lambda ^{-1}\mathbf {d} \end{aligned}$$

(2)

where

$$\begin{aligned} \mathbf {d}={\mathbf {FD,}} \end{aligned}$$

(3)

in which $\mathbf {D}$ is the unit tangent to the fiber trajectory in the reference configuration. Equation (3) can be derived by taking the derivative of $\mathbf {r}(s)=\mathbf {\chi }(\mathbf {X}(s))$, upon making the identifications ${\mathbf {D=X}}^{\prime }(s)$ and $\mathbf {d}=\mathbf {r}^{\prime }(s)$. Here, primes refer to derivatives with respect to arclength along a fiber in the reference configuration (i.e. $(*)^{\prime }=\hbox {d}(*)/\hbox {d}s$). The expression for geodesic curvature of an arc ($\mathbf {r}\left( s\right)$) is then obtained from Eq. (3) as

$$\begin{aligned} \mathbf {g}=\mathbf {r}^{\prime \prime }=\frac{\hbox {d}(\mathbf {r}^{\prime }\left( s\right) )}{\hbox {d}s}=\frac{\partial ({\mathbf {FD}})}{\partial \mathbf {X}}\frac{\hbox {d} \mathbf {X}}{\hbox {d}s}=\nabla [{\mathbf {FD}}]{\mathbf {D}}. \end{aligned}$$

(4)

Further, by using the chain rule, the compatibility condition of $\mathbf {F}$ is given by

$$\begin{aligned} G_{iAB}=F_{iA,B}=F_{iB,A}=G_{iBA}. \end{aligned}$$

(5)

In the present work, we adopt the framework of the virtual work statement $\overset{\cdot }{E}=P$ in the derivation of equilibrium equations. From (1), the potential energy of the system is given by

$$\begin{aligned} E=\int _{w}W(\mathbf {F},\mathbf {G})\hbox {d}A. \end{aligned}$$

(6)

To accommodate the bulk incompressibility condition, we consider the following energy functional

$$\begin{aligned} E=\int _{w}U\left( {\mathbf {F,G,}}\ p\right) \hbox {d}A,\ \ U\left( {\mathbf {F,G,}}\ p\right) =W(\mathbf {F},\mathbf {G})-p(J-1),\ \ \end{aligned}$$

(7)

where J is determinant of $\mathbf {F}$ and p is a Lagrange-multiplier field.

The derivation of the Euler equation and boundary conditions in second-gradient elasticity is well studied [8,9,10, 21]. Here, we reproduce the results for the sake of clarity and completeness of the proposed model. The induced variation of the energy is then evaluated as

$$\begin{aligned} \overset{\cdot }{E}=\int _{w}\overset{\cdot }{U}\left( {\mathbf {F,G,}}\ p\right) \hbox {d}A, \end{aligned}$$

(8)

where

$$\begin{aligned} \ \overset{\cdot }{U}\left( {\mathbf {F,G,}}\ p\right) =W_{\mathbf {F}}{\mathbf { \cdot \overset{\cdot }{F}+W_{G}\cdot }}\overset{\cdot }{\mathbf {G}}-p \overset{\cdot }{J}, \end{aligned}$$

(9)

and subscripts denote corresponding partial derivatives (e.g. $W_{\mathbf {F} }=\partial W/\partial \mathbf {F}).$ We note here that, within the framework of the forgoing model, the fiber’s extensibility can be accounted through the variational computation of the energy density function with respect to $\varepsilon$. In other words, the energy density function is required to be a function of $\varepsilon$ in addition to $\mathbf {F}$, $\mathbf {G}$ and $\rho$ (i.e. $\mathbf {W}=W(\mathbf {F},\ \mathbf {G,}\ \varepsilon ,\ p)$ to accommodate fiber’s extensibility. The corresponding energy variation is computed as

$$\begin{aligned} \overset{\cdot }{U}\left( {\mathbf {F,G,}}\ p,\ \varepsilon \right)= & {} W_{F} \overset{\cdot }{\mathbf {F}}+W_{\varepsilon }\overset{\cdot }{\varepsilon } +W_{\mathbf {G}}\cdot \overset{\cdot }{\mathbf {G,}} \end{aligned}$$

(10)

$$\begin{aligned} \dot{\varepsilon }&\overset{(6)}{=}&\Big [\frac{1}{2}\left( \lambda ^{2}-1\right) \overset{\cdot }{\Big ]}=\overset{\cdot }{\lambda }\lambda . \end{aligned}$$

(11)

and

$$\begin{aligned} \overset{\cdot }{\lambda }\lambda ={\mathbf {FD\cdot \overset{\cdot }{F} D}}=tr({\mathbf {FD\otimes \overset{\cdot }{F}D}})=tr\left( ({\mathbf { FD\otimes D}})\overset{\cdot }{\mathbf {F}}^\mathrm{T}\right) ={\mathbf {F[D\otimes D]\cdot }} \overset{\cdot }{\mathbf {F}}. \end{aligned}$$

(12)

The above computations are excluded from the present study in an effort to obtain mathematically tractable equations.

Now, since $\overset{\cdot }{J}=J_{F}\cdot {\mathbf {\overset{\cdot }{ F}}}=\mathbf {F}^{*}\cdot {\mathbf {\overset{\cdot }{F},}}$ Eq. (8) yields

$$\begin{aligned} \overset{\cdot }{E}=\int _{w}[\left( W_{\mathbf {F}}-p\mathbf {F}^{*}\right) {\mathbf {\cdot \overset{\cdot }{F}}}+{\mathbf {W_{G}\cdot }} \overset{\cdot }{\mathbf {G}}]\hbox {d}A. \end{aligned}$$

(13)

Also, from Eq. (5), $W_\mathbf {\mathbf {G}}\cdot \overset{ \cdot }{\mathbf {G}}$ can be rewritten as

$$\begin{aligned} \frac{\partial W}{\partial G_{iAB}}\overset{\cdot }{G}_{iAB}=\frac{\partial W }{\partial G_{iAB}}u_{i,AB}=\left( \frac{\partial W}{\partial G_{iAB}} u_{i,A}\right) _{,B}-\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}u_{i,A}, \end{aligned}$$

(14)

where $u=\overset{\cdot }{\chi }$ is the variation of the position field. By substituting Eqs. (14) into (13), we find

$$\begin{aligned} \overset{\cdot }{E}=\int _{w}\left[ \left( \frac{\partial W}{\partial F_{iA}} -pF_{iA}^{*}\right) \mathbf {\cdot }\overset{\cdot }{F_{iA}}+\left( \frac{ \partial W}{\partial G_{iAB}}u_{i,A}\right) _{,B}-\left( \frac{\partial W}{ \partial G_{iAB}}\right) _{,B}u_{iA}\right] \hbox {d}A, \end{aligned}$$

(15)

the above becomes

$$\begin{aligned} \overset{\cdot }{E}=\int _{w}\left[ \frac{\partial W}{\partial F_{iA}} -pF_{iA}^{*}-\left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}\right] \overset{\cdot }{F_{iA}}\hbox {d}A+\int _{\partial w}\left( \frac{\partial W}{ \partial G_{iAB}}u_{i,A}\right) N_{B}\hbox {d}S, \end{aligned}$$

(16)

where $\mathbf {N}$ is the rightward unit normal to the boundary curve $\partial w$ in the sense of the Green–Stoke’s theorem. If we assume the material response is uniform (i.e. $C(\mathbf {F})=C)$, Eq. (1) furnishes

$$\begin{aligned} W_{\mathbf {G}}\cdot \overset{\cdot }{\mathbf {G}}\ =C{\mathbf {g\cdot }} \overset{\cdot }{\mathbf {g}}, \end{aligned}$$

(17)

and

$$\begin{aligned} W_{\mathbf {G}}=C{\mathbf {g\otimes D\otimes D.}} \end{aligned}$$

(18)

For initially straight fibers (i.e. $\nabla \mathbf {D}=0$), $\hbox {Div}(W_{\mathbf {G }})$ reduces to

$$\begin{aligned} \hbox {Div}(W_{\mathbf {G}})=Cg_{i,B}D_{A}D_{B}(\mathbf {e}_{i}{\mathbf {\otimes E}} _{A}),\ \because \left( \frac{\partial W}{\partial G_{iAB}}\right) _{,B}=Cg_{i,B}D_{A}D_{B}\mathbf {.} \end{aligned}$$

(19)

Consequently, Eq. (16) becomes

$$\begin{aligned} \overset{\cdot }{E}=\int _{w}P_{iA}\overset{\cdot }{F_{iA}}\hbox {d}A+\int _{\partial w}Cg_{i}D_{A}D_{B}u_{i,A}N_{B}\hbox {d}S, \end{aligned}$$

(20)

where

$$\begin{aligned} P_{iA}=\frac{\partial W}{\partial F_{iA}}-pF_{iA}^{*}-Cg_{i,B}D_{B}D_{A}. \end{aligned}$$

(21)

Therefore, the corresponding Euler equation can be obtained as follows

$$\begin{aligned} P_{iA,A}=0\text { or }\hbox {Div}(\mathbf {P})=0. \end{aligned}$$

(22)

which hold on w.

2.1 Example: Neo-Hookian materials

In the case of incompressible Neo-Hookian materials, the energy density function is given by

$$\begin{aligned} \widehat{W}(\mathbf {F})= & {} \frac{\mu }{2}tr(\mathbf {C})=\frac{\mu }{2}tr( \mathbf {F}^\mathrm{T}\mathbf {F})=\frac{\mu }{2}{\mathbf {F\cdot F}}\text { } \nonumber \\ \text {and }W(\mathbf {F},\mathbf {G})= & {} \frac{\mu }{2}{\mathbf {F\cdot F}}+\frac{ 1}{2}C\left| \mathbf {g}\right| ^{2},\ \ \end{aligned}$$

(23)

where $\mu$ and C are the material constant of the matrix and fiber, respectively. We mention here that the Neo-Hookian model is suitable for deformation analysis involving large rotation and small extension such as bending analysis [23]. Accordingly, from Eqs. (21–22), the corresponding Euler equation can be obtained as

$$\begin{aligned} P_{iA,A}=\mu F_{iA,A}-p_{,A}F_{iA}^{*}-Cg_{i,AB}D_{A}D_{B}=0,\ \ \because F_{iA,A}^{*}=0\text { ( Piola's identity).} \end{aligned}$$

(24)

If a fiber-reinforced material consists of a single family of fibers (i.e.$~ \mathbf {D}=\mathbf {E}_{1},~D_{1}=1,~D_{2}=0$) and subjected to plane deformations, Eq. (24) further reduces to

$$\begin{aligned} \mu F_{iA,A}-p_{,A}F_{iA}^{*}-Cg_{i,11}=0\text { for }i,A=1,2, \end{aligned}$$

(25)

and

$$\begin{aligned} g_{i}=F_{i1,1}=G_{i11},\ \ F_{iA}=\frac{\partial \chi _{i}}{\partial X_{A}}\text { and }F_{iA}^{*}=\varepsilon _{ij}\varepsilon _{AB}F_{jB}, \end{aligned}$$

(26)

where $\varepsilon _{ij}$ is the 2-D permutation; $\varepsilon _{12}=-\varepsilon _{21}=1,\varepsilon _{11}=-\varepsilon _{22}=0$. Therefore, Eq. (26) together with the incompressibility condition ($\det \mathbf {F}=1$) furnishes a coupled PDE system solving for $\chi _{1},\chi _{2}$ and p. i.e.

$$\begin{aligned} \mu \left( \chi _{1,11}+\chi _{1,22}\right) -p_{,1}\chi _{2,2}+p_{,2}\chi _{2,1}-C\chi _{1,1111}= & {} 0, \nonumber \\ \mu \left( \chi _{2,11}+\chi _{2,22}\right) +p_{,1}\chi _{1,2}-p_{,2}\chi _{1,1}-C\chi _{2,1111}= & {} 0, \nonumber \\ \chi _{1,1}\chi _{2,2}-\chi _{1,2}\chi _{2,1}= & {} 1. \end{aligned}$$

(27)

The above systems of PDE can be accommodated by commercial packages (e.g. Matlab, COMSOL etc...).

3 Boundary conditions

From Eq. (16), we have

$$\begin{aligned} \overset{\cdot }{E}=\int _{w}P_{iA}\overset{\cdot }{F_{iA}}\hbox {d}A+\int _{\partial w}\left( \frac{\partial W}{\partial G_{iAB}}u_{i,A}\right) N_{B}\hbox {d}S, \end{aligned}$$

(28)

where

$$\begin{aligned} P_{iA}=\frac{\partial W}{\partial F_{iA}}-pF_{iA}^{*}-\left( \frac{ \partial W}{\partial G_{iAB}}\right) _{,B}. \end{aligned}$$

Decomposing the above as in (15) (i.e. $P_{iA}u_{i,A}=(P_{iA}u_{i})_{,A}-P_{iA,A}u_{i}$), the above yields

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial w}P_{iA}u_{i}N_{A}\hbox {d}S-\int _{w}P_{iA,A}u_{i}\hbox {d}A+\int _{\partial w}\left( \frac{ \partial W}{\partial G_{iAB}}u_{i,A}\right) N_{B}\hbox {d}S, \end{aligned}$$

(29)

and hence the Euler equation $P_{iA,A}=0$ which hold in w. With this satisfied, Eq. (29) reduces to

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial w}P_{iA}u_{i}N_{A}\hbox {d}S+\int _{\partial w}\left( \frac{\partial W}{\partial G_{iAB}}u_{i,A}\right) N_{B}\hbox {d}S. \end{aligned}$$

(30)

Now, we make use of the normal-tangent decomposition of $\nabla \mathbf {u}$ as;

$$\begin{aligned} \nabla \mathbf {u}=\nabla {\mathbf {u(T\otimes T)}}+\nabla {\mathbf {u(N\otimes N)=u}}^{\prime }{\mathbf {\otimes T+u,}}_{\mathbf {N}}{\mathbf {\otimes N}} \end{aligned}$$

(31)

where $\mathbf {T}=\mathbf {X}^{\prime }(s)={\mathbf { k\times N}}$ is the unit tangent to $\partial w;$ and $\mathbf {u}^{\prime }=d\mathbf {u}(\mathbf {X}\left( s\right) )/\hbox {d}s$ and $\mathbf {u}_{,N}$ are the tangential and normal derivatives of $\mathbf {u}$ on $\partial w$ (i.e. $u_{i}^{\prime }=u_{i,A}T_{A},~u_{i,N}=u_{i,A}N_{A}$). Thus, Eq. (30) can be rewritten as

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial w}P_{iA}u_{i}N_{A}\hbox {d}S+\int _{\partial w} \frac{\partial W}{\partial G_{iAB}}\left( u_{i}^{\prime }T_{A}N_{B}+u_{i,N}N_{A}N_{B}\right) \hbox {d}S. \end{aligned}$$

(32)

Since

$$\begin{aligned} \frac{\partial W}{\partial G_{iAB}}T_{A}N_{B}u_{i}^{\prime }=\left( \frac{ \partial W}{\partial G_{iAB}}T_{A}N_{B}u_{i}\right) ^{\prime }-\left( \frac{\partial W}{\partial G_{iAB}}T_{A}N_{B}\right) ^{\prime }u_{i}, \end{aligned}$$

we obtain

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial w}\left\{ P_{iA}N_{A}-\left( \frac{ \partial W}{\partial G_{iAB}}T_{A}N_{B}\right) ^{\prime }\right\} u_{i}\hbox {d}S+\int _{\partial w}\frac{\partial W}{\partial G_{iAB}} u_{i,N}N_{A}N_{B}\hbox {d}S+\int _{\partial w}\left( \frac{\partial W}{\partial G_{iAB}}T_{A}N_{B}u_{i}\right) ^{\prime }\hbox {d}S. \end{aligned}$$

(33)

In view of Eq. (18) (i.e. $W_{\mathbf {G}}=C{\mathbf {g\otimes D\otimes D}}$), the above furnishes

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial w}\left\{ P_{iA}N_{A}-\left( Cg_{i}D_{A}T_{A}D_{B}N_{B}\right) ^{\prime }\right\} u_{i}\hbox {d}S+\int _{\partial w}Cg_{i}D_{A}N_{A}D_{B}N_{B}u_{i,N}\hbox {d}S-\sum \left\| Cg_{i}D_{A}T_{A}D_{B}N_{B}u_{i}\right\| , \end{aligned}$$

(34)

where the double bar symbol refers to the jump across the discontinuities on the boundary $\partial w$ (i.e. $\left\| *\right\| =\left( *\right) ^{+}-\left( *\right) ^{-}$) and the sum refers to the collection of all discontinuities. According to the virtual work statement ($\overset{\cdot }{E}=P$), the admissible mechanical powers are given by

$$\begin{aligned} P=\int _{\partial w_{t}}t_{i}u_{i}\hbox {d}S+\int _{\partial w}m_{i}u_{i,N}\hbox {d}S+\sum f_{i}u_{i}. \end{aligned}$$

(35)

By comparing Eqs. (34) and (35), we obtain

$$\begin{aligned} \mathbf {t}= & {} {\mathbf {PN}}-\frac{d}{ds}\left[ C\mathbf {g}({\mathbf {D\cdot T}})( {\mathbf {D\cdot N}})\right] \mathbf {,} \nonumber \\ \mathbf {m}= & {} C\mathbf {g}({\mathbf {D\cdot N}})^{2}, \nonumber \\ \mathbf {f}= & {} C\mathbf {g}({\mathbf {D\cdot T}})({\mathbf {D\cdot N}}). \end{aligned}$$

(36)

which are expressions of edge tractions, edge moments and the corner forces, respectively. For example, if the fiber’s directions are either normal or tangential to the boundary (i.e. $({\mathbf {D\cdot T}})({\mathbf {D\cdot N}})=0$ ), Eq. (36) further reduces to

$$\begin{aligned} t_{i}= & {} P_{iA}N_{A}, \nonumber \\ m_{i}= & {} Cg_{i}D_{A}N_{A}D_{B}N_{B}, \nonumber \\ f_{i}= & {} 0, \end{aligned}$$

(37)

where

$$\begin{aligned} P_{iA}=\mu F_{iA}-pF_{iA}^{*}-Cg_{i,B}D_{A}D_{B},\ \ g_{i}=F_{iA,B}D_{A}D_{B}. \end{aligned}$$

(38)

3.1 Finite element analysis of the 4th order coupled PDE

It is not trivial to demonstrate numerical analysis procedures for coupled PDE systems, especially for those with high order terms, since the piece wise linear function adopted in FE analysis has limited differentiability up to second order. For pre processing, Eq. (27) can be recast as

$$\begin{aligned} \mu \left( R+\chi _{1,22}\right) -A\chi _{2,2}+B\chi _{2,1}-CR_{,11}= & {} 0,\nonumber \\ \mu \left( Q+\chi _{2,22}\right) +A\chi _{1,2}-B\chi _{1,1}-CQ_{,11}= & {} 0,\nonumber \\ Q-\chi _{1,11}= & {} 0, \nonumber \\ R-\chi _{2,11}= & {} 0, \nonumber \\ A-\mu (\chi _{1,11}+\chi _{1,22})-CR_{,11}= & {} 0, \nonumber \\ B-\mu (\chi _{2,11}+\chi _{2,22})-CQ_{,11}= & {} 0, \end{aligned}$$

(39)

where $Q=\chi _{1,11}$ and $R=\chi _{2,11}.$ By employing the Picard iterative process, the nonlinear terms in the above can be treated as

$$\begin{aligned} -A_\mathrm{initial}\chi _{2,2}^\mathrm{initial}+B_\mathrm{initial}\chi _{2,1}^\mathrm{initial}&\Longrightarrow&-A_{0}\chi _{2,2}^{0}+B_{0}\chi _{2,1}^{0} \nonumber \\ A_\mathrm{initial}\chi _{1,2}^\mathrm{initial}-B_\mathrm{initial}\chi _{1,1}^\mathrm{initial}&\Longrightarrow&A_{0}\chi _{1,2}^{0}-B_{0}\chi _{1,1}^{0}, \end{aligned}$$

(40)

where the values of A and B continue to be refreshed based on their previous estimations (e.g. $A_{1}$ and $B_{1}$ are updated by their previous values $A_{0}$ and $B_{0}$) as iteration progresses. Thus, we write

$$\begin{aligned} -A_{N-1}\chi _{2,2}^{N-1}+B_{N-1}\chi _{2,1}^{N-1}&\Longrightarrow&-A_{N}\chi _{2,2}^{N}+B_{N}\chi _{2,1}^{N} \nonumber \\ A_{N-1}\chi _{1,2}^{N-1}-B_{N-1}\chi _{1,1}^{N-1}&\Longrightarrow&A_{N}\chi _{1,2}^{N}-B_{N}\chi _{1,1}^{N}, \end{aligned}$$

(41)

where N is the number of iterations. The weak form of Eq. (39)$_{1}$ is given by

$$\begin{aligned} 0=\int _{\varOmega }w_{1}(\mu \left( R+\chi _{1,22}\right) -A\chi _{2,2}+B\chi _{2,1}-CR_{,11})\hbox {d}\varOmega . \end{aligned}$$

(42)

By applying integration by parts $\left( \hbox {e.g. } \mu \int \nolimits _{\varOmega ^{e}}w_{1}\chi _{1,22}\hbox {d}\varOmega =-\mu \int \nolimits _{\varOmega ^{e}}w_{1,2}\chi _{1,2}\hbox {d}\varOmega +\mu \int \nolimits _{\varOmega ^{e}}w_{1}\chi _{1,2}N\hbox {d}\varGamma \right)$ and the Green–Stoke’s theorem, the above becomes

$$\begin{aligned} 0= & {} \int _{\varOmega ^{e}}(\mu w_{1}R-\mu w_{1,2}\chi _{1,2}-w_{1}A_{0}\chi _{2,2}+w_{1}B_{0}\chi _{2,1}+Cw_{1,1}R_{,1})\hbox {d}\varOmega \nonumber \\&+\int _{\partial \varGamma ^{e}}\mu w_{1}\chi _{1,2}N\hbox {d}\varGamma -\int _{\partial \varGamma ^{e}}Cw_{1}R_{,1}N\hbox {d}\varGamma . \end{aligned}$$

(43)

Similarly, we obtain

$$\begin{aligned} 0= & {} \int _{\varOmega }(\mu w_{1}R-\mu w_{1,2}\chi _{1,2}-w_{1}A_{0}\chi _{2,2}+w_{1}B_{0}\chi _{2,1}+Cw_{1,1}R_{,1})\hbox {d}\varOmega \nonumber \\&+\int _{\partial \varGamma }\mu w_{1}\chi _{1,2}N\hbox {d}\varGamma -\int _{\partial \varGamma }Cw_{1}R_{,1}N\hbox {d}\varGamma , \nonumber \\ 0= & {} \int _{\varOmega }(\mu w_{2}Q-\mu w_{2,2}\chi _{2,2}++w_{2}A_{0}\chi _{1,2}-w_{2}B_{0}\chi _{1,1}+Cw_{2,1}Q_{,1})\hbox {d}\varOmega \nonumber \\&+\int _{\partial \varGamma }\mu w_{2}\chi _{2,2}N\hbox {d}\varGamma -\int _{\partial \varGamma }Cw_{2}Q_{,1}N\hbox {d}\varGamma , \nonumber \\ 0= & {} \int _{\varOmega }(w_{3}Q+w_{3,1}\chi _{1,1})\hbox {d}\varOmega -\int _{\partial \varGamma }w_{3}\chi _{1,1}N\hbox {d}\varGamma , \nonumber \\ 0= & {} \int _{\varOmega }(w_{4}R+w_{4,1}\chi _{2,1})\hbox {d}\varOmega -\int _{\partial \varGamma }w_{4}\chi _{2,1}N\hbox {d}\varGamma , \nonumber \\ 0= & {} \int _{\varOmega }(w_{5}A+\mu w_{4,1}\chi _{1,1}-\mu w_{5,2}\chi _{1,2}+Cw_{4,1}R_{,1})\hbox {d}\varOmega -\int _{\partial \varGamma }\mu w_{5}\chi _{1,1}N\hbox {d}\varGamma \nonumber \\&+\int _{\partial \varGamma }\mu w_{5}\chi _{1,2}N\hbox {d}\varGamma -\int _{\partial \varGamma }Cw_{5}R_{,1}N\hbox {d}\varGamma , \nonumber \\ 0= & {} \int _{\varOmega }(w_{6}B+\mu w_{6,1}\chi _{2,1}-\mu w_{6,2}\chi _{2,2}+Cw_{5,1}Q_{,1})\hbox {d}\varOmega -\int _{\partial \varGamma }\mu w_{6}\chi _{2,1}N\hbox {d}\varGamma \nonumber \\&+\int _{\partial \varGamma }\mu w_{6}\chi _{2,2}N\hbox {d}\varGamma -\int _{\partial \varGamma }Cw_{6}Q_{,1}N\hbox {d}\varGamma , \end{aligned}$$

(44)

where $\varOmega$, $\partial \varGamma$ and $\mathbf {N}$ are the domain of interest, the associated boundary, and the rightward unit normal to the boundary $\partial \varGamma$ in the sense of the Green–Stoke’s theorem, respectively. The unknowns, $\chi _{1},\ \chi _{2},\ Q,\ R,\ A$ and B can be written in the form of Lagrangian polynomial such that

$$\begin{aligned} (*)=\sum _{j=1}^{n}\left[ (*)_{j}\Psi _{j}(x,y)\right] \text { and }n=1,\text { }2, \text { }3,~4, \end{aligned}$$

(45)

where $\Psi _{i}(x,y)$ are the shape functions; $\Psi _{1}= \frac{(x-2)(y-1)}{2},$ $\Psi _{2}=\frac{x(y-1)}{-2},~\Psi _{3}=\frac{xy}{2}$ and $\Psi _{4}=\frac{y(x-2)}{-2}$ for the 4-node rectangular element. Accordingly, the corresponding test function $w_{m}$ is expressed by

$$\begin{aligned} w_{m}=\sum _{i=1}^{n}w_{m}^{i}\Psi _{i}(x,y)\text { and }m=1,\text { }2,\text { } 3,\ldots ,6, \end{aligned}$$

(46)

where $w_{m}^{i}$ is weight of the test function. In view of Eq. (45), the first of Eq. (44)$_{1}$ can be rewritten as

$$\begin{aligned} 0= & {} \sum _{j=1}^{n}\left\{ \int _{\varOmega }(\mu \Psi _{i}\Psi _{j}+C\Psi _{i,1}\Psi _{j,1})\hbox {d}\varOmega \right\} R_{j}-\sum _{j=1}^{n}\left\{ \int _{\varOmega }(\mu \Psi _{i,2}\Psi _{j,2})\hbox {d}\varOmega \right\} \chi _{1j} \nonumber \\&-\sum _{j=1}^{n}\left\{ \int _{\varOmega }(\Psi _{i}A_{0}\Psi _{j,2}+\Psi _{i}B_{0}\Psi _{j,1})\hbox {d}\varOmega \right\} \mathbf {\chi }_{2}^{j}+\int _{\partial \varGamma }(\mu \Psi _{i}\chi _{1,2})N\hbox {d}\varGamma -\int _{\partial \varGamma }(C\Psi _{i}R_{,1})N\hbox {d}\varGamma , \end{aligned}$$

(47)

and similarly for the rest of equations. In addition, for the local stiffness matrix, we find

$$\begin{aligned} \left[ \begin{array}{cccc} K_{11}^{11} &{}\quad K_{12}^{11} &{}\quad K_{13}^{11} &{}\quad K_{14}^{11} \\ K_{21}^{11} &{}\quad K_{22}^{11} &{}\quad K_{23}^{11} &{}\quad K_{24}^{11} \\ K_{31}^{11} &{}\quad K_{32}^{11} &{}\quad K_{33}^{11} &{}\quad K_{34}^{11} \\ K_{41}^{11} &{}\quad K_{42}^{11} &{}\quad K_{43}^{11} &{}\quad K_{44}^{11} \end{array} \right] _{\mathrm{Local}}\left[ \begin{array}{c} \chi _{1}^{1} \\ \chi _{1}^{2} \\ \chi _{1}^{3} \\ \chi _{1}^{4} \end{array} \right] _{\mathrm{Local}}=\left[ \begin{array}{c} F_{1}^{1} \\ F_{2}^{1} \\ F_{3}^{1} \\ F_{4}^{1} \end{array} \right] _{\mathrm{Local}}, \end{aligned}$$

(48)

or alternatively,

$$\begin{aligned} \left[ K_{ij}^{11}\right] \left\{ \chi _{1}^{i}\right\} =\left\{ F_{i}^{1}\right\} . \end{aligned}$$

(49)

Here

$$\begin{aligned} \left[ K_{ij}^{11}\right]= & {} \int _{\varOmega }(\mu \Psi _{i,2}\Psi _{j,2})\hbox {d}\varOmega , \end{aligned}$$

(50)

$$\begin{aligned} \left\{ F_{i}^{1}\right\}= & {} -\mu \int _{\partial \varGamma ^{e}}\Psi _{i}\chi _{1,2}N\hbox {d}\varGamma +C\int _{\partial \varGamma ^{e}}\Psi _{i}R_{,1}N\hbox {d}\varGamma , \end{aligned}$$

(51)

and similarly for the rest of components (e.g. $[K_{ij}^{21}] \{\chi _{2}^{i}\}=\{F_{i}^{2}\}$ etc.). Finally, we assemble the local stiffness matrices and obtain the following systems of equations in the Global form.

$$\begin{aligned} \left[ \begin{array}{cccccc} \left[ K_{ij}^{11}\right] &{}\quad \left[ K_{ij}^{12}\right] &{}\quad \left[ K_{ij}^{13} \right] &{}\quad \left[ K_{ij}^{14}\right] &{}\quad \left[ K_{ij}^{15}\right] &{}\quad \left[ K_{ij}^{16}\right] \\ \left[ K_{ij}^{21}\right] &{}\quad \left[ K_{ij}^{22}\right] &{}\quad \left[ K_{ij}^{23} \right] &{}\quad \left[ K_{ij}^{24}\right] &{}\quad \left[ K_{ij}^{25}\right] &{}\quad \left[ K_{ij}^{26}\right] \\ \left[ K_{ij}^{31}\right] &{}\quad \left[ K_{ij}^{32}\right] &{}\quad \left[ K_{ij}^{33} \right] &{}\quad \left[ K_{ij}^{34}\right] &{}\quad \left[ K_{ij}^{35}\right] &{}\quad \left[ K_{ij}^{36}\right] \\ \left[ K_{ij}^{41}\right] &{}\quad \left[ K_{ij}^{42}\right] &{}\quad \left[ K_{ij}^{43} \right] &{}\quad \left[ K_{ij}^{44}\right] &{}\quad \left[ K_{ij}^{45}\right] &{}\quad \left[ K_{ij}^{46}\right] \\ \left[ K_{ij}^{51}\right] &{}\quad \left[ K_{ij}^{52}\right] &{}\quad \left[ K_{ij}^{53} \right] &{}\quad \left[ K_{ij}^{54}\right] &{}\quad \left[ K_{ij}^{55}\right] &{}\quad \left[ K_{ij}^{56}\right] \\ \left[ K_{ij}^{61}\right] &{}\quad \left[ K_{ij}^{62}\right] &{}\quad \left[ K_{ij}^{63} \right] &{}\quad \left[ K_{ij}^{64}\right] &{}\quad \left[ K_{ij}^{65}\right] &{}\quad \left[ K_{ij}^{66}\right] \end{array} \right] _{\mathrm{Global}}\left[ \begin{array}{c} \{\chi _{1}^{i}\} \\ \{\chi _{2}^{i}\} \\ Q_{i} \\ R_{i} \\ A_{i} \\ B_{i} \end{array} \right] _{\mathrm{Global}}=\left[ \begin{array}{c} \{F_{i}^{1}\} \\ \{F_{i}^{2}\} \\ \{F_{i}^{3}\} \\ \{F_{i}^{4}\} \\ \{F_{i}^{5}\} \\ \{F_{i}^{6}\} \end{array} \right] _{\mathrm{Global}}. \end{aligned}$$

(52)

Table 1 Maximum numerical error with respect to the number of iterations

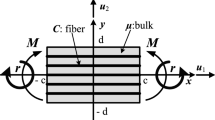
For demonstration purpose, we consider a rectangular fiber composite where one end is fixed and the other end is subjected to uniform bending in order to examine fibers’ reinforcing effects against to flexure. We also note here that data are obtained under the normalized setting (e.g. $\frac{C }{\mu }=150,\,\,\frac{M}{\mu }=5[L]^{3}$ etc.). The convergence criteria are set for both nonlinear terms (i.e. A and B ) and the deformed profiles at $y=0$.

$$\begin{aligned} \left| A_{n+1}-A_{n}\right| =e_{1}\le \varepsilon ,\ \left| B_{n+1}-B_{n}\right| =e_{2}\le \varepsilon \text { and }\varepsilon = \text {maximum error}=10^{-10}. \end{aligned}$$

(53)

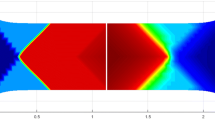
It is clear from Table 1 and Fig. 1 that the adopted numerical method demonstrates fast convergence within 20 iterations. The deformation profile and contour show smooth transitions as they approach the boundary (Figs. 2, 3, 4). In addition, Fig. 3. indicates that magnitude of deformation decreases with increasing fiber’s bending stiffness. This is a clear indication that the obtained model is capable of accounting fibers resistant to flexure. A comparison with experimental results is also presented when a crystalline nanocellulose (CNC) fiber composite ($C=150$ GPa, $\mu =1$ GPa) is subjected to 3 point bending at $-10$ mm, 0, and 10 mm. In the test, the out of plane direction ($x_{3}$) is aligned with the loading cylinder (see, Fig. 5). This is a special case of the proposed model, in the case when $C/\mu =150$ with vanishing thickness in $x_{2}$ direction. The obtained numerical solution successfully predicts the deformation of the CNC composite with maximum error less than 3% (Fig. 6). The result further suggests that the presented model can be employed in the analysis and design of CNC-reinforced composites.

Fig. 1

Convergence of the numerical solutions at $y=0$

Fig. 2

Deformed configurations with respect to $M/\mu$ when $C/\mu =150$

Fig. 3

Deformed configurations with respect to $C/\mu$ when $M/\mu =8$

Fig. 4

Deformation contour $\left( \sqrt{\chi _{1}^{2}+\chi _{2}^{2}}\right)$ when $C/\mu =150$ and $M/\mu =8$

Fig. 5

Deformation profile (image processing) at 2.55 mm: CNC fiber composite

Fig. 6

Comparison: Theoretical prediction versus experimental result at 2.55 mm

4 Linear theory

We consider superposed “small” deformations as

$$\begin{aligned} {\mathbf {\chi =\chi }}_{o}+\varepsilon \overset{\cdot }{\mathbf {\chi }} ;\left| \varepsilon \right| \ll 1, \end{aligned}$$

(54)

where $(*)_{o}$ denote configuration of $*$ evaluated at $\varepsilon =0$ and $(\overset{\cdot }{\mathbf {*}})=\partial (*)/\partial \varepsilon .$ In particular, we denote $\overset{\cdot }{\mathbf { \chi }}=\mathbf {u}$. Here, caution needs to be taken that the present notation is not confused with the one used for the variational computation. Then, the deformation gradient tensor can be written by

$$\begin{aligned} \mathbf {F}=\mathbf {F}_{o}+\varepsilon \nabla \mathbf {u},\ \text {where } \overset{\cdot }{\mathbf {F}}=\nabla \mathbf {u}. \end{aligned}$$

(55)

We assume that the body is initially undeformed and stress free at $\varepsilon =0$ (i.e. $\mathbf {F}_{o}=\mathbf {I}$ and $\mathbf {P}_{o}= \mathbf {0}$). Then, Eq. (55) becomes

$$\begin{aligned} \mathbf {F}=\mathbf {I}+\varepsilon \nabla \mathbf {u,} \end{aligned}$$

(56)

and successively obtain

$$\begin{aligned} \mathbf {F}^{-1}= & {} \mathbf {I}-\varepsilon \nabla \mathbf {u}+o(\varepsilon ), \end{aligned}$$

(57)

$$\begin{aligned} J= & {} \det \mathbf {F}=1+\varepsilon \,\hbox {div}\,\mathbf {u}+o(\varepsilon ) \mathbf {.} \end{aligned}$$

(58)

Further, in view of Eqs. (54), (22) can be rewritten as

$$\begin{aligned} \hbox {Div}(\mathbf {P})=\hbox {Div}(\mathbf {P}_{o})+\varepsilon \hbox {Div}(\overset{\cdot }{\mathbf {P}})+o(\varepsilon )=\mathbf {0}. \end{aligned}$$

(59)

Dividing the above by $\varepsilon$ and let $\varepsilon \rightarrow 0,$ we obtain

$$\begin{aligned} \hbox {Div}(\overset{\cdot }{\mathbf {P}})=0 \end{aligned}$$

(60)

which serves as the linearized Euler equation. Now, from Eq. (21), we evaluate the variation of $\mathbf {P}$ with respect to $\varepsilon$ as

$$\begin{aligned} \overset{\cdot }{\mathbf {P}}=W_{\mathbf {FF}}\overset{\cdot }{ \mathbf {F}}-\overset{\cdot }{p}\mathbf {F}_{o}^{*}-p_{o}\overset{\cdot }{ \mathbf {F}^{*}}-C\nabla \overset{\cdot }{\mathbf {g}}{\mathbf {(D\otimes D)}} \end{aligned}$$

(61)

where, in the case of Neo-Hookian material (Eq. 23); $W_{\mathbf {FF}}=\mu (\mathbf {e}_{i}{\mathbf {\otimes E}}_{A}{\mathbf {\otimes e}}_{i} {\mathbf {\otimes E}}_{A}).$ Thus Eqs. (60–61) furnishes

$$\begin{aligned} \hbox {Div}(\mu \overset{\cdot }{\mathbf {F)}}-\hbox {Div}(\overset{\cdot }{p}\mathbf {F} _{o}^{*})-\hbox {Div}(p_{o}\overset{\cdot }{\mathbf {F}^{*}})-\hbox {Div}(C\nabla \overset{\cdot }{\mathbf {g}}{\mathbf {(D\otimes D))}}=0\mathbf {.} \end{aligned}$$

(62)

However, from Eq. (54), terms in the above further deduce to

$$\begin{aligned} \hbox {Div}(\mu \overset{\cdot }{\mathbf {F}})= & {} \hbox {Div}(\mu \nabla \mathbf {u})=\mu u_{i,AA} \mathbf {e}_{i},\ \ \end{aligned}$$

(63)

$$\begin{aligned} \hbox {Div}(\overset{\cdot }{p}\mathbf {F}_{o}^{*})= & {} \mathbf {F}_{o}^{*}\nabla \overset{\cdot }{p}=\mathbf {I}\nabla \overset{\cdot }{p},\because \hbox {Div}( \mathbf {F}^{*})=0, \end{aligned}$$

(64)

where $\mathbf {I}\nabla \overset{\cdot }{p}$ is on the current basis (i.e. $\mathbf {I}\nabla \overset{\cdot }{p}=\overset{\cdot }{p_{,i}}\mathbf {e}_{i}$ ) and

$$\begin{aligned} \hbox {Div}(p_{o}\overset{\cdot }{\mathbf {F}^{*}})=p_{o}\hbox {Div}(\mathbf {F}^{*})^{\cdot }=0\text {, }\because p_{o}=\mu =\text {constant}. \end{aligned}$$

(65)

We note that $p_{o}=\mu$ to recover initial stress free state at $\varepsilon =0$ (i.e.$\ \mathbf {P}_{o}=\mu \mathbf {F}_{o}-p\mathbf {F} _{o}^{*}-C\nabla \mathbf {g}_{o}{\mathbf {(D\otimes D)=0}}$). In addition, since $\mathbf {g}=\nabla [{\mathbf {FD}}]{\mathbf {D,}}$ we obtain in the case of initially straight fibers (i.e. $\nabla \mathbf {D}=0$)

$$\begin{aligned} \hbox {Div}(C\nabla \overset{\cdot }{\mathbf {g}}{\mathbf {(D\otimes D))}}= & {} C\hbox {Div}[u_{i,ABC}D_{A}D_{B}D_{C}D_{D}\mathbf {e}_{i}{\mathbf {\otimes E}}_{D}] \nonumber \\= & {} Cu_{i,ABCD}D_{A}D_{B}D_{C}D_{D}\mathbf {e}_{i},\ \because \overset{ \cdot }{\mathbf {F}}=\nabla \mathbf {u}\text {.} \end{aligned}$$

(66)

Consequently, from Eqs. (62–66), the linearized Euler equation is given by

$$\begin{aligned} \mu u_{i,AA}-\overset{\cdot }{p_{,i}}-Cu_{i,ABCD}D_{A}D_{B}D_{C}D_{D}=0, \end{aligned}$$

(67)

Further, the corresponding bulk incompressibility condition reduces to

$$\begin{aligned} (J-1)^{\cdot }=\mathbf {F}_{o}^{*}\cdot \overset{\cdot }{\mathbf {F}}= \hbox {div}\,{\mathbf {u=0}}. \end{aligned}$$

(68)

For a single family of fibers (i.e.$~\mathbf {D}=\mathbf {E} _{1},~D_{1}=1,~D_{2}=0$), the Eq. (67) becomes

$$\begin{aligned} \overset{\cdot }{p_{,i}}=\mu u_{i,AA}-Cu_{i,1111}\text { for }i,A=1,2 \end{aligned}$$

(69)

which, together with Eq. (68), serves as a compatible linear model of Eq. (27) for small deformations. Finally, the boundary conditions in Eq. (36) can be linearized similarly as the above (e.g. $\mathbf {t}=\mathbf {t}_{o}+\varepsilon \overset{\cdot }{\mathbf {t}} +o(e)$ etc.)

$$\begin{aligned} \overset{\cdot }{\mathbf {t}}= & {} \overset{\cdot }{\mathbf {P}}\mathbf {N}-\frac{ d}{ds}\left[ C\overset{\cdot }{\mathbf {g}}({\mathbf {D\cdot T}})({\mathbf {D\cdot N}})\right] \mathbf {,} \nonumber \\ \overset{\cdot }{\mathbf {m}}= & {} C\overset{\cdot }{\mathbf {g}}({\mathbf {D\cdot N}})^{2}, \nonumber \\ \overset{\cdot }{\mathbf {f}}= & {} C\overset{\cdot }{\mathbf {g}}({\mathbf {D\cdot T}})({\mathbf {D\cdot N}}). \end{aligned}$$

(70)

In particular, if the fiber’s directions are either normal or tangential to the boundary (i.e. $({\mathbf {D\cdot T}})({\mathbf {D\cdot N}})=0$ ), Eq. (70) further reduces to

$$\begin{aligned} \overset{\cdot }{t}_{i}= & {} \overset{\cdot }{P}_{iA}N_{A}, \nonumber \\ \overset{\cdot }{m}_{i}= & {} C\overset{\cdot }{g}_{i}D_{A}N_{A}D_{B}N_{B}, \nonumber \\ \overset{\cdot }{f}_{i}= & {} 0, \end{aligned}$$

(71)

where

$$\begin{aligned} \overset{\cdot }{P}_{iA}=\mu u_{i,A}-\overset{\cdot }{p}(F_{iA}^{*})_{o}-p_{o}\overset{\cdot }{F_{iA}^{*}}-C\overset{\cdot }{g} _{i,B}D_{A}D_{B},\ \ \overset{\cdot }{g}_{i}=u_{i,AB}D_{A}D_{B}, \end{aligned}$$

(72)

and

$$\begin{aligned} (F_{iA}^{*})_{o}=\delta _{iA},\text { }\because (F_{iA})_{o}=\delta _{iA}\ \text { at }\varepsilon =0. \end{aligned}$$

(73)

Lastly, since $J\partial F_{jB}^{*}/\partial F_{iA}=F_{jB}^{*}F_{iA}^{*}-F_{iB}^{*}F_{jA}^{*}$ at $\mathbf {F}_{o}=\mathbf {I}$ we obtain

$$\begin{aligned} \left( \partial F_{jB}^{*}/\partial F_{iA}\right) _{o}=\delta _{jB}\delta _{iA}-\delta _{iB}\delta _{jA}\text { and }\left( \mathbf {F}_{\mathbf {F}}^{*}[ \overset{\cdot }{\mathbf {F}}]\right) _{jB}=\left( \delta _{jB}\delta _{iA}-\delta _{iB}\delta _{jA}\right) u_{i,A}. \end{aligned}$$

(74)

Thus yields

$$\begin{aligned} \overset{\cdot }{F_{iA}^{*}}=(\hbox {Div}\mathbf {u})\delta _{iA}-u_{A,i}=-u_{A,i}, \end{aligned}$$

(75)

where $\hbox {Div}\mathbf {u}=\hbox {div}\,\mathbf {u}=0$ from the Linearized incompressibility condition. We note that, in the superposed incremental deformations, there is no clear distinction between current and deformed configuration (i.e. $\mathbf {e}_{\alpha }=\mathbf {E}_{\alpha }$).

5 Solution to the linearized problem

We introduce scalar field $\phi ~$as

$$\begin{aligned} \mathbf {u}=\mathbf {k}\times \nabla \phi ,\ \mathbf {k} \text { (unit normal)};\text { }u_{i}=\varepsilon _{\lambda i}\phi _{,\lambda }, \end{aligned}$$

(76)

so that Eq. (68) can be automatically satisfied (i.e. $\phi _{,12}-\phi _{,21}=0$). From Eq. (76), the linearized Euler equation Eq. (69) can be rewritten as

$$\begin{aligned} \overset{\cdot }{p_{,i}}=\mu \varepsilon _{\lambda i}(\phi _{,\lambda 11}+\phi _{,\lambda 22})-C\varepsilon _{\lambda i}\phi _{,\lambda 1111}. \end{aligned}$$

(77)

By utilizing the compatibility condition for $\overset{\cdot }{p_{,i}}$ (i.e. $\overset{\cdot }{p_{,ij}}=\overset{\cdot }{p_{,ji}}$ ), we obtain the following ordinary differential equation as;

$$\begin{aligned} \mu (\phi _{,1111}+2\phi _{,1122}+\phi _{,2222})-C(\phi _{,11}+\phi _{,22})_{,1111}=0 \end{aligned}$$

(78)

The above further reduces to

$$\begin{aligned} \Delta H-\alpha H_{,1111}=0,\text { where}~H=\Delta \phi \text { and }\ \alpha =\frac{C}{\mu }>0\text { (material constants).} \end{aligned}$$

(79)

The general solution for the above equation can be found as (when:$\ 1-4 \frac{C}{\mu }m^{2}<0$)

$$\begin{aligned} \phi= & {} \sum \limits _{m=1}^{\infty }\left[ \left\{ e^{a_{m}x}\left( A_{m}\cos b_{m}x+B_{m}\sin b_{m}x\right) +e^{-a_{m}x}\left( C_{m}\cos b_{m}x+D_{m}\sin b_{m}x\right) \right\} \right. \nonumber \\&\times (E_{m}\cos my+F_{m}\sin my)]+K,~a_{m}=\frac{\sqrt{2m\sqrt{\alpha }+1 }}{2\sqrt{\alpha }},\ b_{m}=\frac{\sqrt{2m\sqrt{\alpha }-1}}{2\sqrt{\alpha }}, \end{aligned}$$

(80)

where K is a solution of Laplace’s equation ($\Delta K=0$) given by

$$\begin{aligned} K=\sum \limits _{n=1}^{\infty }\left[ \left( G_{n}\cosh nx+H_{n}\sinh nx\right) (I_{n}\cos ny+J_{n}\sin ny\right) ] \end{aligned}$$

Fig. 7

schematic of problem

and m is separation constants. We note here that the case of $\ 1-4\frac{C }{\mu }m^{2}>0$ is excluded, since the strength of fibers is usually far more stronger than those of bulk materials (i.e. $C\gg \mu$) and therefore physically less meaningful. The unknown constant real numbers $A_{m},B_{m},C_{m},D_{m},E_{m},F_{m},G_{n},H_{n},I_{n},$ and $J_{n}$ can be completely determined by imposing admissible boundary conditions depicted in Eqs. (71–75). The corresponding stress and displacement fields can be also determined through Eqs. (72) and (76–) (e.g. $u_{1}=-\phi _{,2}$, $u_{2}=\phi _{,1}$ etc.). For example, in the case of symmetric bending where (see Fig. 7)

$$\begin{aligned} \overset{\cdot }{\mathbf {m}}=\overset{\cdot }{m}_{1}\mathbf {e}_{1}+\overset{ \cdot }{m}_{2}\mathbf {e}_{2},\ \ \overset{\cdot }{m}_{1}=5\approxeq \sum \limits _{n=1}^{30}\frac{20}{\pi n}(-1)^{\frac{n-1}{2}}\cos \left( \frac{\pi n }{2d}\right) y\mathbf {e}_{1},\ \overset{\cdot }{m}_{2}=0 \end{aligned}$$

(81)

and

$$\begin{aligned} \mathbf {D}=D_{1}\mathbf {E}_{1}+D_{2}\mathbf {E}_{2},\ \ D_{1}=1,\ \ D_{2}=0. \end{aligned}$$

(82)

We find

$$\begin{aligned} \phi (x,y)= & {} \left[ \left\{ e^{a_{m}x}\left( -C_{m}\cos b_{m}x+D_{m}\sin b_{m}x\right) +e^{-a_{m}x}\left( C_{m}\cos b_{m}x+D_{m}\sin b_{m}x\right) \right\} \nonumber \right. \\&\left. \times \left( \sin \left( \frac{\pi }{2d}\right) y\right) \right] , \nonumber \\ m= & {} \frac{\pi n}{2d},\alpha =\frac{C}{\mu },a_{m}=\ \frac{\sqrt{2m\sqrt{ \alpha }+1}}{2\sqrt{\alpha }},\ b_{m}=\frac{\sqrt{2m\sqrt{\alpha }-1}}{2 \sqrt{\alpha }}, \end{aligned}$$

(83)

and unknown $C_{m}$ and $D_{m}$ can be determined via

$$\begin{aligned} \overset{\cdot }{m}_{1}= & {} Cu_{1,11}=-\phi _{,211}=\sum \limits _{n=1}^{30} \frac{20}{\pi n}(-1)^{(n-1)/2}\cos \left( \frac{\pi n}{2d}\right) y \nonumber \\ \overset{\cdot }{m}_{2}= & {} Cu_{2,11}=\phi _{,111}=0. \end{aligned}$$

(84)

Fig. 8

Deformation profiles with respect to $M/\mu$ when $C/\mu =150$

Fig. 9

Deformation profiles with respect to $C/\mu$ when $M/\mu =5$

More precisely, using the symmetry condition across $x=0$ and the second of Eq. (84), we obtain $A_{m}=-C_{m}$ and $B_{m}=D_{m}$. Therefore, the unknowns in Eq. (83) are completely determined. The applied moment is approximated using Fourier series (see, Eq. 81) indicating fast convergence (within 30 iterations) and the corresponding results are summarized through Figs. 8, 9, 10, 11, 12. Despite the presence of sharp corners, where singular behaviors of response functions are often observed (e.g. discontinuities and oscillations), the obtained solution demonstrates smooth and continuous deformation profiles with sufficient sensitivities to the parameters,C, $\mu$ and M (see, Figs. 8, 9). More precisely, the corresponding deflections are inversely correlated with fibers’ strength $C/\mu$ (Fig. 9), while a positive correlation exists between the deflections and applied bending moments (Fig. 8). In addition, the analytical (linear) solution shows good agreement with nonlinear solution (FEM) for the small deformation regime, while larger values of M induce a significant discrepancy between the linear and nonlinear solution (see, Fig. 12). This is mainly due to the fact that the presented linear model accounts only the leading order terms as depicted in Eqs. (54–55). As a result, the obtained analytical solution has limitations in large deformation analysis. However, it can still be used in the design and analysis of fiber composites, particularly for CNC-reinforced composites, where the deformations of the systems are expected to be relatively ‘small’.

Fig. 10

Deformed configuration of the fiber composite when $C/\mu =150$ and $M/\mu =5$

Fig. 11

Stress distribution $P_{xx}$ when $M/\mu =5,~C/\mu =150$

Fig. 12

Solutions of the bending problem with $C/\mu =150$. Nonlinear solution (dashed line), linear solution (solid line)

6 Conclusion

A continuum-based model is developed in finite plane elastostatics in which fibers resistant to flexure is taken into account. The fibers are regarded as continuously distributed spatial rods of the Kirchhoff type in which the kinematics are based on a position field and a director field. The equilibrium equation of the fiber-reinforced composite materials is derived by the variational computation and method of virtual work. With the equilibrium equation satisfied, the necessary boundary condition is also obtained. These constitute a highly nonlinear coupled PDE system which is treated numerically via the finite element method. The corresponding deformed configurations demonstrate clear dependency on fibers resistant to flexure and show good agreement with the three point bending test of CNC-reinforced composites. Within the prescription of superposed incremental deformations, a complete linear theory is developed through which an analytical solution of the corresponding linearized PDE system is obtained. The obtained analytical solution demonstrates good agreement with nonlinear solution for the small deformation regime, yet has limited predictions for large deformation analysis. In addition, the solution exhibits smooth behavior as it approaches the boundary despite the influences of sharp corners, where singular behaviors of response functions are often observed. Lastly, we mention that the final deformed stage is energetically favorable and therefore stable.