A model for the second strain gradient continua reinforced with extensible fibers in plane elastostatics

Abstract

A second strain gradient theory-based continuum model is presented for the mechanics of an elastic solid reinforced with extensible fibers in plane elastostatics. The extension and bending kinematics of fibers are formulated via the second and the third gradient of the continuum deformation. The Euler equations arising in the third gradient of virtual displacement are then formulated by means of iterated integration by parts and variational principles. A rigorous derivation of the associated boundary conditions is also presented from which the expressions of triple forces and stresses are obtained. The obtained triple forces are found to be in conjugation with the Piola-type triple stress and are necessary to determine energy contributions on edges and points of Cauchy cuts. In particular, a complete linear model including admissible boundary conditions is derived within the description of superposed incremental deformations. The obtained analytical solution predicts smooth deformation profiles and, more importantly, assimilate gradual and dilatational shear angle distributions throughout the domain of interest.

1 Introduction

The mechanics of materials with distinct microstructures has consistently been the subject of intense study that has significantly advanced our understanding of materials science and continuum mechanics in general [1, 2]. The fiber-reinforced composites are a particular class of such materials where fibers act as a reinforcement in order to enhance the mechanical properties of matrix materials. Contemporary continuum approaches incorporating the microstructural effects of fibers on elastic solids are based on the concept of an anisotropic material followed by the postulation of continuously distributed spatial rods (fibers) of Kirchhoff type [3,4,5]. Within this continuum setting, the kinematics of fibers are formulated via the first and second gradient of continuum deformations and integrated into desired response functions which are typically augmented by the constraint of bulk incompressibility or fiber inextensibility (see, for example, [6,7,8]. The second gradient continuum models of Spencer and Soldatos type [9] have been widely adopted in the deformation analysis of fiber-reinforced materials since they offer compact descriptions in the constitutive modeling and associated mathematical framework. The second gradient models also resolved the kinematic over determinacy arising in the earlier studies of first gradient continuum models [10, 11]. The author in [6] devised a generalized second gradient model under the simplified setting of the Cosserat theory of nonlinear elasticity which accommodates extensible and twistable fibers. The generalized model has been further refined for the analyses of meshed structures [12,13,14], bending motions of fiber composite [15, 16] and composites reinforced with extensible fibers [8, 17, 18]. Although the second gradient models offer more realistic descriptions of microstructured continua, they are intrinsically limited in the predictions of phenomena associated with higher-gradient fields such as mechanical contact interactions on edges and points of Cauchy cuts [19,20,21,22], dynamic instability arising in highly inhomogeneous continua [23,24,25,26] and internal boundary layer formations of bone tissues [27,28,29]. The analysis of such exotic responses of microstructured continua requires the consideration of higher-order gradient continua which can offer sufficient smoothness up to the desired gradient fields.

The concept of higher-order continua was discussed in Mindlin’s earlier work (see [30] and the references therein) that has inspired researchers to confront formidable challenges arising in various engineering problems. For example, authors in [31,32,33] examined mechanical contact interactions between 3D and 1D continua in the form of galloping and internal resonance using higher-gradient theory. Recently, the higher-order continuum theory has been revisited for its applications in the analyses of microstructured continua with complex topological boundaries (including boundary layers) and associated forces [19,20,21]. In particular, authors in [34, 35] integrated the third gradient of deformation into the continuum model describing the bending motions of fiber composites and predict smooth shear angle distributions. However, the implementation of higher-order gradient theory, especially those arising in finite plane deformations, is largely absent from the literature due to the intrinsic complexities in the constitutive formulations and the associated mathematical framework.

In the present study, we develop a second strain gradient-based model describing the mechanics of an elastic solid reinforced with extensible fibers and subjected to plane bias extension. Emphasis is placed on the incorporation of the second strain gradient field into the model of continuum deformation while maintaining the rigor and relative simplicity in the corresponding constitutive formulation. The extensible fibers are presumed to be continuously distributed spatial rod of Kirchhoff type in which the kinematics of fibers are defined by their position and director fields [3,4,5]. Within this setting, the energy density function of Spencer and Soldatos type [9] is generalized to accommodate the third gradient of continuum deformation through which contact forces, couples, double forces and triple forces are assimilated together with the extension and bending resistance of fibers. The Euler equations and the admissible boundary conditions are obtained by utilizing iterated integrations by parts and the variational formulations arising in the third gradient of continuum deformations [36,37,38]. More precisely, the rate of change in curvature, defined at points on the convected curves of fibers, is formulated via the third gradient of deformation map through which the mechanical contact interactions between the adjoined fibers and the matrix may be characterized.

In particular, a complete linear model is derived from the proposed nonlinear theory for small deformation analysis superposed on large. The corresponding boundary conditions are also approximated up to the leading order expansion in order to obtain the expressions of compatible triple forces and their energy couples (Piola-type triple stresses) exerted by the third gradient continua (see, also, [19, 37, 38]). By taking adapted iterative reduction and eigenfunction expansion methods [39,40,41], a complete analytical solution is obtained which describes the responses of an elastic solid reinforced with extensible fibers and subjected to plane bias extension. The proposed linear model assimilates smooth and dilatational shear angle distributions unlike those predicted by the first and second gradient-based continuum models where the resulting shear zones display either non-smooth distributions or non-dilatational shear angle transitions (see, for example, [8, 18] and the references therein). Lastly, comparisons with the experimental results of polymeric (PETKM) composites at 20% and 50% elongation have been performed. Despite its limitation for relatively small deformation analyses, the proposed linear model demonstrates reasonably good agreement with the deformation profiles and shear angle distributions of PETKM composites throughout the domain of interest.

Throughout the paper, we make use of a number of well-established symbols and conventions such as $\mathbf {A}^{T},~\mathbf {A}^{-1},\ \mathbf {A}^{*}$ and $tr(\mathbf {A}).$ These are the transpose, the inverse, the cofactor and the trace of a tensor A, respectively. The tensor product of vectors is indicated by interposing the symbol $\otimes ,$ and the Euclidian inner product of tensors A, B is defined by $\mathbf {A\cdot B=}tr(\mathbf {AB}^{T})$ ; the associated norm is $\left| \mathbf {A}\right| =\sqrt{\mathbf { A}\cdot \mathbf { A}}$. The symbol ${\vert }*{\vert }$ is also used to denote the usual Euclidian norm of three vectors. Latin and Greek indices take values in $\{1, 2\}$ and, when repeated, are summed over their ranges. Lastly, the notation $F_{\mathbf {A}}$ stands for the tensor-valued derivatives of a scalar-valued function $F(\mathbf {A})$.

2 Kinematics

Let $\varvec{\tau }$ be the unit tangent to the fiber’s parametric trajectory of $\mathbf {r}(s)$ in the current configuration and $\mathbf {D}$ and $\mathbf {X}(S)$ are their counterparts in the reference frame. The orientations of a particular fiber are then defined by

$$\begin{aligned} \lambda =\left| \mathbf {d}\right| \text { and }\lambda \varvec{\tau }= \mathbf {d; }\,\lambda \equiv \frac{\mathrm{{d}}s}{\mathrm{{d}}S}\text { and }\varvec{\tau }\equiv \frac{\mathrm{{d}}\mathbf {r(}s\mathbf {)}}{\mathrm{{d}}s}, \end{aligned}$$

(1)

where s and S are, respectively, the arc length parameters in current and reference configuration and $\mathbf {d}$ is the director field of fibers in the reference frame which can be expressed as

$$\begin{aligned} \mathbf {d}=\mathbf {FD}\text {, }\mathbf {F=}\lambda \varvec{{\tau } \otimes } \mathbf{D,} \end{aligned}$$

(2)

and $\mathbf {F}$ is the first gradient of the deformation function $(\varvec{\chi }(X)).$ Equation (2) is obtained by taking the derivative of $\mathbf {r}(S)=\varvec{\chi }(X(S))$, upon making the identifications of $\mathbf {D}=dX(S)/dS$ and $\mathbf {d}=d\mathbf {r}(s)/ds$ (see, also, [3,4,5]). Here $d(*)/ds$ and $d\mathbf {(*)/}dS$ refer to the arc length derivative of ($*$) along fibers’ directions in the deformed and reference configurations, respectively. Therefore, from Eq. (2), the geodesic curvature of a parametric curve of fibers ($\mathbf {r }\left( S\right)$) and the associated rate of changes in curvature can be obtained by following equations (see, also, [9] and Eqs. (A2)–(A4) in “Appendix”)

$$\begin{aligned} \mathbf {g=r}^{\prime \prime }=\frac{\mathrm{{d}}^{2}\mathbf {r(}S\mathbf {)}}{ \mathrm{{d}}S^{2}}=\frac{\partial (\mathbf {FD)}}{\partial \mathbf {X}}\frac{\mathrm{{d}} \mathbf {X}}{\mathrm{{d}}S}=\nabla [\mathbf {FD]D}. \end{aligned}$$

(3)

In a typical environment, most of the fibers are straight prior to deformations. Even slightly curved fibers can be idealized as ‘fairly straight’ fibers, considering their length scales with respect to those of matrix materials. This further leads to the assumption of vanishing gradients fields of $\mathbf {D}$ (i.e., $\nabla \mathbf {D=0)}$. Thus, Eq. (3) reduces to

$$\begin{aligned} \mathbf {g(G)=G(D\otimes D),} \end{aligned}$$

(4)

where we adopt the commonly used convention of strain gradient tensor:

$$\begin{aligned} \nabla \mathbf {F\equiv G}. \end{aligned}$$

(5)

The corresponding strain gradient field is compatible in the sense of Leibniz differentiation which can be seen as

$$\begin{aligned} \text { }G_{iAB}=F_{iA,B}=F_{iB,A}=G_{iBA}. \end{aligned}$$

(6)

Equations (3)–(6) constitute a second gradient-based energy function in the description of an elastic solid reinforced with fibers resistant to flexure;

$$\begin{aligned} W(\mathbf {F,g(G)})=\widehat{W}(\mathbf {F})+\frac{1}{2}C\left( \mathbf {F} \right) \left| \mathbf {g(G)}\right| ^{2}, \end{aligned}$$

(7)

where $\widehat{W}(\mathbf {F})$ account for the energy function of a matrix material (e.g., $\widehat{W}(\mathbf {F})=\frac{\mu }{2}(\mathbf {F\cdot F}-3)$) for neo-Hookean (incompressible) type of materials) and $\frac{1}{2} C\left( \mathbf {F}\right) \left| \mathbf {g(G)}\right| ^{2}$ is fiber’s bending energy potential of Spencer and Soldatos type [9]. Further, $C\left( \mathbf {F}\right)$ refers to the material parameter associated Piola-type double stress which is, in general, independent of the deformation gradient, i.e.,

$$\begin{aligned} C\left( \mathbf {F}\right) =C. \end{aligned}$$

(8)

Eq. (7) is based on the kinematic relevance between the bending motions of embedded fibers and the adjoined second gradient fields [9] that has been widely and successfully adopted in the relevant studies (see, for example, [6, 15,16,17, 42]). For the desired applications, the above energy potential is now augmented to accommodate extensible fibers as

$$\begin{aligned} W(\mathbf {F},\varepsilon (\mathbf {F}),\mathbf {g(G)})=\widehat{W}(\mathbf {F})+ \frac{1}{2}E\varepsilon ^{2}+\frac{1}{2}C\left| \mathbf {g(G)}\right| ^{2}, \end{aligned}$$

(9)

where $\frac{1}{2}E\varepsilon ^{2}$ is the quadratic strain potential of fiber’s extension and E is the corresponding modulus. The expression of $\varepsilon$ is given by

$$\begin{aligned} \text { }\varepsilon =\frac{1}{2}(\lambda ^{2}-1). \end{aligned}$$

(10)

Also, in view of Eqs. (1)–(2), $\lambda ^{2}$ can be written in terms of the deformation gradient tensor $\mathbf {F}$ and the director field of fibers $\mathbf {D}$ as

$$\begin{aligned} \lambda ^{2}=\mathbf {FD\cdot FD=F}^{T}\mathbf {FD\cdot D=(\mathbf {F}^{T} \mathbf {F)}\cdot D\otimes D}. \end{aligned}$$

(11)

In particular, the third gradient of deformations is introduced into the models of continuum deformation to achieve a more comprehensive description of generalized continua of higher order. More precisely, we compute the rate of changes in curvature at points of the fibers as (see, also, Eqs. (A5)–(A7) in “Appendix”)

$$\begin{aligned} \varvec{\alpha }=\mathbf {r}^{\prime \prime \prime }=\frac{\mathrm{{d}}(\nabla [\mathbf {FD]D})}{\mathrm{{d}}S}=\frac{\partial (\nabla [\mathbf {FD]D)}}{\partial \mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}=[\nabla \{\nabla [\mathbf {FD]D\}}] \mathbf {D}=[\nabla \{\nabla [\mathbf {FD]\}D+}\nabla [\mathbf { FD](}\nabla \mathbf {D)}]\mathbf {D,} \end{aligned}$$

(12)

such that the interactions between the fibers and the surrounding matrix may be characterized. The required third-order gradient fields can be formulated in the same spirit as Eqs. (4)–(5) that

$$\begin{aligned} \varvec{\alpha }= & {} \nabla (\nabla \mathbf {F}) (\mathbf {D}\otimes \mathbf {D}\otimes \mathbf {D})\text {, }\nonumber \\ \nabla (\nabla \mathbf {F)}= & {} \nabla \mathbf {(G)\equiv H}, \text {and}\nonumber \\ \varvec{\alpha }= & {} \mathbf {H}(\mathbf {D}\otimes \mathbf {D}\otimes \mathbf {D})=\alpha (\mathbf {H,D}). \end{aligned}$$

(13)

Consequently, the energy potential accommodating the third gradient of continuum deformation can be obtained as

$$\begin{aligned} W(\mathbf {F},\varepsilon (\mathbf {F}),\mathbf {g(G),\alpha (H)})=\widehat{W}( \mathbf {F})+\frac{1}{2}E\varepsilon ^{2}+\frac{1}{2}C\left| \mathbf {g(G)} \right| ^{2}+\frac{1}{2}A(\mathbf {H})\left| {\varvec{\alpha }} \mathbf {(H)} \right| ^{2}. \end{aligned}$$

(14)

We note here that, similar to Eq. (8), $A(\mathbf {H})$ pertaining to the third gradient of continuum deformations is assumed to be constant for the sake of simplicity

$$\begin{aligned} A(\mathbf {H})=A. \end{aligned}$$

(15)

The phenomenological implications vis-a-vis the third gradient of deformations (e.g., interactions between fibers and a matrix material) and the identification of the associated coefficient (here, denoted as A) are addressed in the literature [20,21,22, 36,37,38, 43]. In the present study, we place an emphasis on the development of a mathematical framework and the associated analyses in order to promote the implementation of higher-order strain gradient theory in plane elastostatics. For uses in the derivation of Euler equations and the necessary boundary conditions, we continue by evaluating the induced energy variation of the response function with respect to $\mathbf {F}$,$\varepsilon ,$ $\mathbf {g}$, and $\varvec{\alpha }$ as

$$\begin{aligned} \dot{W}(\mathbf {F},\varepsilon ,\mathbf {g,\alpha })=\widehat{W}_{\mathbf {F}} \cdot \dot{\mathbf {F}}+W_{\varepsilon }\dot{\varepsilon }\mathbf {+}W_{\mathbf {g}} \cdot \dot{\mathbf {g}}+W_{\varvec{\alpha }}\cdot \dot{\alpha }, \end{aligned}$$

(16)

where the superposed dot refers to derivatives with respect to a parameter $\epsilon$ at the particular configuration of the composite ($\epsilon =0$) that labels a one-parameter family of deformations.

The desired expressions for the induced energy variation can be obtained from Eqs. (4) and (10)–(14) that

$$\begin{aligned} \dot{\varepsilon }= & {} \frac{1}{2}(\lambda ^{2}-1\dot{)}=\frac{1}{2}({{\mathbf {FD}}\cdot {\mathbf {FD}}-{\varvec{1}}\dot{)}={\mathbf {FD}}\cdot \dot{{\mathbf {F}}}{\mathbf {D}}={\mathbf {FD}}\otimes {\mathbf {D}}\cdot \dot{{\mathbf {F}}},}\text { } W_{\varepsilon }\dot{\varepsilon }=\left( \frac{1}{2}E\varepsilon ^{2}\right) =E\varepsilon \dot{\varepsilon }, \end{aligned}$$

(17)

$$\begin{aligned} W_{\mathbf {g}}\cdot \dot{\mathbf {g}}= & {} C\mathbf {g}\cdot \overset{\cdot }{\mathbf {g}}=Cg_{j}\mathbf {e}_{\mathbf {j}}\cdot \dot{G}_{iAB}D_{A}D_{B} \mathbf {e}_{i}=Cg_{i}D_{A}D_{B}\dot{G}_{iAB}\text {, } \end{aligned}$$

(18)

and

$$\begin{aligned} \dot{W}(\mathbf {H})=A\varvec{\alpha \cdot }\overset{\cdot }{\varvec{\alpha }} =A\alpha _{j}\mathbf {e}_{\mathbf {j}}\cdot \dot{H}_{iABC}D_{A}D_{B}D_{C} \mathbf {e}_{i}=A\alpha _{i}D_{A}D_{B}D_{C}\dot{H}_{iABC}. \end{aligned}$$

(19)

Hence, from Eqs. (16)–(19), we find

$$\begin{aligned} \dot{W}(\mathbf {F},\varepsilon ,\mathbf {g,\alpha })= & {} \widehat{W}_{F_{iA}} \dot{F}_{iA}+\frac{E}{2}(F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A})\dot{F} _{iA} \nonumber \\&+Cg_{i}D_{A}D_{B}\dot{G}_{iAB}+A\alpha _{i}D_{A}D_{B}D_{C}\dot{H}_{iABC}. \end{aligned}$$

(20)

Clearly, the resulting energy variation [Eq. (20)] is dependent on both the second and third gradients of continuum deformations as intended. It will be seen in the later sections that Eq. (20) furnishes the relevant mathematical framework to accommodate the triple force (e.g., interaction forces) and its energy couple (Piola-type triple stress) sustained by the third gradient continua.

3 Equilibrium

The derivation of the Euler equation and boundary conditions arising in the second gradient elasticity are well established (see, for example, [36, 44, 45] and references therein). In this section, we present a variational formulation arising in the third gradient of the continuum deformation by employing the principles of the virtual work statement and iterated integrations by parts ([22, 36,37,38, 43]).

In a typical environment, volumetric changes in materials’ deformations are energetically expensive processes and thus are constrained in most engineering analyses (see, also, [46, 47]). This can be achieved by introducing the weak form of bulk incompressibility condition into the proposed energy potential such that

$$\begin{aligned} U(\mathbf {F},\varepsilon ,\mathbf {g,\alpha ,}p)=W(\mathbf {F},\varepsilon , \mathbf {g,\alpha })-p(J-1), \end{aligned}$$

(21)

where J is determinant of $\mathbf {F}$ and p is a Lagrange multiplier filed. Relevant applications regarding the uses of Lagrange multiplies arising in the continuum-based modeling and analysis may also be found in [48] (and the references therein). The strain energy of the system is then expressed as

$$\begin{aligned} E=\int _{\Omega }U(\mathbf {F},\text { }\mathbf {G},\text { }\mathbf {H,\ }p)\mathrm{{d}}A, \end{aligned}$$

(22)

where $\Omega$ is the referential domain occupied by a fiber-matrix material.

Now, the principle of virtual work states that

$$\begin{aligned} \dot{E}=P. \end{aligned}$$

(23)

In the above, P is the virtual power of the applied load and the superposed dot refers to the variational and/or Gateâux derivative. Since the conservative loads are characterized by the existence of a potential L such that $P=\dot{L}$, the problem of determining equilibrium deformations is then reduced to the problem of minimizing the potential energy $E-L.$ Accordingly, we find

$$\begin{aligned} \overset{\cdot }{E}=\int _{\Omega }\dot{U}(\mathbf {F},\text { }\mathbf {G}, \text { }\mathbf {H,\ }p)\mathrm{{d}}A. \end{aligned}$$

(24)

Using the identity $\dot{J}=J_{\mathbf {F}}{{\mathbf {F}}\cdot \dot{{\mathbf {F}}}={\mathbf {F}}}^{*} \cdot \dot{\mathbf {F}}$ together with the results in Eqs. (20)–(21), the variational derivative of the augmented energy potential can be evaluated as

$$\begin{aligned} \dot{U}= & {} \dot{W}-p\dot{J}=\left[ \widehat{W}_{F_{iA}}u_{i,A}+\frac{E}{2} (F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A})u_{i,A}\right. \nonumber \\&\left. +C(g_{i}D_{A}D_{B})u_{i,AB}+A(\alpha _{i}D_{A}D_{B}D_{C})u_{i,ABC}-pF_{iA}^{*}u_{i,A}\right] , \end{aligned}$$

(25)

where $u_{i}=\dot{\chi }_{i}$ is the variation of the position field. Hence, Eqs. (24) yield

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\Omega }\Bigg [\widehat{W}_{F_{iA}}u_{i,A}+\frac{E}{2} (F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A})u_{i,A} \Bigg . \nonumber \\&\Bigg .+C(g_{i}D_{A}D_{B})u_{i,AB}+A(\alpha _{i}D_{A}D_{B}D_{C})u_{i,ABC}-pF_{iA}^{*}u_{i,A}\Bigg ]\mathrm{{d}}A. \end{aligned}$$

(26)

Applying integration by parts on the third and fourth terms in Eq. (26), we find

$$\begin{aligned} C(g_{i}D_{A}D_{B})u_{i,AB}= & {} C(g_{i}D_{A}D_{B}u_{i,A})_{,B}-C(g_{i}D_{A}D_{B})_{,B}u_{i,A},\text { and}\nonumber \\ A(\alpha _{i}D_{A}D_{B}D_{C})u_{i,ABC}= & {} A(\alpha _{i}D_{A}D_{B}D_{C}u_{i,AB})_{,C}-A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}u_{i,AB}, \end{aligned}$$

(27)

and thereby obtain

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\Omega }\left[ \widehat{W}_{F_{iA}}u_{i,A}+\frac{E}{2} (F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A}) u_{i,A}+C(g_{i}D_{A}D_{B}u_{i,A})_{,B}\right. \nonumber \\&\left. -C(g_{i}D_{A}D_{B})_{,B}u_{i,A}+A(\alpha _{i}D_{A}D_{B}D_{C}u_{i,AB})_{,C}-A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}u_{i,AB}-pF_{iA}^{*}u_{i,A}\right] \mathrm{{d}}A. \nonumber \\ \end{aligned}$$

(28)

Equation (28) may be recast as

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\Omega }\left[ \widehat{W}_{F_{iA}}-pF_{iA}^{*}+ \frac{E}{2} (F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A})-C(g_{i} D_{A}D_{B})_{,B}\right] u_{i,A}\mathrm{{d}}A \nonumber \\&-\int _{\Omega }\big [A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}u_{i,AB}\big ]\mathrm{{d}}A+\int _{\partial \Omega }(Cg_{i}D_{A}D_{B}u_{i,A})N_{B}\mathrm{{d}}S \nonumber \\&+\int _{\partial \Omega }(A\alpha _{i}D_{A}D_{B}D_{C}u_{i,AB})N_{C}\mathrm{{d}}S, \end{aligned}$$

(29)

where $\mathbf {N}$ is the rightward unit normal to the boundary $\partial \Omega$ in the sense of Green–Stokes theorem. To obtain the desired expression, we again apply integration by parts and the Green–Stokes theorem on the second integral of the above; i.e.,

$$\begin{aligned}&\int _{\Omega }\left[ A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}u_{i,AB}\right] \mathrm{{d}}A =\int _{\Omega }\left[ \{A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}u_{i,A}\}_{,B}-A(\alpha _{i}D_{A}D_{B}D_{C})_{,CB}u_{i,A}\right] \mathrm{{d}}A \nonumber \\&\quad =\int _{\partial \Omega }A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}u_{i,A}N_{B}\mathrm{{d}}S -\int _{\Omega }A(\alpha _{i}D_{A}D_{B}D_{C})_{,CB}u_{i,A}]\mathrm{{d}}A. \end{aligned}$$

(30)

The substitution of Eq. (30) into Eq. (29) then furnishes

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\Omega }\left[ \widehat{W}_{F_{iA}}-pF_{iA}^{*}+ \frac{E}{2} (F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A})-C(g_{i}D_{A}D_{B})_{,B}+A( \alpha _{i}D_{A}D_{B}D_{C})_{,CB}\right] u_{i,A}\mathrm{{d}}A \nonumber \\&\int _{\partial \Omega }\left[ \{Cg_{i}D_{A}D_{B}-A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}\}u_{i,A}N_{B}+A\alpha _{i}D_{A}D_{B}D_{C}u_{i,AB}N_{C}\right] \mathrm{{d}}S. \end{aligned}$$

(31)

Finally, we obtain

$$\begin{aligned} \overset{\cdot }{E}=\int _{\Omega }P_{iA}u_{i,A}\mathrm{{d}}A+\int _{\partial \Omega }\left[ \{Cg_{i}D_{A}D_{B}-A(\alpha _{i}D_{A}D_{B}D_{C})_{,C}\}u_{i,A}N_{B}+A\alpha _{i}D_{A}D_{B}D_{C}u_{i,AB}N_{C}\right] \mathrm{{d}}S, \end{aligned}$$

(32)

where

$$\begin{aligned}&P_{iA}(\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)} \nonumber \\&\quad = \left[ \widehat{W}_{F_{iA}}-pF_{iA}^{*}+\frac{E}{2} (F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A})-C(g_{i}D_{A}D_{B})_{,B}+A( \alpha _{i}D_{A}D_{B}D_{C})_{,CB}\right] (\mathbf {e}_{i}\otimes \mathbf {E}_{A}).\nonumber \\ \end{aligned}$$

(33)

Hence, the Euler equation satisfies

$$\begin{aligned} P_{iA,A}\mathbf {e}_{i}=0\text { or }\mathrm{{Div}}(\mathbf {P})=0 \end{aligned}$$

(34)

which holds in $\Omega .$ It is also note here that, for the sake of clarity and completeness, the appropriate tensorial notations of Eqs. (32)–( 33) may be found as

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\partial \Omega }\left[ \left\{ C\mathbf {(g\otimes D\otimes D)}^{T}-(\mathrm{{Div}}(\mathbf {\alpha \otimes D\otimes D\otimes D})^{T}\right\} \mathbf {F} ^{T}+(\mathbf {\alpha \otimes D\otimes D\otimes D)}(\nabla \mathbf {F})^{T}\right] \cdot \mathbf {N}\mathrm{{d}}S \nonumber \\&+\int _{\Omega }\mathbf {P}\cdot \overset{\cdot }{\mathbf {F}}\mathrm{{d}}A, \end{aligned}$$

(35)

and

$$\begin{aligned} \mathbf {P}=\widehat{W}_{\mathbf {F}}-p\mathbf {F}^{*}+\frac{E}{2}(\mathbf { FD}\cdot \mathbf {FD}-1)\mathbf {F}(\mathbf {D\otimes D})-\mathrm{{Div}}(C\mathbf {g\otimes D\otimes D})+\mathrm{{Div}}(\mathrm{{Div}}(A\mathbf {\alpha \otimes D\otimes D\otimes D})), \end{aligned}$$

(36)

which clearly meet the basis agreement requirement arising in multilinear transformations of higher-order tensors with mixed bases.

4 Boundary conditions

The incorporation of the high-order gradient fields into the model of the continuum deformation leads to the necessary existence of their high-order energy conjugate pairs (e.g., triple forces, contact interactions) suitably imposed on the desired boundaries. Although the roles and phenomenological implications regarding these higher-order boundary conditions are discussed in a number of studies (see, for example, [19, 20, 22, 37, 38]), their implementations, particularly those arising in plane elastostatics, in an actual analytical platform have not been well addressed. Throughout the section, we present rigorous derivations vis-a-vis admissible boundary forces of higher-order exerted on the third gradient continua.

To proceed, we apply integration by parts (i.e., $P_{iA}u_{i,A}=(P_{iA}u_{i})_{,A}-P_{iA,A}u_{i}$) on the first term of Eq. (32) and thereby obtain

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial \Omega }P_{iA}u_{i}N_{A}\mathrm{{d}}S-\int _{\Omega }P_{iA,A}u_{i}\mathrm{{d}}A+\int _{\partial \Omega }\left[ \{W_{G_{iAB}}-(W_{H_{iABC}})_{,C} \}u_{i,A}N_{B}+W_{H_{iABC}}u_{i,AB}N_{C}\right] \mathrm{{d}}S, \end{aligned}$$

(37)

where we define:

$$\begin{aligned} W_{G_{iAB}}\equiv Cg_{i}D_{A}D_{B}\text { and }W_{H_{iABC}}\equiv A\alpha _{i}D_{A}D_{B}D_{C}, \end{aligned}$$

(38)

for the notational simplicity in the forgoing derivations. Since the Euler equation, $P_{iA,A}=0,$ holds in $\Omega$, the above reduces to

$$\begin{aligned} \overset{\cdot }{E}=\int _{\partial \Omega }P_{iA}u_{i}N_{A}\mathrm{{d}}S+\int _{\partial \Omega }\left[ \{W_{G_{iAB}}-(W_{H_{iABC}})_{,C} \}u_{i,A}N_{B}+W_{H_{iABC}}u_{i,AB}N_{C}\right] \mathrm{{d}}S, \end{aligned}$$

(39)

Now, the projection of onto normal and tangential direction yields

$$\begin{aligned} \nabla \mathbf {u=}\nabla \mathbf {u(T\otimes T)+}\nabla \mathbf {u(N\otimes N)= \mathbf {u,}_{\mathbf {T}}\otimes T+u,}_{\mathbf {N}}\otimes \mathbf {N,} \end{aligned}$$

(40)

In the above $\mathbf {u,}_{\mathbf {T}}$ and $\mathbf {u}_{,N}$ are, respectively, the tangential and normal derivatives of $\mathbf {u}$ such that

$$\begin{aligned} u_{i,T}\mathbf {e}_{i}=u_{i,A}T_{A} \mathbf {e}_{i},~u_{i,N}\mathbf {e} _{i}=u_{i,A}N_{A}\mathbf {e}_{i}, \end{aligned}$$

(41)

and $\mathbf {T}$ $=\mathbf {X}^{^{\prime }}\mathbf {(}S\mathbf {)}=\mathbf { k\times N}$ is the unit tangent to the boundary ($\partial \Omega$) and $\mathbf {N}$ is the associated unit normal. Hence, invoking Eqs. (40)–(41), the projections of the first and second coordinate derivatives of $u_{i}$ can be found, respectively, as

$$\begin{aligned} u_{i,A}(\mathbf {e}_{i}\otimes \mathbf {E}_{A})= & {} \left( \frac{\mathrm{{d}}u_{i}}{\mathrm{{d}}s} \frac{\mathrm{{d}}s}{\mathrm{{d}}X_{A}}+\frac{\mathrm{{d}}u_{i}}{\mathrm{{d}}N}\frac{\mathrm{{d}}N}{\mathrm{{d}}X_{A}}\right) (\mathbf {e}_{i} \otimes \mathbf {E}_{A}\mathbf {)}=(u_{i,T}T_{A}+u_{i,N}N_{A}) ((\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)}),\text { and} \end{aligned}$$

(42)

$$\begin{aligned}&u_{i,AB}(\mathbf {e}_{i}\otimes \mathbf {E}_{A} \otimes \mathbf {E}_{B}\mathbf {)} \nonumber \\= & {} [u_{i,TT}T_{A}T_{B}+u_{i,T}(T_{A,T}T_{B}+ T_{A,N}N_{B})+u_{i,N}(N_{A,T}T_{B}+N_{A,N}N_{B}) \nonumber \\&+u_{i,TN}(N_{A}T_{B}+T_{A}N_{B})+u_{i,NN}N_{A} N_{B}](\mathbf {e}_{i}\otimes \mathbf { E}_{A}\otimes \mathbf {E}_{B}\mathbf {)}. \end{aligned}$$

(43)

We then substitute Eq. (43) into Eq. (39) and thereby obtain

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\partial \Omega }P_{iA}u_{i}N_{A}\mathrm{{d}}S+\int _{\partial \Omega }[W_{G_{iAB}}-(W_{H_{iABC}})_{,C}](u_{i,T}T_{A}+u_{i,N}N_{A})N_{B}\mathrm{{d}}S \nonumber \\&+\int _{\partial \Omega }W_{H_{iABC}}[u_{i,TT}T_{A}T_{B}+u_{i,T}(T_{A,T} T_{B}+T_{A,N}N_{B})+u_{i,N}(N_{A,T}T_{B}+N_{A,N}N_{B}) \nonumber \\&+u_{i,TN}(N_{A}T_{B}+T_{A}N_{B})+u_{i,NN}N_{A}N_{B}]N_{C}\mathrm{{d}}S. \end{aligned}$$

(44)

In order to obtain desired expressions, we apply iterated integration by parts on the tangential derivatives of $\mathbf {u}$ in Eq. (44). For example,

$$\begin{aligned} W_{G_{iAB}}T_{A}N_{B}u_{i,T}= & {} \left( W_{G_{iAB}}T_{A}N_{B}u_{i}\right) _{,T}-\left( W_{G_{iAB}}T_{A}N_{B}\right) _{,T}u_{i}, \end{aligned}$$

(45)

$$\begin{aligned}&W_{H_{iABC}}(N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})u_{i,TN} \nonumber \\= & {} \left[ W_{H_{iABC}}(N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})u_{i,N}\right] _{,T}- \left[ W_{H_{iABC}}(N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})\right] _{,T}u_{i,N}, \end{aligned}$$

(46)

$$\begin{aligned}&W_{H_{iABC}}T_{A}T_{B}N_{C}u_{i,TT} \nonumber \\= & {} \left( W_{H_{iABC}}T_{A}T_{B}N_{C}u_{i}\right) _{,TT}+\left( W_{H_{iABC}}T_{A}T_{B}N_{C}\right) _{,TT}u_{i}-2\left[ \left( W_{H_{iABC}}T_{A}T_{B}N_{C}\right) _{,T}u_{i}\right] _{,T}, \nonumber \\ \end{aligned}$$

(47)

and similarly for other terms. Therefore, Eq. (44) can be replaced with

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\partial \Omega }\left[ P_{iA}N_{A}-\left\{ W_{G_{iAB}}T_{A}N_{B}-\left( W_{H_{iABC}}\right) _{,C}T_{A}N_{B}\right\} _{,T}\right] u_{i}\mathrm{{d}}S \nonumber \\&-\int _{\partial \Omega }\left[ \left\{ W_{H_{iABC}}(T_{A,T}T_{B}N_{C}+T_{A,N}N_{B}N_{C}) \right\} _{,T}-(W_{H_{iABC}}T_{A}T_{B}N_{C})_{,TT}\right] u_{i}\mathrm{{d}}S \nonumber \\&+\int _{\partial \Omega }\left[ \left\{ W_{G_{iAB}}T_{A}N_{B}-\left( W_{H_{iABC}}\right) _{,C}T_{A}N_{B}-2\left( W_{H_{iABC}}T_{A}T_{B}N_{C}\right) _{,T}\right\} u_{i}\right] _{,T}\mathrm{{d}}S \nonumber \\&+\int _{\partial \Omega }\left[ W_{H_{iABC}}(T_{A,T}T_{B}N_{C}+T_{A,N}N_{B}N_{C})u_{i}\right] _{,T}\mathrm{{d}}S+\int _{ \partial \Omega }\left[ W_{H_{iABC}}(N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})u_{i,N} \right] _{,T}\mathrm{{d}}S \nonumber \\&+\int _{\partial \Omega }\left[ \left\{ \left( W_{G_{iAB}}\right) -\left( W_{H_{iABC}}\right) _{,C}\right\} N_{A}N_{B}+W_{H_{iABC}}(N_{A,T}T_{B}+N_{A,N}N_{B})N_{C}\right] u_{i,N}\mathrm{{d}}S\nonumber \\&-\int _{\partial \Omega }\left[ \left\{ W_{H_{iABC}}(N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})\right\} _{,T}\right] u_{i,N}\mathrm{{d}}S \nonumber \\&+\int _{\partial \Omega }\left( W_{H_{iABC}}T_{A}T_{B}N_{C}u_{i}\right) _{,TT}\mathrm{{d}}S+\int _{\partial \Omega }W_{H_{iABC}}u_{i,NN}N_{A}N_{B}N_{C}\mathrm{{d}}S. \end{aligned}$$

(48)

The above may be further recast as

$$\begin{aligned} \overset{\cdot }{E}= & {} \int _{\partial \Omega }\left[ P_{iA}N_{A}-\left\{ (Cg_{i}-A\alpha _{i,C}D_{C})D_{A}T_{A}D_{B}N_{B}\right\} _{,T}-\left\{ A\alpha _{i}D_{C}N_{C}(D_{A}T_{A,T}D_{B}T_{B}+D_{A}T_{A,N}D_{B}N_{B})\right\} _{,T}\right] u_{i}\mathrm{{d}}S\nonumber \\&+\int _{\partial \Omega }\left[ \left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}D_{C}N_{C}\right) _{,TT}\right] u_{i}\mathrm{{d}}S+\sum \left\| A\alpha _{i}(D_{A}T_{A,T}D_{B}T_{B}D_{C}N_{C}+D_{A}T_{A,N}D_{B}N_{B}D_{C}N_{C})u_{i} \right\| \nonumber \\&+\sum \left\| \left[ (Cg_{i}-A\alpha _{i,C}D_{C})D_{A}T_{A}D_{B}N_{B}-2\left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}D_{C}N_{C}\right) _{,T}\right] u_{i}\right\| \nonumber \\&+\sum \left\| A\alpha _{i}(D_{A}N_{A}D_{B}T_{B}D_{C}N_{C}+D_{A}T_{A}D_{B}N_{B}D_{C}N_{C})u_{i,N} \right\| +\sum \left\| \frac{\mathrm{{d}}}{\mathrm{{d}}s}\left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}N_{C}D_{C}u_{i}\right) \right\| \nonumber \\&+\int _{\partial \Omega }\left[ (Cg_{i}-A\alpha _{i,C}D_{C})D_{A}N_{A}D_{B}N_{B}+A\alpha _{i}D_{C}N_{C}(D_{A}N_{A,T}D_{B}T_{B}+D_{A}N_{A,N}D_{B}N_{B})\right] u_{i,N}\mathrm{{d}}S \nonumber \\&-\int _{\partial \Omega }\left[ \left\{ A\alpha _{i}D_{A}D_{B}D_{C}(N_{A}T_{B}N_{C}+T_{A}N_{B}N_{C})\right\} _{,T}u_{i,N}\right] \mathrm{{d}}S+\int _{\partial \Omega }(A\alpha _{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C}u_{i,NN})\mathrm{{d}}S, \nonumber \\ \end{aligned}$$

(49)

where the double bar symbol refers to the jump across the discontinuities on the boundary $\partial \Omega$ (i.e., $\left\| *\right\| =\left( *\right) ^{+}-\left( *\right) ^{-}$) and the sum refers to the collection of all discontinuities. But the virtual work statement suggests that the admissible powers are of the form

$$\begin{aligned} P=\int _{\partial w_{t}}t_{i}u_{i}\mathrm{{d}}S+\int _{\partial w}m_{i}u_{i,N}\mathrm{{d}}S+\int _{\partial w}r_{i}u_{i,NN}\mathrm{{d}}S+\sum f_{i}u_{i}+\sum h_{i}u_{i,N}, \end{aligned}$$

(50)

Consequently, by comparing Eqs. (49) and (50), we obtain

$$\begin{aligned} t_{i}\mathbf {e}_{i}= & {} P_{iA}N_{A}\mathbf {e}_{i}+\frac{\mathrm{{d}}^{2}}{\mathrm{{d}}s^{2}}\left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}D_{C}N_{C}\right) \mathbf {e}_{i} \nonumber \\&-\frac{\mathrm{{d}}}{\mathrm{{d}}s}\left[ \big (Cg_{i}-A\alpha _{i,C}D_{C}\big )D_{A}T_{A}D_{B}N_{B}-A\alpha _{i}D_{C}N_{C}\big (D_{A}T_{A,T}D_{B}T_{B}+D_{A}T_{A,N}D_{B}N_{B}\big )\right] \mathbf {e}_{i}, \nonumber \\ m_{i}\mathbf {e}_{i}= & {} \big (Cg_{i}-A\alpha _{i,C}D_{C}\big )D_{A}N_{A}D_{B}N_{B} \mathbf {e}_{i}+A\alpha _{i}D_{C}N_{C}\big (D_{A}N_{A,T}D_{B}T_{B}+D_{A}N_{A,N}D_{B}N_{B}\big )\mathbf {e}_{i} \nonumber \\&-\frac{\mathrm{{d}}}{\mathrm{{d}}s}\big (2A\alpha _{i}D_{A}D_{B}D_{C}N_{A}T_{B}N_{C}\big )\mathbf {e}_{i}, \nonumber \\ r_{i}\mathbf {e}_{i}= & {} A\alpha _{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C}\mathbf {e} _{i}, \nonumber \\ f_{i}\mathbf {e}_{i}= & {} \big (Cg_{i}-A\alpha _{i,C}D_{C}\big )D_{A}T_{A}D_{B}N_{B} \mathbf {e}_{i}-\frac{\mathrm{{d}}}{\mathrm{{d}}s}\left( 2A\alpha _{i}D_{A}T_{A}D_{B}T_{B}D_{C}N_{C}\right) \mathbf {e}_{i} \nonumber \\&+A\alpha _{i}\big (D_{A}T_{A,T}D_{B}T_{B}D_{C}N_{C}+D_{A}T_{A,N}D_{B}N_{B}D_{C}N_{C}\big ) \mathbf {e}_{i}, \nonumber \\ \frac{\mathrm{{d}}(f_{i})}{\mathrm{{d}}s}\mathbf {e}_{i}= & {} \frac{\mathrm{{d}}}{\mathrm{{d}}s}\left( A\alpha _{i}D_{A}T_{A}D_{B}T_{B}N_{C}D_{C}\right) \mathbf {e}_{i}, \nonumber \\ h_{i}\mathbf {e}_{i}= & {} 2A\alpha _{i}D_{A}N_{A}D_{B}T_{B}D_{C}N_{C}\mathbf {e} _{i}, \end{aligned}$$

(51)

In the above $t_{i},$ $m_{i}$ and $f_{i}$ are, respectively, the expressions of edge tractions, edge moments and the corner forces. But more importantly, additional interaction boundary conditions (i.e., $r_{i},$ $\mathrm{{d}}(f_{i})/\mathrm{{d}}s,~h_{i}$) are obtained via the introduction of the third gradient of deformations. These boundary conditions can be understood as the set of admissible contact interactions suitably sustained by the third gradient continua (see, for example, [22, 36, 43]). Moreover, the induced interaction forces are, in turn, coupled with the Piola-type triple stress and thus fall into the category of triple forces that characterize the mechanical contacts on the edges and points of Cauchy cuts ([19, 22, 37]). In the present case, the letter would mean the effects of local interactions between the fiber and matrix which are assimilated via the computation of the third gradient of the continuum deformation on the convected curves of fibers.

We remark here that the obtained triple forces are meaningful only if there exist their conjugate pairs (a class of Piola-type triple stresses) and are necessary to capture the internal energy contributions to the mechanical contact interactions induced on the adjoined boundary. In fact, such necessary mutual existence arising in the third gradient of continuum deformation is equally valid to a class of forces and stresses exerted by lower-order continua. For example, the prescribed double force $m_{i}$ is the energy pair of the Piola-type double stress ($Cg_{i,B}D_{A}D_{B}$).

If fibers are aligned along the directions of either normal and/or tangential to the boundary (such cases are commonly observed in meshed composites, fabric composites and particulate composites produced under controlled environment), we find

$$\begin{aligned} D_{A}T_{A}D_{B}N_{B}=0\text { and }T_{A,N}=T_{A,T}=N_{A,N}=N_{A,T}=0, \end{aligned}$$

(52)

and thus Eq. (51) reduces to

$$\begin{aligned} t_{i}\mathbf {e}_{i}= & {} P_{iA}N_{A}\mathbf {e}_{i} \nonumber \\ m_{i}\mathbf {e}_{i}= & {} (Cg_{i}-A\alpha _{i,C}D_{C})D_{A}N_{A}D_{B}N_{B} \mathbf {e}_{i} \nonumber \\ r_{i}\mathbf {e}_{i}= & {} A\alpha _{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C}\mathbf {e} _{i}, \nonumber \\ f_{i}\mathbf {e}_{i}= & {} 0\mathbf {e}_{i}, \nonumber \\ \frac{\mathrm{{d}}(f_{i})}{\mathrm{{d}}s}\mathbf {e}_{i}= & {} 0\mathbf {e}_{i}, \nonumber \\ h_{i}\mathbf {e}_{i}= & {} 0\mathbf {e}_{i}. \end{aligned}$$

(53)

Further, the expression of the associated Piola-type stress now becomes

$$\begin{aligned} P_{iA}(\mathbf {e}_{i}\otimes \mathbf { E}_{A}\mathbf {)}= & {} \left( \widehat{W}_{F_{iA}}-pF_{iA}^{*}+\frac{E}{2} (F_{jC}F_{jD}D_{C}D_{D}-1)(F_{iB}D_{B}D_{A})-Cg_{i,B}D_{A}D_{B}+A\alpha _{i,BC}D_{A}D_{B}D_{C}\right) (\mathbf {e}_{i}\otimes \mathbf { E}_{A}\mathbf {)}, \nonumber \\ g_{i}\mathbf {e}_{i}= & {} F_{iA,B}D_{A}D_{B}\text { }\mathbf {e}_{i}\text {and } \alpha _{i}\mathbf {e}_{i}=F_{iA,BC}D_{A}D_{B}D_{C}\mathbf {e}_{i}. \end{aligned}$$

(54)

It is clear from Eq. (54) that, in the cases of aligned fibers, $r_{i}$ is the only meaningful boundary conditions due to the third gradient of continuum deformations (i.e., $f_{i}$, $\mathrm{{d}}(f_{i})/\mathrm{{d}}s$ and $h_{i}$ vanish identically). We also note that the imposition of $r_{i}$ is necessary to determine unique solution when solving the associated Euler equation [i.e., Eq. (51)]. The classifications of the obtained triple forces and boundary conditions may be of practical interests. In this respect, a number of cases are investigated within the prescription of superposed incremental deformations in the forgoing sections. Lastly, details regarding the implementation of the resulting boundary conditions [Eq. (53)] are reserved in “Appendix”.

5 Linear theory

Based on the constitutive formulations presented in the previous sections, we develop a compatible linear model which describes the mechanical responses of an elastic solid reinforced with fiber’s resistance to extension and flexure.

For this purpose, we consider superposed ‘small’ deformations defined by

$$\begin{aligned} \varvec{\chi } \varvec{\approx \chi }_{\mathrm{{o}}}+\epsilon \varvec{\dot{\chi }}\ ;\left| \epsilon \right| \ll 1, \end{aligned}$$

(55)

where $({\dot{\mathbf {*}}})=\partial (*)/\partial \varepsilon$, ${\dot{\mathbf {\chi }}}=\mathbf {u}$ and $(*)_{\mathrm{{o}}}$ denote configuration of $*$ evaluated at $\epsilon =0$, $(\dot{\varvec{*}})=\partial (*)/\partial \varepsilon$. Here caution needs to be taken that the present notation is not confused with the one used for the variational computation. Therefore, the deformation gradient tensor can be approximated as

$$\begin{aligned} \mathbf {F}\approx \mathbf {F}_{\mathrm{{o}}}+\epsilon \nabla \mathbf {u},\ \text {where} \quad \overset{\cdot }{\mathbf {F}}=\nabla \mathbf {u}. \end{aligned}$$

(56)

In a typical environment, the body is initially undeformed and stress-free. This can be accommodated by imposing the initial conditions of

$$\begin{aligned} \mathbf {F}_{\mathrm{{o}}}=\mathbf {I}\text { and }\mathbf {P}_{\mathrm{{o}}}=\mathbf {0,}\text { at } \varepsilon =0, \end{aligned}$$

(57)

from which we subsequently reduce Eq. (56) to

$$\begin{aligned} \mathbf {F}=\mathbf {I}+\epsilon \nabla \mathbf {u.} \end{aligned}$$

(58)

Eq. (58) further leads to

$$\begin{aligned} \mathbf {F}^{-1}=\mathbf {I}-\epsilon \nabla \mathbf {u+}o(\epsilon \mathbf {)} \text { and }J=\det \mathbf {F=}1+\epsilon \text{ div }\mathbf {u\mathbf {+}} o(\epsilon )\mathbf {,} \end{aligned}$$

(59)

which are the linearized expressions of the inverse and determinant of deformation gradient tensor $\mathbf {F}$. Similarly, the constraint of bulk incompressibility can be approximated as

$$\begin{aligned} (J-1)^{\cdot }=\mathbf {F}_{\mathrm{{o}}}^{*}\cdot \overset{\cdot }{\mathbf {F}}= \text{ div }\mathbf {u=0}. \end{aligned}$$

(60)

Now, using Eq. (55), the Euler equation [Eq. (30)] can be expanded as

$$\begin{aligned} \mathrm{{Div}}(\mathbf {P})=\mathrm{{Div}}(\mathbf {P}_{\mathrm{{o}}})+\epsilon \mathrm{{Div}}(\dot{\mathbf {P}} )+o(\epsilon \mathbf {)=0.} \end{aligned}$$

(61)

Dividing the above by $\varepsilon$ and limiting $\varepsilon \rightarrow 0,$ we obtain

$$\begin{aligned} \mathrm{{Div}}(\dot{\mathbf {P}})=0\text { or }\dot{P}_{iA,A}=0, \end{aligned}$$

(62)

For the use in Eq. (62), the expression of $\dot{P}_{iA}$ can be obtained from Eq. (29) that

$$\begin{aligned}&\dot{P}_{iA}(\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)} \nonumber \\&\quad =\big [(\widehat{W}_{F_{iA}}\dot{)}-\dot{p}(F_{iA}^{*})_{\mathrm{{o}}}-p\dot{F} _{iA}^{*}+E\left\{ \dot{F}_{jC}(F_{jD})_{\mathrm{{o}}}D_{C}D_{D}\right\} \left\{ (F_{iB})_{\mathrm{{o}}}D_{B}D_{A})\right\} \big ](\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)} \nonumber \\&\quad +\frac{E}{2}\big [(F_{jC})_{\mathrm{{o}}}(F_{jD})_{\mathrm{{o}}}D_{C}D_{D}-1\big ](\dot{F} _{iB}D_{B}D_{A})-C\dot{g}_{i,B}D_{A}D_{B}+A(\alpha _{i}D_{A}D_{B}D_{C})_{,CB}\big ](\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)}. \end{aligned}$$

(63)

Further, evaluating at $\epsilon =0$ (e.g., $(F_{jD})_{\mathrm{{o}}}=\delta _{jD},$ $(F_{iA}^{*})_{\mathrm{{o}}}=\delta _{iA}$), we reduce Eq. (63) to

$$\begin{aligned} \dot{P}_{iA}(\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)}= & {} \big [(\widehat{W} _{F_{iA}}\dot{)}+Eu_{j,B}D_{A}D_{B}D_{i}D_{j}-\dot{p}\delta _{iA}-p_{\mathrm{{o}}}\dot{F }_{iA}^{*}-Cu_{i,BCD}D_{C}D_{D}D_{A}D_{B}\big ](\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)} \nonumber \\&+A\big [(u_{i,EFG}D_{E}D_{F}D_{G})D_{A}D_{B}D_{C}\big ]_{,CB}(\mathbf {e}_{i}\mathbf { \otimes E}_{A}\mathbf {)}, \end{aligned}$$

(64)

where $\delta _{jC}\delta _{jD}D_{C}D_{D}=D_{j}D_{j}=1$, $\dot{g}_{i,B}=\dot{ F}_{iC,BD}D_{C}D_{D}$ and $\alpha _{i}=u_{i,EFG}D_{E}D_{F}D_{G}.$ It is noted that the reference and current bases are now merged so that the initial director field $\mathbf {D}$ is represented by the current basis (i.e., $D_{i}\mathbf {e}_{i}$) not by the reference frame (i.e., $D_{A}\mathbf {E }_{A}$). This can be explained by the collapse of the two different bases dictated by the linear theory of elasticity (i.e., $\mathbf {e}_{i}\equiv \mathbf {E}_{A}$; see, also, [46, 47]). Hence, from Eqs. (62) and (64), the linearized Euler equations can be obtained as

$$\begin{aligned} \dot{P}_{iA,A}\mathbf {e}_{i}= & {} [(\widehat{W}_{F_{iA}}\dot{)} _{,A}+E(u_{j,B}D_{A}D_{B}D_{i}D_{j})_{,A}-\dot{p} _{,i}-C(u_{i,BCD}D_{C}D_{D}D_{A}D_{B})_{,A}]\mathbf {e}_{i} \nonumber \\&+A[(u_{i,EFG}D_{E}D_{F}D_{G})D_{A}D_{B}D_{C}]_{,CBA}\mathbf {e}_{i}, \end{aligned}$$

(65)

where $\ \dot{F}_{iA,A}^{*}=0$ (Piola’s identity) and $(\dot{p}\delta _{iA})_{,A}=\dot{p}_{,A}\delta _{iA}=\dot{p}_{,i}.$

In the case of initially straight fibers (i.e., $\nabla \mathbf {D}=0),$ the above further reduces to

$$\begin{aligned} \dot{P}_{iA,A}\mathbf {e}_{i}= & {} (\widehat{W}_{F_{iA}}\dot{)}_{,A}\mathbf {e} _{i}+Eu_{j,AB}D_{A}D_{B}D_{i}D_{j}\mathbf {e}_{i}-\dot{p}_{,i}\mathbf {e} _{i}-Cu_{i,ABCD}D_{C}D_{D}D_{A}D_{B}\mathbf {e}_{i} \nonumber \\&+Au_{i,ABCEFG}D_{A}D_{B}D_{C}D_{E}D_{F}D_{G}\mathbf {e}_{i}=0\mathbf {e}_{i}. \end{aligned}$$

(66)

Lastly, the boundary conditions in Eq. (51) can be approximated similarly as in the above (e.g., $\mathbf {t}=\mathbf {t}_{\mathrm{{o}}}+\varepsilon \dot{\mathbf {t}}+o(e\mathbf {)}$, etc.)

$$\begin{aligned} \dot{t}_{i}\mathbf {e}_{i}= & {} \dot{P}_{iA}N_{A}\mathbf {e}_{i}+\frac{\mathrm{{d}}^{2}}{\mathrm{{d}}s^{2}}\left( A\dot{\alpha }_{i}D_{A}T_{A}D_{B}T_{B}D_{C}N_{C}\right) \mathbf { e}_{i} \nonumber \\&-\frac{\mathrm{{d}}}{\mathrm{{d}}s}[(Cg_{i}-A\dot{\alpha }_{i,C}D_{C})D_{A}T_{A}D_{B}N_{B}-A\dot{ \alpha }_{i}D_{C}N_{C}(D_{A}T_{A,T}D_{B}T_{B}+D_{A}T_{A,N}D_{B}N_{B})]\mathbf { e}_{i}, \nonumber \\ \dot{m}_{i}\mathbf {e}_{i}= & {} (C\dot{g}_{i}-A\dot{\alpha } _{i,C}D_{C})D_{A}N_{A}D_{B}N_{B}\mathbf {e}_{i}+A\dot{\alpha } _{i}D_{C}N_{C}(D_{A}N_{A,T}D_{B}T_{B}+D_{A}N_{A,N}D_{B}N_{B})\mathbf {e}_{i} \nonumber \\&-\frac{\mathrm{{d}}}{\mathrm{{d}}s}(2A\dot{\alpha }_{i}D_{A}D_{B}D_{C}N_{A}T_{B}N_{C})\mathbf {e} _{i}, \nonumber \\ \dot{r}_{i}\mathbf {e}_{i}= & {} A\dot{\alpha }_{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C} \mathbf {e}_{i}, \nonumber \\ \dot{f}_{i}\mathbf {e}_{i}= & {} (C\dot{g}_{i}-A\dot{\alpha } _{i,C}D_{C})D_{A}T_{A}D_{B}N_{B}\mathbf {e}_{i}-\frac{\mathrm{{d}}}{\mathrm{{d}}s}\left( 2A\dot{ \alpha }_{i}D_{A}T_{A}D_{B}T_{B}D_{C}N_{C}\right) \mathbf {e}_{i} \nonumber \\&+A\dot{\alpha } _{i}(D_{A}T_{A,T}D_{B}T_{B}D_{C}N_{C}+D_{A}T_{A,N}D_{B}N_{B}D_{C}N_{C}) \mathbf {e}_{i}, \nonumber \\ \frac{\mathrm{{d}}(\dot{f}_{i})}{\mathrm{{d}}s}\mathbf {e}_{i}= & {} \frac{\mathrm{{d}}}{\mathrm{{d}}s}\left( A\dot{\alpha } _{i}D_{A}T_{A}D_{B}T_{B}N_{C}D_{C}\right) \mathbf {e}_{i}, \nonumber \\ \dot{h}_{i}\mathbf {e}_{i}= & {} 2A\dot{\alpha }_{i}D_{A}N_{A}D_{B}T_{B}D_{C}N_{C} \mathbf {e}_{i}. \end{aligned}$$

(67)

Hence, Eqs. (60), (66) and (67) determine the deformed configurations of fiber composites for small deformations superposed on large. In particular, if the fiber’s directions are either normal or tangential to the boundary [see Eq. (52)], the above becomes

$$\begin{aligned} \dot{t}_{i}\mathbf {e}_{i}= & {} \dot{P}_{iA}N_{A}\mathbf {e}_{i}, \nonumber \\ \dot{m}_{i}\mathbf {e}_{i}= & {} (C\dot{g}_{i}-A\dot{\alpha } _{i,C}D_{C})D_{A}N_{A}D_{B}N_{B}\mathbf {e}_{i}, \nonumber \\ \dot{r}_{i}\mathbf {e}_{i}= & {} A\dot{\alpha }_{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C} \mathbf {e}_{i}, \nonumber \\ \dot{f}_{i}\mathbf {e}_{i}= & {} 0\mathbf {e}_{i}, \nonumber \\ \frac{\mathrm{{d}}(\dot{f}_{i})}{\mathrm{{d}}s}\mathbf {e}_{i}= & {} 0\mathbf {e}_{i}, \nonumber \\ \dot{h}_{i}\mathbf {e}_{i}= & {} 0\mathbf {e}_{i}. \end{aligned}$$

(68)

The imposition of the above boundary conditions will be further discussed in the following section.

5.1 Example: Neo-Hookean-type materials

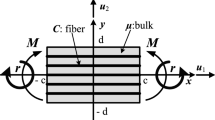
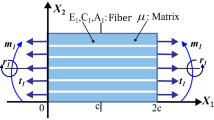
For the implementation of the obtained linear theory, we consider an elastic solid of neo-Hookean type reinforced with a single family of fibers subjected to plane bias extension. In the foregoing analysis, we confine our analysis to the case where fibers are initially straight and aligned along the directions of either normal or tangential to the boundary (i.e., $\mathbf { D}=\mathbf {E}_{1},~D_{1}=1,~D_{2}=0,$ see Fig. 1) such that

$$\begin{aligned} \mathbf {(D\cdot T)(D\cdot N)}=0\text { and }\nabla \mathbf {D=}\nabla \mathbf { T=\nabla N=0.} \end{aligned}$$

(69)

We also note here that different types of boundaries and fibers alignments can be readily accommodated by modifying Eq. (69) (e.g., $\mathbf {D}= \mathbf {E}_{2},$ $D_{1}=0,~D_{2}=1$ and $\mathbf {D\cdot N=1}$, etc.). For example, by expanding the Einstein summation for $A,B...G=1,2$, the last term of Eq. (66) becomes

$$\begin{aligned} Au_{i,ABCEFG}D_{A}D_{B}D_{C}D_{E}D_{F}D_{G}\mathbf {e}_{i}= & {} A\big (u_{i,111111}D_{1}D_{1}D_{1}D_{1}D_{1}D_{1}+u_{i,211111}D_{2}D_{1}D_{1}D_{1}D_{1}D_{1} \nonumber \\&+u_{i,121111}D_{1}D_{2}D_{1}D_{1}D_{1}D_{1}+u_{i,112111}D_{1}D_{1}D_{2}D_{1}D_{1}D_{1}+... \nonumber \\&+u_{i,222222}D_{2}D_{2}D_{2}D_{2}D_{2}D_{2}\big )\mathbf {e}_{i}. \end{aligned}$$

(70)

Since $~D_{1}=1$ and$~D_{2}=0,$, the above further reduces to

$$\begin{aligned} Au_{i,ABCEFG}D_{A}D_{B}D_{C}D_{E}D_{F}D_{G}\mathbf {e} _{i}=A(u_{i,111111}D_{1}D_{1}D_{1}D_{1}D_{1}D_{1})\mathbf {e} _{i}=Au_{i,111111}\mathbf {e}_{i}. \end{aligned}$$

(71)

Accordingly, Eqs. (64) and (66) become

$$\begin{aligned} \dot{P}_{iA}(\mathbf {e}_{i}\otimes \mathbf { E}_{A}\mathbf {)}= & {} \big [(\widehat{W} _{F_{iA}}\dot{)}+Eu_{1,1}D_{A}D_{i}-\dot{p}\delta _{iA}-p_{\mathrm{{o}}}\dot{F} _{iA}^{*}-Cu_{i,111}D_{A}+A(u_{i,11111})D_{A}\big ](\mathbf {e}_{i}\mathbf { \otimes E}_{A}\mathbf {)},\text { and} \nonumber \\ \dot{P}_{iA,A}\mathbf {e}_{i}= & {} \big [(\widehat{W}_{F_{iA}}\dot{)} _{,A}+Eu_{1,11}D_{i}-\dot{p}_{,i}-Cu_{i,1111}+Au_{i,111111}\big ]\mathbf {e}_{i}=0 \mathbf {e}_{i}. \end{aligned}$$

(72)

Now, the neo-Hookean strain energy function is given by

$$\begin{aligned} W(I_{1},I_{3})=\frac{\mu }{2}(I_{1}-3)-\mu \log I_{3}+\frac{\lambda }{2} (\log I_{3})^{2}, \end{aligned}$$

(73)

where $\mu$ and $\lambda$ are the material constants, and $I_{1}=tr( \mathbf {F}^{T}\mathbf {F})$ and $I_{3}=\det (\mathbf {F}^{T}\mathbf {F})$ are, respectively, the first and third invariant of the deformation gradient tensor. In the case of incompressible materials (i.e., $I_{3}=1$), Eq. (73) further reduces to

$$\begin{aligned} \widehat{W}(\mathbf {F})=\frac{\mu }{2}(\mathbf {F\cdot F}-3). \end{aligned}$$

(74)

Thus, we evaluate $W_{F_{iA}}=\mu F_{iA}$ and thereby obtain from Eq. (72) that

$$\begin{aligned} \dot{P}_{iA}(\mathbf {e}_{i}\otimes \mathbf { E}_{A}\mathbf {)}= & {} [\mu u_{i,A}+Eu_{1,1}D_{A}D_{i}-\dot{p}\delta _{iA}-p_{\mathrm{{o}}}\dot{F}_{iA}^{*}-Cu_{i,111}D_{A}+A(u_{i,11111})D_{A}](\mathbf {e}_{i}\otimes \mathbf {E}_{A} \mathbf {)},\text { and} \nonumber \\ \end{aligned}$$

(75)

$$\begin{aligned} \dot{P}_{iA,A}\mathbf {e}_{i}= & {} [\mu u_{i,AA}+Eu_{1,11}D_{i}-\dot{p} _{,i}-Cu_{i,1111}+Au_{i,111111}]\mathbf {e}_{i}=0\mathbf {e}_{i}. \end{aligned}$$

(76)

In the above, the unknown constant $p_{\mathrm{{o}}}$ can be chosen such that the Piola-type stress admits the initial stress free state at $\varepsilon =0;$ i.e.,

$$\begin{aligned} \dot{\mathbf {P}}_{\mathrm{{o}}}=\mu \dot{\mathbf {F}}_{\mathrm{{o}}} -p_{o}\dot{\mathbf {F}}_{\mathrm{{o}}}^{*}=0, \end{aligned}$$

(77)

and thus yielding

$$\begin{aligned} p_{\mathrm{{o}}}=\mu . \end{aligned}$$

(78)

In addition, since $J\partial F_{jB}^{*}/\partial F_{iA}=F_{jB}^{*}F_{iA}^{*}-F_{iB}^{*}F_{jA}^{*}\mathbf {,}$ we evaluate at $\varepsilon =0$ as

$$\begin{aligned} (\partial F_{jB}^{*}/\partial F_{iA})_{\mathrm{{o}}}=\delta _{jB}\delta _{iA}-\delta _{iB}\delta _{jA}, \end{aligned}$$

(79)

and thus find

$$\begin{aligned} \overset{\cdot }{F_{iA}^{*}}=(\partial F_{jB}^{*}/\partial F_{iA}) \dot{F}_{jB}=(\delta _{jB}\delta _{iA}-\delta _{iB}\delta _{jA})u_{j,B}=u_{B,B}\delta _{iA}-u_{A,i}=-u_{A,i}, \end{aligned}$$

(80)

where $u_{B,B}=0$ from Eq. (60).

Consequently, Eq. (76) together with the constraint of bulk incompressibility [Eq. (60)] determines the deformed configuration of composites.

Fig. 1

Schematic of the problem

6 Solution to the linearized problem

For the purpose of illustration, we consider an elastic solid of neo-Hookean type reinforced with the single family of fibers and subjected to the double force $t_{i}$ (extension) and triple force $r_{i}$ (see Fig. 1). Accordingly, we find from Eqs. (60) and (76) that

$$\begin{aligned} \mu (u_{1,11}+u_{1,22})+Eu_{1,11}-Cu_{1,1111}+Au_{\begin{array}{c} 1,111111 \end{array}}- \overset{.}{p}_{,1}= & {} 0, \nonumber \\ \mu (u_{2,11}+u_{2,22})-C_{2,1111}+Au_{2,111111}-\overset{.}{p}_{,2}= & {} 0, \nonumber \\ u_{1,1}+u_{2,2}= & {} 0. \end{aligned}$$

(81)

Let us now introduce scalar field, $\phi ,$as

$$\begin{aligned} \mathbf {u}=\mathbf {k}\times \nabla \phi \mathbf {, k}\text {(unit normal)}\mathbf {;}\, u_{i}=\varepsilon _{\lambda i}\phi _{,\lambda }, \end{aligned}$$

so that the third equation of Eq. (81) can be satisfied (i.e., $\phi _{,12}-\phi _{,21}=0$). We note here that the adopted Ansatz of $\phi$ restricts the possible forms of solutions similarly to those cases arising in the use of complex potentials and plan harmonic functions (see, also, [49,50,51]). However, this does not necessarily mean that the predictions from the resulting solution are limited. In fact, the adopted technique has been successfully adopted in the similar types of problems and produces reasonably accurate prediction results (see, for example, [7, 8, 15, 17, 52]). Accordingly, Eq. (81) becomes

$$\begin{aligned} \dot{p}_{,1}= & {} -\mu (\varphi _{,211}+\varphi _{,222})+C\varphi _{,21111}-A\varphi _{,2111111}, \nonumber \\ \dot{p}_{,2}= & {} \mu (\varphi _{,111}+\varphi _{,122})-C\varphi _{,11111}+A\varphi _{,1111111.} \end{aligned}$$

(82)

In addition, we use the compatibility condition of p (i.e., $\overset{\cdot }{p_{,ij}}=\overset{\cdot }{p_{,ji}}$) and thereby reduce Eq. (82) to

$$\begin{aligned} \mu (\varphi _{,1111}+\varphi _{,2222}+2\varphi _{,1122})-C(\varphi _{,111111}+\varphi _{,221111})+A(\varphi _{,11111111}+\varphi _{,22111111})=0. \end{aligned}$$

(83)

The above may be reacted into the following compact from

$$\begin{aligned} \Delta \left( \Delta \phi -\frac{C}{\mu }\phi _{,1111}\right) +\frac{E}{\mu }\phi _{,1122}+\frac{A}{\mu }\Delta (\phi _{,111111})=0, \end{aligned}$$

(84)

which solves the unknown mapping function, $\phi (x,y)$.

It is noted here that the solution of Eq. (84) is not accommodated by the conventional methods such as the Fourier transform or the separation of variables. Instead, we adopt the methods of iterative reduction and the principle of eigenfunction expansion [39,40,41] to yield

$$\begin{aligned} \phi (x,y)=X(x)sin(my), \end{aligned}$$

(85)

and subsequently obtain from Eq. (84) that

$$\begin{aligned} \big [AX_{,11111111}-\big (C+Am^{2}\big )X_{,111111}+\big (1+Cm^{2}\big ) X_{,1111}-m^{2}(2+E)X_{,1111}+m^{4}X\big ]\sin my=0 \text {.} \end{aligned}$$

(86)

Hence, the general solution of $\phi$ can be found as

$$\begin{aligned} \phi (x,y)= & {} \overset{\infty }{\underset{m=1}{\sum }}\big [\big \{e^{a_{m}x}(A_{m} \sin (b_{m}x)+B_{m}\cos (b_{m}x))+e^{-a_{m}x}(C_{m}\sin (b_{m}x)+D_{m}\cos (b_{m}x)) \nonumber \\&+(E_{m}\sin (c_{m}x)+F_{m}\cos (c_{m}x))+G_{m}e^{d_{m}x}+H_{m}e^{-d_{m}x}\big \}\times \{\sin (my)\}\big ]. \end{aligned}$$

(87)

The expressions of $a_{m},b_{m},c_{m}$ and $d_{m}$ can then be obtained via the simple algebraic procedures (see “Appendix”). We note that other approaches such as the method of Lagrange multipliers in [53] may also be employed in solving the type of PDEs presented in Eq. (81).

Lastly, the unknown constant real numbers $A_{m},B_{m},C_{m},D_{m},E_{m},F_{m},G_{m}$ and $H_{m}$ can be completely determined by imposing the admissible boundary conditions depicted in Eq. (68). In the assimilation, the applied forces and triple forces are approximated using the Fourier series expansion. For example,

$$\begin{aligned} t_{1}= & {} \overset{\cdot }{P}_{11}N_{1}=\mu (u_{1,1}-u_{2,2})+Eu_{1,1}- \overset{\cdot }{p}-Cu_{1,111}+Au_{1,11111}=5\simeq \sum \limits _{n=1}^{30} \frac{20}{n\pi }(-1)^{\frac{n-1}{2}}\cos (\frac{n\pi }{2d}y), \nonumber \\ \dot{r}_{i}= & {} A\dot{\alpha }_{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C},\text { }\dot{r }_{1}=Au_{1,111}=5\simeq \sum \limits _{n=1}^{30}\frac{20}{n\pi }(-1)^{\frac{ n-1}{2}}\cos (\frac{n\pi }{2d}y), \nonumber \\ \text { }\dot{r}_{2}= & {} Au_{2,111}=0. \end{aligned}$$

(88)

The obtained solution, $\phi$, is then substituted into the following expression to configure the deformation maps and the corresponding stress fields.

$$\begin{aligned} \varvec{\chi }=(X_{1}-\phi _{,2})\mathbf {E}_{1}+(X_{2}+\phi _{,1})\mathbf {E} _{2}\text {.} \end{aligned}$$

(89)

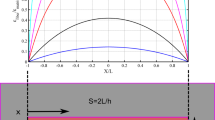
We also remark that the required computational cost is minimum (far less expansive then pure numerical approaches) even with the presence of heavy expressions [Eq. (63)], since Eq. (63) are merely in algebraic structures once implemented. This is also evidenced by the fast convergence rate of the obtained solutions as illustrated in Fig. 2. (within 30 iterations).

Fig. 2

Deformation profiles with respect to the number of iterations (N)

6.1 Model implementation and discussions

In this section, we simulate the responses of fiber-reinforced composite subjected to plane deformations using the obtained linear model. Emphasis is placed on the assimilation of the deformation profiles, strain field distributions and, in particular, the sensitivity analyses of the proposed linear model with respect to the applied loads and the parameters associated with the Piola-type double stresses and triple stresses. It is noted that the data are obtained under the normalized setting unless otherwise specified (e.g., $C/\mu =20$, $A/\mu =50$, etc.). Figure 3 illustrates the post-processed deformation mapping for a composite with fibers axial, bending and triple force moduli of $E/\mu =150,~C/\mu =150$, and $A/\mu =150$ when the composite is subjected to the axial extension load of $t_{1}/\mu =20$. The deformation mapping predicted by the proposed linear solution demonstrates smooth profiles on the boundaries and within the domain of interest (Fig. 3).

Fig. 3

Deformation mapping when $t_{1}/\mu =20\text {,} E/\mu =150,~C/\mu =150$ , and $A/\mu =150$

Further, it is shown in Figs. 4 and 5 that the corresponding deformation configurations are sensitive to both the first and triple stress moduli of Piola-type (i.e., E and A). More precisely, the axial elongation of the composite gradually decreases with increasing the first stress modulus (E). The deformation configuration is also affected by the varying triple stress modulus (A). In this case, the gradients of deformation profiles at each material points become steeper as the triple stress modulus decreases. These results are also closely aligned with the observations in [8, 17, 52]. In fact, the obtained solution accommodates the deformation configurations predicted by the second gradient theory in the limit of the vanishing triple stress modulus (i.e., $A=0$, see Fig. 6).

Fig. 4

Deformation configurations with respect to $E/\mu \text { when }t_{1}/\mu =20,\text { }C/\mu =150\text { and }A/\mu =150$

Fig. 5

Deformation configurations with respect to $A/\mu \text { when }t_{1}/\mu =20,\text { }E/\mu =135\text { and }C/\mu =150$

Fig. 6

Comparison with the second gradient model [8]

In particular, utilizing the following relations [12], we evaluate the shear strain gradients and the associated shear angle contours to examine the effects of the third gradient of deformations on the resulting deformation fields,

$$\begin{aligned} \phi ^{\prime }=\frac{u_{2}^{\prime \prime }(1+u_{1}^{\prime })-u_{2}^{\prime }u_{1}^{\prime \prime }}{u_{2}^{\prime 2}+(1+u_{1}^{\prime })^{2}}, \end{aligned}$$

(90)

and

$$\begin{aligned} \phi =\tan ^{-1}\left( \frac{\chi _{2,1}- \chi _{1,1}}{2+\chi _{1,1}+\chi _{2,1}}\right) . \end{aligned}$$

(91)

Figure 7 clearly indicates that the magnitude of shear strain gradually increases as approach the right and left boundaries when positive triple force is applied (i.e., $\dot{r}_{i}>0$) and vice versa in the case of negative triple force (i.e., $\dot{r}_{i}<0$). The continuous shear strain fields give rise to the smooth and dilatational shear strain distributions where the rate of dilatation is dependent on the applied triple force $\dot{r }_{i}$ (see Fig. 8). This, in turn, suggests that the proposed linear model is capable of predicting multiple configurations of shear angle distributions given the single configuration of the applied force $\dot{t} _{i}$ and double force $\dot{m}_{i}$, whereas only one configuration is possible within the description of second gradient-based models (see [8, 13, 14, 17]). In fact, the shear angle field estimated by the second gradient continuum model is one of the particular configurations predicted by the proposed model in the limit of vanishing triple force (i.e., $\dot{r} _{i}=0,$ see, also, Fig. 6). This also can be seen by setting Eq. (68) as

$$\begin{aligned} \dot{r}_{i}\mathbf {e}_{i}=A\dot{\alpha }_{i}D_{A}N_{A}D_{B}N_{B}D_{C}N_{C} \mathbf {e}_{i}=0\mathbf {e}_{i}. \end{aligned}$$

(92)

Hence, the expressions of force and double force [Eq. (68)] and the associated Piola-type stress [Eq. (75)] become

$$\begin{aligned} \dot{t}_{i}\mathbf {e}_{i}= & {} \dot{P}_{iA}N_{A}\mathbf {e}_{i}\text {, }\dot{m}_{i} \mathbf {e}_{i}=C\dot{g}_{i}D_{A}N_{A}D_{B}N_{B}\mathbf {e}_{i}\text {, and}\\ \dot{P}_{iA}(\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)}= & {} \big [\mu u_{i,A}+Eu_{1,1}D_{A}D_{i}-\dot{p}\delta _{iA}-p_{\mathrm{{o}}}\dot{F}_{iA}^{*}-Cu_{i,111}D_{A}\big ](\mathbf {e}_{i}\otimes \mathbf {E}_{A}\mathbf {)},\text { } \end{aligned}$$

which recover the results in [17] (see Eqs. (61)–(62) therein).

Fig. 7

Shear strain gradient with respect to $\dot{r}_{i}:\dot{r} _{i}>0\text { (Left)}\ \text {and }\dot{r}_{i}<0\text { (Right)}$

Fig. 8

Shear angle contours with respect to $\dot{r}_{i}:\dot{r} _{i}>0$ (a) and $\dot{r}_{i}<0$ (b)

We also summarize the shear strain gradients and the associated shear angle contours computed, respectively, by the first, second and third gradient continuum models for the purpose of further clarification. It is evident from Fig. 9 that the proposed model (third gradient) predicts smooth and continuous shear strain gradient fields as opposed to those obtained from the first and second gradient models where the corresponding strain gradient fields display either zero or constant distributions (see Fig. 9). In results, a comprehensive description of smooth and dilatational shear angle distributions is assimilated by the proposed linear model (see Fig. 10). On the other hand, conventional lower-order models produce limited predictions of either discontinued (first gradient model) or non-dilatational (second gradient model) field distributions (Fig. 10). The obtained results are also aligned with the earlier discussions regarding higher-order continua that Nth-order continua can sustain continuous and smooth deformation gradient fields up to $(N-1)$th order ([19, 20, 22]).

Fig. 9

Shear strain gradients predicted by the first (Left), second (Middle) and third gradient (Right) models

Fig. 10

Shear angle contours predicted by the first (Left), second (Middle) and third gradient (Right) models

6.2 Comparison with the experimental results

Lastly, comparisons with the in-house experimental results are presented to demonstrate the performance and potential utility of the obtained linear model. For the stated purpose, we consider the uniaxial tension test of an elastomeric material (Ecoflex 0050; Smooth-on Inc., USA) reinforced with polyester fibers (PETKM2005 and PETKM2006; Brookfield, CT, USA) (see Fig. 11). We note here that, since the proposed model is linearized model, the comparisons have been made for deformations arising at relatively low strain levels. The corresponding material parameters within the linear regime are found as $\mu =0.11$ MPa (Ecoflex 0050), $E=3.45$ MPa (PETKM2005) and$E=2.35$ MPa (PETKM2006). An aspect ratio of length to width of 2 : 1 is maintained for all samples and a uniform axial tension is applied by using Instron 5943 (Illinois Tool Works Inc., USA) (see Fig. 11). A Sony A6000 camera was used to capture the deformed image of the elastomeric composites and the obtained images are post-processed via the MATLAB image processing toolbox to compute the deformation profiles and the shear angle distributions of PETKM fiber composites.

Fig. 11

Experimental set up (left): uniaxial tension test of elastomeric composite $(50\,\mathrm{{mm}}\times 25\,\mathrm{{mm}})$; schematic illustration of the uniaxial strain of the reinforced elastomer (right)

Fig. 12

Shear angle distributions of PETKM2005 composite at 20% (top) and 50% (bottom) elongations

Fig. 13

$\chi _{2}$ deformations of PETKM2005 and PETKM2006 composites at 50% elongation

Fig. 14

Deformation profiles of PETKM2005 composite at 50% (top) and 100% (bottom) elongations

The shear angle distributions of PETKM2005 composite at $20\%$ and $50\%$ strain levels and transverse deformation ($\chi _{2}$) of PETKM2005 and PETKM2006 composites at $50\%$ elongations are presented in Figs. 12 and 13. We note that, in Fig. 13, the corresponding deformation profiles are normalized by their initial length scales (i.e., $w_{\mathrm{{o}}}$ and $L_{\mathrm{{o}}}$) for compact demonstrations. Despite the uncertainties arising in the MATLAB image processing and curve fittings, the proposed linear model produces reasonably accurate predictions in both the shear strain angle distributions and $\chi _{2}$ deformation of the composites. More precisely, the proposed linear model predicts smooth and continuous shear angle transitions from the minimum shear zone (blue) to the maximum shear zone (red) which captures the major characteristics of the shear angle distributions of the composite under axial tension (Fig. 12). For the transverse deformations ($\chi _{2}$) of PETKM composites, the experimental results show abrupt changes as they move from the center ($x/L_{\mathrm{{o}}}=0$) to the clamped end ($x/L_{\mathrm{{o}}}=0.5$) (see Fig. 13). This may be attributed by the imperfections in fiber’s bonding in the vicinity of the boundaries (refer to the non-symmetric deformation profiles with respect to x axis in Fig. 14) and/or possible reading errors. Except these sharp variations, the proposed model closely estimates the transverse deformations of the composites throughout the domain of interest (Fig. 13). In addition, although the proposed linear model is not intended for relatively large deformation analyses, it produces reasonably good prediction results for the general deformation profiles of PETKM2005 composite at $50\%$ and $100\%$ strain levels (see Fig. 14).

It should be also noted here that the obtained model may be further extended to include practically more important problems such as determination of the triple force moduli, analysis of the residual triple stresses on the mechanical responses of higher-order continua and a microlevel analysis of curved fiber reinforces shell structures [54, 55]. Researches on these subjects certainly deserve further attentions which, however, are beyond the scope of the present study due to the paucity of available experimental resources and data sets (especially with the current outbreak).

7 Conclusion

In this study, we present a second strain gradient-based continuum model for the mechanics of an elastic solid reinforced with extensible fibers and subjected to plane deformations. The fibers are presumed as continuously distributed spatial rods of Kirchhoff type, under which the kinematics of fibers has been formulated via the second and third gradient of continuum deformations. In particular, we incorporated the second strain gradient field into the model of continuum deformation through which mechanical contact forces, couple moments, double forces and triple forces can be assimilated in addition to the extension and bending resistance of fibers. By means of the variational principles and the virtual work statement, the Euler equations and the associated necessary boundary conditions are obtained. The energy density function of Spencer and Soldatos type is augmented by the third gradient of continuum deformations to accommodate the third gradient continua and the associated bulk incompressibility. The rate of change in curvature, defined at points on the convected cures of fibers, is also formulated in terms of the third gradient of deformations which characterizes the mechanical contact interactions between the adjoined fibers and the surrounding matrix.

More importantly, we obtained a complete linear model within the prescription of superposed incremental deformations from which a complete analytical solution has been obtained. The corresponding boundary conditions are also approximated up to the leading order which were then used to assimilate the triple forces and their energy couples exerted by the third gradient continua. The presented linear model predicts smooth deformations profiles and, in particular, predicts gradual and dilatational shear angle distributions of the composite subjected to plane bias extension. This is due to the sufficient continuity in the resulting deformation fields suitably sustained by the third gradient continua unlike those from the lower-order continua where sharp variations are present in the corresponding shear zones. In addition, it is found that the intensity of dilatations is dependent on both the triple stress modulus and the applied triple force. The results may be employed to the strain and failure analyses of composite structures subjected to dilatational shear where significant displacement inconsistencies are often observed. Comparisons with the experimental results of polymeric (PETKM) composites at 20% and 50% elongation are also performed which indicate that the proposed linear model provides reasonably accurate predictions in the deformation and shear angle analyses of polyester fiber (PETKM) composites.

Lastly, we note that the obtained model may be further extended to include practically more important problems such as determination of the triple force moduli, analysis of the residual triple stresses on the mechanical responses of higher-order continua and a microlevel analysis of shell structures reinforced with curved fibers.

Appendix

$\bullet$ Algebraic procedures for $a_{m},b_{m},c_{m}$ and $d_{m}$

$$\begin{aligned} a_{m}= & {} \frac{(T_{2}+T_{1})}{2},b_{m}=\frac{(T_{2}-T_{1})}{2i},c_{m}=\frac{ T_{3}}{i},d_{m}=T_{4}\text {, }m=\frac{n\pi }{2d}(n=1,3,5,etc.), \nonumber \\ T_{1}= & {} \left[ \frac{T_{24}}{4A}-T_{5}-\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}-T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{2}= & {} \left[ \frac{T_{24}}{4A}-T_{5}+\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}-T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{3}= & {} \left[ \frac{T_{24}}{4A}+T_{5}-\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}+T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{4}= & {} \left[ \frac{T_{24}}{4A}+T_{5}+\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}+T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{5}= & {} \frac{T8}{6(T_{9})^{\frac{1}{6}}},T_{6}=3\sqrt{6} T_{19}\left[ 27(T_{19})^{2}+3\sqrt{3}T_{15}-72T_{17}T_{18}-2(T_{18})^{3}\right] ^{0.5}, \nonumber \\ T_{7}= & {} 6(T_{9})^{\frac{1}{6}}\left[ 6T_{18}(T_{9})^{\frac{1}{3}}+9(T_{9})^{\frac{ 2}{3}}-T_{12}+\frac{12m^{4}}{A}+(T_{18})^{2}+T_{11}-\frac{3T_{24}T_{16}}{ A^{2}}\right] ^{\frac{1}{4}}, \nonumber \\ T_{8}= & {} \left[ 6T_{18}(T_{10})^{\frac{1}{3}}+9(T_{10})^{\frac{2}{3}}-T_{12}+\frac{ 12m^{4}}{A}+(T_{18})^{2}-\frac{3T_{24}T_{22}}{A^{2}}+T_{11}\right] ^{\frac{1}{2}}, \nonumber \\ T_{9}= & {} \frac{(T_{14})^{2}}{2}-\frac{4T_{18}T_{13}}{3}+\left( \frac{\sqrt{3}}{18} \right) \Big [12(T_{18})^{2}(T_{13})^{2}+27(T_{14})^{4}+16(T_{18})^{4}T_{13}+256(T_{13})^{3} \nonumber \\&-4(T_{18})^{3}(T_{14})^{2}-144T_{18}(T_{14})^{2}T_{13}-\frac{(T_{18})^{3}}{ 27}\Big ]^{0.5}, \nonumber \\ T_{10}= & {} \frac{(T_{19})^{2}}{2}+\frac{\sqrt{3}T_{15}}{18}-\frac{ 4T_{18}T_{17}}{3}-\frac{(T_{18})^{3}}{27},T_{11}=\frac{3(T_{24})^{2}T_{23}}{ 4A^{3}},T_{12}=\frac{9(T_{24})^{4}}{64A^{4}}, \nonumber \\ T_{13}= & {} T_{21}-\frac{m^{4}}{A}-T_{20}+\frac{T_{24}T_{16}}{4A^{2}},T_{14}= \frac{(T_{24})^{3}}{8A^{3}}+\frac{T_{16}}{A}-\frac{T_{24}T_{23}}{2A^{2}}, \nonumber \\ T_{15}= & {} \Big [27(T_{19})^{4}+T_{16}T_{17}(T_{18})^{4}+256(T_{17})^{3}-4(T_{18})^{3}(T_{19})^{2}, \nonumber \\&+128(T_{18})^{2}(T_{17})^{2}-144T_{18}(T_{19})^{2}T_{17}\Big ]^{0.5}, \nonumber \\ T_{16}= & {} (2+E)m^{2},T_{17}=T_{21}-\frac{m^{4}}{A}+\frac{T_{24}T_{22}}{4A^{2} }-T_{20}, \nonumber \\ T_{18}= & {} \frac{3(T_{24})^{2}}{8A^{2}}-\frac{T_{23}}{A},T_{19}=\frac{ (T_{24})^{3}}{8A^{3}}+\frac{T_{22}}{A}+\frac{T_{24}T_{23}}{2A^{2}},T_{20}= \frac{(T_{24})^{2}T_{23}}{16A^{3}},T_{21}=\frac{3(T_{24})^{4}}{256A^{4}}, \nonumber \\ T_{22}= & {} (2+E)m^{2},T_{23}=Cm^{2}+1\text { and }T_{24}=Am^{2}+C. \end{aligned}$$

(A.1)

$\bullet$ Evaluation of the geodesic curvature of the fibers

The geodesic curvature of a parametric curve ($\mathbf {r}(S)$) can be obtained by evaluating the second derivative of $\mathbf {r}(S)$ with respect to the arc length parameter (S);

$$\begin{aligned} \mathbf {g=r}^{\prime \prime }=\frac{d^{2}\mathbf {r(}S\mathbf {)}}{ dS^{2}}. \end{aligned}$$

(A.2)

Using the chain rule (i.e., $\mathrm{{d}}(*)/\mathrm{{d}}S=\frac{\mathrm{{d}}(*)}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}} \mathbf {X}}{\mathrm{{d}}S}$), we obtain from Eq. (A2) that

$$\begin{aligned} \frac{\mathrm{{d}}^{2}\mathbf {r(}S\mathbf {)}}{\mathrm{{d}}S^{2}}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\mathbf {r(}S \mathbf {)}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\varvec{\chi } (S\mathbf {)}}{\mathrm{{d}}\mathbf {X}} \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}=\left( \frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\varvec{\chi (}S\mathbf {)}}{\mathrm{{d}} \mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}\mathbf {X}}\right) \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}. \end{aligned}$$

(A.3)

Since $\mathbf {F}=\mathrm{{d}}\varvec{\chi }/\mathrm{{d}}\mathbf {X}$ and $\mathbf {D}=(\mathrm{{d}}\mathbf {X} (S))/\mathrm{{d}}S$, the above can be rewritten as

$$\begin{aligned} \mathbf {g=r}^{\prime \prime }=\left( \frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\varvec{\chi (}S \mathbf {)}}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}\mathbf {X}}\right) \frac{\mathrm{{d}}\mathbf { X}}{\mathrm{{d}}S}=\left( \frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}}\right) \mathbf {D=}\nabla [\mathbf {FD]D,} \end{aligned}$$

(A.4)

where $\nabla (\mathbf {FD})=\mathrm{{d}}(\mathbf {FD})/\mathrm{{d}}\mathbf {X}$ is the first gradient of “ $\mathbf {FD}$” .

$\bullet$ Evaluation of the rate of changes in curvature of the fibers

The rate of changes in curvature of the fibers can be formulated by taking third derivative of $\mathbf {r}(S)$ with respect to the arc length parameter (S). Hence, from Eq. (A4), we find

$$\begin{aligned} \varvec{\alpha } =\mathbf{r}^{\prime \prime \prime }=\frac{\mathrm{{d}}^{3}\mathbf {r(}S \mathbf {)}}{\mathrm{{d}}S^{3}}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}^{2}\mathbf {r(}S\mathbf {)}}{\mathrm{{d}}S^{2}}\big )}{\mathrm{{d}}S}= \frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}. \end{aligned}$$

(A.5)

Now applying the chain rule (i.e., $\mathrm{{d}}(*)/\mathrm{{d}}S=\frac{\mathrm{{d}}(*)}{\mathrm{{d}}\mathbf {X}} \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}$), Eq. (A5) Becomes

$$\begin{aligned} \frac{\mathrm{{d}}^{3}\mathbf {r(}S\mathbf {)}}{\mathrm{{d}}S^{3}}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}} \mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}} \mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}=\left[ \frac{\mathrm{{d}}^{2}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}^{2}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}+\frac{\mathrm{{d}}( \mathbf {FD})}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}^{2}\mathbf {X}}{\mathrm{{d}}S^{2}}\right] \frac{\mathrm{{d}}\mathbf {X}}{ \mathrm{{d}}S}. \end{aligned}$$

(A.6)

Since $\mathbf {D}=(\mathrm{{d}}\mathbf {X}(S))/\mathrm{{d}}S$, the above can be rewritten as

$$\begin{aligned} \varvec{\alpha } =\mathbf{r}^{\prime \prime \prime }=\left[ \frac{\mathrm{{d}}^{2}(\mathbf {FD}) }{\mathrm{{d}}\mathbf {X}^{2}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}+\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}} \frac{\mathrm{{d}}^{2}\mathbf {X}}{\mathrm{{d}}S^{2}}\right] \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}=[\nabla \{\nabla ( \mathbf {FD})\}{} \mathbf{D}+\nabla (\mathbf {FD})(\nabla \mathbf {(D))}]\mathbf{D,} \end{aligned}$$

(A.7)

where $\nabla (\nabla (\mathbf {FD}))=\mathrm{{d}}^{2}(\mathbf {FD})/\mathrm{{d}}\mathbf {X}^{2}$ is the second gradient of “ $\mathbf {FD}$ ”.

$\bullet$ Implementation of the boundary conditions [Eq. (53)]

The boundary conditions in Eq. (53) can be readily implemented in the desired boundaries via the tangential and normal vectors of the boundary and the director field of the fibers. For example, in the case of aligned fibers in the direction of $\mathbf {X}_{1}$, we find

$$\begin{aligned} \mathbf {D=}D_{1}\mathbf {E}_{1}+D_{2} \mathbf {E}_{2}=D_{1}\mathbf {E}_{1};\text { \ }D_{1}=1\text { and }D_{2}=0. \end{aligned}$$

(A.8)

Now on $\Omega _{1}$, the unit normal and tangent to the boundary are defined by (see Fig. 15)

$$\begin{aligned} \mathbf {T}^{1}= & {} T_{1}^{1}\mathbf {E}_{1}+T_{2}^{1}\mathbf {E} _{2}=T_{2}^{1}\mathbf {E}_{2};\text { \ }T_{1}^{1}=0\text { and }T_{2}^{1}=1, \nonumber \\ \mathbf {N}^{1}= & {} N_{1}^{1}\mathbf {E}_{1}+N_{2}^{1}\mathbf {E} _{2}=N_{1}^{1}\mathbf {E}_{1};\text { \ }N_{1}^{1}=1\text { and }N_{2}^{1}=0. \end{aligned}$$

(A.9)

Fig. 15

Schematic demonstration of imposed boundary conditions

Hence, on $\Omega _{1}$, the corresponding boundary conditions can be obtained by

$$\begin{aligned} t_{1}^{1}\mathbf {e}_{1}= & {} \big (P_{11}N_{1}^{1}+P_{12}N_{2}^{1}\big ) \mathbf {e}_{1}=P_{11}\mathbf {e}_{1}, \nonumber \\ t_{2}^{1}\mathbf {e}_{2}= & {} \big (P_{21}N_{1}^{1}+P_{22}N_{2}^{1}\big ) \mathbf {e}_{2}=P_{21}\mathbf {e}_{2}, \nonumber \\ m_{1}^{1}\mathbf {e}_{1}= & {} \big (Cg_{1}-A\alpha _{1,1}D_{1}^{1}-A\alpha _{1,2}D_{2}^{1}\big )\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{1} \nonumber \\= & {} (Cg_{1}-A\alpha _{1,1})\mathbf {e}_{1}, \nonumber \\ m_{2}^{1}\mathbf {e}_{2}= & {} \big (Cg_{2}-A\alpha _{2,1}D_{1}^{1}-A\alpha _{2,2}D_{2}^{1}\big )\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{2} \nonumber \\= & {} (Cg_{2}-A\alpha _{2,1})\mathbf {e}_{2}, \nonumber \\ r_{1}^{1}\mathbf {e}_{1}= & {} A\alpha _{1}\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}\nonumber \\&+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{1}=A\alpha _{1}\mathbf {e}_{1},\nonumber \\ r_{2}^{1}\mathbf {e}_{2}= & {} A\alpha _{2}\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}\nonumber \\&+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{2}=A\alpha _{2}\mathbf {e}_{2}, \end{aligned}$$

(A.10)

where $\mathbf {t}^{1}=t_{1}^{1}\mathbf {e}_{1}+t_{2}^{1}\mathbf {e}_{2}$, $\mathbf {m}^{1}=m_{1}^{1}\mathbf {e}_{1}+m_{2}^{1}\mathbf {e}_{2}$ and $\mathbf { r}^{1}=r_{1}^{1}\mathbf {e}_{1}+r_{2}^{1}\mathbf {e}_{2}$ are, respectively, the boundary traction, edge moment and the triple force acting on the $\Omega _{1}$ boundary.

For $\Omega _{2}$ boundary, we find (see Fig. 15)

$$\begin{aligned} \mathbf {T}^{2}= & {} T_{1}^{2}\mathbf {E}_{1}+T_{2}^{2}\mathbf {E} _{2}=T_{2}^{2}\mathbf {E}_{2};\text { \ }T_{1}^{2}=0\text { and }T_{2}^{2}=1,\nonumber \\ \mathbf {N}^{2}= & {} N_{1}^{2}\mathbf {E}_{1}+N_{2}^{2}\mathbf {E} _{2}=N_{1}^{2}\mathbf {E}_{1};\text { \ }N_{1}^{2}=1\text { and }N_{2}^{2}=0. \end{aligned}$$

(A.11)

Therefore, repeating the same process as done in the above, it can be shown that

$$\begin{aligned} t_{1}^{2}\mathbf {e}_{1}= & {} \big (P_{11}N_{1}^{2}+P_{12}N_{2}^{2}\big ) \mathbf {e}_{1}=P_{12}\mathbf {e}_{1}, \nonumber \\ t_{1}^{1}\mathbf {e}_{1}= & {} \big (P_{21}N_{1}^{2}+P_{22}N_{2}^{2}\big ) \mathbf {e}_{2}=P_{22}\mathbf {e}_{2}, \nonumber \\ m_{1}^{1}\mathbf {e}_{1}= & {} 0\mathbf {e}_{1} {{, }} m_{2}^{1}\mathbf {e}_{2}=0\mathbf {e}_{2}, \nonumber \\ r_{1}^{1}\mathbf {e}_{1}= & {} 0\mathbf {e}_{1}, r_{2}^{1}\mathbf {e}_{2}=0\mathbf {e}_{2}. \end{aligned}$$

(A.12)

Lastly, Eq. (A12) indicates that the edge moment and triple force cannot be sustained by the $\Omega _{2}$ boundary where no reinforcing fibers are aligned in $\mathbf {e}_{2}$ direction.