1 Introduction

Functionally graded materials are new composite materials whose material properties vary continuously and smoothly in a specific direction [1, 2]. FGM structures can effectively reduce thermal stresses so that they are applied in extreme thermal environments. However, the FGM structures are usually subjected to dynamic thermal loadings, the temperature variations result in transient thermal stresses, even thermal buckling [1,2,3,4,5]. Up to now, many works on the thermal stability of FGM structures have been published, but most of them were only limited to the static problems. For example, Javaheri and Eslami [3] examined the buckling characteristics of rectangular FGM plates subjected to different thermal loadings and the closed form solutions were provided. Ma and Wang [4, 5] carried out the nonlinear bending and post-buckling studies for the circular FGM plates subjected to the mechanical and thermal loadings according to the first- and third-order plate theories, respectively. The post-buckling behaviors of piezoelectric FGM plates under complicated loadings were investigated by Liew et al. [6]. In addition, Li et al. [7, 8] researched the buckling and post-buckling of functionally graded beams and imperfect FGM plates using the shooting method. It was found that the deformations are still bifurcation buckling for boundary clamped FGM beams and perfect plates, even if they were subjected to non-uniform heating loads, whereas the imperfect FGM plates do not display bifurcation buckling.

Since FGM structures usually serve in high-temperature-gradient environments, the dynamic thermal buckling is very likely to occur. However, the studies on dynamic thermal buckling of functionally graded structures are much fewer than those on static buckling. Mirzavand et al. [9] conducted an investigation on the dynamic post-buckling characteristics of the piezoelectric FGM cylindrical shells under thermal load on the basis of Budiansky’s stability criterion. Mirzavand et al. [10] also dealt with the research on dynamic post-buckling and buckling temperatures of the FGM cylindrical shells based on the third-order shell theory. Additionally, the two-dimensional solutions of FGM partial annular disks subjected to radial thermal shock were presented by Mehrian and Naei [11] based on the Lord–Shulman generalized thermoelastic theory with two relaxation times and the hybrid Fourier–Laplace transformation. Shariyat [12] analyzed the nonlinear dynamic buckling characteristics of the preloaded functionally graded cylindrical shells suffered from transient thermal. He also examined the dynamic buckling behaviors of the FGM plates subjected to thermal, electric and mechanical loads [13]. It should be noted that geometrical imperfections of structures were considered in the above two investigations. Besides these, many investigations on dynamic buckling are limited to functionally graded structures under mechanical loads. Such as Huang and Han [14] researched the buckling of the functionally graded cylindrical shells with imperfection under axial compressed load according to Donnell’s shell theory. Bich et al. [15] examined nonlinear buckling of the axial stiffened FGM cylindrical shells under different types of loads, and the static buckling loads and post-buckling paths were obtained. The nonlinear dynamic buckling of the FGM stiff and soft cylindrical shells was investigated by Gao et al. [16] using Galerkin method and considering damping effect.

All of the above works have used traditional elasticity approaches, for example, finite element method, difference method, Galerkin method, etc. Although the obtained results agree well with the static buckling problems using these methods, it is difficult to solve complex partial differential equations for the dynamic buckling problems. This is due to the complexity of the dynamic behaviors and variableness of space and time. In contrast, based on the symplecticity method in the Hamilton system [17], the equations of structural stability problems can be easily solved by separation of variables and symplectic eigenfunction expansion. This is because solving partial differential equations can be avoided. Xu et al. [18, 19] studied the buckling and post-buckling characteristics of homogeneous cylindrical shells using the symplecticity method. Sun et al. [20, 21] examined the static buckling of FGM cylindrical shells subjected to combined thermal and compressed loads using the symplecticity method. In the light of plenty of researches, of which we can easily get that this method is very efficient and accurate in solving the problem of structural stability.

As far as the authors know, few research results have been published on the dynamic thermal buckling of functionally graded structures using the symplecticity method. Therefore, the present paper examined dynamic thermal buckling behaviors of the functionally graded material cylindrical shells under thermal shock based on this method. In symplectic space, a canonical equation will be established in the Hamilton system, and the buckling mode equations and bifurcation conditions will be solved by analytical methods. The buckling thermal loads and buckling modes will be obtained by solving mode equations and bifurcation conditions. Finally, the dynamic buckling temperatures of the FGM cylindrical shells are obtained via inverse solutions of the buckling thermal membrane force.

2 Mathematical formulas of the problem

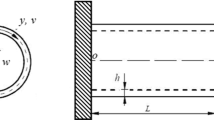
A coordinate system \(({x,\theta ,z})\) is adopted where the x-axis is in the generatrix direction of the mid-surface of undeformed shell, metered from the left end. \(\theta \) denotes the circumferential direction, and z denotes the thickness direction metered from the mid-surface. Thermal shock loads are imposed on the inner surface of the FGM shells and the outer surface exchanges heat with the ambient environment. No initial displacements or velocities exist at any point. Figure 1 shows the sketch of the shell.

Fig. 1
figure 1

The sketch of the thin FGM cylindrical shell subjected to thermal shock

Full size image

2.1 Material properties of FGM

Functionally graded materials are usually made of the metal and ceramic. Effective material properties are often described on the basis of the linear rule of mixtures, which will be convenient to calculate transient non-uniform temperature field and give analytical expressions of stiffness coefficients. Based on the linear rule of mixtures, the material properties P(z) (including Young’s modulus E, mass density \(\rho \), thermal expansion coefficient \(\alpha \), thermal capacity C and thermal conductivity \(\kappa \)) of the FGM cylindrical shell are [22]:

$$\begin{aligned} P(z)=(P_\mathrm{e} -P_\mathrm{i} )V_\mathrm{e} (z)+P_\mathrm{i} \end{aligned}$$
(1)

in which \(P_\mathrm{i}\) and \(P_\mathrm{e}\) indicate the material properties of constituent materials, respectively. Volume fractions \(V_\mathrm{i} \left( z \right) \) and \(V_\mathrm{e} \left( z \right) \) are assumed to be a power function in terms of the thickness coordinate z [22], expressed as

$$\begin{aligned} V_\mathrm{e} (z)=\left( {\frac{h+2z}{2h}} \right) ^{k}, \quad V_\mathrm{e} (z)=1-V_\mathrm{i} \end{aligned}$$
(2)

in which power law index k is employed to measure gradient characteristics of FGM. Since Poisson’s ratio \(\mu \) has a minor variation for different materials, so \(\mu (z)\) is usually chosen as a constant \(\mu \) [22].

2.2 Fundamental equations

The thin FGM cylindrical shell subjected to uniform dynamic thermal loads on its inner surface is considered. Displacement components u, v and w in the mid-surface are relevant to the x, \(\theta \) and z directions, respectively. According to the classical shell theory, the normal strains \(\varepsilon _{xx}^{(z)}\), \(\varepsilon _{\theta \theta }^{(z)} \) and shear strain \(\varepsilon _{x\theta }^{(z)} \) at any point can be given by

$$\begin{aligned} \varepsilon _{xx}^{(z)} =\varepsilon _{xx} +z\kappa _{xx}, \quad \varepsilon _{\theta \theta }^{(z)} =\varepsilon _{\theta \theta } +z\kappa _{\theta \theta },\quad \varepsilon _{x\theta }^{(z)} =\varepsilon _{x\theta } +2z\kappa _{x\theta } \end{aligned}$$
(3a)

in which the strains \(\varepsilon _{xx} \), \(\varepsilon _{\theta \theta } \) and \(\varepsilon _{x\theta } \), curvatures \(\kappa _{xx} \) and \(\kappa _{\theta \theta } \), torsional curvature \(\kappa _{x\theta } \) on the middle surface are

$$\begin{aligned} \varepsilon _{xx}= & {} \frac{\partial u}{\partial x},\quad \varepsilon _{\theta \theta } =\frac{1}{R}\frac{\partial v}{\partial \theta }-\frac{w}{R},\quad \varepsilon _{x\theta } =\frac{1}{R}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial x},\quad \kappa _{xx} =-\frac{\partial ^{2}w}{\partial x^{2}},\quad \kappa _{\theta \theta } =-\frac{1}{R^{2}}\frac{\partial ^{2}w}{\partial \theta ^{2}}, \nonumber \\ \kappa _{x\theta }= & {} -\frac{1}{R}\frac{\partial ^{2}w}{\partial x\partial \theta } \end{aligned}$$
(3b)

By taking into consideration of the linear thermoelastic deformation of the structure [23], the constitutive equations of the shell under thermal shock can be written based on the linear thermoelastic theory as

figure a
figure b

in which \(T=T\left( {z,t} \right) \) is the rise in temperature compared with initial temperature \(T_{0}\). Substituting Eqs. (3) into Eqs. (4), the constitutive equations respecting middle surface strains are expressed as

figure c
figure d

where \(K=\frac{E}{1-\mu ^{2}}\). The membrane forces and moments can be obtained by integrating above stresses, described as

$$\begin{aligned} \left\{ {N_{xx} ,N_{\theta \theta } ,N_{x\theta } ,M_{xx} ,M_{\theta \theta } ,M_{x\theta } } \right\} ^{\mathrm{T}}=\int \limits _{-h/2}^{h/2} {\left\{ {\sigma _{xx} ,\sigma _{\theta \theta } ,\sigma _{x\theta } ,z\sigma _{xx} ,z\sigma _{\theta \theta } ,z\sigma _{x\theta } } \right\} ^{\mathrm{T}}\mathrm{d}z} \end{aligned}$$
(6)

Substituting Eqs. (5) into (6), the membrane forces and moments can be obtained as

figure e
figure f
figure g
figure h

where stiffness coefficients \(\left\{ {A,B,C} \right\} ^{\mathrm{T}}=\int \limits _{-h/2}^{h/2} {\frac{E}{1-\mu ^{2}}\left\{ {1,z,z^{2}} \right\} ^{\mathrm{T}}\mathrm{d}z}\) are adopted. \(N_\mathrm{T} \), \(M_\mathrm{T}\) are given by

$$\begin{aligned} \left\{ {N_\mathrm{T} ,M_\mathrm{T} } \right\} ^{\mathrm{T}}=\int \limits _{-h/2}^{h/2} {\frac{E}{1-\mu }\left\{ {1,z} \right\} ^{\mathrm{T}}~\alpha T\,\mathrm{d}z} \end{aligned}$$
(9)

2.3 Canonical equations

The strain energy of the FGM cylindrical shell is

$$\begin{aligned} U= & {} \frac{1}{2}\int \limits _v {\left[ {\sigma _{xx} \varepsilon _{xx}^{(z)} {+}\sigma _{\theta \theta } \varepsilon _{\theta \theta }^{(z)} {+}\sigma _{x\theta } \varepsilon _{x\theta }^{(z)} } \right] \mathrm{d}V} \\= & {} \frac{1}{2}\int \limits _0^{2\pi } {\int \limits _0^R {\left[ {A(\varepsilon _{xx} +\varepsilon _{\theta \theta } )^{2}} \right. } } -2(1-\mu )A\varepsilon _{xx} \varepsilon _{\theta \theta } +C(\kappa _{xx} +\kappa _{\theta \theta } )^{2}-2(1-\mu )C\kappa _{xx} \kappa _{\theta \theta } +2B\varepsilon _{xx} \kappa _{xx} \\&+\,2B\varepsilon _{\theta \theta } \kappa _{\theta \theta } +\left. 2\mu B\varepsilon _{xx} \kappa _{\theta \theta } +2\mu B\varepsilon _{\theta \theta } \kappa _{xx} +\frac{1-\mu }{2}(A\varepsilon _{x\theta } +BC\kappa _{x\theta } )\varepsilon _{x\theta }\right. \\&\left. +\,\frac{1-\mu }{2}(B\varepsilon _{x\theta } +2C\kappa _{x\theta } )2\kappa _{x\theta } \right] R\mathrm{d}x\mathrm{d}\theta \end{aligned}$$

Thus, the density of it is

$$\begin{aligned} \overline{U}= & {} \frac{1}{2}A(\varepsilon _{xx} +\varepsilon _{\theta \theta } )^{2}-(1-\mu )A\varepsilon _{xx} \varepsilon _{\theta \theta } +\frac{1}{2}C(\kappa _{xx} +\kappa _{\theta \theta } )^{2}-(1-\mu )C\kappa _{xx} \kappa _{\theta \theta } \\&+B\varepsilon _{xx} \kappa _{xx} +B\varepsilon _{\theta \theta } \kappa _{\theta \theta } +\mu B\varepsilon _{xx} \kappa _{\theta \theta } +\mu B\varepsilon _{\theta \theta } \kappa _{xx} +\frac{1-\mu }{{4}}(A\varepsilon _{x\theta } +{2}B\kappa _{x\theta } )\varepsilon _{x\theta }\\&+\frac{1-\mu }{{4}}(B\varepsilon _{x\theta } +2C\kappa _{x\theta } )2\kappa _{x\theta } \end{aligned}$$

For the FGM cylindrical shell after buckling, though the stretching is also existing, the bending deformation energy is far more than the corresponding energy of it [18, 20]. So, only the bending deformation energy is considered here. The Lagrange density function is expressed by displacements as

$$\begin{aligned} \bar{{L}}= & {} \frac{1}{2}I_{0} \left( {\frac{\partial w}{\partial t}} \right) ^{2}-\overline{U} -\frac{1}{2}N_\mathrm{T} \left( {\frac{\partial w}{\partial x}} \right) ^{2} \\= & {} \frac{1}{2}I_{0} \left( {\frac{\partial w}{\partial t}} \right) ^{2}-\left[ {\frac{1}{2}A\left( {\frac{w}{R}} \right) ^{2}+\frac{1}{2}C\left( {\frac{\partial ^{2}w}{\partial x^{2}}+\frac{1}{R^{2}}\frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) ^{2}-(1-\mu )C\frac{1}{R^{2}}\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial ^{2}w}{\partial \theta ^{2}}+B\frac{w}{R^{3}}\frac{\partial ^{2}w}{\partial \theta ^{2}}} \right. \\&\left. {+\,\mu B\frac{w}{R}\frac{\partial ^{2}w}{\partial x^{2}}+2(1-\mu )C\left( {\frac{1}{R}\frac{\partial ^{2}w}{\partial x\partial \theta }} \right) ^{2}} \right] -\frac{1}{2}N_\mathrm{T} \left( {\frac{\partial w}{\partial x}} \right) ^{2}-\frac{1}{2}N_\mathrm{T} \left( {\frac{1}{R}\frac{\partial w}{\partial \theta }} \right) ^{2} \end{aligned}$$

where \(I_{0} =\int \limits _{-h/2}^{h/2} {\rho (z)\mathrm{d}z} \) is the mass per unit area.

The radius R of the shell is defined as the characteristic length and the dimensionless variables \(X=\frac{x}{R}\), \(L=\frac{l}{R}\), \(W=\frac{w}{R}\), \(\alpha =\frac{AR^{2}}{C}\), \(\beta =\frac{BR}{C}~N=\frac{N_\mathrm{T} R^{2}}{C}\), \(I=\frac{I_{0} R^{2}}{C}\) are adopted. In order to introduce the equations into the Hamiltonian system, operator symbols are defined as \(f^{'}=\frac{\partial f}{\partial X}\) and \(\dot{{f}}=\frac{\partial f}{\partial \theta }\). Define rotation angle \(\psi =-\dot{{W}}\), a set of new variables \(\mathbf {q=}\{q_{1} ,q_{2} \}^{\mathrm{T}}=\{W,\psi \}^{\mathrm{T}}\) are also introduced. In the Hamiltonian system, the corresponding dual variables are

$$\begin{aligned} \mathbf {p}=\left\{ {{\begin{array}{*{20}l} {p_{1} } \\ {p_{2} } \\ \end{array} }} \right\} =\frac{\partial L}{\partial \dot{\mathbf{q }}}=\left\{ {{\begin{array}{*{20}c} {-{\mathop {q}\limits ^{\ldots }_{1}} -\dot{{q}}_{1} ''} \\ {q_{1} ''-\dot{{q}}_{2} +\beta q_{1} } \\ \end{array} }} \right\} \end{aligned}$$
(10)

They represent the equivalent shear force and the equivalent bending moment, respectively. Thus, the Hamiltonian function can be expressed as

$$\begin{aligned} H={\mathbf{p}}{\dot{\mathbf{q}}}-L=-p_{1} q_{2} +\frac{1}{2}\left( {-p_{2} +q_{1} ''+\beta q_{1} } \right) ^{2}+\frac{1}{2}\alpha q_{1}^{2}+\frac{1}{2}\left( {q_{1} ''} \right) ^{2}+\mu \beta q_{1} q_{1} ''+\frac{1}{2}N\left( {q'} \right) ^{2} \end{aligned}$$
(11)

Introducing a state vector \(\varvec{\upvarphi }=\{q_{1} ,q_{2} ,p_{1} ,p_{2} \}^{\mathrm{T}}\), the Hamiltonian canonical equations are derived by Legendre transformation as

$$\begin{aligned} \varvec{\dot{{\upvarphi }}}=\left\{ {\begin{array}{l} \dot{\mathbf{q }} \\ \dot{\mathbf{p }} \\ \end{array}} \right\} =\left\{ {\begin{array}{l} \frac{\delta H}{\delta \mathbf {p}} \\ -\frac{\delta H}{\delta \mathbf {q}} \\ \end{array}} \right\} \end{aligned}$$
(12)

The matrix form of Eq. (12) is

$$\begin{aligned} \varvec{\dot{{\upvarphi }}}=\left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {\dot{{q}}_{1} } \\ {\dot{{q}}_{2} } \\ \end{array} }} \\ {\dot{{p}}_{1} } \\ \end{array} }} \\ {\dot{{p}}_{2} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} 0 &{}\quad {-1} &{}\quad 0 &{}\quad 0 \\ {-\partial _{x}^{2} -\beta } &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ {-2\partial _{x}^{4} -[2(1+\mu )\beta +N]\partial _{x}^{2} -\beta ^{2}-\alpha } &{}\quad 0 &{}\quad 0 &{}\quad {\partial _{x}^{2} +\beta } \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ \end{array} }} \\ {p_{1} } \\ \end{array} }} \\ {p_{2} } \\ \end{array} }} \right\} \end{aligned}$$
(13a)

Equation (13a) can also be written as

$$\begin{aligned} \varvec{\dot{{\upvarphi }}}=\mathbf {H} \varvec{\upvarphi } \end{aligned}$$
(13b)

in which \(\mathrm{\mathbf{H}}\) is operator matrix, its specific expression is

$$\begin{aligned} \mathbf {H}=\left[ {{\begin{array}{*{20}c} 0 &{}\quad {-1} &{}\quad 0 &{}\quad 0 \\ {-\partial _{x}^{2} -\beta } &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ {-2\partial _{x}^{4} -[2(1+\mu )\beta +N]\partial _{x}^{2} -\beta ^{2}-\alpha } &{}\quad 0 &{}\quad 0 &{}\quad {\partial _{x}^{2} +\beta } \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ \end{array} }} \right] \end{aligned}$$

The solutions of the Eqs. (13) can be written as the form of separate variables as follows

$$\begin{aligned} \varvec{\upvarphi }(X,\theta )=\sum {\mathbf {b}\varvec{\upvarphi }_{n} (X)\mathrm{e}^{\lambda _{n} \theta }} \end{aligned}$$
(14)

in which eigenvalue \(\lambda _{n} \), eigenvector \(\varvec{\upvarphi }_{n}\) and constant coefficient matrix \(\mathbf {b}\) must satisfy the following eigenequation:

$$\begin{aligned} \mathbf {H}\varvec{\upvarphi }_{n} =\lambda _{n} \varvec{\upvarphi }_{n} \end{aligned}$$
(15)

According to the sealing condition of the cylindrical shell

$$\begin{aligned} \varvec{\upvarphi }(X,0)=\varvec{\upvarphi }_{n} (X)=\varvec{\upvarphi }(X,2\pi )=\varvec{\upvarphi }_{n} (X)\mathrm{e}^{2\lambda _{n} \pi } \end{aligned}$$

the eigenvalues can be calculated are

$$\begin{aligned} \lambda _{n} =in \end{aligned}$$
(16)

where \(i=\sqrt{-1} \), n equals \(\left( {0,\pm 1,\pm 2,\ldots } \right) \). Substituting the eigenvalues into Eq. (15), obtains

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {-in} &{}\quad {-1} &{}\quad 0 &{}\quad 0 \\ {-\partial _{x}^{2} -\beta } &{}\quad {-in} &{}\quad 0 &{}\quad 1 \\ {-2\partial _{x}^{4} -[2(1+\mu )\beta +N]\partial _{x}^{2} -\beta ^{2}-\alpha } &{}\quad 0 &{}\quad {-in} &{}\quad {\partial _{x}^{2} +\beta } \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad {-in} \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ \end{array} }} \\ {p_{1} } \\ \end{array} }} \\ {p_{2} } \\ \end{array} }} \right\} =0 \end{aligned}$$
(17)

Thus \(\varvec{\upvarphi }_{n} \) can be obtained as

$$\begin{aligned} \varvec{\upvarphi }_{n} =c_{1} \left[ {{\begin{array}{*{20}c} {\mathrm{e}^{\lambda _{1} X}} \\ {-in\mathrm{e}^{\lambda _{1} X}} \\ {in\xi \mathrm{e}^{\lambda _{1} X}} \\ {\xi _{1} \mathrm{e}^{\lambda _{1} X}} \\ \end{array} }} \right] +c_{2} \left[ {{\begin{array}{*{20}c} {\mathrm{e}^{\lambda _{2} X}} \\ {-in\mathrm{e}^{\lambda _{2} X}} \\ {in\xi \mathrm{e}^{\lambda _{2} X}} \\ {\xi _{2} \mathrm{e}^{\lambda _{2} X}} \\ \end{array} }} \right] +c_{3} \left[ {{\begin{array}{*{20}c} {\mathrm{e}^{\lambda _{3} X}} \\ {-in\mathrm{e}^{\lambda _{3} X}} \\ {in\xi \mathrm{e}^{\lambda _{3} X}} \\ {\xi _{3} \mathrm{e}^{\lambda _{3} X}} \\ \end{array} }} \right] +c_{4} \left[ {{\begin{array}{*{20}c} {\mathrm{e}^{\lambda _{4} X}} \\ {-in\mathrm{e}^{\lambda _{4} X}} \\ {in\xi \mathrm{e}^{\lambda _{4} X}} \\ {\xi _{4} \mathrm{e}^{\lambda _{4} X}} \\ \end{array} }} \right] \end{aligned}$$
(18)

where \(c_{1} \), \(c_{2} \), \(c_{3}\) and \(c_{4}\) are the undetermined constants, \(\xi =(1+\alpha -2\beta )\), \(\xi _{j} =\lambda _{j} ^{2}+\beta +n^{2}\) (\(\hbox {j}=1,2,3,4\)). \(\lambda _{j}\) (\(j=1,2,3,4\)) are the four solutions of eigen equation:

$$\begin{aligned} \lambda ^{4}+(N-2n^{2}+2\beta \mu )\lambda ^{2}+\alpha -n^{4}=0 \end{aligned}$$
(19)

They are obtained by solving Eq. (19), as

$$\begin{aligned} \lambda _{j} =\pm \frac{1}{2}\sqrt{4n^{2}-2N-4\beta \mu \pm 2\sqrt{4\beta ^{2}\mu ^{2}-8\beta n^{2}\mu +4N\beta \mu -4Nn^{2}+8\beta n^{2}+N^{2}-4\alpha } } \end{aligned}$$

In particular, when \(n=0\), the eigenvector values are independent of the circumferential coordinate \(\theta \) corresponding to the axisymmetric buckling problem of the FGM cylindrical shell. Therefore, the canonical equation also can be obtained by simplifying as

$$\begin{aligned} \frac{\partial ^{4}q_{1} }{\partial X^{4}}+\left( {\eta +N} \right) \frac{\partial ^{2}q_{1} }{\partial X^{2}}+\xi q_{1} =0, \end{aligned}$$
(20)

where \(\eta =2\mu (\beta -1)\). Solutions of Eq. (20) can be written as a simplified form of exponential function by

$$\begin{aligned} q_{1} =c_{1} \mathrm{e}^{\lambda _{1} x}+c_{2} \mathrm{e}^{\lambda _{2} x}+c_{3} \mathrm{e}^{\lambda _{3} x}+c_{4} \mathrm{e}^{\lambda _{4} x}. \end{aligned}$$
(21)

3 Bifurcation conditions

Consider the functionally graded material cylindrical shell fixed at both ends, that is \(x=0\) and l, \(w=0\), \(\frac{\partial w}{\partial x}=0\). Substituting the boundary conditions of fixed supported \(q_{1} =0\), \(\frac{\partial q_{1} }{\partial X}=0~(X=0,~X=L)\) into Eq. (18) obtains

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ {\lambda _{1} } &{}\quad {\lambda _{2} } &{}\quad {\lambda _{3} } &{}\quad {\lambda _{4} } \\ {\mathrm{e}^{\lambda _{1} L}} &{}\quad {\mathrm{e}^{\lambda _{2} L}} &{}\quad {\mathrm{e}^{\lambda _{3} L}} &{}\quad {\mathrm{e}^{\lambda _{4} L}} \\ {\lambda _{1} \mathrm{e}^{\lambda _{1} L}} &{}\quad {\lambda _{2} \mathrm{e}^{\lambda _{2} L}} &{}\quad {\lambda _{3} \mathrm{e}^{\lambda _{3} L}} &{}\quad {\lambda _{4} \mathrm{e}^{\lambda _{4} L}} \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {c_{1} } \\ {c_{2} } \\ {c_{3} } \\ {c_{4} } \\ \end{array} }} \right\} =0 \end{aligned}$$
(22)

If the Eq. (22) have only zero solutions, the FGM cylindrical shell will not occur buckling when subjected to uniform compression. Conversely, the condition of buckling is that Eq. (22) have nonzero solutions. That is, the determinant of the coefficient of Eq. (22) equals to zero.

$$\begin{aligned} \left| {{\begin{array}{*{20}c} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ {\lambda _{1} } &{}\quad {\lambda _{2} } &{}\quad {\lambda _{3} } &{}\quad {\lambda _{4} } \\ {\mathrm{e}^{\lambda _{1} L}} &{}\quad {\mathrm{e}^{\lambda _{2} L}} &{} \quad {\mathrm{e}^{\lambda _{3} L}} &{}\quad {\mathrm{e}^{\lambda _{4} L}} \\ {\lambda _{1} \mathrm{e}^{\lambda _{1} L}} &{}\quad {\lambda _{2} \mathrm{e}^{\lambda _{2} L}} &{}\quad {\lambda _{3} \mathrm{e}^{\lambda _{3} L}} &{}\quad {\lambda _{4} \mathrm{e}^{\lambda _{4} L}} \\ \end{array} }} \right| =0 \end{aligned}$$
(23)

Applying the bifurcation conditions Eq. (23), the buckling loads of the FGM cylindrical shell can be calculated. Then, the relevant buckling modes can be solved by Eq. (18).

In the Eqs. (18) and (22), there are the thermal membrane forces relying on the temperature fields. Therefore, the solutions of the temperature fields have to be first acquired to solve the canonical equations.

4 Transient temperature field

Suppose that the FGM cylindrical shells are under the initial steady-state heat balance and subjected to uniform thermal shock loads on their inner surfaces \(z=-\frac{h}{2}\), while the outer surfaces \(z=\frac{h}{2}\) exchange heat with external environment. Consequently, the thermal conduction problem should be reduced to one-dimension inside the inhomogeneous material. Applying Fourier thermoelasticity theory, the heat conduction equation can be written as [22]

$$\begin{aligned} C\left( z \right) \rho \left( z \right) \frac{\partial T\left( {z,t} \right) }{\partial t}=\frac{\partial }{\partial z}\left[ {\kappa \left( z \right) \frac{\partial T\left( {z,t} \right) }{\partial z}} \right] ,~\left( {t>0,-\frac{h}{2}<z<\frac{h}{2}} \right) \end{aligned}$$
(24)

The dynamic heating loads are taken as an exponential function form, that is \(\bar{{T}}=\Delta T(1-\mathrm{e}^{-at})\) with an amplitude of temperature rise \(\Delta T\) on the inner surface, the parameters of the loads variation a. The heating initial conditions, the boundary conditions of the outer and the inner surfaces are expressed as

$$\begin{aligned} T(z,0)=0,~T\left( {-\frac{h}{2},t} \right) =\Delta T(1-\mathrm{e}^{-at}), ~\left. {-\kappa \left( z \right) \frac{\partial T}{\partial z}} \right| _{z=h / 2} =h_\mathrm{r} T\left( {\frac{h}{2},t} \right) \end{aligned}$$
(25)

where \(h_\mathrm{r} \) indicates the heat exchange coefficient between the outer surface of the shell and surrounding environment. Herein, Eqs. (24, 25) are solved through the Laplace transformation technique in combination with the power series method for obtaining the transient temperature fields which contains the thermal load amplitude parameter \(\Delta T\). The detailed solution process can be found in the Ref. [22]. And then, the thermal membrane force \(N_\mathrm{T} \) with undetermined parameter \(\Delta T\) can be obtained by integrating Eq. (9) in the thickness direction. In this study, the buckling thermal membrane forces are firstly obtained according to the bifurcation condition Eq. (23), and then the thermal buckling temperature amplitude \(\Delta T\) is obtained from the known thermal membrane force.

5 Numerical results

In this section, the FGM cylindrical shell made of ceramic SiC and metal Ni is taken into account. The outer surface is the metal while the inner surface is the ceramic. The material properties of SiC and Ni can be found in Table 1. Poisson’s ratio is \(\mu =0.3\). The dynamic thermal buckling modes and buckling temperature rise of axisymmetric buckling and non-axisymmetric buckling are calculated and discussed.

Table 1 Material properties of the ceramic and metal [22]
Full size table

5.1 Buckling modes

Based on the bifurcation condition Eq. (23), the buckling thermal loads of the FGM cylindrical shell can be obtained by using Newton–Raphson method. Some comparison studies are carried out first so as to verify the effectiveness and accuracy of above derivation and calculation on buckling analysis of the FGM cylindrical shells under thermal shock. Setting \(k\rightarrow \infty \), functionally graded materials are reduced to the homogeneously isotropic ones. Dynamic non-uniform temperatures are also reduced to static uniform ones when we neglect the thermal conduct. Thus, the FGM cylindrical shell buckling problem is reduced to a homogeneous cylindrical shell buckling. In particular, \(h=0.05\) m, \(R=1\) m and \(\mu =0.25\) are chosen to be the same as the corresponding ones by Xu et al. [18]. Comparisons of the buckling loads obtained in this study with the corresponding results by Xu et al. [18] are listed in Table 2. Furthermore, given \(L=1.5\), Table 3 lists the comparison of the non-axisymmetric buckling loads of the cylindrical shell under uniform temperature. It shows the buckling thermal loads in this calculation are all highly consistent with the previous results by Xu et al. [18].

Table 2 Comparison of the axisymmetric buckling loads of the cylindrical shell under uniform temperature (\(m=0\))
Full size table
Table 3 Comparison of the non-axisymmetric buckling loads of the cylindrical shell under uniform temperature (\(m=1\))
Full size table
Fig. 2
figure 2

The variation of the axisymmetric buckling thermal loads N with L\((n=0)\)

Full size image

With confidence in the present derivations and calculations, the dimensionless buckling thermal loads of the FGM cylindrical shell (\(k=1\)) are calculated by using Newton–Raphson method based on the bifurcation condition shown in the Eq. (23). Figure 2 plots the variations of the axisymmetric buckling thermal loads N of the FGM cylindrical shell with length L, given different axial buckling waves m. For non-axisymmetric buckling, Fig. 3 shows the variations of first- to sixth-order buckling thermal loads N with length, given the axial buckling waves \(m=1\) and the different circumferential buckling waves n. These figures indicate the thermal buckling loads decrease with the increase in the length of the cylindrical shell. This is due to the fact that the bending stiffness decreases and the FGM cylindrical shell is prone to instability with the increase in length. When the length is large, the change trend is slow, but when the length is small, the buckling loads change sharply. At the same time, the larger the length, the closer the buckling loads are. And for the same length, the larger the numbers of buckling waves, the higher the buckling thermal loads required.

Fig. 3
figure 3

The variation of the non-axisymmetric buckling thermal loads N with L (\(m=1\))

Full size image

Substituting the dimensionless buckling thermal loads into Eqs. (21) and (14), the axisymmetric and non-axisymmetric buckling modes can be obtained. Obviously, different buckling thermal loads correspond to different buckling modes. The first- to sixth-order buckling modes of the FGM cylindrical shell are demonstrated in Fig. 4a–c. As shown in these figures, the dynamic thermal loads excite more buckling wave numbers, and the number of waves and orders of the corresponding buckling modes increase with the increase in dimensionless eigenvalues. When comparing these buckling modes with ones of a homogeneous cylindrical shell shown by Xu et al. [18], it is found that they are almost the same. That is to say, the variations of the materials properties have no effect on the buckling mode shapes.

Fig. 4
figure 4

a The axisymmetric buckling modes (\(n=0\)). b The non-axisymmetric buckling modes (\(m=1\)). c The non-axisymmetric buckling modes (\(n=2\))

Full size image

5.2 Dynamic thermal buckling temperatures

In this section, the thermal shock buckling temperatures are presented and discussed. And the influence of the material gradient, parameters of structural geometry and thermal loadings on the critical buckling temperatures are also studied. In the following calculation, if not specified, the geometric sizes of the FGM cylindrical shells are \(h=0.01\) m, \(R=1\) m and \(l=4\) m. The thermal shock loads with an exponential function are adopted. The parameter of the load is specified as \(a=20\), the dynamic thermal loading time is \(\Delta t=5\) s and the heat exchange coefficient is \(h_\mathrm{r} =50\).

Table 4 The axisymmetric buckling temperatures \(\Delta T\) (unit: K) \((n=0)\)
Full size table
Table 5 The non-axisymmetric buckling temperatures \(\Delta T\) (unit: K) (\(m=1\))
Full size table
Table 6 The critical buckling temperatures \(\Delta T_\mathrm{{cr}}\) for some specified values of \(\lambda \)
Full size table

Tables 4 and 5 list the first- to sixth-order axisymmetric and non-axisymmetric buckling temperatures of the FGM cylindrical shells for different power law index k, separately. As shown in the tables, the buckling temperatures increase with the increasing circumferential buckling waves n and axial buckling waves m. The critical buckling temperatures, that is, the minimum buckling temperatures are those eigenvalues corresponding to the axisymmetric buckling modes, when \(n=0\) and \(m=1\). As we expect, in the situation of this study, the instability of the FGM cylindrical shell is axisymmetric, and it is due to the fact that the shell is subjected to uniformly distributed thermal shock load.

In the following, the dynamic critical buckling temperatures will be concerned mainly. The variation of the critical buckling temperature with the power law index k representing some specified values of the radius-thickness ratio \(\lambda \) is presented in Table 6 and Fig. 5. It shows that the amount of increase in the critical buckling temperature of the shells subjected to dynamic thermal loads drops significantly as the radius-thickness ratio increases. This is because the bending stiffness of the FGM shells decreases as radius-thickness radio increases. When \(k=0\), the FGM cylindrical shells reduce to homogeneous ceramics ones. When \(k\rightarrow \infty \), the FGM shells reduce to metal. According to Fig. 5 and Table 6, the critical buckling temperatures drop when k increases. It means, with the increase in k, the ability of the shell to withstand dynamic thermal loads is decreased. If \(k<2\), the magnitude of the dropping buckling temperature rise is larger. But if \(k>2\), the curve is levels off. This is because the constituents of the ceramics drop when k increases, the Young’s modulus and bending stiffness decrease.

Fig. 5
figure 5

The variations of the critical buckling temperatures with k for some specified values \(\lambda \)

Full size image

Table 7 shows the variations between the increases in the critical buckling temperature of the FGM cylindrical shells and the heat exchange coefficients \(h_\mathrm{r}\). As Table 7 shows, the amount of increase in critical buckling temperature changes only slightly with the increasing coefficients of heat transfer. That means, the heat transfer coefficients have insignificant influence on critical buckling temperatures.

Table 7 The critical buckling temperatures \(\Delta T_\mathrm{{cr}} \) for some specified values of \(h_\mathrm{r} \)
Full size table
Fig. 6
figure 6

The variations of the critical buckling temperatures with k for different a

Full size image
Table 8 The critical buckling temperatures \(\Delta T_\mathrm{{cr}}\) for different loading time \(\Delta t\) (\(n=0,\;m=1\))
Full size table

The variations in the critical buckling temperatures \(\Delta T_\mathrm{{cr}} \) are shown in Fig. 6 under given some specified values of a. As indicated that the \(\Delta T_\mathrm{{cr}} \) drop as the a increases. Furthermore, variations in parameter of the loads have only slight effect on the \(\Delta T_\mathrm{{cr}} \) with respect to \(a<5\); similarly, there is also almost no effect on \(\Delta T_\mathrm{{cr}} \) when \(a>5\).

Finally, Table 8 shows that the critical buckling temperatures vary with different loading times of thermal shock. According to Table 8, the critical temperatures decline with the increase in loading time. When \(\Delta t<5\) s, the critical temperatures drastically drop as the loading time is lengthened. But it hardly varies and tends to remain constant with the increase in time when \(\Delta t>5\) s. The reason is that the longer the process takes, the temperature distributions inside the shell are more uniform, and the influence on buckling critical temperature gradually disappears as the loading time is lengthened.

6 Conclusions

The dynamic thermal buckling of the ceramic–metal FGM cylindrical shell under the thermal shock is investigated. The Hamiltonian system and the symplectic method are introduced into this problem, which is reduced to the zero eigenvalue in Hamiltonian system. The canonical equations are established in the symplectic space firstly. By means of the characteristics and completeness of the Hamiltonian system, a complete buckling mode space is given. The relationships between the critical loads as well as the buckling modes and the symplectic eigenvalues and the eigen solutions are revealed. It shows that the dynamic thermal buckling of the FGM structures can be effectively investigated applying the symplectic method in Hamiltonian system. It is found that the gradient properties of the functionally graded materials have great effects on the critical buckling temperatures. The buckling temperatures of the metal/ceramic FGM shells decrease monotonously with the increasing of gradient parameter. The critical buckling temperature of the FGM structures can be changed by adjusting the volume fractions of the constituent materials. The ratio of the radius to the thickness and the time of the dynamic loading have great influences on the critical temperatures, but the coefficients of heat transfer and the load parameters have slight influences.