Keywords

1 Introduction

As composite materials, the properties of functionally graded materials (FGM) change continuously and smoothly in a specific direction [1, 2]. The analyses of the mechanical behaviors of FGM structures are more difficult than conventional homogeneous structures. Up to now, considerable research works on the buckling of the FGM structures have been published, but most of them are only limited to static problems. For example, thermal buckling and post-buckling for the FGM plates were investigated in [3,4,5]. Li et al. [6] and Zhang et al. [7] researched the buckling and post-buckling of FGM Timoshenko beams and imperfect FGM plates.

The research on dynamic buckling of the FGM structures is much fewer compared to it on static buckling. The works of [2, 8, 9] investigated the dynamic buckling of FGM thin cylindrical shells under axial compression, a longitudinal constant velocity or thermal load. Additionally, two-dimensional analysis of FGM partial annular disks subjected to radial thermal shock was presented by Mehrian and Naei [10]. All of the above research uses traditional methods, such as the finite element method, Galerkin method, etc. However, it is difficult to solve the complex partial differential equations of the dynamic buckling problems using these methods. In contrast, based on the symplecticity method in the Hamilton system [11], the equations of structural stability will be easily solved by variable separation approach and symplectic eigenfunction expansion. Xu et al. [12] studied the buckling and post-buckling behaviors of homogeneous cylindrical shells based on the symplecticity method. Sun et al. [13] studied the static buckling behaviors of FGM cylindrical shells combined thermal and compressive loads by the symplecticity method, too. They showed this method is very efficient and accurate in solving the problem of structural stability.

To the best of the authors’ knowledge, few researches study on impact buckling of FGM structures by the symplecticity method. Therefore, it is meaningful to exam the torsional impact buckling of FGM cylindrical shells in Hamilton system. In symplectic space, a canonical equation will be established, then buckling mode equations and bifurcation conditions will be solved by analytical methods. Finally, critical buckling loads and buckling modes will be obtained and discussed.

2 Mathematical Formulas

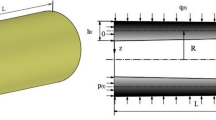
The thin-walled FGM cylindrical shell with length l, mid-surface radius R, and thickness h is considered, which is fixed at one end and subjected to a torsional impact load at the other end. A coordinate system (x, θ, z) is referred, in which the x-axis coincides with the generatrix of the middle surface, measured from the left end. θ is in the circumferential direction and z is in the transverse direction. The corresponding displacements in the mid-surface are designated as u, v , and w. No initial displacement or velocity exists at any point.

For the FGM cylindrical shell [14], the linear rule of mixtures is used to describe the variations in material properties P [15, 16]; and the power law function is used to describe the variation of volume fractions V 1 and V 2, expressed as

$$ P={P}_1{V}_1+{P}_2{V}_2,\kern1em {V}_1={\left(\frac{h-2z}{2h}\right)}^k,\kern1em {V}_2=1-{V}_1 $$
(1)

where k is the power law index used to quantify the inhomogeneous properties of FGM. Since Poisson’s ratio μ does not significantly vary in material gradient direction, so μ(z) is taken as a constant μ.

2.1 Fundamental Equations

Based on the classical thin shell theory, the strains \( {\varepsilon}_{x x}^{(z)},{\varepsilon}_{\theta \theta}^{(z)},{\varepsilon}_{x\theta}^{(z)} \) at any point are expressed as

$$ {\varepsilon}_{x x}^{(z)}={\varepsilon}_{x x}+z{\kappa}_{x x},\kern1em {\varepsilon}_{\theta \theta}^{(z)}={\varepsilon}_{\theta \theta}+z{\kappa}_{\theta \theta},\kern1em {\varepsilon}_{x\theta}^{(z)}={\varepsilon}_{x\theta}+z{\kappa}_{x\theta} $$
(2)

where strains ε xx, ε θθ, ε xθ and curvatures κ xx, κ θθ, κ xθ on the middle surface are

$$ {\varepsilon}_{x x}{=}\frac{\partial u}{\partial x},\kern0.3em {\varepsilon}_{\theta \theta}{=}\frac{1}{R}\frac{\partial v}{\partial \theta }{-}\frac{w}{R},\kern0.3em {\varepsilon}_{x\theta}{=}\frac{1}{R}\frac{\partial u}{\partial \theta }{+}\frac{\partial v}{\partial x},\kern0.5em {\kappa}_{x x}{=}-\frac{\partial^2w}{\partial {x}^2},\kern1em {\kappa}_{\theta \theta}=-\frac{1}{R^2}\frac{\partial^2w}{\partial {\theta}^2},\kern0.5em\\ {} {\kappa}_{x\theta}=-\frac{1}{R}\frac{\partial^2w}{\partial x\partial \theta }\hspace*{18.5pc} $$
(3)

Considering linear elastic deformations, the constitutive equations are expressed as:

$$ {\sigma}_{x x}{=}\frac{E}{1{-}{\mu}^2}{\varepsilon}_{x x}^{(z)}{+}\frac{\mu E}{1{-}{\mu}^2}{\varepsilon}_{\theta \theta}^{(z)},\kern0.3em {\sigma}_{\theta \theta}{=}\frac{\mu E}{1{-}{\mu}^2}{\varepsilon}_{x x}^{(z)}{+}\frac{E}{1{-}{\mu}^2}{\varepsilon}_{\theta \theta}^{(z)},\kern0.3em {\sigma}_{x\theta}{=}\frac{E}{2\left(1{+}\mu \right)}{\varepsilon}_{x\theta}^{(z)} $$
(4)

where σ xx and σ θθ are normal stresses, σ xθ is shear stress.

2.2 Canonical Equations

Taking the geometric equations into account, the density of strain energy \( \overline{U} \) of the shell is expressed as

$$ {\displaystyle \begin{array}{l}\overline{U}=\frac{A}{2}{\left(\frac{\partial u}{\partial x}+\frac{1}{R}\frac{\partial v}{\partial \theta }-\frac{w}{R}\right)}^2-\left(1-\mu \right)\left[A\frac{\partial u}{\partial x}\left(\frac{1}{R}\frac{\partial v}{\partial \theta }-\frac{w}{R}\right)+C\frac{\partial^2w}{\partial {x}^2}\frac{1}{R^2}\frac{\partial^2w}{\partial {\theta}^2}\right]\\ {}\kern1.25em +\frac{C}{2}{\left(\frac{\partial^2w}{\partial {x}^2}+\frac{1}{R^2}\frac{\partial^2w}{\partial {\theta}^2}\right)}^2-B\frac{\partial u}{\partial x}\frac{\partial^2w}{\partial {x}^2}-\frac{B}{R^2}\left(\frac{1}{R}\frac{\partial v}{\partial \theta }-\frac{w}{R}\right)\frac{\partial^2w}{\partial {\theta}^2}-\mu B\frac{\partial u}{\partial x}\frac{1}{R^2}\frac{\partial^2w}{\partial {\theta}^2}\\ {}\kern1.25em -\mu B\left(\frac{1}{R}\frac{\partial v}{\partial \theta }-\frac{w}{R}\right)\frac{\partial^2w}{\partial {x}^2}-2\left(1-\mu \right)\left[\frac{B}{R}\left(\frac{1}{R}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial x}\right)-C{\left(\frac{1}{R}\frac{\partial^2w}{\partial x\partial \theta}\right)}^2\right]\end{array}} $$

in which \( A={\int}_{\!-h/2}^{h/2}\frac{E}{1-{\mu}^2}\mathrm{d}z \), \( B={\int}_{\!-h/2}^{h/2}\frac{Ez}{1-{\mu}^2}\mathrm{d}z \), and \( C={\int}_{\!-h/2}^{h/2}\frac{Ez^2}{1-{\mu}^2}\mathrm{d}z \) are stiffness coefficients. Assuming the shells under torsional impact loading, it is expressed as

$$ {N}_T=\left\{\begin{array}{c}T\kern1.75em 0\le x\le {C}_{\mathrm{e}}t,t\le L/{C}_{\mathrm{e}}\\ {}0\kern1.75em {C}_{\mathrm{e}}t\le x\le L,t\le L/{C}_{\mathrm{e}}\end{array}\right. $$
(5)

where \( {C}_{\mathrm{e}}\approx \sqrt{\frac{\left(1-\mu \right)A}{2{I}_0}} \) is wave velocity; \( {I}_0={\int}_{\!-h/2}^{h/2}\rho (z)\mathrm{d}z \) is mass per unit area; x e = C et is elastic transverse wavefront position. Then the density of Lagrange function can be expressed as

$$ L=\frac{1}{2}{I}_0{\left(\frac{\partial u}{\partial t}\right)}^2+\frac{1}{2}{I}_0{\left(\frac{\partial v}{\partial t}\right)}^2+\frac{1}{2}{I}_0{\left(\frac{\partial w}{\partial t}\right)}^2-\overline{U}-{N}_T\frac{\partial w}{\partial x}\frac{\partial w}{\partial \theta }-{N}_T\frac{\partial v}{\partial x}w $$
(6)

The torsional wave equation can be obtained by variation with respected to v

$$ \frac{\partial^2v}{\partial {t}^2}-{C}_{\mathrm{e}}^2\frac{\partial^2v}{\partial {x}^2}=0 $$
(7)

Define dimensionless variables \( X=\frac{x}{R} \), \( W=\frac{w}{R} \), \( \alpha =\frac{AR^2}{C} \), \( \beta =\frac{BR}{C} \), \( T=\frac{C_{\mathrm{e}}t}{R} \), \( {T}_{\mathrm{cr}}=\frac{N_T{R}^2}{C} \). Introduce the original variables \( \mathbf{q}=\left\{\begin{array}{c}{q}_1\\ {}{q}_2\end{array}\right\}=\left\{\begin{array}{c}W\\ {}\psi \end{array}\right\} \) and the dual variables \( \mathbf{p}=\left\{\begin{array}{c}{p}_1\\ {}{p}_2\end{array}\right\}=\frac{\partial L}{\partial \dot{\mathbf{q}}}=\left\{\begin{array}{c}-{\overset{\dddot{}}{q}}_1-{{\dot{q}}_1}^{\prime \prime}\\ {}{q_1}^{\prime \prime }-{\dot{q}}_2+\beta {q}_1\end{array}\right\} \), where \( \dot{\mathbf{q}}=\frac{1}{R}\frac{\partial \dot{\mathbf{q}}}{\partial \theta } \), \( \psi =-{\dot{q}}_1 \), \( {\mathbf{q}}^{\prime }=\frac{\partial \mathbf{q}}{\partial X} \).

The canonical equation can be obtained by the Hamiltonian variational principle

$$ \left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\dot{q}}_1\\ {}{\dot{q}}_2\end{array}\\ {}{\dot{p}}_1\end{array}\\ {}{\dot{p}}_2\end{array}\right\}=\left[\begin{array}{cccc}0& -1& 0& 0\\ {}-{\partial}_x^2-\beta & 0& 0& 1\\ {}-2{\partial}_x^4-\left[2\left(1+\mu \right)\beta \right]{\partial}_x^2-{\beta}^2-\alpha &\quad -{T}_{\mathrm{cr}}{\partial}_x& 0& {\partial}_x^2+\beta \\ {}-{T}_{\mathrm{cr}}{\partial}_x& 0& 1& 0\end{array}\right]\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{q}_1\\ {}{q}_2\end{array}\\ {}{p}_1\end{array}\\ {}{p}_2\end{array}\right\} $$
(8)

Introducing a state vector \( \dot{\boldsymbol{\upvarphi}}={\left\{{q}_1,{q}_2,{p}_1,{p}_2\right\}}^{\mathrm{T}} \), then the canonical equation becomes

$$ \dot{\boldsymbol{\upvarphi}}=\mathbf{H}\boldsymbol{\upvarphi } $$
(9)

The solution of Eq. (9) is written as the following variable separation form

$$ \boldsymbol{\upvarphi} \left(X,\theta \right)={\boldsymbol{\upvarphi}}_n(X){\mathrm{e}}^{\lambda_n\theta } $$
(10)

where λ n is the eigenvalue of the function; φ n is the eigenvector, and they satisfy the following eigenequation

$$ \mathbf{H}\boldsymbol{\upvarphi } ={\lambda}_n\boldsymbol{\upvarphi} $$
(11)

For the FGM cylindrical shell, the eigenvalue can be obtained from the sealing condition \( \boldsymbol{\upvarphi} \left(X,0\right)={\boldsymbol{\upvarphi}}_n(X)=\boldsymbol{\upvarphi} \left(X,2\pi \right)={\boldsymbol{\upvarphi}}_n(X){\mathrm{e}}^{2{\lambda}_n\pi } \), expressed as

$$ {\lambda}_n= in $$
(12)

where \( i=\sqrt{-1} \), the values of n are 0, ±1, ±2…. For λ n ≠ 0, the eigensolutions φ n(X) are nonzero. Solving Eq. (11) gives the eigenvector φ

$$ {\boldsymbol{\upvarphi}}_n={c}_1\left[\begin{array}{c}{\mathrm{e}}^{\lambda_1X}\\ {}- in{\mathrm{e}}^{\lambda_1X}\\ {} in\xi {\mathrm{e}}^{\lambda_1X}\\ {}{\xi}_1{\mathrm{e}}^{\lambda_1X}\end{array}\right]+{c}_2\left[\begin{array}{c}{\mathrm{e}}^{\lambda_2X}\\ {}- in{\mathrm{e}}^{\lambda_2X}\\ {} in\xi {\mathrm{e}}^{\lambda_2X}\\ {}{\xi}_2{\mathrm{e}}^{\lambda_2X}\end{array}\right]+{c}_3\left[\begin{array}{c}{\mathrm{e}}^{\lambda_3X}\\ {}- in{\mathrm{e}}^{\lambda_3X}\\ {} in\xi {\mathrm{e}}^{\lambda_3X}\\ {}{\xi}_3{\mathrm{e}}^{\lambda_3X}\end{array}\right]+{c}_4\left[\begin{array}{c}{\mathrm{e}}^{\lambda_4X}\\ {}- in{\mathrm{e}}^{\lambda_4X}\\ {} in\xi {\mathrm{e}}^{\lambda_4X}\\ {}{\xi}_4{\mathrm{e}}^{\lambda_4X}\end{array}\right]\vspace*{-3pt} $$
(13)

where c 1~c 4 are constants; ξ j = λ j 2 + β + n 2; λ j (j = 1–4) are solutions of equation

$$ {\lambda}^4+2\left(\beta \mu +{i}^2{n}^2\right){\lambda}^2+2 Tin\lambda +\alpha -{i}^4{n}^4=0\vspace*{-3pt} $$
(14)

2.3 Bifurcation Conditions

Since the shell is considered to be fixed at one end, there are no displacement and rotation, i.e., w = 0, \( \frac{\partial w}{\partial \theta }=0 \). By introducing the boundary conditions and continuity conditions into Eq. (10), homogeneous algebraic equations are obtained. The condition for buckling is the equations have nonzero solutions, and the determinant of coefficient equals to zero

$$ \left|\begin{array}{cccc}1& 1& 1& 1\\ {}{\lambda}_1& {\lambda}_2& {\lambda}_3& {\lambda}_4\\ {}{\mathrm{e}}^{\lambda_1{X}_{\mathrm{e}}}& {\mathrm{e}}^{\lambda_2{X}_{\mathrm{e}}}& {\mathrm{e}}^{\lambda_3{X}_{\mathrm{e}}}& {\mathrm{e}}^{\lambda_4{X}_{\mathrm{e}}}\\ {}\lambda {\mathrm{e}}^{\lambda_1{X}_{\mathrm{e}}}& \lambda {\mathrm{e}}^{\lambda_2{X}_{\mathrm{e}}}& \lambda {\mathrm{e}}^{\lambda_3{X}_{\mathrm{e}}}& \lambda {\mathrm{e}}^{\lambda_4{X}_{\mathrm{e}}}\end{array}\right|=0 $$
(15)

Using the above bifurcation conditions Eq. (15), the torsional buckling loads T cr for FGM shell buckling can be determined. After obtaining the buckling loads, the corresponding buckling modes can be solved by Eq. (13).

3 Numerical Results and Discussions

In this chapter, FGM cylindrical shells are made from ceramic SiC and metal Ni. The material properties of the constituents can be found in [17]. The Poisson’s ratio is μ = 0.3.

The torsional shock buckling modes of the shells with different wavefronts are shown in Figs. 1 and 2. It can be seen that the buckling modes are different for the wavefronts, the more the axial wavenumberm is, the larger the wavefront is. At the same time, they are all local buckling that occurs in areas disturbed by stress waves. Comparing with the torsional buckling modes of homogeneous cylindrical shell in [18], it is found that the buckling modes of the homogeneous FGM cylindrical shells are identical, that is, the material changes do not affect the mode pattern.

Fig. 1
figure 1

Buckling modes of the shells with different circumferential order (m = 1)

Full size image
Fig. 2
figure 2

Buckling modes of the shell with different circumferential order (m = 2)

Full size image

Let k = 0, FGM reduce to homogeneous material. Table 1 shows comparisons between the torsional buckling loads of the homogeneous cylindrical shell calculated in this chapter and the corresponding results in [18]. It can be found the present results are very close to the corresponding results in the literature, indicating that the theoretical derivation and numerical calculation are correct and reliable. Since the critical loads are obtained by numerically solving bifurcation conditions through the Newton iterative method, some differences arise.

Table 1 Variation of torsional critical loads with circumferential order
Full size table

If not specified, the geometries of the cylindrical shells are chosen to be h = 0.05 m, R = 1 m in the subsequent calculation. Table 2 gives the first sixth-order buckling loads for different wavefronts. It can be seen from the table that as the axial mode order increases, the buckling loads increase. And the longer the wavefront is selected, the smaller the buckling load is.

Table 2 First sixth-order buckling loads for different wavefronts (n = 1)
Full size table

Table 3 lists the first sixth-order critical loads of FGM shells with different k when the circumferential wave is n = 4 and wavefront is T = 4. Figures 3 and 4 further show the variations of the first sixth-order circumferential and the first eighth-order radial buckling loads with the wavefront. It can be seen that the torsional buckling loads decrease as the order of the buckling modes increase. Additionally, the buckling loads drop when the power law index k increases, i.e., the ability of the shells to withstand dynamic torsional loads decreases. This is due to the fact that the constituents of the ceramics decrease with the increasing k. And the longer the wavefront of the action is selected, the smaller buckling loads are.

Table 3 Buckling loads of FGM cylindrical shells with different axial waves (unit: N)
Full size table
Fig. 3
figure 3

Variations of the first sixth-order circumferential buckling loads with the wavefront (m = 1)

Full size image
Fig. 4
figure 4

Variations of the first eighth-order axial buckling loads with the wavefront (n = 3)

Full size image

Finally, the variations of critical buckling loads are presented in Table 4 with the changes of k and some specified ratios γ representing ratios of radius to thickness. When the wavefront is T = 4, the circumferential and axial orders are n = 4 and m = 1, respectively. It shows that the critical buckling loads generally decrease as the ratios of radius to thickness γ increase. This is because that the bending stiffness decreases as γ increases.

Table 4 The critical buckling loads for FGM shells with some specified ratio γ (unit: N)
Full size table

4 Conclusions

In this chapter, the torsional impact buckling of the ceramic-metal FGM cylindrical shell is investigated in Hamilton system by symplectic method. The canonical equations are established, and a complete buckling mode space is given. The relationship between the critical loads and the eigenvalues has been revealed, so has it between the buckling modes and eigensolutions. It is found that the gradient properties of FGM have significant effect on the buckling loads. The buckling loads of the metal/ceramic FGM shells are intermediate to those of metal and ceramic shells, and decrease monotonously with the increasing of power law index, furthermore, the ratio of radius to thickness also have great influences on the critical buckling loads.