Dynamic thermal buckling and postbuckling of clamped–clamped imperfect functionally graded annular plates

Abstract

Dynamic thermal buckling and postbuckling of imperfect functionally graded material (FGM) annular plates are investigated based on the nonlinear plate theory. The transient temperature fields of the FGM annular plates under dynamic thermal loadings are obtained by Laplace transform in combination of power series method according to the theory of Fourier heat conduction. The nonlinear dynamic equations of large axisymmetric deformations are numerically solved by series expansions and Runge–Kutta method. The critical bucking and dynamic postbuckling responses are predicted by the maximum deflections of the FGM annular plates with positive or negative initial geometric imperfections. The effects of the loads, the material gradient and the initial geometric imperfections on the dynamic responses and the buckling critical temperatures of the FGM annular plates are analyzed in detail.

1 Introduction

Functionally graded materials (FGM) are new composite materials whose properties vary continuously and smoothly in a specific direction [1, 2]. FGM structures can effectively diminish thermal stresses so that they are applied in the high temperature environments. Since the material properties of FGM are non-uniform, the analyses on thermal characteristics of the FGM structures are much more difficult than traditional homogeneous structures [3,4,5].

Dynamic buckling is an important failure phenomenon of engineering structures. About the research on dynamic buckling of the functionally graded structures, most of works just limited to the structures subjected to mechanical loads. Such as Huang and Han [6], Bich et al. [7] examined the nonlinear buckling of the FGM cylindrical shells subjected to axial compression. Considering the mercurial damping effect and longitudinal constant velocity, the dynamic buckling of the FGM cylindrical shells was presented by Gao et al. [8]. Zhang and Li [9] examined the characteristics of impact stability of the FGM truncated conical shells with the initial geometric imperfection, and so on.

Engineering structures are frequently subjected to dynamic thermal loads, such as aerodynamic heating and laser heating. The rapid temperature variation results in the occurrence of transient thermal stresses, even instability, which lead to loss of the carrying capacity of the structures. There have been some research results on the dynamic thermal buckling of structures. However, most of them are aimed at homogeneous or traditional composite structures [10,11,12,13,14,15]. For the thermal barrier functionally graded material structures, they are often subjected to dynamic thermal loads which lead to the occurrence of instability. However, the studies on the dynamic thermal buckling of the FGM structures are many fewer compared to those on the static buckling. The thermal conduction and the deformation equations of structures subjected to dynamic thermal loadings are variable coefficient partial differential equations because of the inhomogeneity of FGM. The time variable and inertia items are contained in these equations, which greatly brings the difficulty for solving. Using the finite element method, Shariyat [16, 17] addressed the nonlinear dynamic buckling of FGM geometrical imperfect cylindrical shells under thermal shock and thermo-electro-mechanical loads. Taking into consideration of the temperature dependence, Mirzavand et al. [18] conducted a study on the thermal shock postbuckling of piezoelectric cylindrical shells. Mirzavand et al. [19] also presented research on the dynamic postbuckling paths and buckling temperatures of FGM cylindrical shells. In addition, based on the L–S theory, a two-dimensional thermal shock analysis of FGM partial annular disks was presented by Mehrian and Naei [20]. However, inertial terms have been neglected in some of above studies, which leads to the quasi-static problem.

Annular plates are frequently used in structures and device systems and often undergo dynamic thermal loads. As far as the authors know, few research results have been reported on the dynamic thermal buckling and postbuckling of FGM annular plate. Therefore, this study considering the initial geometrical imperfections of the annular plate, dynamic thermal buckling and postbuckling of the FGM annular plate with bottom surface subjected to uniform thermal shock loading are studied. The critical buckling temperatures are calculated using linear perturbation method [15]. The influences of the initial geometric imperfections of the plate and the non-homogeneous parameters of the materials on the buckling and postbuckling are analyzed and discussed.

2 Problem formulations

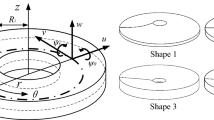
An FGM annular plate with inner radius $R_1$, outer radius R and thickness h is considered, made of ceramic and metal in accordance with varying volume fractions. The upper surface is the metal, while the bottom surface is the ceramic, as schematically shown in Fig. 1. The material properties P(z) of this structure (Young’s modulus E, density $\rho$, specific heat capacity C, coefficient of thermal expansion $\alpha$ and coefficient of thermal conductivity K) are supposed to continuously change from ceramic to metal in thickness direction. Their expressions are the same as in Ref. [21]. The volume fractions are given in form of a power function as $V_{{c}} (z)=\left( {\frac{h-2z}{2h}} \right) ^{n},\;V_m (z)=1-V_{{c}} (z)$, which can also be found in Ref. [21]. And the power law index n represents the inhomogeneous properties of FGM. Usually, Poisson’s ratio $\nu$ varies little with the material constituents hence it is supposed to be constant, i.e., $\nu (z)=\nu$ [21]. The cylindrical coordinates r and $\theta$ on the middle plane are established. Thickness coordinate is z, positive upward. The buckling and postbuckling of the FGM annular plate with the bottom surface subjected to dynamic thermal loads and the upper one exchanging heat with the environment are examined.

Fig. 1

Functionally graded material annular plate

2.1 Fundamental equations

We consider the thin FGM annular plates with initial geometric imperfection and undergoing the axisymmetric deformation. Based on von Kármán nonlinear plate theory, the normal strains can be expressed as [22]:

$$\begin{aligned} \left\{ {\varepsilon _r,\varepsilon _\theta } \right\} ^{\mathrm{T}}=\left\{ {\varepsilon _r^0,\varepsilon _\theta ^0 } \right\} ^{\mathrm{T}}+z\left\{ {\kappa _r,\kappa _\theta } \right\} ^{\mathrm{T}} \end{aligned}$$

where $\varepsilon _r$ and $\varepsilon _\theta$ are the normal strains in r and $\theta$ directions at an arbitrary point (r, $\theta$, z), respectively: $\varepsilon _r^0$ and $\varepsilon _\theta ^0$ are the normal strains in the middle plane: $\kappa _r$ and $\kappa _\theta$ are the curvatures. Their expressions are as follows:

$$\begin{aligned} \left\{ {\varepsilon _r^0,\varepsilon _\theta ^0 } \right\} ^{\mathrm{T}}= & {} \left\{ {\frac{\partial u}{\partial r}+\frac{\partial w}{\partial r}\frac{\partial w_0 }{\partial r}+\frac{1}{2}\left( {\frac{\partial w}{\partial r}} \right) ^{2},\frac{u}{r}} \right\} ^{\mathrm{T}}\nonumber \\ \left\{ {\kappa _r,\kappa _\theta } \right\} ^{\mathrm{T}}= & {} \left\{ {-\frac{\partial ^{2}w}{\partial r^{2}},-\frac{1}{r}\frac{\partial w}{\partial r}} \right\} ^{\mathrm{T}} \end{aligned}$$

(1)

where u(r, t), w(r, t) and $w_0 (r)$ are the displacement in r direction, the deflection and the initial geometric imperfection in the middle plane, respectively. t is time and its unit is expressed in seconds.

Considering the deformations of the FGM annular plate are linearly thermo-elastic, the radial normal stress $\sigma _r$ and the circumferential normal stress $\sigma _\theta$ are expressed as [22]

where $T\left( {z,t} \right)$ is increased temperature compared to reference ambient temperature $T_0$. The membrane force $N_r ,N_\theta$ and bending moment $M_r,M_\theta$ can be obtained by integrating along the thickness of the FGM annular plate. Their expressions are:

$$\begin{aligned} \left\{ {{\begin{array}{l} {N_r } \\ {N_\theta } \\ {M_r } \\ {M_\theta } \\ \end{array} }} \right\}= & {} \int _{\mathrm{-}h/2}^{h/2} {\left\{ {{\begin{array}{l} {\sigma _r } \\ {\sigma _\theta } \\ {z\sigma _r } \\ {z\sigma _\theta } \\ \end{array} }} \right\} } \hbox {d}z\nonumber \\= & {} \left[ {{\begin{array}{llll} A&{}\quad {\nu A}&{}\quad B&{}\quad {\nu B} \\ {\nu A}&{}\quad A&{}\quad {\nu B}&{}\quad B \\ B&{}\quad {\nu B}&{}\quad D&{}\quad {\nu D} \\ {\nu B}&{}\quad B&{}\quad {\nu D}&{}\quad D \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\varepsilon _r^0 } \\ {\varepsilon _\theta ^0 } \\ {\kappa _r } \\ {\kappa _\theta } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {N^{\mathrm{T}}} \\ {N^{\mathrm{T}}} \\ {M^{\mathrm{T}}} \\ {M^{\mathrm{T}}} \\ \end{array} }} \right\} \end{aligned}$$

where A, B and D are the stiffness coefficients; $N^{\mathrm{T}}$ and $M^{\mathrm{T}}$ are the thermal membrane force and the thermal bending moment, which vary with the temperature change of the FGM annular plate. They are defined as

$$\begin{aligned} \left( {A,B,D} \right) ^{\mathrm{T}}= & {} \frac{1}{1-\nu ^{2}}\int _{{-h}/2}^{h/2} {E\left( z \right) \left( {1,z,z^{2}} \right) } ^{\mathrm{T}}\hbox {d}z\nonumber \\ \left( {N^{\mathrm{T}},M^{\mathrm{T}}} \right) ^{\mathrm{T}}= & {} \frac{1}{1-\nu }\int _{{-h}/2}^{h/2} {E\left( z \right) \alpha \left( z \right) T\left( {z,t} \right) \left( {1,z} \right) ^{\mathrm{T}}\hbox {d}z}.\nonumber \\ \end{aligned}$$

(3)

The nonlinear motion equations for the axisymmetrically deformed FGM annular plates are [22]:

$$\begin{aligned}&\frac{\partial \left( {rN_r } \right) }{\partial r}-N_\theta =0 \end{aligned}$$

(4a)

$$\begin{aligned}&\frac{\partial ^{2}\left( {rM_r } \right) }{\partial r^{2}}-\frac{\partial M_\theta }{\partial r}+\frac{\partial }{\partial r}\left[ {rN_r \left( {\frac{\partial w}{\partial r}+\frac{\partial w_0 }{\partial r}} \right) } \right] \nonumber \\&\quad -\,I_0 r\frac{\partial ^{2}w}{\partial t^{2}}=0 \end{aligned}$$

(4b)

where $I_0 =\int _{-h/2}^{h/2} {\rho (z)\hbox {d}z}$ is the mass per unit area.

2.2 Dynamic governing equations

Substituting the membrane force $N_r,N_\theta$ and bending moment $M_r,M_\theta$ into Eqs. (4a,b) and taking into account Eq. (1), the dynamic governing equations regarding the mid-plane displacements can be obtained. In order to facilitate analysis and calculation, the following dimensionless quantities are introduced:

$$\begin{aligned} x= & {} \frac{r}{R}, \left( {W,W_0 } \right) ^{\mathrm{T}}=\frac{\hbox {1}}{h}\left( {w,w_0 } \right) ^{\mathrm{T}}, \\ \tau= & {} t\sqrt{\frac{E_\mathrm{m} }{\rho _\mathrm{m} h^{2}}}, U=\frac{uR}{h^{2}}, D_0 =\frac{I_0 }{h\rho _\mathrm{m} }, \\ D_1= & {} \frac{A}{hE_\mathrm{m} }, D_2 =\frac{B}{h^{2}E_\mathrm{m} }, D_3 =\frac{D}{h^{3}E_\mathrm{m} },\\ D_4= & {} \frac{h}{R}, N_\mathrm{T} =\frac{N^{\mathrm{T}}R^{2}}{E_\mathrm{m} h^{3}}. \end{aligned}$$

in which $E_\mathrm{m}$ and $\rho _\mathrm{m}$ are the Young’s modulus and the mass density of metal, respectively. Thus, the dimensionless dynamic governing equations can be obtained as follows

$$\begin{aligned} \frac{\partial }{\partial x}\left[ {\frac{1}{x}\frac{\partial }{\partial x}\left( {xU} \right) } \right]= & {} \frac{D_2 }{D_1 }F_1 +F_2 \end{aligned}$$

(5a)

$$\begin{aligned} D_3 \nabla ^{4}W= & {} -N_\mathrm{T} F_3 +D_2 \left( {F_4 +F_5 } \right) \nonumber \\&+\,D_1 \left( {F_6 +F_7 } \right) -\frac{D_0 }{D_4 ^{4}}\frac{\partial ^{2}W}{\partial \tau ^{2}}\nonumber \\ \end{aligned}$$

(5b)

where differential operators is $\nabla ^{4}=\frac{\partial ^{4}}{\partial x^{4}}+\frac{2}{x}\frac{\partial ^{3}}{\partial x^{3}}-\frac{1}{x^{2}}\frac{\partial ^{2}}{\partial x^{2}}+\frac{1}{x^{3}}\frac{\partial }{\partial x}$; $F_1\sim F_7$ are partial differential expressions of U and W, which are listed in “Appendix.”

In this study, fixed outer and inner edges are taken into account and their boundary conditions can be expressed by

$$\begin{aligned}&x=x_1, \quad U=W=\frac{\partial W}{\partial x}=0 \end{aligned}$$

(6a)

$$\begin{aligned}&x=1, \quad U=W=\frac{\partial W}{\partial x}=0 \end{aligned}$$

(6b)

where $x_1 =\frac{R_1 }{R}$. The initial state of the annular plate is static. Then the initial conditions can be expressed by

$$\begin{aligned} \tau =0, U(x,0)=W(x,0)=\frac{\partial U}{\partial \tau }=\frac{\partial W}{\partial \tau }=0 \end{aligned}$$

(6c)

Equations (5a,b) and (6a–c) are the non-dimensional governing equations for the dynamic thermal buckling and postbuckling problem of the FGM annular plates, the boundary conditions of the fixed inner and outer edges and the initial conditions, respectively. In the aforementioned equations, the dimensionless thermal membrane forces $N_\mathrm{T}$ which depends on the temperature field in the FGM annular plate is included. Hence, in order to solve the governing equations, the solutions of the temperature field need to be obtained first.

2.3 Transient temperature field

Suppose that the FGM annular plate is subjected to uniform rapid heating loads on the bottom surface. The upper surface exchanges heat with the external environment. Consequently, the thermal conduction can be reduced to one-dimensional problem in the inhomogeneous material. Applying Fourier thermoelasticity theory, the heat conduction equation can be written as

$$\begin{aligned}&C(z)\rho (z)\frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left[ {K(z)\frac{\partial T}{\partial z}} \right] , \nonumber \\&\quad \left( {t>0,-\frac{h}{2}<z<\frac{h}{2}} \right) . \end{aligned}$$

(7)

The dynamic heating load is taken as $\bar{{T}}=\Delta T(1-e^{-at})$, where $\Delta T$, a are the parameters of the load variation, respectively. The heating initial conditions, the boundary conditions are specified as

$$\begin{aligned}&T(z,0)=0, \quad T\left( {-\frac{h}{2},t} \right) =\Delta T(1-e^{-at}), \nonumber \\&\left. {-\,K(z)\frac{\partial T}{\partial z}} \right| _{z=h/2} =h_r T\left( {\frac{h}{2},t} \right) \end{aligned}$$

(8)

where $h_r$ indicates the heat exchange coefficient between the upper surface of plate and the surrounding environment. Herein, Eqs. (7, 8) are solved through the Laplace transformation technique in combination with the power series method for obtaining the transient temperature field in the FGM annular plate which contains the thermal load amplitude parameter $\Delta T$. The detailed solution process can be found in Ref. [21]. And then, the thermal membrane force $N_\mathrm{T}$ with undetermined parameter $\Delta T$ can be obtained by integrating Eq. (3) in the thickness direction.

3 Solutions to governing equations

The axisymmetric deflections and the initial geometrical imperfection of the functionally graded annular plate can be expanded into power series as follows:

$$\begin{aligned}&W=\frac{\delta }{\lambda }\left( {1+\sum _{i=2,4}^\infty {A_i x^{i}} } \right) \nonumber \\&\approx \frac{\delta }{\lambda }\left( {1+A_2 x^{2}+A_4 x^{4}+A_6 x^{6}+A_8 x^{8}} \right) \end{aligned}$$

(9a)

$$\begin{aligned}&W_0 \left( x \right) =\frac{\delta _0 }{\lambda }\left( {1+\sum _{i=2,4}^\infty {A_i x^{i}} } \right) \nonumber \\&\approx \frac{\delta _0 }{\lambda }\left( {1+A_2 x^{2}+A_4 x^{4}+A_6 x^{6}+A_8 x^{8}} \right) \nonumber \\ \end{aligned}$$

(9b)

in which

$$\begin{aligned} \lambda =1+A_2 x_2 ^{2}+A_4 x_2 ^{4}+A_6 x_2 ^{6}+A_8 x_2 ^{8} \end{aligned}$$

(9c)

where $x_2$ is the dimensionless length from the center of the annular plate to the point of maximum deflection which can be considered at the midpoint of the inner radius to the outer radius approximately, i.e., $x_2 =\frac{R+R_1 }{2}$. $\delta$ and $\delta _0$ are deflection and initial displacement at point $x_2$. $A_2\sim A_8$ are constant determined by boundary conditions, which can be calculated for the fixed inner and outer boundary conditions (Eqs. (6a, b)) as:

$$\begin{aligned} A_2= & {} -\frac{2\left( {x_1 ^{2}+1} \right) }{x_1 ^{2}}, \quad A_4 =\frac{x_1 ^{4}+4x_1 ^{2}+1}{x_1 ^{4}}, \\ A_6= & {} -\frac{2\left( {x_1 ^{2}+1} \right) }{x_1 ^{4}}, \quad A_8 =\frac{1}{x_1 ^{4}}. \end{aligned}$$

Substituting Eqs. (9a, b) into the right sides of Eqs. (5a, b) obtains:

$$\begin{aligned}&\frac{\partial }{\partial x}\left[ {\frac{1}{x}\frac{\partial }{\partial x}\left( {xU} \right) } \right] =-\eta _1 \delta ^{2}+\eta _2 \delta \end{aligned}$$

(10a)

$$\begin{aligned}&D_3 \nabla ^{4}W=\lambda _1 \delta ^{3}+\lambda _2 \delta ^{2}+\lambda _3 \delta +\lambda _4 \ddot{\delta }+\lambda _5 \end{aligned}$$

(10b)

where $\ddot{\delta }$ indicate second derivative of $\delta$ with respect to time; $\eta _1$, $\eta _2$, $\lambda _1\sim \lambda _5$ are polynomials with unknown U and variable x. The detailed forms are shown in “Appendix.”

The solution to Eq. (10a) is obtained by using integral method as

$$\begin{aligned} U=\eta _1 ^{\prime }\delta ^{2}+\eta _2 ^{\prime }\delta +C_1 x+\frac{C_2 }{x} \end{aligned}$$

(11)

in which $\eta _1 ^{\prime }$ and $\eta _2 ^{\prime }$ are the polynomials of $\eta _1$ and $\eta _2$ after being integrated with respect to x; the detailed forms are shown in “Appendix.” $C_1$ and $C_2$ are the integral constants which can be calculated by the boundary condition $U=0$ at point $x=x_{1}$ and $x=1$, obtained as

$$\begin{aligned} C_1 =\eta _1 ^{\prime \prime }\delta ^{2}+\eta _2 ^{\prime \prime }\delta , \quad C_2 =\eta _3 ^{\prime \prime }\delta ^{2}+\eta _4 ^{\prime \prime }\delta \nonumber \\ \end{aligned}$$

The expressions of $\eta _1 ^{\prime \prime }$, $\eta _2 ^{\prime \prime }$, $\eta _3 ^{\prime \prime }$ and $\eta _4 ^{\prime \prime }$ are shown in “Appendix.” Substituting Eq. (11) into Eq. (10b) and integrating, we can obtain an ordinary differential equation as

$$\begin{aligned} D_3 D_4 W= & {} \lambda _1 ^{\prime }\delta ^{3}+\lambda _2 ^{\prime }\delta ^{2}+\lambda _3 ^{\prime }\delta +\lambda _4 ^{\prime }\ddot{\delta }+\lambda _5 ^{\prime }\nonumber \\&+\,\frac{C_3 x^{2}\left( {\ln x-1} \right) }{4}+\frac{C_4 x^{2}}{4}+C_5 \ln x+C_6\nonumber \\ \end{aligned}$$

(12)

in which $\lambda _1 ^{\prime }\sim \lambda _5 ^{\prime }$ are the polynomials of integrated $\lambda _1 \sim \lambda _5$ with respect to x. $C_3\sim C_6$ are unknown integral constants, which can be calculated by boundary conditions (6a,b). Substituting Eqs. (9a–c), $C_3 \sim C_6$ and $x=x_2$ into Eq. (12) obtains

$$\begin{aligned} f_1 \ddot{\delta }+f_2 \delta ^{3}+f_3 \delta ^{2}+f_4 \delta +f_5 =0 \end{aligned}$$

(13)

where $f_1\sim f_5$ are polynomials of $x_1$ and $x_2$. Transient deflections at point $x_2$ of the functionally graded material annular plate can be calculated through Eq. (13) by using Runge–Kutta method.

Table 1 Critical buckling temperatures $T_{\mathrm{cr}}$ for the homogeneous annular plates under static uniform temperature rise (unit: K)

Table 2 The material properties of SiC and Ni [21]

In order to determine the critical buckling temperatures, let

$$\begin{aligned} \delta =\delta _0 ^{\prime }+\delta ^{\prime } \end{aligned}$$

(14)

where $\delta _0 ^{\prime }$ and $\delta ^{\prime }$ are stable solutions and small perturbation solutions [15], respectively. Let the small perturbation solutions $\delta ^{\prime }$ have a power function form:

$$\begin{aligned} \delta ^{\prime }{=}Ae^{\beta \tau } \end{aligned}$$

(15)

where A and $\beta$ are constants. Substituting Eq. (14) into Eq. (13), and taking into consideration of Eq. (15), we arrive

$$\begin{aligned}&f_2 \left( {{\delta }'} \right) ^{3}+\left( {3f_2 {\delta }'_0 +f_3 } \right) \left( {{\delta }'} \right) ^{2}+\left( {f_1 \beta ^{2}{+3}f_{2} \left( {{\delta }'_0 } \right) ^{2}} \right) \delta ^{\prime } \nonumber \\&\quad +\,\left( {{2}f_3 \delta _0 ^{\prime }+f_4 } \right) \delta ^{\prime }+f_2 \left( {{\delta }'_0 } \right) ^{3}\nonumber \\&\quad +\,f_3 \left( {{\delta }'_0 } \right) ^{2}+f_4 {\delta }'_0 +f_5 =0 \end{aligned}$$

(16)

The stable solutions can be the same as the initial geometric imperfections when the critical buckling state occurs, i.e., $\delta _0 ^{\prime }=\delta _0$ [15]. Substituting the known parameters of imperfection $\delta _0$ into Eq. (16), we obtain the coefficients of $\left( {\delta ^{\prime }} \right) ^{3}$, $\left( {\delta ^{\prime }} \right) ^{2}$, $\delta ^{\prime }$ and $\left( {\delta ^{\prime }} \right) ^{0}$. Since the values of the coefficients of $\left( {\delta ^{\prime }} \right) ^{3}$, $\left( {\delta ^{\prime }} \right) ^{2}$ and $\left( {\delta ^{\prime }} \right) ^{0}$ are very small, they can be approximated as zero, which results in:

$$\begin{aligned} f_1 \beta ^{2}\delta ^{\prime }{+3}f_{2} \left( {\delta _0 ^{\prime }} \right) ^{2}\delta ^{\prime }{+2}f_3 \delta _0 ^{\prime }\delta ^{\prime }+f_4 \delta ^{\prime }=0 \end{aligned}$$

(17)

When structures are in the critical state of buckling, the critical condition of equilibrium $\beta =0$ requires [15]:

$$\begin{aligned} {3}f_{2} \left( {\delta _0 ^{\prime }} \right) ^{2}{+2}f_3 \delta _0 ^{\prime }+f_4 {=}0 \end{aligned}$$

(18)

The critical buckling thermal loads of the functionally graded annular plate can be acquired by solving Eq. (18) numerically. In this study, the critical thermal membrane forces $N_{\mathrm{T}{\mathrm{cr}}}$ can be obtained first according to the critical condition, and then the critical buckling temperatures $\Delta T_{\mathrm{cr}}$ are obtained from the known thermal membrane force.

4 Numerical results and discussions

First, the accuracies of theoretical derivations and numerical calculations to study dynamic thermal buckling of the FGM annular plates are illustrated. Setting the power law index $n=0$, the FGM plate is reduced into homogeneous ceramic plate. Dynamic non-uniform temperature is also reduced to static uniform when we neglect the thermal conduct. Thus, the problem reduced to static thermal buckling for homogeneous annular plate. In addition, all parameters are chosen to be the same as in Ref. [23]. Comparisons between the present results and the corresponding results in Refs. [23, 24] are shown in Table 1. Dimensionless thermal load parameter was chosen as $\tau =12\left( {1-\nu ^{\mathrm{2}}} \right) \left( {R/h} \right) ^{2}\alpha T$, in Ref. [24]. When given $R/{R_1 }=0.5$, obtaining dimensionless critical temperature for the clamped annular plate is $\tau _{\mathrm{cr}} =105.61$. Convert the result into dimensional critical temperature, and list it as well as the results of Ref. [23] in Table 1. As shown in Table 1, there have been small differences between present results or results in Ref. [24] and those in Ref. [23], which is due to only considering axisymmetric deformation [23]. Present results are very close with those in Ref. [24] by finite difference method, which proves the correctness and reliability of this calculation.

In this section, consider that the FGM annular plate is made of SiC and Ni. The material properties of SiC and Ni are listed in Table 2. Besides, the Poisson’s ratio is taken as $\nu =0.3$.

Herein, the dynamic thermal buckling and postbuckling of the FGM annular plate with positive imperfections and negative imperfections are calculated and discussed, respectively. When the direction of the initial geometric imperfection is consistent with the thermal shock, named positive imperfection, otherwise negative one. In the following calculation, if there is not specified, the geometric parameters of the FGM annular plate are $R=0.3\,\hbox {m}$, $R_1 =0.09\,\hbox {m}$ and $h=0.006\,\hbox {m}$. The parameters of dynamic heating are $\Delta T=300\,\hbox {K}$ and $a=10$. The ambient temperature is $T_0 =300\,\hbox {K}$. The heat exchange coefficient is $h_r =50$.

Fig. 2

Transient deflections at the point $x_2$ of the FGM annular plate with different n. a Positive imperfection $(\delta _0 =0.001)$, b negative imperfection $(\delta _0 =-0.001)$

Fig. 3

Transient deflections at the point $x_2$ of the FGM annular plate with various imperfections. a Positive imperfection, b negative imperfection.

Figure 2a, b first illustrates the transient deflections at the point $x_2$ of the FGM annular plate with parameters of different power law index n, considering positive $\delta _0 =0.001$ and negative $\delta _0 =-0.001$ initial geometric imperfection, respectively. Apparently, the thermal deformations of the plate rapidly increase when the dynamic heating occurs, and the transient deflections have fluctuating effect due to subjected the dynamic thermal loading. The deflections of the dynamic responses are positive when the initial imperfections are positive, and vice versa. As shown in Fig. 2a, b, the transient maximum deflections of the FGM annular plate under the dynamic heating are intermediate to those of the metal and the ceramic annular plates and increase with the increasing n. Similar results can be seen in the works executed by Li and Fan [25], Kar and Kanoria [26]. At the same time, the time for occurrence of dynamic instability is advanced as the n increases. That is, the ability of the structure to withstand dynamic thermal loading decreases as the n increases. It is due to the bending stiffness of FGM annular plate drops with increasing power law index. So, the obvious effects of the n on the dynamic thermal deformation should be paid attention to in the design of FGM structures.

Figure 3a, b shows the transient deflections of the functionally graded annular plate with the power law index $n=2$ and four different parameters of initial geometric imperfection $\delta _0$. As shown in Fig. 3a, b, the variations of the parameters of initial imperfections have a great effect on the dynamic response. With the increase in the parameters of imperfections, the faster the deflections response and the time for the occurrence of the instability will be correspondingly advanced. At the same time, the dynamic maximum deflections increase with the increase in the parameters of imperfection. That is, the stiffness and the ability to withstand dynamic thermal loadings of the FGM annular plate decreases due to the presence of imperfections. These characteristics are in complete agreement with the corresponding results of homogeneous material circular plate in Ref. [15].

Table 3 The critical buckling temperatures $\Delta T_{\mathrm{cr}}$ of the FGM annular plates (unit: K)

The critical buckling temperatures of the functionally graded annular plate with three different parameters of the initial geometric imperfection are listed in Table 3. It can be seen that although the existence of the imperfections leads to the time of the buckling deformations is advanced significantly, but there has little effect on the critical buckling temperatures. And the critical temperatures of the imperfect plates are closer to those of the perfect plate. The characteristics of the variations between the dynamic critical temperatures and the imperfections are completely the same as the corresponding conclusions obtained in Ref. [27] on the static thermal buckling of the FGM circular plates. In addition, since the stiffness and the ability to withstand dynamic heating of the FGM annular plate decreases when power law index increases, the critical buckling temperatures of the FGM annular plate decrease when the power law index n increases.

Fig. 4

Transient deflections at the point $x_2$ of the FGM annular plate with different $R{:}\,R_1$. a Positive imperfection ($\delta _0 =0.001)$, b negative imperfection ($\delta _0 =-0.001)$

Figure 4a, b shows the variations of the transient deflections of the FGM annular plate with the $n=2$ and the parameters of imperfection $\delta _0 =0.001$ and $\delta _0 =-0.001$, given different ratios of outer radius to inner radius $R{:}\,R_1$. As shown in Fig. 4a, b, the ratio $R{:}\,R_1$ has a greater influence on the dynamic buckling and postbuckling. The responses of the deformations are faster and the time for the occurrence of instability is advanced, as the $R{:}\,R_1$ increase. The dynamic maximum deflections or the deformations of dynamic thermal postbuckling increases with the increase in $R{:}\,R_1$. These are due to the fact that the boundary constraints of the functionally graded annular plate drop with the increase in the $R{:}\,R_1$.

Fig. 5

The variations of the critical buckling temperatures with n for some specified values $R{:}\,R_1$

The variations of the critical buckling temperatures $\Delta T_{\mathrm{cr}}$ of the perfect FGM annular plates versus the power law index n for some specified values $R{:}\,R_1$ are analyzed in Fig. 5, in which $R{:}\,R_1$ is the ratio of inner radius to outer radius. $n=0$ corresponds to the FGM annular plates made from homogeneous ceramics. When $n=100{,}000$, the plate can be regarded as one made of metal. It can be seen from Fig. 5 that the critical buckling temperatures decrease when the n increases. That is to say, with the increase in n, the ability of the plate to withstand dynamic thermal loads decreases. If $n<2$, the magnitude of the dropping buckling temperature is larger. But if $n>2$, the curve becomes flat. It is because the constituents of the ceramics decrease and the stiffness of the FGM plate weakened with the increasing n. In addition, as the ratio of outer radius and inner radius $R{:}\,R_1$ decreases, the restraining strength of the plate increases and the critical temperatures also increase.

Fig. 6

Transient deflections versus time for some specified values of $a\,(\delta _0 =0.001)$

The variations of the dynamic thermal deformation of the plate with the load parameter a are examined in Fig. 6. Here, take $n=2$ and the parameter of the initial imperfection $\delta _0 =0.001$. As shown in Fig. 6, as the load parameter a increases, the faster the deflection response, the time for the occurrence of instability is also advanced. At the same time, the dynamic maximum deflections increase with the increase in the load parameter a. The influence on the dynamic thermal deformations is greater when the load parameter a is smaller than 5, and the influence becomes slight when the load parameter a is greater than 5.

Fig. 7

The variations of the critical buckling temperatures with n for some specified values of a

The variations of the critical buckling temperatures with the n are depicted in Fig. 7, given some specified values of a. As shown in Fig. 7, the critical buckling temperature slightly decreases as the parameter a increases. The curves coincide together when a greater than five. That is to say, a has almost no effect on the critical buckling temperatures, although the increase in load parameters has a great influence on the dynamic response.

5 Conclusions

The axisymmetric dynamic thermal buckling and postbuckling of the imperfect ceramic-metal FGM annular plate are carried out based on the nonlinear plate theory. First, the transient temperature fields are calculated by using Laplace transform in combination with power series expansion approach. Then, Runge–Kutta method is adopted to achieve the solutions to the transient thermal deformations. Finally, the buckling critical temperatures are obtained by using the linear perturbation method. The main conclusions are as follows:

• 1. The gradient properties of the functionally graded materials have apparent effects on the critical buckling temperatures of the annular plates. The buckling temperatures of the FGM plates are intermediate to those of the metal and the ceramic shells and decrease monotonously with the increasing power law index. At the same time, increasing the power law index, the time of dynamic instability is advanced and the dynamic maximum deflections increase.

• 2. The dynamic postbuckling of the FGM annular plate is sensitive to the initial imperfections. The stiffness of the functionally graded annular plate and its ability to resist the thermal shock are all decrease because of the presence of imperfections. The response of the transient deflections become faster and the maximum deflections increase, the time for the occurrence of instability is also advanced, as the parameter of imperfection increase.

• 3. The ratio of outer radius and inner radius has a greater influence on the dynamic responses. As the ratio increase, the faster the deflections response, the time for the occurrence of buckling is advanced, and the postbuckling deformations increase.

Appendix

$$\begin{aligned} F_1= & {} \frac{\partial ^{3}W}{\partial x^{3}}+\frac{1}{x}\frac{\partial ^{2}W}{\partial x^{2}}-\frac{1}{x^{2}}\frac{\partial W}{\partial x},\\ F_2= & {} -\left( {\frac{\partial ^{2}W}{\partial x^{2}}-\frac{\partial ^{2}W_0 }{\partial x^{2}}+\frac{1-\nu }{2x}\frac{\partial W}{\partial x}} \right) \frac{\partial W}{\partial x}\\&-\,\left( {\frac{\partial ^{2}W}{\partial x^{2}}+\frac{1-\nu }{x}\frac{\partial W}{\partial x}} \right) \frac{\partial W_0 }{\partial x},\\ F_3= & {} \frac{\partial ^{2}W}{\partial x^{2}}+\frac{\partial ^{2}W_0 }{\partial x^{2}}+\frac{1}{x}\left( {\frac{\partial W}{\partial x}+\frac{\partial W_0 }{\partial x}} \right) , \\ F_4= & {} \frac{1}{x}\frac{\partial }{\partial x}x\frac{\partial }{\partial x}\frac{1}{x}\frac{\partial }{\partial x}\left( {xU} \right) ,\\ F_5= & {} \frac{1-3\nu }{x}\frac{\partial W}{\partial x}\frac{\partial ^{2}W}{\partial x^{2}}+\frac{1-2\nu }{x}\frac{\partial ^{2}W}{\partial x^{2}}\frac{\partial W_0 }{\partial x}\\&+\,\left[ \frac{2\left( {1-\nu } \right) }{x}\frac{\partial W}{\partial x} +\frac{\partial ^{2}W}{\partial x^{2}} \right] \frac{\partial ^{2}W_0 }{\partial x^{2}}+\frac{\partial W}{\partial x}\frac{\partial ^{3}W_0 }{\partial x^{3}},\\ F_6= & {} \frac{1}{x}\frac{\partial }{\partial x}\left[ {x\left( {\frac{\partial U}{\partial x}+\frac{\nu }{x}U} \right) \frac{\partial W}{\partial x}} \right] \\&+\,\left[ {\frac{\partial U}{\partial x}+\frac{\nu }{x}U} \right] \frac{\partial ^{2}W_0 }{\partial x^{2}}+\left( {\frac{\partial ^{2}U}{\partial x^{2}}+\frac{1+\nu }{x}\frac{\partial U}{\partial x}} \right) \frac{\partial W_0 }{\partial x},\\ F_7= & {} \frac{1}{x}\frac{\partial }{\partial x}\left[ {\frac{x}{2}\left( {\frac{\partial W}{\partial x}} \right) ^{2}+\frac{\partial W}{\partial x}} \right] \\&+\,\left( {2\frac{\partial W_0 }{\partial x}+\frac{3}{2}\frac{\partial W}{\partial x}} \right) \frac{\partial W}{\partial x}\frac{\partial ^{2}W_0 }{\partial x^{2}} \\&+\,\left[ \left( {3\frac{\partial W}{\partial x}+\frac{\partial W_0 }{\partial x}} \right) \frac{\partial ^{2}W}{\partial x^{2}}\right. \\&\left. +\left( {\frac{3}{2x}\frac{\partial W}{\partial x}+\frac{1}{x}\frac{\partial W_0 }{\partial x}} \right) \frac{\partial W}{\partial x} \right] \frac{\partial W_0 }{\partial x} \\ \eta _1= & {} \left( {\nu -15} \right) \frac{32A_8 ^{2}x^{13}}{\lambda ^{2}}+\left( {\nu -13} \right) \frac{48A_6 A_8 x^{11}}{\lambda ^{2}}\\&+\,\left( {\nu -11} \right) \left( {18A_6 ^{2}+32A_4 A_8 } \right) \frac{x^{9}}{\lambda ^{2}}\\&+\,\left( {\nu -9} \right) 16A_4 A_6 \frac{x^{7}}{\lambda ^{2}} \\&+\,\left( {\nu -9} \right) 24A_2 A_8 \frac{x^{7}}{\lambda ^{2}}+\left( {\nu -7} \right) \\&\times \,\left( {12A_2 A_6 +8A_4 ^{2}} \right) \frac{x^{5}}{\lambda ^{2}}+\left( {\nu -5} \right) \frac{8A_2 A_4 x^{3}}{\lambda ^{2}}\\&+\,\left( {\nu -3} \right) \frac{2A_2 ^{2}x}{\lambda ^{2}} \end{aligned}$$

$$\begin{aligned} \eta _2= & {} \left( {\nu -15} \right) \frac{64\delta _0 A_8 ^{2}x^{13}}{\lambda ^{2}}+\left( {\nu -13} \right) \frac{96\delta _0 A_8 A_6 x^{11}}{\lambda ^{2}}\\&+\,\left( {\nu -11} \right) \left( {36\delta _0 A_6 ^{2}+64\delta _0 A_4 A_8 } \right) \frac{x^{9}}{\lambda ^{2}} \\&+\,\left( {\nu -9} \right) \left( {48\delta _0 A_4 A_6 +32\delta _0 A_2 A_8 } \right) \frac{x^{7}}{\lambda ^{2}}\\&+\,\left[ \left( {24\delta _0 A_2 A_6 +16\delta _0 A_4 ^{2}} \right) \left( {\nu -7} \right) +\,\frac{384D_2 A_8 }{D_1 } \right] \frac{x^{5}}{\lambda ^{2}}\\&+\left[ \frac{144D_2 A_6 }{D_1 }+16\delta _0 A_2 A_4 \times \,\left( {\nu -5} \right) -12\delta _0 A_2 ^{2} \right] \frac{x^{3}}{\lambda ^{2}}\\&+\,\left( {\delta _0 A_2 ^{2}\nu +\frac{8D_2 A_4 }{D_1 }} \right) \frac{4x}{\lambda ^{2}} \\ \lambda _1= & {} \frac{5632D_1 D_4 ^{4}A_8 ^{3}x^{20}}{\lambda ^{3}}+\frac{11520D_1 D_4 ^{4}A_6 A_8 ^{2}x^{18}}{\lambda ^{3}}\\&\quad +\,\left( 7776A_6 ^{2}A_8 {+}6912A_4 A_8 ^{2}\right. \\&\quad \left. +\,3072A_2 A_8 ^{2} \right) \frac{D_1 D_4 ^{4}x^{16}}{\lambda ^{3}}\\&\quad +\,\left( {9216A_4 A_6 A_8 {+}1728A_6 ^{3}} \right) \frac{D_1 D_4 ^{4}x^{14}}{\lambda ^{3}}\\&\quad +\,\left( 4032A_2 A_6 A_8 {+}2688A_4 ^{2}A_8 \right. \\&\quad \left. +\,3024A_4 A_6 ^{2} \right) \frac{D_1 D_4 ^{4}x^{12}}{\lambda ^{3}}\\&\quad +\,\left( 2304A_2 A_4 A_8 {+}1296A_2 A_{6}^{2}\right. \\&\quad \left. +\,1728A_{4}^{2} A_6 \right) \frac{D_1 D_{4}^{4} x^{10}}{\lambda ^{3}}\\&\quad +\,\left( {320A_{4}^{3} {+}1440A_2 A_4 A_6 {+}480A_{2}^{2} A_8 } \right) \frac{320A_{4}^{3} x^{8}}{\lambda ^{3}} \\&\quad +\,\left( {288A_2 ^{2}A_6 {+}384A_2 A_4 ^{2}} \right) \frac{D_1 D_4 ^{4}x^{6}}{\lambda ^{3}}\\&\quad +\,\frac{144D_1 D_4 ^{4}A_2 ^{2}A_4 x^{4}}{\lambda ^{3}}+\frac{16D_1 D_4 ^{4}A_2 ^{3}x^{2}}{\lambda ^{3}}\\ \end{aligned}$$

$$\begin{aligned} \lambda _2= & {} \frac{16896D_1 D_4 ^{4}\delta _0 A_8 ^{3}x^{20}}{\lambda ^{3}}+\frac{34560A_6 D_1 D_4 ^{4}\delta _0 A_8 ^{2}x^{18}}{\lambda ^{3}}\\&\quad +\,\left( {20736A_4 A_8 ^{2}{+}23328A_6 ^{2}A_8 } \right) \frac{D_1 D_4 ^{4}\delta _0 x^{16}}{\lambda ^{3}}\\&\quad +\,\frac{9216A_2 A_8 ^{2}D_1 D_4 ^{4}\delta _0 x^{14}}{\lambda ^{3}}\\&\quad +\,\left( {27648A_2 A_6 A_8 {+}5184A_6 ^{3}} \right) \\&\quad \times \,\frac{D_1 D_4 ^{4}\delta _0 x^{14}}{\lambda ^{3}}+\left( {1-3\nu } \right) \frac{448D_2 D_4 ^{4}A_8 ^{2}x^{12}}{\lambda ^{3}} \\&\quad +\,\left( {12096A_2 A_6 A_8 +8064A_4 ^{2}A_8 +9072A_4 A_6 ^{2}} \right) \\&\quad \times \,\frac{D_1 D_4 ^{4}\delta _0 x^{12}}{\lambda ^{3}}+3888A_2 A_6 ^{2}\frac{D_1 D_4 ^{4}\delta _0 x^{10}}{\lambda ^{3}} \\&\quad +\,\left( {6912A_2 A_4 A_8 +5184A_{4}^{2} A_6 } \right) \frac{D_1 D_4 ^{4}\delta _0 x^{10}}{\lambda ^{3}}\\&\quad +\,\left( {1-3\nu } \right) \frac{576D_2 D_{4}^{4} A_6 A_8 x^{10}}{\lambda ^{2}}\\&\quad +\,\left( {1-3\nu } \right) \frac{180D_2 D_{4}^{4} A_{6}^{2} x^{8}}{\lambda ^{2}} \\&\quad +\,\left( {1-3\nu } \right) \frac{320D_2 D_4 ^{4}A_4 A_8 x^{8}}{\lambda ^{2}}\\&\quad +\,\left( 960A_4 ^{3}+1440A_2 ^{2}A_8 \right. \\&\quad \left. +\,4320A_2 A_4 A_6 \right) \frac{D_1 D_4 ^{4}\delta _0 x^{8}}{\lambda ^{3}} \\&\quad +\,\left( {1-3\nu } \right) \frac{128D_2 D_4 ^{4}A_2 A_8 x^{6}}{\lambda ^{2}}+\left( {1-3\nu } \right) \\&\quad \times \,\frac{192D_2 D_4 ^{4}A_4 A_6 x^{6}}{\lambda ^{2}}+\left( 864A_2 ^{2}A_6\right. \\&\quad \left. +\,1152A_2 A_4 ^{2} \right) \frac{D_1 D_4 ^{4}\delta _0 x^{6}}{\lambda ^{3}}\\&\quad +\,\left( {1-3\nu } \right) \frac{48D_2 D_4 ^{4}A_4 ^{2}x^{4}}{\lambda ^{2}}+\left( {1-3\nu } \right) \\&\quad \times \,\frac{72D_2 D_4 ^{4}A_2 A_6 x^{4}}{\lambda ^{2}}+\frac{432D_1 D_4 ^{4}\delta _0 A_2 ^{2}A_4 x^{4}}{\lambda ^{3}}\\&\quad +\,\left( {1-3\nu } \right) \frac{32D_2 D_4 ^{4}A_2 A_4 x^{2}}{\lambda ^{2}}\\&\quad +\,\frac{48D_1 D_4 ^{4}\delta _0 A_2 ^{3}x^{2}}{\lambda ^{3}}+\left( {1-3\nu } \right) \frac{4D_2 D_4 ^{4}A_2 ^{2}}{\lambda ^{2}} \\ \end{aligned}$$

$$\begin{aligned} \lambda _3= & {} \frac{11264D_1 D_4 ^{4}\delta _0 ^{2}A_8 ^{3}x^{20}}{\lambda ^{3}}+\frac{23040D_1 D_4 ^{4}\delta _0 ^{2}A_6 A_8 ^{2}x^{18}}{\lambda ^{3}}\\&\quad +\,\left( {13824A_8 ^{2}{+}15552A_6 ^{2}A_8 } \right) \frac{D_1 D_4 ^{4}\delta _0 ^{2}x^{16}}{\lambda ^{3}} \\&\quad +\,\left( {6144A_2 A_8 ^{2}+18432A_4 A_6 A_8 +3456A_6 ^{3}} \right) \\&\quad \times \,\frac{D_1 D_4 ^{4}\delta _0 ^{2}x^{14}}{\lambda ^{3}}+\frac{\left( {4-\nu } \right) 1792D_2 D_4 ^{4}\delta _0 A_8 ^{2}x^{12}}{\lambda ^{2}} \\&\quad +\,\left( {6048A_4 A_6 ^{2}+5376A_4 ^{2}A_8 +8064A_2 A_6 A_8 } \right) \\&\quad \times \,\frac{D_1 D_4 ^{4}\delta _0 ^{2}x^{12}}{\lambda ^{3}}+\frac{\left( {7-2\nu } \right) 2304D_2 D_4 ^{4}\delta _0 A_6 A_8 x^{10}}{\lambda ^{2}} \\&\quad +\,\frac{\left( {3-\nu } \right) 720D_2 D_4 ^{4}\delta _0 A_6 ^{2}x^{8}}{\lambda ^{2}}+\left( 2592A_2 A_6 ^{2}\right. \\&\quad \left. +\,3456A_4 ^{2}A_6 +4608A_4 A_6 A_8 \right) \frac{D_1 D_4 ^{4}\delta _0 ^{2}x^{10}}{\lambda ^{3}} \\&\quad +\,\left( {640A_4 ^{3}+960A_2 ^{2}A_8 +2880A_2 A_4 A_6 } \right) \\&\quad \times \,\frac{D_1 D_4 ^{4}\delta _0 ^{2}x^{8}}{\lambda ^{3}}+\frac{\left( {3-\nu } \right) 1280D_2 D_4 ^{4}\delta _0 A_4 A_8 x^{8}}{\lambda ^{2}} \\&\quad +\,\frac{8D_1 D_4 ^{4}A_8 x^{7}}{\lambda }\frac{\partial ^{2}U\left( x \right) }{\partial x^{2}}+\left( 768A_2 A_4 ^{2}\right. \\&\quad \left. +\,576A_2 ^{2}A_6 \right) \frac{D_1 D_4 ^{4}\delta _0 ^{2}x^{6}}{\lambda ^{3}}\\&\quad +\,\left( {5-2\nu } \right) \frac{256D_2 D_4 ^{4}\delta _0 A_2 A_8 x^{6}}{\lambda ^{2}} \\&\quad +\,\left( {8+\nu } \right) \frac{8\nu D_1 D_4 ^{4}A_8 x^{6}}{\lambda }\frac{\partial U\left( x \right) }{\partial x}-\frac{64N_T D_4 ^{4}A_8 x^{6}}{\lambda }\\&\quad +\,\left( {5-2\nu } \right) \frac{384D_2 D_4 ^{4}\delta _0 A_4 A_6 x^{6}}{\lambda ^{2}}\\&\quad +\,\left( {56A_8 \nu U\left( x \right) +6A_6 \frac{\partial ^{2}U\left( x \right) }{\partial x^{2}}} \right) \frac{D_1 D_4 ^{4}x^{5}}{\lambda }\\&\quad +\,\left( {2-\nu } \right) \frac{192D_2 D_4 ^{4}\delta _0 A_4 ^{2}\nu x^{4}}{\lambda ^{2}}-\frac{36N_T D_4 ^{4}A_6 x^{4}}{\lambda } \\&\quad +\,\left( {2-\nu } \right) \frac{288D_2 D_4 ^{4}\delta _0 A_2 A_6 \nu x^{4}}{\lambda ^{2}}+\left( {6+\nu } \right) \\&\quad \times \,\frac{6D_1 D_4 ^{4}A_6 \nu x^{4}}{\lambda }\frac{\partial U\left( x \right) }{\partial x}+\frac{288D_1 D_4 ^{4}\delta _0 ^{2}A_2 ^{2}A_4 x^{4}}{\lambda ^{3}} \\&\quad +\,\left( {4A_4 \frac{\partial ^{2}U\left( x \right) }{\partial x^{2}}+30A_6 \nu U\left( x \right) } \right) \frac{D_1 D_4 ^{4}x^{3}}{\lambda }\\&\quad +\,\frac{32D_1 D_4 ^{4}\delta _0 ^{2}A_2 ^{3}x^{2}}{\lambda ^{3}}+\left( {4+\nu } \right) \frac{4D_1 D_4 ^{4}A_4 \nu x^{2}}{\lambda }\frac{\partial U\left( x \right) }{\partial x} \\ \end{aligned}$$

$$\begin{aligned}&\quad +\,\left( {3-2\nu } \right) \frac{128D_2 D_4 ^{4}\delta _0 A_2 A_4 \nu x^{2}}{\lambda ^{2}}-\frac{16N_T D_4 ^{4}A_4 x^{2}}{\lambda }\\&\quad +\,\left( {A_2 \frac{\partial ^{2}U\left( x \right) }{\partial x^{2}}+6A_4 \nu U\left( x \right) } \right) \frac{2D_1 D_4 ^{4}x}{\lambda } \\&\quad +\,\left( {2+\nu } \right) \frac{2D_1 D_4 ^{4}A_2 \nu }{\lambda }\frac{\partial U\left( x \right) }{\partial x}\\&\quad -\,\frac{4N_T D_4 ^{4}A_2 }{\lambda }+\frac{2D_1 D_4 ^{4}A_2 \nu U\left( x \right) }{x\lambda } \\ \lambda _4= & {} -\frac{D_0 A_8 x^{8}}{\lambda }-\frac{D_0 A_6 x^{6}}{\lambda }-\frac{D_0 A_4 x^{4}}{\lambda }\\&-\,\frac{D_0 A_2 x^{2}}{\lambda }-\frac{D_0 }{\lambda }\\ \lambda _5= & {} \frac{8D_1 D_4 ^{4}\delta _0 A_8 x^{7}}{\lambda }\frac{\partial ^{2}U}{\partial x^{2}}+\left( {8\frac{\partial U}{\partial x}-\frac{8N_T }{D_1 }+\nu \frac{\partial U}{\partial x}} \right) \\&\times \frac{8D_1 D_4 ^{4}\delta _0 A_8 x^{6}}{\lambda }{+}\left( {56A_8 \nu U+6A_6 \frac{\partial ^{2}U}{\partial x^{2}}} \right) \frac{D_1 D_4 ^{4}\delta _0 x^{5}}{\lambda } \\&+\,\left( {6\frac{\partial U}{\partial x}+\nu \frac{\partial U}{\partial x}-\frac{6N_T }{D_1 }} \right) \frac{6D_1 D_4 ^{4}\delta _0 A_6 x^{4}}{\lambda }\\&+\,\left( {30A_6 \nu U+4A_4 \frac{\partial ^{2}U}{\partial x^{2}}} \right) \frac{D_1 D_4 ^{4}\delta _0 x^{3}}{\lambda }\\&-\,\frac{16N_T D_4 ^{4}\delta _0 A_4 x^{2}}{\lambda }\\&+\,\left( {4+\nu } \right) \frac{4D_1 D_4 ^{4}\delta _0 A_4 x^{2}}{\lambda }\frac{\partial U}{\partial x}+\left( {6\nu A_4 U+A_2 \frac{\partial ^{2}U}{\partial x^{2}}} \right) \\&\times \,\frac{2D_1 D_4 ^{4}\delta _0 x}{\lambda }+\frac{D_2 D_4 ^{4}U}{x^{3}}-\frac{D_2 D_4 ^{4}}{x^{2}}\frac{\partial U}{\partial x} \\&+\,\frac{2D_2 D_4 ^{4}}{x}\frac{\partial ^{2}U}{\partial x^{2}}+\frac{2D_1 D_4 ^{4}\delta _0 A_2 \nu U}{\lambda x}+\left( {\nu +2} \right) \\&\times \,\frac{2D_1 D_4 ^{4}\delta _0 A_2 }{\lambda }\frac{\partial U}{\partial x}+D_2 D_4 ^{4}\frac{\partial U}{\partial x}-\frac{4N_T D_4 ^{4}\delta _0 A_2 }{\lambda } \\ {\eta }'_1= & {} \left( {\nu -15} \right) \frac{A_8 ^{2}x^{15}}{7\lambda ^{2}}+\left( {\nu -13} \right) \frac{2A_6 A_8 x^{13}}{7\lambda ^{2}}+\left( {\nu -11} \right) \\&\times \left( {9A_6 ^{2}+16A_4 A_8 } \right) \frac{x^{11}}{60\lambda ^{2}}+\left( {\nu -9} \right) 3A_4 A_6 \frac{x^{9}}{10\lambda ^{2}} \\&+\,\left( {\nu -9} \right) 2A_2 A_8 \frac{x^{9}}{10\lambda ^{2}}+\left( {\nu -7} \right) \left( {3A_2 A_6 +2A_4 ^{2}} \right) \\&\times \,\frac{x^{7}}{12\lambda ^{2}}+\left( {\nu -5} \right) \frac{A_2 A_4 x^{5}}{3\lambda ^{2}}+\left( {\nu -3} \right) \frac{A_2 ^{2}x^{3}}{4\lambda ^{2}} \\ \end{aligned}$$

$$\begin{aligned} {\eta }'_2= & {} \left( {\nu -15} \right) \frac{2\delta _0 A_8 ^{2}x^{15}}{7\lambda ^{2}}+\left( {\nu -13} \right) \frac{4\delta _0 A_8 A_6 x^{13}}{7\lambda ^{2}}\\&+\,\left( {\nu -11} \right) \left( {9\delta _0 A_6 ^{2}+16\delta _0 A_4 A_8 } \right) \frac{x^{11}}{30\lambda ^{2}} \\&+\,\left( {\nu -9} \right) \left( {12\delta _0 A_4 A_6 +4\delta _0 A_2 A_8 } \right) \frac{x^{9}}{10\lambda ^{2}}\\&\quad +\,\left[ \left( {3\delta _0 A_2 A_6 +2\delta _0 A_4 ^{2}} \right) \left( {\nu -7} \right) \right. \\&\quad \left. +\,\frac{48D_2 A_8 }{D_1 } \right] \frac{x^{7}}{6\lambda ^{2}} +\left[ \frac{36D_2 A_6 }{D_1 }\right. \\&\quad \left. +\,4\delta _0 A_2 A_4 \left( {\nu -5} \right) -3\delta _0 A_2 ^{2} \right] \\&\quad \times \,\frac{x^{5}}{6\lambda ^{2}}+\left( {\delta _0 A_2 ^{2}\nu +\frac{8D_2 A_4 }{D_1 }} \right) \frac{x^{3}}{2\lambda ^{2}} \\ \eta _1 ^{\prime \prime }= & {} -\left( {\nu -15} \right) \frac{A_8 ^{2}\left( {x_1 ^{16}-1} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&-\,\left( {\nu -13} \right) \frac{2A_6 A_8 \left( {x_1 ^{14}-1} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&-\,\left( {\nu -11} \right) \left( {9A_6 ^{2}+16A_4 A_8 } \right) \frac{\left( {x_1 ^{12}-1} \right) }{60\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&-\,\left( {\nu -9} \right) \left( {3A_4 A_6 +2A_2 A_8 } \right) \frac{\left( {x_1 ^{10}-1} \right) }{10\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&-\,\left( {\nu -7} \right) \left( {3A_2 A_6 +2A_4 ^{2}} \right) \frac{\left( {x_1 ^{8}-1} \right) }{12\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&-\,\left( {\nu -5} \right) \frac{A_2 A_4 \left( {x_1 ^{6}-1} \right) }{3\lambda ^{2}\left( {x_1 ^{2}-1} \right) }-\left( {\nu -3} \right) \frac{A_2 ^{2}\left( {x_1 ^{4}-1} \right) }{4\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\ \eta _2 ^{\prime \prime }= & {} -\left( {\nu -15} \right) \frac{2\delta _0 A_8 ^{2}\left( {x_1 ^{16}-1} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&-\,\left( {\nu -13} \right) \frac{4\delta _0 A_8 A_6 \left( {x_1 ^{14}-1} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&-\,\left( {\nu -11} \right) \left( {9A_6 ^{2}+16A_4 A_8 } \right) \frac{\delta _0 \left( {x_1 ^{12}-1} \right) }{30\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&-\,\left( {\nu -9} \right) \left( {3A_4 A_6 +A_2 A_8 } \right) \frac{4\delta _0 \left( {x_1 ^{10}-1} \right) }{10\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&-\,\left[ \left( {3\delta _0 A_2 A_6 +2\delta _0 A_4 ^{2}} \right) \left( {\nu -7} \right) \right. \\&\left. +\,\frac{48D_2 A_8 }{D_1 } \right] \frac{\left( {x_1 ^{8}-1} \right) }{6\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&-\,\left[ {\frac{36D_2 A_6 }{D_1 }+4\delta _0 A_2 A_4 \left( {\nu -5} \right) -3\delta _0 A_2 ^{2}} \right] \\ \end{aligned}$$

$$\begin{aligned}&\times \,\frac{\left( {x_1 ^{6}-1} \right) }{6\lambda ^{2}\left( {x_1 ^{2}-1} \right) }-\left( {\delta _0 A_2 ^{2}\nu +\frac{8D_2 A_4 }{D_1 }} \right) \frac{\left( {x_1 ^{4}-1} \right) }{2\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\ \eta _3 ^{\prime \prime }= & {} \left( {\nu -15} \right) \frac{A_8 ^{2}\left( {x_1 ^{16}-x_1 ^{2}} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }+\left( {\nu -13} \right) \frac{2A_6 A_8 \left( {x_1 ^{14}-x_1 ^{2}} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&+\,\left( {\nu -11} \right) \left( {9A_6 ^{2}+16A_4 A_8 } \right) \frac{\left( {x_1 ^{12}-x_1 ^{2}} \right) }{60\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&+\,\left( {\nu -9} \right) \left( {3A_4 A_6 +2A_2 A_8 } \right) \frac{\left( {x_1 ^{10}-x_1 ^{2}} \right) }{10\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&+\,\left( {\nu -7} \right) \left( {3A_2 A_6 +2A_4 ^{2}} \right) \frac{\left( {x_1 ^{8}-x_1 ^{2}} \right) }{12\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&+\,\left( {\nu -5} \right) \frac{A_2 A_4 \left( {x_1 ^{6}-x_1 ^{2}} \right) }{3\lambda ^{2}\left( {x_1 ^{2}-1} \right) }+\left( {\nu -3} \right) \frac{A_2 ^{2}\left( {x_1 ^{4}-x_1 ^{2}} \right) }{4\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\ \eta _4 ^{\prime \prime }= & {} \left( {\nu -15} \right) \frac{2\delta _0 A_8 ^{2}\left( {x_1 ^{16}-x_1 ^{2}} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&+\,\left( {\nu -13} \right) \frac{4\delta _0 A_8 A_6 \left( {x_1 ^{14}-x_1 ^{2}} \right) }{7\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&+\,\left( {\nu -11} \right) 9\delta _0 A_6 ^{2}\frac{\left( {x_1 ^{12}-x_1 ^{2}} \right) }{30\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&+\,\left( {\nu -11} \right) 16\delta _0 A_4 A_8 \frac{\left( {x_1 ^{12}-x_1 ^{2}} \right) }{30\lambda ^{2}\left( {x_1 ^{2}-1} \right) }+\left( {\nu -9} \right) \\&\times \left( {12\delta _0 A_4 A_6 +4\delta _0 A_2 A_8 } \right) \frac{\left( {x_1 ^{10}-x_1 ^{2}} \right) }{10\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&+\,\left[ {\delta _0 \left( {3A_2 A_6 +2A_4 ^{2}} \right) \left( {\nu -7} \right) +\frac{48D_2 A_8 }{D_1 }} \right] \\&\times \frac{\left( {x_1 ^{8}-x_1 ^{2}} \right) }{6\lambda ^{2}\left( {x_1 ^{2}-1} \right) }+4\delta _0 A_2 A_4 \left( {\nu -5} \right) \frac{\left( {x_1 ^{6}-x_1 ^{2}} \right) }{6\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\&+\,\left( {\frac{36D_2 A_6 }{D_1 }-3\delta _0 A_2 ^{2}} \right) \frac{\left( {x_1 ^{6}-x_1 ^{2}} \right) }{6\lambda ^{2}\left( {x_1 ^{2}-1} \right) }\\&+\,\left( {\delta _0 A_2 ^{2}\nu +\frac{8D_2 A_4 }{D_1 }} \right) \frac{\left( {x_1 ^{4}-x_1 ^{2}} \right) }{2\lambda ^{2}\left( {x_1 ^{2}-1} \right) } \\ \end{aligned}$$