Integrated design optimization of actuator layout and structural ply parameters for the dynamic shape control of piezoelectric laminated curved shell structures

Abstract

Compared with static shape control, dynamic shape control is more difficult due to its time-varying nature. To improve the control precision and reduce the number of actuators needed, an integrated design optimization model of structure and control is proposed. The following three sets of design variables are considered to minimize the time domain variance between the controlled and desired dynamic shapes: the time-varying actuator voltages, the actuator layout and the structural ply parameters. To satisfy the engineering performance requirements to the greatest extent possible, constraints on the structural mass, the energy, the maximum transient voltage and the number of actuators are considered. Because the control voltages are varying in time, a two-level optimization strategy is adopted. In the inner optimization problem, the Newmark integral method is applied to derive discrete time domain expressions for the shape control equations, and then, the Kuhn-Tucker condition is introduced to calculate the optimal time-varying voltage distribution. To solve the outer optimization problem, because of the coexistence of discrete variables and continuous variables, a simulated annealing algorithm is used. To address the shape control of complicated curved shells, a finite element formulation for an eight-node laminated curved shell element with piezoelectric actuators is derived. Numerical examples show that the proposed integrated design optimization method can significantly improve the control effect and that the optimization of the structural ply parameters plays an important role. Moreover, the control system can be simplified by taking the minimum number of actuators as the objective function when the control accuracy allows.

1 Introduction

Laminated curved shells are widely used in transportation engineering, aerospace engineering and other fields due to their excellent performance. However, in some complex and dynamic environments, structures can be easily affected by temperature differences, humidity and external forces, making such structures prone to failure due to undesired deformation. Therefore, it is essential to develop ways of maintaining the shape of structures in a harsh environment. When products are made using traditional materials, it is difficult to achieve active shape control during use. However, the emergence of smart materials has relieved this difficulty, especially piezoelectric materials, which are widely used in active shape and vibration control because of their rapid control capabilities and excellent operability.

At present, methods for the shape control of plates and shells based on piezoelectric actuators are mainly focused on static conditions. Koconis et al. (1994) controlled plates into desired shapes by changing the voltages of actuators. Varadarajan et al. (1998) discussed the quasi-static shape control of laminates with actuators in both open-loop and closed-loop cases. Kang and Tong (2008) used voltage as the design variable to control structural shapes and forced the voltages to converge to one of three sets of values by means of a penalty function. In addition, the static shape control of plate and shell structures was analysed by Zhang et al. (2015) using non-linear theories, and the authors compared the results with those of linear theories. A new explicit analytical solution for the static shape control of smart laminated cantilever piezocomposite hybrid plates was proposed by Gohari et al. (2016). The optimal voltage distribution for the shape control of composite plates was obtained by Zhang et al. (2016) using a GA (genetic algorithm). A closed-loop iterative shape control method was proposed by Song et al. (2019) to solve the problem of the high-precision shape control of an antenna reflector system, and the method was verified through numerical simulations and experiments. The influence of the actuator locations and voltages on the displacement of a plate was studied by Iurlova et al. (2019). In addition, Shao et al. (2018) applied the piezoelectric actuators to the mechanically reconfigurable reflector. However, for designs considering time-varying loads or shape adjustment needs, static shape control methods cannot meet the engineering requirements; consequently, research on dynamic shape control has begun to emerge. A sequential linear least squares algorithm for controlling the dynamic shapes of smart structures was proposed by Luo and Tong (2006). The dynamic shape control of slender beams was studied by Schoeftner et al. (2014). In addition, Wang et al. (2018b) designed a dynamic shape control method with vibration suppression by optimizing a time-varying voltage. The same authors (Wang et al. 2018a) adopted a feedback tracking control method to control the dynamic shape of a piezocomposite actuated flexible wing. Zhang and Wang (2019) applied a piezoelectric composite material to the dynamic distributed morphing of an aeroelastic wing.

In shape control based on piezoelectric actuators, the voltages, locations and number of actuators together influence the control effect. If actuators are spread over the whole surface of a structure, this will increase the weight of the structure itself and result in higher energy consumption, and it may even increase the complexity of the control system. In contrast, if too few actuators are used, it will be impossible to meet the accuracy requirements. Therefore, to improve the control effect while reducing the complexity of the system, the layout of the actuators needs to be optimized. To this end, Onoda and Hanawa (1993) obtained the optimal layout of space trusses using a combination of a GA and an SA (simulated annealing) algorithm. By extending the SIMP (solid isotropic material with penalization) model (Bendsoe and Sigmund 1999), Kögl and Silva (2005) developed a new piezoelectric material interpolation model, and they obtained the optimal layout of the piezoelectric materials by using a sequential linear programming method. Nguyen and Tong (2007) proposed an evolutionary optimization algorithm and obtained the optimal layout of actuators on the basis of sensitivity information. Wang et al. (2016) investigated the optimal design of a smart reflector structure in the context of static shape control by means of SA. Wang et al. (2017) used a GA to optimize the layout and voltages of actuators for the static shape control of an intelligent cantilever plate from the perspectives of accuracy and cost. The layout of piezoelectric actuators in shape control of a beam with load uncertainties was optimized (Adali et al. 2000). The influence of the boundary conditions on the layout of actuators for the shape control of a beam was investigated by Bendine and Wankhade (2017) using a GA. Some studies have also addressed the integrated optimization of actuators and substrate materials: Kang et al. (2011) carried out integrated topology optimization on cantilever beams with piezoelectric plies. A level set model and an independent pointwise density interpolation method were proposed by Wang et al. (2014) to optimize the distributions of piezoelectric actuators and substrate materials. To maximize the static displacement of a laminated composite plate with piezocomposite actuators, the ply parameters of the laminated plate and the actuator parameters were simultaneously optimized by Wang et al. (2019). Notably, however, all of the above studies focused on optimization for static shape control. Although there are many researches on active vibration control using piezoelectric actuators (Padoin et al. 2019; Niu et al. 2019; Zhao et al. 2009), the researches on optimization of dynamic shape control are rare at present. As one example, Liu and Lin (2010) obtained the optimal channel distribution for the dynamic shape control of a plate using an SA algorithm.

Many scholars have studied the shape control or vibration suppression of flat shells. In reality, however, curved shells are often encountered in practical situations. Therefore, to meet practical needs and improve the achievable control accuracy, it is necessary to study finite element models of curved shell structures. To this end, Kumar and Singh (2012) applied an eight-node element for the vibration control of piezoelectric curved panels. Zhai et al. (2016, 2020) used and verified that the calculation accuracy and efficiency achieved with curved shell elements are higher than those achieved with flat shell elements in the vibration control of curved shells.

At present, methods for the shape control of shells mainly focus on static shape control and single-ply shells. There have been few studies on the dynamic shape control of laminated curved shell structures. Nonetheless, laminated curved shells and dynamic deformations are among the most common structural forms and mechanical behaviours, respectively, that are encountered in practical applications. When simulating curved shell structures, curved shell elements offer higher accuracy than flat shell elements. Therefore, it is highly valuable to use laminated curved shell elements to perform calculations for the dynamic shape control of laminated curved shells. In addition, the mechanical behaviours of laminated shells are known to depend not only on the material properties but also on the ply thicknesses and ply angles. The flexibility of these structures has a strong influence on their ease of control; therefore, optimizing the ply parameters of a laminated substrate structure helps reduce the difficulty of controlling its shape. However, at present, the available shape control methods for laminated shells mostly focus on finding the optimal actuator parameters while ignoring the influence of the structural ply parameters; hence, there is room for improvement.

Based on these considerations, the dynamic shape control and integrated design optimization of piezoelectric laminated curved shells are investigated in this paper. The best control effect is achieved by simultaneously optimizing three sets of variables, i.e. the time-varying voltages and layout of the actuators and the ply parameters of the laminated substrate structure. A maximum energy constraint, a maximum voltage constraint, a limit on the number of actuators and a constraint on the mass of the laminated substrate structure are considered. First, the finite element equations for an eight-node laminated curved shell element with piezoelectric curved shell actuators are derived. Second, the objective function is formulated as the time domain variance between the controlled and desired dynamic shapes. To solve for the optimal time-varying voltages, a two-level optimization strategy combining an optimal criterion method and an SA algorithm is adopted. In the inner optimization problem, discrete time domain expressions for the dynamic shape control equations are derived by invoking the Newmark integral method, and then, the Kuhn-Tucker condition is introduced to obtain the optimal time-varying voltage distribution. The outer optimization problem seeks the optimal layout of the actuators and the optimal ply thicknesses and ply angles of the laminated substrate structure to improve the control effect. Due to the coexistence of discrete variables and continuous variables in the outer optimization problem, an SA algorithm is adopted to solve this problem because it is an intelligent random search algorithm that is known to be suitable for optimization problems of this kind. Finally, examples are presented to verify the accuracy of the results obtained using laminated curved shell elements and the effectiveness of the two-level optimization strategy. An analysis of various cases shows that the proposed integrated design optimization method can significantly improve the control effect and that the optimization of the structural ply parameters plays an important role. Furthermore, the number of actuators can be taken as the objective function to be minimized to simplify the control system.

2 Finite element equations for laminated curved shell elements

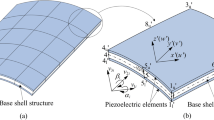
Figure 1a shows an eight-node single-ply curved shell element. In this figure, (x ‐ y ‐ z) is the global coordinate system, (x '  ‐ y '  ‐ z') is the nodal coordinate system, and (ξ ‐ η ‐ ζ) is the natural coordinate system with −1 ≤ ξ, ζ, η ≤ 1. Here, we assume that v_3i is the normal unit vector perpendicular to the middle surface of the element and that v_1i and v_2i are unit vectors that are perpendicular to v_3i and orthogonal to each other. The displacement vector of any point in the element with respect to the global coordinate system can be expressed in the following interpolation form:

$$ \left\{\begin{array}{c}u\\ {}v\\ {}w\end{array}\right\}=\sum \limits_{i=1}^8{N}_i\left(\xi, \eta \right)\left\{\begin{array}{c}{u}_i\\ {}{v}_i\\ {}{w}_i\end{array}\right\}+\sum \limits_{i=1}^8\frac{h_i}{2}\zeta {N}_i\left(\xi, \eta \right)\left[\begin{array}{cc}{l}_{1i}& -{l}_{2i}\\ {}{m}_{1i}& -{m}_{2i}\\ {}{n}_{1i}& -{n}_{2i}\end{array}\right]\left\{\begin{array}{c}{\alpha}_i\\ {}{\beta}_i\end{array}\right\} $$

(1)

where (u_i v_i w_i α_i β_i)^T is the generalized displacement vector of the ith node; α_i and β_i are the rotation angles of v_3i around v_2i and v_1i, respectively; N_i and h_i are the two-dimensional interpolation function and thickness, respectively, of the ith node; and (l_ji m_ji n_ji)^T, with j = 1, 2, are the direction cosines of v_1i and v_2i, respectively, at the ith node. The stiffness matrix of the element can be written as:

$$ {\mathbf{K}}^{\mathbf{e}}={\int}_{-1}^1{\int}_{-1}^1{\int}_{-1}^1{\mathbf{B}}^{\mathrm{T}}\mathbf{CB}\left|\mathbf{J}\right|\ \mathrm{d}\xi \mathrm{d}\eta \mathrm{d}\zeta $$

(2)

where J and B (Zhai et al. 2017) are the Jacobian matrix and strain matrix, respectively, and C is the elastic matrix. For an orthotropic shell, the material coordinate system is different from the global coordinate system due to the influence of the ply angle. Therefore, the elastic matrix C in the material coordinate system needs to be transformed into $\overline{\mathbf{C}}$ in the global coordinate system:

$$ \overline{\mathbf{C}}={\mathbf{TCT}}^{\mathrm{T}} $$

(3)

with:

$$ \mathbf{T}=\left[\begin{array}{cccccc}{c}^2& {s}^2& 0& 2 sc& 0& 0\\ {}{s}^2& {c}^2& 0& -2 sc& 0& 0\\ {}0& 0& 0& 0& 0& 0\\ {}- sc& sc& 0& {c}^2-{s}^2& 0& 0\\ {}0& 0& 0& 0& c& -s\\ {}0& 0& 0& 0& s& c\end{array}\right] $$

(4)

where s = sin θ and c = cos θ, with θ being the ply angle. Therefore, for an orthotropic material, (2) should be converted into:

$$ {\mathbf{K}}^{\mathbf{e}}={\int}_{-1}^1{\int}_{-1}^1{\int}_{-1}^1{\mathbf{B}}^{\mathrm{T}}\overline{\mathbf{C}}\mathbf{B}\left|\mathbf{J}\right|\ \mathrm{d}\xi \mathrm{d}\eta \mathrm{d}\zeta $$

(5)

Fig. 1

Curved shell elements: a single-ply element, b laminated element, c laminated element with actuators

As shown in Fig. 1b, a laminated curved shell element consists of a stack of curved shell elements with different material properties and different ply parameters. For such a laminated curved shell element, the elastic matrix is not a continuous function of the thickness coordinate ζ. Therefore, integration in the thickness direction is achieved by splitting the limits through each ply. For the pth ply, a new natural coordinate ζ^∗ with a value range of [‐1, 1] is introduced; the corresponding positions of − 1 and 1 correspond to ζ_p − 1 and ζ_p, respectively, which are the coordinates of two surfaces of the pth ply in the ζ coordinate. The stiffness matrix of the laminated element can be expressed using the following formula:

$$ {\mathbf{K}}^{\mathbf{e}}=\sum \limits_{p=1}^q{\int}_{-1}^1{\int}_{-1}^1{\int}_{-1}^1{{\mathbf{B}}_p}^{\mathrm{T}}{\overline{\mathbf{C}}}_p{\mathbf{B}}_p{\left|\mathbf{J}\right|}_p{\left|{\mathbf{J}}^{\ast}\right|}_p\mathrm{d}\xi \mathrm{d}\eta \mathrm{d}{\zeta}^{\ast } $$

(6)

where q is the number of plies and the subscript p denotes the pth ply. For a laminated curved shell element with a total thickness of h₀, when calculating the stiffness matrix of each ply, the following relationships can be obtained:

$$ {\displaystyle \begin{array}{c}{\zeta}_{p-1}=\frac{h_{p-1}}{h_0}\times 2-1\\ {}{\zeta}_p=\frac{h_p}{h_0}\times 2-1\end{array}} $$

(7)

Here, h_p − 1 and h_p are the two surface heights of the pth ply in the global coordinate system. Therefore, the following relationship between ζ and ζ^∗ can be obtained:

$$ \zeta =\frac{\zeta_p+{\zeta}_{p-1}}{2}+\frac{\zeta^{\ast}\left({\zeta}_p-{\zeta}_{p-1}\right)}{2} $$

(8)

Combining (7) and (8) yields:

$$ \zeta =\frac{h_p+{h}_{p-1}+{\zeta}^{\ast}\left({h}_p-{h}_{p-1}\right)}{h_0}-1 $$

(9)

Thus, the expression for |J^∗| in (6) is:

$$ \left|{\mathbf{J}}^{\ast}\right|=\frac{d\zeta}{d{\zeta}^{\ast }}=\frac{h_p-{h}_{p-1}}{h_0} $$

(10)

3 Dynamic finite element equations for piezoelectric laminated curved shells

Figure 1c shows a laminated curved shell element with piezoelectric actuators. To control deformation of shells, piezoelectric actuators are placed on the first and last ply surfaces. The voltage polarities of the two surfaces are opposite. The linear constitutive equations of a piezoelectric material are (Takezawa et al. 2014):

$$ {\displaystyle \begin{array}{c}\boldsymbol{\upsigma} =\mathbf{C}\boldsymbol{\upvarepsilon } -{\mathbf{e}}^{\mathrm{T}}\mathbf{E} \\ {}\mathbf{D}=\mathbf{e}\boldsymbol{\upvarepsilon } +\boldsymbol{\Lambda} \mathbf{E}\end{array}} $$

(11)

where σ and ε are the stress vector and strain vector, respectively; C is the elastic matrix; e is the piezoelectric stress coefficient matrix; E is the electric field vector; D is the electric displacement vector; and Λ is the dielectric coefficient matrix.

The dynamic finite element equations can be obtained by applying Hamilton’s variational principle (Zhai et al. 2016):

$$ {\mathbf{M}}_{\mathbf{t}}\ddot{\mathbf{u}}+{\mathbf{K}}_{\mathbf{t}}\mathbf{u}+{\mathbf{C}}_{\mathbf{t}}\dot{\mathbf{u}}+{\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}\boldsymbol{\upvarphi} =\mathbf{F} $$

(12)

with:

$$ {\displaystyle \begin{array}{c}{\mathbf{M}}_{\mathbf{t}}={\mathbf{M}}_{\mathbf{s}}+{\mathbf{M}}_{\mathbf{a}}\\ {}{\mathbf{K}}_{\mathbf{t}}={\mathbf{K}}_{\mathbf{s}}+{\mathbf{K}}_{\mathbf{a}}\\ {}{\mathbf{C}}_{\mathbf{t}}={\mathbf{C}}_{\mathbf{s}}+{\mathbf{C}}_{\mathbf{a}}\end{array}} $$

(13)

where M_t, K_t and C_t are the total mass matrix, stiffness matrix and damping matrix, respectively; the subscripts s and a denote the laminated substrate structure and the actuators, respectively; φ is the time-varying voltage vector; and K_uφ (Zhang et al. 2018) is the electromechanical coupling matrix of the actuators:

$$ {\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}={\int}_{\varOmega }{\mathbf{B}}^{\mathrm{T}}{\left({\boldsymbol{\Gamma}}^{\mathrm{T}}{\mathbf{e}}^{\mathrm{T}}{\mathbf{T}}_{\mathbf{p}}\right)}^{\mathrm{T}}{\mathbf{B}}_{\boldsymbol{\upvarphi}}\mathrm{d}\Omega $$

(14)

with:

$$ \boldsymbol{\Gamma} =\left[\begin{array}{cccccc}{l}_1^2& {m}_1^2& {n}_1^2& {l}_1{m}_1& {m}_1{n}_1& {n}_1{l}_1\\ {}{l}_2^2& {m}_2^2& {n}_2^2& {l}_2{m}_2& {m}_2{n}_2& {n}_2{l}_2\\ {}{l}_3^2& {m}_3^2& {n}_3^2& {l}_3{m}_3& {m}_3{n}_3& {n}_3{l}_3\\ {}2{l}_1{l}_2& 2{m}_1{m}_2& 2{n}_1{n}_2& {l}_1{m}_2+{l}_2{m}_1& {m}_1{n}_2+{m}_2{n}_1& {n}_1{l}_2+{n}_2{l}_1\\ {}2{l}_2{l}_3& 2{m}_2{m}_3& 2{n}_2{n}_3& {l}_2{m}_3+{l}_3{m}_2& {m}_2{n}_3+{m}_3{n}_2& {n}_2{l}_3+{n}_3{l}_2\\ {}2{l}_3{l}_1& 2{m}_3{m}_1& 2{n}_3{n}_1& {l}_3{m}_1+{l}_1{m}_3& {m}_3{n}_1+{m}_1{n}_3& {n}_3{l}_1+{n}_1{l}_3\end{array}\right] $$

(15)

where B is the strain matrix in (2), Γ (Cook et al. 2001) is the strain transformation matrix, (l_i m_i n_i) with i = 1, 2, 3, are the direction cosines between the global coordinate system and local coordinate system, T_p is the coordinate transformation matrix, and B_φ is the electrical strain matrix. For curved shell actuators:

$$ {\mathbf{B}}_{\boldsymbol{\upvarphi}}=\sum \limits_{i=1}^{n_a}\frac{1}{h_a}{N}_i{\left({l}_{3i}\ {m}_{3i}\ {n}_{3i}\right)}^{\mathrm{T}} $$

(16)

Here, N is the same interpolation function as in (1), n_a is the number of actuator nodes, h_a is the actuator thickness, and (l_3i m_3i n_3i)^T is the normal direction cosine of the ith node, which corresponds to the case of j = 3 for (l_ji m_ji n_ji)^T in (1).

In reality, the fourth term K_uφφ in (12) represents the equivalent nodal force produced by piezoelectric actuators. The distributed piezoelectric actuators are adopted in this paper, and each actuator has an independent electrode and voltage. In addition, the actuators are imposed by the voltage boundary conditions rather than the charge boundary conditions. Therefore, the equivalent nodal force of each actuator depends on the applied voltage. At the nodes which are shared by multiple adjacent actuators, the nodal equivalent forces are produced by the joint actions of multiple actuators.

4 Description of dynamic shape control and integrated design optimization

The integrated design optimization of laminated curved shells for dynamic shape control is defined as the process of seeking the optimal actuator parameters and structural ply parameters under certain constraints to deform the laminated curved shells into desired dynamic shapes. The variance f between the desired and controlled dynamic shapes within the period [0, t] can be taken as the objective function of the optimization problem:

$$ f={\int}_0^t{\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)}^{\mathrm{T}}\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)\mathrm{d}t $$

(17)

where u and w_d are the controlled and desired deformations, respectively, in the time domain. To facilitate calculation, the time domain is uniformly divided into k time interpolation points. Thus, the discrete form can be written as:

$$ f={\sum}_{i=1}^k{{\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)}_i}^{\mathrm{T}}{\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)}_i $$

(18)

where i represents the ith time interpolation point.

The design variables include the time-varying voltages φ(t), the layout x of the actuators and the ply thicknesses h and ply angles θ of the laminated substrate structure. The detailed expressions are as follows:

$$ {\displaystyle \begin{array}{c}\boldsymbol{\upvarphi} \left(\mathbf{t}\right)=\left[{\boldsymbol{\upvarphi}}_{\mathbf{1}}\left(\mathbf{t}\right),\dots, {\boldsymbol{\upvarphi}}_{\mathbf{e}}\left(\mathbf{t}\right),\dots, {\boldsymbol{\upvarphi}}_{\mathbf{n}}\left(\mathbf{t}\right)\right]\\ {}\mathbf{x}=\left({x}_1,\dots, {x}_e,\dots, {x}_n\right)\\ {}\mathbf{h}=\left({h}_1,\dots, {h}_p,\dots, {h}_q\right)\\ {}\ \boldsymbol{\uptheta} =\left({\theta}_1,\dots, {\theta}_p,\dots, {\theta}_q\right)\end{array}} $$

(19)

where φ_e(t) is the time-varying voltage vector of the eth actuator; x_e = 1 denotes that the eth actuator is retained, while x_e = 0 denotes that the eth actuator is removed; h_p and θ_p are the thickness and angle, respectively, of the pth ply of the laminated substrate structure; q and n are the numbers of plies and actuators, respectively.

To meet the actual requirements of engineering applications, it is necessary to consider more comprehensive constraints. Considering that actuators have a breakdown voltage value, an excessive voltage can disable them, so the maximum voltage value should be constrained to protect the control system. Moreover, the energy consumption of the actuators is equivalent to the control cost, meaning that an energy constraint is meaningful for cost reduction. In the time period [0, t], the energy P^e consumed by each actuator is:

$$ {P}^e={\int}_0^t\frac{{\varepsilon \varphi}^2(t){l}_a{b}_a}{2{h}_a} dt $$

(20)

where l_a, b_a and h_a are the length, width and thickness, respectively, of a piezoelectric actuator; ε is the dielectric constant; and φ(t) is the time-varying voltage. In addition, limiting the number of actuators can effectively simplify the control system, which is necessary in practical applications. In general, mass reduction is desirable in engineering applications, so the total mass of the laminated substrate structure should also be limited. Considering the manufacturing requirements, the ply angles of the laminated substrate structure can be selected only from among a given set of discrete values. In reality, multiple performance requirements for shell structures need to be considered in practical engineering, such as aeroelastic performance (Wang et al. 2018a, 2018b; Zhang and Wang 2019). To simplify the analysis, only the performance requirement of shape control is considered in our study, although it may cause an adverse influence on the structural and aeroelastic performances. In summary, the integrated design optimization model for the dynamic shape control of a laminated curved shell can be expressed as follows:

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\begin{array}{c}\mathrm{Find}:\kern0.5em \mathbf{x}=\left({x}_1,\dots, {x}_e,\dots, {x}_n\right)\\ {}\mathbf{h}=\left({h}_1,\dots, {h}_p,\dots, {h}_q\right)\\ {}\boldsymbol{\uptheta} =\left({\theta}_1,\dots, {\theta}_p,\dots, {\theta}_q\right)\end{array}\\ {}\boldsymbol{\upvarphi} \left(\mathbf{t}\right)=\left[{\boldsymbol{\upvarphi}}_{\mathbf{1}}\left(\mathbf{t}\right),\dots, {\boldsymbol{\upvarphi}}_{\mathbf{e}}\left(\mathbf{t}\right),\dots, {\boldsymbol{\upvarphi}}_{\mathbf{n}}\left(\mathbf{t}\right)\right]\\ {}\operatorname{Min}:\kern0.5em f\left[\mathbf{x},\mathbf{h},\boldsymbol{\uptheta}, \boldsymbol{\upvarphi} \left(\mathbf{t}\right)\right]={\int}_0^t{\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)}^{\mathrm{T}}\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)\ \mathrm{d}t\end{array}\\ {}\begin{array}{cc}\mathrm{s}.\mathrm{t}:& {\mathbf{M}}_{\boldsymbol{t}}\ddot{\mathbf{u}}\left(\mathbf{t}\right)+{\mathbf{C}}_{\mathbf{t}}\dot{\mathbf{u}}\left(\mathbf{t}\right)+{\mathbf{K}}_{\mathbf{t}}\mathbf{u}\left(\mathbf{t}\right)+{\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}\boldsymbol{\upvarphi} \left(\mathbf{t}\right)=\mathbf{F}\end{array}\\ {}\begin{array}{c}\begin{array}{cc}{x}_e\in \left\{0,1\right\}& e=1,2,\dots, n\end{array}\\ {}\begin{array}{cc}{\theta}_p\in \left\{{\theta}_1,{\theta}_2,\dots, {\theta}_m\right\}& p=1,2,\dots, q\end{array}\\ {}\begin{array}{cc}\underline{h}\le {h}_p\le \overline{h}& p=1,2,\dots, q\end{array}\\ {}P\le \overline{P}\\ {}\begin{array}{c}\max \left[\boldsymbol{\upvarphi} \left(\mathbf{t}\right)\right]\le \overline{\varphi}\\ {}{\sum}_{e=1}^n{x}_e\le \overline{\mathrm{x}}\\ {}{\mathrm{M}}_s\le {\overline{\mathrm{M}}}_s\end{array}\end{array}\end{array}} $$

(21)

where M_s is the mass of the laminated substrate structure; ${\overline{\mathrm{M}}}_s$ is the maximum allowable value of this mass; $\overline{\mathrm{x}}$ is the number of actuators we wish to retain; $\overline{h}$ and $\underline{h}$ are the maximum and minimum thicknesses, respectively, of a single ply; P is the total energy consumption; $\overline{P}$ is the maximum allowable energy consumption; $\overline{\varphi}$ is the upper limit on the transient voltage; and {θ₁, θ₂, …, θ_m} are the possible ply angles. Of course, depending on the practical needs of the situation, it is also valuable in some cases to minimize the number of actuators as the objective function; in this case, the corresponding constraint $f\le \overline{f}$ is added to optimization model (21), where $\overline{f}$ is the upper limit on the control error.

In optimization model (21), the voltage variables are transient and varying in time. Therefore, the voltage variables are solved for separately. The design variables can be divided into two groups: the time-varying voltages and all remaining design variables. These two groups of design variables are independent of each other, but there is a sequential relationship between them. Therefore, a two-level optimization strategy is adopted in this paper.

5 Inner optimization problem: solving for the optimal time-varying voltages

Once the layout of the actuators and the ply parameters of the laminated substrate structure have been determined, the desired dynamic deformation can be obtained by optimizing the voltages of the actuators. To control the deformation to obtain the desired shape at any given time, the voltage value of each piezoelectric actuator as a function of time should be calculated. Here, an optimal criterion method based on the Kuhn-Tucker condition and the Newmark integral method is used. Considering the time period [t_i, t_i + n], the inner optimization problem can be written as:

$$ {\displaystyle \begin{array}{l}\mathrm{Find}:\kern1.5em \boldsymbol{\upvarphi} (t)=\left[{\boldsymbol{\upvarphi}}_1(t),\dots, {\boldsymbol{\upvarphi}}_e(t),\dots, {\boldsymbol{\upvarphi}}_n(t)\right]\\ {}\kern0.19em \operatorname{Min}:\kern1.9em f\left(\boldsymbol{\upvarphi} \right)={\int}_{t_i}^{t_{i+n}}{\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)}^{\mathrm{T}}\left(\mathbf{u}-{\mathbf{w}}_{\mathbf{d}}\right)\mathrm{d}t\end{array}} $$

(22)

First, the Newmark integral method is adopted. According to (12), the equation of motion at time t_i + 1 is:

$$ {\mathbf{M}}_{\mathbf{t}}{\ddot{\mathbf{u}}}_{i+1}+{\mathbf{C}}_{\mathbf{t}}{\dot{\mathbf{u}}}_{i+1}+{\mathbf{K}}_{\mathbf{t}}{\mathbf{u}}_{i+1}={\mathbf{F}}_{i+1}-{\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}{\boldsymbol{\upvarphi}}_{i+1} $$

(23)

In the Newmark integral method, the velocities, accelerations and displacements at times t_i and t_i + 1 satisfy the following equations (Yun and Youn 2017):

$$ {\displaystyle \begin{array}{c}{\dot{\mathbf{u}}}_{i+1}={\dot{\mathbf{u}}}_i+\left[\left(1-\delta \right){\ddot{\mathbf{u}}}_i+\delta {\ddot{\mathbf{u}}}_{i+1}\right]\varDelta t\\ {}{\mathbf{u}}_{i+1}={\mathbf{u}}_i+{\dot{\mathbf{u}}}_i\varDelta t+\left[\left(0.5-\alpha \right){\ddot{\mathbf{u}}}_i+\alpha {\ddot{\mathbf{u}}}_{i+1}\right]{\left(\varDelta t\right)}^2\end{array}} $$

(24)

where Δt represents the time interval between the two time steps. When δ ≥ 0.5 and α ≥ 0.25(0.5 + δ)², the Newmark integral method is unconditionally stable. In the calculation process, all unknowns of the next time step can be iteratively calculated using the values from the previous time step. By analysing each time step, the displacement u_i + 1 at time t_i + 1 is found to be:

$$ \tilde{\mathbf{K}}{\mathbf{u}}_{i+1}={\tilde{\mathbf{F}}}_{i+1}-{\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}{\boldsymbol{\upvarphi}}_{i+1} $$

(25)

where $\tilde{\mathbf{K}}$ and ${\tilde{\mathbf{F}}}_{i+1}$ are the equivalent stiffness matrix and equivalent mechanical load vector, respectively, at time t_i + 1. They can be expressed as:

$$ {\displaystyle \begin{array}{c}\tilde{\mathbf{K}}={\mathbf{K}}_{\mathbf{t}}+{c}_0{\mathbf{M}}_{\mathbf{t}}+{c}_1{\mathbf{C}}_{\mathbf{t}}\\ {}{\tilde{\mathbf{F}}}_{i+1}={\mathbf{F}}_{i+1}+{\mathbf{F}}_{\mathbf{M}}+{\mathbf{F}}_{\mathbf{C}}\\ {}{\mathbf{F}}_{\mathbf{C}}={\mathbf{C}}_{\mathbf{t}}\left({c}_1{\mathbf{u}}_i+{c}_4{\dot{\mathbf{u}}}_i+{c}_5{\ddot{\mathbf{u}}}_i\right)\\ {}{\mathbf{F}}_{\mathbf{M}}={\mathbf{M}}_{\mathbf{t}}\left({c}_0{\mathbf{u}}_i+{c}_2{\dot{\mathbf{u}}}_i+{c}_3{\ddot{\mathbf{u}}}_i\right)\end{array}} $$

(26)

The integration constants can be expressed in terms of δ, α and Δt:

$$ {\displaystyle \begin{array}{c}{c}_0=\frac{1}{\alpha {\left(\varDelta t\right)}^2}{c}_1=\frac{\delta }{\alpha \varDelta t}{c}_2=\frac{1}{\alpha \varDelta t}\\ {}{c}_3=\frac{1}{2\alpha }-1{c}_4=\frac{\delta }{\alpha }-1{c}_5=\frac{\varDelta t}{2}\left(\frac{\delta }{\alpha }-2\right)\end{array}} $$

(27)

By suitably transforming (25), the controlled displacement u_i + 1 at time t_i + 1 can be obtained:

$$ {\mathbf{u}}_{i+1}={\tilde{\mathbf{K}}}^{-1}{\tilde{\mathbf{F}}}_{i+1}-{\tilde{\mathbf{K}}}^{-1}{\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}{\boldsymbol{\upvarphi}}_{i+1} $$

(28)

Second, to extract the displacement in a particular direction of interest, the matrix R is introduced. In this matrix, the element corresponding to the desired displacement direction is one, and the other elements are zero. Therefore, the following expression can be obtained:

$$ {\mathbf{U}}_{i+1}={\mathbf{Ru}}_{i+1}=\mathbf{R}{\tilde{\mathbf{K}}}^{-1}{\tilde{\mathbf{F}}}_{i+1}-\mathbf{R}{\tilde{\mathbf{K}}}^{-1}{\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}{\boldsymbol{\upvarphi}}_{i+1} $$

(29)

Here, we set:

$$ {\displaystyle \begin{array}{c}{\mathbf{S}}_{\mathbf{F}}=\mathbf{R}{\tilde{\mathbf{K}}}^{-1}\\ {}{\mathbf{S}}_{\boldsymbol{\upvarphi}}=\mathbf{R}{\tilde{\mathbf{K}}}^{-1}{\mathbf{K}}_{\mathbf{u}\boldsymbol{\upvarphi }}\end{array}} $$

(30)

Substituting the above equation into (22) yields:

$$ {\displaystyle \begin{array}{c}f\left({\boldsymbol{\upvarphi}}_{i+1}\right)={\left({\mathbf{S}}_{\boldsymbol{\upvarphi}}{\boldsymbol{\upvarphi}}_{i+1}-{\mathbf{d}}_{i+1}\right)}^{\mathrm{T}}\left({\mathbf{S}}_{\boldsymbol{\upvarphi}}{\boldsymbol{\upvarphi}}_{i+1}-{\mathbf{d}}_{i+1}\right)\\ {}{\mathbf{d}}_{i+1}={\mathbf{S}}_{\mathbf{F}}{\tilde{\mathbf{F}}}_{i+1}-{\left({\mathbf{w}}_{\mathbf{d}}\right)}_{i+1}\end{array}} $$

(31)

Finally, the Kuhn-Tucker necessary condition is introduced to solve for the extreme value of the objective function with respect to the voltage vector:

$$ \frac{\partial f}{\partial {\boldsymbol{\upvarphi}}_{i+1}}=0 $$

(32)

Accordingly, the voltage vector φ_i + 1 at time t_i + 1 is as follows:

$$ {\boldsymbol{\upvarphi}}_{i+1}={\left({{\mathbf{S}}_{\boldsymbol{\upvarphi}}}^{\mathrm{T}}{\mathbf{S}}_{\boldsymbol{\upvarphi}}\right)}^{-1}{{\mathbf{S}}_{\boldsymbol{\upvarphi}}}^{\mathrm{T}}{\mathbf{d}}_{i+1} $$

(33)

The controlled deformation and required voltages at each time point can be obtained after completing the cycle in the whole time domain.

6 Outer optimization problem: seeking the optimal structural ply parameters and actuator layout

In the outer optimization problem, we consider the layout x of the actuators as well as the ply thicknesses h and ply angles θ of the laminated substrate structure as the design variables, and the time domain variance between the controlled and desired dynamic shapes is taken as the optimization objective. In our study, there are many design variables, and discrete variables (x and θ) coexist with continuous variables (h). SA is an iterative adaptive heuristic probabilistic search algorithm that can obtain the globally optimal solution with a large probability when applied for the optimization of non-differentiable or even discontinuous functions. In addition, SA can also handle problem of mixed variables, which makes it well suited for the outer optimization problem.

The SA algorithm is derived from the process of solid annealing. Solid annealing refers to the thermodynamic process of heating a solid to a sufficiently high temperature and then slowly cooling it to solidify it into a regular crystal. Heating the solid will cause the thermal motion of the particles in the solid to gradually increase and become disordered, and the energy will also increase with the rise in temperature. Subsequently cooling the solid will cause the thermal motion of the particles to weaken and gradually become orderly, and the energy will gradually decrease and approach a minimum value. The SA algorithm is based on the similarity between the optimization process and the solid annealing process: the objective function to be optimized is equivalent to the internal energy of the solid, and the variable state space of the optimization problem is equivalent to the internal energy state space of the solid.

To apply SA to the constrained optimization problem of interest here, the following method is adopted. A penalty function is added to punish the occurrence of infeasible solutions, thus transforming the constrained optimization problem into an unconstrained optimization problem. The penalty function value L is formulated as follows:

$$ \min\ L=f+\left(1+\overline{\alpha}\left|f\right|\right)\left(\sum \limits_{i=1}^{n_c}\max \left(0,{\overline{g}}_i\right)\right) $$

(34)

where $\overline{g}$ is a normalized inequality constraint; $\overline{\alpha}$ is a penalty factor, which we take to be 1.0 here; and n_c is the number of inequality constraints.

To address the coexistence of discrete and continuous variables in our study, the SA algorithm first considers the discrete variables as continuous variables to generate a new solution X_con, with the corresponding penalty function value L_con. Then, for each component of the new solution X_con, the SA algorithm finds the corresponding discrete value with the smallest distance as the corresponding component of the discrete solution X_dis, with a corresponding penalty function value of L_dis. The real penalty function value can then be obtained in accordance with the following formula:

$$ {L}_{real}={\alpha}_1{L}_{con}+{\alpha}_2{L}_{dis} $$

(35)

where α₁ and α₂ are weight factors, for which we adopt the same values as in (Zhai et al. 2016).

Algorithm 1 Pseudo-code for the SA algorithm

The pseudo-code for the SA algorithm used in this paper is shown in Algorithm 1. The convergence criterion can be described as: the absolute value of the difference between the two adjacent optimal penalty function values is less than 0.0001 times the current optimal penalty function value, and the maximum cooling iteration is set to 5000 to ensure the robustness of algorithm.

Therefore, by combining the inner and outer optimization problems, the whole process of the two-level optimization strategy can be described as represented by the flowchart in Fig. 2.

Fig. 2

Flowchart of the two-level optimization strategy

7 Numerical examples

7.1 Verification analysis

The accuracy of the curved shell element proposed in this paper in dynamic analysis and control analysis was studied here, and the relationship between the optimal voltage and the mesh resolution was also studied.

7.1.1 Verification of the accuracy of the finite element model and dynamic shape control method

To verify the accuracy that can be achieved with the laminated curved shell element proposed in this paper, models of a laminated cylindrical shell were developed that were divided into flat shell elements and curved shell elements for dynamic analysis and dynamic shape control, respectively.

As shown in Fig. 3, we consider a clamped laminated cylindrical shell with a length of 400 mm, a cross-sectional radius of 200 mm and a central angle of 90°. It has eight plies, each with a thickness of 0.5 mm, and the ply angles are [0°, 90°, 90°, 0°]_s. The material properties are as follows: the elastic moduli are E₁ = 50 GPa and E₂ = E₃ = 6 GPa, the shear moduli are G₁₂ = G₂₃ = G₁₃ = 7 GPa, the Poisson’s ratios are ν₁₂ = ν₁₃ = ν₂₃ = 0.3, and the mass density is ρ = 1800 kg/m³. The structure is divided into 10 × 10 curved shell elements or 10 × 10, 30 × 30, 50 × 50 or 60 × 60 flat shell elements. The ANSYS software package was used for calculations based on the models divided into flat shell elements, while the calculations for the model divided into curved shell elements were performed using program codes we compiled ourselves. The first three natural frequencies and the corresponding errors are shown in Table 1.

Fig. 3

Laminated cylindrical shell

Table 1 Natural frequencies and errors calculated using flat shell elements (FSE) and curved shell elements (CSE)

As seen from the results, when we used ANSYS to calculate the natural frequencies with 50 × 50 and 60 × 60 flat shell elements, the resulting errors were very small; therefore, the results of the latter can be regarded as the standard solution. When the shell is divided into only 10 × 10 flat shell elements, there are large errors with respect to the results obtained using 60 × 60 flat shell elements. When the structure is divided into 30 × 30 flat shell elements, the error with respect to the standard solution is reduced. However, when the shell is divided into 10 × 10 curved shell elements, the results are better than those of 30 × 30 flat shell elements, approximately equivalent to those obtained using 60 × 60 flat shell elements. These findings show that with the same number of elements, curved shell elements offer higher precision than flat shell elements. That is to say, for a given accuracy requirement, the number of curved shell elements needed is smaller than the necessary number of flat shell elements.

Next, we distributed actuators with a thickness of 0.2 mm across the two surfaces of the laminated cylindrical shell shown in Fig. 3. The elastic modulus, Poisson’s ratio, density and piezoelectric coefficients of the actuators are E_a = 70 GPa, ν_a = 0.25, ρ_a = 7500 kg/m³ and e₃₁ = e₃₂ =  − 5.2 C/m², respectively. Here, the proportional damping C_t = a₁M_t + a₂K_t with a₁ = 4.73 and a₂ = 2.47 × 10⁻⁴ is adopted. The deformation we desire in the y direction is as follows:

$$ {\mathbf{w}}_{\mathbf{d}}\left(x,z,t\right)=\frac{\left(\cosh z-1\right)\sin \left(5\pi \left|x\right|\right)}{10000}\sin t $$

(36)

Here, 10 × 10 curved shell elements and 10 × 20 flat shell elements were used to simulate the shell. For one time period of calculation, we considered 21 time interpolation points uniformly distributed in the time domain.

For the calculation using 10 × 10 curved shell elements, the variance f is 7.70 × 10⁻⁴ mm², and the consumption energy P is 0.41 J. For the calculation using 10 × 20 flat shell elements, f is 7.49 × 10⁻⁴ mm², and P is 0.77 J. Thus, given the same control accuracy, the number of curved shell elements required is smaller than the required number of flat shell elements. Therefore, for the dynamic shape control of a curved shell structure, the use of curved shell actuators can effectively reduce the number of actuators needed in the control system, reduce the computational burden of finite element analysis and save energy. Figure 4 shows the voltage distributions at the time point with maximum deformation under two-element meshes. It can be seen that there are many actuators with very small voltage values in both meshes, so it is necessary to optimize the layout of the actuators.

Fig. 4

Distributions of optimal voltage: a 10 × 10 curved shell elements, b 10 × 20 flat shell elements

7.1.2 Convergence analysis of the optimal voltage distribution and value

Mesh independency is an important aspect in topology optimization, which can avoid numerical instability and checkerboard modes (Nguyen et al. 2010). To analyse the relationship between the voltage convergence and mesh resolution, the structure shown in Fig. 3 is divided into 10 × 10, 20 × 20, 30 × 30 or 40 × 40 curved shell elements, and the fundamental frequencies for the four mesh schemes are 84.2 Hz, 84.5 Hz, 84.6 Hz and 84.6 Hz, respectively. Therefore, the fundamental frequency of the case with 10 × 10 meshes is convergent.

Figure 5 shows the optimal voltage distributions at the time point with maximum deformation for different resolution meshes. Therefore, in dynamic shape control, the convergence of voltage distribution is demonstrated in the cases with 30 × 30 and 40 × 40 meshes. However, the maximum voltage is not convergent, so the voltage values depend on the mesh. Considering the importance of the relationship between the optimization results and mesh, we first discuss it in the next optimization example.

Fig. 5

Voltage distributions for different resolution meshes: a 10 × 10, b 20 × 20, c 30 × 30, d 40 × 40

7.2 Integrated design optimization for the dynamic shape control of piezoelectric laminated curved shells

To validate the formulas and theories proposed in this paper, two examples of integrated design optimization for dynamic shape control are presented.

7.2.1 Integrated design optimization for part of a spherical shell structure

As shown in Fig. 6, the calculation model is obtained by cutting into a spherical shell with a radius of 1000 mm using a cube with a side length of 600 mm. Furthermore, we distribute actuators across the first and last ply surfaces of the laminated structure, respectively. Here, the plies of the laminated substrate structure are orthotropic, and the actuators are isotropic. The material properties are shown in Table 2.

Fig. 6

Part of a spherical shell and the coordinates of selected nodes

Table 2 Material properties

Discussion for the relationship between the optimal actuator layout and mesh resolution

Here, the shell model shown in Fig. 6 has four plies with angles of [90°, 0°]_s, and each ply has a thickness of 0.5 mm. To study the relationship between the optimal layout and mesh, we distribute 8 × 8 and 16 × 16 actuators with a thickness of 0.2 mm across the surfaces of the structure, respectively. In the Cartesian coordinate system, the desired dynamic twist deformation is given by the following formula:

$$ {\mathbf{w}}_{\mathbf{d}}\left(x,y,t\right)=\frac{\left(\cosh y-1\right)\sin x}{300}\sin t $$

(37)

We consider calculations performed over half a time period, corresponding to 0 ≤ t ≤ π in (37), with 11 time points uniformly distributed in the time domain. The optimization information for the two mesh schemes is shown in Table 3.

Table 3 Information for two optimization schemes

The pair of actuators placed in the same position on the two surfaces of the model are defined as one group. When the surfaces of the spherical shell model are completely covered by 64 groups of actuators, the initial variance, the initial energy consumption and the initial maximum transient voltage are 21.94 mm², 9.88 × 10⁻² J and 252 V after shape control, respectively. When the surfaces of the model are completely covered by 256 groups of actuators, the above values are 15.61 mm², 2.08 × 10⁻¹ J and 513 V, respectively. Here, the higher initial energy consumption value is taken as the upper limit, and the maximum transient voltage is set to 600 V. Since the volume of a single actuator is different for the two mesh schemes, we take 65% of the total actuator volume as the number constraint of actuators.

Table 4 shows the optimized results for two mesh schemes. Figure 7 shows the optimized actuator layouts for two mesh schemes. As can be seen from Fig. 7, the optimized actuator layout for the case with 16 × 16 meshes is not consistent from the result for the case with 8 × 8 meshes. It shows that the optimal layout depends on the mesh resolution for the layout optimization in this paper. The reasons are mainly in two aspects. On the one hand, the initial control variances of the two mesh schemes are not convergent. On the other hand, the voltage values depend on the mesh.

Table 4 Optimized results for two mesh schemes

Fig. 7

Optimized actuator layouts: a 8 × 8 meshes, b 16 × 16 meshes

However, the layout optimization in our study is different from the structural topology optimization. For the latter, the mesh independency is an important aspect. For the layout optimization in this paper, the mesh dependency is allowable. In practical engineering, the structural sizes and number of actuators are generally given, which means that the mesh resolution is determined. As can be seen from Table 4, the objective values for the two mesh schemes are all successfully optimized although the optimal layouts are different. Therefore, the optimized results are reliable and have engineering values. It can be seen from Fig. 7 that the increase of mesh resolution will increase the number of actuators, which will greatly increase the control cost and the operation difficulty in practical engineering. Therefore, for a given mesh resolution (actuator size) that meets the precision requirement of dynamic analysis, the optimal optimization results can be obtained using the method proposed in this paper, which is obviously different from topology optimization. Therefore, although the optimal layout in this paper depends on the mesh resolution, the optimized results are reliable and have great engineering significance.

Taking the minimum variance as the objective function: layout optimization and integrated design optimization

Here, the shell model shown in Fig. 6 has eight plies with angles of [90°, 90°, 0°, 0°]_s, and each ply has a thickness of 0.5 mm. The thickness of each single ply can vary in the range of 0.3~0.7 mm and is considered as a continuous design variable. As discrete variables, the ply angles can take values selected from among {−45°, 0°, 45°, 90°}. Furthermore, we distribute 64 actuators with a thickness of 0.2 mm across the first and last ply surfaces of the laminated structure, respectively. The material properties are shown in Table 2.

In the Cartesian coordinate system, the desired dynamic in-plane deformation in the x direction is given by the following formula:

$$ {\mathbf{w}}_{\mathbf{d}}\left(y,t\right)=\frac{\left(\cosh 2|\mathrm{y}|-1\right)\sin \frac{5\pi \mid \mathrm{y}\mid }{6}}{50000}\sin t $$

(38)

We consider calculations performed over half a time period, corresponding to 0 ≤ t ≤ π in (38), with 11 time points uniformly distributed in the time domain. When sint = 1 at time t₆, the dynamic deformation of each node reaches its maximum value. The maximum desired deformation is shown by the black wire frame in Fig. 8 (the degree of deformation depicted in the figure is 5000 times the true value), and the red wire frame represents the original shape.

Fig. 8

Maximum desired deformation of the laminated shell: a front view, b top view

Different practical applications have different requirements, corresponding to different optimization objectives and constraints. The optimization with minimum variance as the objective function was studied here. The detailed optimization information is shown in Table 5. Therefore, the optimization problems in Case 1 and Case 2 are the layout optimization and the integrated design optimization, respectively.

Table 5 Information for two optimization schemes

When the surfaces of the spherical shell model are completely covered by 64 groups of piezoelectric actuators, the initial variance is 9.76 × 10^‐1 mm² after shape control. The initial energy consumption and the initial maximum transient voltage are 8.29 × 10⁻¹ J and 720 V, respectively. For the two optimization schemes, the initial energy consumption is taken as the upper limit, and the maximum transient voltage is set to 800 V. In addition, the number of actuator groups is set to 50.

Table 6 shows the calculation results for the two optimization schemes. In the initial case, the maximum transient voltage cannot be constrained because there is no outer optimization. Compared with those in the initial case, the variance and the number of actuator groups in Case 1 are reduced by 11.48% and 21.88%, respectively. The energy consumption and maximum voltage are within the constraints, although the maximum voltage is very close to the upper limit. These results show that the optimization of the actuator layout in Case 1 is effective. Similarly, we again adopt 50 groups of actuators in Case 2. Compared with that in the initial case, the variance in Case 2 is reduced by 48.87%. Under the condition of the same number of actuators and structural mass, the variance of Case 2 is reduced by 42.25% compared to Case 1, and the maximum voltage and energy consumption are reduced. Therefore, if only the layout and voltages of the actuators are optimized, although the control effect is improved, this improvement is relatively small. Including the ply parameters of the laminated substrate structure among the design variables can greatly improve the accuracy. Therefore, the optimization of the ply parameters plays an important role in the integrated design optimization. For Case 2, the final ply thicknesses and ply angles of the laminated substrate structure are shown in Table 7. We can see that the ply thicknesses may either increase or decrease within the allowed range and that the ply angles vary greatly, but the structural mass remains unchanged. Figure 9 shows the optimization iterations of SA algorithm, and for the curve of Case 2, the iteration number starts to accumulate from the iteration where feasible solutions are first generated.

Table 6 Objective values and constraint values for two optimization schemes

Table 7 Ply parameters of the laminated substrate structure in Case 2

Fig. 9

Iteration histories of the objective values for three cases

Figure 10 shows the layouts of the actuators in different cases. Although Case 2 has the same number of actuators as Case 1, the layouts are quite different because of the changes in the ply parameters of the laminated substrate structure. This indicates that the structural ply parameters also affect the actuator layout.

Fig. 10

Actuator layouts for three cases: a initial layout, b Case 1, c Case 2

Figure 11 shows the voltage distributions at time t₆ for three cases. Here, t₆ is the time interpolation point with the maximum voltage and deformation. Compared with the initial distribution, the voltage distribution in Case 1 shows little change, and the maximum voltage corresponds to the same actuator. Therefore, optimizing the layout of the actuators has little effect on the voltage distribution. In contrast, the voltage distribution changes greatly in Case 2. This change manifests in three aspects. The first is the position change of the maximum voltage. For the initial distribution and distribution in Case 1, the actuator with the maximum transient voltage is No. 53, where in Case 2, it is No. 60. The second is the reversal of the electrode direction for some actuators, such as No. 8 and No. 44. For the initial case and Cases 1 and 2, the maximum positive voltages are located at the 52nd, 44th and 60th actuators, respectively, and the maximum negative voltages are located at the 53rd, 53rd, and 37th actuators, respectively. Figure 12 shows the voltage histories of the above-mentioned actuators for all cases. As can be seen from Fig. 12, the last aspect is the reduction of the voltage value range, which shows that the voltage distribution is more uniform in the integrated design optimization. Therefore, the ply parameters have a great influence on the voltage distribution.

Fig. 11

Voltage distributions at time t₆ for three cases: a initial distribution, b Case 1, c Case 2

Fig. 12

Voltage histories of selected actuators

Figure 13 shows the displacement curves of node A₁ in different cases and the desired displacement, where node A₁ is the corner node with the maximum deformation in Fig. 6. The control accuracy is highest in Case 2, followed by Case 1 and the initial case. These results indicate that the integrated design optimization of the actuator layout, actuator voltages and structural ply parameters can significantly improve the control accuracy.

Fig. 13

Displacement curves of the node with the maximum deformation

Taking the minimum number of actuators as the objective function: layout optimization

The layout optimization with the minimum number of actuators as the objective function was studied. The calculation model used in the example with minimum variance as the objective function is adopted here. In addition, the detailed optimization information is shown in Table 8.

Table 8 Information for the layout optimization

In the example with minimum variance as the objective function, we have obtained the initial values. Here, the initial energy consumption is taken as the upper limit, and the maximum transient voltage is set to 800 V. To study the number and position of the retained actuators under different variance constraints, we calculated the results for three variance constraint values, namely 1.2 times, 1.4 times and 1.6 times the initial variance.

Table 9 shows the calculation results for the layout optimization with the minimum number of actuators as the objective function. As seen from Table 9, for the all kinds of variance constraints, the maximum transient voltage, energy consumption and variance all satisfy the constraints. When the number of actuators is taken as the optimization objective, there are different number of actuators after optimization for different variance constraints. Figure 14 shows the optimization iterations of SA algorithm. As the variance constraint value decreases, the number of actuators removed gradually decreases. This indicates that the higher the control accuracy, the more actuators are required. For the three cases with 1.2 times, 1.4 times and 1.6 times initial variance constraint, although the control accuracy are not as good as the initial case, the numbers of actuators are further reduced, which are 26 groups, 23 groups and 19 groups, respectively. In engineering, we can choose the appropriate variance constraint to reduce the number of actuators.

Table 9 Objective values and constraint values

Fig. 14

Iteration histories of the objective values for different variance constraints

Figure 15 shows the optimized layouts of the actuators. For all kinds of variance constraints, the actuators are all mainly distributed in areas with large deformations. This indicates that in the dynamic shape control process, the actuators located in the area with large deformation are more important, so they retained more after optimization.

Fig. 15

Optimized actuator layouts: a 1.2 times, b 1.4 times, c 1.6 times

Figure 16 shows the voltage distributions at time t₆. Here, t₆ is the time interpolation point with the maximum voltage. Most of the remaining actuators are those with relatively high voltages in the initial case shown in Fig. 11a. Although the actuator has different distributions among the all kinds of variance constraints, the larger voltages are all distributed in the same region.

Fig. 16

Voltage distributions at time t₆: (a) 1.2 times, (b) 1.4 times, (c) 1.6 times

7.2.2 Integrated design optimization for a simplified wing model

Figure 17 shows a simplified wing model with one clamped edge and the coordinates of some selected nodes in the Cartesian coordinate system. This simplified wing model has ten plies with angles of [0°, 90°, 90°, 0°, 0°]_s, and each ply has a thickness of 0.4 mm. The thickness of a single ply can vary within the range of 0.3~0.5 mm and is considered as a continuous design variable. As discrete variables, the ply angles can take values selected from among {‐45°, 0°, 45°, 90°}. We distribute 144 actuators with a thickness of 0.2 mm across the two surfaces of the laminated structure, respectively. The material properties of the simplified wing model and actuators are shown in Table 2, but e₃₁ = e₃₂ =  − 10 C/m² here.

Fig. 17

Simplified wing model and coordinates of selected nodes

In the Cartesian coordinate system, the desired dynamic deformation in the y direction is given by the following formula:

$$ {\mathbf{w}}_{\mathbf{d}}\left(x,z,t\right)=\frac{z^4\log \left(x+1\right)}{200}\sin t $$

(39)

We consider calculations performed over half a time period, corresponding to 0 ≤ t ≤ π in (39), with 11 time points uniformly distributed in the time domain. The desired deformation of each node reaches its maximum at time t₆. Figure 18a and b show the original shape and the desired shape, respectively, at time t₆ (the degree of deformation depicted in the figure is 600 times the true value).

Fig. 18

Maximum desired deformation of the simplified wing model: a original shape, b desired shape

Taking the minimum variance as the objective function: integrated design optimization

The integrated design optimization for the simplified wing model is studied here; the detailed optimization information is shown in Table 10.

Table 10 Information for the integrated design optimization

When the surfaces of the wing model are completely covered by 144 groups of piezoelectric actuators, the initial variance is 22.96 mm² after shape control. The initial energy consumption and the initial maximum transient voltage are 1.73 × 10⁻¹ J and 779 V, respectively. For the integrated design optimization, the initial energy consumption is taken as the upper limit, and the maximum transient voltage is set to 800 V. In addition, the number of actuator groups is set to 120.

Table 11 shows the calculation results for the integrated design optimization. Although the structural mass is not changed, through integrated design optimization, the variance is reduced by 77.96% compared with the initial variance. In addition, the energy consumption, number of actuators and maximum transient voltage decreased by 63.29%, 16.67% and 70.47%, respectively. Therefore, including the ply parameters of the laminated substrate structure among the design variables can greatly improve the accuracy. This conclusion is similar to that for the example presented in Section 7.2.1. The final optimal structural ply parameters are shown in Table 12. We can see that the ply thicknesses may either increase or decrease within the allowed range and that the ply angles vary greatly, but the structural mass remains unchanged. Figure 19 shows the optimization iterative of SA algorithm for the integrated design optimization. Here, the iteration number starts to accumulate from the iteration where feasible solutions are first generated.

Table 11 Objective value and constraint values for the integrated design optimization

Table 12 Ply parameters of the laminated substrate structure in the integrated design optimization

Fig. 19

Iteration history of the objective value for the integrated design optimization

The top surface of the simplified wing model is labelled surface A, and the bottom surface is labelled surface B. Figure 20 shows the optimal layouts of the actuators for two cases. Here, 60 groups of actuators are retained on both surface A and surface B after integrated design optimization.

Fig. 20

Actuator layouts for two cases: a initial layout, b optimized layout

Figure 21 shows the voltage distributions at time t₆ for two cases. Here, t₆ is the time interpolation point with the maximum voltage. For the initial distribution and the optimized distribution, the maximum positive voltages are located at the 85th and 79th actuators, respectively, and the maximum negative voltages are located at the 84th and 61st actuators, respectively. Figure 22 shows the voltage histories of the above-mentioned actuators. For the optimized distribution, the actuator with the maximum transient voltage is No. 79, whereas it is No. 85 for the initial distribution. The directions of some electrodes, such as those of actuators No. 57, No. 58, and No. 85, are reversed. In addition, the optimized distribution of voltages is more uniform than the initial distribution.

Fig. 21

Voltage distributions at time t₆ for two cases: a initial distribution, b optimized distribution

Fig. 22

Voltage histories of selected actuators

Figure 23 shows the displacement curves of node B₈ for two cases and the desired displacement, where node B₈ is the corner node with the maximum deformation in Fig. 17. The displacement for the case of integrated design optimization is very close to the desired displacement.

Fig. 23

Displacement curves of the node with the maximum deformation

Taking the minimum number of actuators as the objective function: layout optimization

The layout optimization with the minimum number of actuators as the objective function was studied here. The detailed optimization information is shown in Table 13.

Table 13 Information for the layout optimization

The initial energy consumption, the initial maximum voltage and the initial variance have been obtained in the example with the minimum variance as the objective function. The initial energy consumption is taken as the upper limit, and the maximum transient voltage is set to 800 V. In addition, the variance constraint is set to 1.5 times the initial variance.

Table 14 shows the calculation results for the layout optimization. When the minimum number of actuators is taken as the optimization objective, there are only 72 groups of actuators after optimization. The constrained values all satisfy the specified requirements, and the variance is very close to the upper limit. Although the variance is 1.5 times the initial variance, the number of actuators is half the initial number. Figure 24 shows the optimization iterative of SA algorithm for the layout optimization and the layouts of actuators for selected iteration steps. Here, the iteration number starts to accumulate from the iteration where feasible solutions are first generated.

Table 14 Objective value and constraint values for the layout optimization

Fig. 24

Iteration history of the objective value for the layout optimization

As seen from the layout of the final step in Figs. 24, 30 and 42 groups of actuators are retained for surface A and surface B, respectively. The number of actuators in the former varies more. After layout optimization, the actuators are mainly distributed in areas with large deformations. This phenomenon is similar to that for the example presented in Section 7.2.1, indicating that in the dynamic shape control, more actuators are needed in the larger deformation areas.

Figure 25 shows the voltage distribution at time t₆ for the layout optimization. Here, t₆ is the time interpolation point with the maximum voltage. We can see that most of the remaining actuators are those with relatively high initial voltages.

Fig. 25

Voltage distribution at time t₆ for the layout optimization

7.3 Analysis and discussion for computational performance

All examples in this paper were computed on a desktop PC with an Intel Core i7-4790 CPU and 8 GB memory. In addition, the codes of shape control in this paper were implemented in the self-programming MATLAB software.

For the model with 8 × 8 meshes in example 7.2.1, the total number of structural DOF (degrees of freedom) is 1350. For one complete dynamic shape control process, that is, an inner optimization calculation, it takes about 10.2 s. The computational performances for the cases with the minimum variance as the objective function are shown in Table 15, and the computational performances for the cases with the minimum number of actuators as the objective function are shown in Table 16.

Table 15 Computational performances for the cases with the minimum variance as the objective function

Table 16 Computational performances for the cases with the minimum number of actuators as the objective function

As can be seen from Table 15, the number of design variables for the integrated optimization is more than that for layout optimization. Therefore, the integrated optimization requires more outer optimization analyses (cooling iterations).

According to the results in Table 16, under the premise of the same type and number of design variables, the model with more relaxed constraint requires fewer outer optimization analyses.

In example 7.2.2, the total number of structural DOF is 2736. For one complete inner optimization calculation, it takes about 25.3 s. The computational performances can be seen in Table 17.

Table 17 Computational performances in example 7.2.2

As can be seen from Table 17, the case with the minimum variance as the objective function has the same variable type as the integrated optimization in Table 15, but it requires more outer optimization analyses due to the large number of variables.

8 Conclusions

Considering the difficulties caused by the time-varying nature of the dynamic shape control of laminated curved shells, an integrated design optimization model of structure and control is proposed to improve the control precision while reducing the number of actuators. The time domain variance between the controlled and desired dynamic shapes is minimized as the objective function. Constraints on the structural mass, the total energy, the maximum transient voltage and the number of actuators are considered to satisfy the engineering requirements. The time-varying actuator voltages, the actuator layout and the structural ply thicknesses and ply angles are considered as the design variables. Because the control voltages are transient and varying in time, a two-level optimization strategy is adopted. In the inner optimization problem, by combining the Newmark integral method and the Kuhn-Tucker condition, the optimal time-varying voltage distribution of the actuators is obtained. In the outer optimization problem, because of the coexistence of discrete and continuous variables, an SA algorithm is used. A finite element formulation of an eight-node laminated curved shell element with piezoelectric actuators is derived. Numerical examples validate the effectiveness of the two-level optimization strategy proposed in this paper and yield the following main conclusions:

• (1) The dynamic shape of a structure can be successfully controlled by optimizing only the time-varying voltages, but the maximum transient voltage cannot be limited in this case. When the actuator layout and time-varying voltages are optimized simultaneously, a maximum transient voltage constraint can be applied, and the control precision is improved, although the improvement is relatively small. Through integrated design optimization of the actuator layout, time-varying voltages and structural ply parameters, additional constraints can be considered, and the control precision can be greatly improved.

• (2) In the integrated design optimization problem, the actuator layout is coupled with the structural ply parameters. The optimal actuator layout and time-varying voltages will be different with different ply parameters, which is why the integrated design optimization method for dynamic shape control offers higher precision.

• (3) For a given precision requirement in dynamic shape control, the number of curved shell elements required is smaller than the required number of flat shell elements in the finite element model. To reduce the system complexity, we can use curved shell actuators to reduce the necessary number of actuators. Moreover, the number of curved actuators and the acceptable precision can be used as the optimization objective and constraint, respectively, to further reduce the number of actuators.