1 Introduction

Curved shell structures are widely used in engineering applications such as aerospace, submarine and automobile industries. As more and more stringent performance requirements are imposed in these advanced engineering applications, considerable attention should be paid to the control of structural vibration and acoustic radiation of curved shell structures.

One way to reduce vibration and acoustic radiation is to perform passive design with the help of systematic optimization methods. Passive control can be achieved by means of these measures such as using damping materials, tailoring structural material, changing structural thickness or geometry, modifying the boundary conditions and adding auxiliary structures masses, ribs or other stiffeners to the structure. These measures can be applied during the design phase of structural components. Many works have been focused on those measures for minimal sound radiation. Zhang and Kang (2013) implemented the topology design of damping layers to reduce sound radiation of shell structures based on the sensitivity analysis of sound pressure. Yang and Du (2013), Xu et al. (2011) respectively dealt with topology optimization problems of the periodic microstructure and the composite material plate with respect to minimization of the sound power radiation. Belegundu et al. (1994) optimized the thickness of the baffled plate to minimize the radiated acoustic power using gradient-based optimization algorithm. Yuksel et al. (2012) employed differential evolution to find the optimum thickness of the vibrating panels to reduce interior noise. Kaneda et al. (2002) optimized the geometry curvature of a plate to reduce the sound power based on a genetic algorithm. Jeon and Okuma (2004) fulfilled the noise reduction using bending optimization based on the particle swarm algorithm. Cheng et al. (2011) studied the structural shape optimization for minimizing the sound radiation. Denli and Sun (2008) minimized the sound radiation by designing boundary supports of the structures. Joshi et al. (2010) and Kaneda et al. (2003) respectively optimized the placements of the curvilinear stiffeners and masses to reduce the sound radiation.

Unlike passive control, active control can be implemented to reduce the sound radiation without major structural modification. Active noise control (ANC) and active structural acoustic control (ASAC) are considered as two main strategies and have been widely studied (Fuller and Von Flotow 1995; Kuo and Morgan 1999). In ANC system, amplifiers are used to generate the signal out of phase with respect to original noise signal, hence leading to its local reduction. ASAC is different from ANC, since ASAC applies control force inputs to structure itself directly rather than exciting the acoustic medium with loudspeakers. It is a very promising method for reducing the structural radiated sound. The applications of ASAC have been reported (Belanger et al. 2009; Sors and Elliott 2002; Zhang et al. 2011). Many factors affect the performance of ASAC including the number, size, location of the piezoelectric sensors and actuators as well as the control gain, and thus efforts to optimize these parameters are essential to improve the performance of the ASAC system (Kim and Ko 1998). So far there are a limited number of literatures devoted to optimizing some parameters for minimizing the sound radiation. Ruckman and Fuller (1995) optimized the location of actuators to reduce the total radiated power using subset selection. Oude Nijhuis and Ad (2003) used a genetic algorithm to find the optimal actuator and sensor locations for the minimum radiated sound power over a broad-band frequency range. Li et al. (2004) employed genetic algorithms to optimize the locations of PZT actuators in an ASAC system comprising a cylindrical shell with an internal floor partition. Choi (2006) optimized the placement of the piezoelectric actuators for minimal radiated sound power. Zhang et al. (2014) developed a topological design method to find the optimal layout of electrode coverage of piezoelectric sensors/actuators. However, these efforts were focused on the placement optimization of actuators without considering other parameters that affect the control effect. In the work of Wang et al. (1994), although the optimal actuator locations and the optimal control voltages were investigated for reducing the sound radiation, the optimal control voltages were computed using the linear quadratic optimal control theory (LQOCT) separately from solving the optimization problem of actuator configuration. Hence, it remains a challenging problem to simultaneously optimize multiple parameters affecting the control effect of the sound radiation.

The aforesaid design optimizations were carried out based on one of the passive and active measures, and have made certain achievement in the reduction of sound radiation. However, few studies have been done on the minimization of sound radiation simultaneously based on both measures. If such a design issue is explored, it may reduce the sound radiation more.

In many applications, it is usually not practical to apply a full-coverage piezoelectric actuator/sensor layer treatment, which may consume a lot of piezoelectric materials, complicate the circuit of the control system and may not achieve the best control effect. It is thus highly desired to find the optimal distribution of piezoelectric actuators/sensors within the allowable number to improve this situation. In addition, pure active control for reducing the sound radiation may require more control power, in order to maximally reduce the structural sound radiation and save control power, the thickness distribution of the base structure should be considered in the design phase. Therefore, it would be ideal to find a way to minimize the sound radiation.

To address this issue, an acoustic radiation control design problem considering the structural mass constraint and the limitation on number of actuators is formulated as a design optimization of structural thickness and control system. The piezoelectric layers are bonded on both sides of the base shell acting as sensors and actuators and they share the same distribution. Using the velocity feedback algorithm, the sensor and actuator are combined to form the closed-loop control system. The curved shell structure is modeled with the finite element method for the structural dynamic analysis. The sound radiation analysis is approximated by the Rayleigh integral. In the optimization model, the sound power is taken as the objective function, the thickness of the base shell elements and the location of sensors/actuators as well as control gains are chosen as the design variables. Because the continuous variables (thicknesses, control gains) and discrete variables (locations) coexist, the optimization problem is solved by the simulated annealing algorithm.

The remainder of this paper is organized as follows. In Section 2, a finite element formulation of the piezoelectric structure excited by external harmonic load is presented, and the sound radiation analysis is treated by the Rayleigh integral. A eight-node curved shell element is used. The base shell element and the piezoelectric shell element are directly coupled by nodal displacement constraint equations. Section 3 proposes the integrated optimization model and the optimization approach. In Section 4, numerical examples are given to demonstrate the validity of the proposed scheme. Finally, Section 5 contains some concluding remarks.

2 Vibration and sound radiation analysis under piezoelectric active control

2.1 Coupling curved shell element

2.1.1 Curved shell element

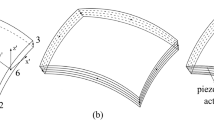
The curved shell element with eight nodes is shown in Fig. 1. The element can be described by the natural coordinate system ξ − η − ζ (ξ,  η,  ζ ∈ [−1, 1]), where the curvilinear coordinates (ξ − η)are in the shell mid-surface while ζ is the linear coordinate in the thickness direction. The displacement field of an arbitrary point in the shell element are derived by Cook et al. (1989)

$$ \left\{\begin{array}{c}\hfill u\hfill \\ {}\hfill v\hfill \\ {}\hfill w\hfill \end{array}\right\}=\sum_{i=1}^n{N}_i\left(\xi, \eta \right)\left\{\begin{array}{c}\hfill {u}_i\hfill \\ {}\hfill {v}_i\hfill \\ {}\hfill {w}_i\hfill \end{array}\right\}+\sum_{i=1}^n{N}_i\left(\xi, \eta \right)\zeta \frac{t_i}{2}\left[\begin{array}{cc}\hfill -{l}_{2 i}\hfill & \hfill {l}_{1 i}\hfill \\ {}\hfill -{m}_{2 i}\hfill & \hfill {m}_{1 i}\hfill \\ {}\hfill -{n}_{2 i}\hfill & \hfill {n}_{1 i}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\alpha}_i\hfill \\ {}\hfill {\beta}_i\hfill \end{array}\right\} $$
(1)
Fig. 1
figure 1

Schematic of a curved shell element

Full size image

where {u i   v i   w i   α i   β i }T is the generalized displacement of ith node. t i is the element thickness. {l ji , m ji , n ji }T( j = 1, 2, 3) is the thickness-direction cosine vector. The shape functions N i (ξ, η) in (1) are given as follows

$$ \begin{array}{l}{N}_i\left(\xi, \eta \right)=\frac{1}{4}\left(1+{\xi}_i\xi \right)\left(1+{\eta}_i\eta \right)\left({\xi}_i\xi +{\eta}_i\eta -1\right)\kern1em \left( i=1,2,3,4\right)\\ {}\kern2.5em {\eta}_i=0,{N}_i\left(\xi, \eta \right)=\frac{1}{2}\left(1+{\xi}_i\xi \right)\left(1-{\eta}^2\right)\kern1em \left( i=5,7\right)\\ {}\kern2.5em {\xi}_i=0,{N}_i\left(\xi, \eta \right)=\frac{1}{2}\left(1-{\xi}^2\right)\left(1+{\eta}_i\eta \right)\kern1em \left( i=6,8\right)\end{array} $$
(2)

Strains of the element can be expressed in terms of displacement derivatives

$$ \left\{\begin{array}{c}\hfill {\varepsilon}_x\hfill \\ {}\hfill {\varepsilon}_y\hfill \\ {}\hfill {\varepsilon}_z\hfill \\ {}\hfill {\gamma}_{x y}\hfill \\ {}\hfill {\gamma}_{y z}\hfill \\ {}\hfill {\gamma}_{z x}\hfill \end{array}\right\}=\varGamma \left\{\begin{array}{c}\hfill {u}_{, x}\hfill \\ {}\hfill {u}_{, y}\hfill \\ {}\hfill {u}_{, z}\hfill \\ {}\hfill {v}_{, x}\hfill \\ {}\hfill {v}_{, y}\hfill \\ {}\hfill {v}_{, z}\hfill \\ {}\hfill {w}_{, x}\hfill \\ {}\hfill {w}_{,\mathrm{y}}\hfill \\ {}\hfill {w}_{, z}\hfill \end{array}\right\}=\varGamma \left[\begin{array}{ccc}\hfill {\mathbf{J}}^{-1}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill {\mathbf{J}}^{-1}\hfill & \hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{J}}^{-1}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {u}_{,\xi}\hfill \\ {}\hfill {u}_{,\eta}\hfill \\ {}\hfill {u}_{,\zeta}\hfill \\ {}\hfill {v}_{,\xi}\hfill \\ {}\hfill {v}_{,\eta}\hfill \\ {}\hfill {v}_{,\zeta}\hfill \\ {}\hfill {w}_{,\xi}\hfill \\ {}\hfill {w}_{,\eta}\hfill \\ {}\hfill {w}_{,\zeta}\hfill \end{array}\right\} $$
(3)

with

$$ \varGamma =\left[\begin{array}{ccccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right] $$
(4)

where J −1is the inverse of Jacobian matrix J. Let ε = {ε x   ε y   ε z   γ xy   γ yz   γ zx }T and \( {\mathbf{d}}_i^e={\left\{{u}_i\kern0.5em {v}_i\kern0.5em {w}_i\kern0.5em {\alpha}_i\kern0.5em {\beta}_i\right\}}^T \), from (1) and (3) the relationship between strain and displacement can be obtained as

$$ \boldsymbol{\upvarepsilon} =\sum_{i=1}^n{\mathbf{B}}_i{\mathbf{d}}_i^e $$
(5)

and

$$ {\mathbf{B}}_i=\varGamma \left[\begin{array}{ccc}\hfill {\mathbf{J}}^{-1}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill {\mathbf{J}}^{-1}\hfill & \hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{J}}^{-1}\hfill \end{array}\right]\left[\begin{array}{ccccc}\hfill {N}_{i,\xi}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\zeta {t}_i{N}_{i,\xi}{l}_{2 i}/2\hfill & \hfill \zeta {t}_i{N}_{i,\xi}{l}_{1 i}/2\hfill \\ {}\hfill {N}_{i,\eta}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\zeta {t}_i{N}_{i,\eta}{l}_{2 i}/2\hfill & \hfill \zeta {t}_i{N}_{i,\eta}{l}_{1 i}/2\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{t}_i{N}_i{l}_{2 i}/2\hfill & \hfill {t}_i{N}_i{l}_{1 i}/2\hfill \\ {}\hfill 0\hfill & \hfill {N}_{i,\xi}\hfill & \hfill 0\hfill & \hfill -\zeta {t}_i{N}_{i,\xi}{m}_{2 i}/2\hfill & \hfill \zeta {t}_i{N}_{i,\xi}{m}_{1 i}/2\hfill \\ {}\hfill 0\hfill & \hfill {N}_{i,\eta}\hfill & \hfill 0\hfill & \hfill -\zeta {t}_i{N}_{i,\eta}{m}_{2 i}/2\hfill & \hfill \zeta {t}_i{N}_{i,\eta}{m}_{1 i}/2\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{t}_i{N}_i{m}_{2 i}/2\hfill & \hfill {t}_i{N}_i{m}_{1 i}/2\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {N}_{i,\xi}\hfill & \hfill -\zeta {t}_i{N}_{i,\xi}{n}_{2 i}/2\hfill & \hfill \zeta {t}_i{N}_{i,\xi}{n}_{1 i}/2\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill {N}_{i,\eta}\hfill & \hfill -\zeta {t}_i{N}_{i,\eta}{n}_{2 i}/2\hfill & \hfill \zeta {t}_i{N}_{i,\eta}{n}_{1 i}/2\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{t}_i{N}_i{n}_{2 i}/2\hfill & \hfill {t}_i{N}_i{n}_{1 i}/2\hfill \end{array}\right] $$
(6)

The complete strain-displacement matrix is B = [B 1  B 2 ⋯  B 8]. Combining the material property matrix D, the stiffness matrix of a curved shell element can be derived as

$$ {\mathbf{K}}^e={\int}_{-1}^1{\int}_{-1}^1{\int}_{-1}^1{\mathbf{B}}^T\mathbf{DB}\left|\mathbf{J}\right| d\xi d\eta d\zeta $$
(7)

2.1.2 Piezoelectric curved shell element

The electric potential φ at any point within the element is related to the corresponding node values φ i (ζ) by \( \varphi =\sum_{i=1}^n{N}_i\left(\xi, \eta \right){\varphi}_i\left(\zeta \right) \). Therefore, the electric field vector E related to the electric potential φ can be expressed in terms of nodal variables as:

$$ \mathbf{E}=-\nabla \varphi =-{\mathbf{B}}_{\varphi}{\boldsymbol{\upvarphi}}^e $$
(8)

where φ e = {φ 1  φ 2  φ 3  φ 4  φ 5  φ 6  φ 7  φ 8}T is the electric potential vector, B φ  = ∇N in which ∇ is the gradient operator and N = [N 1  N 2  N 3  N 4  N 5  N 6  N 7  N 8] is the shape function matrix.

Considering the electrical-mechanical coupled effects of the piezoelectric element, the coupling stiffness matrix can be written as

$$ {\mathbf{K}}_{d\varphi}^e={\int}_{\Omega_e}{\mathbf{B}}^T{\mathbf{e}}^T{\mathbf{B}}_{\varphi} d\Omega $$
(9)

where e is the piezoelectric constant matrix.

2.1.3 Linkage of the piezoelectric shell and base shell elements

The piezoelectric layers are attached to both sides of the base shell structure. In order to reduce the computing scale and improve the computational efficiency, the nodal degrees of freedom of the piezoelectric shell elements are merged into the base shell element. It is assumed that the piezoelectric shell and base shell structure are linked directly, as shown in Fig. 2. According to the nodal displacement constraint equations (Wang et al. 2009), the nodes of the piezoelectric elements and base structure elements can be coupled in the local coordinate system.

Fig. 2
figure 2

Schematic of the connection between the base shell element and piezoelectric shell elements

Full size image

The generalized displacements of nodes in the base shell element and piezoelectric shell element can be respectively depicted in local coordinates as follows:

$$ \begin{array}{l}\kern1em {{\mathbf{d}}^{\hbox{'}}}_{bi}={\left({u^{\hbox{'}}}_{bi}\kern0.5em {v^{\hbox{'}}}_{bi}\kern0.5em {w^{\hbox{'}}}_{bi}\kern0.5em {\alpha^{\hbox{'}}}_{bi}\kern0.5em {\beta^{\hbox{'}}}_{bi}\right)}^T\\ {}{{\mathbf{d}}^{\hbox{'}}}_{pi^{\hbox{'}}}={\left(\begin{array}{ccccc}\hfill {u^{\hbox{'}}}_{pi^{\hbox{'}}}\hfill & \hfill {v^{\hbox{'}}}_{pi^{\hbox{'}}}\hfill & \hfill {w^{\hbox{'}}}_{pi^{\hbox{'}}}\hfill & \hfill {\alpha^{\hbox{'}}}_{pi^{\hbox{'}}}\hfill & \hfill {\beta^{\hbox{'}}}_{pi^{\hbox{'}}}\hfill \end{array}\right)}^T\end{array} $$
(10)

To illustrate the relationship between the piezoelectric elements and base shell element, we take node 1 of the base shell element and node 1′ (1u’ and 1l’) of the piezoelectric shell elements as example (see Fig. 2). The generalized displacements of two nodes satisfy the following constraint equation in the local coordinate system.

$$ {{\mathbf{d}}^{\hbox{'}}}_{p{1}^{\hbox{'}}}={{\mathbf{cd}}^{\hbox{'}}}_{b1} $$
(11)

with

$$ \mathbf{c}=\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \pm \frac{1}{2}\left({t}_p+{t}_b\right)\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \mp \frac{1}{2}\left({t}_p+{t}_b\right)\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right] $$
(12)

where c is the nodal constraint matrix in the local coordinate system. The sign '±' represents the location of the piezoelectric layer, beneath or over the base shell. t p and t b are the thicknesses of the piezoelectric element and base shell element respectively. Considering that the other nodes of two elements also satisfy (11), the constraint equation for all nodes of two elements can be obtained in the global coordinate system.

$$ {{\mathbf{d}}^{\hbox{'}}}_p=\overline{\mathbf{C}}{{\mathbf{d}}^{\hbox{'}}}_b $$
(13)

where \( \overline{\mathbf{C}} \) is the element constraint matrix in the global coordinates. Based on the matrix \( \overline{\mathbf{C}} \), the stiffness of the piezoelectric shell element is added to the stiffness of the base shell element as the additional stiffness of the base structure.

$$ {\overline{\mathbf{K}}}_p^e={\overline{\mathbf{C}}}^T{\mathbf{K}}_p^e\overline{\mathbf{C}} $$
(14)

where \( {\mathbf{K}}_p^e \) is the stiffness matrix of the piezoelectric shell element. Combining with the stiffness \( {\mathbf{K}}_b^e \)of the base shell element, the stiffness \( {\mathbf{K}}_c^e \)of the coupled structure can be obtained:

$$ {\mathbf{K}}_c^e={\mathbf{K}}_b^e+{\overline{\mathbf{K}}}_{p_u}^e+{\overline{\mathbf{K}}}_{p_l}^e $$
(15)

2.2 Governing equations for active control of piezoelectric curved shells

Besides the mechanical displacement degrees of the freedom, every coupling curved shell element has two additional electric degrees of freedom. The piezoelectric structure is modeled by the coupling curved shell elements. Using Hamilton's principle and assembling all the elements, the governing equations of the piezoelectric system are (Liew et al. 2004)

$$ \mathbf{M}\ddot{\mathbf{d}}+{\mathbf{C}}_u\dot{\mathbf{d}}+\mathbf{Kd}+{\mathbf{K}}_{d\varphi}\boldsymbol{\upvarphi} =\mathbf{F} $$
(16)
$$ {\mathbf{K}}_{\varphi d}\mathbf{d}-{\mathbf{K}}_{\varphi \varphi \kern0.5em }\boldsymbol{\upvarphi} =\mathbf{Q} $$
(17)

where M, C u and K are the structural mass, damping and stiffness matrices respectively, K dφ represents the electrical-mechanical coupling matrix, \( {\mathbf{K}}_{\varphi d}^T={\mathbf{K}}_{d\varphi}=\sum_{e=1}^{N_e}{\mathbf{K}}_{d\varphi}^e \), \( {\mathbf{K}}_{\varphi \varphi}=\sum_{e=1}^{N_e}{\int}_{\Omega_e}{\mathbf{B}}_{\varphi}^T{\boldsymbol{\upxi} \mathbf{B}}_{\varphi} d\Omega \) is the dielectric stiffness matrix of piezoelectric layer in which ξ is the dielectric coefficient matrix and N e is the number of piezoelectric elements, F is the mechanical force vector and Q is the electrical charge vector.

For the sensor layer, the applied charge Q s is the zero vector in which subscript ‘s’ denotes the sensors. The distribution of electric potential on the sensor surface is obtained in terms of the mechanical displacement coordinates through electrical-mechanical coupling \( {\mathbf{K}}_{\varphi d}^s \) from (17) as follows:

$$ {\boldsymbol{\upvarphi}}_s={{\mathbf{K}}_{\varphi \varphi}^s}^{-1}{\mathbf{K}}_{\varphi d}^s\mathbf{d} $$
(18)

Substituting (18) into (16) results in a dynamic equation for the sensor layer,

$$ \mathbf{M}\ddot{\mathbf{d}}+{\mathbf{C}}_u\dot{\mathbf{d}}+\overline{\mathbf{K}}\mathbf{d}=\mathbf{F} $$
(19)

with

$$ \overline{\mathbf{K}}=\mathbf{K}+{\mathbf{K}}_{d\varphi}^s{{\mathbf{K}}_{\varphi \varphi}^s}^{-1}{\mathbf{K}}_{\varphi d}^s $$
(20)

For the actuator layer, the converse piezoelectric is applied. The electric potential vector on the actuator surface is the known input and appears as the external force through electrical-mechanical coupling \( {\mathbf{K}}_{d\varphi}^a \) in which subscript ‘a’ denotes the actuator. Thus, the control force term \( {\mathbf{K}}_{d\varphi}^a{\boldsymbol{\upvarphi}}_a \) on the left side of (16) is moved to the right side as

$$ \mathbf{M}\ddot{\mathbf{d}}+{\mathbf{C}}_u\dot{\mathbf{d}}+\mathbf{Kd}=\mathbf{F}-{\mathbf{K}}_{d\varphi}^a{\boldsymbol{\upvarphi}}_a $$
(21)

For the overall system, the governing equation can be expressed as

$$ \mathbf{M}\ddot{\mathbf{d}}+{\mathbf{C}}_u\dot{\mathbf{d}}+\overline{\mathbf{K}}\mathbf{d}=\mathbf{F}-{\mathbf{K}}_{d\varphi}^a{\boldsymbol{\upvarphi}}_a $$
(22)

As a closed loop control system, the sensor output voltage can be fed back through an amplifier to the actuator. Thus,

$$ {\boldsymbol{\upvarphi}}_a=\mathbf{G}{\dot{\boldsymbol{\upvarphi}}}_s={{\mathbf{GK}}_{\varphi \varphi}^s}^{-1}{\mathbf{K}}_{\varphi d}^s\dot{\mathbf{d}} $$
(23)

where \( \mathbf{G}=\operatorname{diag}\left\{{G}_1\kern1em {G}_2\kern1em \dots \kern1em {G}_{N_e}\right\} \) is the feedback gain. Use of (23) in (22) introduces an equivalent velocity feedback in the system as follows:

$$ \mathbf{M}\ddot{\mathbf{d}}+\left({\mathbf{C}}_u+{\mathbf{C}}_A\right)\dot{\mathbf{d}}+\overline{\mathbf{K}}\mathbf{d}=\mathbf{F} $$
(24)

with

$$ {\mathbf{C}}_A={\mathbf{K}}_{d\varphi}^a{{\mathbf{GK}}_{\varphi \varphi}^s}^{-1}{\mathbf{K}}_{\varphi d}^s $$
(25)

where C A is the active damping matrix produced by piezoelectric actuators. Assume the structural vibration is excited by a time-harmonic mechanical loading vector F = f e iωt with the frequency ω and amplitude vector f. (24) can be described as

$$ \left[-{\omega}^2\mathbf{M}+\mathrm{i}\kern0.20em \omega \left({\mathbf{C}}_u+{\mathbf{C}}_A\right)+\overline{\mathbf{K}}\right]\mathbf{u}=\mathbf{f} $$
(26)

where u is the complex amplitude of the displacement response d.

2.3 Sound radiation analysis

For systems having simple near-planar geometry, a Rayleigh integral approximation yields a good approximation (Holland and Fahy 1997; Kaneda et al. 2003). The acoustic pressure at any field point from harmonically vibrating small-curvature plate embedded in infinite baffle is given by

$$ p(P)\approx i\omega \rho {\int}_S{e}^{- ikr}{v}_n(Q)/2\pi RdS(Q) $$
(27)

Here, p(P)is the acoustic pressure at the arbitrary field point P, v n (Q) is the normal velocity at a point Q on the surface of radiating structure, k = ω/c denotes the wave number, c is the sound speed, R = |Q − P| represents the distance between the field point P and source point Q. The sound power radiated from the structure surface can be obtained by

$$ W=\frac{1}{2}{\int}_S\operatorname{Re}\left[ p(P){v}_n^{\ast }(P)\right] dS(P) $$
(28)

where \( {v}_n^{\ast }(P) \) is the complex conjugate of v n (P), respectively; Re[ ] represents the real part of a complex number. Substituting (27) into (28) yields

$$ W=\frac{\omega \rho}{4\pi}{\int}_S{\int}_S{v}_n(Q)\frac{ \sin kR}{R}{v}_n^{\ast }(P) dS(Q) dS(P) $$
(29)

A discretized form for this expression in terms of finite element degrees of freedom can be written in elemental form as

$$ W=\frac{\omega \rho}{4\pi}\sum_{r=1}^{N_e}\sum_{s=1}^{N_e}{J}_r{J}_s{\mathbf{v}}_{nr}^H\frac{ \sin kR}{R}{\mathbf{v}}_{ns} $$
(30)

where N e is the number of elements, J r and J s are the values of the Jacobian matrix, and superscript H denotes conjugation transpose. Assembling \( {v}_n^l \) and the sound power can be written as

$$ W=\frac{1}{2}{\mathbf{v}}_n^H{\mathbf{Zv}}_n $$
(31)

where v n is a global vector of node normal velocity, Z is a global impedance matrix and a symmetric, positive definite matrix, and it is assembled from element matrices as

$$ \mathbf{z}=\frac{\omega \rho}{2\pi}{J}_r{J}_s\frac{ \sin kR}{R}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill \dots \hfill & \hfill 1\hfill \\ {}\hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill \end{array}\right) $$
(32)

here, the rows of matrix z correspond to the node numbers of the receiver element while the columns correspond to those of the source element.

The global normal velocity vector v n in (31) is related to the structural velocity vector by the transformation matrix T

$$ {\mathbf{v}}_n=\mathbf{Tv}=\mathrm{i}\omega \mathbf{Tu} $$
(33)

3 Design optimization modeling and solution algorithm

3.1 Problem formulation

The aim of the considered optimization problem is to simultaneously find the optimal structural thickness and the optimal distribution of actuators/sensors as well as the optimal control gains while minimizing the sound power with the limitation on number of actuators. The optimization problem can be stated as

$$ \begin{array}{l}\mathrm{Find}\kern0.5em \mathbf{G}=\operatorname{diag}\left\{{G}_1,{G}_2,\cdots, {G}_{N_e}\right\}\\ {}\kern2.5em \mathbf{t}={\left({t}_1,{t}_2,\cdots, {t}_{N_e}\right)}^T\\ {}\kern2.4em \mathbf{X}={\left({X}_1,{X}_2,\cdots, {X}_{N_e}\right)}^T\\ {} \min \kern0.5em f\left(\mathbf{X},\mathbf{G},\mathbf{t}\right)= W\\ {}\kern-0.1em \mathrm{s}.\mathrm{t}.\kern0.8em M\le \overline{M}\kern2.7em N\le \overline{N}\\ {}\kern2em {X}_e=1\kern0.5em \mathrm{or}\kern0.5em 0\kern2.5em \\ {}\kern1.9em \underset{\bar{\mkern6mu}}{G}\le {G}_e\le \overline{G}\kern1.5em \\ {}\kern1em \underset{\bar{\mkern6mu}}{t}\kern0.5em \le {t}_e\le \overline{t}\kern2em e=1,2,\cdots {N}_e\end{array} $$
(34)

where M and \( \overline{M} \) are the total mass of the base structure and its upper limit. N and \( \overline{N} \) are the number of sensors/actuators and the allowable number. X is the placement vector of piezoelectric sensors and actuators, X e  = 1 denotes the presence of the eth piezoelectric sensor and actuator, whereas X e  = 0 means the absence. \( \underset{\bar{\mkern6mu}}{G} \) and \( \overline{G} \) are the lower and the upper limits of the control gain. t represents the thickness vector of the base structure. t e is the thickness of the eth base shell element. \( \underset{\bar{\mkern6mu}}{t} \) and \( \overline{t} \) are the lower and upper limits of the thickness of the base structure.

This optimization problem involves the topological design of the piezoelectric actuators/sensors. Up to now, many topological methods have been proposed and successfully applied to various fields. For details, the reader is referred to the review papers by Sigmund and Maute (2013), Deaton and Grandhi (2014), and the studies by Baumann and Kost (2005), and Zhu et al. (2016), and a large number of papers cited therein. Besides, the optimization problem in this paper encompasses the structural size design and control parameter design. This is an optimization problem with mixed design variables. Gradient-based algorithms were used to solve the mixed-variable optimization problems in papers (Zhu et al. 2009; Zhu and Zhang 2010). These algorithms are efficient in computation but may have the risk of misleading, with local optima being found. As an alternative, stochastic methods are believed to be applicable to the optimization problem with irregular constraint and a larger number of local minima (Kane and Schoenauer 1996; Shim and Manoochehri 1997). In this paper a simple and efficient simulated annealing algorithm is adopted for problem-solving.

3.2 Optimization algorithm

The simulated annealing algorithm is a stochastic search optimization technique derived from statistical mechanics. This algorithm cannot guarantee convergence to the global optima (Sigmund 2011). However, it does provide reasonable mechanisms of stochastic search in the entire solution space, and has the ability to jump out of local optimum solutions, thereby improving the probability and ability of finding the global optima. One advantage of this algorithm is that it can provide a clear design because finite elements are explicitly defined as existent or absent. Other advantage is that it does not require the computation of sensitivities. In addition, it can easily handle the optimization problems with mixed variables (Chen and Su 2002). Its applications in various engineering design have been reported, such as Zhang and Wang (1993), Tinnsten et al. (2002), Hasançebi and Erbatur (2002). The simulated annealing algorithm is only applicable to deal with the unconstrained optimization problems. Therefore, penalty function method is used to transform the constrained optimization problem into an unconstrained optimization problem. All constraints can be expressed by g i (X, G, t) ≤ 0. The transformed optimization problem of (34) can be expressed as follows:

$$ \mathrm{M}\mathrm{in}.\kern0.5em L\left(\mathbf{X},\mathbf{G},\mathbf{t}\right)= f\left(\mathbf{X},\mathbf{G},\mathbf{t}\right)+\left(1+\overset{\frown }{\alpha}\left| f\left(\mathbf{X},\mathbf{G},\mathbf{t}\right)\right|\right)\cdot \left(\sum_{i=1}^m\left| \max \Big(0,{g}_i\left(\mathbf{X},\mathbf{G},\mathbf{t}\right)\Big)\right|\right) $$
(35)

where \( \overset{\frown }{\alpha} \) is the penalty factor, m is the number of all constraints.

In the simulated annealing algorithm, the idea of multi-objectives programming is used to solve the discrete variables. Based on the discrete variable \( \mathbf{X}={\left({X}_1,\cdots, {X}_e,\cdots {X}_{N_e}\right)}^{\mathrm{T}} \) with X e  ∈ (0 or 1), the continuous variable \( \mathbf{Y}={\left({Y}_1,\cdots, {Y}_e,\cdots {Y}_{N_e}\right)}^{\mathrm{T}} \) with Y e  ∈ (0, 1) for e ∈ {1, 2, ⋯N e } is introduced where Y e represents the volume density of the eth piezoelectric sensor and actuator. We can rewrite the mass matrix M, the stiffness matrix K and the active damping matrix C A in above equations as

$$ \begin{array}{l}\mathbf{M}=\sum_{e=1}^{N_e}{\mathbf{M}}_b^e+\sum_{e=1}^{N_e}{Y}_e\left({\overline{\mathbf{M}}}_s^e+{\overline{\mathbf{M}}}_a^e\right)\\ {}\mathbf{K}=\sum_{e=1}^{N_e}{\mathbf{K}}_b^e+\sum_{e=1}^{N_e}{Y}_e\left({\overline{\mathbf{K}}}_s^e+{\overline{\mathbf{K}}}_a^e\right)\\ {}{\mathbf{C}}_A=\sum_{e=1}^{N_e}{Y}_e{\mathbf{C}}_A^e\end{array} $$
(36)

where \( {\mathbf{M}}_b^e \) represents the elemental mass matrix of the base shell structure. \( {\overline{\mathbf{M}}}_s^e \) and \( {\overline{\mathbf{M}}}_a^e \) are the additional mass matrices from the piezoelectric sensor and actuator. \( {\overline{\mathbf{K}}}_s^e \) and \( {\overline{\mathbf{K}}}_a^e \) are the additional stiffness matrices from the piezoelectric sensor and actuator. \( {\mathbf{C}}_A^e \) is the active damping matrix of the eth element calculated with the piezoelectric constants of the fully solid material.

The solution of design variable Y e in the kth iteration is generated by

$$ {Y}_e^k={\overline{Y}}_e^k+\varDelta {Y}_e^k $$
(37)

where \( {\overline{Y}}_e^k \) is the initial value of the eth variable; \( \varDelta {Y}_e^k \) is the offset which is dependent on the current temperature and random quantities distributed in [−1,1] as well as the upper and lower bounds of the eth variable in the kth iteration.

The variable \( {\mathbf{Y}}_k={\left({Y}_1^k,\cdots, {Y}_e^k,\cdots {Y}_{N_e}^k\right)}^{\mathrm{T}} \) is corresponding to the variable \( {\mathbf{X}}_k={\left({X}_1^k,\cdots, {X}_e^k,\cdots {X}_{N_e}^k\right)}^{\mathrm{T}} \)by the mapping function \( {X}_e^k=\mathrm{round}\kern0.5em \left({Y}_e^k\right) \), which denotes the integer discrete value nearest to \( {Y}_e^k \).

Assume that L c and L d are the values of the penalty functions L(Y, G, t) and L(X, G, t) respectively. In order to judge whether the design state is accepted in the optimization iteration, the weight value \( \overline{L} \) is defined as

$$ \overline{L}=0.1\cdot {L}_c\kern0.5em +0.9\cdot {L}_d $$
(38)

If \( \min \left[1, \exp \left(-\left({\overline{L}}_k-{\overline{L}}_{k-1}\right)/{KT}_k\right)\right]\ge \mathrm{random}\left(0,1\right) \) in which K is the adaptive factor, accept \( {L}_d^k \), the current value of the variable Y k and the values of variables G k and t k are taken as new solutions for the next iteration. Meanwhile, the values of the variables X k composed of 0 and 1 as well as the values of variables G k and t k are output as current optimal solutions. Figure 3 gives the flow chart of solution strategy based on the SA optimization procedure. For ease of description, the vector x in Fig. 3 is used to represent the design variables in the optimization problem.

Fig. 3
figure 3

Flow chart of the SA optimization procedure

Full size image

4 Numerical examples

The integrated optimization procedure is implemented using MATLAB procedure. Two curved shell structures are simulated to illustrate the validity and applicability of the proposed integrated optimization approach. Here, it is stated that the following optimization examples have not considered gradient control.

4.1 Comparison studies

Example 1: To validate the finite element formulation presented in section 2, in Table 1, the first six natural frequencies of a cylindrical shell panel (18 × 14mesh) with clamped edges are computed and compared to those published in Refs (Cheung et al. 1989; Liew et al. 2000; Petyt 1971; Yang and Shen 2003). The computation data are: L = 0.0762 m, a c  = 0.1016 m,R = 0.762 m, E = 68.948 Gpa, ν = 0.33, ρ s  = 2657.3kg/m3, where a c is the arc length. Good agreement is observed.

Table 1 Comparison of results: natural frequencies (Hz) of a clamped cylindrical shell
Full size table

Example 2: To verify sound power calculation, The radiated sound power level (dB, re: 10−12 W) of a rectangular plate in air is compared with that obtained by (Li and Zhao (2004)), as shown in Fig. 4. The dimensions of the simply supported plate are a = 0.455m ,  b = 0.379m ,  t b  = 0.003m respectively. The material properties of the base plate are E = 210 Gpa, ν = 0.3, ρ s  = 7850kg/m3. A force with amplitude F = 1 N applies at the point located at (0.11375 m, 0.09475 m). Clearly, the comparison shows good agreement.

Fig. 4
figure 4

Radiated sound power versus frequency

Full size image

4.2 Example 3: integrated optimization for the clamped piezoelectric cylindrical shell

4.2.1 Optimal solution

Firstly, we consider the integration optimization of the structural thickness and the placement of actuator as well as control gain for a clamped piezoelectric cylindrical shell, as shown in Fig. 5a. The curvature radius, central angle and thickness of the base shell are 0.5 m, 45 degrees and 3 × 10−3 m respectively. The structural damping is ignored. The Young’s modulus, Poisson’s ratio and mass density of the base material are E = 69 Gpa, ν = 0.33 and ρ = 2700 kg/m3, while those of the piezoelectric material are E p  = 71 Gpa, ν p  = 0.3 and ρ p  = 7600kg/m3. The electrical properties of the piezoelectric material are e 31 = e 32 =  − 5.20C/m2, e 33 = 15.08C/m2, ξ 11 = 13.05nF/m, ξ 22 = 13.054nF/m and ξ 33 = 11.505nF/m respectively. Each piezoelectric layer is 1 × 10−4 m thick. A time-harmonic external force with amplitude F = 1 N is applied at the center point of the structural free end and the excitation frequency is fixed as 153 Hz.. The mass density and sound velocity of the acoustic medium (air) are ρ 0 = 1.21 kg/m3 and c 0 = 343 m/s.

Fig. 5
figure 5

Schematic of the structural geometry (a) and the element mesh (b, c) of a piezoelectric cylindrical shell

Full size image

The structure is discretized by a 8×10 mesh and a 12×15 mesh respectively, as shown in Fig. 5b and c. Then the piezoelectric sensor/actuator layer is also discretized into 8×10 and 12×15 sensor/actuator pairs respectively. The sensor outputs are converted to feedback control voltages via five control gain channels and the control gains are grouped as shown in Fig. 5b and c. From the iteration histories of objective functions shown in Fig. 6, a similar decreasing trend of the objective functions obtained by 8×10 mesh and 12×15 mesh can be observed. The initial and optimized design values obtained by two kinds of meshes are listed in Table 2. The initial sound powers obtained by two kinds of meshes are very close and this proves that the model of 8×10 mesh can achieve the high computational precision. Additionally, the values of control gains and the sound powers of the optimized designs obtained by two kinds of meshes are consistent. The optimized designs for the actuators/sensors and structural thicknesses obtained by two kinds of meshes are shown in Fig. 7. we can find the similarity of optimal solutions obtained by two kinds of meshes. It is also seen from the optimized designs of the two mesh-sizes that the placements of the actuators are substantially consistent with the structural thickness distributions. Figure 8 shows the actuation voltage amplitude distribution in the optimal design. It can be seen that the actuation voltages obtained by the coarse mesh are consistent with those obtained by the finer mesh. But the highest voltage amplitude obtained by the finer mesh is larger than that obtained by the coarse mesh, One reason is that at the position of the actuator with the highest voltage amplitude, the corresponding nodal velocities of the optimized design obtained by the finer mesh are larger than that of the optimized design obtained by the coarse mesh, resulting from the differences between the optimized designs of the two meshes. Another reason is that the coupling matrix and dielectric stiffness matrix of the sensor change with the refinement of mesh. For the model of 8×10 mesh, the iteration history about the number of actuators/sensors and a series of selected intermediate designs of actuators/sensors are shown in Fig. 9. Considering the complexity of the control system and the efficiency of design optimization, the model of 8×10 mesh has been used in the optimization examples.

Fig. 6
figure 6

Iteration histories of the objective functions

Full size image
Table 2 The initial and optimized design parameters of the cylindrical shell modeled by two kinds of mesh
Full size table
Fig. 7
figure 7

Comparison of the optimized results for the distribution of the sensors/actuators (a, c) and structural thickness (b, d) obtained by two kinds of discrete mesh

Full size image
Fig. 8
figure 8

Actuator voltage amplitude distribution for the optimized designs obtained by two kinds of discrete mesh

Full size image
Fig. 9
figure 9

Iteration history about the number of sensors/actuators and a series of selected intermediate designs for the optimization model with 8×10 mesh

Full size image

4.2.2 Comparison of optimal solutions between thickness optimization, control system optimization and integrated optimization

The optimized designs under excitation frequency 64 Hz are obtained by the following three cases:(a) Case 1: the thicknesses of base shell elements are design variables, and the mass of the base structure is constrained; (b) Case 2: the locations of sensors/actuators and the control gains (G1-G5) are design variables, and only the number of sensors/actuators is constrained; (c) Case 3: the locations of sensors/actuators, control gains (G1-G5) and thicknesses of base shell elements are design variables, the number of sensors/actuators and the mass of the base structure are constraints.

The optimization parameters for three cases are listed in Table 3. As shown in the table, the sound power levels decrease from 103.45 dB in initial design to 75.49 dB in optimal design of Case 1, 83.14 dB in Case 2 and 73.62 dB in Case 3, for about 27.96 dB, 20.31 dB and 29.83 dB respectively, which indicates a significant reduction of sound radiation. Additionally, the constraints of the base structure mass and the number of sensors/actuators for these three cases are all satisfied. The sound power in Case 1 is smaller than that in Case 2. But the number of sensors/actuators in Case 1 is greater than that in Case 2. So Case 1 cannot simplify the complexity of control system. In short, Case 1and Case 2 have their own advantages and disadvantages. Additionally, the sound power in Case 3 decreases more than that in Case 1, and the number of sensors/actuators in Case 3 is the same as that in Case 2, reaching the upper limit. The above conclusions show that the integrated optimization (Case 3) achieves the best objective value in these three cases and simplifies the complexity of control system. The thicknesses of the base shell elements and the optimized locations of sensors/actuators for three cases are shown in Fig. 10. Clearly, the thickness distribution of base shell elements in Case 1 neither agrees with the thickness distribution obtained in Case 3 nor with the placements of sensors/actuators in Case 2 and Case 3. Because the structural resonance frequency is reduced from 64 Hz to 58 Hz in Case 1, but the structural resonance frequency is increased from 64 Hz to 68 Hz in Case 2 and from 64 Hz to 72 Hz in Case 3. Control voltages applied to the actuators after optimization of three cases are given in Fig. 11. It is clear that the amplitude of control voltage in Case 3 is smallest.

Table 3 Summary of design parameters of three cases for the initial and optimized designs
Full size table
Fig. 10
figure 10

Optimized results for the distribution of the structural thickness (a, c) and sensors/actuators (b, d): a Case 1; b Case 2; c Case 3; d Case 3

Full size image
Fig. 11
figure 11

Amplitude distribution of the actuation voltage after optimization in the three cases: a Case 1; b Case 2; c Case 3

Full size image

4.2.3 Optimal solution for excitation frequency

The integrated optimization model under the influence of different excitation frequencies is studied. Here, four different excitation frequencies f=40, 122, 153 and 180 Hz are considered.

The initial and optimized values of design parameters are given in Table 4. It is shown that the decrease of the sound power levels is 4.07 dB for 40 Hz, 20.56 dB for 122 Hz and 18.67 dB for 153 Hz, 3.55 dB for 180 Hz respectively. It is also clear that the constraints of the structural mass and the number of sensors/actuators are all satisfied. The optimized placement of sensors/actuators and the optimized thickness distribution of base shell elements are shown in Figs. 12 and 13, respectively. It is observed that the placement of sensors/actuators is agreement with the thickness distribution of the base shell elements at the same excitation frequency. The optimization solutions shown in Figs. 12 and 13 are depended on the structural mechanical property and the effect of active control. For example, the optimization solutions under frequency 40 Hz are mainly determined by increasing the first structural resonant frequency from 64 Hz to 70 Hz. In other words, retaining the piezoelectric sensors/actuators near the clamped end and moving the base materials to the clamped end make excitation frequency away from the structural resonant frequency so that the sound radiation is reduced. The optimization solutions under excitation frequency 180 Hz are consistent with the layout of the relatively large displacement response, which indicates that the sound radiation is reduced by controlling the structural displacement. The displacement responses of the initial and optimal designs under frequencies 40 Hz and 180 Hz are shown in Fig. 14.

Table 4 Summary of design parameters for the initial and optimized designs at different excitation frequencies
Full size table
Fig. 12
figure 12

Optimized results for the distribution of sensors/actuators at different excitation frequencies: a f = 40 Hz; b f = 122 Hz; c f = 153 Hz; d f = 180 Hz

Full size image
Fig. 13
figure 13

Optimized results for the structural thickness distribution at different excitation frequencies: a f = 40 Hz; b f = 122 Hz; c f = 153 Hz; d f = 180 Hz

Full size image
Fig. 14
figure 14

Displacement responses of the initial design (a, b) and final design (c, d) under frequencies 40 Hz and 180 Hz: a and c f = 40 Hz; b and d f = 180 Hz

Full size image

4.2.4 Optimal solution for a specified excitation frequency band

The optimization problem is to minimize the radiated sound power in the given frequency band 114–172 Hz. The average sound power level of the frequency band 114–172 Hz is chosen as the objective function.

The summary of design parameters for the initial and optimal designs under the frequency band 114–172 Hz is given in Table 5, from which we can find that the decrease of the average sound power is 6.27 dB. Moreover, constraints including the masses of base shell and the number of sensors/actuators are satisfied. The optimized placements of piezoelectric sensors/actuators and thickness distribution contours of the base structure are shown in Fig. 15, which indicates that the placement of sensors/actuators is substantially consistent with the thickness distribution of the base shell elements. Obvious differences can be observed between these optimal solutions and those obtained at individual frequencies f = 122 Hz (see Figs. 12b and 13b) and f = 153 Hz (see Figs. 12c and 13c).The radiated sound power levels for the initial design without/with control and the optimized design obtained under frequency band are compared in Fig. 16. It is shown that the radiated power level at specified frequency has the smallest sound power only in the vicinity of this specific frequency and the solution of the frequency band has a smaller value of the sound power over the whole frequency band of concern.

Table 5 Summary of design parameters for the initial and optimized designs under the excitation frequency band
Full size table
Fig. 15
figure 15

Optimized results for the distribution of the sensors/actuators (a) and structural thickness (b) under the excitation frequency band 114–172 Hz

Full size image
Fig. 16
figure 16

Radiated sound power level for the optimized design and initial design without/with control

Full size image

4.2.5 Optimal solutions for the model with structural damping

In this example, assume that the structural damping is considered and regarded as the proportional damping. The optimization problem with damping coefficient α = β =  5 × 10−4 is considered. Here, the excitation frequency is fixed as 153 Hz.

The parameters for the initial design and optimized design are given in Table 6. It can be seen that the sound power decreases from 71.54 dB in the initial design to 60.05 dB in the final design. By comparison of design parameters in Tables 2 and 6, we find that the structural damping can further significantly reduce the sound radiation from 80.07 dB to 71.54 dB before optimization, and the sound radiation of the optimized design with the structural damping is lower than that of the optimized design without the structural damping. Also, the amount of noise reduction in these two cases achieved by optimization is different. The optimal placement of the actuators/sensors and the optimal thickness distribution are shown in Fig. 17. It is shown that the placement of actuators is similar to the thickness distribution of structural elements. By comparing the optimized designs in Fig.17 with the corresponding ones in Fig.7a and b, some small differences can be observed in the optimized designs. These small differences are found in the small central region near the fixed end and the corners of the free end. In short, the structural damping has marginally affected the optimization results.

Table 6 Parameters for the initial and optimized designs of the model with structural damping
Full size table
Fig. 17
figure 17

Optimized results for the distribution of the sensors/actuators (a) and structural thickness (b) obtained with the structural damping

Full size image

4.3 Example 4: integrated optimization for the simply supported piezoelectric spherical shell

The sound radiation from the piezoelectric spherical shell is studied, see Fig. 18. The certain size spherical shell is obtained by using the rectangle with length 0.6 m and width 0.5 m to cut the sphere with radius 1.5 m. The initial thickness of the spherical shell is 2×10−3 m, and each piezoelectric layer is 1×10−4 m thick. The material properties of the base shell and piezoelectric layer are the same as the example 3. Here, the structural damping is neglected. Four corners of the structure are clamped. The smart structure is modeled by 8×8 uniform elements. There are 64 sensors/actuators and they constitute different closed-loop systems with four control gains (G1-G4) as shown in Fig. 18b. The disturbance is assumed to be a harmonic force with amplitude F = 1 Nand its location is shown in Fig. 18b. The mass density and sound velocity of the acoustic medium are the same as those of example 3.

Fig. 18
figure 18

Schematic of the structural geometry (a) and element mesh (b) of a piezoelectric spherical shell

Full size image

In this example, the thicknesses of base shell elements and the locations of sensors/actuators as well as control gains are optimized for minimizing the average sound power of the broad frequency band 40 Hz - 250 Hz. Iteration history of average sound power in optimization process is shown in Fig. 19 and the initial and optimized values are listed in Table 7. It can be seen that the average sound power under the frequency band decreases from 63.06 dB to 59.89 dB, for about 3.17 dB. Constraints of the base structural mass and the number of sensors/actuators are all satisfied. A series of selected intermediate designs and final design of the piezoelectric sensors/actuators are given in Fig. 20. Figure 21 shows the optimized thickness distribution contours of the base shell elements. It is clear that the placement of sensors/actuators is similar to the thickness distribution of base shell elements. The curve chart of the radiated sound power levels for initial and optimized designs with the frequency increasing is plotted in Fig. 22. It is seen that the peaks of the radiated power for the initial design is decreased by active control and the overall sound power level across the frequency band is significantly decreased by optimization. Actuator voltage amplitudes under the excitation frequencies 88 Hz, 146 Hz and 204 Hz are given in Fig. 23. For the same excitation frequency, the actuators attached to the asymmetrical positions are driven by different voltages, because the nodal velocities at the positions of different actuators are different and the corresponding control gains may be different. For the different excitation frequencies, the same actuator is driven by different voltages, because the nodal velocities at its corresponding position are different under different excitation frequencies.

Fig. 19
figure 19

Iteration history of the objective function under the broad frequency range

Full size image
Table 7 Summary of design parameters for the initial and optimized designs with different damping coefficients
Full size table
Fig. 20
figure 20

A series of selected intermediate designs and final design for the sensor/actuator distribution

Full size image
Fig. 21
figure 21

Optimized result for the structural thickness distribution

Full size image
Fig. 22
figure 22

Comparison of the radiated sound power for the initial design without/with control and the optimized design obtained under a broad excitation frequency range

Full size image
Fig. 23
figure 23

Actuator voltage amplitude distribution at different frequencies: a f = 88 Hz; b f = 146 Hz; c f = 204 Hz

Full size image

5 Conclusion

The vibrating curved shell structure integrated with sensors/actuators is discrete with finite element method in structural dynamic analysis and the sound radiation analysis is treated by the Rayleigh integral. The displacement constraint equation is used to couple the base shell and piezoelectric shell. The active damping of the piezoelectric curved shell is formulated by the velocity feedback algorithm. An integrated optimization model of the vibro-acoustic problem is proposed based on both passive and active measures. The radiated sound power is taken as the design objective to be minimized. The thickness of the base shell and the location of sensors/actuators as well as control gains are assigned as design variables and simultaneously optimized. Since the optimization problem simultaneously exists discrete and continuous variables, the simulated annealing algorithm is employed for solving the optimization model. The results of first two numerical examples verify the correctness and accuracy of the finite element model and acoustic procedure through comparing with the results of the references. The last two numerical examples confirm the feasibility and effectiveness of the presented method. The influences of some factors, including mesh-size, design variable, excitation frequency and structural damping, on the optimized design are studied in the numerical examples. It is seen that the integrated optimization of structural thickness and control system can reduce the number of actuators/sensors and the total sound power better than respective optimizations. These two examples also demonstrate that the radiated sound power at specified excitation frequency, or in a certain frequency band can be significantly reduced by integrated optimization. In particular, the overall sound power level for a given broad frequency band can be well controlled.

To minimize the sound radiation from the vibrating piezoelectric curved shells by integrated optimization, the design has been driven by mechanical property and the effect of active control. For a single excitation frequency near the first resonance frequency, the design is determined mainly by moving the nearest resonance frequency far away from the prescribed excitation frequency, while the design is driven by controlling the vibration amplitudes for the higher excitation frequency and the broad frequency range, and this furnishes significant differences in the optimized designs.

The present work provides us a primary view on the characteristics of integrated design of structure size and control system with respect to acoustic criteria, which may help us to understand further how to improve the vibro-acoustic behavior of the structure by integrated optimization.