1 Introduction

High-fidelity computer simulations play an important role in the investigation of modern engineering systems. However, the computational cost of computer simulations is still excessive even with the current fast developed computer technology, especially for the numerical design optimization of engineering systems. It is an efficient way to reduce the computational cost by replacing the computationally expensive simulations with surrogate models in the investigation and design of complex engineering systems.

There are various surrogate models widely used in the investigation of engineering design, such as polynomial response surface (PRS) (Myers and Montgomery 2002), radial basis function (RBF) (Hardy 1971), kriging (KRG) (Sacks et al. 1989), Gaussian process (GP) (MacKay 1998), neural networks (Smith 1993), and support vector regression (SVR) (Gunn 1997).

The surrogate models are widely used in many research fields, such as surrogate-based optimization (Meng et al. 2019; Imani et al. 2018), adaptive sampling (Li et al. 2010), Bayesian control (Imani et al. 2018), and adaptive filtering (Imani et al. 2017). Generally, there is an optimal surrogate model for a specific research object. And it was proved by many researchers that one individual surrogate tends to perform quite differently for different design problems due to their underlying and dissimilar characteristics (Forrester and Keane 2009; Queipo et al. 2005; Wang and Shan 2007). Simpson et al. (2001) and Jin et al. (2001) provided recommendations on the selection of surrogates for different problems by comparing various surrogate models. However, the behavior of an individual surrogate is unknown in advance. Building an ensemble of surrogates by combining different individual surrogates into a weighted-sum formulation is an efficient method to enhance the accuracy and robustness of the surrogate model.

The ensemble of surrogate models can be categorized into average ensemble model and pointwise ensemble model, according to its weight calculation method:

Average ensemble model

The weights of the average ensemble model stay constant over the entire design space, and the weights are calculated by using a global error measure. There are many approaches for average ensemble modeling. For example, Goel et al. (2007) proposed an average ensemble of surrogates. In their work, the generalized mean square cross-validation error (GMSE) was used to determine the weights as global data-based error measure. Acar and Rais-Rohani (2009) proposed an average ensemble of surrogates, wherein the selection of weight factors was treated as an optimization problem. Viana et al. (2009) proposed an average ensemble of surrogates based on minimization of the mean square error (MSE), and they noted that the use of weighted average surrogate does not seem to have the potential of substantial error reduction with a large number of points. Zhou et al. (2011) obtained the average weights through a recursive process. Ferreira et al. (2016) presented an approach to create ensemble of surrogates based on least squares approximation.

Pointwise ensemble model

The weights of pointwise ensemble model change with the variation of prediction point, and the weights are calculated based on a local error measure. For example, Acar (2010) determined the weight factors of individual surrogate by cross-validation error, and he noted that pointwise cross-validation error is not a good surrogate for the error at a point, even though GMSE is a good representative with respect to the global error. Lee and Choi (2014) proposed to construct the ensemble of surrogates by using v nearest points. Liu et al. (2016) presented an optimal weighted pointwise ensemble. Yin et al. (2018) divided the design space into multiple subdomains, and each domain is assigned a set of optimized weight factors. Chen et al. (2018) divided the design space into two parts, and different strategies were introduced to evaluate the weight factors in each of the two parts.

The potential for average ensemble modeling to improve prediction precision is limited because of the constant weights. The optimal average ensemble model proposed by Viana et al. (2009) is one of the best average ensemble models. However, they also noted that the use of weighted average surrogates does not seem to have the potential for substantial error reduction with a large number of points. Thus, it may be a way to build an accurate pointwise ensemble model by determining the pointwise weight factors based on the minimization of the local error.

Besides, the data-based error measure, such as GMSE and cross-validation error, is widely used in the recent investigation of ensemble modeling. This is because the data-based error measure can provide error estimation for any individual surrogate. The local data-based error measure plays an essential role in building the pointwise ensemble model. Ideally, if an accurate local data-based error measure to identify the error between the individual surrogate model and the real model is available, the pointwise ensemble model must be more accurate than the average ensemble model because the ensemble model can adapt to the local characteristics of each individual surrogate. In previous research, however, the pointwise ensemble model did not exhibit obvious advantage over the average ensemble model as there is no sufficiently accurate local data-based error measure. Thus, one could be able to enhance the accuracy of the pointwise ensemble model by improving the accuracy of the data-based local error measure.

Motivated by these findings, we propose an optimal pointwise weight ensemble (OPWE) based on the minimization of the local mean square error (LMSE). The LMSE is proposed in this paper as criteria for the error of the region near the observed points. Meanwhile, a new local data-based error measure, namely the global-local error (GLE), is proposed in this paper to construct the LMSE.

The remainder of this paper is organized as follows. In Section 2, we review the existing ensembles of surrogates. In Section 3, we describe the proposed ensemble of surrogates in detail. In Section 4, we show the example problems. In Section 5, we present the numerical procedure. The results and discussion appear in Section 6, followed by the summary of important conclusions in Section 7.

2 Existing ensembles of surrogates

2.1 The average ensemble of surrogates proposed by Goel et al. (2007)

Goel et al. used the GMSE as the global error measure to determine the weights using a heuristic formulation:

$$ \begin{array}{@{}rcl@{}} w_{i}&=&\frac{w_{i}^{*}}{{\sum}_{j=1}^{n}w_{j}^{*}}\\ w_{i}^{*}&=&(E_{i}+\alpha E_{avg})^{\upbeta}\\ E_{avg}&=&\frac{{\sum}_{i=1}^{n}E_{i}}{n}\\ \upbeta&<&0,\alpha<1 \end{array} $$
(1)

where wi denotes the weight of the i th surrogate model, n is the total number of the individual surrogates, and Ei denotes the GMSE of the i th surrogate model, which is obtained from the leave-one-out strategy and is calculated as

$$ E_{i}=\frac{{\sum}_{k=1}^{m}(y(k)-\hat{y}(k))^{2}}{m} $$
(2)

In the equation, m is the number of points in the training set, y(k) is the true response at the k th observed point, and \(\hat {y}(k)\) is the corresponding predicted value from the individual surrogate constructed by using all except the k th observed points.

There are two user-defined parameters α and β in this method, which are employed to control the importance of averaging surrogate and the importance of individual surrogate, respectively. Goel et al. (2007) set α = 0.05 and β = − 1 in their study.

2.2 The average ensemble of surrogates proposed by Acar and Rais-Rohani (2009)

Acar and Rais selected weights by solving an optimization problem of the form

$$ \begin{array}{@{}rcl@{}} &&Find\ w_{i}\\ &&Minimize\ GMSE\\ &&s.t. \sum\limits_{i=1}^{n}w_{i}=1 \end{array} $$
(3)

where GMSE is the generalized mean square cross-validation error of the ensemble model, wi is the weight of the i th individual surrogate, and n is the total number of the individual surrogates.

2.3 The average ensemble of surrogates proposed by Vinan et al. (2009)

Viana et al. selected weights by following an approach based on the minimization of the mean square error (MSE):

$$ MSE=\frac{{\int}_{V}e^{2}(\mathbf{x})}{V}=\mathbf{w}^{T}\mathbf{C}\mathbf{w} $$
(4)

where the function e(x) is the error of the ensemble model at x, w is the vector of weights of the individual surrogates, and V denotes the sample space. They approximated the value of C by using the vectors of cross-validation errors, e∗, as

$$ c_{ij}\simeq\frac{\mathbf{e}_{i}^{*T}\mathbf{e}_{j}^{*}}{m} $$
(5)

where m is the number of observed points.

The weights are obtained by minimizing the MSE, as

$$ \begin{array}{@{}rcl@{}} &&Find\ \mathbf{w}\\ &&Minimize\ MSE_{WAS}=\mathbf{w}^{T}\mathbf{C}\mathbf{w} \end{array} $$
(6)

which is subject to

$$ \mathbf{1}^{T}\mathbf{w}=1 $$
(7)

The solution is obtained by using Lagrange multipliers, as

$$ \mathbf{w}=\frac{{\mathbf{C}^{-1}\mathbf{1}}}{\mathbf{1}^{T}\mathbf{C}^{-1}\mathbf{1}} $$
(8)

The solution of (8) may include negative weights as well as weights with values larger than one. Viana et al. suggested to solve (8) using only the diagonal elements of C to enforce the positivity.

2.4 The pointwise ensemble of surrogates proposed by Acar (2010)

Acar proposed that the weight of the individual surrogate with the smallest cross-validation error is one while the other individual surrogates have zero weights. And the spatial weights are calculated by

$$ \begin{array}{@{}rcl@{}} w_{i}(\mathbf{x})&=&\sum\limits_{k=1}^{n}W_{i,k}I_{k}(\mathbf{x})\\ I_{k}(\mathbf{x})&=&\frac{1}{{d_{k}^{2}}(\mathbf{x})}\\ d_{k}(\mathbf{x})&=&\Arrowvert\mathbf{x}-\mathbf{x_{k}}\Arrowvert \end{array} $$
(9)

where Wi,k is the pointwise weight of the i th surrogate at the k th observed point. Wi,k is equal to one for the individual surrogate with the smallest cross-validation error at an observed point, and it is equal to zero for all other individual surrogates. dk(x) is the Euclidian distance between x and xk, and n is the total number of the individual surrogates.

3 The proposed ensemble of surrogates

A pointwise ensemble of surrogates named optimal pointwise weighted ensemble (OPWE) is proposed in this section. The pointwise weight of each individual surrogate at an observed point is determined by minimizing the local error of the region around this observed point. The local mean square error (LMSE) is defined in this section to measure the local error of the region around the observed point. And a new local data-based error measure named global-local error (GLE) is proposed in this section to construct the LMSE.

3.1 Determining the weights at observed points by minimizing the local error

Viana et al. (2009) determined the global weight factors by minimizing the MSE. In their work, the MSE represents the global error of the ensemble model. And we determine the pointwise weight factors at an observed point by minimizing the local error of the region around this observed point. And the LMSE is used to measure this local error:

$$ LMSE_{WAS}(\mathbf{x})=\frac{{\int}_{V^{\prime}}e^{2}(\mathbf{x})d\mathbf{x}}{V^{\prime}}=\mathbf{w(\mathbf{x})}^{T}\mathbf{C}(\mathbf{x})\mathbf{w}(\mathbf{x}) $$
(10)

The formulation of LMSE is similar to MSE, except that the weight and C change with x, where \(V^{\prime }\) denotes the region around the observed point and C is the error matrix. And the weights are calculated as

$$ \mathbf{w(\mathbf{x})}=\frac{(\mathbf{C(\mathbf{x})}^{-1}\mathbf{1})}{(\mathbf{1}^{T}\mathbf{C(\mathbf{x})}^{-1}\mathbf{1})} $$
(11)

Similar to (8), the solution of (11) may include negative weights as well as weights with values larger than one. Viana et al. suggested to solve (8) using only the diagonal elements of C to enforce positivity. In this paper, we solve (11) by using the diagonal elements of C if the solution based on the full elements of C include negative weights or weight values larger than one.

3.2 Approximating the local error of the region around the observed points

The local error of the region around an observed point is not only related to the error of the observed point, but also related to the error of the nearby observed points. Thus, we approximate the elements of the C matrix by using an error measure vector. The elements of C matrix are defined in (12), as

$$ c_{ij}(\mathbf{x})=\frac{\mathbf{e}_{i}^{*}(\mathbf{x})^{T}\bullet \mathbf{e}_{j}^{*}(\mathbf{x})}{v} $$
(12)

where \(e_{i}^{*}(\mathbf {x})\) is the local error measure vector of the i th surrogate at x, and it represents the local error of the region around x. The parameter v denotes the vector dimension of \(e_{i}^{*}(\mathbf {x})\). The local error measure vector of an observed point is constructed with the local error measure of nearby observed points. Meanwhile, the distances between observed points are used to correct the local error measure vector. A new local error measure named GLE, which combines the global error measure and the local error measure, is employed to prevent the bias in error estimation of the local error measure.

The details regarding the calculation of \(e_{i}^{*}(\mathbf {x})\) at each observed point will be shown later in this section.

3.2.1 The combination of the global error measure and the local error measure

Some researchers built average ensemble models using GMSE, and GMSE is a good criterion for the global error to determine weights in the average ensemble model. It is difficult to further improve the accuracy of the average ensemble model due to the constant weights. There are also some researches who built pointwise ensemble models using pointwise cross-validation error. The accuracy of the pointwise ensemble model may improve due to the pointwise weights. However, the improvement depends on the accuracy of the local error measure. The accuracy of the pointwise ensemble model may be poor only if the local error measure at an observed point is inaccurate although the local error measure at the other observed points is accurate.

In this paper, we combine the GMSE and the pointwise cross-validation error to enhance the accuracy of the local error measure, as

$$ e_{i}(\mathbf{x})=GMSE_{i}\bullet CV_{i}(\mathbf{x}) $$
(13)

where ei(x) is the local error measure of the i th surrogate at x, GMSEi is the generalized mean square cross-validation error of the i th surrogate, and CVi(x) is the pointwise cross-validation error of the i th surrogate at x.

A similar form of the formula in (13) was first put forward by Liu et al. (2016). Liu et al. proposed that the weight at an observed point of the individual surrogate with the smallest absolute value of ei(x) is equal to one while the other individual surrogates have zero weights. The absolute value of ei(x) is used to identify the individual surrogate with the best accuracy at an observed point. In other words, only the order of the ei(x) is used to determine the weights. In the current work, however, the value of ei(x) is used to calculate weights. In the approach of Liu et al., one only needs to be able to precisely identify the most accurate individual surrogate based on ei(x). In the current approach, however, the value of ei(x) needs to be able to reflect the local error of the i th surrogate at x.

3.2.2 Use of the nearby observed points

The local error measure vector of an observed point is constructed with the local error measure of nearby observed points. On the one hand, the local error measure vector at an observed point represents the local error of the region around this observed point. Thus, all the observed points in the region should be utilized to construct the local error measure. On the other hand, constructing the local error measure vector using nearby points is also a way to prevent the bias in error estimation of the local error measure.

Thus, \(\mathbf {e}_{i}^{*}(\mathbf {x})\) at each observed point is calculated by

$$ \mathbf{e}_{i}^{*}(\mathbf{x})= \left[\begin{array}{l} e_{i}(\mathbf{x}_{1})\bullet l_{i}(\mathbf{x}_{1})\\ e_{i}(\mathbf{x}_{2})\bullet l_{i}(\mathbf{x}_{2})\\ ...\\ e_{i}(\mathbf{x}_{j})\bullet l_{i}(\mathbf{x}_{j})\\ ...\\ e_{i}(\mathbf{x}_{m})\bullet l_{i}(\mathbf{x}_{m}) \end{array}\right] $$
(14)

where \(e_{i}^{*}(\mathbf {x})\) is the error measure vector of the i th surrogate at x, ei(xj) is the local error measure of the i th surrogate at xj, and m is the total number of observed points. where li(xj) is the weight of the i th surrogate at xj:

$$ \begin{array}{@{}rcl@{}} l_{i}(\mathbf{x}_{j})&=& \left\{\begin{array}{ll} 1 &d(\mathbf{x}_{j},\mathbf{x})= d_{low}\\ \overline{d}_{inv}&d_{low}<{d(\mathbf{x}_{j},\mathbf{x})}\leq d_{high}\\ 0&d_{high}<{d(\mathbf{x}_{j},\mathbf{x})} \end{array}\right.\\ d_{low}&=&\underset{1\leq j,k\leq n;j\neq k}{\min}d(\mathbf{x}_{j}.\mathbf{x}_{k})\\ d_{high}&=&\underset{1\leq j,k\leq n;j\neq k}{average}d(\mathbf{x}_{j}.\mathbf{x}_{k}) \end{array} $$
(15)

where d(xj,x) is the Euclidean distance between the observed points xj and x, \(\overline {d}_{inv}\) denotes the inverse-distance relative conversion value, and dlow and dhigh denote the upper and lower bounds of distance, respectively. In particular, dlow is defined as the minimum value of the distance among all the observed points, and dhigh is defined as the average value of the distance among all the observed points.

For each observed point x, the value of li(xj) at the observed point xj is equal to one if the distance between xj and x is less than dlow, the value of li(xj) is zero if the distance between xj and x is greater than dhigh, and the value of li(xj) is set as \(\overline {d}_{inv}\) if the distance between xj and x is within the upper and lower bounds of distance.

The \(\overline {d}_{inv}\) satisfies

$$ \begin{array}{ll} \overline{d}_{inv}= \left\{ \begin{aligned} &1&&d(\mathbf{x}_{j},\mathbf{x})= d_{low}\\ &0&&d(\mathbf{x}_{j},\mathbf{x})= d_{high} \end{aligned} \right.\\ \overline{d}_{inv}^{\prime}= \left\{ \begin{aligned} &0&&d(\mathbf{x}_{j},\mathbf{x})= d_{low}\\ &0&&d(\mathbf{x}_{j},\mathbf{x})= d_{high} \end{aligned} \right. \end{array} $$
(16)

where \(\overline {d}_{inv}^{\prime }\) is the first derivative function of \(\overline {d}_{inv}\).

Thus, the following third-order polynomial is employed to calculate \(\bar {d}_{inv}\) in this paper:

$$ \begin{array}{ll} &\overline{d}_{inv}=2\overline{d}(\mathbf{x}_{j},\mathbf{x}_{k})^{3}-3\overline{d}(\mathbf{x}_{j},\mathbf{x}_{k})^{2}+1\\ &\overline{d}(\mathbf{x}_{j},\mathbf{x}_{k})=\frac{(d(\mathbf{x}_{j},\mathbf{x}_{k})-d_{low})}{d_{high}-d_{low}} \end{array} $$
(17)

3.3 The optimal pointwise weighted ensemble

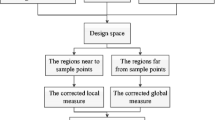
Figure 1 shows the flowchart of the proposed OPWE. And the following points need to be explained:

  1. 1.

    The method described in Section 3.2 is employed in this paper to calculate the error measures (LMSE) at observed points. This method combines the global error measure and the local error measure based on the formula in (13). The nearby points are used to construct the local error measure vector to prevent the negative influence from inaccurate pointwise cross-validation error at an observed point.

  2. 2.

    The method described in Section 3.1 is adopted in this paper to determine the weights at observed points. The LMSE is proposed to represent the local error of the region around the observed point, and the OPWE is obtained from the minimization of the LMSE as described in (10). In addition, the solution of (10) is obtained by using Lagrange multipliers as (11).

  3. 3.

    The weights at unobserved points are predicted by referring to the inverse-distance weighted formulas (9).

Fig. 1
figure 1

The flowchart of the proposed OPWE

Full size image

3.4 The pointwise ensemble models based on GLE

In order to verify the performance of OPWE, two pointwise ensemble models based on GLE are proposed in this paper and they are compared to the other ensemble models in the numerical procedure.

Ensemble model A

Ensemble model A is a pointwise ensemble model. In this model, the weight of the individual surrogate with the smallest local error measure is set equal to one while the other individual surrogates have zero weights. The local error measure used in this model is the GLE proposed in Section 3.2.1. The weights at unobserved points are predicted according to the inverse-distance weighted formulas (9).

Ensemble model B

Ensemble model B is also a pointwise ensemble model. The weights at observed points are calculated by

$$ w_{i}(\mathbf{x})=\frac{{e_{i}^{2}}(\mathbf{x})}{{\sum}_{j=1}^{n}{e_{j}^{2}}(\mathbf{x})} $$
(18)

where n is the total number of the individual surrogates and ei(x) is the local error measure of the i th surrogate at x, and the local error measure is the GLE proposed in Section 3.2.1. The weights at unobserved points are predicted according to the inverse-distance weighted formulas (9).

Summary

The ensemble models A and B are similar to the ensemble models proposed by Acar (2010) except for the local error measure. Ensemble model A is also similar to the ensemble model proposed by Liu (2016) except for the inverse-distance weighted formulation.

In ensemble model A, the order of GLE is used to determine the best individual surrogate model at observed points, and the weight of the best individual surrogate is set equal to one while the other individual surrogates have zero weights. And in ensemble model B, the value of GLE is used to calculate the weight factors at observed points. Ideally, ensemble model A is more accurate than ensemble model B if the GLE is accurate enough to determine the best individual surrogate. However, one may obtain bad weights if there are some cases with bias in error estimation of GLE. In such cases, ensemble model B is more robust than ensemble model A since the weights in model B are calculated by using the local error measure of all individual surrogates. Thus, one obtains better weights with ensemble model B than ensemble model A if there is obvious bias in error estimation of the local error measure.

4 Reference example problems

To verify the performance of the proposed ensemble model in this paper, we consider six well-known mathematical problems and four engineering problems.

4.1 Mathematical problems

4.1.1 Branin-Hoo function (two variables)

$$ \begin{array}{ll} y\left( x_{1},x_{2}\right)=&\left( x_{2}-\frac{5.1{x_{1}^{2}}}{4\pi^{2}}+\frac{5x_{1}}{\pi}-6\right)^{2}\\ &+10\left( 1-\frac{1}{8\pi}\right)\cos\left( x_{1}\right)+10 \end{array} $$
(19)

where \(x_{1}\in \left [-5,10\right ]\) and \(x_{2}\in \left [0,15\right ]\).

4.1.2 Camelback function (two variables)

$$ \begin{array}{ll} y\left( x_{1},x_{2}\right)=&\left( 4-2.1{x_{1}^{x}}+\frac{{x_{1}^{4}}}{3}\right){x_{1}^{2}}\\ &+x_{1}x_{2}+\left( -4+4{x_{x}^{x}}\right){x_{x}^{x}} \end{array} $$
(20)

where \(x_{1}\in \left [-3,3\right ]\) and \(x_{2}\in \left [-2,2\right ]\).

4.1.3 Glodstein-Price function (two variables)

$$ \begin{array}{@{}rcl@{}} y\left( x_{1},x_{2}\right)&=&\left[\right.1+\left( x_{1}+x_{2}+1\right)^{2}\\ &&\times\left( \right.19-4x_{1}+3{x_{1}^{2}}\\ &&-14x_{2}+6x_{1}x_{2}+3{x_{2}^{2}}\left.\right)\left.\right]\\ &&\times\left[\right.30+\left( 2x_{1}-3x_{2}\right)^{2}\\ &&\times\left( \right.18-32x_{1}+12{x_{1}^{2}}\\ &&+48x_{2}-36x_{1}x_{2}+27{x_{2}^{2}}\left.\right)\left.\right] \end{array} $$
(21)

where \(x_{1},x_{2}\in \left [-2,2\right ]\).

4.1.4 Hartman function (six variables)

$$ y(\mathbf{x})=-\sum\limits_{i=1}^{m}c_{i}\exp\left[-\sum\limits_{j=1}^{n}a_{ij}\left( x_{j}-p_{ij}\right)^{2}\right] $$
(22)

where \(x_{i}\in \left [0,1\right ]\). Here, the six-variable model (m= 6) of Hartman function is considered and m is taken as four. The values of the function parameters ci, aij and pij are taken from Goel et al. (2007), and they are provided in Table 1.

Table 1 Parameters used in the six-variable Hartman function (j = 1,...,6)
Full size table

4.1.5 Extended Rosenbrock function (nine variables)

$$ y(\mathbf{x})=-\sum\limits_{i=1}^{m-1}\left[\left( 1-x_{i}\right)^{2}+100\left( x_{i+1}-{x_{i}^{2}}\right)^{2}\right] $$
(23)

where \(x_{i}\in \left [-5,10\right ]\). Here, the nine-variable model (m= 9) of extended Rosenbrock function is considered.

4.1.6 Dixon-Price function (twelve variables)

$$ y(\mathbf{x})=\left( x_{1}-1\right)^{2}+\sum\limits_{i=2}^{m}i\left[2{x_{i}^{2}}-x_{i-1}\right]^{2} $$
(24)

where \(x_{i}\in \left [-10,10\right ]\). Here, the 12-variable model (m= 12) of Dixon-Price function is considered.

4.2 Engineering problems

4.2.1 Four variable I-beam

This four variable I-beam problem (see Fig. 2) is taken from Messac and Mullur (2008). The response for this problem is the maximum bending stress developed in the beam, which is calculated from

$$ \begin{array}{@{}rcl@{}} \sigma_{max}&=&\frac{\frac{P}{2}\frac{x_{1}}{2}}{I}\\ I&=&\frac{1}{12}\left[x_{2} {x_{1}^{3}}-\left( x_{2}-x_{3}\right)\left( x_{1}-2x_{4}\right)^{3}\right] \end{array} $$
(25)
Fig. 2
figure 2

The cross-section of the four variable I-beam design

Full size image

The ranges of the design variables are taken as 0.1m ≤ x1,x2 ≤ 0.8m and 0.009m ≤ x3,x4 ≤ 0.05m as specified in Messac and Mullur.

4.2.2 Fortini’s clutch

The Fourtini’s clutch problem (see Fig. 3) is taken from Lee and Kwak (2006). The response for this problem is the contact angle, which is calculated from

$$ {y=arccos\left[\frac{x_{1}+0.5\left( x_{2}+x_{3}\right)}{x_{4}-0.5\left( x_{2}+x_{3}\right)}\right]} $$
(26)
Fig. 3
figure 3

The clutch assembly

Full size image

The ranges of the design variables are shown in Table 2.

Table 2 The ranges of the design variables for Fortini’s clutch problem
Full size table

4.2.3 Lavel nozzle

A finite volume (FV) model of a Lavel nozzle shown in Fig. 4 is used for flow simulation using the commercial software of CFD, FLUENT. In this example, surrogate models are constructed to estimate the thrust and mass flow rate. The responses are calculated from

$$ \begin{array}{@{}rcl@{}} q_{m}&=&{\int}_{A_{o}}\left( \rho v\right)dA\\ F&=&{\int}_{A_{o}}\left[\rho v^{2}+\left( p-p_{0}\right)\right]dA \end{array} $$
(27)

where, F denotes the thrust, qm denotes the mass flow rate, Ao denotes the nozzle outlet, ρ is the flow density at nozzle outlet, v is the flow velocity at nozzle outlet, p is the flow static pressure at nozzle outlet, and p0 is the standard atmospheric pressure. The input variables include the nozzle pressure ratio (NPR, the ratio of total pressure at nozzle inlet to standart atomspheric presure) and expansion angle (α, see in Fig. 4). And the ranges of input variables are taken as 2 ≤ NPR ≤ 15 and 20 ≤ α ≤ 50.

Fig. 4
figure 4

Three views of Lavel nozzle

Full size image

4.2.4 Variable cycle engine

The variable cycle engine problem (VCE, see Fig. 5) is taken from Zhang et al. (2016). The thrust and specific fuel consumption (sfc) under subsonic cruise condition (Flight Mach number= 0.9, Flight altitude= 11000m) are the responses for this problem. The ranges of design variables are shown in Table 3.

Fig. 5
figure 5

Variable cycle engine

Full size image
Table 3 The ranges of the design variables for VCE problem
Full size table

5 Numerical procedure

The numerical procedure is similar to the publicly available document (Acar 2010) to better evaluate and study the improvement of OPWE. The example problems are considered in this paper with varying dimensions (from 2 to 12) and selected numbers of training points. For all example problems, the Latin hypercube sampling (LHS) technique is adopted to generate the training points. The training points are generated with the MATLAB routine “lhsdesign” and “maximin” criterion with the maximum iteration number of 1000. And the computational time of building each ensemble model is calculated with the MATLAB routine “tic” and “toc.” Meanwhile, random sampling is utilized to generate 1000 test points for each training set. It is noted that the performance of the surrogate model may vary as the training set changes. Thus, some training and test sets are generated to reduce the effect of random sampling. The number of the training and test sets decreases as the dimension of the test problem increases to save the computational cost. In Table 4, we summarized the training and test data used in each problem.

Table 4 Summary of training and test data used in each test problem
Full size table

Four different individual surrogates are considered: PRS, RBF, KRG, and GP. We used the SURROGATES Toolbox (2011) to build these individual surrogates. The SURROGATES Toolbox fits the kriging model using the DACE toolbox of Lophaven et al. (2002), fits the Gaussian process model using the GPML toolbox of Rasmussen and Williams (2006), and fits the radial basis function model using the RBF toolbox of Jekabsons (2009). In the case of kriging, both the constant trend model, KRG0, and the linear trend model KRG1 are used. Therefore, the ensemble of surrogates is composed of five members. The PRS surrogate is represented by fully quadratic polynomial. The RBF surrogate is based on multi-quadric formulation with the constant c = 1. In the kriging surrogates KRG0 and KRG1, a Gaussian correlation function is used. The covariance function in the GP surrogate is selected as the squared exponential function with automatic relevance determination distance measure.

In order to explore the effect of the number of individual surrogates, three tests with different individual surrogates are considered. The number of individual surrogates in the three tests is 5, 4, and 3, respectively. In Table 5, we show the individual surrogates used in each test.

Table 5 The individual surrogates used in each test
Full size table

All the ensemble models considered in the numerical procedure have already been described in detail. The ensemble models based on the heuristic method by Goel et al. (2007) is labeled as EG; the spatial model by Acar (2010) is labeled as SP; the OWSdiag by Viana (2009) is labeled as Od; the OPWE proposed in the current work is labeled as OP; and the two other ensemble models described in Section 3.4 are labeled as EA and EB, respectively.

6 Results and discussion

In this section, the root mean square error (RSME) is chosen as the error metric of interest. The error values are normalized with respect to the most accurate individual surrogate to provide a better comparison of different models. And the most accurate individual surrogates and ensemble models are marked in bold.

In Table 6, we show the mean values of RMSE over various training and test sets for all mathematical test problems. Wherein, the numbers in the bracket are the rank of the accuracy of ensemble models. And in Table 10, we show the computational time among different ensemble models for all mathematical test problems. Wherein, the numbers in the bracket are the normalized computational time, which is normalized with respect to the ensemble model with the fastest modeling speed. Tables 7 and 8 show the comparison of normalized RMSE of individual surrogate and ensemble of surrogates for all mathematical test problems with varying numbers of individual surrogates. Table 9 shows the comparison of normalized RMSE of individual surrogate and ensemble of surrogates for all engineering problems. Wherein, the numbers in the bracket are the rank of the accuracy of ensemble models.

Table 6 Comparison of the normalized RMSE of individual surrogate and ensemble of surrogates for the all mathematical test problems with five individual surrogates
Full size table
Table 7 Comparison of the normalized RMSE of individual surrogate and ensemble of surrogates for the all mathematical test problems with four individual surrogates
Full size table
Table 8 Comparison of the normalized RMSE of individual surrogate and ensemble of surrogates for the all mathematical test problems with three individual surrogates
Full size table
Table 9 Comparison of the normalized RMSE of individual surrogate and ensemble of surrogates for the all engineering test problems with five individual surrogates
Full size table
Table 10 The computational time among different ensemble models for all mathematical test problems with five individual surrogates
Full size table

By comparing the accuracy of individual surrogates with the different number of points in the training set, it is revealed that the best individual surrogate may change as the number of points in the training set increases for the same test problem. This indicates that the accuracy of individual surrogate depends heavily on the training set. The sequential sampling optimization is an efficient optimization framework using surrogate. The sequential sampling procedure continuously generates new observed points until the end of optimization, and of course, it causes a change in the training set. Thus, it is not suitable to use only a certain surrogate model in sequential sampling optimization. However, it is noted that using the ensemble model is much more time-consuming.

As the number of points in the training set increases, the deviation of accuracy for the most accurate individual surrogate and the ensemble models increases in most test problems. However, SP, EA, EB, and OP are more robust than Od. This is because the accuracy of local error measure continuously increases as the number of points in the training set increases. It is also noted that OP exhibits excellent stability along with the increase of the number of points in the training set in comparison with the other ensemble models.

EA is more accurate than SP in most test problems. The difference between EA and SP is only the local error measure. This indicates that GLE is a more accurate criterion for the local error than the cross-validation error. It is also noted that for several low-dimensional test problems (dimension≤ 5), SP shows better accuracy than EA. The cross-validation error provides the local information, and the GLE provides the local and global information. If the cross-validation error is an accurate enough criterion for the local error for a certain test problem, the global information provided by GLE is useless or even harmful for constructing an accurate ensemble model. For example, for the Nozzle flow rate (12.) test problem, SP is more accurate than EA. And it is found that SP is also more accurate than the best individual surrogate obviously. This indicates that the cross-validation error is accurate enough to represent the local error for this test problem.

EB is more accurate than EA in most low-dimensional test problems. This indicates that there is bias in error estimation of GLE. This bias raises the probability for EA to gain bad ensemble models. The deviation in accuracy between EB and EA is enlarged as the number of individual surrogate increases. This is because the increase of the number of individual surrogate raises the probability for bias in error estimation of GLE. It is also noted that EA is more accurate than EB in most of high-dimensional test problems (dimension≤ 6). This indicates that GLE is an accurate criterion of local error for these test problems.

OP is more accurate than EA and EB in most test problems. This implies that using OP with GLE is better than EA and EB in determining the weight factors. The pointwise weights are calculated by minimizing LMSE in OP, wherein LMSE is defined as a representative for the error of the region near the observed points. This method not only offers more efficient use of local error measure but also prevents the bias in error estimation of GLE. Altogether, OP can be utilized to prevent the bias in error estimation of GLE for local error and to improve the accuracy and robustness of ensemble models due to the efficient use of GLE. It is also noted that for several low-dimensional test problems, EB shows better accuracy than OP. In EB and OP, the GLE provides the local information of an observed point, and the LMSE provides the local information of several observed points. Thus, if the local information of an observed point can reflect the local error accurately at observed points, the local information of the other observed points provided by LMSE is useless or even harmful for constructing an accurate ensemble model.

It can be seen from Table 10 that the computational time of building OP is more than that of building the other ensemble models considered in this paper.

Except for building the individual surrogate model, the most time-consuming procedure in building the ensemble models considered in this paper (EG, Od, SP, EA, EB, and OP) is calculating the surrogate error measure. The data-based error measure is used in these ensemble models. The individual surrogate need to rebuilt n times to provide the cross-validation error for data-based error measure, where the n is the number of points in the training set. Thus, the computational time of calculating the surrogate error measure depends on the type of individual surrogate, the dimension of test problem, and the number of points in the training set.

Another time-consuming procedure in OP is calculating the distance between each observed point. The computational time of this procedure depends on the dimension of the test problem and the number of points in the training set.

As the number of points in the training set increases, the computational time of computing surrogate error measure increases. Thus, the computational time of building the ensemble models considered in this paper increases. And the computational time of computing the distance between each observed point also increases. For the high-dimensional test problems, the increasing computation time to compute the cross-validation error is more than that to compute the distance between each observed point. This is the reason why the normalized computational time decreases as the number of points in the training set increases for ExtendedRosen and DixonPrice test problems.

7 Conclusions

In this work, we propose an optimal pointwise weighted ensemble (OPWE) method, wherein the optimal pointwise weight factors are obtained based on minimization of the local mean square error which is constructed by the global-local error (GLE). Via six well-known mathematical functions with varying dimensions and numbers of training points and four engineering problems, it is proved that the proposed OPWE is better than the other ensembles of surrogates in terms of both accuracy and robustness. GLE is a more accurate surrogate than the cross-validation error for the local error at the observed points. The method proposed in this paper can be utilized to prevent the bias in error estimation of GLE for local error and to improve the accuracy and robustness of ensemble models.