Abstract
The reliability analysis of structural systems is generally difficult when limit state function (LSF) is implicitly defined especially by black-box models in engineering. To balance analysis efficiency and accuracy, an improved approach named BIS-FC is proposed in this paper based on the Beta-spherical importance sampling (BIS) framework with the innovative concept of critical region defined by combination with First Order Reliability Method (FORM). The critical region is defined by the hyper-tangent plane of LSF at the Most Probable Point (MPP) and its parallel hyperplanes according to the convex or concave features of LSF, wherein the samples are of both high occurrence probability and high misjudgment risk due to the linearization assumption of FORM. BIS-FC only conducts LSF analysis for the BIS samples located in the critical region, and the other samples are directly identified as safe or failure according to the linearized hyperplanes. Thus large computational cost can be saved compared to the original BIS, and meanwhile, the analysis accuracy can be greatly enhanced compared to FORM. An iterative process is proposed to properly define the critical region, based on which reliability is analyzed sequentially until the stopping criteria for desired estimation error level and stable convergence are satisfied. The algorithms of BIS-FC for both single and multiple MPP situations are developed and testified with six numerical examples and one satellite structural engineering problem. The results demonstrate the effectiveness of BIS-FC regarding good balance between efficiency and accuracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To analyze the reliability of a structural system under various random uncertainties, the typical probabilistic model is defined as follows (Yao et al. 2011):
where R is the reliability, Pf is the probability of failure, x = (x1, … , xn) is an n-dimensional vector of uncertain variables with joint probability density function (PDF) fx(x), and g(x) is the limit state function (LSF) of the system. The limit state boundary is defined as g(x) = 0 and the failure domain is defined as g(x) < 0. As the non-Gaussian random variable vector x in the original X space can be transformed into independent standard normal variable vector u in standard Gaussian U-space (Du and Hu 2012; Rosenblatt 1952), it is reasonable to focus attention in the U-space in the following discussion, and (1) can be transformed as
where φn(u) is the n-variate joint standard normal PDF, and G(u) is the transformation of g(x) in the U-space. It is generally difficult to calculate (2) analytically as G(u) is seldom defined explicitly in engineering and usually involves black-box simulation, e.g., structural finite element analysis (FEA). Thus various approximation approaches have been developed to solve (2), e.g., Laplace multidimensional integral methods based asymptotic approximation (Breitung 1984; Evans and Swartz 1995), dimension-reduction (DR) methodology (Noh et al. 2008; Song 1990), First Order Reliability Method (FORM) (Hasofer and Lind 1974; Hohenbichler and Rackwitz 1982; Du and Hu 2012) and Second Order Reliability Method (SORM) (Breitung 1984), Simulation-based methods (Helton et al. 2006; Kahn and Marshall 1953), etc.
In engineering, FORM is very prevailing for its simplicity (Chen et al. 2016; Jiang et al. 2017; Keshtegar and Hao 2018; Yao et al. 2013a, b). It only requires a significantly small number of LSF analysis to search the Most Probable Point (MPP) and calculate the reliability index β, based on which the reliability can be directly calculated by the linearization assumption. However, this simplicity brings accuracy loss, especially for highly nonlinear problems. For better accuracy, simulation-based method, e.g., Monte Carlo Simulation (MCS), is widely used (Yao et al. 2011). However, the implementation of crude MCS requires a great quantity of samples to achieve acceptable estimation accuracy, which becomes intractable for real-world engineering problems. To alleviate the computational complexity, one popular way is to develop “cheap” surrogate model instead of the expensive LSF model for reliability analysis, e.g., the response surfaces method (RSM) (Gayton et al. 2003; Guan and Melchers 2001), polynomial chaos expansions (PCE) (Crestaux et al. 2009; Hu and Youn 2011), support vector machine (SVM) (Bourinet et al. 2011), Kriging (Cai et al. 2017; Cressie 1990; Wang and Wang 2016) and its variants with active learning (Echard et al. 2011; Hu and Mahadevan 2015; Lv et al. 2015; Sun et al. 2017), etc. Since only a small number of samples are needed for surrogate modeling, the computational burden can be greatly reduced. However, for highly nonlinear problems, especially in the high-dimensional situation, it is still a common difficulty to overcome over-fitting or under-fitting. The surrogate model validation and error estimation also remain open questions, which greatly affect the analysis accuracy. Besides, as Ref. (Yun et al. 2018) pointed out, a post-processing computational cost to evaluate the reliability (e.g., sampling with the surrogate) is needed after the surrogate modeling, which may be expensive and deserves attention for further efficiency enhancement especially for the implicit surrogate models such as Kriging (Lee et al. 2013). Therefore, in addition to the continuous research on the surrogate based method, many research efforts are also devoted to enhance the sampling efficiency, among which importance sampling (IS) (Au and Beck 1999; Melchers 1990; Papaioannou et al. 2016) is a popular direction for its efficiency and simplicity.
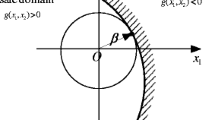
The key step of importance sampling is the proper selection of importance sampling density function (Ang et al. 2015; Hinrichs 2010). One intuitively understandable technique with the advantage of easy implementation is the β-spherical IS method (BIS), which is also called Truncated IS (TIS) or radial-based IS (RBIS) (Harbitz 1986; Engelund and Rackwitz 1993; Grooteman 2008). It defines the “β-sphere” by the reliability index β of MPP, the inner part of which is regarded as safe region. Thus the samples within the β-sphere need not be analyzed with the expensive LSF and can be excluded from sampling to enhance efficiency, as shown in Fig. 1(a). To further reduce the computational burden, a modified IS method (M-ISM) is proposed (Yun et al. 2018). It first shifts the importance sampling center to the MPP, and the IS samples are shown as the black points in Fig. 1(b). Then following the BIS method, the samples inside the β-sphere are excluded. The samples outside the β-sphere are left and divided into two groups according to the contribution of the samples to the failure probability. Only those samples with large contribution specified by the threshold need LSF analysis, which are labeled as blue points in Fig. 1(b). This can save computational cost compared to the original BIS within controlled relative error.
In the aforementioned modified method M-ISM, the sample contribution to the failure probability estimation is only measured according to the original and IS sampling PDF of the samples, which represents the sample occurrence probability. Actually, the contribution of a sample to the estimation accuracy of a reliability analysis method is not only affected by its PDF weight (probability of sample occurrence), but also the sample location where the safe or failure state has great possibility to be misjudged in the analysis method (risk of sample misjudgment). Thus inspired by this idea, an improved BIS method is proposed in this paper by identifying the critical region which contains samples with both high occurrence probability and high misjudgment risk due to the linearization assumption of FORM. The critical region is defined by the hyper-tangent plane of LSF at the MPP and its parallel hyperplanes in the specified direction according to the concave or convex features of the nonlinear LSF. This definition can effectively cover samples near MPP which have high risk of misjudgment due to the LSF nonlinearity as the hyperplanes move along the LSF gradient direction (i.e., the hyperplanes are perpendicular to the LSF gradient). Besides, this definition has the advantage of easy implementation as it is very convenient to generate hyperplanes, based on which the critical region can be easily constructed. The parameters of the hyperplanes are defined according to the gradient of LSF at MPP, which is the byproduct of FORM and needs no extra computation. As illustrated in Fig. 1(c), only the samples in the critical region need LSF analysis, which can save great computational cost compared to the existing BIS methods. The concept of critical region can be easily applied to the multiple-MPP situation, which is also studied in this paper.
To sum up, the main contribution of this paper is the development of an improved reliability analysis method which combines the advantages of BIS and FORM with the concept of Critical region (BIS-FC). On one hand, there exist fruitful researches on FORM which can provide effective MPP search and β estimation algorithms. By adding a modest computational cost to FORM resulting from the LSF analysis of samples in the critical region, the failure probability estimation accuracy can be greatly enhanced especially for the nonlinear LSF problems. On the other hand, based on the BIS framework, the analysis accuracy of BIS can be inherited as the proposed method can converge to the original BIS result, which proves to be efficient and accurate compared to crude MCS (Engelund and Rackwitz 1993; Grooteman 2008; Yun et al. 2018).
The paper is organized as follows. The fundamentals of FORM and BIS are first introduced in section 2. Then the proposed BIS-FC method is developed in section 3 for both the single and multiple MPP situations. The critical region definition for convex and concave LSF features, the iterative procedure to identify the proper size of critical region for the balance of efficiency and accuracy, and the step-by-step algorithm to calculate reliability are presented in detail. In section 4 the proposed BIS-FC is testified with six numerical examples and a practical satellite structure problem, followed by conclusions in the final section.
2 Fundamentals
2.1 FORM
The random vector x = {x1, x2, …xn} in the original X space is first transformed into the uncorrelated Gaussian random vector u = {u1, u2, …un} in U space. Then the MPP on the limit state boundary G(u) = 0 is identified by solving the following minimization problem:
Denote the optimum as u∗ and the reliability index as β = ‖u∗‖. By linearizing the LSF with the hyper-tangent plane at MPP, the reliability can be approximated as
where Φ(⋅) denotes the standard normal cumulative distribution function (CDF), and \( {\widehat{R}}_{FORM} \) represents the approximated reliability obtained by FORM. \( {\widehat{P}}_f^{FORM} \) is the failure probability. It is obvious that if LSF is nonlinear, this approximation could lead to great accuracy loss. SORM can alleviate this problem to some extent by using second-order approximation. However, it may also become inaccurate for highly nonlinear LSF situation; wherein simulation-based method can play an important role.
2.2 Beta-spherical importance sampling
Beta-spherical (BIS), or β-spherical IS, and its variants have been developed in (Harbitz 1986; Grooteman 2008; Yun et al. 2018). The main idea is to exclude the β-sphere from the whole sampling space. Based on the reliability index β of MPP, the β-sphere in the n-dimensional U space can be drawn. The center is located at the origin, and the radius equals to β. As ‖u‖2 follows a chi-square distribution, the probability within the β-sphere can be calculated by:
where \( CD{F}_{\chi}^n\left(\cdot \right) \) denotes the cumulative chi-square distribution function with n degrees of freedom. Since the MPP is defined as the point on the failure boundary which is closest to the origin, it is certain that the failure events will not occur inside the β-sphere. Thus it is reasonable to remove this region from the whole sampling space for importance sampling. Then the sampling domain is greatly reduced, and the occurrence ratio of the failure events is increased. As the probability of the remaining region is \( 1- CD{F}_{\chi}^n\left({\beta}^2\right) \), the reliability can be calculated as
where NBIS is the total BIS sampling size and NS denotes the safe events of G ≥ 0. I(⋅) is an indicator function which is one if G ≥ 0 and zero otherwise.
The preceding derivation of BIS is based on the assumption that the MPP can be accurately identified. However, in practical problems with highly nonlinear LSF, it is generally difficult to search the MPP accurately, and the estimated \( \widehat{\beta} \) may be different from the true value β. If \( \widehat{\beta}\le \beta \), BIS method can be applied without accuracy loss as the samples in the excluded region (\( \widehat{\beta} \)-sphere) are still absolutely safe. Only the efficiency will be sacrificed as the safe samples between \( \widehat{\beta} \)-sphere and the true β-sphere are also analyzed, as shown in Fig. 2(a). In the contrast, if \( \widehat{\beta}>\beta \), BIS accuracy will be greatly affected as the samples between the β and \( \widehat{\beta} \) spheres are partially misclassified to be safe, as shown in Fig. 2(b). To maintain the accuracy of BIS, one way is to use the existing advanced MPP search method to robustly identify MPP (Hasofer and Lind 1974; Hohenbichler and Rackwitz 1982; Keshtegar and Chakraborty 2018) or multiple MPPs (Kiureghian and Dakessian 1998). Another way is to develop adaptive strategy during BIS to search MPP (Grooteman 2008). Since BIS is not much sensitive to the MPP estimation as long as \( \widehat{\beta}\le \beta \), another conservative way is to reduce the estimated \( \widehat{\beta} \) purposefully for high confidence in the reliability analysis accuracy at the cost of certain extra computation. The more efficient and accurate MPP search method for BIS can be an important issue in the future research.
3 The improved approach based on combined FORM and BIS
Without loss of generality, \( \widehat{R}\ge 0.5 \) (i.e. Pf ≤ 0.5) is discussed in this paper. For the situation of \( \widehat{R}<0.5 \), the method proposed in this paper can be directly applied by just switching the failure and safe domain definition.
3.1 The critical region definition and reliability analysis
3.1.1 The single-MPP situation
In this paper, the concept of critical region is introduced to cover the area which has both large occurrence probability and high misclassification risk due to the linearization assumption of FORM. FORM utilizes the hyper-tangent plane GL of the LSF at MPP to approximately divide the space into two parts, namely the safe region and the failure region, based on which the failure probability \( {\widehat{P}}_f^{FORM} \) can be easily calculated. However, this simplification may lead to underestimation or overestimation due to the convexity or concavity of the LSF in the neighborhood of MPP. According to (Lee et al. 2010), LSF is defined as probabilistic concave or convex function as follows:
-
(1)
Probabilistic concave function: if the FORM-based reliability analysis overestimates the probability of failure, i.e., \( {\widehat{P}}_f^{FORM}>{P}_f \), as shown in Fig. 3(a).
-
(2)
Probabilistic convex function: if the FORM-based reliability analysis underestimates the probability of failure, i.e., \( {\widehat{P}}_f^{FORM}<{P}_f \), as shown in Fig. 3(b).
For the concave situation in Fig. 3(a), the region on the safe side of GL can be assured to be safe. The region that contributes most to the inaccuracy of \( {\widehat{P}}_f^{FORM} \) due to the linearization is between GL (the red line) and its parallel hyperplane GL∗ (the red dashed line) on the failure side (further away from the origin), as indicated by the shaded area. Due to the nonlinearity of LSF, large safe part of this region is misclassified as failure in FORM which leads to the overestimation.
For the convex situation in Fig. 3(b), the region on the failure side of GL can be assured to be failure. The region that contributes most to the inaccuracy of \( {\widehat{P}}_f^{FORM} \) due to the linearization is between GL (the red line) and its parallel hyperplane GL∗ (the red dashed line) on the safe side (closer to the origin), as indicated by the shaded area. Due to the nonlinearity of LSF, large failure part of this region is misclassified as safe in FORM which leads to the underestimation.
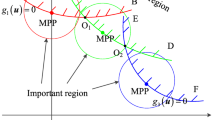
From the preceding analysis, it can be concluded that the estimation inaccuracy of \( {\widehat{P}}_f^{FORM} \) is mainly due to the misclassification of the nonlinear region in the vicinity of MPP. Inspired by this idea, the critical region which needs special analysis can be defined. Describe the hyper-tangent plane GL of the LSF at MPP as
where λ = (λ1, λ2, …λn) is the normalized direction vector from the origin to the MPP, and u = (u1, u2, …un) is the variable vector in the U-space. To define the critical region, the hyper-tangent plane GL∗(u) parallel to GL(u) is defined as
where Δβ is a positive value which defines the critical region width between the two hyperplanes GL∗(u) and GL(u). GL∗(u) with positive Δβ corresponds to the concave situation, and GL∗(u) with minus Δβ corresponds to the convex situation.
With the hyperplanes GL∗(u) and GL(u), the whole sampling space of BIS (the region outside the β-sphere) can be divided into three parts, namely the assured safe region (for the concave situation) or the assured failure region (for the convex situation), the critical region, and the unimportant region, as shown in Fig. 3(a) and 3(b) respectively. The assured safe or failure region needs no LSF analysis. The unimportant region is far away from the origin and has low occurrence probability, which means negligible impact on the failure probability estimation as long as the critical region is reasonably determined (see section 3.2). Therefore this region also needs no LSF analysis and can be directly identified as safe or failure by (8). Only the critical region needs LSF analysis, which can greatly reduce the computational burden compared to the original BIS method.
With the aforementioned critical region definition, the reliability estimation can be stated as:
where NBIS denotes the total sample size of the original BIS method, which is the sum of the sample numbers NA, NC, and NU from the assured safe (or failure) region, the critical region, and the unimportant region, respectively. NS denotes the number of safe samples in BIS population, which is the sum of the safe sample numbers \( {N}_A^S \), \( {N}_C^S \), and \( {N}_U^S \) from the assured safe or failure region, the critical region, and the unimportant region, respectively.
To save the LSF analysis burden of the original BIS method, it is proposed that only the NC samples in the critical region need LSF analysis to obtain the safe sample number \( {N}_C^S \) accurately. The NA samples in the assured safe or failure region, and the NU samples in the unimportant region need no LSF analysis. These samples can be judged as safe or failure simply according to the linear hyperplanes (7) or (8). Thus these part of computational cost can be saved, and \( {N}_A^S \) and \( {N}_U^S \) can be obtained directly as
Then the reliability estimation for the concave and convex situations can be stated as
Thus based on FORM and the concept of Critical region, the computational efficiency of the original BIS can be enhanced. This improved reliability analysis method is named BIS-FC in this paper. The key issue to maintain the accuracy and efficiency of BIS-FC is the proper selection of the critical region width Δβ, which will be discussed in detail in section 3.2.
3.1.2 The multiple-MPP situation
Similar to the critical region definition for the single-MPP in section 3.1.1, the proposed method can be applied to define the critical region for the multiple-MPP situation based on the critical region for each MPP. However, as the concave or convex features of the MPPs may be different, there may be intersection regions (area overlapping) which simultaneously belong to the assured safe, assured failure or unimportant regions of different MPPs. Thus in this section, the region division method for the multiple-MPP situation is further developed.
Denote the multiple MPP set as {M1, M2, ⋯, MN _ mpp}, where N _ mpp is the total number. For each MPP Mi(1 ≤ i ≤ N _ mpp), obtain the reliability index \( {\widehat{\beta}}_i \), generate the hyper-tangent plane GL _ i(u) at Mi with (7), and analyze the concave or convex feature of LSF near Mi. For each Mi, define the same critical region width Δβ and generate the parallel hyperplane GL ∗ _ i(u) with (8) based on \( {\widehat{\beta}}_i\pm \varDelta \beta \) according to the concave or convex features at each MPP. Denote the index set of the MPPs where the LSF local feature is concave as IConcave, and the index set of the MPPs where the LSF local feature is convex as IConvex. These two sets compose the total index set of Mi(1 ≤ i ≤ N _ mpp).
Define the β-sphere with the minimum reliability index \( {\widehat{\beta}}_{\mathrm{min}}=\underset{1\le i\le N\_ mpp}{\min }{\widehat{\beta}}_i \)Denote the BIS sampling space Ω as the total U space excluding the \( {\widehat{\beta}}_{\mathrm{min}} \)-sphere. Following the critical region definition in section 3.1.1, based on GL _ i(u) and its parallel GL ∗ _ i(u), define the critical region ΩC _ i, the unimportant region ΩU _ i, and the assured safe or failure region for each MPP Mi(1 ≤ i ≤ N _ mpp). If i ∈ IConcave, then the assured region for Mi is safe and denoted as \( {\varOmega}_{A\_i}^S \). Otherwise, the assured region is failure and denoted as \( {\varOmega}_{A\_i}^F \).
Define the total critical region as the union of all the MPPs’ critical regions as
It means all the MPPs’ critical regions are regarded important and need LSF analysis.
Define the assured failure region as the union of all the assured failure regions of Mi(i ∈ IConvex) minus its intersection with the critical region ΩC, which is
Define the assured safe region as the intersection of all the assured safe regions of Mi(i ∈ IConcave) and all the unimportant regions of Mi(i ∈ IConvex), which is
It is obvious that
The preceding definition means that a sample is regarded as assured failure if it is located in the assured failure region of any Mi(i ∈ IConcave), except that it is located in the critical region. A sample is regarded as assured safe only if it is located in the assured safe region of all Mi(i ∈ IConcave) and meanwhile it is located in the unimportant region of Mi(i ∈ IConvex). This definition is conservative to prevent aggressive estimation of reliability.
The rest area is defined as the unimportant region, which is
To efficiently analyze the safe or failure state of the samples in unimportant region, it is proposed to compare the projection of the sample on each unit direction of Mi(1 ≤ i ≤ N _ mpp). If there exist Mi such that the projection on this direction is larger than \( {\widehat{\beta}}_i \), then this sample is regarded to be failure, which can be stated that
The rest of ΩU is regarded as safe, which is
Record the total sample number in Ω as NBIS, the number in ΩC as NC, the number in \( {\varOmega}_A^F \) as \( {N}_A^F \), the number in \( {\varOmega}_A^S \) as \( {N}_A^S \), the number in \( {\varOmega}_U^F \) as \( {N}_U^F \), and the number in \( {\varOmega}_U^S \) as \( {N}_U^S \). Based on the preceding region definition, the reliability estimation can be stated as
It is obvious that the critical region definition and reliability analysis of the single-MPP situation is a special case of the multiple-MPP situation.
3.2 Iterative procedure to define the critical region
The selection of Δβ directly affects the accuracy and efficiency of the proposed BIS-FC method. If the critical region is very large and Δβ approaches to infinity as the extreme case, it is equivalent to the original BIS. Then good accuracy can be obtained, but efficiency will be sacrificed in return. If the critical region is very small and Δβ approaches to zero as the extreme case, it is equivalent to the original FORM method. Then good efficiency can be obtained, but accuracy will be sacrificed in return. Thus, the key of BIS-FC is how to properly determine the optimal critical region to achieve the balance between accuracy and efficiency.
3.2.1 The iterative procedure for reliability estimation
To properly define Δβ, a sequential method is proposed which adjusts Δβ step by step until certain stopping criterion is satisfied. The single-MPP and multiple-MPP situations are discussed respectively in this section.
The single-MPP situation
Initialize the reliability estimation as \( {\widehat{R}}^{(0)}=\varPhi \left(\widehat{\beta}\right) \), where \( \widehat{\beta} \) is obtained by FORM at the MPP. Define the initial critical region width as Δβ0. For the kth iteration (k ≥ 1), the critical region width is defined as
where Δβstep is the step increment. According to Δβk, the k th parallel hyperplane \( {G}_{L\ast}^{(k)} \) can be generated, and the critical region of this iteration can be updated. The two parallel hyperplanes of two consecutive iterations are illustrated as the red dashed lines in Fig. 4.
It can be observed that in both concave and convex situations, the assured safe or failure region is fixed during the iteration change of Δβk. Only the critical and the unimportant regions are adjusted according to the move of \( {G}_{L\ast}^{(k)} \). Then the reliability estimation in the k th iteration is
where NA is fixed during iteration. \( {N}_C^{S(k)} \) is the safe sample number in the critical region updated in the kth iteration. If k = 1, \( {N}_C^{S(k)} \) is obtained by running LSF for the samples in the critical region between GL and \( {G}_{L\ast}^{(k)} \). If k > 1, \( {N}_C^{S(k)} \) consists of two parts. One is the safe sample number \( {N}_C^{S\left(k-1\right)} \) obtained in the (k − 1)th iteration. The other is the newly safe sample number \( \varDelta {N}_C^{S(k)} \) obtained by running LSF analysis for the \( \varDelta {N}_C^{(k)} \) samples in the newly expanded critical region between \( {G}_{L\ast}^{\left(k-1\right)} \) and \( {G}_{L\ast}^{(k)} \). The total sample number \( {N}_U^{(k)} \) of the unimportant region can be accordingly updated as \( {N}_U^{(k)}={N}_U^{\left(k-1\right)}-\varDelta {N}_C^{(k)} \). Thus in each iteration, the computational cost only comes from the LSF analysis for the \( \varDelta {N}_C^{(k)} \) samples in the newly expanded critical region between \( {G}_{L\ast}^{\left(k-1\right)} \) and \( {G}_{L\ast}^{(k)} \).
The multiple-MPP situation
For each MPP Mi(1 ≤ i ≤ N _ mpp) with the reliability index \( {\widehat{\beta}}_i \), denote the safe side region of the hyper-tangent plane GL _ i as \( {\varOmega}_{S\_i}^{(0)} \). The intersection of all the safe regions \( {\varOmega}_{S\_i}^{(0)} \) is used for initial reliability estimation, which is
Define the initial critical region width as Δβ0 and the step increment as Δβstep. For the kth iteration (k ≥ 1), the critical region width Δβ(k) for each MPP is the same as defined in (20), according to which the hyperplane \( {G}_{L\ast \_i}^{(k)} \) for each Mi(1 ≤ i ≤ N _ mpp) can be generated by (8). Based on GL _ i and \( {G}_{L\ast \_i}^{(k)} \) for each MPP, the critical region \( {\varOmega}_{C\_i}^{(k)} \), the unimportant region \( {\varOmega}_{U\_i}^{(k)} \), and the assured safe or failure region can be defined. If i ∈ IConcave, then the assured region for Mi is safe and denoted as \( {\varOmega}_{A\_i}^{S(k)} \). Otherwise, the assured region is failure and denoted as \( {\varOmega}_{A\_i}^{F(k)} \).
For the kth iteration (k ≥ 1), the reliability estimation is:
\( {N}_C^{S(k)} \) is the safe sample number in the critical region updated in the kth iteration. The same as the single-MPP situation, if k = 1, \( {N}_C^{S(k)} \) is obtained by running LSF for the samples in the critical region ΩC, which is the union of the regions between GL _ i and \( {G}_{L\ast \_i}^{(k)} \) for each MPP. If k > 1, \( {N}_C^{S(k)} \) consists of two parts. One is the safe sample number \( {N}_C^{S\left(k-1\right)} \) obtained in the (k − 1)th iteration. The other is the newly obtained safe sample number \( \varDelta {N}_C^{S(k)} \) by running LSF analysis for the \( \varDelta {N}_C^{(k)} \) samples in the newly expanded critical region which is the union of the regions between \( {G}_{L\ast \_i}^{\left(k-1\right)} \) and \( {G}_{L\ast \_i}^{(k)} \) for each Mi(1 ≤ i ≤ N _ mpp).
\( {N}_A^{S(k)} \) and \( {N}_U^{S(k)} \) are the safe sample numbers in the assured safe region \( {\varOmega}_A^{S(k)} \) and the unimportant safe region \( {\varOmega}_U^{S(k)} \) respectively, which can be obtained by (14) and (18) based on the updated region division in the kth iteration.
By sequentially increasing Δβk and updating the reliability estimation, the analysis result will gradually converge to the original BIS. The control of the iteration process is mainly to balance the analysis accuracy and efficiency. Thus error analysis of BIS-FC estimation is first studied in section 3.2.2, based on which the iteration process setup and the stopping criteria are developed in section 3.2.3 and 3.2.4 respectively.
3.2.2 The error analysis of BIS-FC estimation
The estimation error of the proposed BIS-FC method, compared to the original BIS method, mainly comes from the misclassification of the samples in the unimportant region which are not accurately analyzed by LSF. The error estimations for the single-MPP and multiple-MPP situations are discussed respectively as follows.
The single-MPP situation
In the concave situation, there are safe areas E in the unimportant region, e.g., the areas E1 and E2 in Fig. 4(a), which are misclassified as failure. In the kth iteration, denote the sample number in the misclassified area \( {E}_{Concave}^{(k)} \) as \( {N}_{E\_ Concave}^{(k)} \). Then the reliability estimation of BIS-FC is smaller than the original BIS result, and the error equals to the probability mass of the misclassified area \( {E}_{Concave}^{(k)} \), which can be stated as
The misclassified sample number decreases as the iteration increases, which is
It means that by conducting LSF analysis for the samples \( \varDelta {N}_C^{(k)} \) in the newly expanded critical region, \( \varDelta {N}_C^{S(k)} \) safe samples are identified and deduced from the misclassified number.
In the U-space, for the concave situation, \( \Pr \left\{{E}_{Concave}^{(k)}\right\} \) can be roughly estimated as
where Φ(⋅) denotes the standard normal CDF, and \( 1-\varPhi \left(\widehat{\beta}+\varDelta {\beta}_{(k)}\right) \) represents the probability mass of the unimportant region defined by the hyperplane \( {G}_{L\ast}^{(k)} \), as shown in Fig. 5. λ(k) is the ratio between the misclassified area and the total unimportant region in the kth iteration, which is determined by the nonlinearity of LSF in this area. Thus λ(k) is named the nonlinearity coefficient in this paper.
For the convex situation, there are failure areas E in the unimportant region, e.g., the areas E1 and E2 in Fig. 4(b), which are misclassified as safe. In the kth iteration, denote the sample number in the misclassified area \( {E}_{Convex}^{(k)} \) as \( {N}_{E\_ Convex}^{(k)} \). Then the reliability estimation of BIS-FC is bigger than the original BIS result, and the error equals to the probability mass of the misclassified area E(k), which can be stated as
And the misclassified sample number is updated in the kth iteration as
The reliability analysis error \( \Pr \left\{{E}_{Convex}^{(k)}\right\} \) can be roughly estimated as
where \( \Pr \left\{{\varOmega}_{\beta - sphere}\cap {\varOmega}_U^{(k)}\right\} \) is the probability of the part of β-sphere which is located in the unimportant region. As the integration of chi-squared distribution is complex, a simplified rough estimation is given as
which decomposes the probability of the β-sphere uniformly into an interval \( \left[-\widehat{\beta},\widehat{\beta}\right] \) along the MPP direction. Then (29) is reformulated as
The error estimation in (26) and (31) first needs determining the nonlinearity coefficient λ(k), which results from the nonlinearity of LSF compared to the hyperplane \( {G}_{L\ast}^{(k)} \). If LSF is highly nonlinear, λ(k) becomes large, which means the linearization of the hyperplane \( {G}_{L\ast}^{(k)} \) leads to great misclassification and accuracy loss. In the contrast, λ(k) becomes small if LSF is not highly nonlinear, i.e., relatively “flat”. Moreover, it approaches to zero when LSF is almost linear and matches closely to \( {G}_{L\ast}^{(k)} \), which means the linearization of the hyperplane \( {G}_{L\ast}^{(k)} \) has little accuracy loss in the unimportant area.
As LSF is generally implicitly formulated or even defined by a black-box model, it is difficult to obtain λ(k) analytically and accurately. In this paper, it is proposed to approximate λ(k) with reference to λ(k − 1). Assume that λ(k) equals to λ(k − 1) for the similar misclassification ratio due to the similar LSF nonlinearity feature in the two consecutive iterations. Then
With λ(k) obtained from (32), the reliability estimation error can be estimated with (26) or (31).
The multiple-MPP situation
Similar to the single-MPP situation, the estimation error mainly comes from the misclassified samples in the unimportant region, which is affected by the probability mass of the unimportant area and the LSF nonlinearity in this area. In the kth iteration, due to the complexity of the area overlapping, each sample in the unimportant region \( {s}_i\in {\varOmega}_U^{(k)} \) may simultaneously belong to the unimportant regions of several MPPs. To analyze the misclassification risk, it is proposed to determine first which MPP’s unimportant region \( {\varOmega}_{U\_i}^{(k)} \) the sample \( {s}_i\in {\varOmega}_U^{(k)} \) is associated to such that it has the biggest risk. The algorithm is proposed as follows.
First, analyze the unimportant failure region \( {\varOmega}_U^{F(k)} \). For each sample \( {s}_i\in {\varOmega}_U^{F(k)} \), there may be several MPPs where the LSF local nonlinearity is concave, and meanwhile, its corresponding unimportant region can cover this sample. The index set of the MPPs which satisfy the preceding conditions can be stated as
The MPP \( {M}_j\left(j\in \left\{l|l\in {I}_{Concave},{s}_i\in {\varOmega}_{U\_l}^{(k)}\right\}\right) \), with which si has the largest misclassification risk \( {\lambda}_j^{(k)}\left[1-\varPhi \left({\widehat{\beta}}_j+\varDelta {\beta}^{(k)}\right)\right] \) defined by (26), is chosen as the reference MPP to calculate the misclassification risk of si. Here \( {\lambda}_j^{(k)} \) is the nonlinearity coefficient of LSF at the jth MPP.
Similar to the unimportant failure region, for each sample \( {s}_i\in {\varOmega}_U^{S(k)} \) in the unimportant safe region, the MPP Mj(j ∈ IConvex) whose LSF local nonlinearity is convex and whose unimportant region covering si has the largest misclassification risk modeled by (29), is chosen as the reference MPP to calculate the misclassification risk of \( {s}_i\in {\varOmega}_U^{S(k)} \).
Denote the misclassification risk at each sample \( {s}_i\in {\varOmega}_U^{(k)} \) in the unimportant region as its misclassification weight, which is
Then the total reliability estimation error is proposed to be the average risk of all the samples in the unimportant region, which is
It is obvious that the error estimation (26) and (31) for the single-MPP situation are exactly the special case of error estimation (34) and (35) for the multiple-MPP situation.
3.2.3 The iteration process setup
The iteration process of BIS-FC is conducted until the estimation error compared to the original BIS drops into an acceptable level. Meanwhile, the proper critical region can be gradually identified to reduce the computational cost effectively. Define the percentage of the saved computational cost compared to the original BIS as
In this section, the factors affecting the iteration process and the efficiency are analyzed, based on which the iteration process parameter setting up is discussed.
From the error estimation (26) for the single-MPP concave situation, (31) for the single-MPP convex situation, and (35) for the multiple-MPP situation, the main factors affecting the reliability estimation error include the nonlinearity coefficient of LSF, the reliability index at MPP, and the critical region width. It is obvious that smaller nonlinearity coefficient and larger critical region are preferred for smaller estimation error.
Due to the similar iteration process and error estimation for both the single and multiple MPP situations, and the similar trends of parameter effects on the estimation error, only the single-MPP situation is discussed here for briefness, which can be directly applied for the multiple-MPP situation. The detailed parameter effects are discussed as follows.
The situation with smaller λ (k)
Smaller λ(k) means the nonlinearity of LSF is not severe and there is small difference between LSF and the hyperplane \( {G}_{L\ast}^{(k)} \). For both the concave and convex situations, small λ(k) can greatly reduce the demand for large Δβ(k). And if \( \widehat{\beta} \) is large, Δβ(k) can be even smaller. Then huge computational burden for critical region analysis can be saved, and great efficiency can be obtained by BIS-FC.
For the extreme situation that LSF is linear and parallel to \( {G}_{L\ast}^{(k)} \), then λ(k) = 0 and Pr{E(k)} = 0. Then the accurate estimation is achieved, and no more iteration is needed. For example, if LSF is linear and accurately matches GL(u) at MPP, then it can be calculated that λ(1) = 0 by analyzing the samples in the initial critical region Δβ(1). Thus it can be concluded that FORM is accurate and no iteration is needed for more analysis.
The situation with larger λ (k)
Larger λ(k) means that LSF is highly nonlinear and there is significant difference between LSF and the hyperplane \( {G}_{L\ast}^{(k)} \). For the concave situation, the small estimation error has to be achieved by large \( \widehat{\beta}+\varDelta {\beta}^{(k)} \). Especially if \( \widehat{\beta} \) is small, then very large Δβ(k) is needed, and the efficiency of BIS-FC will be reduced. For the convex situation, if \( \widehat{\beta} \) is small, small \( \widehat{\beta} \)-sphere is excluded. Thus very large Δβ(k) is also needed. Therefore for both the concave and convex situations, the efficiency of BIS-FC will be greatly reduced if \( \widehat{\beta} \) is small. In the contrast, if \( \widehat{\beta} \) is large, then maybe only small Δβ(k) is enough to achieve small estimation error, which accordingly may not reduce the efficiency too much. To sum up, for the highly nonlinear situation, the efficiency advantage of the proposed BIS-FC method will be not as significant as the linear situation. But compared to the original BIS, the proposed BIS-FC can still significantly reduce the computational burden as the LSF analysis for the assured region can be saved.
According to the preceding analysis, the thumb of rule for the proper setup of the parameters Δβ0 and Δβstep in implementing BIS-FC is summarized as follows:
If it is known in advance that LSF is not highly nonlinear, a small Δβ0 is preferred. If it is known that LSF is highly nonlinear or there is no a priori knowledge about the nonlinear condition, a modest value is preferred, which can leave flexible adjustment room to identify the proper critical region by the followed-up iteration process.
The step increment Δβstep affects the newly expanded critical region in each iteration, which is directly related to the sample number \( \varDelta {N}_C^{(k)}={N}_C^{(k)}-{N}_C^{\left(k-1\right)} \) for LSF analysis in this iteration as
It is obvious that smaller Δβstep relates to fewer samples in the newly expanded critical region of each iteration.
-
If LSF is not highly nonlinear, small critical region is needed. Then small Δβstep is preferred so as to finely adjust the critical region until satisfying the stopping criteria. With the fixed Δβstep value, the sample number \( \varDelta {N}_C^{(k)}={N}_C^{(k)}-{N}_C^{\left(k-1\right)} \) in the newly expanded critical region in the kth iteration will reduce as k increases.
-
If LSF is highly nonlinear, the required critical region size Δβ(k) depends on \( \widehat{\beta} \) of the MPP. If \( \widehat{\beta} \) is small, large Δβ(k) is needed. Then relatively larger Δβstep is preferred so as to prevent tedious iteration process which expands the critical region step by step until the required size is achieved. If \( \widehat{\beta} \) is large, the need for Δβ(k) is less demanding and Δβstep can be set to a modest or small value.
3.2.4 The stopping criteria
As the applicability of the proposed BIS-FC method largely depends on its accuracy, the stopping criterion should be defined such that the estimation error is controlled within the acceptable level. Define the estimation error threshold as γE. Then the stopping criterion for estimation error control can be stated as
In some situations, when the accuracy condition is satisfied, the relative difference between the two consecutive estimations may still be relatively large. For example, if γE is defined to be a relatively large value (e.g. γE = 0.01) to represent a big error tolerance, this threshold may be quickly achieved. However, the reliability estimation may still change greatly during the iteration. Then the researcher may need to check the result when the estimation converges to a stable value if the computational resource is available. In this case, define the relative difference between the two consecutive estimations as
where γε is the preset small tolerance. It is noteworthy that the condition \( {\varepsilon}_r^{(k)}\le {\gamma}_{\varepsilon } \) may not really represent the convergence, as it is also affected by the iteration parameter settings. Take the concave case for example, the estimation difference of two consecutive iterations is
From (32) it is known that \( \varDelta {N}_C^{S(k)}\approx {\lambda}_{(k)}\varDelta {N}_C^{(k)} \). As \( \varDelta {N}_C^{(k)} \) is proportional to the probability mass of the newly expanded area between the two consecutive hyperplanes \( {G}_{L\ast}^{\left(k-1\right)} \) and \( {G}_{L\ast}^{(k)} \) as shown in (37), then
It is obvious that if Δβstep is set to be very small, \( {\varepsilon}_r^{(k)} \) will be accordingly very small and may easily drop into the tolerance γε. Thus special care should be taken when using this convergence criterion. Moreover, it is strongly suggested to use this condition as a supplement to the criterion of estimation error.
To sum up, the stopping criteria of BIS-FC include two parts. The first one is for accuracy control, as shown in (38), which requires the estimation error compared to the original BIS method to be smaller than the threshold. The second one is for stable convergence, as shown in (39), which requires the relative change between the two consecutive estimations to be smaller than the threshold. The second criterion is optional and should be used with special care to avoid misjudgment of the convergence condition.
3.3 The algorithm of BIS-FC
According to the definition of critical region in section 3.1, and the iterative procedure for proper critical region identification developed in section 3.2, the system reliability can be analyzed sequentially until reaching the prescribed small estimation error level compared to the original BIS method; meanwhile efficiency can be enhanced by only conducting expensive LSF for the samples in the critical region. To sum up, the flowchart of the proposed BIS-FC method is illustrated in Fig. 6. The main algorithm is explained as follows. For conciseness, the single-MPP and multiple-MPP situations are stated together. The single-MPP situation is regarded as a special case with the MPP number N _ mpp = 1.
-
Step 1.
Transfer the original random vector x = {x1, x2, …xn} into the uncorrelated standard Gaussian random vector u = {u1, u2, …un} in the U space.
-
Step 2.
Obtain the MPPs {M1, M2, ⋯, MN _ mpp}(N _ mpp ≥ 1) and calculate their corresponding reliability index \( {\widehat{\beta}}_i\left(1\le i\le N\_ mpp\right) \). Obtain the hyper-tangent plane GL _ i(u) of LSF at each MPP according to (7).
-
Step 3.
Determine the probabilistic concave or convex of LSF at the vicinity of each MPP following the method in (Lee et al. 2010), based on which define the direction of the hyperplanes for critical region identification.
-
Step 4.
Generate NBIS samples based on the original BIS method in the area outside the \( {\widehat{\beta}}_{\mathrm{min}} \)-sphere, where \( {\widehat{\beta}}_{\mathrm{min}}=\underset{1\le i\le N\_ mpp}{\min }{\widehat{\beta}}_i \). The sampling can be realized by the acceptance-rejection or MCMC-related methods.
-
Step 5.
Initialize the iterative process. Calculate the initial reliability estimation \( {\widehat{R}}^{(0)} \) by (22), which can be simplified to \( {\widehat{R}}^{(0)}=\varPhi \left(\widehat{\beta}\right) \) for the single-MPP situation. Define the initial critical region width as Δβ0, the step increment as Δβstep, the estimation error tolerance as γE, and the stable convergence threshold as γε. Denote the iteration number as k = 1.
-
Step 6.
For the kth step, set Δβ(k) = Δβ0 + (k − 1) ⋅ Δβstep. Generate the hyperplane \( {G}_{L\ast \_i}^{(k)} \) parallel to GL _ i. According to GL _ i and \( {G}_{L\ast \_i}^{(k)} \), define the critical region, assured safe or failure region, unimportant region for each MPP following the definition in section 3.1.1, based on which the total critical region, assured safe and failure region, unimportant safe and failure region can be defined following equations from (12) to (18) for multiple-MPP situation. Denote the sample number in the critical region as \( {N}_C^{(k)} \).
-
Step 7.
If k = 1, conduct LSF analysis for the \( {N}_C^{(k)} \) samples in the critical region, and record the safe number \( {N}_C^{S(k)} \); otherwise, conduct LSF analysis only for the \( \varDelta {N}_C^{(k)}={N}_C^{(k)}-{N}_C^{\left(k-1\right)} \) samples in the newly expanded critical region.
-
Step 8.
Calculate the reliability \( {\widehat{R}}^{(k)} \) according to (23), which can be simplified to (21) for the single-MPP situation.
-
Step 9.
Check the stopping conditions.
-
Step 9.1.
Check the reliability estimation error e(k) by (38). If e(k) > γE, k = k + 1 and go back to Step 6; otherwise, go to Step 9.2 if it is applicable or go to Step 10 if the stable convergence criterion is not used.
-
Step 9.2.
Calculate the relative difference \( {\varepsilon}_r^{(k)} \) between the two consecutive estimations by (39). If \( {\varepsilon}_r^{(k)}\le {\gamma}_{\varepsilon } \), the stable convergence is achieved and go to Step 10; otherwise, k = k + 1 and go back to Step 6. Special attention is needed for using this criterion, which is discussed in detail in section 3.2.4.
-
Step 9.1.
-
Step 10.
End the iteration procedure and output the reliability result \( {\widehat{R}}^{(k)} \).
4 Examples
In this section, six numerical examples and one engineering example are employed to verify the proposed BIS-FC method. Due to the randomness of sampling, in each example, 100 independent runs are conducted. The average reliability analysis results are used for performance discussion. To demonstrate the effectiveness of BIS-FC which is based on the framework of BIS, the accuracy and efficiency are compared against the original BIS. The efficiency is measured by the saved computational cost defined in (36), and the relative error compared to BIS is defined as
The crude MCS is also used as benchmark to measure the estimation accuracy as
where \( {\widehat{R}}_{BIS} \) and \( {\widehat{R}}_{MCS} \) are the reliability estimations obtained by BIS and MCS respectively.
4.1 Example 1
A two-dimensional LSF is used to demonstrate the original BIS and the effect of the reliability index \( \widehat{\beta}\left(\widehat{\beta}\le \beta \right) \) on reliability estimation. The LSF is defined as:
where both u1 and u2 are independent standard normal random variables, denoted as u1, u2 ∼ N(0, 1). The safe region is defined by G(u) < 0. The reliability analysis results of the crude MCS (the sample size is 107) and the original BIS are listed in Table 1. The HL-RF method (Hasofer and Lind 1974; Hohenbichler and Rackwitz 1982) is used for MPP searching in BIS, and the accurate value \( \widehat{\beta}=\beta =3 \) is obtained. The total number of function calls to the LSF is denoted as Ncalls. For BIS, Ncalls includes the function calls used in FORM for MPP searching and the sample analysis in the importance sampling process (Fig. 7). The results show that BIS can effectively improve the efficiency compared to MCS with good accuracy.
In order to demonstrate the effect of \( \widehat{\beta}\left(\widehat{\beta}\le \beta \right) \) on reliability estimation of BIS, \( \widehat{\beta} \) is purposefully set to be 2, 2.3, 2.6, 2.9 respectively and the results of BIS are listed in Table 2. It can be observed that all the results can achieve good accuracy. The estimation results are not sensitive to the \( \widehat{\beta} \) value (as long as \( \widehat{\beta}\le \beta \)) which is an advantage of robustness. However, the small \( \widehat{\beta} \) leads to the sacrifice of efficiency, as more samples outside the \( \widehat{\beta} \)-sphere need LSF analysis. Thus the accurate estimation of \( \widehat{\beta} \) still plays an important role to enhance both the accuracy and the efficiency of BIS.
4.2 Example 2
The two-dimensional concave LSF from the literature (Zou et al. 2002) is used to demonstrate the proposed BIS-FC method. The LSF is defined as:
where x1 and x2 are random variables and their probabilistic distributions are shown in Table 3. The LSF is probabilistic concave and highly non-linear in the vicinity of the MPP, as shown in Fig. 8. The reliability analysis results obtained by the proposed BIS-FC, the crude MCS, the original BIS, and FORM are compared in Table 4. The crude MCS sample size is 107. The original BIS only needs 2813 samples to achieve good accuracy on average of 100 independent runs. The BIS sampling is shown in Fig. 8(a). For FORM, the MPP is searched by the trust region update method (Zou et al. 2002) (4 iterations with 20 LSF calls), as the HL-RF algorithm does not converge in this case. The reliability index \( \widehat{\beta} \) is calculated as 2.226, and the reliability is estimated as \( \varPhi \left(\widehat{\beta}\right)=0.9870 \) by FORM.
For the proposed BIS-FC method, set the initial critical region width and the step increment as Δβ0 = Δβstep = 0.2. Set the stopping criterion of estimation error tolerance in (38) as γE = 0.001 and the convergence tolerance in (39) as γε = 0.0001. As shown in Fig. 8(b), among the samples of BIS (blacks dots), only a small portion are located in the critical region after convergence (blue-star points) which are analyzed with the accurate LSF. The other samples located in the assured safe or unimportant region are directly identified as safe or failure by the linear hyperplane at MPP (the red line) and its parallel (the red dashed line). Thus great computational cost can be saved. Table 5 and Fig. 9 show the detailed iterative process. It reaches stable convergence after four iterations and the sample number \( \varDelta {N}_C^{(k)} \) in the newly expanded critical region analyzed in each iteration is 189, 106, 59 and 26, respectively. It is obvious that as the iteration proceeds, the function calls to LSF reduce significantly, which complies with the analysis in section 3.2.3. Table 5 shows that the proposed method can greatly improve the analysis accuracy compared with FORM (the relative error compared to MCS is reduced from 0.7% to 0.04%). Meanwhile, its computational cost is much lower than the original BIS (almost reduced by 85%) with minor sacrifice of accuracy. The results demonstrate that the proposed method can achieve a good balance between efficiency and accuracy.
4.3 Example 3
The following probabilistic convex LSF with two independent standard normal random variables is used to demonstrate the effect of Δβstep on estimation:
where u1 and u2 are independent standard normal variables. The analysis results obtained by the crude MCS, the original BIS and FORM, are shown in Table 6.
For FORM, the MPP is identified by the HL-RF algorithm (6 LSF calls), and the reliability index is \( \widehat{\beta}=2.62 \). The reliability estimated by FORM is \( \varPhi \left(\widehat{\beta}\right)=0.9956 \) and the relative error compared to MCS is 0.39%. BIS uses 2564 (6 + 2578) function calls on average (only 0.0256% of the MCS sample number) to achieve a satisfied accuracy in comparison to the crude MCS. The BIS samples are represented by the black dots in Fig. 10(a).
To discuss the effect of different step increment on the iterative convergence and accuracy of BIS-FC, set Δβ0 = Δβstep as 0.5 and 0.2 respectively. Set the stopping criterion of the estimation error tolerance as γE = 0.001 and the convergence tolerance as γε = 0.0001. The analysis results are compared in Table 7, and the iteration processes are compared in Table 8. It is shown that it takes four iterations for convergence when Δβstep = 0.5 (i.e. the final critical region width Δβk = Δβ0 + (k − 1) ⋅ Δβstep = 2.0) and 8 iterations when Δβstep = 0.2 (i.e. Δβk = 1.6). The parallel hyperplanes defining the critical region in each iteration and the convergence histories for both settings are shown in Fig. 10 and Fig. 11 respectively, wherein the samples in the critical regions are labeled as blue-star. With the same stopping criteria, the critical regions for the two settings should be the same. As the step increment of 0.5 is larger than 0.2, it needs less iteration number to reach the stopping criteria. However, smaller step increment can better finely adjust the critical region till reaching the stopping criteria. Thus although BIS-FC needs more iterations with Δβstep = 0.2, it can gradually converge to a smaller critical region width which is skipped over by the large step increment. Accordingly, the function calls to LSF with Δβstep = 0.2 is slightly smaller (Ncalls = 678) than that with Δβstep = 0.5 (Ncalls = 788). But with slightly wider critical region, the analysis accuracy (EBIS = 0.008%) with Δβstep = 0.5 is obviously better than that (EBIS = 0.014%) with Δβstep = 0.2. This clearly demonstrates the thumb of rules for the settings of Δβstep in section 3.2.3.
To demonstrate the convergence capability of the proposed method to the original BIS, continue the iterative process until there is no more sample added to the critical region, i.e., the unimportant region shrinks to zero. For the case of Δβstep = 0.2, the iterative analysis results are shown in Fig. 12. In total, it takes 32 iterations to finally converge to the original BIS, which demonstrates the capability of the proposed BIS-FC to infinitely approach till final convergence to the BIS result.
4.4 Example 4
To further study the effectiveness of BIS-FC under different LSF nonlinearity and reliability level conditions, the following four two-dimensional concave problems are discussed.
where u1 and u2 are independent standard normal variables. For each LSF Gi (i = 1, ⋯, 4), the failure region is defined as Gi > 0. G1 and G2 are a group with the same LSF nonlinear level but different reliability indexes at MPP, which are 0.5 and 3 respectively. G3 and G4 are a group with the same LSF nonlinear level which is much flatter than the first group. Set Δβ0 = Δβstep = 0.2, the stopping criterion of the estimation error tolerance as γE = 0.001, and the convergence tolerance as γε = 0.00001. The analysis results obtained by BIS-FC, FORM and MCS (the sample size is 107) for the four LSFs are shown in Table 9 and Fig. 13.
First, discuss the results of BIS-FC. It can be observed that, with the same reliability index of \( \widehat{\beta}=0.5 \), G1 with higher nonlinear level needs more iterations and function calls to LSF analysis than those of G3. The same comparison can be observed between G2 and G4. This clearly indicates that larger nonlinearity leads to the sacrifice of efficiency of BIS-FC compared to the “flat” LSF situation. With the same nonlinearity level, G1 and G3 with larger failure probability (\( \widehat{\beta}=0.5 \)) need more iterations and function calls to LSF analysis than those of G2 and G4 with smaller failure probability (\( \widehat{\beta}=3 \)). The computational cost saved by BIS-FC compared to BIS is 65% for G1 and 70% for G3, which is lower than the ratio 89% for G2 and 93% for G4. This demonstrates that when \( \widehat{\beta} \) is large, the need for Δβ(k) is less demanding. Thus BIS-FC can be very efficient for both highly nonlinear and flat LSFs under this circumstance. If the reliability index of MPP is small and the LSF is highly nonlinear, the efficiency of BIS-FC will be reduced. However, compared to the original BIS method, the advantage of efficiency is still significant. The preceding results conform to the analysis in section 3.2.3.
Second, compare the results between BIS-FC and FORM. It is obvious that FORM is very efficient with much less function calls to the LSF analysis. In the situations of extremely small failure probability (\( \widehat{\beta}=3 \)), FORM can achieve very good accuracy for both the flat and high nonlinear problems, i.e., G2 and G4. It is because the misclassified region due to the nonlinearity is far from the origin and has small probability mass. However, FORM has large estimation error due to the LSF nonlinearity when the failure probability is large. For the situation \( \widehat{\beta}=0.5 \), the relative error compared to MCS is up to 17.9%. Compared to FORM, the proposed BIS-FC method can greatly enhance the analysis accuracy by only adding a modest extra computational cost. The samples in the critical region, which have both large occurrence probability and high risk of misclassification, are analyzed with LSF. Thus a good balance between the accuracy and efficiency can be achieved. For both flat and high nonlinear LSF, in the situations with either small or large failure probability, BIS-FC can robustly obtain good estimation accuracy.
4.5 Example 5
A roof truss case from (Keshtegar and Hao 2018; Yun et al. 2018) is studied to verify the proposed BIS-FC. As shown in Fig. 14, the perpendicular deflection Δc at the node C should be smaller than a threshold ζ, and the six-dimensional LSF is:
where l is the distance between node A and B, AC and AS are the cross-sectional areas of reinforced concrete and steel bars respectively, and EC and ES are the elastic modulus of the corresponding materials. The random input variables are independent, and the distribution models are listed in Table 10. The failure region is defined as g < 0.
Set the threshold ζ of the node deflection as 0.03 and 0.025 respectively, so as to check the validity of the proposed method in the situations with small and extremely small failure probability. Conduct reliability analysis with the crude MCS, FORM, BIS, the modified important sampling method (M-ISM) from Ref. (Yun et al. 2018), and BIS-FC for the two threshold settings, and the results are listed in Tables 11 and 12 respectively. For the crude MCS, 108 samples are used for accuracy, and the analysis results are used as benchmark for comparison. The HL-RF method is used for MPP identification. The reliability index at MPP is \( \widehat{\beta}=3.4 \) for ζ = 0.03 and \( \widehat{\beta}=2.39 \) for ζ = 0.025. As in both settings, the failure probability obtained by FORM is smaller than MCS, LSF is probabilistic convex near MPP. Then in BIS-FC, the hyperplane for defining the critical region in the kth iteration should be generated by \( \widehat{\beta}-\varDelta {\beta}_k \). Set the reliability estimation error tolerance as γE = 0.001 and the convergence tolerance as γε = 0.00001. Three different step width settings are used for comparison. As the reliability approaches to one when \( \widehat{\beta}=3.4 \), the failure probability \( {\widehat{P}}_f=1-\widehat{R} \) is used for clear demonstration in this example.
For both ζ = 0.03 and ζ = 0.025, the estimation errors of FORM compared to MCS are very large and up to over 30% due to the nonlinearity. BIS can achieve very small estimation error (1.07% and 0.08%) with much less samples (19,169 and 6442), which is much more efficient than crude MCS. The proposed BIS-FC method can further significantly reduce the sample number (by over 95% for ζ = 0.03 and over 80% for ζ = 0.025) compared to BIS, and meanwhile, control the estimation error within 0.5% compared to BIS and around 1% compared to MCS. Thus the effectiveness of the proposed method is verified in good balance of estimation accuracy and efficiency.
The M-ISM method from Ref. (Yun et al. 2018) is also used for comparison. As introduced in section 1, M-ISM can enhance sampling efficiency by only analyzing the samples near MPP and outside the β-sphere which have higher contributive weights measured by the sample occurrence probability (as illustrated in Fig. 1). In Table 11 it shows that M-ISM can achieve good accuracy (EBIS = 1.40% and EMCS = 2.45%) with only 1233 samples, which is very efficient. However, when the sample number is increased to 4778, there is very limited accuracy improvement as EBIS = 0.93% and EMCS = 1.99%. For the proposed BIS-FC, with the gradually increased critical region and slightly increased sample number (from 483 to 905), the accuracy can be effectively improved by reducing EBIS from 2.35% to 0.15% and reducing EMCS from 3.40% to 1.21%. In Table 12, M-ISM can achieve good accuracy (EBIS = 2.38% and EMCS = 2.46%) with the sample size as small as 707. However, when the sample size is gradually increased to 1505, 2974, and 5911, there is no accuracy improvement. For BIS-FC, with the gradually increased critical region and slightly increased sample number (from 539 to 1002), the accuracy can be effectively improved by reducing EBIS from 2.30% to 0.32% and reducing EMCS from 2.38% to 0.40%. Thus in this example, it shows that M-ISM can achieve good accuracy with greatly reduced sampling cost. However, M-ISM may fail to effectively improve the analysis accuracy by increasing the sample number with LSF analysis because the sample selection is based on the sample contributive weight which is measured only by the sample occurrence probability. However, for the proposed BIS-FC, with the step-by-step increase of the critical region, the samples with both large occurrence probability and high risk of misclassification due to the linearization assumption of FORM are analyzed sequentially. Thus BIS-FC can effectively enhance the analysis accuracy with a good balance of computational cost.
By comparing the BIS-FC results obtained with the three different step increment settings, the similar trends as shown in Example 3 can be observed as well. For the same problem, smaller step increment means more iteration number; but the capability to finely adjust the critical region is better. With larger final critical region width, which means more samples need LSF analysis, better accuracy can be achieved. In Table 12, for Δβstep = 0.2 and Δβstep = 0.3, the final critical region widths are the same. Thus similar numbers of LSF calls and analysis results are obtained with small fluctuation due to randomness. Compare the sample numbers of BIS-FC for the two different thresholds 0.03 and 0.025. It can be observed that as the reliability index for ζ = 0.03 is larger than that for ζ = 0.025, less samples are needed for LSF analysis. It conforms to the analysis in section 3.2.3 that with larger reliability index \( \widehat{\beta} \) smaller critical region is needed even in the nonlinear situation.
4.6 Example 6
In this example, a multiple-MPP problem is studied to verify the proposed BIS-FC method. The LSF is defined as
where u1 and u2 are independent standard normal variables. The failure region is defined as G < 0.
As shown in Fig. 15, the LSF (the blue dashed line) has two MPPs. LSF is probabilistic concave at MPP1 and probabilistic convex at MPP2. Set Δβ0 = Δβstep = 0.2, and the stopping criteria as γE = 0.001 and γε = 0.0001. The convergence is achieved after three iterations. With the critical region definition for multiple MPP situation developed in section 3.1.2, the final critical region is obtained with the two tangent lines (the solid red lines) at the two MPPs and their parallel lines (the red dashed lines) respectively. The BIS samples are labeled as black dots, only a small portion of which are located in the critical region (labeled as blue stars) and analyzed with LSF. The rest of the BIS samples are identified as assured failure or safe, unimportant failure or safe, directly according to the algorithm developed in section 3.2.1, based on which reliability can be calculated. The results are compared with the crude MCS and BIS, which are listed in Table 13. And the iteration process is listed in Table 14. The results show that BIS-FC can effectively enhance the computational efficiency of BIS by reducing Ncalls from 2069 to 320. Meanwhile, the analysis accuracy can be maintained with very small estimation error (EBIS = 0.0025%). This example demonstrates the applicability of BIS-FC in solving multiple-MPP problems, and the efficiency and accuracy are also verified.
4.7 Example 7
In this example, a practical engineering problem is studied. The reliability constraint is that the minimal first-order frequency of the frame structure of the micro satellite TT-3, which was launched in 2015 (Li et al. 2017), should be no smaller than the threshold, and the LSF is defined as:
where e1 and e2 denote the Young’s modulus of aluminum and steel respectively, and ρ represents the density of aluminum. F is the system response of first-order frequency, which is calculated by finite element analysis (FEA) with the software ABAQUS (Fig. 16). The three input variables are independent random with the probabilistic models in Table 15. As five minutes are needed for one single FEA simulation, the computational burden of the crude MCS cannot be afforded. Thus only FORM and the original BIS are used for reliability analysis and comparison. The MPP is searched based on the HL-RF algorithm with 52 function calls. It is worth noting that there are two symmetrical MPPs with the same reliability index 2.72 and the LSF is probabilistic concave at both MPPs. Set Δβ0 = Δβstep = 0.2, and the stopping criteria as γE = 0.001 and γε = 0.0001. The results are shown in Table 16.
As shown in Fig. 17, the convergence is achieved after four iterations, and the final critical region is defined with green hyperplanes, wherein the samples are labeled as red circles. Compared to the original BIS, only 301 samples out of the original 3147 BIS samples are analyzed with LSF, which can significantly reduce the computational cost by 89%. Meanwhile, the relative error compared to the original BIS is only 0.003%. Thus the efficiency and accuracy of the proposed method is well verified in this practical engineering application example.
5 Conclusion
In this paper, an improved reliability analysis approach BIS-FC is proposed for both single and multiple MPP situations based on the β-spherical importance sampling (BIS) framework with the innovative concept of critical region by combination with FORM. Unlike the traditional BIS which simply samples the area outside the β-sphere and the modified IS algorithms which improve the efficiency by only analyzing samples with large contributive weights measured by the sample occurrence probability, the proposed method identifies the critical region which contains samples with both high occurrence probability and high misjudgment risk due to the linearization assumption of FORM. According to the concave or convex features of the nonlinear LSF at the MPP, the critical region can be defined by the hyper-tangent plane of LSF at the MPP and its parallel hyperplanes in the specified direction. For multiple-MPP situation, the critical region definition can be directly applied to each MPP and the total critical region can be easily obtained. This definition can effectively cover samples near MPP which have high risk of misjudgment due to the LSF nonlinearity as the hyperplanes move along the LSF gradient direction. Since the MPP can be conveniently obtained with the existing well-developed FORM methods and the gradient information is just the byproduct, the proposed critical region can be easily constructed without complex computation. Thus the proposed BIS-FC has the great advantage of easy implementation.
As BIS-FC needs only conduct LSF analysis for samples in the critical region, it can greatly reduce the computational cost compared to the original BIS. Meanwhile, the analysis accuracy can be greatly enhanced compared to FORM by analyzing samples which are of high misclassification risk near MPP. With the iterative process to gradually enlarge the critical region and improve the estimation accuracy, a good balance of accuracy and efficiency can be obtained. The estimation error level can be controlled by setting the stopping condition of the error tolerance, and BIS-FC can infinitely approach until the final convergence to the original BIS, which guarantees the capability of BIS-FC regarding accuracy convergence. Thus iterative process can be flexibly controlled according to the user’s preference and the computational resources available. The effectiveness of the proposed method is testified with six numerical examples (including convex and concave, single and multiple MPP situations) and one practical engineering application example, and the efficiency and accuracy of BIS-FC are verified. The comparison with the existing methods, as well as the algorithm parameters and LSF nonlinearity effects on the estimation are also comprehensively discussed. As analyzed in section 3.2 and empirically studied in the examples, BIS-FC may sacrifice its efficiency when the LSF is highly nonlinear and the reliability index of MPP is small, which still needs further study in the future.
References
Ang GL, Ang AHS, Tang WH (2015) Kernel method in importance sampling density estimation. Structural Safety and Reliability
Au SK, Beck JL (1999) A new adaptive importance sampling scheme for reliability calculations. Struct Saf 21:135–158
Bourinet JM, Deheeger F, Lemaire M (2011) Assessing small failure probabilities by combined subset simulation and support vector machines. Struct Saf 33:343–353
Breitung K (1984) Asymptotic approximations for multinormal integrals. J Eng Mech ASCE 110:357–366
Cai X, Qiu H, Gao L, Shao X (2017) Metamodeling for high dimensional design problems by multi-fidelity simulations. Struct Multidiscip Optim 56:151–166
Chen X, Yao W, Zhao Y, Ouyang Q (2016) An extended probabilistic method for reliability analysis under mixed aleatory and epistemic uncertainties with flexible intervals. Struct Multidiscip Optim 54(6):1–12
Cressie N (1990) The origins of kriging mathematical. Geology 22:239–252
Crestaux T, MaıTre OL, Martinez JM (2009) Polynomial chaos expansion for sensitivity analysis. Reliab Eng Syst Saf 94:1161–1172
Du X, Hu Z (2012) First order reliability method with truncated random variables. J Mech Design 134:255–274
Echard B, Gayton N, Lemaire M (2011) AK-MCS: an active learning reliability method combining kriging and Monte Carlo simulation. Struct Saf 33:145–154
Engelund S, Rackwitz R (1993) A benchmark study on importance sampling techniques in structural reliability. Struct Saf 12:255–276
Evans M, Swartz T (1995) Methods for approximating integrals in statistics with special emphasis on Bayesian integration problems. Struct Saf 10:254–272
Gayton N, Bourinet JM, Lemaire M (2003) CQ2RS: a new statistical approach to the response surface method for reliability analysis. Struct Saf 25:99–121
Grooteman F (2008) Adaptive radial-based importance sampling method for structural reliability. Struct Saf 30:533–542
Guan XL, Melchers RE (2001) Effect of response surface parameter variation on structural reliability estimates. Struct Saf 23:429–444
Harbitz A (1986) An efficient sampling method for probability of failure calculation. Struct Saf 3:109–115
Hasofer AM, Lind NC (1974) An exact and invariant first order reliability format. J Eng Mech ASCE
Helton JC, Johnson JD, Sallaberry CJ, Storlie CB (2006) Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab Eng Syst Saf 91:1175–1209
Hinrichs A (2010) Optimal importance sampling for the approximation of integrals. J Complex 26:125–134
Hohenbichler M, Rackwitz R (1982) First-order concepts in system reliability. Struct Saf 1:177–188
Hu C, Youn BD (2011) Adaptive-sparse polynomial Chaos expansion for reliability analysis and Design of Complex Engineering Systems. Struct Multidiscip Optim 43:419–442
Hu Z, Mahadevan S (2015) Global sensitivity analysis-enhanced surrogate (GSAS) modeling for reliability analysis. Struct Multidiscip Optim 53:501–521
Jiang C, Qiu H, Gao L et al (2017) An adaptive hybrid single-loop method for reliability-based design optimization using iterative control strategy. Struct Multidiscip Optim 56:1271–1286
Kahn H, Marshall AW (1953) Methods of reducing sample size in Monte Carlo computations. J Oper Res Soc Am 1:263–278
Keshtegar B, Chakraborty S (2018) A hybrid self-adaptive conjugate first order reliability method for robust structural reliability analysis. Appl Math Model 53:319–332
Keshtegar B, Hao P (2018) A hybrid descent mean value for accurate and efficient performance measure approach of reliability-based design optimization. Comput Methods Appl Mech Eng 336:237–259
Kiureghian AD, Dakessian T (1998) Multiple design points in first and second-order reliability. Struct Saf 20:37–49
Lee I, Choi KK, Gorsich D (2010) System reliability-based design optimization using MPP-based dimension reduction method. Struct Multidiscip Optim 41:823–839
Lee I, Shin J, Choi KK (2013) Equivalent target probability of failure to convert high-reliability model to low-reliability model for efficiency of sampling-based RBDO. Struct Multidiscip Optim 48:235–248
Li S, Chen L, Chen X, Zhao Y, Bai Y (2017) Long-range AIS message analysis based on the TianTuo-3 micro satellite. Acta Astronaut 136:159–165
Lv Z, Lu Z, Wang P (2015) A new learning function for kriging and its applications to solve reliability problems in engineering. Comput Math Appl 70:1182–1197
Melchers RE (1990) Search-based importance sampling. Struct Saf 9:117–128
Noh, Y., Choi, K. K., & Lee, I. (2008). MPP-based dimension reduction method for RBDO problems with correlated input variables. AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference
Papaioannou I, Papadimitriou C, Straub D (2016) Sequential importance sampling for structural reliability analysis. Struct Saf 62:66–75
Rosenblatt M (1952) Remarks on a multivariate transformation. Ann Math Stat 23:470–472
Song BF (1990) A numerical integration method for computing structural system reliability. Comput Struct 36:65–70
Sun Z, Wang J, Li R, Tong C (2017) LIF: a new kriging based learning function and its application to structural reliability analysis. Reliab Eng Syst Saf 157:152–165
Wang Z, Wang P (2016) Accelerated failure identification sampling for probability analysis of rare events. Struct Multidiscip Optim 54:1–13
Yao W, Chen X, Huang Y, Van TM (2013a) An enhanced unified uncertainty analysis approach based on first order reliability method with single-level optimization. Reliab Eng Syst Saf 116:28–37
Yao W, Chen X, Luo W, Tooren MV, Guo J (2011) Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Prog Aerosp Sci 47:450–479
Yao W, Chen X, Ouyang Q, Tooren MV (2013b) A reliability-based multidisciplinary design optimization procedure based on combined probability and evidence theory. Struct Multidiscip Optim 48:339–354
Yun W, Lu Z, Jiang X (2018) A modified importance sampling method for structural reliability and its global reliability sensitivity analysis. Struct Multidiscip Optim 57:1625–1641
Zou T, Mahadevan S, Mourelatos Z, Meernik P (2002) Reliability analysis of automotive body-door subsystem. Reliab Eng Syst Saf 78:315–324
Acknowledgements
This work was supported in part by National Natural Science Foundation of China under Grant No.51675525 and 11725211.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor is KK Choi
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Yao, W., Tang, G., Wang, N. et al. An improved reliability analysis approach based on combined FORM and Beta-spherical importance sampling in critical region. Struct Multidisc Optim 60, 35–58 (2019). https://doi.org/10.1007/s00158-019-02193-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-019-02193-y