A modified importance sampling method for structural reliability and its global reliability sensitivity analysis

Abstract

The importance sampling method is an extensively used numerical simulation method in reliability analysis. In this paper, a modification to the importance sampling method (ISM) is proposed, and the modified ISM divides the sample set of input variables into different subsets based on the contributive weight of the importance sample defined in this paper and the maximum super-sphere denoted by β-sphere in the safe domain defined by the truncated ISM. By this proposed modification, only samples with large contributive weight and locating outside of the β-sphere need to call the limit state function. This amelioration remarkably reduces the number of limit state function evaluations required in the simulation procedure, and it doesn’t sacrifice the precision of the results by controlling the level of relative error. Based on this modified ISM and the space-partition idea in variance-based sensitivity analysis, the global reliability sensitivity indices can be estimated as byproducts, which is especially useful for reliability-based design optimization. This process of estimating the global reliability sensitivity indices only needs the sample points used in reliability analysis and is independent of the dimensionality of input variables. A roof truss structure and a composite cantilever beam structure are analyzed by the modified ISM. The results demonstrate the efficiency, accuracy, and robustness of the proposed method.

1 Introduction

Reliability analysis measures the ability that a system or a component fulfills its intended function without failures by taking uncertainties into account. The fundamental problem is to determine the failure probability with a typical expressionP _f  = Pr {g(x) = ε − ψ(x) < 0}, where εis a failure threshold, ψ(x)is the response function such as the deformation of structure, g(x)is a limit state function, and x is a vector of random input variables including the applied loads, material properties, operating condition, and geometry or configuration, etc.

Theoretically speaking, the failure probability can be obtained once the cumulative distribution function (CDF) F _G (g) of the limit state functiong(x), is available, i.e., P _f  = F _G (0). However, analytical derivation of F _G (g)is infeasible for complex limit state function.

During the past several decades, various approximate methods have been developed to estimate the failure probability. The first-order reliability method (FORM) (Hasofer and Lind 1974; Zhao and Ono 1999a) and the second-order reliability method (SORM) (De Der Kiureghian 1991; Zhao and Ono 1999b) are mainly-used method for their efficiency. FORM especially is considered as one of the most acceptable and feasible computational methods, and is developed into two scenarios. One is the mean value FORM (MVFORM) by a linearization of the limit state function around the mean point of input variables, and the other is the advanced FORM (AFORM) by linearizing the limit state function around the most probable point (MPP). However, the accuracy of both FORM and SORM may be abated when encountering the strongly nonlinear cases. Besides, the first-order and second-order partial derivatives of the limit state function g(x) with respect to the model input variables need to be determined in advance, respectively. To overcome the shortcoming of the FORM and the SORM, moment methods for structural reliability are developed (Zhao and Ono 2001; Zhao et al. 2006; Zhao and Ono 2004). Moment methods needn’t the partial derivatives of the limit state function and are simple to implement. However, for some problems with small failure probability, the moment method cannot provide accurate results. Besides, the totally different results may be yielded for different equivalent formulations of the same limit state function by the moment methods (Xu and Cheng 2003). The main reason for error of the moment methods is that the CDF of the limit state function is difficult to be determined only by its first four moments, especially in the tail range. In addition, the high order moments such as the third- and fourth- order moments for strongly nonlinear limit state function are difficult to estimate accurately. Therefore, the fractional moment based maximum entropy is investigated by Zhang and co-workers (Zhang and Pandey 2013) for reliability analysis, where the probability density function (PDF) of the limit state function is approximated by the maximum entropy procedure under the given fractional moment constraints. This method is superior to the integral moment constraints because a fractional moment embodies information about a large number of central moments (Zhang and Pandey 2013). To efficiently estimate the fractional moments, Ref. (Zhang and Pandey 2013) proposed a multiplicative form of dimensional reduction method. The obvious advantage is the rather low computational cost, but it also has some deficiencies. It limits the positive limit state function with low interactive effects and the limit state value cannot be zero when input variables are fixed at their mean values. To reduce the calls of limit state function, the limit state function is usually surrogated by the developed meta-models like quadratic response surface (Kim and Na 1997), neural networks (Papadrakakis and Lagaros 2001), support vector machine (Song et al. 2013; Bourinet et al. 2011) and Kriging (Echard et al. 2011; Hu and Mahadevan 2016). This type of surrogate method needs a post-processing computational cost to evaluate the reliability, although the post-processing computational cost is usually ignored because it is relatively smaller than that of evaluating the limit state function, it dose still exist. Therefore, an efficient post-processing reliability analysis method can enhance the efficiency of meta-model methods effectively.

To avoid estimating the moments and the partial derivatives of the limit state function, Monte Carlo simulation (MCS), a universal method is a good choice since it is adapted for all problems and all distribution types. To improve the efficiency and accuracy of the direct MCS, variance reduction techniques such as importance sampling method (ISM) (Zhang et al. 2014; Melchers 1989; Harbitz 1986; Au and Beck 2002; Zhou et al. 2015) should be preferred. The ISM shifts the sampling center from the mean point of input variables to the MPP. To further construct the more optimal IS density, kernel density estimation (Au and Beck 1999) is employed to estimate the failure probability adaptively.

The modified version of the original ISM is mainly investigated in this paper to save a part of the computational cost and enhance the efficiency of the original ISM. Firstly, truncated importance sampling (TIS) procedure (Grooteman 2008) is employed by introducing the β-sphere, where the sample points dropped into the inner of the β-sphere are all safe. Therefore, the sample points within the inner of the β-sphere don’t need to run the true model, and this process is the first part to save the computational cost for the original ISM. Secondly, contributive weight function is defined in this paper by dividing the original PDF by the importance sampling PDF, which measures the contribution of importance sample points to the failure probability. Thus, the sample points with small contribution are selected by defining a specified tolerance, and these sample points also don’t need to run the true model to decide whether failure or not. Due to that the importance sample points with small contribution usually in the sparse domain with very small PDF, while the inner of the β-sphere are usually in the intensive domain with large PDF, the proposed method decreases the computational cost of the original ISM from two different domains, and these two domains may be independent or have a small intersection.

By the information of the modified ISM in failure probability analysis, space-partition method is extended to estimate the global reliability sensitivity indices which are more useful in reliability-based design optimization and defined in Refs (Cui et al. 2010; Li et al. 2012; Wei et al. 2012). The space-partition method is used in variance-based sensitivity analysis originally. The proposed method is independent of the dimensionality of the model input variables by repeatedly dividing the vector of failure indicator values into different subsets according to different inputs.

The main contributions of this work include: ① modified ISM is investigated by using β-sphere which appears in TIS and the contributive weight function defined in this paper to reduce the computational cost of original ISM from two different domains then to enhance the efficiency of ISM. This amelioration remarkably reduces the number of limit state function evaluations required in the simulation procedure, and it doesn’t sacrifice the precision of the results by controlling the level of relative error. ② space-partition method combined with the modified ISM technique is proposed to estimate the global reliability sensitivity indices efficiently, and this method is independent of the dimension of model input variables; ③ failure probability and global reliability sensitivity indices are estimated simultaneously by one group of model evaluations.

The rest of this paper is organized as follows. Section 2 briefly reviews the definitions of the structural reliability and the global reliability sensitivity indices. Section 3 introduces the original ISM for reliability analysis briefly and the modified ISM proposed in this paper elaborately. Along with the proposed modified ISM, a new computational method of global reliability sensitivity indices is proposed based on the space-partition idea in Section 4. Section 5 analyzes a roof truss structure and a composite cantilever beam structure to verify the accuracy, efficiency, and robustness of the proposed method. Finally, conclusions are summarized in Section 6.

2 Reviews of structural reliability analysis and global reliability sensitivity analysis

2.1 Structural reliability analysis

Suppose the limit state function of the concerned structural system is Y = g(x), where x = (x ₁, x ₂, …, x _n ) is the random input variable vector and f _X (x)is the joint PDF of model input variables. Given all the input variables are mutually independent, the joint PDF can be expressed by a product of the marginal PDF of x _i (i = 1, 2, …, n), i.e., ${f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)=\prod_{i=1}^n{f}_{X_i}\left({x}_i\right)$. We define the region where the limit state function is less than zero as the failure domain. Thereof, the failure probability of this structural system is expressed as follows:

$$ {P}_f=\Pr \left\{g\left(\boldsymbol{x}\right)<0\right\}={\int}_{g\left(\boldsymbol{x}\right)<0}{f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)d\boldsymbol{x} $$

(1)

Equation (1) is a multidimensional integration and the direct method to estimate it is MCS, i.e.,

$$ {\widehat{P}}_{f\_ MCS}=\frac{1}{N}\sum_{i=1}^N{I}_F\left({\boldsymbol{x}}_i\right) $$

(2)

where N is the number of sample points and x _i (i = 1, …, N)is generated from f _X (x). I _F (x _i ) is the indicator function of the failure domain and is defined as follows:

$$ {I}_F\left(\boldsymbol{x}\right)=\left\{\begin{array}{l}1\kern2.00em g\left(\boldsymbol{x}\right)<0\\ {}0\kern1.75em \ g\left(\boldsymbol{x}\right)\ge 0\end{array}\right. $$

(3)

2.2 Global reliability sensitivity analysis

To measure the effect of model input variables on the failure probability, Cui and Li (Cui et al. 2010; Li et al. 2012) proposed the failure probability-based global sensitivity index, and it is depicted as follows:

$$ {\delta}_i^P={E}_{X_i}{\left({P}_f-{P}_{f\mid {X}_i}\right)}^2={\int}_{-\infty}^{+\infty }{\left({P}_f-{P}_{f\mid {X}_i}\right)}^2{f}_{X_i}\left({x}_i\right){dx}_i $$

(4)

where P _f is the unconditional failure probability and ${P}_{f\mid {X}_i}$is the conditional failure probability when X _i is fixed. ${\delta}_i^P$reflects the average effect of the input variable X _i on the failure probability of the model. The higher ${\delta}_i^P$is, the more importance X _i is on the failure probability.

Ref. (Li et al. 2012) proven that (4) has the same form with the variance-based sensitivity index, i.e.,

$$ {\delta}_i^P={E}_{X_i}{\left({P}_f-{P}_{f\mid {X}_i}\right)}^2=V\left(E\left({I}_F|{X}_i\right)\right) $$

(5)

Wei (Wei et al. 2012) standardized it by dividing (5) by the unconditional variance of the failure domain indicator function, that is

$$ {S}_i=\frac{V\left(E\left({I}_F|{X}_i\right)\right)}{V\left({I}_F\right)} $$

(6)

Equation (6) indicates that the failure probability-based global sensitivity index is the first order variance effect of the failure indicator function. Therefore, methods in estimation of Sobol’ index can be extended to this index.

3 Modified importance sampling method (ISM) for structural reliability analysis

3.1 Original ISM for structural reliability analysis

For the problem with large failure probability (10⁻¹~10⁻²), the MCS is efficient and accurate enough. But for the problem with small failure probability (10⁻²~10⁻³or even small), a large number of sample points should be generated (more than 10⁴) to guarantee the calculation accuracy. Aiming at the problem with small failure probability, the ISM is proposed to improve the calculation efficiency. The formula is

$$ {P}_f=\int \dots {\int}_{R^n}{I}_F\left(\boldsymbol{x}\right){f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)d\boldsymbol{x}=\int \dots {\int}_{R^n}{I}_F\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)d\boldsymbol{x} $$

(7)

where h _X (x) is the importance sampling PDF. The optimal h _X (x) is constructed by the following equation (Melchers 1989; Wei et al. 2014):

$$ {h}_{opt}\left(\boldsymbol{x}\right)={I}_F\left(\boldsymbol{x}\right){f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)/{P}_f $$

(8)

Equation (8) indicates that P _f must be obtained in advance for determining the optimal h _X (x), which is impossible because I _F (x)is the integrand and P _f is to be estimated. Thereof, the optimal importance sampling PDF cannot be obtained feasibly in advance. Generally, the importance sampling PDF is constructed by shifting the sampling center from the mean point of input variables to the MPP because MPP is the point with highest probability density in the failure domain.

3.2 Modified ISM for structural reliability analysis

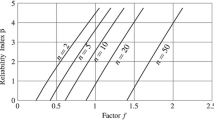
To reduce the calls of model evaluations on ISM, TIS procedure is proposed in Ref (Grooteman 2008) by introducing the β-sphere shown in Fig. 1 where β is the minimum distance from the coordinate origin to the failure surface in the standard normal space, and can be sought by a constrained optimization procedure, i.e.,

$$ {\displaystyle \begin{array}{l}\kern2em \min :\mid \mid \boldsymbol{u}\mid \mid \\ {}\mathrm{subject}\ \mathrm{to}:g\left(\boldsymbol{u}\right)=0\end{array}} $$

(9)

where u is the uncorrelated normalized variables transformed from the random variables x by equivalent probability transformation, i.e.,

$$ \left\{\begin{array}{l}\varPhi \left({u}_i\right)={F}_{X_i}\left({x}_i\right)\\ {}{u}_i={\varPhi}^{-1}\left({F}_{X_i}\left({x}_i\right)\right)\end{array}\right. $$

(10)

where ${F}_{X_i}\left(\cdot \right)$ is the cumulative distribution function (CDF) of X _i , Φ(⋅)and Φ ⁻¹(⋅) are the CDF and inverse CDF of standard normal variable, respectively.

Fig. 1

Geometrical illustration of the TIS procedure

Therefore, the indicator function of the outer of the β-sphere is defined as follows:

$$ {I}_{\beta}\left(\boldsymbol{x}\right)=\left\{\begin{array}{l}0\kern0.75em \mid \mid \boldsymbol{x}\mid \mid <{\beta}^2\\ {}1\kern0.75em \mid \mid \boldsymbol{x}\mid \mid >{\beta}^2\end{array}\right. $$

(11)

where the inner of the β-sphere contains all the safe domain or a part, and the outer of the β-sphere contains the failure domain and a part of safe domain. Thereof, no failure point exists in the β-sphere and the failure domain indicator function is revised as follows:

$$ {I}_F\left(\boldsymbol{x}\right)=\left\{\begin{array}{l}0\kern0.75em \left({I}_{\beta}\left(\boldsymbol{x}\right)=0\right)\kern0.5em \mathrm{or}\kern0.75em \left({I}_{\beta}\left(\boldsymbol{x}\right)=1\ \mathrm{and}\kern0.5em g\left(\boldsymbol{x}\right)>0\right)\\ {}1\kern0.75em {I}_{\beta}\left(\boldsymbol{x}\right)=1\kern0.5em \mathrm{and}\kern0.5em g\left(\boldsymbol{x}\right)\le 0\end{array}\right. $$

(12)

Equation (12) illustrates that a part of safe points dropped into the β-sphere doesn’t need to call the true model to judge whether failure or not. Therefore, the failure probability can be rewritten as follows:

$$ {\displaystyle \begin{array}{l}{P}_f=\int \dots {\int}_{R^n}{I}_F\left(\boldsymbol{x}\right){f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}\kern1.25em =\int \dots {\int}_{R^n}{I}_F\left(\boldsymbol{x}\right){I}_{\beta}\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}\kern1.25em =E\left[{I}_F\left(\boldsymbol{x}\right){I}_{\beta}\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)\right]\end{array}} $$

(13)

The main difference between the ISM and the TIS method is that the latter needs to judge if the sample point is contained in the β-sphere, and if so, the limit state function value doesn’t need to be estimated for this sample point. To estimate (13), N sample points of model inputs are generated, and then the failure probability is estimated by

$$ \widehat{P_f}=\frac{1}{N}\sum_{i=1}^N{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)} $$

(14)

where x _i is the ith sample points of model inputs.

The expectation of the estimator $\widehat{P_f}$ can be derived as

$$ E\left[\widehat{P_f}\right]=E\left[\frac{1}{N}\sum_{i=1}^N{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}\right]=E\left[{I}_F\left(\boldsymbol{x}\right){I}_{\beta}\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}\right]={P}_f $$

(15)

Thus, (14) is an unbiased estimator for the failure probability P _f .

Depending on the definitions of I _F (⋅) and I _β (⋅), the item ${I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}$ can be calculated as

$$ {I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}=\left\{\begin{array}{l}\kern1.00em 0\kern3.25em {I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)=0\\ {}\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}\kern2em {I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)\ne 0\end{array}\right. $$

(16)

The sample point in the inner of the β-sphere is absolutely safe. Generally, the state of the sample point out of the β-sphere need to be judged beforehand. Equation (16) indicates that if the sample point x _i is safe, the contribution of this sample point to the denominator of (14) is zero. In contrast, if the sample point x _i is failure, the contribution of this sample point to the denominator of (14) is $\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}$. Thus, we define a contributive weight of sample point as follows:

$$ W\left(\boldsymbol{x}\right)=\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)} $$

(17)

Equation (17) is suitable for the case of single MPP. For multiple MPPs, the failure probability is estimated by the following equation according to Ref. (Lu and Feng 1995), i.e.,

$$ {\displaystyle \begin{array}{l}{P}_f=\int \dots {\int}_{R^n}{I}_{\boldsymbol{F}}\left(\boldsymbol{x}\right){f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}\kern1.25em =\int \dots {\int}_{R^n}{I}_F\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\sum \limits_{j=1}^m{h}_j\left(\boldsymbol{x}\right)}\sum \limits_{k=1}^m{h}_k\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}\kern1.25em =\sum \limits_{k=1}^m\int \dots {\int}_{R^n}{I}_F\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\sum \limits_{j=1}^m{h}_j\left(\boldsymbol{x}\right)}{h}_k\left(\boldsymbol{x}\right)d\boldsymbol{x}\end{array}} $$

(18)

where m is the number of MPPs and h _k (x) is the kth importance sampling PDF by shifting the sample center to the kth MPP.

Therefore, N number of sample points is generated by h _k (x)(k = 1, 2, …, m), respectively, and the failure probability is estimated as follows:

$$ {\displaystyle \begin{array}{l}{\hat{P}}_f=\sum \limits_{k=1}^m\left\{\frac{1}{N}\sum \limits_{i=1}^N{I}_F\left({\boldsymbol{x}}_{k,i}\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_{k,i}\right)}{\sum \limits_{j=1}^m{h}_j\left({\boldsymbol{x}}_{k,i}\right)}\right\}\\ {}\kern1.5em =\frac{1}{N}\sum \limits_{k=1}^m\sum \limits_{i=1}^N{I}_F\left({\boldsymbol{x}}_{k,i}\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_{k,i}\right)}{\sum \limits_{j=1}^m{h}_j\left({\boldsymbol{x}}_{k,i}\right)}\end{array}} $$

(19)

where x _k, i is the ith sample generated by the kth importance sampling PDF.

Thus, the contributive weight function of the case of multiple MPPs is constructed as follows:

$$ W\left(\boldsymbol{x}\right)=\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\sum_{j=1}^m{h}_j\left(\boldsymbol{x}\right)} $$

(20)

For convenience, the following derivation is based on (17), and the following derivation is also adapted for the case of multiple MPPs by substituting (17) with (20).

The generated N sample points are firstly sorted in a descending order according to the values of their contributive weight indices. Therefore, (14) can be rewritten as

$$ {P}_f=\frac{1}{N}\left[\sum_{i=1}^k{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}+\sum_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}\right] $$

(21)

where $\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}\kern0.5em \left(j\in \left[k+1,N\right]\right)$ is smaller than any $\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}\left(i\in \left[1,k\right]\right)$.

Through ignoring the second sum of the denominator in (21), the estimation of (21) is expressed as

$$ {P}_f^{(k)}=\frac{1}{N}\left[\sum_{i=1}^k{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right)\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}\right] $$

(22)

A convergence criterion should be constructed to choose a proper number of k. Based on the (21) and (22), the relative error of the failure probability between the current ${P}_f^{(k)}$ and the true estimate value P _f is computed by

$$ {\displaystyle \begin{array}{l}{\varepsilon}_k=\frac{P_f-{P}_f^{(k)}}{P_f}\\ {}\kern1em =\frac{\left(1/N\right)\sum \limits_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}{\left(1/N\right)\left[\sum \limits_{i=1}^k{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)+\sum \limits_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)\right]}\\ {}\kern1em =\frac{\sum \limits_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}{\sum \limits_{i=1}^k{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)+\sum \limits_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}\\ {}\kern1em =\frac{1}{1+\frac{\sum \limits_{i=1}^k{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{\sum \limits_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}}\end{array}} $$

(23)

The state of the samples in the first group is identified accurately by calling the limit state function and judging whether the sample point is in the β-sphere, thus, $\sum_{i=1}^k{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)$ is known. In contrast, the state of the sample point in the second group doesn’t need to be judged due to its small contributive weight, and $\sum_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)$ is an unknown value for the analysts. To control the error due to ignoring$\sum_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)$and determine a suitable k, the supremum value of $\sum_{j=k+1}^N{I}_F\left({\boldsymbol{x}}_j\right){I}_{\beta}\left({\boldsymbol{x}}_j\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)$ can be determined by $\sum_{j=k+1}^N{f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)$. Obviously, $\sum_{j=k+1}^N{f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)$ is independent of the indicator function and doesn’t need to call the limit state function. Based on it, the maximum relative error of the failure probability given in (22) is estimated as

$$ {\varepsilon}_k^{\mathrm{max}}=\frac{1}{1+\frac{\sum_{i=1}^k{I}_F\left({\boldsymbol{x}}_i\right){I}_{\beta}\left({\boldsymbol{x}}_i\right){f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{\sum_{j=k+1}^N{f}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)/{h}_{\boldsymbol{X}}\left({\boldsymbol{x}}_j\right)}} $$

(24)

Then, the suitable value of k is searched from one to N by setting ${\varepsilon}_k^{\mathrm{max}}<{C}_r$ (where C _r is the level of accuracy). The incrementation stops if ${\varepsilon}_k^{\mathrm{max}}<{C}_r$.

3.3 Computational cost

The aforementioned modification of ISM reduces the number of limit state function evaluations from two different domains, i.e., the inner of β-sphere and the region with small contributive weight indices. Thereof, the sample set can be divided into three categories, i.e.,

$$ A=\left\{\boldsymbol{x}|||\boldsymbol{u}||<\beta \right\} $$

(25)

$$ B=\left\{\boldsymbol{x}|\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}<\frac{f_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}{h_{\boldsymbol{X}}\left({\boldsymbol{x}}_i\right)}\kern0.5em \forall i\in \left[1,k\right]\right\} $$

(26)

$$ C=U-A\cup B $$

(27)

where U is the universal set containing all the generated sample points. Because the sample points in the set A and B don’t need to call the limit state function, the true number of limit state function evaluations of this improvement is

$$ Ncall=\operatorname{card}\ C $$

(28)

where card represents the number of elements in the set C.

4 Modified ISM for estimating the global sensitivity indices

To estimate (5) by the input sample points and relative output sample points generated in the modified ISM for reliability analysis, the space-partition method proposed in Ref (Zhai et al. 2014) is extended in this paper.

Suppose the sample space of input X _i is (b _l , b _u ), and partition it into s successively equiprobable and non-overlapping subintervals A _k  = [a _k − 1, a _k ), 1 ≤ k ≤ s, where ${p}_k={\int}_{a_{k-1}}^{a_k}{f}_{X_i}\left({x}_i\right){dx}_i$. Then, the (6) is equivalently expressed as

$$ {S}_i=1\hbox{-} \frac{E_{A_k}\left(V\left({I}_F|{X}_i\in {A}_k\right)\right)-\sum_{k=1}^s{p}_k{V}_{X_i}\left(E\left({I}_F|{X}_i\right)|{X}_i\in {A}_k\right)}{V\left({I}_F\right)} $$

(29)

where ${E}_{A_k}\left(\cdot \right)$is the expectation operator when X _i is fixed in A _k  = [a _k − 1, a _k )(k = 1, 2, …, s). Ref (Zhai et al. 2014) proved that $\sum_{k=1}^s{p}_k{V}_{X_i}\left(E\left({I}_F|{X}_i\right)|{X}_i\in {A}_k\right)\to 0$when $\varDelta a=\underset{k}{\max}\mid {a}_k-{a}_{k-1}\mid \to 0$. Thus, the approximate expression of S _i in case of Δa → 0 is

$$ {S}_i\approx 1-\frac{E_{A_k}\left(V\left({I}_F|{X}_i\in {A}_k\right)\right)}{V\left({I}_F\right)} $$

(30)

The law of total expectation in successive intervals without overlapping is proved as follows:

$$ {\displaystyle \begin{array}{l}{E}_{A_k}\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)=\sum \limits_{k=1}^s{\int}_{a_{k-1}}^{a_k}{f}_{X_i}\left({x}_i\right){dx}_i\cdot \frac{1}{\int_{a_{k-1}}^{a_k}{f}_{X_i}\left({x}_i\right){dx}_i}{\int}_{-\infty}^{+\infty }{\int}_{-\infty}^{+\infty}\dots {\int}_{a_{k-1}}^{a_k}{I}_F\left(\boldsymbol{x}\right){f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right){dx}_i\prod \limits_{j=1,j\ne i}^n{dx}_j\\ {}\kern8.25em =\sum \limits_{k=1}^s{\int}_{-\infty}^{+\infty }{\int}_{-\infty}^{+\infty}\dots {\int}_{a_{k-1}}^{a_k}{I}_F\left(\boldsymbol{x}\right){f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right){dx}_i\prod \limits_{j=1,j\ne i}^n{dx}_j\\ {}\kern8.25em ={\int}_{-\infty}^{+\infty }{\int}_{-\infty}^{+\infty}\dots {\int}_{b_1}^{b_2}{I}_F\left(\boldsymbol{x}\right){f}_{\boldsymbol{X}}\left(\boldsymbol{x}\right)d\boldsymbol{x}\\ {}\kern8.25em =E\left({I}_F\right)\end{array}} $$

(31)

Based on (31), the law of total variance in successive intervals without overlapping is proved as follows:

$$ {\displaystyle \begin{array}{l}{V}_{A_k}\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)={E}_{A_k}\left({E}^2\left({I}_F|{X}_i\in {A}_k\right)\right)-{E}_{A_k}^2\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)\\ {}\kern7.75em ={E}_{A_k}\left({E}^2\left({I}_F|{X}_i\in {A}_k\right)\right)-{E}^2\left({I}_F\right)\end{array}} $$

(32)

$$ {\displaystyle \begin{array}{l}{E}_{A_k}\left(V\left({I}_F|{X}_i\in {A}_k\right)\right)={E}_{A_k}\left(E\left({I_F}^2|{X}_i\in {A}_k\right)-{E}^2\left({I}_F|{X}_i\in {A}_k\right)\right)\\ {}\kern8.5em =E\left({I_F}^2\right)-{E}_{A_k}\left({E}^2\left({I}_F|{X}_i\in {A}_k\right)\right)\end{array}} $$

(33)

Then,

$$ {E}_{A_k}\left(V\left({I}_F|{X}_i\in {A}_k\right)+{V}_{A_k}\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)\right.=E\left({I_F}^2\right)-{E}^2\left({I}_F\right)=V\left({I}_F\right) $$

(34)

Thus, (30) can be equivalently written as

$$ {S}_i\approx \frac{V_{A_k}\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)}{V\left({I}_F\right)} $$

(35)

Generally, E(I _F | X _i  ∈ A _k ) is easier to be estimated and requires much fewer sample points in each subinterval A _k than V(I _F | X _i  ∈ A _k ). Thereof, the conflict between the accuracy of estimating E(Y| X _i  ∈ A _k ) and convergence condition Δa → 0 of (35) can be alleviated.

4.1 Estimation of ${V}_{A_k}\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)$

According to (13), E(I _F | X _i  ∈ A _k )is estimated as

$$ {\displaystyle \begin{array}{l}E\left({I}_F|{X}_i\in {A}_k\right)={\int}_{A_k}{I}_F\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}d\boldsymbol{x}\\ {}\kern6.25em ={\int}_{A_k}{I}_F\left(\boldsymbol{x}\right){I}_{\beta}\left(\boldsymbol{x}\right)\cdot \frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}\cdot \frac{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}\cdot \frac{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}d\boldsymbol{x}\\ {}\kern6em =\frac{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}\cdot {\int}_{A_k}\left[{I}_F\left(\boldsymbol{x}\right){I}_{\beta}\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}\right]\cdot \frac{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}d\boldsymbol{x}\\ {}\kern6em =\frac{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}\cdot {E}_{A_k\mid {h}_{\boldsymbol{X}}^{\ast}\left(\boldsymbol{x}\right)}\left[{I}_F\left(\boldsymbol{x}\right){I}_{\beta}\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}\right]\end{array}} $$

(36)

$$ {h}_{\boldsymbol{X}}^{\ast}\left(\boldsymbol{x}\right)=\left\{\begin{array}{l}\frac{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}\kern1.25em {x}_i\in {A}_k\\ {}\kern2.5em 0\kern3.75em {x}_i\notin {A}_k\end{array}\right. $$

(where)

Define $IW\left(\boldsymbol{x}\right)={I}_F\left(\boldsymbol{x}\right){I}_{\beta}\left(\boldsymbol{x}\right)\frac{f_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}{h_{\boldsymbol{X}}\left(\boldsymbol{x}\right)}$ and make IW(x _i ) = 0 (i = k + 1,  .. , N) for its small contributive weight. Then,

$$ E\left({I}_F|{X}_i\in {A}_k\right)=\frac{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}\frac{1}{m_k}\sum_{r=1}^{m_k} IW\left({\boldsymbol{x}}_r^{(k)}\right) $$

(37)

where m _k is the number of sample points ${\boldsymbol{x}}_r^{(k)}\left(r=1,\dots, {m}_k\right)$in subinterval A _k .

According to the relationship between expectation and variance, and combining the proved law of total expectation in successive intervals without overlapping, the estimator of ${V}_{A_k}\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)$is derived as follows:

$$ {\displaystyle \begin{array}{l}{V}_{A_k}\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)={E}_{A_k}\left({E}^2\left({I}_F|{X}_i\in {A}_k\right)\right)-{E}_{A_k}^2\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)\\ {}\kern8.5em ={E}_{A_k}\left({E}^2\left({I}_F|{X}_i\in {A}_k\right)\right)-{E}^2\left({I}_F\right)\end{array}} $$

(38)

where

$$ {\displaystyle \begin{array}{l}{E}_{A_k}\left({E}^2\left({I}_F|{X}_i\in {A}_k\right)\right)=\sum \limits_{k=1}^s\Pr \left\{{X}_i\in {A}_k\right\}{E}^2\left({I}_F|{X}_i\in {A}_k\right)\\ {}\kern9em =\sum \limits_{k=1}^s\Pr \left\{{X}_i\in {A}_k\right\}{\left[\frac{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}\frac{1}{m_k}\sum \limits_{r=1}^{m_k} IW\left({\boldsymbol{x}}_r^{(k)}\right)\right]}^2\\ {}\kern9em =\sum \limits_{k=1}^s\frac{{\left\{{\int}_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i\right\}}^2}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}{\left[\frac{1}{m_k}\sum \limits_{r=1}^{m_k} IW\left({\boldsymbol{x}}_r^{(k)}\right)\right]}^2\end{array}} $$

(39)

$$ {\displaystyle \begin{array}{l}{E}_{A_k}^2\left(E\left({I}_F|{X}_i\in {A}_k\right)\right)={\left[\sum \limits_{k=1}^sP\left\{{X}_i\in {A}_k\right\}E\left({I}_{\boldsymbol{F}}|{X}_i\in {A}_k\right)\right]}^2\\ {}\kern8.5em ={\left[\sum \limits_{k=1}^s{\int}_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i\frac{\int_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i}{\int_{A_k}{f}_{X_i}\left({x}_i\right)d{x}_i}\frac{1}{m_k}\sum \limits_{r=1}^{m_k} IW\left({\boldsymbol{x}}_r^{(k)}\right)\right]}^2\\ {}\kern8.5em ={\left[\sum \limits_{k=1}^s{\int}_{A_k}{h}_{X_i}\left({x}_i\right)d{x}_i\frac{1}{m_k}\sum \limits_{r=1}^{m_k} IW\left({\boldsymbol{x}}_r^{(k)}\right)\right]}^2\end{array}} $$

(40)

$$ {E}^2\left({I}_F\right)={P}_f^2\approx {\left({P}_f^{(k)}\right)}^2 $$

(41)

4.2 Estimation of V(I _F )

According to the relationship between the expectation and the variance, V(I _F ) is estimated by${P}_f^{(k)}$, i.e.,

$$ V\left({I}_F\right)=E\left({I}_F^2\right)-{E}^2\left({I}_F\right)={P}_f-{P}_f^2\approx {P}_f^{(k)}-{\left({P}_f^{(k)}\right)}^2 $$

(42)

4.3 The partition strategies

The partition scheme affects the estimations of the global reliability sensitivity indices notablely. A larger s may improve the accuracy of the outer variance and guarantee the convergence condition, yet also reduce the accuracy of the inner expectation. The inaccurate estimation of the inner expectation will yield mistakes in estimation of S _i . A smaller s may improve the accuracy of the inner expectation, but decrease the accuracy of outer variance and destroy the convergence condition of the space-partition method. Therefore, achieving a compromise is necessary at a given number of input-output sample points. To harmonize the number of subintervals and the number of samples in each subinterval, the medium value $s=\left[\sqrt{N}\right]$is suggested in Ref. (Li and Mahadevan 2016). Another partition scheme is suggested in this paper. Firstly, a certain number of sample points are fixed in each subinterval. In the beginning, when N is small, the each subinterval is long and the number of samples for estimating the variance in the out loop are small. Then the estimates of the global reliability sensitivity indices are quite inaccurate. By increasing N, the length of each subinterval becomes short and the number of samples for estimating the outer variance is increased. Consequently, the accuracy of the inner expectation and outer variance are fulfilled, and the convergence condition of space-partition also is guaranteed by increasing N, the number of sample points. Fig. 2 shows the process of the proposed alternative partition scheme. The blue circle represents the total sample points, and the red circle represents the boundaries of each subinterval.

Fig. 2

The partition scheme

5 Case studies

In this section, a roof truss structure and a composite cantilever beam structure are employed to verify the effectiveness of the proposed method. In these two engineering studies, low discrepancy sequence sampling procedure (Sobol 1976; Sobol 1998) is used to generate the sample points of the model input variables. Moreover, MPP can be searched by many existing methods (Hasofer and Lind 1974; Rashki et al. 2012). In this paper, MPP is computed by the advanced first-order reliability method (AFORM) (Hasofer and Lind 1974). The AFORM algorithm is global convergent when the limit state function is continuous and differentiable (Hasofer and Lind 1974).

5.1 Case study I: A roof truss structure

A roof truss is shown in Fig. 3. The top boom and the compression bars are reinforced by concrete. The bottom boom and the tension bars are steel. The uniformly distribution load q is applied on the roof truss, which can be transformed into the nodal load P = ql/4. The perpendicular deflection Δ _C of the node C can be obtained by the mechanical analysis, which is the function of the input variables, i.e.,

$$ {\varDelta}_C=\frac{ql^2}{2}\left(\frac{3.81}{A_C{E}_C}+\frac{1.13}{A_S{E}_S}\right) $$

(43)

where A _C , A _S , E _C , E _S , and l denote sectional area, elastic modulus, length of the concrete and that of the steel bars, respectively. Considering the safety and the applicability, the limit state function is established as follows:

$$ g\left(\boldsymbol{x}\right)=\varepsilon -{\varDelta}_C $$

(44)

where ε is the failure threshold. Random input variables are assumed as the independent normal variables with the distribution parameters shown in Table 1.

Fig. 3

The schematic diagram of roof truss

Table 1 The distribution parameter of the input variables of Case study I

We define the sample reduction ratio to measure the efficiency of each reliability analysis method. The mathematical expression of the sample reduction ratio is depicted as follows:

$$ \mathrm{Sample}\ \mathrm{reduction}\ \mathrm{ratio}=\frac{N- Ncall}{N} $$

(45)

where N is the number of samples used in MCS and Ncall is the used number of samples in the compared method. Ncall includes the number of samples used to find MPP if used. Therefore, the higher the sample reduction ratio is, the more efficient the method is.

Tables 2, 3, and 4 show the results of failure probability estimated by MCS, ISM, TIS where MPP is searched by 35 model evaluations and the proposed modified ISM with different maximum relative error limits, respectively. From these three tables, five points can be obtained as follows:

• (1). The proposed modified ISM inherits the variance reduction property of the original ISM, and decreases the computational cost remarkably by adjusting the maximum relative error limit flexibly.

• (2). The higher the maximum relative error limit is, the larger the sample reduction ratio is.

• (3). With the reduction of the maximum relative error limit, the estimation of the failure probability by the proposed modified ISM trends towards the true value.

• (4). The sample reduction ratio of the proposed ISM in this case study is more than twice as large as that of the TIS method with the maximum relative error limit being 5%, is twice as large as that of the TIS method with the maximum relative error limit being 2%, and is approximate 1.5 times as large as that of the TIS method with the maximum relative error limit being 0.5%.

• (5). As the number of samples N increases, the sample reduction ratio of the modified ISM increases. The main reason is that as the number of samples N increases, the samples used to find the MPP can be omitted in comparison with the savings of sample evaluations.

Table 2 The estimation of failure probability for the threshold ε = 0.025mwith C _r  = 5%

Table 3 The estimation of failure probability for the threshold ε = 0.025mwith C _r  = 2%

Table 4 The estimation of failure probability for the threshold ε = 0.025mwith C _r  = 0.5%

To further illustrate the capability of dealing with small failure probability of the modified ISM, we adjust the failure threshold for comparison. Tables 3, 5, and Table 6 give the results of failure probability with different failure threshold, and the maximum relative error limit is set as 2%. The MPPs are computed by 35, 56, 49 model evaluations for three different failure thresholds, respectively. The following conclusions from the numerical results are obviously obtained, i.e.,

• (1). The proposed modified ISM method is competent for the case with small failure probability.

• (2). Under the acceptable precision level, sample reduction ratio of the proposed method is twice as large as that of the TIS method.

• (3). Under the same precision level, the smaller the failure probability is, the bigger the sample reduction ratio is. The main reasons is that if the current system is not highly reliable, then the β-sphere will not be larger and thus the samples in the β-sphere could be small so that the savings of function evaluations.

Table 5 The estimation of failure probability for the threshold ε = 0.028mwith C _r  = 2%

Table 6 The estimation of failure probability for the threshold ε = 0.030mwith C _r  = 2%

Table 7 shows the results estimated by MVFORM, AFORM, and MaxEnt + M-DRM. The calls of model evaluations are 8, 35/56/49, 25, respectively. These are more efficient than the sampling-based method. However, the accuracies of these three efficient methods are lower than those of the sampling-based method for this problem. It further illustrates the generality of the sampling-based method.

Table 7 The estimations of failure probability of the roof truss structure by other methods

By reusing the samples generated in failure probability estimation, the global reliability sensitivity indices can be obtained as byproducts.

Fig. 4 and Fig. 5 show the numerical results of global reliability sensitivity indices withε = 0.025. From the results figures, it can be seen that no matter $s=\left[\sqrt{N}\right]$ or fixing a certain number of sample points in each subinterval in advance, the acceptable accuracies can be achieved in the examples. Table 8 shows the numerical results of global reliability sensitivity indices estimated by the proposed modified ISM and the single-loop IS method proposed in Ref. (Wei et al. 2012). The importance ranking of the random input variables obtained by Ref (Wei et al. 2012), modified ISM and MCS are the same, i.e., A _c  > q > E _s  > A _s  > l > E _c . For each estimate, the standard deviation (SD) of estimate ${\widehat{S}}_i$ is employed to measure the convergence. From Table 8, we can clearly see that SDs of our proposed method are small than these of the method in Ref. (Wei et al. 2012), thus it can demonstrate the robustness of the proposed modified ISM. The potential sources of the slight error of the proposed modified ISM in global reliability sensitivity analysis are the slight errors from the modified ISM in reliability analysis and the space-partition method in sensitivity analysis.

Fig. 4

The global reliability sensitivity indices estimated by the modified ISM integration with space-partition method (Modified ISM(1) represents the partition scheme that $s=\left[\sqrt{N}\right]$, and references are the results estimated by MCS with large number of model evaluations)

Fig. 5

The global reliability sensitivity indices estimated by the modified ISM integration with space-partition method (Modified ISM(2) represents the partition scheme that a certain number of sample points are fixed in each subinterval in advance, and references are the results estimated by MCS with large number of model evaluations)

Table 8 Numerical results of global reliability sensitivity indices for the threshold ε = 0.025m with C _r  = 5%

5.2 Case study II: A Composite cantilever beam structure

A composite cantilever beam structure with the load F ₀ is shown in Fig. 6. The displacement Δ _Tip of the free point is obtained by mechanical analysis of composite material structure:

$$ {\varDelta}_{Tip}=\frac{F_0{L}^3}{2{h}^3}\left(\frac{E_L^2-4{G}_{LT}{E}_T{v}_{LT}^2+{E}_L\left({E}_T+4{G}_{LT}+2{E}_T{v}_{LT}\right)}{E_L{G}_{LT}\left({E}_L+{E}_T+2{E}_T{v}_{LT}\right)}\right) $$

(46)

where F ₀, L and h are the applied load per width, length of the beam and the height of the beam, respectively. E _L , E _T , G _LT and v _LT are the longitudinal Young moduli, transverse Young moduli, shear modulus and Poisson ratio, respectively. Considering that the tip displacement cannot exceed 9.59 cm, the limit state function of the reliability analysis can be established as follows:

$$ g=9.59-{\varDelta}_{Tip} $$

(47)

Fig. 6

Composite cantilever beam structure model

All the input variables are normal and mutually independent. The distribution parameters are listed in the Table 9.

Table 9 Distribution parameters of input variables for Case study II

Table 10 shows the numerical results of failure probability while ε = 9.59cm and C _r  = 2%. The results demonstrate that the proposed modified ISM not only inherits the advantages of the original ISM but also reduces more than 5 % model evaluations in comparison with the original ISM. The failure probability of this case is 0.0876. The mainly reductive direction of this case study is the small contributive weight domain, and it hardly has sample points in the β-sphere for β is small in this case. For comparison, ε is adjusted to 19.59 cm and 29.59cm. The failure probabilities of the two cases are 0.00197 and 1.068 × 10⁻⁴, respectively. They are smaller than that of 9.59 cm failure threshold. From Tables 11 and 12, it can be seen that the number of sample points in β-sphere increases, and no matter small failure probability or large failure probability, the reductive number of model evaluations in the small contributive weight domain is as much as that in β-sphere.

Table 10 The estimation of failure probability for this composite cantilever beam with ε = 9.59cm and C _r  = 2%

Table 11 The estimation of failure probability for this composite cantilever beam with ε = 19.59cm and C _r  = 2%

Table 12 The estimation of failure probability for this composite cantilever beam with ε = 29.59cm and C _r  = 2%

Table 13 also shows the failure probability of this composite cantilever beam structure estimated by AFORM and MaxEnt + M-DRM. AFORM uses 24 model evaluations to find the MPPs for different failure thresholds, respectively. MaxEnt + M-DRM only uses 29 model evaluations to estimate the failure probabilities with different failure thresholds. From Table 13, it obvious that AFORM behaves more accurately than MaxEnt + M-DRM which cannot estimate the small failure probability accurately for this case study.

Table 13 The estimations of failure probability of the composite cantilever beam structure by other methods

By $s=\left[\sqrt{N}\right]$ partition scheme and reusing the sample points in failure probability estimation, the global reliability sensitivity indices are computed in Table 14. Results in Table 14 demonstrate the fast convergence of the proposed method compared with the existing efficient single-loop IS method. The importance rank is h > L > F ₀ > G _LT  > E _L  > E _T  = v _LT , which indicates that the uncertainty of h has the most important effect on failure probability. By decreasing the uncertainty of h, the most reduction of failure probability can be obtained. It is also shown that the sensitivity indices of  E _T   and v _LT  are close to zero, thus the uncertainty of these two input variables can be omitted.

Table 14 Numerical results of global reliability sensitivity indices with ε = 9.59cmand C _r  = 2%

6 Conclusion

This paper aims at improving the efficiency of ISM in reliability analysis. The proposed modified ISM inherits the advantages of the original ISM and further reduces the computational cost of ISM. Firstly, based on the idea of TIS, we screen out the samples in β-sphere. Secondly, we define the contributive weight as the ratio of the original PDF to the importance sampling PDF. The samples with small contributive weight are screened out under an acceptable precision level. Because of the samples dropped in β-sphere are safe, they don’t need to run the model to decide their states. The samples with small contributive weights predicate the small contribution to failure probability. Thereof, we consider they are safe directly without running the model. Thus, the proposed modified ISM reduces the computational cost of ISM from two different domains. Because the modified ISM is based on the original ISM some limitations of the original ISM also exist in the modified ISM. To further estimate the global reliability sensitivity indices as byproducts, original space-partition method in variance-based sensitivity analysis is extended to the global reliability sensitivity analysis, and the law of total variance in the successive intervals without overlapping is proved additionally. By analyzing a roof truss structure and a composite cantilever beam structure, the effectiveness of the proposed modified ISM in reliability analysis and global reliability sensitivity analysis is verified.