1 Introduction

The extensive use of stiffened panels in aerospace industry is mainly motivated by their high specific stiffness and strength. Stiffened panels still play a significant role in fuel storage and load-carrying components (see, for example, the study on the new Chinese launch vehicle done by Hao et al. 2012). Metallic materials such as aluminum alloys are the primary choice in the aerospace industry because these can easily be tailored to create an adequate design even working in the post-buckling field. With the advent of new composite materials in aerospace applications, stiffened panels made of composite material were also developed rapidly in the last few decades (Nagendra et al. 1994; Huybrechts and Meink 1997; Noor et al. 2000; Park et al. 2001, 2012).

For thin-walled structures subjected to axial compression, buckling is the main failure mechanism (Calladine 1983; Wang et al. 2013). In general, launch vehicles may be subject to uniform and non-uniform axial compression (see Fig. 1). Stiffened panels in stage cores are usually subjected to uniform compression. Inertia loads generated by acceleration during ascent are transferred from core stages to the noses of the boosters. These elements are hence subject to concentrated forces, by most part axial, that generate a state of non-uniform compression.

Fig. 1
figure 1

Sources of stiffened panels subject to uniform and non-uniform compressions in launch vehicle

Full size image

It is generally recognized that axially compressed cylindrical shells are very sensitive to initial geometric imperfections (Calladine 1995; Lindgaard et al. 2010; Wang et al. 2011; Hao et al. 2013), while flat plates are marginally sensitive to small-amplitude imperfections (Schultz and Nemeth 2010). Among various types of geometric imperfections, eigenmode-shape imperfection is expected to be relatively conservative because it represents deformation shapes with a high bias toward buckling (Lamberti et al. 2003). The newly developed European code for steel shell structures also recommended that eigenmode-shape imperfection should be used, unless a different unfavorable pattern can be justified (Eurocode 3 1999).

Several methods and programs are available for the analysis of stiffened panels, ranging from simple closed form solutions to complicated discrete solutions (Timoshenko and Gere 1961; Calladine 1983; Thompson and Hunt 1984; Croll and Ellinas 1983). Several simple analysis methods, such as Smeared Stiffener Method (SSM) and simple analytical models were utilized to calculate the critical buckling load of stiffened shells for preliminary design (Kidane et al. 2003). However, these methods cannot account for the nonlinearity of buckling behavior. Moreover, the critical buckling mode shape in SSM is assumed to be in form of a double Fourier series and thus distributed uniformly along the shell length, which may be different from the actual condition. FE analysis also can be used to evaluate the load-carrying capacity of stiffened panels, including linear eigenvalue buckling analysis, nonlinear implicit and explicit dynamic methods. In the case of elastic buckling, linear eigenvalue buckling analysis can predict the critical buckling mode shape and thus load-carrying capacity accurately, which is commonly utilized in the preliminary design stage due to the high computational efficiency. However, in the case of plastic buckling, since stiffness reduction caused by yielding before buckling may affect significantly load and equilibrium paths of stiffened panels, material nonlinearity must be taken into account and nonlinear buckling analysis is hence needed. Furthermore, accounting for imperfections requires more detailed modeling of structures and nonlinear analysis for predicting the load redistribution due to pre-buckling bending. Nonlinear implicit methods, such as the Newton-Raphson method (Crisfield 1979) and the modified Riks method (Crisfield 1981), have been commonly employed to simulate the post-buckling behavior of stiffened panels (Bushnell 1981, 1985, 1987; Wu et al. 2010). However, the convergence of an implicit analysis is difficult to guarantee, especially after skin buckling occurs. Compared to nonlinear implicit methods, explicit dynamic method allows to investigate the evolution of the deformed shape of a stiffened panel from pre-buckling to post-buckling field until collapse (Lanzi and Giavotto 2006). In other words, the position where collapse occurs can be captured accurately by the explicit dynamic analysis. The deformed shape of stiffened panels at the collapse load varies considerably from the critical buckling mode shape, especially in the position where buckling or collapse occurs. Specifically, the deformed positions are assumed to distribute uniformly along the shell length in SSM, while the collapse mostly occurs at either the intermediate section or both two shell ends. In the case of elastic buckling, the collapse mainly occurs at the intermediate section of the shell, referred to as ”diamond shaped” buckling mode. Conversely, in plastic buckling, the collapse usually evolves from the both ends of the shell, referred to as ”elephant foot” buckling mode (Mazzolani et al. 2004). Thus it is a logical way to adjust the stiffness of a structure along the axial direction and then increase the load-carrying capacity.

Many optimizations have been carried out for metallic and composite stiffened panels against buckling. In the case of uniform axial compression, Leriche and Haftka (1993) demonstrated the efficiency of genetic algorithms (GA) in dealing with global optimization and discrete design variables for composite stiffened panels. A design strategy for optimum design of stiffened shells subject to global and local buckling constraints as well as strength constraints based on GA was developed by Jaunky et al. (1998). In order to reduce the computational cost of the optimization process, surrogate models (Mack et al. 2007) were also adopted into the optimizations of stiffened panels (Vitali et al. 2002; Lamberti et al. 2003; Venkataraman et al. 2003; Queipo et al. 2005). In the previous work, the variables involved in the optimizations were stiffener size, stiffener spacing, skin laminate sequence and ply-angle, etc. (Leriche and Haftka 1993; Hao et al. 2012). Layout optimization of stiffened panels that allows buckling strength to be increased with no weight penalty is rarely reported in literature. Sadeghifar et al. (2010) performed a multiobjective optimization of stiffened panels for minimum weight and maximum axial buckling load. In their study, size variables and layout variables were optimized simultaneously using GA based on SSM. However, nonlinearity of buckling behavior was not taken into account, which might influence the value of collapse load significantly. Moreover, only critical buckling mode shape, rather than collapse shape, can be obtained by SSM. The critical buckling mode shape, which is assumed to be in form of a double Fourier series, is distributed uniformly along the shell length. Therefore, the optimal design may not be suitable for resisting the collapse. Design optimization of panels for non-uniform axial compression neither is very common in literature. For example, Greenberg and Stavsky (1995) analyzed the buckling response of composite cylindrical shells subject to circumferentially non-uniform axial loads. Another study was carried out by Ahmed (2009). Hao et al. (2012) developed a two-stage optimization framework with adaptive sampling including relatively high-fidelity surrogate models of stiffened panels under non-uniform compression.

A two-stage sizing-layout optimization framework is proposed in this study. In the first stage of the process, sizing optimization is performed with respect to skin thickness, ply-angles, uniform stiffener spacing, stiffener width and height. Based on the buckling or collapse-like deformed shape evaluated for the design optimized in this first stage, the panel can be divided in sub-regions each of which shows characteristic deformations along axial and circumferential directions (e.g. general trend, monotonicity). In the second stage of the process, layout optimization is performed by using a stiffener spacing distribution function to represent the location of each stiffener. A layout coefficient is assigned to each sub-region and the overall layout of the panel is optimized.

Proper analysis methods must be selected for each load (i.e. uniform or non-uniform axial compression) and optimization stage (i.e. sizing or layout optimization) in order to maximize the computational efficiency of the proposed framework yet satisfying requirements on accuracy and limitations on computational resources.

In the case of uniform axial compression, SSM companied with Rayleigh-Ritz method is used to determine the critical buckling load. In the second stage of the optimization process, collapse loads and deformed shapes of stiffened panels with non-uniformly spaced stiffeners are determined via FE analysis with explicit dynamic analysis. In this case, only the layout of circumferential stiffeners needs to be optimized according to the position where FE analysis predicted collapse load to occur.

In the case of non-uniform axial compression, FE analysis must be performed in both sizing and layout optimizations and the layouts of circumferential and axial stiffeners should be simultaneously optimized.

The validity of the proposed optimization framework is fully demonstrated by solving three test problems where the objective is to maximize the load-carrying capacities of a metallic orthogrid cylindrical shell and two composite stiffened plates. Remarkably, collapse load (critical buckling load) can be increased by 17.4 %, 66.2 % and 102.2 % with respect to the initial structural configurations.

2 Analysis methods

2.1 Smeared stiffener method

In SSM, stiffened panel is converted mathematically into an unstiffened uniform thickness panel with equivalent orthotropic stiffness.

The total potential energy of the system is composed of the strain energy U s and the work done by the external force W:

$$ \Pi =U_{s} +W $$
(1)

For a simply supported end condition, the displacement components u, v and w can be defined as follows

$$\mathit{u}=\sum\limits_{m=1}^{\infty} {\sum\limits_{n=1}^{\infty} {A_{mn} \cos ( {m\alpha x} )\sin ( {n\beta y} )} } $$
(2)
$$ \mathit{v}=\sum\limits_{m=1}^{\infty} {\sum\limits_{n=1}^{\infty} {B_{mn} \sin ( {m\alpha x} )\cos ( {n\beta y} )} } $$
(3)
$$ \mathit{w}=\sum\limits_{m=1}^{\infty} {\sum\limits_{n=1}^{\infty} {C_{mn} \sin ( {m\alpha x} )\sin \left( {n\beta y} \right)} } $$
(4)

where α = π/L, β = 2 π/D, m is the number of axial half waves, n is the number of circumferential full waves.

For the equilibrium to be stable, the total potential energy must be a minimum. Appling the Rayleigh-Ritz method, this can be satisfied by finding the first derivative of the total potential energy with respect to A mn , B mn , and C mn and equating to zero, which yields an eigenvalue equation. The minimum eigenvalue is the global buckling load of the structure.

In addition, the skin of per grid cell can be considered as a simply supported rectangular plate. The local buckling load of the structure can then be calculated (Lekhnitskii 1968). The minimum one between global and local buckling loads is the critical buckling load.

2.2 Linear eigenvalue buckling analysis

Complex model details can be taken into account in a FE analysis, such as cutouts, local enhancements, etc. A linear buckling problem can be stated as

$$ \left({\boldsymbol{K}_{0} +P_{cr}^{j} \boldsymbol{G}} \right)\boldsymbol{\varphi}_{j} =\mathbf{0},\quad j=1,2,...,n $$
(5)

where K 0 and G are the geometric stiffness and stress stiffness matrices, respectively. φ j is the jth eigenvector, \(P_{cr}^{j}\) is the jth eigenvalue, and the lowest one is critical buckling load factor.

Since displacements at the critical buckling configuration are assumed to be small in the linear eigenvalue analysis, it turned out to be inaccurate for these structures showed a significantly nonlinear pre-buckling behavior.

2.3 Nonlinear explicit dynamic analysis

Nonlinear explicit dynamic analysis allows to investigate the deformed shape evolution of a stiffened panel from pre-buckling to post-buckling field until collapse. For a dynamic analysis, the equation of motion can be expressed as

$$ \boldsymbol{Ma}_{\mathbf{t}} =\boldsymbol{F_{t}^{ext}} -\boldsymbol{F_{t}^{int}} -\boldsymbol{CV}_{\mathrm{t}} -\boldsymbol{KU}_{\mathrm{t}} $$
(6)

where M is the mass matrix, C is the damping matrix, K is the stiffness matrix, a is the vector of nodal acceleration, V is the vector of nodal velocity, U is the vector of nodal displacement, t is the time, \(\boldsymbol {F_{t}^{ext}}\) is the vector of applied external force, \(\boldsymbol {F_{t}^{int}}\) is the vector of internal force.

Using the explicit time integration with central difference method to approximate velocity and acceleration by

$$ \boldsymbol{a}_{t} =\left( {U_{t-\Delta t} -2U_{t} +U_{t+\Delta t} } \right)/\Delta t^2 $$
(7)
$$ \boldsymbol{V_{t}} =\left( {\boldsymbol{U}_{\boldsymbol{t}+\mathbf{\Delta \boldsymbol{t}}} -\boldsymbol{U}_{\boldsymbol{t}-\mathbf{\Delta \boldsymbol{t}}} } \right)/2\Delta t $$
(8)

where Δt is the time increment, and substituting (7–8) into (6), the equation of motion is then transformed as

$$\begin{array}{@{}rcl@{}} \left( {\frac{\boldsymbol{M}}{\Delta t^{2}}+\frac{\boldsymbol{C}}{2\Delta t}} \right)\boldsymbol{U}_{t+\Delta t}&=&\boldsymbol{F}_{t}^{ext} -\boldsymbol{F}_{t}^{int}+\left( {\frac{2\boldsymbol{M}}{\Delta t^{2}}-\boldsymbol{K}} \right)\boldsymbol{U}_{t}\\ &&-\left( {\frac{\textit{M}}{\Delta t^{2}}-\frac{\boldsymbol{C}}{2\Delta t}} \right)\boldsymbol{U}_{t-\Delta t} \end{array} $$
(9)

Referring to (9), it can be seen that U t+Δt depends on U t and U t−Δt . The geometry of the structure is continuously updated by adding the computed displacements to the initial geometry. Consequently, the equations can be solved directly, and no convergence checks are needed since the equations are uncoupled. Since buckling and collapse are considered as a quasi-static phenomena, load velocity should be slow enough to eliminate the dynamic effects, and damping should also be avoided for such a quasi-static solution, as this could lead to significantly overestimated buckling load.

3 Two-stage framework for size-layout optimization

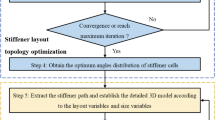
The flow-chart of the two-stage sizing-layout optimization framework developed in this study is shown in Fig. 2. In the first stage of the process, sizing optimization is performed with respect to skin thickness, ply-angles, uniform stiffener spacing, stiffener width and height. Based on the buckling or collapse-like deformed shape evaluated for the design optimized in this first stage, the panel can be divided in sub-regions each of which shows characteristic deformations along axial and circumferential directions (e.g. general trend, monotonicity). In the second stage of the process, layout optimization is performed by using a stiffener spacing distribution function to represent the location of each stiffener. A layout coefficient λ is assigned to each sub-region and the overall layout of the panel is optimized.

Fig. 2
figure 2

Two-stage computational framework for size-layout optimization of stiffened panels

Full size image

In case of uniform axial compression, SSM companied with Rayleigh-Ritz method is used to carry out linear buckling analysis for determining the buckling load in the sizing optimization stage. This could be done because the trends of critical buckling load and collapse load are substantially consistent and allowed computation cost of the optimization process to be substantially reduced. In this way it is possible to carry out large-scale optimization of stiffened panels.

Sizing optimization is carried out to maximize buckling load under a constraint on structural weight. The optimization problem is stated as:

$$\mathrm{Find\!\!:}\quad \boldsymbol{X}=[ {t_{s} , t_{r} , h, N_{a} , N_{c} } ]$$
(10)
$$ \text{Maximize}\!\!: P_{cr}$$
(11)
$$ \text{Subject}\; \text{to}\!\!: W\le W_{0}$$
(12)
$$X_{i}^{l} \le X_{i} \le X_{i}^{u} , i=1, 2,...,5$$
(13)

where W 0 is the structural weight corresponding to the initial design, t s is the skin thickness, t r is the stiffener width, h is the stiffener height, N c is the number of circumferential stiffeners, N a is the number of axial stiffeners, \(X_{i}^{l} \) and \(X_{i}^{u} \) are the lower and upper bounds of the ith variable, respectively.

The suitability of the optimized design must be checked with finite element analysis. For that purpose, in the second stage of the optimization process, the panel is divided in sub-regions along the axial direction according to the tendency of deformed shape to resemble buckling or collapse. This can be done if axial load does not vary in the circumferential direction. A stiffener spacing distribution function is used herein to represent the location of each circumferential stiffener along the shell length (Sadeghifar et al. 2010), and the location of the ith stiffener in jth sub-region can be stated as

$$ Z_{i} =\left\{ {{\begin{aligned} {L_{j} \left( {\frac{i}{N_{j} +1}} \right)^{\lambda} } & {i=1,2,...,N_{j} -1} \\ {\quad \quad L_{j} } &\,\,\, {i \,\,\,=\, N_{j} } \\ \end{aligned} }} \right. $$
(14)

where λ is the layout coefficient governing only the layout of circumferential stiffeners. In most cases, collapse deformed shape is almost axisymmetric, thus the layout of circumferential stiffeners may be assumed axisymmetric with respect to the mid-bay of the panel. For λ = 1, the circumferential stiffeners are evenly spaced. For λ < 1, the circumferential stiffeners in the intermediate section are more close to the adjacent ones than those in the two sides. For λ > 1, the circumferential stiffeners in the two sides are more close to the adjacent ones than those in the intermediate section, as shown in Fig. 3. In this stage, FE analysis simulated the buckling behavior and collapse load of stiffened panels with uneven spacing. The layout of circumferential stiffeners can be optimized according to the position where FE analysis predicts the collapse load to occur.

Fig. 3
figure 3

Distribution of stiffeners in the jth sub-region with various values of λ

Full size image

The optimization formulation set for the second stage of the proposed framework is:

$$ \text{Find}\!\!: \lambda $$
(15)
$$ \text{Maximize}\!\!: P_{co} \left( {P_{cr} } \right) $$
(16)
$$ \text{Subject to:}\; \lambda^{l} \le \lambda \le \lambda^u $$
(17)

where λ l and λ u are the lower and upper bounds of λ, respectively.

In case of non-uniform axial compression, finite element analysis must be performed in both sizing and layout optimizations. The first stage (sizing optimization) of the optimization process is similar to the case of uniform axial compression. However, surrogate models must be used in order to reduce the computational cost of the optimization. Panels must be subdivided along the circumferential direction and layout optimization must be carried out in each sub-region to obtain the final optimum design.

4 Test problems and results

4.1 Cylindrical stiffened shell subjected to uniform compression

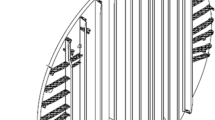
The first test problem regards the cylindrical orthogrid stiffened shell described in Wang et al. (2011). This model is representative of a large lightly loaded launch vehicle cylinder section, with diameter of D = 3000.0 mm, length of L = 2000.0 mm. In Fig. 4, a portion of the cylinder outer skin is removed to show the stiffener layout. The skin thickness t s is 4.0 mm, and the stiffener width t r and height h are 9.0 and 15.0 mm, respectively. The numbers of circumferential and axial stiffeners are 26 and 90, respectively. Typical properties of the aluminum alloy used for stiffened panel are as follows: Young’s modulus E = 70 GPa, Poisson’s ratio υ = 0.33, yield stress σ s = 410 MPa, ultimate stress σ b = 480 MPa, density ρ = 2.7E-6 kg/mm 3. According to literature, the structural weight of the initial design is 358 kg.

Fig. 4
figure 4

Main geometric parameters defined for an orthogrid stiffened panel

Full size image

The bottom edge of the panel is simply-supported while the translations of the top edge are constrained to 0 except for axial displacements. The critical buckling load of stiffened shell P cr0 obtained with SSM is 13412 kN, and the corresponding buckling mode shape includes 4 axial half waves and 9 circumferential full waves.

The FE model was then developed in ABAQUS. The FE model was discretized with shell elements including three translational degrees of freedom and three rotational degrees of freedom per node. A preliminary mesh sensitivity study allowed to set the element size as 30 mm: hence, the FE model included a total number of degrees of freedom equal to 330480. An end-shortening displacement was imposed to the panel top edge, and the reaction force developed in the bottom end were extracted to express the loading-carrying capacity of the panel.

The critical buckling load computed by ABAQUS is 13610 kN. The corresponding buckling mode shape, shown in Fig. 5, is practically the same as its counterpart for SSM. The collapse load P co obtained by explicit dynamic analysis is 16791 kN, and the deformed shape of stiffened shell at the collapse load is given in Fig. 6. Since modeling of initial imperfections is of great importance to evaluate the load-carrying capacity of cylindrical shells, eigenmode-shape imperfection was introduced in the numerical model of this test problem, with a maximum amplitude of 1.9 mm, corresponding to one tenth of the sum of skin thickness and stiffener height. The collapse load P co of the imperfect shell is 10107 kN, and the deformed shape at the collapse load is shown in Fig. 7.

Fig. 5
figure 5

Critical buckling mode shape of the initial design for test problem 1

Full size image
Fig. 6
figure 6

Deformed shape of the orthogrid stiffened panel corresponding to the collapse load evaluated for the initial design of test problem 1

Full size image
Fig. 7
figure 7

Deformed shape of the imperfect stiffened panel corresponding to the collapse load evaluated for the initial design of test problem 1

Full size image

Although Multi-Island Genetic Algorithm (MIGA) is less efficient than several new-developed metaheuristic algorithms (e.g. particle swarm optimization, etc.), which may be very sensitive to control parameters (Engelbrecht 2005), sizing optimization was performed with MIGA in this study, because of its intuitiveness, ease of implementation, and the ability to effectively solve the highly nonlinear problems (Panda and Padhy 2008). MIGA is a stochastic search algorithm reproducing the mechanisms of natural selection and genetics. In MIGA, the population in each generation is divided into several islands, and the genetic operations are performed independently on each island. This allows to avoid converge to local optima (Reiko 1989; Ooka and Komamura 2009). MIGA internal parameters were set as: the rates of crossover, mutation, migration are 1.0, 0.01 and 0.5, respectively. The interval of migration is 0.5. Three sets of population parameters were compared: numbers of islands N I , generations N G , and population per island N P are (10, 20, 20), (20, 10, 20), (20, 20, 10), respectively.

Side constraints of design variables are listed in Table 1, while convergence curves are shown in Fig. 8. As can be seen, three optimum results are similar. In general, larger sub-populations and a larger number of generations allow a better design to be found. In the present case, the optimized design (N P = 20, N I = 10, N G = 20) is as follows: t r = 6.1 mm, h = 17.8 mm, t s = 4.9 mm, N c = 22, N a = 84. The corresponding structural weight is 357 kg. The critical buckling load evaluated with the smeared model is 16201 kN. The optimized design was then given in input to a FE model to carry out buckling and collapse analysis. The critical buckling load of the optimized design computed by ABAQUS is 16344 kN, which is close to the result of SSM. The corresponding collapse load P co is 18646 kN. The critical buckling mode shape is shown in Fig. 9, while the deformed shape at the collapse load is shown in Fig. 10. The collapse load P co of the imperfect panel with an imperfection amplitude of 1.9 mm is 11216 kN, and the corresponding deformed shape at the collapse load is shown in Fig. 11.

Fig. 8
figure 8

Test problem 1: converge curves recorded in the sizing optimization stage for different combinations of the MIGA internal parameters

Full size image
Fig. 9
figure 9

Critical buckling mode shape of the first-stage optimum design of test problem 1

Full size image
Fig. 10
figure 10

Deformed shape of the orthogrid stiffened panel corresponding to the collapse load evaluated for the first-stage optimum design of test problem 1

Full size image
Fig. 11
figure 11

Deformed shape of the imperfect stiffened panel corresponding to the collapse load evaluated for the first-stage optimum design of test problem 1

Full size image
Table 1 Initial values and side constraints of design variables for test problem 1
Full size table

In the layout optimization stage, sub-regions must be defined according to the deformed shape of the optimum design found in the sizing stage. Since deformed shape is almost axisymmetric (see Fig. 11), the layout of circumferential stiffeners may be assumed axisymmetric with respect to the mid-bay of the panel. Then Sequential Quadratic Programming Method (SQP) was adopted. The range of λ was also specified as [0.5, 1.5], and the considered imperfection amplitude was also set as one tenth of the sum of skin thickness and stiffener height. Convergence curve of the layout optimization is shown in Fig. 12. The collapse load of P co = 11869 kN of the imperfect optimum design was obtained at λ = 0.6224. Hence, the collapse load of the imperfect panel improved by 17.4 % with respect to the initial design (see Table 2). The deformed shapes of perfect and imperfect panels at the collapse load are shown in Figs. 13 and 14, respectively.

Fig. 12
figure 12

Convergence curve of the second-stage optimization for test problem 1

Full size image
Fig. 13
figure 13

Deformed shape of the orthogrid stiffened panel corresponding to the collapse load evaluated for the second-stage optimum design of test problem 1

Full size image
Fig. 14
figure 14

Deformed shape of the imperfect stiffened panel corresponding to the collapse load evaluated for the second-stage optimum design of test problem 1

Full size image
Table 2 Comparison of initial and optimized designs for test problem 1
Full size table

4.2 Flat stiffened plate subjected to non-uniform symmetrical compression

The second test problem regarded a simply-supported stiffened plate whose dimensions coincide with those indicated in Jaunky et al. (1996). The nominal dimensions of the panel are as follows (see the schematic of Fig. 15): B = 1524 mm, L = 914.4 mm; the stiffener width t r and height h are 3.0 and 12.7 mm, respectively. The initial design included 5 circumferential stiffeners and 7 axial stiffeners. The stiffened plate is made of graphite-epoxy with the following material properties: E 11 = 169.0 GPa, E 2 = 11.3 GPa, G 12 = 6.0 GPa, υ = 0.3, ρ = 1.578E-6 kg/mm 3. The skin stacking sequence is [ ±45/90/0] s with 0.2032 mm thick plies. Stiffeners include plies oriented in the stiffening direction. Since only uniform axial compression was considered in Jaunky et al. (1996), non-uniform compression was considered in this study according to Ganesh et al. (2013).

Fig. 15
figure 15

Main geometric and load parameters defined for the orthogrid stiffened plate optimized in test problem 2

Full size image

Because of the presence of non-uniform axial compression, SSM could not be used. Furthermore, since panel edges were simply supported and nodal displacements were restricted at panel boundaries, explicit dynamic analysis also was inapplicable. Therefore, the load-carrying capacity of the panel was described by the buckling load computed by ABAQUS. The following boundary conditions were imposed in FE analysis: X =0, u =v =w = 𝜃 x = 0; X =B, v =w = 𝜃 x = 0; Y = 0 and L, u =v =w = 𝜃 y = 0. The non-uniform compression load was applied at X =B (see Fig. 15) according to the following equation:

$$ N_{x} =\sin \left( {\pi Y/L} \right) $$
(18)

The element size in FE mesh was set to 5 mm through convergence analysis. The critical buckling load factor of 34.9 was determined via linear analysis, and the buckling mode shape evaluated for the initial design is shown in Fig. 16. Further, eigenmode-shape imperfection was also introduced in the numerical model of this test problem, with a maximum amplitude of 1.43 mm, corresponding to one tenth of the sum of skin thickness and stiffener height. The corresponding critical buckling load factor is 37.3, with the buckling mode shape shown in

Fig. 16
figure 16

Critical buckling mode shape of the initial design for test problem 2

Full size image

Fig. 17, which is almost identical with the one of the perfect geometry. This demonstrates that flat plates are marginally sensitive to small-amplitude imperfections (see, for example, Schultz and Nemeth 2010) and hence the effect of geometric imperfections may not be considered in the following optimizations.

Fig. 17
figure 17

Critical buckling mode shape of the imperfect initial design for test problem 2

Full size image

Side constraints of sizing variables are listed in Table 3. Ply-angles could take discrete values from the set (-45, 0, 45, 90). The laminate is symmetric and comprised of 8 plies. Because of the existence of discrete variables and in order to limit computational cost of FE analyses, surrogate-based optimization was performed for this test problem. Following literature, the RBF model was selected as it resulted more accurate and robust than Kriging and polynomial regression method (Jin et al. 2001). In view of this, we generated a set of 500 sampling points using Optimal Latin Hypercube Sampling (OLHS) throughout design space and built the RBF model fitting the sampled data. Since percent errors for critical buckling load and structural weight were respectively 1.0 % and 0.1 %, the surrogate model was rated to be adequate.

Table 3 Initial values and side constraints of design variables for test problem 2
Full size table

The MIGA search engine was then adopted in the surrogate-based optimization entailed by the sizing stage. For the sake of clarity, iterations based on the surrogate model are removed and only the history of outer update is shown in Fig. 18. The optimized design is: [-45/90/-45/45] s skin stacking sequence, t r = 3.36 mm, h = 14.57 mm, t s = 0.18 mm, N c = 6, N a = 8. The corresponding structural weight is 4.5 kg. The critical buckling load factor P cr evaluated for the optimized design is 54.3, with the corresponding buckling mode shape shown in Fig. 19. Although the load was axisymmetric, the buckling mode is slightly asymmetrical because of the asymmetry in the skin stacking sequence.

Fig. 18
figure 18

Converge curve (outer updates) recorded in the sizing optimization stage of test problem 2

Full size image
Fig. 19
figure 19

Critical buckling mode shape of the first-stage optimum design of test problem 2

Full size image

In the layout optimization stage, the node with the largest displacement (with coordinates X = 925.29 mm, Y = 553.72 mm) was identified first: the corresponding displacement paths across horizontal and vertical lines passing through that node are shown in Figs. 20 and 21, respectively. Since two axial and two horizontal sub-regions could be identified in terms of monotonicity, a value of λ was assigned to each sub-region. Layout optimization was then performed with SQP. The range of variability set for λ was again [0.5,1.5].

Fig. 20
figure 20

Test problem 2: distribution of displacements along the Y-direction control path passing through the maximum displacement node

Full size image
Fig. 21
figure 21

Test problem 2: distribution of displacements along the X-direction control path passing through the maximum displacement node

Full size image

The critical buckling load factor evaluated for the optimized design is 58.0, hence 66.2 % higher than for the initial design with no penalty in structural weight. The optimum layout design was obtained for λ a1 = 1.0, λ a2 = 0.9882, λ c1 = 0.5 and λ c2 = 0.6721. The convergence curve of the layout optimization process is shown in Fig. 22.

Fig. 22
figure 22

Convergence curve of the second-stage optimization for test problem 2

Full size image

The optimized values of λ a1 and λ a2 are close to those corresponding to the optimum size design. This may be explained looking at the buckling mode corresponding to the optimized design (see Fig. 23). The local skin buckling in the lower-left and lower-right corners of the stiffened plate occurs simultaneously to global buckling. Should spacing of axial stiffeners near panel edges increase, local buckling would occur before global buckling thus limiting the load-carrying capacity of the panel. Finally, the critical buckling load is improved by 66.2 % without any increase in structural weight, as listed in Table 4.

Fig. 23
figure 23

Critical buckling mode shape of the second-stage optimum design of test problem 2

Full size image
Table 4 Comparison of initial and optimized designs for test problem 2
Full size table

4.3 Flat stiffened plate subjected to non-uniform asymmetrical compression

The third test problem solved in this study regarded another simply-supported stiffened plate, with L = 1828.8 mm. The panel is schematized in Fig. 24. The other structural parameters and material properties are the same as in the previous test case. Non-uniform compression, not symmetric with respect to Y-direction, was considered (see Fig. 24):

$$ N_{x} =1+2\sin \left( {\pi Y/L-\pi /3} \right) $$
(19)

Boundary conditions and mesh size were the same as for test case 2. The critical buckling load factor evaluated for this initial design is 8.9. The corresponding buckling mode is shown in Fig. 25.

Fig. 24
figure 24

Main geometric and load parameters defined for the orthogrid stiffened plate optimized in test problem 3

Full size image
Fig. 25
figure 25

Critical buckling mode shape of the initial design for test problem 3

Full size image

In sizing optimization, the number of axial stiffeners N a could range between 11 and 17. Data relative to all other design variables and conventions were the same as for the previous test problem. Surrogate models were generated in the same fashion as for the previous test problem. Since model errors for critical buckling load and structural weight were respectively 4.0 % and 0.6 %, the surrogate model was again considered to be adequate.

The MIGA convergence curve is shown in Fig. 26. The optimized design is as follows: the skin stacking sequence is [0/ ±45/90] s , t r = 3.25 mm, h = 15.24 mm, t s = 0.18 mm, N c = 5, N a = 17. The corresponding structural weight is 9.0 kg. The critical buckling load factor P cr evaluated for this optimized design is 16.6, with the corresponding buckling mode shape shown in Fig. 27 Because of the high asymmetry of the axial load acting on the panel, the buckling mode shape is also non-uniform with respect to Y-axis.

Fig. 26
figure 26

Converge curve (outer updates) recorded in the sizing optimization stage of test problem 3

Full size image
Fig. 27
figure 27

Critical buckling mode shape of the first-stage optimum design of test problem 3

Full size image

In the layout optimization stage, the node with the largest displacement (with coordinates X = 861.61 mm, Y = 675.64 mm) was identified first: the corresponding displacement paths across horizontal and vertical lines passing through that node are shown in Figs. 28 and 29, respectively. It was again possible to identify four sub-regions. Layout optimization was then performed with SQP. The range of variability set for λ was again [0.5,1.5]. The critical buckling load factor evaluated for the optimized design is 18.0, hence 102.2 % higher than for the initial design, as shown in Table 5. The optimum layout design was obtained for λ a1 = 0.6329, λ a2 = 0.5, λ c1 = 0.8544 and λ c2 = 1.0. The convergence curve of the layout optimization process is shown in Fig. 30. The buckling mode corresponding to the optimum design is shown in Fig. 31. It can be seen that buckling deformation is more uniform compared with that evaluated for the initial design. This demonstrates that the benefit of layout optimization is more significant for the case of non-uniform asymmetrical compression.

Fig. 28
figure 28

Test problem 3: distribution of displacements along the Y-direction control path passing through the maximum displacement node

Full size image
Fig. 29
figure 29

Test problem 3: distribution of displacements along the X-direction control path passing through the maximum displacement node

Full size image
Table 5 Comparison of initial and optimized designs for test problem 3
Full size table
Fig. 30
figure 30

Convergence curve of the second-stage optimization for test problem 3

Full size image
Fig. 31
figure 31

Critical buckling mode shape of the second-stage optimum design of test problem 3

Full size image

5 Conclusion

This paper presented a two-stage computational framework for sizing-layout optimization of stiffened panels. In the first stage, traditional sizing optimization is performed. Based on the buckling or collapse shapes of the optimized design, sub-regions can be defined with respect to buckling or collapse deformations along axial and circumferential directions. Layout optimization can then be performed for the entire panel. In order to increase the numerical efficiency of the proposed framework, different analysis methods including surrogate models were utilized in each optimization stage based on the type of loads acting on the panel.

Three test problems were solved in order to demonstrate the validity of the proposed optimization framework. It was found that the improvement deriving from optimization is far more significant in the case of non-uniform compression. However, the proposed framework is only applicable to orthogrid stiffened panels and its suitability for more complicated stiffening patterns (e.g. triangle, Kagome, etc.) will have to be investigated in future studies. Furthermore, the investigation on the lightweight design of stiffened panels by combining both the size and layout optimizations is still worth exploring.