1 Introduction

1.1 Size effect

Micro-beams, as one out of the most important components in micro-electromechanical systems (MEMS) e.g. atomic force microscopes, micro-actuators, and micro-pumps, have been broadly utilizedPelesko and Bernstein 2003). Since dimensions of beams are in micron-order, size dependent behaviors have been observed experimentally in these applications (Lam et al. 2003; McFarland and Colton 2005). Due to lack of length scale parameters in the constitutive relation of classical continuum theory, the classical beam models are not able to interpret the size effects in micro-scale elements. Therefore, several non-classical continuum theories such as the couple stress (Toupin 1962), nonlocal (Eringen 1968), the modified couple stress (Yang et al. 2002) and the modified strain gradient (Lam et al. 2003) theories have been developed to investigate the size effect. Recently, these non-classical continuum theories have been widely utilized to formulate and study the size-dependent thermal and mechanical behavior of micro-beams, plates and shells. Some examples of such works are mentioned here: Ghayesh et al. (2017); Farokhi et al. (2016); Gholipour et al. (2015); Taati et al. (2014a, b); Ghayesh et al. (2013); Taati et al. (2012).

1.2 Functionally graded materials

Functionally graded materials (FGMs) are made from two or more materials in which the properties continuously vary in the defined direction(s) from one point to another. In the most of cases, FGMs are a combination of a metal phase and a ceramic phase which can provide simultaneously both the desired mechanical and thermal properties. Metals give better tensile strength and are not able to withstand exposure to high temperatures. On the contrary, ceramics are advantageous in high compressive strength and thermal environments. The mechanical behavior of FGMs is strongly dependent to spatial distribution of the volume fractions. Hence, the distribution of volume fractions in FG structures can be selected as a design variable in the optimization procedure for achieving desired mechanical performance. In recent years, the abundant requirements have been declared to achieve the multilayer MEMS with variable properties in the thickness. For example, the processes were defined to produce an FG layer in micron size with the desired electrical, thermal and mechanical properties at its bottom and top surfaces (Witvrouw and Mehta 2005). Hence, some studies have been accomplished on the thermal and mechanical analyses of FG microstructures under thermo-mechanical loadings (For instance, please see: Şimşek and Aydın 2017; Taati 2016; Şimşek 2015; Molaei et al. 2014a, b; Asghari and Taati 2013; Kocatürk et al. 2011).

1.3 Multi-objective optimization

Multi-objective optimization algorithms are used to find optimum values of several target functions. These algorithms have been employed in numerous scientific fields namely engineering, physics, chemistry and economics where optimal decisions require to be taken in the presence of trade-offs between two or more conflictive objectives. No single solution can be found that simultaneously optimizes each objective for non-trivial multi-objective problem. Until now, some of multi-objective optimization algorithms have been introduced by researchers that the most important of those are Pareto Archived Evolution Strategy (rey Horn et al. 1993), Multi-Objective Genetic Algorithm (Murata et al. 1996), Strength Pareto Evolutionary Algorithm (Zitzler and Thiele 1999) and The Pareto Envelope-based Selection Algorithm (Corne et al. 2000). Recently, Srinivas and Deb (1994) proposed a non-dominated sorting genetic algorithm to find optimum values which includes several layers of classifications. Deb et al. (2002) improved the NSGA and called it NSGAII. This algorithm generates population and classifies the solutions based on ranks. By applying evolutionary operations such as mutation and crossover, it builds new offspring and combines offsprings with parents. Also, the diversity of algorithms is guaranteed by employing crowding distance for selection the solutions.

1.4 A review of studies accomplished on the optimization of beams

Here, a brief review of studies conducted on the optimization of beams is presented. Dems (1980) developed optimal design of the shape of an internal or external boundary in an elastic bar subjected to torsion. For the formulation of optimization problem, the boundary shape was described by a set of shape functions and a set of shape parameters. Hence, the optimization procedure was reduced to determination of these parameters. Dems and Plaut (1990) designed beams, plates and their elastic foundations for uniform foundation pressure which its main objective was the minimization of the maximum pressure transmitted to the foundation. Three types of loadings including concentrated central force, uniform and parabolic distribution of load per unit length were considered. Lee et al. (1994) proposed a detection technique for the delamination phenomenon in a laminated beam which optimizes the spatial distribution of harmonic excitation so as to magnify the difference in response between the delaminated and intact beam. This technique was evaluated by numerical simulation of two-layered aluminum beams. Kruusing (2000) presented a simple and straightforward analytical model of the mechanical response of cantilever micro-beam loaded normally at the tip. In the both cases of constant total thickness and constant thickness of one layer, the optimal dimensions of two-layer beams with one active and one passive layer was given based on the maximal tip deflection and generated force. Sorokin et al. (2001a) developed a formulation and a solution technique to analyze and optimize energy flows in structures composed of beam elements. They considered the energy outflow integrated within the given frequency range at a given cross-section of the tubular structure as an objective function. They (Sorokin et al. 2001b) employed this method to optimize a model structure consisting of two elements of a finite length and one semi-infinite element. Design parameters were chosen as the stiffness, mass and the location of two of the terminal points. Cardoso et al. (2002) accomplished a design sensitivity analysis and optimal design of composite structures modelled as thin-walled beams subjected to torsion-bending loadings. A two-node Hermitean beam element was used to solve the mathematical model. Optimal design was carried out with respect to the lamina orientations and thickness of the laminates. Liu et al. (2008) formulated a topology optimization technique for beam cross-section using an anisotropic beam theory. They studied effects of section warping and coupling among deformations in this method. In this optimization problem, the minimum averaged compliance of the beam was taken as an objective function, and the material density of each element was utilized as a design variable. Sivanagendra and Ananthasuresh (2009) provided the optimization of the cross-section profile of a cantilever beam under deformation-dependent loads. The criteria of optimization were considered to be minimum moment at the fixed ground support as well as adequate stiffness and strength. Polajnar et al. (2013) performed the geometry optimization of a slender cantilever beam subjected to a concentrated force at the free end. Bernoulli–Euler beam theory was used to obtain two-parametric mathematical model of lateral torsional buckling. The optimization procedure was implemented by use of the optimal control theory and the relation between state and adjoint variables. Shi and Shimoda (2015) proposed an interface shape optimization method to design FG sandwich structures with two different materials to minimize the compliance of FG sandwich structures under the volume constraint. They concluded that the compliance of FG sandwich structures is significantly reduced after optimizing by means of this method with a large difference between Young’s modulus of components.

1.5 Present study

In this study, a multi-objective optimization of simply supported FG micro-beams resting on an elastic medium is carried out using the size dependent analytical expressions of mechanical parameters. The elastic medium is modeled as a two-layered foundation including a shear layer and a linear normal layer which are known Pasternak and Winkler elastic foundations, respectively. To this end, the size dependent equilibrium equation of FG micro-beams is derived using the modified strain gradient theory. Next, by solving this governing equation, the analytical expressions for maximum deflection, maximum stress, minimum natural frequency and critical buckling load are developed. For multi-objective optimization, the lengths to thickness (aspect) ratio, thickness and distribution parameter of FGM are considered as design variables. Also, the target function is defined such that maximum deflection, maximum stress and mass become minimum while values of natural frequency and critical buckling load must be maximized. Multi-objective optimization is performed by use of non-dominated sorting genetic algorithm-II. The optimum patterns of FG micro-beams resting on the elastic foundation including curves of the normalized target function versus pairs of design variables are presented for both exponential and power-law FGMs. For each case, the effects of theory type and foundation on various optimum patterns are discussed in details. Outcomes show that the elastic foundation coefficients and internal length scale parameters of materials have significant influence on the distribution of design variables at optimal states.

2 Preliminaries

2.1 Problem definition and modeling

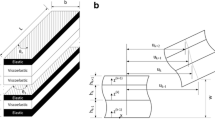
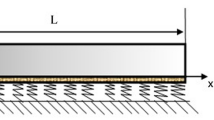
Consider a simply supported FG micro-beam resting on elastic foundations with length L, thickness h, width b, as shown in Fig. 1. It is subjected to axial load N and the constant transverse force per unit length q. The optimization of the aspect ratio L/h, thickness and distribution parameter of FGM in micro-beams is selected as a case study. The optimization procedure will be performed using analytical expressions of size dependent mechanical parameters. To this end, the Euler–Bernoulli beam model is used to describe the deformational behavior of beams under mechanical loadings. According to this model, the components of the infinitesimal displacement field are expressed as follows:

$$ {u}_x=-z\kern0.24em \frac{\partial w\left(x,t\right)}{\partial x},\kern0.6em {u}_2=0,\kern0.6em {u}_3=w\left(x,t\right), $$
(1)
Fig. 1
figure 1

Coordinate system, loading and geometry of a simply supported FG micro-beam resting on elastic foundation

Full size image

The symbol w denotes the displacement of points on the bending plane of the flexible beam in z direction. Moreover, parameter t is the time. The bending plane is a plane perpendicular to the thickness direction and the cross section of beam, wherein no longitudinal strain exists under pure bending condition (without axial force resultant). Parameter z represents the distance of the point from the mid surface.

Here, FGMs are modeled as a non-homogenous isotropic linear elastic material whose properties, Λ vary continuously through the thickness direction. Most researchers utilized the exponential function (E-FGM) and the power-law function (P-FGM) to describe the spatial dependent of FGM properties. Hence, these two kinds of FGMs are introduced in the following:

  • E-FGM

For this case of FGMs, it is supposed that all of mechanical properties are varied through the thickness as the following exponential function:

$$ \frac{\Lambda (z)}{\Lambda_{ref}}={e}^{\alpha \left(z/h+0.5\right)} $$
(2)

In (2), Λ is a material property and the index of ref. stands for any physical property of FGM either metal or ceramic. Moreover, the inhomogeneity parameter is denoted by α.

  • P-FGM

For this case of FGMs, it is assumed that the beam is composed of a ceramic phase and a metal phase whose volume fractions obeying a simple power-law distribution. Therefore, each of beam properties, Λ can be expressed as follows:

$$ \Lambda ={\Lambda}_c{V}_c+{\Lambda}_m{V}_m $$
(3)

where the subscripts c and m stand for ceramic and metal, respectively. Also V c and V m are the volume fractions of ceramic and metal, respectively which are related as V c +V m  = 1. (3) shows the linear rule of mixture, which is the simplest estimate of the effective material properties at a point in a dual-phase metal–ceramic material. The metal volume fraction is considered to follow a power-law distribution as follows:

$$ {V}_m={\left(0.5+z/h\right)}^n\kern0.36em \Rightarrow \kern0.84em {V}_c=1-{\left(0.5+z/h\right)}^n $$
(4)

In (4), n is the power-law index that takes values greater than or equal to zero. Substituting for V c and V m from (4) into (3) results in the effective material property as:

$$ \Lambda (z)={\Lambda}_c+\left({\Lambda}_m-{\Lambda}_c\right){\left(0.5+z/h\right)}^n $$
(5)

In current study, relation (4) will be employed as a model for Young’s modulus E, shear modulus G, and density ρ of micro-beams.

2.2 The modified strain gradient theory

According to the modified strain gradient theory (Lam et al. 2003), the variation of strain energy (δU) for a linear elastic body occupying region Ω can be written as follows:

$$ \delta U=\underset{\Omega}{\int}\left({\sigma}_{ij}{\delta \varepsilon}_{ij}+{p}_i\;{\delta \gamma}_i+{\tau}_{ij k}^{(1)}\;{\delta \eta}_{ij k}^{(1)}+{m}_{ij}^s{\delta \chi}_{ij}^s\right)\kern0.24em d\Omega $$
(6)

where

$$ {\varepsilon}_{ij}=\frac{1}{2}\left(\frac{\partial {u}_i}{\partial {x}_j}+\frac{\partial {u}_j}{\partial {x}_i}\right), $$
(7)
$$ {\gamma}_i=\frac{\partial {\varepsilon}_{mm}}{\partial {x}_i}, $$
(8)
$$ {\displaystyle \begin{array}{c}{\eta}_{ij k}^{(1)}=\frac{1}{3}\left(\frac{\partial {\varepsilon}_{jk}}{\partial {x}_i}+\frac{\partial {\varepsilon}_{ki}}{\partial {x}_j}+\frac{\partial {\varepsilon}_{ij}}{\partial {x}_k}\right)-\frac{1}{15}{\delta}_{ij}\left(\frac{\partial {\varepsilon}_{mm}}{\partial {x}_k}+2\frac{\partial {\varepsilon}_{mk}}{\partial {x}_m}\right)\\ {}-\frac{1}{15}{\delta}_{jk}\left(\frac{\partial {\varepsilon}_{mm}}{\partial {x}_i}+2\frac{\partial {\varepsilon}_{mi}}{\partial {x}_m}\right)-\frac{1}{15}{\delta}_{ki}\left(\frac{\partial {\varepsilon}_{mm}}{\partial {x}_j}+2\frac{\partial {\varepsilon}_{mj}}{\partial {x}_m}\right)\end{array}}, $$
(9)
$$ {\chi}_{ij}^s=\frac{1}{2}\left(\frac{\partial {\theta}_i}{\partial {x}_j}+\frac{\partial {\theta}_j}{\partial {x}_i}\right), $$
(10)
$$ {\theta}_i=\frac{1}{2}{\left(\mathit{\operatorname{curl}}\left(\overrightarrow{u}\right)\right)}_i, $$
(11)

where ε ij , \( {\eta}_{ijk}^{(1)} \) and \( {\chi}_{ij}^s \) are the components of the strain tensor, the deviatoric stretch gradient tensor and the symmetric part of the rotation gradient tensor, respectively. Also, u i , γ i and θ i denote components of the displacement vector, the dilatation gradient vector, and the infinitesimal rotation vector, respectively. In addition, the components of the classical (σ ij ) and higher-order ( p i , \( {\tau}_{ijk}^{(1)} \),\( {m}_{ij}^s\Big) \) stress tensors are defined as follow (Lam et al. 2003):

$$ {\sigma}_{ij}=\lambda tr\left(\overleftrightarrow{\boldsymbol{\upvarepsilon}}\right){\delta}_{ij}+2{\mu \varepsilon}_{ij}, $$
(12)
$$ {p}_i=2\mu {l}_0^2{\gamma}_i={\beta}_0{\gamma}_i, $$
(13)
$$ {\tau}_{ijk}^{(1)}=2\mu {l}_1^2{\eta}_{ijk}^{(1)}={\beta}_1{\eta}_{ijk}^{(1)}, $$
(14)
$$ {m}_{ij}^s=2\mu {l}_2^2{\chi}_{ij}^s={\beta}_2{\chi}_{ij}^s, $$
(15)

where λ and μ are Lame constants.

3 Theoretical formulation

Here, analytical expressions for the mechanical parameters of simply supported FG micro-beams are obtained. To this purpose, the equilibrium equation of FG micro-beams is derived using Hamilton principle and a variational approach. Next, the Fourier series expansion is employed to solve the governing equation.

3.1 Equilibrium equation

Based on the modified strain gradient theory, the variation of strain energy for an FG micro-beam can be computed as follows (Taati et al. 2014b):

$$ \delta U=\underset{0}{\overset{L}{\int }}\delta {U}^{\mathrm{int}}\kern0.24em \delta w\; dx+{\left(\delta {U}^{\mathrm{bound}}\right)}_{x=0}^{x=L}, $$
(16)

where

$$ {\displaystyle \begin{array}{c}\delta {U}^{\mathrm{int}}=-\frac{\partial^2}{\partial {x}^2\kern0em }\left[{M}_{11}+{M}_3^p+\frac{1}{5}\left(-{M}_{333}^{\tau }+4{M}_{113}^{\tau }-{M}_{223}^{\tau}\right)+{M}_{12}^m\right]\;\\ {}+\frac{\partial^3}{\partial {x}^3\kern0em }\left[{H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)\right]\end{array}} $$

and

$$ {\displaystyle \begin{array}{c}\delta {U}^{\mathrm{bound}}=\left[\frac{\partial }{\partial x\kern0em }\left({M}_{11}+{M}_3^p+\frac{1}{5}\left(-{M}_{333}^{\tau }+4{M}_{113}^{\tau }-{M}_{223}^{\tau}\right)+{M}_{12}^m\right)\right.\\ {}\left.-\frac{\partial^2}{\partial {x}^2\kern0em }\left({H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)\right)\right]\kern0.24em \delta w\\ {}-\left[{M}_{11}+{M}_3^p+\frac{1}{5}\left(-{M}_{333}^{\tau }+4{M}_{113}^{\tau }-{M}_{223}^{\tau}\right)+{M}_{12}^m\right.\\ {}\left.-\frac{\partial }{\partial x\kern0em }\left({H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)\right)\right]\kern0.24em \delta \left(\frac{\partial w}{\partial x\kern0em }\right)\\ {}-\left({H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)\right)\delta \left(\frac{\partial^2w}{\partial {x}^2\kern0em }\right)\end{array}} $$
(17)

In (17), the stress resultants are defined as follows:

$$ {\displaystyle \begin{array}{l}{M}_{11}=-{(EI)}_{eq}\frac{\partial^2w}{\partial {x}^2},\kern3.119999em {M}_{12}^m={M}_{21}^m=-\frac{1}{2}{\left({\beta}_2A\right)}_{eq}\frac{\partial^2w}{\partial {x}^2},\\ {}{H}_1^p=-{\left({\beta}_0I\right)}_{eq}\frac{\partial^3w}{\partial {x}^3},\kern2.879999em {M}_3^p=-{\left({\beta}_0A\right)}_{eq}\frac{\partial^2w}{\partial {x}^2},\\ {}{H}_{111}^{\tau }=-\frac{2}{5}{\left({\beta}_1I\right)}_{eq}\frac{\partial^3w}{\partial {x}^3},\kern2.04em {M}_{333}^{\tau }=\frac{1}{5}{\left({\beta}_1A\right)}_{eq}\frac{\partial^2w}{\partial {x}^2},\\ {}{M}_{113}^{\tau }={M}_{311}^{\tau }={M}_{131}^{\tau }=-\frac{4}{15}{\left({\beta}_1A\right)}_{eq}\frac{\partial^2w}{\partial {x}^2},\\ {}{M}_{223}^{\tau }={M}_{232}^{\tau }={M}_{322}^{\tau }=\frac{1}{15}{\left({\beta}_1A\right)}_{eq}\frac{\partial^2w}{\partial {x}^2},\\ {}{H}_{221}^{\tau }={H}_{212}^{\tau }={H}_{122}^{\tau }={H}_{133}^{\tau }={H}_{313}^{\tau }={H}_{331}^{\tau }=\frac{1}{5}{\left({\beta}_1I\right)}_{eq}\frac{\partial^3w}{\partial {x}^3},\end{array}} $$
(18)

in which

$$ {\displaystyle \begin{array}{l}\begin{array}{cc}{(EA)}_{eq}=b\underset{-h/2}{\overset{h/2}{\int }}E(z)\; dz,& {(EI)}_{eq}=b\underset{-h/2}{\overset{h/2}{\int }}E(z)\;{z}^2 dz,\\ {}{\left({\beta}_iA\right)}_{eq}=b\underset{-h/2}{\overset{h/2}{\int }}{\beta}_i(z)\; dz,& {\left({\beta}_iI\right)}_{eq}=b\underset{-h/2}{\overset{h/2}{\int }}{\beta}_i(z)\;{z}^2\; dz, for\kern0.24em i=0,1,2\end{array}\\ {}\kern4.439998em \\ {}\kern3.599998em \end{array}} $$
(19)

The variation of kinetic energy for an FG micro-beam is given by:

$$ {\displaystyle \begin{array}{c}\delta T=-m\underset{0}{\overset{L}{\int }}\ddot{w}\delta w dx+m\underset{0}{\overset{L}{\int }}\frac{\partial }{\partial t}\left(\dot{w}\delta w\right) dx+I\;\underset{0}{\overset{L}{\int }}\left(\frac{\partial^2\ddot{w}}{\partial {x}^2}\delta w\right) dx-I\;{\left(\frac{\partial \ddot{w}}{\partial x}\delta w\right)}_{x=0}^{x=L}\\ {}-I\;\underset{0}{\overset{L}{\int }}\frac{\partial }{\partial t}\left(\frac{\partial^2\dot{w}}{\partial {x}^2}\delta w\right) dx+I\;{\left[\frac{\partial }{\partial t}\left(\frac{\partial \dot{w}}{\partial x}\delta w\right)\right]}_{x=0}^{x=L}\end{array}} $$
(20)

where ρ is the density and a dot over the kinematic variables signifies a time derivative. Furthermore, the parameters m and I are defined as follows:

$$ m=b\underset{-h/2}{\overset{h/2}{\int }}\rho (z)\; dz,\kern0.5em I=b\underset{-h/2}{\overset{h/2}{\int }}\rho (z)\;{z}^2\; dz $$
(21)

Finally, the variation of virtual work done by the external forces is obtained as:

$$ \delta W=\underset{0}{\overset{L}{\int }}\left[q-N\frac{\partial^2w}{\partial {x}^2}-{k}_W\;w(x)+{k}_P\frac{\partial^2w}{\partial {x}^2}\right]\delta w\; dx, $$
(22)

Based on the relation of the Hamilton principle on the time interval between t1 and t2, we have:

$$ {\int}_{t_1}^{t_2}\left(\delta T-\delta U+\delta W\right) dt=0 $$
(23)

Substituting for the variation of strain energy, kinetic energy and external work from (16), (20) and (22), respectively into relation (23) results in the following governing equation:

$$ {\displaystyle \begin{array}{l}\delta w:\frac{\partial^2}{\partial {x}^2\kern0em }\left[{M}_{11}+{M}_3^p+\frac{1}{5}\left(-{M}_{333}^{\tau }+4{M}_{113}^{\tau }-{M}_{223}^{\tau}\right)+{M}_{12}^m\right]-\frac{\partial^3}{\partial {x}^3\kern0em }\left[{H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)\right]\\ {}+q-{k}_W\;w+{k}_P\frac{\partial^2w}{\partial {x}^2}-N\frac{\partial^2w}{\partial {x}^2}-m\ddot{w}+I\frac{\partial^2\ddot{w}}{\partial {x}^2}=0\end{array}}\kern2.759999em $$
(24)

Similarly, the end conditions at x = 0, L are obtained as follows:

$$ {\displaystyle \begin{array}{l}\begin{array}{l}\;\frac{\partial }{\partial x\kern0em }\left({M}_{11}+{M}_3^p+\frac{1}{5}\left(-{M}_{333}^{\tau }+4{M}_{113}^{\tau }-{M}_{223}^{\tau}\right)+{M}_{12}^m\right)\\ {}-\frac{\partial^2}{\partial {x}^2\kern0em }\left({H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)\right)+I\kern0.24em \frac{\partial \ddot{w}}{\partial x}=0\kern0.6em OR\kern0.96em \delta w\left(x,t\right)=0\\ {}{M}_{11}+{M}_3^p+\frac{1}{5}\left(-{M}_{333}^{\tau }+4{M}_{113}^{\tau }-{M}_{223}^{\tau}\right)+{M}_{12}^m\\ {}-\frac{\partial }{\partial x\kern0em }\left({H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)\right)=0,\kern2.04em OR\kern1.32em \delta \left(\frac{\partial w}{\partial x}\right)=0,\\ {}{H}_1^p+\frac{2}{5}\left({H}_{111}^{\tau }-3{H}_{221}^{\tau}\right)=0,\kern6.25em OR\kern1.32em \delta \left(\frac{\partial^2w}{\partial {x}^2\kern0em }\right)=0\end{array}\\ {}\kern2.04em \\ {}\kern7.319995em \end{array}} $$
(25)

Upon substitution of the stress resultants from (18) into the differential equation of motion presented in (24), one can get the governing equation only in terms of kinematic parameter and the material properties as follows:

$$ \delta w:\tilde{D}\frac{\partial^6w}{\partial {x}^6}-\tilde{E}\frac{\partial^4w}{\partial {x}^4}+q-m\ddot{w}+I\frac{\partial^2\ddot{w}}{\partial {x}^2}-{k}_W\;w+{k}_P\frac{\partial^2w}{\partial {x}^2}-N\frac{\partial^2w}{\partial {x}^2}=0 $$
(26)

where,

$$ \tilde{D}={\left({\beta}_0I\right)}_{eq}+\frac{2}{5}{\left({\beta}_1I\right)}_{eq},\kern0.5em \tilde{E}={(EI)}_{eq}+{\left({\beta}_0A\right)}_{eq}+\frac{4}{15}{\left({\beta}_1A\right)}_{eq}+\frac{1}{2}{\left({\beta}_2A\right)}_{eq} $$
(27)

Similarly, the boundary conditions at x = 0 and L can be expressed as follows:

$$ {\displaystyle \begin{array}{cc}\tilde{D}\frac{\partial^5w}{\partial {x}^5}-\tilde{E}\frac{\partial^3w}{\partial {x}^3}+I\frac{\partial \ddot{w}}{\partial x}=0& OR\kern0.96em \delta w\left(x,t\right)=0,\\ {}\tilde{D}\frac{\partial^4w}{\partial {x}^4}-\tilde{E}\frac{\partial^2w}{\partial {x}^2}=0,& OR\kern1.32em \delta \left(\frac{\partial w}{\partial x}\right)=0,\\ {}\tilde{D}\frac{\partial^3w}{\partial {x}^3}=0,& OR\kern1.32em \delta \left(\frac{\partial^2w}{\partial {x}^2\kern0em }\right)=0.\end{array}}\kern1.92em $$
(28)

3.2 Analytical expressions for the mechanical parameters

In this section, the mechanical parameters namely the mass, maximum deflection, stress, natural frequency and buckling load are obtained for simply supported FG micro-beams. The following Fourier series expansion, which is compatible with simply supported boundary conditions, can be proposed for transverse deflection.

$$ w\left(x,t\right)=\sum \limits_{m=1}^{\infty }{w}_m\sin \left(\frac{m\;\pi }{L}\;x\right)f(t) $$
(29)

where f(t) = 1 for static analysis and \( f(t)={e}^{i{\omega}_mt} \) for free vibration analysis. In addition, the constant transverse force per unit length should be expanded as follows:

$$ q=\sum \limits_{m=1}^{\infty }{Q}_m\sin \left(\frac{m\;\pi }{L}\;x\right),\kern0.5em {Q}_m=\frac{2}{L}\underset{0}{\overset{L}{\int }}q\sin \left(\frac{m\;\pi }{L}\;x\right)\; dx=\frac{4\;q}{m\pi}\kern0.5em \left(m=1,3,\cdots \right).\kern0.72em $$
(30)

The mechanical parameters can be obtained by substituting (29) and (30) into governing equation appearing in (26). Analytical expressions of mechanical parameters which will be used for multi-objective optimization of simply supported FG micro-beams are given in Table 1.

Table 1 Analytical expressions of mechanical parameters in multi-objective optimization
Full size table

4 Multi-Objective optimization

In this study, all mechanical parameters developed in the previous section are considered for multi-objective optimizations. The target function is defined such that maximum deflection, maximum stress and mass must be minimized while natural frequency and critical buckling load must be maximized. Hence five target functions are introduced as follow

$$ \mathrm{Target}\ \mathrm{Functions}:\min \left(\frac{M}{M^S}\right);\min \left(\frac{w_{max}}{w_{max}^S}\right);\min \left(\frac{\sigma_{max}}{\sigma_{max}^S}\right);\max \left(\frac{\omega }{\omega^S}\right);\max \left(\frac{N_{cr}}{N_{cr}^S}\right) $$
(31)

where the mechanical parameters with superscript S refer to values relevant to suitable sample beams with L = 10h = 10b = 10μm and E = 70 GPa for each case. The values of mechanical parameters are obtained for three cases as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{Mechanical}\ \mathrm{parameters}\ \mathrm{of}\ \mathrm{sample}\ \mathrm{beam}\ \mathrm{based}\ \mathrm{on}\ \mathrm{the}\ \mathrm{modified}\ \mathrm{strain}\ \mathrm{gradient}\ \mathrm{theory}:\\ {}{M}^S=27\kern0.24em fg,{w}_{\mathrm{max}}^S=2.23\kern0.24em nm,{\sigma}_{\mathrm{max}}=75\;\mu N/{\left(\mu m\right)}^2,\\ {}{\omega}^S=2.3\;{e}^7 Hz,{N}_{cr}^S=575.73\mu N\ \\ {}\mathrm{Mechanical}\ \mathrm{parameters}\ \mathrm{of}\ \mathrm{sample}\ \mathrm{beam}\ \mathrm{based}\ \mathrm{on}\ \mathrm{the}\ \mathrm{modified}\ \mathrm{strain}\ \mathrm{gradient}\ \mathrm{theory}:\\ {}{M}^S=27\kern0.24em fg,{w}_{\mathrm{max}}^S=1.93\kern0.24em nm,{\sigma}_{\mathrm{max}}=64.75\;\mu N/{\left(\mu m\right)}^2,\\ {}{\omega}^S=2.475\;{e}^7 Hz,{N}_{cr}^S=666.99\mu N\\ {}\mathrm{Mechanical}\ \mathrm{parameters}\ \mathrm{of}\ \mathrm{sample}\ \mathrm{beam}\ \mathrm{resting}\ \mathrm{on}\ \mathrm{the}\ \mathrm{elastic}\ \mathrm{foundation}\\ {}{M}^S=27\; fg,{w}_{\mathrm{max}}^S=0.3\kern0.24em nm,{\sigma}_{\mathrm{max}}=9.36\;\mu N/{\left(\mu m\right)}^2,\\ {}{\omega}^S=6.19\;{e}^7 Hz,{N}_{cr}^S=4174\mu N\end{array}} $$
(32)

It is to be noticed that 1 femtogram (fg) ≡ 10−15g ram. The variables of aspect ratio L/h, thickness h and distribution parameter of FGM are chosen as design variables which play important role in the target functions. These are components of a vector with 3 elements which include numerical quantities and denoted by X i (i = 1 to 3) presented in Table 2. It is not possible to evaluate all possible values of design vector, therefore the design variables must be constrained between lower and upper bound which are given in Table 2.

Table 2 Range of design variables in micro-beams
Full size table

4.1 NSGAII Algorithm and settings

As mentioned before, NSGAII is a successful algorithm for multi-objective optimization.it has several layers to maintain both variety and efficiency. The successive steps of optimization on the basis of NSGAII Algorithm are presented in Table 3.

Table 3 NSGAII Algorithm
Full size table

To this algorithm, the number of initial population is firstly generated and amount of objective functions for each number of the initial population is computed. Also, these members are ranked and the crowding distance (CD) for any one of them is determined. In the next stage, parents are chosen based on the rank and CD of each member and then a total population is formed by combination of new population and initial population. N number of upper population of the total population would be separated for the next generations among the total population, whose numbers are higher than initial population. To get acceptable results, the algorithm requires to suitable settings. The settings of the NSGAII algorithm are given in Table 4.

Table 4 Algorithm Settings
Full size table

Crossover and mutation determined in Table 4 are two basic operators of optimization algorithm which are simultaneously employed to generate new population in the algorithm. Crossover is utilized to vary the programming of a chromosome or chromosomes from one generation to the next generation. This process is like to reproduction and biological crossover which takes more than one parent solutions and produces a child solution from them. Many crossover techniques namely single-point crossover, two-point crossover, cut and splice, uniform crossover and half uniform crossover exist for organisms which use different data structures to store themselves. The single-point crossover technique is applied to increase the variety in the answers in this algorithm. Mutation operator often changes randomly a part of a chromosome and maintains genetic diversity from one generation of a population of genetic algorithm chromosomes to the next. It prevents the algorithm to stay in a local minimum so the chance of finding more accurate answers improves.

The non-dominated sorting operator (NS) is the important operator of the multi-objective procedures which eliminates the weak answers and improves the optimum front to reach to the Pareto front. In this algorithm, each population is compared with all other population two by two. For each chromosome, the number of times defeated by other answers is calculated. The answers which are not defeated by other points are placed in the first front. By laying away these non-dominated points, the trend repeats for remain points. It is important to assign a rank for each member of population located in a front. In what follows, the crowding distance (CD) is described to tackle the issue. The CD subprogram plays main role in the NSGAII algorithm which is applied to compare the answers of a united front with similar rank number and sorts these answers. It means that if two answers are from a unique front, the answer with higher crowding distance will be selected and increases the variety of answers. In this study, the objective functions are five, hence the crowding distance is a five-dimensional space.

5 Results and discussion

Here, the results of optimization are obtained for two types of FG beams with constant width b = 1μm. As mentioned in the first section, three design variables including thickness, aspect ratio and the distribution parameters of FGM (α for E-FGM and n for P-FGM) are assumed. In addition, if the material length scales parameters l0, l1 and l2 are considered to be zero, the results predicted by the classical theory are obtained. Without losing generality and for convenience, it is presumed that all the material length scale parameters have the same value as l0 = l1 = l2 = 0.1μm. As mentioned previously, five normalized mechanical parameters have been considered that orders of their amplitudes are not same. We tend to define an output parameter in which the weight of all mechanical parameters is supposed to be equal. To this end, all values for each of outcomes (T i ) is normalized as follows:

$$ {\tilde{T}}_i(j)=\frac{T_i(j)-\min \left[{T}_i(j)\right]}{\max \left[{T}_i(j)\right]-\min \left[{T}_i(j)\right]} $$
(33)

where, index j stand for the population number. As a result, the values of \( {\tilde{T}}_i \) ‘s are in the interval [0,1]. A normalized form of target function is defined as follow:

$$ \Psi ={\tilde{T}}_M+{\tilde{T}}_{w_{\mathrm{max}}}+{\tilde{T}}_{\sigma_{\mathrm{max}}}-{\tilde{T}}_{\omega }-{\tilde{T}}_{N_{cr}} $$
(34)

It is worth mentioning that the sign of values of function Ψ may be negative.

5.1 E-FG beams

For obtaining the numerical results, it is assumed that E-FG beams are composed of aluminum (Al) material with properties E ref  = 70 GPa, G ref  = 26GPa and ρ ref  = 2700 kg/m3 as the reference material. In order to attain the best outcomes, intended algorithm has been utilized in several times and by considering the various population members and various iteration times. Table 5 demonstrates some selected outcomes of multi-objective optimization predicted by classical continuum theory for various design variables (h, L/h and α). From this Table, it can be found that the mass of micro-beams can be reduced more than half of the sample beam as values of α are negative. Hence, these FG micro-beams are suitable for applications that beams are only subjected to the inertial forces. In these applications, the values of maximum deflection, maximum stress and critical load are less important. A range of results of the multi-objective optimization is good for FG micro-beams under compressive traction. In these cases, the thickness of beams and inhomogeneity parameters are larger than the thickness of the sample beam and zero, respectively. Compared to the sample beam, the mechanical parameters except buckling loads are not improved. Figures 2a and b show the values of normalized target function defined in (34) for pairs of design variables (α, L/h) and (α, h), respectively based on the classical continuum theory. It can be readily concluded from these figures that E-FG beams with 0.5 ≤ h(μm) ≤ 2, 10 ≤ L/h ≤ 12, and 0.2 ≤ α ≤ 1.2 are selected in the most of optimized cases. It is to be noted that the point Ψ∗ implies a state of multi-objective optimization at which the value of normalized target function is minimum. The row related to this state is highlighted in all of tables and such beam is applicable when importance of all mechanical parameters is identical.

Table 5 Some results of multi-objective optimization for the classical theory
Full size table
Fig. 2
figure 2

Values of normalized target function Ψ for pairs of optimum decision variables (a) (α, L/h) and (b) (α, h), respectively based on the classical continuum theory

Full size image

In Table 6, some selected outcomes of multi-objective optimization for various design variables (h, L/h and α) are given by use of the modified strain gradient theory. It is to be noted that the mechanical parameters are normalized with respect to the suitable reference values given in (32) for sample beam. For some cases of beams, the thickness and aspect ratio of micro-beams, respectively are significantly lesser and larger than those of the sample beam, the mass and natural frequency of FG beams is decreased approximately to 38–44% and 60–90% of those of the sample beam, respectively. Therefore, these beams are applicable wherein subjected to harmonic forces with excitation frequencies higher than natural frequencies of FG micro-beams. Meanwhile, other range of the optimal design is excellent for application of FG micro-beams which are under compressive tractions and harmonic forces with low excitation frequencies. In these cases, the mass and buckling load of beams are larger than the several times those of the sample beam. Also, a remarkable difference between optimal values of mechanical parameters specially mass and buckling load can be observed. In Figs. 3a and b, the values of normalized target function for pairs of design variables (α, L/h) and (α, h), respectively are depicted using the modified strain gradient theory. By comparing Figs. 2 and 3, it can be readily found that inhomogeneity parameters and aspect ratio of optimal states predicted by the modified strain gradient theory are larger than those obtained by the classical continuum theory. Also, the distributions of optimal statespredicted by these theories are completely different with each other.

Table 6 Some results of multi-objective optimization for the modified strain gradient theory
Full size table
Fig. 3
figure 3

Values of normalized target function Ψ for pairs of optimum decision variables (a) (α, L/h) and (b) (α, h), respectively based on the modified strain gradient theory

Full size image

In Table 7, the effect of elastic foundations on some results of multi-objective optimization for various design variables (h, L/h and α) is studied using the modified strain gradient theory. It is to be noted that the mechanical parameters of the sample beam resting elastic foundations (K w  = 2K p  = 100) based on the modified strain gradient theory are used to normalize outputs. According to Tables 6 and 7, the optimal aspect ratio and inhomogeneity parameters of FG micro-beams resting on the elastic foundations are smaller than those of FG micro-beams without elastic foundations. In the most of optimal cases, values of the inhomogeneity parameters are smaller than zero. Also, the elastic foundations are able to increase values of the buckling load for some optimal states whose thickness are larger than that of the sample beam. In Figs. 4a and b, the effect of elastic foundations on values of normalized target function Ψ for pairs of design variables is investigated based on the modified strain gradient theory. As can be seen, FG micro-beams with 1 ≤ h(μm) ≤ 3,  10.75 ≤ L/h ≤ 12, and −1 ≤ α ≤ 0 are chosen as the optimal cases. It can be readily concluded from Figs. 3 and 4 that the elastic foundation has the considerable influence on the scattering of optimal states. In addition, the thickness, inhomogeneity parameter and aspect ratio of the FG beam under elastic foundations at state Ψ∗ are larger, smaller and approximately equal to those of beam without elastic foundations.

Table 7 The effect of elastic foundations (K w  = 2K p  = 100) on some results of multi-objective optimization for the modified strain gradient theory
Full size table
Fig. 4
figure 4

The effect of elastic foundations (K w  = 2K p  = 100) on values of normalized target function Ψ for pairs of optimum decision variables (a) (α, L/h) and (b) (α, h), respectively based on the modified strain gradient theory

Full size image

In Fig. 5, the distribution of properties through the normalized thickness of E-FG beams at the optimal states Ψ∗ is plotted. As can be observed, the forms of properties distribution are completely different from each other by considering the size effect and the elastic foundation. The difference between the values of properties at top and bottom surfaces is small for the optimal case predicted by the modified strain gradient theory.

Fig. 5
figure 5

The distribution of properties through the normalized thickness at the optimal state Ψ∗

Full size image

5.2 P-FG beams

In this section, it is assumed that constituents of the FG micro-beeams are a mixture of aluminum (Al) and alumina (Al2O3) with material properties E m  = 70 GPa, G m  = 26 GPa and ρ m  = 2700 kg/m3 for Al, and E c  = 380 GPa, G c  = 152 GPa and ρc = 3960 kg/m3 for Al2O3. In Table 8, some of optimal outcomes for various design variables (h, L/h and n) are presented based on the classical continuum theory. As can be seen, the buckling loads and maximum deflections of micro-beams can be improved more than sometimes of the sample beam. While, the maximum stresses are increased more than 50% of the sample beam. In the most of optimal states, values of thickness and power index are larger than 2 and 2.5, respectively. Also, the values of aspect ratio are smaller than 11. By comparison of Tables 5 and 8, it can be found that the optimal mechanical parameters of P-FGM beams except the mass are more advisable than those of E-FGM beams. Figure 6a and b demonstrate the optimal values of normalized target function for pairs of design variables (α, L/h) and (α, h), respectively based on the classical continuum theory. To these Figures, It can be readily found that P-FG beams with 1 ≤ h(μm) ≤ 2.25, 10.4 ≤ L/h ≤ 10.8, and 2 ≤ n ≤ 3.75 are chosen in the most of optimal states. Furthermore, values of normalized target function are smaller than zero in these cases. The comparison of optimal values at state Ψ∗ in Figs. 2 and 6 indicates that all mechanical parameters of the P-FG beams except mass are more appropriate than those of the E-FG beams.

Table 8 Some results of multi-objective optimization for the classical theory
Full size table
Fig. 6
figure 6

Values of normalized target function Ψ for pairs of optimum decision variables (a) (n, L/h) and (b) (n, h), respectively based on the classical continuum theory

Full size image

In Table 9, the size effect on optimal states of P-FG beams is investigated by means of the modified strain gradient theory. Comparing Tables 8 and 9, it can be concluded that P-FG beams with smaller values of the thickness, aspect ratio and power index are chosen as optimal states based on the modified strain gradient theory. Also, values of normalized maximum deflection predicted by the modified strain gradient theory are smaller than those of the classical continuum theory. However, values of other normalized mechanical parameters of optimal states change very slightly considering the effect of size dependency. It is worth mentioning that there are significant differences between values predicted by the classical and modified strain gradient theories of outcomes except mass, which are not normalized. In Figs. 7a and b, the size effect on the values of the normalized target function for pairs of design variables (α, L/h) and (α, h), respectively are studied. As observed in Figs. 6 and 7, the scattering of power indexes predicted by the modified strain gradient theory for optimal states are larger than that of classical continuum theory. To results depicted in Figures 2,3, 6 and 7, it can be readily concluded that the difference between values of design variables and the normalized target function obtained by the modified strain gradient theory and the classical continuum theory for P-FG beam are smaller than those of E-FG beams.

Table 9 Some results of multi-objective optimization for the modified strain gradient theory
Full size table
Fig. 7
figure 7

Values of normalized target function Ψ for pairs of optimum decision variables (a) (n, L/h) and (b) (n, h), respectively based on the modified strain gradient theory

Full size image

In Table 10, the simultaneous effects of elastic foundations and size dependency on the design variables (h, L/h and α) and the mechanical parameters are investigated. Similar to Table 7, the mechanical parameters are normalized using values of the sample beam resting elastic foundations predicted by the modified strain gradient theory. From Tables 9 and 10, the influence of elastic foundation coefficients on the values of outcomes is more significant than the size effect. In the most of optimal states, values of the aspect ratio and power index respectively are in the interval [10, 10.7] and [2, 2.8]. In Fig. 8a and b, the effect of elastic foundations on values of design variables and normalized target function is shown using the modified strain gradient theory. As can be seen in Figs. 7 and 8, the distribution of optimal states for micro-beams resting on the elastic foundations is different from the case of without foundation. For optimal state Ψ∗, the thickness of the P-FG beam under elastic foundations is larger than that predicted for the case without effect of elastic foundations. However, values of power index and aspect ratio of the FG beams are approximately equal to each other. Furthermore, the multi-objective optimization is able to improve the normalized values of mass, maximum deflection and frequency for P-FG micro-beams resting on the elastic foundation (please see the row of Tables 10 which are highlighted).

Table 10 The effect of elastic foundations (K w  = 2K p  = 100) on some results of multi-objective optimization for the modified strain gradient theory
Full size table
Fig. 8
figure 8

The effect of elastic foundations (K w  = 2K p  = 100) on values of normalized target function Ψ for pairs of optimum decision variables (a) (n, L/h) and (b) (n, h), respectively based on the modified strain gradient theory

Full size image

In Fig. 9, the distributions of metal volume fraction, V m through the normalized thickness at the optimal state Ψ∗ are depicted. The volume fraction distributions are clearly different by considering the size effect while a little difference can be seen for micro-beams resting on the elastic foundation. Comparing Figs. 5 and 9, it can be concluded that the effects of size and elastic foundation for E-FG beams are more remarkable than P-FG beams.

Fig. 9
figure 9

The volume fraction of metal through the normalized thickness at the optimal state Ψ∗

Full size image

5.3 History, trade-off and sensitivity analysis

Here, the optimization histories of five target functions, trade-off and sensitivity analysis of E-and P-FG beams for three case studies are discussed in detail. In Figs. 10 and 11, the iteration history of best values of mechanical parameters are presented to show the trade-off of conflicting target functions for each case of E-and P-FG beams, respectively. It is to be noted that best values at different iterations do not necessarily belong to an optimal state. From Figs. 10 and 11, it is seen that the best values of normalized buckling load and natural frequencies become larger when number of iteration increases, contrary to best values of normalized maximum deflection, maximum stress and mass. For E-FG beams, the optimal value of maximum stress, natural frequency and mass are obtained by use of less iteration. For P-FG beams, only the optimal values of normalized buckling load are significantly varied by iteration. Also, it is observed that the best value of some mechanical parameters is remained to be constant after each of iteration for different cases, e.g. the optimal values of normalized maximum deflection and mass in three cases of P-FG beams. As mentioned in the Sections 5.1 and 5.2, many optimal states can be found at each of iteration and it is impossible to discuss all of them. Also, it is obvious that the best values of all target functions are not occurred an optimal state. Hence, the mechanical behavior of FG beams in some aspects may be improved while the other mechanical aspects are unchanged or even more disadvantageous. In Figs. 12 and 13, the trade-off analysis of some optimal states is shown for three cases of E- and P-FG beams, respectively. The values of mechanical parameters at selected optimal states of FG beams discussed to show the trade-off of conflicting target functions. For first example, consider the values of target functions at first data point of E-FF beams predicted by the classical theory (Fig. 12a). It is seen that all mechanical parameters except the normalized maximum stress are improved relative to sample values. For third, fifth and sixth data points in Fig. 12b, it is seen that the values of normalized buckling load and mass become larger than sample beam while values of natural frequency and maximum deflection decreases. Hence, these cases are suitable in application which E-FG beams are only subjected to static loads. For some selected optimal states in the case of P-FG beams resting under elastic foundation (Fig. 13c), it is observed that the values of mass and normalized natural frequency are less than the sample beam the while maximum stress increases. Such optimal states of beam is used somewhere the harmonic load with a high excitation frequency imposed to the device.

Fig. 10
figure 10

The iteration history for the target functions of E-FG beams

Full size image
Fig. 11
figure 11

The iteration history for the target functions of P-FG beams

Full size image
Fig. 12
figure 12

The trade-off analysis for selected optimal states of E-FG beams

Full size image
Fig. 13
figure 13

The trade-off analysis for selected optimal states of P-FG beams

Full size image

A quantitative sensitivity analysis is conducted to show the applicability and feasibility of the multi-objective optimization and better understand optimal states presented in two previous sections. On the basis of this sensitivity analysis, the variation with an arbitrary design variable of outcomes is obtained while two other variables are supposed to be constant at their mean values. Since the design variables such as thickness, distribution parameter of functionally graded materials and aspect ratio have different ranges, a new variable of each design variable should be defined using the Z -score function as follows:

$$ Z- score(X)=\frac{X-\Upsilon}{\Gamma} $$
(35)

In which, ϒ is the mean of arbitrary design variable X and Γ is the standard deviation of X. It is to be noted that values of design variables have same mean value equal to zero and their standard deviation is equal to unit. Figures 14 and 15 illustrate the quantitative sensitivity analysis for all mechanical parameters of E- and P-FG beams embedded in the elastic foundation using the modified strain gradient theory, respectively. As mentioned previously, the horizontal axis represents values of Z -score function and not the exact values of design variables. From Figs. 14 and 15, it can be concluded that the aspect ratio have significant influence on the normalized maximum deflection and buckling load. Also, the variation with thickness of normalized natural frequency and mass are larger than those with other design variables. For E-FG beams, the normalized maximum stress are strongly varied by the positive values of Z− score when α increases. Based on this sensitivity analysis, it can be concluded that the variation of mechanical parameters with an arbitrary design variable may be different each other while two other variables are fixed at their mean values.

Fig. 14
figure 14

The sensitivity analysis for target functions of E-FG beams resting on the elastic foundation based on the MSG theory

Full size image
Fig. 15
figure 15

The sensitivity analysis for target functions of P-FG beams resting on the elastic foundation based on the MSG theory

Full size image

6 Conclusion

In this study, a multi-objective optimization of simply supported FG micro-beams resting on Pasternak and Winkler elastic foundations has been performed using the non-dominated sorting genetic algorithm-I. The analytical expressions of mechanical parameters were chosen as target functions such that maximum deflection, maximum stress and mass become minimum while values of natural frequency and critical buckling load must be maximized. The size and foundation effects on the design variables including thickness, distribution parameter of FGMs, and aspect ratio and values of normalized target functions were discussed in details for both E-FG and P-FG micro-beams. Findings indicated that

  • For some of optimum cases, the mass of micro-beams is reduced more than half of the sample beam based on the classical and the modified strain gradient theories. These cases are suitable for applications of E-FG and P-FG beams subjected to the inertial forces.

  • For cases of optimum states, the thickness and inhomogeneity parameters of micro-beams are larger than those of the sample beam. These cases are suitable for when FG micro-beams are subjected to static in-plane and transverse forces, since the values of buckling load are many times larger than those of sample beam

  • The elastic foundation coefficients and internal length scale parameters of materials have significant influence on the distribution of design variables.

  • For most cases of E-FG beams, the optimal values of thickness and aspect ratio predicted by the modified strain gradient theory respectively are significantly lesser and larger than those of the sample beam. For such states, the mass and natural frequency is decreased approximately to 38–44% and 60–90% of those given for the sample beam.

  • For P-FG micro-beams resting on the elastic foundation, the multi-objective optimization is able to increase values of buckling load more than several times of sample beam and decrease the values of mass and maximum deflection.

  • For E-FG micro-beams embedded in elastic medium, optimum values of the inhomogeneity parameters are smaller than zero in the most of optimal cases.

  • Optimum mechanical parameters of P-FGM beams except the mass are more advisable than those of E-FGM beams based on the classical continuum theory.

Finally, the history and trade-off analysis was provided to demonstrate the shortcomings of the proposed multi-objective optimization. The most main limitation is that there were some conflicts between five target functions which prevents to achieve the best optimal states for each mechanical parameter. However, this obstacle can be removed by reducing a number of target functions and it is possible to reach a better optimal design of FG micro-beams for a specific application. In the iteration history analysis, it was shown that the values of target functions at optimal states may be dominated for next generations. Also, the multi-objective optimization algorithm may be improved by modifying the crowding distance and using a weighted function for each target function.