Keywords

1 Introduction

Functionally graded (FG) materials are increasingly and widely used in different fields such as aerospace, marine, mechanical and structural engineering. FG materials are made of two or more constituents that have a continuous and smooth variation of the relative volume fraction and microstructure [1]. It is well known that the performance of a FG composite depends not only on the material properties and quantity of its constituent materials but also on the distribution of these constituents. Often, the volume fractions of the constituents are tailored to obtain an optimal material composition satisfying design needs. This paper focuses on tailoring the material distribution to maximize the first natural frequency of FG beams. The maximization of natural frequencies of structures is a common optimization objective since an increase in fundamental frequencies can provide an improvement in structural stiffness [2].

The optimal design of volume fraction for maximizing the natural frequencies of FG beams has been a research interest in recent years. Goupee and Vel [3] used the two-dimensional spatial distribution of volume fractions represented by piecewise cubic interpolation of volume fraction values determined at a finite number of grid points to optimize the natural frequencies of functionally graded beams. In the work by Yas et al. [4, 5] and Kamarian et al. [6], the volume fraction optimization in the thickness direction of a FG beam resting on elastic foundation was studied using three-parameter power law distribution. The three-parameter power law distribution of volume fraction has been also employed in recent works by Roque and Martins [7] and Roque et al. [8]. Some researchers tailored the material distribution through the longitudinal direction for maximizing the fundamental frequency of four-parameter or five-parameter FG beams [9] and arches [10].

On the other hand, the determination of the natural frequencies requires the solution of the free vibration problem. There have been many published works on the analysis of the free vibration of FG beams using different shear deformation theories (e.g. see [11,12,13,14,15]). High-order shear deformation theories can be used to obtain precise results in the case of thick beams. Nevertheless, the past works on optimization of FG beams have mostly based on classical beam theory or first-order shear deformation theory.

In this study, various shear deformation theories are employed in the free vibration analysis of FG beams. Navier-type solution method is used to obtain the natural frequencies. Four-parameter power law distribution and five-parameter trigonometric distribution are introduced to describe the volume fraction in beam thickness direction. These distribution formulations are supposed to permit more diverse material distributions when compared with the simple power law or three-parameter power law. The objective is to find optimal parameter values so as the first natural frequency is maximized. Since the optimization problem is highly nonlinear and complex that is not easily solved by traditional gradient-based techniques, a novel population-based metaheuristic algorithm, called Social Group Optimization (SGO), is applied for the first time to optimize the volume fraction of FG beams. Beams with different material properties are examined.

2 Free Vibration of Functionally Graded Beam

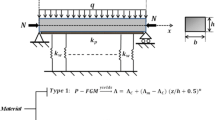
Consider a functionally graded (FG) beam composed of two materials with length \(L\) and rectangular cross section \(b \times h,\) where \(b\) is the width and \(h\) is the height. The \(x,y\) and \(z\) coordinates are taken along the length, width and height of the beam, respectively. The study is limited to linear elastic material behaviour.

2.1 Formulations of Volume Fraction

The material properties of a FG beam are assumed to vary continuously along the thickness of the beam (in the \(z\) direction) and governed by the volume fraction of its constituents according to the rule of mixtures:

$$P(z) = P_{1} V_{1} (z) + P_{2} V_{2} (z);\quad V_{2} (z) = 1 - V_{1} (z)$$
(1)

where \(P\) represents the effective material property such as Young’s modulus \(E\) and mass density \(\rho\); \(V\) is the volume fraction; subscripts 1 and 2 represent the constituent 1 and constituent 2, respectively.

Possible distribution laws for volume fraction are the power law [16], the sigmoid law [17], the exponential law [18] and the three-parameter law [19]. In this study, to spatially tailor the material properties, it is proposed that the volume fraction of constituent 1 follows four-parameter power law distribution formulations or five-parameter trigonometric distribution as given in Table 1.

Table 1 Volume fraction of constituent 1
Full size table

The parameters \(a\), \(b\), \(c\), \(d\) and \(p\) are the control parameters, or the design variables of the optimization problem. The proposed equations allow more diverse material distributions when compared with the simple power law. As shown later in this paper, these distributions are also more advantageous than the three-parameter power law distribution (Eq. 2), which was used in the previous work by Roque and Martins [7] to optimize the volume fraction of the same FG beams.

$$V_{1} = \left[ {\frac{1}{2} + \frac{z}{h} + b\left( {\frac{1}{2} - \frac{z}{h}} \right)^{c} } \right]^{p}$$
(2)

2.2 Analytical Solution for Free Vibration of FG Beams

Based on the higher-order shear deformation theory, the displacement field for the beam is assumed in the following form

$$\begin{array}{*{20}l} {u(x,z,t) = u_{0} (x,t) - z\frac{\partial w(x,z,t)}{\partial x} + f(z)\phi (x,t)} \hfill \\ {v(x,z,t) = 0} \hfill \\ {w(x,z,t) = w_{0} (x,t)} \hfill \\ \end{array}$$
(3)

where \(u\), \(v\) and \(w\) are the displacements at a point of the beam along \(x,y\) and \(z\) directions; \(u_{0}\) and \(w_{0}\) are the axial and transverse displacement of a point on the mid-surface, respectively; \(\phi\) is the rotation of the cross section about the \(y\)-axis; and \(f(z)\) is a shape function characterizing the distribution of the transverse shear strain and shear stress through the thickness of the beam.

With Eq. (3), different shear deformation theories can be introduced to obtain the displacements of the beam by using different shape functions \(f(z)\). In this study, the Euler–Bernoulli beam theory (CBT), the exponential beam theory (EBT) of Karama et al. [20], the hyperbolic beam theory (HBT) of Soldatos [21], the sinusoidal beam theory (SBT) of Touratier [22] and the third-order beam theory (TBT) of Reddy [23] are employed with the corresponding shape functions \(f(z)\) given in Table 2. The Timoshenko beam theory (TMT) is not considered for the analysis since it has been already used in [7].

Table 2 Shape functions
Full size table

The strain–displacement relationships are obtained from:

$$\begin{array}{*{20}l} {\varepsilon_{x} = \frac{\partial u}{\partial x} = \frac{{\partial u_{0} }}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + f(z)\frac{\partial \phi }{\partial x}} \hfill \\ {\gamma_{xz} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} = f^{{\prime }} (z)\phi } \hfill \\ \end{array}$$
(4)

The stresses are of the form:

$$\begin{aligned} \sigma_{x} & = E(z)\varepsilon_{x} \\ \tau_{xz} & = \frac{E(z)}{2(1 + \nu )}\gamma_{xz} = G(z)\gamma_{xz} ;\quad G(z) = \frac{E(z)}{2(1 + \nu )} \\ \end{aligned}$$
(5)

Applying the principle of virtual work to the free vibration problem of the beam leads to:

$$b\int_{0}^{L} {\int_{ - h/2}^{h/2} {(\sigma_{x} } } \delta \varepsilon_{x} + \tau_{xz} \delta \gamma_{xz} )dzdx + b\int_{0}^{L} {\int_{ - h/2}^{h/2} {\rho (z)(\frac{{\partial^{2} u}}{{\partial t^{2} }}\delta u + \frac{{\partial^{2} w}}{{\partial t^{2} }}\delta w)dzdx = 0} }$$
(6)

where the symbol \(\delta\) denotes the variation operator. By substituting Eqs. (4) and (5) into Eq. (6), integrating by parts and noting that the variation \(\delta u_{0}\), \(\delta w_{0}\) and \(\delta \phi\) can be arbitrary, the following governing equations can be derived:

$$\begin{array}{*{20}l} { - A\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + B\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - C\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{3} w_{0} }}{{\partial x\partial t^{2} }} + I_{3} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} = 0} \hfill \\ { - B\frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + D\frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} - F\frac{{\partial^{3} \phi }}{{\partial x^{3} }} + I_{2} \frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} - I_{4} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }} + I_{5} \frac{{\partial^{3} \phi }}{{\partial x\partial t^{2} }} + I_{1} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} = 0} \hfill \\ { - C\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + F\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} - G_{1} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + H_{1} \phi + I_{3} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - I_{5} \frac{{\partial^{3} w_{0} }}{{\partial x\partial t^{2} }} + I_{6} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} = 0} \hfill \\ \end{array}$$
(7)

where the coefficients A, B, C, D, F, G 1 , H 1 , I 1 , I 2 , I 3 , I 4 , I 5 and I 6 are given by:

$$\begin{array}{*{20}l} {(A,B,C,D,F,G_{1} ) = \int_{ - h/2}^{h/2} {E(z)(1,z,f,z^{2} ,zf,f^{2} )dz} ;} \hfill \\ {H_{1} = \int_{ - h/2}^{h/2} {G(z)\left( {f^{{\prime }} } \right)^{2} dz} } \hfill \\ {(I_{1} ,I_{2} ,I_{3} ,I_{4} ,I_{5} ,I_{6} ) = \int_{ - h/2}^{h/2} {\rho (z)(1,z,f,z^{2} ,zf,f^{2} )dz} } \hfill \\ \end{array}$$
(8)

For simply supported beams with length L, the analytical solution can be derived by considering the following expansions for displacements \(u_{0} (x,t)\), \(w_{0} (x,t)\) and \(\phi (x,t)\):

$$\begin{array}{*{20}l} {u_{0} (x,t) = \sum\limits_{m = 1}^{\infty } {u_{m} \cos \left( {\frac{m\pi x}{L}} \right)\sin \,\omega_{m} t} } \hfill \\ {w_{0} (x,t) = \sum\limits_{m = 1}^{\infty } {w_{m} \sin \left( {\frac{m\pi x}{L}} \right)\sin \,\omega_{m} t} } \hfill \\ {\phi (x,t) = \sum\limits_{m = 1}^{\infty } {\phi_{m} \cos \left( {\frac{m\pi x}{L}} \right)\sin \,\omega_{m} t} } \hfill \\ \end{array}$$
(9)

where \(\omega_{m}\) is the mth natural frequency. In this study, only the first natural frequency is optimized and therefore m = 1. Substituting Eq. (9) in Eq. (7), the following set of equations is obtained:

$$\begin{array}{*{20}l} {\left[ {\left( {A\frac{{m^{2} \pi^{2} }}{{L^{2} }}} \right)u_{m} - \left( {B\frac{{m^{3} \pi^{3} }}{{L^{3} }}} \right){\text{w}}_{m} + \left( {C\frac{{m^{2} \pi^{2} }}{{L^{2} }}} \right)\phi_{m} } \right] - \omega^{2} \left[ {I_{1} u_{m} - I_{2} \frac{m\pi }{L}{\text{w}}_{m} + I_{3} \phi_{m} } \right] = 0} \hfill \\ {\left[ { - \left( {B\frac{{m^{3} \pi^{3} }}{{L^{3} }}} \right)u_{m} + \left( {D\frac{{m^{4} \pi^{4} }}{{L^{4} }}} \right){\text{w}}_{m} - \left( {F\frac{{m^{3} \pi^{3} }}{{L^{3} }}} \right)\phi_{m} } \right] - \omega^{2} \left[ { - I_{2} \frac{m\pi }{L}u_{m} + \left( {I_{1} + I_{4} \frac{{m^{2} \pi^{2} }}{{L^{2} }}} \right){\text{w}}_{m} - I_{5} \frac{m\pi }{L}\phi_{m} } \right] = 0} \hfill \\ {\left[ {\left( {C\frac{{m^{2} \pi^{2} }}{{L^{2} }}} \right)u_{m} - \left( {F\frac{{m^{3} \pi^{3} }}{{L^{3} }}} \right){\text{w}}_{m} + \left( {H_{1} + G_{1} \frac{m\pi }{L}} \right)\phi_{m} } \right] - \omega^{2} \left[ {I_{3} u_{m} - I_{5} \frac{m\pi }{L}{\text{w}}_{m} + I_{6} \phi_{m} } \right] = 0} \hfill \\ \end{array}$$
(10)

The system is an eigenproblem of type \([K - \omega^{2} M]\{ \Delta \} = \{ 0\}\), where \(\omega\) is a natural frequency.

3 Optimization Problem

The optimal design of a FG beam is based on the optimization of material distribution throughout beam height, i.e. optimizing the volume fractions of the material constituents. The optimization problem considered in this study is the maximization of the fundamental frequency. The problem is formulated as Eq. (11).

$$\text{Maximize}\,\bar{\omega } = \frac{{\omega L^{2} }}{h}\sqrt {\frac{{\rho_{2} }}{{E_{2} }}}$$
(11)
$$\begin{array}{*{20}l} {{\text{Subject}}\,{\text{to}}} & {0 \le V_{1} \le 1} \\ {} & {a_{{{\text{min}}}} \le a \le a_{{{\text{max}}}} } \\ {} & {b_{{{\text{min}}}} \le b \le b_{{{\text{max}}}} } \\ {} & {c_{{{\text{min}}}} \le c \le c_{{{\text{max}}}} } \\ {} & {d_{{{\text{min}}}} \le d \le d_{{{\text{max}}}} } \\ {} & {p_{{{\text{min}}}} \le p \le p_{{{\text{max}}}} } \\ \end{array}$$

where \(\bar{\omega }\) is the normalized fundamental frequency, with \(\rho_{2}\) and \(E_{2}\) are the density and modulus of elasticity of constituent 1, respectively.

In the above optimization problem, the design variables \(a\), \(b\), \(c\), \(d\) and \(p\) are subjected to bound constraints and they must be chosen such that the volume fraction at any point along the height will stay within the permissible physical limits, i.e. \(0 \le V_{1} \le 1\). To assure that, a set of constraints is introduced as:

$$\begin{array}{*{20}l} {0 \le V_{1,top} ,V_{1,bottom} \le 1} \hfill \\ {0 \le V_{1,\hbox{min} } ;\quad V_{1,\hbox{max} } \le 1} \hfill \\ \end{array}$$
(12)

where \(V_{1,top} ,V_{1,bottom}\) are the volume fractions at the boundaries (at the top and the bottom); and \(V_{1,\hbox{min} } ,V_{1,\hbox{max} }\) are the minima and maxima within the structure domain. The maxima/minima point \(z_{opt}\) can be obtained by solving:

$$V_{1}^{{\prime }} (z) = 0$$
(13)

For four-parameter power law distribution, we obtained:

$$z_{opt} = \frac{h}{2}\left( {1 - 2{\text{e}}^{{\frac{ - \log \left[ b \right] - \log \left[ c \right]}{c - 1}}} } \right)$$
(14)

For five-parameter trigonometric distribution, we obtained:

$$z_{opt} = \left[ {\begin{array}{*{20}c} {\frac{{h\left( {2d - \pi + c\pi } \right)}}{2c\pi }} \\ {\frac{{h\left( {2d + \pi + c\pi } \right)}}{2c\pi }} \\ {\frac{{h\left( {2d + c\pi - 2\arcsin \left[ {\frac{{1 - 20^{{\frac{1}{ - 1 + p}}} }}{b}} \right]} \right)}}{2c\pi }} \\ \end{array} } \right.$$
(15)

After solving for maxima or minima, then the values of the volume fraction at all the points in the structure domain corresponding to these maxima or minima should satisfy the permissible limits.

4 Social Group Optimization

The SGO is one of the most recent optimization techniques, developed by Satapathy and Naik for global optimization [24]. SGO is based on the concept of social behaviour of human towards solving a complex problem, i.e. a problem/task which is too difficult to solve by a single person can be solved by a group of persons. It has been shown in [24] that SGO outperforms several advanced optimization techniques in solving different unconstrained benchmark functions. The technique is quite simple and straightforward to implement. Details of the concept and the mathematical formulation of SGO can be found in [24].

4.1 Basic Procedure of SGO

SGO is a population-based optimizer, where the population of candidate solutions is considered as a group of N persons \(X_{k} (k = 1,2, \ldots ,N)\) and each person is defined by \(X_{k} = (x_{k1} ,x_{k2} , \ldots ,x_{kD} )\), where \(x_{ki} (i = 1,2, \ldots ,D)\) is the traits (design variables) assigned to a person and \(D\) is the dimension of the optimization problem. Each person in the group gets knowledge and has a certain level of capacity for solving the problem, which is corresponding to the ‘fitness’, \(f_{k}\). The best person \(X_{gbest} \;\) is the one with best fitness. The best person intends to propagate knowledge to the other person, which will improve the knowledge level of the whole group.

The procedure of SGO consists of two phases: the ‘improving phase’ and the ‘acquiring phase’. At the ‘improving phase’, each person is influenced by the best person and his/her knowledge level is enhanced. At the ‘acquiring phase’, the knowledge level of each person is improved through mutual interaction with another person and the best person in the group at that time. The basic steps of SGO are given in the following.

Initialization

An initial population is randomly sampled from the solution space as Eq. (16),

$$x_{ki} = x_{i}^{l} + \text{rand} [0,1] \times (x_{i}^{u} - x_{i}^{l} ),\quad i = 1,2, \ldots ,D$$
(16)

where \(x_{i}^{l}\) and \(x_{i}^{u}\) are the lower and the upper bounds of the ith design variable, respectively; \({\text{rand}}[0,1]\) is a uniformly distributed random real value in the range [0, 1]. Then, calculate the fitness of each person in the population \(f_{k}\).

Improving Phase

In this phase, each person \(X_{k}\) acquires knowledge from the group’s best person \(X_{gbest}\). The updating of each person is given as follows:

$$X_{k}^{new} = c\,*\,X_{k}^{old} + {\mathbf{r}}\,*\,(X_{gbest} - X_{k}^{old} ),\quad k = 1,2, \ldots ,N$$
(17)

where \(c\) is a self-introspection parameter and \(0 < c < 1\); \({\mathbf{r}}\) is a vector of D uniformly distributed random numbers within the range [0, 1]. Accept \(X_{k}^{new}\) if it provides a better fitness than \(X_{k}^{old}\) does; otherwise, the \(X_{k}^{old}\) is retained in the group.

Acquiring phase

In this phase, each person interacts with other person of the group for acquiring knowledge. The best knowledgeable person (here known as the person with the best fitness at the end of the improving phase) has the greatest influence on others. A person will also get new information from others if they have more knowledge than he/she has. The updating of each person is as follows.

For each person \(X_{k}\), randomly select another person in the current group \(X_{r}\), where \(r \ne k\):

If \(X_{k}\) is better than \(X_{r}\):

$$X_{k}^{new} = X_{k}^{old} + {\mathbf{r}}_{1}\,*\,(X_{k} - X_{r} ) + {\mathbf{r}}_{2}\,*\,(X_{gbest} - X_{k} )$$
(18)

Otherwise,

$$X_{k}^{new} = X_{k}^{old} + {\mathbf{r}}_{1}\,*\,(X_{r} - X_{k} ) + {\mathbf{r}}_{2}\,*\,(X_{gbest} - X_{k} )$$
(19)

where \({\mathbf{r}}_{1}\) and \({\mathbf{r}}_{1}\) are two vectors of D uniformly distributed random numbers in [0, 1]. Accept \(X_{k}^{new}\) if it gives a better fitness than \(X_{k}^{old}\) does.

The improving and acquiring phases are repeated until a termination criterion is reached.

4.2 Constraint Handling

The SGO has been developed originally for unconstrained optimization problem. In order to adapt SGO to the optimization of FG beams discussed in Sect. 3, constrained handling is required. In the optimization of FG beams, there are two types of constraints: bound constraints and inequality constraints.

Handling of bound constraints

If the value of a design variable \(x_{kj}^{new}\) violates the bound(s) \(b_{j}\), its value is recomputed as:

$$x_{kj}^{new} = \frac{{x_{kj}^{old} + b_{j} }}{2}$$
(20)

Handling of inequality constraints

Consider the inequality constraint of the form:

$$c_{j} (X_{k} ) \le 0,\quad j = 1,2, \ldots ,N_{C}$$
(21)

where \(N_{C}\) is the number of constraints of the optimization problem; \(c_{j} (X_{k} )\) is the jth constraint function. For the FG beam problem, the constraints are the requirement on the volume fraction as given in Eq. (12).

The constraint violation of a solution \(X_{k}\) is then determined by:

$$C_{k} = \hbox{max} \left\{ {\mathop {\hbox{max} }\limits_{j} \{ 0,c_{j} (X_{k} )\} } \right\},\quad j = 1,2, \ldots ,N_{C}$$
(22)

Deb’s rules [25] are employed in this study to handle inequality constraints:

  1. (1)

    A feasible solution is better than any infeasible one.

  2. (2)

    Of two feasible solutions or two solutions with equal constraint violation, the one with better fitness is the better.

  3. (3)

    Of two infeasible solutions, the one with a smaller constraint violation is the better.

Deb’s constraint rules have been successfully applied for genetic algorithm and several metaheuristics.

5 Optimization Results

The FG beam considered in the optimization is composed of two materials. Material properties for material 1, Young’s modulus and mass density are the same as those of aluminium. Material properties for material 2 are obtained by considering different material property ratios s = E2/E1. The choice of these material properties is purely for the illustration of the optimization problem. The properties of the FG beam are the same as those in [7] and listed in Table 3.

Table 3 Data for the FG beam
Full size table

Two optimization problems are considered. In the first problem (Problem 1), volume fraction is followed by the four-parameter power law distribution, and in the second problem (Problem 2), the five-parameter trigonometric distribution is applied. For both problems, the fundamental natural frequencies are obtained for the beam using the shear deformation theories mentioned in Sect. 2. The ranges of the design variables for each problem are given in Table 4. These ranges are chosen based on a preliminary investigation of the proposed models of volume fraction given in Table 1, which ensure a wide range of possibilities for material distribution.

Table 4 Design variable ranges
Full size table

The parameter setting for SGO is the group size N = 50, the maximum iteration T max = 300 and the self-introspection c = 0.2. The computation program is implemented in MATLAB R2012a and executed on a personal computer with an Intel CPU Core i3 2.3 GHz and 2 GB RAM. For each case, the optimization is performed with 25 independent runs.

For Problem 1, the best solutions for each ratio E 2/E 1 are presented in Table 5. Optimization results show that the volume fraction can be tailored with respect to the ratio E 2/E 1 in order to achieve maximum fundamental frequencies. It is found that, for ratios E 2/E 1 < 1, the results obtained with different shear deformation theories are quite consistent. The material profiles obtained by the proposed four-parameter distribution model are similar to those given by the three-parameter power law distribution in [7]. However, the maximum fundamental frequencies by this study are slightly smaller than those obtained by Timoshenko beam theory in [7]. For ratios E 2/E 1 > 1, the optimal solutions given by different shear deformation theories are slightly different from each other. The maximum fundamental frequencies found in this study are higher than those in [7], which implies that the optimal results of four-parameter distribution are better than those of the three-parameter power law distribution.

Table 5 Best optimization results with four-parameter volume fraction model
Full size table

For Problem 2, the best solutions for each ratio E 2/E 1 are presented in Table 6. For all ratios E 2/E 1, the maximum fundamental frequencies are higher than the corresponding results obtained in Problem 1, as shown in Table 6. That means the proposed trigonometric volume fraction can provide better material distribution for maximizing the natural frequencies of FG beams. In this problem, quite consistent material profiles are obtained with different beam theories. It is found that the parameters a and b become unity regardless of ratios E 2/E 1.

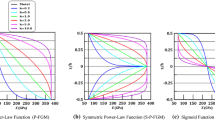
Table 6 Best optimization results with five-parameter volume fraction model
Full size table

The material profiles, V1, along the beam thickness based on the third-order beam theory (TBT) are shown in Fig. 1. The optimized profiles found for different E2/E1 correspond to ‘a sandwich-structured composite, with a smooth transition between face and core properties’. It is noted that these profiles are similar with the finding in [7] for the case E2/E1 < 1. For E2/E1 > 1, optimal solutions found in [7] using three-parameter volume fraction are closer to simple power law distribution.

Fig. 1
figure 1

Best optimal material profiles, V1, after 25 runs

Full size image

6 Conclusion

In this study, the optimization of volume fraction for maximizing the fundamental frequency of FG beam using various shear deformation theories and different distribution laws for volume fraction is investigated. Different ratios of material properties were tested.

For the cases considered, the optimized material profile was found quite consistent for different shear deformation theories. Using the proposed four-parameter and five-parameter formulations for volume fraction, it is able to tailor the material distribution for different design of FG beam. For different ratios of material properties, the optimized solutions correspond to ‘a sandwich-structured composite, with a smooth transition between face and core properties’. Moreover, the five-parameter formulation for volume fraction can provide better material distribution for maximizing the natural frequencies of FG beams.

The recent Social Group Optimization algorithm, which was originally developed for unconstrained optimization, has been adapted to effectively solve highly nonlinear, complex constrained optimization problem like the FG beam design.