1 Introduction

Frame structures composed of laminated composites like glass or carbon fiber-reinforced polymers (GFRP/CFRP) have been extensively used in aerospace structure and civil engineering with excellent performances for the high ratio of stiffness and weight. For convenience, GFRP/CFRP frame structures are simply referred to as composite frames in the following parts of the paper. The composite frame is utilized especially for aerospace vehicles, load-bearing structure of satellites, spatial stations, transmission towers and wind turbine structures, where large-scale, high stiffness and low weight are emphasized (Schutze 1997; Ibrahim et al. 2000). Therefore, optimization of laminated composites has undergone tremendous development in last decades. Some contributions on this topic have been summarized in the review articles of Ghiasi et al. (2009, 2010) and Bakis et al. (2002). It is worth noting that, in recent years, Discrete Material Optimization (DMO) of laminated composites has achieved considerable progress and attracted much attention due to the requirements of manufacturing the optimal design of composite structures. Based on an extension of the multi-phase topology optimization (Sigmund and Torquato 1997) Lund and Stegmann proposed the DMO method for multi-phase optimization of laminated composites (Lund and Stegmann 2005; Stegmann and Lund 2005). The DMO method has been successfully used to dispose many physical problems (Hvejsel et al. 2011; Lund 2009; Niu et al. 2010; Duan et al. 2014). As an alternative to the DMO schemes, Bruyneel (2011) introduced the Shape Functions with Penalization (SFP) scheme based on the shape functions of a quadrilateral first order finite element. Gao et al. (2012) proposed a Bi-valued Coding Parameterization (BCP) scheme which can be considered as a generalization of the SFP scheme.

Despite remarkable achievements have been made for the optimization of laminated composites, there still are two challenging issues for design of laminated composites. The first one is design for practical applications. This means that certain design guidelines or rules, referred to as manufacturing constraints, should be considered to e.g., reduce the risk of local failure in the structure. In Bailie et al. (1997), they mentioned eight weaknesses associated with laminated composites. An efficient way to prevent these weaknesses from happening is to follow a set of fundamental manufacturing constraints based on industrial experiences from tests and analyses. These manufacturing constraints have been developed to help the designers to exploit the material’s strengths while reducing the risk of structure and material failure. Costin and Wang (1993), Wang and Costin (1992) and Liu et al. (2011) considered manufacturing constraints in aircraft structural design with lamination parameters and numbers of plies with the predefined angles (such as [0°, ∓45°, 90°]) as design variables. Manne and Tsai (1998) utilized plydrop tapering for thickness optimization of symmetric layups to avoid warping. Recently, adopting SFP interpolation scheme, Bruyneel et al. (2012) realized the optimal stacking sequence design of laminated composites considering several manufacturing constraints. Irisarri et al. (2014) considered an extensive set of design guidelines to realize the optimal design of laminated composite structures with ply drops using a stacking sequence table (SST) method. Sørensen and Lund (2013), Sørensen et al. (2014) carried out the serial works on thickness and material choice design of laminated composites with certain manufacturing constraints. A more detailed discussion about design guidelines and their justification is provided in Bailie et al. (1997).

Another challenging issue is how to fully exploit the potential of composite structures due to the coupling effects between the macro structures (size, shape of structural components and structural configuration) and material microstructure (Yan et al. 2015a, b; Rodrigues et al. 2002) (fiber orientation, fiber content and layer thickness). As a kind of architecture material, laminated composites offer a good opportunity to tailor the material properties. Many researchers have carried out corresponding multi-scale lightweight material design of composite structures. Gao et al. (2013) proposed a simultaneous optimization of layout design and discrete fiber orientation of laminated structures. Ferreira et al. (2013) adopted Discrete Material Optimization (DMO) approach to perform a hierarchical optimization of laminated composite structures with simultaneous consideration of the fiber orientation and cross-section size/shape. As an immediate extension of the original DMO method, Sørensen et al. (2014) considered the topology variables of layer thickness and fiber orientation as the design variables and presented simultaneous optimization of the thickness and fiber orientation of laminate composites including certain manufacturing constraints. Blasques and Stolpe (2012) carried out a framework of simultaneous topology and material optimization (fiber orientation and laminate thickness) in optimal design of laminated composite beams with specific structural requirements, e.g., compliance, eigenfrequency constraints and structure weight. Liu et al. (2008) proposed the PAMP (Porous Anisotropic Material with Penalization) model, which has also been extended to multi-scale optimal design of composite material accounting for strength optimization (Yan et al. 2014), thermo-mechanical loads (Yan et al. 2015a; Deng et al. 2013) and frequency optimization (Niu et al. 2009). However, in the previous references, few works are related with multi-scale optimization of composite frame structures. Actually, in order to achieve lightweight designs with specific structural performance (e.g., compliance, frequency) for composite frame structure, it is an efficient approach to simultaneously optimize the ply parameters of the composite material and its structural configurations.

The present paper proposes a concurrent multi-scale design optimization model for composite frames with respect to minimum structural compliance under the volume constraint. The cross-section of the beam at the macro-scale and the discrete fiber winding angles at the micro-scale are introduced as the independent design variables to realize the topology and stacking sequence optimization at the two geometrical scales simultaneously. Especially, in the optimization model, six kinds of specific manufacturing constraints have been explicitly expressed as series of linear inequalities or equalities, and the sensitivities of these specific manufacturing constraints are easy to derive and obtain. At the micro-scale the DMO approach has been applied to achieve the micro-scale material interpolation. The extension of the open-source composite beam analysis tool BECAS developed by Blasques and Lazarov (2012), see also Blasques and Stolpe (2011), has been adopted to realize high-fidelity analysis of the composite frame structure. In the numerical examples, we implement four kinds of optimization models, which consider the effect of single-scale optimization, multi-scale optimization, and different constraint parameters on the optimization results.

The organization of the remainder parts of this paper is as follows. In Section 2, the concurrent multi-scale optimization concept and the discrete material optimization model with evaluation of convergence are introduced. Section 3 presents the explicit mathematical formulation of the manufacturing constraints considered in the present paper. Section 4 introduces the mathematical formulation of the optimization problem and the structural analysis model. Sensitivity analysis formulas are presented in Section 5. Section 6 presents the optimal results and the comparison of the single-scale and multi-scale optimization. Finally, a section with conclusions closes the paper.

2 Concurrent multi-scale optimal design of composite frame with Discrete Material Optimization (DMO) approach

2.1 Concurrent optimization of composite frame

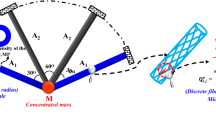
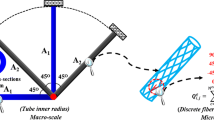
Because frame structures frequently adopt constant circular cross-sections and a fixed number of layers in most aerospace applications, for the ease of derivation and without loss of generality, frames made of tubes with constant circular cross-sections and a fixed number of layers are investigated in the present paper. The joints connecting the composite tubes can transfer moments and are assumed infinitely stiff. At the macroscopic level, the radius of the cross-section is used as the macro design variable, similar as that in the classical size optimization of frame structures. The radius of the tube can be recognized as the size and topology variable at the same time. When the radius reaches its lower limit, the tube can be regarded to be deleted from the ground structure and thereby realize the structural topology optimization (Bendsøe and Sigmund 2003; Eschenauer and Olhoff 2001). As has been shown in the schematic diagram of Fig. 1, the middle hidden beam component means the macro design variable of the beam has reached its lower limit and has been deleted from the ground frame structure.

Fig. 1
figure 1

Schematic diagram of the concurrent optimization of a composite frame composed of three beams

Full size image

At the microscopic level, the discrete fiber winding angle selection is solved by using the DMO approach in the sense that the structural constituents are chosen from among a given set of candidate materials. In most practical applications, the candidate composite ply is restricted to [0°, ∓45°, 90°], which are the conventional orientations used in aeronautics (Baker et al. 2004). Considering the manufacturing process, Mallick (2007) suggested that 0° and 90° fiber winding angles in filament winding process should be implemented by 5° and 85° fiber winding angles, respectively. So in this work, we consider the assembly of [5°, ∓45°, 85°] as a set of candidate composite fiber winding angles. The fiber winding angle is assumed to be constant in a given ply.

2.2 Discrete Material Optimization (DMO) approach

To ensure the integrity of this paper and the reading convenience, the basic idea and formula of the DMO model are briefly introduced in this section. For the detailed description please refer to the references (Stegmann and Lund 2005; Hvejsel and Lund 2011; Lund 2009; Niu et al. 2010; Duan et al. 2014).

The discrete material optimization formulation is implemented in a finite element framework. In the DMO approach the element constitutive matrix per layer \( {\boldsymbol{D}}_{i, j}^e \) (the superscript e refers to “element”, and the subscripts mean the i’th tube and j’th layer) can be expressed as a weighted sum of the constitutive matrices D i , j , c of the candidate materials (the subscript c means the c’th candidate material). In general, for multi-layer structures, the interpolation method can be implemented layer-wise for each element, i.e., for all layers in all elements. Various parameterization schemes have been developed in Lund and Stegmann (2005); Stegmann and Lund (2005). Consequently, the interpolation scheme is written by layers, and the constitutive relation for the j’th layer can be expressed as a sum over the number of candidate materials Ncand for the layer:

$$ {\boldsymbol{D}}_{i, j}^e={\sum}_{c=1}^{{\mathrm{N}}^{\mathrm{cand}}}{\omega}_{i, j, c}{\boldsymbol{D}}_{i, j, c} $$
(1)

where each candidate material is characterized by a constitutive matrix D i , j , c . The weighting functions ω i , j , c all attain values between 0 and 1 because no stiffness or mass matrix can contribute more than the physical material properties, and a negative contribution is physically meaningless. In (1), the parameterization model can be realized for single-layers and layer-wise for multiple layers for a large number of candidate materials. In this paper, the generalization of the SIMP multi-material interpolation schemes (Hvejsel and Lund 2011) is used to push the weighting functions towards 0 or 1 and obtain a distinct material selection. The weighting functions can be expressed as

$$ {\omega}_{i, j, c}={\left({x}_{i, j, c}\right)}^p $$
(2)

where p is a penalty parameter and the design variables x i , j , c are the artificial materials density of candidates. If x i , j , c  = 1, it means that the distinct c’th candidate material has been selected from a set of candidate materials for the j’th layer of the i’th tube. It is worth noting that in the original DMO multi-material interpolation, to keep the physically meaning in the case of a mass constraint or eigenfrequency optimization, a normalized weighting scheme was adopted (Stegmann and Lund 2005).

Hvejsel and Lund (2011) formulated multi-material variations of the SIMP (Bendsoe 1989) and RAMP (Stolpe and Svanberg 2001) interpolation schemes and relied on a large number of sparse linear constraints to enforce the selection of at most one material in each design subdomain. Inspired by Hvejsel and Lund (2011), in the present paper, the simple linear equality constraints on candidate artificial material density and continuous penalty strategy are adopted. The linear equality constraints on candidate artificial material densities can be expressed as

$$ {\sum}_{c=1}^{{\mathrm{N}}^{\mathrm{cand}}}{x}_{i, j, c}=1 $$
(3)

In this paper, the equality constraint in (3) is labeled as DMO normalization constraint (DMOnC), which should be realized layer-wise for laminated composites with multiple layers and solved by SLP (Sequential Linear Programming) method (Fletcher et al. 1998 or Gomes and Senne 2011). The details about DMOnC constraint and other manufacturing constraints will be shown in Section 3. With the micro-scale parameters of the DMO material interpolation recognized as the micro design variable (i.e., x i , j , c ), the manufacturing constraints can be explicitly expressed as linear equalities or inequalities in the form of the micro-scale parameters. Then, considering the coupling effect of design variables at the two geometrical scales and the specific manufacturing constraints, the concurrent multi-scale optimization of composite frames can be established for the specified structural loading and boundary conditions.

2.3 Evaluation of convergence of DMO

A convergence measure given in Stegmann and Lund (2005) is adopted to describe whether the optimization has converged to a satisfactory result, i.e., a single candidate material has been chosen in a specified element and all other materials have been discarded. For each layer, the following inequality is evaluated according to all weighting functions layer-wise.

$$ {\omega}_{i, j, c}\ge \varepsilon \sqrt{\omega_{i, j,1}^2+{\omega}_{i, j,2}^2+\cdots +{\omega}_{i, j,{\mathrm{N}}^{\mathrm{cand}}}^2} $$
(4)

where ε is a tolerance level; typically, ε ∈ [0.95 ~ 0.99]. If inequality (4) is satisfied for any ω i , j , c  in the j’th layer, that layer is flagged as converged. The convergence assessment criterion H ε is defined as the ratio between the number of converged layers \( {\mathrm{N}}_{\mathrm{c}}^{\mathrm{l},\mathrm{tot}} \) and the total number of layers Nl,tot. Nlay is the number of layers in each tube, and it is assumed that each tube has the same number of layers in the present paper. Thus, Nl,tot can be expressed as the number of tubes multiplied by the number of layers in a tube Nl,tot = Ntub ∙ Nlay:

$$ {\mathrm{H}}_{\upvarepsilon}=\frac{{\mathrm{N}}_{\mathrm{c}}^{\mathrm{l},\mathrm{tot}}}{{\mathrm{N}}^{\mathrm{l},\mathrm{tot}}} $$
(5)

If the tolerance level is 95% and fully converged, i.e., Hε = 0.95 = 1, all layers have a single weight factor that contributes more than 95% to the Euclidian norm of the weight factors.

3 Manufacturing constraints

Recent years, manufacturing constraints have attracted more and more attention in design of laminate composites, e.g., minimum percentage of each orientation constraints (10% rule), contiguity constraints, balance constraints, symmetry constraints (e.g., Bruyneel et al. 2012; Seresta et al. 2007; Kassapoglou 2013), damage tolerance constraints, ply-drop design constraints (e.g., Irisarri et al. 2014), thickness variation rate and intermediate constraints (e.g., Sørensen and Lund 2013; Sørensen et al. 2014). Taking into account the relevance of the above mentioned manufacturing constraints for the case of composite frames, the variable stiffness design i.e., thickness variation and ply-drop problems are not considered in this work and will be left for future work. The benefits of obeying these constraints are obvious in designing laminated composites, such as the following lists.

  1. [1]

    Manufacturing constraints make it possible to exploit the strengths of the material while mitigating the adverse effects of the material (e.g., matrix cracking and delamination; warping under thermal loading; out-of-plane failure modes).

  2. [2]

    Manufacturing constraints can furthermore be used to limit the complexity of the optimized design, thereby making it possible to achieve a higher degree of manufacturability (Sørensen et al. 2014).

  3. [3]

    Following certain manufacturing constraints, we can greatly improve the robustness of composite structures and improve service time of equipments.

The explicit linear equality or inequality manufacturing constraints are presented with respect to micro-scale design variables (x i , j , c ). The linear formulations are highly attractive from an optimization point of view and possible to achieve for all the manufacturing constraints presented in this paper.

3.1 Contiguity constraint (CC)

The definition of the contiguity constraint (CC) is that no more than a given number of plies, CL, of the same orientation should be stacked together. The benefit of this manufacturing constraint is to avoid matrix cracking failure (Sørensen et al. 2014). The contiguity constraint with respect to micro-scale parameters can be formulated as a linear inequality described by (6). Let CL ∈ N∗ denote the contiguity limit, then for any i ∈ Ntub , j ∈ Nlay , c ∈ Ncand, it should follow (6), and the loop should meet the dimension of j + CL ≤ Nlay. Ntub is the number of tubes in the frame structure.

The CC can be expressed as

$$ {x}_{i, j, c}+\cdots +{x}_{i, j+ CL, c}\le \mathrm{CL},\kern0.5em j+\mathrm{CL}\le {\mathrm{N}}^{\mathrm{lay}} $$
(6)

Table 1 gives an example of a laminate with four layers and four candidate materials in each layer. To present the contiguity constraint clearly for this example, the first candidate material, i.e., −45∘ and the contiguity constraint with CL = 1 are considered. Then the contiguity constraint can be expressed as linear inequalities:

$$ {\mathrm{x}}_{i,1,1}+{\mathrm{x}}_{i,2,1}\le \mathrm{CL};{\mathrm{x}}_{i,2,1}+{\mathrm{x}}_{i,3,1}\le \mathrm{CL};{\mathrm{x}}_{i,3,1}+{\mathrm{x}}_{i,4,1}\le \mathrm{CL} $$
(7)
Table 1 Example of laminate with four layers and four candidate materials in each layer
Full size table

Here we note that, the contiguity constraint should be implemented layer-wise for every candidate material, i.e., for all four fiber winding angles considered in this work.

For example, if a composite tube has twenty layers i.e., Nlay = 20, and every layer has four candidate materials i.e., Ncand = 4, the total number of contiguity constraints should be calculated as (Nlay − CL)∗Ncand = (20 − 1)∗4 = 76, when the contiguity limit is equal to one i.e., CL = 1.

3.2 10% rule (ten percent rule, TPR)

In the 10% rule, a minimum of 10% of plies of each of the 5∘, ±45∘ and 85∘ angles is required. The benefit of this constraint is to obtain laminates that are more robust in the sense that they are less susceptible to the weaknesses associated with highly orthotropic laminates. It is important to note that the 10% fiber-dominated guideline is often interpreted differently with regard to the ±45∘ plies. Some project directives require there is at least 5% “+45∘” and 5% “−45∘” plies, rather than 10% of +45∘ and −45∘ plies. There are no guidelines that establish a rigorous differentiation between these two alternative minimum 45° ply contents. Other projects have issued guidelines requiring at least 6% (rather than 10%) 85° plies are included when there are at least 20% “±45∘” plies. In most aerospace application, the 10% rule is frequently adopted, and therefore the 10% rule is adopted in the implementation of the present paper.

The TPR is expressed as

$$ {\sum}_{j=1}^{{\mathrm{N}}^{\mathrm{lay}}}{x}_{i, j, c}\ge 10\%\kern0.5em {\mathrm{N}}^{\mathrm{lay}} $$
(8)

Equation (8) can be explained as the sum for every candidate material density (x i , j , c ) in the whole laminate should be greater or equal than 10%. That is to say, if the combination of a laminate is −45∘ (8%); 5∘ (62%); +45∘ (25%); 85∘ (5%), then it does not fulfill the 10% rule, because the layer proportions of the −45∘ and 85∘ candidate materials in the whole laminate are less than 10%.

3.3 Balance constraint (BC)

Balance constraint means that angle plies (those at any angle other than 5∘ and 85∘) should occur only in balanced pairs with the same number of +θ∘and −θ∘ plies (θ∘ ≠ 5∘ , 85∘). For the set of the 5° ,  ∓ 45° , 85° candidate materials, any +45∘ ply should be accompanied by a −45∘ ply. A typical example of the difference between balanced and unbalanced laminates is shown in Fig. 2. The parameterized linear equality constraint with respect to candidate artificial material density x i , j , c can be expressed as (9).

Fig. 2
figure 2

Illustration of balanced and unbalanced symmetric laminates

Full size image

The BC is computed as

$$ {\sum}_{j=1}^{{\mathrm{N}}^{\mathrm{lay}}}{x}_{i, j,+ c}-{\sum}_{j=1}^{{\mathrm{N}}^{\mathrm{lay}}}{x}_{i, j,- c}=0,\kern0.5em c\ne \left({5}^{\circ}\cup {85}^{\circ}\right) $$
(9)

In (9), x i , j ,  + c denotes a positive angle, conversely, x i , j ,  − c denotes an accompanied negative angle. In the set of the 5° ,  ∓ 45° , 85° candidate materials, x i , j ,  + c is +45∘ ply, and x i , j ,  − c is −45∘ ply. An example of the balance constraint for a four layer laminate as shown in Table 1 can expressed as \( {\sum}_{j=1}^4{x}_{i, j,1}-{\sum}_{j=1}^4{x}_{i, j,3}=0 \). This equation guarantees the +45∘ and −45∘ candidates have the same number of plies in the laminate.

3.4 DamTol constraint (DTC)

A damage tolerance constraint, abbreviated as DamTol constraint, is introduced. It states that the 5∘ ply along the axial direction cannot be selected in the inner and outer layer. This manufacturing constraint is very reasonable for composite frames, because it is not easy to wind the fiber on the inner and outer surface of the tube with 5∘ fiber along the axial direction. Furthermore, a composite tube with the layer of 5∘ can easily delaminate, which should be avoided. So this constraint can be expressed as the artificial density of 5∘ candidate material in the outer surface is zero and the same as in the inner surface i.e., \( {x_{i,1, c}=0; x}_{i,{\mathrm{N}}^{\mathrm{lay}}, c}=0,\kern0.5em \left( c\in \left[{5}^{\circ}\right]\right) \). The separated two equality constraints can be compounded as one equality constraint as (10).

The DTC constraint is defined as

$$ {x}_{i,1, c}+{x}_{i,{\mathrm{N}}^{\mathrm{lay}}, c}=0, c\in \left[{5}^{\circ}\right] $$
(10)

As an alternative strategy, the DamTol constraint can also be realized through micro-scale DMO material interpolation strategy. That is to say, the candidate materials set of the outer and inner surfaces does not contain the 5∘ candidate material. For a four layer laminate as shown in Table 1, the damage tolerance constraint can be expressed as x i , 1 , 2 + x i , 4 , 2 = 0.

3.5 Symmetry constraint (SC)

Whenever possible, the winding sequence should be symmetric about the mid-plane, which in the case of the composite tube in the present paper specifically refers to the average radius plane of the tube. There are two reasons why this guideline is representative of a good practice: (1) to uncouple bending and membrane response, and (2) to prevent warping under thermal loading. Clearly, this guideline cannot always be rigorously enforced such as in zones where thickness is tapered. However, any asymmetry existence due to manufacturing constraints should be minimized.

This constraint can be expressed as follows.

$$ {x}_{i, j, c}={x}_{i,{\mathrm{N}}^{\mathrm{lay}}- j+1, c}\kern0.5em $$
(11)

It should be noted that, to guarantee the symmetry of the layers, the fiber winding thickness is fixed at constant thickness, even though fiber winding thickness is not considered as design variable.

3.6 DMO normalization constraint (DMOnC)

As has been mentioned, in order to keep the physical meaning in the case of a mass constraint or eigenfrequency optimization, the sum of the candidate artificial materials density in the same layer should be equal to one, which should be realized layer-wise for laminated composites with multiple layers.

The DMOnC normalization constraint is expressed as

$$ {\sum}_{c=1}^{{\mathrm{N}}^{\mathrm{cand}}}{x}_{i, j, c}=1 $$
(12)

4 Mathematical formulation of the optimization problem and the structural analysis model

4.1 Mathematical formulation of the optimization problem

We consider the concurrent multi-scale optimization of composite frame structures with the objective of minimizing the structural compliance under specific manufacturing and total volume constraints. The details of the specific manufacturing constraints have been presented in Section 3. The macro-scale inner tube radius (r i ) of the circular cross-section and micro-scale artificial materials density (x i , j , c ) related to the discrete fiber winding angles are introduced as the independent design variables to realize the topology and stacking sequence optimization of the two geometrical scales simultaneously. Considering manufacturing constraints, the optimization formulation can be listed as

$$ \mathrm{Find}\kern0.75em \mathbf{X}=\left\{{r}_i,{x}_{i, j, c}\right\}\kern0.5em $$
(13)
$$ \mathrm{Min}\kern0.75em \mathrm{C}={\boldsymbol{U}}^{\mathrm{T}}\boldsymbol{KU} $$
(14)
$$ \left\{\begin{array}{c} S. T.\kern0.75em \boldsymbol{K}\left({\boldsymbol{D}}^e\left({r}_i,{x}_{i, j, c}\right)\right)\boldsymbol{U}=\boldsymbol{F}\\ {} V\left({r}_i\right)={\sum}_{i=1}^{{\mathrm{N}}^{\mathrm{tub}}}\pi \left[{t_i^{t ot}}^2+2{r}_i{t}_i^{t ot}\right]{L}_i\le \overset{-}{V}\\ {} Manufacturing\ Constraints\ \left( CC, TPR, BC, DTC, SC, DMOnC\right)\\ {}{r}_i\in \left[{r}_{min},{r}_{max}\right]\ \\ {}{x}_{i, j, c}\in \left[0,1\right]\kern1em \\ {} i=1,2,\dots, {\mathrm{N}}^{\mathrm{tub}}, j=1,2,\dots, \raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right., c=1,2,\dots, {\mathrm{N}}^{\mathrm{cand}}\end{array}\right. $$
(15)

where x i , j , c is the artificial density of DMO candidate materials, r i is the inner radius of the composite tube, and \( {t}_i^{t ot} \) is the total layer thickness of the tube. The subscripts i, j and c denote the number of tube, layer and candidate material, respectively. Ntub, Nlay and Ncand denote the total number of tubes, layers and candidate materials, respectively.\( \overline{V} \) is the allowable volume of the macro-design domain and L i is the length of the tube. r min (r min  = 0.1mm in the present paper) is a small positive value to avoid singularity of the stiffness matrix during optimization iterations. r max is the upper bound of the inner radius. As mentioned, in the optimization model, the DamTol constraint (DTC) and symmetry constraint (SC) are realized through the micro-scale DMO material interpolation strategy and the association of design variables. Because of the symmetry constraints applied on the micro-scale design variables, only half of layers are considered as design variables, and the range of number of layers is \( j=1,2,\dots, \raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2.$}\right. \)

4.2 Structural analysis of composite frame

The response of the composite frames is analyzed based on an extension of the beam finite element tool called BEam Cross section Analysis Software (BECAS) developed by Blasques and Lazarov (2012). BECAS is an analysis tool of cross sections for anisotropic and inhomogeneous beam sections with arbitrary geometry. It has been successfully used by Blasques and Stolpe (2012) and Blasques (2014) to develop the multi-material topology optimization of wind turbine blades with respect to static and frequency design. In the present paper, the BECAS analysis tool is extended to be applied to the composite frame structures combined with DMO discrete material interpolation scheme. For the detailed description about BECAS, please refer to the references (Blasques and Lazarov 2012; Blasques and Stolpe 2012; Blasques 2014).

4.3 SLP and move limit strategy

The optimization problems to solve contain many linear constraints, which can be efficiently handled using a SLP (Sequential Linear Programming) approach. Thus, SLP is applied in this paper, and the approach is implemented in the Matlab environment. Without precautions, a SLP approach is generally subject to oscillating function and design variable values, and a move limit strategy is required to accommodate inevitable oscillations. Let \( {\delta}_{r_i}^u \) and \( {\delta}_{x_{i, j, c}}^u \) denote the move limits for variables r i and x i , j , c , respectively. Let u denote the iteration number. The initial move limits are set to \( {\delta}_{r_i}^0=0.01 \) and \( {\delta}_{x_{i, j, c}}^0=0.1 \). With the optimization iteration, the macro and micro move limits are changed according to a certain criterion described below. Then the move limit strategy can be expressed as

$$ \max \left({r}_{min},{r}_i^u-{\delta}_{r_i}^u\ \right)\le {r}_i^{u+1}\le \min \left({r}_i^u+{\delta}_{r_i}^u,{r}_{max}\right)\forall i $$
(16a)
$$ \max \left(0,{x}_{i, j, c}^u-{\delta}_{x_{i, j, c}}^u\ \right)\le {x}_{i, j, c}^{u+1}\le \min \left({x}_{i, j, c}^u+{\delta}_{x_{i, j, c}}^u,1\right)\forall i, j $$
(16b)

Let O (u) denote the oscillation indicator for iteration (u) such that

$$ {O}_{r_i}^{(u)}=\frac{r_i^{u-1}-{r}_i^{u-2}}{r_i^u-{r}_i^{u-1}} $$
(17a)
$$ {O}_{x_{i, j, c}}^{(u)}=\frac{x_{i, j, c}^{u-1}-{x}_{i, j, c}^{u-2}}{x_{i, j, c}^u-{x}_{i, j, c}^{u-1}} $$
(17b)

As mentioned, the move limits \( {\delta}_{r_i}^u \) and \( {\delta}_{x_{i, j, c}}^u \) are being adjusted according to a certain criterion. The reduction or expansion of the move limits depends on the oscillation indicator. If \( {O}_{r_i}^{(u)} \) or \( {O}_{x_{i, j, c}}^{(u)} \) is less than 0, then \( {\delta}_{r_i}^u={\delta}_{r_i}^u\bullet {\beta}^2 \), \( {\delta}_{x_{i, j, c}}^u={\delta}_{x_{i, j, c}}^u\bullet {\beta}^2 \), else \( {\delta}_{r_i}^u=\raisebox{1ex}{${\delta}_{r_i}^u$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right. \), \( {\delta}_{x_{i, j, c}}^u=\raisebox{1ex}{${\delta}_{x_{i, j, c}}^u$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right. \). Here, β is the move limit expansion or recovery factor. In this work, β = 0.7 is found appropriate according to our numerical experiences.

4.4 Continuation strategy

In order to obtain discrete designs at the micro-scale, i.e., a distinct selection of one of the candidates in every layer, a continuation strategy for the penalization parameter p in (2) is adopted in this paper. The initial penalty parameter p is set as p = 1. It has been shown by Hvejsel and Lund (2011) that the value of the penalty factor p larger than p = 3 will not help too much to penalize intermediate values of the design variables. So in the present paper the power p is linearly increasing with a slope of 0.1 of every ten iterations from 1 to 3. Numerical examples show that this approach is effective.

5 Design sensitivity analysis

In order to perform gradient-based optimization, gradients should be obtained efficiently. Due to its ease of derivation and implementation, the semi-analytical method (SAM) (Lund 1994; Blasques and Stolpe 2011) is adopted instead of deriving and implementing analytical sensitivities in this work. The SAM is computationally efficient and thus often used for the sensitivity analysis of finite element models. This section only presents the compliance sensitivity analysis with respect to micro design variable x i , j , c . The sensitivity of the compliance with respect to macro-scale design variable r i can be obtained in a similar procedure. Assume the applied static loads are design independent, then the sensitivity of the objective function (i.e., the structure compliance C) in (14) with respect to the micro-scale design variable x i , j , c is given as

$$ \frac{\partial C}{\partial {x}_{i, j, c}}={\sum}_{e=1}^{{\mathrm{N}}^{\mathrm{ele}}}\left(\frac{\partial {U}_e^T}{\partial {x}_{i, j, c}}{\boldsymbol{K}}_e{\boldsymbol{U}}_e+{\boldsymbol{U}}_e^T\left(\frac{\partial {\boldsymbol{K}}_e}{\partial {x}_{i, j, c}}{\boldsymbol{U}}_e+{\boldsymbol{K}}_e\frac{\partial {\boldsymbol{U}}_e}{\partial {x}_{i, j, c}}\right)\right) $$
(18)

where U e is the displacement vector of element e. K e is the corresponding element stiffness matrix of element e . Furthermore, making use of the equilibrium conditions K U = F and assuming design independent loads, (18) can be simplified (see Bendsøe and Sigmund 2003) as

$$ \frac{\partial C}{\partial {x}_{i, j, c}}=-{\sum}_{e=1}^{{\mathrm{N}}^{\mathrm{ele}}}{\boldsymbol{U}}_e^T\frac{\partial {\boldsymbol{K}}_e}{\partial {x}_{i, j, c}}{\boldsymbol{U}}_e $$
(19)

It is possible to rewrite (19) using the element stiffness matrix given by \( {\boldsymbol{K}}_e={\int}_{\Omega^e}{\boldsymbol{B}}^{\mathrm{T}}{\boldsymbol{D}}_e\boldsymbol{B}\mathrm{d}{\Omega}^e \) where B is the strain-displacement matrix and Ωe is the volume of the e’th finite element:

$$ \frac{\partial \mathrm{C}}{\partial {x}_{i, j, c}}=-{\sum}_{e=1}^{{\mathrm{N}}^{\mathrm{ele}}}{\boldsymbol{U}}_e^T{\int}_{\Omega^e}{\boldsymbol{B}}^{\mathrm{T}}\frac{\partial {\boldsymbol{D}}_e\left({x}_{i, j, c},{r}_i\right)}{\partial {x}_{i, j, c}}\boldsymbol{B}\mathrm{d}{\Omega}^e{\boldsymbol{U}}_e $$
(20)

In the current implementation, the sensitivities \( \frac{\partial {\boldsymbol{D}}_e\left({x}_{i, j, c},{r}_i\right)}{\partial {x}_{i, j, c}} \) are determined by central differences. The SAM approach is computationally more efficient than the OFD (Overall Finite Difference) method, because the factorization of global stiffness matrix, which is the most time consuming part in the computation, is only calculated once for N design variables. In the OFD using forward differences, the stiffness matrix needs to be assembled and factored N + 1 times for N design variables. Thus the semi-analytical method is much more efficient. Then the sensitivities of \( \frac{\partial {\boldsymbol{D}}_e\left({x}_{i, j, c},{r}_i\right)}{\partial {x}_{i, j, c}} \) are calculated as

$$ \frac{\partial {\boldsymbol{D}}_e\left({x}_{i, j, c},{r}_i\right)}{\partial {x}_{i, j, c}}\approx \frac{{\boldsymbol{D}}_e\left(\left({x}_{i, j, c}+\varDelta {x}_{i, j, c},{r}_i\right)\right)-{\boldsymbol{D}}_e\left({x}_{i, j, c}-\varDelta {x}_{i, j, c},{r}_i\right)}{{2\varDelta x}_{i, j, c}} $$
(21)

where ∆x i , j , c is a small perturbation parameter of the micro-scale design variable. The sensitivity of the compliance with respect to macro-scale design variable r i can be obtained in a similar semi-analytical procedure. For each of the macro-scale design variables r i , perturbed finite element meshes are generated for the BECAS cross sectional analysis tool, and then the sensitivities \( \frac{\partial {\boldsymbol{D}}_e\left({x}_{i, j, c},{r}_i\right)}{\partial {r}_i} \) are obtained by central difference approximations. The global volume constraint in (15) is only a function of the macro radius design variables. The sensitivity of the volume with respect to the radius r i of the frame is easily obtained as

$$ \frac{\partial V\left({r}_i\right)}{\partial {r}_i}=2\uppi {t}_i^{t ot}{L}_i $$
(22)

The manufacturing constraints in the present paper are formulated as series of linear inequalities or equalities. Thus, the sensitivities of all manufacturing constraints are given explicitly and are easy to derive and implement.

6 Numerical examples

In this section, the classical 10-beam and large-scale thirty-five-beam composite frame structures have been investigated, the 10-beam frame structure is Example 1. In these two numerical examples, considering the engineering practical application, we assume every composite tube has the same number of layers i.e., Nlay = 20, and every layer has a constant thickness i.e., \( {t}_i^{t ot}/{\mathrm{N}}^{\mathrm{lay}}=0.1\mathrm{mm} \), such that the total thickness \( {t}_i^{t ot} \) is 2mm.

The fiber candidate materials are glass fiber reinforced epoxy with orthotropic properties as shown in Table 2.

Table 2 Material properties of the uni-directional glass reinforced epoxy
Full size table

In order to clearly demonstrate the optimization problem, four optimization models labeled as CMsMC1, CMsMC2, MACs and MICsMC are studied in Example 1. For CMsMC1 and CMsMC2 models, to investigate the effects of the contiguity constraint parameter CL (contiguity limit), in CMsMC1 optimization model the CL is set as CL = 1, and in CMsMC2 optimization model the CL is set as CL = 2. The optimization model of single macro-scale (tube inner radius r i ) without considering manufacturing constraints is labeled as MACs, and the optimization model of single micro-scale (candidate material density x i , j , c ) considering manufacturing constraints is labeled as MICsMC. From the above four optimization models, we can gain insight into the interaction effects of the structure and the layup of composite material, and the benefits of the concurrent multi-scale optimization.

In MACs model, fiber winding angles of all the layers are fixed at a constant angle θ i , j  = 14.6° and the initial value of the inner radius is 25 mm i.e., r init  = 25mm. The MACs model thereby has the same initial objective function as the other models. Here, rmin is the lower limit of the inner radius of the tube, and as mentioned previously we adopt r min  = 0.1mm and r max  = 0.1m in the Example 1. When the radius reaches this limit, we assume that the tube can be deleted. θ i , j is the fiber winding angle of the j’th layer in the i’th tube. In MICsMC optimization, with consideration of all the manufacturing constraints mentioned in Section 3, the fiber winding angles are considered as the design variables. r i is fixed at a constant value i.e., r i  = 25mm. The initial values of the micro-scale design variables, x i , j , c , may in principle be any number between 0 and 1, but in general the values should be chosen such that the initial weight is uniform, i.e., ω i , j , c  = ω i , j , k  (k ≠ c) for all i, j, c, k=1 , 2⋯ Ncand. In this way no candidate material is favored a priori. With consideration of the DamTol constraint, the initial outer layer values are x i , 1 , c  = 0.33, and other layer values are x i , j ≠ 1 , c  = 0.25. In the concurrent multi-scale optimization models (CMsMC1 and CMsMC2) the initial macro- and micro-scale design variables are similar with those in MACs and MICsMC, respectively.

6.1 Example 1

The loading/boundary conditions and geometric sizes with tube number are shown in Fig. 3.

Fig. 3
figure 3

10-beam composite frame structure

Full size image

With consideration of all the manufacturing constraints in Section 3, the number of design variables in every tube is 40 in CMsMC1 and CMsMC2 optimization models, for the examples presented in this paper, which contains 1 sizing design variable (r i ) and 39 candidate material density design variables (x i , j , c ). It should be noted that, considering the symmetry constraints, the number of candidate material density design variables (x i , j , c ) is \( {\left(\raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^{\ast }{\mathrm{N}}^{\mathrm{cand}} \), and the DamTol constraint is realized through micro-scale DMO material interpolation strategy. Then, the real number of micro-scale design variables is \( {\left(\raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^{\ast }{\mathrm{N}}^{\mathrm{cand}}-1 \), that is 10*4–1 = 39. Then the total number of design variables is 400 for this 10-beam example. There are 7 kinds of constraints, one is volume constraint, and the others are manufacturing constraints. The symmetry constraint is realized by the technique of design variable linking. So in each tube, there are 36 CC constraints when contiguity limit is 1, 4 TPR (10% rule) constraints, 10 DMOnC constraints and 1 BC constraint. Generally, the computational effort for optimization is non-linearly increasing as the constraint number increases. For the 10- beam example in the present study, each tube has 51 constraints leading to the total 510 constraints which will be larger for a frame composed with more beams. But for present paper’s concurrent multi-scale optimization model with considering specific manufacturing constraints, all these specific manufacturing constraints have been simplified as explicit linear constraints, and then the sensitivity of these constraints with respect to the micro-scale design variable x i , j , c will be easily and explicitly obtained. Meanwhile, the SLP optimization algorithm (Mehrotra 1992; Zhang 1998) can efficiently solve the optimization problem with linear constraints. This makes it possible to solve the concurrent multi-scale optimization model considering specific manufacturing constraints proposed in the present paper.

6.2 Optimization results of example 1

The comparison of the macro-scale optimized configurations, the value of the objective function and DMO convergence measure of the above four different optimization models are presented in Table 3. For MACs model, which only considers the inner tube radius r i as design variables, the convergence measure H ε = 0.95 given by (5) is not relevant. The iteration history is illustrated in Fig. 4. The values of objective functions C in (14) are normalized with respect to the initial objective function, and the four models have the same initial value of the objective function.

Table 3 Optimization results of 10-beam composite frame structure
Full size table
Fig. 4
figure 4

Iteration history of the objective function of Example 1

Full size image

The detailed optimal results of macro and micro-scale designs are provided in Tables 4, 5, and 6. Table 4 presents the macro-scale optimized results of the inner tube radius with the micro-scale variables fixed at θ i , j  = 14.6°. Table 5 presents the micro-scale optimization results of the MICsMC model when the macro variables are fixed at r i  = 25mm. Table 6 presents the two-scale optimization results of the CMsMC1 and CMsMC2 models. In Tables 4 and 6, the label rmin denotes that the macro radius has reached its lower limit. It is worth noting that when the radius reaches its lower limit, the layer thicknesses are still existing with very little total thickness \( {t}_i^{t ot}=2\mathrm{mm} \). Therefore, we calculate the optimum structural compliance with and without the minimum radius tubes (r = rmin) for CMsMC1, CMsMC2 and MACs models, respectively. The analysis results are shown in Table 7. The values of the compliance in the table are true values and have not been normalized with respect to the initial objective function. From Table 7 we observe that, for three kinds of optimization models, the largest difference of the compliance with and without the minimum radius tubes in the models is 1.36% of CMsMC1 model. That means the contribution from the minimum radius tubes to the overall structure stiffness is very small, and thus these minimum radius tubes can be deleted from the ground structure to realize topology optimization on macro-scale.

Table 4 The optimized radius of tubes of MACs optimization model (θ i , j  = 14.6°)
Full size table
Table 5 The detailed optimization results of MICsMC model (r i  = 25mm)
Full size table
Table 6 The detailed optimization results of CMsMC1 and CMsMC2 model of Example 1
Full size table
Table 7 Comparison of compliance values including and excluding minimum radius tubes
Full size table

6.3 Discussion of example 1

From the optimization iteration history shown in Fig. 4, with the same material volume, the objective function values of the four types of optimization model i.e., CMsMC1, CMsMC2, MACs, and MICsMC with respect to the initial values decrease by 51.15%, 56.64%, 32.41% and 28.13%, respectively. We can intuitively observe that when the minimum compliance is applied as the objective function, the values of the objective function of concurrent multi-scale optimization are significantly better than those from the single-scale optimizations. Furthermore, the structural performance improvements are approximately 24 ~ 28%. This is reasonable, because CMsMC1 and CMsMC2 models can account for the coupled effects of the macro-structure topology together with the micro-material selection. Conversely, the single-scale MACs and MICsMC models can only improve the performance of the structure from the macro- or micro-scale. Thus the interaction between the structure and material cannot be considered. In this numerical example, from the value of the objective function, the MACs and MICsMC models result in quite similar structural stiffness with completely different topologies. It should be noted specially that in the concurrent multi-scale optimization model, the CMsMC2 model can obtain a better design than that from the CMsMC1 model. This is because the contiguity limit is 2 in the CMsMC2 model, which relaxes the constraints on micro-scale design variables and enlarges the design domain compared to the CMsMC1 model.

Table 3 shows the optimized configurations of macro-structures based on the four optimization models. The CMsMC1, CMsMC2 and MACs models almost have the same optimized macroscopic structure configuration in which the design variables of tubes 4, 5, 6 and 10 have reached the lower limit of their cross-sectional radius. The optimized macro configurations comply with the loading condition from the view of structural analysis. An interesting observation is that, in CMsMC1 and CMsMC2 models, tube 8 is maintained with a small radius value, which indicates that the material distributed on the eighth tube can further improve the structural performance, while in MACs model tube 8 is deleted from the ground structure. It also reflects the impact of micro-scale design variables on macro-scale structural topology. Here it should be noted that, in MACs optimization model, the micro fiber winding angles are fixed at θ i , j  = 14.6° to guarantee the MACs model has the same initial objective function as other models. Of course, with different fixed micro fiber winding angles, the optimized macro configuration of the MACs model will be different, but it is impossible for engineers to give the optimal initial fiber winding angles directly for a complex structure which shows the necessity of an optimization model for the composite structure.

Observing the micro-scale design variables from Tables 5 and 6, only fiber winding angles of the first ten layers are listed due to the symmetry constraints adopted for the micro-scale design variables. Firstly, because the outer and inner layers do not contain the 5∘ candidate material, there is no 5∘ ply placed in the outer layer of the laminate in Tables 5 and 6. Secondly, when contiguity limit equals one (CL = 1), all arbitrary contiguity layers have different fiber winding angles, as shown in the micro-scale design variables of the MICsMC and CMsMC1 model. That means all the adjacent fiber winding angles are different. With CL = 2 in CMsMC2 model, more 5∘ ply layers are selected than in CMsMC1 and MICsMC models. CMsMC2 model relaxes the constraints on micro-scale design variables and enlarges the design domain. 5∘ ply layers are beneficial to improve the axial stiffness of the structure with respect to the loading case in the present example, then the CMsMC2 model can obtain a lower objective function value. However, the larger CL may lead to crack propagation in the laminate ultimately. So in most engineering applications the CL is settled as 2 ~ 3, especially in aerospace engineering. Finally, if without the 10% rule constraints, the 85∘ fiber winding angles may not appear. The 10% rule effectively avoids a single fiber angle to dominate excessively to make the laminate more robust in the sense that they are less susceptible to the weaknesses associated with highly orthotropic laminates.

Take the third tube as an example. Figure 5 gives the description of the different manufacturing constraints on micro-scale design variables.

Fig. 5
figure 5

Micro-scale fiber winding angle with manufacturing constraints

Full size image

6.4 Example 2

The loading/boundary conditions and geometric sizes with tube number are shown in Fig. 6, and L = 1m. Example 1 has detailed discussions on the pros and cons of the CMsMC1, CMsMC2, MACs and MICsMC models. Therefore, Example 2 only considers the multi-scale CMsMC2 model to further verify the effectiveness of the concurrent multi-scale design optimization method for composite frames considering specific manufacturing constraints.

Fig. 6
figure 6

35-beam composite frame structure

Full size image

For CMsMC2 model in the Example 2, the number of design variables in each tube is 40, which is the same with that in CMsMC2 in Example 1. Then the total number of design variables is 1400 for this 35-beam example. The symmetry constraint is realized by the technique of design variable linking. So in each tube, there are 32 CC constraints when contiguity limit is 2, 4 TPR (10% rule) constraints, 10 DMOnC constraints and 1 BC constraint. Then the number of specific manufacturing constraint is 47 in each tube, which leads to the total 1645 manufacturing constraints. Besides the upper bound of the inner radius is r max  = 0.075 m in the Example 2, all the parameters, initial value of design variables and the material properties are the same with the CMsMC2 model in Example 1.

6.5 Optimization results and discussion of example 2

The iteration history of CMsMC2 model is illustrated in Fig. 7. The value of objective function C in (14) is also normalized with respect to the initial objective function. Table 8 presents the detailed two-scale optimization results of the CMsMC2 model. Figure 8 shows the optimized macro-scale topology configuration of the CMsMC2 model.

Fig. 7
figure 7

Iteration history of the objective function of Example 2 of 35-beam composite frame structure with contiguity limit of 2

Full size image
Table 8 The detailed optimization results of the CMsMC2 model of Example 2
Full size table
Fig. 8
figure 8

Optimized topology configuration of CMsMC2 model

Full size image

From the iteration history of the objective function shown in Fig. 7, with respect to the initial values, the objective function values of CMsMC2 model has decreased by 69.87%. Figure 8 shows that the CMsMC2 model obtains a symmetrical optimized macroscopic structure configurations.

From Table 8, the micro-scale fiber winding angles are strictly following the specific manufacturing constraints for this 35-beam frame example. The detailed discussion about the manufacturing constraints is the same with that for Example 1. And we could clearly observe that, the proposed concurrent multi-scale design optimization method for composite frame is effective to solve a problem with relatively larger number of constraints.

As seen from the above discussion and summary in two examples, the proposed concurrent multi-scale optimization model for composite frames can efficiently realize the optimization on two geometrical scales and obtain better results than that from a single-scale optimization. Based on the DMO approach, some specified important manufacturing constraints have been mathematically expressed and numerically solved, and the optimization results show that the manufacturing constraints are strictly observed.

7 Conclusion

Concurrent multi-scale design optimization of composite frames is established in this paper using the Discrete Material Optimization (DMO) approach with consideration of several different manufacturing constraints. The capabilities of the proposed method are demonstrated for compliance minimization subject to a constraint of specified composite volume. Furthermore, an extensive set of design guidelines referred to as manufacturing constraints are considered in the optimization model. These manufacturing constraints are explicitly expressed as series of linear inequalities or equalities in the optimization model and efficiently solved by a SLP optimization algorithm with move limit strategy and semi-analytical sensitivity analysis. With consideration of the design guidelines, it can help to reduce the risk of structural and material failure and the complexity of the optimal design.

Numerical results show that the concurrent multi-scale optimization of composite frames can further explore the potential of macro-structure and micro-material to achieve light weight design of composite frames. The two-scale optimization model provides a new choice for the design of composite frames in aerospace and other industries. In future work, the concurrent multi-scale optimization of composite frame structures with variable cross-section, thickness and frequency constraint problem will be explored.