A new method for concurrent multi-scale design optimization of fiber-reinforced composite frames with fundamental frequency constraints

Abstract

This paper proposes an efficient methodology for concurrent multi-scale design optimization of composite frames considering specific design constraints to obtain the minimum structure cost when the fundamental frequency is considered as a constraint. To overcome the challenge posed by the strongly singular optimum and the weakness of the conventional polynomial material interpolation (PLMP) scheme, a new area/moment of inertia–density interpolation scheme, which is labeled as adapted PLMP (APLMP) is proposed. The APLMP scheme and discrete material optimization approach are employed to optimize the macroscopic topology of a frame structure and microscopic composite material selection concurrently. The corresponding optimization formulation and solution procedures are also developed and validated through numerical examples. Numerical examples show that the proposed APLMP scheme can effectively solve the singular optimum problem in the multi-scale design optimization of composite frames with fundamental frequency constraints. The proposed multi-scale optimization model for obtaining the minimum cost of structures with a fundamental frequency constraint is expected to provide a new choice for the design of composite frames in engineering applications.

1 Introduction

Concurrent multi-scale design optimization, which aims at realizing an innovative structural configuration and lightweight design through macro-scale structural topology and micro-scale material design, has been a hot topic since the pioneering work of Rodrigues et al. (2002) on hierarchical structure and material design. The hierarchical model was then extended to perform concurrent material and topology optimization of three-dimensional structures and bone tissue adaptation (Coelho et al. 2008). Liu et al. (2008) introduced a porous anisotropic material with a penalty (PAMP) model to optimize both the macro-structure and micro-material simultaneously for maximum fundamental frequency, thermo-elastic, mechanical, thermal load coupling, and multi-objective problems (Niu et al. 2009; Yan et al. (2008); ; Yan et al. 2016; Deng et al. 2013). Based on the bi-directional evolutionary structural optimization (BESO) method, Huang et al. (2013) proposed a mathematical model for simultaneous two-scale topology optimization with different objectives, including minimizing static, dynamic compliance, and maximizing the fundamental frequency (Xu and Xie 2015; Xu et al. 2018). Xia and Breitkopf (2014) presented a model for concurrent topology optimization of materials and structures using nonlinear multi-scale analysis. Recently, the concept of multi-scale design optimization has been extended to thermo-elastic lattice structures (Yan et al. 2020), porous composite materials with multi-domain microstructures (Gao et al. 2019), minimizing the sound radiation power of a vibrating structure (Xuan and Du 2019). Additionally, the isogeometric analysis (IGA) method has attracted much attention in structural topology optimization due to its advantages on meshing independence, boundary reconstruction, explicit geometrical constraints, etc. Costa et al. (2018) reformulated topology optimization of a 2D problem with solid isotropic material with penalization (SIMP) method in the non-uniform rational BSpline (NURBS). Recently, the NURBS-based SIMP method has been extended to the 3D topology optimization problem (Costa et al. 2019a, b) and minimum length scale control (Costa et al. 2019a, b). State-of-the-art researches on multi-scale design optimization of structures with cellular and porous materials were conducted by Zuo et al. (2013) and Andreasen and Sigmund (2012). For reading convenience, a list of acronyms is shown in Table 1.

Table 1 A list of the main acronyms in the paper

Laminated fibrous composite materials have been widely used, especially in aerospace, automotive, advanced shipping, and civil engineering, due to their superior material properties for high specific strength and stiffness. As an architectural material, the material properties of laminated composites can be tailored by adjusting the fiber ply parameters. Thus, many researchers have recently carried out studies on multi-scale lightweight design optimization of composite structures. The pioneering work of multi-scale design optimization of laminated fibrous composites can be traced to Stegmann and Lund (2005), who proposed a discrete material optimization (DMO) approach to realize the selection of fiber-reinforced polymers or isotropic materials for a wind turbine blade. By introducing void material into alternative materials, Duan et al. (2015) proposed an improved Heaviside penalization of discrete material optimization (HPDMO) model to realize multi-scale design optimization of laminated composite plates and shell structures. Then, the related concept had been extended to the maximum fundamental frequency (Duan et al. 2019a, b) and specific design constraints (Yan et al. 2017), which can also be mentioned as design rules or design guidelines. Alternative material interpretation schemes for DMO can be found in Bruyneel (2011) and Gao et al. (2013) using shape functions with penalization (SFP), and binary coded parameterization (BCP), respectively. In addition, some researchers investigated the minimization of the structural compliance problem of laminated composites by considering different types of macro-scale and micro-scale design variables. Such as, Ferreira et al. (2013) considered the orientation, fiber volume fraction, and cross-sectional size and shape of reinforcement fibers as the two-scale design variables, respectively. Coelho et al. (2015) considered the distribution of two materials and the fiber orientation as the micro-scale and macro-scale design variables, respectively. Sørensen et al. (2014) proposed a discrete material and thickness optimization model labeled as DMTO to realize material selection and thickness variation simultaneously. Recently, Tao et al. (2017) investigated multi-scale design optimization of a three-dimensional woven composite. By adopting DMTO, Wu et al. (2019) performed optimization of a laminated engine hood by minimizing the overall compliance. Ma et al. (2020) established a concurrent multi-scale optimization method for hybrid composite plates and shells. A state-of-the-art review and recent developments in this field can be found in the articles of Nikbakt et al. (2018) and Xu et al. (2018).

For design optimization of laminated composites, one of the problems when using fiber laying angles and thicknesses as design variables directly is the lack of convexity of the objective function. Some researchers had proposed attractive approaches to overcome the problem of non-convexity in the design optimization of laminated composites. Based on the polar formalism, Montemurro et al. (2018) proposed a multi-scale two-level design methodology, and the optimization problem is split into two sub-problems to solve hierarchically. Panettieri et al. (2019) investigated blending constraints for composite laminates in the framework of the multi-scale two-level optimization strategy. By integrating a global–local (GL) modeling approach, Izzi et al. (2020) proposed a global–local multi-scale two-level optimization strategy (MS2LOS) to study multi-scale design optimization of composite structures. Duan et al. (2019a, b) proposed a two-step optimization scheme based on equivalent stiffness parameters for forcing convexity of fiber winding angle to investigate the optimum design of composite frames. For more references about the recent progress of global optimum design optimization of laminated composites and applications, the readers can refer to Scardaoni and Montemurro (2020), Scardaoni et al. (2021), and the references therein.

Although remarkable achievements have been made for multi-scale design optimization related to macro-scale structure topology and micro-scale material design, there are still many issues for multi-scale design optimization of composite structures. Among them, numerical singularity problems, which are related to singular optimum problems with stress or frequency as constraints, have attracted much attention (Cheng and Guo 1997; Bruggi 2008; Ni et al. 2014; Yamada and Kanno 2016). In the case of stress-constrained topology optimization of discrete structures, Cheng and Guo (1997) revealed that the singular optimum is not an isolated point but the endpoint of line segments attached to the feasible domain. Similar to the case of stress-constrained topology optimization of discrete structures, Ni et al. 2014, and Yamada and Kanno (2016) pointed that if the fundamental frequency is considered as a constraint, the corresponding eigenmodes of the structure are strongly topology-dependent and may suffer a severe discontinuity. In particular, the feasible domain of the frequency constraint is composed of several disconnected subdomains because its feasible domain is separated, and the optimal global solution is located at the tip of a separate low-dimensional subdomain, which is the strong singularity phenomenon for topology optimization of composite frames.

To overcome the challenge of the strongly singular optimum when the fundamental frequency is considered as a constraint, Ni et al. (2014) proposed a polynomial material interpolation (PLMP) scheme in the form of area/moment of inertia–density interpolation to restore the connectedness of the feasible domain. Yamada and Kanno (2016) formulated the frequency constraint as a positive semidefinite constraint of a certain symmetric matrix and relaxed this constraint to make the feasible set connected. Although the multi-scale design optimization of laminated composites and singularity optimum have attracted much attention and attained significant achievements, to the best of the authors’ knowledge, there is no corresponding research on multi-scale design optimization of composite frames that considers the fundamental frequency and specific design constraints. In addition, as mentioned, the limitation of the PLMP scheme (Ni et al. 2014) is that each tube has the same value of parameter $\beta$. Thus, to ensure the accuracy of the calculation, the value of $\beta$ must be close to 1, which will reduce the accuracy of the frequency analysis and limit the lower bound of the fundamental natural frequency. This is presented in detail in Sects. 3.2–3.3. Even if some achievements have been made for the design optimization of composite frames, the strongly singular optimum for the design optimization of laminated composites remains a challenging problem. Consequently, this paper aims to propose an efficient methodology for concurrent multi-scale design optimization of composite frames by considering the fundamental frequency as a constraint. To overcome the challenge posed by the strongly singular optima and the weakness of the conventional PLMP scheme, a new area/moment of inertia–density interpolation scheme APLMP (Adapted Polynomial Material interpolation) is proposed.

The remainder of this paper is organized as follows. The mathematical formulation and concept of concurrent multi-scale optimization with frequency constraints are introduced in Sect. 2. In Sect. 3, the conventional PLMP scheme is briefly reviewed, and its improved resolution strategy is proposed based on an investigation of its basic nature. Section 4 presents the derivation of the equivalent stiffness parameters of composite beams. The DMO interpolation scheme and some solution strategies are provided in Sect. 5. Section 6 discusses the typical design constraints, sensitivity analysis, and numerical solution steps. Numerical examples of composite frames are presented and discussed in Sect. 7. Finally, Sect. 8 concludes the paper.

2 Concept of multi-scale design optimization of a composite frame and strong singularity phenomenon with the fundamental frequency constraint

To investigate the concurrent multi-scale design optimization problem of composite frames with frequency constraints and overcome the drawbacks of the conventional PLMP scheme, the mathematical formulation, and concept of concurrent multi-scale design optimization are first presented. Then, the aforementioned strong singularity phenomenon is illustrated through an academic example of a three-tube composite frame with a fixed fiber winding angle.

2.1 Concept of multi-scale design optimization of a composite frame with the fundamental frequency constraint

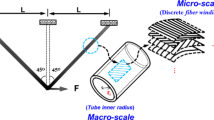
The concept of multi-scale design optimization of a composite frame is shown in Fig. 1. At the microscopic level, considering the cost and process requirements, the most commonly used set of discrete fiber ply angles is ($\left[{0}^{^\circ },\mp {45}^{^\circ },{90}^{^\circ }\right]$) in industrial applications (Rock West Composites). It should be mentioned that the multi-scale design optimization refers to geometric multi-scale in the present research, which is different from the physical multi-scale, and the microscopic level refers to the fiber winding orientation. Usually, in classical laminated theory, the fiber laying orientation is also referred to as mesoscopic. The discrete fiber winding angle selection is solved using DMO, which is briefly explained in Sect. 5.1, because the structural constituents are selected from a given set of candidate ply angles. At the macro-scale, the macro-scale artificial densities (${\chi }_{i}$, as indicated in Fig. 1) of the beam components in the APLMP scheme are considered as design variables.

Fig. 1

Schematic of multi-scale design optimization of a composite frame with a fundamental frequency constraint (adapted from Duan et al. 2020)

Uniform circular cross-sections along the axial direction and a fixed number of layers are often adopted in most composite frames. For ease of derivation and without loss of generality in the engineering application, frames made of tubes with uniform circular cross-sections and a fixed number of layers are investigated in the paper. The joints connecting the composite tubes can transfer moments and are assumed to be infinitely stiff. Composite tubes are mostly manufactured using the filament winding process (Martins et al. 2014), and then Mallick (2017) suggested that the fiber winding angles of ${0}^{^\circ }$ and ${90}^{^\circ }$ in the filament winding process should be replaced by ${5}^{^\circ }$ and ${85}^{^\circ }$, respectively. In the present paper, we consider an assembly of $\left[{5}^{^\circ },\mp {45}^{^\circ },{85}^{^\circ }\right]$ as a set of candidate composite fiber winding angles, and the fiber winding angle is assumed to be constant in a given ply. It’s obvious that the limited set of candidate composite fiber winding angles can effectively reduce the computational cost, especially when considering typical design constraints in Sect. 6.1, but the disadvantage is the reduction of microscopic design space.

2.2 Strong singularity phenomenon in topology design optimization of composite frames

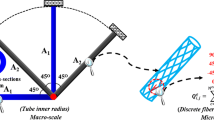
In general, the topology optimization problem is a standard mathematical programming model that can be dealt with gradient-based continuous optimization algorithms without essential difficulty. However, the following in-depth analysis reveals that the topology optimization problem with frequency actually implies the phenomenon of strong singularity, which may prevent gradient-based optimization algorithms from finding the global optimal topology. This is because the fundamental frequency constraint and the corresponding eigenmode of the structure are strongly topology-dependent and may suffer a severe discontinuity, i.e., the feasible domain of the frequency constraint is composed of several disconnected subdomains when the topology of the structure changes, which was also pointed out by Ni et al. (2014) and Yamada and Kanno (2016). In the following, an academic example of a three-tube composite frame is displayed in Fig. 2 to explicitly demonstrate the strong singularity phenomenon of the topology optimization of a composite frame. To reveal the strange singularity phenomenon, the three-tube composite frame is assumed to have a constant fiber winding angle of 0°, as shown in Fig. 2, where only the macro-scale inner tube radii (${r}_{i}$) are considered as the vibrational parameters, i.e., ${r}_{i}$ can change its value in the following numerical analysis. A similar example with an isotropic material was presented by Ni et al. (2014).

Fig. 2

A three-tube composite frame with a constant 0° fiber winding angle

It is assumed that each composite tube in Fig. 2 has the same number of layers, i.e., ${N}^{\text{lay}}=20$, and the 20 layers have identical thicknesses of 0.1 mm, i.e., ${t}_{i}^{\text{tot}}/{N}^{\text{lay}}=0.1\text{ mm}$ with a constant fiber winding angle of ${0}^{^\circ }$. ${t}_{i}^{\text{tot}}$ is the total thickness of the $i$-th tube. The fiber material is CFRE with orthotropic properties, as presented in Table 2.

Table 2 Material properties of uni-directional CFRE

As shown in Fig. 2, ${A}_{1}$ and ${A}_{2}$ are the cross-sectional areas of the middle and side tubes, respectively. The initial three tubes have the same internal radius (${r}_{i}$), fiber winding thickness, and constant fiber winding angle. Table 3 presents the change in the fundamental frequency as a function of the middle tube ${A}_{1}$ when ${A}_{2}={A}_{2}^{\text{ini}}$ is fixed. As indicated in Table 3, ${\omega }_{1}$ tends to approach a small value (0.0155 Hz) as ${\text{A}}_{1}\to 0$ (in fact, the limit of ${\omega }_{1}$ is zero).

Table 3 Change in the fundamental natural frequency of the three-tube composite frame with ${A}_{1}/{A}_{1}^{\text{ini}}$

More specifically, Fig. 3 depicts the trend and change in the structural fundamental natural frequency and the eigenmode of the three-tube composite frame in Table 3, with the reduction in the cross-sectional area of the middle tube, i.e., ${A}_{1}/{A}_{1}^{\text{ini}}$.

Fig. 3

Fundamental natural frequency of the three-tube composite frame with the reduction in ${\text{A}}_{1}/{\text{A}}_{i}^{\text{ini}}$

Further analysis of the data in Table 3 and Fig. 3 shows that the eigenmode corresponding to the fundamental natural frequency changes from an overall eigenmode to a local bending mode of the vertical tube (i.e., ${A}_{1}$), and the fundamental natural frequency decreases rapidly when ${A}_{1}\le 0.1{A}_{1}^{\text{ini}}$, as depicted in Fig. 3. However, if ${A}_{1}=0$ and ${A}_{2}={A}_{2}^{\text{ini}}$, the fundamental natural frequency of the two-tube composite frame is ${\omega }_{1}\left({A}_{1}=0, {A}_{2}={A}_{2}^{\text{ini}}\right)=152.8361 {\text{Hz}},$ as shown in the upper right corner of Fig. 3, which is much larger than 0.0155 Hz in Table 3. This means that the fundamental natural frequency is discontinuous at ${\text{A}}_{1}=0$, i.e., $\underset{{A}_{1}\to 0}{\text{lim}}{\omega }_{1}\left({A}_{1}, {A}_{2}={A}_{2}^{\text{ini}}\right)\ne {\omega }_{1}\left({A}_{1}=0, {A}_{2}={A}_{2}^{\text{ini}}\right)$.

To be more specific, Fig. 4a and b present the corresponding feasible domains with the fundamental natural frequency lower bound of $\underset{\_}{\omega }=50\text{ Hz}$ with and without zero limits for ${A}_{1}$ and ${A}_{2}$.

Fig. 4

Feasible domain of the three-tube composite frame with and without zero lower bound of the cross-sectional area

Here, the area with diagonal cross lines is the feasible domain obtained by the enumeration method throughout the design domain, and the red dashed line is the contour of the objective function. In Fig. 4a, the feasible domain is composed of three disconnected subdomains: one is a two-dimensional subdomain with diagonal cross lines where ${A}_{1}>0, {A}_{2}>0$ and the other two one-dimensional subdomains are characterized by ${A}_{1}>0, {A}_{2}=0$ and ${A}_{1}=0, {A}_{2}>0$, respectively. In Fig. 4b, a small lower bound ${A}_{i}^{\text{low}}$ is introduced into the problem formulation to replace the zero lower limit. The corresponding feasible domain is composed of only one subdomain in a two-dimensional subdomain with diagonal cross lines, where ${A}_{1}>0, {A}_{2}>0$. Hence, in Fig. 4a, there are three optimal solutions, namely, A (0, 23.40), C (113.09, 0), and B (26.83, 15.25), with the structure cost of $W$ as ${W}_{1}=0.1196 \text{kg}$, ${W}_{3}=0.2040 {\text{kg}}$, and ${W}_{2}=0.1259 {\text{kg}}$, respectively. Point A (0, 23.40) with ${W}_{1}=0.1196 {\text{kg}}$ located on the subdomain of the y-axis is the optimal global solution. The conventional gradient-based optimization algorithm can only converge to the optimal local solution of point B.

As indicated in Fig. 4, the feasible domain of the optimization problem is disconnected by several subdomains, and the optimal global solution is located at the tip of a separate low-dimensional subdomain. This is the strong singularity phenomenon for the topology optimization of composite frames. This undesirable behavior may prevent gradient-based optimization algorithms from finding optimal global topologies. Therefore, it is important to establish an efficient and rational formulation that can unify the sizing and topology optimization within the same framework when applying sizing optimization techniques to solve the topology optimization problem (Cheng and Guo 1997).

3 Improved resolution strategies for the PLMP scheme

To overcome the aforementioned challenge posed by the strong singularity for concurrent multi-scale design optimization of composite frames, an improved APLMP scheme is proposed based on PLMP (Ni et al. 2014) in this section.

3.1 Review of the PLMP scheme

According to the basic idea of restoring the continuities of the objective and constraint functions involved in the problem formulation at the critical values of the design variables (Cheng and Guo 1997; Guo and Cheng 2000); , the PLMP scheme (Ni et al. 2014) presents the following particular forms of area/moment of inertia–density interpolation schemes:

$${A}_{i}=f\left({\chi }_{i}\right){A}_{i}^{\text{ini}}$$

(1a)

$${I}_{i}=g\left({\chi }_{i}\right){I}_{i}^{\text{ini}}$$

(1b)

where ${\chi }_{i}$ is the macro-scale artificial density of the APLMP scheme, which is associated with the i-th structural component area, i.e., ${\chi }_{i}={A}_{i}/{A}_{i}^{\text{ini}}$. ${A}_{i}$ is the cross-sectional area of the $i$-th tube. ${A}_{i}^{\text{ini}}$ is the initial cross-sectional area of the i-th structural component. Because ${\text{A}}_{i}$ is a function of ${r}_{i}$, ${\chi }_{i}$ has a unique relationship with the macroscopic tube radius ${r}_{i}$. ${I}_{i}^{ini}$ is the moment of inertia of the i-th structural component when ${\chi }_{i}$ = 1. In Eqs. (1a) and (1b), $f\left({\chi }_{i}\right)$ and $g\left({\chi }_{i}\right)$ should satisfy the following:

$$\frac{g\left({\chi }_{i}\right)}{f\left({\chi }_{i}\right)}=1, {\chi }_{i}=1,$$

(2a)

$$0<\frac{g\left({\chi }_{i}\right)}{f\left({\chi }_{i}\right)}<1, 0<{\chi }_{i}<1,$$

(2b)

$${\left.\frac{g\left({\chi }_{i}\right)}{f\left({\chi }_{i}\right)}\right|}_{{\chi }_{i}=0}=\underset{{\chi }_{i}\to 0}{\text{lim}}\frac{g\left({\chi }_{i}\right)}{f\left({\chi }_{i}\right)}=C1>0, {\chi }_{i}=0.$$

(2c)

where Eqs. (2a) and (2b) guarantee the physical relationship, trends of the cross-sectional area, and moment of inertia, respectively. Equation (2c) ensures a lower limit for the local vibration frequency in the interpolation scheme. With the requirement of Eq. (2), the following forms of $f\left({\chi }_{i}\right)$ and $g\left({\chi }_{i}\right)$ are suggested:

$$f\left({\chi }_{i}\right)={\chi }_{i},$$

(3a)

$$g\left({\chi }_{i}\right)={\beta \chi }_{i}^{p}+\left(1-\beta \right){\chi }_{i}.$$

(3b)

where $0<\beta <1$ is a positive parameter, and $p$ is indexed to the moment of inertia and cross-sectional area. The idea behind the PLMP in Eq. (3) is to avoid the emergence of a very low fundamental frequency, which may correspond to the local bending mode of a single beam or a group of slender beams. Ni et al. (2014) used the frame structure of a homogeneous circular cross-section beam as an example, and the PLMP scheme was proven to be effective in solving the strong singularity phenomenon. The cross-sectional area and moment of inertia of a composite tube with a self-similar cross-section (circular or square cross-section) has the following relationship:

$${I}_{i}^{\text{ini}}=\kappa {\left({\text{A}}_{i}^{\text{ini}}\right)}^{\mu }$$

(4)

where $\kappa$ and $\mu$ are both positive real constants (e.g., $\kappa =\frac{1}{4\pi }, \mu =2$ for a circular cross-section, and $\kappa =1/12$, $\mu =2$ for a square cross-section). For the circular cross-section considered in this paper, the cross-sectional area is controlled by two variables, i.e., the internal diameter and thickness (${r}_{i}$ and ${t}_{i}^{\stackrel{\sim}{\text{tot}}}$). The winding layer thickness penalization strategy, as presented in Sect. 5.2 of Eq. (16), is used, and the thickness of the cross-section is set to change with the inner diameter to satisfy the self-similar property of Eq. (4).

3.2 Investigation of the basic nature of the PLMP scheme

This section will further explore the nature and accuracy of the PLMP scheme and proposes an improved interpolation scheme to overcome the weakness of the PLMP in terms of the accuracy of frequency analysis. First, the three-tube composite frame in Sect. 2.3, is verified for its feasible domain considering the influence of parameter $\beta$. The optimal global solution of three-tube composite frame should be the two-tube frame with the middle tube deleted (i.e., ${\text{A}}_{1}=0$).

With constant ${\text{A}}_{2}$ and decreasing ${\text{A}}_{1}$, Table 4 presents the fundamental natural frequency value for the composite three-tube frame under different values of $\beta$. Based on the results in Table 4, we can conclude that the influence of parameter $\beta$ on the fundamental natural frequency increases gradually with a decrease in ${\chi }_{1}$. As observed in the second column of Table 4, when $\beta =1$, Eq. (3b) does not change the physical relationship between the moment of inertia and the cross-sectional area. Then, if ${\chi }_{1}$ gradually decreases, the eigenmode changes from an overall vibration mode of the global frame to a local vibration of the middle tube.

Table 4 Fundamental natural frequency under different values of $\beta$

For the second row, when the parameter ${\chi }_{1}=1.0$, a change in $\beta$ does not affect the fundamental natural frequency value of the frame. For the last column, when $\beta =0.85$ and ${\chi }_{1}<0.1$, the fundamental natural frequency is not reduced with a decrease in ${\chi }_{1}$. As pointed out in Sect. 2.3, after deleting the middle tube, the fundamental natural frequency of the planar two-tube composite frame is 152.8361 Hz, which is almost the same as $\beta =0.85$. This means that the corresponding cross-sectional area can take a very small value without making the eigenmode of the fundamental natural frequency become the local vibration frequency of the middle tube.

The PLMP method changes the relationship between the original moment of inertia and the cross-sectional area of the beam. By analyzing Table 4, we can observe that by adopting the PLMP scheme, the cross-sectional area variable of the tube can reach the minimum value in the optimization without violating the fundamental frequency constraint, so that the tube is removed from the ground structure, which successfully overcomes the difficulty of the strong singularity for structural topology optimization of composite frames with a fundamental frequency constraint.

However, an important prerequisite for adopting the PLMP scheme is the accuracy of the structural frequency analysis. If the calculated error of the fundamental frequency using the PLMP scheme is relatively large, then it is meaningless to solve the problem of strong singularity. This will cause the optimized fundamental natural frequency to be less than the constraint value, so that the structure loses its robustness and reliability.

Ni et al. (2014) also mentioned one limitation of the PLMP scheme: to ensure accuracy of the calculation, the value of parameter $\beta$ must be close to 1. This is because each tube has the same value of $\beta$, which also limits the lower bound of the fundamental natural frequency. For example, if the parameter $\beta =0.99$ and the design variable ${\chi }_{1}$ = 0.001, then the base frequency constraint $\underset{\_}{\omega }$ of the optimization problem must be less than 51.0190 Hz for the present three-tube composite frame. If $\underset{\_}{\omega }$ is greater than 51.0190 Hz, the design variable ${\chi }_{1}$ cannot reach the lower limit.

Based on Table 4, when ${\chi }_{1}=1$ and $\beta =0.85$, with a decrease in design variable ${\chi }_{1}$, the calculated structural frequency is the fundamental frequency of the actual two-tube frame structure. This is because in Eq. (3), when ${\chi }_{i}=1$, the change in parameter $\beta$ does not affect the relationship between the moment of inertia and the cross-sectional area of the $i$-th composite component.

The accuracy of the frequency analysis is very important, especially when the tube design variable ${\chi }_{i}$ is not equal to 1 and does not reach the lower limit of the design variable. The three-tube composite frame is taken as an example to further explore the nature of the PLMP method, as illustrated in Fig. 5. In this figure, it is assumed that the middle tube area reaches the lower limit, i.e., ${\chi }_{1}=0.00001$. The blue curve with the inverted triangle identification is the two-tube frame structure after removing the middle tube, and the remaining three curves are the three-tube frame using the PLMP scheme with parameter $\beta$ values of 0.85, 0.95, and 0.99, respectively. The blue curve is the true frequency; thus, if the line is closer to the blue curve, the corresponding frequency analysis is more accurate.

Fig. 5

Influence of different values of $\beta$ on the fundamental frequency

As shown in Fig. 5, for the case of $\beta$= 0.85, ${\chi }_{2}=1$ is the demarcation compared with the two-tube model. When ${\chi }_{2}<1$, the fundamental frequency of the three-tube model is greater than that of the two-tube model. As ${\chi }_{2}$ decreases, the error between the two-tube and three-tube models increases in the fundamental frequency analysis using the PLMP. When ${\chi }_{2}>1$, the fundamental natural frequency of the three-tube model is less than that of the two-tube model.

For the cases of $\beta$= 0.95 and $\beta$ = 0.99, when ${\chi }_{2}$ is greater than the critical value, a flat segment appears on the fundamental frequency curve, and the fundamental natural frequency does not change with an increase in ${\chi }_{2}$. According to these two curves of $\beta$ = 0.95 and $\beta$= 0.99, the frequency value of the flat segment decreases gradually as $\beta$ increases.

Based on the fundamental frequency accuracy in Fig. 5, it can be observed that except for the flat segment, when $\beta$ is closer to 1, the fundamental frequency calculated using the PLMP scheme is closer to the two-tube structure, and the specific error tolerance is also related to the value of ${\chi }_{2}$. Therefore, to minimize the error of the fundamental frequency, the value of $\beta$ should be close to 1 to guarantee the original physical relationship. In addition, the lower limit of the frequency constraint in the optimization formulation should be below the flat segment, such as $\beta =0.99$, and $\underset{\_}{\omega }$ should be less than 51 Hz. This undoubtedly reduces the scope of application of the PLMP scheme.

3.3 Improved PLMP method

Considering the limitation of the conventional PLMP on the accuracy of frequency analysis and the limitation of the lower bound of the frequency constraint, the improved APLMP scheme is proposed as follows:

$$f\left({\chi }_{i}\right)={\chi }_{i}$$

(5a)

$$g\left({\chi }_{i}\right)={{\beta }_{i}\chi }_{i}^{p}+\left(1-{\beta }_{i}\right){\chi }_{i}$$

(5b)

The original PLMP scheme described in Eq. (3) has only one parameter $\beta$ for all beams of the entire frame, i.e., the interpolation scheme of the PLMP affects the dynamic performance of the entire structure, regardless of whether the design variable reaches the lower limit. This leads to the problem of inaccurate analysis of the fundamental natural frequency, as discussed in Sect. 3.2. The APLMP scheme presented in Eq. (5b) sets a parameter ${\beta }_{i}$ for each beam in the frame. In the current research, the parameter ${\beta }_{i}$ of each tube at the beginning of optimization has the same value of less than 1. Then, with the feedback of the optimization, the algorithm described in Eq. (7) can automatically change the value of ${\beta }_{i}$. The artificial reinforcement or weakening of the bending stiffness of some beams in the PLMP scheme is eliminated, and the error of the frequency analysis in the optimization process is reduced.

To further investigate the nature of the feasible domain, a symmetrical four-tube composite frame, as displayed in Fig. 6, is considered. The frame is divided into two groups labeled ${\text{A}}_{1}$ and ${\text{A}}_{2}$. The material properties and microstructure parameters are the same as those of the three-tube composite frame.

Fig. 6

Four-tube composite frame

Figures 7 and 8 depict the feasible domain of the four-tube composite frame using the PLMP scheme (with ${\beta }_{1}={\beta }_{2}=0.99$) and the proposed APLMP (with ${\beta }_{1}=0.99$, ${\beta }_{2}=1.0$), respectively. $\underset{\_}{\omega }=50\text{ Hz}$ is set as the lower frequency bound. In Figs. 7 and 8, the area with diagonal cross lines is the original feasible domain without any interpolation scheme, whereas that with single diagonal lines is the design domain using the PLMP or APLMP scheme.

Fig. 7

Feasible domain of the four-tube composite frame using the PLMP scheme (${\beta }_{1}={\beta }_{2}=0.99$)

Fig. 8

Feasible domain of the four-tube composite frame using the APLMP scheme (${\beta }_{1}=0.99 {\text{and}} {\beta }_{2}=1.0$)

As shown in Figs. 7 and 8, by expanding the original feasible domain without any interpolation scheme, the PLMP and the proposed APLMP obtain the optimal solution as point D (0, 21.57) with the objective function of 0.1098 and point E (0, 23.93) with the objective function of 0.1216, respectively. The real global optimum should be (0, 23.40) with a target function value of 0.1196, the D-point error is 8.19%, and the E-point error is only 1.67%, as presented in Table 5. It is obvious that the adoption of the APLMP scheme described in Eq. (5) can make the design domain of the optimization problem closer to the real one and improve the accuracy of the optimization result.

Table 5 Error of analysis results using the PLMP and APLMP schemes

During the optimization process, the value of ${\beta }_{i}$ is set the same for each tube when the optimization is started as ${\beta }_{i}^{\text{ini}}$. That value remains unchanged until the optimization reaches the first convergence and is updated based on the feedback from the optimization iteration. The convergence criterion is presented as

$${H}^{k}=\sum_{i=1}^{{N}^{\text{Tub}}}\frac{\left|{\chi }_{i}^{k}-{\chi }_{i}^{k-1}\right|}{\left|{\chi }_{i}^{\text{max}}-{\chi }_{i}^{\text{min}}\right|}\le \varepsilon ,$$

(6)

where ${\chi }_{i}^{k}$ represents the value of the i-th tube after k iterations, when the convergence criterion value ${H}^{k}$ is less than the value of $\varepsilon$, which is defined as 0.0001 in this study. When the optimization is achieved after the first convergence, the following assessments and changes are adopted in the APLMP scheme to update the parameter ${\beta }_{i}$:

$${\beta }_{i}=\left\{\begin{array}{ll} {\beta }_{i}^{\text{ini}}&\quad if {\chi }_{i}\le \gamma *{\chi }_{\text{min}}\\ { \beta }_{i}+\delta &\quad if{ \chi }_{i}>\gamma *{\chi }_{\text{min}}\end{array}\right.$$

(7)

where $\gamma$ is the lower limit tolerance coefficient, which is set as 1.5 in this study according to numerical data. During convergence, some tubes are close to the lower limit but do not fully reach it. The parameter $\gamma$ is used to determine the tolerance coefficient, which will make it easy for the optimization model to identify the needless tubes. The progressive change in parameter ${\beta }_{i}$ makes the optimization process smoother, with the upper limit of ${\beta }_{i}$ as 1 and $\delta$ set as 0.01.

4 Derivation of equivalent stiffness parameters of composite beams

One prerequisite for realizing the area/moment of the inertia–density interpolation of the APLMP scheme is to derive the equivalent stiffness of composite beams. In this research, because APLMP is a special form of area/moment of inertia–density interpolation scheme, the equivalent stiffness parameters of a composite beam composed of a circular cross-section are derived and expressed as explicit integrals of the fiber winding angles. This will be briefly presented, and for more details, the readers can refer to Duan et al. (2019a, b).

4.1 Equivalent stiffness parameters of a composite beam

A composite beam composed of a circular cross-section is depicted in Fig. 9. The joints connecting the composite tubes can transfer moments and are assumed to be infinitely stiff. In Fig. 9, R represents the distance from the center to the mid-plane, $h$ is the cross-sectional thickness, and $\rho$ is the integration variable along the thickness direction.

Fig. 9

Schematic of the composite beam with a circular cross-section (Duan et al. 2019a, b)

Using Eqs. (32, 33), the equivalent elastic modulus and shear modulus of a multi-layer laminated beam can be expressed as the integral of ${{E}_{x}}^{i,j}$ and ${{G}_{xz}}^{i,j}$ along the thickness direction (as presented in Appendix). Consequently, the equivalent elastic and shear moduli for the multi-layer laminated beam can be obtained as the layer-wise sum of ${{E}_{x}}^{i,j}$ and ${{G}_{xz}}^{i,j}$ as follows:

$${\bar{E}}_{x}^{i}={\int }_{R-h/2}^{R+h/2}{{E}_{x}}^{i,j}{\text{d}}\rho =\sum_{j=1}^{{N}^{\text{layer}}}{{E}_{x}}^{i,j}{t}_{i,j},$$

(8)

$${\bar{G}}_{xz}^{i}={\int }_{R-h/2}^{R+h/2}{{G}_{xz}}^{i,j}{\text{d}}\rho =\sum_{j=1}^{{N}^{\text{layer}}}{{G}_{xz}}^{i,j}{t}_{i,j},$$

(9)

where ${N}^{layer}$ denotes the number of ply layers and ${t}_{i,j}$ is the thickness of the j-th layer of the i-th tube. Then, the equivalent tension, bending, and torsional stiffness, i.e., ${\bar{EA} }^{i}$, ${\bar{EI} }^{i}$, and ${\bar{G{I }_{p}}}^{i}$, respectively, of the i-th tube can be expressed as

$${\bar{EA} }^{i}={\bar{E}}_{x}^{i}{A}^{i}=2\pi {\int }_{R-h/2}^{R+h/2}\rho {{E}_{x}}^{i,j}{\text{d}}\rho ,$$

(10)

$${\bar{EI} }^{i}={\bar{E}}_{x}^{i}{I}^{i}=\pi {\int }_{R-h/2}^{R+h/2}{\rho }^{3}{{E}_{x}}^{i,j}{\text{d}}\rho ,$$

(11)

and

$${\bar{G{I }_{\text{p}}}}^{i}={\bar{G}}_{xz}^{i}{{I}_{\text{p}}}^{i}=2\pi {\int }_{R-h/2}^{R+h/2}{\rho }^{3}{{G}_{xz}}^{i,j}{\text{d}}\rho ,$$

(12)

respectively, where $A$, $I$, and ${I}_{\text{p}}$ are the area, area moment of inertia, and polar moment of inertia, respectively.

5 DMO and solution strategies

5.1 Fundamental DMO theory

The fundamental theory of DMO used to perform discrete material selection is briefly introduced in this section. The DMO approach is implemented using a finite element (FE) framework. Then, the constitutive element matrix per layer ${{\varvec{Q}}}_{i,j}^{e}$ can be expressed as a weighted sum of the constitutive matrices ${{\varvec{Q}}}_{i,j,c}$ of the candidate ply angles, where the superscript e refers to “element,” and the subscripts $i$, $j$, and c refer to the i-th tube, j-th layer, and c-th candidate ply angles, respectively. In general, for multi-layer laminates, the interpolation scheme can be implemented layer-wise for all layers in all elements. The constitutive relationship for the j-th layer can be expressed as the sum of the number of candidate ply angles ${\text{N}}^{\text{cand}}$ as follows:

$${{\varvec{Q}}}_{i,j}^{e}=\sum_{c=1}^{{\text{N}}^{\text{cand}}}{\omega }_{i,j,c}{{\varvec{Q}}}_{i,j,c}$$

(13)

where ${\omega }_{i,j,c}$ is a weighting function with the bounds of 0 and 1 since no stiffness or mass matrix can contribute more than the physical material properties, and a negative contribution is physically meaningless. A generalized SIMP for multi-material interpolation scheme (Hvejsel and Lund 2011) is used in this paper to push the weighting function to either 0 or 1 to obtain a distinct material selection. Then, the weighting function can be expressed as

$${\omega }_{i,j,c}{=\left({x}_{i,j,c}\right)}^{\alpha }$$

(14)

where $\alpha$ is a penalty parameter and ${x}_{i,j,c}$ is an artificial material density of the candidate ply angles that satisfies

$$\sum_{c=1}^{{\text{N}}^{\text{cand}}}{x}_{i,j,c}=1$$

(15)

5.2 Solution strategies

To obtain discrete designs in the micro-scale, a continuation strategy for the penalization parameter $\alpha$ in Eq. (15) is adopted in this paper. The initial penalty parameter $\alpha$ is set as 1. Hvejsel and Lund (2011) showed that an $\alpha$ value larger than 3 will not contribute much to penalize the intermediate values of the design variables. Hence, $\alpha$ linearly increases with a slope of 0.5 in every 10 iterations from 1 to 3 in this study.

To realize topology optimization at the macro-structural scale and reduce the number of design variables, a linear penalization relationship between the micro winding layer thickness and macro-scale tube radius is adopted as

$${t}_{i}^{\stackrel{\sim}{\text{tot}}}=\frac{{r}_{i}}{{r}_{i}^{\text{ini}}}\times {t}_{i}^{\text{ini}},\quad i\in {N}^{\text{Tub}}\quad \text{ if}\; {r}_{i}<{r}_{i}^{\text{ini}}$$

(16)

where ${t}_{i}^{\stackrel{\sim}{\text{tot}}}$ is the layer thickness of the $i$-th tube after penalization, ${t}_{i}^{\text{ini}}$ is the initial layer thickness, and ${r}_{i}^{\text{ini}}$ is the initial inner radius of the tube. In Eq. (16), the layer thickness changes as the inner radius changes when ${r}_{i}<{r}_{i}^{\text{ini}}$. Otherwise, the layer thickness is maintained as ${t}_{i}^{\text{ini}}$. Based on the ground structure approach of topology optimization, a small ${r}_{i}$ means that the tube has a smaller contribution to the stiffness of the entire structure, so that more material can be allocated to other tubes to improve the stiffness. For more details on this strategy, the readers can refer to Duan et al. (2018, 2019).

6 Typical design constraints, sensitivity analysis, numerical solution steps, and mathematical formulation

The design constraints in Eqs. (17) and (21), labeled as $MC1 \text{to} MC6$, are briefly introduced in this section. The explicit linear equality and inequality equations for the design constraints are expressed in terms of ${x}_{i,j,c}$ in the DMO. For a more detailed explanation of the six typical design constraints of laminated fibrous composite structures, the readers can refer to Yan et al. (2017) and Duan et al. (2019a, b).

6.1 Design constraints and numerical solution steps

The first manufacturing constraint is a contiguity constraint with a contiguity limit of $\text{CL}\in \text{N}$ and is formulated as a linear inequality as follows:

$${x}_{i,j,c}+\cdots +{x}_{i,j+{\text{CL}},c}\le {\text{CL}},\quad j+{\text{CL}}\le {N}^{\text{lay}},\quad MC1$$

(17)

Any $i\in {N}^{\text{tub}}, j\in {N}^{\text{lay}},\;\text{ and }\; c\in {N}^{\text{cand}}$ should follow Eq. (17), and the loop should satisfy the dimension $j+\text{CL}\le {\text{N}}^{\text{lay}}$. For example, if a composite tube has 20 layers, i.e., ${N}^{\text{lay}}=20$, and every layer has four candidate materials, i.e., ${N}^{\text{cand}}=4$, then, the total number of contiguity constraints should be calculated as ${(N}^{\text{lay}}-\text{CL})\times {N}^{\text{cand}}=(20-1)\times 4=76$, when $\text{CL}=1$.

The second manufacturing constraint is the 10% rule, which means that a minimum of 10% of plies of each candidate angle (${5}^{^\circ },\mp {45}^{^\circ },{85}^{^\circ }$) are required. It is frequently adopted in engineering applications and is expressed as follows:

$$\sum_{j=1}^{{\text{N}}^{\text{lay}}}{x}_{i,j,c}\ge 0.1{\text{N}}^{\text{lay}}, \; MC2$$

(18)

The third manufacturing constraint is the balance constraint, which means that the angle plies (those at any angle other than ${5}^{\circ }$ and ${85}^{\circ }$) should be only in balanced pairs with the same number of ${+\uptheta }^{\circ }$ and ${-\uptheta }^{\circ }$ plies. The parameterized linear equality constraint with respect to ${x}_{i,j,c}$ can be expressed as

$$\sum_{j=1}^{{\text{N}}^{\text{lay}}}{x}_{i,j,+c}-\sum_{j=1}^{{\text{N}}^{\text{lay}}}{x}_{i,j,-c}=0, c\ne \left({5}^{\circ }\cup {85}^{\circ }\right), \; MC3$$

(19)

where ${x}_{i,j,+c}$ and ${x}_{i,j,-c}$ denote a positive and an accompanying negative angle, respectively.

The fourth manufacturing constraint is the damage tolerance constraint, which means that a ${5}^{\circ }$ ply along the axial direction cannot be selected for the inner and outer layers. This constraint can be expressed as the artificial density of ${5}^{\circ }$ candidate material in the outer surface, which is set as zero, and the same as in the inner surface, i.e., ${{x}_{i,1,c}=0; x}_{i,{\text{N}}^{\text{lay}},c}=0, \left(c\in \left[{5}^{\circ }\right]\right)$, which are combined into one equality constraint as

$${x}_{i,1,c}+{x}_{i,{\text{N}}^{\text{lay}},c}=0, c\in \left[{5}^{\circ }\right],\; MC4$$

(20)

As an alternative strategy, the $MC4$ constraint can also be realized through the micro-scale DMO interpolation strategy, which means that the candidate material set of the outer and inner surfaces does not contain a ${5}^{\circ }$ candidate material.

The fifth manufacturing constraint is the symmetry constraint, which means that the fiber winding sequence should be symmetric with respect to the mid-plane. In the case of the composite tube in this study, the mid-plane specifically refers to the average radius plane of the tube. Then, the symmetry constraint can be formulated as a linear equality:

$${x}_{i,j,c}={x}_{i,{N}^{\text{lay}}-j+1,c},\; MC5$$

(21)

The sixth manufacturing constraint ($MC6$) is the normalization constraint in Eq. (15) to maintain the physical meaning in the case of a volume constraint or eigenfrequency optimization.

6.2 Mathematical formulation of multi-scale design optimization of composite frames with frequency constraints

Considering that the fundamental natural frequency is greater than a given lower limit, i.e., $\underset{\_}{\omega }$, the concurrent multi-scale design optimization of composite frames with specific design constraints can be formulated as Eq. (22), where the structure cost is selected as the objective function.

$$\begin{array}{*{20}l} {\mathop {\min }\limits_{{\chi _{i} ,x_{{i,j,c}} }} W\left( {\chi _{i} } \right) = \sum\limits_{{i = 1}}^{{N^{{{\text{Tub}}}} }} {A_{i} } \left( {\pi \left[ {t_{i}^{{\mathop {{\text{tot}}}\limits^{{\sim } }} ^{2}} + {2r_{i}} ({\chi _{i}} ,{r_{i}}^{{{\text{ini}}}} )t_{i}^{{\mathop {{\text{tot}}}\limits^{\sim } }} } \right]} \right)L_{i} \rho } \hfill \\ {{\text{Subject to}}:\left\{ {\begin{array}{*{20}l} {K\Phi _{k} = \omega _{k}^{2} M\Phi _{k} } \\ {\omega _{1} \ge \mathop \omega \limits_{\_} } \\ {\begin{array}{*{20}l} {\chi _{i} \in \left[ {\chi _{{\min }} ,\chi _{{\max }} } \right]} \\ {A_{i} = \pi \left[ {t_{i}^{{\mathop {{\text{tot}}}\limits^{{\sim } }} ^{2}} + {2r_{i}}{t_{i}}^{{\mathop {{\text{tot}}}\limits^{\sim } }} } \right]} \\ \end{array} } \\ {x_{{i,j,c}} \in \left[ {0,1} \right]} \\ {i = 1,2, \ldots ,N^{{{\text{tub}}}} ,j = 1,2, \ldots ,N^{{{\text{lay}}}} /2,c = 1,2, \ldots ,N^{{{\text{can}}}} } \\ {{\text{Design constraints }}({\text{MC }}1{\text{ to MC}}6)} \\ \end{array} } \right.} \hfill \\ \end{array}$$

(22)

where $\text{W}\left({\chi }_{i}\right)$ is the structure cost of the composite frame; ${\chi }_{i}$ and ${x}_{i,j,c}$ are the macro-scale artificial density of the APLMP scheme, which is associated with the i-th structural component area, i.e., ${\chi }_{i}={A}_{i}/{A}_{i}^{\text{ini}}$, and micro-scale artificial material density. The subscripts i, j, and c denote the number of tubes, layers, and candidate materials, respectively; $\rho$ is the mass density of carbon fiber-reinforced epoxy (CFRE); ${t}_{i}^{\stackrel{\sim}{\text{tot}}}$ is the current total thickness after the penalization strategy; ${L}_{i}$, ${r}_{i}$, and ${A}_{i}$ are the length, inner radius, and cross-sectional area of the $i$-th tube, respectively; ${r}_{i}^{\text{ini}}$ and ${\text{A}}_{i}^{\text{ini}}$ are the initial inner radius and cross-sectional area of the i-th structural component, respectively; ${\omega }_{k}$ is the $k$-th order eigenfrequency and ${{\varvec{\Phi}}}_{k}$ is the corresponding eigenvector; ${\omega }_{1}$ is the fundamental natural frequency of the composite frame and $\underset{\_}{\omega }$ is its lower bound. $\mathbf{K}$ and ${\mathbf{M}}$ are the symmetric and positive definite stiffness and mass matrix, respectively. The ground structure approach (Bendsøe and Sigmund 2013) is adopted to optimize the topology of the composite frame. For the structure cost $\text{W}\left({\chi }_{i}\right)$, ${A}_{i}$ is the area of the circular cross-section, which is a function of ${r}_{i}$ and is derived as ${A}_{i}=\uppi \left[{{t}_{i}^{\stackrel{\sim}{\text{tot}}}}^{2}+2{r}_{i}{t}_{i}^{\stackrel{\sim}{\text{tot}}}\right]$; ${\chi }_{\text{min}}$ and ${\chi }_{\text{max}}$ are the lower and upper bounds of the artificial density of the APLMP scheme, respectively; ${N}^{\text{tub}}$, ${N}^{\text{lay}}$, and ${N}^{\text{cand}}$ denote the total number of tubes, layers, and candidate ply angles, respectively; and $MC1 \text{to} MC6$ are the design constraints, which are explained in Sect. 6.1. In the mathematical formulation of Eq. (22), because the symmetry constraints are applied to the micro-scale design variables, only half of the layers are considered, and therefore, $j=1, 2,\ldots ,{N}^{\text{lay}}/{2}$ for the macroscopic topology optimization of Eq. (22), which is in fact a formulation of size optimization. As a common practice in the ground structure approach, it is always believed that topology optimization can be achieved by setting ${\text{r}}_{\text{min}}=0$.

6.3 Design sensitivity analysis

The structure cost of Eq. (22) is a function of ${\chi }_{i}$, considering the winding layer thickness penalization strategy presented in Sect. 5.2.2. The sensitivity with respect to ${\chi }_{i}$ is given by

$$\frac{\partial {\text{W}}\left({\chi }_{i}\right)}{\partial {\chi }_{i}}=2{r}_{i}\frac{\partial {r}_{i}}{\partial {\chi }_{i}}\frac{{t}_{i}^{\text{ini}}}{{r}_{i}^{\text{ini}}}\left(\pi \frac{{t}_{i}^{\text{ini}}}{{r}_{i}^{\text{ini}}}+2\right){L}_{i}\uprho$$

(23)

where ${t}_{i}^{\text{ini}}$ and ${r}_{i}^{\text{ini}}$ are the initial total thickness and macro-scale inner tube radius, respectively. ${r}_{i}$ is a function of ${\chi }_{i}={A}_{i}/{A}_{i}^{\text{ini}}$ and ${A}_{i}=\uppi \left[{{t}_{i}^{\stackrel{\sim}{\text{tot}}}}^{2}+2{r}_{i}{t}_{i}^{\stackrel{\sim}{\text{tot}}}\right].$ The design constraints in this study are formulated as a series of linear inequalities or equalities, as presented in Sect. 6.1. Thus, the sensitivities of all design constraints are explicitly obtained without further derivation.

For the sensitivity analysis of the structural frequency constraint, the semianalytical method (SAM) (Lund 1994; Cheng and Olhoff 1993) is adopted instead of deriving and implementing analytical sensitivities because of its ease of derivation and implementation. SAM is computationally efficient and is thus often used for the sensitivity analysis of FE models. This section only presents the fundamental natural frequency sensitivity analysis with respect to ${x}_{i,j,c}$ because the derivatives of ${\chi }_{i}$ can be obtained in a similar manner. A direct approach for obtaining the eigenvalue sensitivities is to differentiate the generalized vibration eigenvalue equation without damping, i.e., $\mathbf{K}{{\varvec{\Phi}}}_{k}={\omega }_{k}^{2}{\mathbf{M}}{{\varvec{\Phi}}}_{k}$, with respect to ${x}_{i,j,c}$ as follows:

$$\frac{\partial \mathbf{K}}{\partial {x}_{i,j,c}}{{\varvec{\Phi}}}_{k}+\mathbf{K}\frac{\partial {{\varvec{\Phi}}}_{k}}{\partial {x}_{i,j,c}}=\frac{\partial {\omega }_{k}^{2}}{\partial {x}_{i,j,c}}{{\mathbf{M}}{{\varvec{\Phi}}}_{k}+\omega }_{k}^{2}\frac{\partial {\mathbf{M}}}{\partial {x}_{i,j,c}}{{\varvec{\Phi}}}_{k}+{\omega }_{k}^{2}{\mathbf{M}}\frac{\partial {{\varvec{\Phi}}}_{k}}{\partial {x}_{i,j,c}}$$

(24)

With a simple derivation, as in the study by Wittrick (1962), $\frac{\partial {\omega }_{k}^{2}}{\partial {x}_{i,j,c}}$ can be expressed as

$$\frac{\partial {\omega }_{k}^{2}}{\partial {x}_{i,j,c}}={{{\varvec{\Phi}}}_{k}}^{\text{T}}\frac{\partial \mathbf{K}}{\partial {x}_{i,j,c}}{{\varvec{\Phi}}}_{k}{-\omega }_{k}^{2}{{{\varvec{\Phi}}}_{k}}^{\text{T}}\frac{\partial {\mathbf{M}}}{\partial {x}_{i,j,c}}{{\varvec{\Phi}}}_{k}$$

(25)

In the current implementation, the sensitivities $\frac{\partial \mathbf{K}}{\partial {x}_{i,j,c}}$ and $\frac{\partial {\mathbf{M}}}{\partial {x}_{i,j,c}}$ are determined by a semianalytical central difference method. This approach has a higher computational efficiency than the overall finite difference (OFD) method because the computation of the generalized vibration eigenvalue equation with the global stiffness and mass matrices, which is the most time-consuming part in the optimization, will be performed only once for $\text{N}$ design variables. In contrast, in the OFD method, the frequency equation needs to be calculated at least $\text{N}+1$ times for $\text{N}$ design variables.

Thus, the sensitivities of $\mathbf{K}$ and ${\mathbf{M}}$ with respect to ${x}_{i,j,c}$ are obtained as

$$\frac{\partial \mathbf{K}({x}_{i,j,c})}{\partial {x}_{i,j,c}}\approx \frac{\mathbf{K}\left({x}_{i,j,c}+\text{s}\right)-\mathbf{K}\left({x}_{i,j,c}-\text{s}\right)}{2\text{s}}; \frac{\partial {\mathbf{M}}({x}_{i,j,c})}{\partial {x}_{i,j,c}}\approx \frac{{\mathbf{M}}\left({x}_{i,j,c}+\text{s}\right)-{\mathbf{M}}\left({x}_{i,j,c}-\text{s}\right)}{2\text{s}}$$

(26)

where $s$ is the step size set as $2.5\times {10}^{-6}$ and $1\times {10}^{-3}$ for ${r}_{i}$ and ${x}_{i,j,c}$, respectively, in this implementation. As ${x}_{i,j,c}$ is a weighting function of the fiber winding angles, changing ${x}_{i,j,c}$ will not affect the mass matrix, i.e., the sensitivities $\frac{\partial {\mathbf{M}}}{\partial {x}_{i,j,c}}$ are equal to 0. For higher-order eigenfrequencies sensitivity analysis method, the author can refer to Giulio and Montemurro (2020).

6.4 Process of numerical implementation

The major numerical procedures for the concurrent multi-scale design optimization of composite frames with frequency constraints based on the APLMP scheme are shown schematically in Fig. 10. The method of moving asymptotes (MMA) with default parameters suggested by (Svanberg 2007) is adopted to update the design variables.

Fig. 10

Flowchart of concurrent multi-scale design optimization of composite frames under frequency and design constraints

7 Numerical examples and discussions

In this section, two numerical examples are presented to validate the effectiveness of the proposed APLMP scheme in concurrent multi-scale design optimization of composite frames with frequency constraints.

It is assumed that each composite tube has the same number of layers, i.e., ${\text{N}}^{\text{lay}}=20$, and the 20 layers have identical thicknesses of 0.1 mm in the initial design, i.e., ${t}_{i}^{\text{tot}}/{\text{N}}^{\text{lay}}=0.1\text{ mm}$. The artificial density ${\chi }_{i}$ is associated with the i-th structural component of the area, which is a function of ${r}_{i}$. The initial value of the artificial density of the APLMP scheme is ${\chi }_{i}=1$, i.e., ${A}_{i}={A}_{i}^{\text{ini}}$, and the corresponding upper and lower limits are ${\chi }_{\text{max}}=10$ and ${\chi }_{\text{min}}=0.00001$, respectively. The contiguity limit $\text{CL}$ is set as $1$. The fiber candidate material is CFRE with orthotropic properties, as presented in Table 2. Since the equivalent stiffness parameters have been derived, the dynamic analysis of composite frames can be regarded as an isotropic material structure, the linear elastic beam element has been adopted to simulate the structural dynamic response, and the element density is 100 per meter for the two numerical examples.

7.1 Two-dimensional (2D) 10-beam composite frame

For the first example, an academic 2D 10-beam composite frame is introduced for the concurrent multi-scale design optimization of a composite frame with a frequency constraint. The initial geometric sizes, concentrated masses, and boundary conditions are shown in Fig. 11. The magnitude of each concentrated mass is 5 kg. The initial value of the inner radius is ${r}_{i}^{\text{ini}}=20\text{ mm}.$ The total numbers of design variables of the macro-scale artificial density, micro-scale artificial material density, design constraints, and frequency constraint are 10, 390 ((N^lay/2 × N^cand − 1) × 10, i.e., (10 × 4 − 1) × 10 = 390), $51\times 10$ (as presented in Sect. 6.1), and 1, respectively. The fundamental natural frequency lower bound is $70$ Hz, i.e., ${\omega }_{1}\ge 70$ Hz. The proposed APLMP scheme in Sect. 3.3 is utilized to solve the frame optimization problem with corresponding strong singularity.

Fig. 11

Ten-beam composite frame

Figures 12 and 13 and Tables 6 and 7 present the optimized topology configurations, fundamental vibration modes, and detailed optimization results of the concurrent multi-scale design optimization of the 10-beam composite frame with and without using the APLMP scheme, respectively.

Fig. 12

Optimized topology configuration of the 10-beam composite frame: a without using the APLMP scheme (optimized structure cost = 2.235 kg) and b using the APLMP scheme (optimized structure cost = 2.211 kg)

Fig. 13

Fundamental vibration mode of the 10-beam composite frame with fundamental eigenfrequencies of a 71.756 Hz and b 71.705 Hz

Table 6 Concurrent multi-scale design optimization results of the 10-beam composite frame without using the APLMP scheme and the optimized structure cost of 2.235 kg

Table 7 Concurrent multi-scale design optimization results of the 10-beam composite frame using the APLMP scheme (${\beta }_{5}$ = 0.95 and the others are ${\beta }_{i}$ = 1) and the optimized structure cost of 2.211 kg

Based on Figs. 12 and 13 and Tables 6 and 7, the following observations can be made:

• 1. Using the APLMP scheme, the 5th vertical beam in the original structure is deleted because it reaches the lower limit, which realizes the topological change in the structural configuration. Thus, we can conclude that by adopting the proposed APLMP scheme, the optimized topology shows a 9-beam configuration, which is different from the conventional optimization configuration of a 10-beam frame. In addition, the proposed APLMP scheme can successfully overcome the aforementioned strong singularity challenge.

• 2. Comparing the optimization results in Tables 6 and 7, with the exception of the 5th tube, the macroscopic optimization results of the remaining tubes change only slightly with all microscopic discrete fiber winding angles.

• 3. The objective function of the APLMP scheme (2.211 kg) is slightly smaller than that of the conventional optimization model (2.235 kg), with a reduction of 1.1% for the present simple 10-beam example.

• 4. Figure 16 presents the fundamental vibration modes and frequencies of the two optimized composite frames with 10 and 9 tubes, respectively. The corresponding fundamental frequencies are 71.756 Hz and 71.705 Hz using direct numerical simulation (DNS) in Abaqus, respectively.

• 5. Compared with the frequency analysis results of DNS, the relative errors of the frequency obtained by the present optimization model are 2.45% and 2.38%, respectively. This indicates that the APLMP scheme can provide more accurate optimization results to satisfy engineering requirements.

• 6. For the final topology optimization results, the ${\beta }_{i}$ parameters in the APLMP scheme are ${\beta }_{5}$ = 0.95 and the others are ${\beta }_{i}$ = 1, which effectively guarantee that the proposed APLMP overcomes the strong singularity difficulty and ensures accuracy of the frequency analysis.

• 7. Tables 6 and 7 indicate that all micro-scale fiber winding angles strictly follow the specific design constraints.

Figure 14 illustrates the detailed design constraints on the micro-scale design variables using the 1st tube of the APLMP scheme. For more discussion about design constraints, the readers are suggested to refer to Bailie et al. (1997), Yan et al. (2017), Duan et al. (2019a, b).

Fig. 14

Detailed design constraints of the 1st tube in the APLMP scheme

Figure 15 presents the frequency iteration history for the APLMP scheme with the 1st and 2nd eigenfrequencies, where the iteration histories of the initial 12 and the final 20 iterations are separately shown for clearer demonstration.

Fig. 15

Iteration history of first two eigenfrequencies of the 10-beam composite frame using the APLMP scheme

Generally, the trend of the fundamental natural frequency is to increase and then decrease, which is reasonable because the microscopic design variable is 0.333 or 0.25 at the initial stage with the DMO interpolation. The corresponding composite frame structural stiffness is relatively low, which results in a lower initial frequency. With the optimization, macro-variables, and micro-variables are adjusted in the direction of increasing stiffness; thus, the structural frequency increases rapidly. When the microscopic variables reach the optimal value, the fundamental frequency of the structure decreases to the lower frequency limit with the reduction in the macro-variables. It should be noted from Fig. 15 that the eigenfrequencies do not have intersections or a coincident frequency, which means that multiple eigenfrequency and model switch problems do not occur (Du and Olhoff 2007).

7.2 Investigation of 2D 174-beam composite frames

To further verify the capability of the proposed APLMP scheme for the concurrent multi-scale design optimization of a composite frame with a specified frequency constraint, 2D 174-beam composite arched frames with different arch heights $\text{H of }0$, $2$, and $4\text{ m}$ on circles with radii of 0, 26, and 14.5 m, respectively, are investigated. Figure 16 depicts the initial geometric sizes, concentrated masses, and boundary conditions. The magnitude of each concentrated mass is 500 kg. The total numbers of design variables of the macro-scale artificial density, micro-scale artificial material density, design constraints, and frequency constraint are 174, 6786 ((N^lay/2 × N^cand − 1) × 174, i.e., (10 × 4 − 1) × 174 = 6786), $51\times 174=8874$ (as presented in Sect. 6.1), and 1, respectively. The fundamental natural frequency lower bound is $7$ Hz, i.e., ${\omega }_{1}\ge 7$ Hz. Yamada and Kanno (2016) and Ohsaki et al. (1999) investigated a similar geometry isotropic frame structure to minimize the structure cost under fundamental frequency and multiple eigenvalue constraints, respectively. The initial value of the inner radius is ${r}_{i}^{\text{ini}}=80\text{ mm}$.

Fig. 16

Illustration of 174-beam composite arched frames of initial structure with different arch heights H: a $H=0\text{ m}$, b $H=2\text{ m}$, and c $H=4\text{ m}$

Figures 17 and 18 display the corresponding beam number with the arch height of $\text{H}=4\text{ m}$ as an example and the optimized topology configurations of the arched frames with $\text{H}=0$, $2$, and $4\text{ m}$.

Fig. 17

Beam numbers with arch height $\text{H}=4\text{ m}$ as an example

Fig. 18

Optimized topology configurations of the 174-beam composite arched frames with different arch heights H: a $H=0\text{ m}$, b $H=2\text{ m}$, and c $H=4\text{ m}$

Figures 19 and 20 depict the frequency constraint iteration histories for the 1st and 2nd eigenfrequencies, and the structure cost, respectively, of the 174-beam composite arched frame with $\text{H}=4\text{ m}$ as an example.

Fig. 19

Iteration history of first two eigenfrequencies of the 174-beam composite arched frame with $\text{H}=4\text{ m}$ using the APLMP scheme

Fig. 20

Iteration history of the structure cost of the 174-beam composite arched frame when $\text{H}=4\text{ m}$ using the APLMP scheme (the optimized structure cost is 481.91 kg)

Table 8 presents the concurrent multi-scale optimized results (i.e., macroscopic radius r_i and microscopic fiber winding angle ${\theta }_{i,j}$) of the first and last 10 tubes of the 174-beam composite arched frame with $H=4\text{ m}$ as an example.

Table 8 Concurrent multi-scale design optimization results of the 174-beam composite arched frame with $H=4\text{ m}$ using the APLMP scheme

Based on Figs. 18, 19, 20 and Table 8, the following observations can be made:

• 1. The proposed APLMP scheme can successfully realize concurrent multi-scale design optimization of composite frames and overcome the challenge of strongly singular optimum with frequency constraints for the large-scale design variables (174 + 6786 = 6960) and linear design constraints (8874) of the 174-beam example.

• 2. The optimized topology configurations of the 174-beam differ for different arch heights. However, the final optimized topology configurations perfectly present the best transmission path for the dynamic mechanism. For example, the left and right upper corner tubes that are away from the concentrated mass have reached the lower limit of their cross-sectional radius, and the left and right bottom tubes are relatively thicker than the others, which provides a more stable base.

• 3. Compared with the 10-tube example, the iteration history of the first two eigenfrequencies of the 174-beam composite arched frame is more oscillatory because there are more tubes that are deleted or recovered during the optimization process.

• 4. As illustrated in Fig. 20, with the height of the arched frame $\text{H}=4\text{ m}$ as an example, the structure cost decreases by 69.20% from 1564.953 to 481.91 kg.

• 5. Table 8 indicates that all the micro-scale fiber winding angles strictly follow the specific design constraints.

8 Conclusion

This paper proposes an efficient area/moment of inertia–density interpolation scheme, which is labeled as APLMP, to overcome the challenge of strong singularity when the fundamental frequency is considered as a constraint. The methodology of the conventional PLMP scheme is thoroughly explored, and the improved APLMP scheme is proposed to enhance the accuracy of frequency analysis and overcome the limitation of the frequency lower bound of the conventional PLMP. The capabilities of the proposed method are demonstrated in the structure cost minimization of composite frames by considering the fundamental natural frequency to be greater than a given lower limit and specific manufacturing issues as constraints.

Numerical examples have been presented to verify the effectiveness of the proposed APLMP scheme with large-scale design variables and design constraints using a gradient-based optimization method. It is shown that the proposed APLMP scheme is more robust and can successfully realize concurrent multi-scale design optimization of composite frames with frequency and design constraints as well as overcome the challenge of strong singularity. The proposed APLMP scheme provides a new choice for the design of composite frames in aerospace and other industries. In future work, the concurrent reliability-based multi-scale design optimization of composite frame structures with variable cross-sections, fiber winding angles, and frequency constraint will be explored.

9 Replication of Results

The raw/processed data required to reproduce these findings are available from the corresponding authors upon request.

Appendix Layer-wise constant shear beam theory

The transformed stress–strain relation of an orthotropic single lamina under the assumption of plane stress in the x–y plane without the transverse normal stress component in the structure coordinates [$x$ $y$ $z$] (see Fig. 21) can be written as

$$\left(\begin{array}{c}\begin{array}{c}{\sigma }_{x}\\ {\sigma }_{y}\\ {\sigma }_{xy}\end{array}\\ {\sigma }_{yz}\\ {\sigma }_{xz}\end{array}\right)=\left(\begin{array}{c}\begin{array}{c}{\bar{Q} }_{11}\\ {\bar{Q} }_{12}\\ {\bar{Q} }_{16}\end{array}\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}{\bar{Q} }_{12}\\ {\bar{Q} }_{22}\\ {\bar{Q} }_{26}\end{array}\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}{\bar{Q} }_{16}\\ {\bar{Q} }_{26}\\ {\bar{Q} }_{66}\end{array}\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ {\bar{Q} }_{44}\\ {\bar{Q} }_{45}\end{array}\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ {\bar{Q} }_{45}\\ {\bar{Q} }_{55}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}{\varepsilon }_{x}\\ {\varepsilon }_{y}\\ {\gamma }_{xy}\end{array}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\right)$$

(27)

where ${\bar{Q} }_{pq}$ ($p,q\in$ 1, 2, 4, 5, 6) is the transformed reduced stiffness. The reduced stiffness ${Q}_{pq}$ can be expressed as follows:

$${Q}_{11}=\frac{{E}_{11}}{1-{\nu }_{12}{\nu }_{21}}, {Q}_{22}=\frac{{E}_{22}}{1-{\nu }_{12}{\nu }_{21}}, {Q}_{12}=\frac{{{\nu }_{21}E}_{11}}{1-{\nu }_{12}{\nu }_{21}}=\frac{{{\nu }_{12}E}_{22}}{1-{\nu }_{12}{\nu }_{21}}$$

(28a)

$${Q}_{44}={G}_{23}, {Q}_{55}={G}_{13}, {Q}_{66}={G}_{12}$$

(28b)

Fig. 21

Schematic of the fiber winding angle of a composite beam with a circular cross-section

The invariant parameters ${U}_{1}-{U}_{6}$ are defined to efficiently calculate ${\bar{Q} }_{pq}$ as.

$${U}_{1}=\left(3{Q}_{11}+3{Q}_{22}+2{Q}_{12}+4{Q}_{66}\right)/8$$

(29a)

$${U}_{2}=\left({Q}_{11}-{Q}_{22}\right)/2$$

(29b)

$${U}_{3}=\left({Q}_{11}+{Q}_{22}-2{Q}_{12}-4{Q}_{66}\right)/8$$

(29c)

$${U}_{4}=\left({Q}_{11}+{Q}_{22}+6{Q}_{12}-4{Q}_{66}\right)/8$$

(29d)

$${U}_{5}=\left({Q}_{44}+{Q}_{55}\right)/2$$

(29e)

$${U}_{6}=\left({Q}_{44}-{Q}_{55}\right)/2$$

(29f)

Then, ${\bar{Q} }_{pq}$ can be expressed as.

$$\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{\bar{Q} }_{11}\\ {\bar{Q} }_{22}\\ {\bar{Q} }_{12}\end{array}\\ {\bar{Q} }_{44}\end{array}\\ {\bar{Q} }_{55}\end{array}\\ {\bar{Q} }_{45}\\ {\bar{Q} }_{66}\end{array}\\ {\bar{Q} }_{16}\end{array}\\ {\bar{Q} }_{26}\end{array}\right\}=\left[\begin{array}{ccccc}{U}_{1}& {U}_{2}& 0& {U}_{3}& 0\\ {U}_{1}& {-U}_{2}& 0& {U}_{3}& 0\\ {U}_{4}& 0& 0& {-U}_{3}& 0\\ {U}_{5}& {U}_{6}& 0& 0& 0\\ {U}_{5}& {-U}_{6}& 0& 0& 0\\ 0& 0& {-U}_{6}& 0& 0\\ \frac{1}{2}({U}_{1}{-U}_{4})& 0& 0& {-U}_{3}& 0\\ 0& 0& \frac{1}{2}{U}_{2}& 0& {U}_{3}\\ 0& 0& \frac{1}{2}{U}_{2}& 0& {-U}_{3}\end{array}\right]\left\{\begin{array}{c}1\\ {\text{cos}}\left(2{\theta }_{i,j}\right)\\ {\text{sin}}\left(2{\theta }_{i,j}\right)\\ {\text{cos}}\left(4{\theta }_{i,j}\right)\\ {\text{sin}}\left(4{\theta }_{i,j}\right)\end{array}\right\}$$

(30)

where ${\theta }_{i,j}$ is the fiber winding angle for layer $j$ of tube $i$. The layers are numbered with the inner layer as the first layer. The schematic of the fiber winding angle definition is shown in Fig. 21 for a single layer, where $+{\theta }_{i,j}$ denotes the positive fiber winding angle; $x$, $y$, and $z$ are the beam structure coordinates; and 1, 2, and 3 are the principal material coordinates.

Assuming that the laminated beam is a one-dimensional component, the coordinate $y$ is the circumferential direction along a circular cross-section beam; thus, ${\sigma }_{y}={\sigma }_{yz}={\sigma }_{xy}=0$ (Jones 2014) is applied in Eq. (27), which yields

$${\sigma }_{x}={{E}_{x}}^{i,j}{\varepsilon }_{x} {\sigma }_{xz}={{G}_{xz}}^{i,j}{\gamma }_{xz}$$

(31)

where the equivalent elastic modulus along the x-direction and shear modulus in the x–z plane of the j-th layer of the i-th tube, ${{E}_{x}}^{i,j}$ and ${{G}_{xz}}^{i,j},$ are given respectively by

$${{E}_{x}}^{i,j}={\bar{Q} }_{11}+{\bar{Q} }_{12}\frac{({\bar{Q} }_{16}{\bar{Q} }_{26}-{\bar{Q} }_{12}{\bar{Q} }_{66})}{({\bar{Q} }_{22}{\bar{Q} }_{66}-{\bar{Q} }_{26}{\bar{Q} }_{26})}+{\bar{Q} }_{16}\frac{({\bar{Q} }_{12}{\bar{Q} }_{26}-{\bar{Q} }_{16}{\bar{Q} }_{22})}{({\bar{Q} }_{22}{\bar{Q} }_{66}-{\bar{Q} }_{26}{\bar{Q} }_{26})}$$

(32)

and

$${{G}_{xz}}^{i,j}=\left({\bar{Q} }_{55}-\frac{{{\bar{Q} }_{45}}^{2}}{{\bar{Q} }_{44}}\right),$$

(33)

respectively. With the derivation above, ${{E}_{x}}^{i,j}$ and ${{G}_{xz}}^{i,j}$ are expressed as a function of the fiber winding angles with fixed orthotropic material properties.