1 Introduction

Frame structures composed of glass or carbon fiber-reinforced polymers (GFRP/CFRP) have been extensively used in aerospace vehicles [1], main load-bearing structures of satellite [2, 3], space stations [4], transmission towesr [5], wind turbines [6], etc., where large-scale space, high strength, high stiffness and light weight are emphasized. For reading convenience, the frame composed of GFRP/CFRP laminates are simply referred to as composite frame in the following parts of the presented paper.

To realize the light weight design of the structure of a composite frame, there are usually two main classes of approach: one is to adopt innovative structural configurations, and the other is to select lightweight materials. For the first class of approach, the structural optimization, especially the structural topology optimization can give an inspiration of the innovative frame structure. There is the majority of the literature focused on this topic, such as the ground structure approach (see, e.g., Refs. [7–10] and the references therein), which is adopted to realize topology optimization of the frame structure in the paper. For the second class of approach, the GFRP/CFRP is treated as structural materials and usually stacked with a number of layers, each consisting of fibers bonded together by resin to form a laminate. So the fiber ply parameters, e.g., fiber winding angle, layer thickness, and ply stacking sequence could be recognized as design variables. This characteristic offers many opportunities for designers to meet the specific design criterion in practical engineering practices, such as the optimization of compliance, stress, and natural frequency by adjusting the microscopic parameters of the laminates. To realize the optimization of the fiber ply parameters, some researchers adopted a variety of evolutionary techniques, such as the genetic algorithm (An et al. [11]), branch and bound (Todoroki and Terada [12]), simulated annealing (Deng et al. [13]), ant colony (Aymerich and Serra [14]), and particle swarm optimization (Nan et al. [15]). In addition, the lamination parameters method is also widely reported in the literature to deal with the global optimization for the ply parameters, e.g., Tsai and Pagano [16], Miki and Sugiyama [17]. Another approach inspired by the ideas of multi-phase material topology optimization has been presented by Lund and Stegmann [18] and Stegmann and Lund [19]. Recently, Bruyneel et al. [20] introduced the shape functions with a penalization (SFP) scheme. The SFP scheme is based on the shape functions of a quadrangular first order finite element, using only two natural coordinates to interpolate four material candidates. Also, Gao et al. [21] proposed a bi-valued coding parameterization (BCP) scheme, which distinguishes itself from SFP schemes in that it does not have a limit on the number of applied material candidates and has a relatively higher efficiency.

In the most of the references cited above, the structural lightweight design is focused on the single geometrical scale, macro-structural scale, or micro-material scale, respectively. In order to achieve higher structural efficiency, one may extend the model to optimize the structure and its composed material parameters concurrently. Multi-scale design optimization of structure is a recent and very active research area covering a variety of the physical problems. In one case, Rodrigues [22] adopted a hierarchical method to optimize porous materials and structures. On the other hand, Ferreira et al. [23] considered cross section of reinforcement fiber as the microscopic design variable presented a simultaneous macroscopic and microscopic design of composite structures in the structure and its material. For his work, Liu et al. [24] adopted solid isotropic material with penalization (SIMP) and porous anisotropic material penalization (PAMP) penalization approaches in micro-scale and macro-scale, respectively, to realize the concurrent topology optimization of ultra-light structures. In addiiton, Deng et al. [25] applied the concurrent optimization model to study multi-objective design of thermo-elastic structures composed of homogeneous porous material. Alternatively, Huo and Yang [26] realized the concurrent optimization of materials selection, topology, and size of hybrid steel-composite skeletal structures based on laminate component and solid isotropic microstructure withthe penalty method. For their work, Ni et al. [27] studied the integrated size and topology optimization of skeletal structures under natural frequency constraints. Another scheme was proposed by Gao and Zhang [28] to optimize the layout design of structures composed of multiphase material with the mass constraint. In addition, Niu et al. [29] presented a two-scale optimization method to realize the optimization of configurations of cellular materials with maximum structural fundamental frequency. Recently, An et al. [30, 31] implemented an adaptive genetic algorithm to realize the simultaneous optimization of stacking sequence and the cross-sectional size of composite laminate.

So considering the coupling effects between the macro-structural and micro-material, the present paper proposed a novel method to investigate the concurrent multi-scale optimization of composite frame structure in respect to minimum structural compliance with specified volume constraints. The inner radius of a circular tube’s cross-section and fiber winding angle are introduced as the independent design variables on the macro-structural and micro-material scales. In most practical applications, the candidate materials are restricted to \(\left[ {0^{{\circ }},\mp 45^{{\circ }},90^{{\circ }}} \right] \) plies which are the conventional orientations used in aeronautics (Baker et al. [32]) considering the cost requirement of manufacturing. So in this work the set of \(\left[ {0^{{\circ }},\mp 45^{{\circ }},90^{{\circ }}} \right] \) fiber winding angles are considered as the candidate materials. However, there will be the indistinct material selection problem if we adopt the classical discrete material optimization (DMO) scheme [18, 19]. Therefore, Gao and Zhang [28] in their recent works found that the normalized weights of the design variables weaken the punishment and make the elements difficult to converge to a clear choice of fiber ply angle in the discrete composite optimization. The un-convergent problem has been recognized in previous references, and several methods were proposed, but they remain insufficient. The improved Heaviside penalization discrete material optimization (HPDMO) interpolation scheme [33, 34] is adopted in this study to realize the discrete optimization of the micro design variable and to obtain a clear choice of composite material ply among the above set of candidate materials. In numerical examples, we compared the optimization results from the multi-scale (concurrently macro-structural and micro-material scales) optimization model with those of single scale optimization models focused on the macro-structural topology or micro-material scale optimization of fiber winding angle (discrete or continuous), respectively, to show its merits.

The organization of the remainder of this paper is as follows. The concurrent multi-scale optimization conception and optimization formula are described in Sect. 2. In Sect. 3, the DMO model and evaluation of convergence are introduced. Section 4 introduces the parameterization for the composite laminate frame structure, and the sensitivity analysis formulas are presented in Sect. 4.2. Section 5 presents the comparison of the single-scale and multi-scale concurrent optimization results. Finally, a section with conclusions closes the paper.

Fig. 1
figure 1

Schematic figure of the concurrent optimization of composite frame

Full size image

2 Concurrent multi-scale optimization of composite frame structure

In most cases, the structural configuration optimization and material design are often carried out independently, which generally requires several iterations, costing a lot of time and computational resources. For composite frame, the micro fiber ply parameters (i.e., fiber winding angle, layer thickness, and ply stacking sequence) and the macro structural characteristics (i.e., cross-sectional area of components and topology configuration) can definitively affect the stiffness performance of the structure. So in this paper, a concurrent multi-scale optimization model is established, which can fully consider the coupling effect of macro- and micro-scale design variables to fully use the potential of composite structures.

2.1 Concept of concurrent multi-scale optimization of composite frame

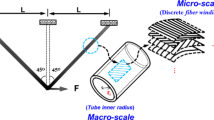
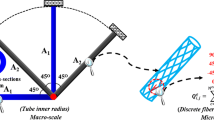
The schematic figure of concurrent multi-scale optimization of composite frame structure is shown in Fig. 1. For ease of deduction and no loss of generality, we assume the composite frame structure studied in this paper is composed of circular tubes. In macro-scale, the radius of cross-section is recognized as a macro design variable. As in classical topology, for optimization of the frame structure, the tube’s radius can be recognized as the size and topology variables at the same time. When the radius reaches its lower limit, the tube can be regarded to be deleted from the ground structure to realize the structural topology optimization. It should be pointed out specially that to avoid the heavy burden of reconstruction of the stiffness matrix, the tube with very little radius is kept in the Finite Element Model in practical implementation. So it can be restored with the optimization iterations, but in the current step the tube has little contribution to the stiffness of the frame structure since its radius is already approaching its lower bound, a very little value. In the micro-scale, the fiber winding angle (i.e., \({\theta }_{{i},{j}} \) for continuous optimization model and \({x}_{{i},{j},{k}}\) for the discrete optimization model) is recognized as the micro design variable. Considering the constraint of practical manufacturing, the fiber winding angle is assumed to be the same in the same layer. Detailed discussion about continuous or discrete micro-material models for the design variable of micro-scale fiber winding angle will be given in Sect. 2.2.

2.2 Optimization formulation with consideration of the discrete fiber winding angle

Considering the constraints of manufacturing, the fiber winding angle used in practical engineering is generally with a discrete character, which means the candidate fiber winding angles are restricted to a pre-specified set of candidate fiber winding angles, such as \(\left[ {0^{{\circ }},\mp 45^{{\circ }},90^{{\circ }}} \right] \). This character will create a difficulty for the solution of the optimization of composite frame structure with gradient based algorithms if we directly introduce the winding angle as the design variables. So some special treatment must be taken to cope with the difficulty in the optimization model. Based on the minimum structural compliance, the concurrent multi-scale optimization of the composites frame in this case can be expressed as Eqs. (1–3). The structural compliance \(\hbox {C}\) is the objective function, which can be stated as \(\textit{C}={\varvec{U}}^{\mathrm{T}}{\varvec{KU}}\), and the structural volume is recognized as a material constraint, where \({\varvec{U}}\) and \({\varvec{K}}\) are global vectors of the displacements and global stiffness matrix, respectively. The micro-scale design variable is set as the artificial candidate material density of \({x}_{{i},{j},{k}} \), where the subscripts i, j and k mean the number of tubes, layers, and the number of candidate materials, respectively. For convenience of description, we label this discrete fiber concurrent multi-scale optimization model as DCMO.

$$\begin{aligned}&\hbox {Find }{\varvec{X}}=\left\{ {{x}_{{i},{j},{k}} ,{r}_{\textit{i}} } \right\} \,{i}\in {N}^{\mathrm{tub}},{j}\in {N}^{\mathrm{lay}},{k}\in {N}^{\mathrm{can}}, \end{aligned}$$
(1)
$$\begin{aligned}&\hbox {Min}\,C={\varvec{U}}^{\mathrm{T}}{\varvec{KU}}, \end{aligned}$$
(2)
$$\begin{aligned}&\hbox {S}.\hbox {T} K\left( {{\varvec{D}}\left( {{x}_{{i},{j},{k}} ,r_{i} } \right) } \right) {\varvec{U}}={\varvec{F}}, \nonumber \\&{V}\left( {{r}_{i} }\right) =\sum \limits _{{i}=1}^{{N}^{\mathrm{tub}}} \uppi \left( {{t_{\text {tot}}^i}^{2}+2r_i t_{\text {tot}}^i } \right) L_i \leqslant {f}_{\mathrm{{v}}} \bar{{{V}}}, \nonumber \\&0\leqslant {x}_{{i},{j},{k}} \leqslant 1, \nonumber \\&0\leqslant {r}_{\mathrm{min}} \leqslant {r}_{i} \leqslant 0.1\,\hbox {m}. \end{aligned}$$
(3)

In Eq. (1), \({N}^{\mathrm{tub}}\) is the number of tubes in the frame structure. \({N}^{\mathrm{can}}\) is the number of candidate materials in each layer. \({N}^{\mathrm{lay}}\) is the number of layers in each tube, and in this paper the number of layers, i.e., \({N}^{\mathrm{lay}}\) is assumed as the same in all tubes. The macro-scale design variable \({r}_{i}\) is the inner radius of the tube. \(L_{i} \) is the length of the tube, \(t_{\text {tot}}^{i} \) is the total thickness of the tube. In the present paper, we only consider the macro radius and micro fiber winding angle as the design variables, so the fiber layer thickness is constant in the optimization process. \(\bar{{V}}\) is the entire volume of the macro-design domain, \({f}_{\mathrm{{v}}} \) is the volume fraction of materials. \({r}_{\mathrm{min}} \) is the lower limit of the tube’s radius and generally adopts a small positive value. In the presented paper, \({r}_{\mathrm{min}} =0.1\,\hbox {mm}\). We consider four kinds of fiber winding angles \(\left[ {0^{{\circ }},\mp 45^{{\circ }},90^{{\circ }}} \right] \) (Baker et al. [32]) as the candidate materials, and adopt the HPDMO interpolation scheme [33, 34] to solve the discrete micro-scale optimization problem. In Eq. (1), if \({x}_{{i},{j},{k}} =1\), indicates the i-th tube’s j-th layer chooses the k-th material from the set of candidate materials; and if \({x}_{{i},{j},{k}} =0\), the i-th tube’s j-th layer does not contain the k-th candidate material. More details about the HPDMO formulation can be found in Sect. 3.

With a few differences from the DCMO model, if the fiber winding angle (\({\theta }_{{i},{j}} )\) can change continually within the range of [\(-90^{\circ },\mathrm{}90^{\circ }]\) and be directly recognized as the design variable, then the design variable \({x}_{{i},{j},{k}}\) in Eq. (1) of the DCMO model can be changed to \({\theta }_{{i},{j}}\) in the mathematical formulation of the continuous fiber concurrent multi-scale optimization model (label as CCMO).

3 Parameterization model for discrete composite material optimization

Based on an extension of the multi-phase material topology optimization (Sigmund and Torquato [35]), Lund and Stegmann [18] and Stegmann and Lund [19] proposed a method to realize a single choice of material among a finite set of candidate materials labeled as the DMO interpolation scheme. Then the discrete optimization problem can be solved by a continuous approach with a penalty to exclude intermediate values of the artificial design variables. With this parameterization, it is possible to determine the optimal orientation along with the presence or absence of plies in each region of a composite structure. To overcome the difficulty of non-convergent elements [36] in the classical DMO model [18, 19, 37, 38] and obtain clear fiber ply angle choices, Duan et al. [33, 34] introduced the modified Heaviside penalty function (Guest et al. [39], Sigmund [36]) to replace the polynomial material interpolation formula in the classical DMO, and proposed an improved discrete material penalty model labeled as HPDMO. The HPDMO method is adopted in the presented paper to realize the micro-scale optimization of the discrete fiber winding angle.

3.1 Improved discrete material optimization interpolation scheme

To ensure the integrity of this paper and for reading convenience, the basic ideas and formula of the HPDMO model are briefly introduced in this section. For the detailed description about the HPDMO model please refer to Refs. [33, 34].

The DMO formulation is encompassed in the same parameterization and can be solved in the finite element framework. The elemental constitutive matrix \({\varvec{D}}^{{ i},{j}} \) (the superscript i and j have the same meaning as those in Eq. (1) expressed as a weighted sum of the candidate materials, which is shown as Eq.(4).

$$\begin{aligned} \varvec{D}^{{i},{j}} =\sum \limits _{k=1}^{{N}^{\mathrm{can}}} {\underbrace{\left( {{x}_{{i},{j},{k}} } \right) }_{{\omega }_{{i},{j},{k}}}}^{p}{\varvec{D}}_{{i},{j},{k}}, \end{aligned}$$
(4)

where \({\omega }_{{i},{j},{k}} \) is the weight of k-th candidate material of the i-th tube’s j-th layer, which is the function of artificial density \({x}_{{i},{j},{k}}\). p is a penalty index, which has the same function as that in SIMP [40] which is one of the most popular algorithms in the field of structural topology optimization with single material composition to push the design variable to 0 or 1. \({\varvec{D}}_{{i},{j},{k}} \) is the constitutive matrix, the subscripst i, j, k have the same meaning as those defined in Sect. 2.2. The weighting function \({\omega }_{{i},{j},{k}} \) should satisfy the following two formulas, which take a value between 0 and 1 because no matrix can contribute more than the physical material properties, and a negative contribution is physically meaningless.

$$\begin{aligned}&0\ll {\omega }_{{i},{j},{k}} \ll 1, \end{aligned}$$
(5)
$$\begin{aligned}&\sum \limits _{k=1}^{{N}^{\mathrm{can}}} {\omega }_{{i},{j},{k}} =1. \end{aligned}$$
(6)

Then, in general, for multi-layer structures, the interpolation method must be implemented layer-wise for each element, i.e., for all layers in all elements.

In this paper, the fiber winding angle is assumed to be the same in the same layer. So the total number of design variables for a composite frame structure in DCMO model is \({N}^{\mathrm{tub}}\times {N}^{\mathrm{lay}}\times {N}^{\mathrm{can}}\). Stegmann and Lund [19] extended the interpolation scheme to a multi-materials form, which considered the coupling effect between the artificial densities, and can be expressed as Eq. (7):

$$\begin{aligned} {\varvec{D}}^{{i},{j}}= & {} \sum \limits _{k=1}^{{N}^{\mathrm{can}}} \underbrace{\frac{1}{\sum _{k=1}^{{N}^{\mathrm{can}}} {\omega }_{{i},{j},{k}} }\left( {{x}_{{i},{j},{k}} } \right) ^{{p}}\prod \nolimits _{m=1}^{{N}^{\mathrm{can}}} \left[ {1-\left( {\left( {{x}_{{i},{j},{m}\ne {k}} } \right) ^{{p}}} \right) } \right] }_{{\bar{\omega }}_{{i},{j},{k}} }\nonumber \\&\times {\varvec{D}}_{{i},{j},{k}}.\nonumber \\ \end{aligned}$$
(7)

Duan [33, 34] introduced the modified Heaviside penalty function (see Refs. [36, 39] and the literature there) shown as Eq. (8) into the DMO material interpolation formula to help the design to obtain a clear choice of the candidate ply angle. The HPDMO material interpolation model can be shown in Eq. (9).

$$\begin{aligned}&{\bar{{x}}}_{{i},{j},{k}} =\hbox {e}^{-{\beta }\left( {1-{x}_{{i},{j},{k}} } \right) }-\left( {1-{x}_{{i},{j},{k}} } \right) \hbox {e}^{-{\beta }}, \end{aligned}$$
(8)
$$\begin{aligned}&{\varvec{D}}^{{i},{j}} =\sum \limits _{k=1}^{{N}^{\mathrm{can}}} \underbrace{\frac{1}{\sum _{k=1}^{{N}^{\mathrm{can}}} {\omega }_{{i},{j},{k}} }\left[ {\hbox {e}^{-{\beta }\left( {1-{v}} \right) }-\left( {1-x_{{i},{j},{k}} } \right) \hbox {e}^{-{\beta }}} \right] \times \prod \nolimits _{{m}=1}^{{N}^{\mathrm{can}}} \left[ {1+\left( {1-{x}_{{i},{j},{m}\ne {k}} } \right) \hbox {e}^{-{\beta }}-\hbox {e}^{-{\beta }\left( {1-{x}_{{i},{j},{m}\ne {k}} } \right) }} \right] }_{{{\bar{\omega }}}_{{i},{j},{k}} }{\varvec{D}}_{{i},{j},{k}}, \end{aligned}$$
(9)

where \({\bar{{x}}}_{{i},{j},{k}} \) is the artificial density after the nonlinear penalty, and \(\beta \) is the parameter of the nonlinear penalty.

3.2 Evaluation of convergence

To determine whether the optimization has converged to a satisfactory result, then a single candidate material has been chosen in a specified element and all other materials have been discarded. The convergence criterion is defined as Eq. (10). For each layer, the following inequality is evaluated according to all weight factors.

$$\begin{aligned} \varpi _{{i},{j},{k}} \geqslant {\xi }\sqrt{\varpi _{{i},{j},1}^2 +\varpi _{{i},{j},2}^2 +\cdots +\varpi _{{i},{j},{N}^{\mathrm{can}}}^2}\,, \end{aligned}$$
(10)

where \({\xi }\) is a tolerance level; typically, \({\xi }\in \left[ 0.95\ 0.99 \right] \) suggested by Stegmann and Lund [19]. If inequality (10) is satisfied for any \(\varpi _{{i},{j},{k}} \) in the layer, the layer is flagged as converged. The convergence assessment criterion \({H}_{\xi } \) is defined as the ratio of converged layers for a total number of layers: \({H}_{\xi } =\frac{{N}_\mathrm{c}^{\mathrm{l},\mathrm{tol}} }{{N}^{\mathrm{l},\mathrm{tol}}}\), where \({N}_\mathrm{c}^{\mathrm{l},\mathrm{tol}} \) is the total number of convergent layers, \({N}^{\mathrm{l},\mathrm{tol}}\) is the total number of layers. The convergent assessment criterion is denoted as \({H}_{{\xi }=0.95} \) in this study. If the tolerance level is 95.0 % and fully converges, i.e., \({H}_{{\varepsilon }=0.95} =1\), all the layers have a single weight that contributes more than 95.0 % to the Euclidian norm of the weight factors.

4 Laminate stiffness and sensitivity analysis

In this paper, the composite frame is modelled using a shell element and the classical composite laminate theory is used to model the laminate.

4.1 Laminate stiffness

According to the classical composite laminate theory, the stress in the j-th layer can be expressed in terms of the laminate middle-surface strains and curvatures as in Eq. (11):

$$\begin{aligned} \left[ {{\begin{array}{l} {{\sigma }_{x} } \\ {{\sigma }_{y} } \\ {{\sigma }_{{xy}} } \\ \end{array} }} \right] _{j} =\left[ {{\begin{array}{lll} {\bar{{\mathcal{Q}}}_{11} }&{} {\bar{{\mathcal{Q}}}_{12} }&{} {\bar{{\mathcal{Q}}}_{16} } \\ {\bar{{\mathcal{Q}}}_{12} }&{} {\bar{{\mathcal{Q}}}_{22} }&{} {\bar{{\mathcal{Q}}}_{26} } \\ {\bar{{\mathcal{Q}}}_{16} }&{} {\bar{{\mathcal{Q}}}_{26} }&{} {\bar{{\mathcal{Q}}}_{66} } \\ \end{array} }} \right] _{j} \left\{ {\left[ {{\begin{array}{l} {{\varepsilon }_{x}^0 } \\ {{\varepsilon }_{y}^0 } \\ {{\gamma }_{{xy}}^0 } \\ \end{array} }} \right] +{z}\left[ {{\begin{array}{l} {{K}_{x} } \\ {{K}_{y} } \\ {{K}_{{xy}} } \\ \end{array} }} \right] } \right\} ,\nonumber \\ \end{aligned}$$
(11)

where \({\varepsilon }_{x}^{0}, {\varepsilon }_{y}^{0}, {\gamma }_{{xy}}^{0} \) are the middle-surface strains, \({K}_{x} , {K}_{y} \) are the bending curvature of the middle-surface, and \({K}_{{xy}} \) is the twist curvature of the middle-surface. z is the integration variable in thickness. The curvatures \({K}_{x} , {K}_{y} , {K}_{{xy}} \) are constant in each layer, and not to be indicated with the subscript j. The transformed reduced stiffness \(\bar{{\mathcal{Q}}}_{pq} ,p,q\in 1,2,6\) can be given in the term of the reduced stiffness of \(\mathcal{Q}_{pq} \) as defined in Eqs.  (14) and (15). For convenience, we define laminated invariant parameters \({\varGamma }_1 -{\varGamma }_4 \), which can be expressed as Eqs. (12) and (13):

$$\begin{aligned} {\varGamma }_1= & {} {\left( {3\mathcal{Q}_{11} +3\mathcal{Q}_{22} +2\mathcal{Q}_{12} +4\mathcal{Q}_{66} } \right) }/8,\nonumber \\ {\varGamma }_2= & {} {\left( {\mathcal{Q}_{11} -\mathcal{Q}_{22} } \right) }/2,\end{aligned}$$
(12)
$$\begin{aligned} {\varGamma }_3= & {} {\left( {\mathcal{Q}_{11} +\mathcal{Q}_{22} -2\mathcal{Q}_{12} -4\mathcal{Q}_{66} } \right) }/8,\nonumber \\ {\varGamma }_4= & {} {\left( {\mathcal{Q}_{11} +\mathcal{Q}_{22} +6\mathcal{Q}_{12} -4\mathcal{Q}_{66} } \right) }/8. \end{aligned}$$
(13)

For the orthotropic material, the reduced stiffness \(\mathcal{Q}_{11}, \mathcal{Q}_{22} , \mathcal{Q}_{12} , \mathcal{Q}_{66} \) can be expressed as the function of engineering constants as Eqs. (14) and (15).

$$\begin{aligned} \mathcal{Q}_{11}= & {} \frac{{E}_{11} }{1-{\upnu }_{12} {\upnu }_{21} },\mathcal{Q}_{22} =\frac{{E}_{22} }{1-{\upnu }_{12} {\upnu }_{21} }, \end{aligned}$$
(14)
$$\begin{aligned} \mathcal{Q}_{12}= & {} \frac{{\upnu }_{21} {E}_{11} }{1-{\upnu }_{12} {\upnu }_{21} }=\frac{{\upnu }_{12} {E}_{11} }{1-{\upnu }_{12} {\upnu }_{21} }, \quad \mathcal{Q}_{66} ={G}_{12} ={G}_{31}.\nonumber \\ \end{aligned}$$
(15)

Then the transformed reduced stiffness \(\bar{{\mathcal{Q}}}_{pq} \) can easily be expressed as Eqs. (16) and (17):

$$\begin{aligned}&\left\{ {{\begin{array}{l} {\bar{{\mathcal{Q}}}_{11} } \\ {\bar{{\mathcal{Q}}}_{22} } \\ {{\begin{array}{l} {\bar{{\mathcal{Q}}}_{12} } \\ {\bar{{\mathcal{Q}}}_{66} } \\ {{\begin{array}{l} {\bar{{\mathcal{Q}}}_{16} } \\ {\bar{{\mathcal{Q}}}_{26} } \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right\} ^{{j}}=\left[ {{\begin{array}{lllll} {{\varGamma }_1 }&{} {{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 }&{} 0 \\ {{\varGamma }_1 }&{} {-{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 }&{} 0 \\ {{\varGamma }_4 }&{} {{\varGamma }_2 }&{} 0&{} {-{\varGamma }_3 }&{} 0 \\ {\frac{1}{2}\left( {{\varGamma }_1 -{\varGamma }_4 } \right) }&{} 0&{} {\frac{1}{2}{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 } \\ 0&{} 0&{} {\frac{1}{2}{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 } \\ 0&{} 0&{} {\frac{1}{2}{\varGamma }_2 }&{} 0&{} {-{\varGamma }_3 } \\ \end{array} }} \right] \nonumber \\&\qquad \qquad \quad \times \left\{ {{\begin{array}{l} 1 \\ {\cos \left( {2{\theta }_{{i},{j}} } \right) } \\ {\sin \left( {2{\theta }_{{i},{j}} } \right) } \\ {\cos \left( {4{\theta }_{{i},{j}} } \right) } \\ {\sin \left( {4{\theta }_{{i},{j}} } \right) } \\ \end{array} }} \right\} , \end{aligned}$$
(16)
$$\begin{aligned}&\varvec{\varGamma }=\left[ {{\begin{array}{lllll} {{\varGamma }_1 }&{} {{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 }&{} 0 \\ {{\varGamma }_1 }&{} {-{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 }&{} 0 \\ {{\varGamma }_4 }&{} {{\varGamma }_2 }&{} 0&{} {-{\varGamma }_3 }&{} 0 \\ {\frac{1}{2}\left( {{\varGamma }_1 -{\varGamma }_4 } \right) }&{} 0&{} {\frac{1}{2}{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 } \\ 0&{} 0&{} {\frac{1}{2}{\varGamma }_2 }&{} 0&{} {{\varGamma }_3 } \\ 0&{} 0&{} {\frac{1}{2}{\varGamma }_2 }&{} 0&{} {-{\varGamma }_3 } \\ \end{array} }} \right] . \end{aligned}$$
(17)

The matrices \({\varvec{A}}_{pq}^{i} , {\varvec{B}}_{pq}^{i} , {\varvec{D}}_{pq}^{i} \) can be expressed as Eqs. (18–20), where \(p,q\in 1,2,6\) and the superscripts have the same meaning with Eq. (4), i.e., i is the number of the tube, \({\theta }_{{i},{j}} \) is the fiber winding angle of the i-th tube’s j-th layer:

$$\begin{aligned} {A}_{pq}^{i}= & {} \sum \limits _{{j}=1}^{{N}^{\mathrm{lay}}} \left( {{z}_{j} -{z}_{{j}-1} } \right) \nonumber \\&\varvec{\varGamma }\left\{ 1\quad {\cos \left( {2{\theta }_{{i},{j}} } \right) } \quad {{ {\sin \left( {2{\theta }_{{i},{j}} } \right) }\quad {\cos \left( {4{\theta }_{{i},{j}} } \right) }\quad {\sin \left( {4{\theta }_{{i},{j}} } \right) }}} \right\} ^{\mathrm{T}},\nonumber \\&\quad p,q\in 1,2,6, \end{aligned}$$
(18)
$$\begin{aligned} {B}_{pq}^{i}= & {} \frac{1}{2}\sum \limits _{{j}=1}^{\mathrm{N}^{\mathrm{lay}}} \left( {{z}_{j}^{2}-{z}_{{j}-1}^{2}} \right) \nonumber \\&\varvec{\varGamma }\left\{ 0\quad {\cos \left( {2{\theta }_{{i},{j}} } \right) }\quad {\sin \left( {2{\theta }_{{i},{j}} } \right) } \quad {\cos \left( {4{\theta }_{{i},{j}} } \right) } \quad {\sin \left( {4{\theta }_{{i},{j}} } \right) } \right\} ^{\mathrm{T}},\nonumber \\&\quad p,q\in 1,2,6, \end{aligned}$$
(19)
$$\begin{aligned} {D}_{pq}^{i}= & {} \frac{1}{3}\sum \limits _{{j}=1}^{{N}^{\mathrm{lay}}} \left( {{z}_{j}^{3}-{z}_{{j}-1}^{3}} \right) \nonumber \\&\varvec{\varGamma }\left\{ 1\quad {\cos \left( {2{\theta }_{{i},{j}}}\right) } \quad {\sin \left( {2{\theta }_{{i},{j}} } \right) } \quad {\cos \left( {4{\theta }_{{i},{j}}} \right) }\quad {\sin \left( {4{\theta }_{{i},{j}} } \right) }\right\} ^{\mathrm{T}},\nonumber \\&\quad p,q\in 1,2,6. \end{aligned}$$
(20)

where \({A}_{pq}^{i} , {B}_{pq}^{i},\) and \({D}_{pq}^{i}\) are in-plane extensional stiffness, bending-stretching coupling stiffness, and bending stiffness matrices, respectively.

The finite element method is used to analyze the response of the composite frame subjected to a given set of loading and boundary conditions. For the optimization in the case of the continuous fiber winding angle, the elemental stiffness matrix of element n tube \({i}, {\varvec{K}}^{{i},n}\) is obtained as the integration of the constitutive matrix in the elements, as shown in Eq. (21). The element constitutive matrix can be expressed as Eq. (22).

$$\begin{aligned}&{\varvec{K}}^{{i},n}=\int \limits _{{\varOmega }^{n}} {\varvec{B}^{\mathrm{{T}}}}{\varvec{D}}_{\mathrm{{c}}}^{i} B\mathrm{{d}}{\varOmega }^{n}, \end{aligned}$$
(21)
$$\begin{aligned}&{\varvec{D}}_{\mathrm{{c}}}^{i} =\left[ {{\begin{array}{lll} {{A}_{pq}^{i} \left( {{\theta }_{{i},{j}} ,{r}_{i} } \right) }&{} {{B}_{pq}^{i} \left( {{\theta }_{{i},{j}} ,{r}_{i} } \right) } \\ {{B}_{pq}^{i} \left( {{\theta }_{{i},{j}} ,{r}_{i} } \right) }&{} {{D}_{pq}^{i} \left( {{\theta }_{{i},{j}} ,{r}_\mathrm{i} } \right) } \\ \end{array} }} \right] . \end{aligned}$$
(22)

In Eq. (21), \({\varvec{D}}_\mathrm{{c}}^{i} \) is the elemental constitutive matrix of tube i, element n. The superscript c denotes the continuous micro fiber model. \({\varvec{B}}\) is the strain–displacement matrix. The global stiffness matrix can be obtained as the sum of elemental stiffness over all \(N^\mathrm{ele}\) elements, i.e., \({\varvec{K}}=\sum _{n=1}^{{N}^{\mathrm{{ele}}}} {\varvec{K}}^{{i},n}\).

For the discrete material model, as we have mentioned in Sect. 3.1, the interpolation method must be implemented layer-wise for each element, i.e., for all layers in all elements. Then the elemental stiffness of \({A}_{pq}^{{i}}, {B}_{pq}^{{i}}\), and \({D}_{pq}^{{i}}\) should firstly be expressed as the summary of the candidate material stiffness similar as in Eq. (9) in this case. \({A}_{pq}^{{i,j,k}}, {B}_{pq}^{{i,j,k}}, {D}_{pq}^{{i,j,k}}\) are the stiffness of k-th candidate materials of the i-th tube’s j-th layer. They can be obtained through Eqs. (18)–(21). Then we can obtain the stiffness expressions of the n-th element of the i-th tube using a new discrete material model based on the HPDMO interpolation scheme as Eqs. (23)–(25):

$$\begin{aligned}&A_{pq}^{i} =\sum \limits _{{j}=1}^{{N}^{\mathrm{lay}}} \sum \limits _{{k}=1}^{{N}^{\mathrm{can}}} \underbrace{\frac{1}{\sum _{{k}=1}^{{N}^{\mathrm{can}}} {\omega }_{{ i},{j},{k}} }\left[ {\hbox {e}^{-{\beta }\left( {1-{V}} \right) }-\left( {1-x_{{i},{j},{k}} } \right) \hbox {e}^{-{\beta }}} \right] \times \prod \nolimits _{{m}=1}^{{ N}^{\mathrm{can}}} \left[ {1+\left( {1-\hbox {x}_{{i},{j},{ m}\ne {k}} } \right) \hbox {e}^{-{\beta }}-\hbox {e}^{-{\beta }\left( {1-{ x}_{{i},{j},{m}\ne {k}} } \right) }} \right] }_{{{\bar{\omega }}}_{{i},{j},{k}}} A_{pq}^{{i},{j},{k}}, \nonumber \\\end{aligned}$$
(23)
$$\begin{aligned}&B_{pq}^{i} =\sum \limits _{{j}=1}^{{N}^{\mathrm{lay}}} \sum \limits _{{k}=1}^{{N}^{\mathrm{can}}} \underbrace{\frac{1}{\sum _{{k}=1}^{{N}^{\mathrm{can}}} {\omega }_{{i},{j},{k}} }\left[ {\hbox {e}^{-{\beta }\left( {1-{V}} \right) }-\left( {1-x_{{i},{j},{k}} } \right) \hbox {e}^{-{\beta }}} \right] \times \prod \nolimits _{{m}=1}^{{ N}^{\mathrm{can}}} \left[ {1+\left( {1-x_{{i},{j},{ m}\ne {k}} } \right) \hbox {e}^{-{\beta }}-\hbox {e}^{-{\beta }\left( {1-x_{{i},{j},{m}\ne {k}} } \right) }} \right] }_{{{\bar{\omega }}}_{{i},{j},{k}} }B_{pq}^{{i},{j},{k}}, \nonumber \\\end{aligned}$$
(24)
$$\begin{aligned}&D_{pq}^{i} =\sum \limits _{{j}=1}^{{N}^{\mathrm{lay}}} \sum \limits _{{k}=1}^{{N}^{\mathrm{can}}} \underbrace{\frac{1}{\sum _{{k}=1}^{\mathrm{N}^{\mathrm{can}}} {\upomega }_{{i},{j},{k}} }\left[ {\hbox {e}^{-{\beta }\left( {1-{V}} \right) }-\left( {1-x_{{i},{j},{k}} } \right) \hbox {e}^{-{\beta }}} \right] \times \prod \nolimits _{{m}=1}^{{N}^{\mathrm{can}}} \left[ {1+\left( {1-x_{{i},{j},{m}\ne {k}} } \right) \hbox {e}^{-{\beta }}-\hbox {e}^{-{\beta }\left( {1-x_{{i},{j},{m}\ne {k}} } \right) }} \right] }_{{{\bar{\upomega }}}_{{i},{j},{k}} }D_{pq}^{{i},{j},{k}}.\nonumber \\ \end{aligned}$$
(25)

Then the structural constitutive matrix in the discrete material model can be expressed as Eq. (26):

$$\begin{aligned} {\varvec{D}}_\mathrm{{d}}^{i} =\left[ \begin{array}{ll} {A_{pq}^{i} } &{} {B_{pq}^{i} }\\ {B_{pq}^{i} } &{} {D_{pq}^{i} } \end{array}\right] , \end{aligned}$$
(26)

where \({\varvec{D}}_\mathrm{{d}}^{i} \) has the same meaning with \({\varvec{D}}_\mathrm{{c}}^{i} \), just the superscript d denotes the discrete micro fiber model. Then we can solve the linear static equilibrium: \({\varvec{KU}}={\varvec{F}}\), where \({\varvec{U}}\) and \({\varvec{F}}\) are global vectors of the displacements and external forces of the composite structure, respectively.

4.2 Sensitivity analysis of compliance optimization of composite frame

In order to perform gradient-based optimization efficiently, the design sensitivity analysis is done semi-analytically (Lund [41]; Cheng [42]). In this paper, two optimization models (DCMO and CCMO) consider two kinds of design variables, e.g., micro design variables \(\theta _{{i,j}}\) (continuous fiber winding angle) or \(x_{{i},{j},{ k}} \) (discrete fiber winding angle), and macro design variable \({r}_{{i}}\). Considering the limit of the pages of this paper, this section only presents the compliance sensitivity analysis with respect to micro design variable \(x_{{ i},{j},{k}}\). The sensitivity of the compliance with respect to \(\uptheta _{{i,j}}\) and \(r_{{i}}\) can be obtained in a similar procedure. Assumed that the applied static loads are design independent, then the sensitivity of the objective function (i.e., the structural compliance C) in Eq. (5) with respect to the micro-scale design variable \(x_{{i},{ j},{k}}\) is given as Eq. (27):

$$\begin{aligned} \frac{\partial C}{\partial x_{{i},{j},{k}} }= & {} {\sum \limits _{n=1}^{{N}^\mathrm{ele}}} \left[ {\frac{\partial {\varvec{U}}_n^\mathrm{T}}{\partial x_{{i},{j},{k}} }{\varvec{K_n}} {\varvec{U}}_n }\right. \nonumber \\&\left. {+{\varvec{U}}_n^\mathrm{T} \left( {\frac{\partial {\varvec{K_n}} }{\partial x_{{i},{j},{k}} }{\varvec{U}}_n +{\varvec{K}_{n}} \frac{\partial {\varvec{U}}_n }{\partial x_{{i},{j},{k}} }} \right) } \right] , \end{aligned}$$
(27)

where \({\varvec{U}}_n \) are the displacement of element n, and \({\varvec{K}}_n \) is the corresponding elemental stiffness of element n. Furthermore, after a further simplification, Eq. (27) can be simplified (see Ref. [7]) as Eq. (28):

$$\begin{aligned} \frac{\partial C}{\partial x_{{i},{j},{ k}}}=\sum \limits _{{ n}=1}^{{N}^\mathrm{ele}} -{\varvec{U}}_\mathrm{n}^\mathrm{T} \frac{\partial {\varvec{K}}_{n}}{\partial x_{{i},{ j},{k}}}{\varvec{U}}_{n}. \end{aligned}$$
(28)

It is possible to further extend the above equation with the elemental stiffness matrix defined in Eqs. (21) and (26). Then the derivative of the compliance with respect to the design variable \(x_{{i},{j},{k}}\) becomes as Eq. (29).

$$\begin{aligned}&\frac{\partial C}{\partial {x}_{{i},{j},{k}} }=\sum \limits _{n=1}^{{N}^\mathrm{ele}} -{\varvec{U}}_\mathrm{n}^\mathrm{T} \int _{{\varOmega }^{\mathrm{n}}} {\varvec{\mathcal{B}}}^{\mathrm{T}}\frac{\partial {\varvec{D}}_\mathrm{d}^{i} }{\partial x_{{i},{ j},{k}} }{\varvec{\mathcal{B}}}\mathrm{d}{\varOmega }^{n}{\varvec{U}}_{n}, \nonumber \\&\quad =\sum \limits _{{n}=1}^{{N}^\mathrm{ele}} -{\varvec{U}}_{n}^\mathrm{T} \int _{{\varOmega }^{n}} {\varvec{\mathcal{B}}}^{\mathrm{T}}\left[ \begin{array}{ll} {\frac{\partial A_{pq}^{i}}{\partial x_{{i},{j},{k}} }}&{} {\frac{\partial B_{pq}^{i} }{\partial x_{{i},{j},{k}} }}\\ {\frac{\partial B_{pq}^{i}}{\partial x_{{ i},{j},{k}} }} &{}{\frac{\partial D_{pq}^{i} }{\partial x_{{i},{j},{k}} }}\\ \end{array}\right] {\varvec{\mathcal{B}}}\mathrm{d}{\varOmega }^{n}{\varvec{U}}_{n}. \end{aligned}$$
(29)

As we have mentioned, in the current implementation, the sensitivities \(\frac{\partial {\varvec{D}}_\mathrm{d}^{i} }{\partial x_{{i},{j},{k}} }\) are determined semi-analytically (Lund [41]; Cheng [42]) with forward differences. Furthermore, the sensitivities of \(\frac{\partial {\varvec{D}}_\mathrm{d}^{i} }{\partial x_{{i},{j},{k}} }\) with respect to micro variables \(x_{{i},{j},{k}} \) are implemented as follows

$$\begin{aligned}&\frac{\partial {\varvec{D}}_\mathrm{d}^{i} \left( {x_{{i},{j},{ k}} ,r_{i} } \right) }{\partial x_{{i},{ j},{k}} }\nonumber \\&\quad \approx \frac{{\varvec{D}}_\mathrm{d}^{i} \left( {\left( {x_{{i},{j},{k}} ,r_{i} } \right) +s\cdot \mathbf {e}_{k} } \right) -{\varvec{D}}_\mathrm{d}^{i} \left( {x_{{i},{j},{k}} ,r_{i} } \right) }{s}, \end{aligned}$$
(30)

where s is the step size and \(\mathbf{e}_{k}\) is the unit vector of k-th candidate material. The step size s is set to \(1\times 10^{-6}\) in our implementations.

The global volume constraint in Eq. (3) is only a function of the macro radius. The sensitivity of the structural volume constraint with respect to the radius \(r_{i}\) of the frame is easily obtained as

$$\begin{aligned} \frac{\partial {V}\left( r_{i} \right) }{\partial r_{i} }=\sum \limits _{{i}=1}^{{N}^{\mathrm{tub}}} 2\uppi \left( {t_\mathrm{tot}^{i} +2r_{i} } \right) L_{i}. \end{aligned}$$
(31)

5 Numerical examples and discussions

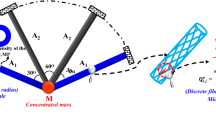
In this paper we consider a classical ten-beam composite frame as an academic example. Loading/boundary conditions and geometric sizes are shown in Fig. 2. The left part of the frame structure is fixed and the right end corner of the structure is applied with an in-plane bending moment \(\hbox { M}_\mathrm{Z} =100~\hbox {kN}\cdot \hbox {m}\) and out-plane concentrated force \(\hbox { F}_\mathrm{Z} =100~\hbox {kN}\), respectively.

Fig. 2
figure 2

Ten-beam composite frame

Full size image
Table 1 Comparison of optimized results of ten-beam composite structure
Full size table
Table 2 Concurrent multi-scale optimized results of DCMO and CCMO model
Full size table

The fiber candidate materials are glass fiber reinforced epoxy with the orthotropic properties, \(E_{11} =201~\hbox {GPa}, E_{22} =8.4~\hbox {GPa}, \upsilon _{12} =0.25, G_{12} =4.2~\hbox {GPa}, {G}_{23} =2.1~\hbox {GPa}\). For easy of computation and no loss of generality, every tube is assumed to be composed with four winding layers, and the thickness of the circular tube is assumed to be with constant value \(t_\mathrm{tot}^{i} =0.4\) mm. The inner tube radius \(r_{i} \) is chosen as the macro-scale design variable, and the value range is \(0\leqslant r_{\mathrm{min}} \leqslant r_{i} \leqslant 100~\hbox {mm}, {r}_{\mathrm{min}} \) is the lower limit of the radius, which is set as \(r_{\mathrm{min}} =0.1~\mathrm{mm}\) in this paper. For the discrete fiber winding angles, the most commonly used fiber winding angle \(\left[ {0^{{\circ }},\mathrm{}\mp 45^{{\circ }}, \mathrm{}90^{{\circ }}} \right] \) are adopted as the four candidate materials in model DCMO. The \(90^{{\circ }}\) winding angle means the fiber is along the tube axial direction. Initial values of the micro-scale artificial density design variables are \(x_{{i},{ j},{k}} =0.25\), i.e., the initial design of the candidate materials is uniformly distributed in each layer. In model CCMO, the fiber winding angle \({\theta }_{{i},{j}} \) is directly consideredto be the micro-scale design variable. The fiber winding angle range is \(-90^{{\circ }}\leqslant {\theta }_{{ i},{j}} \leqslant 90^{{\circ }}\). Here, according to the numerical experience, we suggest to use the \({\theta }_{{i},{j}} =14.3^{{\circ }}\), as the initial value of micro-scale design variables. In the \(\hbox {CCMO}_{\mathrm{{rad}}}\) optimization model, the radius of components in the composite frame is optimized with the micro fiber winding angles fixed at \({\theta }_{{i},{j}} =90^{{\circ }}\). In the two optimization models, the initial value of the macro-scale design variable is set as \(r_{i} =50~\hbox {mm}\). Then we can realize the topology optimization of frame structure through the macro-scale optimization, and realize the micro-scale material optimization through the optimization of the fiber winding angle.

In this numerical example, five kinds of optimization models have been investigated and compared. They are concurrent multi-scale optimization models with consideration of continuous or discrete fiber winding angles anda macro-structural radius as design variables, which can be denoted as CCMO and DCMO. Single-scale optimization models denoted as \(\hbox {CCMO}_\mathrm{{fib}}\) or \(\hbox {CCMO}_\mathrm{{rad}}\) are with either a consideration of continuous fiber winding angle or macro-structural radius as design variables, respectively. We also defined the single scale optimization denoted as \(\hbox {DCMO}_\mathbf{fib}\) in which only the discrete micro material optimization is carried out.

Table 1 shows the initial value of macro- and micro- variables and the comparison of the optimized compliance from the above five models, where \(x_{{i},{j},{k}} \) is the artificial candidate material density. Table 2 gives the comparison of the concurrent optimized results of DCMO and CCMO models, respectively. Figure 3 gives the iteration history of the objective function. It can be directly observed from Table 1 and Fig. 3 that the multi-scale optimization results from DCMO are obviously better than the single-scale optimization results \(\hbox {CCMO}_\mathrm{{rad}}, \hbox {DCMO}_\mathrm{{fib}}\) and \(\hbox {CCMO}_\mathrm{{fib}}\), with a decrease of 41.94 %, 33.98 % and 32.63 %, respectively. It fully reflects the advantages of concurrent multi-scale optimization of the composite frame. It also can give a reasonable explanation from the point of view of a wider design domain in the concurrent optimization. The concurrent multi-scale optimization sufficiently takes into account the coupling effects of the macro-structure and micro-material to maximize the potential of composite frame structures. From the comparison with other three single-scale optimization models in the optimization iteration history of Fig. 3, DCMO model can give better optimization results with the same or less iteration steps. The convergence rate in Table 1 shows that the micro fiber winding angles are completely convergent in the DCMO model with a HPDMO interpolation scheme.

While, if we compare the CCMO and the DCMO, we can find that the structural compliance from the CCMO model decreases further by 10.63 %, i.e., the averaged structural stiffness is increased by 10.63 %. This is because the candidate winding fiber angles are limited within \(\left[ {0^{{\circ }},\mp 45^{{\circ }}, 90^{{\circ }}} \right] \) in the DCMO model. This actually forced a restraint on the design variables, thus reducing the design optimization space of DCMO model on the micro-scale and led to a relatively higher structural compliance. However, it should be especially pointed out that the optimal result from the DCMO model can be manufactured with a relatively lower cost.

Furthermore, as observed from the following Fig. 4a, b, the multi-scale optimization models DCMO and CCMO can give the consistent optimized configurations in the macro-scale. For example, the tubes 7, 9, and 10 have nearly reach the lower limit of the macro design variable and can be regarded as deleted from the original ground structure. It should be pointed out that, in the DCMO model, the micro fiber winding angles are restricted in a specific candidate angle set, which led to the macro- and micro- design variables than cannot be freely coupled, and, thus, the tube’s number 7, 9, and 10 do not fully reach the lower limit (however, they are much lower than the cross-sectional areas of other tubes in the optimized structure). The details of the macro-scale radius can be found in Table 2.

Fig. 3
figure 3

Iteration history of objective function

Full size image
Fig. 4
figure 4

Optimized configurations and objective functions of DCMO and CCMO model. a DCMO, OBJ=135617.20. b CCMO, OBJ=121204.87

Full size image

Then from the point view of the micro fiber winding angle, the tubes of the optimal composite frame can be divided into 4 groups denoted as G1–G4 with different representative colours. The G1 group contains tubes 1 and 3, the G2 group has tubes 2, 4, 7, 8, 10, the G3 group contains tubes 5, 6, and the G4 group contains tube 9.

The tubes in the same group share the similar micro fiber winding properties in the two concurrent optimization models. As shown in Table 2, the fiber winding angles of the tubes in G1 from the DCMO model are all \(90^{{\circ }}\), and the optimized winding angles of the inner and outer layers in G1 are \(89.62^{{\circ }}\) (tube 1), \(88.58^{{\circ }}\) (tube 1), \(89.89^{{\circ }}\) (tube 3), \(89.47^{{\circ }}\) (tube 3) in the CCMO model, which can be rounded to approximately \(90^{{\circ }}\). The fiber winding angles of the middle two layers in G1 are \(74.91^{{\circ }}\) (tube 1), \(72.47^{{\circ }}\) (tube 1), \(70.56^{{\circ }}\) (tube 3), and \(71.78^{{\circ }}\) (tube 3), which are close to the \(90^{{\circ }}\) in CCMO model. G2 and G3 also have similar data. Only G4 (i.e., tube 9) does not have this similarity. But this tube has achieved the lower limit of the macro design variable, which means it is actually deleted from the initial ground structure and has little influence on the overall structural stiffness. So from the above analysis, we can see that the optimal fiber winding angle in DCMO and CCMO models is almost consistent, which can verify the correctness and reliability of the DCMO model and its optimized results to some extent, Table 3.

Table 3 Macro-scale optimized results of \(\hbox {CCMO}_\mathrm{{rad}}\) model
Full size table
Table 4 Optimized results of \(\hbox {DCMO}_\mathbf{fib}\) and \(\hbox {CCMO}_\mathrm{{fib}}\) models
Full size table

When we compare the optimization results from Figs. 4a and  6, we can find the structural compliance from the DCMO model is much lower than that from the \(\hbox {CCMO}_\mathrm{{rad}}\) model. The configurations of macro structure are different. In the \(\hbox {CCMO}_\mathrm{{rad}}\) optimization model, the radius of components in the composite frame is optimized with the micro fiber winding angles fixed at \({\theta }_{{i},{j}} =90^{{\circ }}\). Then we can conclude that the optimized macro configuration of the \(\hbox {CCMO}_\mathrm{{rad}}\) will be different with the different fixed micro fiber winding angles. But it is impossible for engineers to give the optimal initial fiber winding angles for a complex composite frame before the optimization. So this actually reflects the significance of the concurrent multi-scale optimization of the composite frame, which fully considers the coupling effect of the structural configuration and material design, thereby saving a great deal of design iterations and computational resources. From the comparison of Figs. 4a and 6, Tubes 7, 10 have reached the lower limit of the macro design variable in both the figures, while the cross sectional area is different for tube 5. We think the configuration of Fig. 4a is more consistent with the loading characteristics of the bending moment \({M}_\mathrm{Z} \) and concentrated force \({F}_\mathrm{Z} \), which can partly verify the effectiveness of the DCMO optimization model Fig. 5.

Fig. 5
figure 5

Schematic figure of the group classification

Full size image
Fig. 6
figure 6

Optimized configuration and objective function of \(\hbox {CCMO}_\mathrm{{rad}}\), OBJ = 233608.53

Full size image
Fig. 7
figure 7

Optimized configurations and objective functions of \(\hbox {DCMO}_{\mathrm{{fib}}}\) and \(\hbox {CCMO}_\mathrm{{fib}}\) models a \(\hbox {DCMO}_\mathrm{{fib}}\), OBJ = 215737.97. b \(\hbox {CCMO}_\mathrm{{fib}}\), OBJ = 201324.62

Full size image

Table 4 gives the results of the single scale optimization of the fiber winding angle from \(\hbox {DCMO}_\mathrm{{fib}}\) and \(\hbox {CCMO}_\mathrm{{fib}}\). Because only the fiber winding angle is considered as the design variable, the structural configuration is fixed as shown in Fig. 7a and b. The macro radius is kept at a constant value \(r_{i} =0.05~\)m in the optimization procedure. The different coloured numbers Fig. 7 mean they are classified into different groups as used in the following discussions.

From the optimization results of Table 4, we can find that the optimized fiber winding angle from the \(\hbox {DCMO}_\mathrm{{fib}}\) model is \(90^{{\circ }}\) in tubes 1, 2, 3, 10, and the optimized angle is a combination of the four candidates for the other six tubes (4, 5, 6, 7, 8, 9). Observing the structural loading conditions shown in Fig. 2, tubes 1, 2, 3, and 10 mainly bear the tension or compression along their axial of the beam caused by the applied concentrated forces and bending moment. Thus, the filament along the axial i.e., \(90^{{\circ }}\) fiber winding angle is the best choice to transfer the axial loads. However, the tubes 4, 7, 8, and 9 not only bear the axial force, but also the shear force. Thus, the outer and inner layers with a \(90^{{\circ }}\) fiber winding angle can effectively resist the axial loads, while the middle layer with \(\mp 45^{{\circ }}\) fiber winding angle can effectively resist the deformation caused by shear force, then leading to a greater contribution to the overall stiffness than that from the angle of \(90^{{\circ }}\). Tubes 5, 6 are with the combination of \(\mp 45^{{\circ }}\) fiber winding angles because tubes 5, 6 mainly bear the shear loads, which is consistent with the optimal angle designs.

It should be pointed that, as discussed above, the \(\hbox {CCMO}_\mathrm{{fib}}\) model has a larger design space compared with the \(\hbox {DCMO}_\mathbf{fib}\) model in the micro-scale. So the \(\hbox {CCMO}_{\mathrm{{fib}}}\) model can obtain better optimization results than the \(\hbox {DCMO}_{\mathrm{{fib}}}\) model. For the \(\hbox {CCMO}_\mathrm{{fib}}\) model, the optimized fiber winding angles of tubes 1, 2, 3, and 10 are close to \(90^{{\circ }}\) after rounding, the same as the design of \(\hbox {DCMO}_{\mathrm{{fib}}}\).

6 Conclusions

In this paper, a concurrent multi-scale optimization method is proposed for the optimization of the composite frame. The DCMO model based on the HPDMO interpolation scheme is established and the optimized macro structural configuration and the material winding angle are compared with those from single-scale optimization models to demonstrate the effectiveness of the DCMO model. The optimized results verify the effectiveness of the optimization model, and present an effective new way to achieve the lightweight design of composite frame structures in a multi-scale way.

  1. (1)

    The concurrent multi-scale optimization model of DCMO can realize the optimal design of structural compliance of composite frame with better structural stiffness and less iteration steps, comparing with the \(\hbox {CCMO}_{\mathrm{{rad}}}, \hbox {DCMO}_{\mathrm{{fib}}}\), and \(\hbox {CCMO}_\mathrm{{fib}}\) models. From the point view of the design domain, the concurrent multi-scale optimization sufficiently takes into account the coupling effects of the macro-structure and micro-material to maximize the potential of composite structures. Furthermore, the convergence rate shows that the micro-scale fiber winding angles are completely convergent in DCMO and \(\hbox {DCMO}_{\mathrm{{fib}}}\) models with a HPDMO interpolation scheme.

  2. (2)

    The multi-scale optimization models (DCMO and CCMO) get the consistent optimized configurations in macro-scale, which are in accordance with the characteristics of the loading conditions of the numerical example. The optimal results from the DCMO model can be manufactured with a relatively lower cost.

  3. (3)

    From the observations of the optimization results, we can find that the optimized macro configuration of the composite frame will be different with the different fixed micro fiber winding angles. Then the concurrent multi-scale optimization can help engineers design the composite frame more efficiently.

Therefore, the technique of concurrent multi-scale optimization can further explore the potential of macro-structure and micro-material to achieve an ultra-light design of composite frame. The two-scale optimization technique provides a new choice for the design of the composite frame structures in aerospace and other industries.