Topology optimization of continuum structures subjected to the variance constraint of reaction forces

Abstract

In this paper, the attainment of uniform reaction forces at the specific fixed boundary is investigated for topology optimization of continuum structures. The variance of the reaction forces at the boundary between the elastic solid and its foundation is firstly introduced as the evaluation criterion of the uniformity of the reaction forces. Then, the standard formulation of optimal topology design is improved by introducing the variance constraint of the reaction forces. Sensitivity analysis of the latter is carried out based on the adjoint method. Numerical examples are dealt with to reveal the effect of the variance constraint in comparison with solutions of standard topology optimization.

1 Introduction

In last decades, topology optimization of continuum structures is recognized as a challenging research topic in engineering design community. The standard formulation of compliance minimization with applied mechanical loads was initially developed and then extended to various complicated design problems for the achievement of optimal material layout (Deaton and Grandhi 2014; Sigmund and Maute 2013; Zhu et al. 2015). To this end, much effort was made to develop different formulations with required definitions of objective functions and design constraints.

In static problems, the compliance or strain energy of the whole structure is the most popular objective function and usually minimized to obtain the stiffest structures subjected to the volume constraint (Bendsøe 1989). Recently, the summation of the strain energies of all finite elements within the specific shape preserving zones were assigned as an additional design constraint to control the local deformation (Zhu et al. 2016). Displacement of the given DOF (degree of freedom) was also used (Kočvara 1997). In the case of a single concentrated force, the minimization of the displacement magnitude at the applied node along the direction of the applied force is equivalent to the minimization of the global structural compliance. Stress constraint is another important design criterion and deeply investigated (Cheng and Guo 1997; Duysinx and Bendsøe 1998). Besides, structural topology and support locations were simultaneously optimized (Buhl 2002).

In thermo-elastic problems, the structural compliance (Rodrigues and Fernandes 1995) was also minimized for the stiffest structure. However, it was found that the elastic strain energy minimization and mean compliance minimization led to different configurations (Zhang et al. 2014). Both optimization formulations are equivalent only under pure mechanical loads. Moreover, the minimization of the maximum von-Mises stress was achieved by seeking the uniform energy density (Pedersen and Pedersen 2012). Besides, the magnitudes of the reaction forces at specific nodes were introduced as design constraints to indirectly limit the thermal loading (Deaton and Grandhi 2013).

In dynamic problems, most researches were focused on maximization of fundamental, high-order eigenfrequencies or the gap between two consecutive eigenfrequencies (Díaz and Kikuchi 1992; Hilding 2000). In case of the harmonic or stationary random force excitation, the objective function was defined by the so-called dynamic compliance (Jog 2002; Ma et al. 1995) or the displacement amplitude (Liu et al. 2015b; Zhang et al. 2015b).

In stability problems, the buckling critical load constraint was introduced into the topology optimization model (Neves et al. 1995).

Some other design criteria have been studied as well. For multicomponent optimization problems, physical properties, e.g., gravity centre (Zhu et al. 2009) and moment of inertia of a structure (Takezawa et al. 2006) were considered and well recognized in aircraft and aerospace structure designs. In the case of multiple materials, it has been demonstrated that the mass constraint is more beneficial and physically more significant than the volume constraint (Gao and Zhang 2011), although both kinds of constraints are identical when only one single solid material phase is present.

The variance constraint of nodal forces at the interface between the main section and connection section was introduced into the topology optimization formulation as the evaluation criterion in the design of the connection section to transfer concentrated external forces to its main section (Zhang et al. 2015a). In that work, the nodal forces are located at the interface between two elastic solids.

This paper focuses on the design constraint on the reaction forces at the specific fixed boundary, i.e., the reaction forces between an elastic solid and its foundation. According to engineering experience, uniform reaction forces, i.e., uniform stress distribution in the connectors or welds, usually benefit the structural performance (Chang et al. 1999). Particularly, in the long-term usage of high- or ultra-precision machines, an uniform distribution of vertical reaction forces over the pedestal supports greatly avoid non-uniform creep relaxation of the supports that deteriorates the levelness of the bench surface and the machining accuracy (Liu et al. 2015a). The configuration and flexibility of the machine frame remarkably affect the distribution of the vertical loads at each support, which is usually uneven in practice but is treated as uniform forces (Kono et al. 2015). However, the design of the machine frame to improve the reaction forces distribution has not been a popular aspect of optimization design in spite of its significant effect on the long-term performance of machine tools. Therefore, it is of great importance to investigate the appropriate evaluation criterion of the uniformity of the reaction forces and the topology optimization formulation for the machine frame at the early concept stage. This is the motivation of the current work.

This paper is organized as follows. In Section 2, a basic formulation of finite element analysis is firstly presented for calculation of reaction forces. In Section 3, the variance of the reaction forces is introduced as the evaluation criterion of the uniformity of the reaction forces. In Section 4, topology optimization problem subjected to the variance constraint of the reaction forces is formulated. Sensitivity analysis is carried out and detailed in the Appendix. The validity of the proposed formulation is illustrated with 2D and 3D numerical examples in Section 5. Finally, conclusions are drawn out.

2 Finite element analysis

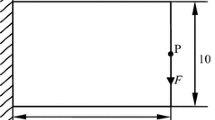
Fig. 1 illustrates a structural domain Ω with applied force F ^a and homogeneous Dirichlet boundary condition. The static linear analysis corresponds to the solution of finite element eq.

$$ \mathbf{F}=\mathbf{K}\mathbf{U} $$

(1)

Fig. 1

Illustration of a structure with applied force and homogeneous Dirichlet boundary condition

Herein, K denotes the global stiffness matrix. U and F are the nodal displacement vector and nodal force vector, respectively.

By rewriting the finite element equilibrium equation with the separation of the matrix and vectors, we have

$$ \left\{\begin{array}{c}{\mathbf{F}}^{\mathrm{a}}\\ {}\mathbf{R}\end{array}\right\}=\left[\begin{array}{cc}{\mathbf{K}}_{\mathrm{c}\mathrm{c}}& {\mathbf{K}}_{cs}\\ {}{\mathbf{K}}_{cs}^{\mathrm{T}}& {\mathbf{K}}_{ss}\end{array}\right]\left\{\begin{array}{c}{\mathbf{U}}_{\mathrm{c}}\\ {}{\mathbf{U}}_{\mathrm{s}}\end{array}\right\} $$

(2)

with

$$ \mathbf{K}=\left[\begin{array}{cc}{\mathbf{K}}_{\mathrm{cc}}& {\mathbf{K}}_{cs}\\ {}{\mathbf{K}}_{cs}^{\mathrm{T}}& {\mathbf{K}}_{ss}\end{array}\right] $$

(3)

Herein, subscript s and c represent DOFs with and without imposed values, respectively. F ^a represents the applied load vector and R is the nodal reaction force vector.

In this work, homogeneous Dirichlet boundary condition refers to

$$ {\mathbf{U}}_{\mathrm{s}}=\mathbf{0} $$

(4)

and (2) can be simplified as

$$ \left\{\begin{array}{c}{\mathbf{F}}^{\mathrm{a}}\\ {}\mathbf{R}\end{array}\right\}=\left[\begin{array}{cc}{\mathbf{K}}_{\mathrm{c}\mathrm{c}}& {\mathbf{K}}_{cs}\\ {}{\mathbf{K}}_{cs}^{\mathrm{T}}& {\mathbf{K}}_{ss}\end{array}\right]\left\{\begin{array}{c}{\mathbf{U}}_{\mathrm{c}}\\ {}\mathbf{0}\end{array}\right\} $$

(5)

where the following two parts can be used to solve U _c and to calculate R, respectively.

$$ \begin{array}{l}{\mathbf{F}}^{\mathrm{a}}={\mathbf{K}}_{\mathrm{c}\mathrm{c}}{\mathbf{U}}_{\mathrm{c}}\\ {}\mathbf{R}={\mathbf{K}}_{cs}^{\mathrm{T}}{\mathbf{U}}_{\mathrm{c}}\end{array} $$

(6)

3 Variance of the considered reaction forces

The purpose of this work is to seek the stiffest topology configuration under the applied forces and the constraint of distribution uniformity of the reaction forces. A proper quantitative description of the uniformity of the reaction forces is necessary.

Theoretically, variance is defined as the expectation of the squared deviation of a measurable variable from its mean. It is often used to measure how far a set of variable values are spread out from their mean. Here, the variance of the reaction forces on the specific DOFs is introduced as a measure of the uniformity of the reaction forces.

Assume that Γ_RV is the set of the specific DOFs on which the reaction forces are expected to be uniformly distributed. Usually, all reaction forces normal to the fixed boundary are included in Γ_RV. And then, the variance of the reaction forces is calculated as

$$ D\left(\mathbf{R}\right)=\frac{1}{n_{\mathrm{r}}}{\sum}_j{\left({R}_j-\overline{R}\right)}^2\kern0.24em \mathrm{or}\kern0.24em D\left(\mathbf{R}\right)=\frac{1}{n_{\mathrm{r}}}{\left(\mathbf{R}-\overline{\mathbf{R}}\right)}^{\mathrm{T}}\left(\mathbf{R}-\overline{\mathbf{R}}\right)\kern0.72em j\in {\Gamma}_{\mathrm{RV}} $$

(7)

where the mean of these reaction forces is expressed as

$$ \overline{R}=\frac{1}{n_{\mathrm{r}}}{\sum}_j{R}_j\kern0.6em j\in {\Gamma}_{\mathrm{RV}} $$

(8)

n _r represents the member numbers of the set Γ_RV. R _j is reaction force at the jth specific DOF and R is the vector consisting of all reaction forces at the specific DOFs.

Obviously, D(R) is always positive. A small value of D(R) implies the attainment of a uniform distribution of the reaction forces on the specific DOFs. If D(R) = 0, the reaction forces in Γ_RV are absolutely the same and distributed uniformly.

4 Optimization formulation

Firstly, two formulations are studied comparatively for topology optimization: one is the standard compliance minimization; the other includes the variance of the reaction forces as an additional constraint.

4.1 Formulation 1: minimization of the global compliance

$$ \begin{array}{l}\mathrm{find}\kern2.75em \mathbf{x}=\left\{{x}_i\right\}\kern1em i=1,2,\dots, {n}_{\mathrm{e}}\\ {} \min \kern2.5em C={\mathbf{U}}^{\mathrm{T}}\mathbf{K}\mathbf{U}\\ {}\mathrm{s}.\mathrm{t}\kern3.5em \mathbf{F}=\mathbf{K}\mathbf{U}\\ {}\kern4.25em \sum_i{V}_i{x}_i\le {f}_{\mathrm{U}}\cdot V\\ {}0<\kern-0.35em {x}_{\mathrm{L}}\le {x}_i\le 1\end{array} $$

(9)

Herein, x denotes the set of design variables. x _i represents the presence (1) or absence (0) of the solid material in the i ^th finite element. To avoid the singularity of the structural stiffness matrix in the finite element analysis, a lower bound of x _L = 10⁻³ is introduced for the design variables. In this formulation, n _e is the number of designable elements. The upper bound of the volume fraction, f _U, is defined as the ratio of the upper bound of the volume constraint (V _U) to the total volume of all designable elements (V) with f _U = V _U/V.

4.2 Formulation 2: minimization of the global compliance subjected to the variance constraint of the reaction forces

Based on Formulation 1, a variance constraint of reaction forces is introduced and the corresponding optimization problem is stated as

$$ \begin{array}{l}\mathrm{find}\kern2.75em \mathbf{x}=\left\{{x}_i\right\}\kern1em i=1,2,\dots, {n}_{\mathrm{e}}\\ {} \min \kern2.5em C={\mathbf{U}}^{\mathrm{T}}\mathbf{K}\mathbf{U}\\ {}\mathrm{s}.\mathrm{t}\kern3.5em \mathbf{F}=\mathbf{K}\mathbf{U}\\ {}\kern4.25em D\left(\mathbf{R}\right)\le {D}_{\mathrm{U}}\\ {}\kern4.25em \sum_i{V}_i{x}_i\le {f}_{\mathrm{U}}\cdot V\\ {}0<\kern-0.35em {x}_{\mathrm{L}}\le {x}_i\le 1\end{array} $$

(10)

Here, D _U, the upper bound of D(R), is usually determined based on the variance of the specific reaction forces obtained in topology optimization using Formulation 1. For example, D _U can be 20% of D(R) in topology optimization using Formulation 1.

Additionally, an optimization formulation to minimize the variance of the reaction forces is also studied to identify the extrema of D(R).

4.3 Formulation 3: minimization of the variance constraint of the reaction forces

$$ \begin{array}{l}\mathrm{find}\kern2.75em \mathbf{x}=\left\{{x}_i\right\}\kern1em i=1,2,\dots, {n}_{\mathrm{e}}\\ {} \min \kern2.5em D\left(\mathbf{R}\right)\\ {}\mathrm{s}.\mathrm{t}\kern3.5em \mathbf{F}=\mathbf{K}\mathbf{U}\\ {}\kern4.25em \sum_i{V}_i{x}_i\le {f}_{\mathrm{U}}\cdot V\\ {}0<\kern-0.35em {x}_{\mathrm{L}}\le {x}_i\le 1\end{array} $$

(11)

SIMP (Solid Isotropic Material with Penalization) model is used in this work and the penalized Young’s modulus is expressed as

$$ {E}_i={x}_i^p{E}^{(0)} $$

(12)

in which the superscript (0) indicates the properties of the solid material. The penalty factor p=3 is adopted in this work.

Gradient-based optimizers are usually used to solve topology optimization problems. Therefore, it is necessary to carry out sensitivity analysis with respect to design variables. The sensitivity of the global compliance corresponds to

$$ \frac{\partial C}{\partial {x}_i}=-{\mathbf{U}}_i^{\mathrm{T}}\frac{\partial {\mathbf{K}}_i}{\partial {x}_i}{\mathbf{U}}_i $$

(13)

By means of the adjoint method, the sensitivity of the variance of the reaction forces could be derived by only one additional finite element analysis.

$$ \frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}={\boldsymbol{\Lambda}}^{\mathrm{T}}\frac{\partial {\mathbf{K}}_{cs}^{\mathrm{T}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}}-{\boldsymbol{\uplambda}}^{\mathrm{T}}\frac{\partial {\mathbf{K}}_{\mathrm{c}\mathrm{c}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}} $$

(14)

In (13, 14), $\frac{\partial {\mathbf{K}}_i}{\partial {x}_i}$, $\frac{\partial {\mathbf{K}}_{cs}^{\mathrm{T}}}{\partial {x}_i}$ and $\frac{\partial {\mathbf{K}}_{\mathrm{cc}}}{\partial {x}_i}$ can be easily derived at the element level. The meanings of the artificial vector Λ and the adjoint vector λ, and details of the sensitivity analysis are presented in the Appendix.

5 Numerical tests

In this section, the proposed formulation is tested with several numerical examples. It is assumed that Young’s modulus of the solid material is 105GPa and the Poisson’s ratio is 0.34. Filter methods, including the sensitivity filter (Sigmund 2001) and the density filter (Bourdin 2001), are the most popular regularization methods in the pseudo-density method. A sensitivity filtering technique, whose underlying concepts was rigorously derived from principles in continuum mechanics and nonlocal elasticity (Sigmund and Maute 2012), is adopted herein to yield checkerboard-free topology configuration owing to its ease of application. The ConLin (Convex Linearization) (Fleury and Braibant 1986) is applied to solve the topology optimization problem with the convergence criterion that the relative variations of the objective function and constraints between two consecutive iterations are all less than 0.5%.

5.1 Test 1

Consider a plane structure with a non-designable domains (the dark areas), as shown in Fig. 2. The structure is meshed into 120 × 60 four-node finite elements. Each element has a size of 2.5 mm. A vertical force (1000 N) is applied. The upper bound of the volume fraction is f _U = 0.3. The reaction forces along vertical direction at all fixed nodes are considered.

Fig. 2

Structure 1 (unit: mm)

Fig.3(a) shows the topology optimization result using Formulation 1. The variance of the considered reaction forces is D(R) = 106.1 for this configuration. In order to realize a more uniform distribution of these reaction forces, Formulation 2 is used with different values of D _U. Optimized configurations are shown in Fig.3(b)-(d). It is found that the constraint of the variance of reaction forces makes the structure bifurcate, and that smaller values of D _U produce more refined branches with the reduction of the stiffness of the optimized structures, as shown in Fig.4. It should be noted that in all three tests, the constraints of the material volume and the variance of reaction forces involved in Formulation 2 are both active.

Fig. 3

Topological configurations in Test 1

Fig. 4

Relation between the structural compliance and the variance of the specific reaction forces in Test 1

For all tests shown in Fig.3, reaction forces along the vertical direction at all fixed nodes are compared in Fig.5. Obviously, the constraint of the variance of reaction forces makes the applied force be transferred to more fixed nodes and thus reduces the maximum reaction forces greatly.

Fig. 5

Distribution of the Y-axis reaction forces in Test 1

In the case of D _U = 1, the reaction forces at all nodes are smoothed into a nearly uniform distribution. The iteration processes of the compliance and D(R) are plotted in Fig.6. For the considered optimization problem, it is very difficult to find a feasible initial solution. In this paper, the initial values for all design variables are set to be the upper bound of the volume fraction. Clearly, the variance constraint of reaction forces is violated at the beginning. In order to achieve the feasible solutions, the ConLin algorithm combined with the augmented Lagrangian method is utilized. When the iterative solution reaches the upper bound of the variance constraint of reaction forces, it is pushed back into the feasible space and some oscillations occur in the iteration. Finally, both iteration curves converge to the optimized solution.

Fig. 6

Iteration histories of structural compliance and D(R) (Structure 1, D _U = 1)

5.2 Test 2

A plane structure is clamped on both parts of the bottom and two vertical forces are applied, as shown in Fig. 7. The size of four-node finite element is 2.5 mm and a mesh of 120 × 80 elements is used. The upper bound of the volume fraction is f _U = 0.3. The reaction forces along vertical direction at all fixed nodes are considered.

Fig. 7

Structure 2 (unit: mm)

Topology optimization results are shown in Fig.8. Formulation 1 leads to the stiffest configuration and the stiffness of the optimized structures decreases with D _U if the variance of reaction forces is constrained. Note that the constraints of the material volume and the variance of reaction forces are both active in the tests using Formulation 2.

Fig. 8

Topological configurations in Test 2

Here, the case of D _U = 17,000 should be highlighted. The optimized configuration is quite different. Unfortunately, D(R) cannot decrease below its upper bound D _U even after 300 iterations in this case. Besides, the structural compliance of this test is clearly larger than others. Further investigation is made here to clarify this case. Using Formulation 3, D(R) =17,928 is found as the extrema of the variance of reaction forces, as shown in Fig. 8(f). It means that it is impossible to obtain absolutely uniform distribution of the reaction forces under the prescribed loads and boundary conditions in this test.

Fig.9 shows the relation between the structural compliance and the variance of specific reaction forces. Around solution (f), the global compliance decreases quickly while the uniformity of the reaction forces increases slightly. Comparatively, around solution (a), the global compliance decreases slowly while the variance of the reaction forces quickly increases. The reaction forces in vertical direction at all fixed nodes are shown in Fig. 10.

Fig. 9

Relation between the structural compliance and the variance of the specific reaction forces in Test 2

Fig. 10

Reaction force distributions of Structure 2

5.3 Test 3

The proposed method is now tested for a large-scale engineering problem. The pedestal of a milling machine is shown in Fig.11. Assume that the dark areas are non-designable. The structure is fixed on the six areas of the bottom and undergoes pressures on several plane surfaces. The whole structure is meshed into 120,558 solid elements. The mass of the whole structures should be less than 1500 kg. The reaction forces along Z-axis at all fixed nodes are considered.

Fig. 11

Structure 3 (Pedestal of a milling machine)

In the design of the pedestal of a milling machine, the stiffness of the whole structure is one of the most important requirements. Therefore, Formulation 1 is firstly utilized to obtain the configuration involving the maximum stiffness and Formulation 2 is then adopted to improve the uniformity of the reaction forces. Fig.12 illustrates that obvious differences exist between the topology optimization results due to the presence of the variance constraint of the reaction forces. The additional variance constraint reduces the max value and the variance of the reaction forces along Z-axis on the supports, as shown in Fig. 13.

Fig. 12

Topological configurations in Test 3

Fig. 13

Reaction force distributions in Test 3

6 Conclusions

In topology optimization, the exploration and development of new optimization formulations constructed for various design criterions are of significant engineering importance. In this paper, variance constraint of reaction forces is introduced into structural topology optimization to meet the engineering design needs. The variance of the reaction forces is introduced as the quantitative description of uniformity of these reaction forces on the fixed nodes. Based on the traditional formulation of the compliance minimization subject to the volume constraint, the variance constraint of the specific reaction forces is added. Its upper bound is determined by a relaxation of the variance value obtained in traditional optimization formulation. Besides, an optimization formulation to minimize the variance of the reaction forces is also studied to identify its extrema. By means of the adjoint method, the sensitivities of the variance of the reaction forces are derived by one additional finite element analysis.

Numerical tests indicate that variance constraint of reaction forces could reduce the maximum value and improve the uniformity of the reaction forces, to some extent. An extrema exists for the variance of reaction forces if the support positions are prescribed. Therefore, if the upper bound of the variance constraint of reaction forces is smaller than its extrema, the optimization process might fail to find the optimal solution. In order to further improve the distribution uniformity of the reaction forces, support positions could be included in the optimization formulation as constraints or design variables in future work.

Appendix: Sensitivity analysis

The sensitivity analysis of the global compliance and the variance of reaction forces with respect to design variables is detailed as follow.

1.1 Sensitivity analysis of the global compliance

Based on the definition of the global compliance, the sensitivity of the latter then corresponds to

$$ \frac{\partial C}{\partial {x}_i}=2{\mathbf{U}}^{\mathrm{T}}\frac{\partial \mathbf{F}}{\partial {x}_i}-{\mathbf{U}}^{\mathrm{T}}\frac{\partial \mathbf{K}}{\partial {x}_i}\mathbf{U}=2{\mathbf{U}}_{\mathrm{c}}^{\mathrm{T}}\frac{\partial {\mathbf{F}}^{\mathrm{a}}}{\partial {x}_i}-{\mathbf{U}}_i^{\mathrm{T}}\frac{\partial {\mathbf{K}}_i}{\partial {x}_i}{\mathbf{U}}_i $$

(A.1)

In this work, the applied forces are supposed to be design-independent. This implies that

$$ \frac{\partial {\mathbf{F}}^{\mathrm{a}}}{\partial {x}_i}=0 $$

(A.2)

The sensitivity of the global compliance is then rewritten as

$$ \frac{\partial C}{\partial {x}_i}=-{\mathbf{U}}_i^{\mathrm{T}}\frac{\partial {\mathbf{K}}_i}{\partial {x}_i}{\mathbf{U}}_i $$

(A.3)

1.2 Sensitivity analysis of the variance of reaction forces

Based on the definition in Section 3, the sensitivity of the variance of the specific reaction forces corresponds to

$$ \frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}=\frac{1}{n_{\mathrm{r}}}{\sum}_j2\left({R}_j-\overset{-}{R}\right)\left(\frac{\partial {R}_j}{\partial {x}_i}-\frac{\partial \overset{-}{R}}{\partial {x}_i}\right) $$

(A.4)

where the partial derivative of the mean reaction force is expressed as

$$ \frac{\partial \overset{-}{R}}{\partial {x}_i}=\frac{1}{n_{\mathrm{r}}}{\sum}_{\zeta}\frac{\partial {R}_{\zeta }}{\partial {x}_i} $$

(A.5)

Thus, we have

$$ \begin{array}{l}\frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}=\frac{1}{n_{\mathrm{r}}}\sum_j2\left({R}_j-\overline{R}\right)\left(\frac{\partial {R}_j}{\partial {x}_i}-\frac{1}{n_{\mathrm{r}}}\sum_{\zeta}\frac{\partial {R}_{\zeta }}{\partial {x}_i}\right)\\ {}=\frac{2}{n_{\mathrm{r}}}{\sum}_j\left({R}_j-\overline{R}\right)\left(\left(1-\frac{1}{n_{\mathrm{r}}}\right)\frac{\partial {R}_j}{\partial {x}_i}-\frac{1}{n_{\mathrm{r}}}{\sum}_{{}_{\zeta }{,}_{\zeta}\ne j}\frac{\partial {R}_{\zeta }}{\partial {x}_i}\right)\end{array} $$

(A.6)

This expression can be rewritten as

$$ \frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}={\boldsymbol{\Lambda}}^{\mathrm{T}}\frac{\partial \mathbf{R}}{\partial {x}_i} $$

(A.7)

in which Λ is a vector

$$ \boldsymbol{\Lambda} =\left\{\begin{array}{c}{\varLambda}_1\\ {}\begin{array}{c}\vdots \\ {}{\varLambda}_j\\ {}\vdots \end{array}\\ {}{\varLambda}_{n_{\mathrm{s}}}\end{array}\right\} $$

(A.8)

with each term being calculated by

$$ {\Lambda}_j=\left\{\begin{array}{cc}\frac{2}{n_{\mathrm{r}}}\left(\left({R}_{\boldsymbol{j}}-\overset{-}{R}\right)\left(1-\frac{1}{n_{\mathrm{r}}}\right)-\frac{1}{n_{\mathrm{r}}}{\sum}_{\boldsymbol{\zeta}, \boldsymbol{\zeta} \ne \boldsymbol{j}}\left({R}_{\boldsymbol{\zeta}}-\overset{-}{R}\right)\right)& j\in {\Gamma}_{\mathrm{RV}}\\ {}0& j\notin {\Gamma}_{\mathrm{RV}}\end{array}\right. $$

(A.9)

To calculate $\frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}$, the partial derivative of the reaction force vector R is necessary. According to (6), we have

$$ \frac{\partial \mathbf{R}}{\partial {x}_i}=\frac{\partial {\mathbf{K}}_{cs}^{\mathrm{T}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}}+{\mathbf{K}}_{cs}^{\mathrm{T}}\frac{\partial {\mathbf{U}}_{\mathrm{c}}}{\partial {x}_i} $$

(A.10)

and

$$ \frac{\partial {\mathbf{U}}_{\mathrm{c}}}{\partial {x}_i}={\mathbf{K}}_{\mathrm{c}\mathrm{c}}^{-1}\left(\frac{\partial {\mathbf{F}}^{\mathrm{a}}}{\partial {x}_i}-\frac{\partial {\mathbf{K}}_{\mathrm{c}\mathrm{c}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}}\right) $$

(A.11)

Under the assumption of design-independent force (i.e., $\frac{\partial {\mathbf{F}}^{\mathrm{a}}}{\partial {x}_i}=0$), the above relation can be simplified as

$$ \frac{\partial {\mathbf{U}}_{\mathrm{c}}}{\partial {x}_i}=-{\mathbf{K}}_{\mathrm{c}\mathrm{c}}^{-1}\frac{\partial {\mathbf{K}}_{\mathrm{c}\mathrm{c}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}} $$

(A.12)

The substitution of (A.12) into (A.10) yields

$$ \frac{\partial \mathbf{R}}{\partial {x}_i}=\frac{\partial {\mathbf{K}}_{cs}^{\mathrm{T}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}}-{\mathbf{K}}_{cs}^{\mathrm{T}}{\mathbf{K}}_{\mathrm{c}\mathrm{c}}^{-1}\frac{\partial {\mathbf{K}}_{\mathrm{c}\mathrm{c}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}} $$

(A.13)

Now, the sensitivity of the variance of the considered reaction forces can be derived as

$$ \frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}={\boldsymbol{\Lambda}}^{\mathrm{T}}\frac{\partial {\mathbf{K}}_{cs}^{\mathrm{T}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}}-{\boldsymbol{\Lambda}}^{\mathrm{T}}{\mathbf{K}}_{cs}^{\mathrm{T}}{\mathbf{K}}_{\mathrm{c}\mathrm{c}}^{-1}\frac{\partial {\mathbf{K}}_{\mathrm{c}\mathrm{c}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}} $$

(A.14)

in which the adjoint method is applied to calculate the second term.

Suppose

$$ {\boldsymbol{\Lambda}}^{\mathrm{T}}{\mathbf{K}}_{cs}^{\mathrm{T}}{\mathbf{K}}_{\mathrm{cc}}^{-1}={\boldsymbol{\uplambda}}^{\mathrm{T}} $$

(A.15)

The adjoint vector λ can then be obtained by

$$ {\mathbf{K}}_{\mathrm{cc}}\boldsymbol{\uplambda} ={\mathbf{K}}_{cs}\boldsymbol{\Lambda} $$

(A.16)

or

$$ \left[\begin{array}{cc}{\mathbf{K}}_{\mathrm{cc}}& {\mathbf{K}}_{cs}\\ {}{\mathbf{K}}_{cs}^{\mathrm{T}}& {\mathbf{K}}_{ss}\end{array}\right]\left\{\begin{array}{c}\boldsymbol{\uplambda} \\ {}\mathbf{0}\end{array}\right\}=\left\{\begin{array}{c}{\mathbf{K}}_{cs}\boldsymbol{\Lambda} \\ {}{\mathbf{R}}_{\uplambda}\end{array}\right\} $$

(A.17)

Here, ${\mathbf{R}}_{\uplambda}$ is the reaction forces in the additional analysis related to (A.17). Obviously, only one additional finite element analysis needs to be carried out under the same boundary conditions as the original structural analysis in (2) no matter what the adjoint load is.

Thus, by virtue of the adjoint method, $\frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}$ is established as

$$ \frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}={\boldsymbol{\Lambda}}^{\mathrm{T}}\frac{\partial {\mathbf{K}}_{cs}^{\mathrm{T}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}}-{\boldsymbol{\uplambda}}^{\mathrm{T}}\frac{\partial {\mathbf{K}}_{\mathrm{c}\mathrm{c}}}{\partial {x}_i}{\mathbf{U}}_{\mathrm{c}} $$

(A.18)

In this expression, $\frac{\partial {\mathbf{K}}_{cs}^{\mathrm{T}}}{\partial {x}_i}$ and $\frac{\partial {\mathbf{K}}_{\mathrm{cc}}}{\partial {x}_i}$ can be easily derived at the element level.

A particular case should be mentioned herein. If the applied force is constant during optimization and the variance constraint is applied to all fixed nodes, the mean reaction force $\overset{-}{R}$ is constant as well. As a result, the derivative of the mean reaction force with respect to all design variables in (A.5) is zero and the sensitivity of the variance of specific reaction forces in (A.4) could be simplified as

$$ \frac{\partial D\left(\mathbf{R}\right)}{\partial {x}_i}=\frac{1}{n_{\mathrm{r}}}\sum_j2\left({R}_j-\overset{-}{R}\right)\frac{\partial {R}_j}{\partial {x}_i} $$

(A.19)

Thus, the artificial vector Λ is simplified as

$$ {\boldsymbol{\Lambda}}_j=\left\{\begin{array}{cc}\frac{1}{n_{\mathrm{r}}}{\sum}_j2\left({R}_j-\overset{-}{R}\right)& j\in {\Gamma}_{\mathrm{RV}}\\ {}0& j\notin {\Gamma}_{\mathrm{RV}}\end{array}\right. $$

(A.20)