Stiffening of restrained thermal structures via topology optimization

Abstract

The majority of work in the thermal structures field has focused on reducing or eliminating thermal stresses by accommodating thermal expansion. In the modern day, several new applications, including engine exhaust-washed structures for embedded engine aircraft, are posing new design scenarios where this prescription is not possible. Thus it becomes necessary to utilize new design techniques to solve the problem of stiffening and stress reduction in thermal structures with restrained thermal expansion. In this work, a design scenario is presented to demonstrate the challenges associated with the design of thin shell structures in a thermal environment and the breakdown of common design methodologies. These challenges include a fundamental non-intuitiveness in the design space and the design dependency that occurs with thermal loading. Three different topology optimization formulations are investigated to solve this problem. The effectiveness of each of these methods is benchmarked against one another and general recommendations are made regarding effective design solutions for restrained thermal structures.

1 Introduction

Thermal structures have been an active area of research in the aerospace industry since the early 1950s and the advent of supersonic flight. In general the field is concerned with the effects of elevated temperatures or large spatial and temporal temperature gradients on structural components. These effects lead to thermal expansion in addition to a degradation of mechanical properties for standard aerospace materials (Thornton 1996). If not properly accounted for, thermal expansion can lead to damaging thermal stresses and component failure. These stresses and failure are the focus of this paper.

Regarding design against thermal stresses, the most fundamental design solution for structures in a thermal environment is to simply accommodate the expansion. By allowing some or all of the displacement created by the thermal environment, the resulting thermal stresses can be significantly reduced or altogether eliminated (Gatewood 1957). This design solution is demonstrated by the expansion joints in concrete structures, gas turbine engine components, and the notable corrugated wing skins of the SR-71 Blackbird (Merlin 2009). While this basic consideration is widely accepted as the best practice to prevent thermal stresses, in the modern day increased requirements on mission capability, combat survivability, and versatility of military aircraft have created design scenarios in which freely accommodating thermal expansion is not possible. These include exhaust-washed components of low observable, embedded engine aircraft and integrated thermal protection systems on hypersonic vehicles. In these situations, platform level design criteria necessitate strict fixivity requirements on critical structural components that are subjected to elevated temperatures (Haney 2005).

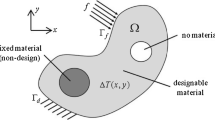
In low observable aircraft, such as the B-2 Spirit and future concepts, engines are buried inside the aircraft. This configuration allows for a smooth outer mold line (OML), which decreases radar observability, in addition to reducing infrared detectability by preventing direct line-of-sight to hot turbine components with a ducted exhaust system (Paterson 1999). The structural components located aft of the embedded engines that make up this exhaust system are known as engine exhaust-washed structures (EEWS). A conceptual EEWS configuration is shown in Fig. 1. The structure consists of a duct of exhaust-washed surfaces through which high temperature exhaust gasses are passed. These components are attached to a supporting structure and the entire system is contained inside the aircraft skins. In this configuration it is important to note that strict design constraints are placed on the shape of the exhaust path and structural fixivity of exhaust-washed surfaces. These constraints result from the desired configuration level performance capabilities and create a situation where it is difficult to freely accommodate thermal expansion of the hot exhaust structures (Deaton and Grandhi 2011).

Fig. 1

Conceptual engine exhaust-washed structure located aft of embedded engines on a low observable aircraft and its primary components

From Fig. 1, we see that the structure is largely made up of thin plate- or shell-like structures, which are common in aerospace applications. When thin shell structures are subjected to elevated temperatures with sufficient fixivity at their boundary conditions, they undergo either buckling or bowing. Both behaviors lead to out-of-plane deformation with respect to the original shell geometry. This deformation can generate excessive thermal stresses and lead to component failure. Since thermal expansion cannot be easily accommodated to prevent these stresses, more advanced design methods are necessary to generate effective and reliable structures that can survive the restrained expansion.

In the following section, a design scenario is presented using a characteristic beam strip model to demonstrate the complications with design of thin shell structures in a thermal environment and boundary conditions that prohibit thermal expansion. The strip model is selected because it idealizes the behavior of thin structures under restrained expansion such as the EEWS. Following this investigation, Section 3 provides a review of topology optimization as applied to thermoelasticity and thermally loaded structures. Section 4 presents three formulations of topology optimization and their application to the design scenario from Section 2. Finally, Section 5 gives the results of optimization along with an evaluation of the resulting configurations with respect to achieving design objectives.

2 Demonstration of restrained expansion scenario

To demonstrate the case of restrained thermal expansion we refer to the characteristic beam strip geometry with elastic end conditions shown in Fig. 2. While this model is simple, its thermoelastic behavior is representative of common thin, thermally restrained components including curved shells and post-buckled flat plates where bending is important (Barron and Barron 2012; Haney and Grandhi 2009). As noted in Fig. 2, the geometry has a curvature of radius R of 144 inches, a rectangular cross-section with thickness t of 0.16 inches and unit width w, and covers a span L of 12 inches. Material properties include a constant (temperature independent) elastic modulus of 10 × 10⁶ psi and constant coefficient of thermal expansion of 5.0 × 10⁻⁶ in/in/° F, which correspond closely with properties of titanium at high temperature. A uniform elevated temperature $\Delta T$ is applied to the model. The commercial finite element program MD Nastran is used to investigate the structural response (MSC.Software 2010). Since behavior under these conditions is geometrically nonlinear, a nonlinear solver is used to capture the effects of large displacements, follower forces, and stress stiffening. Two-noded beam elements are used to model the structure and a mesh convergence study was performed, which indicated that a mesh size of 0.05 inches along the length was required. In addition to an exploration of the basic response to elevated temperature, parametric studies for variability in the thickness and deformation state of the model are performed to gain insight into the design problem posed when attempting to strengthen or stiffen a thin, thermally restrained structure.

Fig. 2

Schematic of a thin shallow curved beam strip model subjected to thermal loading

Figure 3 shows the deformation response of the model at various elevated temperature levels for the case of fully clamped ends. Since the model has an initial curvature, buckling does not occur as it might in an initially flat beam, but rather the beam continuously deforms or bows out-of-plane.

From Fig. 3, it is evident that higher temperature states correspond directly to greater out-of-plane deformation with the highest displacement at the center of the model. Note that the contour in Fig. 3 represents the displacement in the vertical direction. From strictly a strength of materials standpoint, we recognize that such a deformation state is dominated by bending stresses with a maximum tensile stress at the clamped ends of the beam on the side opposite the direction of deformation. In a design application, these areas represent the most likely failure modes for the structure. Assuming that no control over the temperature level of the environment is available, any design modification for stress reduction must be done structurally.

Fig. 3

Out-of-plane deformation of the thermally loaded beam model with fully clamped end conditions at various levels of elevated temperature

2.1 Effect of material addition in thermal environment

A common practice in mechanical design to reduce deformation and decrease stress is stiffening by structural material addition. For a thin shell structure like that considered here, this corresponds to increasing the thickness of the component. We now explore the effectiveness of this approach in an elevated temperature environment for various magnitudes of restraint placed on the thermal expansion.

In physical application, the boundary conditions are finite and dependent upon the stiffness of fasteners and the adjoining substructure. To represent this, a linear spring is included to provide an elastic boundary condition in the x-direction as shown previously in Fig. 2. Rotations at the edges of the beam and translation in the y-direction remain fixed. Various finite stiffness values of the elastic end conditions are represented using (1) where k is a stiffness ratio parameter, $K_{s}$ is the stiffness of the spring, and $EA/L$ represents the beam stiffness including the elastic modulus E, cross sectional area A (which is dependent upon thickness t), and length L.

$$ k = \frac{K_{s}}{EA / L} $$

(1)

Varying the stiffness parameter k provides a convenient mechanism to compare the relative stiffness of the boundary condition to the stiffness of the structure itself. A higher k value corresponds to a stiffer boundary with more resistance to thermal expansion while a low k value represents a boundary that will allow more expansion in the x-direction. An infinite value of k corresponds to the fully clamped end condition. Finally, a uniform elevated temperature of ΔT = 900° F is used.

Figure 4 shows the effect of increasing the thickness of the beam on the stress response at the critical location on the edge of the beam. Results are presented as the stress ratio, which represents the stress that occurs for a beam of thickness t to the stress at the nominal thickness $t_{o} = 0.16$ inches, versus thickness ratio, which is the thickness t divided by nominal thickness $t_{o}$. Different stiffness parameters are shown as multiple curves on the plot.

Fig. 4

Stress ratio versus thickness ratio for various values of relative spring stiffness ratio

We note several important observations from Fig. 4. For low values of the stiffness parameter k, increasing the thickness of the structures does in fact reduce the stress; however, for higher values of k, increasing the thickness actually increases the stress at the root of the beam. This results from the fundamental design dependency of thermal loads. By adding material to the structure via an increase in thickness, we have added more material that must also undergo thermal expansion. With high values of the stiffness ratio parameter, or physically speaking, a thin, low stiffness structure, such as an aircraft skin panel or exhaust-washed surface, affixed to a very rigid supporting structure, such as a rib or spar, the additional material from the thickness increase can be detrimental. In this case, the added thickness results in a thermal load increase that can actually cause greater out-of-plane deformation and higher stresses in critical locations. We note that this effect can eventually be overcome, but only by significant thickness increases. For example, for a stiffness parameter of $k = 5$, at least a doubling of thickness is required before any reduction in stress is observed. In a large built-up structural system, this results in a substantial increase in weight.

Another drawback of a simple thickness increase in a thermal environment is evidenced in Figs. 5 and 6. In these figures, the effects of thickness increase on the reaction load and reaction moment taken at the boundary conditions of the structure are demonstrated.

Fig. 5

Increase in boundary reaction force ratio with increases in thickness for various values of relative stiffness ratio

Fig. 6

Increase in boundary moment with increases in thickness for various values of relative stiffness ratio

From Figs. 5 and 6, we note that increasing thickness increases both the reaction load and reaction moment regardless of the stiffness parameter k. While the effect is most severe with higher stiffness boundaries, it is nonetheless significant everywhere. Just as with the increase in stress results previously observed, this occurs due to the increase in thermal loading that accompanies material addition in elevated temperature environments. For the doubling of thickness for $k = 5$ considered previously, which only just begins to decrease stress in Fig. 4, we now observe approximately a 7 fold increase in reaction load and a 5 fold increase in reaction moment. In a real world design application, these increases correspond directly to increased thermal load that will be imposed on adjoining structures. This poses significant challenges to both a redesign of an existing component and in the development of entirely new structures. For a redesign or retrofit, existing adjoining structure will likely be unable to sustain such a significant increase in loading as it was not previously designed to do so. In the design of new thermal structures, such sensitivity of thermal and boundary loading to local design modification means that the design space must be expanded to include adjoining structures that experience the effects of design modification of any local structural member.

2.2 Displacement-stress relationship

In the previous section, it was demonstrated that simply adding structural material in an attempt to stiffen a thermally restrained structure is not only ineffective, but can actually be detrimental to both the primary component and any structures it is affixed to. It was also identified that the tensile stresses in critical locations of the model are a result of the out-of-plane displacement of the structure. We now focus on the relationship between the overall magnitude of deformation and the stress level that is developed to discover the necessary criteria of an effective stiffening technique to reduce stresses.

Since the fully clamped edge scenario, or an infinite stiffness parameter k, seemed to place an upper bound on the detrimental effects of material addition, we select the fully clamped boundary condition with a thickness of $t = 0.16$ inches. We first subject the structure to the elevated temperature ΔT = 900° F to obtain the deformed shape. A series of enforced displacement conditions are then imposed on the structure so as to incrementally return it to the undeformed state. At each step of this process the stress in the beam and the boundary reaction load is measured and plotted in Figs. 7 and 8, respectively. In the plots, the displacement is measured at the center of the model, which corresponds to the location of maximum out-of-plane displacement.

Fig. 7

Relationship between out-of-plane displacement and stress at critical locations during loading and enforced displacement

Fig. 8

Effect on boundary reaction load resulting from loading and enforced displacement conditions

From Fig. 7, we observe that significant gains in stress reduction can be obtained by reducing the out-of-plane displacement. For example, from the deformed state with a center displacement of 0.39 inches a 50 % reduction in stress can be achieved by reducing the displacement to only 0.32 inches. Physically, it is impossible to reduce displacement as done here, but it becomes evident that to reduce thermal stress levels induced by restrained thermal expansion a design solution should be emoloyed that directly reduces out-of-plane deformation.

In addition, while displacement reduction does achieve the desired effect on the stress response, an increase in boundary loading is still evident as demonstrated by Fig. 8. This stems from the reorientation of the thermal loading by the enforced displacement conditions. When the structure can freely deform, thermal loads result in out-of-plane bending. When deformation is reduced, thermal loading is reoriented such that higher in-plane, or axial-type, loading exists, which leads to increases in boundary reaction load.

With the findings of the exercises in this section in mind, it becomes clear that to achieve the desired stress reduction without significant reaction increase, the design space must be expanded past modification of the thin structure itself and more advanced design methods should be employed. For the remainder of this paper, we investigate the application of structural topology optimization to generate a stiffening structure that can simultaneously reduce stress in critical locations and limit reaction loads. Such a solution will require satisfying several competing design critiera and managing both the amount and direction of thermal expansion within the structural system.

3 Topology optimization

Structural topology optimization is the process of determining the optimal layout of material within a given design space (Bendsøe and Sigmund 2003). The bulk of research has been focused on purely mechanical load cases, but some progress has also been made for other types of loading including thermal loads. As a result of the inherent design dependency of thermoelastic loading, a number of additional challenges with topology optimization arise when considering these problems. Rodrigues and Fernandes (1995) first studied topology optimization of thermally loaded structures using a homogenization method. Li et al. (1999, 2001) applied the Evolutionary Structural Optimization (ESO) method with element thickness as design variables and varying temperature fields. Sigmund and Torquato (1997) used topology design to generate structures with extremal thermal expansion properties, which included structures that exhibit zero or even negative global expansion when subjected to an elevated temperature. Jog (1996) extended the application of topology optimization to non-linear thermoelastic systems. In addition, thermally compliant mechanisms have also been derived via topology optimization, which control the amount and direction of thermal expansion, for use in micro-electronic mechanism applications (Sigmund 2001).

More recently, Pedersen and Pedersen (2010) considered both minimum compliance and uniform energy density objectives with thermal loading for strength optimized designs of graded material structures. Gao and Zhang (2010) studied the effects of different material interpolation schemes and proposed the use of a thermal stress coefficient to consistently penalize both the element stiffness and thermal stress load. Pedersen and Pedersen (2012) also explored concepts of penalization and interpolation in thermoelastic topology optimization. Xia and Wang (2008) applied the level set method to circumvent the formation of gray intermediate material areas that commonly occur in compliance minimization of thermoelastic structures. Finally, practical examples of thermoelastic topology optimization can be found in works by Penmetsa et al. (2006) and Kim et al. (2006) where topology optimization was utilized in the design of thermal protection systems (TPS) that are subjected to both intense thermal and vibro-acoustic loads during atmospheric reentry. Wang et al. (2011) studied the topological design of the support structure for a space camera subjected to thermal loading. The design objectives in their study of high stiffness thermoelastic structures with low amounts of thermal expansion in critical directions are similar to the concepts we explore in this paper.

3.1 The stiffening problem

As observed in the demonstration scenario, simple material addition via thickness increase is not a suitable stiffening technique for thin structures subjected to restrained expansion. Thus we propose topology optimization as a means to generate effective stiffening structures that may be attached to either side of a thin shell structure to reduce out-of-plane deformation and decrease thermal stresses. We also seek to prevent the excessive reaction load increases.

The application case in this work is motivated by an EEWS application. It is assumed that a designable domain exists below a thin curved structure like that explored in the demonstration case, which we now call the non-design domain, over which hot exhaust gases pass. This is demonstrated by Fig. 9. The thermal environment created is idealized as a uniform elevated temperature on both the non-design and designable regions. Structural boundary conditions are fully clamped conditions on the edges of the non-design domain. An edge that forms in the designable region remains a traction free boundary. Under these conditions, any topological designs that are developed represent stiffening structures that may be affixed to the underside of the thin component with restrained expansion for stress reduction. The following section presents the topology optimization formulation investigated to accomplish these design objectives.

Fig. 9

Topology optimization design space

4 Topology optimization formulation

Static Equilibrium in a finite element system including both mechanical and thermal loading is given by (2):

$$ \mathbf{KU}=\mathbf{F} $$

(2)

where K is the global stiffness matrix, U is the nodal displacement vector, and F is the nodal load vector. Depending on the problem, F consists of either design-independent mechanical loading $\mathbf {F}^{m}$, design-dependent thermal loads $\mathbf {F}^{th}$, or a combination of both as:

$$ \mathbf{F} = \mathbf{F}^{m} + \mathbf{F}^{th} $$

(3)

Stiffness matrix K is assembled in the usual way as a sum over element matrices. It is parameterized similar to typical density-based topology optimization (Bendsøe and Sigmund 2003); however, a non-SIMP interpolation scheme, described later, is used. $\mathbf {F}^{th}$ is parameterized using the thermal stress coefficient (TSC) introduced by Gao and Zhang (2010) and described briefly below. The nodal load vector for the element e is given as:

$$ \mathbf{F}_{e}^{th} =\int\limits_{\Omega_{e}}\mathbf{B}_{e}^{T}\mathbf{C}_{e}\boldsymbol{\varepsilon}_{e}^{th} d \Omega $$

(4)

$\mathbf {B}_{e}$ is the element strain-displacement matrix, which consists of derivatives of the element shape functions that are independent of topology design variables. $\mathbf {C}_{e}$ is the element elasticity matrix, which for isotropic materials can be written as a linear function of elastic modulus:

$$ \mathbf{C}_{e} =E(x_{e})\overline{\mathbf{C}}_{e} $$

(5)

where $\overline {\mathbf {C}}_{e}$ consists of constant terms related to the material constitutive matrix and $E(\rho _{e})$ is the elastic modulus of element e that is dependent on element density $x_{e}. \;\ \boldsymbol {\varepsilon }_{e}^{th}$ is the thermal strain vector for the element given by:

$$ \boldsymbol{\varepsilon}_{e}^{th} =\alpha (x_{e})\Delta T_{e}\boldsymbol{\varphi}^{T} $$

(6)

Here, $\alpha (x_{e})$ is the thermal expansion coefficient that is also dependent on element density, $\Delta T_{e}$ is the temperature change on the element and $\varphi$ is simply [1 1 0] or [1 1 1 0 0 0] for two and three dimensional problems, respectively. Substitution of (5) and (6) into (4) yields:

$$ \mathbf{F}_{e}^{th} =E(x_{e})\alpha (x_{e})\Delta T_{e} \int\limits_{\Omega_{e}} \mathbf{B}_{e}^{T} \overline{\mathbf{C}}_{e} \boldsymbol{\varepsilon}_{e}^{th} \boldsymbol{\varphi}^{T}d \Omega $$

(7)

in which we note that both $E(x_{e})$ and $\alpha (x_{e})$ are dependent on density design variables and thus both necessitate material interpolation. To simplify, we combine these parameters into a single thermal stress coefficient (TSC) as:

$$ \beta (x_{e})=E(x_{e})\alpha (x_{e}) $$

(8)

The TSC is then treated as an inherent material property and $\mathbf {F}_{e}^{th}$ can be rewritten as:

$$ \mathbf{F}_{e}^{th} =\beta (x_{e})\Delta T_{e} \int\limits_{\Omega_{e}}\mathbf{B}_{e}^{T}\overline{\mathbf{C}}_{e}\boldsymbol{\varepsilon}_{e}^{th}\boldsymbol{\varphi}^{T}d \Omega $$

(9)

4.1 Material interpolation

It is known that in the presence of design dependent type loading, including thermal loads, the Solid Isotropic Material with Penalization (SIMP) interpolation scheme presents numerical difficulties. This occurs because the scheme has zero sensitivity at zero density. As a result, in this work we adopt the Rational Approximation of Material Properties (RAMP) model, which has nonzero slope at zero density. In this model the stiffness and TSC are interpolated according to:

$$ E(x_{e})=\frac{x_{e}}{1+R_{E}(1-x_{e})}E_{o} $$

(10)

$$ \beta (x_{e})=\frac{x_{e}}{1+R_{\beta}(1-x_{e})}E_{o} \alpha_{o} $$

(11)

where $R_{E}$ and $R_{\beta }$ are RAMP parameters that have different values for elastic modulus and TSC. In addition, $E_{o}$ and $\alpha _{o}$ are baseline material properties for the elastic modulus and the coefficient of thermal expansion, respectively.

4.2 Density filter and heaviside projection

To prevent checkerboarding and enforce length scale a basic density filter is employed (Bruns and Tortorelli 2001). In addition, to eliminate transition areas of gray material along structural boundaries and obtain more complete black/white designs a Heaviside projection filter is utilized (Guest et al. 2004). The criteria of black/white design is desirable because while intermediate density material may result in superior thermoelastic performance (as evidenced by the usage of bi-material structures in other works) in practical application it is difficult to physically realize these structural characteristics when using high temperature aerospace metals or even composites. The Heaviside filter, which is applied immediately after the density filter in the algorithm takes the form of a smooth Heaviside function:

$$ \overline{x}_{e} =1-e^{-\gamma \widetilde{x}_{e}} +\widetilde{x}_{e} e^{-\gamma} $$

(12)

where $\widetilde {x}_{e}$ is the intermediate density resulting from density filtering and $\overline {x}$ is the physical density that describes the structure after Heaviside projection. The parameter $\gamma \ge 0$ describes the curvature of the projection which is linear at $\gamma = 0$ and approaches a Heaviside step as $\gamma$ approaches infinity. In this work, a continuation scheme is utilized where $\gamma$ is initial equal to zero and increased to 1 after 50 iterations. It is then gradually increased from 1 to 256 by doubling its value every 50 iterations or when the maximum change between design variables in consecutive iterations is less than 0.01. Sensitivity analysis is also modified with the appropriate chain rules for application of both the density filter and projection as discussed by Guest et al. (2004) and Andreassen et al. (2011).

4.3 Computational model and implementation

The topology optimization algorithm and finite element analysis is developed in MATLAB. This represents a divergence from Nastran in the demonstration problem because a custom implementation allows for topology optimization with thermal loads and ease of coupling between FEA and topology optimization with analytical sensitivity analysis. The structure is discretized using 2D bilinear quadrilateral plane strain elements with 52 elements in the vertical direction and 150 elements in the horizontal direction. This results in a design problem with 7,500 topology variables as the upper most elements lie in the non-design domain as shown in Fig. 10. We also note the elements are not perfectly rectangular due to the curvature of the top of the domain. Boundary conditions consist of fixed degrees of freedom on each node along the edges of the non-design domain. This is consistent with clamped boundaries of the original thin component in the demonstration case. Loading conditions that are specific to each topology optimization formulation are described in following sections.

Fig. 10

Finite element model for topology optimization

4.4 Minimum compliance with thermal loading

The first formulation investigated is the basic minimum compliance (maximum stiffness) objective with a volume fraction constraint. This is the most common problem setup for topology optimization. A uniform temperature change of ΔT = 900° F is applied to the entire model with no externally applied mechanical loads. This represents a design scenario where thermal effects are orders of magnitude more significant than mechanical loading. While the validity of the compliance objective for topology optimization with thermal loads has been questioned, we nonetheless investigate it to gain further insights into why it fails to yield useful results for these types of problems. The mathematical statement of the topology optimization problem is given as:

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} \mathrm{minimize:} & c(\mathbf{x})=\mathbf{U}^{T}\mathbf{KU} \\ \mathrm{subject \; to:} & \sum\limits_{e=1}^{N}(x_{e} \mathit{v}_{e} - \mathit{v}f \cdot \mathit{v}_{e}) \le 0 \\ & \mathbf{KU}=\mathbf{F}^{th} \\ & \mathbf{0} < \mathbf{x}_{\mathrm{min}} \le \mathbf{x} \le \mathbf{1} \\ \end{array} \end{array} $$

(13)

where c is compliance, x is the vector of density design variables, U is the displacement vector, K is the stiffness matrix, $\mathbf {F}^{th}$ is the thermal load vector resulting from the uniform elevated temperature, $\mathit {v}_{e}$ is the volume of element e, and vf is the allowable volume fraction. The sensitivity of the compliance objective to design variable j with a design dependent load is obtained via the adjoint method as:

$$ \frac{\partial c}{\partial x_{j}} =\mathbf{U}^{T} \left(2\frac{\partial \mathbf{F}^{th}}{\partial x_{j}} -\frac{\partial \mathbf{K}}{\partial x_{j}}\mathbf{U} \right) $$

(14)

4.5 Fictitious mechanical load method

The second topology optimization formulation takes a different approach to stiffness design for restrained expansion. It was first demonstrated in the dissertation by Haney (2005) and attempts to derive a structure using only mechanical loading that behaves favorably in a thermal environment. The problem statement here takes the form of a basic minimum compliance case with mechanical loading:

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} \mathrm{minimize:} & c(\mathbf{x})=\mathbf{U}^{T}\mathbf{KU} \\ \mathrm{subject \; to:} & \sum\limits_{e=1}^{N}(x_{e} \mathit{v}_{e} -\mathit{v}f \cdot \mathit{v}_{e}) \le 0 \\ & \mathbf{KU} = \mathbf{F}^{m} \\ & \mathbf{0} < \mathbf{x}_{\mathrm{min}} \le \mathbf{x} \le \mathbf{1} \\ \end{array} \end{array} $$

((15))

In this case, we note that there is no thermal load and $\mathbf {F}^{m}$ is simply an externally applied mechanical load. To determine the application of this load we recognize the fact that the optimum structure resulting from a problem of the form in (15) contains stiffness aligned in directions to best resist the load $\mathbf {F}^{m}$. Simply put, a structure is developed that is resistant to deformation in the direction of the applied load, but has very little stiffness in any other direction. Recalling our original design goal of reducing out-of-plane deformation of the original thin structure with restrained expansion, it follows that this may be accomplished by applying a fictitious mechanical load (in the absence of thermal loads) in the direction we wish to reduce displacement. Logically, it also follows that since the mechanically derived structure has little stiffness in off-load directions, it is rendered incapable of generating large reaction loads due to a lack of material to undergo expansion in those orientations.

While intuitively suitable designs may be generated if only the fictitious loads are oriented in the proper direction, in reality resulting designs are sensitive to exactly how they are applied (for example, a uniformly distributed load case or fewer discrete loads). To illustrate this sensitivity two different fictitious load configurations, shown in Fig. 11, are demonstrated. Both sets of fictitious loads are oriented in the out-of-plane direction with respect to the original thin structure, which represents the direction we desire to reduce deformation, and each sum to 1,000 lb.

Fig. 11

Fictitious Load Case 1 (a) and 2 (b) for the second topology optimization formulation, the fictitious mechanical load method

4.6 Thermoelastic combination method

The final technique to solve the stiffening problem is a proposed extension of the previous fictitious mechanical load method. While the previous problem setup exploits the fundamental mechanics of minimum compliance topology optimization, it does not directly address the boundary reaction increases that usually result from adding material in a thermal environment. In addition, the resulting designs are dependent upon the exact application of fictitious load cases. In an effort to both remove this dependency and directly place limits on the additional reaction loads generated by a stiffening structure, we propose to place a constraint in optimization directly on the in-plane thermal reaction loads.

The minimum compliance objective function is utilized, where the compliance is determined from a purely mechanical finite element analysis with fictitious mechanical loading. In addition, a separate thermoelastic simulation is performed where loading consists of a only a uniform elevated temperature of ΔT = 900° F applied to the entire domain. The in-plane reaction load from this analysis is utilized to directly enforce constraints in the topology optimization problem. The mathematical statement of the topology design problem is given as:

$$ \begin{array}{ll} \mathrm{minimize:} & c(\mathbf{x})=\mathbf{U}_{1}^{T}\mathbf{KU}_{1} \\ \mathrm{subject to:} & \sum\limits_{e=1}^{N}(x_{e} \mathit{v}_{e} - \mathit{v}f \cdot \mathit{v}_{e}) \le 0 \\ & R-R_{L} \le 0 \\ & \mathbf{KU}_{1} = \mathbf{F}^{m} \\ & \mathbf{KU}_{2} = \mathbf{F}^{th} \\ & \mathbf{0} < \mathbf{x}_{\mathrm{min}} \le \mathbf{x} \le \mathbf{1} \\ \end{array} $$

(16)

In (16), we note the presence of two finite element systems with $\mathbf {U}_{1}$ representing the displacement vector for the system with fictitious mechanical load set $\mathbf {F}^{m}$ and $\mathbf {U}_{2}$ representing the displacement vector for the system with the thermal load $\mathbf {F}^{th}$. The compliance c is computed using $\mathbf {U}_{1}$, and is thus dependent only on the fictitious mechanical load. R is the in-plane reaction load for the thermal load system and $R_{L}$ is the limiting load for the new constraint. This quantity may be determined from the vector of reaction loads obtained following the solution of the second finite element problem using (17) and (18):

$$ \mathbf{R} = \mathbf{KU}_{2} - \mathbf{F}^{th} $$

(17)

$$ R = \sum\limits_{i\in D}R_{i} $$

(18)

Here R is a vector of loads that contains reaction forces at degrees of freedom on which boundary conditions are applied and zeros elsewhere. $\mathbf {F}^{th}$ in this case is the load vector before the elimination of degrees of freedom by boundary condition application in the finite element solution process. The total reaction load R is determined via (18) as the summation of individual loads $R_{i}$ on degrees of freedom i in the set D, which consists of x-direction components on nodes along the edge of the non-design region where boundary conditions are applied. The sensitivity of the resultant load to design variable j is obtained as:

$$ \frac{\partial R}{\partial x_{j}} =\sum\limits_{i \in D}\frac{\partial R_{i}} {\partial x_{j}} $$

(19)

where the sensitivity of the resultant load at a particular degree of freedom is determined by the adjoint method and (20).

$$ \frac{\partial R_{i}} {\partial x_{j}} =\frac{\partial \mathbf{K}_{i}} {\partial x_{j}} \mathbf{U}_{2} + \boldsymbol{\lambda}_{i}^{T} \left( \frac{\partial \mathbf{F}^{th}}{\partial x_{j}} -\frac{\partial \mathbf{K}}{\partial x_{j}} \mathbf{U}_{2} \right)-\frac{\partial F_{i}^{th}}{\partial x_{j}} $$

(20)

In this case, K$_{i}$ represents a 1 by n (number of degrees of freedom in the entire model) vector equal to row i of the global stiffness matrix and $F_{i}^{th}$ is the load vector element at degree of freedom i. $\lambda _{i}$ is the adjoint vector obtained by solving the adjoint system given in (21).

$$ \mathbf{K}\boldsymbol{\lambda}_{i} = \mathbf{K}_{i}^{T} $$

(21)

We note that we must solve one adjoint equation for each degree of freedom to include in the summation of reaction forces for the sensitivity analysis as presented here.

A basic summary of the solution of the two finite element systems required for this method is demonstrated in Fig. 12 with associated loading conditions. Numerical results are provided in the results section for a variety of reaction load limits to illustrate its significance in stiffening material distribution.

Fig. 12

Pure mechanical fictitious load problem (a) used to compute compliance objective and thermoelastic problem (b) used to determine reaction constraint

5 Topology optimization results

The topology optimization results obtained for the three methods are presented in the following sections. In addition, an assessment of the generated topologies is performed to compare their performance from both a displacement reduction and reaction load perspective. In each problem, material properties are identical to those in the demonstration case. Unless otherwise noted, the initial design vector is equal to the volume fraction. The MMA algorithm is used for optimization (Svanberg 1987).

5.1 Minimum compliance with thermal load

The result for the minimum compliance topology optimization problem with purely thermal loading outlined in (13) is shown in Fig. 13, where the dotted line indicates the boundary of the designable region. In this case, the RAMP parameters are $R_{E} = 8$ and $R_{\beta } = 0$ and the allowable volume fraction is taken as 0.20. We observe that the optimum structure contains only trace amounts of added material near the application of the boundary conditions. This occurs due to the participation of thermal loading directly in the compliance objective. In this scenario, where thermal loads heavily dominate mechanical effects, any material addition with the exception of in localized regions that may deformation in the non-design domain actually increases the compliance of the entire structure. This becomes obvious in iteration history of compliance and volume shown in Fig. 14. It is readily obvious that to achieve a minimum compliance design, as little material as possible should be utilized. This parallels the conclusions of the demonstration case where it was observed material addition isn’t always beneficial in a thermal environment.

Fig. 13

Resulting topology for the minimum compliance with thermal load problem formulation

Fig. 14

Iteration history for the minimum compliance with thermal load problem formulation

To further demonstrate, the sensitivity of the compliance objective to element density design variables is shown in Fig. 15. Sensivities for a design variable field with all elements equal to 0.001, 0.10, and 0.20 are provided. We see in each case the majority of elements, with the exception of small localized regions which were retained in the optimum structure in Fig. 13, have a positive gradient. This indicates that the existance of these elements, and the accompanying increased thermal load, serves to only increase compliance.

Fig. 15

Compliance sensitivity for each element at (a) $x = 0.001$, (b) $x = 0.10$, and (c) $x = 0.20$

From these results it becomes evident that in cases with significant thermal loads and an absence of mechanical effects, the minimum compliance topology optimization formulation is unable to produce suitable designs. In fact, the majority of thermoelastic topology optimization literature only investigates cases where the amount of thermal loading is benign compared with mechanical loading and thus these effects are avoided. With the fictitious mechanical load and thermoelastic combination results that follow, we demonstrate that alternative problem formulations can lead to usable results.

5.2 Fictitious mechanical load method

Figure 16 shows the optimum topology designs obtained via the fictitious mechanical load method of (15) for the two fictitious load sets in Fig. 11. Two volume fractions, 0.20 and 0.30, respectively, are given. The RAMP parameter for all cases of this method was $R_{E} = 8$.

Fig. 16

Topology optimization results for volume fractions of 0.20 (left column) and 0.30 (right column) for fictitious load case 1 (a, b) and case 2 (c, d). Reaction load ratio ($R/R_{o}$) for each design a 2.18, b 2.32, c 1.73, and d 1.81

In contrast to the previous method, it is obvious that potentially useful stiffening structures are obtained. This is to be expected because in fact, a well posed minimum compliance with purely mechanical loading problem was posed. We note that in each case, optimum structures span the entire depth of the designable region and contain a lower inverted arch structure. This inverted arch is connected to the upper non-design region at locations where the fictitious loads are applied. We also note that increasing the allowable volume fraction results in an identical design with thicker members. These results are characteristic of the particular type of topology optimization problem that was solved. The iteration history for compliance objective and volume fraction constraint is given in Fig. 17. Note the sharp jumps in responses correspond to points when the $\beta$ parameter in the Heaviside filter is increased.

Fig. 17

Iteration histories for the fictitious mechanical load method with (a) load case 1 and (b) load case 2 for a volume fraction of 0.20

To investigate the thermoelastic performance of each of structure, a thermoelastic analysis was performed wherein the fictitious loads were removed, and the structures were subjected to a uniform elevated temperature of ΔT = 900° F. The reaction ratio $R/R_{o}$, which is the reaction load for a particular design divided by that of the unstiffened non-design domain, was obtained to assess the designs from a reaction increase perspective. $R/R_{o}$ for the designs in Fig. 16 are (a) 2.18, (b) 2.32, (c) 1.73, and (d) 1.81. From these results we draw two conclusions. First, regardless of the application of fictitious loading, increased material usage leads to greater reaction loading. This is supported by evidence from the demonstration case, where adding material to the domain yielded increases in reactions. Second, it is apparent from the slightly lower reaction load from fictitious load case 2 that some configurations of fictitious loading may lead to superior designs from a thermoelastic point-of-view. Results obtained by the thermoelastic combination method presented in the next method further investigate this conclusion.

5.3 Thermoelastic combination method

Figure 18 gives the results for the thermoelastic combination method in (16) for reaction constraints corresponding to reaction ratio $R/R_{o}$ of 1.25, 1.50, and 1.75. Results for both fictitious load cases utilized previously are presented. The allowable volume fraction is taken as 0.2 and the RAMP parameters are $R_{E} = 16$ and $R_{\beta } = 2$.

Fig. 18

Topology optimization rsults for the thermoelastic combination problem using fictitious load case 1 (a, c, e) and case 2 (b, d, f) with constraints on reaction load corresponding $R/R_{o}$ a, b 1.25, c, d 1.50, and e, f 1.75

It is observed that for lower allowable reaction loading ($R/R_{o} = 1.25$) in Fig. 18a and b that nearly identical designs are obtained for both fictitious load cases. This indicates that the thermoelastic problem formulation has removed the sensitivity of results on the application of fictitious loading when trying to better control the magnitude of reaction loads. It also appears that a structure has been generated in which the in-plane expansion of the upper non-design domain and the lower arch-like structure, which now appears more rounded when compared to earlier results, is counteracted by the mechanics of the internal connecting members. This apparent tailoring of thermoelastic behavior allows for the satisfaction of tighter limits on reaction load.

If the reaction constraint is relaxed such that $R/R_{o}$ is 1.50, we observe from Fig. 18b and c that the resulting structures still resemble fundamentally the same basic configuration. The designs now contain less complex internal connecting members that in fact resemble those in Fig. 16c for strictly fictitious load case 2. Continuing to relax the reaction constraint to allow $R/R_{o}$ of 1.75 in Fig. 18e and f, which is near to the reaction values obtained from cases with only fictitious load designs, leads to structures that differ for each fictitious load case, but resemble those obtained previously. The primary differences compared to designs in Fig. 16a and c is that the internal connecting members appear to be angled slightly more towards the horizontal and the structures do not span the entire depth of the designable region. This demonstrates that as one seeks to obtain stiffening structures that lead to more benign reaction loading, additional information must be directly included in the design problem because it is difficult, if not impossible, to identify which fictitious load case will lead to suitable designs a priori.

The iteration history of the compliance, volume constraint, and reaction constraint for each case is given in Fig. 19. It is notable from the iteration history that by introducing thermal loading into the problem by way of the reaction constraint, rather than directly in the compliance objective (as was done with the minimum compliance with thermal load case) the volume constraint remains active in the final design. This results in a problem from which we may obtain suitable designs. From this exercise it also becomes obvious that some stiffening configurations are much more suitable to controlling the amount of reaction load that is generated from the added material.

Fig. 19

Iteration history for compliance, volume constraint, and reaction constraint, corresponding to the topology thermoelastic combination topology optimization problems

5.4 Qualitative comparisons

In this section the thermoelastic qualities of the structures produced by the fictitious mechanical load and thermoelastic combination methods are studied. Designs are compared in terms of the reaction ratio $R/R_{o}$ and the displacement ratio $U/U_{o}$. Similar to the reaction ratio, the displacement ratio is the out-of-plane displacement measured at the top center node of the non-design domain for a particular stiffened design to that of purely the non-design domain with no stiffening material. As analogy to metrics used in Section 2.2, these ratios indicate the true effectiveness of the stiffening designs obtained by topology optimization. They also provide insight into the unique mechanics by which they accomplish a reduction in deformation while limiting reaction load (Table 1).

Table 1 Reaction and displacement comparison for all structural topologies

We note from the table that in all cases, the displacement ratio is reduced. This indicates that the minimum compliance problem using the fictitious mechanical load cases does resulting in structures that are resistant to deformation out-of-plane and satisfy the basic design goals for displacement reduction. This holds true even when the structure is subjected to the elevated temperature environment after having been derived using mechanical loads. As evidenced by negative displacement ratios that for all of the designs, excluding those with the tightest reaction constraints, deformation at the middle of the non-design domain actually occurs downwards. This indicates the mechanics that produce the reduction in displacement, when compared to the undeformed case, result in a pull-down effect due to the expansion of the stiffening structure. For the designs produced by the thermoelastic combination method and reaction ratio limited to 1.25, we note the non-design domain still deforms in the positive direction, but only do so with roughly half the magnitude of the unstiffned structure. In practical application, this may result in a halving of out-of-plane displacement, which was shown previously in the demonstration case to remove nearly all tensile bending stresses, at only a 25 % increase in reaction loading. This is achieved only by harnessing the potential thermoelastic tailoring capabilities of topology optimization in which the proper thermoelastic responses are included in the problem formulation.

6 Conclusions

It is important to keep in mind that whenever possible, when designing a structure that is subjected to a thermal environment, one should attempt to accommodate thermal expansion/contraction to avoid the damaging effects of thermal stresses. From purely a thermal stress perspective, this is universally the best design solution. However, there exist a number of design scenarios in which accommodating thermal expansion is not possible due to additional design constraints or desired qualities for the system being considered. The fundamental challenges and some potential design solutions for such a case have been explored. Using a curved beam model, it was demonstrated that some fundamental practices for mechanical design at room temperature may not be applicable to design with restrained thermal expansion due to the design dependency of thermal loading. In this case, more advanced alternative design methodologies must be utilized. In this work, three different topology optimization problems were presented and applied. It was demonstrated that a typical minimum compliance objective in the presence of thermal loading does not generate favorable designs. Methods using a fictitious mechanical load applied in such a way to generate a structure with favorable thermoelastic qualities showed better performance. However, since results obtained are dependent upon the application of fictitious loads, additional constraints on reaction loading were introduced to help desensitize the design to the loading configuration. With proper problem setup, a topology representing the necessary stiffening material that should be applied to a restrained thermal structure can be obtained that prevents out-of-plane deformation while simultaneously maintaining a reasonable amount of reaction load at structural boundaries.