1 Introduction

The topology optimization design of the continuum structures is one of the most challenging research topics in the field of the structural optimization (Bendsøe and Sigmund 2003). The purpose of the topology optimization design is to find the optimal lay-out of a structure within a specified region. The topology optimization design of the continuum structures is essentially a discretized 0–1 variables problem. Some familiar formulations including homogenization method (Bendsøe and Kikuchi 1988), variable density approach (Zhou and Rozvany 1991; Bendsoe and Sigmund 1999), evolutionary structural optimization approach (Xie and Steven 1993), level set-based approach (Sethian and Wiegmann 2000; Wang et al. 2003; Allaire et al. 2004) and ICM (Independent Continuous Mapping) method (Sui and Peng 2006) have been developed for topology optimization. The current investigations mainly focus on the problems, whose objective function are compliance or potential energy subjected to the global constraints, such as volume or natural frequency constraints. Less effort has devoted to topology optimization of continuum structures subjected to the displacement constraints. The displacement constraints are very important in practicable structures, and the design can not be put into use without considering the constraints.

To date, the prevailing numerical method in topology optimization is the finite element method (FEM). The finite elements are utilized not only to describe the fields of displacements and strains but also to represent the topology of structures. It can be seen that the standard SIMP model and most of its variants were formulated based on elemental design variables, in which the relative densities of elements are often treated as design variables. However, in topology optimization of continuum structures, the element density variables may be one of the reasons for the occurrence of numerical instabilities, for example, checkerboards, mesh-dependence, and a non-smooth zigzag boundary (Zhou et al. 2001; Sigmund and Petersson 1998). In addition, frequent remeshing is unavoidable when dealing with large deformation or moving boundary problems based on FEM. Recently, there have emerged several methods for topology optimization of structures based on nodal design variables of finite elements. Matsui and Terada (2004) studied the nodal density approximant for topology optimization problems by using finite element shape functions. Rahmatalla and Swan (2004) presented a nodal variable based topology optimization method to ensure C0 continuity of the design variables for suppressing checkerboards using finite elements. Kang and Wang (2011) discussed the merits of standard Shepard interpolations in preserving the physical meaning of density variables for topology optimization of structures.

In recent years, a group of meshless methods have been developed and achieved remarkable progress (Belytschko et al. 1996; Liu and Gu 2005), such as smooth particle hydrodynamics method (SPH) (Monaghan 1992), element free Galerkin method (EFG) (Belytschko et al. 1994), reproducing kernel particle method (RKPM) (Liu et al. 1995), meshless local Petrov–Galerkin method (MLPG) (Atluri and Shen 2002), collocation meshless method (Zhang et al. 2001), and so on. These are methods in which the approximate solution is constructed entirely in terms of a set of nodes, and no element or characterization of the interrelationship of the nodes is needed. The element free Galerkin method (EFG) is one of the popularly used meshless methods, as it generally exhibits very good numerical stability and possesses excellent rate of convergence and reasonably accurate results. The EFG method has been successfully applied to large variety of problems including two-dimension and three-dimension linear and nonlinear elastic problems (Belytschko et al. 1997), fracture and crack growth problems (Belytschko et al. 1994), plate and shell structures (Liu and Chen 2001), and so on. In EFG, the shape function is constructed by moving least square (MLS), and control equation is produced from the weak form of variational equation. Because the EFG shape function constructed using the MLS approximation lacks the Kronecker delta function property, special techniques are needed in the implementation of essential boundary conditions, for example, the penalty method, the Lagrange multiplier method, and so on. At present, some researchers have already explored structural topology optimization using meshless methods. Zhou and Zou (2008) introduced the implicit topology description function method into meshless method for optimization of continua. Zheng et al. (2008) applied the meshless radial point interpolation method (RPIM) to carry out a topology optimization design for the continuum structure. Cho and Kwak (2006) formulated a structural topology optimization method using the meshless method for geometric non-linearly modeling. Luo et al. (2013) proposed a structural topology optimization method using a dual-level point-wise density approximant and the meshless Galerkin weak-forms. Luo et al. (2012) also proposed a meshless Galerkin level set method for shape and topology optimization of continuum structures and used CSRBFs techniques to parameterize the level set surface and to construct the meshless shape functions.

This study aims to propose the topology optimization of continuum structures with displacement constraints using the element free Galerkin method (EFG). Considering the relative density at Gauss quadrature points as design variable, and the minimization of weight as an objective function, the mathematical formulation of the topology optimization is developed using the SIMP interpolation scheme. The approximate explicit function expression is given between topological variables and displacement constraint. The sensitivity analysis of topology optimization under displacement constraints is derived in detail, and the filtering technique is adopted to eliminate the checkerboard pattern with the point state. The problem is well solved by using optimality criteria. Three numerical examples are used to prove the feasibility of the approach adopted in this paper.

2 Element free Galerkin method for plane elasticity

2.1 Moving least square approximation

With the moving least square (MLS) method (Belytschko et al. 1994), if field variable is a function such as \(u({{\bf x}})\), the interpolation function \(u^{h} ({{\bf x}})\) in a sub-domain Ω s can be defined over a number of scattered local points x i (i = 1, 2, …, n) by

$$u^{h} ({{\bf x}}) = {{\bf P}}^{{{\bf T}}} ({{\bf x}}){{\bf a}}({{\bf x}}), \quad \forall {{\bf x}} \in \varOmega_{s}$$
(1)

where \({{\bf P}}({{\bf x}})\) is the basis function of the spatial coordinates. For two-dimensional problems, the complete polynomial basis functions are chosen as

$$\begin{array}{*{20}l} {\text{linear basis function}} \hfill & {{{\bf P}}^{{{\bf T}}} ({{\bf x}}) = \left[ {1,x_{1} ,x_{2} } \right]} \hfill & {{\text{m}} = 3} \hfill \\ {\text{quadratic basis function}} \hfill & {{{\bf P}}^{{{\bf T}}} ({{\bf x}}) = \left[ {1,x_{1} ,x_{2} ,x_{1}^{2} ,x_{1} x_{2} ,x_{2}^{2} } \right]} \hfill & {{\text{m}} = 6} \hfill \\ \end{array}$$

In Eq. (1), \({{\bf a}}({{\bf x}})\) is a vector containing coefficients which are functions of the global Cartesian coordinates \(\left[ {x_{1} ,x_{2} } \right]^{\text{T}}\), depending on the polynomial basis.

These coefficients can be obtained by minimizing a weighted discrete \({{\bf L}}_{2}\) norm defined as

$$J({{\bf x}}) = \sum\limits_{i = 1}^{n} {w({{\bf x}}_{i} ,{{\bf x}})[{{\bf P}}^{{{\bf T}}} ({{\bf x}}_{i} ){{\bf a}}({{\bf x}}) - {\hat{u}}_{i} ]^{2} }$$
(2)

where n is the number of nodes in the support domain of \({{\bf x}}\) for which the weight function \(w({{\bf x}}_{i} ,{{\bf x}}) \ne 0\); u i is the nodal parameter of u at \({{\bf x}} = {{\bf x}}_{i}\); and \(w({{\bf x}}_{i} ,{{\bf x}})\) is the weight function associated with the node i. In this paper, weight function is cubic spline weight function as below

$$w({{\bf x}}_{i} ,{{\bf x}}) = \left\{ {\begin{array}{*{20}l} {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3} - 4r_{i}^{2} + 4r_{i}^{3} } \hfill & {r_{i} \le 0. 5} \hfill \\ {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3} - 4r_{i} + 4r_{i}^{2} - {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}r_{i}^{3} } \hfill & { 0. 5 { < }r_{i} \le 1} \hfill \\ 0\hfill & {r_{i} > 1 \, } \hfill \\ \end{array} } \right.$$

where \(r_{i} = \frac{{d_{i} }}{{r_{w} }} = \frac{{\left| {{{\bf x}} - {{\bf x}}_{i} } \right|}}{{r_{w} }}\) in which \(d_{i} = \left| {{{\bf x}} - {{\bf x}}_{i} } \right|\) is the distance from node \({{\bf x}}_{i}\) to the interest point \({{\bf x}}\), and r w is the size of the support domain for the weight function.

The stationary of J with respect to \({{\bf a}}({{\bf x}})\) leads to the following set of linear relation

$${{\bf A}}({{\bf x}}){{\bf a}}({{\bf x}}) = {{\bf B}}({{\bf x}}){{\bf U}}_{s}$$
(3)

where \({{\bf U}}_{s}\) is the vector that collects the nodal parameters of the field function for all the nodes in the support domain, \({{\bf U}}_{s} = \left[ {{\hat{u}}_{1} ,{\hat{u}}_{2} , \ldots ,{\hat{u}}_{n} } \right]^{\text{T}}\); and \({{\bf A}}({{\bf x}})\) is called the weighted moment matrix defined by

$${{\bf A}}({{\bf x}}) = {{\bf P}}^{\text{T}} {{\bf WP}}\,{ = }\,\sum\limits_{i = 1}^{n} {w({{\bf x}}_{i} ,{{\bf x}}){{\bf P}}({{\bf x}}_{i} ){{\bf P}}^{{{\bf T}}} ({{\bf x}}_{i} )}$$
(4)

The matrix \({{\bf B}}({{\bf x}})\) in Eq. (3) is defined as

$${{\bf B}}({{\bf x}}) = {{\bf P}}^{\text{T}} {{\bf W}}\,{ = }\,\left[ {w({{\bf x}}_{1} ,{{\bf x}}){{\bf P}}({{\bf x}}_{1} ),w({{\bf x}}_{2} ,{{\bf x}}){{\bf P}}({{\bf x}}_{2} ), \ldots ,w({{\bf x}}_{n} ,{{\bf x}}){{\bf P}}({{\bf x}}_{n} )} \right]$$
(5)

Solving Eq. (3) for \({{\bf a}}({{\bf x}})\), we have

$${{\bf a}}({{\bf x}}) = {{\bf A}}^{ - 1} ({{\bf x}}){{\bf B}}({{\bf x}}){{\bf U}}_{s}$$
(6)

Substituting the above equation back into Eq. (1), we have

$$u^{h} ({{\bf x}}) = \sum\limits_{i = 1}^{n} {\phi_{i} ({{\bf x}}){\hat{u}}_{i} } = {\varvec{\Phi}}^{\text{T}} ({{\bf x}}){{\bf U}}_{s}$$
(7)

where \({\varvec{\Phi}}({{\bf x}})\) is the vector of MLS shape functions corresponding n nodes in the support domain of the point \({{\bf x}}\), and can be written as

$${\varvec{\Phi}}^{\text{T}} ({{\bf x}}) = \left[ {\phi_{1} ({{\bf x}}),\phi_{2} ({{\bf x}}), \ldots ,\phi_{n} ({{\bf x}})} \right] = {{\bf P}}^{{{\bf T}}} ({{\bf x}}){{\bf A}}^{ - 1} ({{\bf x}}){{\bf B}}({{\bf x}}).$$
(8)

2.2 Discrete equations in 2D problem

Considering the following standard two-dimension problem of linear elasticity defined in the domain Ω bounded by the boundary Γ

$$\left\{ {\begin{array}{*{20}l} {{{\bf L}}^{\text{T}} {\varvec{\sigma}} + {{\bf b}} = 0} \hfill & {{\text{in }}\varOmega } \hfill \\ {{\varvec{\sigma}} {{\bf n}} = {{\bf \bar{t}}}}\hfill & {{\text{on }}\varGamma_{\text{t}} } \hfill \\ {{{\bf u = \bar{u}}}} \hfill & {{\text{on }}\varGamma_{\text{u}} } \hfill \\ \end{array} } \right.$$
(9)

where \({{\bf L}}\) is the differential operator; \({\varvec{\upsigma}}\) is the stress vector; \({{\bf u}}\) is the displacement vector; \({{\bf b}}\) is the body force vector; \({\bar{{\bf t}}}\) is the prescribed traction on the natural boundaries; \({\bar{{\bf u}}}\) is the prescribed displacement on the essential boundaries; \({{\bf n}}\) is the vector of unit outward at a point on the natural boundary.

The element free Galerkin method uses the moving least squares (MLS) shape functions. Because the MLS approximation lacks the Kronecker delta function property, the constrained Galerkin weak form should be posed as follows

$$\int_{\varOmega } {\delta ({{\bf Lu}})^{\text{T}} {{\bf D}}({{\bf Lu}})} {\text{d}}\varOmega - \int_{\varOmega } {\delta {{\bf u}}^{\text{T}} {{\bf b}}} {\text{d}}\varOmega - \int_{{\varGamma_{t} }} {\delta {{\bf u}}^{\text{T}} {\bar{{\bf t}}}} {\text{d}}\varGamma - \delta \int_{{\varGamma_{u} }} {\frac{1}{2}({{\bf u - \bar{u}}})^{\text{T}} {\varvec{\upalpha}}({{\bf u - \bar{u}}})} {\text{d}}\varGamma = 0$$
(10)

where \({\varvec{\upalpha}} = \left| \!{\overline {\, {} \,}} \right. \alpha_{1} \, \alpha_{2} \, \cdots \, \alpha_{k} \left. {\underline {\, {} \,}}\! \right|\) is a diagonal matrix of penalty factors.

The displacement at any point can be approximated using n nodes in the local support domain of the point

$${{\bf u}} = \left\{ {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\phi_{1} } & 0 & \cdots & {\phi_{n} } & 0 \\ 0 & {\phi_{1} } & \cdots & 0 & {\phi_{n} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\hat{u}}_{1} } \\ {{\hat{v}}_{1} } \\ \vdots \\ {{\hat{u}}_{n} } \\ {{\hat{v}}_{n} } \\ \end{array} } \right\} = {\varvec{\Phi}} {\hat{{\bf u}}}$$
(11)

where \({\varvec{\Phi}}\) is the matrix of the shape functions, \({\hat{{\bf u}}}\) is the vector of the displacements at the field nodes in the support domain, and n is the number of nodes in the support domain of a quadrature point.

In terms of the integration by parts and the divergence theorem, the discrete governing equation corresponding to the weak formulation can be expressed by

$$\left[ {{{\bf K}} + {{\bf K}}^{\alpha } } \right]{{\bf U = F}} + {{\bf F}}^{\alpha }$$
(12)

where

$${{\bf K}} = \int_{\varOmega } {{{\bf B}}_{{}}^{\text{T}} {{\bf DB}}{\text{d}}\varOmega } ,\quad {{\bf F}} ={{\bf F}}^{b} + {{\bf F}}^{t} = \int_{\varOmega } {{\varvec{\Phi}}_{{}}^{\text{T}} {{\bf b}}{\text{d}}\varOmega } + \int_{{\varGamma_{\text{t}} }} {{\varvec{\Phi}}_{{}}^{\text{T}} {\bar{{\bf t}}}{\text{d}}\varGamma }$$
(13)
$${{\bf K}}_{{}}^{\alpha } = \int_{{\varGamma_{u} }} {{\varvec{\Phi}}_{{}}^{\text{T}} {\varvec{\alpha \varPhi }}{\text{d}}\varGamma ,\quad } {{\bf F}}^{\alpha } = \int_{{\varGamma_{u} }} {{\varvec{\Phi}}_{{}}^{\text{T}} {\varvec{\alpha}} {{\bf \bar{u}}}}{\text{d}}\varGamma$$
(14)
$${{\bf B}}_{I} = \left[ {\begin{array}{*{20}c} {\phi_{I,x} } & 0 \\ 0 & {\phi_{I,y} } \\ {\phi_{I,y} } & {\phi_{I,x} } \\ \end{array} } \right],\quad {{\bf D}} = \frac{E}{{1 - \mu^{2} }}\left[ {\begin{array}{*{20}c} 1 & \mu & 0 \\ \mu & 1 & 0 \\ 0 & 0 & {\left( {1 - \mu } \right)/2} \\ \end{array} } \right]$$
(15)

In the numerical implementation, the above equations will be assembled by using Gauss quadrature scheme over the problem domain. With the Gauss quadrature, these matrixes can be further expressed by

$${{\bf K}} = \sum\limits_{i = 1}^{ng} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} {{\bf B}}_{{}}^{\text{T}} \left( {{{\bf x}}_{i} } \right){{\bf DB}}\left( {{{\bf x}}_{i} } \right)\left| {{{\bf J}}\left( {{{\bf x}}_{i} } \right)} \right|}$$
(16)
$${{\bf F}} =\sum\limits_{i = 1}^{ng} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} {\varvec{\Phi}}_{{}}^{\text{T}} \left( {{{\bf x}}_{i} } \right){{\bf b}}\left( {{{\bf x}}_{i} } \right)\left| {{{\bf J}}\left( {{{\bf x}}_{i} } \right)} \right|} + \sum\limits_{i = 1}^{ng} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} {\varvec{\Phi}}_{{}}^{\text{T}} \left( {{{\bf x}}_{i} } \right){\bar{{\bf t}}}\left( {{{\bf x}}_{i} } \right)\left| {{{\bf J}}\left( {{{\bf x}}_{i} } \right)} \right|}$$
(17)

where ng is the number of gauss quadrature points, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i}\) is the weighting factors for the ith gauss point, \({{\bf J}}\left( {{{\bf x}}_{i} } \right)\) is the Jacobian matrix.

3 Formulation of the topology optimization

3.1 The optimization model with displacement constraints

SIMP (solid isotropic microstructures with penalization) is a common density interpolation model (Zhou and Rozvany 1991). In SIMP model, a penalization factor which has the effect of penalizing the intermediate density is introduced to ensure that the continuous design variables are forced towards to a 0–1 solution. The relation between the density and the material tensor is written as

$$E_{ijkl} \left( x \right) = \rho^{\text{p}} \left( x \right)E_{ijkl}^{0}$$
(18)

where E 0 ijkl and E ijkl represent the elastic modulus of a given solid material and interpolated elastic modulus, respectively; ρ(x) is design variable; p is a penalization factor, p ≥ 1.

In element free Galerkin (EFG) method, the global stiffness matrix in discrete equation is assembled by the stiffness matrix of Gauss points. So in order to reduce the computational tasks, the design variable is set at the Gauss quadrature point. Considering the relative density at Gauss quadrature points as design variable, and the minimization of weight as an objective function, the topology optimization problem of a continuum structure subjected to displacement constraints can be stated as follows

$$\begin{array}{*{20}l} {\hbox{min} . \, M = \sum\limits_{i = 1}^{ng} {\rho_{i} m_{i} } } \hfill \\ {s.t. \, u_{rl} \le \bar{u}_{r} \, (r = 1, \ldots ,R \, , \, l = 1, \ldots ,L)} \hfill \\ \quad {0 < \rho_{\hbox{min} } \le \rho_{i} \le 1} \hfill \\ \end{array}$$
(19)

where ρ i is the relative density of the ith Gauss points, and is the design variable; m i is the inherent weight of the ith Gauss points; u rl is the \(r{\text{th}}\) constrained displacement under the \(l{\text{th}}\) load condition; \(\bar{u}_{r}\) is the prescribed limit of u r ; R is the total number of displacement constraints in the design; L is the total number of load cases; ng is the number of Gauss quadrature points; ρ min is a lower bound on density, introduced to prevent any possible singularity, in the typical application, we set ρ min = 0.001.

To solve the optimization problem (19), the explicit function expression between topological variables and displacement constraints should be given firstly. According to Mohr theorem, the displacement of arbitrary point to the j direction can be calculated by

$$u_{j} = \sum\limits_{i = 1}^{ng} {D_{i} } = \sum\limits_{i = 1}^{ng} {\int {({\varvec{\upsigma}}_{i}^{v} )^{\text{T}} ({\varvec{\upvarepsilon}}_{i}^{R} )} {\text{d}}v}$$
(20)

where \({\varvec{\upsigma}}_{i}^{v}\) is the stress vector of the ith Gauss points under the unit pseudo load; \({\varvec{\upvarepsilon}}_{i}^{R}\) is the strain vector of the ith Gauss points under the real load.

By virtual work principle,

$$D_{i} = \int {({\varvec{\upsigma}}_{i}^{v} )^{\text{T}} ({\varvec{\upvarepsilon}}_{i}^{R} )} {\text{d}}v = ({{\bf F}}_{i}^{v} )^{\text{T}} {{\bf u}}_{i}$$
(21)

By system Eq. (12), we can have

$$u_{j} = ({{\bf F}}_{{}}^{v} )^{\text{T}} {{\bf U}} = ({\hat{{\bf U}}}^{v} )^{\text{T}} {\hat{{\bf K}}}(\rho ){{\bf U}}.$$
(22)

3.2 Sensitivity analysis

In general, the adjoint sensitivity method (Bendsoe and Sigmund 1999) is more effective for the sensitivity analysis when the number of design variables far exceeds that of structural performance functions. For this reason, the adjoint method is used to calculate the sensitivity of the objective function.

By the derivative of Eq. (22) with respect to the design variable ρ i , we can obtain as

$$\frac{{\partial u_{j} }}{{\partial \rho_{i} }} = \left( {{{\bf F}}^{v} } \right)^{\text{T}} \frac{{\partial {{\bf U}}}}{{\partial \rho_{i} }} = \left( {{{\bf F}}^{v} } \right)^{\text{T}} {\varvec{\Phi}}\frac{{\partial {\hat{{\bf U}}}}}{{\partial \rho_{i} }}$$
(23)

By the derivative of Eq. (12) with respect to the design variable ρ i , we can have

$$\frac{{\partial {{\bf K}}}}{{\partial \rho_{i} }}{\hat{{\bf U}}} + {\hat{{\bf K}}}\frac{{\partial {\hat{{\bf U}}}}}{{\partial \rho_{i} }} = 0$$
(24)

It can be rewritten as

$$\frac{{\partial {\hat{{\bf U}}}}}{{\partial \rho_{i} }} = - {\hat{{\bf K}}}^{ - 1} \frac{{\partial {{\bf K}}}}{{\partial \rho_{i} }}{\hat{{\bf U}}}$$
(25)

Substituting Eq. (25) into Eq. (23), we can have

$$\frac{{\partial u_{j} }}{{\partial \rho_{i} }} = - \left({{{\bf F}}^{v} } \right)^{\text{T}} {\varvec{\Phi}}{\hat{{\bf K}}}^{- 1} \frac{{\partial {{\bf K}}}}{{\partial \rho_{i}}}{\hat{{\bf U}}}$$
(26)

In solutions, there would appear some dispersed and no structural continuity points, analogous to so-call checkerboard pattern in FEM. In this paper, the phenomenon is termed the checkerboard pattern with the point state. The filtering of sensitivities is adopted to eliminate the checkerboard pattern with the point state. The filter modifies the design sensitivity of a specific Gauss point based on a weighted average of the Gauss point sensitivities in a fixed neighborhood. The filter works by modifying the Gauss point sensitivities as follows

$$\frac{{\overline{{\partial u_{j} }} }}{{\partial \rho_{e} }} = \frac{1}{{\rho_{e} \mathop \varSigma \limits_{f = 1}^{n} \overline{H}_{f} }}\mathop \varSigma \limits_{f = 1}^{n} \overline{H}_{f} \rho_{f} \frac{{\partial u_{j} }}{{\partial \rho_{i} }}$$
(27)

where \(\bar{H}_{f}\) is the convolution operator, and can be written as

$$\bar{H}_{f} = r_{\hbox{min} } - dist\left( {e,f} \right)$$

in which, r min is the filter radius; dist (e, f) is the distance between the Gauss points e and f.

3.3 Optimality criteria

After obtaining the design sensitivities, a number of efficient optimization algorithms can be used as the optimizer to find the solution. According to the mathematical formulation of the optimization problem, this study will choose the optimality criteria (OC) method (Rozvany et al. 1995).

The OC method is derived based on Kuhn-Tucker optimality conditions. The OC method is simple to understand and implement, and is especially efficient for problems with large number of design variables and few constraints. The effectiveness of the method comes from the fact that each design variable is updated independently of the update of the other design variables

The Lagrange function of the optimization problem (19) can be constructed as

$$L = m + \sum\limits_{l = 1}^{L} {\sum\limits_{r = 1}^{R} {\lambda_{rl} \left( {u_{rl} - \bar{u}_{r} } \right)} } + \sum\limits_{i = 1}^{ng} {\mu_{1}^{i} \left( {\rho_{\hbox{min} } - \rho_{i} } \right)} + \sum\limits_{i = 1}^{ng} {\mu_{2}^{i} \left( {\rho_{i} - 1} \right)}$$
(28)

where λ rl , μ 1 and μ 2 are Lagrangian multipliers and they must be non-negative.The well-known necessary condition for a stationary solution of the problem (19) is the Kuhn-Tucker condition, which here takes the form:

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial L}{{\partial \rho_{i} }} = \frac{\partial m}{{\partial \rho_{i} }} + \sum\limits_{l = 1}^{L} {\sum\limits_{r = 1}^{R} {\lambda_{rl} \frac{{\partial u_{rl} }}{{\partial \rho_{i} }}} } - \mu_{1} + \mu_{2} = 0} \hfill \\ {u_{rl} - \bar{u}_{r} = 0} \hfill \\ {\mu_{1} \left( {\rho_{\hbox{min} } - \rho_{i} } \right) = 0} \hfill \\ {\mu_{2} \left( {\rho_{i} - 1} \right) = 0} \hfill \\ {\rho_{\hbox{min} } \le \rho_{i} \le 1} \hfill \\ {\mu_{1} \ge 0{ , }\quad \mu_{2} \ge 0} \hfill \\ \end{array} } \right.$$

The above Kuhn-Tucker condition is equivalent to

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial m}{{\partial \rho_{i} }} + \sum\limits_{l = 1}^{L} {\sum\limits_{r = 1}^{R} {\lambda_{rl} \frac{{\partial u_{rl} }}{{\partial \rho_{i} }}} } = 0 \quad \rho_{\hbox{min} } < \rho_{i} < 1 \, } \hfill \\ {\frac{\partial m}{{\partial \rho_{i} }} + \sum\limits_{l = 1}^{L} {\sum\limits_{r = 1}^{R} {\lambda_{rl} \frac{{\partial u_{rl} }}{{\partial \rho_{i} }}} } \ge 0 \quad \rho_{i} \,{ = }\,\rho_{\hbox{min} } } \hfill \\ {\frac{\partial m}{{\partial \rho_{i} }} + \sum\limits_{l = 1}^{L} {\sum\limits_{r = 1}^{R} {\lambda_{rl} \frac{{\partial u_{rl} }}{{\partial \rho_{i} }}} } \le 0 \quad \rho_{i} = 1} \hfill \\ {u_{rl} - \bar{u}_{r} = 0} \hfill \\ \end{array} } \right.$$
(29)

Considering Eq. (29) is equivalent to 0, that is

$$\frac{\partial m}{{\partial \rho_{i} }} + \sum\limits_{l = 1}^{L} {\sum\limits_{r = 1}^{R} {\lambda_{rl} \frac{{\partial u_{rl} }}{{\partial \rho_{i} }}} } = 0$$

We define

$$B_{i} = - \frac{{\frac{\partial m}{{\partial \rho_{i} }}}}{{\sum\limits_{l = 1}^{L} {\sum\limits_{r = 1}^{R} {\lambda_{rl} \frac{{\partial u_{rl} }}{{\partial \rho_{i} }}} } }} = 1$$
(30)

an update scheme for the design variables is formulated as follows

$$\rho_{i}^{new} = \left\{ {\begin{array}{*{20}l} {\hbox{max} (\rho_{\hbox{min} } ,\rho_{i} - m)\quad{\text{ if }}\rho_{i} B_{i}^{\eta } \le \hbox{max} (\rho_{\hbox{min} } ,\rho_{i} - m)} \hfill \\ {\rho_{i} B_{i}^{\eta }\quad {\text{ if }}\hbox{max} (\rho_{\hbox{min} } ,\rho_{i} - m) < \rho_{i} B_{i}^{\eta } < \hbox{min} (1,\rho_{i} + m)} \hfill \\ {\hbox{min} (1,\rho_{i} + m)\quad{\text{ if }}\hbox{min} (1,\rho_{i} + m) \le \rho_{i} B_{i}^{\eta } } \hfill \\ \end{array} } \right.$$
(31)

where m is a positive move-limit, η is a numerical damping coefficient. The introduction m and η is to ensure the stability of the iteration.

4 Numerical examples

4.1 Example 1

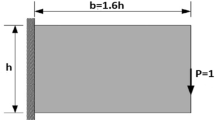
A cantilever beam, as shown in Fig. 1, is now discussed. The left-hand side of the beam is fixed and a concentrated force \(F = 10\,{\text{kN}}\) is applied at the middle of the free end. The problem domain is discretized by 651 field nodes, and 600 rectangular background cells are used for the numerical integration, in each background cell 2 × 2 Gauss quadrature points are employed. The elastic material properties are chosen as Young’s modulus \(E = 3 \times 10^{8} \,{\text{Pa}}\), Possion’s ratio μ = 0.3. The initial total weight of the structure is 600 ton, the initial displacement of the loaded point P in the vertical direction is 0.006 mm, and the vertical downward displacement constraint at point P is 0.019 mm.

Fig. 1
figure 1

Example 1

Full size image

The optimization result of the beam obtained by the present method without sensitivity filtering is shown in Fig. 2a, and the checkerboard pattern exists in the final result. The optimization result with sensitivity filtering is shown in Fig. 2b. It can be seen from these results that the filtering can effectively eliminate the checkerboard pattern phenomenon.

Fig. 2
figure 2

Optimization results

Full size image

The variation of the objective function with iterative number is shown in Fig. 3. Without sensitivity filtering, the value of the objective function decreases from 600 to 204.2 ton, and the number of iteration is 82. With sensitivity filtering, the value of the objective function decreases from 600 to 227.8 ton, and the number of iteration is 81. The variation of the value of the displacement at the point P with iterative number is shown in Fig. 4. Without sensitivity filtering, the final displacement at the point P in the vertical direction is 0.01879 mm. With sensitivity filtering, it is 0.0188 mm.

Fig. 3
figure 3

Variation curve of the objection function

Full size image
Fig. 4
figure 4

Variation curve of the displacement at the point P

Full size image

4.2 Example 2

The initial structural model is shown in Fig. 5, which is fixed at both lower corners and subject to a concentrate force \(F = 1\,{\text{kN}}\) at the center of the lower edge. The problem domain is discretized by 21 × 41 field nodes, and 800 rectangular background cells are used for the numerical integration, in each background cell 2 × 2 Gauss quadrature points are employed. The elastic material properties are chosen as Young’s modulus \(E = 3 \times 10^{8} \,{\text{Pa}}\), Possion’s ratio μ = 0.3, and mass density \(\rho = 7800{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\). The initial displacement of the loaded point P in the vertical direction is 0.02 mm, the vertical downward displacement constraint at point P is 0.06 mm.

Fig. 5
figure 5

Example 2

Full size image

The optimization result of the structure obtained by the present method is shown in Fig. 6. The objective function (mass) optimization history with iterative number is shown in Fig. 7. The value of the objective function decreases from 3900 to 1181 kg. The optimization history of the displacement at the point P with iterative number is shown in Fig. 8.

Fig. 6
figure 6

Optimization results

Full size image
Fig. 7
figure 7

Mass optimization history of the structure

Full size image
Fig. 8
figure 8

Optimization history of displacement at point P

Full size image

4.3 Example 3

We consider the cantilever beam as shown in Fig. 9. The left-hand side of the beam is fixed, a concentrated force \(F_{1} = - 1\,{\text{kN}}\) is applied at the point P1 and a concentrated force \(F_{2} = 1\,{\text{kN}}\) is applied at the point P2. The problem domain is discretized by 441 field nodes, and 400 rectangular background cells are used for the numerical integration, in each background cell 2 × 2 Gauss quadrature points are employed. The elastic material properties are chosen as Young’s modulus \(E = 3 \times 10^{8} {\text{Pa}}\), Possion’s ratio μ = 0.3. The initial total weight of the structure is 100 ton, the initial displacement of the loaded point P 1 in the vertical direction is −0.047 mm, the initial displacement of the loaded point P 1 in the vertical direction is 0.049 mm, the vertical downward displacement constraints at point P 1, P 2 are 0.14 mm.

Fig. 9
figure 9

Example 3

Full size image

The optimization result obtained by the present method under the action of F 1 is shown in Fig. 10a, the optimization result under the action of F 2 is shown in Fig. 10b, and the optimization result by the co-action of F 1 and F 2 is shown in Fig. 10c. In Ref (Zhou and Rozvany 1991), considering the minimization of compliance as objective function and the volume as constraint, the same model is solved by the finite element method (FEM). The optimization result is shown in Fig. 10d. From these results, it can be seen that similar optimization results were obtained by two different algorithms, and a smoother optimization result can be obtained by the present method.

Fig. 10
figure 10

Optimization results

Full size image

The variation of the objective function with iterative number is shown in Fig. 11, the value of the objective function decreases from 100 to 36.52 ton, and the number of iteration is 77. The variation of the value of the displacement at the point P 1, P 2 with iterative number is shown in Fig. 12. The final displacement at the point P 1 in the vertical direction is −0.14, and is 0.14 mm at the point P 2.

Fig. 11
figure 11

Variation curve of the objection function

Full size image
Fig. 12
figure 12

Variation curve of the displacement at the point P 1 and P 2

Full size image

5 Conclusions

In this paper, the element free Galerkin method (EFG) is applied to solve the topology optimization problem of the continuum structures subjected to displacement constraints. Based on the EFG method, a set of field nodes are used to constructed numerical simulation and optimization problem in the design domain, without requiring to consider the mesh connectivity. Considering the relative density at Gauss quadrature points as design variables, and the minimization of weight as an objective function, the mathematical formulation of the optimization is developed using the SIMP interpolation scheme. The approximate explicit function expression between topological variables and displacement constraints are derived. The filtering technique of sensitivity is applied to eliminate the checkerboard pattern with the point state. Several numerical examples are shown to prove the validity and feasibility of the present method. And the examples also show the simplicity and fast convergence of the proposed method. In future work the proposed method can be straightforwardly extended to more advanced topology optimization problems, involving geometrical nonlinearity problems, material nonlinearity problems, discontinuity problems and singularity problems, to which the meshless methods are more applicable than FEM method.