1 Introduction

Repetitive analysis is usually needed when the structure is modified and optimized. One of the main obstacle of repetitive analysis is the high computational cost in the large scale problems solution. Reanalysis technology, which aims to evaluate the structural response for changed structures, such as displacements, stresses, frequencies and so on, without solving the complete set of modified equations, came into being from the 1970s (Arora 1976; Phansalkar 1974). Many approximate (Kirsch and Rubinstein 1972) and exact (Level et al. 1996) reanalysis methods were proposed to analyze structures which are modified due to changes in design and optimization. Approximate methods are more efficient and popular. Combined approximations (CA) method proposed by Kirsch is one of the effective approximate methods for solving static displacement equations (Kirsch 2000, 2003b). Responses of the original structures are used in the solution procedures, and then the computational efficiency is improved compared to the repetitive analysis.

Based on CA method, extended CA methods were proposed to solve the structural static reanalysis. A hybrid Fox and CA method combined the merits of Fox’s polynomial fitting reanalysis and CA reanalysis was suggested, which had the advantage of globe-local approximation (Zuo et al. 2012). To determine the number of basis vectors of CA method, an adaptive technique is used (Sun et al. 2014). Based on the symmetric successive over-relaxation and corresponding sparse raw, Wang et al. improved the efficiency of CA method on GPU platform (Huang et al. 2014; Wang et al. 2013).

Research of vibration reanalysis methods have been discussed since the early 2000s (Chen et al. 2000; Kirsch and Bogomolni 2007). Kirsch firstly transplanted the CA approach to solve eigenproblems (Kirsch 2003a), where approximation results can be obtained by solving smaller eigenproblems in a reduced Krylov subspace composed of several approximation vectors. CA method could not give enough accuracy in many large modification cases of structural design. To improve the accuracy of the eigenvalues reanalysis of large modifications of structural parameters, combining CA and Rayleigh quotient, Chen developed an extended CA method (Chen and Yang 2000). Then Epsilon algorithm was then applied in the eigenproblem reanalysis associated with the Neumann series expansion (Chen et al. 2006). A modified combined approximations method for reanalysis of dynamic problems with many dominant mode shapes was discussed (Zhang et al. 2009). Using a suitable frequency-shift method, the frequency-shift combined approximations approach allowed to calculate higher modes accurately (Xu et al. 2011). Combined with CA method and Newmark-β method, an adaptive reanalysis algorithm was suggested for dynamic analysis (Gao et al. 2013). Then, with the multi-GPU acceleration (He et al. 2015), real large-scale structural design problem can be reanalyzed and the vehicle design cycle was reduced (Wang et al. 2016).

In structural design process, the sensitivity, which can provide search direction, is indispensable to the engineer. Based on reanalysis of displacements, efficient sensitivity of displacement was first presented by Kirsch (Kirsch 1994). A unified approach for accurate approximations of displacement derivatives with respect to design variables was then presented (Kirsch and Papalambros 2001). Currently, analytical sensitivity reanalysis of static displacement was investigated by using Taylor series expansion and CA method to improve the efficiency (Zuo et al. 2016). Finite-difference derivatives of static, vibration and dynamic response were given by Kirsch (Kirsch and Bogomolni 2005; Kirsch et al. 2007). Topology optimization for specified eigenfrequency was accelerated by using CA method and corresponding frequency sensitivity analysis (Bogomolni 2010). Reanalysis and sensitivity reanalysis by CA method was summarized by Kirsch in his article (Kirsch 2010). However, rather less attention has been paid to the analytical sensitivity reanalysis of vibration problem, which is also essential information in many flexible structural optimizations.

In this study, a novel sensitivity reanalysis method of vibration problem is proposed to acquire the derivatives of the eigenvalues and eigenvectors. In this method, only a much smaller eigenproblem and its derivative problem are needed to be calculated. The formulas of sensitivity reanalysis of vibration problem are expressed in Section 2, and then three numerical examples of 8-bar truss structure, truss grid and a monocoque bus frame are demonstrated for the accuracy in Section 3. Finally, efficiency consideration and conclusion are summarized in Section 4.

2 Sensitivity reanalysis formulations

In this paper, sensitivity reanalysis of vibration problem is proposed in the framework of CA method. Therefore, the reanalysis of eigenvalue and eigenvector is firstly introduced here from CA method.

2.1 Kirsch’s reanalysis of vibration problem

Given an initial design with stiffness matrix K 0 and mass matrix M 0. The corresponding eigenvector r 0 and eigenvalue λ 0 are calculated by solving the set of initial equations

$$ {\mathbf{K}}_0{\mathbf{r}}_0={\lambda}_0{\mathbf{M}}_0{\mathbf{r}}_0 $$
(1)

where K 0 is given from the initial analysis in the decomposed form

$$ {\mathbf{K}}_0={\mathbf{U}}_0^{\mathbf{T}}{\mathbf{U}}_0 $$
(2)

and U 0 is an upper triangular matrix. λ 0 = ω 20 , ω 0 is the circle free-vibration frequency.

Assuming there is a change in the design, then corresponding changes in the stiffness matrix and mass matrix can be expressed respectively

$$ \mathbf{K}={\mathbf{K}}_0+\varDelta \mathbf{K},\kern1.12em \mathbf{M}={\mathbf{M}}_0+\varDelta \mathbf{M} $$
(3)

Then the modified equations are given by

$$ \mathbf{K}\mathbf{r}=\lambda \mathbf{M}\mathbf{r} $$
(4)

For new eigenpairs λ and r, the CA method can obtain them efficiently and accurately. Calculation of r in (4) by the CA method involves the following steps (Kirsch 2003a):

  1. (a)

    Calculate the basis vectors by steps of iteration. The detailed explanation has been demonstrated in CA method. Here we directly give the form of the basis vectors

    $$ {\mathbf{r}}_1={\lambda}_0{\mathbf{K}}_0^{-1}\mathbf{M}{\mathbf{r}}_0 $$
    (5)

    For k = 2 to s

    $$ {\mathbf{r}}_k=-\mathbf{B}{\mathbf{r}}_{k-1} $$
    (6)

    where s is the number of basis vector which is much smaller than the structural degrees of freedom (DoFs), and B = K − 10 ΔK. Notice that we have acquired the decomposed form of K 0 in process of solving the original equations, so the calculations of basis vectors involve only forward and back substitutions of (6).

  2. (b)

    Calculate the new eigenvector r. Assume r can be approximated by the linear combination of s pre-selected linearly independent basis vectors r 1, r 2, ⋯, r s , i.e.

    $$ \mathbf{r}={y}_1{\mathbf{r}}_1+{y}_2{\mathbf{r}}_2+\cdots +{y}_s{\mathbf{r}}_s={\mathbf{r}}_B\mathbf{y} $$
    (7)

    where \( {\mathbf{r}}_B=\left[\begin{array}{cccc}\hfill {\mathbf{r}}_1,\hfill & \hfill {\mathbf{r}}_2,\hfill & \hfill \cdots, \hfill & \hfill {\mathbf{r}}_s\hfill \end{array}\right] \) and y = [y 1, y 2, ⋯, y s ]T.

    Now substitute (7) into (4) and pre-multiply r T B

    $$ {\mathbf{r}}_B^T\mathbf{K}{\mathbf{r}}_B\mathbf{y}={\mathbf{r}}_B^T\lambda \mathbf{M}{\mathbf{r}}_B\mathbf{y} $$
    (8)

    With the notation

    $$ {\mathbf{K}}_R={\mathbf{r}}_B^T\mathbf{K}{\mathbf{r}}_B,{\mathbf{M}}_R={\mathbf{r}}_B^T\mathbf{M}{\mathbf{r}}_B $$
    (9)

    (8) is reduced as a s × s eigenproblem

    $$ {\mathbf{K}}_R\mathbf{y}=\lambda {\mathbf{M}}_R\mathbf{y} $$
    (10)

    This small-scale equation can be efficiently solved by Jacobi method. And then substituting the obtained λ and y into (7), r is yielded.

2.2 The proposed sensitivity reanalysis of vibration problem

In the following, we derive the sensitivity of eigenvector r with respect to the design variable x i . Differentiating (7) directly with respect to x i gives the first-order derivative equations at the modified design

$$ \frac{\partial \mathbf{r}}{\partial {x}_i}=\frac{\partial {\mathbf{r}}_B}{\partial {x}_i}\mathbf{y}+{\mathbf{r}}_B\frac{\partial \mathbf{y}}{\partial {x}_i} $$
(11)

In order to acquire ∂r/∂x i , we should firstly calculate ∂r B/∂x i and ∂y/∂x i . The stiffness matrix K is usually explicit functions of the design variables. K 0, r 0 and λ 0 are constant for arbitrary change of design variable x i , so ∂r 1/∂x i can be expressed as

$$ \frac{\partial {\mathbf{r}}_1}{\partial {x}_i}={\mathbf{K}}_0^{-1}{\lambda}_0\frac{\partial \mathbf{M}}{\partial {x}_i}{\mathbf{r}}_0 $$
(12)

For k = 2 to s

$$ \frac{\partial {\mathbf{r}}_k}{\partial {x}_i}=-{\mathbf{K}}_0^{-1}\frac{\partial \Delta \mathbf{K}}{\partial {x}_i}{\mathbf{r}}_{k-1}-{\mathbf{K}}_0^{-1}\Delta \mathbf{K}\frac{\partial {\mathbf{r}}_{k-1}}{\partial {x}_i}=-{\mathbf{K}}_0^{-1}\left(\frac{\partial \Delta \mathbf{K}}{\partial {x}_i}{\mathbf{r}}_{k-1}+\Delta \mathbf{K}\frac{\partial {\mathbf{r}}_{k-1}}{\partial {x}_i}\right) $$
(13)

Accordingly, we obtain

$$ \frac{\partial {\mathbf{r}}_B}{\partial {x}_i}=\left[\begin{array}{cccc}\hfill \frac{\partial {\mathbf{r}}_1}{\partial {x}_i},\hfill & \hfill \frac{\partial {\mathbf{r}}_2}{\partial {x}_i},\hfill & \hfill \cdots, \hfill & \hfill \frac{\partial {\mathbf{r}}_s}{\partial {x}_i}\hfill \end{array}\right] $$
(14)

Additionally, ∂y/∂x i is the derivative of the eigenvector from the reduced eigenproblem (10). Since we have calculated λ and y, ∂y/∂x i can be solved by using Nelson method (Nelson 1976). Rewrite (10) as

$$ \left({\mathbf{K}}_R\mathbf{\hbox{-}}\lambda {\mathbf{M}}_R\right)\mathbf{y}=0 $$
(15)

Besides, y and M R satisfy the following normal equation

$$ {\mathbf{y}}^T{\mathbf{M}}_R\mathbf{y}=1 $$
(16)

Differentiate (15) and (16) directly with respect to x i and rearrange them as

$$ \left({\mathbf{K}}_R\mathbf{\hbox{-}}\lambda {\mathbf{M}}_R\right)\frac{\partial \mathbf{y}}{\partial {x}_i}=-\left(\frac{\partial {\mathbf{K}}_R}{\partial {x}_i}-\frac{\partial \lambda }{\partial {x}_i}{\mathbf{M}}_R-\lambda \frac{\partial {\mathbf{M}}_R}{\partial {x}_i}\right)\mathbf{y} $$
(17)
$$ {\mathbf{y}}^T{\mathbf{M}}_R\frac{\partial \mathbf{y}}{\partial {x}_i}=-\frac{1}{2}{\mathbf{y}}^T\frac{\partial {\mathbf{M}}_R}{\partial {x}_i}\mathbf{y} $$
(18)

Premultiply (17) by y T, and noting (15) and (16), we obtains the derivative of eigenvalue

$$ \frac{\partial \lambda }{\partial {x}_i}={\mathbf{y}}^T\left(\frac{\partial {\mathbf{K}}_R}{\partial {x}_i}-\lambda \frac{\partial {\mathbf{M}}_R}{\partial {x}_i}\right)\mathbf{y} $$
(19)

Noting (9), one can obtain the derivative of reduced matrix K R and M R , respectively

$$ \frac{\partial {\mathbf{K}}_R}{\partial {x}_i}=\frac{\partial {\mathbf{r}}_B^T}{\partial {x}_i}\mathbf{K}{\mathbf{r}}_B+{\mathbf{r}}_B^T\frac{\partial \mathbf{K}}{\partial {x}_i}{\mathbf{r}}_B+{\mathbf{r}}_B^T\mathbf{K}\frac{\partial {\mathbf{r}}_B}{\partial {x}_i} $$
(20)
$$ \frac{\partial {\mathbf{M}}_R}{\partial {x}_i}=\frac{\partial {\mathbf{r}}_B^T}{\partial {x}_i}\mathbf{M}{\mathbf{r}}_B+{\mathbf{r}}_B^T\frac{\partial \mathbf{M}}{\partial {x}_i}{\mathbf{r}}_B+{\mathbf{r}}_B^T\mathbf{M}\frac{\partial {\mathbf{r}}_B}{\partial {x}_i} $$
(21)

Because y = [y 1, y 2, ⋯, y s ]T is obtained in (10), we select the maximum element of vector y, for example y k . Then, introducing the notation

$$ \mathbf{R}=-\left(\frac{\partial {\mathbf{K}}_R}{\partial {x}_i}-\frac{\partial \lambda }{\partial {x}_i}{\mathbf{M}}_R-\lambda \frac{\partial {\mathbf{M}}_R}{\partial {x}_i}\right)\mathbf{y} $$
(22)

we let the elements of matrix K R  ‐ λ M R and R are, respectively

$$ \begin{array}{l}{\left({\mathbf{K}}_R\mathbf{\hbox{-}}\lambda {\mathbf{M}}_R\right)}_{ki}=0,\ {\left({\mathbf{K}}_R\mathbf{\hbox{-}}\lambda {\mathbf{M}}_R\right)}_{ik}=0,\ i=1,2,\cdots, s,\ i\ne k\\ {}{\left({\mathbf{K}}_R\mathbf{\hbox{-}}\lambda {\mathbf{M}}_R\right)}_{kk}=1,\ {\mathbf{R}}_k=0\end{array} $$
(23)

Solve (17) to obtain vector v, and

$$ \frac{\partial \mathbf{y}}{\partial {x}_i}=\mathbf{v}+c\mathbf{y} $$
(24)

where c is an unknown parameter which can be determine by substituting (24) into (18)

$$ c=-{\mathbf{y}}^T\left(\frac{1}{2}\frac{\partial {\mathbf{M}}_R}{\partial {x}_i}\mathbf{y}+{\mathbf{M}}_R\mathbf{v}\right) $$
(25)

In summary, the DoFs of the reduced (17) is much smaller than that of the corresponding equation of complete structure, so it is efficient to calculate ∂y/∂x i by the Nelson method.

3 Numerical examples

Three examples are used to demonstrate the efficiency and accuracy of the proposed sensitivity reanalysis method in application of structural modifications.

3.1 8-bar truss structure

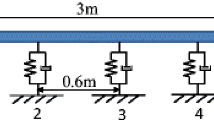
A 8-bar truss structure is shown in Fig. 1, where l = 36cm, elastic modulus is 72,000 MPa, and density is 2700 kg/m3. Design variables are the cross-sectional area of bar members, i.e. \( \mathbf{x}={\left[\begin{array}{cccc}\hfill {x}_1,\hfill & \hfill {x}_2,\hfill & \hfill \cdots, \hfill & \hfill {x}_8\hfill \end{array}\right]}^T \). The initial cross-sectional areas are \( {\mathbf{x}}_0={\left[\begin{array}{cccc}\hfill 10,\hfill & \hfill 10,\hfill & \hfill \begin{array}{cccc}\hfill \begin{array}{cc}\hfill 10,\hfill & \hfill 10,\hfill \end{array}\hfill & \hfill 10,\hfill & \hfill 10,\hfill & \hfill 10\hfill \end{array},\hfill & \hfill 10\hfill \end{array}\right]}^T \) whereas the arbitrarily modified cross-sectional areas are listed in vector \( \mathbf{x}={\left[\begin{array}{cccc}\hfill 11,\hfill & \hfill 10,\hfill & \hfill \begin{array}{cccc}\hfill \begin{array}{cc}\hfill 8,\hfill & \hfill 9,\hfill \end{array}\hfill & \hfill 10,\hfill & \hfill 11,\hfill & \hfill 10\hfill \end{array},\hfill & \hfill 10\hfill \end{array}\right]}^T \). Three basis vectors are used to approximately solve the modified structure. The approximate and accurate eigenvalue and eigenvector sensitivities are compared in Table 1. To concisely present the results, u 4y1 and u 4y2 are selected to list in Table 1, which denote modal displacements of the 1st and 2nd orders at the 4th node in the y direction, respectively. It can be seen that the reanalysis error of eigenvalue sensitivity is less than 1%. For the eigenvector sensitivity, the accuracy of the 1st order is higher than that of the 2nd order. However, the accuracy of eigenvector sensitivity is lower than that of eigenvalue sensitivity. Therefore, the proposed method can provide highly accurate frequency sensitivity for structural optimization with the constraint of frequencies. Next, the efficiency of this method is further investigated by large-scale structures.

Fig. 1
figure 1

8-bar truss structure

Full size image
Table 1 Eigenvalue and eigenvector sensitivities of 8-bar truss structure
Full size table

3.2 Truss grid

A truss grid with six groups is shown in Fig. 2, whose elastic modulus is E = 2.1 × 105MPa and density is 7.85 × 10− 9 t/mm 3. It consists of 906 bars, 259 nodes and 518 DOFs. All these 906 bar members are classified into six groups and each bar which belongs to the same group has the identical cross-sectional area, so there are six design variables \( \mathbf{x}={\left[\begin{array}{cccc}\hfill {x}_1,\hfill & \hfill {x}_2,\hfill & \hfill \cdots, \hfill & \hfill {x}_6\hfill \end{array}\right]}^T \) for this structure. The initial and modified design variables are \( {\mathbf{x}}_0={\left[\begin{array}{cccc}\hfill 120,\hfill & \hfill 160,\hfill & \hfill \begin{array}{ccc}\hfill 100,\hfill & \hfill 80,\hfill & \hfill 60\hfill \end{array},\hfill & \hfill 40\hfill \end{array}\right]}^T \) and \( \mathbf{x}={\left[\begin{array}{cccc}\hfill 123,\hfill & \hfill 158.5,\hfill & \hfill \begin{array}{ccc}\hfill 103.5,\hfill & \hfill 77.5,\hfill & \hfill 59\hfill \end{array},\hfill & \hfill 38.5\hfill \end{array}\right]}^T \), respectively. We choose the first order eigenvalue λ 1 and the u 1y1 component of the corresponding eigenvector u 1 with respect to six design variables to concisely demonstrate the results, as listed in Table 2. For eigenvalue sensitivity, all the approximate solution is equal to the exact solution. The accuracy of eigenvector sensitivity increases with the number of basis vector. In the case of 3 basis vector, the error of eigenvector sensitivity is reduced to 1.5%, which can be accepted in engineering design. Computational cost spent on the sensitivity reanalysis of λ 1 and u 1 with respect to six design variables is 3.2 s, while that of exact analysis is 15.6 s. The proposed approximate method has improved the efficiency by almost 5 times, compared with the exact method.

Fig. 2
figure 2

6-groups truss grid structure

Full size image
Table 2 First order eigenvalue and eigenvector sensitivities of truss grid structure
Full size table

3.3 Bus frame

A monocoque bus frame, as shown in Fig. 3, is used as an example to demonstrate the effectiveness of the proposed method for real large-scale structure. This bus frame has 172 nodes, 1032 DoFs and 333 thin-walled box beam elements which are grouped into 12 components. The thin-walled box cross section of each component has three design variables height h, breadth b and thickness t, as marked in Fig. 4. The material is Q235 steel with elastic modulus 2.05 × 105 MPa, poisson ratio 0.27 and density 7.85 × 10− 9 t/mm3. The initial and modified cross-sectional sizes of three components are listed in Table 3. The first 20 orders eigenvectors of the initial bus frame is selected as the basic vectors. In this numerical example, we calculate the sensitivities of eigenvalues and eigenvectors for the first two orders with respect to the cross-sectional variables of the ceiling component (denoted as b 1, h 1, t 1) and the lower floor component (denoted as b 2, h 2, t 2). In the design of bus body structure, the vibration of driver’s position should be controlled to satisfy the demand of comfort. Accordingly, the first two order eigenvector sensitivities ∂u z1 /∂x i and ∂u z2 /∂x i in the z direction at the driver’s position are calculated and listed in Table 4. The maximum error is 13.0%, which may be completely accepted at the conceptual design stage of bus frame. During the structural optimization, move limit technology is extensively used to calculate the step size of design variables, so as to control the magnitude of design modification. The design variables approach to the optimal solution step by step, and each step can belong to small modification (Thomas et al. 2002).

Fig. 3
figure 3

Monocoque bus frame

Full size image
Fig. 4
figure 4

Thin-walled box cross section and its design variables

Full size image
Table 3 Comparisons between the initial and modified cross-sectional sizes
Full size table
Table 4 Eigenvalue and eigenvector sensitivities of bus frame
Full size table

Besides, the average time spent on the exact analysis is 52s, while the approximate method only needs 14s, which saves 73.1% of computational cost. There are 12 components in the bus frame, meanwhile each component has 3 design variables. During the structural optimization, more than 200 iterations often occur. If that, the sensitivity analysis will cost 200 × 52 s (about 3 h) for the exact analysis, while it needs only 200 × 14 s (about 45 min) by using the proposed method. The efficiency of optimization may be obviously improved.

4 Conclusion

This paper proposes a sensitivity reanalysis of vibration problem in the framework of CA method. Three numerical examples verify the accuracy and efficiency of the presented method. For the eigenvector sensitivity, the accuracy of the 1st order is higher than that of the 2nd order. Also, the accuracy of eigenvector sensitivity increases with the number of basis vector. However, the accuracy of eigenvector sensitivity is lower than that of eigenvalue sensitivity. Additionally, the proposed approximate method has greatly improved the efficiency, compared with the exact method. In terms of the accuracy of sensitivity reanalysis, truss structure is superior to frame structure. It is because that each bar element in truss structure has only one design variable, while each box beam element in frame structure has three. Therefore, the accuracy of sensitivity reanalysis is determined by both modification and the number of design variables.

The proposed method can be applied in any structural optimization problem constrained with frequency or modal shape responses. Sensitivity calculation occupies a large part of the optimization process. Using the proposed method, almost three quarters of calculating time can be reduced. During the process of structural optimization, exact analysis and approximate reanalysis should be alternately used to calculate the responses and its derivatives, where exact solution can provide the initial values for approximate reanalysis. In this way, the accumulated reanalysis error can be truncated and independent of the iteration number of structural optimization.