A reanalysis method for local modification and the application in large-scale problems

Abstract

A novel reanalysis method, named independent coefficients (IC) method is suggested in this study. This method is proposed to reanalyze structures with local modification which leads to a low-rank change in the stiffness matrix. IC method requires only initial solution as input, and can determine the independent coefficients for each degree of freedoms (DOFs) influenced by structural modifications. Since any extra operations such as decomposition of the initial stiffness matrix is not involved in computation procedure, the IC is a “cheap” algorithm and can be an alternative choice for reanalysis. In order to verify the performance of IC method, several large scale numerical examples are tested. The results demonstrate that the IC method has high accuracy as well as efficiency when the modification is local. The cases involving beyond 1,500,000 DOFs and 3,000,000 DOFs show that IC method has low demands on computer storage, and large scale problems can be easily reanalyzed by this method.

1 Introduction

Reanalysis is an important research area for structure optimization, and the studies have made some significant improvements. The combined approximation (CA) might be the most popular method of reanalysis. The advantage of CA is that the efficiency of local approximations and the accuracy of global approximation are integrated to construct a feasible method. The classical CA method (Kirsch 2002, 2010; Kirsch and Papalambros 2001) uses an initial solution by complete analysis and binomial series to construct basis vectors for predicting the modified structure. It is only suitable for small modification, and the DOFs of structure must be fixed (Kirsch 2002). In order to deal with the bottleneck of the classical CA, Kirsh and Papalambros suggested an unified approach (Kirsch and Papalambros 2001) by introducing a modified initial design (MID), and Chen developed an approximate two-step method (Chen and Yang 2004) for modified structure with added DOFs. To solve the case with large modification of structure, Chen also proposed an iterative combined approximation (ICA) method (Yang et al. 2004). The ICA method divides the large modification into some pieces, and uses CA method to deal with small changes of stiffness matrix in an iterative way. The CA method is also developed for ill-conditioned system of equations (Huang et al. 2011) using singular value decomposition. Rational approximation (Wu et al. 2003) is another kind of fast algorithm which uses an accurate initial solution and binomial series to construct basis vectors just like CA method do. The difference is that CA method obtains the coefficient of each basis vector by resolving the reduced equations, while rational approximation uses rational approximation method, such as Padé approximation to achieve the coefficients for reduced equations.

Above mentioned methods have the capability to reanalyze all kinds of real engineering problems, such as structural static reanalysis (Kirsch 2000), eigenvalue reanalysis (Kirsch 2000; Huang et al. 2000; He et al. 2007), nonlinear dynamic reanalysis (Kirsch et al. 2006) topological optimization (Bogomolny 2010; Amir et al. 2009) and can be combined with genetic algorithm (Zuo et al. 2011). However, among these methods, the initial requirements for each method commonly are different, such as decomposition of initial stiffness matrix. Furthermore, the initial solvers are various, which include direct method such as matrix decomposition, and iterative method such as conjugate gradient (CG) (Wu et al. 2004) and so on, and some of them cannot provide the data that the reanalysis methods really need. If a reanalysis method needs only the initial solution as input, it will be more convenient and flexible, since it can be integrated with any solvers ideally.

Therefore, a reanalysis method named as independent coefficients (IC) is suggested in this study. This method requires only the initial solution for input, and determines the independent coefficient for each DOF influenced by structural modifications. The distinctive characteristic of the IC method is to avoid using any extra information such as decomposition of initial stiffness matrix, and the storage space is also reduced significantly. In the IC method, the change of the solution after modification is approximated by a linear combination of some basis vectors, which are constructed by some preselected DOFs. The basis vectors are used to reduce the scale of the equilibrium equation, and the coefficients of basis vectors are obtained by solving the reduced equations. The IC method is efficient to the modifications in a relatively small number of elements and nodes. When the modification is local, the efficiency of IC method is much higher than complete analysis, and the accuracy can be ensured as well. With the increasing of scale of FE model, the advantage of IC should prevail.

The rest of this paper is described as follows. The basic theories of IC method are described in details in Section 2. In Section 3, three numerical examples are shown to test the performance of the IC method. Finally, the conclusions are summarized in Section 4.

2 Independent coefficients method

2.1 Background description

Assuming that the initial equilibrium equations of the structure are

$$ {\mathbf{K}}_{0} {\mathbf{r}}_{0} =\mathbf{F}, $$

(1)

where, r $_{0}$ are initial displacements, which can be obtained by any available method include direct methods and iterative methods. After modifications, the new equilibrium equations are

$$ {\mathbf{Kr}}=\mathbf{F}. $$

(2)

The mission of reanalysis is to solve (2) as efficient and accurate as possible, which usually means not to solve (2) directly.

2.2 Formulation

The IC method replaces solving (2) directly with calculating the displacements of the DOFs influenced by the corresponding modifications. Major strategy of IC is summarized as follows.

Assuming that the solution of the modified equations is

$$ \mathbf{r}={\mathbf{r}}_{0} +\Delta \mathbf{r}, $$

(3)

Equation (2) can be written as

$$ \mathbf{K}\left( {\mathbf{r}}_{0} +\Delta \mathbf{r} \right)=\mathbf{F}. $$

(4)

Transforming (4) into

$$ \mathbf{K}\Delta {\mathbf{r}=\mathbf{F}-\mathbf{Kr}}_{0}, $$

(5)

and defining

$$ \boldsymbol{\delta }={\mathbf{F}-\mathbf{Kr}}_{0}, $$

(6)

Equation (5) becomes

$$ \mathbf{K}\Delta \mathbf{r}={\boldsymbol{\delta }}. $$

(7)

$\boldsymbol {\delta }$ can be defined as the residual value of the initial solution ${\mathbf {r}}_{0}$. Since the modification is local, only some members of $\boldsymbol {\delta }$ are non-zero. Pre-select a small tolerance $\varepsilon ,$ all the DOFs related to the non-zero members of $\boldsymbol {\delta }$ should be recorded for the rest steps of IC method. For instance, if $\left | \boldsymbol {\delta } ( i ) \right | > \varepsilon ,$ the i-th row of K should be checked to choose the DOFs influenced by modifications. If K(i,j) is not 0, the j-th DOF influenced by the modification is recorded. Assume that the selected DOFs are recorded in ${\mathbf {S}}_{d}$, and the number of the selected DOFs is $n_{d}$. For example, if the first 3 DOFs are selected, then ${\mathbf {S}}_{d}= [1 2 3]^{T}$ and $n_{d}= 3$.

In the IC method, a series of basis vectors are selected and the linear combination of these basis vectors is used to approximate $\Delta \mathbf {r}$ in (7). Assuming that

$$ \Delta \mathbf{r}={\mathbf{v}}_{1} y_{1} +{\mathbf{v}}_{2} y_{2} +\cdots +{\mathbf{v}}_{s} y_{s} ={\mathbf{r}}_{B} \mathbf{y}, $$

(8)

where ${\mathbf {v}}_{1}, {\mathbf {v}}_{2}, \ldots , {\mathbf {v}}_{s}$ are the basis vectors, and $y_{1},y_{2},$ $\ldots , y_{s}$ are the coefficients of every basis vector. s is the number of the basis vectors, corresponding value equals to $n_{d}$. In (8),

$$ {\mathbf{r}}_{B} =\left[ {v_{1} \quad v_{2} \quad \cdots \quad v_{s} } \right], $$

(9)

$$ \mathbf{y}=\left[ {y_{1} \quad y_{2} \quad \cdots \quad y_{s} } \right]^T. $$

(10)

The independent coefficient for every selected DOF can be determined as follows.

For every $i= 1, 2, \ldots ,$ s, if the i-th selected DOF is DOF $j, {\mathbf {v}}_{i}$ can be constructed as

$$ {\mathbf{v}}_{i} =\left[ {0\,\, \cdots \,\, 0\,\, 1\,\, 0\,\, \cdots 0} \right]^{T},\left(1~\text{is\, the\,} j-\text{th\, element\, of\,} {{\mathbf{v}}_{\mbox{i}} } \right). $$

(11)

By this way, an independent coefficient can be determined for every displacement of the selected DOF.

Substituting (8) into (7), and premultiplying both side by ${\mathbf {r}}_{B}^{T}$, (7) becomes

$$ {{\mathbf{r}}_{B}^{T} \mathbf{Kr}}_{B} \mathbf{y}={\mathbf{r}}_{B}^{T} \boldsymbol{\delta}. $$

(12)

Defining

$$\begin{array}{@{}rcl@{}} {\mathbf{K}}_{R} ={\mathbf{r}}_{B}^{T} \mathbf{Kr}_{B} \\ {\mathbf{F}}_{R} ={\mathbf{r}}_{B}^{T} \boldsymbol{\delta} \end{array} $$

(13)

Equation (12) can be written as

$$ {\mathbf{K}}_{R} \mathbf{y}={\mathbf{F}}_{R} . $$

(14)

By solving (14), y is obtained. Substituting y into (8), the approximation of $\Delta$ r is achieved. Afterwards, r can be obtained by (3).

Assuming that the complete analysis solution of (2) is ${\mathbf {r}^{\ast }}$, (15) is used for evaluating the error of approximate solution:

$$ \Delta =\frac{\left\| \mathbf{r}-{\mathbf{r}}^{\ast} \right\|}{\left\| {\mathbf{r}}^{\ast} \right\|}. $$

(15)

The main procedure of the IC method is summarized as the flow chart shown in Fig. 1a. For comparison, the flow chart of the CA method is shown in Fig. 1b. From the figures, it is obviously to see that, the IC method pays more attention to compute $\Delta {\mathbf {r}}$, while the CA method computes the approximation of r directly.

Fig. 1

Flow chart of IC and CA. a IC method. b CA method

2.3 Computational efficiency and storage cost of IC method

Assuming that the scale of K is $n\times n$ and the half-bandwidth of the matrix is m. If (2) is solved directly such as triangular decomposition, the computation should be O($nm^{2}$). In topological optimization, local modification is frequently applied to the structure, which means $n_{d}$ will not be too large. For example, $n_{d}=n/10$ means there are 10 % DOFs influenced by the modification. In this case, the scale of ${\mathbf {K}}_{R}$ is $n_{d}\times n_{d}$, and the compute time of solving (17) is O($n_{d}m^{2}$). The value of O($n_{d}m^{2}$) is O($nm^{2}$)/10. In other words, it will cost 1/10 of the computation time of resolving (2) to resolving (14). Actually for most of local modification problems, especially in large scale cases, the influenced DOFs are much less than 10 %, which means the efficiency of IC method can be higher.

To discuss the computer storage space cost by the IC method, the features of ${\mathbf {R}}_{B}$ and ${\mathbf {K}}_{R}$ should be addressed. In the IC method, the number of basis vectors is much larger than other reanalysis methods. If ${\mathbf {R}}_{B}$ and ${\mathbf {K}}_{R}$ are not sparse, computer storage space cannot be saved. According to Section 2.2, it is easy to know that, there is only one non-zero element in every column of ${\mathbf {R}}_{B}$, thus ${\mathbf {R}}_{B}$ is sparse. For ${\mathbf {K}}_{R}$, a more special structure can be observed in this discussion compared with (13). Assuming that the i-th member of ${\mathbf {S}}_{d}$ is k, namely the i-th selected DOF is DOF k, and the j-th member of ${\mathbf {S}}_{d}$ is$~l$, namely the j-th selected DOF is DOF l, the matrix ${\mathbf {K}}_{R}$ can be computed as

$$ {\mathbf{K}}_{R} ( {i,j} )= {\mathbf{K}}( {k,l} ). $$

(16)

If ${\mathbf {S}}_{d}$ is arranged in ascending order, it is easily to observe that ${\mathbf {K}}_{R}$ is a $n_{d}$-rank sub-matrix of K. In other words, the sparsity of ${\mathbf {K}}_{R}$ is increasing along $n_{d}$.

Therefore, ${\mathbf {R}}_{B}$ and ${\mathbf {K}}_{R}$ are both sparse. In fact, the matrix ${\mathbf {R}}_{B}$ won’t appear in the procedure of the IC method summarized below.

However, the accuracy and efficiency are influenced by the scale of the modification. If the scale of the modification increases, $n_{d}$ will become larger, it means more computational time should be cost for solving more reduced equations. Theoretically, the accuracy won’t be influenced much if enough DOFs are selected to be reanalyzed. Considering an extreme case, if all of the DOFs are selected (all DOFs are influenced), IC method becomes a complete analysis and the result is accurate.

2.4 The procedure of IC method

According to the discussion in the above sections, the procedure of IC method can be summarized as follows:

• 1. Select a small value $\varepsilon$;

• 2. Calculate ${\boldsymbol {\delta }}={{\mathbf {F}}-{\mathbf {Kr}}_{0}}$;

• 3. Select the DOFs to be reanalyzed:

  For $i=1$ to n (n is the number of the DOFs)

  If $\left |\boldsymbol {\delta }(i)\right |>\varepsilon$

  For $j=1$ to n

  If K $(i,j)\neq 0$

  Save the number j in the vector ${\mathbf {S}}_{{d}}$

  End if

  End for

  End if

  End for

  Calculate $n_{{d}}$: $n_{{d}}$ is the number of the DOFs saved in ${\mathbf {S_{d}}}$

• 4. Reduce the equation:

  For $i=1$ to $n_{{d}}$

  $k={S_{d}}(i), {{\mathbf {F}}_{{R}}}(i)=\boldsymbol {\delta }(k)$

  For $j=1$ to $n_{{d}}$

  $l={\mathbf {S}}_{{d}}(j), {\mathbf {K}}_{{R}}(i,j)={\mathbf {K}}(k,l)$

  End for

  End for

• 5. Solve the reduced equation ${{\mathbf {K}}_{R}} {\mathbf {y}}={{\mathbf {F}}_{R}}$;

• 6. Calculate ${\mathbf {r}}={{\mathbf {r}}_{0}} +\Delta {\mathbf {r}}$:

  ${\mathbf {r}}={\mathbf {r}}_{0}$

  For $i=1$ to $n_{{d}}$

  $j={\mathbf {S}}_{\mathrm {d}}(i),$ ${\mathbf {r}}(j)={\mathbf {r}}(j)+{\mathbf {y}}(i)$

  End for

3 Numerical examples

3.1 Benchmark

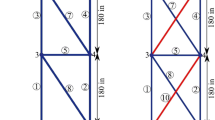
A stretch rod is shown in Fig. 2a. The rod is discretized into 4 nodes and 3 truss elements. The displacement of node 1 is restrained and a load P is enforced on node 4. The modulus of elasticity is E and the cross section of the rod is A. The length of each element is l.

Fig. 2

Stretch rod. a initial structure. b modified structure

According to the FEM theory, the initial equilibrium equation is

$$ \frac{AE}{l}\left[ {{\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 2 & {-1} & 0 \\ 0 & {-1} & 2 & {-1} \\ 0 & 0 & {-1} & 1 \\\end{array} }} \right]{\mathbf{r}_{0}} =\left[ {{\begin{array}{*{20}c} 0\\ 0\\ 0\\ P\\\end{array} }} \right].$$

(17)

The solution of (17) is

$$ {\mathbf{r}}_{0} =\frac{Pl}{AE}\left[ {0\quad 1\quad 2\quad 3} \right]^{T}. $$

(18)

Another node and element are added to the structure as a modification as shown in Fig. 2b, and the equilibrium equation of the modified structure is

$$ \frac{AE}{l}\left[ {{\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 0 & 2 & {-1} & 0 & 0 \\ 0 & {-1} & 2 & {-1} & 0 \\ 0 & 0 & {-1} & 2 & {-1} \\ 0 & 0 & 0 & {-1} & 1 \\\end{array} }} \right]{\mathbf{r}}=\left[ {{\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ P \\ 0 \\\end{array} }} \right]. $$

(19)

According to (6), the residual value of ${\mathbf {r}}_{0}$ is

$$ {\boldsymbol{\delta }}={\mathbf{F}-\mathbf{Kr}}_{0}=\left[ {0\quad 0\quad 0\quad -3P\quad 3P} \right]^T. $$

(20)

Therefore, ${\mathbf {S}}_{d} =\left [ {3\quad 4\quad 5} \right ]$ and $n_{\mathrm {d}}= 3$.

The reduced equation is

$$ \frac{AE}{l}\left[ {{\begin{array}{*{20}c} 2 & {-1} & 0 \\ {-1} & 2 & {-1} \\ 0 & {-1} & 1 \\\end{array} }} \right]{\mathbf{y}}=\left[ {{\begin{array}{*{20}c} 0 \\ {-3P} \\ {3P} \\\end{array} }} \right]. $$

(21)

Solving (21), obtains

$$ {\mathbf{y}}=\left[ {0\quad 0\quad \frac{3Pl}{AE}} \right]^T. $$

(22)

Thus, the change of the displacement is

$$ \Delta {\mathbf{r}}=\left[ {0\quad 0\quad 0\quad 0\quad \frac{3Pl}{AE}} \right]^T. $$

(23)

According to (3), the solution of the modified equation is

$$ {\mathbf{r}}={{\mathbf{r}}_{0}} +\Delta {\mathbf{r}}=\frac{Pl}{AE}\left[ {0\quad 1\quad 2\quad 3\quad 3} \right]^T. $$

(24)

By solving (19) directly, the exact solution can be obtained, which is

$$ {{\mathbf{r}}\ast} =\frac{Pl}{AE}\left[ {0\quad 1\quad 2\quad 3\quad 3} \right]^T. $$

(25)

Comparing (24) and (25), it is obviously to see that the IC method obtains the exact solution in this example.

Substituting some specific values for A, E, l and P, for example $A=E=l=P=1,$ the CA method is used to reanalyze the same problem.

By initial analysis, the inverse of the stiffness matrix is

$$ {\mathbf{K}_0^{-1}}=\left[ {{\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 2 & 2 \\ 0 & 1 & 2 & 3 \\\end{array} }} \right]. $$

(26)

Extending the dimensions of the inverse matrix, thus

$$ {\mathbf{K}_0^{-1}} =\left[ {{\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 1 & 2 & 2 & 0 \\ 0 & 1 & 2 & 3 & 0 \\ 0 & 0 & 0 & 0 & {10000} \\\end{array} }} \right]. $$

(27)

The change of the stiffness matrix is

$$ \Delta {\mathbf{K}={\mathbf{K}-{\mathbf{K}_{0}}}} =\left[ {{\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & {-1} \\ 0 & 0 & 0 & {-1} & {0.9999} \\\end{array} }} \right].$$

(28)

Then 2 basis vectors can be obtained, which are

$$ {\mathbf{R}_{b}} =\left[ {{\begin{array}{*{20}c} 0 & 0 \\ 1 & 3 \\ 2 & 6 \\ 3 & 9 \\ 0 & {-30000} \\\end{array} }} \right].$$

(29)

The reduced stiffness matrix and the reduced load vector are

$$ {\mathbf{K}_{r}} =\left[ {\begin{array}{l} \quad \quad 12\quad \quad \quad 9.0036\times 10^4 \\ 9.0036\times 10^4\quad 9.0045\times 10^8 \\ \end{array}} \right]\mbox{and}\, {\mathbf{F}_{r}} =\left[ {{\begin{array}{*{20}c} 3 \\ 9 \\\end{array} }} \right]. $$

(30)

Solve the reduced equations, obtaining

$$ {\mathbf{y}}={\mathbf{K}_{r}^{-1}} {\mathbf{F}_{r}} =\left[ {{\begin{array}{*{20}c} {1.0006} \\ {-0.0001} \\\end{array} }} \right].$$

(31)

The solution r then can be approximated as

$$ \mathbf{r}={\mathbf{R}}_{b} {\mathbf{y}}=\left[ {0\quad 1.0003\quad 2.0006\quad 3.0009\quad 3.0012} \right]^T. $$

(32)

Comparing with the exact solution

$$ {\mathbf{r}}^{\ast}= {\mathbf{R}}_{b} \mathbf{y} =\left[ {0\quad 1\quad 2\quad 3\quad 3} \right]^{T}, $$

(33)

The error of the approximation is 0.034 %.

3.2 Car frame

A simplified model and the main body size of a car frame are shown in Fig. 3. The shape and size of cross-section of the longitudinal and traverse beam are shown in Fig. 4.

Fig. 3

Simplified car frame model

Fig. 4

An illustration of cross section of frame model. a longitudinal beam b traverse beam

The frame FE model is composed of 118,200 elements and 120,546 nodes, involving 723,276 DOFs. To simulate bending of the frame, constraints can be applied according to Table 1. The vertically downward loads are enforced on the nodes marked E with the value of 500N and the nodes marked F with the value of 100N as shown in Fig. 5.

Table 1 DOF constraints

Fig. 5

Mesh model of frame

The modulus of elasticity is 200 GPa, and the Poisson’s ratio is 0.3. A direct method using matrix decomposition is used for solving the initial equations. The initial deformation solution is shown in Fig. 6.

Fig. 6

Initial deformation

As a modification, the thickness of traverse beam 1 shown in Fig. 5 becomes 20 mm and the one traverse beam 2 becomes 5 mm. The IC method and CA method and complete analysis method are used for analyzing structure with fixed constraints and loads. The IC method uses 5280 basis vectors and the CA method uses 6 basis vectors. The deformation results are shown in Figs. 7, 8 and 9, respectively.

Fig. 7

Deformation result by IC method

Fig. 8

Deformation result by CA method

Fig. 9

Deformation result by complete analysis

According to these figures, it is easy to observe that both the deformation results of the IC method and the CA method are close to the one of complete analyze, and a particular comparison of the displacements is shown in Table 2. Table 2 shows that the displacements of the IC method and the CA method are close to the complete analysis ones. According to (15), the error of the IC method is 0.38 %, and the error of the CA method is 0.037 %.

Table 2 Comparison for displacements of Car frame

The complete analysis cost 39.13 s to solve this problem, and the IC method takes 2.69 s and the CA method takes 6.95 s. The efficiency of the IC method and the CA method are much higher than complete analysis. Compared with the complete analysis, the IC method only takes 6.87 % of the computational time to solve this problem, and the corresponding ratio of CA is 17.76 %. The comparison of the efficiency is also shown in Fig. 10.

Fig. 10

Computational cost of car frame

3.3 Side panel

A side panel model is shown in Fig. 11. The mesh model is composed of 273,816 nodes and 538,332 elements, involving 1,642,896 DOFs. To calculate the torsional stiffness, the 3 translational DOFs of nodes A, B and C are restrained, and a force is applied on node D with the value of 400N along Y direction. A direct method using matrix decomposition is used to solve the initial equations. The displacements in Y axis are shown in Fig. 12.

Fig. 11

Side panel

Fig. 12

Initial solution

The modified side panel is shown in Fig. 13. A rib is added to the structure. And then, the structure is reanalyzed with the IC method using 402 basis vectors and the CA method with 6 basis vectors. The corresponding solutions are shown in Figs. 14, 15 and 16. It is shown that the solutions of IC method and complete analysis are almost the same.

Fig. 13

The modified inner door panel. a modified side panel. b partial enlargement

Fig. 14

Analysis results by IC method. a IC solution. b partial enlargement

Fig. 15

Analysis results by CA method. a CA solution. b partial enlargement

Fig. 16

Analysis results by complete method. a complete analysis. b partial enlargement

To further compare the accuracy of the IC method and the CA method, the displacements of some selected DOFs are listed in Table 3. It can be found that all the errors of the selected DOFs are smaller than 0.1 % and the error of the IC method calculated by (15) is 0.19 %, and the error of the CA method is 0.07 %.

Table 3 Comparisons of the selected DOFs

The computational cost of the IC method is 4.295 s, and the CA method 43.06 s, while the one of complete analysis is 177.828 s. The IC method takes only 2.42 % of complete analysis, and the CA method takes 24.2 %. The comparison of efficiency is also shown in Fig. 17.

Fig. 17

Computational cost of side panel

3.4 Inner door panel

An inner door panel model is shown in Fig. 18. The mesh model is composed of 545,659 nodes and 1,083,336 elements, involving 3,273,954 DOFs. As shown in Fig. 19, the 3 translational DOFs of nodes A and B are restrained. For node C, the translational DOF along Y direction is restrained and a force is applied along Z direction with a value of -800N. In order to reduce the computational cost, a preconditioned conjugate gradient (PCG) method(Helfenstein and Koko 2011) is used to solve the initial equations. The displacements in Z axis are shown in Fig. 20.

Fig. 18

Inner door panel

Fig. 19

Constraints and loads

Fig. 20

Initial solution

The modified inner door panel is shown in Fig. 21. A hole is added to the structure. Since the initial analysis is done using PCG method, only the IC method is applied to this structure and the solutions of both the IC method and complete analysis are shown in Figs. 22–23, respectively. It is shown that the solutions of the IC method and complete analysis are almost the same.

Fig. 21

The modified inner door panel. a modified inner door panel. b partial enlargement

Fig. 22

Analysis results by IC method. a IC solution. b partial enlargement

Fig. 23

Analysis results by complete method. a complete analysis. b partial enlargement

To further observe the accuracy of IC, the displacements of some selected nodes are listed in Table 4. It can be found that the errors of the displacements of these nodes are about 0.4 % and the error calculated by (15) is 1.23 %. The computational cost of IC method is 17.85 s, while the one of complete analysis is 3574.97 s. The IC method takes only 0.5 % computation time of complete analysis. The comparison of the efficiency is also shown in Fig. 24.

Table 4 Comparisons of the selected nodes

Fig. 24

Computational cost of inner door panel

3.5 IC based topology optimization

The size and shape of the design domain are shown in Fig. 25. The left side of the domain is fixed and a unit force is applied on the center position of the right side. The area is discretized into $100 \times 40$ elements. The material parameters are modulus of elasticity $E =1$ and Possion’s ratio $\mu = 0.3$. The BESO method (Querin et al. 1998) is used for solving the topology optimization problem and 40 % of the elements are planned to be deleted. Two strategies are used to solve the optimization problem – complete analysis for every iterative step and complete analysis and IC method used alternately. Several selected iterative steps in procedure of topology optimization completed by complete and IC methods are presented in Fig. 26, respectively. According to the Fig. 26, compared with the complete analysis, the results by the IC method made are a bit different due to the approximation strategy and error accumulation. However, the result is consistent with the one of complete analysis. The final compliance value of complete analysis is 46.5303, and the one of IC method is 46.5859.

Fig. 25

Topology optimization model

Fig. 26

Structures of selected iterative steps. a complete analysis. b IC method

4 Conclusions

This study suggests a novel method named IC method to reanalyze structures with local modification. The IC method is a “cheap” algorithm, because it requires only initial solution as input. Avoiding using any extra information such as decomposition of initial stiffness matrix is the most remarkable advantage, so that this method can be used together with any available initial analysis method. The applications in large scale numerical examples show that the proposed method also achieves much higher efficiency than complete analysis, and the accuracy can be ensured as well.