1 Introduction

The optimization of water turbines is an interesting and heavily studied area for many researchers (Lewis et al. 2012; Patel et al. 2013), since a relatively small increase in the turbine’s performance can produce big revenues. The real-world tests are very expensive and time-consuming, meaning that in most cases the optimizations are done with the computational fluid dynamics (CFD) methods. But even if the CFD methods are used during the optimization, the direct optimization approaches, such as the Newton method or the steepest gradient method (Nocedal et al. 2000), would take a couple of months to find the optimum. The core of the problem is the long computational time of a single CFD calculation, possible multi-modality, discontinuity, noisiness or ill-definition of the fitness function and a large number of fitness function evaluations. A different type of optimization methods, namely the Evolutionary algorithms (EA), were proposed (Schmitt 2001) in order to lower the needed number of objective function evaluations.

The EA have been proven to be powerful global optimizers in many real-world optimizations in (Hornby et al. 2006) and in (Stanković et al. 2006). However, without the fitness function approximation (Won et al. 2003), the EA needs quite a large number of the fitness function evaluations (NFE). The fitness function approximation can reduce the NFE to a factor of at least five and is performed with the surrogate models (SM). The SM can be a different type of approximation or interpolation method or a very simplified computational model with a small computational cost. While the use of the SM reduces the NFE significantly, an additional problem arises in connection to the fidelity of the incorporated SM (Jin 2005). If the SM has low fidelity, it is very likely that the EA will converge to the false optimum. The approximation with the artificial neural networks (ANN) (Hornik et al. 1989) is prone to such an effect if not trained correctly. Different techniques are suggested in order to improve the accuracy of the SM and therefore the result of the EA optimization. The design of experiments (Myers et al. 2009) for defining the initial data of the SM construction is just one of such techniques. Another technique is the model management of evolution control. In this case the original fitness function is used to evaluate the optima from the optimization of the SM and to update the SM with the real fitness value of the optima. The evolution control can be either fixed (Bull 1999; Jin et al. 2002), where found optima of the SM are evaluated with the original fitness function based on the predefined rule, or adaptive, where found optima of the SM are evaluated based on the fidelity of the SM (Afonin 2011).

A new approach to lower the NFE is presented in this paper and used in the optimization of the guide vane blade. An optimization problem is decomposed into several smaller optimization problems based on the measurement of the separability of the input arguments. Such an approach lowers the NFE of the optimization and increases the fidelity of the SM. The overall computational time of the optimization is lowered due to the smaller NFE.

As aforementioned, the new approach is used to optimize a guide vane blade of a reversible water turbine, which can operate as a turbine or as a pump. The addressed problem is the insufficient strength of the guide vane blade. Some cracks appeared near the blade’s pin. The objective of the optimization is to find such blade geometry that will bear the maximal pressure loads and the maximal pressure fluctuations, while at the same time the volume of the blade will be minimized and the hydraulic efficiency of the whole turbine will not be impaired.

Two different continua are treated in the optimization problem. The first is the fluid (water) and the second is the solid body (steel blade). Numerical analysis methods are incorporated in order to obtain the fitness function value during the optimization. The fluid problem is treated with the CFD and the solid body problem is treated with two different structural analysis methods, namely, the finite element method (FEM) (Zienkiewicz et al. 2005) and the meshless method (MM) (Liu 2010). The FEM has been used for many different optimization problems as reported in (Amoiralis et al. 2008; Rajan et al. 2004; Toropov et al. 1993; Wang and Liu 2012), while the MM is not commonly used. There are several different MM formulations and just a few were successfully applied for the optimization problems. The use of the reproducing kernel particle method (RPKM) (Chen et al. 2001) as the fitness function evaluator was reported in (Grindeanu et al. 1999) and the moving-least squares (MLS) (Atluri et al. 2004) was used as the fitness function evaluator in (Kim et al. 2002). The MM formulation used in this paper is the weak form radial point interpolation method (RPIM) formulation (Wang and Liu 2002).

Both FEM and MM use some sort of mesh during the computation. The mesh is the basis of the FEM where the problem’s region is discretized with the finite elements. On the other hand, the mesh in the MM is a background mesh, used only at the numerical integration of the Galerkin weak form formulation. The key difference between the FEM and the MM is the effect of the mesh on the method’s results. If the mesh is of poor quality, the error of the FEM can be significant and thus the results can be deceptive or wrong. This is not the case if the MM is used. This effect can greatly impair the optimization results if obtained meshes during the optimization are of poor quality and the FEM is used for the structural analysis. The optimization of the guide vane blade is performed with the FEM and separately with the MM in order to assess the effect of the structural analysis method on the optimization results.

The decomposition of the optimization problem is presented and tested on mathematical functions in Section 2. Used numerical methods in the optimization of the guide vane blade are discussed in Section 3 and a brief comparison of the structural analysis methods is presented in Subsection 3.1. The guide vane blade optimization problem and its results are depicted in Section 4 and Subsection 4.1, respectively. Finally, the conclusion, open questions and the promising research topics are covered in Section 5.

2 Method for the decomposition of the optimization problem

The decomposition of the optimization problem is to be performed on the input arguments of the objective function and consequently on the input arguments of the fitness function. The decomposition divides the space of input arguments of the dimension n into the multiple spaces of smaller dimensions n i <n and is based on the value of the separability measurement s i,j of the two input arguments i and j, defined by

$$ \begin{array}{rcl}\mathsf{s}_{i,j}&=\big|f({\mathbf{x}}_{(+i,+j)})-f({\mathbf{x}}_{+i})-f({\mathbf{x}}_{+j})+f({\mathbf{x}})\big|\\ &+\big|f({\mathbf{x}}_{(-i,+j)})-f({\mathbf{x}}_{-i})-f({\mathbf{x}}_{+j})+f({\mathbf{x}})\big|\\ &+\big|f({\mathbf{x}}_{(+i,-j)})-f({\mathbf{x}}_{+i})-f({\mathbf{x}}_{-j})+f({\mathbf{x}})\big|\\ &+\big|f({\mathbf{x}}_{(-i,-j)})-f({\mathbf{x}}_{-i})-f({\mathbf{x}}_{-j})+f({\mathbf{x}})\big|.\\ \end{array} $$
(1)

In the (1) f(⋅) presents the function of multiple arguments \(\mathbf{x}\) (dimension of \(\mathbf{x}\) is greater than 2) and subscripts near the arguments present the change of value of the subscripted argument. The s i,j is defined only for different arguments, meaning i≠j. Figure 1 graphically explains the meaning of the subscripts near the arguments.

Fig. 1
figure 1

Position of the points x +i , x −i , x +j , x −j , x (+i,+j), x (−i,+j), x (−i,−j) and x (+i,−j) around the point x in the x i ,x j plane. h i is the change of i-th argument and h j is the change of j-th argument

Full size image

In order to define the decomposition of the input space, one has to calculate the s i,j for each pair (i,j). Based on these values, the input space is decomposed into the list with the pairs of arguments or single arguments. This list is called the Optimization Strategy (OpS) and its elements are called the Optimization Tuple (OpT). The OpS is created in such a way that the arguments with the largest absolute value of |s i,j | are optimized first, while the arguments with the smallest separability or even separable arguments are optimized at the end of the OpS. Figure 2 depicts a detailed procedure of the OpS construction. The arguments x i and x j are separable, if it holds s i,j =0, and could be optimised in two different OpTs (e.g. if the fitness function is \(f(x_{1},x_{2})={x_{1}^{2}}+{x_{2}^{2}}\), then the optimizations could be performed individually for each of the arguments x 1 and x 2). Each argument of the input space must appear at least once in the OpS and maximal twice. The optimization is performed on each OpT in the OpS after the OpS has been created. The optimization of single OpT is performed only on the input arguments, contained in the OpT. If the OpT ={x 3,x 5} and the input arguments are \(\mathbf{x}=\{x_{1},x_{2},x_{3},x_{4},x_{5}\}\), the optimization is performed only on arguments x 3 and x 5, meaning that during the optimization only those two arguments are allowed to change, while others remain the same.

Fig. 2
figure 2

Algorithm of the Optimization Strategy construction. Mind that f is the index of the current input argument and s in the index of the next input argument, while i and j are indices of arbitrary argument

Full size image

The OpS construction requires n 2 evaluations and is thus computationally very expensive to construct for cases, where the fitness function has a large computational cost. In these cases, an additional function can be used in order to construct the OpS. It is obvious, that the additional function should adequately decompose the problem and should not have an impact on the solution itself. Computationally expensive fitness functions are different numerical simulations, such as the finite element method, finite volume method, etc. If the fitness function contains some sort of mesh, we propose to define the additional function as the mesh volume. The additional function definitions for other optimization problems are currently not known and are above the scope of this research. The proposed method is applicable for those problems, where the function used for the decomposition of the original optimization problem is known.

The problem arises when one argument is not separable from two other arguments and is contained in two different OpTs. In this case, the optimization process on the second OpT could impair the found optimum of the first OpT. The solution to this problem is a few repetitions of the OpS creation and optimization through the new OpS.

There are two expected benefits of the optimization decomposition, namely, the smaller NFE and the increase of the fidelity of the SM. The first benefit is expected based on the fact that the NFE is smaller if the number of input arguments of the optimizing function is small. If the number of input arguments is high, then the NFE during the optimization is also high. The maximal number of arguments in one OpT is two and therefore small, consequently the NFE should be small during the optimization of one OpT. It is expected that the sums of the NFEs of all optimizations in one OpS should be smaller than the NFE of the optimization of the original (whole) function. The second benefit is quite obvious since the fidelity of the SM is dependent on the dimension of the input space (Jin et al. 2002). If the dimension is large, the fidelity is lowered and vice-versa. Since the dimension of the SM’s input space in the decomposed optimization is two at most, the fidelity of the SM is high.

In order to use the decomposition of the optimization problem, the OpS must be constructed before the optimization occurs. If one decides to use several iterations of the optimizations through the whole OpS, the future OpS should be constructed before the iteration starts. Figure 3 depicts the pseudo-code of the optimization algorithm with the included decomposition of the problem and optimization with the use of the SM.

Fig. 3
figure 3

Algorithm of the optimization procedure with included decomposition of the optimization problem

Full size image

2.1 Numerical test of the decomposition of the optimization problem

The proposed decomposition of the optimization problem was tested on a multidimensional spherical function

$$ f(\mathbf{x})=\sum\limits_{i=1}^{n}{x_{i}^{2}} $$
(2)

with optimum f(0)=0 and on a multidimensional Rosenbrock function

$$ f(\mathbf{x})=\sum\limits_{i=1}^{n-1}(x_{i}-1)^{2}+100({x_{i}^{2}}-x_{i-1})^{2} $$
(3)

with optimum f(1)=0. While the spherical function is separable for all input arguments, this is not the case with the Rosenbrock function. The latter is separable just for some input arguments. The n in (2) and (3) represents the dimension of the input space or the number of optimization arguments. The tested n were 5, 10 and 20. Each optimization was repeated 10 times. Three different SM were used, namely the radial basis function interpolation (Wendland 1997), inverse distance weighting interpolation (Shepard 1968) and approximation with the artificial neural networks (Hornik et al. 1989). The search intervals were x i ∈[−10,5] for all arguments and for all test cases. The functions were optimized with the decomposition method and compared to the results from (Won et al. 2003) which were obtained without the decomposition method. The observed results were the average of the found optima (\(\overline {f_\text{{o}}}\)), best found optima (f o,b e s t ) and the average NFE (\(\overline {\text {NFE}}\)). The results of the optimizations and their comparisons are gathered in Table 1 for the spherical function and in Table 2 for the Rosenbrock function.

Table 1 Results of the optimization of the spherical function with and without decomposition method (Won et al. 2003) (column Dec.)
Full size table
Table 2 Results of the optimization of the Rosenbrock’s function with and without decomposition method (Won et al. 2003) (column Dec.)
Full size table

The search intervals of the optimizations without the decomposition were smaller (see (Won et al. 2003) for their definition) than the search intervals of the optimizations with the decomposition method in case of functions with 20 input arguments. The method decomposes the optimization problems properly, meaning that the OpT optimizations are performed on single input argument in case of the spherical function and on two sequential arguments (x i ,x i+1) in case of the Rosenbrock’s function. During the optimization of the spherical function, the proposed decomposition method lowers the NFE at least for the factor of 13 and still the found optima are under the value of 10−10. Observing only the optima value shows that the results obtained without the decomposition method are far better than the results obtained with the decomposition method. But the results of the decomposition method are good enough for the mechanical engineers, since the measurement tolerances are of order 10−6, defined by the ISO standard (International organization for standardization 2010). This only occurs at the optimization of spherical function which is strictly convex function. At the optimization of Rosenbrock function, the decomposed optimization is worse only in the case of the averaged results of the five input arguments. In all other cases of the Rosenbrock function optimization, the decomposed optimization method produced better results than the optimization without the decomposition method. Another great property of the decomposition method is that the results are not impaired as much with the larger number of input arguments as in the case of the optimization without the decomposition method.

The main conclusion of this test is that the optimization with the decomposition has similar or better performance than the optimization without the decomposition no matter if the function’s input arguments can be separated or not.

3 Numerical methods for the fitness value calculation

Three different numerical methods are used in order to obtain the value of the fitness function of the problem, defined in Section 4. The structural analysis is a static analysis and is performed with the Finite Element Method (FEM) (Zienkiewicz et al. 2005) or the Meshless Method (MM) (Liu 2010). The transient fluid analysis is dealt with the Finite Volume Method (FVM) (Hirsch 1988). Because the FVM method is computationally more expensive than the FEM or MM method, one would like to minimize the necessary number of FVM calculations. The pseudo-code of the whole optimization procedure used in the optimization in Section 4 is depicted in Fig. 4.

Fig. 4
figure 4

Algorithm of the optimization procedure with the included decomposition method and numerical analysis tools (FVM, FEM or MM). This optimization procedure is used to optimize the guide vane in Section 4

Full size image

A program with the decomposed optimization method, FEM and MM, was developed using the C# language with the support of the .NET framework, version 3.5, and the MUMPS solver (Amestoy et al. 2013) for the solving of the sparse matrices in the FEM and MM. For the FVM an external solver was used, namely the Numeca FINE TM Turbo, version 8.9-3. The meshes needed for the numerical methods were created with the mesh deformation technique, based on the radial basis function interpolation (de Boer et al. 2007) that was included in the aforementioned program. For the FVM calculation, meshes were saved in an external file and then read with the external solver. The fluid loads on the solid body were interpolated with the RBF interpolation method. The decomposition of the input space is performed based on the volume of the solid region instead of the fitness function. The main reason for this is the computational cost of the fitness calculation.

3.1 Comparison of the FEM and the MM analysis

The main reason to incorporate two different structural analysis methods is the ability to compare their effect on the optimization results. The formulation of FEM is straight forward, but still several different elements exist, e.g. 8-node Brick, 20-node Brick, etc. Additionally, one can use the different quadrature rules or weighted or reduced integration (Barlow 1989) in order to improve the accuracy of the FEM analysis. The situation is more complicated with the MM formulations. Several different MM formulations are reported in literature (Atluri et al. 2006; Gu and Liu 2002; Kee et al. 2006; Dolbow and Belytschko 1999) with the main difference in the discretization of the problem domain Ω. In order to give the best comparison between the optimization with FEM and optimization with MM, the used FEM element is 8-node Brick element (Zienkiewicz et al. 2005) and the used MM formulation is a weak form radial point interpolation method (RPIM) defined in (Liu et al. 2005). The quadrature rule is of the order of two for both methods. Chosen formulations are very similar to each other, and therefore the most suitable for the comparison of each other.

Both MM and FEM are used to approximate the solution of a three-dimensional problem of solid mechanics, defined by

$$ \sigma_{ij,j}+f_{i}=0\quad\text{ in }{\Omega}, $$
(4)

where σ i j is a stress tensor, f i is a body force and Ω is a body domain, bounded by Γ. The relations between the displacement field u i and strain field ε i j are described with kinematic equations and strains are linked to the stresses with constitutive equations. The boundary conditions are given as

$$ \begin{array}{rcl} \sigma_{ij}n_{i}&=\hat{f_{i}}\quad\text{ on the natural boundary }{\Gamma}_{f},\\ u_{i}&=\hat{u_{i}}\quad\text{ on the essential boundary }{\Gamma}_{u}, \end{array} $$
(5)

in which the superposed hat denotes the prescribed boundary values and n i is the unit outward normal to the domain Ω. Equations (4) and (5) can be expressed in the weak form as

$$ {\int}_{\Omega}\sigma_{ij}\delta \varepsilon_{ij}\mathrm{d}{\Omega}-{\int}_{\Omega}\delta u_{i} f_{i}\mathrm{d}{\Omega} -{\int}_{{\Gamma}_{f}}\delta u_{i} \hat{f_{i}}\mathrm{d}{\Gamma}=0. $$
(6)

The above equation can be discretized according to the FEM or MM. In both cases one obtains

$$\mathbf{K u_{\mathbf{N}}}={\mathbf{f}},$$
(7)

where \(\mathbf {K}\) is the stiffness matrix, \(\mathbf {u_{N}}\) is the vector of node displacement and \(\mathbf {f}\) is a load vector. A submatrix of \(\mathbf {K}\) is calculated by

$$\mathbf{K_{\text{sub}}}=\int_{\Omega \text{sub}}\mathbf{B}^{T}\mathbf{EB}\mathrm{d} \Omega, $$
(8)

where \(\mathbf {B}\) is the strain displacement matrix and \(\mathbf {E}\) is the material matrix. In case of three-dimensional elastic body problems the strain displacement matrix \(\mathbf {B}\) is composed of block matrices

$$\mathbf{B}_{\text{sub}}=\left[\begin{array}{ccc}N_{i,x}&0&0 \\0&N_{i,y} &0\\0&0&N_{i,z}\\N_{i,y} & N_{i,x}&0\\0&N_{i,z}&N_{i,y}\\N_{i,z}&0&N_{i,x}\\\end{array}\right], $$
(9)

where the N i is a shape function and depends on the used method, FEM or MM. The way of composing \(\mathbf {B}\) from the block matrices \(\mathbf {B}_{\text {sub}}\) also varies of the used method. Elements \(\mathbf {f_{\mathrm {i}}}\) of the load vector \(\mathbf {f}\) corresponding to node i are calculated by

$$\mathbf{f_{\mathrm{i}}}=\int_{\Gamma_{f\mathrm{i}}}N_{i}\hat{f_{i}}\mathrm{d}\Gamma+\int_{\Omega_{\mathrm{i}}}N_{i} f_{i}\mathrm{d}\Omega. $$
(10)

Since the body forces can be neglected, the right integral in (10) vanishes. The integration in (8) and (10) is performed with the Gauss quadrature technique for both methods, FEM and MM.

In the FEM, the shape function construction and integration of the (8) and (10) is based on the elements (Zienkiewicz et al. 2005), as depicted in Fig. 5(a). In case of the MM, the shape function construction is based on the choice of the support nodes and the integration of (8) and (10) can be done based on the background mesh. More on the selection of the support nodes and on the integration schemes in the MM can be seen in (Liu 2010). In the MM, it is possible to define the support nodes based on the background mesh, which simplifies the computational implementation of the MM. In this case, the scheme of choosing the support nodes for the shape function construction from the nodes of background mesh is needed. The integration region and the support nodes for the shape function construction of the MM is depicted in Fig. 5(b).

Fig. 5
figure 5

Selection of the nodes (circles) for the shape function construction and integration area (hatched area) for one Gauss quadrature point for: (a) FEM and (b) MM with the T2L selection scheme.

Full size image

In order to obtain the best possible comparison, the FEM is based on an 8-node Brick element (Felippa and Clough 1969) and the MM is based on the hexahedral background mesh with the modified T2L-scheme for choosing the support nodes (Kee et al. 2006).

A preliminary comparison of both structural analysis methods is performed on the cube with the edge of length a=50 mm and the compression load p=10 MPa, as depicted in Fig. 6(a). The material is elastic Hooke’s material with the properties of E=210000 MPa and \(\nu =\frac {1}{3}\). Both methods are compared on two different meshes, one completely orthogonal mesh and the other a distorted mesh (depicted in Fig. 6(b)), in order to observe the effect of the mesh on the results. The number of elements in both meshes were 10×10×10=1000.

Fig. 6
figure 6

3D structural test case for the preliminary comparison of the structural analysis methods. Front face is compressed with p=10 MPa and the back face is freely supported in the opposite direction of the compression, except in one point where is it clamped

Full size image

The observed result is the value of the maximal von Mises stress σ VM in the body since the fitness function value in Section 4 depends on it. The analytical solution is σ VM,max=10 MPa. The results of the preliminary tests and their errors are gathered in Table 3.

Table 3 The effect of the mesh orthogonality on the different structural analysis results
Full size table

The MM method did not obtain 0.0% error for the orthogonal mesh, but the result is much better in case of the distorted mesh. The error of results obtained with the FEM and distorted mesh is greater than 25% and as such greater than the error of the result with the MM and the distorted mesh which is 11.5%. From the test case it seems, that the MM results are less sensitive to the mesh distortion as the FEM results. One can apply different quadrature rule in order to improve the accuracy of the FEM. The result of different quadrature rule applied to the FEM method are presented in parenthesis in Table 3 which resulted in the similar FEM results to the MM results. Nonetheless, in order to perform the best possible comparison between the MM and the FEM, the quadrature rule of two is used in the optimization processes.

4 Optimization of the Guide Vane Blade

The optimization of the guide vane blade of the reversible water turbine is presented in this section. The reversible water turbine is a turbine that can also act as a pump. The pumping regime represents the problem, since the pressure fluctuations can vary from the value of p min=700 kPa to the value of p max=1200 kPa resulting in the dynamic loading of the guide vane blades.

The optimization is performed in such a way that at given dynamic pressure loads the optimal blade geometry would have minimal volume and at the same time, the efficiency of the pump η p would not be impaired. These objectives can be expressed mathematically as

$$\begin{array}{@{}rcl@{}} \text{Minimize}&:& V(\vec{x})=\int\limits_{V}\mathrm{d} V,\end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} \textrm{subjected to}&:& (\sigma_{VM,max}(\vec{x}))\leq\sigma_{y}, \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} \text{and}&:& ({\Delta}_{max}\sigma_{VM}(\vec{x}))\leq{\Delta}\sigma_{y}, \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \text{and}&:& \eta_{\mathrm{p}}(\vec{x})\geq\eta_{p,0}. \end{array} $$
(14)

The two corresponding fitness functions with penalty functions are defined as

$$\begin{array}{@{}rcl@{}}&&\mathrm{min}~f_{\rm{struct}}(\mathbf{x})=\mathrm{min} \left(V(\mathbf{x})+f_{p1}(\mathbf{x})+f_{p2}(\mathbf{x})\right), \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}}&&\mathrm{max} ~f_{\rm{fluid}}(\mathbf{x})=\mathrm{max}~\eta_{\mathrm{p}}(\mathbf{x}), \end{array} $$
(16)
$$ {\begin{aligned} f_{p1}(\mathrm{x})=\begin{cases} 0&\text{if}~\sigma_{\mathrm{VM,max}}(\mathrm{x})\leq\sigma_{y},\\ \left(\sigma_{\mathrm{VM,max}}(\mathrm{x})-\sigma_{y}\right)^{2}&\text{if}~\sigma_{\mathrm{VM,max}}(\mathrm{x})>\sigma_{y}. \end{cases},\\ \end{aligned}} $$
(17)
$$ {\begin{aligned} f_{p2}(\mathrm{x})=\begin{cases} 0&\text{if}~{\Delta}_{\text{max}}\sigma_{\text{VM}}(\mathrm{x})\leq{\Delta}\sigma_{y},\\ \left({\Delta}_{\text{max}}\sigma_{\text{VM}}(\mathrm{x})-{\Delta}\sigma_{y}\right)^{2}&\text{if}~{\Delta}_{\text{max}}\sigma_{\text{VM}}(\mathrm{x})>{\Delta}\sigma_{y}. \end{cases}. \end{aligned}} $$
(18)

The used numerical methods are: FEM, MM and FVM. The meshes for the FEM and MM contained 19 492 8-node hexahedral elements, while the FVM mesh contained 7 535 350 finite volumes. A preliminary transient CFD calculation of the reference point with two complete rotations of the rotor was made in order to define CFD time parameters used during the optimization. A pressure fluctuation was noticed in this preliminary calculation, which needed approximately 2.3×10−3 s to change its position from one blade to its neighbouring blade. The transient fluid velocity field from the runner/guide vane interface was recorded in the last 0.11 s in order to use it in the FVM analysis of the optimization procedure. The latter procedure was transient with 45 time steps in order to correctly capture the dynamic pressure loads. A time of one time step is 2.44×10−3 s. First 35 time steps were neglected and only the last ten time steps were observed in the structural analysis. This approach ensures the elimination of the transient effect in the CFD calculation and that the pressure fluctuation will move from one blade to its neighbouring blade. Four different pressure loads on the blade are captured within this ten time steps:

  • Pressure loading with the maximal resulting torque on the blade,

  • Pressure loading with the minimal resulting torque on the blade,

  • Pressure loading with the maximal resulting force on the blade,

  • Pressure loading with the minimal resulting force on the blade.

These four different loading spectrums are used in the structural analysis in order to obtain the maximal von Mises stress σ VM,max due to the pressure loading and maximal amplitude of the von Mises stress Δmax σ VM due to the different loading spectrums.

The results of the analysis for the reference (starting) point and blade material data are gathered in Table 4.

Table 4 The results for the reference (starting) geometry of the guide vane blade and the blade material data. The efficiency is normalized to the reference point
Full size table

The results in Table 4 show that the σ VM,max and Δmax σ VM are small, compared to the maximal allowable values. Apparently, the aforementioned cracks are not the result of the treated fluid loads, but are caused by some other event or dynamic structure behaviour, which is beyond the scope of this investigation. From the reference results it is expected for the blade to get thinner during the optimization process and the efficiency of the turbine η p should rise as a consequence. This is taken into account in the optimization procedure, where only the fitness function \(f_{\text{struct}}(\mathbf{x})\) is optimized, as it is expected that the fitness function \(f_{\text {fluid}}(\mathbf{x})\) will be fulfilled automatically.

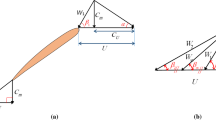
The blade geometry of the reference (starting) point is depicted in Fig. 7. All dimensions are normalized to the unit length of the profile chord.

Fig. 7
figure 7

The blade geometry at the start of the optimization

Full size image

The blade profile is parameterized with the leading and trailing circles and with the polynomials of the pressure and the suction sides. The polynomials of the pressure and the suction sides are

$$\begin{array}{*{20}l} f_{\mathrm{P}}(x)&=a_{\mathrm{P}}x^{6}+b_{\mathrm{P}}x^{5}+c_{\mathrm{P}}x^{4}+d_{\mathrm{P}}x^{3}+e_{\mathrm{P}}x^{2}+f_{\mathrm{P}}x+g_{\mathrm{P}},\\ f_{\mathrm{S}}(x)&=a_{\mathrm{S}}x^{5}+b_{\mathrm{S}}x^{4}+c_{\mathrm{S}}x^{3}+d_{\mathrm{S}}x^{2}+e_{\mathrm{S}}x+f_{\mathrm{S}}. \end{array} $$
(19)

The leading and the trailing circles are described with its radii, namely r L and r T, and the conditions of the static leading and the static trailing edge (the leading and trailing edges do not move during the optimization). Two different sets of parameterization variables are selected and thus defining two different optimization problems. The parameters of the first optimization problem are

$${\mathbf{x}}_{\text{P1}}=\{b_{\mathrm{P}},c_{\mathrm{P}},d_{\mathrm{P}},c_{\mathrm{S}},d_{\mathrm{S}}\}, $$
(20)

and of the second optimization problem

$${\mathbf{x}}_{\text{P2}}=\{r_{\mathrm{L}},b_{\mathrm{P}},c_{\mathrm{P}},d_{\mathrm{P}},c_{\mathrm{S}},d_{\mathrm{S}}\}. $$
(21)

The search intervals and the starting values for the selected optimization parameters are gathered in Table 5.

Table 5 Search intervals for the optimization parameters of the guide vane blade
Full size table

The search intervals are defined in such a way to ensure the regular profiles and meshes for arbitrary value of the parameters within them. Due to the occurrence of singular geometries, the search intervals of parameters b P and c P do not contain the starting value.

With two different sets of the optimization parameters and two different methods for the structural analysis there are four different optimizations defined. All optimizations incorporate the decomposition of the input space with two iterations through the OpS and four different SM to approximate or interpolate the population values. The used SM are:

  • multilayered perceptron ANN approximation with three hidden layers and 10, 7, 9 neurons in them,

  • RBF interpolation with CP C 2 function and the support radius of value r=0.15,

  • RBF interpolation with CP C 2 function and the support radius of value r=0.3,

  • IDW interpolation with the power parameter of value 2.0.

4.1 Results of the optimizations

The parameter values of the found optima x Opti and the optima values f(xOpti) are depicted in Tables 6 and 7, respectively. The subscripts P1 and P2 represent the parameter set, defined by (20) and (21), respectively, while the subscripts MM and FEM indicate the used structural analysis method. The efficiencies are normalized to the reference value. The contours of the \({\mathbf{x}}^{\text{Opti}}_{\text{P1,MM}}\) blade and of the \({\mathbf{x}}^{\text{Opti}}_{\text{P2,MM}}\) blade are depicted in Figs.8 and 9, respectively.

Table 6 Parameter values of the found optima for all four different optimizations
Full size table
Table 7 Optima values of the found optima for all four different optimizations
Full size table
Fig. 8
figure 8

The contour of the optimal blade (solid line) found by the first set of the optimization parameters x P1 and the MM structural analysis. The reference geometry is depicted with dashed line

Full size image
Fig. 9
figure 9

The contour of the optimal blade (solid line) found by the second set of the optimization parameters \(\mathbf{x}_{\text {P2}}\) and the MM structural analysis. The reference geometry is depicted with dashed line

Full size image

All of the performed optimizations are successful. The optimization of the first set of the optimization parameters \(\mathbf{x}_{\text {P1}}\) gives worse results than the optimization of the second set of the optimization parameters \(\mathbf{x}_{\text {P2}}\). The main reason for this is the parameterization of the leading circle, which itself thins the blade a lot more than the parameterizations of the suction side and the pressure side combined. The optimizations with the MM as the structural analysis method give better results than with the FEM. The difference is bigger in case of the second set of the optimization parameters, in which the FEM violated the first penalty function, defined by (17). The penalty function violation in case of the FEM can appear due to the poor mesh quality, as shown in the results in Subsection 3.1.

An interesting conclusion can be made about the efficiency. The efficiency is not directly optimized, only the volume of the blade is. Nevertheless, the efficiency is better than the reference point’s efficiency for all found optima. The biggest rise is achieved with the use of the MM as the fitness evaluator and the first set of the optimization parameters. The optimization with the MM produces better efficiency results for both sets of the optimization parameters. The smallest rise of the efficiency is obtained with the second set of the optimization parameters and the use of FEM as the fitness evaluator. This is expected, since the FEM violated the first penalty function during the optimization process. The main conclusion on the efficiency results is that for some cases it is better to optimize the volume of the blade than the performance of the blade, since the structural analysis methods are computationally less expensive.

5 Conclusions

This paper presents a new method for the decomposition of the optimization problem. The decomposition is based on the separability measurement of the function input arguments. The function can be the original fitness function in case of the mathematical fitness functions or the volume of the region in case of the fitness functions expressed with the numerical analysis methods. The decomposition of the optimization problem is used for the optimization of two mathematical functions and a real world problem – the optimization of the guide vane blade. The results of all performed tests show that the proposed decomposition method gives similar or better results while lowering the computational cost of the optimization.

The optimizations of the guide vane of the reversible water turbine are performed separately using two different structural analysis methods, namely the finite element method and the meshless method. Found optima are compared based on the used method to show the effect of the used structural analysis method on the found optima. The obtained optima are better than the reference point no matter the structural analysis method used or the blade parameterization. An interesting phenomenon occurred at the optimization of the turbine efficiency. The efficiency was not optimized directly, but still the optima have better efficiency than the reference point. The efficiency rise is achieved solely through the minimization of the blade volume. This phenomenon can be exploited for a similar optimization problem, since the structural analysis is computationally less expensive that the computational fluid dynamics analysis.

Future research will focus on the improvement of the decomposition method and its implementation into the multiobjective optimization. Another promising research topic is the aforementioned efficiency phenomena. For the optimization problems, where multiple fitness functions can be defined and the optimization result would be the same no matter the used fitness function, it is more efficient to optimize a fitness function with a lower computational cost. In such a case, it would be desirable to detect in advance which fitness function will have the smallest computational cost of the optimization and will produce sufficient optimization results at the same time.