Aerodynamic shape optimization of wind turbine rotor blades using the continuous adjoint method

Abstract

This paper presents the development of the continuous adjoint method for incompressible fluid flows, solved for the absolute velocity in the relative reference frame, allowing the optimization of rotating machines. The development is conducted using an extended version of the OpenFOAM-based continuous adjoint solver adjointOptimisationFoam. This implements and solves the adjoint to the Navier–Stokes system of equations, coupled with the differentiation of the Spalart–Allmaras turbulence model. Its application to the aerodynamic shape optimization of the MEXICO and NREL Phase VI wind turbines blades follows, targeting the maximization of the axial moment. The flow solution for the two cases is compared with the outcome of other CFD solvers and experimental data, where available. Blades and the displacements of the surrounding grid nodes are parameterized using a volumetric B-Splines morphing box. A number of optimizations are conducted using different operating conditions and geometric constraints.

1 Introduction

The consumption of energy has increased dramatically over the past few decades, with an increasing trend to replace fossil fuels with clean renewable energies. Wind energy has been a big part of this effort, due to its geographically wide availability and zero pollution Liu et al. (2013). A significant increase in wind turbine (WT) installations is expected as this stands for the fastest growing installed alternative-energy production Lindenberg et al. (2008). Maximizing wind energy extraction is the key to increase the annual energy production. One of the possible approaches is to increase the swept area of the WT blades by simply upscaling the turbine which leads to an increase in mass by the cube of the rotor radius, introducing structural challenges for the WT Ashuri and Zaayer (2008). Alternatively, wind energy extraction can be increased by using shape optimization techniques, without increasing the rotor radius.

Several numerical approaches have been applied to simulate WT flows, based on either the Blade Element Momentum (BEM) method Glauert (1983); Bai and Wang (2016) or standard Computational Fluid Dynamics (CFD) software Castelli et al. (2011). BEM models are the most widely used as they predict the WT aerodynamic performance at low cost and with a rather simple implementation. However, one obstacle in using BEM codes is that lift and drag data must be at hand. Moreover, BEM results highly depend on the accuracy of the above aerodynamic data, which might be challenging to obtain; on the contrary, CFD is able to predict the flow field around the WT, compute forces exerted on its blades and, thus, predict aerodynamic performance.

CFD-based aerodynamic shape optimization is used on a regular basis to design air and ground vehicles.Chen et al. (2016); Papoutsis-Kiachagias et al. (2019); He et al. (2020). CFD has also been deemed as a promising tool to optimize WTs performance. The choice of the aerodynamic model has a large impact on the optimal design Barrett and Ning (2016). Shape optimization has been used to optimize WT blades using 3D CFD and gradient-free methods. In order to provide optimal configurations for different design objectives using a BEM model and Evolutionary Algorithms, an extended database generation procedure validated with adopting numerical optimization methods for vertical axis WT design Bedon et al. (2013) was introduced. The optimization of a vertical axis WT to maximize torque by using unsteady CFD simulations along with a differential evolution search method is presented in Carrigan et al. (2012). In Vučina et al. (2016), a WT blade was optimized in terms of power extraction using a 3D CFD model and a gradient-free method using 25 design variables. Furthermore, in Díaz-Casás et al. (2013), an evolutionary algorithm is used to develop an automatic design environment for WT blades. The design process includes a fast aerodynamic simulator and an Artificial Neural Network (ANN) correction to reduce computational costs. Despite the use of ANN, in case of many design variables, the optimization turn-around time of gradient-free methods might become infeasible. For this reason, whenever dealing with a large number of design variables, gradient-based algorithms assisted by the adjoint method become the only viable technique at a reasonable cost solving the optimization problem.

Among the methods to compute gradients, the adjoint method Jameson (1988); Strang (1986) has been receiving a lot of attention, due to the fact that the cost of computing the objective function gradient is independent of the number of the design variables. This makes the method an excellent choice for large scale optimization problems. To formulate the adjoint method, a Lagrangian function is defined by adding the sum/integral of the residuals of the flow equations (a.k.a. primal equations) multiplied by the adjoint (or co-state) variables to the objective function to be minimized. Then, the Lagrangian is differentiated with respect to (w.r.t.) the design variables yielding sensitivity derivatives expressions that include the derivatives of the flow w.r.t. the design variables. Their computation is costly and, to overcome it, their multipliers are set to zero, giving rise to the adjoint equations and their boundary conditions. In the continuous adjoint approach (Kyle and Venkatakrishnan 1999; Jameson 1988, 1995; Jameson and Reuther 1994; Alexias and Giannakoglou 2020), the objective function is augmented using the flow equations in continuous form (PDEs) and this results to the adjoint equations in the form of PDEs, to be discretized and numerically solved.

The first time the adjoint to the RANS equations was used to optimize the lift-to-drag ratio of a WT blade airfoil was in Ritlop and Nadarajah (2009). Several 3D adjoint-based shape optimizations considered rotation effects in configurations other than those presented here. In one of them, Dhert et al. (2017), the NREL Phase VI rotor was optimized using the RANS equations to maximize the torque coefficient by changing the blade shape using discrete adjoint. The frozen turbulence assumption was made for the same WT Vorspel et al. (2018), meaning that the adjoint turbulence model equations were not included into the system of adjoint equations to optimize the thrust. The continuous adjoint to the RANS equations, was used in Tsiakas et al. (2019) to maximize the power of the MEXICO WT rotor with the flow and adjoint solvers running on GPUs. In Madsen et al. (2019), a modern 10 MW offshore wind turbine blade planform and cross-sectional shape were simultaneously optimized using discrete adjoint.

This work presents the development of continuous adjoint for incompressible fluid flows, solved for the absolute velocity in the relative reference frame. Compared to the continuous adjoint method corresponding to a stationary reference frame, new terms emerge in the adjoint mean flow equations and the sensitivity derivatives, computed with the so-called FI adjoint approach Kavvadias et al. (2015). The newly developed method is implemented within the open-source toolbox OpenFOAM and includes the adjoint to the Spalart-Allmaras turbulence model equation. This is used for the shape optimization of the MEXICO and NREL Phase VI WTs. The goal is to maximize the axial moment, thereby enhancing power production. Even though this paper focuses on WTs, the developed continuous adjoint method can be used for the optimization of other kinds of rotating machines, too. An equality constraint, stating that the optimized blade should have the same volume with the initial blade, is imposed in the second case. At a first step, the CFD analysis of the WT blades is verified/validated vis-a-vis to other CFD solvers and experimental data, where available. Then, the adjoint method is used to compute the gradient and support the optimization. A number of optimizations are performed for the MEXICO and NREL Phase VI WTs, all targeting the increase of axial moment. For the MEXICO WT, in specific, optimization is performed for both nominal and off-design conditions and the resulting shapes are re-evaluated at other operating conditions too.

The rest of the paper is structured as follows: in Sect. 2, the flow and adjoint equations are presented in brief, focusing mainly on the additional and modified terms in the adjoint equations, emerging due to the reference frame change; a comparison with finite differences is included. Section 3 includes the verification of the flow solver and the optimization of the two aforementioned WT blades. Finally, Sect. 4 summarizes the findings of this work.

2 Flow and adjoint equations

2.1 Flow (primal) equations

The flow model is based on the steady-state RANS equations for incompressible flows, coupled with the Spalart-Allmaras turbulence model Spalart and Allmaras (1992). The flow equations are solved for the absolute velocity $v_i,\ i=1,2,3$ in the relative reference frame. These equations coincide with those of the Multiple Reference Frame (MRF) approach Luo et al. (1994), with a uniform angular velocity $\upvarpi$ along the entire computational domain in our case. By representing the relative velocity components as $w_i$ ($v_i = w_i + e_{ijk} \upvarpi _j x_k$ where $x_k$ is measured from the origin that lies on the rotation axis and $e_{ijk}$ stands for the Levi-Civita symbol), the flow equations read

$$\begin{aligned} R^{p} \!&=\! -\frac{\partial w_j}{\partial x_j}\!=\!0 \end{aligned}$$

(1a)

$$\begin{aligned} R^{v}_{i} \!&=\! w_j \frac{\partial v_i}{\partial x_j} \!-\! \frac{\partial \tau _{ij}}{\partial x_j} \!+\! \frac{\partial p}{\partial x_i} + e_{ijk} \upvarpi _j v_k \!=\!0 ~,~~~~~i=1,2,3 \end{aligned}$$

(1b)

$$\begin{aligned} R^{\widetilde{\nu }} \!&=\! w_j \frac{\partial \widetilde{\nu }}{\partial x_j} \!-\! \frac{\partial }{\partial x_j}\! \left[ \left( \! \nu \!+\! \frac{\widetilde{\nu }}{\sigma } \!\right) \frac{\partial \widetilde{\nu }}{\partial x_j} \right] \!-\! \frac{c_{b2}}{\sigma } \left( \frac{\partial \widetilde{\nu }}{\partial x_j} \right) ^2 - \widetilde{\nu }~\! P(\widetilde{\nu }) \!+\! \widetilde{\nu }~\! D(\widetilde{\nu }) \!=\!0 \end{aligned}$$

(1c)

$$\begin{aligned} R^{\varDelta } \!&=\! \frac{\partial }{\partial x_j} \left( \frac{\partial \varDelta }{\partial x_j} \varDelta \right) - \varDelta \frac{\partial ^2 \varDelta }{\partial x_j^2} -1 \!=\!0 \end{aligned}$$

(1d)

where p is the static pressure divided by the constant fluid density, $\tau _{ij}=(\nu + \nu _t)\left( \frac{\partial v_i}{\partial x_j}+\frac{\partial v_j}{\partial x_i}\right)$ and $\nu$ and $\nu _t =\widetilde{\nu }f_{v_1}$ are the bulk and turbulent viscosities. Also, $f_{v_1} = \frac{\chi ^3}{\chi ^3 + C_{v1}^3}$, $\chi = \frac{\widetilde{\nu }}{\nu }$, $c_{v1}=7.1$, $c_{b2} = 0.622$. Equation (1c) is solved for $\widetilde{\nu }$, with $P(\widetilde{\nu })$ and $D(\widetilde{\nu })$ standing for the production and destruction terms of the Spalart-Allmaras turbulence model. Equation (1d) is the Hamilton–Jacobi equation, Tucker (2003), computing distances $\varDelta$ from the nearest wall, to be used by the turbulence model. The objective function to be maximized is the axial moment,

$$\begin{aligned} J = \frac{\int _{S_W} {r_i}^M e_{ijk} x_j \left( -\tau _{kl} n_l + p n_k\right) dS}{\frac{1}{2} l A U_\infty ^2} \end{aligned}$$

(2)

where $\textbf{r}^M$ is the unit vector in the axial direction. The blade length is l, $U_\infty$ is the inlet velocity magnitude, A is the blade area perpendicular to the flow direction and $S_W$ is the blade surface. In some of the cases presented in Sect. 3, a geometric constraint retaining the volume blade throughout the optimization is also used, formulated as $\frac{V - V_{init}}{V_{init}} = 0$ (where V denotes the volume of the blades and $V_{init}$ is the initial volume), and imposed through the gradient projection method (Rosen 1960). The boundary conditions used to “close” the primal problem are (a) Dirichlet conditions for $v_i$ and the $\widetilde{\nu _a}$ along with a zero Neumann condition for p at the inlet and wall boundaries, (b) a zero Dirichlet condition for p along with zero Neumann conditions for $v_i$ and $\widetilde{\nu _a}$ at the outlet and (c) periodic conditions over the periodic boundaries of the CFD domain.

2.2 Continuous adjoint formulation

The Lagrangian function is first defined as

$$\begin{aligned} L = J + \int _\Omega \left( u_i R^v_i + q R^p + \widetilde{\nu _a}R^{\widetilde{\nu }} + \varDelta _a R^{\varDelta } \right) d\Omega \end{aligned}$$

(3)

where $u_i$ denote the adjoint velocity components, q is the adjoint pressure, $\widetilde{\nu _a}$ is the adjoint turbulence variable, $\varDelta _a$ is the adjoint distance and $\Omega$ stands for the computational domain. The derivatives of L w.r.t. the design variables $b_n$, $n\in [1,N]$, yield

$$\begin{aligned} \frac{\delta L}{\delta b_n} = \frac{\delta J}{\delta b_n} + \int _\Omega \left( u_i \frac{\delta R^v_i}{\delta b_n} + q \frac{\delta R^p }{\delta b_n} + \widetilde{\nu _a}\frac{\delta R^{\widetilde{\nu }}}{\delta b_n} + \varDelta _a \frac{\delta R^{\varDelta }}{\delta b_n} \right) d\Omega \end{aligned}$$

(4)

where $\frac{\delta }{\delta b_n}(.)$ represents total (or material) derivatives and

$$\begin{aligned} \frac{\delta J}{\delta b_n} \!&=\! \frac{1}{\frac{1}{2} l A U_\infty ^2} \bigg [\int _{S_W} r_i^M e_{ijk}(-\tau _{kl} n_l + p n_k) \frac{\delta x_j}{\delta b_n}dS \!-\! \int _{S_W} r_i^M e_{ijk} x_j \frac{\delta \tau _{kl}}{\delta b_n} n_l dS \nonumber \\ \!&\quad +\! \int _{S_W} r_i^M e_{ijk} x_j (-\tau _{kl} + p \delta _k^l) \frac{\delta (n_l dS)}{\delta b_n} \!+\! \int _{S_W} r_i^M e_{ijk} x_j \frac{\delta p}{\delta b_n} n_k dS \bigg ] \end{aligned}$$

(5)

Eq. (4) is developed by using $\frac{\delta }{\delta b_n} \left( \frac{\partial (.) }{\partial x_j} \right) = {\frac{\partial }{\partial x_j} \left( \frac{\delta (.) }{\delta b_n} \right) } {-\frac{\partial (.)}{\partial x_k} \frac{\partial }{\partial x_j} \left( \frac{\delta x_k}{\delta b_n}\right) }$ (see Papadimitriou and Giannakoglou (2007)), and the Gauss divergence theorem. Here, only the differentiation of the continuity equation is indicatively shown,

$$\begin{aligned} \int _\Omega q \frac{\delta R^p }{\delta b_n} d\Omega&= {-\int _\Omega q \left[ \frac{\partial }{\partial x_j} \left( \frac{\delta w_j}{\delta b_n} \right) {-\frac{\partial w_j}{\partial x_k} \frac{\partial }{\partial x_j} \left( \frac{\delta x_k}{\delta b_n}\right) } \right] d\Omega } \nonumber \\&= -\int _S q n_j \frac{\delta w_j}{\delta b_n} dS + \int _\Omega \frac{\partial q}{\partial x_j} \frac{\delta w_j}{\delta b_n} d\Omega + \int _\Omega q \frac{\partial w_j}{\partial x_k} \frac{\partial }{\partial x_j} \left( \frac{\delta x_k}{\delta b_n} \right) d\Omega \nonumber \\&= \int _{S} -q n_j \frac{\delta w_j}{\delta b_n} d{S} + \int _\Omega \bigg [ \frac{\partial q}{\partial x_j} \frac{\delta v_j}{\delta b_n} - \frac{\partial q}{\partial x_j} e_{jlk} \upvarpi _l \frac{\delta x_k}{\delta b_n} \nonumber \\ \!&\quad +\! q \left( \frac{\partial v_j}{\partial x_k} - e_{jlk} \upvarpi _l \right) \frac{\partial }{\partial x_j}\left( \frac{\delta x_k}{\delta b_n}\right) \bigg ]d\Omega \end{aligned}$$

(6)

In Eq. (6), all terms including the so-called grid sensitivities, $\frac{\delta x_k}{\delta b_n}$, contribute to the sensitivity derivatives. The remaining integrals in Eq. (4) are expanded in a similar manner. Boundary integrals including derivatives of the flow variables w.r.t. $b_n$ contribute to the adjoint boundary conditions whereas field integrals of the same quantities contribute to the field adjoint equations.

2.2.1 Field adjoint equations and boundary conditions

The process described above can be applied to all terms of Eq. (4) and leads to the following field adjoint equations (for a detailed derivation see Kavvadias et al. (2015) and Papoutsis-Kiachagias and Giannakoglou (2016))

$$\begin{aligned} R^q \!&=\! -\frac{\partial u_j}{\partial x_j} = 0 \end{aligned}$$

(7a)

$$\begin{aligned} R^u_i \!&=\! u_j \frac{\partial v_j}{\partial x_i} - \underbrace{\frac{\partial (w_j u_i) }{\partial x_j}}_\text {M.T.} \!-\! {\ } \frac{\partial \tau _{ij}^a}{\partial x_j} \!+\! \frac{\partial q}{\partial x_i} \!+\! \underbrace{e_{ijk} u_j \upvarpi _k}_\text {A.T.}\nonumber \\ \!&\quad +\! \widetilde{\nu _a}\frac{\partial \widetilde{\nu }}{\partial x_i} \!-\!\frac{\partial }{\partial x_l} \left( \widetilde{\nu _a}\widetilde{\nu }\frac{\mathcal {C}_Y }{\mathbf {|Y|}} e_{mjk} \frac{\partial v_{k}}{\partial x_{j}} e_{mli} \right) \!=\!0 ~,~i\!=\!1,2,3 \end{aligned}$$

(7b)

$$\begin{aligned} R^{\widetilde{\nu _a}} \!&=\! - \underbrace{\frac{ \partial (w_j\widetilde{\nu _a}) }{\partial x_j}}_\text {M.T.} - \frac{\partial }{\partial x_j}\! \left[ \! \left( \nu \!+\!\frac{\widetilde{\nu }}{\sigma } \right) \frac{\partial \widetilde{\nu _a}}{\partial x_j} \right] \!+\! \frac{1}{\sigma }\frac{\partial \widetilde{\nu _a}}{\partial x_j} \frac{\partial \widetilde{\nu }}{\partial x_j} \nonumber \\ \!&\quad +\!2\! \frac{c_{b2}}{\sigma } \frac{\partial }{\partial x_j}\!\! \left( \widetilde{\nu _a}\frac{\partial \widetilde{\nu }}{\partial x_j} \right) \!+\! \widetilde{\nu _a}\widetilde{\nu }\mathcal {C}_{\widetilde{\nu }}\! \!+\! \frac{\partial \nu _t}{\partial \widetilde{\nu }} \frac{\partial u_i}{\partial x_j}\! \left( \frac{\partial v_i}{\partial x_j} \!+\! \frac{\partial v_j}{\partial x_i} \right) \!+\! \left( -P \!+\! D \right) \widetilde{\nu _a}\!=\! 0 \end{aligned}$$

(7c)

$$\begin{aligned} R^{\varDelta _a} \!&=\! -2 \frac{\partial }{\partial x_{j}} \left( \varDelta _a \frac{\partial \varDelta }{\partial x_{j}} \right) \!+\! \widetilde{\nu }\widetilde{\nu _a}\mathcal {C}_{\varDelta } \!=\!0 \end{aligned}$$

(7d)

emerge, where $\tau _{ij}^a = \left( \nu +\nu _t \right) \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right)$ is the adjoint stress tensor and $\textbf{Y}$ is the vorticity vector. The $C_{\widetilde{\nu _a}}$, $C_Y$ and $C_{\varDelta }$ terms are defined in Zymaris et al. (2009). Terms marked with A.T. in Eq. 7 emerge due to switching from $\frac{\delta w_j}{\delta b}$ to $\frac{\delta v_j}{\delta b}$ when formulating the field adjoint equations and their boundary conditions whereas terms marked with M.T. are different than their counterparts for stationary flows, due to the presence of $w_j$ instead of $v_j$ in the convection terms of the momentum and turbulence model equations (Eqs. (7b) and (7c), respectively). The adjoint boundary conditions are listed in Table 1 (see Papoutsis-Kiachagias and Giannakoglou (2016) for the derivation).

Table 1 Adjoint boundary conditions. $t_i^{l}, l\in [1, 2]$ are the components of the two tangent to the surface unit vectors, forming a local Frenet system with $n_i$, $u_t^l$ are the tangent adjoint velocity components aligned with these vectors and $u_n$ is the normal component of the adjoint velocity

The primal and adjoint PDEs, Eqs. (1) and (7), are discretized and solved on unstructured grids using the cell-centered, collocated, finite-volume infrastructure of OpenFOAM. For the primal and adjoint pressure equations, a SIMPLE-like algorithm is used. All convection terms are discretized using second-order upwind schemes; central schemes are used for the diffusive fluxes, including a correction for non-orthogonality. The Gauss divergence scheme is used for the computation of spatial gradients, with a linear interpolation of the differentiated values from cell-centers to cell-faces.

2.3 Sensitivity derivatives

After eliminating all other integrals in the developed form of Eq. (4), by satisfying the adjoint field equations and boundary conditions (see Papoutsis-Kiachagias and Giannakoglou (2016) for a detailed derivation), the remaining terms constitute the sensitivity derivatives of J, which read

$$\begin{aligned} \frac{\delta L}{\delta b_n} \!&=\! \underbrace{\int _{S_W} \tau _{ij}^a n_j e_{ikl} \upvarpi _k \frac{\delta x_l}{\delta b_n} d{S}}_\text {A.T.} + \frac{1}{\frac{1}{2} l A U_\infty ^2} \bigg [\int _{S_W} r_i^M e_{ijk}(-\tau _{kl} n_l + p n_k) \frac{\delta x_j}{\delta b_n} dS \nonumber \\ \!&\quad -\! \int _{S_W} r_i^M e_{ijk} x_j (\tau _{kl} + p \delta _k^l) \frac{\delta (n_l dS)}{\delta b_n} \bigg ] \nonumber \\ \!&\quad -\! \underbrace{\int _\Omega \left( \frac{\partial q}{\partial x_j} + u_i \frac{\partial v_i}{\partial x_j} + \widetilde{\nu _a}\frac{\partial \widetilde{\nu }}{\partial x_{j}} + u_i\right) e_{jlk} \upvarpi _l \frac{\delta x_k}{\delta b_n} d\Omega }_\text {A.T.} \nonumber \\ \!&\quad -\! \int _\Omega \bigg [q \frac{\partial v_j}{\partial x_k} + \underbrace{q e_{jlk} \upvarpi _l}_\text {A.T.} + \underbrace{u_i w_j \frac{\partial v_i}{\partial x_j}}_\text {M.T.} + \tau ^a_{ij} \frac{\partial v_i}{\partial x_k} + u_j \frac{\partial p}{\partial x_k} \nonumber \\ \!&\quad +\! \underbrace{\widetilde{\nu _a}w_j \frac{\partial \widetilde{\nu }}{\partial x_{k}}}_\text {M.T.} \!+\! \left( \! \nu \!+\! \frac{\widetilde{\nu }}{\sigma } \!\right) \frac{\partial \widetilde{\nu _a}}{\partial x_{j}} \frac{\partial \widetilde{\nu }}{\partial x_{k}} - 2 \widetilde{\nu _a}\frac{c_{b2}}{\sigma } \frac{\partial \widetilde{\nu }}{\partial x_{j}} \frac{\partial \widetilde{\nu }}{\partial x_{k}} \nonumber \\ \!&\quad +\! \widetilde{\nu _a}\widetilde{\nu }\mathcal {C}_{Y} \frac{Y_i}{\Vert \textbf{Y}\Vert } e_{ijl} \frac{\partial v_l}{\partial x_{k}} \!+\! 2 \varDelta _a \frac{\partial \varDelta }{\partial x_{j}} \frac{\partial \varDelta }{\partial x_{k}} \bigg ] \frac{\partial }{\partial x_j}\left( \frac{\delta x_k}{\delta b_n}\right) d\Omega \end{aligned}$$

(8)

2.4 Verification of sensitivity derivatives

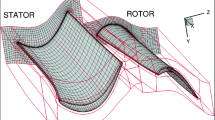
The continuous adjoint-based sensitivity derivatives computed by the proposed method and software are firstly verified against finite-differences (FDs). Since FDs are computationally expensive due to the need to solve the flow equations twice for each design variable, a less costly 2D mixer case, Fig. 1, is used for this purpose. The mesh consists of 12288 elements, with an average $y^+ = 9.7/4.5$ of the first cell centers off the rotating/stationary walls. The Reynolds number, based on the diameter of the rotor and peripheral velocity at its tip, is $R_e = 26,000$, the volumetric B-Splines morphing box shown in Fig. 1a is used to parameterize the rotor of the mixer and the objective function is the axial moment. The four blue and red blades shown in the same figure are rotating and stationary, respectively. A study on the step value of FDs (not shown here) indicated that the FD results do not change significantly for step size $10^{-6}$ (used in Fig. 1) and $10^{-7}$. As it can seen from Figs. 1b and c, the adjoint-based sensitivities are in a good agreement with FDs. The same figures also present sensitivities computed based on an adjoint approach that does not include the differentiation of terms emerging from the change in the reference frame system (i.e. terms marked with A.T. in Eqs. (7) and (8) are omitted and terms marked with M.T. use $v_i$ instead of $w_i$). This approach is referred to as ’adjoint-stationary’. It is evident that, apart from computing the wrong sensitivity magnitude, such as approach can occasionally compute wrongly signed sensitivities (control points 49, 58, 61 in Fig 1b and 45, 62 in Fig 1c), which can be detrimental for the convergence of an optimization loop. This highlights the importance of the adjoint development presented in this paper.

Fig. 1

2D mixer: Verification of the adjoint-based sensitivity derivatives with FDs. a Case geometry; blue/red lines correspond to rotating/stationary walls. The grey area indicates the rotating part of the computational domain in which the last term of Eq. (1b) is active. The lattice of control points parameterizing the rotor is also shown. The coordinates of the control points in red act as the design variables. b, c Comparison of the adjoint-based derivatives with FDs,, and the adjoint-stationary approach, for the x and y coordinates of the control points. (Color figure online)

3 WT Shape Optimization Results

Based on the aforementioned method, blade shapes of two Horizontal Axis WTs, namely the MEXICO and NREL Phase VI WT ones, are optimized. In both cases, the flow equations presented in section 2 are used to numerically predict the flow around the WT blades.

3.1 The MEXICO WT case

The MEXICO WT is associated with the EU project "Model Rotor Experiments In Controlled Conditions" Schepers and Snel (2007). The computational domain $\Omega$ includes one third of the WT disk, with periodic conditions. The tip radius is $R = 2.25$ m and the domain and mesh are presented in Fig. 2; the distance of the blade to the inlet, outlet and top boundaries is 5R, 10R and 7R, respectively. The hybrid mesh consists of about $10^7$ cells, with an average $y^{+} = 0.14$ of the first cell centers of the walls. A structured mesh is generated on the blade surface, followed by structured layers of hexahedra around the blade; the mesh over the remaining of the domain is unstructured with tetrahedra. The global pitch angle of the blade is $-2.3^{\circ }$ and the rotational speed is 424.49 rpm.

Fig. 2

MEXICO WT: CFD domain and mesh around the WT blade

3.1.1 Flow solver verification

The wind speed and yaw angle are 10 m/s and $0^{\circ }$, respectively. The pressure coefficient distribution on a number of different spanwise positions over the blade is shown in Fig. 3. OpenFOAM results are compared with the outcome of the MaPFlow code Papadakis et al. (2014) of the Lab. of Aerodynamics of NTUA and the in-house GPU-enabled PUMA code Tsiakas et al. (2019); in all codes, the Spalart-Allmaras turbulence model is used. It can be seen that all CFD predictions are in good agreement and small differences appear only over the suction side, at $25\%$ and $35\%$ span, Fig. 3a and b.

Fig. 3

MEXICO WT, $U_\infty = 10$ m/s: Comparison of the pressure coefficient distribution computed by OpenFOAM (Present(OF)), PUMATsiakas et al. (2019) and MaPFlowPapadakis et al. (2014), at four spanwise positions

To further verify our CFD analysis against other CFD solvers, thrust and power coefficient ($C_{p} = \frac{Power}{\frac{1}{2} \rho {U_{\infty }}^3 A}$, where Power is computed by multiplying the aerodynamic axial moment with the number of blades and the rotational speed, and A is the rotor disk area) are computed for $U_\infty = 10$ m/s, and compared in Table 2. It can be seen that all CFD codes compute similar power coefficient and thrust values slightly over-estimation only by the MapFlow code.

Table 2 MEXICO WT: $U_\infty = 10$ m/s: Power coefficient and thrust values of the baseline geometry computed by four different CFD codes. Over and above to the CFD solvers used in Fig. 3 to verify our results, values from the CENTER CFD solver Schepers et al. (2012) are also included here

Experimental Svorcan et al. (2018) and CFD (CENTER CFD Schepers et al. (2012)) results showed that the highest power coefficient of the WT blade occurs at $U_\infty =15$ m/s, at a Tip Speed Ratio ($TSR = \omega R / U_\infty$) of approximately 6.67. CFD runs (using OpenFOAM) for six different inlet velocities namely 8, 10, 12, 15, 16, 25 m/s, were performed and the computed power coefficient and thrust force curves are plotted in terms of TSR in Fig. 4. This figure reconfirms the experimentally found point of max. $C_{p}$.

Fig. 4

MEXICO WT: Power coefficient (right) and thrust force (left) curves over a range of TSR, computed by OpenFOAM (Present(OF)) and CENTER CFD Schepers et al. (2012)

3.1.2 Blade optimization

After verifying our CFD results, we proceed with the aerodynamic shape optimization of the WT blade at two inlet velocities, namely $U_{\infty } = 10$ m/s (case A) and $U_{\infty } = 15$ m/s (case B), with the axial moment, Eq. (2), being the objective function to be maximized. The shape of the blade is parameterized using a $6\times \!12\!\times \!6$ volumetric B-Splines morphing box, with 432 control points (CPs) in total, Fig. 5. After 15 optimization cycles, the axial moment has increased by $11.13\%$ and $2.89\%$, in case A and case B, respectively, Table 3; from the latter, it can also be seen that thrust increased in case B and decreased in A. In addition, Fig. 6 presents the convergence of the axial moment for case A. No stopping criterion was used; instead, it was decided to run for 15 optimization cycles at which point, results are considered as indeed no more changing.

Fig. 5

MEXICO WT: The morphing box parameterizing the blade and part of the surrounding mesh. CPs in red can be displaced during the optimization whereas CPs in blue remain still. (Color figure online)

Fig. 6

MEXICO WT: Convergence of the objective function of Case A; all values have been normalized with the objective function value of the initial geometry

Table 3 MEXICO WT: Power coefficient and thrust values of the baseline and optimized geometries, at $U_{\infty } = 10$ m/s and $U_{\infty } = 15$ m/s

In both cases, the optimization has mainly changed the shape of the blades close to its tip, Fig. 7. It bended the tip towards the axial flow direction and slightly increased the blades yaw angle at the same position (Fig. 7d). The part from the root to the mid of the blade was displaced mostly over the pressure side, whereas the rest remained practically unchanged. The part from the mid to the tip experienced noticeable displacements mostly close to the trailing edge and over the pressure side. This was expected because most of the power extraction occurs near the tip. Figure 7c and d show that the optimized geometry of case A is thinner than that of case B; practically, this causes the reduction in the thrust of case A (Table 3). Additionally, to get a clear view on local displacements along the blade span, the cumulative normal displacement of the optimized blade surfaces are presented in Figs. 8 and 9, respectively. Table 4 displays the Reynolds numbers at various spanwise positions for both $U_{\infty } = 10$ m/s and $U_{\infty } = 15$ m/s. As the chord length of the optimized geometry remains unchanged compared to the baseline, the Reynolds numbers for both baseline and optimized designs are identical.

Fig. 7

MEXICO WT: Comparison of the baseline (black), and the optimized for case A (green) and case B (magenta) blade geometries, at four spanwise positions. (Color figure online)

Table 4 MEXICO WT: The Reynolds number at four spanwise positions, at $U_{\infty } = 10$ m/s and $U_{\infty } = 15$ m/s

Fig. 8

MEXICO WT, optimized geometry of case A: Cumulative normal displacement over the blade surface. Positive/negative signs (red/blue colors) indicate inward/outward displacements. (Color figure online)

Fig. 9

MEXICO WT, optimized geometry of case B: Cumulative normal displacement over the blade surface; color interpretation as in Fig. 8

The pressure coefficient and peripheral force distributions of the baseline and optimized geometries for cases A and B are also plotted in Figs. 10 and 11, respectively, at a number of spanwise positions. It is evident that changes in the peripheral force, and hence in the axial moment, are more pronounced in the upper part of the blade. The part close to the root of case A (Fig. 10a and b) contributes to the change in the pressure coefficient more than that of case B (Fig. 11a and b). Another interesting observation is that, in case A, no significant pressure coefficient difference is observed close to the leading and trailing edges of the initial and optimized geometries. On the other hand, these are the positions with the highest pressure coefficient changes between the optimized blade of case B and the initial one. To help interpret the local flow changes and their impact on the generated moment, the sum of the peripheral force $(F_p)$ at each spanwise position is also given, for the baseline $(F^{Base}_{p} [N])$ and optimized $(F^{Opt}_{p}[N])$ geometries (sub-captions of Figs. 10 and 11). From the peripheral force curves, it can be seen that the decrease in the local peripheral force close to the leading edge on the suction side is compensated by an increase close to the leading edge on the pressure side and an increase over the mid-chord of the blade, over both sides; this general trend is observed in both cases.

Fig. 10

MEXICO WT, $U_\infty = 10$ m/s: Comparison of the pressure coefficient distributions and peripheral force integrands $[N/m^2]$ of the baseline and optimized (case A) blades at four spanwise positions. The left and right axes correspond to the pressure coefficient (magenta/blue indicate baseline/optimized) and peripheral force (green/yellow indicate baseline/optimized), respectively. $F^{Base}_{p}$ [N] and $F^{Opt}_{p}$ [N] present the integral of the peripheral force of the baseline and optimized blades in each spanwise position. Colored arrows indicate the correspondence between the colored curves and the left or right axes. (Color figure online)

Fig. 11

MEXICO WT, $U_\infty = 15$ m/s: Comparison of pressure coefficient distributions and the peripheral forces integrands of the baseline and optimized (case B) blades at four spanwise positions, notations as in Fig. 10

Similar comments can be made by examing Figs. 12 and 13 which illustrate the contribution of the blade surface points to the change in axial moment. Mid and tip blade areas contribute more compared to the practically negligible contributions of the root. Figures 12a and 13a show that, in both cases, the highest increase in axial moment results from shape changes over the pressure side at mid-to-tip, close to the leading part.

Fig. 12

MEXICO WT, optimized blade in case A: Contribution of blade surface nodes to the increase in axial moment after the optimization

Fig. 13

MEXICO WT, optimized blade in case B: Contribution of blade surface nodes to the increase in axial moment after the optimization

It is interesting to evaluate geometries from case A (optimized at 10 m/s) and B (optimized at 15 m/s) at operating points they weren’t optimized for. Figure 14 illustrates the power coefficient curve of the baseline geometry (see also Fig. 4) and the performance of the blades optimized in case A and B, both evaluated at 15 m/s and 10 m/s. It can be seen that the geometry optimized in case A not only outperforms the baseline one at the conditions this was optimized for, but also has a slightly higher power coefficient than the baseline one at 15 m/s (TSR=6.67) too. On the contrary, the geometry optimized in case B has a power deficit compared to the baseline one, when evaluated at conditions it was not optimized for (10 m/s, TSR=10).

Fig. 14

MEXICO WT: Power coefficient curve as a function of the tip-speed ratio (TSR) of baseline and optimized geometries

3.2 NREL phase VI WT case

The National Renewable Energy Laboratory (NREL) completed an experimental test for a Phase VI WT in a wind tunnel (24.4 $\times$ 36.6 m) at NASA’s Ames Research Center Simms et al. (2001). Herein, the computational domain $\Omega$ includes half of the WT disk, with periodic boundary conditions. The tip radius is $R=5.029 m$, the domain and mesh are presented in Fig. 15 (the distance of the blade to the inlet, outlet and top boundaries is 5R, 10R and 7R, respectively). A hybrid CFD mesh with $\sim 7 \times 10^6$ cells was generated, with an average non-dimensional distance of the first cell centers off the walls equal to 36. The rotational speed is $71.9\ rpm$ and the global pitch angle is $5^\circ$.

Fig. 15

NREL VI WT Case: CFD domain

3.2.1 Flow solver verification

The wind speed and yaw angle are 7 m/s and $0^{\circ }$, respectively. The pressure coefficient distribution at a number of different spanwise positions over the blade is shown in Fig. 16. OpenFOAM predictions are compared with wind tunnel measurements from the NREL wind tunnel Simms et al. (2001) and predictions using ANSYS FLUENT published in Mo and Lee (2012). Despite the use of different meshes, the two CFD results are in good agreement with measurements.

Fig. 16

NREL Phase VI WT Blade: Comparison of the pressure coefficient distribution computed by the present (OpenFOAM) code, ANSYS FLUENT (Mo. et al) (Mo and Lee 2012) and measurements Simms et al. (2001), at five spanwise positions

3.2.2 Wind turbine blade optimization

The objective function to be maximized is still the axial moment, Eq. (2). In addition, a constraint on the blade volume to be equal to that of the baseline geometry is also applied. The gradient of the constraint function is taken into account using the method presented in Rosen (1960). 864 CPs were used to parameterize the blade using the volumetric B-Splines morphing box presented in Fig. 17. After 15 cycles, the axial moment has increased by $11.65\%$, Table 5. In addition, Fig. 18 illustrates the convergence of the axial moment during the optimization process.

Fig. 17

NREL Phase VI WT: A $6\times \!24\!\times \!6$ volumetric B-Splines morphing box parameterizes the blade and part of the surrounding mesh. CPs in red can be displaced during the optimization whereas those in blue remain still. (Color figure online)

Fig. 18

NREL Phase VI WT: Convergence of the objective function; all values have been normalized with the objective function value of the initial geometry. (Color figure online)

Table 5 NREL Phase VI WT: Power coefficient and thrust values of the baseline and optimized geometries

It can be seen from Fig. 19 that the optimization method has mainly changed the shape of the blade close to its tip, as expected. Smaller changes can also be seen close to the root, where the blade is bended towards the flow direction. From the mid to the tip of the blade, the trailing edge practically remained intact, whereas the largest deformation occurred at the leading part of the blade. Even though the parameterization was not setup in such a way, it is as if the optimization rotated the blade sections around the trailing edge, towards the flow direction. Table 6 presents the Reynolds numbers at different spanwise positions. Since the chord length of the optimized geometry remains unchanged relative to the baseline, the Reynolds numbers for both the baseline and optimized designs are identical.

Fig. 19

NREL Phase VI WT: Comparison of the baseline (black) and optimized (red) blade sections at a number of spanwise positions. (Color figure online)

Table 6 NREL Phase VI: The Reynolds number at five spanwise positions

Fig. 20 presents the cumulative normal displacement of the optimized NREL Phase VI blade surface. It can be observed that the highest displacement occurs at the leading edge, at the mid and upper part of the blade, whereas the trailing edge displacement is almost zero (see Fig. 19).

Fig. 20

NREL Phase VI WT: Cumulative normal displacement over the blade surface. Positive/negative signs (red/blue colors) indicate inward/outward displacements. (Color figure online)

The pressure coefficient and the peripheral force distributions of the baseline and optimized geometries of the NREL Phase VI WT are plotted in Fig. 21 at a number of spanwise positions. It can be seen that the largest increase in the pressure coefficient occurs at the tip. The leading edge of the optimized blade experiences the highest change in the pressure coefficient, with minor changes close to the trailing edge. The trailing part of the optimized blade doesn’t exhibit high peripheral force differences compared to the baseline one. The largest changes in the peripheral force occur between the mid-chord to the leading part of the blade; moreover, it is shown that the optimization run increased $F^{Opt}_{p}$ with respect to $F^{Base}_{p}$ from the root to the tip of the blade, approximately by the same percentage.

Fig. 21

NREL Phase VI WT: Comparison of pressure coefficient distributions and peripheral force integrands of the baseline and optimized blade, at five spanwise positions; notation as in Fig. 10

Figure 22 demonstrates the local axial moment change along the NREL Phase VI blade after 15 optimization cycles. It can be seen that the optimized blade exhibits high axial moment change close to the tip, with almost negligible changes close to the root. The leading part of the blade contributed the most to the increase in axial moment, whereas the value at the trailing part remains almost unchanged compared to the baseline design. Figure 22b shows that the largest increase in axial moment occurs at the leading edge on the suction side of the blade, close to its tip. This coincides with the areas of high peripheral force variations (Fig. 21c, d and e). The largest decrease in the axial moment occurs over the pressure side, close to the tip of the blade, at about mid-chord.

Fig. 22

NREL Phase VI WT: Contribution of blade surface nodes to the increase in axial moment after the optimization

4 Conclusions

This paper demonstrates the application of an enhanced version of the publicly available adjointOptimisationFoam software, an adjoint-based optimizer developed in-house for OpenFOAM, in the context of optimizing the MEXICO and NREL Phase VI wind turbines, with a focus on maximizing the axial moment. The software’s capabilities were augmented through the inclusion of adjoint terms that account for the computational domain’s rotation, resulting in additional terms in the adjoint continuity, momentum equations and sensitivity derivatives expressions. Applying this extended software to the MEXICO wind turbine revealed a remarkable 11.13% increase in the axial moment for the blade optimized at $U_\infty =10$ m/s. This improvement was achieved primarily by bending the blade tip in the axial direction and adjusting the blade yaw angle near the tip. For the MEXICO blade optimized at $U_\infty =15$ m/s, a 2.89% increase in the axial moment was observed. Analyzing TSR-$C_{p}$ curves, it becomes evident that the blade optimized at $U_\infty =10$ m/s exhibited more robust performance compared to both the initial design and the blade optimized for $U_\infty =15$ m/s. Additionally, the axial moment of the NREL Phase VI wind turbine increased by 11.65%. This enhancement was predominantly attributed to changes in the leading part on the suction side of the optimized geometry, primarily stemming from peripheral force variations on the suction side. Notably, the volume of the optimized geometry remained consistent with that of the initial design throughout the optimization process. The most significant deformations occurred at the blade’s leading edge, near the tip, where substantial alterations in the pressure coefficient distribution between the baseline and optimized blade were observed.