1 Introduction

Renewable energy technologies are strong driving force in diminishing greenhouse gas emissions which are expected to supply as much as 29.4% of world electricity production by 2023 [1]. VLH hydropower is a reliable source of renewable energy that is particularly beneficial for remote regions in developing countries where centralized electricity generation is not available or sufficient, and helps to offset the cost of other sources of electricity generation [2, 3]. Kaplan turbines are used for low heads in the range of approximately 10–30 m, and low head turbines are designed for 2–10 m head. The main problem of these two types of turbine is the high cost of constructions [4, 5]. VLH turbines are used for sites with head lower than 4.5 m, and their power outputs are below 500 KW. All aforementioned turbine types are classified as reaction turbines. Moreover, turbines should be able to work in variable conditions. The flow behavior inside the reaction turbines is very complex and alters through the blade passages from hub to tip regarding the interaction between guide vane and runner blades. Also, flow conditions change with respect to guide vane angle and runner rotational speed [6].

VLH turbine is installed in a slanted position with 30°–50° from vertical axis. The turbine is used in channels with low head and velocity, and its frame works as a dam which eliminates the need to construct a dam. Also, the low velocity of flow in channel obviates the necessity for mounting a draft tube as there is not considerable hydrokinetic energy to recuperate. These features reduce civil work and make the technology more cost competitive, particularly for rural areas. Channel geometry and turbine installation angle affect upstream flow. Hence, depth of upstream flow must be controlled for the turbine installation and this criterion should be considered in the design of channel [7, 8].

Since VLH turbine is designed based on the simplistic assumptions, its performance should be controlled in different conditions. Generally, performance curves are extracted from experimental tests based on variations in flow rate, rotational speed and head [9]. The most important part of a VLH turbine is the runner which conducts the fluid flow through the blade passages. Twist of flow inside the runner causes a change in angular momentum and leads to power production. Extracting turbine performance curves helps to obtain a suitable design in different conditions; however, obtaining these curves from model tests is expensive and time-consuming. Computational fluid dynamics (CFD) is used extensively by engineers to investigate the performance of hydro turbines, and its accurate results makes it an efficient tool to simulate flow conditions in VLH turbines and also to save time and cost [10, 11].

VLH turbine’s design has been investigated in the literature. Alexander et al. [12] designed an axial flow turbine with cylindrical hub and five flat blades and efficiency of 68% and considering hub-to-tip ratio about 0.6. Also, they considered three different parameters of geometry to improve the runner performance. These changes included blade inlet and outlet angles at tip and blade inlet angle at hub. They also investigated relative variations in shaft output power and flow rate at the constant head and rotational speed. Runner performance is highly dependent on the tip outlet angle. Moreover, the turbine performance enhances because of flow rate reduction at the design point caused by the tip inlet angle modification [13]. Since the transferred torque and blade length are great, the solidity usually should be between 1 and 1.5. One particular characteristic of Kaplan turbines that does not exist in other types of turbine is the ability to control stagger angle. Although commercial VLH turbines are classified as axial turbines, the guide vanes of the turbines are stationary. In lower loads, the blades are adjusted in a specific way to obtain best efficiency which needs supplementary adjustments of guide vanes stagger angel to create fully axial flow at the runner outlet [14]. Muis and Sutikno [15] considered swirl velocity, free vortex, and forced vortex to design the runner of a VLH turbine using Goettingen0480 airfoil. They applied kω-SST model to solve the 3D flow in the turbine, and their numerical results showed that the generated power for forced vortex criterion is 15% higher than the power produced by free vortex criterion. Hoghooghi et al. [16] performed experimental tests to investigate the hydrodynamic performance of a low head axial flow turbine by applying free vortex method. Their results indicated two regions in the performance curves of the turbine that the turbine’s efficiency is highly dependent on head. Sotoude Haghighi et al. [6] designed a VLH turbine based on free vortex theory and coupling a MATLAB code with XFOIL. They investigated the impact of runner blade opening angles on the turbine’s performance and also studied cavitation phenomenon by implementing the homogeneous multiphase model. Their results revealed the restrictive effect of cavitation on the turbine’s performance at large opening angles. In an attempt to present a simple methodology for design of VLH turbine, Sutikno and Adam [17] applied free vortex theory and minimum pressure coefficient for their numerical simulations. Their results for heads lower than 1.2 m showed that minimum pressure coefficient is an effective criterion to obtain minimum loss in the shock-free flow and maximum efficiency.

Optimization of VLH turbine’s geometry is of great importance to improve the performance of the turbines. Janjua et al. [10] used five blade models to perform numerical analyses on blade profiles at different blade angles and optimized the profile of the blades for different flow rates and pressure heads. Based on reduced polytrophic ratio, Banaszek and Tesch [18] optimized the blade profiles of a Kaplan turbine by applying genetic algorithm and artificial neural network and considering middle camber line and airfoil thickness. They found inverse correlation between power dissipation and thickness distribution coefficient. Optimization of hydrofoils of other types of turbine like ocean current turbines is also studied by researchers. In Ref. [19], drag-to-lift ratio reduction and cavitation limits have been defined as the objective functions to optimize the hydrofoil’s geometry. A multipoint optimization technique is used by applying genetic algorithm to perform multiobjective optimizations. Results of CFD simulations for optimized hydrofoils showed that the optimized geometry has better hydrodynamic performance in three different angles of attacks in comparison with the original design. Blade optimizations are also performed for turbine runner blades with 1.5–2 m head and 75 ls−1 flow rate conditions using free vortex theory. Dixon, Saravanmuttoo and Hothersall presented a comprehensive review of free vortex theory in axial turbomachinery [14, 20].

During the initial stage of turbomachinery design, there is not sufficient information to apply CFD codes. At this step of design, some limits should be considered such as optimization of performance parameters, aerodynamic load on the blades, cavitation, shock effect, and stall limits. Initial geometry can be designed by optimized axial cascades with minimum loss according to minimum suction pressure effect [17]. For VLH turbines, both airfoil and cascade must be considered for optimization. Because of low rotational speed, the airfoils are optimized in a way to give optimum lift-to-drag ratio [21]. The position of airfoil maximum thickness influences other parameters such as position of minimum pressure and created pressure distribution. As far as possible, the position of minimum pressure should be close to trailing edge in order to provide slight transition from laminar flow and decrease friction coefficient. Therefore, the airfoil maximum thickness should be between 30 and 60% of blade length [22]. Determination of maximum thickness, airfoil profile, lift-to-drag ratio and its effect on turbine performance depends on operating conditions.

Although design of VLH turbine is well studied in the literature, less attention has been paid to the optimization of these turbines. The novelty of this work lies in using CST method to optimize the profile of runner blades and increasing the efficiency of the turbine. So far, there is not any report of using CST method for VLH turbines installed in channels. In this paper, effect of 2D optimization on 3D optimization has been considered. At first, initial turbine design is performed according to the Euler law in turbomachinery and assuming constant and equal axial velocity at different sections of blades which are standard airfoils. To optimize the geometry, airfoils are presented by two curves for upper and lower surfaces. These curves are defined in the form of continuous polynomials with respective coefficients. Then, these coefficients are corrected by coupling XFOIL with a MATLAB code and implementing fminsearch minimum navigation algorithm to find optimum profiles of the blades. The main goal is to investigate the performance of the optimized 3D turbine prototype and compare it with the initial design and periodic simulations. To obtain accurate results, multiphase model with standard free surface flow condition is applied on the whole domain including the runner, guide vanes, and channel.

2 Design of the initial turbine

The VLH turbine designed in this study has 1.82 m tip diameter that operates at 2.9 m head with a flow rate and a rated power of 12.187 m3 s−1 and 295 kW, respectively (Table 1). The turbine has eight runner blades and 24 guide vanes that is common for axial flow hydraulic turbines which usually have three to ten runner blades [23]. It is suggested that for VLH turbines installed in inclined position, unit rotational speed (\(N_{11} = nD/H^{0.5}\)) should be within the range of 65–280 [7]. For the initial design of this study, the value of N11 is 69.5.

Table 1 Design parameters of the initial turbine
Full size table

Definition of specific speed for hydro turbine is [4]:

$$N_{s} = \frac{n\sqrt Q }{{\left( {\text{Hg}} \right)^{3/4} }}$$
(1)

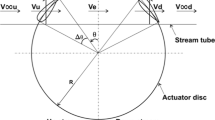
in which n is defined as revolutions per second. The specific speed of the turbine is approximately 0.3 which is suitable for Kaplan turbines [4]. According to principles of design of axial flow hydraulic turbines presented by Lewis [9], the velocity triangles at inlet and outlet of the runner blades are depicted in Fig. 1. According to Euler equation for hydro turbines, hydraulic efficiency can be written as [9]:

Fig. 1
figure 1

a Velocity triangles for runner blades, b relative stream velocity and angle [6]

Full size image
$$\eta_{H} = \frac{\Delta W}{{gH_{E} }} = \frac{{U_{1} C_{\theta 1} - U_{2} C_{\theta 2} }}{{gH_{E} }} .$$
(2)

To achieve maximum efficiency, the last term in Eq. 2 must be equal to zero and hence, it can be written as Eq. 3. Also, according to Fig. 1, angle of relative and absolute velocities can be calculated from Eqs. 4–6:

$$\eta_{H} = \frac{\Delta W}{{gH_{E} }} = \frac{{U_{1} C_{\theta 1} }}{{gH_{E} }}$$
(3)
$$\alpha_{\text{inlet}} = \tan^{ - 1} \left( {\frac{{C_{{\theta ,{\text{inlet}}}} }}{{C_{{m,{\text{inlet}}}} }}} \right)$$
(4)
$$\beta_{\text{inlet}} = \tan^{ - 1} \left( {\frac{\omega \times r}{{C_{{m,{\text{inlet}}}} }} - \tan \alpha_{\text{inlet}} } \right)$$
(5)
$$\beta_{\text{outlet}} = \tan^{ - 1} \left( {\frac{\omega \times r}{{C_{{m,{\text{outlet}}}} }}} \right)$$
(6)

Because of constant cross-area in axial turbine, we suppose axial velocity is constant:

$$C_{m} = \frac{Q}{{\frac{\pi }{4}\left( {D_{\text{tip}}^{2} - D_{\text{hub}}^{2} } \right)}}.$$
(7)

Other parameters which are used in design calculation are as follows:

$$\tan (\beta_{\infty } ) = 0.5 [\tan (\beta_{1} ) + \tan (\beta_{2} )]$$
(8)
$$W_{\infty } = C_{m} /{ \cos }\left( {\beta_{\infty } } \right)$$
(9)
$${\text{Pitch}} = 2*3.14*r/N_{b}$$
(10)
$$C = {\text{Pitch*}}S$$
(11)

in which S is solidity (ratio of chord length to pitch) and in this study varies from 1.05 (at hub) to 1.20 (at tip) linearly.

$$\text{Re} = \rho W_{\infty } C/\mu$$
(12)
$${\text{Mach}} = W_{\infty } /C_{s}$$
(13)
$$L/D = 2*\tan \left( {\beta_{\infty } } \right)/z - \, \tan (\beta_{\infty } )$$
(14)

The last equation calculates the required lift-to-drag ratio, and the selected airfoil should satisfy this criterion. Also z can be obtained as:

$$z = \left( {1 - \eta } \right)\frac{{C_{m} }}{r \times \omega }.$$
(15)

It should be noted that Re and Mach numbers are defined based on relative velocity and are used as XFOIL inputs as well as incidence angle and airfoil’s set of points. Also, in this case, fluid is incompressible and Mach number is smaller than 0.3 which is ignored by XFOIL automatically.

Design process is done for 11 sections according to the Euler law in turbomachinery and considering equal axial velocity and outlet angle of 90° from blade (α2 = 90). Results are shown in Table 2. Also, the sections have been reduced for easiness in design and decrease in optimization calculations as shown in Table 3. Figure 2 shows the initial runner blades and guide vanes, and their positions in the channel. Stagger angle is the angle between the chord line and the turbine axial direction.

Table 2 Cascade design calculation
Full size table
Table 3 Reduced cascade sections
Full size table
Fig. 2
figure 2

Turbine components and their positions

Full size image

3 Numerical setup

3.1 Governing equations

The continuity and Reynolds-averaged Navier–Stokes (RANS) equations in conservation form are [24, 25]:

$$\frac{\partial \rho }{\partial t} + \frac{{\partial \left( {\rho u_{i} } \right)}}{{\partial x_{i} }} = 0$$
(16)
$$\frac{{\partial \left( {\rho u_{i} } \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{j} u_{i} } \right)}}{{\partial x_{j} }} = - \frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {2\mu S_{ij} } \right)$$
(17)

where Sij is strain-rate tensor:

$$S_{ij} = \frac{1}{2} \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right).$$
(18)

Flow through the VLH turbine is turbulent, and therefore, ui and p must be defined as a sum of mean (Ui and P) and fluctuating parts [24]:

To solve the above-mentioned equations, appropriate turbulence models should be applied. The shear stress transport (SST) k–ω turbulence model is widely used for hydro turbine simulations as it is efficient for both free stream flow and turbulent boundary layer modeling. Indeed, its high accuracy for near-wall calculations is beneficial for hydro turbine simulations where accurate boundary layer modeling is demanded [26, 27]. Also, it exhibits less sensitivity to free stream conditions. The transport equations for k and ω are as follows [26, 28]:

$$\frac{{\partial \left( {\rho k} \right)}}{\partial t} + \frac{{\partial \left( {\rho ku_{i} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left( {\varGamma_{k} \frac{\partial k}{{\partial x_{j} }}} \right) + G_{k} - Y_{k}$$
(19)
$$\frac{{\partial \left( {\rho \omega } \right)}}{\partial t} + \frac{{\partial \left( {\rho \omega u_{i} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left( {\varGamma_{\omega } \frac{\partial \omega }{{\partial x_{j} }}} \right) + G_{\omega } - Y_{\omega } + D_{\omega }$$
(20)

where Gk represents the production of turbulence kinetic energy, Gω represents the generation of ω, \(\varGamma_{k}\) and \(\varGamma_{\omega }\) represent the effective diffusivity of k and ω, respectively. \(Y_{k}\) and \(Y_{\omega }\) represent the dissipation of k and ω due to turbulence. Dω represents the cross-diffusion term and Sk and Sω are user-defined source terms.

$$\varGamma_{k} = \mu + \mu_{t} /\sigma_{k}$$
(21)
$$\varGamma_{\omega } = \mu + \mu_{t} /\sigma_{\omega }$$
(22)

where σk and σω are the turbulent Prandtl numbers for k and ω, respectively. Also μt (turbulent viscosity) is calculated as:

$$\mu_{t} = \frac{\rho *k}{\omega }/{ \hbox{max} }\left[ {\frac{1}{{a^{*} }},\frac{{SF_{2} }}{{a_{1} \omega }}} \right]$$
(23)
$$\sigma_{k} = {1 \mathord{\left/ {\vphantom {1 {\left[ {\frac{{F_{1} }}{{\sigma_{k,1} }} + \frac{{1 - F_{1} }}{{\sigma_{k,2} }}} \right]}}} \right. \kern-0pt} {\left[ {\frac{{F_{1} }}{{\sigma_{k,1} }} + \frac{{1 - F_{1} }}{{\sigma_{k,2} }}} \right]}}$$
(24)
$$\sigma_{\omega } = {1 \mathord{\left/ {\vphantom {1 {\left[ {{\raise0.7ex\hbox{${F_{1} }$} \!\mathord{\left/ {\vphantom {{F_{1} } {\sigma_{\omega ,1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{\omega ,1} }$}} + {\raise0.7ex\hbox{${\left( {1 - F_{1} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {1 - F_{1} } \right)} {\sigma_{\omega ,2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{\omega ,2} }$}}} \right]}}} \right. \kern-0pt} {\left[ {{\raise0.7ex\hbox{${F_{1} }$} \!\mathord{\left/ {\vphantom {{F_{1} } {\sigma_{\omega ,1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{\omega ,1} }$}} + {\raise0.7ex\hbox{${\left( {1 - F_{1} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {1 - F_{1} } \right)} {\sigma_{\omega ,2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{\omega ,2} }$}}} \right]}}$$
(25)
$$F_{1} = { \tanh }\left( {\left[ {{ \hbox{min} }\left( {\hbox{max} \left( {{\raise0.7ex\hbox{${\sqrt k }$} \!\mathord{\left/ {\vphantom {{\sqrt k } {0.09\omega y}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${0.09\omega y}$}},500\mu /\rho \omega y^{2} } \right),4k\rho /\sigma_{\omega ,2} y^{2} D^{ + } } \right)} \right]^{4} } \right)$$
(26)
$$F_{2} = { \tanh }\left( {\hbox{max} \left( {{\raise0.7ex\hbox{${2*\sqrt k }$} \!\mathord{\left/ {\vphantom {{2*\sqrt k } {0.09\omega y}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${0.09\omega y}$}},500\mu /\rho \omega y^{2} } \right)^{2} } \right)$$
(27)
$$Y_{k} = \rho \beta^{*} k\omega$$
(28)
$$Y_{\omega } = \rho \beta \omega^{2}$$
(29)
$$\beta = F_{1} \beta_{i,1} + \left( {1 - F_{1} } \right)\beta_{i,2}$$
(30)
$$D_{\omega } = 2\left( {1 - F_{1} } \right)\rho \frac{1}{{\omega \sigma_{\omega ,2} }}\frac{\partial k}{{\partial x_{j} }}\frac{\partial \omega }{{\partial x_{j} }}$$
(31)

The model constants are \(\sigma_{k,1} = 1.176\), \(\sigma_{\omega ,1} = 2.0\), \(\sigma_{k,2} = 1.0\), \(\sigma_{\omega ,2} = 1.168\), \(a_{1} = 0.31\), \(\beta_{i,1} = 0.075\), \(\beta_{i,2} = 0.0828,\) and all additional model constants have the same values as for the standard k-ω model.

The commercial ANSYS CFX 15.0 solver is used to solve the RANS equations by applying SST k–ω turbulence formulations. ANSYS CFX is an implicit solver which solves continuity and momentum equations simultaneously. In this way, there is no need for pressure correction term to enforce mass conservation, and as a result, converged solutions are obtained with lesser iterations compared to other methods such as SIMPLE algorithm [29]. Discretization of equations is carried out by implementing element-based finite-volume combined method which uses shape functions to describe related variables.

3.2 Mesh generation and boundary conditions

After creating the initial geometry, the computational domain is discretized in terms of structured mesh for the turbine runner and guide vane passages using ANSYS meshing software. Boundary layer mesh is generated around the runner blades and in the tip-clearance region. Size of the first layer of mesh in these regions must be small to retain the values of non-dimensional wall distance (y+) within acceptable limit (less than 2). Regarding severe separation of flow and adverse pressure gradients near the runner blades and generated vortices in the tip-clearance region, it is essential to ensure this criterion, particularly when SST k–ω model is applied for turbulence modeling.

In this paper, two cases are simulated: periodical simulation and complete simulation, when the turbine runner and guide vanes are installed in the channel. After meshing, boundary conditions including rotational speed, free flow speed, flow rate, walls boundary, and definition of periodic and angle of flow due to designed guide vanes are defined in the CFX setup. It should be noted that these conditions alter to obtain performance charts. Residual convergence is determined equal to 1e−6, and head of turbine and torque convergence are monitored. Output results may depend on mesh statistics due to the applied turbulence model (SST k–ω).

Mesh independence study is performed by considering different refinement levels of the mesh with minimum and maximum number of elements of 1,065,965 and 7,230,916, respectively (Table 4), in order to justify validity of the numerical results. Hydrodynamic torque of the turbine is calculated for different grids, and the results in Table 4 indicate that the third grid with 4,321,231 elements is suitable for further numerical simulations. Also, average y+ values on pressure and suction sides are 2.057 and 2.165, respectively.

Table 4 Mesh independency test
Full size table

The generated mesh for the runner and guide vane passages along with the boundary layer mesh for leading and trailing edges of the runner blades is illustrated in Fig. 3.

Fig. 3
figure 3

Overview of a fluid domain with boundary layer mesh and b boundary conditions

Full size image

4 Validation of numerical simulations

Numerical results obtained by Sutikno and Adam [17] are used for validation of numerical simulations of the present study. The designed VLH turbine in Ref. [17] produces 2038 watts in head of 0.8 m and efficiency of 90%. They used stagger angle in each section, guide vanes outlet angle, tip diameter, and chord length to create the turbine geometry. Characteristics of 11 sections of their runner blades are shown in Table 5. Using the design methodology of the present study described in Sect. 2 and the design parameters of Ref. [17], the geometry of Sutikno and Adam’s turbine is recreated (Table 6). It should be noted that for the recreated turbine, the stagger angle varies between 7.9° and 54.54° (instead of 6°–54.5° in Ref. [17]) because of constant axial velocity assumption in the present study.

Table 5 Cascade design on radial sections in Ref. [17]
Full size table
Table 6 Cascade design on radial sections for recreated turbine of the present study
Full size table

The numerical setup discussed in Sect. 3 is used to investigate the hydrodynamic performance of recreated turbine. Obtained results show that the recreated turbine generates 2048 watts of power with 0.81 m of head and efficiency of 91% in 180 rpm rotational speed at the design flow rate which indicates the maximum error of 0.49% compared to numerical results of Ref. [17]. This error is attributable to the change in stagger angle at the vicinity of hub.

5 Turbine blade optimization method

5.1 Airfoil characteristics

Optimization of airfoil and cascade of axial flow turbine is studied in the literature. Airfoil characteristics such as radius at leading edge, maximum chamber, and position of maximum thickness have a impact on flow through turbine. Low leading edge radius leads to flow separation in high incidence angle positions because of increasing flow acceleration. An increase in separation between blades leads to an increase in friction losses and a decrease in lift coefficient. A change in the position of maximum chamber in constant Reynolds number influences lift coefficient produced by airfoil. This coefficient is dependent on static pressure on upper and lower surfaces of blades and has effect on output power [30].

Lift, drag, and pressure coefficients are main and basic characteristics of airfoils. The values of these coefficients depend on incidence angle and are determined from numerical solutions or experiment results. One approach for blade optimization is to find an optimum lift-to-drag ratio for a specific incidence angle, and another one is to obtain optimum incidence angle for constant Reynolds and Mach numbers. Since the goal of this study is to investigate effects of 2D optimization on 3D performance of the VLH turbine, minimizing the drag-to-lift ratio is chosen as the objective of the 2D optimization process. Also, the objective function in this approach can be defined in terms of drag-to-lift ratio in a specific incidence angle or several incidence angles (Eq. 32):

$${ \hbox{min} }_{ - } f\left( x \right) = f((C_{\text{L}} /C_{\text{D}} )_{\alpha 1}$$
(32a)

Or

$${ \hbox{min} }_{ - } f\left( x \right) = \frac{{(C_{\text{L}} /C_{\text{D}} )_{\alpha 1} + (C_{\text{L}} /C_{\text{D}} )_{\alpha 2} + (C_{\text{L}} /C_{\text{D}} )_{\alpha 3} }}{3 }$$
(32b)

Deviation of flow in blade cascades is of great importance in rotor and stator design procedure as it has a strong effect on lift force. The definitions of lift and drag coefficients of airfoils are as follows:

$$C_{\text{L}} = \frac{L}{{0.5\rho lW_{\infty }^{2} }}$$
(33a)
$$C_{\text{D}} = \frac{D}{{0.5\rho lW_{\infty }^{2} }}$$
(33b)

in which l is the chord length. Therefore, the drag force and coefficient are:

$$D = Y\sin (\beta_{\infty } ) - X\cos (\beta_{\infty } ) = \Delta p_{0} t\cos (\beta_{\infty } )$$
(34)
$$C_{\text{D}} = \frac{D}{{0.5\rho lW_{\infty }^{2} }} = \left[ {\frac{{\Delta p_{0} }}{{0.5\rho W_{\infty }^{2} }}} \right]\frac{t}{l}\cos (\beta_{\infty } ) = \xi_{\infty } \frac{t}{l}\cos (\beta_{\infty } )$$
(35)

β∞ is defined by Eq. 8:

In a similar way, the lift force and coefficient can be obtained as:

$$L = X\sin (\beta_{\infty } ) + Y\cos (\beta_{\infty } ) = \rho W_{\infty }^{2} t[\tan (\beta_{1} ) - \tan (\beta_{2} )]\cos (\beta_{\infty } ) - \Delta p_{0} t\sin (\beta_{\infty } )$$
(36)
$$C_{\text{L}} = 2\frac{t}{l}\left[ {\tan (\beta_{1} ) - \tan (\beta_{2} )} \right]\cos (\beta_{\infty } ) - C_{\text{D}} \tan (\beta_{\infty } )$$
(37)

In the following section, CST method is described to present airfoil profiles in the form of polynomial coefficients in order to minimize the drag-to-lift ratio as the objective function.

5.2 CST method and airfoil optimization

The CST method is an effective tool to parameterize airfoils by amalgamating analytical class functions with parametric shape functions. In this method, fundamental classes of airfoils are characterized by class functions, and shape functions which are created by Bernstein polynomial equations, characterize geometric shapes in each fundamental class. In this way, 2D profiles of airfoil are generated in the form of set of points using specific equations. The profiles and set of points can be applied for aerodynamic optimization in different flow conditions caused by Reynolds and Mach number variations. [30,31,32].

In addition to the parameterization of 2D geometries such as airfoils, the CST method’s applications can be extended to asymmetric shapes and also 3D geometries like aerodynamic wings, ducts, and nozzles by using proper class and shape functions [33, 34]. This method is powerful and has less estimation error than other methods such as Bezier polynomials, B-splines and NURBS. The last two methods have problem with oscillating curves but CST has not this problem. In other words, this method is similar to Bezier method but with additional class functions.

Any smooth 2D airfoil can be expressed by “CST” general equation. Two different airfoils are distinguished from each other by two sets of coefficients. The coefficients control upper and lower surfaces of airfoils [35, 36]. Definitions of airfoil characteristics are depicted in Fig. 4.

Fig. 4
figure 4

Airfoil nomenclature

Full size image

The CST equations are as follows [32]:

For the upper surface of airfoil, we can write:

$$\xi_{u} \left( \varPsi \right) = C_{{N_{2} }}^{{N_{1} }} \left( \varPsi \right) \times S_{u} \left( \varPsi \right) + \varPsi \Delta \xi_{u}$$
(38)

in which Ψ and ξ are equal to x/c and y/c, respectively. For the lower surface,

$$\xi_{\text{l}} \left( \varPsi \right) = C_{{N_{2} }}^{{N_{1} }} \left( \varPsi \right) \times S_{\text{l}} \left( \varPsi \right) + \varPsi \Delta \xi_{\text{l}} .$$
(39)

The last terms in the right-hand side of Eqs. 38 and 39 represent the thickness at the trailing edge of the upper and lower surfaces. \(C_{N1}^{N2} \left( \varPsi \right)\) is the class function which is defined as [32]:

$$C_{{N_{2} }}^{{N_{1} }} \left( \varPsi \right) = \varPsi^{{N_{1} }} \times \left( {1 - \varPsi } \right)^{{N_{2} }} .$$
(40)

For standard airfoils, N1 and N2 are equal to 0.5 and 1, respectively. It should be noted that these coefficients can be modified for optimization purpose. The shape functions for upper and lower surfaces of airfoil are as follows:

$$S_{\text{u}} \left( \varPsi \right) = \mathop \sum \limits_{i = 0}^{{N_{\text{u}} }} A_{\text{u}} \left( i \right) \times S\left( {\varPsi ,i} \right)$$
(41)
$$S_{\text{l}} \left( \varPsi \right) = \mathop \sum \limits_{i = 0}^{{N_{\text{l}} }} A_{\text{l}} \left( i \right) \times S\left( {\varPsi ,i} \right)$$
(42)

A is set of coefficients that represent airfoil, N is degree (exponent) of polynomials for both upper and lower surfaces, and S is a part of shape function obtained from Bernstein polynomial:

$$S\left( {\varPsi ,i} \right) = K_{\text{i}}^{N} \times \varPsi^{{N_{1} }} \left( {1 - \varPsi } \right)^{{N_{2} }}$$
(43)

and

$$K_{i}^{\text{n}} = \frac{n!}{{i!\left( {n - i} \right)!}}$$
(44)

Substituting Eqs. 40–44 into Eqs. 38 and 39 results in the following equations:

$$\xi_{\text{u}} \left( \varPsi \right) = \varPsi^{0.5} \left( {1 - \varPsi } \right)\mathop \sum \limits_{i = 0}^{{N_{\text{u}} }} [A_{\text{u}} \left( i \right) \times \frac{{N_{\text{u}} !}}{{i!\left( {N_{\text{u}} - i} \right)!}} \varPsi^{i} \left( {1 - \varPsi } \right)^{{N_{\text{u}} - i}} ] + \varPsi \Delta \xi_{\text{u}}$$
(45)
$$\xi_{\text{l}} \left( \varPsi \right) = \varPsi^{0.5} \left( {1 - \varPsi } \right)\mathop \sum \limits_{i = 0}^{{N_{\text{l}} }} \left[ {A_{\text{l}} \left( i \right) \times \frac{{N_{l} !}}{{i!\left( {N_{l} - i} \right)!}}\varPsi^{i} \times \left( {1 - \varPsi } \right)^{{N_{\text{l}} - i}} } \right] + \varPsi \Delta \xi_{\text{l}}$$
(46)

These equations completely describe profile of airfoils and include all of the coefficients for upper and lower surfaces which can be used for optimization purpose. These equations can be rewritten by introducing matrix D:

$$\xi = D \times \vec{A} + \varPsi \Delta \xi$$
(47)

in which D is defined as:

$$D_{i,j} = C_{{N_{2} }}^{{N_{1} }} \left[ {\varPsi \left( i \right)} \right] \varPsi \left( i \right)^{j} K_{j}^{N} \left( {1 - \varPsi \left( i \right)} \right)^{N - j} .$$
(48)

Therefore, coefficients can be calculated by Eq. 49:

$$A = D^{ + } \times \left( {\xi - \varPsi \Delta \xi } \right)$$
(49)

D+ is pseudo-matrix for D.

For sections 1 to 4, NACA2408, NACA2410, NACA2413, and NACA2421 are selected, respectively, by applying specific chord and thickness. The CST method with fourth-degree polynomials is applied for these airfoils. According to the definition of polynomials in CST method, there are five coefficients for the fourth-degree polynomials. Optimization is performed by coupling a MATLAB code with XFOIL. The objective function (drag-to-lift ratio on the 2D airfoil) is calculated by XFOIL and then minimized through fminsearch optimization algorithm to obtain corrected coefficients. Fminsearch is a predefined code in MATLAB which finds the minimum of an unconstrained multivariable function using derivative-free method. In other words, fminsearch tries to find the minimum of a certain function starting with a point or set of points given. Here, the starting points are the coefficients that are obtained from initial airfoil and the output of fminsearch is the corrected coefficients. The search is done using a method called “Nelder-Mead simplex direct search algorithm,” which is one of the best known algorithms for multidimensional unconstrained optimization without derivatives. The corrected coefficients are applied in CST equations to create new airfoil profile. XFOIL is called in MATLAB to analyze the new airfoil, and some parameters are applied on geometry such as Reynolds and Mach numbers, and also angle of incidence for each section. This procedure continues until optimized airfoils are obtained for each section. Flowchart of optimization process is illustrated in Fig. 5. Each section has a special Reynolds and Mach which are calculated from triangle of velocity. Also, the angle of incidence is constant for all of the sections. Initial and optimized data of airfoils are shown in Tables 7 and 8, respectively.

Fig. 5
figure 5

Flowchart of optimization process

Full size image
Table 7 Characterization of the initial airfoils by “CST”
Full size table
Table 8 Characterization of the optimized airfoils obtained by “CST” method
Full size table

The optimization results showed that the drag-to-lift ratio for NACA2408, NACA2410, and NACA2421 decreased from 0.0102 to 0.0074 (27.5% reduction), 0.0087 to 0.0068 (21.8% reduction), and 0.0098 to 0.007 (28.6% reduction), respectively. Also, the optimized NACA2413 indicated a maximum decrease of 31.1% in drag-to-lift ratio (from 0.009 to 0.0062). Comparing the performance of optimized and initial airfoils at different incidence angles in the range of 0°–25° (Fig. 6) reveals that for the most part, optimized airfoils have higher lift-to-drag ratios, particularly around the predetermined incidence angle used in the optimization process. Furthermore, corresponding incidence angles of maximum lift-to-drag ratios moved toward higher incidence angles for all optimized airfoils.

Fig. 6
figure 6

Comparison of lift-to-drag ratio for the initial and optimized airfoils: a NACA2408, b NACA 2410, c NACA 2413, d NACA 2421

Full size image

Figure 7 shows velocity vectors around tip and hub airfoils for initial and optimized airfoils. It should be noted that the velocity vectors are obtained for operating conditions with maximum lift-to-drag ratio for each airfoil.

Fig. 7
figure 7

Comparison of velocity vectors for a initial tip airfoil, b optimized tip airfoil, c initial hub airfoil, d optimized hub airfoil

Full size image

6 Results and discussions

Based on the optimization results obtained in the previous section and the design methodology explained in Sect. 2, the 3D geometry of the optimized VLH turbine is created. To compare the hydrodynamic performance of the optimized and initial turbines, numerical simulations are performed for three different flow rates of 12.187, 10, and 7 m3 s−1 and several rotational speeds based on numerical setup described in Sect. 3. Total power of water and obtained power of turbine from CFD simulations are calculated as follows:

$$P_{\text{water}} = \rho gQH$$
(50a)
$$P_{{t{\text{urbine}}}} = T\omega$$
(50b)

Hence, the efficiency can be calculated:

$$\eta = \frac{{P_{\text{turbine}} }}{{P_{\text{water}} }} = \frac{T\omega }{\rho gQH}$$
(51)

where ρ is the water density, g is the gravity acceleration, Q is the flow rate, H is the available head, T is the produced torque by turbine, and ω is the turbine rotational speed. In Fig. 8, variations in efficiency, power, and effective head with rotational speed at 12.187 m3 s−1 flow rate are illustrated for both initial and optimized turbines. It can be seen that the efficiency of optimized turbine is 87.9% at a rotational speed of 65 rpm, which indicates a considerable increase of 2.4% compared to the initial turbine’s efficiency (85.5%). For rotational speeds higher than approximately 50 rpm, the optimized turbine has greater efficiencies; however, the optimized turbine’s efficiency is lower than the initial turbine for rotational speeds below 50 rpm. Similar behavior can be observed for the power and effective head curves. Also, in low rotational speeds, the slope of variations in efficiency with rotational speed is greater for optimized turbine.

Fig. 8
figure 8

Comparison of a efficiency, b power, and c effective head of optimized turbine with initial turbine at different rotational speeds in a constant flow rate of 12.187 m3 s−1

Full size image

Similar results are obtained for flow rates of 10 and 7 m3 s−1 for both the initial and optimized turbines (Figs. 9 and 10). Results for 10 and 7 m3 s−1 of flow rates showed that the maximum efficiencies increased by 0.72% (from 86.88 to 87.6%) and 0.92% (from 86.53 to 87.45%), respectively, which are relatively significant. Unsurprisingly, when flow rate increases, maximum efficiency occurs at higher rotational speeds. Also, in all flow rates, efficiency is more dependent on rotational speed reduction than rotational speed increase.

Fig. 9
figure 9

Comparison of a efficiency, b power, and c effective head of optimized turbine with initial turbine at different rotational speeds in a constant flow rate of 10 m3 s−1

Full size image
Fig. 10
figure 10

Comparison of a efficiency, b power, and c effective head of optimized turbine with initial turbine at different rotational speeds in a constant flow rate of 7 m3 s−1

Full size image

Around the design point, effective head for the optimized turbine is more than the initial turbine for similar flow rates and rotational speeds. For flow rates of 12.187, 10, and 7 m3 s−1, maximum effective heads of the initial turbine are 2.48, 1.73, and 0.0817 m, respectively, and for the optimized turbine, they are 2.55 (2.82% increase), 1.7 (0.7% decrease), and 0.839 m (2.69% increase), respectively. Furthermore, there is a direct correlation between effective head and flow rate for both initial and optimized turbines. Since the optimized turbine works at higher effective heads than the initial turbine (except for a flow rate of 10 m3 s−1), it has more output power. For the initial turbine at flow rates of 12.187, 10, and 7 m3 s−1, maximum powers are 295.53, 167.56, and 55.97 kW, respectively, and for the optimized turbine, they are 303.28 (2.62% increase), 166.2 (0.8% decrease), and 57.5 kW (2.73% increase), respectively. It is clear that both maximum power and maximum effective head happened at a specific rotational speed and a flow rate, while this rotational speed may not be equal to the corresponding speed of maximum efficiency. Differences in efficiency increase with an increase in rotational speed variations because optimization is done for the design point with specific incidence angles for airfoils. For rotational speeds higher than 50 rpm, output power and effective head of the optimized turbine are more than the initial turbine. Figure 11 shows generated torque by optimized turbine for the three mentioned flow rates. From Fig. 11, it is conspicuous that there is an inverse correlation between generated torque and rotational speed.

Fig. 11
figure 11

Variation in torque with rotational speed for the optimized turbine

Full size image

Three important non-dimensional parameters in VLH turbine design are head, flow, and power coefficients. These parameters provide complete characteristics of VLH turbines and are defined below:

$${\text{Power}}\;{\text{coefficient: }} \bar{P} = \frac{P}{{\rho N^{3} D^{5} }}$$
(52)
$${\text{Head}}\;{\text{coefficient:}} \;\bar{H} = \frac{gH}{{N^{2} D^{2} }}$$
(53)
$${\text{Flow}}\;{\text{coefficient:}}\; \bar{Q} = \frac{Q}{{ND^{3} }}$$
(54)

Figures 12 and 13 show variations in power and flow coefficients with head coefficient for flow rates of 12.187 and 7 m3 s−1. From Fig. 12, one can conclude that in both flow rates, the optimized and initial turbines have equal power coefficients at low head coefficients; however, by increasing the head coefficient, the optimized turbine’s power coefficient becomes lesser than the initial turbine. Similar behavior in variation of flow coefficient with head coefficient is observed in Fig. 13.

Fig. 12
figure 12

Variation in power coefficient with head coefficient for a flow rates of 12.187 m3 s−1 and b 7 m3 s−1

Full size image
Fig. 13
figure 13

Variation in flow coefficient with head coefficient for a flow rates of 12.187 m3 s−1 and b 7 m3 s−1

Full size image

Figure 14 shows static pressure contour on both pressure and suction sides of the optimized blade at the design point (12.187 m3 s−1, 65 rpm). According to Fig. 14, minimum pressure occurs at the leading edge of the suction side of the blade, and also no occurrence of cavitation is observed. It should be mentioned that the values of pressure are relative, while the reference pressure is 1 atm in the CFX software inputs. Figure 15 shows pressure contour and streamlines from inlet to the channel outlet when the optimized turbine is installed in the channel with considering the effect of gravity.

Fig. 14
figure 14

Pressure contour on the a pressure side and b suction side of the optimized runner blade

Full size image
Fig. 15
figure 15

a Pressure contour for the optimized turbine installed in the channel, b streamlines from inlet to the channel outlet

Full size image

7 Conclusion

Performance optimization of a VLH turbine operating in different flow conditions is done using the CST method and coupling of a MATLAB code with XFOIL. Euler law in turbomachinery is implemented for the initial design of the turbine runner and guide vanes with specific design parameters. The continuity and RANS equations are solved using ANSYS CFX 15.0 by applying SST k–ω turbulence model and element-based finite-volume combined method for discretization of governing equations. Then, validation study is conducted by comparing the numerical simulations with available results for a VLH turbine. To investigate the impact of 2D optimization on 3D hydrodynamic performance of the turbine, profiles of four types of NACA airfoils are optimized using the CST method, fminsearch minimum navigation algorithm for minimizing drag-to-lift ratio, and XFOIL. The 2D numerical results showed that the optimized airfoils have greater lift-to-drag ratios in most incidence angles.

The 3D geometry of the optimized VLH turbine is created using the optimized NACA airfoils, and its hydrodynamic performance is investigated at different flow rates and rotational speeds. The numerical results indicated a remarkable increase of 2.4% for efficiency of the optimized turbine compared to the initial turbine at a flow rate of 12.187 m3 s−1 and a rotational speed of 65 rpm. Also, power and effective head of the optimized turbine increased by 7.75 kW and 0.07 m, respectively, compared to the initial turbine. The minimum increase in efficiency (0.83%) is observed at a flow rate of 10 m3 s−1, while optimization resulted in approximately 1.1% increase in efficiency at a flow rate of 7 m3 s−1. Although the optimized turbine has higher efficiencies at all flow rates at 65 rpm of rotational speed, the power of optimized turbine reduced by 0.8% in comparison with the initial turbine at a flow rate of 10 m3 s−1. Furthermore, the generated torque of the turbine decreased by increasing rotational velocity at all flow rates. Pressure contours on the blade suction and pressure sides revealed that the turbine runner operates without cavitation.

To further improve the performance of VLH turbines, it is recommended to study the effect of geometry of other parts of the turbine such as guide vane and channel geometry. Also, the optimization of performance of a VLH turbine array is worth investigating further.