1 Introduction

Multidisciplinary design optimization (MDO), a tool of concurrent engineering for large-scale and complex system design, has gained a great deal of research attention and application (De Weck et al. 2007). The MDO methods are classified into single-level methods and multilevel methods. For complex coupling problems, the key approaches are the multilevel MDO methods that mainly include concurrent subspace optimization (CSSO), bi-level integrated system synthesis (BLISS), collaborative optimization (CO) and analytic target cascading (ATC). Due to the high degree of disciplinary autonomy, CO becomes an attractive method. The basic idea in CO method is the decomposition of the design problem into two levels, the system level and the subsystem level. The system level objective is minimized under consistency requirements among the disciplines by enforcing equality constraints that coordinate the interdisciplinary couplings (Zadeh et al. 2009).

Although many advantages are involved in CO, certain features of the framework cause a few difficulties (Alexandrov and Lewis 2002). For example, it may be difficult for CO to find a feasible solution under the system level equality constraints. Therefore, the following methods were introduced: (1) The equality constraints were replaced by the inequality constraints and the determination of a reasonable relaxation factor was studied (Alexandrov and Lewis 2002; Li et al. 2008). (2) The penalty-function method was provided to yield approximate solutions (Lin 2004). (3) The equality constraints were approximated by the response surface methodology and the approximation models were addressed (Jang et al. 2005; Huang et al. 2008).

The experimental data and analysis in Alexandrov and Lewis (2002) and Lin (2004) show that CO obtains different solutions from several initial points. This phenomenon indicates that the CO using equality constraints, relaxation method and penalty-function method is sensitive to the initial point for some problems. To the best knowledge of the authors, the studies mainly focus on the computational difficulties caused by equality constraints, but no attention is concentrated on the influence caused by the initial point.

In many industrial environments, engineering design of complex systems is inherently multidisciplinary and multi-objective, the character of which enhances the complexity to obtain a satisfactory solution. Some research works focus on re-formulating the problem so as to improve the trade-off between multiple and conflicting objectives due to the specific multi-objective nature of the MDO problem. For example, Tappeta and Renaud (1997) used the weighted-sum method to resolve the multi-objective collaborative optimization (MOCO) problem. The goal programming and linear physical programming (LPP) approaches (McAllister and Simpson 2003; McAllister et al. 2004, 2005) were introduced to resolve the MOCO problem. Huang et al. (2008) applied the fuzzy satisfaction degree and fuzzy sufficiency degree methods to handle the MOCO problem. The multi-objective evolutionary algorithm (MOEA) was presented at both the system and subsystem levels to handle the MOCO problem in Vikrant and Shapour (2006) and Sébastien et al. (2007).

In most previous studies on the MOCO problem, the subsystem objective that minimizes the incompatibility function is independent to the physical problem (Vikrant and Shapour 2006). In the original CO framework, the sole objective function in subsystem is to minimize the incompatibility function (McAllister et al. 2004). However, the study on the MOCO problem with physical objectives in subsystem is important because a subsystem instead of the system level sometimes involves one or more objectives. For example, in the design of an aircraft, the wing subsystem has weight and deflection as physical objectives while the system level has total weight and stress as the system level objectives (Li and Azarm 2008). Obviously, MDO problems with multi-objective subsystems are really involved in some engineering problems.

In this paper, the modifications on CO framework are presented for the employment of CO technique in MDO problems with physical objectives in subsystem. First, in the system level optimization framework, a multi-stage optimization strategy is proposed to decrease the influence for the optimization result caused by the initial point. Second, in the multi-objective subsystem optimization, two transformation methods are presented to transform the incompatibility function into a disciplinary constraint. Therefore, one can avoid the difficulty in setting preference value for the incompatibility function while using the preference-based multi-objective optimization algorithm.

The remainder of the paper is organized as follows. Section 2 describes collaborative optimization framework and provides a multi-stage optimization strategy for the system level optimization. Section 3 presents the modification on the multi-objective subsystem optimization and adopts LPP as the optimization method. Two engineering examples are provided to demonstrate the applicability of the proposed methods in Section 4. Finally, Section 5 closes the paper with conclusion.

2 Formulation of collaborative optimization

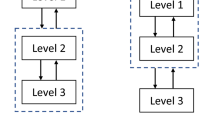
Figure 1 illustrates CO proposed by Kroo et al. (1994). CO is a bi-level optimization approach in which each subsystem consists of a disciplinary level optimizer and disciplinary constraints. The sole objective at the subsystem level is to minimize the incompatibility function that represents the violation of compatibility constraints.

Fig. 1
figure 1

Collaborative optimization framework

Full size image

2.1 Description of system level optimization

The system level attempts to optimize the design objective subject to n interdisciplinary compatibility constraints. The interdisciplinary compatibility constraint J i ∗ related to subsystem i is given by:

$$ J_{i}^{\ast} (\mathbf{z},\mathbf{x}_{i}^{\ast}(\mathbf{z}))=0, \quad i=1,2,\cdots n $$
(1)

where x i ∗ (z) (i.e. the optimal value of subsystem i) is the function with respect to the system level design vector z.

As the analytic expression of x i ∗ (z) is usually difficult to obtain, some approximation methods are introduced. Li et al. (2008) and Braun and Kroo (1995) adopted a constant instead of the function with respect to the system level design variables. Meanwhile, a new post optimality sensitivity analysis (POSA) was presented with a simple formula in which x i ∗ is independent of the system level design variables (Braun and Kroo 1995; Lin 2004). This result indicates that x i ∗ is a constant instead of a function in the POSA definition. In this simplified form, the value of x i ∗ is computed via the optimization procedure of subsystem i. Then, the following simplified interdisciplinary compatibility constraint can be adopted.

$$ J_{i}^{\ast} \left(\mathbf{z},\mathbf{x}_{i}^{\ast}\right)=0,\quad i=1,2,\cdots,n $$
(2)

2.2 Modification on system level optimization

Generally, relaxing the system level constraints can reduce the computational difficulty that is caused by the nature of CO (Alexandrov and Lewis 2002). The system level constraints are relaxed as

$$ J_{i}^{\ast} \left(\mathbf{z},\mathbf{x}_{i}^{\ast}\right)\le \varepsilon,\quad \varepsilon >0,\quad i=1,2,\cdots,n $$
(3)

where ε is the relaxation factor.

However, the solution obtained by this relaxation may be infeasible. It is difficult to give an ideal relaxation factor that allows one to solve the problem while not distorting the solution to an unacceptable level. Furthermore, some starting points may affect the optimization result (Alexandrov and Lewis 2002; Lin 2004).

We present a multi-stage optimization strategy to decrease the influence for the optimization result caused by the starting point. An overall compatibility constraint is introduced to restrict the distance from the solution to the feasible region of the original problem at each optimization stage. Then, the expression of the system level optimization is given as follows:

$$ {\begin{array}{*{20}c} {\min \;F(\mathbf{z})} \\ {s.t.\;J_{i}^{\ast} (\mathbf{z})=\sum\limits_{j=1}^{s_{i}}\left({z_{j}-x_{ij}}^{\ast}\right)^{2}\le \varepsilon \quad i=1,2,\cdots ,n} \\ {\quad {J_{n+1}}^{\ast} (\mathbf{z})=\sum\limits_{i=1}^{n} {J_{i}^{\ast} (\mathbf{z})} = \sum\limits_{i=1}^{n} {\sum\limits_{j=1}^{s_{i}} {\left({z_{j}-x_{ij}}^{\ast}\right)^{2}}} \le E} \end{array}} $$
(4)

where E is the control parameter. The values of ε and E are adjusted according to the inconsistency between subsystems.

The optimization process of CO, in a sense, starts from the infeasible region of the original problem. The process in which the intermediate solution point enters the feasible region of the original problem is illustrated in Fig. 2. The process where an optimization stage shifts to the next one repeats until the solution enters the feasible region.

Fig. 2
figure 2

The process of solution point entering the feasible region

Full size image

If the initial point is within the feasible region of the original problem, the system level optimization is converted into an unconstrained problem. Usually, the solution of unconstrained problem is not the solution of constrained problem. In this case, the solution point moves outside the feasible region.

The inconsistency between subsystems is given by:

$$ I={\sum\limits_{i=1}^{n} {\sqrt {J_{i}(\mathbf{x}_{i})}}} \mathord{\left/ {\vphantom {{\sum\limits_{i=1}^{n} {\sqrt {J_{i} ({\rm \textbf{x}}_{i} )} } } n}} \right. \kern-\nulldelimiterspace} n $$
(5)

where J i is the incompatibility function of subsystem i.Then, the values of E and ε are given with the following principles:

$$ E\propto I,\;E\propto 1 \mathord{\left/ {\vphantom {1 {S^{2}}}} \right. \kern-\nulldelimiterspace} {S^{2}},\;\varepsilon \propto E $$
(6)

where S is the number of optimization stage. The values of E and ε vary with I and S during each optimization stage.

An optimization stage completes as the system level objective becomes stable, and set S = S + 1. The values of E and ε decrease as the number of optimization stage increases. The initial value of I is obtained from the Formula (5) under the condition in which the optimum value of unconstrained problem is designed as the target value allocated by the system level.

3 Multi-objective subsystem optimization

LPP is an engineering method to deal with multi-objective optimization problems by using the designer’s preference (Messac et al. 1996). It is one of the typical preference-based algorithms that require less running time than the MOEA method does. Since the smoothness on performance and convenience in study, we concentrate on LPP for the multi-objective subsystem optimization.

As LPP is a preference-based algorithm, we should set the ranges of desirability for all objective functions. However, it is difficult to set the ranges of desirability for the incompatibility function. The incompatibility function without physical meaning is more important than physical objectives in CO framework. To avoid the difficulty, we propose a new method, in which the incompatibility function is transformed into a disciplinary constraint.

3.1 Transformation of the incompatibility function

The incompatibility function is used to make the optimal value match the target value allocated by the system level as closely as possible, the value of which trends to zero gradually as the bi-level optimization proceeds.

Considering these characters, the transformation is expressed as follows:

$$ \sum\limits_{j=1}^{s_{i}} {\left({x_{ij} -z_{j}}^{\ast}\right)}^{2} - J_{\mbox{cnst}} \le 0 $$
(7)

where J c n s t is the transformation constant and z j ∗ is the jth target value allocated by the system level.

The value of J c n s t influences the distance from the optimization result to the target point allocated by the system level. Two transformation methods, namely, closest distance and relaxed distance, are proposed to define the value of J c n s t .

  • Closest distance transformation    The value of J c n s t is defined by the closest distance from the target point to the feasible region of subsystem i. The closest distance d d s t n is calculated as follows:

    $$ {\begin{array}{rll} {\min \;d_{\mbox{dstn}} =\sum\limits_{j=1}^{s_{i}} {\left( {x_{ij} -z_{j}}^{\ast}\right)^{2}}} \\ {\mbox{s.t}.\;\;c_{i} (\mathbf{x}_{i}) \le 0} \\ \end{array} } $$
    (8)

    Then, J c n s t is defined by

    $$ J_{\mbox{cnst}} =d_{\mbox{dstn}} $$
    (9)

    In addition, the effect of the closest distance transformation method is similar to the method provided in McAllister et al. (2005) where minimization of physical objectives was addressed preemptively only after minimization of the incompatibility function.

  • Relaxed distance transformation    Through the closest distance transformation, the feasible region of the subsystem greatly decreases leading to the points closest to the target point allocated by the system level. Therefore, the closest distance transformation is usually disadvantage of physical objectives obtaining better solutions.

To get better solutions for physical objectives, a dynamic intermediate parameter is given to adjust the value of J c n s t . The dynamic intermediate parameter is expressed by:

$$ d_{\mbox{dnmc}} = k_{d} \cdot d_{0} \left({1-\frac{SS_{i}}{SS_{N}}}\right) $$
(10)

where S S i is the iteration number of the bi-level optimization, S S N is the estimated value of the maximum iteration number, k d is the control parameter given by a decision maker, and d 0 is the distance from the optimum point of unconstrained problem to the feasible region of the original problem. Formula (10) guarantees that d d n m c gradually decreases as the bi-level optimization proceeds.Choose the larger one from d d s t n and d d n m c as the final value of J c n s t , i.e.,

$$ J_{\text{cnst}} =\max \left\{ {d_{\text{dstn}} ,d_{\text{dnmc}} } \right\} $$
(11)

Formula (11) guarantees that the multi-objective subsystem is feasible. When d d s t n ≥ d d n m c , d d s t n is chosen as the value of J c n s t to guarantee the feasibility. When d d s t n < d d n m c (i.e. the interdisciplinary consistency is strengthening), d d n m c is chosen as the value of J c n s t to obtain better solutions for physical objectives.

3.2 Formulation of multi-objective subsystem optimization

Transforming the incompatibility function into a disciplinary constraint yields the formulation of the multi-objective subsystem optimization:

$$ {\begin{array}{*{20}c} {\min \left\{ {f_{i1} ({\mathbf{x}}_{i}),f_{i2} ({\mathbf{x}}_{i}),\cdots ,f_{in_{s}} ({\mathbf{x}}_{i})} \right\}} \\ {\mbox{s.t}.\;\;c_{i} ({\mathbf{x}}_{i})\le 0} \\ {\quad \;\;\sum\limits_{j=1}^{s_{i}} {\left({x_{ij} -z_{j}}^{\ast}\right)^{2}} -J_{\mbox{cnst}} \le 0} \\ \end{array} } $$
(12)

where f i1(x i ) ∼ f i n s (x i ) denotes physical objectives of subsystem i. When LPP method is utilized to solve these conflicting objectives, the formulation is given as follows:

$$\begin{array}{@{}rcl@{}} {\begin{array}{rll} &&{\kern2.5pc}{\min \;\tilde{{J}}_{i} =\sum\limits_{p=1}^{n_{s}} {\sum\limits_{s=2}^{5} {\left( {\tilde{{w}}_{_{ps}}^{-} d_{ps}^{-} +\tilde{{w}}_{_{ps}}^{+} d_{ps}^{+}} \right)} } } \\ &&\mbox{s.t}.\;\;f_{ip} (x_{i})-d_{ps}^{+} \le t_{p(s-1)}^{+},\;f_{ip} (x_{i})\le t_{p5}^{+},\\ &&{\kern4.8pc} d_{ps}^{+} \ge 0\left({\mbox{Classes}\;1\mbox{S},\;3\mbox{S},\;4\mbox{S}} \right), \\ [3pt] &&\quad \;\;f_{ip} (x_{i})+d_{ps}^{-} \ge t_{p(s-1)}^{-},\;f_{ip} (x_{i})\ge t_{p5}^{-},\\ &&{\kern4.8pc} d_{ps}^{-} \ge 0\left({\mbox{Classes}\;2\mbox{S},\;3\mbox{S},\;4\mbox{S}} \right). \\ [3pt] &&{\kern1.5pc} {c_{i} (x_{i} )\le 0} \\ [3pt] &&{\kern1.4pc}{\sum\limits_{j=1}^{s_{i}} {\left({x_{ij} -z_{j}}^{\ast}\right)^{2}} -J_{\mbox{cnst}} \le 0} \\ \end{array} } \end{array} $$
(13)

where d p s − denotes the negative deviation value between f i p and t p(s − 1) − , and d p s + denotes the positive deviation value between f i p and t p(s − 1) + . The calculation of the weight w ~ p s − and w ~ p s + is referred to Messac et al. (1996).

4 Engineering examples

4.1 Speed reducer

The speed reducer example is a typical MDO problem with two formulations (Li et al. 2008; Vikrant and Shapour 2006; Li and Azarm 2008; Gong et al. 2009; Kodiyalam 1998). One is the single objective MDO problem, and the other is the multi-objective MDO problem with multi-objective subsystems.

4.1.1 Formulation without multi-objective subsystems

First of all, the proposed multi-stage optimization strategy in the system levle is used to demonstrate its effectiveness for the problem without multi-objective subsystems. Li et al. (2008) and Kodiyalam (1998) gave the single-objective formulation as follows:

$$\begin{array}{@{}rcl@{}} {\begin{array}{rll} &&{}\min f({\mathbf{x}})=0.7854x_{1} x_{2}^{2} \left( {3.3333x_{3}^{2} +14.9334x_{3} -43.0934} \right) \\ &&{}-1.5079x_{1} \left( {x_{6}^{2} + x_{7}^{2} } \right){+7.477\left( {x_{6}^{3} + x_{7}^{3}} \right) + 0.7854\left( {x_{4} x_{6}^{2} +x_{5} x_{7}^{2} } \right)} \\ \\ \\ \\ \\ \end{array}} \end{array} $$
(14)
$${\begin{array}{rll} {\mbox{s}.\mbox{t}.\quad g_{1} =27/\left( {x_{1} x_{2}^{2} x_{3} } \right)-1.0\le 0} \\ {\quad \quad g_{2} =397.5/\left( {x_{1} x_{2}^{2} x_{3}^{2} } \right)-1.0\le 0} \\ {\quad \quad g_{3} =1.93x_{4}^{3} /\left( {x_{2} x_{3} x_{6}^{4} } \right)-1.0\le 0} \\ {\quad \quad g_{4} =1.93x_{5}^{3} /\left( {x_{2} x_{3} x_{7}^{4} } \right)-1.0\le 0} \\ {\quad \quad g_{5} =\frac{\sqrt {\left( {\frac{745x_{4} }{x_{2} x_{3} }} \right)^{2}+1.69\times 10^{7}} }{110x_{6}^{3} }-1.0\le 0} \\ {\quad \quad \quad g_{6} =\frac{\sqrt {\left( {\frac{745x_{5} }{x_{2} x_{3} }} \right)^{2}+1.575\times 10^{8}} }{85x_{7}^{3} }-1.0\le 0} \\ {\quad \quad g_{7} =x_{2} x_{3} /40-1.0\le 0} \\ {\quad \quad g_{8} =5x_{2} /x_{1} -1.0\le 0} \\ {\quad \quad g_{9} =x_{1} /12x_{2} -1.0\le 0} \\ {\quad \quad g_{10} =(1.5x_{6} +1.9)/x_{4} -1.0\le 0} \\ {\quad \quad g_{11} =(1.1x_{7} +1.9)/x_{5} -1.0\le 0} \\ {\quad \quad 2.6\le x_{1} \le 3.6\quad 0.7\le x_{2} \le 0.8} \\ {\quad \quad 17\le x_{3} \le 28\,\,\,\,\,\,\,\,\, 7.3\le x_{4} \le 8.3} \\ {\quad \quad 7.3\le x_{5} \le 8.3\quad 2.9\le x_{6} \le 3.9} \\ {\quad \quad 5.0\le x_{7} \le 5.5} \\ \end{array} } $$

where x 1 is gear face width; x 2 is teeth module; x 3 is number of teeth pinions; x 4 and x 5 are respectively distances between bearings 1 and bearings 2; x 6 and x 7 are respectively diameters of shaft 1 and shaft 2; g 1 is upper bound on the bending stress of the gear tooth; g 2 is upper bound on the contact stress of the gear tooth; g 3 and g 4 are upper bound on the transverse deflection of the shaft; g 5 and g 6 are upper bound on the stresses of the shaft; g 7, g 8 and g 9 are dimensional restrictions based on experience; g 10 and g 11 are design conditions for the shaft based on experience.

The decomposed formulation involves several cases (Li and Azarm 2008). We follow the decomposed formulation reported by Li et al. (2008). This problem is decomposed into two subsystems: the first and second gear shafts. The constraints are grouped into each subsystem: the first gear shaft with constraints g 1 ∼ g 3, g 5, g 7 ∼ g 10 and the second gear shaft with constraints g 4, g 6, g 11.

The experimental data in Alexandrov and Lewis (2002) and Lin (2004) indicate that the optimization result of CO is sometimes affected by the initial point. The relaxing method was used in Alexandrov and Lewis (2002) and the penalty-function method was used in Lin (2004).

The equality constraints, the relaxing method, the penalty-function method and the proposed multi-stage optimization strategy are adopted. The initial points are listed in Table 1.

Table 1 Design of initial points
Full size table

The “fmincon” function of Matlab optimization toolbox is used. Tables 2, 3, 4 and 5 present the optimization results. The optimization result of single-objective formulation using single-level formulation (Azam and Li 1989) is x0 ∗ = 3. 5, 0. 7, 17, 7. 3, 7. 71, 3. 35, 5. 29 and f 0 x0 ∗ = 2996. The solution for a single-level formulation is also a solution for the CO problem (Lin 2004). The error of objective f(x ∗) to objective f 0 x0 ∗ is calculated by

$$ \mbox{error}=\left| {\frac{f-f_{0} }{f_{0} }} \right|\times 100~\% $$
(15)

Table 2 lists the results obtained from equality constraints. From the error calculated by Formula (15), the solutions starting from points 1 and 3 are the worst with an error of 55.77 % and the best with an error of 0.05 %, respectively. Therefore, the results obtained from equality constraints are affected by the initial point. Fortunately, the iteration times and the interdisciplinary inconsistency (i.e. I) are almost not affected by the starting point. The values of I in Table 2 can be treated as zero, which indicates that the interdisciplinary consistency is satisfactory.

Table 2 Optimization results from CO using equality constraints (\(\varepsilon \) = 0)
Full size table
Table 3 Optimization results from the relaxing CO
Full size table
Table 4 Optimization results from CO using the penalty-function method
Full size table
Table 5 Optimization results from CO using the multi-stage optimization strategy \(\left ({E=\frac {0.5I}{S^{2}},\;\varepsilon =\frac {2}{3}E} \right )\)
Full size table

Table 3 lists the results obtained from the relaxing CO method. The solutions obtained from ε = 0.0001 are better than those obtained from ε = 0.001 with respect to the values of error and I, which indicates that smaller the relaxation factor (i.e. ε) is better the interdisciplinary consistency and objective function are. However, the iteration times increases as the relaxation factor decreases. In this case, the values of I can not be treated as zero, which indicates that the relaxing CO method is accomplished by staying away from realizable design.

In addition, the values of iteration times are larger when initial points 1 and 2 are used, which indicates that the iteration times of the relaxing CO method is affected by the initial point.

Table 4 lists the results obtained from the penalty-function method with penalty factors p = 1, 000 and p = 100, 000. The system level minimizes

$$ F(\mathbf{z})=f(\mathbf{z}) + p\left({{J_{1}^{\ast}}(\mathbf{z}) + {J_{2}^{\ast}}(\mathbf{z})}\right) $$
(16)

The values of I obtained from p = 100, 000 are smaller than those obtained from p = 1, 000. The interdisciplinary consistency becomes better as the penalty factor enlarges, where the effect of the penalty factor (i.e. p) is similar to that of the relaxation factor in the relaxing CO. The data in Table 4 show that the interdisciplinary consistency is not satisfactory.

When p = 1, 000, the solutions are not affected by the starting point. When p = 100, 000, the solutions starting from points 1 and 3 are the worst with an error of 53.60 % and the best with an error of 0.15 %. Therefore, the solutions are still affected by the initial point.

Referring to the results in Table 5, the solutions obtained from four initial points are similar to the result provided by Azam and Li (1989). The errors calculated by Formula (15) are small enough to be accepted. Therefore, the solutions are not affected by the initial point like the cases in which the equality constraints and the penalty-function method are used.

The values of I can be treated as zero, which indicates that the interdisciplinary consistency is satisfactory. The bi-level optimization is implemented with less iteration times due to the larger relaxation factor at the earlier optimization stage. The iteration times is not affected by the initial point like the case in which the relaxing CO method is used.

4.1.2 Formulation with multi-objective subsystems

A three-objective formulation, namely, minimization of the total speed reducer volume, minimization of the maximum stress in the first and second gear shafts, is given in Vikrant and Shapour (2006) and Li and Azarm (2008). The formulation is given by Formulas (17)–(19):

$$ {\begin{array}{rll} &&{\kern-.9pc} \min f_{1} ({\mathbf{x}})=0.7854x_{1} x_{2}^{2} \left( {3.3333x_{3}^{2} +14.9334x_{3} -43.0934} \right)\\ &&-1.5079x_{1} \left( {x_{6}^{2} +x_{7}^{2}} \right) {+ 7.477\left( {x_{6}^{3} +x_{7}^{3}} \right) + 0.7854\left( {x_{4} x_{6}^{2} +x_{5} x_{7}^{2}} \right)} \\ \end{array}} $$
(17)
$$ \min \;f_{2} ({\mathbf{x}})=\frac{\sqrt {\left({\frac{745x_{4}}{x_{2} x_{3}}} \right)^{2} + 1.69\times 10^{7}} }{0.1x_{6}^{3}} $$
(18)
$$ \min \;f_{3} ({\mathbf{x}})=\frac{\sqrt {\left( {\frac{745x_{5} }{x_{2} x_{3}}} \right)^{2} + 1.575\times 10^{8}} }{0.1x_{7}^{3}} $$
(19)

The decomposed formulation for objective functions reported in Vikrant and Shapour (2006) is stated as follows. The first objective f 1 is split into two objectives f 11 and f 21, the sum of which forms one of the system level objectives. The objectives of the system level are f 1, f 2 and f 3. The objectives of the first gear shaft are f 11 and f 12 (i.e. f 2). The objectives of the second gear shaft are f 21 and f 22 (i.e. f 3).

Class-1 of LPP method is used for the multi-objective optimization problems in the system and subsystem levels. The preferences are listed in Table 6.

Table 6 Desirable ranges of each criterion
Full size table

Four initial points listed in Table 1 are chosen as the target points allocated by the system level. The “closest distance” and “relaxed distance” methods presented in Section 3.2 are adopted to calculate the transformation constant of the incompatibility function. The relaxing method and the multi-stage optimization strategy are used in the system level. The optimization results obtained from these four cases are listed in Tables 7, 8, 9 and 10.

Table 7 Optimization results obtained from the relaxing method with the closest distance (\(\varepsilon \) = 0.001)
Full size table
Table 8 Optimization results obtained from the relaxing method with the relaxed distance (\(\varepsilon \) = 0.001)
Full size table
Table 9 Optimization results obtained from the multi-stage optimization strategy with the closest distance
Full size table
Table 10 Optimization results obtained from the multi-stage optimization strategy with the relaxed distance
Full size table

Referring to the results listed in Tables 7 and 8, the values of I are similar to those listed in Table 3, which indicates that the interdisciplinary consistency is not affected by the transformation of the incompatibility function. Meanwhile, the relaxation factor distorts the solutions to an unacceptable level.

Referring to the results listed in Tables 9 and 10, the values of I are similar to those listed in Table 5, which also indicates that the interdisciplinary consistency is not affected by the transformation of the incompatibility function.

Therefore, the method of transforming the incompatibility function into a disciplinary constraint proposed in Section 3.2 is reasonable. Meanwhile, the multi-stage optimization strategy avoids the phenomenon where the solutions stay away from realizable design in the relaxing CO method.

The results listed in Tables 7 and 9 are similar to those listed in Tables 8 and 10 respectively, indicating that the closest distance and the relaxed distance have the same effect. The main reason is that the objectives of the system level are similar to the objectives of the subsystem level.

4.2 Parameter design of rolling mill stand

The parameter design of rolling mill stand is modeled as a MDO problem (Cui 1989; Bai and Li 2006) with multi-objective subsystems. The formulation is given as follows:

$$\begin{array}{@{}rcl@{}} f_{1} (\boldsymbol{x}) = 1.91 \times 10^{-6} \times (x_{1} + 0.59)^{3} \times \left({\frac{1}{x_{4} x_{3}^{3}} + \frac{1}{x_{6} x_{5}^{3}}} \right) \left\{ {1-\frac{3}{4} \times \left[ {1 + \frac{\left( {x_{3} + x_{5} + 4.3} \right)x_{4} x_{2}^{3} x_{6} x_{5}^{3}}{\left( {x_{1} +0.59} \right)x_{2} x_{1}^{3} \left( {x_{4} x_{3}^{3} + x_{6} x_{5}^{3}} \right)}} \right]^{-1}} \right\} \end{array} $$
(20)
$$ f_{2} (\boldsymbol{x}) = 3.704 \times 10^{-6} \times (x_{1} +0.59) \times \left( {\frac{1}{x_{3} x_{4}} + \frac{1}{x_{5} x_{6}}}\right) $$
(21)
$$ f_{3} (\boldsymbol{x}) = 5.119 \times 10^{-6} \times \frac{1}{x_{1} x_{2}} $$
(22)
$$ f_{4} (\boldsymbol{x}) = 0.9671 \times 10^{-6} \times \left[ {8\left( {x_{2} + 0.656}\right)^{3} - 0.64\left( {x_{2} + 0.656}\right) + 0.064 + 8\left( {x_{2} +0.256}\right)^{3} \times \left( {218.8x_{7}^{4} -1} \right)} \right]/x_{7}^{4} $$
(23)
$$ f_{5} (\boldsymbol{x}) = 1.533 \times 10^{-5} \times \left[ {\left( {x_{2} +0.656}\right)-0.2 + \left( {x_{2} +0.256}\right) \times \left( {14.79x_{7}^{2} -1}\right)} \right]/x_{7}^{2} $$
(24)
$$ f_{6} (\boldsymbol{x}) = 0.263 \times 10^{-4} \ln \left[ {0.5904 \times 10^{5} \times \left( {x_{7} + 0.28}\right)}\right] $$
(25)
$$ f_{7} (\boldsymbol{x}) = 15.6 \times \left[ {2.15x_{1} x_{2} + (x_{3} x_{4} + x_{5} x_{6})(x_{1} + 0.295)}\right] $$
(26)
$${\begin{array}{rll} {\mbox{s}.\mbox{t}.\quad g_{1} (\boldsymbol{x})=x_{7} -0.42\le 0} \\ {\kern1.9pc}{g_{2} (\boldsymbol{x})=0.336-x_{7} \le 0} \\ {\kern1.9pc}{g_{3} (\boldsymbol{x})=0.829\times 10^{6}\times \sqrt {1+0.28/x_{7} } -1.61\times 10^{6}\le 0} \\ {\kern1.9pc}{g_{4} (\boldsymbol{x})=0.1678\times 10^{6}\times (x_{2} +0.256)-0.125\times 10^{6}\le 0}\\ {\kern1.9pc}{g_{5} (\boldsymbol{x})=\frac{500}{x_{1} x_{2} }+\frac{750(x_{1} +0.59)}{x_{1}^{2} x_2 }\times \frac{1}{\left[ {1+\frac{(x_{3} +x_{5} +4.3)x_{4} x_{3}^{3} x_{6} x_{5}^{3} }{(x_1 +0.59)x_{2} x_{1}^{3} \left( {x_{4} x_{3}^{3} +x_{6} x_{5}^{3} } \right)}}\right]}-0.055\times 10^{6}\le 0} \\ {\kern1.9pc}{g_{6} (\boldsymbol{x})=\frac{1.5\times 10^{3}(x_{1} +0.59)}{x_{4} x_{3}^{2} }\times \left\{{1-\frac{1}{2\left[{1+\frac{(x_{3} +x_{5} +4.3)x_{4} x_{3}^{3} x_{6} x_{5}^{3} }{(x_1+0.59)x_{2} x_{1}^{3} \left( {x_{4} x_{3}^{3} +x_{6} x_{5}^{3} } \right)}} \right]}}\right\}-0.055\times 10^{6}\le 0} \\ [1.8pc] {\kern1.9pc}{g_{7} (\boldsymbol{x})=\frac{1.5\times 10^{3}(x_{1} +0.59)}{x_{6} x_{5}^{2} }\times \left\{{1-\frac{1}{2\left[{1+\frac{(x_{3} +x_{5} +4.3)x_{4} x_{3}^{3} x_{6} x_{5}^{3} }{(x_1+0.59)x_{2} x_{1}^{3} \left( {x_{4} x_{3}^{3} +x_{6} x_{5}^{3} } \right)}} \right]}}\right\}-0.055\times 10^{6}\le 0} \\ {\kern1.9pc}{g_{8} (\boldsymbol{x})=x_{2} -x_{1} \le 0} \\ {\kern1.9pc}{g_{9} (\boldsymbol{x})=x_{4} -x_{3} \le 0} \\ {\kern1.6pc}{g_{10} (\boldsymbol{x})=x_{6} -x_{5} \le 0} \\ {\kern1.6pc}{g_{11} (\boldsymbol{x})=0.26-x_{2} \le 0} \\ {\kern1.6pc}{g_{12} (\boldsymbol{x})=-x_{4} \le 0} \\ {\kern1.6pc}{g_{13} (\boldsymbol{x})=-x_{6} \le 0} \\ {\kern1.6pc}{g_{14} (\boldsymbol{x})=x_{3} -2.5x_{4} \le 0} \\ {\kern1.6pc}{g_{15} (\boldsymbol{x})=x_{5} -2.5x_{6} \le 0} \\ {\kern1.6pc}{g_{16} (\boldsymbol{x})=15.6\times \left[ {2.15x_{1} x_{2} +(x_{1} +0.295)(x_{3} x_4 +x_{5} x_{6} )} \right]-7.484\le 0} \\ \end{array} } $$

This problem has seven objectives: the sum of bending deflection caused by bending moment of upper and lower beam ( f 1), the sum of bending deflection caused by shearing force of upper and lower beam ( f 2), the tensile deformation of column ( f 3), the sum of bending deflection caused by bending moment of backup roll ( f 4), the sum of bending deflection caused by shearing force of backup roll ( f 5), the sum of elastic flattening between working roll and backup roll ( f 6), and the weight of stand ( f 7). In addition, the design is subject to sixteen inequality constraints. The constraints are diameter restrictions of backup roll body ( g 1 and g 2), contact strength restriction of roll ( g 3), bending strength restriction of dangerous section of roll neck on the juncture of body and neck of backup roll ( g 4), composite strength restriction of bending and tensile strength of column ( g 5), bending strength restrictions of upper and lower beam ( g 6 and g 7), the geometric restrictions of column and beam ( g 8 ∼ g 15), and weight restriction of stand ( g 16).

The decomposed formulation consists of one system level sub-problem (i.e. weight), and three subsystem level sub-problems (i.e. column, beam and backup roll). The objective in the system level sub-problem is to minimize objective f 7. The column sub-problem is to minimize objective f 3 with constraints g 5, g 8 and g 11. The beam sub-problem is to minimize objectives f 1 and f 2 with constraints g 6, g 7, g 9, g 10 and g 12 ∼ g 15. The backup roll sub-problem is to minimize objectives f 4, f 5 and f 6 with constraints g 1 ∼ g 4.

The target value allocated by the system level is z 0 = 16. 8, 985. 3, 1110. 8, 1008. 1, 348. 5, 150. 1, 350. 5. The optimum objective values provided by Cui (1989) are f 1 = 2. 53 × 10− 2, f 2 = 3. 67 × 10− 2, f 3 = 5. 71 × 10− 2, f 4 = 0. 416, f 5 = 0. 137, f 6 = 0. 279 and f 7 = 7. 11. The preference values of physical objectives are listed in Table 11 with the data provided by Cui (1989).

Table 11 Desirable ranges of each criterion for beam and backup roll disciplines
Full size table

Referring to the experimental analysis in Section 4.1, it can be declared that the solutions obtained from the equality constraints method and multi-stage optimization strategy have a satisfactory interdisciplinary consistency. The relaxing and penalty-function methods distort the solutions to a certain unacceptable level that is determined by the relaxation factor and penalty factor, respectively.

A good interdisciplinary consistency is the most important property of MDO problem. Therefore, the equality constraints method and multi-stage optimization strategy are adopted in the system level optimization. Two transformation methods (i.e. the closest distance and relaxed distance) are used to transform the incompatibility function into a disciplinary constraint in the subsystem level optimization.

Table 12 lists the optimization results obtained from the following four cases. (i) The equality constraints in the system level with the relaxed distance transformation in multi-objective subsystems. (ii) The equality constraints in the system level with the closest distance transformation in multi-objective subsystems. (iii) The multi-stage optimization strategy in the system level with the relaxed distance transformation in multi-objective subsystems. (iv) The multi-stage optimization strategy in the system level with the closest distance transformation in multi-objective subsystems.

Table 12 Table 12 Optimization results from the four cases
Full size table

Referring to the results obtained from cases (iii) and (iv), the values of system level objective f 7 are better than those obtained from cases (i) and (ii). The multi-stage optimization strategy contributes to achieving better solutions for system level objective f 7. The reason is that the CO using the multi-stage optimization strategy in the system level is improved on decreasing the sensitivity to the initial point, which can be observed from the experimental analysis in Section 4.1 (i.e. the comparisons of several CO methods). The values of f 7obtained from cases (iii) and (iv) are also better than the result provided in Cui (1989) where the result is obtained from the weighted-sum method without the multidisciplinary decomposed formulation.

Using the equality constraints in the system level optimization, physical objectives of three subsystems obtained from the relaxed distance transformation (i.e. cases (i)) are better than those obtained from the closest distance transformation (i.e. cases (ii)) except for a slight difference for objective f 6.

Using the multi-stage optimization strategy in the system level optimization, case (iii) achieves better results for objectives f 3, f 4 and f 5 than case (iv) does. The value of f 2obtained from case (iii) is larger than that obtained from case (iv). The results obtained from cases (iii) and (iv) show no significant difference on the values of f 1 and f 6.

The relaxed distance method, in a sense, contributes to obtaining better solutions for physical objectives of subsystems than the closest distance method does. This character can be observed from the results obtained by using the equality constraints and the multi-stage optimization strategy in the system level optimization.

5 Conclusion

On the one hand, the modification on the system level is studied for reducing the influence for optimization results of CO caused by the starting point. The multi-stage optimization strategy is employed to guide the solution point to enter the feasible region of the original problem. The disadvantage of the multi-stage optimization strategy is that the setting of the control parameter for the relaxation factor may affect the performance improvement. The value of the control parameter will be studied in the future work to get the best performance for the system level optimization.

On the other hand, the modification on the subsystem level is studied for MDO problems with multi-objective subsystems when the preference-based multi-objective optimization algorithm is used. The difference between the incompatibility function and physical objectives is considered. Two transformation methods, namely, closest distance and relaxed distance, are proposed to transform the incompatibility function into a disciplinary constraint.

Two engineering examples with multi-objective subsystems are used to demonstrate the effectiveness of the proposed methods. In the speed reducer example, it is observed that the solutions obtained from the multi-stage optimization strategy are less sensitive to the initial point than the classic cases (i.e. the equality constraints, the relaxing method and the penalty-function method) do. Meanwhile, the interdisciplinary consistency is satisfactory, which indicates that the proposed method (i.e. transforming the incompatibility function into a disciplinary constraint) is reasonable when the preference-based multi-objective optimization algorithm is adopted.

During the parameter design of rolling mill stand, it is observed that the relaxed distance transformation method achieves better physical objectives of the subsystem level than the closest distance transformation method does, at the expensive of worse objectives of the system level. Therefore, the relaxed distance transformation method can contribute to achieving better solutions for physical objectives of the subsystem level. The multi-stage optimization strategy may contribute to achieving better solutions for objectives of the system level.

Although the proposed method of transforming the incompatibility function into a disciplinary constraint can resolve the difficulty in setting the preference value when the preference-based multi-objective optimization algorithm is used, some efforts are still required to provide more specific parameters on a decision-maker’s preference for the relaxed distance transformation method. This is a motivation for further development of the proposed method.