Keywords

1 Introduction

Multidisciplinary design optimization (MDO) is an area of research that handles optimization problems involving multiple disciplines, subsystems or components. MDO recognises that large, complex or interwoven engineered systems are often partitioned into smaller subsystems. This decomposition can arise for a number of interrelated reasons: from engineering practitioners taking a ‘divide-and-conquer’ approach to solving complex design problems, to the way in which engineering disciplines have emerged over time as discrete entities, to the functional organisation of teams in large engineering companies and institutions. Whilst MDO arose in the design of complex engineered products, such as exist in the aerospace and automotive sectors, its application is not limited to engineering, but is equally applicable to other complex systems contexts such as environmental and public policy [14, 18].

One important consideration in MDO is the need to model the interactions between subsystems, because the performance of a system is not necessarily defined just by its components, but also by the interactions between those components. It is common to model the interactions by using linking (or coupling) variables that are exchanged between the subsystems. However, when the subsystems have circular dependencies, it is not trivial to determine the values of the linking variables, and it might be necessary to use numerical approximation techniques, such as a multidisciplinary analysis (MDA) solver.

Several architectures have been proposed for dealing with MDO problems—see, for example, the seminal survey paper by Martins & Lambe [17]. These MDO architectures specify how to organize the discipline analysis models (and other types of models) within the problem formulation, in order to facilitate the process of finding the optimal design for the entire system. Some typical examples are the individual discipline feasible and the multidisciplinary feasible (MDF) architectures [4]. However, the focus of the MDO literature is primarily on single-objective problems. Multiple conflicting objectives are often found in real-world applications and, given that MDO problems are traditionally aimed at engineering applications, it is perhaps surprising that, to our knowledge, no multi-objective multidisciplinary optimization (MO-MDO) test suite has yet been proposed. Such a test suite would provide an opportunity for researchers and others to develop and test new optimization algorithms making them better equipped for dealing with multi-objective MDO problems.

In earlier work, we proposed an MDO version of a bi-objective benchmark problem known as ZDT1 [13]. This problem was then solved using an MDF architecture, encompassing a conventional multi-objective evolutionary optimization algorithm, NSGA-II [5], as the system optimizer, and a Newton-based method as the MDA solver. The present paper builds upon [13] and its distinctive contribution is as follows:

  1. 1.

    the approach used to transform the original ZDT1 problem into an MDO variant is extended to the remaining continuous ZDT problems;

  2. 2.

    the way the linking variables are integrated into the optimization problem is improved, in that the deviation of the linking variables from their optimal values is used to perturb the decision variables; and

  3. 3.

    two new topologies for connecting the disciplines via their linking variables are proposed, and we show how it is possible to create arbitrary problem structures.

The scope of this work encompasses bi-objective MDO problems with both varying number of variables and number of disciplines. The discipline analysis models are mutually interdependent. Although all optimization problems in this work contain only continuous variables, discrete variables are also within scope as long as they are supported by the optimization algorithm. We have only considered the MDF architecture in this work, but other architectures could be used instead as long they are compatible with the problem formulation.

The remainder of this paper is organised as follows. Section 2 discusses and analyses the current state of multidisciplinary and multi-objective benchmark problems. Section 3 introduces the proposed MO-MDO test suite. Several topologies for connecting the disciplines via linking variables are proposed in Sect. 4. The experimental setup is in Sect. 5, while the obtained experimental results are in Sect. 6. Section 7 gives a short summary of the work undertaken and proposes directions for future work.

2 Related Literature

The MDO paradigm originated in industrial settings, where different parts of complex engineered products are designed or optimised by different disciplinary teams. MDO codifies this arrangement via the structure of the optimization problem, including concepts such as: global variables, which are accessible by more than one discipline; local variables, which are used only within one discipline; and linking variables that are exchanged between disciplines as a way to model disciplinary interdependencies. The MDO literature is extensive [17], and we therefore focus our review on the benchmark problems that have been proposed for testing MDO approaches, since this is the area most pertinent to our paper’s aims, and contrast these to popular benchmarks for multi-objective optimization.

2.1 Multi-disciplinary Benchmarks

There are comparatively few MDO benchmark problems compared with multi-objective benchmarks. Many of these derive from the NASA MDO test suite [19], which contains 14 problems, including the Golinski speed reducer problem, propane combustion and aerospike nozzle design. While some of the benchmark problems have been expanded, such as the speed reducer problem, other problems are outdated and do not fulfil the needs of current MDO research in terms of complexity and scalability. Further, the original test suite is no longer available from its primary source, with the suite now distributed across a number of secondary sources, e.g. [21].

Another popular MDO benchmark problem is the Sellar (also known as the ‘analytical’) problem [20]. This problem is small, consisting of only two disciplines, each containing one equation for the multidisciplinary analysis, one local variable, two global variables and two linking variables. As such, the problem cannot provide an indication of how a complex MDO architecture will perform. Further MDO problems are esoteric, having been proposed for specific applications and typically solved only by the problem proposers; examples include building envelope design [23], robotic fish [2], automotive design [1] and wing design [3]. These problems are unsuitable as benchmarks because of the narrowness of the application and/or lack of availability of the MDA equations in the public domain.

2.2 Multi-objective Benchmarks

The literature on multi-objective benchmark problems is very extensive and we focus only on some popular examples in this section. The ZDT test suite, proposed by Zitzler et al. [24], consists of six two-objective test problems, five of which are continuous and one of which is discrete. For the purposes of this paper, we will only discuss the continuous problems. In each problem, the first objective \(f_1\) is a function of the first design variable, and the second objective \(f_2\) comprises the product of a so-called g(.) function, which is a variation of the sum of all design variables except the one found in the first objective, and an h(.) function which defines the relationship between the first design variable (and, by extension, \(f_1\)) and the remainder. The ZDT test suite can be criticised as unrealistic or incomparable with real-world problems, with structures that provide only a limited reflection of the challenges posed by the current state of research in multi-objective optimization. However, the problems are also simple to modify and are scalable in the number of design variables.

Other test suites include those with similar g(.) functions, such as the DTLZ problems which are scalable in the number of objectives [6], modular problems such as WFG [12], and problems with varied constraints such as those provided by DAS-CMOP [7] and MW [16].

2.3 Multi-objective Multidisciplinary Benchmarks

All the MDO problems mentioned above contain a single objective. Existing multi-objective multidisciplinary optimization problems are derived from single-objective MDO benchmarks which are not scalable, such as the Golinski speed reducer problem [8, 11, 15]. More recently, we proposed a MO-MDO problem based on the bi-objective ZDT1 problem [13], which is scalable in the number of variables and disciplines but has a cost landscape that is not otherwise challenging to an optimizer.

3 Proposed MO-MDO Test Suite: ZDT-MDO

The proposed MO-MDO test suite is based on the ZDT benchmark problems and we therefore label it ZDT-MDO. Despite the limitations of ZDT as a test set, the original structure of the problems makes them amenable to restructuring into MDO problems in which the original Pareto front is recoverable (which is highly advantageous from an analysis perspective). Here, we consider the five continuous ZDT problems, with ZDT5 omitted because it is binary encoded. For all problems, the first decision variable controls the position across the Pareto front, while the others are called distance decision variables because they control the convergence towards the Pareto front.

The multidisciplinary system contains global variables that are shared between the disciplines, and each discipline has its own set of local variables. The decision variables of the original ZDT problem are partitioned into global and local ones, where the first \(n_z\) are global and are represented by the vector \(\textbf{z}=(z_1,\ldots ,z_{n_z})^T\). The remaining ones are local variables and are distributed across N disciplines as given by the vector \(\textbf{x}=(\textbf{x}_1,\ldots ,\textbf{x}_N)^T\). Each \(\textbf{x}_i=(x_{i,1},\ldots ,x_{i,n_{x_i}})^T\) contains a total of \(n_{x_i}\) local variables at the ith discipline where \(i\in \{1,\ldots ,N\}\).

The disciplines exchange linking variables to model the interactions of the overall system. These linking variables are the output of an analysis conducted by each discipline that simulates the behaviour of a particular component of the multidisciplinary system. There is a total of \(n_{y_i}\) output linking variables at the ith discipline, given by the vector \(\textbf{y}_i=(y_{i,1},\ldots ,y_{i,n_{y_i}})^T\), and \(\textbf{y}=(\textbf{y}_1,\ldots ,\textbf{y}_N)^{T}\) contains the output linking variables of all disciplines. Each discipline may require one or more linking variables from other disciplines to conduct its own disciplinary analysis. To keep track of the linking variable connections in the system consider the following:

  1. 1.

    let \(n_{p_i}\) (\(1 \le n_{p_i} < N\)) denote the number of disciplines that provide linking variables to the ith discipline;

  2. 2.

    the indices of the disciplines that provide linking variables to the ith discipline are stored in the set \(\textbf{p}_i=\{p_{i,1},\ldots ,p_{i,n_{p_i}}\}\) where \(p_{i,j}\in \{1,\ldots ,N\} {\setminus } \{i\}\) \(\forall _{j=1,\ldots ,n_{p_i}}\).

For instance, for a hypothetical four-discipline system, if the second and fourth disciplines provide linking variables to the first discipline, then \(\textbf{p}_{1} = \{2,4\}\). The discipline analysis at the ith discipline is to find \(\textbf{y}_i\) that satisfies the following expression:

$$\begin{aligned} A_{i,i}\textbf{y}_i + \sum _{j = 1}^{n_{p_i}} (A_{i,p_{i,j}}\textbf{y}_{p_{i,j}}) = - C_i\bar{\textbf{z}} - D_i\textbf{x}_i, \end{aligned}$$
(1)

where \(\bar{\textbf{z}}=(z_2,\ldots ,z_{n_z})^T\) excludes the first decision variable of the original ZDT problem. The above expression only relies on the decision variables of the distance type, implying that the positional decision variable (\(z_1\)) is not included to ensure that there is a single solution to the systems of equations. The matrices in Eq. 1 are defined as follows:

  1. 1.

    \(A_{i,i} \in \mathbb {R}^{n_{y_i} \times n_{y_i}}\), \(C_i \in \mathbb {R}^{n_{y_i} \times (n_z-1)}\), and \(D_i \in \mathbb {R}^{n_{y_i} \times n_{x_i}}\) \(\forall _{i=1\ldots ,N}\),

  2. 2.

    \(A_{i,p_{i,j}} \in \mathbb {R}^{n_{y_i} \times n_{y_j}}\) \(\forall _{i=1\ldots ,N}\) and \(\forall _{j=1,\ldots ,n_{p_i}}\).

An important aspect of Eq. 1 is that, depending on how the disciplines are connected, determining the linking variables for one discipline may require knowing the values of the linking variables from the other disciplines. It can become even harder to solve in case there are cyclic connections in the system. The complete set of equations across disciplines can form a full system of equations as given by:

$$\begin{aligned} \begin{bmatrix} A_{1,1} &{} A_{1,2} &{} \ldots &{} A_{1,N} \\ A_{2,1} &{} A_{2,2} &{} \ldots &{} A_{2,N} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_{N,1} &{} A_{N,2} &{} \ldots &{} A_{N,N} \\ \end{bmatrix} \begin{bmatrix} \textbf{y}_1\\ \textbf{y}_2\\ \vdots \\ \textbf{y}_N\\ \end{bmatrix} = - \begin{bmatrix} C_1\\ C_2\\ \vdots \\ C_N\\ \end{bmatrix} \bar{\textbf{z}} - \begin{bmatrix} D_1 &{} 0 &{} \ldots &{} 0 \\ 0 &{} D_2 &{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} D_N \end{bmatrix} \begin{bmatrix} \textbf{x}_1\\ \textbf{x}_2\\ \vdots \\ \textbf{x}_N\\ \end{bmatrix} \end{aligned}$$
(2)

or equivalently given by:

$$\begin{aligned} \boldsymbol{A}\textbf{y}= -\boldsymbol{C}\bar{\textbf{z}} - \boldsymbol{D}\textbf{x}. \end{aligned}$$
(3)

To ensure that the full system of equations has a unique solution, \(\boldsymbol{A}\) needs to be invertible. Additionally, any column in \(\boldsymbol{A}^{-1}\boldsymbol{C}\) or \(\boldsymbol{A}^{-1}\boldsymbol{D}\) cannot be all zeros to ensure that there are no redundant design variables. Finding all \(\mathbf {y_i}\)s for the entire system requires the use of numerical techniques, such as Gauss–Seidel and Newton-based methods that are often called multidisciplinary analysis solvers in the MDO literature [17].

The linking variables are incorporated into the optimization problem by penalising the local variables as given by the function:

$$\begin{aligned} \xi (\textbf{x}_i, \textbf{y}_i) = \textbf{x}_i + \Vert \textbf{y}_i - \textbf{y}_i^* \Vert _1 , \end{aligned}$$
(4)

where \(\textbf{y}_i^*\) are the linking variable optimal values for the ith discipline, and the operator \(\Vert \bullet \Vert _1\) is the \(L^1\)-norm. Let the output of Eq. 4 be the vector \(\hat{\textbf{x}}_i=(\hat{x}_{i,1},\ldots ,\hat{x}_{i,n_{x_i}})^T\), and the function that applies the same transformation to all \(\textbf{x}_i\)s is denoted by \(\boldsymbol{\xi }(\textbf{x},\textbf{y})\). The proposed MO-MDO problem formulation based on ZDT1 is given by:

$$\begin{aligned} \begin{aligned} \text {min} \quad&f_1(\textbf{z}) = z_1\\ \text {min} \quad&f_2(\textbf{z}, \boldsymbol{\xi }(\textbf{x},\textbf{y})) = g(\textbf{z}, \boldsymbol{\xi }(\textbf{x},\textbf{y}))h(\textbf{z}, \boldsymbol{\xi }(\textbf{x},\textbf{y}))\\ \text {s.t.} \quad&g(\textbf{z}, \boldsymbol{\xi }(\textbf{x},\textbf{y})) = 1 + \frac{9}{n_v - 1}\left( \sum _{i = 2}^{n_z}z_i + \sum _{i = 1}^{N}\sum _{j = 1}^{n_{x_i}}\hat{x}_{i,j}\right) \\&h(\textbf{z}, \boldsymbol{\xi }(\textbf{x},\textbf{y})) = 1 - \sqrt{\frac{f_1(\textbf{z})}{g(\textbf{z},\boldsymbol{\xi }(\textbf{x},\textbf{y}))}} \end{aligned} \end{aligned}$$
(5)

where \(n_v=n_z+\sum _{i=1}^N n_{x_i}\). For the remaining ZDT problems, \(f_1(\textbf{z})=z_1\), with the exception of ZDT6 which is \(f_1(\textbf{z}) = 1-\exp (-4z_1)\sin ^6(6\pi z_1)\), while the g and h functions are shown in Table 1. For optimality, all decision variables (global and local) with the exception of \(z_1\) have to be zero for the given \(g(\cdot )\) functions, unless transformations are applied. This means that Eq. 2 becomes an homogeneous system of linear equations which is solved when all the \(\textbf{y}_i\)s are zero vectors. The benchmarks established in this section can be found in the project’s github repositoryFootnote 1.

Table 1. The g and h functions of the proposed MO-MDO test suite
Full size table

4 Defining Dependencies Between Disciplines

The proposed formulation in Eq. 2 offers the flexibility to connect the disciplines in different ways via linking variables. For instance, for a three-discipline system, in case the second and third disciplines receive linking variables from the first discipline, then \(A_{2,1}\) and \(A_{3,1}\) have non-zero elements. If there are no more connections between the disciplines (except \(A_{i,i}\) \(\forall _{i=1\ldots N}\) which are set to the identity matrix), then the remaining matrices in \(\boldsymbol{A}\) are set to zero. On the other hand, in case the first discipline receives linking variables from either the second or third discipline (implying that \(A_{1,2}\) and/or \(A_{1,3}\) have non-zero elements), then it can be said that the topology contains cyclic connections.

Fig. 1.
figure 1

Different topologies showcasing the dependencies between disciplines on a five-discipline system.

Full size image

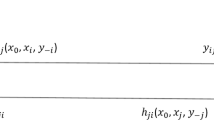
Figure 1a shows a five-discipline system where each discipline is only connected to the next one, and a cyclic connection is created by connecting the last discipline to the first one. The same topology is depicted by an extended design structure matrix (XDSM) as shown in Fig. 1b. This technique has been popularised by [17] to visualise the interconnections between the components of a complex system. It is useful in particular to visualise both data dependencies and process flow. The discipline analysis are represented in a diagonal, the input data flows along the vertical direction, while the output data flows along the horizontal direction. The data is labelled inside parallelograms, and the way the data flows is shown as thick grey lines. Other possible ways of connecting the disciplines are shown in the remaining subfigures in Fig. 1. We now propose the following three topologies for connecting the disciplines:

  1. 1.

    OIOO: stands for “one-in-one-out” since each discipline only receives and sends linking variables to a single discipline. We adopt a circular topology where the first discipline receives linking variables from the last discipline. This is given by \(\textbf{p}_1=\{N\}\) and \(\textbf{p}_i=\{i-1\}~ \forall _{i=2,\ldots ,N}\), and the XDSM is shown in Fig. 1b.

  2. 2.

    TITO: stands for “two-in-two-out” since each discipline sends and receives linking variables to two disciplines. This is given by \(\textbf{p}_1=\{N,i+1\}\), \(\textbf{p}_i=\{i-1,i+1\}\) and \(\textbf{p}_N=\{i-1,1\}\), and the XDSM is shown in Fig. 1d.

  3. 3.

    AIAO: stands for “all-in-all-out” since each discipline sends and receives linking variables to all disciplines. This is given by \(\textbf{p}_i=\{1,\ldots ,N\} {\setminus } \{i\}\) \(\forall _{i=1,\ldots ,N}\), and the XDSM is shown in Fig. 1f.

5 Experimental Setup

The matrices in Eq. 1 are randomly generated and then row-normalised. The only exception is \(A_{i,i}\) \(\forall _{i=1,\ldots ,N}\) which is set to the identity matrix. The number of global variables are set to 10 (\(n_z = 10\)) and for all disciplines the number of local variables and the size of the linking variables vector is set to 5 (i.e. \(n_{x_i} = 5\) and \(n_{y_i} = 5\) \(\forall _{i=1,\ldots ,N}\)). The lower and upper bounds for the decision variables of all the problems are set to 0 and 1, respectively. The only exception is ZDT4 where the lower bounds are \({-}\)5 and 5 for all decision variables with the exception of \(z_1\) which takes values in the range [0, 1].

For dealing with the MO-MDO problems, we adopt an MDF architecture involving a system optimizer and a MDA solver that conducts the disciplinary analysis one discipline at a time. For the system optimizer we use a popular multi-objective optimization algorithm known as NSGA-II [5]. The crossover and mutation probabilities are set to 90% and \(1/n_v\), respectively, while the crossover and mutation index are both set to 20. The number of generations is set to 1000 with a population size of 100. The initial population is randomly initialised. The MDF architecture is provided by the OpenMDAO package in Python [10], and NSGA-II implementation by PyOptSparse [22]. The MDA solver is also provided by OpenMDAO and uses a combination of a nonlinear and linear solver. The nonlinear solver is a Newton method while the linear solver relies on linear algebra techniques such as LU decomposition. The MDA solver runs for a maximum of 1000 iterations. For comparing different problem instances the hypervolume indicator is used. To compute the hypervolume we have used a dimension-sweep algorithm, taken from [9]. The reference point used in the hypervolume computations is \(\{1.1, 14\}\) for ZDT1, \(\{1.1, 13\}\) for ZDT3, \(\{1.1, 1620\}\) for ZDT4, and \(\{1.1, 17\}\) for ZDT6.

6 Experimental Results

In this section we show the obtained results for the MDO version of ZDT1, ZDT3, ZDT4 and ZDT6 problems. Due to space limitations, ZDT2 results are omitted, since they are very similar to those obtained for ZDT1. For all cases the MDA solver has run for sufficient number of iterations to guarantee convergence, implying that the correct linking variables were obtained for the given global (\(\bar{\textbf{z}}\)) and local variables (\(\textbf{x}\)). Therefore our analysis will be mostly focused on the performance of the system optimizer (NSGA-II) in dealing with these problems.

The convergence across generations is captured by the hypervolume metric in Fig. 2 for five and 10 discipline problems with different linking variable topologies. Figure 3 depicts the non-dominated solutions obtained at the end of the optimization run shown alongside the Pareto optimal front (POF). In all plots, the notation D5 and D10 denotes the number of disciplines. Good convergence is achieved for all problems instances involving ZDT1, ZDT3 and ZDT6, although not all solutions are co-located on the POF for ZDT6. ZDT4 shows constant improvement in terms of hypervolume across the generations, but achieves poor convergence overall within the given computational budget.

Fig. 2.
figure 2

Hypervolume across generations.

Full size image
Fig. 3.
figure 3

Non-dominated solutions at the end of the optimization run.

Full size image
Fig. 4.
figure 4

Decision variable values obtained across the generations for 5 disciplines.

Full size image

An increase in the number of disciplines from five to 10 is expected to make the problem more difficult, since it implies an increase in the number of decision variables (30 and 60 decision variables for five and 10 disciplines, respectively). This difficulty is mostly reflected on ZDT4 where the values of \(f_2\) are relatively higher for the 10 discipline case when compared with the five discipline problem. The same trend is captured by the hypervolume for ZDT4, where the five-discipline instances show better convergence when compared with the 10-discipline instances.

The values of the global and local variables across generations are shown in Fig. 4. We only focus on the five discipline problem since similar results are obtained for the 10 discipline case. At the end of each NSGA-II generation, we take the median of the variable values across the population of solutions. This means that there are 9 lines for the global variables and 25 lines for the local variables in these plots. Figures 4a and 4b show the global and local variable values, respectively, for ZDT1. Both variables converge towards the optima in less than 200 generations. The same pattern is observed for the other problems with the exception of ZDT4, and it took slightly longer to converge for ZDT6 (Figs. 4g and 4h). The decision variables for ZDT4 become trapped in local optima after a few generations as shown in Figs. 4c–4f. The values of the decision variables for AIAO are relatively close to the optima when compared with OIOO, implying that AIAO achieves better performance when compared with OIOO as shown in Fig. 3e. Given that the MDA solver has converged in all cases, the differences in performance observed between topologies are likely attributable to the stochasticity of the optimizer at the system level.

7 Summary and Future Work

In this paper we have proposed an MO-MDO test suite based on the continuous ZDT problems. The test suite is scalable in the number of disciplines, as well as the number of global and local decision variables. It offers a flexible approach to defining dependencies between the disciplines, allowing for the construction of more complex systems with multiple dependencies between disciplines. This test suite offers the opportunity for researchers and others to develop MDO architectures in combination with multi-objective optimization techniques. The experimental results have shown that for easier ZDT problems, such as ZDT1 and ZDT3, it can be straightforward for an optimizer like NSGA-II and an MDA solver to find a set of solutions with good convergence across the PF. For problems that are harder to solve, such as ZDT4, it may require using an impractical number of generations (beyond 1000) to find a well-converged set of solutions, or a system optimizer more capable of dealing with multimodality in the fitness landscape.

Future work will include an expansion of MDO problems to more complex multi-objective test suites. This will allow for greater scalability in objectives, as well as being potentially more representative of real-world problems. Extending some of these problems to MDO formulations is not straightforward and will require revisions to the present architecture. Additionally, alternative MDO architectures will be considered for application to MO-MDO benchmarks.