1 Introduction

Within the complex nature of physical, social and technical systems, their exist interconnected subsystems whose interactions need to be accounted for when making system-wide decisions. This allows the decision maker to make globally optimal decisions for the overall system. However, the complex nature of these systems introduces a computational burden that may be too large to justify system-wide optimization, where the problem is solved All-At-Once (AAO). Due to this widespread problem, many algorithms try to address these specific problem structures that consist or inter-connected disciplines with shared variables and parameters. Such problems are referred to as Multidisciplinary Optimization (MDO) problems which are tackled by decomposing the different disciplines into subproblems in distributed methods, or through monolithic formulations Tedford and Martins (2010). Monolithic formulations include approaches that have a single system-wide optimization, where the decomposed system interactions are determined in a single iteration. Monolithic formulations, such as multidisciplinary design feasible formulations, tend to be easy to implement and solve, but their solutions could scale poorly with the complexity of the problem Tedford and Martins (2010) and this motivates new studies that use Machine Learning methods for solving MDO problems Ramu et al. (2022). Similarly, for staged problems, the different stages could be treated as disciplines, however, their is tight coupling across the stages that needs to be accounted for Hamdan et al. (2019). On the other hand, the performance of decomposition schemes is dependent on the complexity of the subproblems as well as the connections between them Santiago et al. (2014). The term complexity, here, refers to the number of constraints and the dimensionality and number of variables in the problem that could make solving each discipline difficult, in addition to the number of constraints and variables that link the different disciplines together.

Decomposition-based methods use iterative solution schemes to coordinate between the different subproblems. This coordination strategy allows the discrepencies between the different subproblems to be minimized with each iteration, approaching a global optimal solution to the problem. The behavior of such methods is highly dependent on the interactions between the subproblems Martins and Kennedy (2021). Therefore, such methods are ideal for problems where the subproblems are modular and have little connections between the other subproblems. When it comes to real-life systems, these links are not always trivial and could cause iterative schemes to diverge or result in a far from optimal solution Lizier et al. (2018). To tackle these complex system structures, the links between the subproblems are usually oversimplified from the true system to facilitate solving the problem. This can make the problem solution not representative of reality or could even result in solutions that are not feasible to the real problem. In order to handle the coordination of MDO problems with complicating variables and constraints, the links across the subproblems need to be reduced to facilitate their coordination with existing MDO methods. As the dimensionality of the problem increases, the links become more intricate. Therefore, decomposing the links across disciplines greatly facilitates their solution, especially when considering iterative MDO solution approaches.

In this paper, a decomposition-based solution scheme is proposed to tackle complex dependencies between modular systems for non-decomposable multidisciplinary optimization problems, while maintaining the quality of the solutions and mitigating the solution complexity. We present a nested Analytical Target Cascading - Lagrangian Relaxation (LR-ATC) solution scheme which can relax complicated links between subproblems to enable tractable solutions. The proposed method can be applied to problems where the relationship between subproblems is complex and can therefore result in improved system-wide optimization for modular problems. Numerical case studies are implemented to measure the effectiveness of the proposed approach over benchmark methods in the literature as well as study the scalability of the proposed solution scheme. A physical system case study is also implemented to highlight the applicability of the proposed method to real case studies.

The rest of the paper is organized as follows. Section 2 introduces the relevant methods in the literature. Section 3 presents the proposed solution scheme. Section 4 presents two numerical case studies and details how the proposed scheme was implemented to solve the problem and how well it scales with the size of the problem. It also highlights the benefit of the proposed method when it comes to the quality of the solution as well as the computational time. Section 5 presents the Golinski Speed Reducer case study and showcases the applicability of the ATC-LR method to real system applications as well as highlights the benefit of the method. Lastly, Sect. 6 concludes the paper.

2 Relevant literature

In this section, some of the most prominent solution methods for coupled systems are reviewed. A comparison between the different methods is drawn and the benefit and applicability of each method is highlighted.

Analytical Target Cascading (ATC) is a hierarchical decomposition method for solving problems with coupled systems Kim et al. (2003). The method was first proposed by Kim et al. (2003) to create a tool to propagate top level targets down in a hierarchical scheme. Since then, many studies formalize this solution scheme in a framework and integrate it with lagrangian methods to improve its applicability to complex problems Kim et al. (2006), Kim et al. (2003), Tosserams et al. (2010), Kang et al. (2014). ATC is a framework that decomposes formulation through hierarchical levels where the top level contains the system targets and the bottom levels try to match the targets from above. Additionally, there is target matching across different sub-models within the same level that have shared variables. ATC is an iterative scheme where the exterior objective is to minimize the discrepancies between the targets. The method is generally applied in three stages: dividing the formulation into coupled sub-problems (in the case of clearly coupled systems, identification of each subsystem and linking variables), setting the targets for each subsystem depending on system links and solving the sub-problems in a coordinated scheme Kim et al. (2003).

Lagrangian Relaxation (LR) is an exterior penalty method which approximates difficult problems with simpler problems in order to facilitate solving complicated problems. LR is implemented by identifying (a set of) complicating constraints and removing them from the constraint space. However, the model penalizes violation of these constraints through including a penalty term in the objective function. This penalty term usually consists of the constraint violation multiplied by a penalty parameter. LR is then usually solved in an iterative solution scheme where the value of the penalty parameter is optimized Fisher (1985). Different ways of updating the penalty parameter exist (subgradient method, ect.), however, in most cases setting a high penalty parameter value tends to improve the quality of the solution. Nonetheless, a trade-off exists between solution time and the quality of the solution when it comes to a choice of a penalty parameter. That is why iterative solution schemes to select the best penalty parameter values exist Hamdan and Diabat (2020). Eqn 1 shows the general form of the relaxed problem given the original objective, \(c^{T}x\), the original constraint \(Ax \le B\) and the penalty parameter \(\lambda\).

$$\begin{aligned} {\displaystyle \mathop {\textrm{Maximize}}\limits _{\lambda }} \;&\quad \min _{x} c^{T}x + \lambda \left( Ax-B \right) \end{aligned}$$
(1)

Augmented Lagrangian (AL) method is an extension to the LR method where the penalty term is augmented with an additional term which is added to avoid ill-conditioning of the problem Afonso et al. (2010). This parameter is a quadratic penalty function that also serves as a convexifying term. The main benefit of this method is that the penalty parameter does not need to be too large in order to obtain an optimal solution to the original problem Papalambros and Wilde (2000). The updated form of the objective is now shown in Eqn. 2. In this equation, \(\mu\) is an additional penalty parameter for the augmenting term.

$$\begin{aligned} {\displaystyle \mathop {\textrm{Maximize}}\limits _{\lambda }} \;&\quad \min_{x} c^{T}x + \lambda \left( Ax-B \right) + \frac{\mu }{2} \Vert Ax-B \Vert ^{2} \end{aligned}$$
(2)

The method has been extended further by using the Alternating Direction Method of Multipliers (ADMM) to reduce the cost incurred with coordination among different levels of the decomposed problem Tosserams et al. (2006). The updated method is referred to as AL-AD ATC which represents an Augmented Lagrangian ATC approach with an Alternating Direction Method of Multipliers. ADMM is an extension to the Method of Multipliers (MM) where instead of iteratively solving an inner loop problem as shown in Fig. 1. The ADMM takes into consideration that in a hierarchical scheme, the odd levels and even levels can each be solved in parallel since odd levels only need responses from even levels and vice versa. Additionally, since in ATC, models along the same level can be solved in parallel, the ADMM method can drastically reduce computational time by parallelizing model optimization along a single level and throughout the levels Tosserams et al. (2005). It also solves each inner loop once instead of the iterative inner loop structure that is very computationally expensive. The results of ADMM are also shown to converge to the results of the original ATC formulation for certain conditions on the problem structure.

Fig. 1
figure 1

Inner loop coordination strategy for the method of multipliers

Full size image

3 A new Lagrangian solution scheme

This section details the developed new Lagrangian solution scheme for the multidisciplinary optimization problems with non-decomposable subsystems. Section 3.1 explains the non-decomposable problem structures, and Sect. 3.2 then details the developed the LR-AL ATC algorithms for the non-decomposable MDO problems. The motivation for the proposed algorithm is that it can handle non-decomposable problem structures with strong links across subproblems. This is done by relaxing the complicating constraints and solving a meta-heuristic, iterative algorithm that can update the relaxation penalties while coordinating the different subproblems.

3.1 Non-decomposable problem structures

In this section we define non-decomposable subsystems. This work targets systems that have an embedded grouping of subsystems that are tightly connected. This hinders the ability of the model to be decomposed into subsystems which can greatly increase the computational time of large and complex problems. In order to illustrate the class of problems targeted in this work, a simple mathematical example is presented in Eqns. 3a to 3g. In this problem, there are six local decision variables represented by \(x_{i}\), two partially shared variables across two subproblems, \(u_{i}\), and a shared variable across all subproblems, v. Although this simple mathematical model has an inherent subgrouping of its variables that make it a strong candidate for solving the problem through decomposition, the existence of constraint Eqn. 3g makes the problem non-decomposable. Figure 2 illustrated the decomposition matrix of the problem. A clear decomposition structure exists for the local variables and partially shared variables, yet, the shared variable found in Eqn. 3g creates strong links along all three subproblems. The gray shaded areas in the figure represent the shared variables. Current decomposition methods have been shown to be effective with partially shared variables (highlighted in light gray), however, strong links between the subproblems (highlighted in dark gray) greatly hinder the effectiveness of decomposition schemes.

$$\begin{aligned} \min\,f =\, & \, x_{2}^{2} + 5x_{6} \end{aligned}$$
(3a)
$$\begin{aligned} \text {s.t.}\, & \, x_{1}^{2}+3x_{2} +2 \le 0 \end{aligned}$$
(3b)
$$\begin{aligned}\, & \, x_{1} - u_{1} + x_{2} +2 \le 0 \end{aligned}$$
(3c)
$$\begin{aligned}\, & \, -x_{3} + 3x_{4}-4 \le 0 \end{aligned}$$
(3d)
$$\begin{aligned}\, & \, -u_{1}+x_{5} - u_{2} + 2 \le 0 \end{aligned}$$
(3e)
$$\begin{aligned}\, & \, 2x_{6}-u_{2} +3 \le 0 \end{aligned}$$
(3f)
$$\begin{aligned}{} & {} x_{2} +vx_{6} - x_{4} + 2 \le 0 \end{aligned}$$
(3g)
$$\begin{aligned}{} & {} x_{i}; \qquad u_{i} \ge 0, \qquad \forall i \nonumber \\{} & {} v \ge 0 \end{aligned}$$
(3h)
Fig. 2
figure 2

Decomposed outline of the subgroups found in the model structure highlighting the non-decomposable nature of the problem. Shared variables across subgroups are highlighted in gray

Full size image

3.2 The LR-AL ATC methodology

In this section, a new Lagrangian Relaxation solution scheme is introduced, which can be used to solve analytical mathematical models that have a non-decomposable or slightly decomposable structures. In order to illustrate how the algorithm can be applied to a general set of problems, general variable and constraint sets will be used. The general form of the problem being studied is presented in Eqn 4. In this formulation, x represents the vector of decision variables, indexed by i, where the full set of decision variables is given by \(x=[x_{1}^{T},x_{2}^{T},\ldots ,x_{n}^{T}]^{T}\). \(c^{T}\) represents the cost vector indexed by i. The objective function is to minimize the total cost of the chosen decision, given by the product \(C^{T}x\). The matrix A represents the left hand side of the constraints and B represents the vector of the right hand side of the constraints.

$$\begin{aligned} {\displaystyle \mathop {\textrm{Minimize}}\limits _{x}} \;&\quad c^{T}x \nonumber \\ S.t.&\quad Ax \le B \end{aligned}$$
(4)

The proposed method combines an AL-AD ATC solution scheme in an iterative Lagrangian Relaxation solution scheme. This approach can handle the added complexity of complicating constraints that make ATC inapplicable for applications where the system is not perfectly modular, or where the links between the subsystems are complex. LR can be used to relax the complicating constraints that link the subsystems in order to improve the ability of ATC to coordinate between the subproblems. Figure 3 shows how the simple mathematical example presented in Eqns. 3 can be converted into a decomposable structure through relaxing the coupling constraint. The constraint causing the strong linkage between subproblems, highlighted in Fig. 2, is relaxed. Due to the additive property of the objective function, the relaxed constraint is distributed over the subproblems in their respective objective functions.

Fig. 3
figure 3

Benefit of relaxing a single complicating constraint for non-decomposable systems

Full size image

The proposed solution scheme is shown in Fig 4, where the structure is outlined for a general implementation of the solution algorithm. The psuedocode presented in Fig 5 presents the proposed nested solution framework. The overall solution scheme is presented in Fig 5 where the outer loop is defined for a general problem structure. The inputs to the algorithm include the Cost vector for the objective function, C, the matrix, A, which represents the left-hand side coefficients for the constraints, and the vector, B, which represents the right hand side constants for the constraints. For this case, the relaxed set of constraints is represented by inequality constraints, however, for equality constraints, this can be easily modified. In the case of equality constraints, the absolute value of the difference \(Ax-B\) is used to determine the stepsize. The Lower Bound (LB) and the Upper Bound (UB) are calculated based on the values of the objectives of the Relaxed MDO solution and the heuristic solution. For a minimization problem, the LB value is the optimal but not necessarily feasible solution obtained from the MDO formulation. The UB, on the other hand, represents the feasible, yet not necessarily optimal solution obtained from the heuristic model. Moreover, the pseudocode shows the case for a minimization problem, in the case of a maximization objective, the UB and LB values can be reversed. The parameters for the algorithm include the stepsize, \(\alpha\), the penalty parameter (this can be a vector in the case of relaxing a set of constraints), \(\lambda\), and the number of consecutive iterations with no improvement in the value of the upper bound (for a minimization problem), noimp.

Fig. 4
figure 4

Proposed LR-AL ATC Method Framework

Full size image

The algorithm then enters a loop until the upper bound and lower bound converge within a predefined tolerance, \(\tau _{1}\) or the scale factor, \(\varepsilon\) falls below a tolerance, \(\tau _{2}\). Inside the outer loop, the Relaxed Master Problem (RMP) is solved using ATC. This is described in the ATC Subroutine pseudocode defined in Fig. 6. Once the ATC code terminates, the solution is recorded and the objective function value is recorded as the current lower bound, CLB, solution. Next, the relaxed constraint is checked with the recorded solution from the RMP to check if it was violated. If the constraint was not violated, that means that the solution of the RMP is feasible to the original formulation and the objective function value is recorded as a potential upper bound value, PotUB. If the constraint was violated, then a heuristic model is solved to obtain a feasible solution to the original problem. This is described in the Heuristic Subroutine presented in Fig. 7.

Once a feasible solution is obtained, the objective function value is calculated and it is recorded as the PotUB. If the value of the PotUB is lower than the UB, then the UB is updated with the objective function solution for the heuristic model. Otherwise, the UB value is not updated and the noimp parameter is incremented by 1. Next, the stepsize is calculated as in Eqn. 5, where \(\delta\) corresponds to the constraint violation. If the constraint is active, then the stepsize is set as 0. However, if the constraint is violated or inactive, then the stepsize is calculated based on the values of the UB and the CLB as well as the slack or surplus from the relaxed constraint. The scale factor also impacts the stepsize value and as the number of iterations increases, the stepsize is decreased by the stepsize value. This allows the model to fine tune the change in \(\lambda\) as the constraint activity is reached as shown in Eqn. 6. As seen in the constraint, \(\lambda\) can either increase or decrease depending on whether the relaxed constraint was violated or not (\(\delta\) can either be positive or negative). Lastly, the LB and the stepsize are updated based on whether there is an improvement in the lower and upper bounds and if the noimp parameter is greater than 5. The algorithm terminates when the conditions of the while loop are no longer met.

$$\begin{aligned} \alpha = \frac{\varepsilon \left( UB-CLB \right) }{\sqrt{\delta ^{2}}} \end{aligned}$$
(5)
$$\begin{aligned} \lambda _{i} = \max \{0, \lambda _{i-1} + \alpha \delta \} \end{aligned}$$
(6)
Fig. 5
figure 5

The LR-ATC Algorithm pseudocode

Full size image

The ATC Subroutine is detailed in Fig. 6, for a general problem decomposition of N levels and each level can have multiple subproblems. The notation in the algorithm is based on the work in Kim et al. (2003), where \(T_{v}\) denotes the design targets, and \(\varepsilon _{v}\) and \(\varepsilon _{y}\) denote the deviation tolerance for coordinating the system responses and the and system linking variables. The problem formulation is set up as in Kim et al. (2003) and the ATC algorithm is initialized by solving the top level optimization problem without including the deviation constraints (since no lower level response has been recorded yet). The algorithm then iterates between levels, where all subproblems in a single problem are solved simultaneously with deviation targets for the shared variables between them, if any. In each iteration, the values of the shared lower and upper levels are shared so as to ensure that the discrepancy between their values is minimized. This pseudocode focuses on the traditional ATC method, for the AL ATC and the AL-AD ATC, the readers are referred to the relevant references Tosserams et al. (2006), Tosserams et al. (2005).

Fig. 6
figure 6

The ATC Subroutine

Full size image

As for the heuristic algorithm that is shown in Fig. 7, an example of a generalized heuristic solution scheme is presented. Although any heuristic method could be used, in order to present a solution scheme that can be easily applied to all applications, a simple procedural method is proposed. The method in Fig. 7, starts off by selecting a subset of decision variables whose values have been determined from the RMP, and setting them as parameters in the original formulation (before constraint relaxation). This is referred to as the first heuristic model. In terms of the decision variables that are fixed, although any combination can be selected, in order to leverage the decomposable nature of the problem, the shared variables between subproblems can be fixed. This allows the subproblems to be solved completely in parallel, which will drastically decrease the computational time required to obtain a feasible solution. Any resulting solution can be suboptimal to the original formulation, however, if it is feasible to the heuristic model, then it is feasible to the original formulation. If a feasible solution is obtained, the objective function value is stored as a PotUB for the problem and the LR-ATC scheme is continued. On the other hand, in the case that the problem has an empty feasible solution space, the second heuristic model can be solved. This is similar to the first heuristic model, however, a smaller subset of decision variables is fixed in order to increase the feasible region to the problem. The advantage of this method is that as the LR outer loop approaches a feasible solution while refining the Langrangian penalty parameter, the heuristic solution also improves with the improving values of the decision variables from the RMP. While any number of heuristic models can be introduced until a feasible solution is obtained, in order to limit the number of inner loop iterations, the heuristic models are limited to two models.

Fig. 7
figure 7

The Heuristic Subroutine

Full size image

4 Numerical case studies

4.1 Geometric programming problem

In this section, a numerical example is used to illustrate the benefit of the proposed nested solution scheme in handling complex dependencies between subsystems. The proposed LR-AL ATC solution method is applied to the numerical example and is shown to perform well for even the simple numerical example presented in this section. The results show that the advantage of the solution scheme over the existing methods in the literature.

4.1.1 Problem description

The numerical example used in this study is based on the non-convex geometric programming problem formulation presented in Kim et al. (2006). However, one of the contributions of the proposed method is its applicability to sub-problems that are highly coupled. Therefore, the a constraint in the model has been modified to further increase the coupling in the numerical model. Specifically, Eqns. 7 represent the updated formulation for the non-convex, geometric programming model presented in Kim et al. (2006), where Eqn. 7b has been updated from Eqn. 8.

$$\begin{aligned} \min\,f ={} & {} x_{1}^{2}+x_{2}^{2} \end{aligned}$$
(7a)
$$\begin{aligned} \text {s.t.}{} & {} g_{1}:\frac{x_{3}^{-2}+x_{4}^{2}}{x_{5}^2} \le 1 \end{aligned}$$
(7b)
$$\begin{aligned}{} & {} g_{2}:\frac{x_{9}^{2}+x_{6}^{-2}}{x_{7}^2} \le 1 \end{aligned}$$
(7c)
$$\begin{aligned}{} & {} g_{3}:\frac{x_{8}^{2}+x_{9}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(7d)
$$\begin{aligned}{} & {} g_{4}:\frac{x_{8}^{-2}+x_{10}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(7e)
$$\begin{aligned}{} & {} g_{5}:\frac{x_{11}^{2}+x_{12}^{-2}}{x_{13}^2} \le 1 \end{aligned}$$
(7f)
$$\begin{aligned}{} & {} g_{6}:\frac{x_{11}^{2}+x_{12}^{2}}{x_{14}^2} \le 1 \end{aligned}$$
(7g)
$$\begin{aligned}{} & {} R_{1}=x_{1}=r_{1}(x_{3},x_{4},x_{5})=(x_{3}^{2}+x_{4}^{-2}+x_{5}^{2})^{1/2} \end{aligned}$$
(7h)
$$\begin{aligned}{} & {} R_{2}=x_{2}=r_{2}(x_{5},x_{6},x_{7})=(x_{5}^{2}+x_{6}^{2}+x_{7}^{2})^{1/2} \end{aligned}$$
(7i)
$$\begin{aligned}{} & {} R_{3}=x_{3}=r_{3}(x_{8},x_{9},x_{10},x_{11})=(x_{8}^{2}+x_{9}^{-2}+x_{10}^{-2}+x_{11}^{2})^{1/2} \end{aligned}$$
(7j)
$$\begin{aligned}{} & {} R_{4}=x_{6}=r_{4}(x_{11},x_{12},x_{13},x_{14})=(x_{11}^{2}+x_{12}^{2}+x_{13}^{2}+x_{14}^{2})^{1/2} \nonumber \\{} & {} x_{i} \ge 0, \qquad \forall i \in 1-14 \end{aligned}$$
(7k)
$$\begin{aligned} g_{2}:\frac{x_{5}^{2}+x_{6}^{-2}}{x_{7}^2} \le 1 \end{aligned}$$
(8)

This model is used since it provides a simple numerical example for a non-linear problem with non-trivial coupling between subsystems. Such problems are underrepresented in the literature and need tools that can handle the intricate relationships between the sub-models. For this reason, the numerical example presented in Eqns. 7 is used to illustrate the proposed method’s ability to handle problems that are more representative of real-world, complex systems.

4.1.2 Heuristic models

In order to generate quick, feasible solutions to the original problem, heuristic models are used. However, in order to bridge the gap between the lower-bound solution (the solution to the Relaxed Master Problem), there needs to be a link between the heuristic and the solution to the RMP. For this reason, three heuristic models are introduced that utilize partial results from the solution of the RMP. The reason that multiple heuristics are generated, is due to the fact that in some cases, utilizing the results of the RMP in the original problem could result in an infeasible solution depending on if the introduced constraints are within the feasible region for the original problem, which tends to be smaller than that of the RMP.

The first heuristic is divided into three models that can be solved in parallel. This parallel solution scheme is achieved by fixing the values of the linking variables between the different sub-models. The first heuristic model is shown in Eqns. 9, Eqns. 10 and Eqns. 11. The three models make up the heuristic where the objective value can be calculated from just solving Eqns. 9, and the values of the remaining decision variables can be determined by solving all three sub-models. The linking variable values selected are \(x_{3}\), \(x_{6}\), and \(x_{11}\). Given that the values of these variables are fixed to be the result of the corresponding variables in the RMP, then the three sub-models can be solved individually on different machines or in parallel. This greatly reduces the computational cost of retrieving a feasible solution to the original problem. The objective functions of 10 and 11 are set to 1 in order to get the first feasible solution available for the variable values that are not in the objective of the original problem.

$$\begin{aligned} \min\,f ={} & {} x_{1}^{2}+x_{2}^{2} \end{aligned}$$
(9a)
$$\begin{aligned} \text {s.t.}{} & {} g_{1}:\frac{x_{3}^{-2}+x_{4}^{2}}{x_{5}^2} \le 1 \end{aligned}$$
(9b)
$$\begin{aligned}{} & {} R_{1}=x_{1}=r_{1}(x_{3},x_{4},x_{5})=(x_{3}^{2}+x_{4}^{-2}+x_{5}^{2})^{1/2} \end{aligned}$$
(9c)
$$\begin{aligned}{} & {} R_{2}=x_{2}=r_{2}(x_{5},x_{6},x_{7})=(x_{5}^{2}+x_{6}^{2}+x_{7}^{2})^{1/2} \nonumber \\{} & {} x_{i} \ge 0, \qquad \forall i \in 1-7 \end{aligned}$$
(9d)
$$\begin{aligned} \min\,f ={} & {} 1 \end{aligned}$$
(10a)
$$\begin{aligned} \text {s.t.}{} & {} g_{3}:\frac{x_{8}^{2}+x_{9}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(10b)
$$\begin{aligned}{} & {} g_{4}:\frac{x_{8}^{-2}+x_{10}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(10c)
$$\begin{aligned}{} & {} R_{3}=x_{3}=r_{3}(x_{8},x_{9},x_{10},x_{11})=(x_{8}^{2}+x_{9}^{-2}+x_{10}^{-2}+x_{11}^{2})^{1/2} \nonumber \\{} & {} x_{i} \ge 0, \qquad \forall i \in 3,8-11 \end{aligned}$$
(10d)
$$\begin{aligned} \min\,f ={} & {} 1 \end{aligned}$$
(11a)
$$\begin{aligned} \text {s.t.}{} & {} g_{5}:\frac{x_{11}^{2}+x_{12}^{-2}}{x_{13}^2} \le 1 \end{aligned}$$
(11b)
$$\begin{aligned}{} & {} g_{6}:\frac{x_{11}^{2}+x_{12}^{2}}{x_{14}^2} \le 1 \end{aligned}$$
(11c)
$$\begin{aligned}{} & {} R_{4}=x_{6}=r_{4}(x_{11},x_{12},x_{13},x_{14})=(x_{11}^{2}+x_{12}^{2}+x_{13}^{2}+x_{14}^{2})^{1/2} \nonumber \\{} & {} x_{i} \ge 0, \qquad \forall i \in 6,11-14 \end{aligned}$$
(11d)

In the case that fixing the values of \(x_{3}\), \(x_{6}\), and \(x_{11}\) results in an empty feasible space, then the second heuristic model can be solved. The second heuristic model consists of two sub-models and is represented in Eqns. 12 and 13. Note that the main difference between the Heuristic 1 and 2 is that the second and third sub-models in Heuristic 1 have been combined in one model. This means that the number of variables to be fixed can be reduced to only fixing \(x_{3}\) and \(x_{6}\). This increases the search space within the feasible region and improves the probability of finding a feasible solution.

$$\begin{aligned} \min\,f ={} & {} x_{1}^{2}+x_{2}^{2} \end{aligned}$$
(12a)
$$\begin{aligned} \text {s.t.}{} & {} g_{1}:\frac{x_{3}^{-2}+x_{4}^{2}}{x_{5}^2} \le 1 \end{aligned}$$
(12b)
$$\begin{aligned}{} & {} R_{1}=x_{1}=r_{1}(x_{3},x_{4},x_{5})=(x_{3}^{2}+x_{4}^{-2}+x_{5}^{2})^{1/2} \end{aligned}$$
(12c)
$$\begin{aligned}{} & {} R_{2}=x_{2}=r_{2}(x_{5},x_{6},x_{7})=(x_{5}^{2}+x_{6}^{2}+x_{7}^{2})^{1/2} \nonumber \\{} & {} x_{i} \ge 0, \qquad \forall i \in 1-7 \end{aligned}$$
(12d)
$$\begin{aligned} \min\,f ={} & {} 1 \end{aligned}$$
(13a)
$$\begin{aligned} \text {s.t.}{} & {} g_{3}:\frac{x_{8}^{2}+x_{9}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(13b)
$$\begin{aligned}{} & {} g_{4}:\frac{x_{8}^{-2}+x_{10}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(13c)
$$\begin{aligned}{} & {} g_{5}:\frac{x_{11}^{2}+x_{12}^{-2}}{x_{13}^2} \le 1 \end{aligned}$$
(13d)
$$\begin{aligned}{} & {} g_{6}:\frac{x_{11}^{2}+x_{12}^{2}}{x_{14}^2} \le 1 \end{aligned}$$
(13e)
$$\begin{aligned}{} & {} R_{3}=x_{3}=r_{3}(x_{8},x_{9},x_{10},x_{11})=(x_{8}^{2}+x_{9}^{-2}+x_{10}^{-2}+x_{11}^{2})^{1/2} \end{aligned}$$
(13f)
$$\begin{aligned}{} & {} R_{4}=x_{6}=r_{4}(x_{11},x_{12},x_{13},x_{14})=(x_{11}^{2}+x_{12}^{2}+x_{13}^{2}+x_{14}^{2})^{1/2} \nonumber \\{} & {} x_{i} \ge 0, \qquad \forall i \in 3,6,8-14 \end{aligned}$$
(13g)

Given that both the first and the second heuristic models have an empty feasible region, the third heuristic model is solved. The disadvantage of the third model is that it is costly, although still less computationally expensive than the original problem. The third heuristic model is described in Eqns. 14. Here, only one model is solved, since the equations are linked as only \(x_{3}\)’s value is known. Therefore, none of the constraints can be decoupled.

$$\begin{aligned} \min\,f ={} & {} x_{1}^{2}+x_{2}^{2} \end{aligned}$$
(14a)
$$\begin{aligned} \text {s.t.}{} & {} g_{1}:\frac{x_{3}^{-2}+x_{4}^{2}}{x_{5}^2} \le 1 \end{aligned}$$
(14b)
$$\begin{aligned}{} & {} g_{3}:\frac{x_{8}^{2}+x_{9}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(14c)
$$\begin{aligned}{} & {} g_{4}:\frac{x_{8}^{-2}+x_{10}^{2}}{x_{11}^2} \le 1 \end{aligned}$$
(14d)
$$\begin{aligned}{} & {} g_{5}:\frac{x_{11}^{2}+x_{12}^{-2}}{x_{13}^2} \le 1 \end{aligned}$$
(14e)
$$\begin{aligned}{} & {} g_{6}:\frac{x_{11}^{2}+x_{12}^{2}}{x_{14}^2} \le 1 \end{aligned}$$
(14f)
$$\begin{aligned}{} & {} R_{1}=x_{1}=r_{1}(x_{3},x_{4},x_{5})=(x_{3}^{2}+x_{4}^{-2}+x_{5}^{2})^{1/2} \end{aligned}$$
(14g)
$$\begin{aligned}{} & {} R_{2}=x_{2}=r_{2}(x_{5},x_{6},x_{7})=(x_{5}^{2}+x_{6}^{2}+x_{7}^{2})^{1/2} \end{aligned}$$
(14h)
$$\begin{aligned}{} & {} R_{3}=x_{3}=r_{3}(x_{8},x_{9},x_{10},x_{11})=(x_{8}^{2}+x_{9}^{-2}+x_{10}^{-2}+x_{11}^{2})^{1/2} \end{aligned}$$
(14i)
$$\begin{aligned}{} & {} R_{4}=x_{6}=r_{4}(x_{11},x_{12},x_{13},x_{14})=(x_{11}^{2}+x_{12}^{2}+x_{13}^{2}+x_{14}^{2})^{1/2} \nonumber \\{} & {} x_{i} \ge 0, \qquad \forall i \in 1-14 \end{aligned}$$
(14j)

Note that the three heuristic models are arranged based on the computational cost needed to solve them, starting with the heuristic that has the smallest feasible region, to the heuristic model with the largest feasible region (if any exists). This is done intentionally to reduce the computational cost required to retrieve an updated upper bound for the minimization problem. In the case that all three heuristic models have an empty feasible region, the previous upper bound (for a minimization problem) is used.

4.1.3 Results

The numerical model was solved using ATC, AL ATC, AL-AD ATC, LR and LR-AL ATC. A comparison of the results is provided in Table 1, where the objective value of the problem, the computational time, as well as the number of iterations, are compared. The purpose of this case study is to validate the proposed method using a common numerical case study from the MDO literature. The number of iterations is compared for the inner loop as well as the outer loop and the total number of iterations is detailed in the table. The inner and outer loop definition changes based on the solution algorithm used. In ATC, the iterative scheme aims to coordinate the shared values across the decomposed subproblems, therefore, it is a single-loop method where the targets for variable discrepancies are updated. In the AL ATC method, the inner loop coordinates between the different subproblems as in the ATC method. The main difference lies in the formulation of the penalty term. so the total number of iterations is equivalent to the number of iterations in the inner loop. For the AL-AD ATC method, since the subproblems are solved once in each iteration, the number of iterations in the outer loop are determined as the number of times all three subproblems are solved. As for the LR method, it is a single-loop solution scheme (assuming that the UB heuristic is not an iterative method) where the value of the penalty parameter is updated in each iteration and the new upper bound and lower bound values are calculated until the termination criteria is reached. The LR-AL ATC method on the other hand is a double-loop method where the outer loop is the LR loop to update the value of the penalty parameter, and the inner loop is an AL ATC loop that aims to reduce discrepancies between the decomposed subproblems. The computational cost is calculated as the total solution time in GAMS modeling software using the Time Elapsed feature.

To compare the results of the proposed algorithm against existing methods, the objective function values are compared. In this case, the proposed LR-ALAD ATC solution method is able to achieve the same result as the AL ATC method, however, only the LR algorithm is able to achieve an objective value equivalent to the AAO solution. The ATC method attains the worst objective value since it indicates an infeasible solution (has an objective value that is lower than the optimal value of a minimization problem). The reason for the infeasible solution is that the model was terminated at 300 iterations due to limited computational power. Besides the ATC method, all other methods return close to feasible solutions, with AL-ATC and ALAD ATC having less optimal results. This is due to the difficulty when coordinating between the subproblems when strong coupling exists between them.

Although the number of iterations is compared in Table 1, the computational cost per iteration changes drastically from one algorithm to the next. Therefore, the total computational time is compared alongside the number of inner and outer loop iterations. The computational time recorded is obtained from the Time Elapsed feature in GAMS. In this case, the computational time is compared for the overall solution scheme until convergence or termination of the algorithm. The best solution is achieved from the LR model. Not only is it able to obtain an optimal solution, but it was also able to obtain it within a single iteration and it took a total of around 1 s. This is much faster than even the AAO solution, even for a simple example. Although ATC was able to achieve the best results when compared with the rest of the methods, it is expected for such a simple example where the entire problem can be solved to optimality within 4 s. ATC methods show reduced efficiency when compared with relaxation methods and an AAO approach. This is also expected for such a simple problem when introducing an iterative approach, since the benefit of decomposition does not outweigh the cost introduced by iterating through the method. Moreover, this is justified by the fact that a complicating constraint, Eqn 7c, exists, where it increases the coupling between the subproblems and increases the number of iterations needed to reach a feasible solution to the original problem. A clear improvement is seen when integrating the relaxation method with a decomposition method such as ATC. Although in some cases the number of iterations could be higher for the integrated approach, such as comparing the total iterations for the AL ATC method and that of the LR-ATC method, the computational cost for the integrated approach is greatly reduced from over 14,000 s to approximately 241 s. This is attributed to the fact that a single iteration of the integrated approach is expected to be faster since three simple problems are solved as opposed to a single difficult problem. This improvement is even evident on a simple problem such as the numerical example studied here. The benefits are expected to be greater for more complicated problem structures.

Table 1 Comparison of Results For Different Solution Schemes
Full size table

In Table 2, the optimal solution is compared for the different approaches. Most of the methods provide solutions close to the optimal solution of the original problem, with the LR and LR-ATC methods providing optimal solutions. However, the ATC, AL-ATC and ALAD ATC methods have a reduced efficiency when compared with the other methods. This is mostly due to the added coupling between the decomposed subproblems that make coordinating between the problems difficult and add more constraints to achieving a feasible solution to the AAO formulation. If we are to take closer look at the decision variable results, we could see that for the methods with objective function values further from the optimal solution, the variables that have the biggest discrepancies from their optimal values are mostly the shared variables along the decomposed problems, \(x_{3},x_{6},x_{9},x_{11}\). This pattern is evident in the results of the ATC method, where \(x_{11}\) has the biggest deviation from the optimal value and it is shared among the three decomposed problems and the model had difficulty coordinating between them. This reinforces the benefit of the proposed method, since it can relax complicating, coupling constraints to ensure that the embedded decomposition scheme can obtain close to optimal solutions for the relaxed problem. Then, the relaxed constraints are optimized in the outer loop. Therefore, we can see improved solutions for the relaxation schemes that are integrated with modified versions of the ATC method.

Table 2 Comparison of results for the modified numerical example
Full size table

4.2 Scalability study

The following subsection presents a numerical example to study how well the proposed solution scheme scales with the uncertainty. The problem formulation is presented in Sect. 4.2.1 and the results of the comparison study are presented in Sect. 4.2.2.

4.2.1 Problem formulation

The proposed numerical problem is presented in Eqns. 15a to 15i. This numerical formulation has two characteristic problem groupings. The proposed decomposition scheme is presented in Fig. 8 and the two subproblems are highlighted. The figure shows the benefit of component aggregation through relaxation of complicating constraints and how the relaxation can provide a benefit over traditional MDO techniques.

$$\begin{aligned} \min\,f ={} & {} x_{1}^{2}+x_{1}x_{2}+x_{4}x_{5}+x_{3}^{2} \end{aligned}$$
(15a)
$$\begin{aligned} \text {s.t.}{} & {} -\frac{x_{1}^{2}}{5} + \frac{4x_{1}x_{2}}{3} - \frac{6x_{2}^{2}x_{1}}{5} -6 \le 0 \end{aligned}$$
(15b)
$$\begin{aligned}{} & {} -\frac{4x_{4}x_{5}}{3} - \frac{2x_{3}^{2}}{3} - \frac{3x_{3}x_{4}}{8} -5 \le 0 \end{aligned}$$
(15c)
$$\begin{aligned}{} & {} \frac{x_{1}}{3} + \frac{x_{2}}{2} - \frac{4x_{3}}{3} \le 0 \end{aligned}$$
(15d)
$$\begin{aligned}{} & {} -\frac{x_{5}}{2} - \frac{5x_{3}x_{5}}{3} - x_{4}^{2} -3 \le 0 \end{aligned}$$
(15e)
$$\begin{aligned}{} & {} x_{5}^{2} + x_{4} -x_{3}x_{4} -2 \le 0 \end{aligned}$$
(15f)
$$\begin{aligned}{} & {} x_{3} -10x_{4} \ge 2r_{t}^{s} \end{aligned}$$
(15g)
$$\begin{aligned}{} & {} x_{4} = x_{5} + 0.6 \end{aligned}$$
(15h)
$$\begin{aligned}{} & {} x_{1} = x_{4} + x_{5} - x_{3}^{2} + 3 \end{aligned}$$
(15i)
$$\begin{aligned}{} & {} x_{1} \ge 10q_{t}^{s} \end{aligned}$$
(15j)
Fig. 8
figure 8

Decomposition for the numerical example with the numbered blocks corresponding to the constraints in Eqns. 15a to 15j

Full size image

4.2.2 Results

In order to test the impact of increasing the size of the problem on the efficiency of the proposed algorithm. The mathematical example is used to vary the number of parameters in the model as well as decision variables and test how well it scales computationally. It is solved with the proposed solution scheme and compared with an ATC decomposition scheme, an LR solution scheme, and the AAO approach. The same set of randomly generated scenarios are used for all the problems in order to ensure a fair comparison. Additionally the same constraints are relaxed for both LR and the LR-ATC method. In terms of the decomposition, the scheme presented in Sect. 4.2 is used for both the ATC method and the proposed LR-ATC method.

Fig. 9
figure 9

Scalability of the proposed solution method with the size of the problem

Full size image

Figure 9 shows the results comparing the proposed solution method with the All-In-One (AIO) approach, using ATC for decomposition and LR for relaxation, separately. The results show that as the number of scenarios considered for the stochastic parameters increases, so does the computational benefit of the proposed approach. After 500 scenarios, the proposed hybrid approach outperforms the other solution methods. The benefit of the proposed scheme becomes more evident against the other methods. This is due to the fact that the cost of coordinating the subproblems is no longer dominating when compared with the benefit of decomposing the problem when the size of the problem increases. This is for the case where no parallelization is used to solve the subproblems. In the case that parallelization is to be used, the benefit of the proposed scheme increases drastically.

5 Golinski speed reducer problem

5.1 Problem description

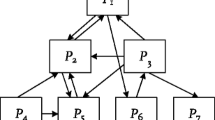
The Golinski Speed Reducer problem is a popular problem from the NASA Langley center for MDO problems Ray (2003) for which the schematic is shown in Fig. 10. The model aims to minimize the volume of the speed reducer, while accounting for physical system constraints Tosserams et al. (2007). The main design variables considered include designing the shaft and gear diameters.

Fig. 10
figure 10

Schematic of the Golinski Speed Reducer from Tosserams et al. (2007)

Full size image

5.2 Problem formulation

The formulation of the problem is extracted from Tosserams et al. (2007), for the multidisciplinary problem. In order to solve the MDO problem using a hierarchical solution scheme such as ATC, the subproblems have to be linked hierarchically. The proposed hierarchical decomposition scheme is presented in Fig 11. Here the model consists of three levels and each level has only one single subproblem. The decomposition into three subproblems is based on the scheme presented in Tosserams et al. (2007) but modified in order to be solved hierarchically.

Fig. 11
figure 11

Hierarchical decomposition scheme for the Golinski Speed reducer problem

Full size image

5.3 Results

The Golinski Speed Reducer problem was solved using an AAO approach and compared with an ATC solution scheme, an AL-ATC solution scheme and an ALAD solution scheme. In all cases, the hierarchical structure depicted in Fig 11 is utilized. The results are presented in Tables 3 and 4, where the objective value, decision variable values and number of iterations are compared for each of the methods studied. The different models were coded using GAMS modeling software and BARON solver was used for Non-linear Programming models. In order to limit the computational time to a reasonable time, the maximum number of iterations was set to be 300 iterations and the best feasible solution identified up to that iteration was used.

Table 3 shows a comparison of ATC methods with the AAO formulation for the Golinski Speed Reducer problem. As expected, the ALAD ATC method is able to reach a solution within only 85 iterations, which is greatly reduced as compared with the number of iterations of the ATC and AL-ATC methods. The ATC method needed more than 300 iterations to converge, however, the results closely matched the AAO results for the Golinski Speed Reducer problem. The reduced computation of the AL-ATC and ALAD ATC methods have a much reduced computational time and are still able to provide results that are close to optimal. Not only is the difference in objective values over 3.2%, the decision variable results also varied drastically for \(X_{6}\), where the percentage difference was over 20% for all the ATC methods. Although ATC did not converge within 300 iterations, its solution more closely matched the AAO solution to the problem. Although it should be noted that all the results were within 4%.

Table 3 Comparison of Results for the Golinski Speed Reducer Problem using ATC
Full size table

As for the proposed solution scheme, it was compared with the AAO solution for the Golinski Speed Reducer problem as well as LR and LR-ATC in Table 4. For the LR methods, the same constraint set was relaxed to allow for fair comparison of the models. The relaxed constraints correspond to constraints \(g_{1}\) and \(g_{8}\) in the formulation of the Golinski Speed Reducer problem in Tosserams et al. (2007). These constraints are shown in Eqns. 16 and 17, since the LR algorithm depicted in Fig 5 provides a lower and upper bound, when the algorithm terminates, if the lower bound is feasible to the original problem (for a minimization problem), then it is taken as the objective value. However, if the lower bound is not feasible, then the upper bound (which should always be feasible to the original formulation) is taken as the objective value. The results of the comparison of LR methods show that LR alone needs less iterations than ATC methods, especially since only two constraints are relaxed. Combining LR with ATC, we see an improvement in the iteration count for ATC, however, in this case, the objective value was much lower than the objective value for the AAO solution, with some discrepancies in the optimal values of the decision variables. In this case, the use of ATC within the LR scheme did not perform better than using LR alone in terms of the iteration count and the objective value alone. In fact, the difference in the objective value was over 22%.

The results were also compared for the computational time for this simple example. It should be noted however, that for a small-scale example, we expect the presented iterative methods to take less time than the AAO solution. However, for a simple solution such as this, we expect that the AAO will have the least computation time. We compare the computational time of the algorithms for this small example and expect to see an exaggerated trend for larger problems. It should also be noted that although the LR-ATC method actually needed more iterations to terminate than the LR approach, it took less time than LR since a single iteration took less time when solving the decomposed ATC problem. In fact, the combined LR-ATC method improved the computational time by approximately 5%, at the cost of a 23% deterioration in the quality of the objective function value. The reduced quality of the objective function value is overcome by utilizing the proposed LR-ALAD ATC solution approach. In this case, the objective function is within 0.2% of the optimal solution obtained from the AAO approach. Moreover, the computational time is further improved to over 91% of the LR method alone.

$$\begin{aligned}&\quad g_{1}: \frac{1}{110x_{6}^{3}}\sqrt{\left( \frac{745x_{4}}{x_{2}x_{3}} \right) ^{2} + 1.69*10^{7}}-1 \end{aligned}$$
(16)
$$\begin{aligned}&\quad g_{8}: \frac{1.93x_{5}^{3}}{x_{2}x_{3}x_{7}^{4}}-1 \end{aligned}$$
(17)
Table 4 Comparison of Results for the Golinski Speed Reducer Problem with LR approaches
Full size table

In terms of the proposed LR-ALAD ATC method, the number of iterations is greatly reduced to only 6 iterations as compared with 96 iterations by using LR alone. Moreover, although the objective function value is not comparable to the LR method alone, since the ALAD ATC method embedded in LR allows for paralleling the subproblems and decomposing them into smaller problems, one run of LR should be faster for the proposed scheme, as evident by the computational time. In fact, in the worst case, a single iteration of the LR-ALAD ATC method should be drastically shorter than a single iteration of the LR method, or the problem decomposition is not optimal. Overall, the proposed method can be seen to greatly reduce the number of iterations for the LR method while maintaining a close accuracy of the results.

In this case, when comparing the LR-ALAD ATC method with the ALAD ATC method, not only is the objective function value improved slightly (approximately 3%), the number of iterations is also diminished by over 66.6% and the computational time decreased by 41.3%. When comparing with AL-ATC, the results follow a similar trend, with an equivalent improvement in the objective function value for the proposed solution scheme and a time improvement of approximately 37%. These results are expected to be even more improved for problems with complex structures where decomposing the problem should result in drastic improvements on the computational time.

6 Conclusions

A novel hybrid solution scheme the decomposes complex constraints across subproblems in MDO problems is presented for coupled non-decomposable systems. The proposed method integrates the benefits of utilizing an outer relaxation solution scheme such as Lagrangian Relaxation while leveraging MDO methods such as Analytical Target Cascading and its variations to decompose the problem. A generalized framework is presented for such problems and the proposed methodology has been applied to a numerical problem as well as the Golinski Speed Reducer problem set provided by NASA Langley. The soltion scheme was compared with several variations and hybrid algorithms based on LR and ATC and the proposed scheme is shown to drastically reduce the computational cost of the solution scheme while maintaining close to optimal solutions. An advantage of utilizing LR-based schemes is that an optimality gap based on the relaxed formulation can be used to provide an estimate of how far the feasible solution is from the best possible estimate. Moreover, a major advantage of ATC is that the complex system can be decomposed, and based on the application and target problem, in some cases that could allow for parallelisation when solving the subproblems. ALAD ATC also allows odd levels and even levels to be parallelised independently. For large applications the benefit is expected to be further heightened.

The proposed methodology has some limitations when implementing it for real-case studies. One limitation is that it is not always straightforward to identify the decomposability of mathematical models with strong coupling. Future work includes identifying systematic methods to identify different decomposition hierarchies for problems. Another limitation of the proposed work is the selection of the MDO method used in the proposed integrated scheme. As seen in the results, some integration schemes could be less optimal than others. There is a need to identify the best MDO solution scheme for different problems to ensure that the integrated solution approach is optimal.

For future work, the application of the proposed methodology to a time-staged application should be studied to quantify the benefit of the proposed methodology to time dependant problems. The decomposition of the problem can be made based on the different time-dependant stages, where the connection between the different stages can be relaxed in the outer loop of the problem. This is contingent on an explicit relationship between stages, in the case of non-explicit relationships, surrogate modeling could be utilized to extract that relationship explicitly. Moreover, the proposed methodology should be applied to large-scale applications where traditional solution schemes are unable to handle the size and complexity of the problem structure. Furthermore, it would be interesting to study and introduce a metric to measure the benefit of applying the proposed methodology to different problem structures. Although general guidelines can be set to determine how suitable the LR-ALAD ATC scheme is, a quantitative metric could be useful to estimate the benefit of using the method with only preliminary results.