Microstructural topology optimization with respect to sound power radiation

Abstract

The paper deals with the problem of topological design of microstructure with respect to minimization of the sound power radiation from a vibrating macrostructure. The macrostructure is excited at a single or a band of excitation frequencies by a time-harmonic mechanical loading with prescribed amplitude and spatial distribution. The structural damping is considered to be proportional damping. The sound power is calculated using a high frequency approximation formulation and thus the sensitivity analysis may be performed in a very efficient manner. The microstructure composed of two different solid isotropic materials is assumed to be identical from point to point at the macro-level which implies that the interface between the structure and the acoustic medium is unchanged during the design process. The equivalent material properties of the macrostructure are calculated using homogenization method and the bi-material SIMP model is employed to achieve zero-one design at the micro-scale. Numerical examples are given to validate the model developed. Some interesting features of acoustic microstructure topology optimization are revealed and discussed.

1 Introduction

In the field of structural acoustics, one of the most important issues is noise and vibration control. Unlike active control, which requires an external interference source imposed upon the system, passive control can be achieved by using sound/vibration insulation/absorbing materials, or even by direct design of sound/vibration source. For example, sound radiation from a vibrating structure may be reduced by optimization of the stiffness, mass and damping of the structure, i.e., structural and material design plays a very important part in passive control of noise and vibration.

In the literature concerning structural acoustic and vibration design, a vast majority of works have been focused on optimization of the size, shape, position parameters and material parameters of the structure (see e.g. Olhoff 1976, 1977; Cheng and Olhoff 1982; Pedersen 1982; Olhoff and Parbery 1984; Bendsøe and Olhoff 1985; Koopmann and Fahnline 1997; Christensen et al. 1998a, b; Kollmann 2000; Marburg 2002; Munjal 2002; Sorokin et al. 2006). With the advent of the method of topology optimization (Bendsøe and Kikuchi 1988; Bendsøe 1989; Rozvany et al. 1992), structural design may be performed in a space with substantially more freedom, thus a better solution than that obtained by the traditional methods can be expected. During the last two decades, topology optimization methods have been developed to a great extent and extensively applied to various fields of engineering. For details, the reader is referred to the books by Bendsøe (1995), Bendsøe and Sigmund (2003), and the survey papers by Eschenauer and Olhoff (2001), Rozvany (2001, 2009), and Guo and Cheng (2010). Specifically, topology optimization has been found to be a powerful tool for vibration and acoustic design to predict the optimal structural layout or material distribution (Pedersen 2000; Sigmund and Jensen 2003; Luo and Gea 2003; Lee et al. 2004; Diaz et al. 2005; Wadbro and Berggren 2006; Jensen and Pedersen 2006; Du and Olhoff 2007a, b, 2010; Yoon et al. 2007; Dühring et al. 2008; Olhoff and Du 2009; Yamamoto et al. 2008, 2009).

Computational models developed by far for topology optimization of acoustic structure may be classified into three sets: (a) finite element based analysis combined with the SIMP model based material interpolation (named as FEM-FEM+SIMP), see e.g. Yoon et al. (2007); (b) finite element and boundary element based analysis combined with the SIMP model (FEM-BEM+SIMP), see e.g., Du and Olhoff (2007a, 2010), Du et al. (2011a, b); (c) level set based approach (Shu et al. 2011). Yoon et al. (2007) used a mixed finite element formulation (Sigmund and Clausen 2007) to circumvent the difficulty of the explicit boundary representation in structural-acoustic interaction problems. An alternative way based on the level set method, which inherently has a well-described boundary, has been proposed recently by Shu et al. (2011). Du and Olhoff (2007a, 2010) developed a high frequency approximation based model to deal with problems of topology optimization of vibrating bi-material elastic structures placed in an open acoustic medium, where the acoustic analysis and the corresponding sensitivity analysis can be carried out in a very efficient manner. In the recent works by Du et al. (2011a, b), a model combining the FEM-BEM formulation and the mixed formulation has been proposed to handle the exterior acoustic problem, where the acoustic boundary integral is performed along a design-independent nominal interface instead of the real interface between the structure and the acoustic medium. This way, the complicated sensitivity analysis due to change of the interface may be avoided. Moreover, the design domain discretized by the mixed finite elements is enclosed by the initial structural boundaries and thus has a finite volume. This is highly advantageous to reduction of the computational scale of the exterior acoustic design problem.

Up to now, most of the research concerning structural acoustic topology optimization has concentrated on the macro scale, i.e. the macro structural layout or material distribution. However, if we look into in detail some real acoustic structures or materials used in engineering, a pattern of composites with periodic microstructure can be often found. Therefore, it is natural to extend the models for structural acoustic topology optimization to the micro scale, or even an integration of the two scales. Topology optimization of microstructure, sometimes mentioned as topology optimization of material, was first realized by using the technique of inverse homogenization by Sigmund (1994, 1995). Since then, plenty of work on the basis of this technique has been carried out for different application areas to obtain the material with prescribed or extremum properties, such as mechanical properties, thermal or thermal-elastic properties, electro-magnetic properties, piezoelectric properties and so on (see e.g. Sigmund and Torquato 1997; Silva et al. 1997; Gibiansky and Sigmund 2000; Yi et al. 2000; Hyun and Torquato 2001; Diaz and Benard 2003; Guest and Prevost 2006; Zhou and Li 2008; Prasad and Diaz 2009; Choi and Yoo 2010).

The effect of boundary conditions of the macrostructure on the optimum layout of the microstructure was studied by Fujii et al. (2001), where the micro unit cell was assumed to have the same configuration and was uniformly distributed over the macroscopic design domain. If the material properties at the macro level are allowed to be varied from point to point, a two-scale design is necessary, which is also known as hierarchical optimization of material and structure (Rodrigues et al. 2002; Coelho et al. 2011). This model implemented the concurrent two-scale optimization to the largest extent, however, in spite of the great computational cost, the optimum result consisting of macro materials varying form point to point is a big challenge for manufacturing. In consideration of this, Liu et al. (2008) introduced two independent groups of design variables, i.e. micro densities and macro densities, to describe the configuration of the microstructure and the distribution of the materials (with the specific microstructure) over the macroscopic design domain respectively. Under the same framework, Yan et al. (2009) extended the problem of minimization of the compliance to thermal-elastic structures and materials, and Niu et al. (2009) studied the problem of maximization of the fundamental eigenfrequency of the macrostructure. In the two-scale optimization problems, the homogenization method is usually adopted to calculate the equivalent material properties and link the two scales together. However, the method itself cannot reveal the size effect when the characteristic inhomogeneity dimension is finite instead of infinitesimal. Some work concerning the size effect on microstructure topology optimization has been reported (see e.g. Zhang and Sun 2006; Liu and Su 2010; Su and Liu 2010).

The present paper is mostly motivated by the work mentioned above, aiming at topology optimization of the periodic microstructure to minimize the total sound power radiation from the boundaries of a vibrating macrostructure. The macrostructure is excited at a single or a band of excitation frequencies by a time-harmonic external mechanical loading with prescribed amplitude and spatial distribution. The structural damping is considered to be Rayleigh damping. The microstructure composed of two different solid isotropic material phases is assumed to be identical from point to point at the macro level, which implies that the interface between the structure and the acoustic medium will not change during the design process. The upper limit of the volume fraction of the strong material is given in the design.

The rest of the paper is organized as follows. In Section 2, the problem formulation is set up with a detailed discussion on the methods of two-scale structural-acoustic analysis and the corresponding sensitivity analysis. Based on a general analysis-optimization procedure, topology optimization of the microstructure to minimize the total sound power radiation from the macrostructure is demonstrated by numerical examples in Section 3. Here no damping is considered and the macrostructure is excited at several single frequencies. The results are also compared with that of minimum dynamic compliance design. Section 4 studies the effect of the structural damping on the optimum layout of the micro unit cell. In Section 5, the design with respect to multiple excitation frequencies is considered, which is formulated as a multiple objective optimization problem. Some interesting results are revealed and discussed. Finally, a conclusion together with some discussion on future work is given in Section 6.

2 Topology optimization of microstructure for minimization of the sound power radiation

2.1 Structural-acoustic analysis model

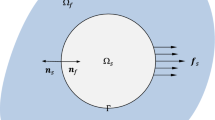
The linear stationary structural-acoustics model is considered in the present paper where both the structure and the acoustic medium (here the air) satisfy the linear constitutive equations and the acoustic medium is assumed to be inviscid, compressible and small fluctuation. Hereby at the interface only the normal displacement of the structure is coupled with the fluid and the fluid just exerts normal loads on the structure.

Under the above assumption, the governing equations of the acoustic field can be described by the standard wave equation:

$$ \nabla^2p_f \left( t \right)-\frac{1}{c^2}\frac{\partial p_f \left( t \right)}{\partial t^2}=0, $$

(1)

where the symbol p _f (t) is the pressure, c is the sound speed and t is the time. When the pressure is considered to be harmonically varied, the wave equation can be simplified as the Helmholtz equation by omitting the time term:

$$ \nabla^2p_f +k^2p_f =0, $$

(2)

where the symbol k represents the wave number and p _f represents the amplitude of the pressure.

In the present paper, we focus on the exterior problem where the vibrating structure is assumed to be surrounded by an infinitely large acoustic medium and is excited by a time-harmonic mechanical loading. Starting from the Helmholtz equation (2) and using the continuity conditions at the coupling interface and the boundary conditions, the Helmholtz integral equation can be derived by following a standard acoustic boundary integral analysis (see e.g. Christensen 1999), where the pressure at the coupling interface satisfies the following equation:

$$ C_a \left( P \right)p_f \left( P \right)=-\int\limits_S {\left[ {i\gamma_f \omega_p Gv_{\boldsymbol{n}} +p_f \frac{\partial G}{\partial {\bf n}}} \right]dS} . $$

(3)

Here the symbol P denotes the objective field point where the sound pressure will be calculated and C _α is the spatial angle at the point. The integration of (3) is performed along the structural surface S (i.e. the coupling interface), where the symbols γ _f , ω _p and v _n represent the mass density, frequency and normal velocity of the acoustic medium, respectively. The symbol G denotes the Green function which is the fundamental solution of the Helmholtz equation under unit impulse. The symbol n is the normal vector of the structural surface and points to the structural part.

The velocity at the coupling interface in (3) is unknown. In order to establish the whole coupling equations, the structural equation should be introduced. Taking into consideration the equilibrium equation, continuity conditions at the coupling interface and the boundary conditions, the governing equation of the structural part may be formulated in an equivalent integral equation by using the Galerkin-method (Zienkiewicz et al. 2005), which gives the following equation:

$$ \begin{aligned}[b] &\mathop\int\limits_V {\delta u_i \left( {\sigma_{ij,j} +f_i -\gamma_s \ddot{u}_i -\mu \dot{u}_i} \right)dv} \\ &\quad +\mathop\int\limits_{S_\sigma } {\delta u_i \left( {\sigma_{ij} n_j +\overline T _i } \right)ds} \\ &\quad +\mathop\int\limits_S {\delta u_i \left( {\sigma_{ij} n_j +p_f n_i } \right)ds} =0. \end{aligned} $$

(4)

Here the symbols V and S _σ denotes the structural domain and the prescribed mechanical loading boundary. The symbol σ _ij denotes the stress (tensor expression). The symbols u _i and δu _i denote the real and virtual displacements, respectively. The symbol γ _s is the mass density of the macro-structure and μ is the damping coefficient (here the linear damping model is used). The symbols f _i and $\overline T_i$ represent the body force and the mechanical traction force of the structure. The third term in (4) corresponds to the continuity conditions at the coupling interface.

For numerical computation, the Helmholtz integral equation (3) may be discretized using the standard boundary element method which gives the following discretized equation:

$$ {\bf C}_\alpha {\bf P}_f ={\rm {\bf GU}}-{\rm {\bf HP}}_f . $$

(5)

Where the symbols P _f and U represent the amplitude vectors of the discretized steady pressure and displacement. The symbols H _, G and C _α are the acoustic matrices and spatial angle matrix, and the detailed expressions of the matrices may be referred to the paper by Christensen et al. (1998a, b).

Similarly, the structure (4) may be discretized using the standard finite element method and simplified by integration by parts which gives the following discretized equation (ignoring the time term):

$$ \left( {{\bf K}+i\omega_P {\bf C}-\omega_p^2 {\bf M}} \right){\bf U}={\bf P}+{\rm {\bf LP}}_f . $$

(6)

Here the symbol P is the amplitude vector of the discretized mechanical loading applied to the structure. The symbols K, C and M denote stiffness, damping and mass matrices of the macrostructure respectively. Here ${\bf K}+i\omega_P {\bf C}-\omega_p^2 {\bf M}$ is also known as the dynamic stiffness matrix denoted by K _d . The symbol L represents fluid-structural coupling matrix which is given by (element expression) ${\bf L}_e =\int\limits_{S_e } {{\bf N}_s^T {\bf nN}_f ds}$, where N _s and N _f are the shape function matrices of the structural element and fluid element, respectively.

2.2 Problem formulation for micro-structural topology optimization

Following the notation of the paper (Du and Olhoff 2007a, b), the macrostructure surrounded by acoustic medium is assumed to be excited by a time-harmonic mechanical loading vector ${\rm {\bf p}}\left( t \right)={\bf P}e^{-i\omega_p t}$ with prescribed forcing frequency ω _p and amplitude vector P _. The corresponding steady structural displacement response vector is ${\bf U}e^{-i\omega_p t}$, where U is a complex or a real vector depending on whether damping is considered or not. The discretized microstructure optimization model for minimization of the total sound power flow (denoted by Π here) from the vibrating macrostructure is formulated as follows (ignoring the time term):

$$ \begin{aligned} &\mathop{\min }\limits_{\kappa_i } \left\{ {\Pi =\int\limits_S {I_n dS} =\int\limits_S {\frac{1}{2}Re\left( {p_f v_n^\ast } \right)dS} } \right\}\\ &\emph{s.t.} \\ & \quad \left( {{{\bf K}}+i\omega_P {{\bf C}}-\omega_p^2 {{\bf M}}} \right){{\bf U}}={{\bf P}}+{{\bf LP}}_f , \\ & \quad \left( {{{\bf C}}_\alpha +{{\bf H}}} \right){{\bf P}}_f ={{\bf GU}}, \\ & \quad \sum\limits_{i=1}^{n_e } {\kappa_i V_i -V^1\le 0, \left( {V^1=\gamma V_0 } \right)} , \\ & \quad 0\le \kappa_i \le 1,\,\left( {i=1,\ldots ,n_e } \right). \end{aligned} $$

(7)

Here the symbols p _f and $v_n^\ast$ are the steady sound pressure (amplitude) and the complex conjugate of the normal velocity (amplitude) at the boundaries of the macrostructure. The symbol I _n is defined as $\frac{1}{2}\mathrm{Re}\left( {p_f v_n^\ast } \right)$ which represents the sound power per unit area. The symbol S is the integration boundary of the macrostructure of which the sound power radiation is minimized.

Now let us consider that the macrostructure is constructed by a kind of composite material with periodic microstructure, where the micro unit cell is composed of two different solid isotropic materials, and is assumed to be identical from point to point at the macro level. The micro unit cell is discretized by n _e finite elements, and the symbol κ _i denotes the relative volumetric density of the stiffer material in element i and plays the role of the design variable at the micro level. The symbol γ denotes the fraction of the given volume V ¹ of the stiffer material (material 1) and is given by V ¹/V ₀, where V ₀ is the volume of the admissible design domain of the micro unit cell. The remaining part of the total volume V ₀ is occupied by a softer material (material 2).

2.3 Two-scale structure-acoustic analysis

It is known that the coupling analysis of the macro structural-acoustic equations (i.e. the first two constraint equations in (7)) is normally very time-consuming. Here we introduce a high frequency approximation of the sound pressure at the structural boundaries (Herrin et al. 2003; Lax and Feshbach 1947)

$$ p_f =\gamma_f cv_n , $$

(8)

where c is the sound speed and γ _f is the mass density of the acoustic medium. We further ignore the acoustic pressure in the structural equation by assuming weak coupling between the structure and the acoustic medium, and we have

$$ \left( {{\bf K}+i\omega_p {\bf C}-\omega_p^2 {\bf M}} \right){\bf U}={\bf P}. $$

(9)

With the above simplification, the first two constraint equations in (7) can be replaced by (8) and (9). The sound power radiation from the boundaries of the macrostructure can now be calculated in a very efficient way by

$$ \Pi =\frac{1}{2}\gamma_f c\omega_p^2 {\bf U}^\ast {\bf S}_n {\bf U}, $$

(10)

where

$$ {\bf S}_{\boldsymbol n} =\mathop\sum\limits_{j=1}^{N_e } {{\bf S}_{nj} } =\mathop\sum\limits_{j=1}^{N_e } {\mathop\sum\limits_{k=1}^{N_{Sj} } {\left(\, {\mathop\int\limits_{S_{jk} } {{\bf N}^{\rm T}{\bf nn}^{\rm T}{\bf N}dS} } \right)} } $$

(11)

is termed as the surface normal matrix (Du and Olhoff 2007a, b). The symbol N _e represents the number of finite elements used to discretize the macrostructure and N is the shape function matrix. The symbol N _Sj is the number of the boundaries located at the interface between the structure and the acoustic medium of the jth structural element. The vector n denotes the unit normal on the corresponding boundary. (Further study has shown that, even for low frequency design, the design result derived from high frequency approximation may often be close to the optimum solution obtained from accurate analysis, c.f. Song (2009).)

The macrostructure is constructed by periodic microstructures and thus the stiffness matrix of the macrostructure can be formulated as

$$ {\bf K}=\sum\limits_{j=1}^{N_e } {{\bf K}_j } =\sum\limits_{j=1}^{N_e } {\left(\, {\int\limits_{\Omega_j } {{\bf B}^T{\bf D}^H{\bf B}d\Omega } } \right)} , $$

(12)

where B is the strain matrix at the macro scale and D ^H is the equivalent macro constitutive matrix of the periodic microstructure that may be obtained by using the classical homogenization method (see e.g. Bendsøe and Kikuchi 1988; Hassani and Hinton 1998a, b):

$$ {\bf D}^H=\frac{1}{\left| Y \right|}\int_Y {{\bf D}^{{\rm MI}}\left( {{\bf I}-{\rm {\bf bu}}} \right)dY} . $$

(13)

Here ∣ Y ∣ is the area (for 2D case) of the micro unit cell. The symbol D ^MI represents the constitutive matrix of the elements consisting of the micro unit cell. In order to achieve a zero-one design, the SIMP model (Rozvany et al. 1992; Sigmund 1994; Bendsøe and Sigmund 1999) extended for bi-material interpolation is employed in the micro scale as

$$ {\bf D}^{{\rm MI}}=\kappa^p{\bf D}^1+\left( {1-\kappa^p} \right){\bf D}^2, $$

(14)

where D ¹ and D ² represent the constitutive matrices of the two given solid isotropic base materials 1 and 2 as described in Section 2.2, which will be used for filling up the design domain of the micro unit cell The symbol κ denotes the relative volumetric density of the stiffer material (material 1) and may be varied from element to element in a discretized micro unit cell. That is to say, if κ = 1, the corresponding element is occupied by the stiffer material (i.e. D ^MI = D ¹), and if κ = 0, the corresponding element is occupied by the softer material (i.e. D ^MI = D ²), and if κ ∈ (0, 1), which is often mentioned as intermediate density, the corresponding micro-scale element is occupied by an artificial material mixed by both the stiffer material and the softer material. Therefore, the zero-one distribution of κ actually determines the bi-material topology of the microstructure and hereby affects the equivalent property of the composite material constructing the macrostructure, and finally affects the dynamic response of the macrostructure and the design objective. The symbol p in (14) is a penalty factor for stiffness (normally taking the value between 3∼4 in topology optimization) which aims to suppress the intermediate density during the design process. The symbol I is a unit matrix. The symbol b in (13) is the strain matrix at the micro scale. The displacement field u of the microstructure can be calculated by the analysis of the unit cell subject to periodic boundary conditions and equivalent forces corresponding to uniform strain fields, i.e.

$$ {\rm {\bf ku}}=\int\limits_Y {{\rm {\bf b}}^{\rm T}{\bf D}^{{\rm MI}}dY} , $$

(15)

where k is the stiffness matrix of the micro unit cell and is given by

$$ {\rm {\bf k}}=\int\limits_Y {{\rm {\bf b}}^{\rm T}{\bf D}^{{\rm MI}}{\rm {\bf b}}dY} . $$

(16)

Calculation of the mass matrix of the macrostructure is much more straightforward, which is given below:

$$ {\bf M}=\sum\limits_{j=1}^{N_e } {{\bf M}_j } =\sum\limits_{j=1}^{N_e } {\left(\, {\int\limits_{\Omega_j } {\overline \eta {\bf N}^T{\bf N}d\Omega } } \right)} , $$

(17)

where $\overline \eta$ denotes the average mass density of the micro unit cell, defined by

$$ \overline \eta =\frac{1}{\left| Y \right|}\int\limits_Y {\eta ^{{\rm MI}}dY} . $$

(18)

Here, η ^MI is the mass density of the element in the base cell and is again interpolated by the bi-material SIMP model as

$$ \eta^{{\rm MI}}=\kappa^q\eta^1+\left( {1-\kappa^q} \right)\eta^2. $$

(19)

Where η ¹ and η ² represent the mass densities of the two given solid isotropic base materials 1 and 2, and q is a penalty factor for mass. We have tested several combinations of p (3∼4) and q (1∼2), and found that the combination of p = 4 and q = 2 can normally achieve good 0–1 result within a relatively large range of the excitation frequency, and thus we choose them as the values of the penalty factors in the numerical examples of the present paper.

The damping of the macrostructure is considered as the Rayleigh damping, which can be expressed by a linear combination of the stiffness and mass matrices K and M as

$$ {\bf C}=\alpha {\bf M}+\beta {\bf K}, $$

(20)

where α and β are the mass damping and stiffness damping coefficients respectively.

Theoretically, one of basic assumptions of homogenization method is that the size of the periodically distributed microstructure (i.e. the unit cell) should be infinitely small and infinitely many in the macrostructure (see e.g. Bendsøe 1995). However, when we consider the possibility of the manufacture, the microstructure always has the finite size, therefore, some size limitations should be introduced so that the basic assumption on homogenization method may be maintained in the sense of approximation. In the present paper, the size of the microstructure is assumed to be small enough in comparison to both the size of the macrostructure and the wave length $(\lambda =\frac{2\pi c}{\omega_p })$ of the dynamic loads considered in the vibro-acoustic design problem (1) so that the asymptotic expansion for homogenization calculation and dynamic analysis is valid.

2.4 Sensitivity analysis

The objective function, i.e. the sound power radiated from the boundaries of the macrostructure, is determined by the dynamic displacement response of the macrostructure (c.f. (10)). The dynamic displacement response is determined by the distribution of mass, damping and stiffness of the macrostructure (c.f. (9)). Each point of the macrostructure is assumed to be constructed by periodic microstructure which can be regarded as a kind of composite material point with equivalent property given by homogenization (c.f. (12) and (13)). Therefore, when the topology of the microstructure is changed (which is directly controlled by the zero-one distribution of the design variables in the unit cell, c.f. (14)), the corresponding equivalent property of the composite material constructing the macrostructure will change, then the dynamic displacement response of the macrostructure will change, and finally the objective function will change.

The sensitivity of the objective function in (10) with respect to the design variables can be derived by the standard adjoint method (similar to that used by Du and Olhoff (2007a, b) except for the damping part), and the result is given as follows

$$ \begin{array}{rll} \frac{\partial \Pi }{\partial \kappa_i }&=&\gamma_f c\omega_p^2 \mathrm{Re}\\&&\times\,\left[ {{\bf U}_S^\ast \frac{\partial {\bf P}}{\partial \kappa_i }-{\bf U}_S^\ast \left( {\frac{\partial {\bf K}}{\partial \kappa _i }+i\omega_p \frac{\partial {\bf C}}{\partial \kappa_i }-\omega _p^2 \frac{\partial {\bf M}}{\partial \kappa_i }} \right){\bf U}} \right]. \end{array} $$

(21)

Here U _s is given by the solution of the equation

$$ \left( {{\bf K}-\omega_p^2 {\bf M}+i\omega {\bf C}} \right)^\ast {\bf U}_s ={\bf S}_n {\bf U}\equiv {\rm {\bf f}}_s , $$

(22)

where f _s may be regarded as a pseudo loading vector. In the present paper, we only consider the case of design-independent mechanical loading, and that means ${\partial {\bf P}} \mathord{\left/ {\vphantom {{\partial {\bf P}} {\partial \kappa_i =0}}} \right. \kern-\nulldelimiterspace} {\partial \kappa_i =0}$ in (21). The sensitivities of the stiffness, mass and damping matrices of the macrostructure can be derived from (12), (17) and (20) as

$$ \frac{\partial {\bf K}}{\partial \kappa_i }=\sum\limits_{j=1}^{N_e } {\left(\, {\int\limits_{\Omega_j } {{\bf B}^T\frac{\partial {\bf D}^H}{\partial \kappa_i }{\bf B}d\Omega } } \right)} , $$

(23)

$$ \frac{\partial {\bf M}}{\partial \kappa_i }=\sum\limits_{j=1}^{N_e } {\left(\, {\int\limits_{\Omega_j } {\frac{\partial \overline \eta }{\partial \kappa_i }{\bf N}^T{\bf N}d\Omega } } \right)} , $$

(24)

$$ \frac{\partial {\bf C}}{\partial \kappa_i }=\alpha \frac{\partial {\bf M}}{\partial \kappa_i }+\beta \frac{\partial {\bf K}}{\partial \kappa_i }, $$

(25)

where the derivative of D ^H can be calculated using the mapping method (Liu et al. 2002) as

$$ \frac{\partial {\bf D}^H}{\partial \kappa_i }=\frac{1}{\left| Y \right|}\int_Y {\left( {{\bf I}-{\rm {\bf bu}}} \right)^T\frac{\partial {\bf D}^{{\rm MI}}}{\partial \kappa_i }\left( {{\bf I}-{\rm {\bf bu}}} \right)dY} , $$

(26)

and the derivative of D ^MI is given by (14) as

$$ \frac{\partial {\bf D}^{{\rm MI}}}{\partial \kappa_i }=p\kappa ^{p-1}\left( {{\bf D}^1-{\bf D}^2} \right). $$

(27)

The derivative of $\overline \eta$ can be calculated from (18) and (19) straightforwardly, and is omitted here.

3 Computational scheme for topology optimization of acoustic microstructure

A computational scheme for the design of acoustic microstructure is illustrated in Fig. 1. The sound power flow of the vibrating macrostructure and the corresponding sensitivities with respect to the micro topological design variables (i.e. the relative volumetric density of elements of the unit cell) are obtained by a two-scale analysis. Then an approximate sub-problem can be generated and solved by using the MMA method (Svanberg 1987), by which the topological design variables are updated. If the design result meets prescribed convergence criteria, the design process will be stopped. Otherwise a new design cycle will be started.

Fig. 1

Flow chart for topology optimization of acoustic microstructure

4 Numerical examples

4.1 Code validation for microstructure topology optimization

A homemade computer program written in MATLAB has been developed for handling the problem of acoustic microstructure topology optimization. In order to validate the code, a benchmark example of microstructure design aiming at minimization of the static compliance of the macrostructure (see Fujii et al. 2001) has been selected for testing and comparison.

The size, boundary and loading conditions of the macrostructure are illustrated in Fig. 2a (see also Fujii et al. 2001). Due to non-convexity of the design problem, there may exist different locally optimal solutions. Some tests have been performed and it was found that the local optimum solution strongly depends on selection of the initial designs. In order to reproduce the optimum topology in the reference, we tested several different initial designs and found one of them converged to a local optimum solution which was most similar to that obtained in the reference, and so that the comparison here makes sense. The initial material distribution within the micro unit cell is shown in Fig. 2b. Under the assumption of plane stress, the macrostructure and the unit cell are discretized by 10 × 10 and 40 × 40 mesh respectively using the 8-node isoparametric elements. The meshing for the macrostructure seems to be a little coarse, but since high order finite elements are used in our calculation, the accuracy of analysis for the mesh adopted is acceptable. Moreover, we have investigated the convergence of the result as a function of mesh refinement and found that, at least for the test example, the optimal topologies with respect to different mesh refinement are similar and consistent. On the other hand, the computational cost of sensitivity analysis in our model is proportional to the multiply of the numbers of elements used for macrostructure and microstructure. In order to finely define the micro-structural topology and at the same time keep a balance between the efficiency and accuracy, it is better to use a fine mesh for the microstructure and “relatively coarse” mesh for the macrostructure.

Fig. 2

Shear plate. a Configuration, boundary and loading conditions of the macrostructure; b Initial material distribution within the micro unit cell where the relative material volumetric densities of elements are denoted by grey scale figure

The given stiffer material has the Young’s modulus E ¹ = 72.4 GPa, Poisson’s ratio v ¹ = 0.15, and the softer material has the properties E ² = 3 GPa and v ² = 0.25. The upper limit of the volume fraction of the stiffer material is 0.5. The symmetric condition with respect to the transverse axis, the longitudinal axis and the diagonal lines of the unit cell is imposed as that of the reference.

Figure 3 gives the optimal bi-material topologies of the micro unit base cell (2 × 2 array) obtained in our test and the reference, as well as the corresponding minimized static compliance of the macrostructure. The two results are similar except that the latter has more details emerged, and the explanation lies in the different techniques used for suppressing the checkerboard problem. In our test, the sensitivity filter (Sigmund and Petersson 1998) is applied, while a perimeter control approach is adopted in the reference.

Fig. 3

Comparison of optimum configurations of the micro unit base cell (2 × 2 array). a Present paper; b Reference (Fujii et al. 2001)

4.2 Minimization of the total sound power radiation from a simply supported vibrating beam excited at a single frequency

The upper surface of a simply supported 2D beam is excited by a uniformly distributed time- harmonic loading, as is illustrated in Fig. 4a. The design objective is minimization of the total sound power radiation from all the boundaries of the beam. The initial design of the micro unit cell is given in Fig. 4b. A small disturbance of material volume density is introduced into the central elements of the design domain to avoid the trivial solution that all the elements have the same material volume density in the final design. Under the assumption of plane stress, the macrostructure and the base cell are discretized by 10 × 3 and 40 × 40 mesh respectively using the 8-node isoparametric elements.

Fig. 4

Simply supported beam. a Configuration, boundary and loading conditions of the macro beam; b Initial material distribution within the micro unit cell

The given stiffer material has the Young’s modulus E ¹ = 210 GPa, Poisson’s ratio v ¹ = 0.3, mass density η ¹ = 7800 kg/m³ and the softer material has the properties E ² = E ¹/10, v ² = 0.25 and $\eta^2={\eta^1} \mathord{\left/ {\vphantom {{\eta^1} {10}}} \right. \kern-\nulldelimiterspace} {10}$. The mass density of the acoustic medium (i.e. air) is γ _f  = 1.29 kg/m³, and the sound speed is c = 343.4 m/s. The upper limit of the volume fraction of the stiffer material is 0.5. No filter is applied in this example.

The optimum bi-material topologies of the micro unit cell with respect to six different single excitation frequencies are given in Fig. 5 (without damping). The sound power radiation values of the initial design and the optimum design are compared in Table 1 with the unit dB transformed in the following way

$$ \widetilde{\Pi }\left( {{\rm dB}} \right)=10\cdot \lg \left( {\Pi /\Pi_0 } \right) $$

(28)

where $\Pi_0 =1\times 10^{-12}{\rm W}$ is a reference sound power. The results in Table 1 indicate that the gain of the reductions of sound power radiation obtained by the current bi-material topology optimization of the microstructure are much less than that obtained by topology optimization of the macro-scale structure consisting of the same amounts of the two materials in isotropic form (Du and Olhoff 2007a). This is perhaps less surprising because in the present model it is assumed that the periodic microstructure is uniformly distributed within the macro-structural domain (i.e. the material properties at the macro-scale are identical from point to point over the macro-structural domain), and obviously the design freedom of the problem in the current setting is much less than that of the problem on topology optimization of the macrostructure itself (see e.g. Du and Olhoff 2007a).

Fig. 5

Optimum bi-material topologies of the micro unit cell at six different single excitation frequencies (without damping). The total sound power flow of the macro beam is minimized

Table 1 Sound power radiation values of the initial design and optimal design

Taking ω _p  = 800 rad/s for example, the effect of a 6 × 6 array of the optimal base cell is illustrated in Fig. 6, and a typical iteration history curve of the objective function is given in Fig. 7a. The curve is not monotonically decreasing because we relax the material volume fraction constraint a little bit at the very beginning and then gradually modify it approaching the prescribed value (i.e. 0.5) as shown in Fig. 7b, by which we have found that the design process is much more stable and easier to converge to a zero-one solution.

Fig. 6

6 × 6 array of the base cell (ω _p  = 800 rad/s)

Fig. 7

Iteration history curves (ω _p  = 800 rad/s). a Objective function, i.e. the total sound power flow of the beam; b Volume fraction of stiffer material

Obviously the optimal configuration of the base cell is very sensitive to the excitation frequency when no damping is considered. Moreover, it is also found that as the excitation frequency increases, the iteration process may possibly become unstable, e.g. in some cases it is difficult to converge to a clear 0–1 solution in the high frequency interval (compared with the fundamental eigenfrequency of the macrostructure which is about ω ₀ = 327.8 rad/s).

It was discussed in the paper by Du and Olhoff (2007a) that substantial reductions in sound power radiation from a structure immersed in a light acoustic medium can also be achieved by minimization of the dynamic compliance of the structure placed in vacuum. For microstructure design of the present paper, the minimum dynamic compliance design problem can be formulated in a similar way as

$$ \begin{aligned} &\mathop{\min }\limits_{\kappa_i } \left\{ {C_d =\left| {{\bf P}^{\rm T}{\bf U}} \right|=\left| {{\bf U}^{\rm T}{\bf K}_d {\bf U}} \right|} \right\} \\ &\emph{s.t.} \\ &\quad \left( {{\bf K}-\omega_p^2 {\bf M}} \right){\bf U}={\bf K}_d {\bf U}={\bf P}, \\ &\quad \sum\limits_{i=1}^{n_e } {\kappa_i V_i -V^1\le 0, \left( {V^1=\gamma V_0 } \right)} , \\ &\quad 0\le \kappa_i \le 1,\,\left( {i=1,\ldots ,n_e } \right). \end{aligned} $$

(29)

Solution of the above problem for the current test gives the following results shown in Fig. 8. It should be mentioned that ω _p  = 0 rad/s in Fig. 8 corresponds to minimization of the static compliance of the macrostructure. In comparison with Fig. 5, the optimum microstructures obtained by minimum dynamic compliance design remain more elements with intermediate density at high excitation frequency levels after the same steps of iteration. A possible explanation is that the dynamic stiffness matrix K _d in (29) may not be positive definite when the excitation frequency is higher (compared with the fundamental eigenfrequency of the initial macrostructure ω ₀ = 327.8 rad/s). On the other hand, the surface normal matrix S _n in (10) is always positive definite, which in some sense implies that the former is a “more well-posed” problem relative to the latter.

Fig. 8

Optimum bi-material topologies of the micro unit cell at six different single excitation frequencies (without damping). The dynamic (or static for the first case) compliance of the macro beam is minimized

4.3 Damping effect

As we know, there is always some damping in a real-life structure. The damping, even with a small value, may possibly have remarkable effect on the dynamic/acoustic behavior of the structure. Therefore, in this section the impact of structural damping on optimal configuration of the base cell is studied. Here the structural damping is considered as Rayleigh damping.

Taking the same problem settings as in Section 4.2, in the first test, we fix the excitation frequency at a moderate value ω _p  = 800 rad/s and a larger value ω _p  = 40000 rad/s, respectively. We assign a small value to the stiffness damping coefficient i.e. β = 1 × 10^− 5 and vary the mass damping coefficient within a certain range (α = 1 × 10^− 5 ∼ 1 × 10^− 2). The optimum microstructure topologies with respect to minimization of the total sound power radiation from the macro beam are given in Fig. 9.

Fig. 9

Effect of the mass damping coefficient on the acoustic microstructure design (β = 1 × 10^− 5)

It is seen form Fig. 9 that the effect of the mass damping on the optimum topology of the micro unit cell is very small. On the other side, we assign a small value to the mass damping coefficient (α = 1 × 10^− 5) and vary the stiffness damping coefficient in a certain range (β = 1 × 10^− 5 ∼ 1 × 10^− 2), and the results are shown in Fig. 10. The effect of the stiffness damping on the optimal topology of the micro unit cell is quite remarkable, especially when β > 1 × 10^− 4. An explanation is given below: the macro-structural damping model considered here is the Rayleigh damping, i.e. the damping matrix is a linear combination of stiffness matrix and mass matrix. It has been found that in the present example the magnitude of the values of the elements in stiffness matrix is approximately 10⁹ larger than that in mass matrix, and thus it is less surprise that the stiffness damping coefficient has more remarkable effect on the result of topology optimization than the mass damping coefficient dose.

Fig. 10

Effect of the stiffness damping coefficient on the acoustic microstructure design (ω _p  = 800 rad/s)

In the second test, the damping coefficients are fixed at large values α = 1 × 10^− 2 and β = 1 × 10^− 2, the optimum bi-material topologies of the micro unit cell with respect to different excitation frequencies are given in Fig. 11. It is found that the optimal design of the base cell is insensitive to the change of the excitation frequency within a broad frequency interval when the structural damping, especially the stiffness damping, is large. Moreover, the iteration process becomes more stable even in the high excitation frequency interval as the structural damping increases.

Fig. 11

Optimal bi-material topologies of the micro base cell at different excitation frequencies with large structural damping (α = 1 × 10^− 2 and β = 1 × 10^− 2)

5 Multiple-frequency optimization

When the value of the excitation frequency varies within a prescribed interval, e.g. [ω _p1, ω _p2], and the total sound power radiation from the structure is minimized for all possible frequencies simultaneously, a multiple objective optimization (or multiple-frequency optimization) should be performed, where the design objective may be formulated in a weighted form as

$$ \widetilde{\Pi }=\int_{\omega_{p1} }^{\omega_{p2} } {w\left( {\omega_p } \right)\Pi \left( {\omega_p } \right)d\omega_p } . $$

(30)

Here w(ω _p ) is the prescribed weight coefficient which satisfies $\int_{\omega_{p1} }^{\omega_{p2} } {w\left( {\omega_p } \right)d\omega _p } =1$. For numerical implementation, the sound power radiation is normally calculated at a group of selected sampling points in the prescribed frequency interval, and a linearly weighted summation of these values is taken as the design objective. The multiple-frequency optimization problem can be stated as

$$ \begin{aligned} & \mathop{\min }\limits_{\kappa_i } \left\{ {\widetilde{\Pi }=\sum\limits_{k=1}^N {w_k \Pi \left( {\omega_{pk} } \right)} } \right\} \\ &\emph{s.t.} \\ &\quad {\begin{array}{*{20}c} {\left( {{\bf K}+i\omega_{p_k } {\bf C}-\omega_{p_k }^2 {\bf M}} \right){\bf U}={\bf P},} & {\left( {k=1,2,\cdots ,N} \right),} \\ {p_{f_k } =\gamma_f cv_{n_k } ,} & {\left( {k=1,2,\cdots ,N} \right)} \\ {\sum\limits_{i=1}^{n_e } {\kappa_i V_i -V^1\le 0,\;\left( {V^1=\gamma V_0 } \right)} ,} & \\ {0\le \kappa_i \le 1,\;\left( {i=1,\ldots ,n_e } \right).} & \\ \end{array} } \end{aligned} $$

(31)

where N is the number of sampling points and the weight coefficients satisfy $\sum\limits_{k=1}^N {w_k } =1$.

Now let us consider again the problem in Section 4.2. We fix the mass damping coefficient at the value α = 1 × 10⁻² and first assign a small value to the stiffness damping coefficient i.e. β = 1 × 10^− 4. Multiple-frequency optimization with respect to a low excitation frequency interval (ω _p  = 200 ∼ 1000 rad/s) with 9 equally distributed sampling points (with the same weight coefficients) and a high excitation frequency interval (ω _p  = 3000 ∼ 5000 rad/s) with 11 equally distributed sampling points (with the same weight coefficients) are performed, respectively. The optimum bi-material topologies of the micro unit base cell are shown in Fig. 12. Frequency responses of the sound power radiation associated with the initial design and the optimum designs respectively are calculated within the frequency interval ω _p = 10∼5000 rad/s. The corresponding frequency response curves are plotted in Fig. 13. Figure 14 compares the frequency response curves between the optimum designs obtained by the multiple-frequency optimization (ω _p = 200∼1000 rad/s) and the single frequency optimization (ω _p  = 500 rad/s).

Fig. 12

Optimum bi-material topologies of the micro unit base cell obtained by multiple-frequency optimization with small stiffness damping (α = 1 × 10^− 2, β = 1 × 10^− 4) a ω _p = 200∼1000 rad/s (9 uniformly distributed sampling points), b ω _p = 3000∼5000 rad/s (11 uniformly distributed sampling points)

Fig. 13

Sound power radiation versus excitation frequency (α = 1 × 10^− 2, β = 1 × 10^− 4)

Fig. 14

Comparison between single-frequency optimization and multiple-frequency optimization (α = 1 × 10^− 2, β = 1 × 10^− 4)

It is seen from Figs. 13 and 14 that the frequency response curve of the initial design has two peak values at the resonance frequencies (ω _p  = 328 rad/s and ω _p  = 913 rad/s) within the frequency interval [200, 1000]. The single-frequency design, as we have expected, makes the sound power take the smallest value at the specific excitation frequency (ω _p  = 500 rad/s) in comparison with the initial design and multiple-frequency design. On the other hand, multiple-frequency design makes the area under the frequency response curve take the “smallest value” (strictly saying, this is true just for the case that the design objective takes the form of (30) with a constant weight coefficient over the frequency interval), which implies that the sound power is the lowest in the sense of mean value within the frequency interval considered. Moreover, the peak values of the frequency response curve within the frequency interval considered are decreased effectively (e.g. ω _p = 200∼1000 rad/s) or even totally disappear (e.g. ω _p = 3000∼5000 rad/s).

Another interesting phenomenon in Fig. 14 is that the two peaks of the frequency response curve of the multiple-frequency design (i.e. ω _p = 200∼1000 rad/s) locate at the frequency values about 350 and 950, which are in the middle of two adjacent sampling frequencies, respectively (the 9 sampling points are taken at the frequency values 200, 300, 400, ..., 900 and 1000 for this case). We may imagine that as the number of sampling points increases, the design will make the peak of the frequency response curve settle down at a proper location in the gap between the adjacent sampling frequencies in order to prevent the resonance from happening at the sampling points. One of the problems for such a design is that as the gap between the adjacent sampling points becomes smaller, the resonance peak of the frequency response curve corresponding to the optimal solution may be very close to some sampling points, the design process will become unstable due to the resonance. On the other side, if the resonance peaks of the frequency response curve of the initial design locate out of the given design frequency interval, it is always possible for the design to drive the peaks far away from the given frequency interval and the resonance can be avoided effectively. This can be illustrated by Fig. 15, where the multiple-frequency design is performed in the interval ω _p = 400∼900 rad/s which locates between the first two resonance frequencies of the initial design.

Fig. 15

Comparison between two different multiple-frequency optimizations (α = 1 × 10^− 2, β = 1 × 10^− 4)

If we increase the stiffness damping coefficient to a larger value (i.e. β = 1 × 10^− 2) and run the test again, the corresponding results are shown in Figs. 16 and 17. The optimum bi-material topologies in Fig. 16 are very similar to each other and are also close to those of Fig. 11, and this proves again that a large structural stiffness damping makes the optimal configuration rather insensitive to variation of the excitation frequency and the design converges to a more consistent result in a broad frequency interval.

Fig. 16

Optimum bi-material topologies of the micro unit base cell by multiple-frequency optimization with large stiffness damping (α = 1 × 10^− 2, β = 1 × 10^− 2). a ω _p = 200∼1000 rad/s (9 uniformly distributed sampling points), b ω _p = 3000∼5000 rad/s (11 uniformly distributed sampling points)

Fig. 17

Multiple-frequency optimization with large stiffness damping (α = 1 × 10^− 2, β = 1 × 10^− 2)

6 Conclusions

Topology optimization of the periodic microstructure with respect to minimization of the total sound power radiation from the boundaries of the macrostructure is studied in the present paper. A high frequency approximation model is employed to implement calculation of the sound power and the corresponding sensitivity analysis in a very efficient manner. The design results of minimum sound power radiation are compared with those of minimum dynamic compliance. Similarity can be viewed in the low excitation frequency interval, while differences appear in the high frequency interval. Numerical examples show that a larger structural stiffness damping coefficient may not only reduce the sensitivity of the optimum topology of the micro unit cell with respect to variation of excitation frequency, but also make the iteration process more stable. The effect of mass damping coefficient is not as remarkable as that of stiffness damping. Tests for multiple-frequency design show that the frequency response of the macrostructure can be decreased to a lower level in a mean sense within the frequency interval considered. At the same time, if the peaks of the frequency response curve locate out of the frequency interval considered, the design will move the peaks far away from the frequency interval considered.

Numerical problems have been encountered in some tests and are briefly reported here. One of the problems is that the micro unit cell is filled out with the softer material after several (few) steps and cannot be changed any more. Another problem is that the base cell still contains many elements with intermediate density after a large number of iteration steps. It is found that the above phenomenon always occurs when the excitation frequency is close to one of the resonance frequencies of the initial design, and they more often happen when the structural damping is small or is not considered. A possible explanation is given as follows. When we start the design from the neighborhood of a resonance frequency (i.e. the excitation frequency is close to a resonance frequency of the initial design that we have chosen), the optimization problem is not well-posed due to the fact that the dynamic stiffness matrix is close to singularity. As a result, numerical instability may easily occur if the moving limit (the MMA method is used in the present paper) is not controlled very well. It is possible to overcome this difficulty by imposing a better control on the iteration process (e.g. reducing the step-size of iteration or using GCMMA to construct a more convex sub-problem) which, in spite of how the effect is (in some tests that we have performed using the reduced step-size, the design converged to a local optimum with many “grey” elements which is not a preferred result), may increase the computational cost of the design remarkably. In order to overcome the above difficulty, we suggest another solution for this problem which is based on “continuity technique”. The idea is, since it is not necessary for us to start the design from an ill-posed problem that is defined in the neighborhood of resonance point, we may possibly redefine the initial design problem as a well-posed one by keeping it away from the resonance point. Here two approaches are proposed to implement the above idea: a) frequency moving approach, i.e. starting the design with an excitation frequency far away from the resonance frequency, then moving the excitation frequency continually to the prescribed value during the design process; b) damping variation approach, i.e. starting the design with a larger damping, then decreasing the damping continually to the prescribed value in the later design process. For multiple-frequency design, approach b) is much easier implemented than approach a) due to that the former has nothing to do with the frequency interval considered. Tests based on the above methods show that numerical instability has been suppressed to a large extent, and the design can normally converge to a “better” optimum solution with less grey elements and smaller value of the objective function, which we believe is closer to the global optimum. Further detailed studies on numerical instability problem in acoustic and dynamic design will be carried out in the future work.

Another work being performed is to check the effects of shape parameter of the micro unit base cell, where the shape parameter is defined as the ratio between the length and the width of the unit cell and is dealt with as an additional design variable. Computational results show that in very few cases, introduction of shape parameter as additional design variable may improve the optimal solution, while in most cases the effect of shape parameter is insignificant. It should be pointed out that the problems discussed here concerning numerical instability and the effect of shape parameter is preliminary. Further detailed studies are necessary and will be performed in the future work.

The work of the present paper provides us a primary view on the characteristics of topology design of microstructure with respect to acoustic criteria, which, together with previous work on macrostructure design, may help us to understand further how to improve the vibration and acoustic behavior of the structure by structural and material topology optimization.