Microstructural topology optimization of structural-acoustic coupled systems for minimizing sound pressure level

Abstract

The aim of this paper is to present a microstructural topology optimization methodology for the structural-acoustic coupled system. In the structural-acoustic system, the structure is considered to be a thin composite plate composed of periodic uniform microstructures. The discrete design variables are used in the microstructural topology optimization, and the constitutive matrix is interpolated by the power-law scheme at the micro scale. The equivalent macro material properties of the microstructure are computed through the homogenization method. The design objective is to minimize the sound pressure level (SPL) in an interior acoustic medium. The sensitivities of the SPL with respect to design variables are derived. The bi-directional evolutionary structural optimization (BESO) method is extended to solve the structural-acoustic coupled optimization problem to find the optimal material distribution of the microstructure. Numerical examples of a hexahedral box and an automobile passenger compartment are given to demonstrate the efficiency of the presented microstructural topology optimization method.

1 Introduction

With the increasing of people’s awareness of the performance of NVH (Noise, Vibration and Harshness), the issues concerning structural acoustic and vibration design have been extensively studied. In literatures, a vast majority of researches have been focused on optimization of the size, shape, position parameters and material parameters of the structure (Koopmann and Fahnline 1997; Christensen et al. 1998a, b; Marburg 2002; Sorokin et al. 2006; Ranjbar et al. 2012). With the advent of the method of topology optimization (Bendsøe and Kikuchi 1988; Bendsøe and Sigmund 2003), structural design can be performed in a space with adequately more freedom and a better solution can be expected compared with the traditional methods. During the last two decades, several topology optimization techniques including the Solid Isotropic Material with Penalization (SIMP) model (Zhou and Rozvany 1991; Rozvany et al. 1992), the level set method (Sethian and Wiegmann 2000; Wang et al. 2003), the Evolutionary Structural Optimization (ESO) method (Xie and Steven 1993, 1997) and its advanced version the Bi-directional ESO (BESO) (Huang and Xie 2009, 2010) method have been developed and extensively applied to various fields of engineering. Thankfully, topology optimization provides a promising approach to tackle the challenging on non-intuitive multi-physics design problem, such as thermomechanical, electro-static, and fluid-structure interaction problems (Maute 2014). Naturally, the topology optimization has been applied in the structural-acoustic problem to seek the optimal structural layout or material distribution for improving the NVH performance (Wadbro and Berggren 2006; Shu et al. 2009; Yamamoto et al. 2009; Du and Olhoff 2007; Shu et al. 2011).

Through exploiting topology optimization, many studies have been done on noise reduction. A topology optimization-based approach has been proposed by Luo et al. to study the optimal configuration of stiffeners for interior sound reduction (Luo and Gea 2003). Dühring et al. have studied the acoustic design of a rectangular room using the topology optimization method (Dühring et al. 2008). Du et al. have researched the topological design of vibrating bi-material structures in a surrounding acoustic medium (Du and Olhoff 2010). The topology optimization of composite material plate concerning the minimization of sound power radiation has been investigated by Xu et al. (2011). Zhang et al. have presented a study on topology optimization of damping layers of a shell structure for minimizing sound radiation (Zhang and Kang 2013). A level set-based topology optimization method has been proposed by Shu et al. for interior noise reduction of the structural–acoustic coupled system (Shu et al. 2014). Considering the minimization of the frequency response of fluid–structure systems, Vicente et al. have proposed a topology optimization methodology using a modified BESO (Vicente et al. 2015). Shang et al. have investigated topology optimization of a bi-material model for acoustic-structural coupled system based on optimality criteria (Shang and Zhao 2016).

Up to now, most of the researches on structural acoustic topology optimization have concentrated on the macro scale, that is, the macro structural layout or material distribution. However, composites with periodic microstructure can often be found being used in some real acoustic structures or materials engineering application, such as automobile engineering and aerospace engineering. Therefore, it is promising to extend the structural acoustic topology optimization to the micro scale. Microstructural topology optimization, sometimes mentioned as topology optimization of material, was first realized by using the technique of inverse homogenization (Sigmund 1994, 1995). Based on this technique, numerous works have been carried out to obtain the material with tailored physical properties in different application areas (de Kruijf et al. 2007; Guest and Prévost 2007; Prasad and Diaz 2009; Choi and Yoo 2010; Huang et al. 2011, 2013; Nakshatrala et al. 2013). Certainly, some significant progress has been made on the application of the microstructural topology optimization in structural acoustic design. Yang and Du have investigated the microstructural topology optimization of a beam and a plate with respect to minimizing their sound power radiation (Yang and Du 2013; Du and Yang 2015; Olhoff and Du 2009). In these literatures, the boundary element method combined with the finite element method is employed to carry out the exterior acoustic field analysis and the response sensitivity analysis in topology optimization. However, the effect of the coupling between structure and acoustic in these works is ignored. Namely, the microstructural topology optimization for minimizing the sound pressure level (SPL) of a structural-acoustic coupled system has not been researched yet. The interior noise control is an important way to improve the riding comfort of automobile and aircraft cabins. Usually, damping materials are used to reduce the internal noise through attaching them to structure. But the development of material science and manufacture techniques offers tremendous opportunities in using composite materials with tailored NVH performance. From this perspective, the design method of the composite material for the interior noise control is demanding.

Motivated by the summary above, the presented work aims to develop a topology optimization methodology of the periodic microstructure to minimize the SPL of the structural-acoustic coupled system. Because of the simplicity and computational efficiency of the BESO method (Xie and Steven 1997; Huang and Xie 2009; Huang et al. 2011), this paper will investigate the microstructural topology optimization on the structural-acoustic coupled system by using the BESO method with discrete design variables. In the structural-acoustic coupled system, the macro structure is considered to be constructed with periodic microstructures, and the microstructure is assumed to have the same configuration and uniform distribution within the macroscopic domain. The finite element model for structural-acoustic coupled system is adopted in this paper as the finite element method has been widely used in engineering applications (Xia et al. 2013; Xia and Yu 2014; Chen et al. 2016). The optimization objective is to minimize the sound pressure level (SPL) in an interior acoustic medium. The binary design variables are employed to represent two different material phases of the unit cell of the microstructure. The homogenization theory will be used to compute the equivalent macro material properties of the microstructure, and the constitutive matrix is interpolated by the power-law scheme at the micro scale. Then the BESO method is extended to find the optimal material distribution of the microstructure.

The remainder of this paper is organized as follows. In Sections 2 and 3, the finite element equilibrium equation of the structural–acoustic system and the homogenization theory is introduced. In Section 4, the microstructural topology optimization of two-scale structural-acoustic problem is set up and the formulations of the corresponding sensitivity analysis are deduced. Two numerical examples are presented in Section 5 and some conclusions are given in Section 6.

2 Equilibrium equation of the structural–acoustic system

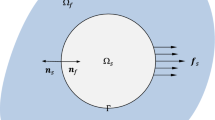
Let us consider the case in which a Kirchhoff plate constructed with periodic microstructures is coupled with an acoustic cavity. Both the plate and the acoustic medium satisfy the linear constitutive equations and the acoustic medium is assumed to be inviscid and incompressible. The interaction between the acoustic field and the vibrating plate cannot be neglected. On the interface between the structure and the fluid, only the normal displacement of the structure is coupled with the fluid and the fluid just exerts normal loads on the structure.

Assuming that the external excitation is time harmonic, the dynamic equilibrium equation of the structural-acoustic system neglecting damping can be expressed as

$$ \left[\begin{array}{cc}\hfill {\mathbf{K}}_s-{\omega}^2{\mathbf{M}}_s\hfill & \hfill -\mathbf{H}\hfill \\ {}\hfill {\rho}_f{\omega}^2{\mathbf{H}}^{\mathrm{T}}\hfill & \hfill {\mathbf{K}}_f-{\omega}^2{\mathbf{M}}_f\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\mathbf{u}}_s\hfill \\ {}\hfill \mathbf{p}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill {\mathbf{F}}_s\hfill \\ {}\hfill {\mathbf{F}}_f\hfill \end{array}\right\} $$

(1)

where ω represents the angle frequency, ρ _f is the density of the acoustic fluid; K _s and M _s. stand for the structural stiffness matrix and structural mass matrix; K _f and M _f stand for the acoustic stiffness matrix and the acoustic mass matrix; H is the spatial coupled matrix; u _s and p are the displacement vector of structure and the sound pressure vector in the acoustic domain; F _s and F _f are the generalized force vectors related to the structure and to the internal acoustic cavity. The detailed derivation of (1) is provided in reference (Xia et al. 2013).

The structural stiffness matrix K _s and mass matrix M _s. , can be expressed as

$$ {\mathbf{K}}_s=\sum_{i=1}^{N_{cell}}\left({\int}_{\Omega_i}{\mathbf{B}}^{\mathrm{T}}{\mathbf{D}}^{\mathrm{H}}\mathbf{B}\mathrm{d}\Omega \right) $$

(2)

$$ {\mathbf{M}}_s=\sum_{i=1}^{N_{cell}}{\int}_{\Omega_i}{\eta}^{\mathrm{H}}{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{N}}_s\mathrm{d}\Omega $$

(3)

where B is the strain matrix at the macroscale; D ^H is the equivalent macro constitutive matrix of the periodic microstructure; η ^H is the average mass density of the micro unit cell; N _s is the Lagrange shape function of the isoparametric quadrilateral element; the summation represents an assembly process of the system matrices and vectors; N _cell is the total number of elements in the structural domain; Ω _i is the i-th element in the structural domain.

The acoustic mass matrix M _f and acoustic stiffness matrix K _f can be expressed as

$$ {\mathbf{M}}_f=\sum_{j=1}^{n_{c ell}}\frac{1}{c^2}{\int}_{\Omega_j}{\mathbf{N}}_f^{\mathrm{T}}{\mathbf{N}}_f\mathrm{d}\Omega $$

(4)

$$ {\mathbf{K}}_f=\sum_{j=1}^{n_{cell}}{\int}_{\Omega_j}{\left(\nabla {\mathbf{N}}_f\right)}^{\mathrm{T}}\cdot \left(\nabla {\mathbf{N}}_f\right)\mathrm{d}\Omega $$

(5)

in which n _cell is the total number of elements in the acoustic domain; Ω _j is the j-th element in the acoustic domain; N _f is the Lagrange shape function of the isoparametric hexahedral element; c is the speed of the sound.

The coupled interface between the plate and the acoustic fluid domain satisfies the continuity conditions of normal particle velocity and pressure u _s n = u _f n. n is the normal vector on the interface; u _s is the displacement of the plate on the interface; u _f is the displacement of the acoustic fluid on the interface. The spatial coupled matrix H is $\mathbf{H}=\sum_{i=1}^{N_{cell}}\left({\int}_{\Omega_i}{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{nN}}_f\mathrm{d}\Omega \right)$.

In order to simplify the process of analyzing the dynamic equilibrium equation of the structural–acoustic system, we rewrite (1) as the following form

$$ \mathbf{ZU}=\mathbf{F} $$

(6)

where Z is the acoustic impedance matrix (Sgard et al. 1994); U is the frequency response vector; F is the external excitation vector. They can be expressed as

$$ \mathbf{Z}=\left[\begin{array}{cc}\hfill {\mathbf{K}}_s-{\omega}^2{\mathbf{M}}_s\hfill & \hfill -\mathbf{H}\hfill \\ {}\hfill {\rho}_f{\omega}^2{\mathbf{H}}^{\mathrm{T}}\hfill & \hfill {\mathbf{K}}_f-{\omega}^2{\mathbf{M}}_f\hfill \end{array}\right]\ \mathbf{U}={\left\{{\mathbf{u}}_s\kern0.5em \mathbf{p}\right\}}^{\mathrm{T}}\ \mathbf{F}={\left\{\begin{array}{cc}\hfill {\mathbf{F}}_s\hfill & \hfill {\mathbf{F}}_f\hfill \end{array}\right\}}^{\mathrm{T}} $$

(7)

3 Homogenization-based microstructural analysis

The macro plate is assumed to be constructed by periodic microstructures. Thus, the equivalent macro constitutive matrix D ^H of the periodic microstructure can be computed through the homogenization method (Bendsoe and Kikuchi 1988; Bendsoe et al. 1993).

$$ {\mathbf{D}}^{\mathrm{H}}=\frac{1}{\left|\Omega \right|}\underset{\Omega}{\int }{\mathbf{D}}_e\left(\mathbf{I}\hbox{-} \mathbf{b}\boldsymbol{\upchi } \right) d\Omega $$

(8)

Where Ω is the domain of the micro unit cell and |Ω| represents its area; D _e stands for the constitutive matrix of the eth element in the micro unit cell; the symbol I is a unit matrix; the symbol b is the strain matrix at the micro scale; χ represents the characteristic displacement of the microstructure, which is the solution of the auxiliary equation given by

$$ \mathbf{k}\boldsymbol{\upchi } =\mathbf{f} $$

(9)

here, the stiffness matrix k and the force vector f at the microscale can be expressed as

$$ \mathbf{k}=\underset{\Omega}{\int }{\mathbf{b}}^T{\mathbf{D}}_e\mathbf{b} d\Omega $$

(10)

$$ \mathbf{f}=\underset{\Omega}{\int }{\mathbf{b}}^T{\mathbf{D}}_e d\Omega $$

(11)

in which the constitutive matrix D _e can be interpolated by the power-law scheme (Huang and Xie 2009), that is

$$ {\mathbf{D}}_e={x}_e^q{\mathbf{D}}^1+\left(1-{x}_e^q\right){\mathbf{D}}^2 $$

(12)

where D ¹ and D ² stand for the constitutive matrices of the two given solid isotropic base material 1 and 2, respectively; x _e is the relative volumetric density, which describe the layout of the micro structure. The symbol q is the exponent of penalization, which usually taken to be equal to 3. In the present paper, the Kirchhoff plate element is employed in the finite element model. The elasticity constitutive matrix of the given solid isotropic material can be expressed as

$$ \mathbf{D}=\frac{Eh^3}{12\left(1-{v}^2\right)}\left[\begin{array}{ccc}\hfill 1\hfill & \hfill v\hfill & \hfill 0\hfill \\ {}\hfill v\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1- v}{2}\hfill \end{array}\right] $$

(13)

where h is the thickness of the plate; the symbols E and ν are the Young’s modulus and the Poisson’s ratio of the given material, respectively.

The average mass density η ^H of the micro unit cell can be calculated as following

$$ {\eta}^{\mathrm{H}}=\frac{1}{\left|\Omega \right|}\underset{\Omega}{\int }{\eta}_e d\Omega $$

(14)

Here, η _e is the mass density of the eth element in the micro unit cell and can also be interpolated as

$$ {\eta}_e={x}_e{\eta}^1+\left(1-{x}_e\right){\eta}^2 $$

(15)

where η ¹ and η ² stand for the mass density of the two given solid isotropic base material 1 and 2, respectively.

4 Microstructural topology optimization for the coupled systems

4.1 Problem statement

In the coupled structural–acoustic system, the macro plate is considered to be constructed by a kind of composite material with a periodic microstructure, and the microstructure is assumed to have the same configuration and uniform distribution within the macroscopic domain. The micro unit cell is composed of two different solid isotropic materials and is assumed to be identical from point to point at the macrolevel. In this paper, the aim of topology optimization for the coupled structural-acoustic systems is to find a material distribution of the microstructure that satisfies prescribed constrains and minimizes the sound pressure level (SPL). Usually two distinct situations should be considered when harmonic loads are acting in a system. The first one is that the external force is acting under just one specified frequency, and the other one is that the applied load can vary in a frequency interval. For the first situation, the objective function and the sensitivity can be calculated directly. Considering the latter situation, a number of approaches can be employed to determine the objective function and the sensitivity in the frequency domain. In literatures, Yoon used an integral function to calculate the objective function in an frequency interval range (Yoon 2010). Zhang et al. calculated the objective function using the Kreisselmeier–Steinhauser (KS) aggregated function and took sampling frequencies in the frequency interval range analyzed (Zhang et al. 2014). In the present work, a linear approximation is used to interpolate the objective function in the analyzed frequency interval. The analyzed frequency range is divided equally into n discrete frequencies. The objective function and the sensitivity for the structural-acoustic system are calculated for each frequency. Then, the arithmetic mean values of the objective function and sensitivity for n discrete frequencies are computed as the effective objective function and sensitivity. Here, the topology optimization model for the coupled systems can be stated as

$$ \begin{array}{r} \min \kern0.5em \sum_{\omega}{\mathrm{SPL}}_{\omega, j}\\ {}\mathrm{s}.\mathrm{t}.\kern0.5em \mathbf{ZU}=\mathbf{F}\\ {}\sum_e{x}_e{v}_e\le V\\ {}{x}_e={x}_{\min }\ or\ 1\end{array} $$

(16)

where x _e is a binary design variable corresponding to element e in the microstructural domain and v _e is the element volume; here, the microstructure is considered to be composed of a soft material (Material 1) and a stiff material (Material 2); V is the predefined upper bound of the volume occupied with soft material; x _e  = 1 and x _e  = x _min denote the soft material elements and stiff material elements, respectively; A small value x _min = 0.001 is used to denote the stiff material elements; here, the SPL _ω,j is defined as following

$$ {\mathrm{SPL}}_{\omega, j}=10{ \log}_{10}{\left(\frac{p_{\omega, j}}{p_0}\right)}^2 $$

(17)

where p _ω,j is the amplitude of the sound pressure at the jth degree of freedom when the angle frequency is ω; p ₀ is the reference sound pressure, which is equal to 2 × 10⁻⁵ Pa.

4.2 Sensitivities analysis

In this paper, the BESO is extended to solve the microstructural topology optimization for the minimization of the SPL of the structural-acoustic coupled systems. The direct-variable sensitivity analysis is conducted here. However,it should be noted that the adjoint-variable method is more efficient than the direct variable method in the problems involving a large number of design variables but only a few behavior functions, as in the case of a topology optimization (Kang et al. 2012). In the extended microstructural BESO, the sensitivity is defined as the derivative of the objective function SPL _ω,j with respect to the design variable x _e , which can be expressed as

$$ \frac{\partial {\mathrm{SPL}}_{\omega, j}}{\partial {x}_e}=\frac{20}{p_{\omega, j} \log (10)}\ \frac{\partial {p}_{\omega, j}}{\partial {x}_e} $$

(18)

In order to determine the derivative of the response sound pressure in the jth degree of freedom with respect to the design variable, a load vector ξ _j is introduced. This load vector has the unity value in the jth degree of freedom and zero in all other positions. Thus, $\frac{\partial {p}_{\omega, j}}{\partial {x}_e}$ can be expressed as

$$ \frac{\partial {p}_{\omega, j}}{\partial {x}_e}={\xi}_j^T\frac{\partial \mathbf{U}}{\partial {x}_e} $$

(19)

Taking derivatives of (6) with respect to design variable x _e , one gets

$$ \frac{\partial \mathbf{U}}{\partial {x}_e}=-{\mathbf{Z}}^{\hbox{-} 1}\frac{\partial \mathbf{Z}}{\partial {x}_e}\mathbf{U} $$

(20)

Combining with (19), (20) and (18), the sensitivity of SPL _ω,j can be rewritten as

$$ \frac{\partial {\mathrm{SPL}}_{\omega, j}}{\partial {x}_e}=\frac{-20}{p_{\omega, j} \log (10)}\ {\xi}_j^T{\mathbf{Z}}^{\hbox{-} 1}\frac{\partial \mathbf{Z}}{\partial {x}_e}\mathbf{U} $$

(21)

where

$$ \frac{\partial \mathbf{Z}}{\partial {x}_e}=\left[\begin{array}{cc}\hfill \frac{\partial {\mathbf{K}}_s}{\partial {x}_e}-{\omega}^2\frac{\partial {\mathbf{M}}_s}{\partial {x}_e}\hfill & \hfill -\frac{\partial \mathbf{H}}{\partial {x}_e}\hfill \\ {}\hfill {\rho}_f{\omega}^2\frac{\partial {\mathbf{H}}^{\mathrm{T}}}{\partial {x}_e}\hfill & \hfill \frac{\partial {\mathbf{K}}_f}{\partial {x}_e}-{\omega}^2\frac{\partial {\mathbf{M}}_f}{\partial {x}_e}\hfill \end{array}\right] $$

(22)

Due to x _e is only associated with the eth microstructural element, (22) can be simplified as

$$ \frac{\partial \mathbf{Z}}{\partial {x}_e}=\left[\begin{array}{cc}\hfill \frac{\partial {\mathbf{K}}_s}{\partial {x}_e}-{\omega}^2\frac{\partial {\mathbf{M}}_s}{\partial {x}_e}\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill \end{array}\right] $$

(23)

where

$$ \frac{\partial {\mathbf{K}}_s}{\partial {x}_e}=\sum_{i=1}^{N_{cell}}\left({\int}_{\Omega_i}{\mathbf{B}}^{\mathrm{T}}\frac{\partial {\mathbf{D}}^{\mathrm{H}}}{\partial {x}_e}\mathbf{B}\mathrm{d}\Omega \right) $$

(24)

$$ \frac{\partial {\mathbf{M}}_s}{\partial {x}_e}=\sum_{i=1}^{N_{cell}}{\int}_{\Omega_i}\frac{\partial {\eta}^{\mathrm{H}}}{\partial {x}_e}{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{N}}_s\mathrm{d}\Omega $$

(25)

where the derivative of D ^H can be computed as following through mapping method (Liu et al. 2002)

$$ \frac{\partial {\mathbf{D}}^{\mathrm{H}}}{\partial {x}_e}=\frac{1}{\left|\Omega \right|}\underset{\Omega}{\int }{\left(\mathbf{I}\hbox{-} \mathbf{b}\boldsymbol{\upchi } \right)}^{\mathrm{T}}\frac{\partial {\mathbf{D}}_e}{\partial {x}_e}\left(\mathbf{I}\hbox{-} \mathbf{b}\boldsymbol{\upchi } \right) d\Omega $$

(26)

The derivative of D _e can be expressed as

$$ \frac{\partial {\mathbf{D}}_e}{\partial {x}_e}={px}_e^{q-1}\left({\mathbf{D}}^1-{\mathbf{D}}^2\right) $$

(27)

The derivative of η ^H in (25) can be calculated as follows

$$ \frac{\partial {\eta}^{\mathrm{H}}}{\partial {x}_e}=\frac{1}{\left|\Omega \right|}\underset{\Omega}{\int}\frac{\partial {\eta}_e}{\partial {x}_e} d\Omega $$

(28)

where

$$ \frac{\partial {\eta}_e}{\partial {x}_e}={\eta}^1-{\eta}^2 $$

(29)

4.3 Solution algorithm

In this paper, the microstructural BESO is developed to minimize the SPL of the structure-acoustic coupled system. The binary design variables are employed to represent two different material phases of the unit cell of the microstructure. The constitutive matrix is interpolated by the power-law scheme at the micro scale, and the equivalent macro material properties of the microstructure are computed through the homogenization method in each iteration of the optimization procedure. The main steps of the microstructural BESO method for coupled systems are given as follows

• Step 1: Discretize the macro structural–acoustic system and microstructure design domain by a finite element mesh with given boundary and loading condition.

• Step 2: Define the BESO parameters, such as the material volume constraint V, evolutionary ratio ER, penalty factor p, filter radius r _min ect. The detail of BESO parameters can be found in literatures (Huang et al. 2011) and (Huang et al. 2013).

• Step 3: Perform the finite element analysis on the micro scale to calculate the effective elastic matrix D ^H and the average mass density η ^H based on the homogenization method presented in section 3.

• Step 4: Carry out the finite element analysis for the coupled system using the effective elastic matrix D ^H and the average mass density η ^H.

• Step 5: Compute the sensitivity numbers α _e for minimizing the SPL in the structural-acoustic coupled systems, which is

$$ {\alpha}_e=-\frac{\partial {\mathrm{SPL}}_{\omega, j}}{\partial {x}_e}=\frac{20}{p_{\omega, j} \log (10)}\ {\xi}_j^T{\mathbf{Z}}^{\hbox{-} 1}\frac{\partial \mathbf{Z}}{\partial {x}_e}\mathbf{U} $$

(30)

here, the sensitivity numbers can be negative or positive. Positive sensitivity number means the design variable has a positive effect on the optimization objective function, and vice versus.

• Step 6: Update sensitivity numbers by a mesh-independency filter scheme, which is defined as

$$ {\hat{\alpha}}_i=\frac{\sum_{j=1}^M w\left({r}_{i j}\right){\alpha}_j}{\sum_{j=1}^M w\left({r}_{i j}\right)} $$

(31)

where M is the total number of nodes in the sub-domain Ω _i ; the sub-domain Ω _i is generated by drawing a circle of radius r _min centered at the centroid of ith element; r _ij denotes the distance between the center of the element i and node j; α _j is the nodal sensitivity numbers; w(r _ij ) is the weight factor defined as (Xie and Steven 1997)

$$ w\left({r}_{ij}\right)=\left\{\begin{array}{c}\hfill {r}_{\min }-{r}_{ij}\kern0.75em for\ {r}_{ij}<{r}_{\min}\hfill \\ {}\hfill 0\kern3em for\ {r}_{ij}\ge {r}_{\min}\hfill \end{array}\right. $$

(32)

• Step 7: Average sensitivity numbers with historical information as

$$ {\hat{\alpha}}_i=\frac{{\hat{\alpha}}_i^k+{\hat{\alpha}}_i^{k-1}}{2} $$

(33)

where k is the current iteration number. In this way, the updated sensitivity number considers the sensitivity information in the previous iterations.

• Step 8: Determine the target soft material volume for the next design. When the current soft material volume V _k is larger than the objective soft material volume V, the target soft material volume for the next design can be calculated by

$$ {V}_{k+1}={V}_k\left(1- ER\right) $$

(34)

If the calculated soft material volume for the next design is less than the objective soft material volume V, the target soft material volume for the next design V _k+1 is set to be V.

• Step 9: Reset the design variables of all elements. For soft material elements, the elemental density is switched from 1 to x _min if the criterion ${\widehat{\alpha}}_i\le {\alpha}_{th}$ is satisfied. Whereas, for stiff material elements, the elemental density is switched from x _min to 1 if the criterion ${\widehat{\alpha}}_i>{\alpha}_{th}$ is satisfied. In these criterions, α _th is the threshold of the sensitivity number. The detail of determining α _th can refer to literature (Huang and Xie 2009).

• Step 10: Repeat 2–9 until the prescribed material volume constraint is achieved and the convergent criterion with a predefined error tolerance τ = 0.001 is satisfied. The variation in the objective function is calculated as following

$$ \frac{\left|{\sum}_{j=1}^3{R}_{k- j+1}\hbox{-} {\sum}_{j=1}^3{R}_{k- j\hbox{-} 2}\right|}{\sum_{j=1}^3{R}_{k- j+1}}\le \tau $$

(35)

where R _k denotes the objective function value in the kth iteration.

The flow chart of the iterative procedure for the microstructural BESO method for coupled systems is shown in Fig.1.

Fig. 1

Flowchart of the procedure of the solution algorithm

5 Numerical example

5.1 A hexahedral box

A three-dimensional cavity is enclosed with a hexahedral box of dimensions 0.25 m × 0.25 m × 0.25 m, as shown in Fig. 2. The top surface of the box is a clamped plate with thickness 1 mm and the other surfaces are rigid. A concentrated harmonic loading F = 10 N is applied to the midpoint of the top surface. The density and the sound speed of the air are 1.21 kg/m³ and 343 m/s, respectively. The clamped plate is discretized by 64 four-node Kirchhoff plate elements and the acoustic domain is discretized by 512 hexahedral elements. The reference point A is used to observe the sound pressure response in the acoustic field.

Fig. 2

A hexahedral box

The macro clamped palate is considered to be composed of a periodic uniform material, thus the homogenization theory can be applied. The microstructure unit cell is composed of two prescribed materials, namely, the strong material (Red color) and the soft material (Blue color). The strong material has a Young’s modulus E ₁ = 71 GPa, Poisson’s ratio v ₁ = 0.3, and mass density ρ ₁ = 2700 kg/m³. The soft material has a Young’s modulus E ₂ = E ₁ / 10, Poisson’s ratio v ₂ = 0.3, and mass density ρ ₂ = ρ ₁ / 10. Figure 3 depicts the initial design of the microstructure unit cell. A small disturbance of material volume density is introduced to the central elements of the design domain to avoid the trivial solution, in which all the elements have the same material volume density in the final design (Yang and Du 2013). For simplicity the unit cells in the micro scale are assumed to be squared and with a dimensionless length of 1 × 1. The microstructure design domain is discretized into 30×30 quadrilateral elements. The parameters in the BESO procedure are set as: the evolutionary ratio is set to be 2%; the radius r _min of the filter is chosen to be 3; the volume fraction of the solid material is constrained to 50% of the total volume. In order to obtain the symmetric designs, only quarter of the microstructure is designed. Simulations of this hexahedral box are carried out by MATLAB R2014a on a 2.93GHz Core(TM) 8 CPU E7500.

Fig. 3

Initial uniform design with slight perturbation in the center of the mirco unit cell

Firstly, cases of microstructural topology optimization for the coupled box model with respect to discrete frequency are considered. The optimum topologies of the micro unit cell under four different frequencies harmonic loading are shown in Fig. 4. It can be seen from Fig. 4 that the optimal topology varies with frequency. Figure 5 presents the evolutionary history of the SPL in these microstructural topology optimization processes. The corresponding sound pressure at the reference point of the initial design and the optimum design are compared in Table 1. The sound pressure at the reference point can be decreased effectively through microstructural topology optimization. It can be found out from Fig. 5 that the sound pressure reduction at f = 150 Hz is the largest among these four different frequencies. As shown in Table 1, the sound pressure is reduced from 102.8 dB to 78.83 dB when the excitation frequency is 150 Hz, a drop of almost 23.3%. This means that the presented microstructural BESO can achieve a good result on the noise reduction of a coupled structural-acoustic system. Furthermore, Fig. 6 shows the comparison of the sound pressure at the reference point between the initial and optimum designs of the coupled box model considering the target frequency f = 250 Hz. It can be found out from Fig. 6 that the sound pressure at the reference point of the optimum design is smaller than that of the original design at the target frequency. Besides, it can be seen that the resonance frequency of optimum design has a shifting compared with original design.

Fig. 4

Optimum topologies of the micro unit cell and the corresponding 6 × 6 arrays for the different excitation frequencies

Fig. 5

The evolutionary history of the SPL at different excitation frequencies

Table 1 The sound pressure at the reference point in the initial design and optimum design

Fig. 6

The comparison of the sound pressure at the reference point between the initial and optimum designs of the coupled box model considering the target frequency f = 250 Hz

Then the situation of the coupled box model considering a frequency interval loading is investigated. The frequency range is set to be 125–175 Hz and is divided into n = 11 discrete frequency values. Using the algorithm mentioned in section 4.1, the optimum topology of the micro unit cell considering the frequency interval of f = 125–175 Hz are shown in Fig. 7. Sound pressures at the reference point associated with the initial design and the optimum designs are calculated respectively within the frequency interval f = 50–200 Hz. The corresponding sound pressure curves are plotted in Fig. 8 and the target frequency interval is shadowed. It can be observed from Fig. 8 that the resonance frequency is shifted away from the interval of the applied excitation and the sound pressure at the reference point in the target frequency interval decrease obviously in the optimum design. This further indicates that the presented microstructural BESO for structural-acoustic coupled system has a good performance in noise control.

Fig. 7

Optimum topology of the micro unit cell and the corresponding 6 × 6 arrays considering the frequency interval of f = (125–175) Hz

Fig. 8

The comparison of the sound pressure at the reference point between the initial and optimum designs of the coupled box model considering the frequency interval f = (125–175) Hz

5.2 An automobile passenger compartment

Figure 9 shows an automobile passenger compartment with flexible roof panel. A harmonic point force F = 10 N is applied at the central of the roof. The thickness of the roof panel is 1 mm. The four sides of the roof panel are set to be fixed. The density and the sound speed of the air are 1.21 kg/m³ and 343 m/s, respectively. The node A is near the driver’s ear. The macro roof panel is assumed to be composed of a periodic uniform material. The microstructure unit cell is composed of two prescribed materials. The two materials employed and the initial design of the microstructure unit cell are the same as those in Section 5.1. The unit cells in the micro scale are assumed to be squared and with a dimensionless length of 1 × 1. The microstructure design domain is discretized into 30×30 quadrilateral elements. Here, the proposed microstructural BESO for structural-acoustic systems is used to perform the topology design. The evolutionary ratio is set to be 2%. The radius r _min of the filter is chosen to be 3. The volume fraction of the solid material is constrained to 50% of the total volume. In order to obtain the symmetric designs, only quarter of the microstructure is designed. Simulations of this automobile passenger compartment are carried out by MATLAB R2014a on a 2.93GHz Core(TM) 8 CPU E7500.

Fig. 9

An automobile passenger compartment

Simulations of microstructural topology optimization for the automobile passenger compartment model with respect to discrete frequency are performed firstly. The optimum topologies of the micro unit cell under three different frequencies harmonic loading are shown in Fig. 10. The comparison of the corresponding sound pressure at the node A in the initial design and the optimum design are made, as shown in Table 2. It can be seen from Fig. 10 that the optimal topology varies seriously with frequency. The sound pressure at the node A can be decreased effectively through microstructural topology optimization. Specifically, the sound pressure is reduced from 67.29 dB to 42.41 dB when the excitation frequency is 180 Hz, a reduction of almost 37.0%. This indicates that the proposed microstructural BESO for structural-acoustic systems can be employed to acquire better NVH performance in practical engineering. Figure 11 shows the comparison of the sound pressure at the reference point between the initial and optimum designs of the automobile passenger compartment model considering the target frequency f = 180 Hz. It can be found out from Fig. 11 that the sound pressure at the reference point of the optimum design is smaller than that of the original design at the target frequency. Besides, the phenomenon that the resonance frequency of optimum design has a shifting compared with original design can be observed as well.

Fig. 10

Optimum topologies of the micro unit cell and the corresponding 6 × 6 arrays for the different excitation frequencies

Table 2 The sound pressure at the node A in the initial design and optimum design

Fig. 11

The comparison of the sound pressure at node A between the initial and optimum designs of the automobile passenger compartment considering the target frequency f = 180 Hz

The case of the automobile passenger compartment model considering a frequency interval loading is also investigated. The frequency range is set to be 110–130 Hz and is divided into n = 11 discrete frequency values. Through the algorithm presented in section 4.1, the optimum topology of the micro unit cell considering the frequency interval of f = 110–130 Hz are given in Fig. 12. The first twelve order non-zero resonance frequencies of original design and optimum design are listed in Table 3. It can be found out that the resonance frequencies of optimum design move to low values compared with original design. Also, resonance frequencies located in the target frequency interval are 117.98 Hz and 127.36 Hz in the original design, whereas the resonance frequency in the optimum design is 129.84 Hz. Sound pressures at the node A associated with the initial design and the optimum designs are computed respectively within the frequency interval f = 20–200 Hz. The corresponding sound pressure curves are plotted in Fig. 13 and the target frequency interval is shadowed. It can be observed from Fig. 13 that the resonance peaks are shifted away from the interval of the applied excitation and the sound pressure at the node A in the target frequency interval decrease obviously in the optimum design. Besides, it can be found out from Fig. 13 that the SPL is decreased at most of the frequencies within the frequency interval f = 20–200 Hz. Therefore, the presented microstructural BESO for structural-acoustic systems is practicable and available for reducing low-frequency noise in engineering problems.

Fig. 12

Optimum topology of the micro unit cell and the corresponding 6 × 6 arrays considering the frequency interval of f = (110–130) Hz

Table 3 The first twelve order non-zero resonate frequencies of original design and optimum design

Fig. 13

The comparison of the sound pressure at node A between the initial and optimum designs of the automobile passenger compartment considering the frequency interval f = (110–130) Hz

6 Conclusions

Motivated by the requirement of the design approach for the composite material in the field of the interior noise control, this paper has presented a microstructural topology optimization methodology for the structural-acoustic coupled system to minimize the SPL generated by the vibrating structure. In the structural-acoustic system, the macro plate is assumed to be composed of a periodic uniform microstructure. The binary design variables are employed to represent two different material phases of the unit cell of the microstructure. The constitutive matrix is interpolated by the power-law scheme at the micro scale, and the equivalent macro material properties of the microstructure are computed using the homogenization method in each iteration of the optimization procedure. The BESO method is extended to find the optimal material distribution of the microstructure. Numerical examples of a hexahedral box and an automobile passenger compartment excited at a single or a band of excitation frequencies by a time-harmonic external loading are performed using the proposed microstructural BESO. The results indicate that the microstructural BESO for structural-acoustic coupled systems presented in this article is practicable and available for reducing noise in engineering problems.