Hybrid model of clustering and kernel autoassociator for reliable vehicle type classification

Abstract

Automatic vehicle classification is an important area of research for intelligent transportation, traffic surveillance and security. A working image-based vehicle classification system is proposed in this paper. The first component vehicle detection is implemented by applying histogram of oriented gradient features and SVM classifier. The second component vehicle classification, which is the emphasis of this paper, is accomplished by a hybrid model composed of clustering and kernel autoassociator (KAA). The KAA model is a generalization of auto-associative networks by training to recall the inputs through kernel subspace. As an effective one-class classification strategy, KAA has been proposed to implement classification with rejection, showing balanced error–rejection trade-off. With a large number of training samples, however, the training of KAA becomes problematic due to the difficulties involved with directly creating the kernel matrix. As a solution, a hybrid model consisting of self-organizing map (SOM) and KAM has been proposed to first acquire prototypes and then construct the KAA model, which has been proven efficient in internet intrusion detection. The hybrid model is further studied in this paper, with several clustering algorithms compared, including k-mean clustering, SOM and Neural Gas. Experimental results using more than 2,500 images from four types of vehicles (bus, light truck, car and van) demonstrated the effectiveness of the hybrid model. The proposed scheme offers a performance of accuracy over $95~\%$ with a rejection rate $8~\%$ and reliability over $98~\%$ with a rejection rate of $20~\%$. This exhibits promising potentials for real-world applications.

1 Introduction

With the increasing demand for security awareness of motor-vehicles and widespread installation of surveillance cameras, there is a pressing need for technologies that are able to automatically identify vehicle types through imaging [1–3]. The identified vehicle type could provide valuable information for the vehicle, which enables the functionalities of the conventional number-plate recognition systems to be extended. Information on vehicle type is serviceable to many applications such as traffic management and transportation infrastructure planning. In controlled areas such as airports, a license plate recognition system augmented with the vehicle type recognition feature can be installed at access lanes, automatically monitoring the vehicles entering and exiting the area, and detect any discrepancies between the vehicle type and its license plate number.

Early AVC technology mainly employed inductive loop [4, 5], which has certain disadvantages such as being costly and impractical for relocation. As vision systems are relatively cheap and easy to install and operate, vision-based vehicle classification has attracted much attention in recent years [1, 3, 6–8]. The issues and problems of vehicle type recognition are similar to other forms of object recognition in computer vision, with a number of challenging characteristics. Vehicle images are always captured with a large degree of variations due to the ever-changing road environments, backgrounds and lighting conditions. Motion-induced variability in the shape, size, color, and appearance of vehicles all add to the limiting factors of the development of vehicle type recognition systems. Although classification of vehicle types has been a subject of interest for several years, most of the published works mainly focused either on detection (determining vehicle or background) or tracking [2, 3, 6, 7]. A few of the past works attempted to apply different feature analysis from images and use advanced machine learning algorithms to classify vehicles into some categories such as cars, buses, heavy goods vehicles (HGVs), etc. [9–11].

As a pre-requisite for image-based vehicle classification, the region of vehicle has to be located from the image. Due to the variability present in imaging conditions caused by occlusions, illuminations and shadows, vehicle detection itself is a challenging task. A number of vehicle detection approaches have been reported in the computer vision literature [6, 7, 11]. Among the proposed approaches, the dominant ones are those based on the pioneering object detection method introduced by Viola and Jones [12]. Viola and Jones’ object detection mainly consists of two main steps: (i) hypothesis generation and (ii) hypothesis verification, which generate the tentative locations of vehicles in an image and then validate the true existence of the vehicles in turn. A recent work by Negri [13] further extends VJ’s strategy in vehicle detection by exploiting two features, i.e., Haar-like feature and histogram of oriented gradient (HOG) [14], together with an AdaBoosting classifier. The joint application of the two features and cascade classifier makes the algorithm computationally expensive. This paper explores a simpler yet more efficient method which exploits HOG and SVM.

Given the significance of vehicle type information, assessment of confidence for classification results should be addressed. A clear indication of classification reliability would allow users’ control over the system’s performance. Typically, image classification methods implicitly assume that a testing case must fall onto one of the predefined classes and subsequently classify all of the examples, even if a result is somehow ambiguous. For most of the real-world applications, such a close-set classification assumption is not acceptable. A preferred practice is to classify an example only when there is a sufficiently high degree of confidence. Known as rejection option in classifier design [15–18], the techniques would allow the accuracy be set prior to classification and hence each classification is given with a predefined confidence level. However, how to implement a rejection option in a multi-class classifier has not been sufficiently addressed by and large, with the exception of a few publications [17–19].

Among the first works to study classification with rejection option, Chow [20] proposed a Bayes optimum recognition framework to reject the most unreliable objects that have the lowest class posterior probabilities. In real problems, however, it is not realistic to accurately estimate the posterior probabilities. It was later proved that Chow’s rule does not perform well if a significant error in probability estimation is present [16]. For vehicle type classification, it is more difficult to accurately estimate class conditional probabilities because of the curse of dimensionality problem. The possibility of having objects from unknown classes also needs to be taken into account. Fumera et al. [16] demonstrated that per-class thresholds have advantages over a single global threshold with regard to an error–reject trade-off. However, the values of the multiple thresholds must be estimated, which is not a trivial task due to the computational intensiveness.

Recently, one-class classification paradigm has been proven efficient in the implementation of rejection options in vehicle type classification [21]. Conventional multi-class classification algorithms classify an unknown object into one of several pre-defined categories, which has an unavoidable problem when the unknown object does not belong to any one of those given categories. In one-class classification, a class known as the positive class or target class, is well characterized by instances in the training data [22, 23]. By class-specific description models using distance among samples, one-class classification can bypass the estimation of class conditional probabilities.

Among the statistical methods and neural learningschemes proposed for one-class classification, auto-associative neural network (AANN) has proved to be a valuable tool in many applications. Auto-associative neural network models [24, 25] are feedforward neural networks, performing an identity mapping of the input space. To improve the performance of a simple AANN model, Zhang et al. [26] proposed a kernel auto-associator (KAA) which maps the data into a high-dimensional feature space via the utilization of a kernel function. Compared with the simple auto-associative network models, KAA model has the benefit of finding complex nonlinear features. The applications of the KAA model to recognition and classification have been reported previously [27, 28].

The main issue of applying the KAA model in one-class classification is to create the kernel matrix. In an earlier paper, we proposed that the prototypes of training samples could be selected by self-organizing map (SOM) and the kernel matrix is then created using the prototypes [29]. This study focuses on the hybrid model and how to exploit its use for vehicle type classification, comparing with two more popular clustering algorithms, i.e., k-means and Neural gas. The clustering algorithms extract prototypes for each of the data categories. The implementation of rejection option is then addressed, aiming at building a reliable classifier that is able to measure the appropriateness of its decisions. Such a system is highly expected when the user requires to be notified about the confidence level of each classification or rejecting the query. The reliable hybrid classification model is applied to classify vehicle types, which are represented by simple edge histogram features.

This paper is structured as follows. Section 1 briefly introduces some background and related research issues of image-based automatic vehicle type classification, Sect. 2 outlines the data acquisition from surveillance cameras and explains the necessary step of vehicle segmentation. Section 3 introduces the hybrid model of KAA and clustering, with three clustering algorithms included; k-means, SOM and Neural Gas. The implementation of confidence estimation via rejection option is discussed in Sect. 4. Section 5 is dedicated to the experiments of vehicle classifications using the hybrid model, followed by conclusion in Sect. 6.

2 Image collection and vehicle detection

A large collection of vehicle images was provided by police in a collaborated project for traffic surveillance. The images were recorded with traffic surveillance cameras over a 1-week period between 7:30 a.m. to 21:50 p.m., encompassing a wide range of weather and illumination conditions. From the recorded images ($>$50,000), 6,000 images of different vehicles of four categories were selected, including car, van, truck and bus. All of the images contained frontal views of a single vehicle captured from variable distances. The original images have $1{,}024\times 1{,}360$ color pixels. A sample of the selected images is shown in Fig. 1.

Fig. 1

Samples of the frontal vehicle images

2.1 Vehicle detection

Vehicle detection is a special topic of object detection in computer vision, which has seen many progresses in recent years, particularly appearance-based methods. Examples include the seminal work of Viola and Jones and many extensions [12]. Support vector machines (SVM) with HOGs [14] have also been extensively applied for object detection, including vehicle detection [13]. In the following, two kinds of vehicle detector that combines the HOG feature descriptor and SVM were proposed. Figure 2 shows the first simple vehicle detection scheme.

Fig. 2

Illustration of the HOG-SVM vehicle detection scheme

The essential idea of HOG is to describe the appearance and shape of a local object in an image can often be characterized well by the distribution of local intensity gradients or edge directions. The main steps of HOG consist of first dividing the image window into small spatial regions (or “cells”), and then accumulating a weighted local 1-D HOG directions over the pixels of the cell. We adopted the most popular R-HOG, which uses rectangular cell. To minimize the effect from illumination variance, contrast-normalization is carried by accumulating local histogram over a larger regions (blocks) to normalize all of the cells in the block.

The vehicle detection is performed by window searching at different scales with the HOG feature using an appropriate classifier, which will locate the bounding boxes for potential vehicles. Training samples were prepared with two types: 6,358 negative samples and 4,557 positive samples. Negative samples correspond to non-object images, which are taken from arbitrary outdoor images free of any vehicles. Positive samples are manually cropped vehicle objects from traffic surveillance images as shown in Fig. 1, with different durations of time and weather conditions being taken into account. Some of the positive and negative examples are illustrated in Figs. 3 and 4.

Fig. 3

Examples of vehicle images as the positive samples

Fig. 4

Examples of non-vehicle images as the negative samples

The parameters of HOG are as follow: The convolution of the image with a 1D $[-1, 0, 1]$ filter mask is applied to approximate the gradient. There are four ($2\times 2$) cells in each block, with each cell of $8 \times 8$ pixels. The bin number of gradient orientation is taken as 9 over the range of $0^{\circ }{-}180^{\circ }$. The block normalization is implemented by L2-norm as follows:

$$\begin{aligned} \nu \rightarrow \frac{\nu }{\sqrt{\Vert \nu \Vert ^2_2+\epsilon ^2}} \end{aligned}$$

(1)

where $\nu$ stands for the local histogram and $\epsilon$ is a small number. The final HOG feature for each sample image is of 1,764 dimension, as illustrated in Fig. 5.

Fig. 5

Illustration of the HOG features extracted for both of the positive and negative samples

The first vehicle detection scheme is implemented by applying HOG feature and a SVM [30]. Given labeled training data, SVM will generate an optimal hyperplane to categorize new examples. Intuitively, the operation of the SVM algorithm is based on finding the hyperplane that gives the largest minimum distance to the training examples. And the optimal separating hyperplane maximizes the margin of the training data. During detection, HOG features from the searching windows are calculated and inputted to the SVM classifier. The SVM’s output will correspond to the detection result. By incorporation of the idea of rescaling the Region of Interests (RoIs) as proposed in [31], such a single SVM detector with HOG feature provides better results than the AdaBoost algorithm with composite features of HOG and Haar described in [31].

To further improve the detection performance, we developed a cascade of linear SVM classifiers for fast vehicle detection. Our motivation is based on the proved efficiency of cascade classifiers such as the AdaBoost algorithms. A cascade SVM was proposed in [32] for object detection, with independently trained SVMs. Being different from theirs, the cascade SVM scheme we proposed can be demonstrated in Fig. 6, with details expounded in the following. A SVM’s existence and performance in the cascade is dependent upon the previous one. Specifically, the original training samples are divided into two sets: training set and validation set, where training set accounts for 10 % of the training samples while validation set 90 %. The training set was used to train the first SVM, and 5 % random samples without replacement from the validation set were taken to test the SVM’s performance. If the error rate exceeds a predefined threshold ($10^{-4}$), then the correctly classified and wrongly classified examples were, respectively, added to the positive and negative training samples exploited by the first SVM, and the resulting augmented training samples will be applied to next SVM’s training. The procedure continues until the error rate from a SVM in the cascade is less than the threshold ($10^{-4}$), which will terminate the training.

Fig. 6

Illustration of cascade SVMs for vehicle detection scheme

Proceeding with the trained cascaded SVMs, a multi-scale vehicle detection is implemented by scaling up the detection windows. Specifically, the hypothesis images delineated by rectangular boxes, which indicate potential vehicle objects, will undergo scaling up operations with appropriate amplification coefficients. Two factors were taken into account in the selection of the coefficients. Too large amplification coefficients will omit some small vehicle objects while too small coefficients will generate unnecessarily many detection windows thus slowing down the detection speed. We selected the detection parameters by trial and error. The initial detection window is of $128\times 128$ pixels, which will be shifted 64 pixels, and scaled up with coefficient 1.3.

As there will be more than one detected windows generated by the cascade SVM from the hypothesis images, proper decision fusion is necessary to produce single detection result. There are two possible different relationships among the detected windows. The first is containment relation, which means one detected window may locate inside another. The second relation is intersection relation, which means different detected windows cross each other. For the first relation, only the largest window will be kept. For the second relation, the positions of the boxes will be averaged and rounded. The two situations and their handling were further explained in Figs. 7 and 8.

Fig. 7

The containment relations for the bounding boxes and the final result from deleting the smaller ones

Fig. 8

The intersection relations for the bounding boxes and the averaged result

3 Hybrid model of clustering algorithms and kernel auto-associator

3.1 Kernel auto-associator construction

A kernel auto-associator (KAA) finds an identity mapping through an implicit kernel space, which can be formally defined as follows [26, 27]. Let $H_k$ be a reproducing kernel Hilbert space and $k(\cdot , \cdot )$ be a positive-definite function in $H_k$. The inner product in $H$ is defined by

$$\begin{aligned} \langle k_x,k_t\rangle =k(x,t) \end{aligned}$$

(2)

and $k(\cdot , \cdot )$ is called the reproducing kernel for $H_k$.

Let $F_b$ be a linear mapping function from $H_k$ to the input space $R^N$. The principle of kernel auto-associator is to perform auto-associative mapping via the kernel feature space, i.e., reconstructing patterns from their counterparts in $H_k$:

$$\begin{aligned} {\hat{\mathbf{x}}}=F_b^{(m)} (\varPhi (\mathbf{x})),\quad \hbox {for}\ {\mathbf{x}} \in \hbox {class}\ m \end{aligned}$$

(3)

where $\varPhi (\mathbf{x}) = k(\mathbf{x}, \cdot )$ represents the feature in functional form in $H_k$ and the subscript $b$ denotes the function for reverse mapping.

When the patterns to be reproduced are multidimensional, $F_b$ will be composed of a set of functions $\{f_{b_n}\}$, each corresponding to an element of the output space: $F_b = [f_{b_1},\ldots ,f_{b_N}]^\mathrm{T}$. Consider an element function $f_{b_n}$ and omit the element label $n$, the function in linear form is

$$\begin{aligned} {{\hat{x}}}=f_b(\varPhi (\mathbf{x}))=\langle \beta _{\phi },\varPhi (\mathbf{x})\rangle \end{aligned}$$

(4)

Here, ${\hat{x}}$ represents an element of the output vector ${\hat{\mathbf{x}}}$, and $\beta _{\phi }$ is a vector in the feature space. Suppose the vector $\beta _{\phi }$ can be spanned by the images of $M$ training samples:

$$\begin{aligned} \beta _{\phi } = \sum _{i=1}^M b_i \varPhi (\mathbf{x}_{i}) \end{aligned}$$

(5)

then the linear function $f_b$ can be rewritten as

$$\begin{aligned} {\hat{x}}=\left\langle \sum _{i=1}^M b_i \varPhi (\mathbf{x}_{i}), \varPhi (\mathbf{x})\right\rangle =\sum _{i=1}^{M}b_{i}k(\mathbf{x}_{i}, \mathbf{x})=\mathbf{b}^\mathrm{T}\mathbf{k} \end{aligned}$$

(6)

where $\mathbf{b}=[b_1,\ldots ,b_{M}]^\mathrm{T}$ is the vector of expansion coefficients, and $\mathbf{k}=[k(\mathbf{x}_1,\mathbf{x}),\ldots , k(\mathbf{x}_{M},\mathbf{x})]^\mathrm{T}$ represents the vector of kernel products. So the complete output vector ${\hat{\mathbf{x}}}$ is given by

$$\begin{aligned} {\hat{\mathbf{x}}} = B \mathbf{k} \end{aligned}$$

(7)

where $B=[b_1,\ldots ,b_N]$ denotes the collection of linear projections for each output element. Given a set of samples, for example, $(\mathbf{x}_1, \mathbf{x}_2,\ldots ,\mathbf{x}_{M})$ for training, we can first compute the kernel product vectors $(\mathbf{k}_1, \mathbf{k}_2,\ldots , \mathbf{k}_{M})$. The desired output of the network can be expressed as

$$\begin{aligned} X = BK \end{aligned}$$

(8)

where $X$ is the matrix with each column an example pattern, $X=(\mathbf{x}_1, \mathbf{x}_2,\ldots ,\mathbf{x}_{M})$, and $K$ represents the matrix with each column a corresponding kernel product vector, $K=(\mathbf{k}_1, \mathbf{k}_2,\ldots ,\mathbf{k}_{M})$.

In [26], a simple method of learning the projection matrix $B$ was proposed by minimizing the empirical square error $\sum _i ||\mathbf{x}_{i}-B\mathbf{k}_{i}||^2$, which gives:

$$\begin{aligned} B=XK^{+} \end{aligned}$$

(9)

where $K^{+}$ is the pseudo-inverse of the kernel product matrix $K: \,K^{+} = (K^\mathrm{T} K)^{-1} K^\mathrm{T}$.

For the $k$th query, the distance between the query input $\mathbf{x}$ and the reconstruction $\mathbf{x}_{k}$ can be simply given by their Euclidean distance:

$$\begin{aligned} d(\mathbf{x}_{k},{\hat{\mathbf{x}}}_{k})=\Vert \mathbf{x}_{k}-{\hat{\mathbf{x}}}_{k}\Vert ^2. \end{aligned}$$

(10)

The kernel auto-associator constructed from Eq. (8) shares the structure of the Radial Basis Function (RBF) network, as shown in Fig. 9, in which $B_{ij}$ is the connection weight from the unit $j$ to the linear output unit $i$. Here, the activity of the unit $j$ is same as the kernel function, for example, a Gaussian kernel of the distance from the input $\mathbf{x}$ to its center $\mathbf{x}_j$.

Fig. 9

Structure of a KAA network

An important issue in KAA is about the selection of the $\sigma$ value in Gaussian kernel function. An appropriate value of $\sigma$ would allow a direct measurement of confidence in the reconstruction for a particular input. We choose a simple method to effectively calculate the $\sigma$ value by taking an average of the similarity measure (in $L_2$ norm sense) between every pair of training samples.

3.2 Hybrid model of clustering algorithms and KAA

The KAA model is particularly valuable when the training samples are scarce, which makes most of the traditional classifiers inapplicable. However, when there is a relatively large number of training data, the direct application of KAA becomes impractical as the kernel matrix in Eq. (8) becomes larger, which makes the inversion computationally expensive. A simple intuition to solve this problem is by appropriate selection of representative samples (prototypes) to build the kernel matrix. In [29], the SOM model [33] was chosen to generate the prototypes. In the following, the hybrid model is further extended with different clustering methods compared, including SOM, k-means clustering and Neural Gas. The training can be explicitly described into two steps:

Step 1::

Unsupervised training to find the prototypes, for example, by applying appropriate clustering algorithms;

Step 2::

Self-supervised training of the KAA models using the prototypes.

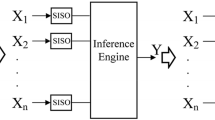
The training process can be further illustrated in Fig. 10. After the prototypes are generated from the training data and the KAA network is trained, a testing pattern will be reconstructed by each of the KAA model during the recognition phase. The reconstruction errors of the KAA define the indicators that the input vector is assigned to the corresponding category.

Fig. 10

Demonstration of the hybrid classification structure, which mainly consists of clustering and KAA

3.3 k-Means clustering

The k-means clustering [34] is one of the most commonly used unsupervised learning methods, which categorizes the input data points into a number ($k$) of different clusters based on an appropriately defined distance, e.g., Euclidean distance, from each other. In another word, the data points are clustered around centroids $\mu _i,\,i=1,2,\ldots ,k$, which are obtained by minimizing the following objective

$$\begin{aligned} J=\sum _{i=1}^k \sum _{x_j \in S_i}\Vert \mathbf{x}_{j}-{{\mu }} \mathrm{_i}||^2 \end{aligned}$$

(11)

where there are $k$ clusters $S_i,\,i=1,2,\ldots ,k$, and $\mu _i$ is the centroid of all the points $\mathbf{x}_{j}\in S_{i}$.

3.4 Self-organizing map

Self-organizing map [24, 33] aims at generating a mapping of an input signal vector $\mathbf{x}$ from a high-dimensional space $R^L$ onto a 2D spatial space through a correspondence between input vectors and the weight vectors of neurons, $\mathbf{w}\in R^{L}$, such that the topological relationships of weight vectors associated with each neuron faithfully preserve the essential features of the inputs.

In the learning process, from a given data sample $\mathbf{x}$, the best matching reference vector $\mathbf{w}_{c}$, together with those $\mathbf{w}_{m}$ adjacent to $c$, are updated, $m=1,\ldots ,M$, with a step size decreasing with the lattice distance between $m$ and $c$. Specifically, SOM can be realized by first selecting a winning unit $c$ as the one with minimal representation error and then choosing a neighborhood set $N_c$ around $c$, which determine those units within $c$’s neighborhood. All the units within the $N_c$ adapt their weights according to the following learning rule

$$\begin{aligned} \varDelta \mathbf{w}_{m}= \left\{ \begin{array}{ll} \mu _k(\mathbf{x}-\mathbf{w}_{m})&{}\quad \mathrm{for}\ m \in N_c \\ 0 &{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

In Kohonen’s model, the size of $N_c$ starts large and slowly decreases over time. For a two-dimensional network, a square array or hexagonal array topological neighborhood shape can be selected. If the learning rate $\mu _k$ decreases gradually over the learning course, the reference vectors $\mathbf{w}_{m}$ tend to become evenly distributed over the input probability distribution.

The above neighborhood selection procedure usually results in slow convergence. A better alternative is to replace the neighborhood set $N_c$ by a continuous neighborhood interaction function $h_{ij}$ of the distance between units $i$ and $j$ in the lattice. The corresponding learning algorithm becomes:

$$\begin{aligned} \varDelta \mathbf{w}_{m}=\mu _{k}h_{mc}(\mathbf{x}-\mathbf{w}_{m}),\quad m=1,\ldots ,M \end{aligned}$$

(12)

where the neighborhood interaction function $h_{mc}$ is a monotonically decreasing function of the geometrical distance $d_{mc}$ between units $m$ and $c$ in the topological map, typically selected as a Gaussian function

$$\begin{aligned} h_{mc}=\exp \left( -\frac{d_{mc}^2}{2\sigma ^2}\right) ,\quad \text{ for } m\in N_c \end{aligned}$$

(13)

3.5 Neural ‘Gas’ algorithm

The idea of Neural ‘Gas’ (NG) model [35, 36] is to partition the input space by competition while ordering the neurons based on a distance metric defined in the input space. Each neuron associates a reference vector. The information about neighborhood relationship among the reference vectors can be provided by an matching score between a reference vector and the input.

With a training sample $\mathbf{x}$, the ranking of distortions $\Vert \mathbf{x}-\mathbf{w}_{m_0}\Vert ^2,\,\Vert \mathbf{x}-\mathbf{w}_{m_1}\Vert ^2,\ldots ,\Vert \mathbf{x} - \mathbf{w}_{m_{M-1}}\Vert ^2$ will be first sorted out, with $\mathbf{w}_{m_0}$ being closest to $\mathbf{x}, \mathbf{w}_{m_1}$ being second closest to $\mathbf{x},\mathbf{w}_{m_k},k=0,\ldots ,M-1$ being the reference vector for which there are $k$ vectors $\mathbf{w}_{j}$ with $\Vert \mathbf{x}-\mathbf{w}_{j}\Vert <\Vert \mathbf{x}-\mathbf{w}_{m_k}\Vert$. Each neuron adjusts its own weight via a dynamical learning rate which depends on the ranking of its distortion.

Denote the number $k$ associated with each neural unit $m$ by $k_m$. The following learning rule realizes the Neural ‘Gas’ algorithm in [35].

$$\begin{aligned} \varDelta \mathbf{w}_{m}={\mu _{k}}h_{\lambda }(k_{m})(\mathbf{x}-\mathbf{w}_{m}),\quad m=1,\ldots ,M \end{aligned}$$

(14)

where $h_{\lambda }(k_m)$ is 1 for $k_m=0$ and decays to zero for increasing $k_m$. In the simulation we choose the same one as in [35], $h_{\lambda }(k_m)=\exp (-k_m/\lambda )$, with $\lambda$ being a decay constant.

Comparing with k-means clustering, Neural ‘Gas’ model is less sensitive to the initial conditions. It has also been proven that NG achieves both robustness and best asymptotic quantization error [36].

4 Hybrid KAA classification with controlled confidence

Classical classification problem is to assign an unknown pattern to one of some pre-defined categories, even if the example is not belonging to any existed category. In practice, the assumption that all classes are known beforehand may not always be true. For example, there may exist a large number of classes, some of which are scarce and difficult to be collected for training the classifier. Another common situation in image classification is the inclusion of poorly segmented samples in the training sets. The poor segmentation results may not be similar to any of the types defined. It is therefore preferable to have a rejection option, by which the ambiguous input can be relayed to human expert to be operated accurately. A rejection option allows the misclassification rate be kept beneath an acceptable threshold, thus ensuring the reliability.

4.1 Chow’s theory of classification with rejection

For applications with known probability distributions, the Bayes classifier is optimal which also explicitly defines the posterior probability of the chosen class. The posterior probability is a natural measure of classification confidence. Based on this institution, Chow [20] has carried out some fundamental research on classification with reject option. For two-class classification problems, an example is represented by a $n$-dimensional feature vector $\mathbf{x}\in \mathfrak {R}^{n}$ and a label $y\in C, \,C =\{-1, +1\}$. Following the Bayes’ theorem, posterior probability is defined:

$$\begin{aligned} p(C_i|\mathbf{x})=\frac{p(C_{i})p(\mathbf{x}|C_{i})}{p(\mathbf{x})},\quad i=1,2. \end{aligned}$$

(15)

where $p(C_i)$ is the prior probability of class $C_i, \,p(\mathbf{x} |C_{i})$ is the conditional densities of $\mathbf{x}$ given $C_i$ and $p(\mathbf{x})=\sum _{i=1}^2 p(\mathbf{x}|C_{i})p(C_{i})$ represents the unconditional density of $\mathbf{x}$.

If we use $\text {risk}(x)$ to denote the risk of making a wrong decision for $\mathbf{x}$, the Bayes decision rule assigns $\mathbf{x}$ to the class of maximum posterior probability (14) by minimizing the error probability, which can be defined by

$$\begin{aligned} \text{ error }=\int _{\mathbf{x}} \text {risk}(\mathbf{x})p(\mathbf{x})~\hbox {d}x \end{aligned}$$

(16)

The Bayes classifier predicts the class having the highest posterior probability and is optimal if true posterior probabilities are available. However, when some classes are not known or when classes overlap in feature space, Bayes classifier may not be always efficient. An alternative approach is to classify only those samples for which the posterior probability is sufficiently high and reject the remaining ones. Based on this principle, Chow presented an optimal classifier with reject option [20]. A binary decision rule with reject option is optimum if for a given error rate (error probability) it minimizes the reject rate (reject probability). Chow demonstrated that the optimum rule is to reject the pattern if the maximum of the a posteriori probabilities is less than a certain threshold.

More explicitly, an example $\mathbf{x}$ is accepted only if the probability that $\mathbf{x}$ belongs to $C_i$ is higher than or equal to a given probability threshold $t$:

$$\begin{aligned} f(\mathbf{x})= \left\{ \begin{array}{ll} \text{ argmax }_{C_i} (p(C_i|\mathbf{x}))&{}\,\,\text{ if }\ \text{ max }_{C_i} p(C_i|\mathbf{x}) \ge t, \\ \text{ reject } &{}\,\,\text{ if }\ p(C_i|\mathbf{x}) \le t \ \forall i. \end{array}\right. \end{aligned}$$

(17)

where $f:\mathfrak {R}^n \rightarrow C$ represents the classification function, which divides the feature space into two regions $R_1,R_2$, one for each predicted class, such that $\mathbf{x}\in R_{i}$ means that $f(\mathbf{x})=C_{i}$.

The classifier rejects an example if the prediction is not sufficiently reliable. The rejection rate is the probability that the classifier rejects the example,

$$\begin{aligned} p(\text{ reject })=\int _{R_\mathrm{reject}} p(\mathbf{x})~\hbox {d}x =p(\max (p(C_{i}|\mathbf{x}))\le t) \end{aligned}$$

(18)

where $R_\mathrm{reject}$ denotes rejection region defined in the feature space and all examples belonging to this region are rejected by the classifier. Accordingly, the acceptance rate is the probability that the classifier accepts an example,

$$\begin{aligned} p(\mathrm{accept}) = 1 - p(\mathrm{reject}) \end{aligned}$$

(19)

There is a general relation between the error and rejection rate: the error rate decreases monotonically while the rejection rate increases [30]. The following basic properties can be easily verified:

$$\begin{aligned}&\!\!\!p(\mathrm{accept}) + p(\mathrm{reject})=1 \nonumber \\&\!\!\!p(f (\mathbf{x})=y)+p(f(\mathbf{x}) \ne y)+p(\hbox {reject})=1 \\&\!\!\!p(f (\mathbf{x})=y|\hbox {accept})+p(f(\mathbf{x})\ne y|\hbox {accept})=1\nonumber \end{aligned}$$

(20)

In Chow’s theory, an optimal classifier can be found only if the true posterior probabilities are known. This is rarely the case in practice. Fumera et al. [16] showed that Chow’s rule does not perform well if a significant error in probability estimation is present. In this case, the authors of [16] claimed that defining different thresholds for each class yields better results.

4.2 Hybrid KAA model with confidence

Chow’s theory is fundamental for classification with reject option. However, in real-world applications, the class distributions are rarely known and the posterior probabilities have to be estimated. Though there are some algorithms for density estimation, most of them are difficult to apply, particularly when the “curse of dimensionality” exists. Among the proposed methods for posterior probability approximation, a commonly applied approach, called soft-max function, can be defined for the hybrid kernel auto-associator:

$$\begin{aligned} {\hat{P}}(C_j|\mathbf{x})=\frac{\exp (-\mathrm{err}_{j}(\mathbf{x})) }{\sum _{k=1}^{N}\exp (-\mathrm{err}_{k}(\mathbf{x}))} \end{aligned}$$

(21)

where $\mathrm{err}_j(\mathbf{x})$ represents the output reconstruction error from $j$th KAA, and $N$ is the number of classes. ${\hat{P}}(C_j|\mathbf{x})$ is an estimated posterior which can be also treated as the confidence of the hybrid classifier in predicting class $C_j$ for instance $\mathbf{x}$.

With posterior estimation for the each of the KAA models, the simplest rejection strategy is by thresholding, following Chow’s theoretical guidance Eq. (16). Specifically, assume the estimated posteriors of a given pattern $\mathbf{x}$ be ${\hat{P}}(\mathbf{x})=\{{\hat{P}}_1(\mathbf{x}), {\hat{P}}_2 (\mathbf{x}),\ldots , {\hat{P}}_{N} (\mathbf{x})\}$, where probabilities ${\hat{P}}_i(\mathbf{x})$ are in descending order. The decision function would be based on $\mathrm{sgn}({\hat{P}}_1(\mathbf{x})-T)$, where $T$ is an empirically chosen threshold. Such a simple thresholding, however, cannot effectively detect patterns for which the classifier is likely to confuse. In another word, those errors which are caused by the samples near the decision boundaries are most pertinent to classification reliability in real applications. In such a case, the scores of at least two classes will be nearly equal.

To cater for the confusion reject, a better scheme is by the comparison of relative difference between the probabilities ${\hat{P}}_1(\mathbf{x})$ and ${\hat{P}}_2(\mathbf{x})$ of the first two ranks. A possible condition of rejection could be based on an appropriate measurement function in the form of $||{\hat{P}}_1(\mathbf{x})-{\hat{P}}_2(\mathbf{x})||$, where $||.||$ is a suitably defined distance, and the decision function is based on a thresholding of the difference.

In the hybrid KAA-based classification system, due to the monotonicity of exponential function, the comparison of the probabilities ${\hat{P}}_1(\mathbf{x})$ and ${\hat{P}}_2(\mathbf{x})$ of the first two ranks can be simplified to the direct comparison of the reconstruction errors of the first two ranks. Specifically, a test pattern can be rejected if the smallest reconstruction error and the second smallest error differ by less than a threshold. An indicator variable $\eta$ can be defined as

$$\begin{aligned} \eta =1-\frac{\mathrm{err}_j}{\mathrm{err}_i} \end{aligned}$$

(22)

where $\mathrm{err}_j$ and $\mathrm{err}_i$ are the smallest and second smallest reconstruction errors, respectively. A decision is then made by the following rule

$$\begin{aligned}&\mathbf{x}\ \text{ is } \text{ rejected } \text{ from } \text{ classification } \text{ if }\ \eta \le \eta _\mathrm{T} \nonumber \\&\mathbf{x}\ \text{ is } \text{ accepted } \text{ for } \text{ classification } \text{ if }\ \eta > \eta _\mathrm{T} \end{aligned}$$

(23)

where $\eta _\mathrm{T}$ is a threshold which can be experimentally decided. We undertook an experiment by varying the threshold $\eta _\mathrm{T}$ from 0.05 to 0.3.

With the rejection option for the hybrid KAA classification system, error rate can be lowered by rejecting some testing vehicle images. In practical applications, user can set a prior high accuracy because potential errors are converted into rejections. The error rate and rejection rate can be defined as

$$\begin{aligned}&\!\!\!\text{ Error } \text{ rate } = \frac{\#~\text{ misrecognized } \text{ instances }}{\#~\text{ testing } \text{ instances }} \end{aligned}$$

(24)

$$\begin{aligned}&\!\!\! \text{ Rejection } \text{ rate } = \frac{\#~\text{ rejected } \text{ instances }}{\#~\text{ testing } \text{ instances }} \end{aligned}$$

(25)

$$\begin{aligned}&\!\!\!\text{ Recognition } \text{ rate } = \frac{\#~\text{ Correctly } \text{ recognized } \text{ instance }}{\#~\text{ testing } \text{ instances }} \end{aligned}$$

(26)

Obviously, error rate can be lowered by increasing the threshold $\eta _\mathrm{T}$ and a larger $\eta _\mathrm{T}$ means a higher rejection rate.

The reliability of a classification system can be defined as the probability of the decision to be correct on a given input object. With the rejection mechanism defined above, reliability can be assessed as the portion of correctly recognized patterns in all the test patterns:

$$\begin{aligned} \hbox {Reliability}=\frac{\mathrm{Recognition rate}}{100~\%-\mathrm{Recognition rate}} \end{aligned}$$

(27)

Such a reliability metric directly suggests that the error rate should be reduced by rejecting suspicious results.

Accordingly, for hybrid KAA classification with reject option, the trade-off between accuracy and the rejection rate can be controlled. The more the system rejects, the better the accuracy. However, with a high rejection rate, some samples that otherwise would have been correctly classified, are rejected. Therefore, a compromise has to be made in practice. The relationship between the error rate and the reject rate is often represented as an error–reject trade-off curve, which can be used to set the desired operating point of the classification system.

5 Experiments

5.1 Vehicle detection

An integrated software toolbox for support vector classification, LIBSVM (http://www.csie.ntu.edu.tw/~cjlin/libsvm/), was exploited for the cascade SVM detection. As both of the dimensionality of HOG feature and the size of training samples are relatively high, we chose the linear kernel to accelerate the calculation.

To demonstrate the superb detection performance of cascade SVM, the single SVM classifier with the same HOG feature was compared without inclusion of the decision fusion stage for both of the methods. As illustrated in the left column in Fig. 11, many no-vehicle objects were generated from the single SVM detector, thus yielding high false detection rate. As a sharp comparison as shown in the right column in Fig. 11, the majority of the those no-vehicle windows will be filtered out by the cascaded SVMs, which means a much higher correct detection rate and lower false detection rate.

Fig. 11

Comparison of the detection results from a single SVM classifier and cascaded SVMs. Left column results were from single SVM. Right column results were from the cascaded SVMs. Both detectors exploited the same HOG feature, without decision fusion

For the cascaded SVMs, the false detection rate is generally decreased with the inclusion of more SVMs. As illustrated in Fig. 12, a total number of 684 traffic surveillance images were used in the experiment for the detection of vehicles using the cascaded SVM. When there is only one SVM, the number of falsely detected windows is 180 per image on average. With one more SVM added, the number of falsely detected windows drops to 50 per image on average. The dependence of the detection performance over the number of stages is clear from Fig. 12. Based on this experiment, we applied 12 SVMs in the final detection experiment to generate the segmented vehicle objects for classification.

Fig. 12

False detection rate versus the number of SVMs in the cascaded SVMs detector

5.2 Feature extraction

After vehicle objects were detected and segmented from original image, appropriate features should be defined for the subsequent classification. Though HOG can still be applied, the relative high dimension makes it less competitive when the trade-off between performance and computational cost has to be taken into account. As geometrical features pertinent to edge are important in the representation of vehicle, another well-known simple feature, Edge Orientation Histogram (EOH) [37, 38], is employed. EOH represents the local edge distribution by dividing image space into $4 \times 4$ sub-images and describing the local distribution of each sub-image by a histogram. More specifically, histograms are created by categorizing edges in all sub-images into five types: vertical, horizontal, diagonal and nondirectional edges, resulting in a total of $5 \times 16 = 80$ histogram bins. Each sub-image can be further divided into nonoverlapping square image blocks with particular size which depends on the image resolution. Each of the image blocks is then classified into one of the five mentioned edge categories or as a nonedge block. For the vehicle images of different types, Fig. 13 demonstrates the extracted EOH features.

Fig. 13

Demonstration of the EOH features extracted from different vehicles

5.3 Vehicle classification

The proposed recognition system was tested on an extensive data set of frontal images (${>}6{,}000$) of a single vehicle detected and segmented from the images captured in a traffic control photographic system, using the cascade SVM detection scheme introduced in Sect. 2. The segmented vehicles are quite different with the manually cropped positive samples used the training of the cascade SVMs. Some of the examples are illustrated in Fig. 14. In addition to the within-class appearance differences, other obvious variations of the detected images include scale, orientation, illumination and remaining background.

Fig. 14

Some of the detected vehicles images (total 6,000) used for the classification experiment. The four rows from top to bottom are cars, buses, vans and light trucks, respectively

The whole training process can be divided into two phases as described in Sect. 3. As the process starts from prototypes generation, the first step of the experiment is to create prototypes via SOM, Neural Gas and k-means for comparison. The number of prototypes for each class is first chosen as 64. For SOM, other parameters are chosen as the default values in the Matlab SOM Toolbox (http://www.cis.hut.fi/somtoolbox/). The learning parameter is varying from 1 to 0.1 dynamically. The decay constant appeared in the interaction function explained in Sect. 3 changes from $s$ to $s/100$, where $s$ is the size of the pre-defined square grid. For the Neural Gas algorithm, the parameter chosen are based on the work of [36, 37]. The learning rate decays from 0.3 to 0.01. The neighborhood size dynamically changes from $0.2\times$ training sample size to 0.01. Finally, the number of training epoch is set to be $40\times$ training sample size.

The training of the kernel auto-associative networks has been elaborated in Sect. 3. During the training process, the value of $\sigma$ in the Gaussian kernel function will be chosen experimentally as the 1/6 time of the centers variance which generated by clustering algorithm.

For all of the experiment, the training set and testing set are randomly split, with 80 % of the patterns for training and 20 % patterns for testing. The results are from the averages of 100 runs. Figure 15 shows the performance of the classifiers based on three clustering algorithms without reject option, respectively, which shows over $91.5~\%$ accuracy from Neural Gas model. The better performance of Neural Gas model over other clustering algorithms including SOM is consistent with our previous studies on handwriting digits recognition [39].

Fig. 15

Comparison of the classification accuracies from the three clustering algorithms exploited in the hybrid model

The subsequent experiments focus on the performance evaluation of the KAA classification scheme taking account of rejection option. A common practice to study a classifier with a rejection option is to perform the comparison for different values of a threshold and then plot the reject-error curve. In the experiment, the threshold for KAA classification ranges from 0 to 0.3. The interplay of classification and rejection can be illustrated by Fig. 16, showing the dependence of error rate on the threshold when SOM, Neural Gas and k-means model are applied, respectively. It is clear that Neural Gas model produces smaller error rate comparing SOM at a given threshold, and a bigger threshold brings smaller error rate.

Fig. 16

The interplay of error rate and the rejection threshold

Rejection avoids some errors, but often has its own cost, e.g., incurring human inspection of the ambiguous examples. When rejection option is activated, the rejection rate should be reported along with error estimates. A complete description of the relationship between the error rate and rejection rate is via error–reject trade-off curve, which can be computed by changing rejection threshold and counting the resulting error. As shown in Fig. 17, the error rate of the KAA classification system reduces when reject option is included, which is due to the fact that the reject option discards those examples whose classification has a high risk. For the Neural Gas model, an error rate (${\sim }4.4~\%$) has been achieved when the rejection rate is about $10~\%$. With a larger rejection rate $20~\%$, the error rates drop to ${<}2.5~\%$ for both of Neural Gas and k-means clustering. Following the same experiment procedures, the relationship between reliability defined in Eq. (26) and reject rate is shown in Fig. 18.

Fig. 17

Error–reject tradeoff curve

Fig. 18

The relationship between reliability defined in Eq. (26) and reject rate

In the hybrid model, size of the prototypes provided by a clustering algorithm is an important factor that influences the system’s performance. Table 1 demonstrates the classification accuracies when the size of prototypes changes, where no rejection has been adopted. It can be observed again that Neural Gas model demonstrates better performance. On the other hand, the performance improvement from increasing the number of prototypes is more obvious when the number is relatively small. When the number is larger than $8\times 8 =64$, no further improvement could be observed.

Table 1 Classification accuracies versus the sizes of prototype provided by three clustering methods (%)

To comprehensively assess the quality of a multiclass classification, the confusion matrix is a significant performance measure. For $C$ classes, a $C \times C$ dimensional confusion matrix evaluates the respective classification errors between classes (off-diagonal), and correct classifications (diagonal elements). Tables 2, 3 and 4 summarize the confusion matrices generated from the hybrid classification system with SOM, Neural Gas and k-means, respectively, without reject option. From the tables, it is obvious that car can be more accurately classified than other three categories, for all of the three clustering algorithms. On the other hand, truck and van seem to be more easily confused with each other due to their overlapping features.

Table 2 Confusion matrix from the hybrid model of SOM–KAA without rejection (%)

Table 3 Confusion matrix from the hybrid model of NG–KAA without rejection (%)

Table 4 Confusion matrix from the hybrid model of k-means–KAA without rejection (%)

With the inclusion of rejection option, the identification rate for individual classes can be calculated from the confusion matrix, as shown in Figs. 19, 20 and 21. Among the four classes, it is evident that car always has the highest identification rates from different clustering methods. In contrast, van and truck show much lower identification rates. However, with the introduction of rejection, all of the four classes will increase the identification rates.

Fig. 19

The identification rate from the hybrid model of SOM–KAA

Fig. 20

The identification rate from the hybrid model of k-means–KAA

Fig. 21

The identification rate from the hybrid model of NG–KAA

6 Conclusions

Vision-based automatic vehicle classification (AVC) is still a big challenge in traffic surveillance. A practical system is studied in this paper, which includes vehicle detection and vehicle classification. An example-based algorithm for vehicle detection was proposed based on cascade SVMs with the HOG features. To implement vehicle classification, a hybrid model composed of clustering and kernel auto-associator (KAA) was investigated. As a generalization of auto-associative networks, KAA offers an effective one-class classification strategy with rejection option to avoid errors on ambiguous inputs. The important issue of KAA, namely, the creation of kernel matrix was emphasized. Three commonly used clustering methods were applied and compared to generate prototypes. Experimental results using more than 6,000 detected vehicle images from four types of vehicles (bus, light truck, car and van) demonstrated the effectiveness of the hybrid model. The proposed scheme offers a performance of accuracy of $95.6~\%$ with a rejection rate $10~\%$ when the Neural Gas model was used for the creation of prototypes. This exhibits promising potentials for real-world applications.