1 Introduction

The cooperative control of multi-agent systems (MASs) has received much attention in the last decade [20, 42, 52]. It has extensive applications in many fields, such as unmanned air vehicles [35], autonomous systems [40] and distributed sensor networks [25]. For the MASs, researchers mainly study the consensus issues, which can be divided into leaderless consensus and leader-follower consensus [49]. Researchers are especially interested in how to coordinate group behavior arising in the MASs, and many meaningful results have been obtained in [8, 11, 18, 34, 38]. The consensus problem of continuous-time MASs with discontinuous information transmission was studied in [38]. Consensus protocol was designed in [11] for a group of agents with quantized communication links and limited data rate. In [18], the consensus problem in continuous-time MASs with switching topology and time-varying delays was considered. In [34], an adaptive control method was studied to realize the cooperative tracking of uncertain MASs.

It is well known that system faults in a dynamic system can take many forms, such as actuator faults and sensor faults. The actuator plays a crucial role in the cooperative tracking problem of MASs [28]. If it undergoes certain failures, it can cause unsatisfactory performance and lead to catastrophic accidents. Hence, many results have solved the problem of actuator faults to increase security and reliability of systems, and a series of meaningful results have been presented. The problem of observer-based adaptive fuzzy fault-tolerant optimal control for SISO nonlinear systems was considered in [15]. The problem of fault detection for fuzzy semi-Markov jump systems based on interval type-2 fuzzy approach was studied in [43]. The problem of flight tracking control against actuator faults based on linear matrix inequality method and adaptive control method was proposed in [3]. The adaptive fuzzy fault-tolerant control method with error constrain was presented in [13] to solve the problem of fault for non-triangular structure nonlinear systems. The active fault-tolerant control problem was studied in [26] for nonidentical high-order MASs with the network disconnections.

On the other hand, the control direction is usually unknown for the control design in many application requirements [2, 30, 37]. Many controllers have been designed for MASs with unknown control direction in the past few years. In most of the existing works, the controller design relys on the information of control direction of each agent. Nussbaum in [27] presented an efficient method to deal with the problem of unknown control direction. The adaptive consensus problem of MASs with unknown identical control directions was studied in [1]. The problem of neural control with unknown control directions was studied for uncertain non-affine nonlinear MASs in [29]. In [36], the consensus problem was solved for uncertain nonlinear MASs with unknown control directions. For time-varying delay systems in [12], an output-feedback adaptive neural network control method was presented to overcome the problem of unknown control directions.

Motivated by the aforementioned discussions, the output-constrained control problem is considered in this paper. First, the error-transformation method is presented to keep initial connectivity patterns in the non-affine MASs. Secondly, the agent state transformation technique is proposed to convert the original MASs to an unconstrained one, where the outputs do not have any restrictions. The Nussbaum function is introduced to overcome partially unknown control direction problem. Further, the fault-tolerant tracking controller is presented to compensate the effects of actuator faults and dead zones. Finally, simulation results demonstrate the effectiveness of the proposed control strategy. Compared with some existing results, the contributions are summarized as follows

  1. 1.

    An error transformation method is presented to preserve initial connectivity patterns of non-affine MASs by using nonlinear error transformation surfaces.

  2. 2.

    Compared with the results in [7, 16, 44], the controller designed in this paper can solve the unknown dead-zone and actuator faults problems simultaneously.

  3. 3.

    Unlike the existing results [17, 24, 50], an output-constrained control algorithm is presented for non-affine MASs. The actuator faults, unknown control directions and unknown dead-zones are considered in this paper. The designed control algorithm can guarantee system stability and ensure that the output constraint cannot be violated during operation.

The remaining of the paper is arranged below. In Sect. 2, some preliminaries are presented. The controller is designed and the stability analysis is described in Sect. 3. The numerical simulation is provided in Sect. 4, and the conclusion is shown in Sect. 5.

2 Preliminaries

2.1 Basic Graph Theory

By regarding the followers and the leaders as nodes, the directed graph is denoted by a directed graph \(\zeta =({\mathcal {V}},{\mathcal {E}},{\mathcal {A}}),\) where \({\mathcal {V}}=\left\{ v_{1},v_{2},...,v_{N}\right\} \), the edge set \( \mathcal {E\subseteq V\times V}\) and the adjacency matrix \(\mathcal {A=}\left[ a_{ij}\right] \in {\mathbb {R}}^{N\times N}\). \(a_{i,j}>0,\) if \( (i,j)\in {\mathcal {E}},\) and \(a_{i,j}=0\) otherwise. For node i and node j, if node i can receive the information sending from node j, then \( (i,j)\in {\mathcal {E}},\) and node j is called a neighbors of node i. The interaction relationships among the leader and followers are noted by matrix \({\mathbb {B}}=\hbox {diag}\left[ b_{1},...,b_{n}\right] \). The Laplacian matrix is defined as \({\mathcal {L}}=D-{\mathcal {A}}\), where \(L=\left[ l_{ij} \right] \in {\mathbb {R}}^{N\times N}\) is defined as \(l_{ii}=\mathop {\sum }\limits _{i\ne j}^{{\varvec{N}}}a_{i,j}\) and \(l_{ij}=-a_{ij},\) \(i\ne j.\) \(D= \hbox {diag}\{d_{1},\ldots ,d_{N}\}\) is diagonal matrix,  and the in-degree is defined as \(d_{{i}}=\mathop {\sum }\limits _{j=1,j\ne i}^{N}a_{ {i},j}.\) The node i is called the neighbor of node j when the edge (j, i) exists. The more details can be found in [9] and references therein.

2.2 Problem Formulation

The system model of the ith agent is

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}_{i,l}&=x_{i,l+1}\text {, }l=1,...,n-1 \\ {\dot{x}}_{i,n}&=f_{i}(x_{i},{\normalsize \kappa }_{i}(u_{i},t))+\omega _{i}(t) \\ y_{i}&=x_{i,1} \end{aligned} \right. \end{aligned}$$
(1)

where \(x_{i,l}\in {\mathbb {R}} \), \(u_{i}\in {\mathbb {R}} \) are the state and control input, respectively, \(f_{i}(\cdot )\) is an unknown function, and \(\kappa _{i}(\cdot )\) is the actuator input–output characteristic.

Assumption 1

Functions \(\frac{\partial f_{i}(x_{i},{\normalsize \kappa }_{i})}{\partial {\normalsize \kappa }_{i}},i=1,2,...,n\) are bounded, and \(0<f_{\min }\le \left| \frac{\partial f_{i}(x_{i},{\normalsize \kappa }_{i})}{\partial {\normalsize \kappa }_{i}}\right| \le f_{\max }\).

Assumption 2

\(\omega _{i}(t)\) is an unknown modeling error and \(\left| \omega _{i}(t)\right| \le \omega _{iM}\), where \(\omega _{iM}\) is an unknown positive constant.

Assumption 3

The function \({\normalsize \kappa }_{i}(u_{i},t)=\sigma _{i}(t)u_{i}+\mu _{i}(t)\) is a nonlinearity model, where the time-varying function is \(\sigma _{i}(t)\) \(\in \left[ \sigma _{\min },\sigma _{\max }\right] \), and \( \left| \mu _{i}(t)\right| \le \mu _{iM}\), \(\sigma _{\min }\), \( \sigma _{\max }\) and \(\mu _{iM}\) are unknown positive constants, \( i=1,2,...,n.\)

Remark 1

Similar to [6], it is assumed that some agents’ control directions \(\frac{\partial f_{i}(x_{i},{\normalsize \kappa }_{i})}{\partial {\normalsize \kappa }_{i}}\) are unknown but identical in this paper.

Remark 2

Assumptions 1–3 are introduced from [6]. Based on these assumptions and the mean value theorem [4], we can get a new dynamic model.

The RBF NNs are utilized to the approximate unknown functions, where \( f_{i}(x_{i},0)=W_{i}^{T}S_{i}\left( x_{i}\right) ,\) and the dynamic model can be described by

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}_{i,l}&=x_{i,l+1} \\ {\dot{x}}_{i,n}&=W_{i}^{T}S_{i}\left( x_{i}\right) +g_{i}(t)u_{i}+h_{i}(t) \\ y_{i}&=x_{{i},1} \end{aligned} \right. \end{aligned}$$
(2)

where

$$\begin{aligned} g_{i}(t)= & {} \left. \frac{\partial f_{i}(x_{i},\kappa _{i})}{\partial \kappa _{i}}\right| _{\kappa _{i}=\kappa _{i}^{0}}\sigma _{i}(t) \nonumber \\ h_{i}(t)= & {} \left. \frac{\partial f_{i}(x_{i},\kappa _{i})}{\partial \kappa _{i}}\right| _{\kappa _{i}=\kappa _{i}^{0}}\mu _{i}(t)+\omega _{i}(t) \end{aligned}$$
(3)

with \(\kappa _{i}^{0}=\varsigma _{i}\kappa _{i},0<\varsigma _{i}<1.\) Hence, it can be verified that \(0<g_{\min }\le \left| g_{i}(t)\right| \le g_{\max }\) and \(\left| h_{i}(t)\right| \le h_{iM}\) with \( g_{\min }=f_{\min }\sigma _{\min },g_{\max }=f_{\max }\sigma _{\max },\) and \( h_{iM}=f_{\max }\mu _{iM}+\omega _{iM}.\)

The state constraint interval is given as follows

$$\begin{aligned} {\underline{x}}(t)<x_{i,1}<{\bar{x}}(t), i=1,2,...,n \end{aligned}$$
(4)

where \({\underline{x}}(t)\) and \({\bar{x}}(t)\) are boundary functions.

2.3 Nussbaum Gain Technique

The Nussbaum-type function \(N(\cdot )\) satisfies the following properties

$$\begin{aligned} \left\{ \begin{array}{c} \mathop {\lim }\limits _{R\rightarrow +\infty }\sup \frac{1}{R}\int _{0}^{R}N(\Pi )d\Pi =+\infty \\ \mathop {\lim }\limits _{R\rightarrow +\infty }\inf \frac{1}{R}\int _{0}^{R}N(\Pi )d\Pi =-\infty \end{array} \right. \end{aligned}$$
(5)

The Nussbaum functions are commonly chosen as \(\Pi ^{2}\cos (\Pi ),\) \(\Pi ^{2}\sin (\Pi )\) and \(-j\exp (\Pi ^{2}\big / 2 )(\Pi ^{2}+2),\) where \( \Pi \) is a real variable, and j is a positive constant.

Lemma 1

[27] V(t) and \(\Pi (t)\) are defined on \( \left[ 0,t_{\chi }\right) \). If there exist continuously differentiable functions \(\vartheta _{i}(t),\) one has

$$\begin{aligned} V(t)\le \int _{0}^{t}\mathop {\sum }\limits _{i=1}^{N}(g_{i}(\chi )N(\vartheta _{i}(\chi ))+\beta _{i}^{-1}){\dot{\vartheta }}_{i}(\chi )d\chi +\varphi \end{aligned}$$
(6)

where \({\dot{\vartheta }}_{i}(t),\) V(t),  and \(\int _{0}^{t}\mathop {\sum }\limits _{j=1}^{N}(g_{i}(\chi )N(\vartheta _{i}(\chi ))+\beta _{i}^{-1}) {\dot{\vartheta }}_{i}(\chi )d\chi \) are bounded on \(\left[ 0,t_{\chi }\right) ,\) and \(\varphi \) is a constant.

2.4 Agent State Transformation

In this paper, according to the literature [6], the agent state transformation technique is described as

$$\begin{aligned} z_{i,1}=M(x_{i,1},{\underline{x}},{\bar{x}}), i=1,2,...,n \end{aligned}$$
(7)

where \(M(\cdot )\) is an increasing function, and

$$\begin{aligned} \left\{ \begin{aligned} \lim _{x_{i,1}\rightarrow {\bar{x}}}z_{i,1}&=+\infty \\ \lim _{x_{i,1}\rightarrow {\underline{x}}+}z_{i,1}&=-\infty \end{aligned} \right. \end{aligned}$$
(8)

Next, define \(Y_{i,l}=[x_{i,1},\) \(x_{i,2},...,x_{i,l},\) \({\underline{x}},\) \( \underline{{\dot{x}}},...,{\underline{x}}^{(l)},\) \({\bar{x}},\) \(\dot{{\bar{x}}},... {\bar{x}}^{(l)}]^{T},\) \(l=1,2,...,m.\)

The derivative of \(z_{i,1}\) is

$$\begin{aligned} {\dot{z}}_{i,1}=H_{i,1}(Y_{i,1})+q_{i}{\dot{x}} _{i,1}=H_{i,1}(Y_{i,1})+q_{i}x_{i,2}\triangleq z_{i,2} \end{aligned}$$
(9)

where \(q_{i}=\frac{\partial z_{i,1}}{\partial x_{i,1}}\) and

$$\begin{aligned} H_{i,1}=\frac{\partial z_{i,1}}{\partial {\underline{x}}}\underline{{\dot{x}}}+ \frac{\partial z_{i,1}}{\partial {\bar{x}}}\dot{{\bar{x}}} \end{aligned}$$
(10)

for \(i=1,2,...,n.\)

Then, differentiating \(z_{i,2}\), it gives

$$\begin{aligned} {\dot{z}}_{i,2}=H_{i,2}(Y_{i,2})+q_{i}{\dot{x}} _{i,2}=H_{i,2}(Y_{i,2})+q_{i}x_{i,3}\triangleq z_{i,3} \end{aligned}$$
(11)

where

$$\begin{aligned} H_{i,2}=\frac{\partial H_{i,1}}{\partial Y_{i,1}}{\dot{Y}}_{i,1}+\left( \frac{ \partial q_{i}}{\partial x}\underline{{\dot{x}}}+\frac{\partial q_{i}}{ \partial x}\dot{{\bar{x}}}+\frac{\partial q_{i}}{\partial x_{i,1}} x_{i,2}\right) x_{i,2} \end{aligned}$$
(12)

Similarity, we have

$$\begin{aligned} {\dot{z}}_{i,p}=H_{i,p}(Y_{i,p})+q_{i}{\dot{x}} _{i,p}=H_{i,p}(Y_{i,p})+q_{i}x_{i,p+1}\triangleq z_{i,p+1} \end{aligned}$$
(13)

and

$$\begin{aligned} H_{i,p}=\frac{\partial H_{i,p-1}}{\partial Y_{i,p-1}}{\dot{Y}}_{i,p-1}+\left( \frac{ \partial q_{i}}{\partial x}\underline{{\dot{x}}}+\frac{\partial q_{i}}{ \partial x}\dot{{\bar{x}}}+\frac{\partial q_{i}}{\partial x_{i,1}} x_{i,2}\right) x_{i,p} \end{aligned}$$
(14)

Finally, differentiating \(z_{i,n}\) yields

$$\begin{aligned} {\dot{z}}_{i,n}= & {} H_{i,n}(Y_{i,n})+q_{i}{\dot{x}}_{i,n}\nonumber \\= & {} H_{i,n}(Y_{i,n})+q_{i}(W_{i}^{T}S_{i}\left( x_{i}\right) +g_{i}(t)u_{i}+h_{i}(t)) \end{aligned}$$
(15)

Then, the resulting system is given as follows

$$\begin{aligned} \left\{ \begin{aligned} {\dot{z}}_{i,l}&=z_{i,l+1} \\ {\dot{z}}_{i,n}&=H_{i,n}(Y_{i,n})+q_{i}(W_{i}^{T}S_{i}\left( x_{i}\right) +g_{i}(t)u_{i}+h_{i}(t)) \\ y_{i}&=z_{i,1} \end{aligned} \right. \end{aligned}$$
(16)

The actuator fault model is

$$\begin{aligned} u_{i,j}^{F}(t)= & {} k_{i,j,o}u_{i,j}(t)+{\bar{u}}_{i,j,o}(t),t\in [t_{i,j,o}^{s},t_{i,j,o}^{e}]\nonumber \\&\kappa _{i,j,h}{\bar{u}}_{i,j,o}(t)=0 \end{aligned}$$
(17)

where \(k_{i,j,o}\in [0,1],\) \(t_{i,j,o}^{s},\) \(t_{i,j,o}^{e}\) are unknown constants. \({\bar{u}}_{i,j,o}(t)\) is an unknown fault, where \( j=o=1,2,...,m,\) and \(0\le t_{i,j,1}^{s}\le t_{i,j,1}^{e}\le t_{i,j,2}^{s}\le t_{i,j,2}^{e}\le ...\le +\infty .\)

We define

$$\begin{aligned} \kappa _{i,j}(t)= & {} \left\{ \begin{array}{l} \kappa _{i,j,o} \\ 1 \end{array} \right. \begin{array}{l} \text {if }t\in [t_{i,j,o}^{s},t_{i,j,o}^{e}] \\ \text {if }t\in [t_{i,j,h}^{e},t_{i,j,o+1}^{s}] \end{array}\nonumber \\ {\bar{u}}_{i,j}(t)= & {} \left\{ \begin{array}{l} {\bar{u}}_{i,j,o}(t) \\ 0 \end{array} \right. \begin{array}{l} \text {if }t\in [t_{i,j,o}^{s},t_{i,j,o}^{e}] \\ \text {if }t\in [t_{i,j,h}^{e},t_{i,j,o+1}^{s}] \end{array} \end{aligned}$$
(18)

The actuator failures can be expressed as

$$\begin{aligned} u_{i,j}^{F}(t)=\kappa _{i,j,o}u_{i,j}(t)+{\bar{u}}_{i,j,o}(t) \end{aligned}$$
(19)

Assumption 4

The \({\bar{u}}_{i,j}\) is an unknown positive constant and satisfies \(\left| {\bar{u}} _{i,j}(t)\right| \le {\bar{u}}_{i,j}.\)

In this paper, the dead zone is defined as

$$\begin{aligned} \begin{array}{l} u_{i,j}(t)=D(\Lambda _{i,j}(t)) \\ \triangleq \left\{ \begin{array}{l} m_{i,j,p}(\Lambda _{i,j}(t)-o_{i,j,p}), \\ 0, \\ m_{i,j,l}(\Lambda _{i,j}(t)+o_{i,j,l}), \end{array} \right. \begin{array}{l} \Lambda _{i,j}(t)\ge o_{i,j,p} \\ -o_{i,j,l}<\Lambda _{i,j}(t)<o_{i,j,p} \\ \Lambda _{i,j}(t)\le -o_{i,j,l} \end{array} \end{array} \end{aligned}$$
(20)

where \(D(\Lambda _{i,j})\) is the dead zone actuator input. The unknown constants \(m_{i,j,r},\) \(o_{i,j,r},\) \(m_{i,j,l}\) and \(o_{i,j,l}\) are positive.

The dead zone is given as follows

$$\begin{aligned} u_{i,j}(t)=m_{i,j}(t)\Lambda _{i,j}(t)+\xi _{i,j}(t) \end{aligned}$$
(21)

where

$$\begin{aligned} m_{i,j}(t)=\left\{ \begin{array}{c} m_{i,j,p,} \\ m_{i,j,l}, \end{array} \right. \begin{array}{l} \Lambda _{i,j}(t)\ge 0 \\ \Lambda _{i,j}(t)\le 0 \end{array} \end{aligned}$$
(22)

and

$$\begin{aligned} \xi _{i,j}(t)=\left\{ \begin{array}{l} -m_{i,j,p}o_{i,j,p}, \\ -m_{i,j}(t)v_{i,j}(t), \\ m_{i,j,l}o_{i,j,l}, \end{array} \right. \begin{array}{l} \Lambda _{i,j}(t)\ge o_{i,j,p} \\ -o_{i,j,l}<\Lambda _{i,j}(t)<o_{i,j,p} \\ \Lambda _{i,j}(t)\le -o_{i,j,l} \end{array} \end{aligned}$$
(23)

From (23), we have

$$\begin{aligned} \left| \xi _{i,j}(t)\right|\le & {} {\bar{\xi }}_{i,j}(t) \nonumber \\ {\bar{\xi }}_{i,j}(t)= & {} \max \{m_{i,j,p}o_{i,j,p},m_{i,j,l}o_{i,j,l}\} \end{aligned}$$
(24)

Then, it follows that

$$\begin{aligned} \left\{ \begin{aligned} {\dot{z}}_{i,k}&=z_{i,k+1} \\ {\dot{z}}_{i,n}&=H_{i,n}(Y_{i,n})+q_{i}W_{i}^{T}S_{i}\left( x_{i}\right) +q_{i}g_{i}(t)\kappa _{i,j}m_{i,j}(t)\Lambda _{i,j}(t) \\&\quad +q_{i}g_{i}(t)\kappa _{i,j}\xi _{i,j}(t)+q_{i}g_{i}(t){\bar{u}} _{i,j}+q_{i}h_{i}(t) \\ y_{i}&=z_{i,1} \end{aligned} \right. \end{aligned}$$
(25)

2.5 Radial Basis Function Neural Networks

The RBF NNs will be utilized to estimate nonlinear functions with the following form

$$\begin{aligned} g\left( {\mathbb {Z}}\right) =W^{*T}S\left( {\mathbb {Z}}\right) +\digamma \left( {\mathbb {Z}}\right) ,\forall {\mathbb {Z}}\in \Omega _{{\mathbb {Z}}}\subset {\mathbb {R}}^{m},\text { }\left| \digamma \left( {\mathbb {Z}}\right) \right| \le \varepsilon \end{aligned}$$
(26)

where \(\digamma \left( {\mathbb {Z}}\right) \) is the approximation error, \( S\left( {\mathbb {Z}}\right) =\left[ S_{1}\left( {\mathbb {Z}}\right) ,S_{2}\left( {\mathbb {Z}}\right) ,...,S_{K}\left( {\mathbb {Z}}\right) \right] ^{T}\) is the basis function vector, and \(k>1\). \(S_{i}\left( {\mathbb {Z}}\right) \) denotes the Gaussian basis function as follows

$$\begin{aligned} S_{i}\left( {\mathbb {Z}}\right) =\exp \left[ -\frac{\left( {\mathbb {Z}}-\iota _{i}\right) ^{T}\left( {\mathbb {Z}}-\iota _{i}\right) }{M_{i}^{2}}\right] \end{aligned}$$
(27)

where \(\iota _{i}=\left[ \iota _{i1},\iota _{i2},\ldots ,\iota _{iq}\right] ^{T}\) is the center vector, and \(M_{i}\) is the width of the Gaussian function.

The ideal weight matrix \(W^{*}\) is designed as

$$\begin{aligned} W^{*}=\arg \mathop {\min }\limits _{W\in {\mathbb {R}}^{k}}\left\{ \mathop {\sup }\limits _{{\mathbb {Z}}\in \Omega }\left| g\left( {\mathbb {Z}}\right) -W^{T}S\left( {\mathbb {Z}}\right) \right| \right\} \end{aligned}$$
(28)

where \(W\in {\mathbb {R}}^{k}\).

Lemma 2

[31] Choose \(S\left( {\bar{x}}_{c}\right) = \left[ S_{1}\left( {\bar{x}}_{c}\right) ,S_{2}\left( {\bar{x}}_{c}\right) ,\ldots ,S_{k}\left( {\bar{x}}_{c}\right) \right] ^{T}\), where\(\ {\bar{x}}_{c}= \left[ x_{1},\ldots ,x_{c}\right] ^{T}\) is the RBF NNs basis function vector. For any positive integer, the following inequality can be obtained

$$\begin{aligned} \left\| S\left( {\bar{x}}_{c}\right) \right\| ^{2}\le \left\| S\left( {\bar{x}}_{p}\right) \right\| ^{2} \end{aligned}$$
(29)

where \(c\le p\).

3 Control Law Design and Stability Analysis

Based on dynamic surface control technology [32, 41], the new nonlinear error transformation surfaces \(s_{i,1}\) and \(s_{i,k}\) are presented as follows

$$\begin{aligned} \begin{aligned} s_{i,1}&=\mathop {\sum }\limits _{j=1}^{N}a_{i,j}\ln \left( \frac{1+e_{i,j} }{1-e_{i,j}}\right) +b_{i}\ln \left( \frac{1+e_{i,0}}{1-e_{i,0}}\right) \\ s_{i,k}&=z_{i,k}-{\bar{\alpha }}_{i,k} \\ L_{i,k}&={\bar{\alpha }}_{i,k}-\alpha _{i,k} \end{aligned} \end{aligned}$$
(30)

where \(k=2,...,N\) and \(i=1,...,N\). \(e_{i,j}=\frac{(z_{i}-z_{j})}{R},\) \( e_{i,0}=\frac{(z_{i}-y_{0})}{R},\) and \(L_{i,k\text { }}\) is the boundary layer error. \(a_{i,j}\) is the weighting parameter described as

$$\begin{aligned} a_{i,j}= & {} \left\{ \begin{array}{c} {\bar{a}}_{i,j}, \\ 0, \end{array} \right. \begin{array}{l} \left| y_{i}(0)-y_{j}(0)\right|<R \\ \hbox {otherwise} \end{array} \nonumber \\ {\bar{a}}_{i,j}= & {} \left\{ \begin{array}{c} R, \\ 0, \end{array} \right. \begin{array}{l} \left| y_{i}-y_{j}\right| <R \\ \hbox {otherwise} \end{array} \end{aligned}$$
(31)

and \(a_{ii}=0.\) \(b_{i}\) is defined as

$$\begin{aligned} \ b_{i}= & {} \left\{ \begin{array}{c} {\bar{b}}_{i}, \\ 0, \end{array} \right. \begin{array}{l} \left| y_{i}(0)-y_{j}(0)\right|<R \\ \hbox {otherwise} \end{array} \nonumber \\ {\bar{b}}_{i}= & {} \left\{ \begin{array}{c} R, \\ 0, \end{array} \right. \begin{array}{l} \left| y_{i}-y_{0}\right| <R \\ \hbox {otherwise} \end{array} \end{aligned}$$
(32)

and \(\tau _{i,k}\dot{{\bar{\alpha }}}_{i,k}+{\bar{\alpha }}_{i,k}=\alpha _{i,k},\) where \(\tau _{i,k}>0\) and \({\bar{\alpha }}_{i,k}(0)=\alpha _{i,k}(0).\) \({\bar{\alpha }}_{i,k}\) are the signals obtained by the first-order filters.

Theorem 1

For the MASs (25) with dead zones, actuator faults and unknown control directions, under Assumptions 1–3, the virtual control signals, the adaptive laws and the actual controller, all the signals in the closed-loop system are cooperatively semi-globally ultimately bounded (CSGUUB). The agent outputs remain within the time-varying constraints for all time.

By using the consensus error \(e_{i,j}=\frac{(y_{i}-y_{j})}{R}\), one has

$$\begin{aligned} {\dot{e}}_{i,j}= & {} \frac{(s_{i,2}+L_{i,2}+\alpha _{i,2}-z_{j,2})}{R} \end{aligned}$$
(33)
$$\begin{aligned} {\dot{e}}_{i,0}= & {} \frac{(s_{i,2}+L_{i,2}+\alpha _{i,2}-{\dot{y}}_{0})}{R} \nonumber \\ {\dot{s}}_{i,k}= & {} s_{i,k+1}+L_{i,k+1}+\alpha _{i,k+1}-\dot{{\bar{\alpha }}}_{i,k} \nonumber \\ {\dot{s}}_{i,n}= & {} {\dot{z}}_{i,n}-\dot{{\bar{\alpha }}}_{i,n} \end{aligned}$$
(34)

where \(k=2,...,n-1.\)

Step 1 For \(k=1\), the derivative of \(s_{{i},1}\) is given as follows

$$\begin{aligned} {\dot{s}}_{i,1}=(\phi _{i}+\psi _{i})({\dot{y}}_{i})-\phi _{i}{\dot{y}}_{j}-\psi _{i}{\dot{y}}_{0} \end{aligned}$$
(35)

where \(\phi _{i}=\mathop {\sum }\limits _{j=1}^{N}a_{i,j}\frac{2}{R(1-e_{ {i},j}^{2})}\) and \(\psi _{i}=b_{i}\frac{2}{R(1-e_{i,0}^{2})}\) are bounded parameters.

We consider the following Lyapunov candidate function

$$\begin{aligned} V_{i,1}=\frac{1}{2}s_{i,1}^{2}+\frac{1}{\gamma _{i,1}}{\tilde{W}}_{i,1}^{T} {\tilde{W}}_{i,1}+\frac{1}{\Gamma _{i,1}}{\tilde{\theta }}_{i,1}^{T}{\tilde{\theta }} _{i,1} \end{aligned}$$
(36)

where \(m_{i,1}\), \(\gamma _{i,1}\), and \(\Gamma _{i,1}\) are positive designed constants.

Differentiating \(V_{i,1}\), one has

$$\begin{aligned} {\dot{V}}_{i,1}= & {} s_{i,1}{\dot{s}}_{i,1}-{\tilde{W}}_{i,1}r_{i,1}^{-1}\dot{{\hat{W}} }_{i,1}-{\tilde{\theta }}_{i,1}^{T}\Gamma _{i,1}^{-1}\dot{\hat{\theta }}_{ {i},1} \\= & {} s_{i,1}[\phi _{i}{\dot{y}}_{i}+\psi _{i}{\dot{y}}_{i}-\phi _{i}{\dot{y}} _{j}-\psi _{i}{\dot{y}}_{0}] \\&-{\tilde{\theta }}_{i,1}^{T}\Gamma _{i,1}^{-1}\dot{\hat{\theta }}_{{ i},1}-{\tilde{W}}_{i,1}r_{i,1}^{-1}\dot{{\hat{W}}}_{i,1} \\= & {} s_{i,1}[(\phi _{i}+\psi _{i})({\dot{y}}_{i})-\phi _{i}{\dot{y}}_{j}-\psi _{i} {\dot{y}}_{0}] \\&-{\tilde{\theta }}_{i,1}^{T}\Gamma _{i,1}^{-1}\dot{\hat{\theta }}_{{ i},1}-{\tilde{W}}_{i,1}r_{i,1}^{-1}\dot{{\hat{W}}}_{i,1} \\= & {} s_{i,1}[(\phi _{i}+\psi _{i})(s_{i,2}+L_{i,2}+\alpha _{i,2}) \\&+P_{i,1}(\alpha _{i,1})]-(\phi _{i}+\psi _{i})^{2}s_{i,1}^{2}\\&-{\tilde{\theta }}_{i,1}^{T}\Gamma _{i,1}^{-1}\dot{\hat{\theta }}_{i,1}-\tilde{ W}_{i,1}r_{i,1}^{-1}\dot{{\hat{W}}}_{i,1} \end{aligned}$$

where \(\hat{\theta }_{i,j}\) is the estimation of \(\theta _{i,j}^{*}\) with \({\tilde{\theta }}_{i,j}=\theta _{i,j}^{*}-\hat{\theta }_{i,j}\). \({\hat{W}}_{i,{j}}\) is the estimation of \(W_{i,j}\) with \( {\tilde{W}}_{i,j}=W_{i,j}^{*}-{\hat{W}}_{i,j},\) \(i=j=1,\ldots ,N\). The unknown nonlinear function \(P_{i,1}\left( \alpha _{i,1}\right) \) is given as follows

$$\begin{aligned} P_{i,1}\left( \alpha _{i,1}\right) =-\phi _{i}x_{j,2}-\psi _{i}{\dot{y}} _{0}+(\phi _{i}+\psi _{i})^{2}s_{i,1}^{2} \end{aligned}$$

where \(\alpha _{i,1}=\left[ z_{i,1},s_{i,1},\mathop {\sum }\limits _{j=1}^{N} a_{i,j}x_{j,1},\mathop {\sum }\limits _{j=1}^{N} a_{i,j}x_{j,2},b_{i}e_{i,0},b_{i}{\dot{y}}_{0}\right] ^{T}.\)

Construct the virtual variable \(\alpha _{i,2}\) as follows

$$\begin{aligned} \alpha _{i,2}= & {} \frac{1}{\phi _{i}+\psi _{i}}\left[ -\varrho _{i,1}s_{i,1}- {\hat{P}}_{i,1}(\alpha _{i,1}\left| {\hat{W}}_{i,1}\right. )\right] \nonumber \\&-\frac{1}{\phi _{i}+\psi _{i}}\hat{\theta }_{i,1}\tanh \left( \frac{s_{i,1}}{ \epsilon _{i,1}}\right) \end{aligned}$$
(37)

and the property \(0\le \left| s_{i,1}\right| -s_{i,1}\tanh (\frac{ s_{i,1}}{\epsilon _{i,1}})\le 0.2785\epsilon _{i,1}\) is used.

The adaptive laws \(\hat{\theta }_{i,1}\) and \({\hat{W}}_{i,1}\) are defined as

$$\begin{aligned} \dot{\hat{\theta }}_{i,1}= & {} \Gamma _{i,1}s_{i,1}\tanh \left( \frac{s_{i,1}}{\epsilon _{i,1}}\right) -\Gamma _{i,1}\xi _{i,1}\hat{\theta }_{i,1} \end{aligned}$$
(38)
$$\begin{aligned} \dot{{\hat{W}}}_{i,1}= & {} \gamma _{i,1}\Theta _{i,1}s_{i,1}-\gamma _{i,1}\sigma _{i,1}{\hat{W}}_{i,1} \end{aligned}$$
(39)

where \(\Gamma _{i,1}>0\) and \(\gamma _{i,1}>0\) are tuning gains, \(\xi _{i,1}>0 \) and \(\sigma _{{i},1}>0\) are constants, and \(\Theta _{i,1}=\frac{\partial {\hat{P}}_{i,1}(\alpha _{i,1})}{\partial {\hat{W}}_{i,1}}\). Substituting (37)–(39) into (36), it gives

$$\begin{aligned} {\dot{V}}_{i,1}\le & {} -\varrho _{i,1}s_{i,1}^{2}+(\phi _{i}+\psi _{i})s_{i,1}(s_{i,2}+L_{i,2}) \nonumber \\&-\,(\phi _{i}+\psi _{i})^{2}s_{i,1}^{2}+{\tilde{\theta }}_{i,1}\left( s_{i,1}\tanh \left( \frac{s_{i,1}}{\epsilon _{i,1}}\right) \right. \nonumber \\&-\,\left. \frac{\dot{\hat{\theta }}_{i,1}}{\Gamma _{i,1}}\right) +{\tilde{W}} _{i,1}^{T}\left( \Theta _{i,1}s_{i,1}-\frac{{\hat{W}}_{i,1}}{\gamma _{i,1}}\right) \nonumber \\&+\,0.2785\epsilon _{i,1}{\bar{\theta }}_{i,1} \nonumber \\\le & {} -\varrho _{i,1}s_{i,1}^{2}+(\phi _{i}+\psi _{i})s_{i,1}(s_{i,2}+L_{i,2}) \nonumber \\&+\,\xi _{i,1}{\tilde{\theta }}_{i,1}\hat{\theta }_{i,1}-(\phi _{i}+\psi _{i})^{2}s_{i,1}^{2} \nonumber \\&+\sigma _{i,1}{\tilde{W}}_{i,1}^{T}{\hat{W}}_{i,1}+0.2785\epsilon _{i,1}\bar{ \theta }_{i,1} \end{aligned}$$
(40)

where \(\varrho _{i,1}>0\) and \(\epsilon _{i,1}>0\).

Step k The derivative of \(s_{i,k}\) is given as follows

$$\begin{aligned} {\dot{s}}_{{i},k}=s_{i,k+1}+L_{i,k+1}+\alpha _{i,k+1}-{\bar{\alpha }} _{i,k} \end{aligned}$$
(41)

Define

$$\begin{aligned} V_{i,k}=V_{i,k-1}+\frac{1}{2}s_{i,k}^{2}+\frac{1}{\gamma _{i,k}}{\tilde{W}} _{i,k}^{T}{\tilde{W}}_{i,k}+\frac{1}{\Gamma _{{i},k}}{\tilde{\theta }} _{{i},k}^{T}{\tilde{\theta }}_{{i},k} \end{aligned}$$
(42)

\(V_{{i},k}\) is derived as

$$\begin{aligned} {\dot{V}}_{i,k}= & {} {\dot{V}}_{i,k-1}+s_{i,k}{\dot{s}}_{i,k}-{\tilde{\theta }}_{ {i},k}^{T}\Gamma _{{i},k}^{-1}\dot{\hat{\theta }}_{ {i},k}-{\tilde{W}}_{i,k}r_{i,k}^{-1}\dot{{\hat{W}}}_{i,k} \nonumber \\= & {} s_{i,k}(s_{i,k+1}+L_{i,k+1}+\alpha _{i,k+1}-{\bar{\alpha }}_{i,k}) \nonumber \\&-{\tilde{\theta }}_{i,k}^{T}\Gamma _{i,k}^{-1}\dot{\hat{\theta }}_{i,k}-\tilde{ W}_{i,k}r_{i,k}^{-1}\dot{{\hat{W}}}_{i,k} \end{aligned}$$
(43)

Construct the virtual variable \(\alpha _{i,k+1}\) as

$$\begin{aligned} \alpha _{i,k+1}=-\varrho _{i,k}s_{i,k}-\hat{\theta }_{i,k}\tanh \left( \frac{s_{i,k} }{\epsilon _{i,k}}\right) +\frac{\alpha _{i,k}-{\bar{\alpha }}_{i,k}}{\tau _{i,k}} \end{aligned}$$
(44)

and the property \(0\le \left| s_{i,k}\right| -s_{i,k}\tanh \left( \frac{ s_{i,k}}{\epsilon _{i,k}}\right) \le 0.2785\epsilon _{i,k}\) is used.

The adaptive parameter \(\dot{\hat{\theta }}_{i,k}\) is designed as

$$\begin{aligned} \dot{\hat{\theta }}_{i,k}=\Gamma _{i,k}s_{i,k}\tanh \left( \frac{s_{i,k}}{\epsilon _{i,k}}\right) -\Gamma _{i,k}\xi _{i,k}\hat{\theta }_{i,k} \end{aligned}$$
(45)

The adaptive parameter \(\dot{{\hat{W}}}_{i,k}\) is designed as

$$\begin{aligned} \dot{{\hat{W}}}_{i,k}=\gamma _{i,k}\Theta _{i,k}s_{i,k}-\gamma _{i,k}\sigma _{i,k}{\hat{W}}_{i,k} \end{aligned}$$
(46)

where \(\Gamma _{i,k}>0\) and \(\gamma _{i,k}>0\) are tuning gains, \(\xi _{i,k}>0 \) and \(\sigma _{{i},k}>0\) are constants, and \(\Theta _{i,k}=\frac{1}{\partial {\hat{W}}_{i,k}}\).

By using (44)–(46), we get

$$\begin{aligned} {\dot{V}}_{i,k}\le & {} {\dot{V}}_{i,k-1}+s_{i,k}(s_{i,k+1}+L_{i,k+1}+\alpha _{i,k+1}-{\bar{\alpha }}_{i,k}) \nonumber \\&-{\tilde{\theta }}_{i,k}\left( s_{i,k}\tanh \left( \frac{s_{i,k}}{\epsilon _{i,k}}\right) -\frac{ \dot{\hat{\theta }}_{i,k}}{\Gamma _{i,k}}\right) \nonumber \\&+{\tilde{W}}_{i,k}^{T}\left( \Theta _{i,k}s_{i,k}-\frac{{\hat{W}}_{i,k}}{\gamma _{i,k}}\right) \nonumber \\&+0.2785\epsilon _{i,k}{\bar{\theta }}_{i,k} \nonumber \\\le & {} -\mathop {\sum }\limits _{l=1}^{\varvec{k}}\varrho _{i,l}s_{i,l}^{2}+\mathop {\sum }\limits _{l=2}^{\varvec{k-1}} s_{i,l}(s_{i,l+1}+L_{i,l+1}) \nonumber \\&+\mathop {\sum }\limits _{l=1}^{\varvec{k}}\Gamma _{i,l}{\tilde{\theta }} _{i,l}\hat{\theta }_{i,l}+\mathop {\sum }\limits _{l=1}^{\varvec{k}} \gamma _{i,l}{\tilde{W}}_{i,l}^{T}{\hat{W}}_{i,l} \nonumber \\&+(\phi _{i}+\psi _{i})s_{i,1}(s_{i,2}+L_{i,2}) \nonumber \\&-(\phi _{i}+\psi _{i})^{2}s_{i,1}^{2}+\mathop {\sum }\limits _{l=1}^{\varvec{k}}0.2785\epsilon _{i,l}{\bar{\theta }}_{i,l} \end{aligned}$$
(47)

where \(\varrho _{i,k}\) and \(\epsilon _{i,k}\) are positive constants.

Step n Based on (34), we get

$$\begin{aligned} {\dot{s}}_{i,n}={\dot{z}}_{i,n}-\dot{{\bar{\alpha }}}_{i,n} \end{aligned}$$
(48)

Define \(V_{i,n}\) as

$$\begin{aligned} V_{i,n}={\dot{V}}_{i,n-1}+\frac{1}{2}s_{i,n}^{2}+\frac{1}{\gamma _{i,n}}\tilde{ W}_{i,n}^{T}{\tilde{W}}_{i,n}+\frac{1}{2}{\tilde{h}}_{i,n}\Gamma _{i,n}^{-1} {\tilde{h}}_{i,n} \end{aligned}$$
(49)

The derivative of \(V_{i,n}\) is

$$\begin{aligned} {\dot{V}}_{i,n}= & {} {\dot{V}}_{i,n-1}+s_{i,n}[H_{i,n}+q_{i}(g_{i}(t)(\kappa _{i,j}(m_{i,j}(t)\Lambda _{i,j}(t) \nonumber \\&+\,\xi _{i,j}(t))+{\bar{u}}_{i,j})+h_{i}(t))-\dot{{\bar{\alpha }}}_{i,n} \nonumber \\&+q_{i}W_{i,n}^{T}S_{i}\left( x_{i}\right) ]-{\tilde{h}}_{i,n}\Gamma _{i,n}^{-1}\dot{{\hat{h}}}_{i,n} \nonumber \\&-\,{\tilde{W}}_{i,n}^{T}r_{i,n}^{-1}\dot{{\hat{W}}}_{i,n} \nonumber \\= & {} {\dot{V}}_{i,n-1}+s_{i,n}[H_{i,n}+q_{i}g_{i}(t)\kappa _{i,j}m_{i,j}(t)\Lambda _{i,j}(t) \nonumber \\&+\,q_{i}g_{i}(t)\kappa _{i,j}\xi _{i,j}(t)+q_{i}g_{i}(t){\bar{u}}_{i,j} \nonumber \\&+\,q_{i}h_{i}(t)-\dot{{\bar{\alpha }}}_{i,n}+q_{i}W_{i,n}^{T}S_{i}\left( x_{i}\right) ] \nonumber \\&-\,{\tilde{h}}_{i,n}\Gamma _{i,n}^{-1}\dot{{\hat{h}}}_{i,n}-{\tilde{W}} _{i,n}^{T}r_{i,n}^{-1}\dot{{\hat{W}}}_{i,n} \nonumber \\= & {} {\dot{V}}_{i,n-1}+s_{i,n}H_{i,n}+s_{i,n}q_{i}g_{i}(t)\kappa _{i,j}m_{i,j}(t)\Lambda _{i,j}(t) \nonumber \\&-\,s_{i,n}\dot{{\bar{\alpha }}}_{i,n}+s_{i,n}g_{i}(t)\kappa _{i,j}\xi _{i,j}(t)+s_{i,n}q_{i}g_{i}(t){\bar{u}}_{i,j} \nonumber \\&+\,s_{i,n}q_{i}h_{i}(t)+s_{i,n}q_{i}W_{i,n}^{T}S_{i}\left( x_{i}\right) - {\tilde{h}}_{i,n}\Gamma _{i,n}^{-1}\dot{{\hat{h}}}_{{i},n} \nonumber \\&-{\tilde{W}}_{i,n}^{T}r_{i,n}^{-1}\dot{{\hat{W}}}_{i,n} \end{aligned}$$
(50)

The control law \(\Lambda _{i,j}\) is given as

$$\begin{aligned} \Lambda _{i,j}=\beta _{i}q_{i}^{-1}N(\vartheta _{i})\Phi _{i} \end{aligned}$$
(51)

where \(\beta _{i}>0.\) The \(\vartheta _{i}\) is a variable, and the derivative of \(\vartheta _{i}\) is given by

$$\begin{aligned} {\dot{\vartheta }}_{i}=k_{i,1}^{-1}\beta _{i}s_{i,n}\Phi _{i} \end{aligned}$$
(52)

Furthermore, \(\Phi _{i}\) is given as

$$\begin{aligned} \Phi _{i}=H_{i,n}+q_{i}W_{i,n}^{T}S_{i}\left( x_{i}\right) -\dot{{\bar{\alpha }} }_{i,n}+\frac{s_{i,n}q_{i}^{2}{\hat{h}}_{i,n}^{2}}{\left| s_{i,n}\right| q_{i}{\hat{h}}_{i}+\exp (-\Upsilon _{i}t)} \end{aligned}$$
(53)

where \(\Upsilon _{i}>0\), and \({\hat{W}}_{i,n},\) \({\hat{h}}_{i,n}\) are the estimates of \(W_{i,n},\) \(h_{i,n}.\)

Utilizing (52) and (53), it follows that

$$\begin{aligned} {\dot{V}}_{i,n}\le & {} {\dot{V}}_{i,n-1}+s_{i,n}q_{i}g_{i}(t)\kappa _{i,j}m_{i,j}(t)\beta _{i}q_{i}^{-1}N(\vartheta _{i})\Phi _{i} \\&-\,s_{i,n}\dot{{\bar{\alpha }}}_{i,n}+s_{i,n}g_{i}(t)\kappa _{i,j}\xi _{i,j}(t)+s_{i,n}q_{i}g_{i}(t){\bar{u}}_{i,j} \\&+\,s_{i,n}q_{i}h_{i}(t)+s_{i,n}q_{i}W_{i,n}^{T}S_{i}\left( x_{i}\right) +s_{i,n}H_{i,n} \\&-\,{\tilde{W}}_{i,n}^{T}r_{i,n}^{-1}\dot{{\hat{W}}}_{i,n}-{\tilde{h}}_{i,n}\Gamma _{i,n}^{-1}\dot{{\hat{h}}}_{{i},n} \\\le & {} {\dot{V}}_{i,n-1}+s_{i,n}[(g_{i}(t)\kappa _{i,j}m_{i,j}(t)\beta _{i}N(\vartheta _{i})+1)\Phi _{i}-\Phi _{i}] \\&-\,s_{i,n}\dot{{\bar{\alpha }}}_{i,n}+s_{i,n}g_{i}(t)\kappa _{i,j}\xi _{i,j}(t)+s_{i,n}q_{i}g_{i}(t){\bar{u}}_{i,j} \\&+\,s_{i,n}q_{i}h_{i}(t)+s_{i,n}q_{i}W_{i,n}^{T}S_{i}\left( x_{i}\right) +s_{i,n}H_{i,n} \\&-\,{\tilde{W}}_{i,n}^{T}r_{i,n}^{-1}\dot{{\hat{W}}}_{i,n}-{\tilde{h}}_{i,n}\Gamma _{i,n}^{-1}\dot{{\hat{h}}}_{{i},n} \end{aligned}$$

Further, notice that \(-\frac{s_{i,n}^{2}q_{i}^{2}{\hat{h}}_{i,n}^{2}}{ \left| s_{i,n}\right| q_{i}{\hat{h}}_{i,n}+\exp (-\Upsilon _{i},t)} \le -\left| s_{i,n}\right| q_{i}{\hat{h}}_{i,n}+\exp (-\Upsilon _{i}t).\) It follows that

$$\begin{aligned} {\dot{V}}_{i,n}\le & {} s_{{i},n}q_{i}{\tilde{W}}_{i,n}^{T}S_{i}\left( x_{i}\right) +\left| s_{i,n}\right| q_{i}{\tilde{h}}_{i,n}+\exp (-\Upsilon _{i}t) \nonumber \\&+\,k_{i,1}(g_{i}(t)\kappa _{i,j}m_{i,j}N(\vartheta _{i})+\beta _{i}^{-1}) {\dot{\vartheta }}_{i} \nonumber \\&+\,s_{i,n}q_{i}g_{i}(t){\bar{u}}_{i,j}+s_{i,n}q_{i}g_{i}(t)\kappa _{i,j}\xi _{i,j}(t) \nonumber \\&-\,{\tilde{h}}_{i,n}\Gamma _{i,n}^{-1}\dot{{\hat{h}}}_{i,n}-{\tilde{W}} _{i,n}r_{i,n}^{-1}\dot{{\hat{W}}}_{i,n} \end{aligned}$$
(54)

According to Young’s inequality and Lemma 2, it has

$$\begin{aligned} s_{i,n}q_{i}g_{i}(t)\kappa _{i,j}\xi _{i,j}(t)\le & {} \frac{ s_{i,n}mq_{i}^{2}g_{i}^{2}(t)}{2}+\frac{s_{i,n}\kappa _{i,j}^{2}\xi _{i,j}^{2}(t)}{2} \nonumber \\ s_{i,n}q_{i}g_{i}(t){\bar{u}}_{i,j}\le & {} \frac{s_{i,n}q_{i}^{2}g_{i}^{2}(t)}{ 2}+\frac{s_{i,n}{\bar{u}}_{i,j}^{2}}{2} \end{aligned}$$
(55)

Design

$$\begin{aligned} \dot{{\hat{W}}}_{i,n}= & {} \gamma _{i,n}\left| s_{i,n}\right| q_{i}S_{i}\left( {\mathbb {Z}}_{i}\right) \end{aligned}$$
(56)
$$\begin{aligned} \dot{{\hat{h}}}_{i,n}= & {} \Gamma _{i,n}\left| s_{i,n}\right| q_{i} \end{aligned}$$
(57)

Utilizing (55)–(57), one has

$$\begin{aligned} {\dot{V}}_{i,n}\le & {} k_{i,1}(g_{i}(t)\kappa _{i,j}m_{i,j}N(\vartheta _{i})+\beta _{i}^{-1}) {\dot{\vartheta }}_{i}+\exp (-\Upsilon _{i},t) \nonumber \\&+s_{i,n}q_{i}^{2}g_{i}^{2}(t)+s_{i,n}\left( \frac{\kappa _{i,j}\xi _{i,j}^{2}+ {\bar{u}}_{i,j}^{2}}{2}\right) \nonumber \\&-\mathop {\sum }\limits _{l=1}^{\varvec{n-1}}\varrho _{i,l}s_{i,l}^{2}+\mathop {\sum }\limits _{l=2}^{\varvec{n-1}} s_{i,l}(s_{i,l+1}+L_{i,l+1}) \nonumber \\&+\mathop {\sum }\limits _{l=1}^{\varvec{n-1}}\Gamma _{i,l}\tilde{ \theta }_{i,l}\hat{\theta }_{i,l}+\mathop {\sum }\limits _{l=1}^{\varvec{n-1}} \gamma _{i,l}{\tilde{W}}_{i,l}^{T}{\hat{W}}_{i,l} \nonumber \\&+\mathop {\sum }\limits _{l=1}^{\varvec{n-1}}0.2785\epsilon _{i,l} {\bar{\theta }}_{i,l}+(\phi _{i}+\psi _{i})s_{i,1}(s_{i,2}+L_{i,2}) \nonumber \\&-(\phi _{i}+\psi _{i})^{2}s_{i,1}^{2} \end{aligned}$$
(58)

Define

$$\begin{aligned} V=\mathop {\sum }\limits _{i=1}^{\varvec{N}}k_{i,1}^{-1}V_{i,n} \end{aligned}$$
(59)

and we can obtain

$$\begin{aligned} {\dot{V}}\le & {} \mathop {\sum }\limits _{i=1}^{\varvec{N}} \mathop {\sum }\limits _{l=1}^{\varvec{n-1}}k_{i,1}^{-1}\left( -\varrho _{i,l}s_{i,l}^{2}+\Gamma _{i,l}{\tilde{\theta }}_{i,l}\hat{\theta }_{i,l}+\gamma _{i,l}{\tilde{W}}_{i,l}^{T}{\hat{W}}_{i,l}\right) \nonumber \\&+\mathop {\sum }\limits _{l=1}^{\varvec{n-1}}k_{i,1}^{-1}(\phi _{{i}}+\psi _{{i}})s_{i,1}(s_{i,2}+L_{i,2}) \nonumber \\&-\mathop {\sum }\limits _{i=1}^{\varvec{N}}k_{i,1}^{-1}(\phi _{ {i}}+\psi _{{i}})^{2}s_{i,1}^{2}+\mathop {\sum }\limits _{i=1}^{\varvec{N}} \mathop {\sum }\limits _{l=1}^{\varvec{n-1}}k_{i,1}^{-1}0.2785\epsilon _{i,l}{\bar{\theta }}_{i,l} \nonumber \\&+\mathop {\sum }\limits _{i=1}^{\varvec{N}}\mathop {\sum }\limits _{l=1}^{\varvec{n-1}}k_{i,1}^{-1}s_{i,l}(s_{i,l+1}+L_{i,l+1}) \nonumber \\&+\mathop {\sum }\limits _{i=1}^{\varvec{N}} \left[ k_{i,1}^{-1}s_{i,n}(q_{i}^{2}g_{i}^{2}(t)+\frac{\kappa _{i,j}\xi _{i,j}^{2}+ {\bar{u}}_{i,j}^{2}}{2})\right] \nonumber \\&+\mathop {\sum }\limits _{i=1}^{\varvec{N}}(g_{i}(t)\kappa _{i,j}m_{i,j}N(\vartheta _{i})+\beta _{i}^{-1}){\dot{\vartheta }}_{i} \nonumber \\&+\mathop {\sum }\limits _{i=1}^{\varvec{N}}k_{i,1}^{-1}\exp (-\Upsilon _{i},t) \end{aligned}$$
(60)

By applying Young’s inequality, \({\tilde{W}}_{i,k}^{T}{\hat{W}}_{i,k}\le \frac{1}{2}\left( {\bar{W}}_{i,k}^{2}-\left\| {\tilde{W}}_{i,k}\right\| ^{2}\right) ,\) and \(\left| {\tilde{\theta }}_{i,k}\right| {\bar{\theta }}_{i,k}-\tilde{ \theta }_{i,k}^{2}\le \frac{1}{2}({\bar{\theta }}_{i,k}^{2}-{\tilde{\theta }} _{i,k}^{2}),\) we have

$$\begin{aligned} {\dot{V}}\le & {} -\mathop {\sum }\limits _{i=1}^{\varvec{N}}\mathop {\sum }\limits _{l=1}^{\varvec{n-1}}k_{i,1}^{-1}\varrho _{i,l}s_{i,l}^{2}+ \mathop {\sum }\limits _{i=1}^{\varvec{N}}\left[ \frac{1}{2} k_{i,1}^{-1}\left( s_{i,2}^{2}+L_{i,2}^{2}\right) \right. \nonumber \\&+\left. \mathop {\sum }\limits _{i=1}^{\varvec{N}} \mathop {\sum }\limits _{l=1}^{\varvec{n-1}} k_{i,1}^{-1}\left( \frac{1}{2}s_{i,l+1}^{2}+s_{i,l}^{2}+ \frac{1}{2}L_{i,l+1}^{2}\right) \right] \nonumber \\&+\mathop {\sum }\limits _{i=1}^{\varvec{N}} \left[ k_{i,1}^{-1}s_{i,n}\left( q_{i}^{2}g_{i}^{2}(t)+\frac{\kappa _{i,j}\xi _{i,j}^{2}+ {\bar{u}}_{i,j}^{2}}{2}\right) \right] \nonumber \\&+\mathop {\sum }\limits _{i=1}^{\varvec{N}}\left[ k_{i,1}^{-1}\exp (-\Upsilon _{i},t)+(g_{i}(t)\kappa _{i,j}m_{i,j}N(\vartheta _{i})\right. \nonumber \\&+\left. \beta _{i}^{-1}){\dot{\vartheta }}_{i}\right] +\varphi \end{aligned}$$
(61)

and

$$\begin{aligned} \varphi =\mathop {\sum }\limits _{i=1}^{\varvec{N}}\left[ \mathop {\sum }\limits _{i=1}^{\varvec{n}}\left( \frac{\Gamma _{i,l}}{2}{\bar{\theta }} _{i,l}^{2}+\frac{\gamma _{i,l}}{2}{\bar{W}}_{i,l}^{2}+0.2785\epsilon _{i,l} {\bar{\theta }}_{i,l}\right) \right] \end{aligned}$$

Similar to [41], choosing positive constants \(\varrho _{i,1}=\varrho _{i,k}^{*},\) \(\varrho _{i,k}=\frac{3}{2}+\varrho _{i,k}^{*},\) \(\varrho _{i,n}=\frac{1}{2}+\varrho _{i,n}^{*}\) and integrating both sides of (62), we have

$$\begin{aligned} V(t)\le & {} V(0)-\int _{0}^{t}\mathop {\sum }\limits _{i=1}^{\varvec{N}} \kappa _{i,j}(g_{i}(\chi )m_{i,j}N(\vartheta _{i}(\chi )) \nonumber \\&+\,\beta _{i}^{-1}){\dot{\vartheta }}_{i}(\chi )d\chi +\mathop {\sum }\limits _{i=1}^{\varvec{N}}\frac{1}{k_{i,1}\Upsilon _{i}} \nonumber \\&-\,\int _{0}^{t}\mathop {\sum }\limits _{i=1}^{\varvec{N}} \mathop {\sum }\limits _{i=1}^{\varvec{N}}k_{i,1}^{-1}\varrho _{i,l}s_{i,l}^{2}(\chi )d\chi \nonumber \\&+\,\int _{0}^{t}\mathop {\sum }\limits _{i=1}^{\varvec{N}}\left[ \frac{1}{2} (s_{i,2}^{2}(\chi )d\chi +L_{i,2}^{2}(\chi )d\chi ) \right. \nonumber \\&+\,\int _{0}^{t}\mathop {\sum }\limits _{i=1}^{\varvec{N}} \mathop {\sum }\limits _{l=1}^{\varvec{n-1}} \left( \frac{1}{2}s_{i,l+1}^{2}(\chi )d\chi +s_{i,l}^{2}(\chi )d\chi \right) \nonumber \\&+\,\frac{1}{2}\int _{0}^{t}\mathop {\sum }\limits _{i=1}^{\varvec{N}} \mathop {\sum }\limits _{l=1}^{\varvec{n-1}} L_{i,l+1}^{2}(\chi )d\chi \nonumber \\&+\,\int _{0}^{t}\mathop {\sum }\limits _{i=1}^{\varvec{N}}\left( \frac{ k_{i,j}\xi _{i,j}^{2}+{\bar{u}}_{i,j}^{2}}{2}\right) d\chi \nonumber \\&+\,\int _{0}^{t}\mathop {\sum }\limits _{i=1}^{\varvec{N}} s_{i,n}(q_{i}^{2}g_{i}^{2}(\chi )d\chi +\varphi \end{aligned}$$
(62)

Through above analysis, we can conclude that \(\vartheta _{i}(t),\) V(t),  and \( \int _{0}^{t}\kappa _{i,j}(g_{i}(\chi )m_{i,j}N(\vartheta _{i}(\chi ))+\beta _{i}^{-1}){\dot{\vartheta }}_{i}(\chi )d\chi \) are bounded on \(t\in \left[ 0,t_{\chi }\right) ,\) and the initial value V(0) is bounded.

Remark 3

Compared with the existing results in [14, 39], an error transformation technique is considered to generate an equivalent MAS. In addition, the controller designed in this paper can deal with the unknown dead-zone and actuator faults problems simultaneously.

4 Simulation Results

The following simulation example is used to verify the effectiveness of the designed control method. We consider a MASs with four pendulums [36], whose dynamics are governed as

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}_{i,1}&=x_{i,2} \\ {\dot{x}}_{i,2}&=-\frac{g}{l_{i}}\sin (x_{i,1})-\frac{k_{i}}{m_{i}}x_{i,2}+ \frac{\chi _{i}}{m_{i}l_{i}^{2}}+\varpi _{i},i=1,2,3,4 \\ y_{r}&=0.05\sin \left( 5t+4.9\right) \end{aligned} \right. \end{aligned}$$
(63)

where \(x_{i,1}\) is the anticlockwise angle. g is the gravitational acceleration. \(l_{i}=4\) is the length of the rod, \(k_{i}=0.2\) is the friction coefficient, and \(m_{i}=2\) is the mass of the bob. The torque \(\chi _{i}\) is described as

$$\begin{aligned} \chi _{1}= & {} \left\{ \begin{array}{l} -1.2(u_{1}-0.2), \\ 0, \\ -0.8(u_{1}+0.2), \end{array} \right. \begin{array}{l} u_{1}\ge 0.2 \\ -0.2<u_{1}<0.2 \\ u_{1}\le -0.2 \end{array} \nonumber \\ \chi _{2}= & {} -u_{2} \nonumber \\ \chi _{3}= & {} \left\{ \begin{array}{l} (1-0.3\sin (u_{3}))\left( u_{3}-0.2\right) , \\ 0, \\ (0.8-0.2\cos (u_{3}))(u3+0.1), \end{array} \right. \begin{array}{l} u_{3}\ge 0.2 \\ -0.1<u_{3}<0.2 \\ u_{3}\le -0.1 \end{array} \nonumber \\ \chi _{4}= & {} u_{4} \end{aligned}$$
(64)

The fault model is given as

$$\begin{aligned} u_{1.1}^{F}= & {} \left\{ \begin{array}{c} u_{1.1} \\ 0.5u_{1.1} \end{array} \right. \begin{array}{l} \text {if }t\in \left[ 2E,2E+1\right] \\ \text {if }t\in \left[ 2E+1,2E+2\right] \end{array} \nonumber \\ u_{1.2}^{F}= & {} \left\{ \begin{array}{c} 0.3u_{1.2} \\ 0 \end{array} \right. \begin{array}{l} \text {if }t\in \left[ 2E,2E+1\right] \\ \text {if }t\in \left[ 2E+1,2E+2\right] \end{array} \nonumber \\ u_{2.1}^{F}= & {} \left\{ \begin{array}{c} u_{2.1} \\ 0.6u_{2.1} \end{array} \right. \begin{array}{l} \text {if }t\in \left[ 2E,2E+1\right] \\ \text {if }t\in \left[ 2E+1,2E+2\right] \end{array} \nonumber \\ u_{2.2}^{F}= & {} \left\{ \begin{array}{c} u_{2.2} \\ 0.2+0.2\sin (t) \end{array} \right. \begin{array}{l} \text {if }t\in \left[ 0,1\right) \\ \text {if }t\in \left[ 1,\infty \right) \end{array} \end{aligned}$$
(65)

where \(E=0,1,...,N.\)

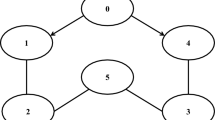
Apparently, the matrices of \({\mathcal {A}}\) and \({\mathcal {L}}\) can be written as

$$\begin{aligned} {\mathcal {A}}=\left[ \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0 \\ 1 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \end{array} \right] ,\text { }{\mathcal {L}}=\left[ \begin{array}{cccc} 1 &{} -1 &{} 0 &{} 0 \\ -1 &{} 3 &{} -1 &{} -1 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} 1 \end{array} \right] \end{aligned}$$
(66)
Fig. 1
figure 1

Topology of communication graph

Full size image
Fig. 2
figure 2

The trajectories of system states

Full size image
Fig. 3
figure 3

The trajectories of outputs

Full size image
Fig. 4
figure 4

The trajectories of actuator faults

Full size image
Fig. 5
figure 5

The trajectories of dead zones inputs

Full size image
Fig. 6
figure 6

The trajectories of controller signals

Full size image

From Fig. 1, we know \(B=\hbox {diag}(1,0,1,0)\). The simulation results are shown by Figs. 2, 3, 4, 5 and 6 and the correlative design parameters are chosen as \( k_{1}=0.1,\) \(\ k_{2}=0.1,\) \(k_{3}=0.1,\) \(k_{4}=0.1,\) \(e_{1,1}=10.1,\) \( e_{2,1}=10.1,\) \(e_{3,1}=10.1,\) \(e_{4,1}=10.1,\) \(\beta _{1,2}=0.75,\) \(\beta _{2,2}=0.22,\) \(\beta _{3,2}=0.82,\) \(\beta _{4,2}=0.81,\) \(\varrho _{1,1}=1.1,\) \( \varrho _{2,1}=1.1,\) \(\varrho _{3,1}=1.1,\) \(\varrho _{4,1}=1.1,q_{1,1}=20.1,q_{2,2}=70.2,q_{3.2}=1,q_{4,2}=1,\zeta _{1,1}=30,\zeta _{2,1}=12.1,\zeta _{3,1}=44.1,\zeta _{4,1}=18,\epsilon _{1,1}=\epsilon _{2,1}=\epsilon _{3,1}=\epsilon _{4,1}=1,\) \(o_{1,1,p}=0.4,\) \(o_{1,1,l}=0.5,\) \(m_{1,1,p}=1.1,\) \(m_{1,1,l}=1.4,\) \(o_{2,1,p}=1.1,\) \(o_{2,1,l}=4.1,\) \( m_{2,1,p}=0.8,\) \(m_{2,1,l}=1.1,\) \(o_{3,1,p}=6.1,\) \(o_{3,1,l}=1.6,\) \( m_{3,1,p}=0.9,\) \(m_{3,1,l}=1.3,\) \(o_{4,1,p}=6.1,\) \(o_{4,1,l}=1.6,\) \( m_{4,1,p}=0.9,\) and \(m_{4,1,l}=1.3.\) The external disturbances are given as \( \varpi _{1}=0.2\cos (5t),\) \(\varpi _{2}=0.1\cos (10t),\) \(\varpi _{3}=0.2\sin (10t),\) and \(\varpi _{4}=0.1\sin (5t).\) \({\underline{x}}=-0.6\exp (-t)-0.1\) and \({\bar{x}}=0.4\exp (-0.8t)+0.2\ \)are constraints, and \(M(x_{i,1}, {\underline{x}},{\bar{x}})=2\ln ((x_{i,1}-{\underline{x}})({\bar{x}} -x_{i,1}))+x_{i,1}\) is a transformation function. The trajectories of constraints on agent outputs as shown in Fig. 2, and the consensus tracking trajectories are shown in Fig. 3. In Fig. 4, the trajectories of actuator failures with unknown dead zones are plotted. Figure 5 shows the trajectories of dead zone input, and Fig. 6 shows the trajectories of control input.

5 Conclusions

This paper has presented a state transformation method to solve the constrained control problem for MASs in non-affine form. A fault-tolerant consensus tracking protocol has been designed to solve the problems of actuator faults and dead zones. The RBF NNs have been utilized to estimate the unknown nonlinear functions. The results indicate that the controller guarantees all the signals are bounded, and all follower’s outputs can follow the leader’s outputs. Finally, simulation results have been utilized to show the effectiveness of proposed consensus control scheme. In our future research, based on the NNs approximation property, we will extend the results of this paper to the event-triggered control [51, 53], digital twin-driven control [10, 22], sampled-data control [47, 48] and some intelligence algorithms [5, 19, 21, 23, 33, 45, 46, 54] for MASs.