Consensus Tracking Algorithm Via Observer-Based Distributed Output Feedback for Multi-Agent Systems Under Switching Topology

Abstract

This paper is devoted to consensus tracking algorithm via observer-based distributed output feedback with adaptive coupling gains for leader-follower multi-agent systems under arbitrary switching topology. The full state of neighboring followers in our work is not available, and the leader’s input might be nonzero and bounded generally. We design the actual observer and adaptive coupling gains to ensure the consensus tracking in a fully distributed fashion for the connected switching topologies. Both the observer gain and feedback gain are determined simultaneously. Sufficient conditions for the multi-agent system to reach consensus are obtained in terms of linear matrix inequalities by a cone complementary linearization technology. An illustrative example is provided to validate the theoretical results.

1 Introduction

Consensus is a major research topic in the area of cooperative control of multi-agent systems. In recent decades, the consensus problem and methods of multi-agent systems have received more extensive consideration nowadays [16, 20, 22, 25]. This is due to the broad applications of multi-agent systems in many areas, e.g., multiple mobile robots [3, 9, 17], flocking or swarming behaviors [15, 21, 24], formation control [2, 13], sensor network [18], and so on. Multi-agent systems possess the distributed coordination nature in that no agent in the systems has a full global view of the system and can only communicate local information with neighbors to achieve certain global behaviors.

The consensus problem arising from multi-agent systems, which is one basic problem in distributed coordination, requires all agents to achieve an agreement on some variables of interest under distributed control laws/protocols based on local information. Existing consensus algorithms can be roughly categorized into two classes, consensus without a leader (i.e., leaderless consensus) and consensus with a leader. In [16, 20, 22] and therein, the leaderless consensus is studied. On the other hand, a particularly interesting study is the consensus tracking of a group of agents with a leader, i.e., the leader-follower multi-agent systems, in which the leader is usually independent of their followers, but has influence on the followers’ behaviors. Such a problem is usually called leader-following consensus. In the leader-following consensus, there is one leader and some informed agents who have the leader’s information, together with the other uninformed agents who only follow their neighbors by designing local control protocols, and the task is for all followers to track desired leader’s trajectories. It was informed that the leader-follower configuration is able to save the control energy and cost [5, 22], and the leader-following consensus has been an active area of research. To mention a few, Ni and Cheng [19] considered the leader-following consensus problem of higher-order multi-agent systems under fixed and switching topologies. In [6], the synchronization for leader-following agents described by linear time-invariant discrete-time dynamics was concerned. It is worth pointing out that most consensus control has focused on the relative state feedback consensus protocols [6, 19, 25] often realized with the assumption that the state information of its neighboring agents is available. However, in most practical cases, such an assumption does not hold, and only the output information of its neighbors is accessible for feedback. Using the outputs of neighboring agents, two basic types of consensus protocols are proposed generally, namely, the static output feedback consensus protocol, and the dynamic output feedback consensus protocol. The controller with static output feedback consensus protocols is limited [1, 26]; so, it is more realistic to design observers that produce the estimation of the system state on-line, i.e., design a dynamic output feedback controller. Therefore, it is not surprising that the observer-based control problem has attracted so much attention, see [7, 28], etc.

In addition, the adaptive control has been discussed very recently for reaching actions in MASs with second-order dynamics or even higher-order dynamics [11, 12, 27], in which some distributed adaptive laws are designed on the weights of the network and uniformly ultimately boundedness is achieved for MASs with second-order, higher-order, or even nonlinear dynamics. However, under the assumption that the full state information of followers is not available, it is still a challenging issue to design a distributed local protocol without using the global information for reaching higher-order consensus in MASs, especially design an actual observer to estimate the neighboring states directly with arbitrary switching topology generally. This motivates us to design a fully distributed consensus tracking algorithm without both global spectrum information and measured states for MASs to reach consensus by devising the actual observer directly.

In this work, we propose a consensus tracking algorithm via the observer-based dynamic output feedback in a fully distributed fashion without any global information of the communication graph for the leader-follower multi-agent system. Under the assumption that the full state of the neighboring followers is not available and in general case that the leader’s input is nonzero and bounded, the actual observer and adaptive coupling gains are designed. In addition, we determine both the observer gain and feedback gain of the proposed algorithm synchronously, which increases the difficulty to obtain the consensus condition of this tracking problem. Here, utilizing a cone complementary linearization approach, sufficient conditions in the form of linear matrix inequalities (LMIs) to complete consensus tracking for any arbitrary and connected switching topologies are deduced, in which the fix topology can be as a special case.

Notations The notation used throughout the paper is fairly standard. The superscript $T$ stands for matrix transposition. $R^{n}$ denotes the $n$-dimensional Euclidean space. The notation $*$ is used as an ellipsis for terms induced by symmetry. The notation $P>0(\ge 0)$ means that $P$ is real symmetric and positive definite (semidefinite). $Z^{+}$ are the sets of positive integers. $\otimes$ denotes the Kronecker product. $\mathbf 1 _{n}$ represents the vector $[1,1, \ldots , 1]^{T}$ with dimension $n$. $0$ denotes zero value or zero matrix with appropriate dimensions. For a vector $x\in R^{n}$, denote $\parallel \cdot \parallel _{1}$ and $\parallel \cdot \parallel _{\infty }$ as its 1-norm and $\infty$-norm, respectively. sgn $(\cdot )$ is the signum function defined componentwise.

2 Graph Theory and Problem Formulation

2.1 Graph Theory

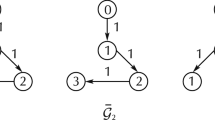
Graph theory is an effective mathematical tool to describe the coordination problems and model the information exchange among agents by means of directed or undirected graphs. Here, consider a modified leader-follower (MLF) multi-agent system consisting of one leader and n followers and the graph is shown in Fig. 1 similar to [23] but not identical actually. In the MAS with MLF structure in our work, the leader denoted as $0$ provides the goal directly, and other $n$ agents should follow the leader by communicating with the neighboring followers and leader. Additionally, we assume the leader receives no information from the followers. Let $G=(V,E)$ be a directed graph with $n+1$ nodes which express $n+1$ agents where there is one leader indexed by $0$ and $n$ followers indexed by $1,\ldots , n$. The directed graph $G$ has a directed spanning tree with the leader as the root, and the subgraph consisting of $n$ followers is undirected. Denote $V=\{0,1,2,\ldots ,n\}$ as the vertex set, and $E$ as edges set, $a_{ij}$ is the count of edges connecting the vertex $i$ and $j$. Hence, we get $A_{L}(G)=(a_{ij})\in R^{(n+1)\times (n+1)}$, which is called weighted adjacent matrix of $G$ with nonnegative elements, where if $i$ is adjacent to $j,\,a_{ij}=1$; otherwise, $a_{ij}=0$. It is obvious that $A_{L}(G)$ is a matrix with $\{0,1\}$, and the main diagonal elements are zeros.

Fig. 1

Directed graph of the leader-follower multi-agent system

Denote $\bar{G}=(\bar{V},\bar{E})$ as the subgraph of $G$, which is formed by $n$ followers, where $\bar{A}_{L}(\bar{G})=(a_{ij}), \forall i,j={1,\ldots , n}$. $\bar{D}(\bar{G})$ is defined as the diagonal matrix of vertex degrees, and $\bar{D}(\bar{G})=\mathrm{diag}\{\bar{d}(1),\ldots ,\bar{d}(n)\}\in R^{n\times n}$, where $\bar{d}(n)$ is the degree of the vertex $i$, that is the number of the edges connected with $i$. Then, the Laplacian matrix of $\bar{G}$ can be defined as

$$\begin{aligned} \bar{L}(\bar{G})=\bar{D}(\bar{G})-\bar{A}_{L}(\bar{G}). \end{aligned}$$

(1)

Let $\bar{L}(\bar{G})=(l_{ij})\in R^{n\times n}$ and

$$\begin{aligned} l(i,j)= \left\{ \begin{array}{ll} &{} \bar{d}(i), \quad i=j\\ &{} -a_{ij},~~~i\ne j \\ \end{array}\right. . \end{aligned}$$

(2)

The connection weight between $i$th follower and the leader is denoted by $\bar{B}$ where

$$\begin{aligned} \bar{B}=\mathrm{diag}\left\{ b_{1},b_{2},\ldots ,b_{n}\right\} \end{aligned}$$

(3)

with $b_{i}>0$ if there is an edge between the $i$th agent and the leader, and otherwise, $b_{i}=0$.

We call the set of agents from which agent $i$ can receive information a neighboring set $N^{i}$ [23], that is $\forall ~i=1,\ldots ,n,~~N^{i}=\{j=1,2,\ldots ,n|(i,j)\in \bar{E}\}$. Therefore, $\bar{d}(i)$ in Laplacian matrix of $\bar{G}$ equals to the cardinality of the set $N^{i}$, and $|N^{i}|$ is called the degree of vertex $i$.

Remark 1

In this paper, we employ a piecewise constant switching signal function $\sigma (t):[0,\infty ) \mapsto \{{1,2, \ldots , M}\}\triangleq \varTheta$ to describe the arbitrary switching topologies as $G_{\sigma (t)}$ [14], and each one has a directed spanning tree, where $M \in Z^{+}$ presents the total number of all possible connected directed graphs. Then, denote the subgraph by $\bar{G}_{\sigma (t)}$ and its corresponding Laplacian matrix by $\bar{L}_{\sigma (t)}$, and denote $\bar{B}$ by $\bar{B}_{\sigma (t)}$. Hence, the matrix $H_{\sigma (t)}$ corresponding to the graph $G_{\sigma (t)}$ satisfies $H_{\sigma (t)}=\bar{L}_{\sigma (t)}+\bar{B}_{\sigma (t)}$. For further analysis, denote $\lambda _{\sigma (t)i}$ as the $i$th eigenvalue of matrix $H_{\sigma (t)},\,i=1,\ldots , n$, and let $\sigma ^{*}i^{*}$ and $\sigma _{*}i_{*}$ be, respectively, the maximum and minimum eigenvalues of all matrices $H_{\sigma (t)}$.

In order to derive the main results of this work, the following lemma is needed.

Lemma 1

For the connected switching graphs $G_{\sigma (t)}$ as described in Remark 1 and Fig. 1, in which the piecewise constant switching signal function $\sigma (t):[0,\infty ) \mapsto \{{1,2, \ldots , M}\}\triangleq \varTheta$, the minimum eigenvalue $\lambda _{\sigma _{*}i_{*}}$ of all matrices $H_{\sigma (t)}$ satisfies $\lambda _{\sigma _{*}i_{*}}\le \mathrm{min}_{x\ne 0}\frac{x^{T}H_{\sigma (t)}x}{x^{T}x}$.

Proof

Since $\lambda _{min}(H_{\sigma (t)})={\min }_{x\ne 0}\frac{x^{T}H_{\sigma (t)}x}{x^{T}x}$ [8], in which $\lambda _{min}(H_{\sigma (t)})$ is the minimum eigenvalue of the matrix $H_{\sigma (t)}$, the proof can be completed according to $\lambda _{\sigma _{*}i_{*}} \le \lambda _\mathrm{min}(H_{\sigma (t)})$.

2.2 Problem Formulation

In this paper, consider a set of $n+1$ agents with general dynamics, containing $n$ followers and one leader, where the $i$th follower’s dynamic equation is expressed by

$$\begin{aligned}&\dot{x}_{i}(t)=Ax_{i}(t)+Bu_{i}(t), \nonumber \\&y_{i}(t)=C{x}_{i}(t),~i=1,\ldots ,n, \end{aligned}$$

(4)

and the dynamics of the leader labeled as $i=0$ is described as

$$\begin{aligned}&\dot{x}_{0}(t)=Ax_{0}(t)+Bu_{0}(t),\nonumber \\&y_{0}(t)=C{x}_{0}(t), \end{aligned}$$

(5)

where ${x}_{i}(t)\in R^{p}$ and $u_{i}(t)\in R^{m}$ are the state and the control input vector of the $i$th agent and $y_{i}(t) \in R^{q}$ is the measured output for $\forall i=0, 1, \ldots , n$. $A,\,B$, and $C$ are real constant matrices with appropriate dimensions, and it is assumed that the pair $(A,B,C)$ is stabilizable and detectable. Moreover, the leader (5) is assumed as the general case that the leader’s input $u_{0}$ is considered as $f(x_{0},t)$, which may be nonzero, time varying, and with the assumption in the following:

Assumption 1

The leader’s control input $u_{0}=f(x_{0},t)$ is continuously differentiable vector-valued function, and $\Vert f(x_{0},t)\Vert _{\infty } \le \kappa ,~\forall t>0$, where $\kappa$ is a nonnegative constant.

It is said that the consensus tracking problem of the leader-follower multi-agent system (4)–(5) is achieved, i.e., the states of all $n$ followers converge to the state of the leader if

$$\begin{aligned} \lim _{t\rightarrow \infty }(x_{i}(t)-x_{0}(t))=0, ~~\forall i = 1,\ldots ,n. \end{aligned}$$

(6)

3 Observer-Based Distributed Output Feedback Consensus Tracking

In this section, we assume the states of the leader are available to its neighbors only, and the full state of followers is not available. Then, denote $\hat{x}_{i}\in R^{p}$ as the estimate of the state $x_{i},\,\hat{y}_{i}=C\hat{x}_{i}$ as the consequent estimate of the output $y_{i}$, and $\tilde{y}_{i}=y_{i}-\hat{y}_{i}$ as the output estimation error for node $i$.

Here, we define the neighborhood state estimation error in the following

$$\begin{aligned} \varepsilon _{i}(t)=\sum _{j\in N^{i}(t)}a_{ij}(t)\left( \hat{x}_{j}(t)-\hat{x}_{i}(t)\right) +b_{i}(t)\left( \hat{x}_{0}(t)-\hat{x}_{i}(t)\right) , \end{aligned}$$

(7)

and hence get

$$\begin{aligned} \upsilon _{i}(t)&= \sum _{j\in N^{i}(t)}a_{ij}(t)\left( \hat{y}_{j}(t)-\hat{y}_{i}(t)\right) +b_{i}(t)\left( \hat{y}_{0}(t)-\hat{y}_{i}(t)\right) \nonumber \\&= C\varepsilon _{i}(t). \end{aligned}$$

(8)

Define the neighborhood output estimation error as

$$\begin{aligned} \zeta _{i}(t)=\sum _{j\in N^{i}(t)}a_{ij}(t)\left( \tilde{y}_{j}(t)-\tilde{y}_{i}(t)\right) +b_{i}(t)\left( \tilde{y}_{0}(t)-\tilde{y}_{i}(t)\right) . \end{aligned}$$

(9)

The observer for each node $i$ is designed as

$$\begin{aligned} \dot{\hat{x}}_{i}(t)=A\hat{x}_{i}(t)+Bu_{i}(t)-c_{i}(t)F\zeta _{i}(t). \end{aligned}$$

(10)

We consider the following observer-based distributed output feedback consensus protocol

$$\begin{aligned} u_{i}(t)&= c_{i}(t)K\varepsilon _{i}(t)+c_{i}(t)\mathrm{sgn}\left( K\varepsilon _{i}(t)\right) ,\nonumber \\ \dot{c}_{i}(t)&= \rho _{i}\big (\varepsilon _{i}^{T}\varPsi \varepsilon _{i}-\upsilon _{i}^{T}\zeta _{i}+\bar{\tau } \zeta _{i}^{T}\zeta _{i}+\Vert K\varepsilon _{i}\Vert _{1}\big ), \end{aligned}$$

(11)

where $c_{i}(t)$ is the time-varying distributed coupling gain of the $i$th agent. $\varPsi ,\,K$, and $F$ in (11) are constant matrix, feedback gain, and observer gain determined later. $\rho _{i}>0$ and $\bar{\tau }>0$ are constants, $\forall i=1,\ldots ,n$.

Define $\delta _{i}=x_{i}-x_{0}$ and $\tilde{x}_{i}=x_{i}-\hat{x}_{i}$ as the consensus tracking error and observer error, respectively. Let $\delta =[\delta _{1}^{T},\ldots ,\delta _{n}^{T}]^{T},\,\tilde{x}=[\tilde{x}_{1}^{T},\ldots ,\tilde{x}_{n}^{T}]^{T}$ and $\hat{C}(t)=\mathrm{diag}(c_{1}(t),\ldots ,c_{n}(t))$. The leader node $0$ is assumed to know its state, i.e., $\hat{x}_{0}=x_{0}$ and hence $\tilde{y}_{0}=0$. Noting that the identity $(L_{\sigma (t)}\otimes BK)(\mathbf 1 _{n}\otimes x_{0})=0$ since $L_{\sigma (t)}\mathbf 1 _{n}=0$, the global closed-loop dynamics can be written as

$$\begin{aligned} \dot{\delta }&= (I_{n}\otimes A-\hat{C}(t)H_{\sigma (t)}\otimes BK)\delta +(\hat{C}(t)H_{\sigma (t)}\otimes BK)\tilde{x}+(\hat{C}(t)\otimes B)\nonumber \\&\quad \times \,\mathrm{sgn}\big (-(H_{\sigma (t)}\otimes K)(\delta -\tilde{x})\big )-(I_{n}\otimes B)\big (\mathbf 1 _{n}\otimes f(x_{0},t)\big ),\nonumber \\ \dot{\tilde{x}}&= (I_{n}\otimes A-\hat{C}(t)H_{\sigma (t)}\otimes FC)\tilde{x}. \end{aligned}$$

(12)

Then, let $\xi =[\delta ^{T},\tilde{x}^{T}]^{T}$, we have

$$\begin{aligned} \dot{\xi }(t)=\hat{A}\xi +\hat{F}(x,t), \end{aligned}$$

where

$$\begin{aligned} \hat{A}&= \left( \begin{array}{c@{\quad }c} I_{n}\otimes A-\hat{C}(t)H_{\sigma (t)}\otimes BK &{} \hat{C}(t)H_{\sigma (t)}\otimes BK \\ 0 &{} I_{n}\otimes A-\hat{C}(t)H_{\sigma (t)}\otimes FC \\ \end{array} \right) ,\\ \hat{F}(x,t)&= \left( \begin{array}{c@{\quad }c} (\hat{C}(t)\otimes B)\mathrm{sgn}\big (-(H_{\sigma (t)}\otimes K)(\delta -\tilde{x})\big )-(I_{n}\otimes B)\big (\mathbf 1 _{n}\otimes f(x_{0},t)\big ) \\ 0 \\ \end{array}\!\!\!\right) . \end{aligned}$$

Theorem 1

Consider the leader-follower multi-agent system (4)–(5) with the variable communication topologies described in Fig. 1 and Remark 1 and leader’s control input given by Assumption 1. The consensus tracking satisfying (6) under the adaptive protocol (11) can be achieved, if for scalars $\rho _{i}>0,\,\bar{\tau }>0$, design $K=B^{T}P^{-1},\,F=PC^{T}$, and $\varPsi =P^{-1}BB^{T}P^{-1}$, where $P>0$ is a solution to the following LMIs:

$$\begin{aligned}&AP+PA^{T}-2 BB^{T}<0,\end{aligned}$$

(13)

$$\begin{aligned}&AP+PA^{T}-2M<0, \left( \begin{array}{cc} C^{T} C &{} * \\ \hat{P} &{} \hat{M} \end{array} \right) \ge 0, \hat{P}P=I, \hat{M}M =I. \end{aligned}$$

(14)

Proof

We construct a Lyapunov function candidate

$$\begin{aligned} V(\xi ,c,t)=\frac{1}{2}\xi ^{T}\left( \varOmega \otimes P^{-1}\right) \xi +\sum _{i=1}^{n}\frac{\mu }{2\rho _{i}}(c_{i}(t)-\alpha )^{2}, \end{aligned}$$

(15)

where $\varOmega =\left( \begin{array}{cc} \mu H_{\sigma (t)} &{} -\mu H_{\sigma (t)} \\ -\mu H_{\sigma (t)} &{} \eta H_{\sigma (t)} \\ \end{array} \right) ,\,\alpha >0,\,\eta \gg \mu >0$. It will be shown that $V(\xi ,c,t)\ge 0$, and $V(\xi ,c,t)=0$ if and only if $\xi =0$ and $c_{i}(t)=\alpha ,\,\forall i=1,\ldots ,n$. According to Lemma 1, one obtains

$$\begin{aligned} V(\xi ,c,t)\ge \frac{1}{2}\xi ^{T}(\hat{\varOmega }\otimes P^{-1})\xi +\sum _{i=1}^{n}\frac{\mu }{2\rho _{i}}(c_{i}(t)-\alpha )^{2}, \end{aligned}$$

(16)

where $\hat{\varOmega }=\left( \begin{array}{cc} \mu \lambda _{\sigma _{*}i_{*}}I_{n} &{} -\mu H_{\sigma (t)} \\ -\mu H_{\sigma (t)} &{} \eta \lambda _{\sigma _{*}i_{*}}I_{n} \\ \end{array} \right)$. By Schur complement and Lemma 1, $\hat{\varOmega }>0$ is equivalent to that $\eta \lambda _{\sigma _{*}i_{*}}>0$, and $\mu \lambda _{\sigma _{*}i_{*}}I_{n}-\frac{\mu ^{2}}{\eta \lambda _{\sigma _{*}i_{*}}}H^{2}_{\sigma (t)}>0$, which hold as $\eta \gg \mu >0$. Hence, $V(\xi ,c,t)\ge 0$, and $V(\xi ,c,t)=0$ if and only if $\xi =0$ and $c_{i}(t)=\alpha ,\,\forall i=1,\ldots ,n$.

$$\begin{aligned} \dot{V}(\xi ,c,t)&= \xi ^{T}(\varOmega \otimes P^{-1})\big (\hat{A}\xi +\hat{F}(x,t)\big )+\sum _{i=1}^{n}\frac{\mu }{\rho _{i}}(c_{i}(t)-\alpha )\dot{c}_{i}(t)\nonumber \\&= \frac{1}{2}\xi ^{T}\left( \left( \varOmega \otimes P^{-1}\right) \hat{A}+\hat{A}^{T}\left( \varOmega \otimes P^{-1}\right) \right) \xi +\xi ^{T}(\varOmega \otimes P^{-1})\hat{F}(x,t)\nonumber \\&\quad +\,\sum _{i=1}^{n}\frac{\mu }{\rho _{i}}(c_{i}(t)-\alpha )\dot{c}_{i}(t). \end{aligned}$$

(17)

Design $K=B^{T}P^{-1}$ and $F=PC^{T}$, in which $P$ is a positive definite matrix. Then, we obtain

$$\begin{aligned} \left( \varOmega \!\otimes \! P^{-1}\right) \hat{A}\!+\!\hat{A}^{T}(\varOmega \!\otimes \! P^{-1}) \!=\! \left( \begin{array}{cc} \mu \left( {H_{A}-2H_{B}}\right) &{} * \\ \mu \left( -H_{A}\!+\!2H_{B}\!+\!H_{C}\right) &{} \eta (H_{A}\!-\!2H_{C})\!-\!2\mu H_{B} \\ \end{array}\right) , \end{aligned}$$

(18)

where

$$\begin{aligned} H_{A}&= H_{\sigma (t)}\otimes P^{-1}A+H_{\sigma (t)}\otimes A^{T}P^{-1},\\ H_{B}&= H_{\sigma (t)}\hat{C}(t)H_{\sigma (t)}\otimes P^{-1}BB^{T}P^{-1},\\ H_{C}&= H_{\sigma (t)}\hat{C}(t)H_{\sigma (t)}\otimes C^{T}C, \end{aligned}$$

and

$$\begin{aligned}&\xi ^{T}\left( \varOmega \otimes P^{-1}\right) \hat{F}(x,t) \nonumber \\&\quad =(\delta -\tilde{x})^{T}(\mu H_{\sigma (t)}\hat{C}(t)\otimes P^{-1}B)\mathrm{sgn}\big (-\left( H_{\sigma (t)}\otimes K\right) \left( \delta -\tilde{x}\right) \big )\nonumber \\&\quad -\left( \delta -\tilde{x}\right) ^{T}(\mu H_{\sigma (t)}\otimes P^{-1}B)\left( \mathbf 1 _{n}\otimes f(x_{0},t)\right) . \end{aligned}$$

(19)

As $K=B^{T}P^{-1}$, by simple calculation, one has

$$\begin{aligned}&(\delta -\tilde{x})^{T}(\mu H_{\sigma (t)}\hat{C}(t)\otimes P^{-1}B)\mathrm{sgn}\left[ -\left( H_{\sigma (t)}\otimes K\right) (\delta -\tilde{x})\right] \nonumber \\&\quad =(\delta -\tilde{x})^{T}(\mu H_{\sigma (t)}\hat{C}(t)\otimes P^{-1}B)\mathrm{sgn}\left[ -(H_{\sigma (t)}\otimes B^{T}P^{-1})(\delta -\tilde{x})\right] \nonumber \\&\quad =-\mu \sum _{i=1}^{n}c_{i}(t)\left( \varepsilon _{i}^{T}P^{-1}B\right) \mathrm{sgn}\big ( B^{T}P^{-1}\varepsilon _{i}\big )\nonumber \\&\quad =-\mu \sum _{i=1}^{n}c_{i}(t) \Vert B^{T}P^{-1}\varepsilon _{i} \Vert _{1}, \end{aligned}$$

(20)

and

$$\begin{aligned}&-(\delta -\tilde{x})^{T}(\mu H_{\sigma (t)}\otimes P^{-1}B)(\mathbf 1 _{n}\otimes f(x_{0},t))\nonumber \\&\quad \le \mu \Vert f(x_{0},t)\Vert _{\infty }\Vert (H_{\sigma (t)}\otimes B^{T}P^{-1})\left( \delta -\tilde{x}\right) \Vert _{1}. \end{aligned}$$

(21)

Combining (17)–(21), one obtains

$$\begin{aligned}&\dot{V}(\xi ,c,t)\\&\quad \le \frac{1}{2}\mu \delta ^{T}\big (H_{\sigma (t)}\!\otimes \! P^{-1}A+H_{\sigma (t)}\!\otimes \! A^{T}P^{-1}-2H_{\sigma (t)}\hat{C}(t)H_{\sigma (t)}\!\otimes \! P^{-1}BB^{T}P^{-1}\big )\delta \\&\qquad +\mu \tilde{x}^{T}\big (-H_{\sigma (t)}\!\otimes \! P^{-1}A\!-\!H_{\sigma (t)}\!\otimes \! A^{T}P^{-1}+2H_{\sigma (t)}\hat{C}(t)H_{\sigma (t)}\otimes P^{-1}BB^{T}P^{-1}\\&\qquad +\,H_{\sigma (t)}\hat{C}(t)H_{\sigma (t)}\otimes C^{T}C\big )\delta \\&\qquad +\,\frac{1}{2}\eta \tilde{x}^{T}\big ((H_{\sigma (t)}\otimes P^{-1}A+H_{\sigma (t)}\otimes A^{T}P^{-1}-2H_{\sigma (t)}\hat{C}(t)H_{\sigma (t)}\otimes C^{T}C)\\&\qquad -\,2\frac{\mu }{\eta } H_{\sigma (t)}\hat{C}(t)H_{\sigma (t)}\otimes P^{-1}BB^{T}P^{-1}\big )\tilde{x}-\mu \sum _{i=1}^{n}c_{i}(t) \Vert B^{T}P^{-1}\varepsilon _{i} \Vert _{1}\\&\qquad +\,\mu \Vert f(x_{0},t)\Vert _{\infty }\Vert (H_{\sigma (t)}\otimes B^{T}P^{-1})(\delta -\tilde{x})\Vert _{1}+\sum _{i=1}^{n}\frac{\mu }{\rho _{i}}(c_{i}(t)-\alpha )\dot{c}_{i}(t). \end{aligned}$$

Under the observer-based adaptive control law (11) and Assumption 1, denote $\bar{\tau }=\frac{\eta }{\mu }-1$ and design $K=B^{T}P^{-1},\,\varPsi =P^{-1}BB^{T}P^{-1}$ in (11), and hence, we get

$$\begin{aligned} \dot{V}&\le \frac{1}{2}\mu \delta ^{T}\big (H_{\sigma (t)}\otimes P^{-1}A+H_{\sigma (t)}\otimes A^{T}P^{-1}-2\alpha H_{\sigma (t)}^{2}\otimes P^{-1}BB^{T}P^{-1}\big )\delta \nonumber \\&\quad +\,\mu \tilde{x}^{T}\big (-H_{\sigma (t)}\otimes P^{-1}A-H_{\sigma (t)}\otimes A^{T}P^{-1}+2\alpha H_{\sigma (t)}^{2}\otimes P^{-1}BB^{T}P^{-1}\nonumber \\&\quad +\,\alpha H_{\sigma (t)}^{2}\otimes C^{T}C\big )\delta +\frac{1}{2}\eta \tilde{x}^{T}\big ((H_{\sigma (t)}\otimes P^{-1}A+H_{\sigma (t)}\otimes A^{T}P^{-1}\nonumber \\&\quad -\,2\alpha H_{\sigma (t)}^{2}\otimes C^{T}C)-2\frac{\mu }{\eta } \alpha H_{\sigma (t)}^{2}\otimes P^{-1}BB^{T}P^{-1}\big )\tilde{x}\nonumber \\&\quad -\,\mu (\alpha -\kappa ) \Vert (H_{\sigma (t)}\otimes B^{T}P^{-1})(\delta -\tilde{x}) \Vert _{1}. \end{aligned}$$

(22)

Letting $\bar{\xi }=(I_{2n}\otimes P^{-1})\xi$, i.e., $\bar{\delta }=(I_{n}\otimes P^{-1})\delta$ and $\bar{\tilde{x}}=(I_{n}\otimes P^{-1})\tilde{x}$, from (22), one has

$$\begin{aligned} \dot{V}\le&\frac{1}{2}\bar{\xi }^{T} \left( \begin{array}{cc} \mu ({\bar{H}_{A}-2\bar{H}_{B}})&{} * \\ \mu (-\bar{H}_{A}+2\bar{H}_{B}+\bar{H}_{C}) &{} \eta (\bar{H}_{A}-2\bar{H}_{C}-2\frac{\mu }{\eta } \bar{H}_{B}) \\ \end{array}\right) \bar{\xi }\nonumber \\&-\mu (\alpha -\kappa ) \Vert (H_{\sigma (t)}\otimes B^{T})(\bar{\delta }-\bar{\tilde{x}}) \Vert _{1}, \end{aligned}$$

(23)

where

$$\begin{aligned} \bar{H}_{A}&= H_{\sigma (t)}\otimes AP+H_{\sigma (t)}\otimes PA^{T},\\ \bar{H}_{B}&= \alpha H_{\sigma (t)}^{2}\otimes BB^{T},\\ \bar{H}_{C}&= \alpha H_{\sigma (t)}^{2}\otimes PC^{T}CP. \end{aligned}$$

Since matrix $H_{\sigma (t)}$ described in Fig. 1 and remark 1 is positive definite, there exits a unitary matrix $U_{\sigma (t)}\in R^{n\times n}$ such that $U_{\sigma (t)}^{T}H_{\sigma (t)}U_{\sigma (t)}=\varLambda _{\sigma (t)} =\hbox {diag}(\lambda _{\sigma (t)1}, \ldots , \lambda _{\sigma (t)n})$, and denote $\tilde{\xi }=(U_{\sigma (t)}^{T}\otimes I_{p})\bar{\xi }$. Then, we get

$$\begin{aligned} \dot{V} \le&\frac{1}{2}\tilde{\xi }^{T} \left( \begin{array}{cc} \mu ({\tilde{H}_{A}-2\tilde{H}_{B}})&{} * \\ \mu (-\tilde{H}_{A}+2\tilde{H}_{B}+\tilde{H}_{C}) &{} \eta (\tilde{H}_{A}-2\tilde{H}_{C}-2\frac{\mu }{\eta } \tilde{H}_{B}) \\ \end{array}\right) \tilde{\xi }\nonumber \\&-\mu (\alpha -\kappa ) \Vert (H_{\sigma (t)}\otimes B^{T})(\bar{\delta }-\bar{\tilde{x}}) \Vert _{1}\nonumber \\ =&\frac{1}{2}\sum \limits _{i=1}^{n}\lambda _{\sigma (t)i}\tilde{\xi }_{i}^{T}\varPi \tilde{\xi }_{i}-\mu (\alpha -\kappa ) \Vert (H_{\sigma (t)}\otimes B^{T})(\bar{\delta }-\bar{\tilde{x}}) \Vert _{1}, \end{aligned}$$

(24)

where

$$\begin{aligned} \tilde{H}_{A}&= \varLambda _{\sigma (t)}\otimes AP+\varLambda _{\sigma (t)}\otimes PA^{T},\\ \tilde{H}_{B}&= \alpha \varLambda _{\sigma (t)}^{2}\otimes BB^{T},\\ \tilde{H}_{C}&= \alpha \varLambda _{\sigma (t)}^{2}\otimes PC^{T}CP, \end{aligned}$$

and

$$\begin{aligned} \varPi =\left( \begin{array}{cc} \mu ({\hat{H}_{A}-2\hat{H}_{B}})&{} * \\ \mu (-\hat{H}_{A}+2\hat{H}_{B}+\hat{H}_{C}) &{} \eta (\hat{H}_{A}-2\hat{H}_{C}-2\frac{\mu }{\eta } \hat{H}_{B}) \\ \end{array}\right) \end{aligned}$$

(25)

in which

$$\begin{aligned} \hat{H}_{A}&= AP+ PA^{T},\\ \hat{H}_{B}&= \alpha \lambda _{\sigma (t)i} BB^{T},\\ \hat{H}_{C}&= \alpha \lambda _{\sigma (t)i} PC^{T}CP. \end{aligned}$$

Choose $\alpha$ to satisfy $\alpha \lambda _{\sigma (t) i}\ge 1$ for $\sigma (t)i=\sigma _{*}i_{*}$ and $\sigma ^{*}i^{*}$; then, based on (13) and $\mu >0,\,\mu ({\hat{H}_{A}-2\hat{H}_{B}})<0$, i.e., $\mu (AP+PA^{T}-2\alpha \lambda _{\sigma (t)i} BB^{T})<0$ holds. Then, giving $\eta$ in $\eta \gg \mu >0$ sufficiently large, we can ensure $\eta (\hat{H}_{A}-2\hat{H}_{C}-2\frac{\mu }{\eta } \hat{H}_{B})<0$, i.e., $\eta (AP+PA^{T}-2\alpha \lambda _{\sigma (t)i} PC^{T}CP -2\frac{\mu }{\eta }\alpha \lambda _{\sigma (t)i} BB^{T})<0$ if $AP+PA^{T}-2 PC^{T}CP<0$ holds. Then, by Schur complement, we get $\varPi <0$. Moreover, choosing $\alpha \ge \kappa$, and from (24), one obtains

$$\begin{aligned} \dot{V} \le \frac{1}{2}\sum _{i=1}^{n}\lambda _{\sigma (t)i}\tilde{\xi }_{i}^{T}\varPi \tilde{\xi }_{i} \end{aligned}$$

(26)

and hence $\dot{V}\le 0$ satisfies, which implies that $V$ is nonincreasing. Hence, by selecting $\alpha$ sufficiently large such that $\alpha \lambda _{\sigma (t) i}\ge 1$ and $\alpha \ge \kappa$, i.e., $\alpha \ge \mathrm{max}\{\frac{1}{\lambda _{\sigma _{*}i_{*}}},\kappa \}$, and in view of (15), we know that $\xi ,\,\tilde{\xi }$, and $c_{i}$ are bounded. Since by Assumption 1, $u_{0}$ is bounded, implying from the Eq. (11) and $\dot{\xi }(t)=\hat{A}\xi +\hat{F}(x,t)$ that $\dot{\xi },\,\dot{\tilde{\xi }}$, and $\dot{c}_{i}$ are bounded. Combining $\dot{V}$ in (17), one finally has that $\ddot{V}$ is bounded. Then, using the well-known Barbalat’s Lemma [10], we get that $\dot{V}\rightarrow 0$ as $t\rightarrow \infty$, and hence, $\xi \rightarrow 0$ as $t\rightarrow \infty$. Since $\varPsi \ge 0$ and $\rho _{i}>0$, $c_{i}$ is monotonically increasing. Thus, the boundedness of $c_{i}(i=1,\ldots ,n)$ implies that each $c_{i}$ converges to some finite value.

It should be noted that the obtained conditions in Theorem 1 are not strict LMIs conditions due to (14). However, using the idea of the cone complementarity [4], we can solve this problem by converting it into a sequential optimization problem subject to LMI constraints:

$$\begin{aligned}&\mathrm{Min}~~ \mathrm{tr}(\hat{P}P+\hat{M}M)\nonumber \\&\mathrm{subject\,to\,(13), (14)\,and}\nonumber \\&\quad \left( \begin{array}{cc } \hat{P} &{} * \\ I&{} P \\ \end{array} \right) \ge 0,~~ \left( \begin{array}{cc} \hat{M} &{} * \\ I&{} M \\ \end{array} \right) \ge 0. \end{aligned}$$

(27)

The aforementioned minimization problem can be solved by the following iterative algorithm.

Algorithm 1

• (1) For given constants $\alpha \ge \mathrm{max}\{\frac{1}{\lambda _{\sigma _{*}i_{*}}},\kappa \}$, and $\bar{\tau }>0$, find a feasible set ($\hat{P}_{0}, {P}_{0}, \hat{M}_{0}, {M}_{0}$) under the LMIs conditions in (27). set $k=1$.

• (2) Solve the following LMI problem with a feasible solution ($\hat{P}, {P}, \hat{M}, {M}$)

  $$\begin{aligned}&\mathrm{Min~~ tr}(\hat{P}_{k}P+P_{k}\hat{P}+\hat{M}_{k}M+M_{k}\hat{M})\\&\mathrm{subject\,to\,LMIs\,in} (27)\\&\mathrm{Set}~ \hat{P}_{k+1}=\hat{P}, P_{k+1}=P, \hat{M}_{k+1}=\hat{M}, M_{k+1}=M. \end{aligned}$$

• (3) If the conditions (13) and (14) are satisfied, then the controller gain, observer gain, and constant matrix are designed as $K=B^{T}P^{-1},\,F=PC^{T}$, and $\varPsi =P^{-1}BB^{T}P^{-1}$ and exit. If the conditions (13) and (14) are not satisfied within a specified number of iterations, then say “no solution” and exit. Otherwise, set $k=k+1$ and return to Step (2).

Remark 2

Here, we study the leader-follower MAS with general dynamics, which includes first-order and second-order integrator dynamics as a special case and is different from the existing literature [27]. Unlike [19, 25], the proposed consensus tracking algorithm is fully distributed without using any global spectrum information for multi-agent systems, when we choose $\alpha$ sufficiently large. In addition, the leader’s nonzero input in our work is considered, which implies the leader-following multi-agent system here is in essence heterogeneous. Moreover, distinct from [11, 19, 25] where the state feedback consensus protocol is designed under the assumption that all the followers’ state vectors are accessible for feedback, in our work, the full state of followers is not available. We design the actual observer to implement the observer-based distributed output feedback consensus tracking algorithm, such that the state estimates $\hat{x}_{i}$ could converge to the real states $x_{i}$. Hence, this is also different from [12], where the so-called “state estimate” $v_{i}$ does not converge to the real state $x_{i}$, but only acts as the intermediate variables for consensus. Furthermore, both the feedback gain and the observer gain are determined but not chosen simultaneously, and by the cone complementary linearization method, sufficient conditions to ensure consensus tracking for the MAS are obtained. These key distinctions we solve in this paper may be more practical in applications.

4 Illustrative Example

In this section, a simulation example is provided for testing the observer-based distributed output feedback consensus algorithm developed for leader-follower multi-agent systems under switching topology in this paper. The matrices in (4) and (5) are $A= \left( \begin{array}{cc} 0 &{} -1 \\ 1 &{} -2 \\ \end{array} \right) ,\,B= \left( \begin{array}{ c } 0 \\ 1 \\ \end{array} \right) ,\,C= \left( \begin{array}{cc} 1 &{} -1 \\ 0 &{} 2 \\ \end{array} \right)$, and the states $x_{i}= \left( \begin{array}{ c } x_{i1} \\ x_{i2} \\ \end{array} \right) ,\,\forall i=0,1,\ldots , 5$. The leader’s input is given as $f(x_{0},t)=[0~~ 2]x_{0}$, and obviously, it satisfies Assumption 1. The communication structure described like Fig. 1 of MASs (4) and (5) dynamically switches among three topologies based on a specific switching signal mode shown in Fig. 2, where $\sigma (t)=1,2,3$ presents three possible and different connected topologies changing one another at each switching instant, and $\tau$ is chosen to be 1 s. The adjacent matrices and Laplacian matrices corresponding to the three switching topologies are given in the following

$$\begin{aligned} \bar{A}_{L_{1}}&= \left( \begin{array}{ccclr} 0 &{} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{}1&{} 0 &{}0 &{}0 \\ 1&{} 0 &{}0 &{}0 &{}0 \\ \end{array} \right) ,~~~\bar{L}_{1}=\left( \begin{array}{ c c c l r } 2 &{} -1&{} 0 &{}0 &{}-1 \\ -1 &{} 3 &{} -1 &{}-1 &{} 0 \\ 0 &{} -1 &{} 1 &{}0 &{} 0 \\ 0 &{} -1 &{} 0 &{} 1 &{} 0 \\ -1 &{} 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right) ;\nonumber \\ \bar{A}_{L_{2}}&= \left( \begin{array}{ c c c l r } 0 &{} 0 &{} 1 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 &{} 1 &{} 0 \\ 1 &{}0&{} 1 &{}0 &{}1 \\ 1&{} 1 &{}0 &{}1 &{}0 \\ \end{array} \right) ,~~~\bar{L}_{2}=\left( \begin{array}{ c c c l r } 3 &{} 0&{} -1 &{}-1 &{}-1 \\ 0 &{} 1&{} 0 &{}0 &{} -1 \\ -1 &{} 0 &{} 2 &{}-1 &{} 0 \\ -1 &{} 0 &{} -1 &{} 3 &{} -1 \\ -1 &{} -1 &{} 0 &{} -1 &{} 3\\ \end{array} \right) ;\nonumber \\ \bar{A}_{L_{3}}&= \left( \begin{array}{ c c c l r } 0 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 0 &{} 1 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0 &{} 0 &{} 0 \\ 1 &{}0&{} 0 &{}0 &{}1 \\ 0&{} 0 &{}0 &{}1 &{}0 \\ \end{array} \right) ,~~~\bar{L}_{3}=\left( \begin{array}{ c c c l r } 3 &{} -1&{} -1 &{}-1 &{}0 \\ -1 &{} 2 &{} -1 &{}0 &{} 0 \\ -1 &{} -1 &{} 2 &{}0 &{} 0 \\ -1 &{} 0 &{} 0 &{} 2 &{} -1 \\ 0 &{} 0 &{} 0 &{} -1 &{} 1\\ \end{array} \right) . \end{aligned}$$

(28)

The interconnection relationship between the leader and the followers is described as the diagonal matrix $\bar{B}_{1}=\mathrm{diag}(1~~0~~0~~ 1~~0),\,\bar{B}_{2}=\mathrm{diag}(1~~0~~1~~ 0~~0)$, and $\bar{B}_{3}=\mathrm{diag}(0~~1~~1~~ 0~~0)$.

Fig. 2

Switching signal $\sigma (t)$.

Then, the maximum and the minimum eigenvalues of these three Laplacian matrices are $5.0464$ and $0.1864$. Using our proposed observer-based distributed output feedback consensus tracking algorithm, and by solving the LMIs (13) and (14), we obtain the feedback gain matrix $K$, observer gain matrix $F$, and the constant matrix $\varPsi$ as

$$\begin{aligned} K= \left( \begin{array}{cc} 0.2114 &{} 0.9004 \\ \end{array} \right) ,~~~F=\left( \begin{array}{cc} 4.3550 &{} -1.6560\\ -2.1330 &{} 2.6101 \\ \end{array} \right) ,~~~\varPsi =\left( \begin{array}{cc} 0.0447 &{} 0.1903\\ 0.1903 &{} 0.8106\\ \end{array} \right) . \end{aligned}$$

In the following, we will show the effectiveness of the aforementioned controller and observer gains. Choose $\eta =55,\,\mu =0.5,\,\alpha =6$, and $\rho _{i}=1,\,\forall i=1,\ldots ,5$ in (11); select $c_{i}(0)$ and $\delta ,\,\tilde{x}$ of global closed-loop dynamics (12) randomly, and we get the following results described by Figs. 3, 4, 5.

Fig. 3

Observer errors $x_{i}-\hat{x}_{i}$ of all followers

Fig. 4

Consensus tracking errors $x_{i}-x_{0}$ of all followers

Fig. 5

Adaptive coupling weights $c_{i}$ of all followers

The simulation results show that, under the three switching topologies given in (28) and the control protocol (11) for the leader-follower multi-agents (4)–(5), the global observer error $x_{i}-\hat{x}_{i} (\forall i=1,\ldots ,5)$ is shown in Fig. 3, suggesting that our designed observers can estimate the actual states actually. Figure 4 displays all the consensus tracking error $x_{i}-x_{0}$ for $i=1,\ldots ,5$ and implies that the consensus tracking is indeed achieved within 15 s. Fig. 5 indicates the adaptive coupling gain $c_{i}$ of each follower, which remains unchanged after about $t=5$ s.

5 Conclusion

In this paper, the consensus tracking algorithm via observer-based distributed and dynamic output feedback control for leader-follower MASs under arbitrary switching topology is investigated. Specially, the full state information of followers is not available and the leader’s input is nonzero in general case. The actual observer is designed to estimate the state directly, and the adaptive laws with distributed control gains are proposed to complete the tracking in a fully distributed fashion without the global graph information. Also, both the observer gain and feedback gain are designed, simultaneously. Moreover, by employing a cone complementary linearization approach, sufficient conditions for reaching consensus tracking for the MAS without the follower’s states measurable under switching topology are first deduced. A simulation example is exploited to demonstrate the effectiveness of the proposed algorithm.