1 Introduction

Distributed consensus control (including consensus seeking and consensus tracking) of multi-agent systems (MASs) has recently emerged as an important topic in the control community [1, 2]. Since pioneering works of Jadbabaie et al. [3] and Olfati et al. [4], many results on consensus have been obtained for MASs with distinct agent dynamics, such as single-integrator dynamics [5, 6], double-integrator dynamics [7,8,9] and general linear dynamics [10, 11]. For the state of art of consensus research, readers can refer to recent research monograph and surveys [12, 13].

Due to the fact that nonlinearities exist widely in the control systems, much progress has been achieved for the consensus problem of nonlinear MASs. For nonlinearities satisfying the Lipschitz condition, the consensus problem of second-order nonlinear MASs is considered in [14, 15] by resorting to the matrix theory and linear Lyapunov method. For nonlinearities that can be “linearly parameterized,” adaptive control for the consensus problem was developed in [16, 17] with the regression matrices being known. For nonlinearities without the Lipschitz condition and the “linearity-in-parameters” assumption, neural networks (NNs) and fuzzy logic systems are promising strategies to neutralize the nonlinear effects due to their “universal approximation” property [18]. In [19,20,21,22,23], NNs were constructed in consensus controllers to directly confront the nonlinearities with matching condition. However, wider applications of the above methods are limited as they require agent nonlinearities to meet the matching condition, while many practical systems are so complicated that nonlinearities are unmatched with the input.

As a powerful technique to study nonlinear systems without matching condition, backstepping technique was proposed in [24]. In early literature, many results of adaptive neural or fuzzy backstepping design have been reported for strict-feedback or pure-feedback nonlinear systems [25,26,27,28]. Even though a single system of strict-feedback or pure-feedback form has been well studied, it is nontrivial to extend the methods therein to nonlinear MASs. The work of Yoo [29] represents the first paper on this topic, where the consensus tracking problem of nonlinear MASs under a direct graph was studied. Along this line, further results are presented in [30,31,32] for multiple nonlinear strict-feedback systems, where adaptive neural backstepping technique was applied. In [30], the command filtered backstepping technique was employed to study the consensus problem of MASs of strict-feedback dynamics under fixed undirected topology. In [31], the author proposed a consensus tracking approach for multiple nonlinear strict-feedback systems under a jointly switching topology. The author in [32] studied the leader-following consensus problem for nonlinear MASs in strict-feedback form with state time delays. More recently, observer-based consensus control schemes were considered in [33,34,35,36]. In [33, 34], authors constructed observers in each follower agent to observe the state of the leader, which enable some techniques in single systems to be available. To avoid measuring all agents’ states directly, the authors in [35, 36] proposed an observer-based adaptive backstepping consensus protocol for MASs with second-order dynamics and semi-strict-feedback dynamics, respectively. However, actuators of real MASs often encounter the hysteresis phenomena which could severely deteriorate the actuator performance [37,38,39]. It is notable that distributed protocols in previous works were designed on the basis that the actuator of each agent works without any hysteresis constraint, which is not applicable in practice when hysteresis constraints exist [40,41,42,43].

Motivated by the above discussions, we investigate the consensus tracking problem for a class of unmatched nonlinear MASs using observer-based control. Each follower is assumed to be in output-feedback form with unknown nonlinear dynamics and external disturbances. Moreover, considering the actuator hysteresis, our problem is more important and challenging in both theory and real-world applications. We use radial basis function (RBF) NNs to approximate the unknown nonlinearities. Under this circumstance, a state observer is designed to estimate the unmeasurable states of each follower. Then, using the backstepping technique, an observer-based distributed adaptive NN controller is proposed. For a directed graph containing a spanning tree, we show that all signals of the closed-loop system are semi-globally uniformly ultimately bounded, and both the consensus tracking error and the observer error converge to an adjustable neighborhood of the origin. Compared with existing results, the main contributions of our paper are twofold:

  1. 1.

    For nonlinear MASs in output-feedback form [44], our work represents the first trial to design distributed adaptive NN controllers for them without full state information. Even nonlinear dynamics considered in [45] is in the output-feedback form, the authors required the nonlinearities to be subjected by an inequality, which limits the choice of the nonlinearities.

  2. 2.

    Actuator of each follower suffering from the Bouc–Wen hysteresis is introduced to the consensus problem of nonlinear MASs. In our previous work [46], we considered MASs of Brunovsky form nonlinearity with actuators suffering from backlash-like hysteresis. However, the controller design is easier in [46] as nonlinearities in Brunovsky form satisfy the matching condition.

The rest of the paper is organized as follows. Problem formulation is introduced in Sect. 2. In Sect. 3, a novel observer-based distributed controller and its stability are presented. Simulation examples are presented in Sect. 4 to demonstrate the effectiveness of the proposed protocols. Section 5 concludes the paper.

Notations\(I_n\) denotes the \(n \times n\) identity matrix and \(1_{n}\) denotes a vector in \({\mathbb {R}}^{n}\) with elements being all ones. \(\Vert \cdot \Vert \) refers to the standard Euclidean norm or the induced matrix 2-norm. We say \(P> 0\) (\(P< 0\)) if the matrix P is positive (negative) definite. \(\text{ diag }\{z_{1},\ldots ,z_{m}\}\) denotes the diagonal matrix with diagonal entries \(z_{1}\) to \(z_{m}\).

2 Preliminaries and problem formulation

2.1 Algebraic graph theory

A directed graph \({\mathcal {G}}=({\mathcal {V}},{\mathcal {E}})\) consists of a set of nodes \({\mathcal {V}}=\{1,\ldots ,N\}\) and a set of directed edges \({\mathcal {E}}\subseteq {\mathcal {V}}\times {\mathcal {V}}\) of the form (j, i). If \((j,i)\in {\mathcal {E}}\), we say i can receive information from j and j is a neighbor of i. The set of neighbors of node i is denoted by \(N_{i}=\{j\in {\mathcal {V}}:(j,i)\in {\mathcal {E}}\}\). A sequence of edges \((i_1, i_2), (i_2, i_3), \ldots , (i_{k-1}, i_k)\) is called a directed path from node \(i_1\) to node \(i_k\). \({\mathcal {G}}\) is said to contain a spanning tree if there exists a node, called the root, which has a directed path to every other nodes in the graph. Denote the adjacency matrix of \({\mathcal {G}}\) as \({\mathcal {A}}=[a_{ij}] \in {\mathbb {R}}^{N \times N}\) where \(a_{ij}>0\)\(\Leftrightarrow \)\((j,i)\in {\mathcal {E}}\). The Laplacian matrix \(L=[l_{ij}] \in {\mathbb {R}}^{N \times N}\) of \({\mathcal {G}}\) is defined by \(L={\mathcal {D}}-{\mathcal {A}}\), where \({\mathcal {D}}=\text{ diag }\{d_1,\ldots ,d_N\}\) is the degree matrix with \(d_i=\sum _{j\in N_{i}}a_{ij}\).

2.2 RBF neural networks

The RBF NN \(h_{nn}(z)\) is described by

$$\begin{aligned} h_{nn}(z)=W^{T}\varPsi (z) \end{aligned}$$
(1)

where \(z\in \varOmega _{z}\subset {\mathbb {R}}^{q}\) is the input with q being the input dimension, the weight \(W=[w_{1},\ldots ,w_{p}]^{T}\in {\mathbb {R}}^{p}\), and \(p>1\) is the number of the NN nodes. \(\varPsi (z)=[\varphi _{1}(z),\ldots ,\varphi _{p}(z)]^{T}\) denotes the basis function vector with \(\varphi _{i}(z)\) being the Gaussian function

$$\begin{aligned} \varphi _{i}(z)=\mathrm {exp}\left[ \frac{-(z-\mu _{i})^T(z-\mu _{i})}{\eta _{i}^2}\right] \quad (i=1,\ldots ,p) \end{aligned}$$

where \(\mu _{i}=[\mu _{i 1},\ldots ,\mu _{i q}]^{T}\) is the center of the receptive field and \(\eta _{i}\) is the width of the Gaussian function.

As shown in [18], when the number p of NN nodes is sufficiently large, the RBF NN (1) can approximate any continuous function h(z) over a compact set \(\varOmega _{z}\subset {\mathbb {R}}^{q}\) to arbitrary accuracy \(\varepsilon _{0}>0\) as

$$\begin{aligned} h(z)=W^{*T}\varPsi (z)+\varepsilon (z),\quad \forall z\in \varOmega _{z} \end{aligned}$$
(2)

where \(W^{*}\) is the ideal weight vector defined by

$$\begin{aligned} W^{*}=\mathrm {arg}\min _{W\in {\mathbb {R}}^{p}}\left\{ \sup _{z\in \varOmega _{z}}\left| h(z)-W^{T}\varPsi (z)\right| \right\} \end{aligned}$$

and \(\varepsilon (z)\) is the approximation error satisfying \(|\varepsilon (z)|\le \varepsilon _{0}\).

2.3 Hysteresis nonlinearity

Various hysteresis models have been constructed to describe the hysteresis nonlinearity [40], such as Duhem model, Maxwell model, Preisach model and Bouc–Wen model. Among them, the Bouc–Wen model has become increasingly popular in the literature due to its capability of capturing a range of shapes of hysteretic cycles. Moreover, a new perfect inverse for the Bouc–Wen model has been proposed [41], which facilitates the observer-based distributed controller design in the framework of MASs and thus is adopted in this paper.

The Bouc–Wen hysteresis nonlinearity [41] is described by

$$\begin{aligned} u=H(v)=\rho _{1}v+\rho _{2}\theta \end{aligned}$$
(3)

where \(\rho _{1}\) and \(\rho _{2}\) are constants with the same sign. \(\theta \in {\mathbb {R}}\) is generated by

$$\begin{aligned} {\dot{\theta }}={\dot{v}}f(\theta ,{\dot{v}}),\quad \theta (t_{0})=0 \end{aligned}$$
(4)

with

$$\begin{aligned} f(\theta ,{\dot{v}})=1-\mathrm {sign}({\dot{v}})\beta |\theta |^{m-1}\theta -\chi |\theta |^{m} \end{aligned}$$
(5)

where \(\beta >|\chi |\), \(m\ge 1\), \(\beta \) and \(\chi \) are parameters describing the shape and amplitude of the hysteresis. m governs the smoothness of the transition from the initial slope to the slope of the asymptote.

In [41], Zhou et al. proposed a new inverse for the Bouc–Wen hysteresis model (3)–(5):

$$\begin{aligned} v=HI(u)=\frac{1}{\rho _{1}}u-\frac{\rho _{2}}{\rho _{1}}\theta _{1} \end{aligned}$$
(6)

where

$$\begin{aligned} \begin{aligned} {\dot{\theta }}_{1}&=\frac{{\dot{u}}}{\rho _{1}+\rho _{2}f\left( \theta _{1},\frac{{\dot{u}}}{\rho _{1}}\right) }f\left( \theta _{1},\frac{{\dot{u}}}{\rho _{1}}\right) ,\quad \theta _{1}(t_{0})=0\\ {\dot{v}}&=\frac{{\dot{u}}}{\rho _{1}+\rho _{2}f\left( \theta _{1},\frac{{\dot{u}}}{\rho _{1}}\right) } \end{aligned} \end{aligned}$$
(7)

and \(f(\cdot ,\cdot )\) is defined as in (5).

Lemma 1

([41]) For Bouc–Wen hysteresis model (3)–(5), the right hysteresis inverse can be constructed as (6)–(7) such that

$$\begin{aligned} \begin{aligned} u(t_{0})&=H(HI(u^{d}(t_{0})))=u^{d}(t_{0})\\&\Rightarrow u(t)=H(HI(u^{d}(t)))=u^{d}(t),\quad \forall ~t\ge t_{0} \end{aligned} \end{aligned}$$
(8)

where \(u^{d}\) is a designed control signal.

Figures 1 and 2 show the hysteresis and hysteresis inverse effects with parameters from the simulation part. Figure 3 shows how hysteresis inverse works.

Fig. 1
figure 1

Bouc–Wen hysteresis

Full size image
Fig. 2
figure 2

Inverse of Bouc–Wen hysteresis

Full size image
Fig. 3
figure 3

Control signal under Bouc–Wen hysteresis and its inverse

Full size image

2.4 Problem formulation

We consider a MAS consisting of \(N+1\) agents, where the agent indexed by 0 is assigned as the leader and the agents indexed by \(1,\ldots ,N\) are followers.

The dynamics of the ith follower is described by

$$\begin{aligned}&\left\{ \begin{array}{l} {\dot{x}}_{i,k}=x_{i,k+1}+f_{i,k}(y_{i})+\omega _{i,k}(t)\\ {\dot{x}}_{i,n}=u_i+f_{i,n}(y_i)+\omega _{i,n}(t)\\ y_{i}=x_{i,1},\quad k=1,\ldots ,n-1\\ u_i=H(u_i^{d}),\quad i=1,\ldots ,N \end{array}\right. \end{aligned}$$
(9)

where \(x_i=[x_{i,1},\ldots ,x_{i,n}]^T\in {\mathbb {R}}^{n}\) and \(y_i\in {\mathbb {R}}\) denote the state and output, respectively. The function \(f_{i,l}(\cdot )~(l=1,\ldots ,n)\) is the unknown nonlinear function; \(\omega _{i,l}\) stands for the external disturbance bounding by an unknown positive constant \(\omega _{i,l,0}\), i.e., \(|\omega _{i,l}(\cdot )|\le \omega _{i,l,0}\). \(u_i^{d}\in {\mathbb {R}}\) is the control input to be designed, and \(u_i\) is the output of the unknown Bouc–Wen hysteresis \(H(u_i^{d})\) defined by (3)–(5). Here, we assume that the motion of virtual leader 0 is independent of that of followers, whose measurable output is a time-varying reference state \(y_{0}\).

The topology of the information flow between N followers is modeled by the directed graph \({\mathcal {G}}=({\mathcal {V}},{\mathcal {E}})\). Furthermore, we define an augmented graph \(\mathcal {{\bar{G}}}=(\mathcal {{\bar{V}}},\mathcal {{\bar{E}}})\) to model the interaction topology of the system consisting of N followers and the leader, where \(\mathcal {{\bar{V}}}=\{0,1,\ldots ,N\}\) and \(\mathcal {{\bar{E}}}\subseteq \mathcal {{\bar{V}}}\times \mathcal {{\bar{V}}}\). Let \(B=\text{ diag }\{b_{1},\ldots ,b_{N}\} \in {\mathbb {R}}^{N \times N}\) be the leader adjacency matrix associated with \(\mathcal {{\bar{G}}}\), where \(b_{i}>0\) if follower i can receive information from leader 0 and \(b_{i}=0\) otherwise.

Remark 1

Regardless of the hysteresis nonlinearity and disturbance, the agent dynamics in (2.4) are in the so-called output-feedback form, in which system nonlinearities depend only on the measured output. As indicated in [47], many systems can be transformed into this form by a global state space diffeomorphism. Although continuous progress has been made toward the control of nonlinear systems in the output-feedback form (see [44, 48] and references therein), there are no results related to observer-based cooperative control of nonlinear MASs in the output-feedback form. This kind of system also facilitates the design of state observers, which will be shown later. An application of the output-feedback form nonlinear systems was discussed in [44], where the position of an electric motor is required to follow a periodic reference signal.

Remark 2

Previous works were focused on nonlinearities in the dynamics of the agents, while supposing that the actuators are free from hysteresis nonlinearities. In the control system area, controlling systems with Bouc–Wen hysteresis nonlinearity has become an important topic and several control schemes for single agent systems to mitigate hysteresis effect have been developed [41,42,43]. However, little progress has been achieved to extend the technique for the nonlinear MASs. This concern directly motivates this study.

Our objective is to design distributed NN control laws \(u_i^{d}\) for followers such that: (1) all signals in the closed-loop system remain semi-globally uniformly ultimately bounded and (2) the follower output \(y_i\) synchronizes to the leader output \(y_0\) in such manner that the tracking error \(y_i-y_0\) converges to a small neighborhood of the origin. For this objective, the following lemma is required in the subsequent sections.

Lemma 2

([8]) If the directed graph \(\mathcal {{\bar{G}}}\) has a spanning tree, then all eigenvalues of \(H=L+B\) have positive real parts.

3 Main results

3.1 State observer design

Since the agent nonlinearity \(f_{i,l}(\cdot )~(l=1,\ldots ,n)\) in (2.4) is unknown, then they cannot be used to construct the state observer and the controller. To avoid this trouble, we first employ a RBF NN to approximate the unknown nonlinear function \(f_{i,l}(\cdot )\) as follows

$$\begin{aligned} f_{i,l}(y_i)=W_{i,l}^{*T}\varPsi _{i,l}(y_i)+\varepsilon _{i,l}(y_i),\quad \forall y_i\in \varOmega _{y_{i}} \end{aligned}$$
(10)

where \(W_{i,l}^{*}\) is the ideal constant weight, \(\varPsi _{i,l}(y_i)\) is the Gaussian basis function and \(\varepsilon _{i,l}(y_i)\) is the approximation error satisfying \(|\varepsilon _{i,l}(y_i)|\le \varepsilon _{i,l,0}\).

By using Lemma 1, the MAS (2.4) can be rewritten as

$$\begin{aligned}&\left\{ \begin{array}{l} {\dot{x}}_{i,k}=x_{i,k+1}+W_{i,k}^{*T}\varPsi _{i,k}(y_i)+\varepsilon _{i,k}(y_i)+\omega _{i,k}(t)\\ {\dot{x}}_{i,n}=u_i^{d}+W_{i,n}^{*T}\varPsi _{i,n}(y_i)+\varepsilon _{i,n}(y_i)+\omega _{i,n}(t)\\ y_{i}=x_{i,1},\quad k=1,\ldots ,n-1,\;\; i=1,\ldots ,N \end{array}\right. \nonumber \\ \end{aligned}$$
(11)

where \(u_i^{d}\) is a designed control signal for the ith follower from a feedback law.

Then, a state observer for the ith follower is designed as

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{{\hat{x}}}_{i,k}={\hat{x}}_{i,k+1}+{\hat{W}}_{i,k}^{T}\varPsi _{i,k}(y_i)+l_{i,k}(y_{i}-{\hat{y}}_{i})\\ \dot{{\hat{x}}}_{i,n}=u_i^{d}+{\hat{W}}_{i,n}^{T}\varPsi _{i,n}(y_i)+l_{i,n}(y_{i}-{\hat{y}}_{i})\\ {\hat{y}}_{i}={\hat{x}}_{i,1},\quad k=1,\ldots ,n-1,\;\; i=1,\ldots ,N \end{array}\right. \nonumber \\ \end{aligned}$$
(12)

where \({\hat{x}}_i=[{\hat{x}}_{i,1},\ldots ,{\hat{x}}_{i,n}]^T\) and \({\hat{W}}_{i,l}~(l=1,\ldots ,n)\) are the estimates of the state \(x_i\) and \(W_{i,l}^{*}\), respectively. \(l_i=[l_{i,1},\ldots ,l_{i,n}]^T\) is the observer gain such that \(A_{i}=A-l_{i}c^{T}\) is a Hurwitz matrix, where \(A=\left[ \begin{array}{lllll} 0 &{}\quad 1 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad \ldots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad {\ddot{s}} &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ \end{array} \right] \in {\mathbb {R}}^{n\times n}\) and \(c=[1,0,\ldots ,0]^{T}\in {\mathbb {R}}^{n}\). Thus, for any given \(Q_{i}>0\), there exists a \(P_{i}>0\) satisfying the Lyapunov equation

$$\begin{aligned} \displaystyle A_{i}^{T}P_{i}+P_{i}A_{i}=-Q_{i}. \end{aligned}$$
(13)

Let \(e_{i}=x_{i}-{\hat{x}}_{i}\) be the observer error, then from (11) and (12), one can obtain the dynamics of the observer error

$$\begin{aligned}&\left\{ \begin{array}{l} {\dot{e}}_{i}=A_{i}e_{i}+\delta _{i}(y_i)+\varepsilon _{i}(y_i)+\omega _{i}(t)\\ {\hat{y}}_{i}=c^{T}{\hat{x}}_{i},\quad i=1,\ldots ,N \end{array}\right. \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{aligned} \delta _{i}(y_i)&=[\delta _{i,1}(y_i),\ldots ,\delta _{i,n}(y_i)]^{T}\\&=(W_{i}^{*}-{\hat{W}}_{i})^{T}\varPsi _{i}(y_i)\\ W_{i}^{*}&=\mathrm {diag}\{W_{i,1}^{*},\ldots ,W_{i,n}^{*}\}^{T}\\ {\hat{W}}_{i}&=\mathrm {diag}\{{\hat{W}}_{i,1},\ldots ,{\hat{W}}_{i,n}\}^{T}\\ \varPsi _{i}(y_{i})&=[\varPsi _{i,1}^{T}(y_{i}),\ldots ,\varPsi _{i,n}^{T}(y_{i})]^{T}\\ \varepsilon _{i}(y_i)&=[\varepsilon _{i,1}(y_i),\ldots ,\varepsilon _{i,n}(y_i)]^{T}\\ \omega _{i}(t)&=[\omega _{i,1}(t),\ldots ,\omega _{i,n}(t)]^{T}. \end{aligned} \end{aligned}$$

Also the observer (12) can be rewritten as:

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{{\hat{x}}}_{i}=A_{i}{\hat{x}}_{i}+{\hat{W}}_{i}^{T}\varPsi _{i}(y_i)+bu_{i}^{d}+l_{i}y_{i}\\ {\hat{y}}_{i}=c^{T}{\hat{x}}_{i},\quad i=1,\ldots ,N \end{array}\right. \end{aligned}$$
(15)

with \(b=[0,\cdots ,0,1]^{T}\in {\mathbb {R}}^{n}\).

With the designed state observer (12), we are now ready to develop a distributed adaptive NN output-feedback controller to achieve the desired control objectives. Note that in this section, the adaptive control law \(u_i^{d}\) will be designed for each follower i. The control signal \(v_i\) can then be calculated by \(v_i=HI(u_i^{d})\) and \(u_i=H(v_i)\).

To facilitate the control design later, the following assumptions are needed.

Assumption 1

There exists a known constant \(\delta _{i,l,0}\), such that \(|\delta _{i,l}(\cdot )|\le \delta _{i,l,0},~\forall l=1,\ldots ,n, i=1,\ldots ,N.\)

Assumption 2

The output of the leader and its first derivative (i.e., \(y_{0}\) and \({\dot{y}}_{0}\)) are known and bounded.

Assumption 3

The graph \(\mathcal {{\bar{G}}}\) contains a directed spanning tree with the leader 0 as the root node.

3.2 Distributed controller design

Before proceeding the controller design through the backstepping technique [24], the following change of coordinates is defined:

$$\begin{aligned} \left\{ \begin{array}{l} z_{i,1}=\sum _{j\in N_i}a_{ij}(y_{i}-y_{j})+b_{i}(y_{i}-y_{0})\\ z_{i,k}={\hat{x}}_{i,k}-{\bar{\alpha }}_{i,k-1}\\ s_{i,k-1}={\bar{\alpha }}_{i,k-1}-\alpha _{i,k-1},\quad k=2,\ldots ,n \end{array}\right. \end{aligned}$$
(16)

where \(\alpha _{i,k-1}\) and \({\bar{\alpha }}_{i,k-1}\) are the virtual control and the filtered virtual control at the \((k-1)\)th step, respectively; \(z_{i,k}\) and \(s_{i,k-1}\) are the error surface and the output error of the first-order filter, respectively. The actual control input \(u_{i}^{d}\) will be designated in the last step.

Step 1 We start with the equation for the local consensus tracking error \(z_{i,1}\). From (11), one can get

$$\begin{aligned} {\dot{z}}_{i,1}= & {} \sum _{j\in N_i}a_{ij}({\dot{y}}_{i}-{\dot{y}}_{j})+b_{i}({\dot{y}}_{i}-{\dot{y}}_{0})\nonumber \\= & {} (d_{i}+b_{i})\left( {\bar{f}}_{i,1}+z_{i,2}+s_{i,1}\right. \nonumber \\&\quad \left. +\,\alpha _{i,1}+{\bar{e}}_{i,2}+{\bar{\omega }}_{i,1}\right) \nonumber \\&\quad -\,\sum _{j\in N_i}a_{ij}{\hat{x}}_{j,2}-b_{i}{\dot{y}}_{0}\nonumber \\= & {} (d_{i}+b_{i})\left( M_{i,1}^{*T}\varPhi _{i,1}+\epsilon _{i,1}+z_{i,2}+s_{i,1}+\alpha _{i,1}\right. \nonumber \\&\quad \left. +\,{\bar{e}}_{i,2}+{\bar{\omega }}_{i,1}\right) -\sum _{j\in N_i}a_{ij}{\hat{x}}_{j,2}-b_{i}{\dot{y}}_{0} \end{aligned}$$
(17)

where

$$\begin{aligned} \begin{aligned} {\bar{f}}_{i,1}&=f_{i,1}-\frac{1}{d_{i}+b_{i}}\sum _{j\in N_i}a_{ij}f_{j,1}\\ {\bar{e}}_{i,2}&=e_{i,2}-\frac{1}{d_{i}+b_{i}}\sum _{j\in N_i}a_{ij}e_{j,2}\\ {\bar{\omega }}_{i,1}&=\omega _{i,1}-\frac{1}{d_{i}+b_{i}}\sum _{j\in N_i}a_{ij}\omega _{j,1}. \end{aligned} \end{aligned}$$

Note here that \({\bar{f}}_{i,1}({\bar{y}}_i)\) containing unknown functions \(f_{i,1}(y_i)\) and \(f_{j,1}(y_j) (j\in N_i)\) has been approximated by \({\bar{f}}_{i,1}({\bar{y}}_i)=M_{i,1}^{*T}\varPhi _{i,1}({\bar{y}}_i)+\epsilon _{i,1}({\bar{y}}_i)\), where \({\bar{y}}_i=[y_i,~y_j,~j\in N_i]^T\), \(M_{i,1}^{*}\) is the ideal constant weight, \(\varPhi _{i,1}({\bar{y}}_i)\) is the Gaussian basis function and \(\epsilon _{i,1}({\bar{y}}_i)\) is the approximation error satisfying \(|\epsilon _{i,1}({\bar{y}}_i)|\le \epsilon _{i,1,0}\).

For the initial step, the Lyapunov function candidate \(V_{i,1}\) is chosen as

$$\begin{aligned} \begin{aligned} V_{i,1}&=e_{i}^{T}P_{i}e_{i}+\frac{1}{2}z_{i,1}^{2}+\frac{1}{2}{\tilde{M}}_{i,1}^{T}\varGamma _{i,1}^{-1}{\tilde{M}}_{i,1}\\&\quad +\,\frac{1}{2\eta _{i,1}}{\tilde{\varDelta }}_{i,1}^{2} \end{aligned} \end{aligned}$$

where \({\tilde{M}}_{i,1}=M_{i,1}^{*}-{\hat{M}}_{i,1}\) and \({\tilde{\varDelta }}_{i,1}=\varDelta _{i,1}-{\hat{\varDelta }}_{i,1}\); \({\hat{M}}_{i,1}\) and \({\hat{\varDelta }}_{i,1}\) are estimates of \(M_{i,1}^{*}\) and \(\varDelta _{i,1}\), respectively; \(\varGamma _{i,1}=\varGamma _{i,1}^{T}>0\) and \(\eta _{i,1}>0\) are design parameters.

Differentiating \(V_{i,1}\) along (14) and (17) yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_{i,1}&=2e_{i}^{T}P_{i}{\dot{e}}_{i}+z_{i,1}{\dot{z}}_{i,1}\\&\quad -\,{\tilde{M}}_{i,1}^{T}\varGamma _{i,1}^{-1}\dot{{\hat{M}}}_{i,1}-\frac{1}{\eta _{i,1}}{\tilde{\varDelta }}_{i,1}\dot{{\hat{\varDelta }}}_{i,1}\\&=-e_{i}^{T}Q_{i}e_{i}+2e_{i}^{T}P_{i}\left[ \delta _{i}+\varepsilon _{i}+\omega _{i}\right] \\&\quad +\,z_{i,1}\left[ (d_{i}+b_{i})\left( M_{i,1}^{*T}\varPhi _{i,1}+z_{i,2}\right. \right. \\&\quad \left. \left. +\,s_{i,1}+\alpha _{i,1}\right) \right. \\&\quad \left. -\,\sum _{j\in N_i}a_{ij}{\hat{x}}_{j,2}-b_{i}{\dot{y}}_{0}\right] \\&\quad +\,(d_{i}+b_{i})z_{i,1}\left( {\bar{e}}_{i,2}+\epsilon _{i,1}+{\bar{\omega }}_{i,1}\right) \\&\quad -\,{\tilde{M}}_{i,1}^{T}\varGamma _{i,1}^{-1}\dot{{\hat{M}}}_{i,1}-\frac{1}{\eta _{i,1}}{\tilde{\varDelta }}_{i,1}\dot{{\hat{\varDelta }}}_{i,1}. \end{aligned} \end{aligned}$$
(18)

Using the Young’s inequality \(a^{T}b\le \frac{1}{2}a^{T}a+\frac{1}{2}b^{T}b\), the Cauchy–Schwartz inequality \((\sum _{k}a_{k}b_{k})^{2}\le (\sum _{k}a_{k}^{2})(\sum _{k}b_{k}^{2}),\) we obtain the following inequalities from Assumption 1:

$$\begin{aligned}&2e_{i}^{T}P_{i}\left[ \delta _{i}+\varepsilon _{i}+\omega _{i}\right] \le e_{i}^{T}e_{i}+\varDelta _{i,0}\Vert P_{i}\Vert ^{2}, \end{aligned}$$
(19)
$$\begin{aligned}&z_{i,1}{\bar{e}}_{i,2}\le \frac{1}{2}\left( 1+\frac{1}{d_{i}+b_{i}}\right) z_{i,1}^{2}+\frac{1}{2}e_{i}^{T}e_{i}\nonumber \\&\quad +\,\frac{k_{i}}{2(d_{i}+b_{i})}\sum _{j=1}^{N}e_{j}^{T}e_{j}, \end{aligned}$$
(20)
$$\begin{aligned}&z_{i,1}\left( \epsilon _{i,1}+{\bar{\omega }}_{i,1}\right) \le \varDelta _{i,1}|z_{i,1}|, \end{aligned}$$
(21)

where \(k_{i}=\sum _{j\in N_i}a_{ij}^{2}\), \(\varDelta _{i,0}=(\delta _{i,0}+\varepsilon _{i,0}+\omega _{i,0})^{2}\), \(\delta _{i,0}=\sqrt{\sum _{j=1}^{n}\delta _{i,j,0}^{2}}\), \(\varepsilon _{i,0}=\sqrt{\sum _{j=1}^{n}\varepsilon _{i,j,0}^{2}}\), \(\omega _{i,0}=\sqrt{\sum _{j=1}^{n}\omega _{i,j,0}^{2}}\), and \(\varDelta _{i,1}\) is the upper bound of \(|\epsilon _{i,1}+{\bar{\omega }}_{i,1}|\).

Substituting (19)–(21) into (18), it can be verified that

$$\begin{aligned} \begin{aligned} {\dot{V}}_{i,1}&\le -e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}}{2}I_{n}\right) e_{i}+\frac{k_{i}}{2}\sum _{j=1}^{N}e_{j}^{T}e_{j}\\&\quad +\,z_{i,1}\left[ (d_{i}+b_{i})\left( M_{i,1}^{*T}\varPhi _{i,1}\right. \right. \\&\left. \left. \quad +\,z_{i,2}+s_{i,1}+\alpha _{i,1}\right) \right. \\&\left. \quad -\,\sum _{j\in N_i}a_{ij}{\hat{x}}_{j,2}-b_{i}{\dot{y}}_{0}\right] +\varDelta _{i,0}\Vert P_{i}\Vert ^{2}\\&\quad +\,\frac{1+d_{i}+b_{i}}{2}z_{i,1}^{2}+(d_{i}+b_{i})\varDelta _{i,1}|z_{i,1}|\\&\quad -\,{\tilde{M}}_{i,1}^{T}\varGamma _{i,1}^{-1}\dot{{\hat{M}}}_{i,1}-\frac{1}{\eta _{i,1}}{\tilde{\varDelta }}_{i,1}\dot{{\hat{\varDelta }}}_{i,1}. \end{aligned} \end{aligned}$$
(22)

Under Assumption 2, we design virtual control function \(\alpha _{i,1}\) and adaptive laws for \({\hat{M}}_{i,1}\) as

$$\begin{aligned} \alpha _{i,1}= & {} \frac{1}{d_{i}+b_{i}}\left[ -\left( \rho _{i,1}+\frac{1+d_{i}+b_{i}}{2}\right) z_{i,1}\right. \nonumber \\&\left. \quad +\,\sum _{j\in N_i}a_{ij}{\hat{x}}_{j,2}+b_{i}{\dot{y}}_{0}\right] -{\hat{M}}_{i,1}^{T}\varPhi _{i,1}\nonumber \\&\quad -\,{\hat{\varDelta }}_{i,1}\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) ,\nonumber \\ \dot{{\hat{M}}}_{i,1}= & {} \varGamma _{i,1}\left[ (d_{i}+b_{i})z_{i,1}\varPhi _{i,1}-\sigma _{i,1}{\hat{M}}_{i,1}\right] , \end{aligned}$$
(23)

and adaptive laws for \({\hat{\varDelta }}_{i,1}\) as

$$\begin{aligned} \begin{aligned} \dot{{\hat{\varDelta }}}_{i,1}&= \eta _{i,1}\left[ (d_{i}+b_{i})z_{i,1}\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) -\gamma _{i,1}{\hat{\varDelta }}_{i,1}\right] \end{aligned} \end{aligned}$$
(24)

where \(\rho _{i,1}\), \(\varepsilon \), \(\sigma _{i,1}\) and \(\gamma _{i,1}\) are positive design parameters.

Substituting (23) and (24) into (22), we obtain

$$\begin{aligned} {\dot{V}}_{i,1}&\le -e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}}{2}I_{n}\right) e_{i}+\frac{k_{i}}{2}\sum _{j=1}^{N}e_{j}^{T}e_{j}\nonumber \\&\quad -\,\rho _{i,1}z_{i,1}^{2}+(d_{i}+b_{i})z_{i,1}(z_{i,2}+s_{i,1})\nonumber \\&\quad +\,(d_{i}+b_{i})\varDelta _{i,1}\left( |z_{i,1}|-z_{i,1}\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) \right) \nonumber \\&\quad +\,\varDelta _{i,0}\Vert P_{i}\Vert ^{2}+\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\hat{M}}_{i,1}+\gamma _{i,1}{\tilde{\varDelta }}_{i,1}{\hat{\varDelta }}_{i,1}\nonumber \\&\le -e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}}{2}I_{n}\right) e_{i}+\frac{k_{i}}{2}\sum _{\iota =1}^{N}e_{\iota }^{T}e_{\iota }\nonumber \\&\quad -\,\rho _{i,1}z_{i,1}^{2}+(d_{i}+b_{i})z_{i,1}(z_{i,2}+s_{i,1})\nonumber \\&\quad +\,0.2785(d_{i}+b_{i})\varepsilon \varDelta _{i,1}+\varDelta _{i,0}\Vert P_{i}\Vert ^{2}\nonumber \\&\quad +\,\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\hat{M}}_{i,1}+\gamma _{i,1}{\tilde{\varDelta }}_{i,1}{\hat{\varDelta }}_{i,1} \end{aligned}$$
(25)

where the inequality \(|z_{i,1}|-z_{i,1}\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) \le 0.2785\varepsilon \)\((\varepsilon >0)\) has been used.

In order to avoid repeatedly differentiating \(\alpha _{i,1}\), let \(\alpha _{i,1}\) pass through a first-order filter to obtain the first filtered virtual control vector \({\bar{\alpha }}_{i,1}\), namely

$$\begin{aligned} \tau _{i,1}\dot{{\bar{\alpha }}}_{i,1}+{\bar{\alpha }}_{i,1}=\alpha _{i,1},~{\bar{\alpha }}_{i,1}(0)=\alpha _{i,1}(0) \end{aligned}$$
(26)

where \(\tau _{i,1}\) is a small positive constant.

Step 2 From (12), the derivative of \(z_{i,2}\) can be expressed as

$$\begin{aligned} \begin{aligned} {\dot{z}}_{i,2}&=\dot{{\hat{x}}}_{i,2}-\dot{{\bar{\alpha }}}_{i,1}\\&={\hat{x}}_{i,3}+{\hat{W}}_{i,2}^{T}\varPsi _{i,2}+l_{i,2}(y_{i}-{\hat{y}}_{i}) -\dot{{\bar{\alpha }}}_{i,1}\\&=z_{i,3}+s_{i,2}+\alpha _{i,2}-{\tilde{W}}_{i,2}^{T}\varPsi _{i,2}+W_{i,2}^{*T}\varPsi _{i,2}\\&\quad +\,l_{i,2}(y_{i}-{\hat{y}}_{i})-\dot{{\bar{\alpha }}}_{i,1}, \end{aligned} \end{aligned}$$
(27)

where \({\tilde{W}}_{i,2}=W_{i,2}^{*}-{\hat{W}}_{i,2}\).

Consider the Lyapunov candidate function \(V_{i,2}\) as

$$\begin{aligned} V_{i,2}=V_{i,1}+\frac{1}{2}z_{i,2}^2+\frac{1}{2}s_{i,1}^2+\frac{1}{2}{\tilde{W}}_{i,2}^{T}\varGamma _{i,2}^{-1}{\tilde{W}}_{i,2}. \end{aligned}$$
(28)

where \(\varGamma _{i,2}=\varGamma _{i,2}^{T}>0\) is the adaptive gain matrix.

Design virtual control function \(\alpha _{i,2}\) and adaptive law for \({\hat{W}}_{i,2}\) as

$$\begin{aligned} \begin{aligned} \alpha _{i,2}&=-\rho _{i,2}z_{i,2}-(d_{i}+b_{i})z_{i,1}-{\hat{W}}_{i,2}^{T}\varPsi _{i,2}+\dot{{\bar{\alpha }}}_{i,1}\\&\quad -\,\delta _{i,2,0}\tanh \left( \frac{z_{i,2}\delta _{i,2,0}}{\varepsilon }\right) +l_{i,2}{\hat{y}}_{i}-l_{i,2}y_{i},\\ \dot{{\hat{W}}}_{i,2}&= \varGamma _{i,2}\left[ z_{i,2}\varPsi _{i,2}-\sigma _{i,2}{\hat{W}}_{i,2}\right] , \end{aligned} \end{aligned}$$
(29)

where \(\rho _{i,2}\) and \(\sigma _{i,2}\) are positive design parameters.

According to the definition of the output error \(s_{i,1}\) in (16), one has \(\dot{{\bar{\alpha }}}_{i,1}=-\frac{s_{i,1}}{\tau _{i,1}}\) and

$$\begin{aligned} \begin{aligned} {\dot{s}}_{i,1}&=\dot{{\bar{\alpha }}}_{i,1}-{\dot{\alpha }}_{i,1}\\&=-\frac{s_{i,1}}{\tau _{i,1}}+\frac{1}{d_{i}+b_{i}}\left[ \phantom {\sum _{j\in N_i}}\left( \rho _{i,1}+\frac{1+d_{i}+b_{i}}{2}\right) {\dot{z}}_{i,1}\right. \\&\left. \quad -\,\sum _{j\in N_i}a_{ij}\dot{{\hat{x}}}_{j,2}-b_{i}{\ddot{y}}_{0}\right] \\&\quad +\,\dot{{\hat{M}}}_{i,1}^{T}\varPhi _{i,1}+{\hat{M}}_{i,1}^{T}\frac{d\varPhi _{i,1}}{dy_{i}}{\dot{y}}_{i}\\&\quad +\,\dot{{\hat{\varDelta }}}_{i,1}\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) +{\hat{\varDelta }}_{i,1}\frac{d\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) }{dz_{i,1}}{\dot{z}}_{i,1}\\&=-\frac{s_{i,1}}{\tau _{i,1}}+B_{i,1} \end{aligned} \end{aligned}$$
(30)

where

$$\begin{aligned} \begin{aligned} B_{i,1}&=\frac{1}{d_{i}+b_{i}}\left[ \phantom {\sum _{j\in N_i}}\left( \rho _{i,1}+\frac{1+d_{i}+b_{i}}{2}\right) {\dot{z}}_{i,1}\right. \\&\left. \quad -\,\sum _{j\in N_i}a_{ij}\dot{{\hat{x}}}_{j,2}-b_{i}{\ddot{y}}_{0}\right] \\&\quad +\,\dot{{\hat{M}}}_{i,1}^{T}\varPhi _{i,1}+{\hat{M}}_{i,1}^{T}\frac{d\varPhi _{i,1}}{dy_{i}}{\dot{y}}_{i}\\&\quad +\,\dot{{\hat{\varDelta }}}_{i,1}\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) +{\hat{\varDelta }}_{i,1}\frac{d\tanh \left( \frac{z_{i,1}}{\varepsilon }\right) }{dz_{i,1}}{\dot{z}}_{i,1} \end{aligned} \end{aligned}$$

which is a continuous function.

From (27)–(30), the derivation of \(V_{i,2}\) becomes

$$\begin{aligned} {\dot{V}}_{i,2}= & {} {\dot{V}}_{i,1}+z_{i,2}{\dot{z}}_{i,2}+s_{i,1}{\dot{s}}_{i,1}-{\tilde{W}}_{i,2}^{T}\varGamma _{i,2}^{-1}\dot{{\hat{W}}}_{i,2}\nonumber \\&\le -e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}}{2}I_{n}\right) e_{i}+\frac{k_{i}}{2}\sum _{j=1}^{N}e_{j}^{T}e_{j}\nonumber \\&\quad -\,\sum _{j=1}^{2}\rho _{i,j}z_{i,j}^{2}+(d_{i}+b_{i})z_{i,1}s_{i,1}\nonumber \\&\quad +\,z_{i,2}s_{i,2}+z_{i,2}z_{i,3}\nonumber \\&\quad +\,0.2785\varepsilon \left[ (d_{i}+b_{i})\varDelta _{i,1}+1\right] +\varDelta _{i,0}\Vert P_{i}\Vert ^{2}\nonumber \\&\quad +\,\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\hat{M}}_{i,1}+\sigma _{i,2}{\tilde{W}}_{i,2}^{T}{\hat{W}}_{i,2}+\gamma _{i,1}{\tilde{\varDelta }}_{i,1}{\hat{\varDelta }}_{i,1}\nonumber \\&\quad -\,s_{i,1}^{2}/\tau _{i,1}+s_{i,1}B_{i,1} \end{aligned}$$
(31)

Let \(\alpha _{i,2}\) pass through a low-pass first-order filter to obtain the 2nd filtered virtual control vector \({\bar{\alpha }}_{i,2}\), namely

$$\begin{aligned} \tau _{i,2}\dot{{\bar{\alpha }}}_{i,2}+{\bar{\alpha }}_{i,2}=\alpha _{i,2},~{\bar{\alpha }}_{i,2}(0)=\alpha _{i,2}(0) \end{aligned}$$
(32)

where \(\tau _{i,2}\) is a small positive constant.

Step\(l~(l=3,\ldots ,n-1)\) Differentiating \(z_{i,l}\) along (12) yields

$$\begin{aligned} \begin{aligned} {\dot{z}}_{i,l}&=\dot{{\hat{x}}}_{i,l}-\dot{{\bar{\alpha }}}_{i,l-1}\\&={\hat{x}}_{i,l+1}+{\hat{W}}_{i,l}^{T}\varPsi _{i,l}+l_{i,l}(y_{i}-{\hat{x}}_{i,1}) -\dot{{\bar{\alpha }}}_{i,l-1}\\&=z_{i,l+1}+s_{i,l}+\alpha _{i,l}-{\tilde{W}}_{i,l}^{T}\varPsi _{i,l}+W_{i,l}^{*T}\varPsi _{i,l}\\&\quad +\,l_{i,l}(y_{i}-{\hat{y}}_{i})-\dot{{\bar{\alpha }}}_{i,l-1} \end{aligned} \end{aligned}$$
(33)

where \({\tilde{W}}_{i,l}=W_{i,l}^{*}-{\hat{W}}_{i,l}\).

Consider the Lyapunov candidate function \(V_{i,l}\) as

$$\begin{aligned} V_{i,l}=V_{i,l-1}+\frac{1}{2}z_{i,l}^2+\frac{1}{2}s_{i,l-1}^2+\frac{1}{2}{\tilde{W}}_{i,l}^{T}\varGamma _{i,l}^{-1}{\tilde{W}}_{i,l}, \nonumber \\ \end{aligned}$$
(34)

where \(\varGamma _{i,l}=\varGamma _{i,l}^{T}>0\) is the adaptive gain matrix.

Design virtual control function \(\alpha _{i,l}\) and adaptive law for \({\hat{W}}_{i,l}\) as

$$\begin{aligned} \begin{aligned} \alpha _{i,l}&=-\rho _{i,l}z_{i,l}-z_{i,l-1}-{\hat{W}}_{i,l}^{T}\varPsi _{i,l}+\dot{{\bar{\alpha }}}_{i,l-1}\\&\quad -\,\delta _{i,l,0}\tanh \left( \frac{z_{i,l}\delta _{i,l,0}}{\varepsilon }\right) +l_{i,l}{\hat{y}}_{i}-l_{i,l}y_{i},\\ \dot{{\hat{W}}}_{i,l}&= \varGamma _{i,l}\left[ z_{i,l}\varPsi _{i,l}-\sigma _{i,l}{\hat{W}}_{i,l}\right] , \end{aligned} \end{aligned}$$
(35)

where \(\rho _{i,l}\) and \(\sigma _{i,l}\) are positive design parameters.

Similar to (30), for \(l=3,\ldots ,n-1\)

$$\begin{aligned} {\dot{s}}_{i,l-1}= & {} \dot{{\bar{\alpha }}}_{i,l-1}-{\dot{\alpha }}_{i,l-1}\nonumber \\&=-\frac{s_{i,l-1}}{\tau _{i,l-1}}+\left[ \rho _{i,l-1}{\dot{z}}_{i,l-1}+{\dot{z}}_{i,l-2}\right. \nonumber \\&\left. \quad -\,l_{i,l-1}\dot{{\hat{y}}}_{i}+l_{i,l-1}{\dot{y}}_{i}\right] +\frac{{\dot{s}}_{i,l-2}}{\tau _{i,l-2}}\nonumber \\&\quad +\,\dot{{\hat{W}}}_{i,l-1}^{T}\varPsi _{i,l-1}+{\hat{W}}_{i,l-1}^{T}\frac{d\varPsi _{i,l-1}}{dy_{i}}{\dot{y}}_{i}\nonumber \\&\quad +\,\delta _{i,l-1,0}\frac{d\tanh \left( \frac{z_{i,l-1}\delta _{i,l-1,0}}{\varepsilon }\right) }{dz_{i,l-1}}{\dot{z}}_{i,l-1}\nonumber \\&=-\frac{s_{i,l-1}}{\tau _{i,l-1}}+B_{i,l-1} \end{aligned}$$
(36)

where

$$\begin{aligned} \begin{aligned} B_{i,l-1}&=\left[ \rho _{i,l-1}{\dot{z}}_{i,l-1}+{\dot{z}}_{i,l-2}-l_{i,l-1}\dot{{\hat{y}}}_{i}+l_{i,l-1}{\dot{y}}_{i}\right] \\&\quad +\,\frac{{\dot{s}}_{i,l-2}}{\tau _{i,l-2}}+\dot{{\hat{W}}}_{i,l-1}^{T}\varPsi _{i,l-1}\\&\quad +\,{\hat{W}}_{i,l-1}^{T}\frac{d\varPsi _{i,l-1}}{dy_{i}}{\dot{y}}_{i}\\&\quad +\,\delta _{i,l-1,0}\frac{d\tanh \left( \frac{z_{i,l-1}\delta _{i,l-1,0}}{\varepsilon }\right) }{dz_{i,l-1}}{\dot{z}}_{i,l-1} \end{aligned} \end{aligned}$$

which is also a continuous function.

Applying the virtual control and adaptive law in (35), the derivation of \(V_{i,l}\) along (33) becomes

$$\begin{aligned} \begin{aligned} {\dot{V}}_{i,l}&={\dot{V}}_{i,l-1}-\rho _{i,l}z_{i,l}^{2}+z_{i,l}\left( z_{i,l+1}+s_{i,l}-z_{i,l-1}\right) \\&\quad +\,s_{i,l-1}{\dot{s}}_{i,l-1}\\&\le -e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}}{2}I_{n}\right) e_{i}\\&\quad +\,\frac{k_{i}}{2}\sum _{j=1}^{N}e_{j}^{T}e_{j}\\&\quad -\,\sum _{k=1}^{l}\rho _{i,k}z_{i,k}^{2}+(d_{i}+b_{i})z_{i,1}s_{i,1}+\sum _{k=2}^{l}z_{i,k}s_{i,k}\\&\quad +\,z_{i,l}z_{i,l+1}+0.2785\varepsilon \left[ (d_{i}+b_{i})\varDelta _{i,1}+(l-1)\right] \\&\quad +\,\varDelta _{i,0}\Vert P_{i}\Vert ^{2}+\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\hat{M}}_{i,1}\\&\quad +\,\sum _{k=2}^{l}\sigma _{i,k}{\tilde{W}}_{i,k}^{T}{\hat{W}}_{i,k}\\&\quad +\,\gamma _{i,1}{\tilde{\varDelta }}_{i,1}{\hat{\varDelta }}_{i,1}+\sum _{k=1}^{l-1}\left( -s_{i,k}^{2}/\tau _{i,k}+s_{i,k}B_{i,k}\right) . \end{aligned} \end{aligned}$$
(37)

Let \(\alpha _{i,l}\) pass through the lth low-pass first-order filter to obtain the lth filtered virtual control vector \({\bar{\alpha }}_{i,l}\), namely

$$\begin{aligned} \tau _{i,l}\dot{{\bar{\alpha }}}_{i,l}+{\bar{\alpha }}_{i,l}=\alpha _{i,l},\quad {\bar{\alpha }}_{i,l}(0)=\alpha _{i,l}(0) \end{aligned}$$
(38)

where \(\tau _{i,l}\) is a small positive constant.

Stepn At this step, we will construct the control law \(u_{i}^{d}\). Viewing (12), the derivative of \(z_{i,n}\) satisfies

$$\begin{aligned} \begin{aligned} {\dot{z}}_{i,n}&=\dot{{\hat{x}}}_{i,n}-\dot{{\bar{\alpha }}}_{i,n-1}\\&=u_{i}^{d}-{\tilde{W}}_{i,n}^{T}\varPsi _{i,n}+W_{i,n}^{*T}\varPsi _{i,n}\\&\quad +\,l_{i,n}(y_{i}-{\hat{x}}_{i,1})-\dot{{\bar{\alpha }}}_{i,n-1}. \end{aligned} \end{aligned}$$
(39)

The Lyapunov function at this step is chosen as

$$\begin{aligned} V_{i,n}=V_{i,n-1}+\frac{1}{2}z_{i,n}^2+\frac{1}{2}s_{i,n-1}^2+\frac{1}{2}{\tilde{W}}_{i,n}^{T}\varGamma _{i,n}^{-1}{\tilde{W}}_{i,n}, \end{aligned}$$
(40)

where \(\varGamma _{i,n}=\varGamma _{i,n}^{T}>0\) is the adaptive gain matrix.

The control signal \(u_{i}^{d}\) and adaptive law for \({\hat{W}}_{i,n}\) are designed as

$$\begin{aligned} \begin{aligned}&u_{i}^{d}=-\rho _{i,n}z_{i,n}-z_{i,n-1}-{\hat{W}}_{i,n}^{T}\varPsi _{i,n}\\&\qquad \quad +\,l_{i,n}{\hat{y}}_{i}-l_{i,n}y_{i}+\dot{{\bar{\alpha }}}_{i,n-1},\\&\dot{{\hat{W}}}_{i,n}= \varGamma _{i,n}\left[ z_{i,n}\varPsi _{i,n}-\sigma _{i,n}{\hat{W}}_{i,n}\right] , \end{aligned} \end{aligned}$$
(41)

where \(\rho _{i,n}\) and \(\sigma _{i,n}\) are positive design parameters.

The \({\dot{V}}_{i,n}\) is then obtained as

$$\begin{aligned} \begin{aligned} {\dot{V}}_{i,n}&={\dot{V}}_{i,n-1}-\rho _{i,n}z_{i,n}^{2}-z_{i,n}z_{i,n-1}\\&\quad +\,s_{i,n-1}{\dot{s}}_{i,n-1}-{\tilde{W}}_{i,n}^{T}\varGamma _{i,n}^{-1}\dot{{\hat{W}}}_{i,n}\\&\le -e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}}{2}I_{n}\right) e_{i}+\frac{k_{i}}{2}\sum _{j=1}^{N}e_{j}^{T}e_{j}\\&\quad -\,\sum _{k=1}^{n}\rho _{i,k}z_{i,k}^{2}+(d_{i}+b_{i})z_{i,1}s_{i,1}+\sum _{k=2}^{n-1}z_{i,k}s_{i,k}\\&\quad +\,0.2785\varepsilon \left[ (d_{i}+b_{i})\varDelta _{i,1}+(n-1)\right] \\&\quad +\,\varDelta _{i,0}\Vert P_{i}\Vert ^{2}\\&\quad +\,\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\hat{M}}_{i,1}+\sum _{k=2}^{n}\sigma _{i,k}{\tilde{W}}_{i,k}^{T}{\hat{W}}_{i,k}\\&\quad +\,\gamma _{i,1}{\tilde{\varDelta }}_{i,1}{\hat{\varDelta }}_{i,1}+\sum _{k=1}^{n-1}\left( -s_{i,k}^{2}/\tau _{i,k}+s_{i,k}B_{i,k}\right) . \end{aligned} \end{aligned}$$
(42)

To date, the distributed controller design is completed.

3.3 Stability analysis

In this subsection, stability of the resulting closed-loop system and consensus tracking performance analysis for the proposed control scheme will be analyzed. The main results are summarized in the following theorem.

Theorem 1

Consider MAS (1) under Assumptions 1–3. For initial conditions satisfying \(V(0)\le \alpha _{0}\) with \(\alpha _{0}>0\), the observer-based distributed adaptive NN controller law (41) with intermediate control laws (23), (29) and (35) and parameter adaptive law (24) guarantee that all signals in the closed-loop systems are semi-globally uniformly ultimately bounded. Moreover, the tracking error \(y_i-y_0\) can be made as small as possible by appropriately choosing design parameters.

Proof

The total Lyapunov function is considered as

$$\begin{aligned} V(t)=\sum _{i=1}^{N}V_{i,n} \end{aligned}$$
(43)

where \(V_{i,n}\) is given by (40).

Substituting (42) into the derivative of (43) yields

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)&=\sum _{i=1}^{N}{\dot{V}}_{i,n}\\&\le \sum _{i=1}^{N}\Bigg [-e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}+\sum _{j=1}^{N}k_{j}}{2}I_{n}\right) e_{i}\\&\quad -\,\sum _{k=1}^{n}\rho _{i,k}z_{i,k}^{2}+(d_{i}+b_{i})z_{i,1}s_{i,1}+\sum _{k=2}^{n-1}z_{i,k}s_{i,k}\\&\quad +\,0.2785\varepsilon \left[ (d_{i}+b_{i})\varDelta _{i,1}+(n-1)\right] \\&\quad +\,\varDelta _{i,0}\Vert P_{i}\Vert ^{2}\\&\quad +\,\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\hat{M}}_{i,1}+\sum _{k=2}^{n}\sigma _{i,k}{\tilde{W}}_{i,k}^{T}{\hat{W}}_{i,k}\\&\quad +\,\gamma _{i,1}{\tilde{\varDelta }}_{i,1}{\hat{\varDelta }}_{i,1}+\sum _{k=1}^{n-1}\left( -s_{i,k}^{2}/\tau _{i,k}+s_{i,k}B_{i,k}\right) \Bigg ]. \end{aligned} \end{aligned}$$

Using the following facts with the design parameter \(\varsigma >0\)

$$\begin{aligned} {\tilde{M}}_{i,1}^{T}{\hat{M}}_{i,1}\le & {} -\frac{1}{2}{\tilde{M}}_{i,1}^{T}{\tilde{M}}_{i,1}+\frac{1}{2}M_{i,1}^{*T}M_{i,1}^{*}\\ {\tilde{W}}_{i,k}^{T}{\hat{W}}_{i,k}\le & {} -\frac{1}{2}{\tilde{W}}_{i,k}^{T}{\tilde{W}}_{i,k}+\frac{1}{2}W_{i,k}^{*T}W_{i,k}^{*}\\ {\tilde{\varDelta }}_{i,1}{\hat{\varDelta }}_{i,1}\le & {} -\frac{1}{2}{\tilde{\varDelta }}_{i,1}^{2}+\frac{1}{2}\varDelta _{i,1}^{2}\\ z_{i,j}s_{i,k}\le & {} \frac{1}{2}z_{i,k}^{2}+\frac{1}{2}s_{i,k}^{2},\,s_{i,j}B_{i,k}\le \frac{1}{2\varsigma }s_{i,k}^{2}B_{i,k}^{2}+\frac{\varsigma }{2} \end{aligned}$$

gives

$$\begin{aligned} \begin{aligned}&{\dot{V}}(t)\\&\quad \le -\sum _{i=1}^{N}\left[ e_{i}^{T}\left( Q_{i}-\frac{2+d_{i}+b_{i}+\sum _{j=1}^{N}k_{j}}{2}I_{n}\right) e_{i}\right. \\&\left. \qquad +\,\frac{1}{2}\sum _{k=1}^{n}(2\rho _{i,k}-\max \{d_{i}+b_{i},1\})z_{i,k}^{2}\right. \\&\left. \qquad +\,\frac{1}{2}\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\tilde{M}}_{i,1}\right. \\&\left. \qquad +\,\frac{1}{2}\sum _{k=2}^{n}\sigma _{i,k}{\tilde{W}}_{i,k}^{T}{\tilde{W}}_{i,k}+\frac{1}{2}\gamma _{i,1}{\tilde{\varDelta }}_{i,1}^{2}\right. \\&\left. \qquad +\,\frac{1}{2}\sum _{k=1}^{n-1}\left( \frac{2}{\tau _{i,k}}-\max \{d_{i}+b_{i},1\}-\frac{B_{i,k}^{2}}{\varsigma }\right) s_{i,k}^{2}\right] \\&\qquad +\,\varUpsilon _{1} \end{aligned} \end{aligned}$$
(44)

where \(\varUpsilon _{1}=\sum _{i=1}^{N}[0.2785\varepsilon [(d_{i}+b_{i})\varDelta _{i,1}+(n-1)]+\varDelta _{i,0}\Vert P_{i}\Vert ^{2}+\frac{1}{2}\sigma _{i,1}M_{i,1}^{*T}M_{i,1}^{*}+\frac{1}{2}\sum _{k=2}^{n}\sigma _{i,k}W_{i,k}^{*T}W_{i,k}^{*}+ \frac{1}{2}\gamma _{i,1}\varDelta _{i,1}^{2}+\frac{(n-1)\varsigma }{2}]\).

Since for any constants \(\alpha _{0}>0\) and \(\beta _{0}>0\), the sets \(\varXi _{i,k}=\{2e_{i}^{T}P_{i}e_{i}+\frac{1}{\eta _{i,1}}{\tilde{\varDelta }}_{i,1}^{2}+{\tilde{M}}_{i,1}^{T}\varGamma _{i,1}^{-1}{\tilde{M}}_{i,1}+\sum _{l=2}^{k}{\tilde{W}}_{i,l}^{T}\varGamma _{i,l}^{-1}{\tilde{W}}_{i,l}+\sum _{l=1}^{k}z_{i,l}^{2}+\sum _{l=1}^{k-1}s_{i,l}^{2}\le 2\alpha _{0}\}\) and \(\varXi =\{y_{0}^{2}+{\dot{y}}_{0}^{2}+{\ddot{y}}_{0}^{2}\le \beta _{0}\}\) are compact in \({\mathbb {R}}^{n+(2+p)k}\) and \({\mathbb {R}}^{3}\), respectively. \(\varXi _{i,k}\times \varXi \) is also compact in \({\mathbb {R}}^{n+(2+p)k+3}\). Then, there exists a positive constant \(M_{i,k}>0\) such that \(|B_{i,k}|\le M_{i,k}\) on \(\varXi _{i,k}\times \varXi \).

Choose the design parameters \(Q_{i}\), \(\rho _{i,k}\), \(\tau _{i,k}\) and \(\varsigma \) such that

$$\begin{aligned} \begin{aligned} {\bar{Q}}_{i}&=Q_{i}-\frac{2+d_{i}+b_{i}+\sum _{j=1}^{N}k_{j}}{2}I_{n}>0\\ {\bar{\rho }}_{i,k}&=2\rho _{i,k}-\max \{d_{i}+b_{i},1\}>0\\ {\bar{\tau }}_{i,k}&=\frac{2}{\tau _{i,k}}-\max \{d_{i}+b_{i},1\}-\frac{M_{i,k}^{2}}{\varsigma }>0. \end{aligned} \end{aligned}$$
(45)

Then, substituting (45) into (44), we obtain

$$\begin{aligned} {\dot{V}}(t)&\le -\sum _{i=1}^{N}\left[ e_{i}^{T}{\bar{Q}}_{i}e_{i}+\,\frac{1}{2}\sum _{k=1}^{n}{\bar{\rho }}_{i,k}z_{i,k}^{2}\right. \nonumber \\&\left. \quad +\frac{1}{2}\sigma _{i,1}{\tilde{M}}_{i,1}^{T}{\tilde{M}}_{i,1}\right. \nonumber \\&\left. \quad +\,\frac{1}{2}\sum _{k=2}^{n}\sigma _{i,k}{\tilde{W}}_{i,k}^{T}{\tilde{W}}_{i,k}+\frac{1}{2}\gamma _{i,1}{\tilde{\varDelta }}_{i,1}^{2}\right. \nonumber \\&\left. \quad +\,\frac{1}{2}\sum _{k=1}^{n-1}{\bar{\tau }}_{i,k}s_{i,k}^{2}\right] \nonumber \\&\quad +\,\varUpsilon _{1}\nonumber \\&\le -\sum _{i=1}^{N}\left[ \frac{\lambda _{\min }({\bar{Q}}_{i})}{\lambda _{\max }(P_{i})}e_{i}^{T}P_{i}e_{i}+\frac{1}{2}\sum _{k=1}^{n}{\bar{\rho }}_{i,k}z_{i,k}^{2}\right. \nonumber \\&\left. \quad +\,\frac{1}{2}\sigma _{i,1}\lambda _{\min }(\varGamma _{i,1}){\tilde{M}}_{i,1}^{T}\varGamma _{i,1}^{-1}{\tilde{M}}_{i,1}\right. \nonumber \\&\left. \quad +\,\frac{1}{2}\sum _{k=2}^{n}\sigma _{i,k}\lambda _{\min }(\varGamma _{i,k}){\tilde{W}}_{i,k}^{T}\varGamma _{i,k}^{-1}{\tilde{W}}_{i,k}\right. \nonumber \\&\left. \quad +\,\frac{1}{2}\gamma _{i,1}{\tilde{\varDelta }}_{i,1}^{2}+\frac{1}{2}\sum _{k=1}^{n-1}{\bar{\tau }}_{i,k}s_{i,k}^{2}\right] +\varUpsilon _{1}\nonumber \\&\le -\varUpsilon _{0}V(t)+\varUpsilon _{1} \end{aligned}$$
(46)

where \(\varUpsilon _{0}=\min \{\frac{\lambda _{\min }({\bar{Q}}_{i})}{\lambda _{\max }(P_{i})},{\bar{\rho }}_{i,k},\sigma _{i,1}\lambda _{\min }(\varGamma _{i,1}), \sigma _{i,k}\lambda _{\min }(\varGamma _{i,k}), \gamma _{i,1}\eta _{i,1},{\bar{\tau }}_{i,k}\}\).

From inequality (46), we have that \({\dot{V}}(t)<0\) on \(V(t)=\alpha _{0}\) when \(\varUpsilon _{0}>\frac{\varUpsilon _{1}}{\alpha _{0}}\). This demonstrates that \(V(t)\le \alpha _{0}\) is an invariant set, i.e., if \(V(0)\le \alpha _{0}\), then \(V(t)\le \alpha _{0}\) for all \(t\ge 0\). Then, solving inequality (46) gives

$$\begin{aligned} \begin{aligned} 0&\le V(t) \le \frac{\varUpsilon _{1}}{\varUpsilon _{0}}+\left( V(0)-\frac{\varUpsilon _{1}}{\varUpsilon _{0}}\right) e^{-\varUpsilon _{0}t},\quad t\ge 0, \end{aligned} \end{aligned}$$
(47)

which means that all signals of the closed-loop system are uniformly ultimately bounded.

Furthermore, by defining the global consensus tracking error \(z_{1}=(z_{1,1},\ldots ,z_{N,1})^{T}\) and using \(\frac{1}{2}\Vert z_{1}(t)\Vert ^{2}\le V(t)\), we obtain \(\frac{1}{2}\Vert z_{1}(t)\Vert ^{2}\le \frac{\varUpsilon _{1}}{\varUpsilon _{0}}+(V(0)-\frac{\varUpsilon _{1}}{\varUpsilon _{0}})e^{-\varUpsilon _{0}t}\). Therefore, as \(t\rightarrow \infty \), \(\Vert z_{1}(t)\Vert \) exponentially converges to the compact set \(\varTheta =\{z_{1}|\Vert z_{1}\Vert \le \sqrt{2\varUpsilon _{1}/\varUpsilon _{0}}\}\) which can be kept arbitrarily small by increasing \(\varUpsilon _{0}\) or decreasing \(\varUpsilon _{1}\). On the other hand, from the definition of \(z_{i,1}\) in (16), the global consensus tracking error \(z_{1}\) can be expressed as

$$\begin{aligned} z_{1}=(L+B)(y-1_{N}y_{0}) \end{aligned}$$

where \(y=(y_{1},\ldots ,y_{N})^{T}\). Under Assumption 3, Lemma 2 indicates that the matrix \(H=L+B\) is invertible and we can obtain \(y-1_{N}y_{0}=(L+B)^{-1}z_{1}\). According to \(\Vert y-1_{N}y_{0}\Vert \le \Vert z_{1}\Vert \Vert (L+B)^{-1}\Vert \), the tracking error \(y-1_{N}y_{0}\) can also be made arbitrarily small by choosing appropriate design parameters. \(\square \)

Remark 3

From the designed consensus tracking controller consisting of virtual/actual control [(23), (29), (35), (41)] and adaptive laws of parameters (24), one can see that each agent only uses the output information from itself and its neighbors. This demonstrates that the designed control algorithm could be completed in a distributed manner which meets the requirement of MASs. To better understand the reason of designing theses virtual controls and adaptive laws, readers should derive the Lyapunov function in every steps and be clear about the position of each term.

Remark 4

To improve the efficiency of selecting design parameters, some guidelines are as follows: (1) specify a positive matrix \(Q_{i}\) and design parameters \(\rho _{i,k}\) and \(\tau _{i,k}\) to satisfy (45); (2) for the specified matrix \(Q_{i}\), choose \(l_{i}=[l_{i,1},\ldots ,l_{i,n}]^{T}\) such that matrix \(A_{i}\) is Hurwitz and then solve the Lyapunov function (13) to get \(P_{i}\); and 3) choose \(\sigma _{i,k}>0\), \(\gamma _{i,1}>0\) and \(\eta _{i,1}>0\). Moreover, it can be seen from (47) that we can improve the tracking performance by increasing \(\varUpsilon _{0}\) and decreasing \(\varUpsilon _{1}\). Specifically, we can reduce the tracking error by choosing large \(\rho _{i,k}\), \(\eta _{i,1}\), \(\lambda _{\min }(\varGamma _{i,k})\) and small \(\sigma _{i,k}\), \(\gamma _{i,1}\), \(\tau _{i,k}.\)

Remark 5

To help potential readers complete the controller in this paper, we take a second-order system as an example to explain the construction process of the controller. According to (41), we need to construct \(u_{i}^{d}=-\rho _{i,2}z_{i,2}-z_{i,1}-{\hat{W}}_{i,2}^{T}\varPsi _{i,2}+l_{i,2}{\hat{y}}_{i}-l_{i,2}y_{i}+\dot{{\bar{\alpha }}}_{i,1}\)

  1. (S1)

    According to (16), \(z_{i,1}\) is obtained and \(z_{i,2}\) requires \({\hat{x}}_{i,2}\) and \({\bar{\alpha }}_{i,1}\);

  2. (S2)

    \({\hat{x}}_{i,2}\) is obtained by (11);

  3. (S3)

    By (29), we have \(\alpha _{i,2}\);

  4. (S4)

    Then, with (26), \({\bar{\alpha }}_{i,1}\) is solved;

  5. (S5)

    \({\hat{W}}_{i,2}^{T}\varPsi _{i,2}\) is constructed by (10);

  6. (S6)

    \({\hat{y}}_{i}={\hat{x}}_{i,1}\).

With the above guidance and Remark 4 for choosing parameters, the controller for a second-order system is constructed. To handle the hysteresis actuator, the hysteresis inverse could be completed according to (6)–(7). For higher-order systems, the construction processes are similar to that of the second-order system.

Fig. 4
figure 4

Communication topology for Examples 1 and 2

Full size image
Fig. 5
figure 5

Follower output \(y_i~(i=1,\ldots ,12)\) and leader output \(y_0\) in Example 1

Full size image

4 Simulation examples

Example 1

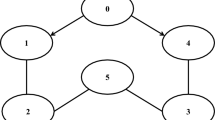
(Numerical example) Consider a MAS composed of 12 followers and a leader. The directed communication topology is shown in Fig. 4, where the numbers on the edges denote the weights between two corresponding agents. The dynamics of each follower is described in the form of (2.4) with

$$\begin{aligned}&\left\{ \begin{array}{l} {\dot{x}}_{i,1}=x_{i,2}+\sin (y_{i})+\omega _{i,1}(t)\\ {\dot{x}}_{i,2}=x_{i,3}+y_{i}^2+\omega _{i,2}(t)\\ {\dot{x}}_{i,3}=u_{i}+y_{i}\cos (y_{i})+\omega _{i,3}(t)\\ y_{i}=x_{i,1}\\ u_{i}=H(u_i^{d}),\quad i=1,\ldots ,12 \end{array}\right. \end{aligned}$$
(48)

where \(\omega _{i,1}(t)=\exp (-t)\), \(\omega _{i,2}(t)=\cos (t^2)\sin (3t)\) and \(\omega _{i,3}(t)=\sin (-t)\).

Fig. 6
figure 6

Observer error \(e_{i}=x_{i}-{\hat{x}}_{i}~(i=1,\ldots ,12)\) in Example 1. a\(e_{i1}=x_{i1}-{\hat{x}}_{i1}\); b\(e_{i2}=x_{i2}-{\hat{x}}_{i2}\); c\(e_{i3}=x_{i3}-{\hat{x}}_{i3}\)

Full size image
Fig. 7
figure 7

Control signals \(u_i~(i=1,\ldots ,12)\) in Example 1

Full size image

In the simulations, we set parameters \(\rho _{1}=\rho _{2}=1\), \(\beta =1\), \(\chi =0.5\) and \(m=2\) for the Bouc–Wen hysteresis (3)–(5) as in [41]. Design parameters for the distributed adaptive NN controller (41) with intermediate control laws (23), (24), (29) and (35) are chosen as \(\varGamma _{i,1}=\varGamma _{i,2}=I_{12}\), \(\rho _{i,1}=12\), \(\rho _{i,2}=15\), \(\rho _{i,3}=13\)\(\tau _{i,1}=\tau _{i,2}=0.01\), \(\varepsilon =0.001\), \(\sigma _{i,1}=\sigma _{i,2}=\sigma _{i,3}=2\), \(\eta _{i,1}=1.5\) and \(\gamma _{i,1}=1.2\). From Fig. 4, we know \(B=\mathrm {diag}\{4, 0, \ldots ,0\}\). The output of the leader is \(y_0=\sin (t)+\sin (2t)+\cos (3t)\). The initial states of \(x_i(0),{\hat{W}}_i,{\hat{\varDelta }}_i\) are pseudorandom values drawn from normal distribution. By solving the Lyapunov equation (13) with \(l_{i,1}=5,~l_{i,2}=8,~l_{i,3}=4\) and \(Q_{i}=\mathrm {diag}\{1, 1, 1\}\), the positive matrices \(P_i\) is calculated as

$$\begin{aligned} P_{i}=\left[ \begin{array}{lll} 0.1424 &{}\quad 0.2118 &{}\quad 0.1250\\ 0.2118 &{}\quad 2.0729 &{}\quad 1.1944\\ 0.1250 &{}\quad 1.1944 &{}\quad 1.8472 \end{array} \right] , \end{aligned}$$

where \(i=1,\ldots ,12\).

Figure 4 depicts the output of 12 followers and the leader. The consensus tracking trajectories, observer errors and control signals are shown in Figs. 5, 6 and 7, respectively. From Figs. 5, 6 and 7, it can be seen that the developed observer-based distributed adaptive NN controller guarantees both stability and good consensus tracking performance of the MAS (48) in the presence of unmatched unknown nonlinearities and unmeasurable state information.

Fig. 8
figure 8

Follower output \(y_i~(i=1,\ldots ,12)\) and the leader output \(y_0\) in Example 2

Full size image

Example 2

(Practical example) Consider a group of 12 single-link robot arms, which are also linked through the graph topology in Fig. 4. The dynamics of the ith robot arm can be modeled as the second-order Lagrangian dynamics [20]

$$\begin{aligned}&\left\{ \begin{array}{l} {\dot{x}}_{i,1}=x_{i,2}+0.3\cos (\pi t)\\ {\dot{x}}_{i,2}=J_{i}^{-1}\left( u_{i}-K_{i}g\omega _{i}\sin (x_{i,1})+0.1\sin (\pi t)\right) \\ y_{i}=x_{i,1}\\ u_{i}=H(u_i^{d}),\quad i=1,\ldots ,12 \end{array}\right. \nonumber \\ \end{aligned}$$
(49)

where \(x_{i,1}\) is the angle velocity and \(x_{i,2}\) is the angular velocity, \(J_i\) is the total rotational inertia of the link and the motor, \(K_i\) is the total mass of the link, g is the gravitational acceleration, and \(\omega _i\) is the distance from the joint axis to the link center of mass for node i. In the simplified form of (44), namely \(J_i=1\), \(K_i=0.3\), \(g=9.8\) and \(k_i=0.2\), it has exactly the structure of (2.4).

In the simulations, we set parameters \(\rho _{1}=\rho _{2}=1\), \(\beta =1\), \(\chi =0.5\) and \(m=2\) for the Bouc–Wen hysteresis (3)–(5) as in [41]. Design parameters for the distributed adaptive NN controller (41) with intermediate control laws (23), (24), (29) and (35) are chosen as \(\varGamma _{i,1}=\varGamma _{i,2}=I_{12}\), \(\rho _{i,1}=12\), \(\rho _{i,2}=18\), \(\tau _{i,1}=\tau _{i,2}=0.01\), \(\varepsilon =0.001\), \(\sigma _{i,1}=\sigma _{i,2}=2\), \(\eta _{i,1}=1.5\) and \(\gamma _{i,1}=1.2\). From Fig. 4, we know \(B=\mathrm {diag}\{4, 0, \ldots ,0\}\). The output of the leader is \(y_0=2\sin (0.5\pi t)\). The initial state of \(x_i(0),{\hat{W}}_i,{\hat{\varDelta }}_i\) are pseudorandom values drawn from normal distribution. By solving the Lyapunov equation (13) with \(l_{i,1}=5,~l_{i,2}=8\) and \(Q_{i}=\mathrm {diag}\{1, 1\}\), the positive matrices \(P_i\) are calculated as

$$\begin{aligned} P_{i}=\left[ \begin{array}{ll} 0.1125 &{}\quad 0.0625\\ 0.0625 &{}\quad 1.2125 \end{array} \right] , \end{aligned}$$

where \(i=1,\ldots ,12\).

Fig. 9
figure 9

Observer error \(e_{i}=x_{i}-{\hat{x}}_{i}~(i=1,\ldots ,12)\) in Example 2. a\(e_{i1}=x_{i1}-{\hat{x}}_{i1}\); b\(e_{i2}=x_{i2}-{\hat{x}}_{i2}\)

Full size image
Fig. 10
figure 10

Control signals \(u_i~(i=1,\ldots ,12)\) in Example 2

Full size image

The consensus tracking trajectories, observer errors and control signals are shown in Figs. 8, 9 and 10, respectively. As expected, the designed distributed adaptive NN controller has achieved good control performances for networked robot arms (49) in the presence of unknown functions, unmeasured states and unknown hysteresis.

5 Conclusion

In this paper, the consensus tracking problem for a class of nonlinear MASs under directed communication graph has been investigated. It is assumed that each follower is in output-feedback form with unknown nonlinear agent/input dynamics and unknown disturbances, and the leader gives its commands only to a small portion of followers. By the function approximation capability of NNs, we have presented a framework of designing observer-based distributed adaptive NN control laws for the consensus problem of nonlinear MASs in output-feedback form. Based on algebraic graph theory and Lyapunov theory, it was proved that both the consensus tracking error and the observer error converge to an adjustable neighborhood of the origin. Note that MASs in triangular form with measured output information and/or switching topology have not been addressed so far in the literature and the consensus control of these systems remains an open problem.