1 Introduction

Distributed adaptive technique is an emerging and promising topic to estimate parameters of interest from the streaming data collected at nodes (or agents) of wireless sensor networks [42, 43]. In distributed adaptive algorithms, each node is allowed to estimate parameters of interest in an adaptive loop and to share its local estimate with the neighboring nodes each other, obtaining better estimation performance than the no cooperation way among nodes. In contrast with the centralized processing over networks, on the other hand, the distributed processing does not require a powerful central processor, thus being more flexible and saving communication bandwidth resources. Due to these advantages, distributed adaptive algorithms have been used in a variety of applications such as the frequency estimation in power grids [22, 26], the spectrum estimation in cognitive radio networks [17, 21, 34], the source localization over unmanned aerial vehicle networks [2, 55], and the compressed estimation [50].

According to different cooperation strategies between interconnected nodes, existing distributed adaptive algorithms can be categorized as incremental [27, 51], consensus [23, 46], and diffusion [1, 8, 13, 25, 30, 56] types. For the incremental type, a Hamiltonian cycle path [27] that runs across all the nodes must be determined and retained until the final estimate is achieved. The incremental type has the lowest communication burden among these three types. However, maintaining such a path is very difficult especially in large-scale networks, since it does not permit any failure of nodes and links. Both consensus and diffusion types have no Hamiltonian cycle, due to the fact that interconnected nodes exchange information each other. The consensus strategy enforces a property to the network that all the nodes obtain the same estimate. Nonetheless, studies in [47] have revealed that the stability of the diffusion algorithm does not rely on the network topology so that it is more stable than the consensus algorithm. Also, the diffusion algorithm exhibits better performance than the consensus algorithm in terms of convergence rate and steady-state estimation error (i.e., estimation accuracy). Comparatively speaking, therefore, the diffusion distributed strategy has got more attention. The diffusion least mean square (dLMS) algorithm is one of the most popular distributed algorithms, due to its simplicity and stable performance in Gaussian noise environment [8]. However, the range of step sizes ensuring the dLMS convergence is dependent of the covariance matrix of input signal. Benefited from the advantage of the normalized LMS (NLMS) to weaken such dependence, the diffusion NLMS (dNLMS) algorithm was proposed [20]. To overcome the trade-off between fast convergence rate and low steady-state estimation error for the dLMS and dNLMS algorithms, many variable step-size (VSS) variants have been promoted, see [20, 24] and references therein.

In signal processing area, Gaussian noise is concerned frequently by researchers. However, the noise may also be non-Gaussian, which includes not only Gaussian noise but also impulsive noise [6, 18, 33]. Although realizations of impulsive noise are sparse and random, the amplitude is far higher than that of Gaussian noise; in this case, the noise is best modeled by heavy-tailed distributions, e.g., the contaminated Gaussian (CG) and the \(\alpha \)-stable distributions. Such noise scenarios exist in many applications such as echo cancelation, underwater acoustics, audio processing, communications, cognitive radio, and extreme learning [6, 9, 10, 18, 33, 58, 59]. In distributed estimation, even if impulsive noise appears only at one node in the network, its adverse influence could be propagated over the entire network due to information exchange among nodes. That is to say, the dLMS/dNLMS algorithms suffer from performance degradation in impulsive noise, owing to the squared error-based minimization criteria. In standalone adaptive filter, several approaches have been presented to deal with impulsive interferences [11, 12, 16, 44, 57]. At present, some of these approaches have been used in distributed networks to develop robust distributed adaptive algorithms in combating impulsive noise.

In [49], the diffusion least mean pth power (dLMP) algorithm by minimizing the cost function consisting of the p-power of the output errors at nodes was proposed, where the parameter p, \(1\le p <2\), controls the robustness of dLMP against impulsive noise. As a special case of the dLMP with \(p=1\), the diffusion sign error LMS (dSE-LMS) algorithm [37] provides good robustness in resisting impulsive noise, while the disadvantage is slow convergence. Based on the weighted combination of the preselected sign-preserving basis functions, the diffusion error nonlinearity LMS (dEN-LMS) algorithm was proposed [40]; however, the basis functions need to be chosen properly according to noise distributions. In [31], the diffusion maximum correntropy criterion (dMCC) algorithm was presented by maximizing the cost function defined as the correntropy of error signals. This algorithm is able to suppress impulsive noise, but this capability relies on the proper choice of the kernel width parameter. By detecting whether impulsive noise occurs or not, reference [3] proposed a robust variable weighting coefficients dLMS (RVWC-dLMS) algorithm, which rejects the cooperation with the nodes at which impulsive noise occurs. Due to the robustness of Huber function against outliers, in [14], it has been used to devise a robust diffusion projection algorithm by resorting to the adaptive projected subgradient rule; and in [29], the diffusion Huber-based NLMS (dHNLMS) algorithm was proposed by resorting to the gradient-descent (GD) rule. However, setting the threshold in the Huber function requires the prior knowledge of the noise distribution. In [5], by minimizing the pseudo-Huber-based cost function over nodes in the network, a robust dLMS algorithm was developed, while its performance needs to choose properly the threshold-like parameter. It is worth noting that the above robust diffusion algorithms involve the choice of step sizes which leads to a performance balance problem between convergence rate and steady-state estimation error. For the sake of addressing this problem, a diffusion robust VSS LMS (dRVSS-LMS) algorithm was developed based on the Huber function [19], but its implementation requires the prior knowledge of background and impulsive noises.

In this paper, we propose a variable threshold (VT) dHNLMS algorithm, referred to as VT-dHNLMS. The thresholds are recursively adjusted with the diffusion cooperation of neighboring nodes and with the diminishing property, which ensures good robustness against impulsive noise. Furthermore, this algorithm can be considered as a variable step-size dNLMS algorithm, with fast convergence and low steady-state estimation error simultaneously. We provide the convergence and steady-state analyses for the algorithm in the presence of impulsive noise. To recover the tracking capability of the VT-dHNLMS algorithm when parameters of interest experience a sudden change, a diffusion cooperation-based nonstationary control (NC) method is devised that resets the thresholds. Although we have discussed similar idea for adjusting the thresholds in the incremental distributed NLMS algorithm [51], here the extension to the diffusion distributed algorithm is not straightforward. Similar approach has also been studied by us to improve the performance of diffusion recursive least squares (dRLS) algorithm in impulsive noise [54], while the dRLS algorithm requires high computational complexity. Thus, it is necessary to further generalize the VT approach to improve the dHNLMS performance, with low-complexity.

This paper is organized as follows. In Sect. 2, the dHNLMS algorithm is introduced. Then, in Sect. 3, the VT-dHNLMS algorithm is proposed. The convergence and steady-state behaviors of the proposed algorithm are analyzed in Sect. 4. In Sect. 5, simulation results in various noise scenarios are presented to verify the effectiveness of the proposed algorithm. Finally, conclusions are given in Sect. 6.

The notations adopted in this paper include \((\cdot )^{\mathrm{T}}\) for the transpose, \(E\{ \cdot \}\) for the expectation, \(\Vert \cdot \Vert _2\) for the \(l_2\)-norm of a vector, \(\Vert \cdot \Vert _\infty \) for the \(\infty \)-norm, \(\text {col}\{\cdot \}\) for a column vector formed by stacking its arguments on top of each other, \(\text {diag}\{\cdot \}\) for the (block) diagonal operation, \(\text {Tr}(\cdot )\) for the trace of a matrix, and \(\otimes \) for the Kronecker product. Also, we denote the identity matrix of size \(M \times M\) as \({\varvec{I}}_M\).

2 dHNLMS Algorithm

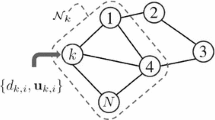
Consider a network that consists of N nodes distributed in a geographic region as shown in Fig. 1, where \(\mathcal {N}_k\) is the set of nodes with a direct link to node k (including itself) and known as the neighborhood of node k. The links among nodes indicate that these nodes can communicate with each other. At every time instant i, every node k has access to an \(M\times 1\) input regressor \({\varvec{u}}_k(i)\) and a scalar measurement \(d_k(i)\) following the linear model:

$$\begin{aligned} d_k(i) = {\varvec{u}}_k^{\mathrm{T}}(i){\varvec{w}}^o + v_k(i), \end{aligned}$$
(1)

where all the nodes in the network are to estimate the \(M\times 1\) vector \({\varvec{w}}^o\). The model (1) has been widely used in applications [41, 42].

Fig. 1
figure 1

Schematic diagram of diffusion network

Full size image

For estimating \({\varvec{w}}^o\), the well-known mean square error (MSE) criteria over networks are defined as

$$\begin{aligned} \begin{aligned} {\varvec{w}}&=\min _{{\varvec{w}}} \sum \limits _{k=1}^N E\left\{ (d_k(i)-{\varvec{u}}_k^{\mathrm{T}}(i){\varvec{w}})^2 \right\} . \end{aligned} \end{aligned}$$
(2)

In the light of the diffusion cooperation of interconnected nodes, (2) equivalently becomes that every node k solves the following estimation problem:

$$\begin{aligned} \begin{aligned} {\varvec{w}}_k&=\min _{{\varvec{w}}_k} J_k^\text {loc}({\varvec{w}}_k),\\ J_k^\text {loc}({\varvec{w}}_k)&= \sum \limits _{m\in {\mathcal {N}_k}}c_{m,k} E\left\{ (d_m(i)-{\varvec{u}}_m^{\mathrm{T}}(i){\varvec{w}}_k)^2 \right\} , \end{aligned} \end{aligned}$$
(3)

for \(k=1,\ldots ,N\). The combination coefficients \(\{c_{m,k}\}\) in (3) are nonnegative and satisfy:

$$\begin{aligned} \sum \limits _{m\in \mathcal {N}_k}c_{m,k} =1 \text {, and } c_{m,k}=0\quad \text {if} \,\, m\notin \mathcal {N}_k , \end{aligned}$$
(4)

where \(c_{m,k}\) accounts for the weight that node k assigns to the data received from its neighboring node m. In general, \(\{c_{m,k}\}\) are determined by either static rules (e.g., the Metropolis rule [45]) which keep them constant, or adaptive rules [35]. From (3), both dLMS and dNLMS algorithms can be derived. Note that, the expectation term in (3) is normalized by input regressors for the dNLMS algorithm, which show good performance in Gaussian additive noise. In many practical situations, however, the additive noise \(v_k(i)\) at node k may compose of the Gaussian component and the impulsive component with low occurrence probability. In this scenario, the data \(\{{\varvec{u}}_k(i), d_k(i)\}\) have more outliers so that the MSE criteria are not favorable. Therefore, in order to seek a good estimate of \({\varvec{w}}^o\) in impulsive noise, the dHNLMS algorithm solves the Huber function-based estimation problem:

$$\begin{aligned} \begin{aligned} {\varvec{w}}_k&=\min _{{\varvec{w}}_k} J_k^\text {loc}({\varvec{w}}_k),\\ J_k^\text {loc}({\varvec{w}}_k)&= \sum \limits _{m\in {\mathcal {N}_k}}c_{m,k} E\left\{ \varphi \left( \frac{d_m(i)-{\varvec{u}}_m^{\mathrm{T}}(i){\varvec{w}}_k}{\Vert {\varvec{u}}_m(i)\Vert _2}\right) \right\} , \end{aligned} \end{aligned}$$
(5)

where the Huber function \(\varphi (\cdot )\) is given by [38]

$$\begin{aligned} \varphi (r_m)=\left\{ \begin{aligned}&r_m^2/2, \quad \text { if }\,\, |r_m|\le \sqrt{\xi }\\&\sqrt{\xi }|r_m|-\xi /2, \quad \text { if }\,\, |r_m|> \sqrt{\xi }, \end{aligned} \right. \end{aligned}$$
(6)

and \(\xi >0\) denotes the threshold. As can be seen in (6), the Huber function can be interpreted as a piecewise combination of the MSE criteria (when \(|r_m| \le \sqrt{\xi }\)) and the sign criteria (when \(|r_m|> \sqrt{\xi }\)). The sign criteria are a popular benchmark in resisting impulsive noise [32, 36], which has prompted some robust algorithms such as the dSE-LMS.

By applying the instantaneous GD principle into (5) and following the Adapt-then-Combine (ATC) version of diffusion cooperation strategy among nodes, the update equations of the ATC dHNLMS algorithm are described as [29]:

$$\begin{aligned}&\begin{aligned} {\varvec{\psi }}_k(i+1)={\varvec{w}}_k(i) + \mu \left\{ \begin{aligned}&\frac{e_k(i){\varvec{u}}_k(i)}{\Vert {\varvec{u}}_k(i)\Vert _2^2}, \quad \text {if }\,\, |e_k(i)|\le \sqrt{\xi }\\&\sqrt{\xi }\frac{\text {sign}(e_k(i)){\varvec{u}}_k(i)}{\Vert {\varvec{u}}_k(i)\Vert _2}, \quad \text {if }\,\, |e_k(i)|> \sqrt{\xi }, \end{aligned} \right. \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned}&{\varvec{w}}_k(i+1) = \sum \limits _{m\in \mathcal {N}_k}c_{m,k} {\varvec{\psi }}_m(i+1), \end{aligned}$$
(8)

where

$$\begin{aligned} e_k(i)=d_k(i)-{\varvec{w}}_k^{\mathrm{T}}(i){\varvec{u}}_k(i) \end{aligned}$$
(9)

is the output error of node k, \(\text {sign}(x)\) is the signum function of variable x, and \(\mu >0\) is the constant step size.

It is clear that the ATC dHNLMS algorithm consists of an adaptation step (7) and a combination step (8). In the adaptation step, each node k updates the estimate from \({\varvec{w}}_k(i)\) to an intermediate estimate \({\varvec{\psi }}_k(i+1)\) using its own data \(\{d_k(i),{\varvec{u}}_k(i)\}\). In the combination step, the intermediate estimates \(\{{\varvec{\psi }}_m(i+1)\}\) from the neighborhood of node k are linearly fused based on the combination coefficients \(\{c_{m,k}\}\), thereby yielding a more reliable estimate \({\varvec{w}}_k(i+1)\). Note that, the Combine-then-Adapt (CTA) version of the dHNLMS algorithm can also be obtained in a straightforward way, namely by reversing the orders of (7) and (8). However, we only discuss the ATC diffusion implementation for brevity, since it generally outperforms the CTA version [8, 43]. Hereafter, the notation ATC is omitted.

3 Proposed Algorithm

In this section, we develop the VT-dHNLMS algorithm and analyze the computational complexity.

3.1 Algorithm Design

The adverse effect of impulsive noise on the dHNLMS performance occurs in the adaptation step (7). Specifically, the robustness of the algorithm against impulsive noise is determined by the preselected threshold \(\xi \). To remedy this flaw, we propose to replace \(\xi \) with the time-varying threshold \(\xi _k(i)\), thus (7) becomes

$$\begin{aligned} \begin{aligned} {\varvec{\psi }}_k(i+1)={\varvec{w}}_k(i) + \mu \left\{ \begin{aligned}&\frac{e_k(i){\varvec{u}}_k(i)}{\Vert {\varvec{u}}_k(i)\Vert _2^2},\quad \text {if }\,\, |e_k(i)|\le \sqrt{\xi _k(i)}\\&\sqrt{\xi _k(i)}\frac{\text {sign}(e_k(i)){\varvec{u}}_k(i)}{\Vert {\varvec{u}}_k(i)\Vert _2}, \quad \text {if }\,\, |e_k(i)|> \sqrt{\xi _k(i)}. \end{aligned} \right. \end{aligned} \end{aligned}$$
(10)

From (10), we are able to obtain the following relation:

$$\begin{aligned} \begin{aligned} \left\| {\varvec{\psi }}_k(i+1)-{\varvec{w}}_k(i)\right\| _2^2&= \mu ^2 \min \left[ \xi _k(i),\; \frac{e_k^2(i)}{\Vert {\varvec{u}}_k(i)\Vert _2^2} \right] \\&{\mathop {\le }\limits ^{(a)}} \xi _k(i), \end{aligned} \end{aligned}$$
(11)

where \(0<\mu \le 1\) is for satisfying the inequality (a). It means that for every node k, the updated distance from \({\varvec{w}}_k(i)\) to \({\varvec{\psi }}_k(i)\) in the adaptation (10) is limited to at most the amount of the threshold \(\xi _k(i)\) for any disturbance (including impulsive noise). Therefore, \(\xi _k(i)\) controls not only the robust level of the algorithm to suppress impulsive noise but also its convergence behavior. Generally, it is desired to have relatively large values of \(\xi _k(i)\) at the beginning of the adaptation, thereby leading to a good initial speed of convergence. Also, it should not be too large to guarantee the robust performance against impulsive noise. On the other hand, at the steady-state stage of the algorithm, smaller values of \(\xi _k(i)\) lead to a lower estimation error. Hence, according to the above requirements, a simple and effective way is that the adaptation of \(\xi _k(i)\) depends on the maximum updated distance of the estimates shown in (11). Also, taking advantage of the diffusion cooperation for \(\xi _k(i)\), we propose to adaptively update it as follows:

$$\begin{aligned} \zeta _k(i+1)= & {} \upsilon \xi _k(i) + (1-\upsilon ) \mu ^2 \min \left[ \frac{e_k^2(i)}{\Vert {\varvec{u}}_k(i)\Vert _2^2},\xi _k(i) \right] , \end{aligned}$$
(12)
$$\begin{aligned} \xi _k(i+1)= & {} \sum \limits _{m\in \mathcal {N}_k}c_{m,k} \zeta _m(i+1), \end{aligned}$$
(13)

where \(\upsilon \) is the forgetting factor with \(0<\upsilon < 1\) and \(\zeta _k(i)\) denotes the intermediate variable of \(\xi _k(i)\). In (12), at every node k, \(\xi _k(i)\) can be initialized as \(\xi _k(0)=\sigma _{d,k}^2/(M\sigma _{u,k}^2)\), where \(\sigma _{d,k}^2\) and \(\sigma _{u,k}^2\) are the powers of signals \(d_k(i)\) and \(u_k(i)\), respectively. As a result, (8), (9), (10), (12) and (13) constitute the VT-dHNLMS algorithm, and for clarity which is summarized in Table 1 after rearranging (10).

Table 1 Summary of the VT-dHNLMS algorithm
Full size table

Remark 1

Intuitively, from (10) we can get some insights. In most of time instants, impulsive noise does not happen due to small probability, which means \(( \left| e_k(i)\right| / \Vert {\varvec{u}}_k(i)\Vert _2) \le \sqrt{\xi _k(i)}\) and the VT-dHNLMS algorithm works as a dNLMS algorithm with the fixed step size \(\mu \le 1\). Whenever impulsive noise appears, due to its large amplitude we have \(( \left| e_k(i)\right| / \Vert {\varvec{u}}_k(i)\Vert _2) >\sqrt{\xi _k(i)}\). In this case, (10) reduces to

$$\begin{aligned} {\varvec{\psi }}_k(i+1) = {\varvec{w}}_k(i) +\mu _k(i) \text {sign}(e_k(i)) {\varvec{u}}_k(i), \end{aligned}$$

which reveals that the VT-dHNLMS algorithm becomes the dSE-LMS algorithm with time-varying step sizes \(\mu _k(i) = \mu \sqrt{\xi _k(i)}/\Vert {\varvec{u}}_k(i)\Vert _2\), thereby providing good robustness against impulsive noise. Furthermore, \(\xi _k(i)\) given in (12) and (13) is decreasing as the algorithm converges, which further ensures the robustness of the algorithm. In a nutshell, the proposed VT-dHNLMS algorithm has good anti-jamming capability by switching automatically modes from the dNLMS to the dSE-LMS when impulsive noise appears.

On the other hand, we rearrange (10) as:

$$\begin{aligned} {\varvec{\psi }}_k(i+1) = {\varvec{w}}_k(i) +\mu _k(i)\frac{{\varvec{u}}_k(i)e_k(i)}{\Vert {\varvec{u}}_k(i)\Vert _2^2}, \end{aligned}$$
(14)

where

$$\begin{aligned} \mu _k(i) = \mu \min \left[ \frac{\sqrt{\xi _k(i)} \Vert {\varvec{u}}_k(i)\Vert _2 }{\left| e_k(i)\right| },\; 1\right] . \end{aligned}$$
(15)

Evidently, (14) and (15) illustrate that the proposed algorithm can be interpreted as a modified dNLMS algorithm with time-dependent step sizes. Moreover, whenever impulsive noise occurs, (15) will immediately force the step size \(\mu _k(i)\) to a tiny value. It is well-known that for the GD-based adaptive algorithms, reducing the step size is also able to mitigate the adverse influence of impulsive noise on the performance of algorithms [44, 52]. In an ideal case, we should set \(\mu _k(i)=0\) for the occurrence instant of impulsive noise meaning that the adaptation is halted. In addition, the step sizes given by (15) are always limited in the range of 0 to \(\mu \) and go toward zero as \(i\rightarrow \infty \) since \(\xi _k(i)\) converges to zero as \(i \rightarrow \infty \) (see “Appendix A” for the proof). Therefore, (15) is a novel VSS approach (which can also be observed in Fig. 7) so that the proposed VT-dHNLMS algorithm not only speeds up the convergence but also reduces the steady-state estimation error.

Remark 2

The adaptation of \(\xi _k(i)\) given by (12) and (13) is the decreasing function with respect to the iteration i. Accordingly, after \({\varvec{w}}^o\) changes suddenly, \(\xi _k(i)\) will continue to become small rather than a desired large value so that the convergence of the algorithm again to the steady-state (i.e., the tracking capability) is poor. To overcome this limitation, by referring to our previous NC method in [54], we take advantage of similar method to reset \(\xi _k(i)\) for adapting the sudden change of \({\varvec{w}}^o\). Table 2 gives this method, where \(\varTheta _{\text {old},k}\) denotes the past value of \(\varTheta _{\text {new},k}\), and \(0<\kappa < 1\) is the weighting factor. As one can see, if \(\varDelta _k(i)>l_\text {th}\) meaning that \({\varvec{w}}^o\) undergoes a sudden change, \(\xi _k(i)\) will be reset as \(\xi _k(0)\), where \(l_\text {th}>0\) is predefined. Differing from [54], we here employ the median operator, median(\(\cdot \)), to remove the abnormal data disturbed by impulsive noise from the sliding data window with the length of \(N_w\) so that \(\varDelta _k(i)\) is insensitive to impulsive noise. It is stressed that larger \(N_w\) leads to a more robust \(\varDelta _k(i)\) but requires a higher complexity, so \(N_w\) should be properly chosen. Since \(\varDelta _k(i)\) is computed only every \(V_t\) iterations, large \(V_t\) reduces the computational cost but with delayed tracking capability; typically, good choice is \(V_t=\varrho M\) with \(1\leqslant \rho \leqslant 3\). Note that these parameters in the NC method are not coupled each other, i.e., each parameter plays a specific role, and thus, their choices are easy.

Table 2 The NC method
Full size table

3.2 Computational Complexity

Table 3 compares the computational complexity of the dSE-LMS [37], dNLMS, VSS-dNLMS presented in [20], dHNLMS [29] algorithms with that of the proposed VT-dHNLMS algorithm for node k per iteration, where \(|\mathcal {N}_k|\) denotes the cardinality of \(\mathcal {N}_k\). Compared with the dHNLMS, the additional complexity of the proposed algorithm arises from equations (12) and (13), which requires \(\left| \mathcal {N}_k\right| +3\) multiplications, \(\left| \mathcal {N}_k\right| \) additions, and 1 comparison. Also, the proposed algorithm requires extra communication cost for transmitting \(\zeta _k\) to its neighbors, i.e., \(|\mathcal {N}_k|-1\) scalars per node k. In comparison with the VT-dHNLMS algorithm, the computational complexity of the NC method is negligible due mainly to \(V_t\ge M\).

Table 3 Computational complexity of algorithms for node k per iteration
Full size table

4 Performance Analyses

4.1 Stability Analysis

From (15) and inequality (11), we obtain, for any node k:

$$\begin{aligned} \mu _k(i)\le \mu \le 1 \;\text {and} \; E\left\{ \mu _k(i) \right\} \le \mu \le 1. \end{aligned}$$
(16)

This means that \(\mu \) is the upper bound of the time-varying step sizes. Remark 1 has analyzed whenever impulsive noise happens, \(\mu _k(i)\) will become very small for preventing the proposed algorithm from divergence. Hence, we can indirectly determine the stability of the proposed algorithm from the convergence condition of the dNLMS algorithm with constant step sizes. For diffusion algorithms with only exchanging the estimates between nodes [42, 43, 47], there is a conclusion that the diffusion algorithm is stable only if each node is stable to independently perform the estimation task using its own adaptation rule. Following this conclusion, the convergence condition of the dNLMS algorithm is that the step sizes \(\mu _k\) for nodes \(k=1,\ldots ,N\) satisfyFootnote 1

$$\begin{aligned} 0<\mu _k<2,\; \end{aligned}$$
(17)

which is also the step-size range of independently running the NLMS algorithm per node. In addition, references [15, 41] have been proved that the step size \(\mu =1\) leads to the fastest convergence of the NLMS algorithm; likewise, we can simply extend it to the dNLMS algorithm. It follows that the proposed VT-dHNLMS algorithm is stable. Moreover, we recommend \(\mu =1\) for the proposed algorithm to obtain the fastest initial convergence.

In the sequel, we study the steady-state and evolution behaviors of the proposed algorithm with \(\mu =1\) in impulsive noise.

4.2 Steady-State Behavior

Let us suppose the unknown vector \({\varvec{w}}^o\) to be stationary. Then, subtracting \({\varvec{w}}^o\) from (10) and applying (12), we have the following equation:

$$\begin{aligned} \widetilde{{\varvec{\psi }}}_k(i+1) = \widetilde{{\varvec{w}}}_k(i) - \sqrt{\frac{\zeta _k(i+1)-\upsilon \xi _k(i)}{1-\upsilon }} \frac{{\varvec{u}}_k(i)\text {sign}(e_k(i))}{\Vert {\varvec{u}}_k(i)\Vert _2}, \end{aligned}$$
(18)

where \(\widetilde{{\varvec{w}}}_k(i) \triangleq {\varvec{w}}^o - {\varvec{w}}_k(i)\) and \(\widetilde{{\varvec{\psi }}}_k(i) \triangleq {\varvec{w}}^o - {\varvec{\psi }}_k(i)\) denote the estimation error vector and the intermediate estimation error vector at node k, respectively. Similarly, using \({\varvec{w}}^o\) we change the combination step (8) to

$$\begin{aligned} \widetilde{{\varvec{w}}}_k(i+1) = \sum \limits _{m\in \mathcal {N}_k}c_{m,k} \widetilde{{\varvec{\psi }}}_m(i+1). \end{aligned}$$
(19)

Equations (18) and (19) will be the start point of the following analyses for the VT-dHNLMS algorithm. For convenience of analysis, some commonly used assumptions are given.

Assumption 1

The input regressors \(\{{\varvec{u}}_k(i)\}\) are zero mean with covariance matrices \({\varvec{R}}_k=E\{{\varvec{u}}_k(i){\varvec{u}}_k^{\mathrm{T}}(i)\}\) and spatially independent.

Assumption 2

The input regressors \(\{{\varvec{u}}_k(i)\}\) are independent of the additive noises \(\{v_m(j)\}\) for all k, m, i, and j.

Assumption 3

The input regressors \(\{{\varvec{u}}_k(i)\}\) are independent of the estimates \(\{{\varvec{w}}_m(j)\}\) for \(j\le i\) and all k, m. It is so-called independence assumption, which is customary for (distributed) adaptive algorithms [41, 42, 53].

Assumption 4

The additive noise \(v_k(i)\) is described by the CG process, i.e., \(v_k(i)=\theta _k(i)+\eta _k(i)\). The background noise \(\theta _k(i)\) is a white Gaussian process with zero mean and variance \(\sigma _{\theta ,k}^2\). The impulsive noise \(\eta _k(i)\) is given by the Bernoulli–Gaussian process, i.e., \(\eta _k(i)=b_k(i) g_k(i)\), where \(b_k(i)\) is a Bernoulli process with \(P[b_k(i)=1]=p_{r,k}\) and \(P[b_k(i)=0]=1-p_{r,k}\), and \(g_k(i)\) is a zero-mean white Gaussian process with variance \(\sigma _{g,k}^2=\hbar \sigma _{\theta ,k}^2, \hbar \gg 1\). Note that, \(p_{r,k}\) is also considered as the probability of occurring impulsive noise. Accordingly, the mean and variance of \(v_k(i)\) are zero and \(\sigma _{v,k}^2 = p_{r,k}(\hbar +1)\sigma _{\theta ,k}^2 + (1-p_{r,k})\sigma _{\theta ,k}^2\), respectively. The CG model is used frequently for analyzing the performance of robust algorithms in impulsive noise environmentsFootnote 2 [28, 37, 48, 54].

First, taking the squared \(l_2\)-norm of the both sides of (18), we obtain

$$\begin{aligned} \begin{aligned} \Vert \widetilde{{\varvec{\psi }}}_k(i+1)\Vert _2^2&= \Vert \widetilde{{\varvec{w}}}_k(i) \Vert _2^2 \\&\quad -\,2\sqrt{\frac{\zeta _k(i+1)-\upsilon \xi _k(i)}{1-\upsilon }} \frac{\text {sign}(e_k(i))e_{k,a}(i)}{\Vert {\varvec{u}}_k(i)\Vert _2} \\&\quad +\, \frac{\zeta _k(i+1)-\upsilon \xi _k(i)}{1-\upsilon },\;\;\;\; \end{aligned} \end{aligned}$$
(20)

where \(e_{k,a}(i)\triangleq \widetilde{{\varvec{w}}}_k^{\mathrm{T}}(i) {\varvec{u}}_k(i)\) denotes the a priori output error at node k. Usually, the forgetting factor \(\upsilon \) is close to 1 so that the fluctuations of \(\xi _k(i)\) and \(\zeta _k(i)\) computed by (12) and (13) are relatively small compared to that of the input regressors and the error signals. As such, the variances of \(\xi _k(i)\) and \(\zeta _k(i)\) can be assumed to be small enough, namely \(\xi _k(i)- E\{\xi _k(i)\}\approx 0\) and \(\zeta _k(i)- E\{\zeta _k(i)\}\approx 0\); thereby, the following approximation can be established:

$$\begin{aligned} \begin{aligned}&E\left\{ \sqrt{\frac{\zeta _k(i+1)-\upsilon \xi _k(i)}{1-\upsilon }} \frac{\text {sign}(e_k(i))e_{k,a}(i)}{\Vert {\varvec{u}}_k(i)\Vert _2} \right\} \approx \\&\quad \sqrt{\frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\}}{1-\upsilon }} E\left\{ \frac{\text {sign}(e_k(i))e_{k,a}(i)}{\Vert {\varvec{u}}_k(i)\Vert _2}\right\} . \end{aligned} \end{aligned}$$
(21)

By incorporating (21), the expectation for both sides of (20) is expressed as

$$\begin{aligned} \begin{aligned} E\{\Vert \widetilde{{\varvec{\psi }}}_k(i+1)\Vert _2^2\}&= E\{\Vert \widetilde{{\varvec{w}}}_k(i) \Vert _2^2\} \\&\quad -\,2\sqrt{\frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\}}{1-\upsilon }} \mathop {\underbrace{E\left\{ \frac{\text {sign}(e_k(i))e_{k,a}(i)}{\Vert {\varvec{u}}_k(i)\Vert _2}\right\} }}\limits _{(b)} \\&\quad +\, \frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\} }{1-\upsilon }.\;\;\;\; \end{aligned} \end{aligned}$$
(22)

For \(M\gg 1\), we can assume that the fluctuation of \(1/\Vert {\varvec{u}}_k(i)\Vert _2\) be small so that the term (b) in (22) is simplified as

$$\begin{aligned} \begin{aligned} E\left\{ \frac{\text {sign}(e_k(i))e_{k,a}(i)}{\Vert {\varvec{u}}_k(i)\Vert _2}\right\}&\approx r_k E\{ \text {sign}(e_k(i))e_{k,a}(i) \}\\&= r_k E\{\text {sign}(e_{k,a}(i) + v_k(i))e_{k,a}(i) \}, \end{aligned} \end{aligned}$$
(23)

where \(r_k \triangleq E\left\{ \frac{1}{\Vert {\varvec{u}}_k(i)\Vert _2}\right\} \). Based on the conditioned expectation property, we have

$$\begin{aligned} \begin{aligned} E\{ \text {sign}(e_{k,a}(i) + v_k(i))e_{k,a}(i) \} = E\left\{ E\{ \text {sign}(e_{k,a}(i) + v_k(i))e_{k,a}(i) | \widetilde{{\varvec{w}}}_k(i) \} \right\} , \end{aligned} \end{aligned}$$
(24)

where the notation \(E\{s|q\}\) represents the expectation of s conditioned on q.

Applying the law of total probability under Assumption 4, the follow equation is established:

$$\begin{aligned} \begin{aligned} E\{ \text {sign}&(e_{k,a}(i) + v_k(i))e_{k,a}(i) | \widetilde{{\varvec{w}}}_k(i) \} \\&=(1-p_{r,k}) E\{ \text {sign}(e_{k,a}(i) +\theta _k(i))e_{k,a}(i) | \widetilde{{\varvec{w}}}_k(i) \} \\&\quad + p_{r,k} E\{ \text {sign}(e_{k,a}(i) + \theta _k(i)+\eta _k(i))e_{k,a}(i) | \widetilde{{\varvec{w}}}_k(i) \}. \end{aligned} \end{aligned}$$
(25)

Also, it is assumed that \(e_{k,a}(i)\) is zero-mean Gaussian when \(M\gg 1\). As in [4], this assumption can be verified by the central limit theorem. Hence, variables \((e_{k,a}(i) +\theta _k(i))\) and \((e_{k,a}(i) + \theta _k(i)+\eta _k(i))\) can also be assumed to be Gaussian, and then we can use Price’s theorem in [39] and Assumptions 2 and 3 to further change (25) to

$$\begin{aligned} \begin{aligned} E\{ \text {sign}&(e_{k,a}(i) + v_k(i))e_{k,a}(i) | \widetilde{{\varvec{w}}}_k(i) \} = h_k E\{e_{k,a}^2(i) | \widetilde{{\varvec{w}}}_k(i) \}, \end{aligned} \end{aligned}$$
(26)

where

$$\begin{aligned} \begin{aligned} h_k = \sqrt{\frac{2}{\pi }}\left\{ \frac{p_{r,k}}{\sqrt{E\{e_{k,a}^2(i)\}+(\hbar +1)\sigma _{\theta }^2\}}} + \frac{1-p_{r,k}}{\sqrt{E\{e_{k,a}^2(i)\}+\sigma _{\theta }^2\}}} \right\} \ne 0. \end{aligned} \end{aligned}$$
(27)

Substituting (23), (24) and (26) into (22), we obtain

$$\begin{aligned} \begin{aligned} E\{\Vert \widetilde{{\varvec{\psi }}}_k(i+1)\Vert _2^2\}&= E\{\Vert \widetilde{{\varvec{w}}}_k(i) \Vert _2^2\}\;\; \\&\quad - 2h_k r_k \sqrt{\frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\} }{1-\upsilon } } E\{e_{k,a}^2(i)\} \\&\quad +\frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\} }{1-\upsilon }. \end{aligned} \end{aligned}$$
(28)

Second, by means of Jensen’s inequality [7, p.77], we take the squared \(l_2\)-norm for both sides of (19) and the expectation to arrive at

$$\begin{aligned} \begin{aligned} E\left\{ \left\| \widetilde{{\varvec{w}}}_k(i+1) \right\| _2^2 \right\} \le \sum \limits _{m\in \mathcal {N}_k}c_{m,k} E\left\{ \Vert \widetilde{{\varvec{\psi }}}_m(i+1) \Vert _2^2 \right\} . \end{aligned} \end{aligned}$$
(29)

To proceed, let us define two vectors over the network:

$$\begin{aligned} \begin{aligned} \varvec{\mathcal {X}}(i)&\triangleq \text {col} \left\{ E\{\Vert \widetilde{{\varvec{\psi }}}_1(i) \Vert _2^2\} , \ldots , E\{ \Vert \widetilde{{\varvec{\psi }}}_N(i) \Vert _2^2\}\right\} , \\ \varvec{\mathcal {W}}(i)&\triangleq \text {col} \left\{ E\{\Vert \widetilde{{\varvec{w}}}_1(i) \Vert _2^2\} , \ldots , E\{\Vert \widetilde{{\varvec{w}}}_N(i) \Vert _2^2\}\right\} , \\ \end{aligned} \end{aligned}$$
(30)

and two diagonal matrices over the network

$$\begin{aligned} \begin{aligned} \varvec{\mathcal { H}} \triangleq&\text {diag}\left\{ h_1 r_1,\ldots ,h_N r_N \right\} ,\\ \varvec{\mathcal {S}}_e(i) \triangleq&\text {diag}\left\{ E\{e_{1,a}^2(i)\},\ldots ,E\{e_{N,a}^2(i)\} \right\} .\\ \end{aligned} \end{aligned}$$
(31)

Also, the matrix \({\varvec{C}}\) collects the combination coefficients \(\{c_{m,k}\}\), i.e., \([{\varvec{C}}]_{m,k}=c_{m,k}\). Then, using these definitions in (30), (31) and (A.1), we formulate (28) and (29) for call the nodes as a unified form:

$$\begin{aligned} \begin{aligned} \varvec{\mathcal {W}}(i+1)&\le {\varvec{C}}^{\mathrm{T}} \varvec{\mathcal {X}}(i+1) \\&= {\varvec{C}}^{\mathrm{T}} \left[ \varvec{\mathcal {W}}(i) - 2\varvec{\mathcal { H}} \varvec{\mathcal {S}}_e(i) \sqrt{{\varvec{\varsigma }}(i)} +{\varvec{\varsigma }}(i)\right] , \end{aligned} \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned} {\varvec{\varsigma }}(i)&\triangleq \frac{E\{{\varvec{\zeta }}(i+1)\}-\upsilon E\{{\varvec{\xi }}(i)\} }{1-\upsilon }. \end{aligned} \end{aligned}$$
(33)

By taking the \(\infty \)-norm of both sides of (32) and using \(\Vert {\varvec{C}}^{\mathrm{T}}\Vert _\infty =1\), we obtain

$$\begin{aligned} \begin{aligned} \Vert \varvec{\mathcal {W}}(i+1)\Vert _\infty&\le \Vert {\varvec{C}}^{\mathrm{T}} \Vert _\infty \Vert \varvec{\mathcal {W}}(i) - 2\varvec{\mathcal { H}} \varvec{\mathcal {S}}_e(i) \sqrt{{\varvec{\varsigma }}(i)} +{\varvec{\varsigma }}(i) \Vert _\infty \\&=\Vert \varvec{\mathcal {W}}(i) - 2\varvec{\mathcal { H}} \varvec{\mathcal {S}}_e(i) \sqrt{{\varvec{\varsigma }}(i)} +{\varvec{\varsigma }}(i) \Vert _\infty . \end{aligned} \end{aligned}$$
(34)

Since \(\varvec{\mathcal { H}}\) and \(\varvec{\mathcal {S}}_e(i)\) are diagonal matrices and their elements are positive, (34) can be equivalently rewritten as

$$\begin{aligned} \begin{aligned} E\{\Vert \widetilde{{\varvec{w}}}_k(i+1)\Vert _2^2\}&\le E\{\Vert \widetilde{{\varvec{w}}}_k(i) \Vert _2^2\} \\&\quad -\,2h_k r_k \sqrt{\frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\} }{1-\upsilon } } E\{e_{k,a}^2(i)\}\\&\quad +\,\frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\} }{1-\upsilon }, \end{aligned} \end{aligned}$$
(35)

for \(k=1,\ldots ,N\). Assuming that the algorithm has reached the steady-state, i.e., taking the limits of all the terms in (35) at \(i\rightarrow \infty \), it is established that

$$\begin{aligned} \begin{aligned} 2h_k r_k E\{e_{k,a}^2(\infty )\} \le \sqrt{\frac{E\{\zeta _k(\infty )\}-\upsilon E\{\xi _k(\infty )\} }{1-\upsilon } }, \end{aligned} \end{aligned}$$
(36)

where \(E\{e_{k,a}^2(\infty )\} \triangleq \lim \nolimits _{i\rightarrow \infty }E\{e_{k,a}^2(i)\}\), \(E\{\zeta _k(\infty ) \triangleq \lim \nolimits _{i\rightarrow \infty }E\{\zeta _k(i)\}\), and \(E\{\xi _k(\infty ) \triangleq \lim \nolimits _{i\rightarrow \infty }E\{\xi _k(i)\}\). As pointed out in “Appendix A”, \(E\{\zeta _k(\infty )\}\) and \(E\{\xi _k(\infty )\}\) approximate zero, and under Assumption 3, (36) leads further to

$$\begin{aligned} \begin{aligned} E\{e_{k,a}^2(\infty )\} = \text {Tr}\left\{ \lim \limits _{i\rightarrow \infty }E\{\widetilde{{\varvec{w}}}_k(i)\widetilde{{\varvec{w}}}_k^{\mathrm{T}}(i)\}{\varvec{R}}_k\right\} \approx 0. \end{aligned} \end{aligned}$$
(37)

Since \({\varvec{R}}_k\) is positive definite, we obtain from (37) that

$$\begin{aligned} \begin{aligned} E\{\Vert \widetilde{{\varvec{w}}}_k(\infty ) \Vert _2^2\}= \text {Tr}\left\{ \lim \limits _{i\rightarrow \infty } E\{\widetilde{{\varvec{w}}}_k(i)\widetilde{{\varvec{w}}}_k^{\mathrm{T}}(i)\}\right\} \approx 0, \end{aligned} \end{aligned}$$
(38)

for \(k=1,\ldots ,N\). The relation (38) illustrates that after a sufficiently many iterations, the proposed algorithm can converge to the true parameter vector \({\varvec{w}}^o\) in the mean square sense, in spite of the presence of impulsive noise.

4.3 Evolution Behavior

Although (38) reveals the convergence of the proposed algorithm in impulsive noise, this is a qualitative analysis due mainly to Eq. (29). For a quantitative analysis, we define the following vectors over the network:

$$\begin{aligned} \begin{aligned} \widetilde{{\varvec{w}}}(i)&\triangleq \text {col}\{\widetilde{{\varvec{w}}}_1(i), \ldots , \widetilde{{\varvec{w}}}_N(i)\}, \\ \widetilde{{\varvec{\psi }}}(i)&\triangleq \text {col}\{\widetilde{{\varvec{\psi }}}_1(i), \ldots , \widetilde{{\varvec{\psi }}}_N(i)\}, \\ \end{aligned} \end{aligned}$$
(39)

and the block diagonal matrix over the network

$$\begin{aligned} \begin{aligned} {\varvec{\varPhi }}(i)&\triangleq \text {diag}\left\{ {\varvec{\varPhi }}_1(i),\ldots ,{\varvec{\varPhi }}_N(i) \right\} ,\\ \end{aligned} \end{aligned}$$
(40)

where

$$\begin{aligned} \begin{aligned} {\varvec{\varPhi }}_k(i) = \sqrt{\frac{\zeta _k(i+1)-\upsilon \xi _k(i)}{1-\upsilon }} \frac{{\varvec{u}}_k(i)\text {sign}(e_k(i))}{\Vert {\varvec{u}}_k(i)\Vert _2} \text {, for } k=1,\ldots ,N. \end{aligned} \end{aligned}$$
(41)

Then, equations (18) and (19) for all the nodes are formulated as the matrix form:

$$\begin{aligned} \begin{aligned} \widetilde{{\varvec{w}}}(i+1)&= \mathcal {{\varvec{C}}}^{\mathrm{T}} \widetilde{{\varvec{\psi }}}(i)\\&= \mathcal {{\varvec{C}}}^{\mathrm{T}} [\widetilde{{\varvec{w}}}(i) - {\varvec{\varPhi }}(i) ]. \end{aligned} \end{aligned}$$
(42)

where \(\mathcal {{\varvec{C}}} \triangleq {\varvec{C}}\otimes {\varvec{I}}_M\).

Enforcing the autocorrelation operation to both sides of (42), we get the following recursion:

$$\begin{aligned} \begin{aligned} {\varvec{\varXi }}(i+1)&= \mathcal {{\varvec{C}}}^{\mathrm{T}} \left[ {\varvec{\varXi }}(i) - \mathop {\underbrace{E\{\widetilde{{\varvec{w}}}(i) {\varvec{\varPhi }}^{\mathrm{T}}(i)\}}}\limits _\text {I} - \mathop {\underbrace{E\{{\varvec{\varPhi }}(i) \widetilde{{\varvec{w}}}^{\mathrm{T}}(i)\}}}\limits _\text {II} + \right. \\&\quad \left. \mathop {\underbrace{E\{{\varvec{\varPhi }}(i){\varvec{\varPhi }}^{\mathrm{T}}(i)\}}}\limits _\text {III} \right] \mathcal {{\varvec{C}}}, \end{aligned} \end{aligned}$$
(43)

where

$$\begin{aligned} \begin{aligned} {\varvec{\varXi }}(i) \triangleq E\{\widetilde{{\varvec{w}}}(i) \widetilde{{\varvec{w}}}^{\mathrm{T}}(i)\} \end{aligned} \end{aligned}$$
(44)

is the autocorrelation matrix of the network estimation error vector \(\widetilde{{\varvec{w}}}(i)\). The kth diagonal block of \({\varvec{\varXi }}(i)\) with size of \(M \times M\), defined as \({\varvec{\varXi }}_k(i) \triangleq E\{\widetilde{{\varvec{w}}}_k(i) \widetilde{{\varvec{w}}}_k^{\mathrm{T}}(i)\}\), is the autocorrelation matrix of the estimation error vector \(\widetilde{{\varvec{w}}}_k(i)\) at node k.

Next, we will show how to evaluate terms I–III in (43).

Applying the conditioned expectation into the (m, k)th block of the term I, we have

$$\begin{aligned} \begin{aligned} E\{\widetilde{{\varvec{w}}}_m(i) {\varvec{\varPhi }}^{\mathrm{T}}_k(i)\}&= E\{ E\{\widetilde{{\varvec{w}}}_m(i) {\varvec{\varPhi }}^{\mathrm{T}}_k(i)|\widetilde{{\varvec{w}}}(i)\}\} \\&\simeq E\{ \widetilde{{\varvec{w}}}_m(i) E\{{\varvec{\varPhi }}^{\mathrm{T}}_k(i)|\widetilde{{\varvec{w}}}_k(i)\}\}. \end{aligned} \end{aligned}$$
(45)

By recalling the Price’s theorem, Assumptions 2, 3 and 4, and the law of total probability (similar to manipulations in Sect.4.2), we arrive at the relation that

$$\begin{aligned} \begin{aligned} E\{{\varvec{\varPhi }}^{\mathrm{T}}_k(i)|\widetilde{{\varvec{w}}}_k(i)\} = h_k(i) \sqrt{\frac{E\{\zeta _k(i+1)\}-\upsilon E\{\xi _k(i)\}}{1-\upsilon }} \widetilde{{\varvec{w}}}_k^{\mathrm{T}}(i) E\left\{ \frac{{\varvec{u}}_k(i){\varvec{u}}_k^{\mathrm{T}}(i)}{||{\varvec{u}}_k(i)||_2}\right\} , \end{aligned} \end{aligned}$$
(46)

where \(h_k(i)\) in (27) is rewritten as

$$\begin{aligned} \begin{aligned} h_k(i) = \sqrt{\frac{2}{\pi }}\left\{ \frac{p_{r,k}}{\sqrt{\text {Tr}({\varvec{\varXi }}_k(i) {\varvec{R}}_k)+(\hbar +1)\sigma _{\theta }^2\}}} + \frac{1-p_{r,k}}{\sqrt{\text {Tr}({\varvec{\varXi }}_k(i) {\varvec{R}}_k)+\sigma _{\theta }^2\}}} \right\} . \end{aligned} \end{aligned}$$
(47)

By combining (45) and (46), the term I can be arranged as

$$\begin{aligned} \begin{aligned} E\{\widetilde{{\varvec{w}}}(i) {\varvec{\varPhi }}^{\mathrm{T}}(i)\} = {\varvec{\varXi }}(i) {\varvec{A}}(i) ({\varvec{h}}(i) {\varvec{\chi }}(i) \otimes {\varvec{I}}_M), \end{aligned} \end{aligned}$$
(48)

where

$$\begin{aligned} \begin{aligned} {\varvec{A}}(i)&\triangleq \text {diag}\left\{ E\left\{ \frac{{\varvec{u}}_1(i){\varvec{u}}_1^{\mathrm{T}}(i)}{||{\varvec{u}}_1(i)||_2}\right\} ,\ldots , E\left\{ \frac{{\varvec{u}}_N(i){\varvec{u}}_N^{\mathrm{T}}(i)}{||{\varvec{u}}_N(i)||_2}\right\} \right\} ,\\ {\varvec{h}}(i)&\triangleq \text {diag}\left\{ h_1(i),\ldots ,h_N(i) \right\} ,\\ {\varvec{\chi }}(i)&\triangleq \text {diag}\left\{ \sqrt{\frac{E\{\zeta _1(i+1)\}-\upsilon E\{\xi _1(i)\}}{1-\upsilon }},\ldots ,\right. \\&\qquad \left. \sqrt{\frac{E\{\zeta _N(i+1)\}-\upsilon E\{\xi _N(i)\}}{1-\upsilon }} \right\} .\\ \end{aligned} \end{aligned}$$
(49)

The term II equals to the transpose of (48).

The evaluation of the term III is divided into two parts. For the kth diagonal block of \(E\{{\varvec{\varPhi }}(i){\varvec{\varPhi }}^{\mathrm{T}}(i)\}\), it is expressed as

$$\begin{aligned} \begin{aligned} E\{{\varvec{\varPhi }}_k(i){\varvec{\varPhi }}_k^{\mathrm{T}}(i)\} = \chi _k^2(i) E\left\{ \frac{{\varvec{u}}_k(i){\varvec{u}}_k^{\mathrm{T}}(i)}{||{\varvec{u}}_k||_2^2}\right\} , \end{aligned} \end{aligned}$$
(50)

where \(\chi _k(i)\) is the kth diagonal entry of \({\varvec{\chi }}(i)\). For the (m, k)th off-diagonal block of \(E\{{\varvec{\varPhi }}(i){\varvec{\varPhi }}^{\mathrm{T}}(i)\}\), it is calculated by

$$\begin{aligned} \begin{aligned} E\{{\varvec{\varPhi }}_m(i){\varvec{\varPhi }}_k^{\mathrm{T}}(i)\}&= E\{E\{{\varvec{\varPhi }}_m(i){\varvec{\varPhi }}_k^{\mathrm{T}}(i)| \widetilde{{\varvec{w}}}(i)\}\} \\&\simeq E\left\{ E\{{\varvec{\varPhi }}_m(i)|\widetilde{{\varvec{w}}}_m(i)\} E\{{\varvec{\varPhi }}_k^{\mathrm{T}}(i)| \widetilde{{\varvec{w}}}_k(i)\} \right\} \\&=h_m(i) \chi _m(i) {\varvec{A}}_m(i) E\{\widetilde{{\varvec{w}}}_m(i) \widetilde{{\varvec{w}}}_k^{\mathrm{T}}(i)\} {\varvec{A}}_k(i) \chi _k(i) h_k(i), \end{aligned} \end{aligned}$$
(51)

where \({\varvec{A}}_k(i)\) is the kth diagonal block of \({\varvec{A}}(i)\). Thus, according to (50) and (51), we obtain the term III:

$$\begin{aligned} \begin{aligned} E\{{\varvec{\varPhi }}(i){\varvec{\varPhi }}^{\mathrm{T}}(i)\}&= ({\varvec{h}}(i) {\varvec{\chi }}(i) \otimes {\varvec{I}}_M) {\varvec{A}}(i) \left[ {\varvec{\varXi }}(i)- \breve{{\varvec{\varXi }}}(i) \right] \\&\quad \times \,{\varvec{A}}(i) ({\varvec{h}}(i) {\varvec{\chi }}(i) \otimes {\varvec{I}}_M) + \breve{{\varvec{A}}}(i), \end{aligned} \end{aligned}$$
(52)

where

$$\begin{aligned} \begin{aligned} \breve{{\varvec{\varXi }}}(i)&\triangleq \text {diag}\left\{ {\varvec{\varXi }}_1(i),\ldots , {\varvec{\varXi }}_N(i) \right\} ,\\ \breve{{\varvec{A}}}(i)&\triangleq \text {diag}\left\{ \chi _1^2(i) E\left\{ \frac{{\varvec{u}}_1(i){\varvec{u}}_1^{\mathrm{T}}(i)}{||{\varvec{u}}_1(i)||_2^2}\right\} ,\ldots , \chi _N^2(i) E\left\{ \frac{{\varvec{u}}_N(i){\varvec{u}}_N^{\mathrm{T}}(i)}{||{\varvec{u}}_N(i)||_2^2}\right\} \right\} .\\ \end{aligned} \end{aligned}$$
(53)

By inserting (48) and (53) into (43), we establish the recursion expression for \({\varvec{\varXi }}(i)\):

$$\begin{aligned} \begin{aligned} {\varvec{\varXi }}(i+1)&= \mathcal {{\varvec{C}}}^{\mathrm{T}} \left\{ {\varvec{\varXi }}(i) - {\varvec{\varXi }}(i) {\varvec{A}}(i) ({\varvec{h}}(i) {\varvec{\chi }}(i) \otimes {\varvec{I}}_M) - ({\varvec{h}}(i) {\varvec{\chi }}(i) \otimes {\varvec{I}}_M)^{\mathrm{T}} \right. \\&\quad \times \,{\varvec{A}}^{\mathrm{T}}(i) {\varvec{\varXi }}^{\mathrm{T}}(i) + ({\varvec{h}}(i) {\varvec{\chi }}(i) \otimes {\varvec{I}}_M) {\varvec{A}}(i) \left[ {\varvec{\varXi }}(i)- \breve{{\varvec{\varXi }}}(i) \right] \\&\quad \times \,\left. {\varvec{A}}(i) ({\varvec{h}}(i) {\varvec{\chi }}(i) \otimes {\varvec{I}}_M) + \breve{{\varvec{A}}}(i) \right\} \mathcal {{\varvec{C}}}. \end{aligned} \end{aligned}$$
(54)

The network mean square deviation (MSD) over all the nodes is defined as \(\text {MSD}_\text {net}(i) \triangleq \frac{1}{N}\text {Tr}\{{\varvec{\varXi }}(i)\} = \frac{1}{N} \sum _{k=1}^N \text {MSD}_k(i)\), where \(\text {MSD}_k(i)=\text {Tr}\{{\varvec{\varXi }}_k(i)\}\) is the MSD per node k. Thus, (54) formulates the MSD evolution of the proposed algorithm in impulsive noise. It is necessary for stressing that the implementation of (54) requires knowing \(E\{\zeta _k(i+1)\}\) and \(E\{\xi _k(i)\}\) beforehand. However, evaluating \(E\{\zeta _k(i+1)\}\) and \(E\{\xi _k(i)\}\) is difficult from (12) and (13), due mainly to the minimum operation of two random variables in impulsive noise. Consequently, we suggest that \(E\{\zeta _k(i+1)\}\) and \(E\{\xi _k(i)\}\) are obtained by the ensemble average in simulations. In a word, (54) is a semi-analytic result, but which is also useful for clarifying the evolution behavior of the proposed algorithm.

5 Simulation Results

In this section, simulation examples in the estimation of parameters are presented to assess the proposed algorithm and verify the performance analysis. The connected distributed network with \(N=20\) nodes is shown in Fig. 2. The entries in the vector \({\varvec{w}}^o\) with length of \(M=16\) are generated randomly from a zero-mean uniform distribution and then are normalized by \({\varvec{w}}{^o}^{\mathrm{T}}{\varvec{w}}^o =1\). The input regressor \({\varvec{u}}_k(i)\) per node has a shifted structure, i.e., \({\varvec{u}}_k(i)=[u_k(i),u_k(i-1),\ldots ,u_k(i-M+1)]^{\mathrm{T}}\) [14, 27, 54], where \(u_k(i)\) is drawn from a first-order autoregressive (AR) system:

$$\begin{aligned} u_k(i) = t_k u_k(i-1) + \epsilon _k(i), \end{aligned}$$

\(\epsilon _k(i)\) is a zero-mean white Gaussian process with variance \(\sigma _{\epsilon ,k}^2 \), and \(t_k\) is the AR coefficient. Figure 3a, b gives values of \(\sigma _{\epsilon ,k}^2\) and \(t_k\) at nodes in the network, respectively. The network MSD is used for measuring the algorithm performance. Unless otherwise specified, the combination coefficients \(\{c_{m,k}\}\) for all the diffusion algorithms are given by the Metropolis rule [45]. The following figures are obtained by averaging the results over 200 independent trails.

Fig. 2
figure 2

Topology of network with \(N=20\) nodes

Full size image
Fig. 3
figure 3

Values of a\(\sigma _{\epsilon ,k}^2\), b\(t_k\) and c\(\sigma _{\theta ,k}^2\) at nodes

Full size image

5.1 Comparison of Algorithms

Case (1): CG noise

The additive noise is randomly generated from a CG process, as in Assumption 4, where the variance of the background noise, \(\sigma _{\theta ,k}^2\), is given in Fig. 3c, and the variance of the impulsive component is set to \(\sigma _{g,k}^2=1000\sigma _{y,k}^2\) with \(\sigma _{y,k}^2\) being the power of \(y_k(i) = {\varvec{u}}_k^{\mathrm{T}}(i){\varvec{w}}^o\).

To begin with, Fig. 4 compares the performance of the VT-dHNLMS algorithm with that of the dNLMS, VSS-dNLMS, and dSE-LMS algorithms in Gaussian noise (i.e., the impulsive noise is absent, \(p_{r,k}=0\)). The parameters of algorithms are set based on the fact that they have the same either initial convergence rate or steady-state MSD, where the notations of parameters are the same as references. As one can see, the dSE-LMS algorithm has the slowest convergence rate. Both the VSS-dNLMS and VT-dHNLMS algorithms have the convergence as fast as the dNLMS algorithm with large step size \(\mu _k=1\), and they have lower steady-state MSD. With small step size \(\mu _k=0.14\), the steady-state MSD of the dNLMS algorithm is as small as that of the VSS-dNLMS algorithm, but it converges slowly. It is worth noting that the proposed VT-dHNLMS algorithm behaves lower MSD than the VSS-dNLMS algorithm in the steady-state. In addition, the VSS-dNLMS algorithm requires the priori knowledge about the variances of the background noises at nodes, \(\{\sigma _{\theta ,k}^2\}_{k=1}^N\), while the VT-dHNLMS algorithm does not require it.

Fig. 4
figure 4

Network MSD curves of various diffusion algorithms. [No impulsive noise]. Parameter setting of algorithms is as follows: \(\mu _k=0.008\) (dSE-LMS); \(\mu _k=1\) and 0.14 (dNLMS); \(\beta =1.2, p_{k,0}=10\) (VSS-dNLMS); \(\upsilon =0.97\) (VT-dHNLMS)

Full size image

Then, Fig. 5 shows the performance of the algorithms in Fig. 4 in the situation that only node 1 in Fig. 2 is disturbed by impulsive noise with \(p_{r,1}=0.01\). It is seen from Fig. 5 that the dNLMS and VSS-dNLMS algorithms have performance deterioration, due to the fact that the wrong estimate (caused by impulsive noise) at node 1 is propagated to its neighboring nodes. In comparison, the dSE-LMS and VT-dHNLMS algorithms are insensitive to impulsive noise.

Fig. 5
figure 5

Network MSD curves of various diffusion algorithms in the case of node 1 with impulsive noise. Parameter setting of algorithms is the same as Fig. 4

Full size image

In addition to the algorithms in Fig. 5, Fig. 6 also examines the performance of the dLMP and RVWC-dLMS [3] algorithms,Footnote 3 in another scenario that all the nodes are affected by impulsive noise with \(p_{r,k}=0.01\). It is clear that the dNLMS and VSS-dNLMS algorithms suffer from substantial degradation in learning performance, since they are based on the squared output errors minimization with sensitivity to impulsive noise. The dSE-LMS (i.e., the dLMP with \(p=1\)) outperforms the dLMP with \(p=1.5\) in the convergence, which illustrates that dLMP’s performance in impulsive noise relies on the choice of p. Since the dSE-LMS does not use the amplitude information of output errors to update the estimates, its convergence is slower than that of the RVWC-dLMS. It is remarkable that the proposed VT-dHNLMS algorithm obtains faster convergence and lower steady-state MSD than these robust algorithms.

Fig. 6
figure 6

Network MSD curves of various diffusion algorithms. [Impulsive noise occurs at all the nodes.] Parameter setting of algorithms is the same as Fig. 4, except \(\mu _k=0.008,p=1.5\) for the dLMP; \(L=16\), \(\alpha =2.58\), \(\lambda =1-1/M\), \(\mu _k=0.048\) for the RVWC-dLMS. Also, the weighting coefficients in the combination step of RVWC-dLMS are specified in [3]; the Metropolis rule is used for the weighting coefficients in the adaptation step

Full size image

Moreover, to show the tracking capability of the algorithms in Fig. 6, the vector \({\varvec{w}}^o\) to be estimated is changed to \(-\,{\varvec{w}}^o\) at iteration \(i=2000\). As can be seen, the VSS-dNLMS and VT-dHNLMS algorithms can not track the sudden change of \({\varvec{w}}^o\). Figure 7 depicts the evolution of the step size \(\mu _1(i)\) at node 1 (the results at other nodes are similar), for the VT-dHNLMS algorithm with and without the proposed NC method. The parameters of the NC method are chosen as \(N_w=12\), \(\kappa =0.99\), \(l_{th}=30\) and \(\varrho =3\). Without the NC method, after \({\varvec{w}}^o\) suddenly changes, the magnitude of the normalized output error, \(|e_k(i) |/||{\varvec{u}}_k(i)||_2\), becomes much larger than \(\sqrt{\xi _k(i)}\) due to the mismatch of the estimate so that the step size through (15) jumps to a much smaller value rather than a desired larger value. This is why the VT-dHNLMS algorithm has no tracking capability. However, the NC method can make the step size through (15) jump to a large value in response to the change of \({\varvec{w}}^o\) so that it equips the VT-dHNLMS algorithm with the tracking capability, meanwhile not degrading the algorithm’s convergence performance.

Fig. 7
figure 7

Evolution of step size \(\mu _1(i)\) at node 1

Full size image

Figure 8 gives the performance comparison of the proposed VT-dHNLMS with NC, the dHNLMS with the fixed threshold \(\xi \), and the DRVSS-LMS [19] algorithms. The notation “non-coop” denotes the VT-dHNLMS with no cooperation (\({\varvec{C}}={\varvec{I}}_N\)), i.e., each node performs independently the estimation task. To fairly compare the DRVSS-LMS algorithm, we choose parameters of impulsive noise as \(p_{r,k}=0.05\) and \(\sigma _{g,k}^2=10000\sigma _{\theta ,k}^2\), since this algorithm needs these priori information; also, the input regressors of nodes are white Gaussian, i.e., by setting \(t_k=0\) in the first-order AR system. As expected, due to the cooperation among interconnected nodes, the VT-dHNLMS algorithm improves the estimation performance for parameters of interest relative to the non-coop version. Compared with the dHNLMS, due to the adaptation of the threshold in (12) and (13), the VT-dHNLMS obtains faster convergence and lower steady-state MSD simultaneously. Although both DRVSS-LMS and VT-dHNLMS are robust VSS diffusion variants based on the Huber function, the proposed VT-dHNLMS has better steady-state and tracking performance.

Fig. 8
figure 8

Network MSD curves of the VT-dHNLMS algorithm and its counterparts. For the DRVSS-LMS, we use \(\text {median}(d_k^2(1),d_k^2(2),\ldots ,d_k^2(M))\) to initialize \(\sigma _{e_{l,k}}^2\), because how to initialize it has not been claimed in [19]. We choose the parameters \(\alpha =2.8\) and \(\lambda _{1,2,3}=0.99\) for the DRVSS-LMS and \(\upsilon =0.94\) for the VT-dHNLMS

Full size image

Table 4 shows the time required by the algorithms in Figs. 6 and 8, implemented in MATLAB R2013a, to be run on a PC with Intel(R) Core(TM) i7-7700 CPU @3.60 GHz processor and 8.00GB RAM. It is seen that the time cost of the proposed algorithm is moderate among these algorithms, which is significantly lower than that of the RVWC-dLMS and DRVSS-LMS algorithms.

Table 4 Run time of various diffusion algorithms
Full size table

Case (2): \(\alpha \)-stable noise

In this example, we investigate the performance of the above shown algorithms in \(\alpha \)-stable noise.Footnote 4 The characteristic function of \(\alpha \)-stable noise is \(\phi (t)=\text {exp}(-\gamma |t |^\alpha )\), where \(\alpha \) denotes the characteristic exponent (a small value leads to more outliers), and \(\gamma \) is the dispersion of the noise [18, 49]. When \(\alpha =1\) and \(\alpha =2\), it reduces to the Cauchy distribution and the Gaussian distribution, respectively. Here, we set \(\alpha =1.25\) and \(\gamma =2/15\). The comparison results are shown in Fig. 9. As can be seen, among these robust algorithms (i.e., excluding the dNLMS and the VSS-dNLMS), the proposed VT-dHNLMS with NC behaves the best performance in terms of convergence rate, steady-state estimation error and tracking capability.

Fig. 9
figure 9

Network MSD curves of various diffusion algorithms in \(\alpha \)-stable noise. Referring to Fig. 6, parameters of some algorithms are tuned as follows: \(\mu _k=0.008\) for the dSE-LMS; \(p=1.2\), \(\mu _k=0.008\) for the dLMP; \(\xi =0.01\) for the dHNLMS

Full size image
Fig. 10
figure 10

Network MSD curves of the VT-dNLMS algorithm in CG noise. a\(p_{r,k}=0.01\), b\(p_{r,k}=0.05\), c\(p_{r,k}=0.1\)

Full size image

5.2 Verification of Analysis

Figure 10 compares the simulated MSD evolution with the theoretical MSD evolution computed by (54) for the proposed algorithm. Only \(E\{\xi _1(i)\}\) at node 1 is shown due to having similar results at other nodes. We set the impulsive parameters in the CG model to \(p_{r,k}=\) 0.01, 0.05 or 0.1, and \(\sigma _{g,k}^2=10000\sigma _{\theta ,k}^2\). As can be seen, the theoretical results are in agreement with the simulated results. Moreover, the deceasing property of \(E\{\xi _1(i)\}\) also supports the analysis in “Appendix A.”

6 Conclusion

In this study, we have improved the dHNLMS algorithm by adaptively adjusting the thresholds in a recursive way and proposed the VT-dHNLMS algorithm. Such recursive adjustment leads to that the proposed algorithm switch automatically from the dNLMS mode to the dSE-LMS mode with time-varying step sizes whenever impulsive noise appears. Theoretical analysis has shown that the proposed algorithm has good stability and learning performance in impulsive noise environments. Moreover, to respond quickly to the abrupt change of parameters of interest, we proposed a NC method for the thresholds. Simulation results have demonstrated the superiority of the proposed algorithm in Gaussian noise, CG impulsive noise, and \(\alpha \)-stable noise cases as compared to the competing diffusion algorithms.