1 Introduction

Over the last decade, distributed estimation has received increased attention in the multi-task network and single-task network [3, 11, 15, 16, 21, 29], especially for the parameter estimation of linear frequency modulation (LFM) signals [24], as well as heat and mass transfer [34]. In a single-task network, the same target parameters are collaboratively estimated for all network nodes, while in a multi-task network, target parameters of each network node need to be estimated separately [20]. This can be improved since diffusion is important for distributed estimation. Diffusion is a common physical phenomenon in the complex transport process. For example, Yang et al. proposed some novel methods to deal with the analytical solution in heat and mass transfer, such as fractional derivatives [33, 37] and kernel functions [35, 36]. Local cooperation and data processing are two important components of distributed data processing technology, and there are three cooperative strategies widely used for the distributed network estimation, namely incremental, consensus, and diffusion strategies [20]. However, the incremental strategy has the same limitation with consensus strategy, which is the asymmetry problem. The asymmetry problem is likely to cause unstable growth of a network state. As the diffusion strategy is more adaptive to environmental changes, it is not limited by this asymmetry problem. The diffusion strategy includes the adapt-then-combine (ATC) scheme [20] and the combine-then-adapt (CTA) scheme [3]. For the ATC scheme, the first step is to update the local estimation by using an adaptive filtering algorithm, and then, the intermediate estimates for the neighbors are fused. For the CTA scheme, first data fusion is performed, and then the local estimation is updated by using the adaptive filtering algorithm. Cattivelli and Sayed analyzed the performance of both schemes, and demonstrated that the ATC scheme outperformed the CTA scheme [20]. After that, a variety of diffusion estimation algorithms using ATC scheme have been proposed [2, 4, 9, 12,13,14, 17, 18, 31, 32, 38].

For the distributed estimation, a significant challenge is how to cope with the impulsive noise, since most of diffusion estimation algorithms over a network are highly susceptible to various impulsive noises with different types of input signals. Therefore, it is necessary to design a robust diffusion estimation algorithm to impulse noises of different intensities. Recently, using a fixed power p, Wen [31] proposed the diffusion least mean p-power (DLMP) algorithm, which is robust to the interference of generalized Gaussian distribution environments. But the performance of the DLMP algorithm is limited by the selected parameter p. On the other hand, minimizing the L1-norm subject to a constraint on the estimation vectors, Ni [22] designed a diffusion sign subband adaptive filtering (DSSAF) algorithm. The DSSAF algorithm is robust against impulsive interferences while its complexity is relatively large. By modifying the diffusion least mean square (DLMS) algorithm [3] and then applying the sign operation to the estimated error signals at each iteration moment point, Ni et al. [17] proposed a diffusion sign-error LMS (DSE-LMS) algorithm. Ye et al. [7] provided steady-state and stability analyses of the DSE-LMS algorithm, showing that although the DSE-LMS algorithm architecture is simple and easy to implement, the DSE-LMS algorithm has a major drawback, i.e., the steady-state error is high. Additionally, based on the Huber objective function, a similar set of algorithms have been proposed by Zhi [13], Wei et al. [9], and Soheila et al. [1], which are the Diffusion Normalized Huber adaptive filtering (DNHuber) [13], the diffusion robust variable step-size LMS (DRVSSLMS) [9], and the Robust Diffusion LMS (RDLMS) [1] algorithms, respectively. But, the RDLMS algorithm is not designed for impulse noise. For the DNHuber algorithm, its robustness against the impulsive interference and input signal need to be explored more comprehensively. The DRVSSLMS algorithm has high computational complexity. Last but not the least, inspired by the least logarithmic absolute difference operation, Chen et al. [4] designed another distributed cost function for the diffusion least logarithmic absolute difference (DLLAD) algorithm. But it is unclear whether the DLLAD algorithm is robust to the input signal and impulse noise.

In many engineering applications, the impulsive interference is present with various characteristics so that the input signal may not behave in an ideal fashion as assumed. For example, if the input signal is strongly correlated in time, different intensity sparsity ratios might lead to the performance degradation of parameter estimation algorithms, even when the algorithms could eventually stop. As stated above, the DSE-LMS, DRVSSLMS, and DLLAD algorithms may not be robust against the input signal and impulsive noise. Therefore, it becomes essential to design a distributed, adaptive algorithm that is more robust to the input signal and impulsive noise than the DSE-LMS, DRVSSLMS, and DLLAD algorithms. These factors, such as various types of the input signals or impulsive noises, usually reinforce the randomness and non-stationarity of system identification. Approximating the posterior distribution can be used to tackle this problem. In a recent study, Fernandez-Bes et al. [6] proposed the probabilistic LMS algorithm, and the theoretical stochastic behavior of the probabilistic LMS algorithm has since been analyzed [10].

In earlier studies, the problem of identification was considered in either a deterministic framework or with the assumption that the observation noise has a Gaussian distribution. However, it is known that in some realistic studies, there will be outliers due to the non-Gaussian noise. For such instances, based on the modified and extended Masreliez-Martin filter, Stojanovic et al. [26] proposed an algorithm for the joint state estimation and parameter estimation of stochastic nonlinear systems in the presence of non-Gaussian noises. To cope with outliers in the estimation of unknown system problems, they also designed an identification of the output error model by using a constraint on the output power [25], and proposed an adaptive two-stage procedure for generating the input signal [28]. Besides, for the state estimation of nonlinear multivariable stochastic systems, they derived the robust extended Kalman filter algorithm [27]. It should be noted that in the probabilistic LMS algorithm, the system coefficients are considered to be an unknown time-varying system whose time-varying characteristics satisfy the Gaussian distribution while the observation noise is a stationary additive noise with zero mean and constant variance. Moreover, the α-stable distribution has been used to model the non-Gaussian noise and is widely utilized as an impulsive noise [22]. That is, the characteristic function of impulsive noise is defined as the α-stable distribution. Then, Bayes’ theorem and the maximum a posteriori (MAP) estimate were used as an approximation for the predictive step. Thus, regardless the noise distribution, the probabilistic LMS algorithm is more robust to impulsive interference. From the probabilistic perspective, the probabilistic LMS algorithm has two major advantages. First, this algorithm has an adaptable step size, making it suitable for both stationary and non-stationary environments, and having less free parameters. Second, the use of a probabilistic model provides an estimation of the error variance, which is useful in many applications. Thus, from approximating the posterior distribution with an isotropic Gaussian distribution, we propose a diffusion probabilistic least mean square (DPLMS) algorithm, which combines the ATC diffusion strategy and the probabilistic LMS algorithm [6, 10] at all distributed network nodes. The stability of the mean estimation error and the computational complexity of this proposed algorithm are analyzed theoretically. Also, simulation experiments are conducted to explore the mean estimation error for the DPLMS algorithm with varied conditions for input signal and impulsive interference, compared to the DSE-LMS, DRVSSLMS, and DLLAD algorithms.

This paper is organized as follows: The proposed DPLMS algorithm is derived in Sect. 2. The theoretical stability of the mean estimation error, mean square performance, and the computational complexity is analyzed in Sect. 3. Then, in Sect. 4, we design several simulation experiments. Finally, in Sect. 5, conclusions are drawn.

2 The Proposed DPLMS Algorithm

2.1 The Modified Probabilistic LMS Algorithm

The probabilistic LMS is a VSS-LMS algorithm [10]. It has been derived from a probabilistic perspective, such as MAP estimation. Now, we will review and modify the probabilistic LMS algorithm in this subsection. Firstly, consider an unknown time-varying system with length M, with its coefficients at iteration moment i,

$${\mathbf{W}}_{o} \left( i \right) = {\mathbf{W}}_{o} \left( {t - 1} \right) + {\varvec{p}}\left( i \right)$$
(1)

In Eq. (1), \({\varvec{p}}\left(i\right)\) is a white Gaussian noise with zero-mean. The time-varying \({\mathbf{W}}_{o} \left( i \right)\) obeys Eq. (2), which is a Gaussian distribution:

$$p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{W}}_{o} \left( {i - 1} \right)} \right) = {\rm N}\left( {{\mathbf{W}}_{o} \left( i \right);{\mathbf{W}}_{o} \left( {i - 1} \right),{\varvec{I}}\sigma_{{\varvec{p}}}^{2} } \right)$$
(2)

where \({\varvec{I}}\sigma_{{\varvec{p}}}^{2} = {\text{E}}\left[ {{\varvec{p}}\left( i \right){\varvec{p}}^{{\text{T}}} \left( i \right)} \right], \sigma_{{\varvec{p}}}^{2}\) is variance for \({ }{\varvec{p}}\left( i \right)\), and \({\varvec{I}}\) is a matrix with the appropriate size.

For this unknown time-varying system, when we input a signal \({\mathbf{X}}\left( i \right) = \left[ {x\left( i \right),x\left( {i + 1} \right),x\left( {i + 2} \right), \ldots ,x\left( {i + M - 1} \right)} \right]^{T}\), the desired signal is \({ }d\left( i \right)\),

$$d\left( i \right) = {\mathbf{W}}_{o}^{{\text{T}}} \left( i \right){\mathbf{X}}\left( i \right) + \varepsilon \left( i \right)$$
(3)

where \(\varepsilon \left( i \right)\) is a stationary additive noise with zero mean and variance of \(\sigma_{\varepsilon }^{2}\). Also, we assume that Eq. (3) obeys Eq. (4), which is a Gaussian distribution also,

$$p\left( {d\left( i \right){|}{\mathbf{X}}\left( i \right),{\mathbf{W}}_{o} \left( i \right)} \right) = {\rm N}\left( {d\left( i \right);{\mathbf{W}}_{o}^{{\text{T}}} \left( i \right){\mathbf{X}}\left( i \right),\sigma_{\varepsilon }^{2} } \right)$$
(4)

supposing that the estimation mean vector and variance of \({\mathbf{W}}_{o} \left( i \right)\) at iteration \(i\) are \({\uptheta }\left( i \right)\) and \(\sigma^{2} \left( i \right)\), respectively. So, by using an isotropic spherical Gaussian distribution [as Eq. (5)] to approximate the posterior distribution, we can obtain the probabilistic LMS algorithm.

$$p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{Z}}_{i} } \right) = {\rm N}\left( {{\mathbf{W}}_{o} \left( i \right);{\uptheta }\left( i \right),{\varvec{I}}\sigma^{2} \left( i \right)} \right)$$
(5)

where \({\mathbf{Z}}_{i} = \left\{ {{\mathbf{X}}\left( k \right),d\left( k \right)} \right\}_{k = 1}^{i}\).

So, based on Eq. (5), we can get

$$\begin{aligned} p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{Z}}_{i - 1} } \right) & = \int p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{W}}_{o} \left( {i - 1} \right)} \right)p\left( {{\mathbf{W}}_{o} \left( {i - 1} \right){|}{\mathbf{Z}}_{i - 1} } \right)d{\mathbf{W}}_{o} \left( {i - 1} \right) \\ & = {\rm N}\left( {{\mathbf{W}}_{o} \left( i \right);{\uptheta }\left( {i - 1} \right),{\varvec{I}}\left( {\sigma^{2} \left( {i - 1} \right) - \sigma_{\rho }^{2} } \right)} \right) \\ \end{aligned}$$
(6)

where \(p\left( {{\mathbf{W}}_{o} \left( {i - 1} \right){|}{\mathbf{Z}}_{i - 1} } \right) = {\rm N}\left( {{\mathbf{W}}_{o} \left( {i - 1} \right);{\uptheta }\left( {i - 1} \right),{\varvec{I}}\sigma^{2} \left( {i - 1} \right)} \right)\) at iteration \(i - 1\). By combining Bayes’ rule and Eq. (6), then we approximate the posterior with an isotropic Gaussian as Eq. (7).

$$\begin{aligned} p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{Z}}_{i} } \right) & = p\left( {d\left( i \right){|}{\mathbf{u}}\left( i \right),{\mathbf{W}}_{o} \left( i \right)} \right)p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{Z}}_{i - 1} } \right) \\ & = {\rm N}\left( {{\mathbf{W}}_{o} \left( i \right);{\uptheta }\left( i \right),{\varvec{I}}\sigma^{2} \left( i \right)} \right) \\ \end{aligned}$$
(7)

where

$${\uptheta }\left( i \right) = {\uptheta }\left( {i - 1} \right) + \alpha \left( i \right)\left[ {d\left( i \right) - {\mathbf{X}}^{{\text{T}}} \left( i \right){\uptheta }\left( {i - 1} \right)} \right]{\mathbf{X}}\left( i \right)$$
(8)

and

$$\sigma^{2} \left( i \right) = \left[ {1 - \frac{{\frac{{\sigma^{2} \left( {i - 1} \right) + \sigma_{\rho }^{2} }}{{\left[ {\sigma^{2} \left( {i - 1} \right) - \sigma_{\rho }^{2} } \right]\left\| {{\mathbf{X}}\left( i \right)} \right\|^{2} + \sigma_{\varepsilon }^{2} }}\left\| {{\mathbf{X}}\left( i \right)} \right\|^{2} }}{L}} \right]\left[ {\sigma^{2} \left( {i - 1} \right) - \sigma_{\rho }^{2} } \right]$$
(9)

Set \(\alpha \left( i \right) = \frac{{\sigma^{2} \left( {i - 1} \right) + \sigma_{\rho }^{2} }}{{\left[ {\sigma^{2} \left( {i - 1} \right) - \sigma_{\rho }^{2} } \right]\left\| {{\mathbf{X}}\left( i \right)} \right\|^{2} + \sigma_{\varepsilon }^{2} }}\), then \(\sigma^{2} \left( i \right) = \left[ {1 - \frac{{\alpha \left( i \right)\left\| {{\mathbf{X}}\left( i \right)} \right\|^{2} }}{L}} \right]\left[ {\sigma^{2} \left( {i - 1} \right) - \sigma_{\rho }^{2} } \right]\).

So, based on Eq. (7), by using MAP, i.e., \({\mathbf{W}}\left( i \right) = {\text{argmax}}_{{{\mathbf{W}}_{o} \left( i \right)}} p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{Z}}_{i} } \right)\), we can get the recursive estimation weight-vector equation of the probabilistic LMS algorithm.

$${\mathbf{W}}\left( {i + 1} \right) = {\mathbf{W}}\left( i \right) + \alpha \left( i \right)e\left( i \right){\mathbf{X}}\left( i \right)$$
(10)

where \(e\left( i \right)\) is the error signal, as \(e\left( i \right) = d\left( i \right) - y\left( i \right)\),

$$\begin{aligned} e\left( i \right) & = d\left( i \right) - {\mathbf{W}}^{{\text{T}}} \left( {i - 1} \right){\mathbf{X}}\left( i \right) \\ & = {\mathbf{W}}_{o}^{{\text{T}}} \left( i \right){\mathbf{X}}\left( i \right) + \varepsilon \left( i \right) - {\mathbf{W}}^{{\text{T}}} \left( {i - 1} \right){\mathbf{X}}\left( i \right) \\ & = {\mathbf{X}}^{{\text{T}}} \left( i \right)\left( {{\mathbf{W}}_{o} \left( {i - 1} \right) + {\varvec{p}}\left( i \right)} \right) - {\mathbf{W}}^{{\text{T}}} \left( {i - 1} \right){\mathbf{X}}\left( i \right) + \varepsilon \left( i \right) \\ & = {\mathbf{X}}^{{\text{T}}} \left( i \right)\left[ {{\mathbf{W}}_{o} \left( {i - 1} \right) - {\mathbf{W}}\left( {i - 1} \right)} \right] + {\mathbf{X}}^{{\text{T}}} \left( i \right){\varvec{p}}\left( i \right)) + \varepsilon \left( i \right) \\ & = {\mathbf{X}}^{{\text{T}}} \left( i \right){\hat{\mathbf{W}}}\left( {i - 1} \right) + {\mathbf{X}}^{{\text{T}}} \left( i \right){\varvec{p}}\left( i \right)) + \varepsilon \left( i \right) \\ \end{aligned}$$
(11)

and \({\hat{\mathbf{W}}}\left( {i - 1} \right) = {\mathbf{W}}_{o} \left( {i - 1} \right) - {\mathbf{W}}\left( {i - 1} \right)\) is the weight-deviation vector.

To facilitate comparative analysis, we make a slight adjustment to the probabilistic LMS that is to add a constant value parameter in Eq. (8) and Eq. (10), as Eq. (12) and Eq. (13).

$${\uptheta }\left( i \right) = {\uptheta }\left( {i - 1} \right) + \tau \alpha \left( i \right)\left[ {d\left( i \right) - {\mathbf{X}}^{{\text{T}}} \left( i \right){\uptheta }\left( {i - 1} \right)} \right]{\mathbf{X}}\left( i \right)$$
(12)
$${\mathbf{W}}\left( {i + 1} \right) = {\mathbf{W}}\left( i \right) + \tau \alpha \left( i \right)e\left( i \right){\mathbf{X}}\left( i \right)$$
(13)

where \(0 < \tau \le 1\) is a constant value parameter.

2.2 The Diffusion Probabilistic LMS (DPLMS) Algorithm

Now in this subsection, we will extend the modified probabilistic LMS algorithm [as Eqs. (12)–(13)] to the diffusion probabilistic LMS algorithm. In the beginning, we set a distributed network consisting of N network nodes (or agents), where each node measures its data \(\{ {\mathbf{X}}_{n} \left( i \right), d_{n} \left( i \right)\}\) to estimate an unknown parameter vector \({\mathbf{W}}_{o}\) of length \(M\) vector through a linear model at agent n \(\in \left\{ {1,2, \ldots ,N} \right\}\).

$$d_{n} \left( i \right) = {\mathbf{X}}_{n} \left( i \right){\mathbf{W}}_{o} + \varepsilon _{n} \left( i \right)$$
(14)

In Eq. (14) \({\mathbf{X}}_{n} \left( i \right)\) is the input signal at n-node, \(d_{n} \left( i \right)\) is the desired signal at n-node,\(\varepsilon_{n} \left( t \right)\) is the measurement noise at \(n\)-node with variance \({ }\sigma_{\varepsilon ,n}^{2}\) and independent of any other data. Under reference [13], we also set \({\mathbf{X}}_{n} \left( i \right){ }\) as temporally white Gaussian with zero mean and spatially independent with \({\mathbf{R}}_{xx,n} \left( i \right) = {\text{E}}\left[ { {\mathbf{X}}_{n}^{{\text{T}}} \left( i \right) {\mathbf{X}}_{n} \left( i \right)} \right] > 0\).

The global cost function of DPLMS can be formulated as:

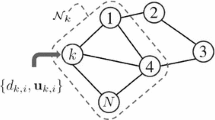
$$\begin{aligned} J^{{{\text{global}}}} \left( {{\mathbf{W}}\left( i \right)} \right) & = \mathop \sum \limits_{n} J_{n}^{{{\text{local}}}} \left( {{\mathbf{W}}\left( i \right)} \right) \\ & = \mathop \sum \limits_{n} J_{n}^{{{\text{local}}}} \left( {{\text{argmax}}_{{{\mathbf{W}}_{o} \left( i \right)}} p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{Z}}_{i} } \right)} \right) \\ & = \mathop \sum \limits_{n} \mathop \sum \limits_{{l \in N_{n} }} c_{l,n} \left( {{\text{argmax}}_{{{\mathbf{W}}_{o} \left( i \right)}} p\left( {{\mathbf{W}}_{o} \left( i \right){|}{\mathbf{Z}}_{i} } \right)} \right) \\ \end{aligned}$$
(15)

In Eq. (15) \(N_{n}\) is the neighborhood of node n and its definitions, the set of nodes that are connected to n node (including n node itself); \(\{ c_{l,n } \}\) is the weighting coefficients (nonnegative real value) for each the neighborhood of nodes n and meet \({ }\mathop \sum \nolimits_{{l \in N_{n} }} c_{l,n} = 1\). For all network nodes, \(\{ c_{l,n } \}\) forms a whole combination matrix C.

Therefore, inspired by the DLMS algorithm in [3], we get the motivation that we can refer to this process to design the DPLMS algorithm via an adaptation step and combination step.

Adaptation step at node n:

$${\boldsymbol{\varphi }}_{n} \left( i \right) = {\mathbf{W}}_{n} \left( {i - 1} \right) + \mu \alpha_{n} \left( i \right)e_{n} \left( i \right){\mathbf{X}}_{n} \left( i \right)$$
(16)

Combination step at node n:

$${\mathbf{W}}_{n} \left( i \right) = \mathop \sum \limits_{{l \in N_{n} }} a_{l,n} {\boldsymbol{\varphi }}_{l} \left( i \right)$$
(17)

In Eq. (16), μ denotes the DPLMS algorithm step size, and \({ }{\boldsymbol{\varphi }}_{n} \left( i \right)\) is the estimated vectors at node n. \(\{ a_{l,n} \}\) is the nonnegative real weighting diffusion coefficients, and if \({ }l \notin N_{n} , a_{l,n} = 0\). \(\{ a_{l,n} \}\) forms a whole diffusion coefficients matrix A and AT1 = 1. Then, we combine the ATC diffusion strategy and the probabilistic least mean square (PLMS) at all distributed network nodes. For convenience, based on Eqs. (14)–(17), Table 1 is a summary of the DPLMS algorithm. Since the convergence speed and the steady-state error will increase (decrease) as the step size μ increases (decreases), the step size \(\mu\) should be appropriately set at the beginning of the DPLMS algorithm. Because improperly initialized weights may cause the DPLMS algorithm to slow down, the most common way is used. \(\left\{ {w_{n,0} = 0} \right\}\) was set at zero for each network node \(n\). Furthermore, the diffusion method was used in this algorithm, so at the beginning nonnegative combination weights, \(\{ a_{l,n} , c_{l,n} \}\) were set at the beginning.

Table 1 The DPLMS algorithm summary
Full size table

3 Performance of the DPLMS Algorithm

Performances of the DPLMS algorithm including mean behavior and computational complexity will be discussed in this subsection. Firstly, let us give some equations,\(\widehat{{ {\mathbf{W}}}}_{n} \left( {i - 1} \right) = {\mathbf{W}}_{o} - {\mathbf{W}}_{n} \left( {i - 1} \right)\), \({\hat{\boldsymbol{\varphi }}}_{n} \left( {i - 1} \right) = {\mathbf{W}}_{o} - {\boldsymbol{\varphi }}_{n} \left( {i - 1} \right)\),\({\mathbf{W}}\left( i \right) = {\text{col}}\left\{ {{\mathbf{W}}_{1} \left( i \right),{\mathbf{W}}_{2} \left( i \right), \ldots ,{\mathbf{W}}_{M} \left( i \right) } \right\}\), \({\boldsymbol{\varphi }}\left( i \right) = {\text{col}}\left\{ {{\boldsymbol{\varphi }}_{1} \left( i \right),{\boldsymbol{\varphi }}_{2} \left( i \right), \ldots ,{\boldsymbol{\varphi }}_{M} \left( i \right) } \right\}\), \({\hat{\mathbf{W}}}\left( i \right) = {\text{col}}\left\{ {{\hat{\mathbf{W}}}_{1} \left( i \right),{\hat{\mathbf{W}}}_{2} \left( i \right), \ldots ,{\hat{\mathbf{W}}}_{M} \left( i \right) } \right\}\), \({\hat{\boldsymbol{\varphi }}}\left( t \right) = {\text{col}}\left\{ {{\hat{\boldsymbol{\varphi }}}_{1} \left( i \right),{\hat{\boldsymbol{\varphi }}}_{2} \left( i \right), \ldots ,{\hat{\boldsymbol{\varphi }}}_{M} \left( i \right) } \right\}\).

To facilitate performance analysis, we make the following assumptions:

Assumption 1

Both the additive noise \(v _{n} \left( i \right)\) and the regression vector \({\mathbf{X}}_{n} \left( i \right)\), ∀k, i, are spatially and temporally independent. Besides, \(v _{n} \left( i \right)\) and \({\mathbf{X}}_{n} \left( i \right)\) are independent of each other.

Assumption 2

The regression vector \({\mathbf{X}}_{n} \left( i \right)\) is independent of \(\widehat{{ {\mathbf{W}}}}_{k} \left( j \right)\) for all k and j < i.

Although these assumptions are not true in general, they have been widely used in the field of adaptive filtering [8, 20], which can help facilitate performance analysis.

3.1 Mean Performance Analysis

Using the above definitions \(\widehat{{ {\mathbf{W}}}}_{n} \left( {i - 1} \right) = {\mathbf{W}}_{o} - {\mathbf{W}}_{n} \left( {i - 1} \right)\), Eq. (16) can be shown as

$${\hat{\boldsymbol{\varphi }}}\left( i \right) = {\hat{\mathbf{W}}}_{n} \left( {i - 1} \right) - {\mathbf{S}}\left( i \right)\left[ {{\mathbf{R}}\left( i \right){\hat{\mathbf{W}}}_{n} \left( {i - 1} \right) + {\mathbf{O}}\left( i \right)} \right]$$
(18)

where \({ }{\mathbf{S}}\left( i \right) = {\text{diag}}\left\{ {\mu \alpha_{n} \left( i \right){\mathbf{I}}_{M} , \ldots ,\mu \alpha_{n} \left( i \right){\mathbf{I}}_{M} } \right\}\), \({\mathbf{R}}\left( i \right) = {\text{diag}}\left\{ {\mathop \sum \nolimits_{l = 1}^{N} c_{l,1} {\mathbf{X}}_{l}^{{\text{T}}} \left( i \right){\mathbf{X}}_{l} \left( i \right), \ldots ,\mathop \sum \nolimits_{l = 1}^{N} c_{l,N} {\mathbf{X}}_{l}^{{\text{T}}} \left( i \right){\mathbf{X}}_{l} \left( i \right)} \right\}\), \({\mathbf{O}}\left( i \right) = {\mathbf{C}}^{{\text{T}}} {\text{col}}\left\{ {{\mathbf{X}}_{n}^{{\text{T}}} \left( i \right)\varepsilon_{n} \left( i \right), {\mathbf{X}}_{n}^{{\text{T}}} \left( i \right)\varepsilon_{n} \left( i \right), \ldots ,{\mathbf{X}}_{n}^{{\text{T}}} \left( i \right)\varepsilon_{n} \left( i \right)} \right\}\), \({\mathbf{C}} = {\mathbf{C}} \otimes {\varvec{I}}_{M}\), and \(\otimes\) denotes the Kronecker product operation.

Also, from combining \({\hat{\boldsymbol{\varphi }}}_{n} \left( {i - 1} \right) = {\mathbf{W}}_{o} - {\boldsymbol{\varphi }}_{n} \left( {i - 1} \right)\) and Eq. (17), we can get

$${\hat{\mathbf{W}}}\left( i \right) = {\mathbf{A}}^{{\text{T}}} {\hat{\boldsymbol{\varphi }}}\left( i \right)$$
(19)

where \({\mathbf{A}} = {\mathbf{A}} \otimes {\varvec{I}}_{M}\).

So, taking Eq. (18) into Eq. (19), we can get Eq. (20), as

$${\hat{\mathbf{W}}}\left( i \right) = {\mathbf{A}}^{{\text{T}}} \left[ {{\mathbf{I}} - {\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right]{\hat{\mathbf{W}}}\left( {i - 1} \right) + {\mathbf{A}}^{{\text{T}}} {\mathbf{S}}\left( i \right){\mathbf{O}}\left( i \right)$$
(20)

Then taking the expectation at both ends of the equal sign of Eq. (20).

$$\begin{aligned} {\text{E}}\left[ {{\hat{\mathbf{W}}}\left( i \right)} \right] & = {\text{E}}\left\{ {{\mathbf{A}}^{{\text{T}}} \left[ {{\mathbf{I}} - {\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right]{\hat{\mathbf{W}}}\left( {i - 1} \right) + {\mathbf{A}}^{{\text{T}}} {\mathbf{S}}\left( i \right){\mathbf{O}}\left( i \right)} \right\} \\ & = {\mathbf{A}}^{{\text{T}}} \left[ {{\mathbf{I}} - {\text{E}}\left\{ {{\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right\}} \right]{\text{E}}\left\{ {{\hat{\mathbf{W}}}\left( {i - 1} \right)} \right\} + {\text{E}}\left\{ {{\mathbf{A}}^{{\text{T}}} {\mathbf{S}}\left( i \right){\mathbf{O}}\left( i \right)} \right\} \\ & = {\mathbf{A}}^{{\text{T}}} \left[ {{\mathbf{I}} - {\text{E}}\left\{ {{\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right\}} \right]{\text{E}}\left\{ {{\hat{\mathbf{W}}}\left( {i - 1} \right)} \right\} \\ \end{aligned}$$
(21)

where \({\text{E}}\left[ {{\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right] = \mu {\text{diag}}\left\{ {\mathop \sum \nolimits_{l = 1}^{N} \alpha_{l} \left( i \right)c_{l,1} {\mathbf{R}}_{xx,l} \left( i \right), \ldots ,\mathop \sum \nolimits_{l = 1}^{N} \alpha_{l} \left( i \right)c_{l,N} {\mathbf{R}}_{xx,l} \left( i \right)} \right\}\).

Then, based on Eq. (21), we will get the condition for stability, as Eq. (22).

$$0 < \mu < \frac{2}{{\rho_{\max } \left( {\mathop \sum \nolimits_{l = 1}^{N} \alpha_{l} \left( i \right)c_{l,l} {\mathbf{R}}_{xx,l} \left( i \right)} \right)}}$$
(22)

In Eq. (22), \(\rho_{\max }\) is the maximal eigenvalue of \(\mathop \sum \nolimits_{l = 1}^{N} \alpha_{l} \left( i \right)c_{l,l} {\mathbf{R}}_{xx,l} \left( i \right)\). So, based on Eq. (22), and under that condition, we obtain \({\text{ E}}\left[ {{\hat{\mathbf{W}}}\left( \infty \right)} \right] = 0\), this means that the DPLMS algorithm can achieve accurate estimation, theoretically.

3.2 Mean Square Performance

To characterize the mean square behavior of the DPLMS algorithm, we define the mean square of weight error as weighted by a Hermitian positive-definite matrix \({\Sigma }\) that we are free to choose, which is shown as

$${\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{{\Sigma }}^{2} = {\hat{\mathbf{W}}}^{{\text{T}}} \left( i \right){\Sigma }{\hat{\mathbf{W}}}\left( i \right)$$
(23)

The matrix \(\Sigma\) can be freely chosen so that \({\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{{\Sigma }}^{2}\) can describe various kinds of mean square behaviors. From Eq. (20) and using Assumptions 1 and 2, if we compute the weighted norm on both sides of the equality and use the fact that \({\mathbf{O}}\left( i \right)\) is independent of \({\hat{\mathbf{W}}}\left( i \right)\) and \(\widehat{{ {\mathbf{W}}}}\left( {i - 1} \right)\), we can rewrite (23) more compactly as the following recursive expression:

$${\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{\Sigma }^{2} = {\text{E}}\left\| {{\hat{\mathbf{W}}}\left( {i - 1} \right)} \right\|_{{\Sigma^{\prime}}}^{2} + {\text{E}}\left\{ {{\mathbf{O}}^{{\text{T}}} \left( i \right){\mathbf{S}}\left( i \right){\text{A}}\Sigma {\mathbf{A}}^{{\text{T}}} {\mathbf{S}}\left( i \right){\mathbf{O}}\left( i \right)} \right\}$$
(24)

where \(\Sigma^{\prime} = {\text{E}}\left\{ {\left[ {{\mathbf{I}} - {\mathbf{R}}\left( i \right){\mathbf{S}}\left( i \right)} \right]{\text{A}}\Sigma {\mathbf{A}}^{{\text{T}}} \left[ {{\mathbf{I}} - {\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right]} \right\}\).

Moreover, setting

$${\mathbf{G}} = {\text{E}}\left\{ {{\mathbf{O}}\left( i \right){\mathbf{O}}^{{\text{T}}} \left( i \right)} \right\} = {\varvec{C}}^{{\varvec{T}}} {\text{diag}}\left\{ {{\boldsymbol{\sigma}}_{{{\varvec{v}},1}}^{2} {\varvec{R}}_{{{\varvec{u}},1}} ,\user2{ } \ldots ,{\boldsymbol{\sigma}}_{{{\varvec{v}},{\varvec{N}}}}^{2} {\varvec{R}}_{{{\varvec{u}},{\varvec{N}}}} ,\user2{ }} \right\}{\varvec{C}}$$
(25)

we can rewrite (24) in the form

$${\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{\Sigma }^{2} = {\text{E}}\left\| {{\hat{\mathbf{W}}}\left( {i - 1} \right)} \right\|_{{\Sigma^{\prime}}}^{2} + {\text{Tr}}\left[ {{\Sigma }{\mathbf{A}}^{{\text{T}}} {\mathbf{S}}\left( i \right){\mathbf{GS}}\left( i \right){\text{A}}} \right]$$
(26)

where \({\text{Tr}}\left[ \, \right]\user2{ }\) denotes the trace operator. Let \(\sigma = {\text{vec}}\left( \Sigma \right)\) and \(\sigma^{\prime} = {\text{vec}}\left( {\Sigma^{\prime}} \right)\), where the \({\text{vec}}\left( { } \right)\) notation stacks the columns of \(\Sigma\) on top of each other and \({\text{vec}}^{ - 1} \left( { } \right)\) is the inverse operation. We will use interchangeably the notation \(\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{\sigma }^{2} \user2{ }\) and \(\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{\Sigma }^{2} \user2{ }\) to denote the same quantity \({\hat{\mathbf{W}}}^{{\text{T}}} \left( i \right){\Sigma }{\hat{\mathbf{W}}}\left( i \right)\). Using the Kronecker product property \({\text{vec}}\left( {U\Sigma {\text{V}}} \right) = \left( {{\text{V}}^{T} { } \otimes U} \right){\text{vec}}\left( \Sigma \right)\), we can vectorize both sides of \(\Sigma^{\prime} = {\text{E}}\left\{ {\left[ {{\mathbf{I}} - {\mathbf{R}}\left( i \right){\mathbf{S}}\left( i \right)} \right]{\text{A}}\Sigma {\mathbf{A}}^{{\text{T}}} \left[ {{\mathbf{I}} - {\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right]} \right\}\) and conclude that \(\Sigma^{\prime} = {\text{E}}\left\{ {\left[ {{\mathbf{I}} - {\mathbf{R}}\left( i \right){\mathbf{S}}\left( i \right)} \right]{\text{A}}\Sigma {\mathbf{A}}^{{\text{T}}} \left[ {{\mathbf{I}} - {\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right]} \right\}\) can be replaced by the simpler linear vector relation:\(\sigma^{\prime} = {\text{vec}}\left( {\Sigma^{\prime}} \right) = F\sigma\), where \(F\) is the following \(N^{2} M^{2} \times N^{2} M^{2}\) matrix with block entries of size \(M^{2} \times M^{2}\) each:

$$F = \left( {I \otimes I} \right)\left\{ {I - I \otimes \left( {{\mathbf{R}}\left( i \right){\mathbf{S}}\left( i \right)} \right) - \left( {{\mathbf{R}}^{{\varvec{T}}} \left( i \right){\mathbf{S}}\left( i \right)} \right) \otimes I + {\text{E}}\left\{ {{\mathbf{R}}^{{\varvec{T}}} \left( i \right){\mathbf{S}}\left( i \right)} \right\} \otimes \left( {{\mathbf{R}}^{{\varvec{T}}} \left( i \right){\mathbf{S}}\left( i \right)} \right)} \right\}\left( {A \otimes A} \right)$$
(27)

Using \({\text{Tr}}\left[ {{ }\Sigma {\text{X}}} \right] = {\text{vec}}\left( {{\text{X}}^{T} } \right)^{T} \sigma\), we can then rewrite Eq. (26) as follows:

$${\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{\sigma }^{2} = {\text{E}}\left\| {{\hat{\mathbf{W}}}\left( {i - 1} \right)} \right\|_{F\sigma }^{2} + \left[ {{\text{vec}}\left( {{\text{A}}^{T} {\mathbf{S}}\left( i \right)G^{T} {\mathbf{S}}\left( i \right)A} \right)} \right]^{T} \sigma$$
(28)

Based on Assumptions 1 and 2, then the DPLMS algorithm (21) will be mean square stable if the step sizes are sufficiently small such that (26) is satisfied, and the matrix in (27) is stable.

$$\begin{aligned} F & \approx \left( {I \otimes I} \right)\left\{ {I - I \otimes \left( {{\mathbf{R}}\left( i \right){\mathbf{S}}\left( i \right)} \right) - \left( {{\mathbf{R}}^{{\varvec{T}}} \left( i \right){\mathbf{S}}\left( i \right)} \right) \otimes I + {\mathbf{R}}^{{\varvec{T}}} \left( i \right){\mathbf{S}}\left( i \right) \otimes {\mathbf{R}}\left( i \right){\mathbf{S}}\left( i \right)} \right\}\left( {A \otimes A} \right) \\ & = \left[ {{\text{A}}^{T} \left( {I - {\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right)} \right]^{T} \left[ {{\text{A}}^{T} \left( {I - {\mathbf{S}}\left( i \right){\mathbf{R}}\left( i \right)} \right)} \right] \\ \end{aligned}$$
(29)

Taking the limit as \(i \to \infty\) as (assuming the step-sizes are small enough to ensure convergence to a steady-state), we deduce from (28) that:

$$\mathop {\lim }\limits_{i \to \infty } {\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{{\left( {I - F} \right)\sigma }}^{2} = \left[ {{\text{vec}}\left( {{\text{A}}^{T} {\mathbf{S}}\left( i \right)G^{T} {\mathbf{S}}\left( i \right)A} \right)} \right]^{T} \sigma$$
(30)

Equation (30) is a useful result: it allows us to derive several performance metrics through the proper selection of the free weighting parameter \(\sigma\) (or \({\Sigma }\)), as was done in [16]. For example, the MSD for any node n is defined as the steady-state value \({\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|^{2}\), as \(i \to \infty\), and can be obtained by computing \(\mathop {\lim }\nolimits_{i \to \infty } {\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{{T_{n} }}^{2}\) with a block weighting matrix \(T_{n}\) that has the \(M \times M{ }\) identity matrix at block \(\left( {n,n} \right)\) and zeros elsewhere. After, denoting the vectorized version of the matrix \(T_{n}\) by \(t_{n} = {\text{vec}}\left( {{\text{diag}}\left( {e_{n} } \right) \otimes I_{M} } \right)\), where \(e_{n}\) is the vector whose n-th entry is one and zeros elsewhere, and if we are selecting \(\sigma\) in (30) as \(\sigma_{n} = \left( {I - F} \right)^{ - 1} t_{n}\), we arrive at the MSD for node \(n\):

$${\text{MSD}}_{n} = \left[ {{\text{vec}}\left( {{\text{A}}^{T} {\mathbf{S}}\left( i \right)G^{T} {\mathbf{S}}\left( i \right)A} \right)} \right]^{T} \left( {I - F} \right)^{ - 1} t_{n}$$
(31)

The average network \({\text{MSD }}\) is given by:

$${\text{MSD}} = \mathop {\lim }\limits_{i \to \infty } \frac{1}{N}\mathop \sum \limits_{n = 1}^{N} {\text{E}}\left\| {{\hat{\mathbf{W}}}_{{\varvec{n}}} \left( i \right)} \right\|^{2}$$
(32)

Then, to obtain the network MSD from Eq. (30), the weighting matrix of \(\mathop {\lim }\nolimits_{i \to \infty } {\text{E}}\left\| {{\hat{\mathbf{W}}}\left( i \right)} \right\|_{T}^{2}\) should be chosen as \({\text{T}} = \frac{{I_{MN} }}{N}\). Let \(q\) denote the vectorized version of \(I_{MN}\), i.e., \(q = {\text{vec}}\left( {I_{MN} } \right)\), and selected \(\sigma\) in (30) as \(\sigma = \frac{{\left( {I - F} \right)^{ - 1} q}}{N}\), the network MSD is given by:

$${\text{MSD}} = \frac{1}{N}\left[ {{\text{vec}}\left( {{\text{A}}^{T} {\mathbf{S}}\left( i \right)G^{T} {\mathbf{S}}\left( i \right)A} \right)} \right]^{T} \left( {I - F} \right)^{ - 1} q$$
(33)

3.3 Computational Complexity

For the adaptive filtering algorithm, the computational complexity previously mentioned is the number of arithmetic operations per iteration for a weight vector or coefficients vector, which includes, the number of multiplications, additions, divisions, and comparisons and so on. Moreover, the time-consuming operation of a multiplication operation is much more than that of addition, so that the multiplication operation takes a major proportion in the computational complexity of an adaptive algorithm. Therefore, the computational complexity is an important parameter, which influences the performance of an adaptive filtering algorithm. Compared to the probability LMS algorithm, there are more multiplications and additions in the adaptive and combined parts. For convenience, the computational complexity of some diffusion algorithms is summarized in Table 2, which includes the DSE-LMS [7], DRVSSLMS [9], DLLAD [4], probability LMS [6], and DPLMS algorithms. From Table 2, compared to the DSE-LMS, DRVSSLMS, and probability LMS [6] algorithms, the DPLMS algorithm is smaller. The computational complexity of DLLAD and DPLMS is the same. The computational complexity of the probability LMS algorithm is the lowest. This is understandable because, in the distributed strategy, each node is the executor of the adaptive algorithm, so that the computational complexity of the distributed algorithm is large.

Table 2 The computational complexity of the DSE-LMS, DRVSSLMS, DLLAD, DPLMS, and probability LMS algorithms
Full size table

4 Simulation Results

In this paper, we focus on the distributed adaptive algorithms, and compare the DPLMS algorithm with the DSE-LMS [7], DRVSSLMS [9], and DLLAD [4] algorithms in system identification. So, in this part, to demonstrate the robustness performance of the proposed DPLMS algorithm in the presence of different intensity levels of impulsive interferences and input signal, we conduct simulation experiments with various impulsive interferences and different types of input signals. For this unknown system, we set \({ }M = 16\), and the parameters vector was selected randomly. Each distributed network topology consists of \(N = 20\) nodes. For impulse noise, according to [13], we can compute the Bernoulli-Gaussian impulse noise. We set impulse noise as \(v\left( i \right) = f\left( i \right)g\left( i \right)\), which is a product of a Bernoulli process \({ }g\left( i \right) = \left\{ {0,1} \right\}{ }\) with the probabilities \({ }p\left( 1 \right) = {\Pr}\), \({ }p\left( 0 \right) = 1 - {\Pr}\) and a Gaussian process \(f\left( i \right)\). Besides, we set the impulse noise as spatiotemporally independent. For the adaptation weights in the adaptation step and combination weights in combination step, we apply the uniform rule i.e., \(a_{l,n} = c_{l,n} = 1/N_{n}\). We use the network mean square deviation (MSD) to evaluate the performance of diffusion algorithms, where \({\text{ MSD}}\left( i \right) = \frac{1}{N}\mathop \sum \nolimits_{n = 1}^{N} {\text{E}}\left[ {\left| {{\mathbf{W}}_{o} - {\mathbf{W}}_{n} \left( i \right)} \right|^{2} } \right]\) [8]. In addition, the independent Monte Carlo number is 60 and each run has 4000 iteration numbers.

4.1 Simulation Experiment 1

To illustrate that our algorithm is more robust to the input signal, has a faster convergence rate and a lower steady-state estimation error than the DSE-LMS [7], DRVSSLMS [9] and DLLAD [4] algorithms, the simulation experiment 1 considered the same network topology and the same impulsive interference with the different input signals. If any two nodes in network topology are declared neighbors, with a connect probability greater than or equal to 0.2, the network topology is shown in Fig. 1. The MSD iteration curves for DRVSSLMS (\(\mu\) equal to 0.6), DSE-LMS (\(\mu\) equal to 0.6), DNLMS (\(\mu\) equal to 0.6), and DLLAD (\(\mu\) equal to 0.6) algorithms in Figs. 2, 3, and 4 are different types of the input signal when the measurement noise in an unknown system is impulse noise with Pr = 0.4 and \({ }\sigma_{f}^{2} = 0.2\).

Fig. 1
figure 1

Random network topology to be decided by probability

Full size image
Fig. 2
figure 2

(Left_top) the input signals \({ }\left\{ {{\mathbf{X}}_{n} \left( i \right)} \right\}\) variances of at each network node with \({\mathbf{R}}_{xx,n} = \sigma_{x,n}^{2} {\mathbf{I}}_{M}\) with possibly different diagonal entries chosen randomly, (Left_bottom) the measurement noise variances \(\left\{ {\varepsilon_{n} \left( i \right)} \right\}\) at each network node; (Right) Transient network MSD (dB) iteration curves of the DSE-LMS, DRVSSLMS, DLLAD, and DPLMS algorithms

Full size image
Fig. 3
figure 3

(Left_top) the input signals \({ }\left\{ {{\mathbf{X}}_{n} \left( i \right)} \right\}\) variances of at each network node with \({\mathbf{R}}_{xx,n} = \sigma_{x,n}^{2} {\mathbf{I}}_{M} \user2{ }\) with the same value in each diagonal entries, (Left_bottom) the measurement noise variances \(\left\{ {\varepsilon_{n} \left( i \right)} \right\}\) at each network node; (Right) Transient network MSD (dB) iteration curves of the DSE-LMS, DRVSSLMS, DLLAD, and DPLMS algorithms

Full size image
Fig. 4
figure 4

(Left_top) the input signals \({ }\left\{ {{\mathbf{X}}_{n} \left( i \right)} \right\}\) variances of at each network node with \({\mathbf{R}}_{xx,n} = \sigma_{x,n}^{2} \left( t \right){\mathbf{I}}_{M} ,t = 1,2,3, \ldots ,M\) with a different values in each diagonal entries, (Left_bottom) the measurement noise variances \(\left\{ {\varepsilon_{n} \left( i \right)} \right\}\) at each network node; (Right) Transient network MSD (dB) iteration curves of the DSE-LMS, DRVSSLMS, DLLAD, and DPLMS algorithms

Full size image

In this experiment, we want to show that the DPLMS algorithm is more robust to the input signal, so we set three sub-experiments with different types of input signals, same impulsive noise and same distributed network topology. From Figs. 2, 3, and 4, we can find that although different types of the input signals are used, the DPLMS algorithm has the faster convergence rate and lowest steady-state error than the DSE-LMS, DRVSSLMS, and DLLAD algorithms. Besides, the DPLMS algorithm is more robust to the input signal. In conclusion, from Simulation experiment 1, we can get that the DPLMS algorithm is superior to the DSE-LMS, DRVSSLMS, and DLLAD algorithms.

4.2 Simulation Experiment 2

To illustrate that our algorithm is more robust to the input signal, has a faster convergence rate, and a lower steady-state estimation error than the DSE-LMS [7], DRVSSLMS [9], and DLLAD [4] algorithms, the simulation experiment 2 considered the same network topology and the same input signal with the different probability densities of impulsive interference. If any two nodes in network topology are declared neighbors, with a certain radius for each node large than or equal to 0.3, the network topology is shown in Fig. 5 (Left). The MSD iteration curves for DRVSSLMS (\(\mu\) equal to 0.4), DSE-LMS (\(\mu\) equal to 0.4), DNLMS (\(\mu\) equal to 0.4), and DLLAD (\(\mu\) equal to 0.4) algorithms were shown in Fig. 6 with Pr = 0.1, Pr = 0.4, and Pr = 0.7 under same \({ }\sigma_{f}^{2} = 0.2\), respectively.

Fig. 5
figure 5

(Left) Random network topology to be decided by a certain radius; (Right_top) the input signals \({ }\left\{ {{\mathbf{X}}_{n} \left( i \right)} \right\}\) variances of at each network node with \({\mathbf{R}}_{xx,n} = \sigma_{x,n}^{2} {\mathbf{I}}_{M}\) with possibly different diagonal entries chosen randomly, (Right_bottom) the measurement noise variances \(\left\{ {\varepsilon_{n} \left( t \right)} \right\}\) at each network node

Full size image
Fig. 6
figure 6

Transient network MSD (dB) iteration curves of the DSE-LMS, DRVSSLMS, DLLAD, and DPLMS algorithms. (Left) with Pr = 0.1, (middle) with Pr = 0.4 and (Right) with Pr = 0.7

Full size image

In this experiment, we aim to show that the DPLMS algorithm is more robust to different the probability densities of impulsive interference. So we set three sub-experiments with different probability densities of impulsive interference, the same input signal (correlation coefficient is 0.7) and same distributed network topology. From Fig. 6, we can find that although different probability densities of impulsive interference is considered, the DPLMS algorithm is slightly faster than that of the DSE-LMS, DRVSSLMS, and DLLAD algorithms, and the DPLMS algorithm still has a smaller steady-state error than the DSE-LMS, DRVSSLMS, and DLLAD algorithms. In other words, from Simulation experiment 2, we can observe that the DPLMS algorithm is more robust to impulsive interference than the DSE-LMS, DRVSSLMS, and DLLAD algorithms.

4.3 Simulation Experiment 3

To illustrate that our algorithm is more robust to the input signal, has a faster convergence rate and a lower steady-state estimation error than the DSE-LMS [7], DRVSSLMS [9], and DLLAD [4] algorithms, the simulation experiment 3 considered the same network topology and the same input signal with the different probability densities and variance of impulsive interference. If any two nodes in network topology are declared neighbors, with a certain radius for each node large than or equal to 0.3, the network topology is shown in Fig. 7. The MSD iteration curves for DRVSSLMS (\(\mu\) equal to 0.4), DSE-LMS (\(\mu\) equal to 0.4), DNLMS (\(\mu\) equal to 0.4), and DLLAD (\(\mu\) equal to 0.4) algorithms in Fig. 8 (Left-top, Pr = 0.7, \(\sigma_{f}^{2} = 0.2\); Right-top, Pr = 0.7, \(\sigma_{f}^{2} = 0.4\); Left-bottom, Pr = 0.4, \(\sigma_{f}^{2} = 0.4\); Right-down, Pr = 0.4, \(\sigma_{f}^{2} = 0.6\), respectively.

Fig. 7
figure 7

Random network topology to be decided by a certain radius

Full size image
Fig. 8
figure 8

Transient network MSD (dB) iteration curves of the DSE-LMS, DRVSSLMS, DLLAD, and DPLMS algorithms with \({\mathbf{R}}_{xx,n} = \sigma_{x,n}^{2} \left( t \right){\mathbf{I}}_{M} ,t = 1,2,3, \ldots ,M\) with different values in each diagonal entries. (Left-top): Pr = 0.7, \(\sigma_{f}^{2} = 0.2\); (Right-top): Pr = 0.7, \(\sigma_{f}^{2} = 0.4\); (Left-bottom): Pr = 0.4, \(\sigma_{f}^{2} = 0.4\); (Right-down): Pr = 0.4, \(\sigma_{f}^{2} = 0.6\)

Full size image

Comparing Fig. 8 (Left_top) with Fig. 8 (Right_top), the DPLMS algorithm can perform better in identifying the unknown coefficients under different impulsive interference intensities. From Fig. 8 (Left_bottom) with Fig. 8 (Right_bottom), the same conclusion can be obtained. However, for the DSE-LMS, DRVSSLMS, and DLLAD algorithms, the identification performance is easily interfered with by different characteristics that is to say that the DPLMS algorithm is more robust. The DPLMS algorithm is superior to the DSE-LMS, DRVSSLMS, and DLLAD algorithms. So, for distributed network estimation in impulsive interference environments, from Simulation experiment 1–Simulation experiment 3 (total ten sub-experiments), we know that the DPLMS algorithm has a superior performance when estimating an unknown linear system under the changeable impulsive noise environments.

5 Conclusion

In this paper, we propose a novel DPLMS algorithm, which is a distributed algorithm robust to various input signal and impulsive interference environments. The method is developed based on the combination and modification of the DLMS algorithm and the probabilistic LMS algorithm at all nodes in a distributed network. The theoretical analysis demonstrates that the DPLMS algorithm can achieve an effective estimation from a probabilistic perspective. It is shown that the computational complexity of the DPLMS algorithm is smaller than that of the DRVSSLMS and DSE-LMS algorithms, despite being equal to that of the DLLAD algorithm. Besides, theoretical mean behavior interpretes that the DPLMS algorithm can achieve accurate estimation, and simulation results show that the DPLMS algorithm is more robust to the input signal and impulsive interference than the DSELMS, DRVSSLMS, and DLLAD algorithms. In short, the DPLMS algorithm has a superior performance when estimating an unknown linear system under changeable impulsive noise environments, which will have a significant impact on real-world applications. Additionally, we wish to bring more probability theory-based techniques to distributed adaptive filtering algorithms. Although the DPLMS algorithm has superior performance compared to the DSE-LMS, DRVSSLMS, and DLLAD algorithms, the environment in actual engineering applications is complex and time-varying, which means DPLMS algorithm needs to be adjusted accordingly for different application scenarios. First, the delay caused by the communication of different nodes needs to be considered [30], because the delay will cause asynchronization. Second, we need to consider whether the parameters to be evaluated are sparse (such as brain networks) [5, 19]. In such cases, it will be better to add a regularized constraint terms (L1-norm) to this algorithm. Lastly, the external environment factors such as the temperature where the system is located should also be considered, because earlier study reported that high temperature could make the system unstable and time-varying [23]. In such cases, it is best to increase the parameters of the external environment in this algorithm.